case study questions from chemical kinetics

Not Able To Find Desired Paper or Worksheet SEARCH

Find papers & worksheets search, case study questions for class 12 chemistry chapter 4 chemical kinetics.

case study questions from chemical kinetics

(0) Comments
3 Downloads

Related Papers

Click to view more related papers, display_name = "class 11" && $paper->display_name = "class 12") { // echo $paper->display_name." questions papers and worksheets"; } //else { // echo $paper->display_name." sample papers and previous year papers"; //} //>, important questions, mcq's, ncert solutions - class 12 chemistry.

Get here all the Important questions for Class 12 Chemistry chapter wise as free PDF download. Here you will get Extra Important Questions with answers, Numericals and Multiple Choice Questions (MCQ's) chapter wise in Printable format. Solving Chapter wise questions is one of the best ways to prepare for the examination. Students are advised to understand the concepts and theories of Chemistry properly before the exam. You can easily find 1 Mark, 2 marks, 3 marks, and 5 marks questions from each chapter of Class 12 Chemistry and prepare for exam more effectively. These preparation material for Class 12 Chemistry , shared by teachers, parents and students, are as per latest NCERT and CBSE Pattern syllabus and assure great success in achieving high score in Final CBSE Board Examinations.

Latest MCQ's and Important Questions for CBSE Class 12 Chemistry

class 12 chemistry chapter 1 important questions with answers class 12 chemistry chapter 2 important questions with answers class 12 chemistry chapter 3 important questions with answers class 12 chemistry chapter 4 important questions with answers class 12 chemistry chapter 5 important questions with answers class 12 chemistry chapter 6 important questions with answers class 12 chemistry chapter 7 important questions with answers class 12 chemistry chapter 8 important questions with answers class 12 chemistry chapter 9 important questions with answers class 12 chemistry chapter 10 important questions with answers class 12 chemistry chapter 11 important questions with answers class 12 chemistry chapter 12 important questions with answers class 12 chemistry chapter 13 important questions with answers class 12 chemistry chapter 14 important questions with answers class 12 chemistry chapter 15 important questions with answers class 12 chemistry chapter 16 important questions with answers mcqs of chemistry class 12 chapter 1 mcqs of chemistry class 12 chapter 2 mcqs of chemistry class 12 chapter 3 mcqs of chemistry class 12 chapter 4 mcqs of chemistry class 12 chapter 5 mcqs of chemistry class 12 chapter 6 mcqs of chemistry class 12 chapter 7 mcqs of chemistry class 12 chapter 8 mcqs of chemistry class 12 chapter 9 mcqs of chemistry class 12 chapter 10 mcqs of chemistry class 12 chapter 11 mcqs of chemistry class 12 chapter 12 mcqs of chemistry class 12 chapter 13 mcqs of chemistry class 12 chapter 14 mcqs of chemistry class 12 chapter 15 mcqs of chemistry class 12 chapter 16 The Solid State Class 12 Case Study Questions Solutions Class 12 Case Study Questions Notes Electrochemistry Class 12 Case Study Questions Chemical Kinetics Class 12 Case Study Questions Surface Notes Class 12 Case Study Questions General Principles and Processes of Isolation of Elements Class 12 Case Study Questions The p-Block Elements Class 12 Case Study Questions The d and f Block Elements Class 12 Case Study Questions Coordination Compounds Class 12 Case Study Questions Haloalkanes and Haloarenes Class 12 Case Study Questions Alcohols, Phenols and Ethers Class 12 Case Study Questions Aldehydes, Ketones and Carboxylic Acids Class 12 Case Study Questions Amines Class 12 Case Study Questions Biomolecules Class 12 Case Study Questions Polymers Class 12 Case Study Questions Chemistry in Everyday Life Class 12 Case Study Questions

Total Papers :

CBSE Class 12 Chemistry Syllabus

Solid State
Electrochemistry
Chemical Kinetics
Surface Chemistry
General Principles and Processes of Isolation of Elements
p-Block Elements
d- and f-Block Elements
Coordination Compounds
Haloalkanes and Haloarenes.
Alcohols, Phenols and Ethers
Aldehydes, Ketones and Carboxylic Acids
Organic compounds containing Nitrogen
Biomolecules
Chemistry in Everyday life

Unit II: Solutions 15 Periods

Types of solutions, expression of concentration of solutions of solids in liquids, solubility of gases in liquids, solid solutions, Raoult's law, colligative properties - relative lowering of vapour pressure, elevation of boiling point, depression of freezing point, osmotic pressure, determination of molecular masses using colligative properties, abnormal molecular mass, Van't Hoff factor.

Unit III: Electrochemistry 18 Periods

Redox reactions, EMF of a cell, standard electrode potential, Nernst equation and its application to chemical cells, Relation between Gibbs energy change and EMF of a cell, conductance in electrolytic solutions, specific and molar conductivity, variations of conductivity with concentration, Kohlrausch's Law, electrolysis and law of electrolysis (elementary idea), dry cell-electrolytic cells and Galvanic cells, lead accumulator, fuel cells, corrosion.

Unit IV: Chemical Kinetics 15 Periods

Rate of a reaction (Average and instantaneous), factors affecting rate of reaction: concentration, temperature, catalyst; order and molecularity of a reaction, rate law and specific rate constant, integrated rate equations and half-life (only for zero and first order reactions), concept of collision theory (elementary idea, no mathematical treatment), activation energy, Arrhenius equation.

Unit VIII: d and f Block Elements 18 Periods

General introduction, electronic configuration, occurrence and characteristics of transition metals, general trends in properties of the first-row transition metals – metallic character, ionization enthalpy, oxidation states, ionic radii, colour, catalytic property, magnetic properties, interstitial compounds, alloy formation, preparation and properties of K2Cr2O7 and KMnO4.

Lanthanoids – Electronic configuration, oxidation states, chemical reactivity and lanthanoid contraction and its consequences.

Actinoids - Electronic configuration, oxidation states and comparison with lanthanoids.

Unit IX: Coordination Compounds 18 Periods

Coordination compounds - Introduction, ligands, coordination number, colour, magnetic properties and shapes, IUPAC nomenclature of mononuclear coordination compounds. Bonding, Werner's theory, VBT, and CFT; structure and stereoisomerism, the importance of coordination compounds (in qualitative analysis, extraction of metals and biological system).

Unit X: Haloalkanes and Haloarenes. 15 Periods Haloalkanes: Nomenclature, nature of C–X bond, physical and chemical properties, optical rotation mechanism of substitution reactions.

Haloarenes: Nature of C–X bond, substitution reactions (Directive influence of halogen in monosubstituted compounds only). Uses and environmental effects of - dichloromethane, trichloromethane, tetrachloromethane, iodoform, freons, DDT.

Unit XI: Alcohols, Phenols and Ethers 14 Periods

Alcohols: Nomenclature, methods of preparation, physical and chemical properties (of primary alcohols only), identification of primary, secondary and tertiary alcohols, mechanism of dehydration, uses with special reference to methanol and ethanol.

Phenols: Nomenclature, methods of preparation, physical and chemical properties, acidic nature of phenol, electrophilic substitution reactions, uses of phenols.

Ethers: Nomenclature, methods of preparation, physical and chemical properties, uses.

Unit XII: Aldehydes, Ketones and Carboxylic Acids 15 Periods

Aldehydes and Ketones: Nomenclature, nature of carbonyl group, methods of preparation, physical and chemical properties, mechanism of nucleophilic addition, reactivity of alpha hydrogen in aldehydes, uses.

Carboxylic Acids: Nomenclature, acidic nature, methods of preparation, physical and chemical properties; uses.

Unit XIII: Amines 14 Periods

Amines: Nomenclature, classification, structure, methods of preparation, physical and chemical properties, uses, identification of primary, secondary and tertiary amines.

Diazonium salts: Preparation, chemical reactions and importance in synthetic organic chemistry.

Unit XIV: Biomolecules 18 Periods

Carbohydrates - Classification (aldoses and ketoses), monosaccharides (glucose and fructose), D-L configuration oligosaccharides (sucrose, lactose, maltose), polysaccharides (starch, cellulose, glycogen); Importance of carbohydrates.

Proteins - Elementary idea of - amino acids, peptide bond, polypeptides, proteins, structure of proteins - primary, secondary, tertiary structure and quaternary structures (qualitative idea only), denaturation of proteins; enzymes. Hormones - Elementary idea excluding structure.

Vitamins - Classification and functions. Nucleic Acids: DNA and RNA.

Structure of CBSE Chemistry Sample Paper for Class 12 Science is

For Preparation of exams students can also check out other resource material

CBSE Class 12 Chemistry Sample Papers

CBSE Class 12 Chemistry Worksheets

CBSE Class 12 Chemistry Question Papers

CBSE Class 12 Chemistry Test Papers

CBSE Class 12 Chemistry Revision Notes

Question Bank of Other Subjects of Class 12

Importance of Question Bank for Exam Preparation?

There are many ways to ascertain whether a student has understood the important points and topics of a particular chapter and is he or she well prepared for exams and tests of that particular chapter. Apart from reference books and notes, Question Banks are very effective study materials for exam preparation. When a student tries to attempt and solve all the important questions of any particular subject , it becomes very easy to gauge how much well the topics have been understood and what kind of questions are asked in exams related to that chapter.. Some of the other advantaging factors of Question Banks are as follows

Since Important questions included in question bank are collections of questions that were asked in previous exams and tests thus when a student tries to attempt them they get a complete idea about what type of questions are usually asked and whether they have learned the topics well enough. This gives them an edge to prepare well for the exam.Students get the clear idea whether the questions framed from any particular chapter are mostly either short or long answer type questions or multiple choice based and also marks weightage of any particular chapter in final exams.
CBSE Question Banks are great tools to help in analysis for Exams. As it has a collection of important questions that were asked previously in exams thereby it covers every question from most of the important topics. Thus solving questions from the question bank helps students in analysing their preparation levels for the exam. However the practice should be done in a way that first the set of questions on any particular chapter are solved and then solutions should be consulted to get an analysis of their strong and weak points. This ensures that they are more clear about what to answer and what can be avoided on the day of the exam.
Solving a lot of different types of important questions gives students a clear idea of what are the main important topics of any particular chapter that needs to focussed on from examination perspective and should be emphasised on for revision before attempting the final paper. So attempting most frequently asked questions and important questions helps students to prepare well for almost everything in that subject.
Although students cover up all the chapters included in the course syllabus by the end of the session, sometimes revision becomes a time consuming and difficult process. Thus, practicing important questions from Question Bank allows students to check the preparation status of each and every small topic in a chapter. Doing that ensures quick and easy insight into all the important questions and topics in each and every individual. Solving the important questions also acts as the revision process.

Question Bank of Other Classes

To Prepare better for CBSE paperclass; ?> " title="Download Free CBSE Papers">Ribblu.com brings to you all the previous years papers & worksheets of subject; ?//> for CBSE paperclass; ?>. This CBSE paper and worksheet can be instrumental in students achieving maximum marks in their exams. These Papers and worksheets help students gain confidence and make them ready to face their school examinations. These Papers and worksheets school wise, covers important concepts from an examination perspective. Students and parents can download all the available papers & worksheets directly in the form of PDF. One can use these papers and worksheets to get extensive practice and familiarise themselves with the format of the question paper.

You can help other users

Be the first to write comment .

Upload papers and the more your paper get downloaded the more you earn the points

You may send papers on email [email protected] along with userid

Downloaded by: SUDHAKAR VYTLA
Downloaded by: Abhishek Sehgal

Rules and regulations for uploads

Write your comment, report this paper, how to earn points.

Upload Papers / Worksheets and Earn 50 Points.

The uploaded material should be original paper or worksheet of any school. Check out some videos on how to upload papers on ribblu

Rate & Review your school and Earn 25 Points.

Review any school that you may be knowing and once your review is approved, you will be credited with 25 points.

Answer on question posted on JustAsk and earn 15 points.

JustAsk is a platform where you can help others to find answers of any question. Share your Knowledge. Answer questions and once approved you will earn 15 points

Complete your profile and earn upto 25 Points.

Edit and complete your user profile and earn points. The more details you submit, the more points you will earn.

Download Ribblu Mobile App and you will (Earn 20 Points) (one time only)

CBSE Schools

CBSE Schools In Delhi
CBSE Schools In Noida
CBSE Schools In Greater Noida
CBSE Schools In Faridabad
CBSE Schools In Ghaziabad
CBSE Schools In Gurgaon
CBSE Schools In Mumbai
CBSE Schools In Pune
CBSE Schools In Bangalore
CBSE Schools In Hyderabad
CBSE Schools In Kolkata
CBSE Schools In Chennai
CBSE Schools In Patna
CBSE Schools In Meerut
CBSE Schools In Kanpur
CBSE Schools In Indore
CBSE Schools In Ludhiana
CBSE Schools In Dehradun

Top Schools

Schools In Delhi
Schools In Noida
Schools In Greater Noida
Schools In Faridabad
Schools In Ghaziabad
Schools In Gurgaon
Schools In Mumbai
Schools In Pune
Schools In Bangalore
Schools In Hyderabad
Schools In Kolkata
Schools In Chennai
Schools In Patna
Schools In Meerut
Schools In Kanpur
Schools In Indore
Schools In Ludhiana
Schools In Dehradun

Other Schools

Pre Nursery Schools In Noida
Day Boarding Schools In Noida
Pre Nursery Schools In Gurgaon
Pre Nursery Schools In Delhi
Play Schools In Delhi
Day Boarding Schools In Delhi

CBSE Papers

CBSE Class 1 Sample Papers
CBSE Class 2 Sample Papers
CBSE Class 3 Sample Papers
CBSE Class 4 Sample Papers
CBSE Class 5 Sample Papers
CBSE Class 6 Sample Papers
CBSE Class 7 Sample Papers
CBSE Class 8 Sample Papers

Case Study Questions for Class 12 Chemistry Chapter 4 Chemical Kinetics

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Category: Case Study Based Questions for Class 12 Chemistry

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 12 Chemistry Chapter 15 Polymers

Case study questions for class 12 chemistry chapter 12 aldehydes, ketones and carboxylic acids, case study questions for class 12 chemistry chapter 4 chemical kinetics, case study questions for class 12 chemistry chapter 9 coordination compounds, case study questions for class 12 chemistry chapter 10 haloalkanes and haloarenes, case study questions for class 12 chemistry chapter 11 alcohols, phenols and ethers, case study questions for class 12 chemistry chapter 13 amines, case study questions for class 12 chemistry chapter 14 biomolecules, case study questions for class 12 chemistry chapter 8 the d- and f-block elements, case study questions for class 12 chemistry chapter 7 the p-block elements, case study questions for class 12 chemistry chapter 5 surface chemistry, case study questions for class 12 chemistry chapter 3 electrochemistry, case study questions for class 12 chemistry chapter 2 solutions, case study questions for class 12 chemistry chapter 1 the solid state.

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

4.9: Exercises on Chemical Kinetics

Last updated
Save as PDF
Page ID 61438

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here . In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.

In the reaction $\mathrm{A \rightarrow products}$, at $\mathrm{t = 0}$, $\mathrm{[A]=0.1563\,M}$. After 1.00 minute, $\mathrm{[A]=0.1496\,M}$, and after 2.00 minutes, $\mathrm{[A]=0.1431\,M}$.

Calculate the average rate of reaction during the first minute and during the second minute.
Why are these two rates not equal?

In the reaction $\mathrm{A \rightarrow products}$, 4.50 minutes after the reaction is started, $\mathrm{[A]=0.587\,M}$. The rate of reaction at this point is $\mathrm{rate = -\dfrac{\Delta[A]}{\Delta t} = 2.1 \times 10^{-2}\, M\, min^{-1}}$. Assume that this rate remains constant for a short period of time.

What is $\mathrm{[A]}$ 6.00 minutes after the reaction is started?
At what time after the reaction is started with $\mathrm{[A] = 0.56\,M}$?

Refers to figure in book. What do we do????

For the reaction $\mathrm{A + 2B \rightarrow 2C}$, the rate of reaction is 1.75 x 10 -5 M s -1 at the time when $\mathrm{[A] = 0.3575\,M}$.

What is the rate of formation of $\mathrm{C}$?
What will $\mathrm{[A]}$ be 1 minute later?
Assume the rate remains at 1.75 x 10 -5 M s -1 . How long would it take for $\mathrm{[A]}$ to change from 0.3580 to 0.3500M?

At 65°, the half-life for the first-order decomposition of $\ce{N2O5(g)}$ is 2.35 minutes.

$\ce{N2O5(g) \rightarrow 2NO2(g) + \dfrac{1}{2}O2(g)}$

If 1.00g of $\ce{N2O5}$ is introduced into an evacuated 10L flask at 65°C,

What is the initial partial pressure, in mmHg, of $\ce{N2O5(g)}$?
What is the initial partial pressure, in mmHg, of $\ce{N2O5(g)}$ after 2.35 minutes?
What is the total gas pressure, in mmHg, after 2.35 minutes?

The initial rate of the reaction $\ce{A + B \rightarrow C + D}$ is determined for different initial conditions, with the results listed in the table.

What is the order of reaction with respect to $\ce{A}$ and to $\ce{B}$?
What is the overall reaction order?
What is the value of the rate constant, $\ce{k}$?

For the reaction $\ce{A + B \rightarrow C + D}$ the following initial rate of reaction were found. What is the rate law for this reaction?

The following rates of reaction were obtained in three experiments with the reaction $\ce{2NO(g) + Cl2(g) \rightarrow 2NOCl (g)}$.

What is the rate of law of this reaction?

The following was obtained for the initial rates of reaction in the reaction $\ce{A + 2B + C \rightarrow 2D + E}$.

What are the reaction orders with respect to $\ce{A}$, $\ce{B}$, and $\ce{C}$?
What is the value of $\ce{R5}$ in terms of $\ce{R1}$?

One of the following statements is true and the other is false regarding the first-order reaction $\ce{A \rightarrow B + C}$. Identify the true statement and the false one, and explain your reasoning.

The rate of the reaction decreases as more of $\ce{B}$ and $\ce{C}$ form.
The time required for one-half of substance $\ce{A}$ to react is directly proportional to the quantity of $\ce{A}$ present initially.

One of the following statements is true and the other is false regarding the first-order reaction $\ce{4A \rightarrow B + C}$. Identify the true statement and the false one, and explain your reasoning.

A graph of $\ce{[A]}$ versus time is a straight line.
The rate of the reaction is one half the rate of disappearance of $\ce{A}$.

The reaction $\ce{A + B \rightarrow C + D}$ is second order in $\ce{A}$ and zero order in $\ce{B}$. The value of $\ce{k}$ is 0.0107 M -1 min -1 . What is the rate of this reaction when $\mathrm{[A] = 0.106\, M}$ and $\mathrm{[B] = 3.73\, M}$?

A reaction 50% complete in 40.0 min. How long is the start will the reaction by 75% complete if it is (a) first order (b) zero order?

The decomposition of $\mathrm{HI\,(g)}$ at 500K is followed for 00s, yielding the following data; at $\mathrm{t = 0}$, $\mathrm{[HI] = 1.00\, M}$; at $\mathrm{t =125\, s}$, $\mathrm{[HI] = 0.90\,M}$; at $\mathrm{t = 250\,s}$, $\mathrm{[HI] = 0.81\,M}$; $\mathrm{t = 375\,s}$, $\mathrm{[HI] = 0.74\,M}$; at $\mathrm{t = 500\,s}$, $\mathrm{[HI] = 0.68\,M}$. What are the reaction order and the rate constant for the reaction:

$\ce{HI(g) \rightarrow \dfrac{1}{2} H2(g) + \dfrac{1}{2} I2(g)}$

Write the rate law for the reaction at 500 K.

For the disproportionation of p-toluenesulfinic acid,

$\ce{3ArSO2H \rightarrow Ar SO2SAr + ArSO3H + H2O}$

(where $\mathrm{Ar = \textrm{p-}CH_3C_6H_4}$), the following data were obtained: $\mathrm{t = 0\, min}$, $\mathrm{[ArSO_2H] = 0.140\, M}$; $\ce{15\, min}$, $\ce{0.0965\, M}$; $\ce{30\, min}$, $\ce{0.0852\, M}$, $\ce{45\, min}$, $\ce{0.0740\, M}$; $\ce{60\, min}$, $\ce{0.0668\, M}$; $\ce{120\, min}$, $\ce{0.0493\, M}$; $\ce{180\, min}$, $\ce{0.0365\, M}$; $\ce{300\, min}$, $\ce{0.0196\, M}$.

Show that this reaction is second order
At what time would $\mathrm{[ArSO_2H] = 0.0600\,M}$?
At what time would $\mathrm{[ArSO_2H] = 0.0300\,M}$?
At what time would $\mathrm{[ArSO_2H] = 0.0150\,M}$?

Explain why

A reaction rate cannot be calculated from solely the collision frequency.
The rate of a chemical reaction may increase dramatically with temperature, whereas the collision frequency rises a lot more slowly.
Introducing a catalyst to a reaction mixture can have such a significant impact on the rate of the reaction, even if the temperature is held constant.

If even a small spark is introduced into a mixture of $\ce{H2(g)}$ and $\ce{O2(g)}$, a highly exothermic explosive reaction occurs. Without the spark, the mixture remains unreacted indefinitely.

Explain this difference in behavior.
Why is the nature of the reaction independent of the size of the spark?

For the reversible reaction $\ce{A + B \leftrightarrow A + B}$ the enthalpy change of the forward reaction is +11 kj/mol. The activation energy of the forward reaction is 74 kj/mol.

A + B ßàA + B

What is the activation energy for the reverse reaction?

By an appropriate draft, indicate why there is some relationship between the enthalpy change of the activation energy for an endothermic reaction but not for the endothermic reaction.

exothermic?

The following statements about catalysis are not stated completely correct. What slight changes would you make to them?

A catalyst is a substance that speeds up a chemical reaction but does not take part in the reaction.
The function of a catalyst is to lower the activation energy allowed for a chemical reaction.

The following substrate's concentration $\ce{[S]}$ versus time data were obtained during an enzyme-catalyzed reaction: $\mathrm{t = 0\, min}$; $\mathrm{[S] = 1.00\,M}$; $\mathrm{30\, min}$, $\mathrm{0.90\,M}$; $\mathrm{90\, min}$, $\mathrm{0.70\,M}$; $\mathrm{120\, min}$, $\mathrm{0.50\,M}$; $\mathrm{180\, min}$, $\mathrm{0.20\,M}$. What order is this reaction with respect to $\ce{S}$ in the concentration

Chapter 24: Chemical Kinetics

4. In the reaction A àproducts, at t = 0 [A]=0.1563M. After 1.00 minute, [A]=0.1496, and after 2.00 minutes [A]=0.1431M.

a. Calculate the average rate of reaction during the first minute and during the second minute.

First minute: -.0067Mmin -1

Second minute: -.0065Mmin -1

b. Why are these two rates not equal?

Since the reaction is not a zero order reaction, the rate of reaction changes as time passes.

5. In the reaction A àproducts, 4.50 minutes after the reaction is started, [A]=0.587M. The rate of reaction at this point is rate = -Δ[A]/Δt = 2.1 x 10 -2 M min -1 . Assume that this rate remains constant for a short period of time.

a) What is [A] 6.00 minutes after the reaction is started?

.6185 = [A] @ 6 minutes

b) At what time after the reaction is started with [A] = 0.56M?

time = 3.21 minutes

7. For the reaction A + 2B à2C, the rate of reaction is 1.75 x 10 -5 M s -1 at the time when [A] = 0.3575M.

a)What is the rate of formation of C?

3.5 x 10 -5 Msec -1

b) What will [A] be 1 minute later?

[A] = .35645M @ 1 minute

c) Assume the rate remains at 1.75 x 10 -5 M s -1 . How long would it take for [A] to change from 0.3580 to 0.3500M

time = 428.5 seconds

10 .At 65°, the half-life for the first-order decomposition of N 2 O 5 (g) is 2.35 minutes.

N 2 0 5 (g) à2NO 2 (g) + ½0 2 (g)

If 1.00g of N 2 0 5 is introduces into an evacuated 10L flask at 65°C,

a) What is the initial partial pressure, in mmHg, of N 2 0 5 (g)?

b) What is the initial partial pressure, in mmHg, of N 2 0 5 (g) after 2.35 minutes?

c) What is the total gas pressure, in mmHg, after 2.35 minutes?

11. The initial rate of the reaction A + B àC + D is determined for different initial conditions, with the results listed in the table.

a) What is the order of reaction with respect to A and to B?

[A] x ; x = 1 st order

[B] y ; y = 2 nd order

b) What is the overall reaction order?

c) What is the value of the rate constant, k?

k = .087 M 2 s

For the reaction A + B àC+ D the following initial rate of reaction were found. What is the rate law for this reaction?

Rate = 2.16 x 10 -3 M 2 min[A] 1 [B] 2

The following rates of reaction were obtained in three experiments with the reaction 2NO(g) + Cl 2 (g) à2NOCl (g).

What is the rate law of this reaction?

Rate = 5.597 M 2 sec[NO] 2 [Cl 2 ] 1

14. The following was obtained for the initial rates of reaction in the reaction A + 2B + C à2D + E.

a) What are the reaction orders with respect to A, B, and C?

[A] = 1 st order

[B] = 2 nd order

[C] = 1 st order

b) What is the value of R 5 in terms of R 1 ?

R 5 = ½ R 1

15. One of the following statements is true and the other is false regarding the first-order reaction A àB + C. Identify the true statement and the false one, and explain your reasoning.

(a) The rate of the reaction decreases as more of B and C form.

True: Since rate = k[A] 1 ; if [A] decreases, the rate will drop.

(b) The time required for one-half of substance A to react directly proportional to the quantity of A present initially.

False: Since rate = k[A] 1 ; as the [A] drops, the reaction rate becomes disproportional to the concentration. Reaction starts fast at high concentrations but will slow down at low [A]

16. One of the following statements is true and the other is false regarding the first-order reaction 2A àB + C. Identify the true statement and the false one, and explain your reasoning.

(a) A graph of [A] versus time is a straight line.

False: Since rate=k[A] 1 ; as [A] decreases, time and concentration become disproportional and graph will curve.

(b) The rate of the reaction is one half the rate of disappearance of A.

True: Since rate is dependent on balanced coefficients. [A] is actually twice the amount in rate = k[A]

33. The reaction A + B àC + D is second order in A and zero order in B. The value of k is 0.0107 M -1 min -1 . What is the rate of this reaction when [A] and = 0.106 M and [B] = 3.73 M?

Rate = 1.2 x 10 -5 M -1 min -1

34. A reaction 50% complete in 40.0 min. How long is the start will the reaction by 75% complete if it is (a) first order (b) zero order?

(a) Cannot be determined without concentration of reactant(s)

(b) 60 minutes

35. The decomposition of HI(g) at 500K is followed for 500s, yielding the following data; at t = 0 [HI] = 1.00 M; at t =125 s, [HI] = 0.90M; at t = 250s, [HI] = 0.81M; t = 375s, [HI] = 0.74M; at t = 500s, [HI] = 0.68M. What are the reaction order and the rate constant for the reaction:

HI(g) à½ H 2 (g) + ½ I 2 (g)”

36. For the disproportionation of p-toluenesulfinic acid,

3ArSO 2 H àAr SO 2 SAr + ArSO 3 H + H 2 0

(where Ar = p-CH 3 C 6 H 4 ), the following data were obtained: t = 0 min, [ArSO 2 H] = 0.140 M; 15 min, 0.0965 M; 30 min, 0.0852 M, 45 min, 0.0740 M; 60 min, 0.0668 M; 120 min, 0.0493 M; 180 min, 0.0365 M; 300 min, 0.0196 M.

(a) Show that this reaction is second order

(b) What is the value of the rate constant, k?

(d) At what time would [ArSO 2 H] = 0.0300M?

(e) At what time would [ArSO 2 H] = 0.0150M?

45. Explain why

(a) A reaction rate cannot be calculated from the solely collision frequency.

Collision Frequency does not solely determine the rate of the reaction because in order to overcome the activation energy to react, temperature and concentrations will also dictate the rate of the reaction.

(b) The rate of a chemical reaction may increase dramatically with temperature, whereas the collision frequency rises a lot more slowly.

A rise in temperature results in higher kinetic energies in the molecules thus increasing the % chance of colliding AND reacting rather than colliding and staying inert. Having a steady collision frequency with higher kinetic energy will result in spiked rates of reactions.

(c) Introducing a catalyst to a reaction mixture can have such a significant impact on the rate of the reaction, even if the temperature is held constant.

Catalysts induce reactants to react with one another by lowering the activation energy of the chemical reaction. This can be done without any sort of flux in the enthalpy of the system.

46. If even a small spark is introduced into a mixture of H 2 (g) and O 2 (g) a highly exothermic explosive reaction occurs. Without the spark, the mixture remains unreacted indefinitely.

(a) Explain this difference in behavior.

Without a super increase in the temperature which acts as a sort of catalyst, the lone diatomics do not possess the energy to overcome the activation barrier.

(b) Why is the nature of the reaction independent of the size of the spark?

Once a single reaction occurs, it independently releases more heat which in turn passes on kinetic energy to its neighboring atoms resulting in a exponential chain reaction.

47. For the reversible reaction A + B ßàAB the enthalpy change of the forward reaction is +11 kj/mol. The activation energy of the forward reaction is 74 kj/mol. What is the activation energy for the reverse reaction? 63 kJ/mol

59. The following statements about catalysis are not stated completely correct. What slight changes would you make to them?

(a) A catalyst is a substance that speeds up a chemical reaction but does not take part in the reaction.

A catalyst is a substance that speeds up a chemical reaction but does get consumed in the reaction.

(b) The function of a catalyst is to lower the activation energy allowed for a chemical reaction.

The function of a catalyst is to lower the activation energy needed for a chemical reaction.

60. The following substrates concentration [S] versus time date were obtained during an enzyme-catalyzed reaction: t = 0 min; [S] = 1.00M; 30 min, 0.90M; 90 min, 0.70M; 120 min, 0.50M; 180 min, 0.20M. What order is this reaction with respect to S in the concentratio

For the reaction $\mathrm{3A + 2B \rightarrow C + 2D}$ reactant $\ce{A}$ is found to disappear at the rate of 4.6 X 10 -5 Ms -1

What is the rate of reaction?
What is the rate of disappearance of the reactant $\ce{B}$ ?
What is the rate of appearance for product $\ce{D}$ ?
$\mathrm{-\dfrac{1}{3} \left(\dfrac{- \Delta[A]}{\Delta t}\right) = \dfrac{1}{3} (4.6 \times 10^{-5}\, Ms^{-1}) = 1.5 \times 10^{-5}\, Ms^{-1}}$
Rate disappearance of $\mathrm{B = (rate\: of\: reaction) \times 2(coefficient\: of\: B)}$ $\mathrm{(1.5 \times 10^{-5}\,Ms^{-1})(2) = 3.1 \times 10^{-5}\, Ms^{-1}}$
Same process as B) (multiply rate of reaction by 2) OR: Rate of appearance of $\mathrm{D = -\dfrac{1}{3}(2)\left(\dfrac{\Delta[A]}{\Delta t}\right) = -\dfrac{2}{3}(4.6 \times 10^{-5}\, Ms^{-1}) = 3.1 \times 10^{-5}\, Ms^{-1}}$

In the reaction $\mathrm{A \rightarrow B}$ , $\mathrm{[A]}$ is found to be 0.675M at $\mathrm{t = 51.1\,s}$ and 0.605M at $\mathrm{t = 61.5\,s}$ . Find the average rate of the reaction during this time interval.

$\mathrm{Rate = -\left(\dfrac{\Delta[A]}{\Delta t}\right) = \dfrac{0.675\,M-0.605\,M}{61.5\,s-51.1\,s} = 0.00673 = 6.73 \times 10^{-3}\, Ms^{-1}}$

The initial rate of the reaction $\mathrm{A + B \rightarrow C + D}$ is determined for difference initial conditions, with the results listed in the table:

What is the order of the reaction with respect of $\mathrm{A}$ and $\mathrm{B}$? Write out respective rate laws for $\mathrm{A}$ and $\mathrm{B}$
What is the value of the $\ce{k}$, the rate constant?
m and n are the respective orders according to $\mathrm{A}$ and $\mathrm{B}$: $\mathrm{R1 = 1.261 \times 10^{-4} = [0.241]^m[0.153]^n}$ $\mathrm{R2 = 5.044 \times 10^{-4} = [0.241]^m[0.306]^n}$ $\mathrm{R3 = 2.522 \times 10^{-4} = [0.482]^m[0.153]^n}$ $\mathrm{R4 = 6.741 \times 10^{-4} = [0.482]^m[0.306]^n}$ Now utilize the rate laws / solve: Divide reaction 2 by reaction 1 ($\mathrm{A}$ is constant $\mathrm{B}$ changes concentration) $\mathrm{\dfrac{R2}{R1} = \dfrac{5.044 \times 10^{-4}}{1.261 \times 10^{-4}} = \dfrac{[0.241]^m[0.306]^n}{[0.241]^m[0.151]^n}}$ $\mathrm{\dfrac{R2}{R1} = 4 = 2^n}$ $\mathrm{n = 2}$ Reaction is second order with respect to $\mathrm{B}$. Do the same for $\mathrm{A}$. Use reactions 3 and 1 ($\mathrm{[B]}$ is constant, $\mathrm{[A]}$ changes) $\mathrm{\dfrac{R3}{R1} = \dfrac{2.522 \times 10^{-4}}{1.26 \times 10^{-4}} = \dfrac{[0.482]^m[0.153]^n}{[0.241]^m[0.153]^n}}$ $\mathrm{\dfrac{R3}{R1} = 2 = 2^m}$ $\mathrm{m = 1}$ Reaction is first order with respect to $\mathrm{A}$
Overall reaction order = (reaction order of A + reaction order of B) = 1 + 2 = 3rder order overall
Substitute in for one of the reactions $\mathrm{Rate\: law = k[A][B]^2}$ For example use reaction 1 Rate: $\mathrm{1.261 \times 10^{-4} = k[A][B]^2}$ $\mathrm{1.261 \times 10^{-4} = k[0.241][0.153]^2}$ $\mathrm{k = 0.0224\, M^{-2}s^{-1}}$

The following rates of reactions were obtained in three experiments with the reaction $\ce{2NO(g) + Cl2 \rightarrow 2NOCl(g)}$

What is the order of the reaction with respect of $\ce{A}$ and $\ce{B}$? Write out respective rate laws for $\ce{A}$ and $\ce{B}$

m and n are the respective orders according to $\ce{A}$ and $\ce{B}$:

$\mathrm{R1 = 1.45 \times 10^{-5} = [0.362]^m[0.730]^n}$

$\mathrm{R2 = 2.90 \times 10^{-5} = [0.362]^m[1.46]^n}$

$\mathrm{R3 = 5.80 \times 10^{-5} = [0.724]^m[0.730]^n}$

Now utilize the rate laws and solve:

Divide R2 by R1 ($\ce{[A]}$ stays constant while $\ce{[Cl2]}$ changes)

$\mathrm{\dfrac{R2}{R1} = \dfrac{2.9 \times 10^{-5}}{1.45 \times 10^{-5}} = \dfrac{[0.362]^m[1.46]^n}{[0.362]^m[0.730]^n}}$

$\mathrm{\dfrac{R2}{R1} = 2 = 2^n}$

$\mathrm{n = 1}$

First order with respect to $\ce{Cl2}$

Divide R3 by R1 ($\ce{[Cl2]}$ is constant $\ce{[NO]}$ changes)

$\mathrm{\dfrac{R3}{R1} = \dfrac{5.8 \times 10^{-5}}{1.45 \times 10^{-5}} = \dfrac{[0.724]^m[0.730]^n}{[0.362]^m[0.730]^n}}$

$\mathrm{\dfrac{R3}{R1} = 4 = 2^m}$

$\mathrm{n = 2}$

Second order with respect to $\mathrm{[NO]}$

$\mathrm{Rate\: Law = k[NO]^2[Cl_2]}$

Using the rate law we can solve for $\ce{k}$, the rate constant

Use any set of experimental data

Lets use exp. 2

$\mathrm{2.9 \times 10^{-5}\, Ms^{-1} = k[NO]^2[Cl_2] = k[0.362]^2[1.46]}$

$\mathrm{k = 1.52 \times 10^{-4}\, M^{-2}s^{-1} [NO]^2[Cl_2]}$

The first order reaction has t 1 /2 of 250s

What percent of a sample of $\ce{A}$ remains unreacted 1500s after a reaction starts.
What if the rate of the reaction is 1/2 the rate of disappearance of $\ce{A}$.
$\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{0.693}{250\, s} = 0.00277\,s^{-1}}$ $\begin{align} \mathrm{\ln(\%\, unreacted)} &= \mathrm{-kt} \\ &=\mathrm{(-.00277\,s^{-1})(1500\,s) = -4.155} \end{align}$ $\mathrm{\%\, unreacted = 0.0157 \times 100\% = 1.57 \%\textrm{ of the original quantity}}$
$\mathrm{Rate = k[A] = 0.00277\,s^{-1})(0.5\,M) = 0.00139\, M/s}$

The reaction A to product is first order in $\ce{A}$.

If 2.4 g of $\ce{A}$ is allowed to decompose for 30 minutes, the mass of $\ce{A}$ remaining undecomposed is found to be .6g. What is the halflife, t 1 /2 , of this reaction.
Starting with 2.4g of $\ce{A}$ what is the mass of $\ce{A}$ remaining undecomposed after 1 hour
Mass has decreased to 1/4 of the original mass. Since $\mathrm{\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right) = \dfrac{1}{4}}$. 2 halflives have elapsed. As a result $\mathrm{2 \times t_{1/2} = 30\: minutes}$ $\mathrm{t_{1/2} = 15\: minutes}$
$\mathrm{k = \dfrac{0.693}{15\:minutes} = 0.0462\: min^{-1}}$ Use equation $\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}$ $\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0}= (-0.0462\:min^{-1})(60\: min) = -2.8}$ $\mathrm{\dfrac{[A]_t}{[A]_0} = e^{-2.8}}$ $\mathrm{[A]_t = [A]_0 e^{-2.8}}$ $\mathrm{[A]_t = (2.4\:g)(e^{-2.8}) = 0.146\:g\: A}$

In the first order reaction $\mathrm{D \rightarrow products}$ it is found that 90% of the original amount of reactant $\ce{D}$ decomposes in 140 minutes. Find the half life of the decomposition reaction.

Use the equation. $\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}$

$\mathrm{100\%-90\% = 10\%\: left}$

$\mathrm{\dfrac{\ln[0.1]}{1.00} = -k(140\: min)}$ $\mathrm{k = 0.0164\: min^{-1}}$

$\mathrm{Half\: life = \dfrac{\ln (2)}{0.0164} = 42.3\: min}$

Acetoacetic acid, $\ce{CH3COCH2COOH(aq)}$, a reagent used in organic synthesis, decomposes in acidic solution, producing acetone and carbon dioxide gas: $\ce{CH3COCH2COOH(aq)\rightarrow CH3COCH3(aq) + CO2(g)}$

This is a first-order decomposition with a halflife of 144 minutes.

How long with it take for a sample of acetoacetic acid to be 55% decomposed?

Start with the decomposed $\mathrm{= 100\% - 55\% = 45\%}$ decomposed

$\mathrm{\ln\dfrac{\dfrac{45}{100}[A]_0}{[A]_0} = \ln 0.45 = -kt}$

Find the value of $\mathrm{k \rightarrow k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{144\: minutes} = 0.00481\: min^{-1}}$

Plug the $\ce{k}$ value back in

$\mathrm{\ln 0.45 = (-0.00481\: min^{-1})(t) }$

$\mathrm{t = 166\: seconds}$

Which sets of data correspond to a:

Zero order reaction
First order reaction
Second order reaction

Graph out each graph for:

1) Concentration vs Time

2) ln(Concentration) vs Time

3) $\mathrm{\dfrac{1}{Concentration}}$ vs Time

Whichever one gives a straight linear line will correlate with the correct order of the reaction:

If Concentration vs Time straight: Zero Order

If ln(Concentration) vs Time straight: First Order

If $\mathrm{\dfrac{1}{Concentration}}$ vs Time straight: Second Order

The correct graphs are shown below for each set of data points provided:

What is the approximate half life of the first order reaction?

Set III is first order. We can analyze the data points to get the half life. Since at the 100 second time period, the concentration decreased by a little more than half. Around 70 seconds. We can obtain a more accurate half life by obtaining a value for $\ce{k}$ from the relation of $\mathrm{\ln\dfrac{[A]_t}{[A]_0} = -kt}$ and $\mathrm{t_{1/2} = \dfrac{0.693}{k}}$

$\mathrm{\ln\dfrac{0.77}{100} = -k(25\,s)}$

$\mathrm{k = 9.92 \times 10^{-3}\, s^{-1}}$

thus $\mathrm{t_{1/2} = \dfrac{0.693}{9.92 \times 10^{-3}\, s^{-1}} = \textrm{around 70 seconds}}$ .

The reaction $\mathrm{A + B \rightarrow C + D}$ is second order and first order with respect to $\ce{B}$. The value of $\ce{k}$ is .0351 M^-1min^-1. What is the rate of this reaction when $\mathrm{[A] = 0.120\, M}$ and $\mathrm{[B] = 4.6\,M}$?

Simply substitute in the values for the rate equation to get the rate of reaction:

$\mathrm{Rate = k[A]^2[B] = (0.0351\, M^{-1}min^{-1})[0.12]^2[4.6] = 0.0023\, M/min}$

The decomposition of $\ce{HF(g)}$ at 750 degrees kelvin is followed for 500s, yielding the following data: at t:0 $\mathrm{[HF] = 1.05\:M}$. t:100s $\mathrm{[HF]=1.25\:M}$. t: 200s $\mathrm{[HF] = 1.54\,M}$. t=300s $\mathrm{[HF] = 2\,M}$.

What are the reaction order and the rate constant for the reaction? $\ce{HF(g) \rightarrow \dfrac{1}{2} H2(g) + \dfrac{1}{2} F2(g)}$

Write the rate law for the reaction at 750 degrees K.

Make a table as follows:

From the above data, plot time vs $\ce{[HF]}$, $\ce{\ln[HF]}$, and $\ce{\dfrac{1}{[HF]}}$. Which ever one gives a straight linear line with a positive slope is the correct corresponding order.

If $\ce{\dfrac{1}{Concentration}}$ vs Time straight: Second Order

$\ce{\dfrac{1}{[HF]}}$. Which ever one gives a straight linear line with a positive slope is the correct corresponding order. will provide a straight line with a positive slope. The decomposition of From the above data, plot time vs $\ce{[HF]}$ is a second order reaction.

Zero order?

First order?

Second order:

In order to calculate the value of $\ce{k}$, the rate constant, you must find the slope of the line:

$\mathrm{\dfrac{2\,M-1.05\,M}{300\,s-0\,s} = 0.0032\: M^{-1}s^{-1}}$

Rate law: $\mathrm{0.0032\: M^{-1}s^{-1}\: [HF]}$

For the reaction $\mathrm{F \rightarrow products}$, the following data was obtained. $\mathrm{t=0\,s}$ $\mathrm{[F] = 0.79\,M}$, $\mathrm{t=50\,s}$ $\mathrm{[F] = 0.67\,M}$, $\mathrm{t = 100\,s}$ $\mathrm{[F] = 0.55\,M}$, $\mathrm{t = 150\,s}$ $\mathrm{[F]=0.43\,M}$

Find the order of the reaction
Find the half life of the reaction
Make a table like the following:

For this reaction $\mathrm{[F]}$ is decreasing consistantly .12M overtime. Plot $\mathrm{[A]}$, M versus time(s), $\mathrm{\ln[F]}$ versus time(s) and $\mathrm{\dfrac{1}{[F]}}$ versus time(s).

Only $\mathrm{[F]}$ versus time will gve a straight line with a negative slope: Zero order reaction

Zero order:

First order?:

Second order?:

The half life will need one half of the initial $\mathrm{[F]}$ to react $\mathrm{\Delta[F] = \dfrac{0.79\,M}{2} = 0.395\,M}$ and $\mathrm{t_{1/2} = \dfrac{0.395\,M}{Slope}}$ $\mathrm{Slope = \dfrac{0.430\, M - 0.790\,M}{150\,s-0\,s} = 0.0024\, M^{-1}s^{-1}}$ Plug the rate constant k back into the half life equation: $\mathrm{t_{1/2} = \dfrac{0.395\,M}{-0.0024} = 165\: seconds}$

Although initially the rate laws of first order and second order reactions may seem similar, they are also very different. Write out the equations of the two half life equations and explain why the situation aren’t the same for two different reactions rates.

First Order: $\mathrm{t_{1/2} = \dfrac{0.693}{k}}$

Second order: $\mathrm{t_{1/2} = \dfrac{1}{[A]_0k}}$

Based on the formula, a first order reaction’s half-life stays constant and this depends on the value of the rate constant, $\ce{k}$. A second order reaction on the other hand has a half-life that fluctuates and varies inversely proportional to $\ce{[A]_0}$. As $\ce{[A]_0}$ increase, the half-life decreases. In a second order reaction the rate of reaction increases as the $\ce{[A]}$ does and so the higher the concentration of initial $\ce{A}$, the higher the rate, and the lower the concentration the lower the rate of reaction. For a reaction order of one, all that is taken into account if the value of the rate constant, $\ce{k}$. This means that the half-life of this order is constant and will not depend on the concentration of initial $\ce{A}$.

Explain why:

Even though the necessary components collide together, a reaction may not occur
The addition of a catalyst doesn't cause it to be included in the chemical equation.
Temperature increases the rate of a chemical reaction.
This is due to the fact that rates of a reaction depend on at least two factors other than the frequency of collisions. One of the most important aspects is whether of the not the collisions have enough energy to get over the energy barriers to the products. The higher the activation energy, the less frequencies of the collisions being energetic enough. Second of all the molecules in a given collision have to be orientated in a certain way. The more complex the molecules are, the more motion the molecules can have. This will result in a lower fraction o the collisions being correctly orientated.
Addition of a catalyst merely speeds up the reaction due to the lowering of the activation energy. It enables an alternate mechanism. The lower activation energy will mean a larger fraction of the molecules having the sufficient energy to react (leading to increased r
This is due to the increase frequency of the collisions(more chances of a reaction occurring). In addition, the molecules collide with more force and is able to overcome the activation energy necessary for the process to proceed.

For the reversible reaction $\mathrm{A + B \leftrightarrow A + B}$ the enthalpy change of the forward reaction is +20kj/mol. The activation energy of the forward reaction is 84 kj/mol.

What is the activation energy of the reverse reaction?
Sketch the reaction plot for this reaction
The products are 20kj/mol closer in energy to the energy activated complex than that of the reactants(the activation energy of the reverse): $\mathrm{84\:jk/mol - 20\: kj/mol = 64\: kj/mol}$

How many intermediates are there in this reaction?
How many transition states are there?
What is the fastest step?
Is the reaction exothermic or endothermic?
Is the second step exothermic or endothermic?
What is the slowest step?
There are 5 peaks/min max: 5
E has the lowest activation energy required
Endothermic reaction absorbs energy from A-F
Endothermic
First step, the activation energy is the highest

The rate constant for the reaction $\ce{H2(g) + F2(g) \rightarrow 2HF}$ has been determined at the following temperatures 650 degrees k, $\mathrm{k = 4.8 \times 10 ^{-4}\, M^{-1}s^{-1}}$; 700 degrees K, $\mathrm{k = 3.0 \times 10^{-2}\,M^{-1}s^{-1}}$. Calculate the activation energy for the reaction.

Use the Arrhenius equation:

$\mathrm{\ln\dfrac{k_1}{k_2} = \dfrac{E_a}{R} \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right) =\ln\dfrac{4.80 \times 10^{-4}\, M^{-1}s^{-1}}{3.00 \times 10^{-2}\, M^{-1}s^{-1}} = \dfrac{E_a}{R} \left(\dfrac{1}{700 K} -\dfrac{1}{650 K}\right)}$

$\mathrm{(E_a)(-1.099 \times 10^{-4}) = -4.135R}$ $\mathrm{R=8.314\: j/(mol\: k)}$

$\mathrm{E_a =\dfrac{(-4.135)(8.314\: J/(mol\: k))}{-1.099 \times 10^{-4}} = 313\: kj/mol}$

True or false? Modify the statement so it is more accurate:

Catalysts speed up a reaction Describe what a catalyst is
Catalysts remain part of the overall equation
True; Catalysts are able to speed up a reaction. They lower the activation energy and let the reaction proceed at a lower energy level. Not all catalyst quickens a reaction. Some catalysts, called inhibitors, actually slow down the rate of reaction.
False. Although catalysts are part of the reaction, they are not part of the chemical equation. It "takes part" in the reaction but is only there to change the mechanism of a reaction. Catalysts are not included in the equation, they only change the activation energy.

What are the similarities and differences between the catalystic activity and properties of an enzyme and that of a metal such as platinum or other metallic catalyst or ever activated carbon?

Platinum and enzymes both have a center that acts as the active site where reactions occur. There are two types of catalysts: heterogeneous and homogenous. While platinum(hetero) doesn't dissolve into the mixture, enzymes(homo) are usually soluable. The most important aspect that enzymes are very specific while platinum catalyzes almost everything. Enzymes have certain configurations and shapes that are unique to each one. They will only catalyze certain reactions if it is is the correct one.

Describe the effect of enzyme concentration on the rate of the enzyme reaction. What effect is going on?

Although enzyme concentration increase resulted in an increase in reaction initially, the increase leveled out eventually. This is due to the fact that substrate may be running out. The leveling off shows that the reactions are at their maximum capacity upon the catalyst. This may be due to the limited amount of the substrate.

The reaction $\mathrm{2A + 2B \leftrightarrow 2C + 2D}$ is second order in respect to $\mathrm{[A]}$ and first order in respect to $\mathrm{[B]}$. A three step mechanism has been proposed. The third fast step is the $\mathrm{second\: intermediate + B \rightarrow 2C + D}$. The first step is $\mathrm{2A \rightarrow first\: intermediate}$. Propose an entire three step mechanism to show that it conforms to experimentally determined reaction order.

Write out the proposed three set of reactions:

$\mathrm{2A \leftrightarrow Intermediate\: 1 \quad (Fast)}$
Unknown (Slow)
$\mathrm{Intermediate\: 2 + B \rightarrow C + D \quad (Fast)}$

First: Find the rate law for this reaction: $\mathrm{Rate = k[A]^m[B]^n}$

m=2nd order n=1st order

as a result: $\mathrm{Rate = k[A]^2[B]^1}$

Consider the three equations and calculate step 2:

$\mathrm{2A \leftrightarrow Intermediate\: 1\quad (Fast)}$
$\mathrm{Intermediate\: 1 + B \rightarrow D + Intermediate\: 2\quad (Slow)}$

Crossing out:

$\mathrm{2A \leftrightarrow }$ Intermediate 1 $\mathrm{\quad(Fast)}$
Intermediate 1 $\mathrm{+ B \rightarrow D +}$ Intermediate 2 $\mathrm{\quad(Slow)}$
Intermediate 2 $\mathrm{+ B \rightarrow C + D \quad(Fast)}$

$\mathrm{= 2A + 2B \leftrightarrow 2C + 2D }$

Through the concepts of mechanism and reactions, we know that the rate determining step is going to be the slowest one.

The rate law of reaction 1 is $\mathrm{Rate = k_1[A]^2}$

The rate law of reaction 2 is $\mathrm{Rate = k_2[B][I_1]}$

The rate law of reaction 3 is $\mathrm{Rate = k_3[B][I_2]}$

We can not have intermediates in our reaction rate law

Step 1 can also be written as $\mathrm{Rate = k_{-1}[I_1]}$

The two reaction 1 equations are equal, set them equal to each other:

$\mathrm{k_1[A]^2 = k_{-1}[I_1]}$

$\mathrm{[I_1] = \dfrac{k_1}{k_{-1}} [A]^2}$

let $\mathrm{\dfrac{k_1}{k_{-1}} = k}$

$\mathrm{[I_1] = k[A]^2}$

Substitute this back into the rate determining step. Combine the $\ce{k}$ value like the previous part of this problem

As a result, the rate $\mathrm{= k[A]^2[B]}$

note that this is the same as the original equation.

For a second order reaction what are the units of $\ce{k}$

$\mathrm{rate = \dfrac{-d[A]}{A} = k[A][A] = k[A]^2}$

=> k has units of M/sec

Find the general rate law and the magnitude of $\ce{k}$ for the overall reaction.

$\ce{2(N2O5 \rightarrow NO2 + NO3)}$
$\ce{NO2 \rightarrow NO3 \rightarrow NO2 + O2 + NO}$
$\ce{NO + NO3 \rightarrow 2NO2}$

$\ce{2N2O5 + NO2 + NO3 + NO + NO3 \rightarrow 2NO2 + 2NO3 + NO2 + O2 + NO + 2NO2}$ $\ce{\Rightarrow 2N2O5 \rightarrow 4NO2 + O2 \: (overall\: reaction)}$

$\ce{NO + Br2 \leftrightarrow NOBr2 \: [Fast,\: revers.]}$
$\ce{NOBr2 + NO \rightarrow 2NOBr \: [Slow, \: RDS]}$

$\mathrm{\Rightarrow Rate = Rate_2 = k_2[NO][NOBr_2]}$ $\mathrm{\rightarrow Rate_1 = Rate_{-1} \rightarrow k_1[NO][Br_2] = k-1[NOBr_2]}$ $\mathrm{\rightarrow [NOBr_2] = \dfrac{k_1}{k_{-1}}[NO][Br_2]}$ $\mathrm{\Rightarrow Rate = k_2[NO][NOBr_2] = k_2[NO]\dfrac{k_1}{k_{-1}}[NO][Br_2]}$ $\mathrm{\Rightarrow Rate = \dfrac{k_2k_1}{k_{-1}}[NO]^2[Br_2] = k[NO]^2[Br_2]}$ $\mathrm{\rightarrow \textrm{Experimental rate law:}\: Rate = k[NO]^2[Br_2]}$ $\mathrm{\rightarrow \textrm{Consistent with the exp. rate law}\: (k = \dfrac{k_2k_1}{k_{-1}})}$

In the reaction $\ce{3A + B \rightarrow 3C + 3D}$, $\ce{A}$ has a disappearance rate of 3.4 × 10 -3 Ms -1 .

What is the rate of reaction at point $\ce{A}$?
What is the rate of disappearance of $\ce{B}$?
What is the rate of formation of $\ce{C}$?

For more help see: The Rate of a Chemical Reaction

$\mathrm{-\dfrac{1}{3} \left( -\dfrac{\Delta[A]}{\Delta t}\right) = \dfrac13 (3.4 \times 10^{-3}\, Ms^{-1}) = 1.13 \times 10^{-3}\, Ms^{-1}}$
$\mathrm{\textrm{Rate of disappearance of B} = reaction\: rate \times coefficient\: of\: B}$ $\mathrm{(1.13 \times 10^{-3}\,Ms^{-1})(1) = 1.13 \times 10^{-3}\,Ms^{-1}}$
$\mathrm{\textrm{Rate of formation of C} = reaction\: rate \times coefficient\: of\: C}$ $\mathrm{(1.13 \times 10^{-3}\,Ms^{-1})(2) = 2.26 \times 10^{-3}\, Ms^{-1}}$

What is the average rate of reaction over a time interval for $\ce{[A]}$ if it is 0.455 M at $\mathrm{t = 80.25\, s}$ and 0.474 M at $\mathrm{t = 82.4\, s}$?

$\mathrm{-\dfrac{\Delta[A]}{\Delta t} = \dfrac{0.474\,M-0.455\,M}{82.4\,s-80.25\,s} = 8.8 \times 10^{-3}\, Ms^{-1}}$

Use the table below to answer the following questions:

Find the order of the reaction $\ce{A}$ vs. $\ce{B}$
Find the overall order
Find the rate constant

$\mathrm{Reaction\: 1 =3.75 \times 10^{-4} = k \times [0.175]^m [0.138]^n}$

$\mathrm{Reaction\: 2 =1.25 \times 10^{-3} = k \times [0.175]^m [0.185]^n}$

$\mathrm{Reaction\: 3 =3.75 \times 10^{-4}= k \times [0.365]^m [0.138]^n}$

$\mathrm{Reaction\: 4 =1.25 \times 10^{-3}= k \times [0.365]^m [0.185]^n}$

Order of reaction with respect to B: 1. Find where $\ce{A}$ is constant and $\ce{B}$ changes (Reaction 1 and Reaction 2) 2. Divide: $\mathrm{\dfrac{Reaction\: 2}{Reaction\: 1} = \dfrac{1.25 \times 10^{-3}}{ 3.75 \times 10^{-4}} = \dfrac{[0.175]^m [0.185]^n}{[0.175]^m[0.138]^n}}$ $\mathrm{\dfrac{Reaction\: 2}{Reaction\: 1}= 4 = 2^n \rightarrow n=2}$ 3. Therefore the reaction is second order with respect to $\ce{B}$ . Order of reaction with respect to A: 1. Find where $\ce{B}$ is constant and $\ce{A}$ changes (Reaction 3 and Reaction 1) 2. Divide: $\mathrm{\dfrac{Reaction\: 3}{Reaction\: 1} = \dfrac{4.41 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.406]^m[0.662]^n}{[0.203]^m[0.662]^n}}$ $\mathrm{\dfrac{R3}{R1} = 2 = 2^m}$ $\mathrm{m = 1}$ 3. Thus the reaction is first order with respect to $\ce{A}$
$\mathrm{Reaction\: order = \textrm{reaction order of A} + \textrm{reaction order of B} = 3^{rd}\textrm{ order reaction}}$
$\mathrm{2.205 \times 10^{-4} = k \times [0.331][0.203]^2}$ $\mathrm{k=1.6 \times 10^{-2}}$

Use the date table below to determine the rate law of the reacton: $\ce{A + B \rightarrow 2D}$

From looking at the table, $\ce{[A]}$ is first order and $\ce{[B]}$ is first order

overall rxn is 2nd order

$\mathrm{R= k[A][B]}$

$\mathrm{4.3E\textrm{-3}\,Ms^{-1}= k(1.5\,M)(1.5\,M)}$

$\mathrm{k=1.2E\textrm{-3}\,(M^{-1})(s^{-1})}$

A first order reaction $\ce{A \rightarrow products}$ has a half life of 120 seconds calculate the following:

What percentage of $\ce{A}$ remains unreacted after 800 seconds of reaction.
What is the rate of reaction at $\mathrm{[A] = 0.25\, M}$?

For more help see: The Rate Law

$\mathrm{t_{1/2} (first\: order) = \dfrac{\ln 2}{k}}$ $\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{120\: s} = 5.77\times10^{-3}}$ percent unreacted defined by $\mathrm{\dfrac{[A]_t}{[A]_0}}$ $\begin{align} \mathrm{\dfrac{[A]_t}{[A]_0}} &= \mathrm{e^{-kt}}\\ &= \mathrm{e^{\large{(-5.77\times10^{-3}\times800)}} \times 100 = 0.98\% \:remains\: unreached.} \end{align}$
For a first order reaction, $\mathrm{rate = k[C]}$ $\mathrm{= 0.0046/s \times 0.25 }$ $\mathrm{= 1.15\times10^{-3}\, M/s}$

Consider another first order reaction $\mathrm{A \rightarrow products}$.

5g of $\ce{A}$ is allowed to decompose for 45 minutes leaving 0.8 grams excess. What is the half life?
If we start with 1.8g of $\ce{A}$ how much is remaining after 1 hour?
First we determine the value of $\ce{k}$ $\mathrm{ln\dfrac{[A]_t}{[A]_0}= -kt}$ $\mathrm{ln\dfrac{[0.8]}{[5]}= -k(45\,min)}$ $\mathrm{k= 4.07E\textrm{-2}\, min^{-1}}$ Next, we find the half life $\begin{align} \mathrm t_{1/2} &= \mathrm{\dfrac{0.693}{k}}\\ &= \mathrm{\dfrac{0.693}{4.07E\textrm{-2}}}\\ &= \mathrm{17\, mins} \end{align}$

$\mathrm{A \rightarrow products}$ is a first order reaction. 97% of reactants decompose in 137 minutes. What is the half-life, t 1 /2 , of this decomposition?

For more help see: Half-lives and Pharmacokinetics

$\mathrm{0.03 = \dfrac{[A]_t}{[A]_0} = e^{-kt}}$

$\mathrm{\ln (0.03) = \ln e^{-kt}}$

$\mathrm{\ln (0.03) = - kt}$

$\mathrm{\ln (0.03) = - k (137\, minutes)}$

$\mathrm{= \dfrac{\ln 2}{-0.0255}}$

= ln 2/ -.0255

$\mathrm{= 27\, minutes}$

The decomposition reaction of 5g of reactant $\ce{A}$ has a half-life of 50 minutes. Given the reaction is first order, how long will it take for reactant $\ce{A}$ to decompose 40%?

Use the following data sets for questions 27 and 29.

Data Set 1 $\mathrm{k= 4.56E\,\textrm{-2}}$

Data Set 2 $\mathrm{k=5.87E\,\textrm{-2}}$

Data Set 3 $\mathrm{k= 6.2E\,\textrm{-2}}$

If 40% of reactant $\ce{A}$ decomposes, that means that 60% of reactant $\ce{A}$ is remaining 60% of 5g is 3g

Next we find $\ce{k}$,

$\mathrm{t_{1/2}= \dfrac{0.693}{k}}$

$\mathrm{k= 0.01386\: min^{-1}}$

Next we solve for $\ce{t}$,

$\mathrm{\ln\left(\dfrac{3}{5}\right)= -(0.01386)(t)}$

$\mathrm{t= 36.86\: min}$

Determine the orders of the above data sets. In other words whether they are zero, first, or second order.

Data Set 1 is First Order

Data set 2 is Zero Order

Data set 3 is Second Order

Find the half-life, t 1 /2 of the first order reaction.

For more help see:

$\mathrm{t_{1/2}= \dfrac{0.693}{4.56E\,\textrm{-2}}}$

$\mathrm{t_{1/2}= 15.2\, s}$

$\begin{align} \mathrm{t_{1/2}} &= \mathrm{\dfrac{[A]_0}{2k}}\\ &= \mathrm{\dfrac{2}{(2)(5.87E\,\textrm-2)}}\\ &= \mathrm{17.0\,s} \end{align}$

$\begin{align} \mathrm t_{1/2} &= \mathrm{\dfrac{1}{[A]_0k}}\\ \mathrm t_{1/2} &= \mathrm{\dfrac{1}{(2.0)(6.2E\,\textrm-2)}}\\ &= \mathrm{8.06\,s} \end{align}$

The reaction $\ce{A + B \rightarrow C + D}$ is a first order in $\ce{A}$ and first order in $\ce{B}$. $\ce{K}$ is equal to 0.0234 M -1 min -1 . What is the rate of this reaction when $\mathrm{[A]=0.245\,M}$ and $\mathrm{[B]=4.45\,M}$?

$\begin{align} \mathrm R &= \mathrm{k[A][B]}\\ &= \mathrm{(0.0234\,M^{-1}\, min^{-1})(0.245\,M)(4.45\,M)}\\ &= \mathrm{0.0255\,M\, min^{-1}} \end{align}$

A common decomposition reaction is observed at constant temperature for 600s with the following data recorded: at $\mathrm{t=0}$, $\mathrm{[Reactant]=2.00\,M}$; at $\mathrm{t=200\,s}$, $\mathrm{[Reactant]=1.80\,M}$; at $\mathrm{t=400\,s}$, $\mathrm{[Reactant]=1.62\,M}$; at $\mathrm{t=600\,s}$, $\mathrm{[Reactant]=1.48\,M}$; at $\mathrm{t=800\,s}$, $\mathrm{[Reactant]=1.36\,M}$. Please provide the reaction order, rate constant, and the rate law for this reaction at this temperature.

For more help see:by graphing the reaction in a log vs x plot we see that it is a second order reaction.

$\mathrm{k = \dfrac{0.617\,M^{-1}-0.500\,M^{-1}}{400\,s-0\,s} = 5.77\times10^{-3}}$

A reaction $\mathrm{A \rightarrow products}$ resulted in the following data. What is the order of the reaction? What is the half life?

Second Order:

Solve for $\ce{k}$ using this equation:

$\mathrm{\dfrac{1}{[A]_t} = kt + \dfrac{1}{[A]_0}}$

Evidently, all the k values for the 3 different times will come out to equal approximately 0.400

Half lives of zeroth and second order reactions are dependent on half life. The situations are different in both cases. Explain why this is so.

Explain the following:

Why can a reaction rate not be determined from a collision rate.
Why is it that rates of reactions change with temperature quickly whereas collision is slower.
Why does addition of catalyst effect the reaction even without change in temperature.
reactions must have collision rates higher than the activation energy.
just because there is an increase in collisions does not mean that the reactions occur more frequently.
when we increase concentration although we increase the collisions we do not really increase the energy.

Consider a reversible reaction with a enthalpy change of the forward reaction of 28kJ/mol, and a activation energy of the forward reaction of 75 kJ/mol.

Find the activation energy of the reverse reaction.
Sketch a reaction profile for the above reaction.
a graph with $\ce{k}$ as the slope and $\ce{[A]}$ as the y intercept. Should have a negative slope.

Visually analyze the following graph.

Count the intermediates of the reaction.
How many transition states are present?
Which segment in the reaction is the fastest?
Which step has the smallest rate constant?
Is step A endothermic or exothermic?
What is the energy change of the overall reaction: endothermic or exothermic
overall exothermic

The following observations of a reaction’s rate constant have been made: at $\mathrm{T=325\,K}$, $\mathrm{k=3.2\times10^{-6}\, M^{-1}s^{-1}}$; at $\mathrm{T=456\,K}$, $\mathrm{k=2.8\times10^{-5}\, M^{-1}s^{-1}}$. What is the activation energy of this reaction?

For more help see: Section on Ahraneous's equation

Solution: use $\mathrm{\ln\dfrac{k_1}{k_2} = \dfrac{E_a}{R} \left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)}$ $\mathrm{\ln\dfrac{2.8\times10^{-5}}{3.2\times10^{-6}} = \dfrac{E_a}{8.3145\, J/mol\, K} \left(\dfrac{1}{325}-\dfrac{1}{456}\right)}$ $\mathrm{-4.21 = \dfrac{E_a(-2.22 \times 10^{-4})}{8.314}}$ $\mathrm{-35.004 = E_a(-2.22 \times 10^{-4})}$ $\mathrm{E_a = 2.25 \times 10^4\: J/mol\: or\: 159\: kJ/mol}$

The following statements are incorrect. What slight modifications would you make to them?

A catalyst speeds up a reaction but dues not take part in it.
A catalyst functions to effectively lower the activation energy of a reaction.
Catalysts do not go throught permenent change.
This only applies to homogeneous catalysts.

Name some of the similarities and differences between the catalytic activity of platinum metal and of an enzyme?

Similarities: Metal activity site

Differences: Platinum is a universal catalyst where as enzymes are specific.

What reaction conditions are required to produce a straight-line graph of reaction rate vs. enzyme concentration?

The catalyst took a different pathway in order to lower activation energy more effectively. Both graphs are accurate.

In the reaction $\ce{4A + 3B \rightarrow 2C + 3D}$ reaction $\ce{A}$ is found to disappear at a rate of 5.1 X 10 -5 Ms -1

$\mathrm{-\dfrac{1}{4} \left (\dfrac{-\Delta[A]}{\Delta t} \right ) = \dfrac{1}{4} (5.1 \times 10^{-5}\, Ms^{-1}) = 1.3 \times 10^{-5}\, Ms^{-1}}$
Rate of disappearance of $\ce{B}$ = reaction rate X coefficient of $\ce{B}$ $\mathrm{(1.3 \times 10^{-5}\,Ms^{-1})(3) = 3.9 \times 10^{-5}\, Ms^{-1}}$
Rate of formation of $\ce{C}$ = reaction rate X coefficient of $\ce{C}$ $\mathrm{(1.3 \times 10^{-5}\,Ms^{-1})(2) = 2.6 \times 10^{-5}\, Ms^{-1}}$

In the reaction $\ce{A \rightarrow B}$, $\ce{[A]}$ is found to be 0.750 M at $\mathrm{t = 61.2\, s}$ and 0.704 M at $\mathrm{t = 73.5\, s}$. Determine the average rate of the reaction during this time interval.

$\mathrm{-\dfrac{\Delta[A]}{\Delta t} = \dfrac{0.704\,M-0.750\,M}{61.2\,s-73.5\,s} = 3.7 \times 10^{-3}\, M s^{-1}}$

The initial rate of the reaction $\ce{A + B \rightarrow C + D}$ is determined for different initial conditions, with the results listed in the table:

What is the order of reaction with respect to $\ce{A}$ and $\ce{B}$?
What is the value of the rate constant $\ce{k}$?

The Rate of a Chemical Reaction

$\mathrm{Reaction\, 1 = 2.205 \times 10^{-4} = k \times [0.331]^m [0.203]^n}$ $\mathrm{Reaction\, 2 = 8.82 \times 10^{-4} = k \times [0.331]^m [0.406]^n}$ $\mathrm{Reaction\, 3 = 4.41 \times 10^{-4}= k \times [0.662]^m [0.203]^n}$ $\mathrm{Reaction\, 4 = 1.7 \times 10^{-3}= k \times [0.662]^m [406]^n}$

Order of Reaction with respect to B:

Find where $\ce{A}$ is constant and $\ce{B}$ changes (Reaction 1 and Reaction 2)
Divide: $\mathrm{\dfrac{Reaction\, 2}{Reaction\, 1} = \dfrac{8.82 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.331]^m [0.406]^n}{[0.331]^m[0.203]^n}}$ $\mathrm{\dfrac{Reaction\, 2}{Reaction\, 1}= 4 = 2^n \rightarrow n=2}$
Thus the reaction is second order with respect to $\ce{B}$.

Order of Reaction with respect to A:

Find where $\ce{B}$ is constant and $\ce{A}$ changes (Reaction 3 and Reaction 1)
Divide: $\mathrm{\dfrac{Reaction\, 3}{Reaction\, 1} = \dfrac{4.41 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.406]^m[0.662]^n}{[0.203]^m[0.662]^n}}$ $\mathrm{\dfrac{R3}{R1} = 2 = 2^m}$ $\mathrm{m = 1}$
Thus the reaction is first order with respect to $\ce{A}$
Reaction order = reaction order of A + reaction order of B = 3 rd order reaction

The following rates of reactions were obtained in three experiments with the reaction $\ce{2NO(g) + Cl2(g) \rightarrow 2NOCl(g)}$

What is the rate law for this reaction?

Order of Reaction with respect to [Cl 2 ] :

Find where $\ce{[NO]}$ is constant and $\ce{[Cl2]}$ changes (Reaction 1 and Reaction 2)
Divide: Reaction 2 by Reaction 1 $\mathrm{\dfrac{2.48 \times 10^{-5}}{1.24 \times 10^{-5}}= \dfrac{[0.145]^m[0.81]^n}{[0.145]^m[0.405]^n} \rightarrow 2 = 2^n}$
Thus $\ce{[Cl2]}$ is first order

Order of Reaction with respect to [NO]:

Find where $\ce{[Cl2]}$ is constant and $\ce{[NO]}$ changes (Reaction 1 and Reaction 3)
Divide: Reaction 3 by Reaction 1 $\mathrm{\dfrac{4.96 \times 10^{-5}}{1.24 \times 10^{-5}} = \dfrac{[0.29]^m [0.405]^n}{[0.145]^m[0.405]^n} \rightarrow 4=2^m}$
Thus $\ce{[NO]}$ is second order

$\mathrm{Rate\, Law = k[NO]^2[Cl_2]}$

The first-order reaction $\mathrm{A \rightarrow products}$ has $\mathrm{t_{1/2} = 300\, s}$

What percent of sample A remains unreacted 1000 s after the reaction starts?
What is the rate of reaction when $\mathrm{[A] = 0.25\,M}$
$\mathrm{\ln(\%\, unreacted) = -kt}$ $\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{300\,s} = 0.0023\, s^{-1}}$ $\mathrm{ln(\%\, unreacted) = -(0.0023\,s^{-1})(1000\,s) = -2.3}$ $\mathrm{e^{-2.3} = 0.1 \times 100\% = 10\%\, unreacted}$
$\mathrm{Rate = k[A]}$ $\mathrm{Rate = 0.0023\,s^{-1}[0.25\,M] = 5.74 \times 10^{-4}\, Ms^{-1}}$

The reaction $\mathrm{A \rightarrow products}$ is first order in $\ce{A}$

If 4.2g $\ce{A}$ decomposes for 45 minutes, the undecomposed $\ce{A}$ is measured to be 1.05g. What is the half-life, $\mathrm{t_{1/2}}$, of this reaction?
Starting with the same 4.2 g, what is the mass of undecomposed $\ce{A}$ after 75 minutes?
$\mathrm{(4.2\,g)\left (\dfrac{1}{4}\right ) = 1.05\,g \rightarrow 2}$ halflives have passed $\mathrm{\rightarrow \dfrac{45\, minutes}{2} = t_{1/2} = 22.5\, minutes}$
$\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}$ $\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{22.5\, minutes} = 0.0308\, min^{-1}}$ $\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0}= (-0.0308\, min^{-1})(75\, min) = -2.31}$ $\mathrm{[A]_t = [A]_0 e^{-2.31}}$ $\mathrm{[A]_t = (4.2\,g)(0.09926) = 0.417\, g\, A}$

In a first order reaction, 95% of the original amount of reactant decomposes in 122 minutes. What is the half-life of this reaction?

In order to determine the half-life of the first-order reaction, we first need to determine the rate constant, $\ce{k}$. $\mathrm{[Reactant]_t=0.05}$ if $\mathrm{[Reactant]_0=1.00}$ since only 5% of the original reactant remains after 122 minutes.

$\mathrm{\ln \dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{0.05}{1}=-2.996=-k(122\,min)}$

$\mathrm{k=\dfrac{-2.996}{-122\,min}=0.024555\,min^{-1}}$

$\mathrm{t_{1/2}=\dfrac{0.693}{k}=\dfrac{0.693}{0.024555\,min^{-1}}=28.2\,min}$

If a first order decomposition reaction has a half-life of 107 minutes, in what amount of time will the original reactant be ¼ of its original concentration?

In order to determine the amount of time for this decomposition reaction to occur, we must first determine the rate constant $\ce{k}$ by using the half-life.

$\mathrm{t_{1/2}=\dfrac{0.693}{k}}$

$\mathrm{k=\dfrac{0.693}{t_{1/2}}=\dfrac{0.693}{107\,min}=0.00648\,min^{-1}}$

$\mathrm{\ln\dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{0.25}{1}=-1.386=-0.00648\,min^{-1}t}$

$\mathrm{t=\dfrac{-1.386}{-0.00648\,min^{-1}}=214\,min}$

Using Table A , determine whether each set is zero-order, first-order, or third-order.

Data set I must be second-order because $\mathrm{\dfrac{1}{[Reactant]_t}-\dfrac{1}{[Reactant]_0}=kt}$. For the first 40s in set I, $\mathrm{\dfrac{1}{2.00\,M}-\dfrac{1}{4.00\,M}=0.25\,L\,mol^{-1}=k(40\,s)}$, $\mathrm{k=0.00625\,L\,mol^{-1}\,s^{-1}}$. For the first 80s in set I, $\mathrm{\dfrac{1}{1.33\,M}-\dfrac{1}{4.00\,M}=0.5\,L\,mol^{-1}=k(80\,s)}$, $\mathrm{k=0.00625\,L\,mol^{-1}\,s^{-1}}$. Since both give the same rate constant, $\ce{k}$, using the second-order kinetics equation, set I must be a second-order reaction.
Data set II must be first-order because the half-life is constant. The first half-life is approximately 40s because the reactant concentration goes from 4.00M to 2.01M (about half). The second half-life is also 40s because the reactant concentration goes from 2.01M to 0.99M (about half) from 40s to 80s.
Data set II must be zero-order because it is decomposing at a constant rate. Every single ten seconds, the reactant concentration decreases by another 1M.

With the information given in Table A , are you able to find the half-life of the first-order reaction? If so, give t 1 /2 .

Yes, we can determine the half-life of the first-order reaction of data set II.

$\mathrm{\ln\dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{2.01}{4.00}=-k(40\,s)}$ , $\mathrm{k=0.0172\,s^{-1}}$

$\mathrm{t_{1/2}=\dfrac{0.693}{k}=\dfrac{0.693}{0.0172\,s^{-1}}=40.3\,s}$

The reaction $\ce{W + X \rightarrow Y + Z}$ is zero order in $\ce{X}$ and second order in $\ce{W}$. The rate constant, $\ce{k}$, is found to be 0.0115 M -1 min -1 . What is the rate of the reaction when $\mathrm{[W]=0.095\,M}$ and $\mathrm{[X]=2.67\,M}$?

Using the rate equation, $\mathrm{Rate=k[W]^2[X]^0=(0.0115\,M^{-1}min^{-1})(0.095\,M)^2(2.67\,M)^0=0.00109\,M/min}$ .

A decomposition reaction is observed at constant temperature for 800s, and the following data is recorded: at $\ce{t=0}$, $\mathrm{[Reactant]=2.00\,M}$; at $\ce{t=200\,s}$, $\mathrm{[Reactant]=1.80\,M}$; at $\ce{t=400\,s}$, $\mathrm{[Reactant]=1.62\,M}$; at $\ce{t=600\,s}$, $\mathrm{[Reactant]=1.48\,M}$; at $\ce{t=800\,s}$, $\mathrm{[Reactant]=1.36\,M}$. Please provide the reaction order, rate constant, and the rate law for this reaction at this temperature.

This reaction is of second-order because a plot of $\ce{\dfrac{1}{[Reactant]}}$ vs. $\ce{t}$ gives a straight line.

The rate constant, $\ce{k}$, is given by the slope of this straight line.

$\mathrm{k\approx \dfrac{0.617\,M^{-1}-0.500\,M^{-1}}{400\,s-0\,s}\approx 2.925E\,\textrm{-4}M^{-1}s^{-1}}$ .

$\mathrm{Rate=k[Reactant]^2}$ .

For a certain decomposition reaction, the following observations have been made: at $\mathrm{t=0\,s}$, $\mathrm{[Reactant]=1.43\,M}$; at $\mathrm{t=44\,s}$, $\mathrm{[Reactant]=1.21\,M}$; at $\mathrm{t=148\,s}$, $\mathrm{[Reactant]=0.69\,M}$; and at $\mathrm{t=264\,s}$, $\mathrm{[Reactant]=0.11\,M}$. Determine the order and half-life of this reaction.

This reaction is of zero-order because a plot of $\mathrm{[Reactant]}$ vs. $\ce{t}$ gives a straight line.

$\mathrm{k=\dfrac{0.69\,M-1.43\,M}{148\,s-0\,s}=-0.00500\,M/s}$ .

$\mathrm{[Reactant]_t=\dfrac{[Reactant]_0}{2}=\dfrac{1.43\,M}{2}=0.715\,M}$

$\mathrm{t_{1/2}=\dfrac{0.715\,M}{0.00500\,M/s}=143\,s}$ .

Does the half-life of a reaction get longer or shorter as initial reactant concentration increases and why? Please answer for a) zero-order reactions b) second-order reactions.

$\mathrm{t_{1/2}=\dfrac{[Reactant]_0}{2k}}$ In a zero-order reaction, half-life is proportional to initial reactant concentration, so the half-life of a zero-order reaction would get longer if the initial reactant concentration increased.
$\mathrm{t_{1/2}=\dfrac{1}{k[Reactant]_0}}$ In a second-order reaction, half-life is inversely proportional to initial reactant concentration, so the half-life of a second-order reaction would get shorter if the initial reactant concentration increased.

Answer the following:

What two factors does the rate of a reaction depend on other than the frequency of collisions?
Why does the rate of reaction increase dramatically with temperature?
What is the net effect of the addition of a catalyst?
1) Whether or not the collisions occurring have enough energy to get over the activation energy and become products. 2) Whether or not the molecules involved in the collisions are situated properly for the reaction to occur.
Collision frequency does not increase dramatically with temperature; however, the percentage of molecules with enough energy to get over the activation energy and become products does.
The net effect of the addition of a catalyst is the decreasing of the energy barrier to products. The catalyst does so by enabling an alternative mechanism with a lower activation energy.

For a reversible reaction, the enthalpy change of the forward reaction is 37kJ/mol, and the activation energy of the forward reaction is 96kJ/mol.

With the information provided, are you able to determine the activation energy of the reverse reaction? If so, please determine it.
Provide a sketch of the potential energy vs. progress of reaction.
Yes we are able to determine the activation energy of the reverse reaction. Because the enthalpy change of the forward reaction is 37kJ/mol, the products are 37kJ/mol closer to the transition state than the reactants. The activation energy for the reverse reaction is $\mathrm{96\,kJ/mol-37\,kJ/mol=59\,kJ/mol}$.
$\mathrm{\Delta H=+37\,kJ}$ $\mathrm{E_a(forward)=96\,kJ}$ $\mathrm{E_a(reverse)=59\,kJ}$

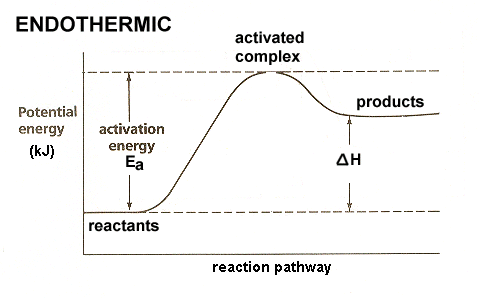
Given the following graph:

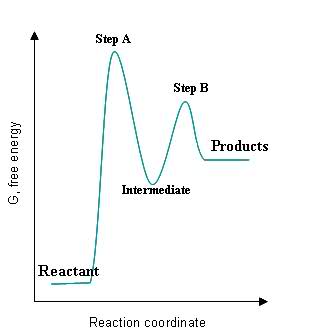
Please answer the following,

How can you tell where the intermediate is on the graph?
How can you tell where the transition state(s) is/are on the graph?
How can you tell where the fastest step of the reaction is on the graph?
How can you tell which step has the smallest rate constant?
How can you tell whether the steps of the reaction are exothermic or endothermic?
How can you tell whether the entire reaction is exothermic and endothermic?
The intermediate is a local minimum and must be brought back up to a transition state before becoming the final product(s).
The transition states, labeled Step A and Step B, are local maxima of the graph because they have reached the activation energy state needed to become intermediates/products.
The fastest step of the reaction is the one with the smallest activation energy, which in this case would be Step B because the energy gap between the intermediate and the Step B transition step is much smaller than the gap between the original reactant and the Step A transition state.
The smallest rate constant would correspond to the slowest reaction, which would correspond to the largest activation energy. In this case, Step A would have the smallest rate constant.
The steps are exothermic if their intermediates/products are lower in energy than their reactants, and the steps are endothermic if their intermediates/products are higher in energy than their reactants. Step A and Step B are endothermic because their intermediates/products are higher in energy than their reactants.
The overall reaction is exothermic if the initial reactant is higher in energy than the final products, and it is endothermic if the initial reactant is lower in energy than the final products. This reaction is endothermic because the reactant is lower in energy than the final products.

The following observations of a reaction’s rate constant have been made: at $\mathrm{T=325\,K}$, $\mathrm{k=3.2E\,\textrm{-6}M^{-1}s^{-1}}$; at $\mathrm{T=456\,K}$, $\mathrm{k=2.8E\,\textrm{-5}M^{-1}s^{-1}}$. What is the activation energy of this reaction?

$\mathrm{\ln\dfrac{k_1}{k_2}=\dfrac{E_a}{R}\left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)=\ln\dfrac{3.2E-6M^{-1}s^{-1}}{2.8E-5M^{-1}s^{-1}}=\dfrac{E_a}{8.3145\,J\,mol^{-1}K^{-1}}\left(\dfrac{1}{456\,K}-\dfrac{1}{325\,K} \right)}$

$\mathrm{-2.2=-1.06\,mol\,J^{-1}(E_a)}$ , $\mathrm{E_a=2.1E4\,J\,mol^{-1}}$

Do catalysts take part in the reaction they catalyze? Do catalysts always speed up a reaction? Explain.
What is the function of a catalyst?
No, catalysts do not take part in the reactions they catalyze. No, catalysts do not always speed up a reaction; some negative catalysts, called inhibitors, can slow down the rate of a reaction.
Catalysts main function is to provide an alternative pathway for a reaction. By changing the mechanism for a reaction, a catalyst provides a pathway with a lower activation energy, resulting in a faster reaction.

Please answer the following about the catalytic activity of both platinum metal and enzymes:

Where are there active sites?
Are they heterogeneous or homogeneous?
Are they specific or nonspecific?
The active site of platinum and of enzymes are at a metal center.
Enzymes are usually homogeneous, meaning they are soluble in the reactant; platinum, however, is heterogeneous, meaning it cannot be dissolved in the reactant.
Enzymes are extremely specific to their substrates, while platinum is usually more nonspecific.

What reaction conditions are necessary to produce a straight-line graph of reaction rate vs. enzyme concentration?

An excess of reactant (substrate) must be available.

The following reaction, $\mathrm{2W+2X \rightarrow Y+Z}$, consists of a three-step mechanism. The first step is fast, and is as follows: $\mathrm{W+W \leftrightarrow A}$. The third step is fast as well, and is as follows: $\mathrm{B+X \rightarrow Z}$. Comprise a three-step mechanism that conforms to $\ce{W}$ being of second order and $\ce{X}$ being of first order.

The first criterion for the reaction mechanism is that it must add up to produce the overall reaction $\mathrm{2W+2X \rightarrow Y+Z}$. We already have two of the three steps of the mechanism, so in order to find the second step, all we need to do is subtract the first and third steps from the overall reaction.

Overall Reaction: $\mathrm{2W+2X \rightarrow Y+Z}$

-First Step: $\mathrm{-(W+W \leftrightarrow A)}$

-Third Step: $\mathrm{-(B+X \rightarrow Z)}$

____________________

$\mathrm{X+A \leftrightarrow Y+B}$ for the second step.

$\mathrm{r_2=k_2[X][A]}$

$\mathrm{r_f=k_f[W]^2}$

$\mathrm{r_r=k_r[A]}$

At equilibrium, rate forward=rate reverse so,

$\mathrm{k_f[W]^2=k_r[A]}$

$\mathrm{[A]=\dfrac{k_f}{k_r}[W]^2}$

$\mathrm{r=k_2\dfrac{k_f}{k_r}[W]^2[X]}$ ; $\mathrm{k= k_2\dfrac{k_f}{k_r}}$

Rate Law: $\mathrm{r=k[W]^2[X]}$, which conforms to $\ce{W}$ being of second order and $\ce{X}$ being of first order.

Find an expression to describe the units of rate constant, $\ce{k}$, for a reaction in terms of order of the reaction ($\ce{n}$) , concentration ($\ce{M}$), and time ($\ce{s}$). Then use this expression to find the units of the rate constant, $\ce{k}$, for a zero, first, and second order reaction.

The rate equation is $\mathrm{rate=k[Reactant]_n}$. Rate has the units of M/s, $\mathrm{[Reactant]}$ has the units of M, so when substituting in units for the rate equation you get, $\mathrm{M/s=(units\: of\: k)M_n}$. By rearranging this equation you get, $\mathrm{(units\: of\: k)=\dfrac{Ms^{-1}}{M_n}=M_{1-n}s^{-1}}$.

When $\mathrm{n=0}$,

$\mathrm{(units\: of\: k)=M_{1-0}s^{-1}=M/s}$

When $\mathrm{n=1}$,

$\mathrm{(units\: of\: k)=M_{1-1}s^{-1}=s^{-1}}$

When $\mathrm{n=2}$,

$\mathrm{(units\: of\: k)=M_{1-2}s^{-1}=M^{-1}s^{-1}}$

The overall reaction $\ce{H2 + Br2 \rightarrow 2HBr}$ occurs in the following three step mechanism:

$\mathrm{Br_2 \overset{k_1}{\underset{k_{-1}}{\longleftrightarrow}} 2Br\: (forward\: and\: reverse\: reactions\: are\: fast)}$
$\mathrm{ Br+H_2 \xrightarrow{k_2} HBr+H\:(slow)}$
$\mathrm{H+Br_2 \xrightarrow{k_3} HBr+Br \:(fast)}$

$\mathrm{k_1=5.7E4}$ ; $\mathrm{k_{-1}=4.5E4}$ ; $\mathrm{k_2=2.7E\,\textrm{-1}}$ ; $\mathrm{k_3=1.6E3}$. What is the rate constant, $\ce{k}$, and the rate law for the entire reaction?

Because step ii is the slow step, it is the rate determining step and the rate law should be derived according to it.

$\mathrm{\dfrac{1}{2}\left (\dfrac{d[HBr]}{dt} \right )=k_2[Br][H_2]}$

The ½ coefficient is needed to account for the two $\ce{HBr}$ being made. $\ce{[Br]}$ is an intermediate, so its rate of formation must equal its rate of decomposition:

$\mathrm{k_1[Br_2]=k_{-1}[Br]^2}$, $\mathrm{[Br]=\dfrac{k_1}{k_{-1}}[Br_2]^{1/2}}$

We can now replace $\ce{[Br]}$ in the original rate law expression, giving:

$\mathrm{Rate=k_2\left(\dfrac{k_1}{k_{-1}}\right)^{1/2}[H_2][Br_2]^{1/2}}$

Meaning $\mathrm{k= k_2 \left(\dfrac{k_1}{k_{-1}}\right)^{1/2}=(2.7E-1)\left(\dfrac{5.7E4}{4.5E4}\right)^{1/2}=0.30}$

Serving Quality Education

Case Study Question 1 on Chemical Kinetics – Chapter 4 CBSE Class 12 Chemistry

April 6, 2022
Chemistry , CBSE , Class 12

Case Study Question 1 on Chemical Kinetics – Chapter 4

Read the given passages and answer the questions that follow..

Question. The rate of a chemical reaction is expressed either in terms of decrease in the concentration of a reactant per unit time or increase in the concentration of a product per unit time. Rate of the reaction depends upon the nature of reactants, concentration of reactants, temperature, presence of catalyst, surface area of the reactants and presence of light. Rate of reaction is directly related to the concentration of reactant. Rate law states that the rate of reaction depends upon the concentration terms on which the rate of reaction actually depends, as observed experimentally. The sum of powers of the concentration of the reactants in the rate law expression is called order of reaction while the number of reacting species taking part in an elementary reaction which must collide simultaneously in order to bring about a chemical reaction is called molecularity of the reaction.

1. Express the rate of the following reaction in terms of different reactants and products.

4NH 3 (g) + 5O 2 (g) —–> 4NO 2 (g) + 6H 2 O(g)

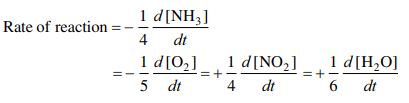
2. Why do pieces of wood burn faster than a log of wood of the same mass?

Ans. Pieces of wood have larger surface area than the log of wood of the same mass. Greater the surface area, faster is the reaction.

3. Why does the rate of any reaction generally decrease during the course of the reaction?

Ans. The rate of reaction depends on the concentration of reactants. As the reaction progresses, reactants start getting converted to products so the concentration of reactants decreases hence the rate of reaction decreases.

4. Why is molecularity applicable only for elementary reactions and order is applicable for elementary as well as complex reactions?

Ans. A complex reaction proceeds through several elementary reactions. Number of molecules involved in each elementary reaction may be different, i.e., the molecularity of each step may be different. Therefore, discussion of the molecularity of overall complex reaction is meaningless. On the other hand, order of a complex reaction is determined by the slowest step in its mechanism and is not meaningless even in the case of complex reactions.

5. The kinetics of the reaction

mA + nB + pC —–> m′X + n′Y + p′Z

obey the rate expression dx/dt = k[A] m [B] n

Calculate total order and molecularity of the reaction.

Ans. The total order of reaction = m + n

The molecularity of the reaction = m + n + p

Ncert solutions class 11 maths chapter 9 exercise 9.2 straight lines.

January 13, 2024

Handwritten Notes of Chapter 2, Physics, Electrical Potential and Capacitance

August 20, 2023

EMF, Chapter 6, Worksheet- 1 (2023-24)

July 9, 2023

Class 12 Chemistry Case Study Questions PDF Download

Post author: studyrate
Post published:
Post category: Class 12 / 12 board
Post comments: 0 Comments

Looking for Class 12 Chemistry Case Study Based Questions in PDF format? This comprehensive article provides expert insights, engaging content, and answers to frequently asked questions to help you excel in your studies. Download the PDF now and boost your chemistry knowledge!

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

You need to improve your preparation for the Class 12 Chemistry Case Study Questions exams if you want to achieve a 95+% on the boards. You may find case study questions from every chapter that will be covered in the CBSE Class 12 Chemistry Board Exams in this post.

Table of Contents

Case Study-Based Questions for Class 12 Chemistry

Welcome to the world of Class 12 Chemistry Case Study Questions! As a student pursuing Chemistry in the 12th grade, you have already shown dedication and commitment to the subject. However, dealing with case study-based questions can be both intriguing and challenging. In this article, we will explore the nuances of such questions and offer valuable guidance to excel in your exams.

Class 12 Physics Case Study Questions Class 12 Chemistry Case Study Questions Class 12 Biology Case Study Questions Class 12 Maths Case Study Questions

Importance of Class 12 Chemistry Case Study-Based Questions

Class 12 Chemistry case study-based questions play a vital role in your overall understanding of the subject. They enable you to:

Apply Theoretical Knowledge : Case studies allow you to apply the concepts you have learned in real-life situations, bridging the gap between theory and practical application.
Develop Analytical Skills : By critically analyzing case scenarios, you enhance your analytical abilities, which are essential in various professional fields.
Enhance Problem-Solving Abilities : Tackling case study-based questions hones your problem-solving skills, preparing you to face challenges with confidence.
Gain Deeper Insights : Exploring different case studies exposes you to a wide range of chemical reactions and phenomena, broadening your understanding of Chemistry.

Tips to Excel in Class 12 Chemistry Case Study Questions

Thoroughly Understand the Concepts: Before attempting case study questions, ensure you have a strong grasp of the underlying concepts and theories.
Analyze the Scenario Carefully: Take your time to read and comprehend the given case study. Pay attention to every detail to identify the key points.
Relate to Real-Life Scenarios: Try to connect the case study with real-life situations, as this will make the problem-solving process more intuitive.
Practice Regularly: Practice a wide variety of case study questions to familiarize yourself with different scenarios and improve your problem-solving skills.
Collaborate with Peers: Engage in group discussions and brainstorming sessions with your peers. This will provide diverse perspectives and enhance your critical thinking.

Best Books for Class 12 Chemistry

Strictly in accordance with the new term-by-term curriculum for the Class 12 Chemistry Case Study Questions exams to be held in the academic session 2024, including the new board-introduced multiple-choice question types, Stand-Alone MCQs, and MCQs based on Assertion-Reason Case-based MCQs. Included are inquiries from the official CBSE Question Bank that was released in April 2024. What changes have been made to the book: strictly in accordance with the term-by-term syllabus for the board exams that will be held during the 2024 academic year? Chapter- and topic-specific multiple-choice questions based on the unique assessment plan for the Class 12 Chemistry Case Study Questions Board Examination.

Chemistry Syllabus for 2024

Unit II: Solutions (15 Periods)

Types of solutions, expression of concentration of solutions of solids in liquids, solubility of gases in liquids, solid solutions, Raoult’s law, colligative properties – relative lowering of vapour pressure, elevation of boiling point, depression of freezing point, osmotic pressure, determination of molecular masses using colligative properties, abnormal molecular mass, Van’t Hoff factor.

Unit III: Electrochemistry (18 Periods)

Redox reactions, EMF of a cell, standard electrode potential, Nernst equation and its application to chemical cells, Relation between Gibbs energy change and EMF of a cell, conductance in electrolytic solutions, specific and molar conductivity, variations of conductivity with concentration, Kohlrausch’s Law, electrolysis and law of electrolysis (elementary idea), dry cell-electrolytic cells and Galvanic cells, lead accumulator, fuel cells, corrosion.

Unit IV: Chemical Kinetics (15 Periods)

Unit VIII: d and f Block Elements (18 Periods)

Lanthanoids – Electronic configuration, oxidation states, chemical reactivity and lanthanoid contraction and its consequences.

Actinoids – Electronic configuration, oxidation states and comparison with lanthanoids.

Unit IX: Coordination Compounds (18 Periods)

Coordination compounds – Introduction, ligands, coordination number, colour, magnetic properties and shapes, IUPAC nomenclature of mononuclear coordination compounds. Bonding, Werner’s theory, VBT, and CFT; structure and stereoisomerism, the importance of coordination compounds (in qualitative analysis, extraction of metals and biological system).

Unit X: Haloalkanes and Haloarenes (15 Periods)

Haloalkanes: Nomenclature, nature of C–X bond, physical and chemical properties, optical rotation mechanism of substitution reactions.

Haloarenes: Nature of C–X bond, substitution reactions (Directive influence of halogen in monosubstituted compounds only). Uses and environmental effects of – dichloromethane, trichloromethane, tetrachloromethane, iodoform, freons, DDT.

Unit XI: Alcohols, Phenols and Ethers (14 Periods)

Phenols: Nomenclature, methods of preparation, physical and chemical properties, acidic nature of phenol, electrophilic substitution reactions, uses of phenols.

Ethers: Nomenclature, methods of preparation, physical and chemical properties, uses.

Unit XII: Aldehydes, Ketones and Carboxylic Acids (15 Periods)

Carboxylic Acids: Nomenclature, acidic nature, methods of preparation, physical and chemical properties; uses.

Unit XIII: Amines (14 Periods)

Amines: Nomenclature, classification, structure, methods of preparation, physical and chemical properties, uses, identification of primary, secondary and tertiary amines

Diazonium salts: Preparation, chemical reactions and importance in synthetic organic chemistry.

Unit XIV: Biomolecules (18 Periods)

Carbohydrates – Classification (aldoses and ketoses), monosaccharides (glucose and fructose), D-L configuration oligosaccharides (sucrose, lactose, maltose), polysaccharides (starch, cellulose, glycogen); Importance of carbohydrates.

Proteins – Elementary idea of – amino acids, peptide bond, polypeptides, proteins, structure of proteins – primary, secondary, tertiary structure and quaternary structures (qualitative idea only), denaturation of proteins; enzymes.

Hormones – Elementary idea excluding structure.

Vitamins – Classification and functions.

Nucleic Acids: DNA and RNA.

FAQ on Class 12 Chemistry Case Study Questions

Q: can i rely solely on class 12 chemistry case study based questions exam preparation.

Yes, case study-based questions are an essential part of your preparation. However, it is advisable to supplement them with other study materials and revision of theoretical concepts for comprehensive preparation.

Q: How often should I practice Class 12 Chemistry Case Study Based Questions?

Frequent practice is crucial for mastering case study-based questions. Set aside dedicated practice sessions and gradually increase the difficulty level of the questions.

Q: Can I discuss case study questions with my teachers?

Absolutely! Engaging with your teachers regarding case study questions will provide valuable insights and clarifications.

Class 12 physics case study questions chapter 8 electromagnetic waves, class 12 physics case study questions chapter 10 wave optics, mcq class 12 english the third level questions with answers english chapter 1, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

Contains the Latest NCERT in just 350 flashcards.
Colourful and Interactive
Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

Chemistry Concept Questions and Answers

Chemical Kinetics Questions

Modern chemical (reaction) kinetics is a branch of science that studies and describes chemical reactions as we know them now. It is the study of the rate of chemical reactions or the transformations of reactants into products that take place according to a specific mechanism, i.e. the reaction mechanism.

Kinetic studies are useful for comprehending reactions and have practical applications. In industry, for example, reactions are carried out in reactors, where compounds are mixed together, perhaps heated and stirred for a short time, and then transferred on to the next stage of the process. It’s critical to know how long to hold a reaction at one stage before moving on to the next, in order to ensure that the previous reaction has been completed before moving on to the next.

Chemical Kinetics Chemistry Questions with Solutions

Q1: Define Reaction Rate.

The reaction rate is determined by how rapidly the products are created and the reactants are consumed. It is usual to deal with substance concentrations in chemical systems, which are defined as the amount of substance per unit volume. The concentration of a material consumed or produced in unit time can thus be described as the rate. It’s sometimes easier to express rates as the number of molecules generated or consumed per unit of time.

Q2: What is meant by the Half-Life?

The half-life of a reactant, which is defined as the time it takes for half of the initial amount to undergo reaction, is a useful rate metric. The half-life is independent of the initial amount for a certain form of kinetic behaviour (first-order kinetics).

Radioactive substances are a simple and typical example of a half-life that is independent of the initial amount. Uranium-238, for example, has a half-life of 4.5 billion years, meaning that half of an initial amount of uranium will have decayed in that time. Many chemical reactions exhibit the same behaviour.

Q3: Write the rate equation for the reaction 2A + B → C if the order of the reaction is zero.

The rate equation for the reaction 2A + B → C in the zero order reaction is,

Rate = k [A] 0 [B] 0 = k.

Q4: Although the reaction between H 2 (g) and O 2 (g) is highly feasible, leaving the gases in the same vessel at room temperature does not result in the creation of water. Explain.

Although the reaction between H 2 (g) and O 2 (g) is very feasible, leaving the gases to remain at room temperature in the same vessel does not result in the creation of water because the reactants’ activation energy is very high at room temperature and not readily available.

Q5: Match the statements given in Column I and Column II

a) – (iii); (b) – (i); (c) – (iv); (d) – (vi); (e) – (ii); (f) – (v)

Q6: Match the items of Column I and Column II.

(a) – (ii); (b) – (i); (c) – (iv); (d) – (iii)

Q7: Define each of the following:

i) Specific rate of a reaction

ii) Activation energy of a reaction

i) Specific rate of a reaction : When the molar concentration of each of the reactants is equal, the rate of reaction is called the specific rate of reaction.

ii) Activation energy of a reaction : The activation energy is the minimum extra amount of energy absorbed by the reactant molecules in need of their energy to equal the threshold value. The addition of a catalyst reduces the reaction’s activation energy.

Q8: Which among the following is a false statement?

(i) Rate of zero order reaction is independent of initial concentration of reactant.

(ii) Half-life of a third order reaction is inversely proportional to the square of initial concentration of the reactant.

(iii) Molecularity of a reaction may be zero or fraction.

(iv) For a first order reaction, t 1/2 = 0.693/K

Answer: (iii) Molecularity of a reaction may be zero or fraction.

Q9: The average rate and instantaneous rate of a reaction are equal

(i) at the start

(ii) at the end

(iii) in the middle

(iv) when two rates have a time interval equal to zero

Answer: (iv) when two rates have a time interval equal to zero

Q10: For a chemical reaction A→B, it is found that the rate of reaction doubles when the concentration of A is increased four times. The order of the reaction is

Answer: (iv) Half

Q11: Differentiate between the Order and Molecularity of a reaction.

Q12: With the help of an example explain what is meant by pseudo first order reaction.

Consider the reaction of ethyl acetate hydrolysis, which can be expressed as

CH 3 COOC 2 H 5 + H 2 O → CH 3 COOH + C 2 H 5 OH

The rate equation can be given as Rate = k [CH 3 COOC 2 H 5 ] [H 2 O]

The concentration of water is relatively high in this case and consequently does not change much during the process. As a result, the rate of the reaction is independent of the change in H 2 O concentration. We might write the effective rate equation as if the term for a change in water concentration in the above reaction is set to zero.

Rate = k [CH 3 COOC 2 H 5 ]

The term here takes into account the value of the water’s constant concentration.

where K = K’ [H 2 O]

The reaction is a first-order reaction, as we can see. These reactions are termed pseudo-first-order reactions .

Q13: What is the use of the integrated rate equation?

Uses of integrated rate equation are as follows:

(i) When the concentration of a reactant at different intervals is known, the value of the rate constant can be calculated.

(ii) The knowledge of reaction concentration at different intervals can be used to establish the order of a reaction.

Q14: How does collision theory explain the formation of products in a chemical reaction?

The reactant molecules are considered to be hard spheres in Collision Theory, and the reaction occurs when these molecules collide. The production of a product is induced by collisions between molecules with sufficient kinetic energy (called threshold energy) and proper orientation. The conditions for effective collision, and hence the rate of a reaction, are determined by the activation energy and proper orientation of the molecules.

Q15: The time required to decompose SO 2 Cl 2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.

We know that for a 1st order reaction,

It is already given that t 1/2 = 60mins

= 0.693/60 = 0.01155 min -1 = 1.155 min -1

Practise Questions on Chemical Kinetics

Q1: Mention the factors that affect the rate of a chemical reaction.

Q2: For a reaction, A + B → Product; the rate law is given by, R = k [A] 1/2 [B] 2 . What is the order of the reaction?

Q3: Define the following terms:

i) Pseudo first order reaction.

ii) Half-life period of reaction (t 1/2 ).

Q4: Distinguish between Rate Expression and Rate Constant of a reaction.

Q5: Write the Arrhenius equation.

Click the PDF to check the answers for Practice Questions. Download PDF

JEE Chemical Kinetics and Surface Chemistry | Target JEE | Solved Questions | JEE Chemistry

Concept of the Day: Initial Rate Method | CHEMISTRY | JEE 2021/2022 l Basir Sir | BYJU’S JEE

Applying Concepts: Collision Theory- States of Matter | Chemistry | JEE

Concept of the Day: Zero Order Reaction | CHEMISTRY | JEE 2021/2022 l Basir Sir | BYJU’S JEE

Register with BYJU'S & Download Free PDFs

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam
STATE WISE BOOKS
ENGINEERING EXAM
SCHOLARSHIP OLYMPIAD
STATE BOOKS

CBSE Board Class 12 Chemistry Case Based Questions With Solutions

CBSE Board Class 12 Chemistry Case Based Questions With Solutions to prepare for the upcoming term 1 board exams are given here. It is extremely helpful since the expert team has crafted this by following the Syllabus of class 12th. Case study questions are also known as passage based problems because it includes the paragraph from which 5 or more problems are curated.

To solve these types of problems students need to have a thorough understanding of all the basics and fundamental concepts. Also, a student who is good in problem solving skills can easily answer such questions.

Those who are preparing for their CBSE Class 12 board exam term 1 can use it to practice the questions on a daily basis. Also, the experts have given step by step solutions to all those problems so that students can cope up with the given problem very easily.

CBSE Class 12 Chemistry Case Based Questions, Assertion & Reason, MCQs

CBSE Class 12 Chemistry includes many chemical reactions, chemical bondings, theories, experiments, discoveries, etc. All of these types of things should be well versed by the students to answer the Case study, Multiple Choice Questions, Assertion and Reason. So, practicing the given CBSE Class 12 Chemistry Case Study PDF will be very handy in boosting the basic knowledge and preparing for the final papers.

We have provided the complete set of PDFs so that candidates can prepare for the board examination very easily. Before attempting the given PDF candidates are suggested here to complete their syllabus for the term 1 exam. Doing so will aid in self-assessment and give a sense of board exam preparation.

Class 12 Chemistry Case Study Questions For Term 1 Exam

Class 12 Chemistry Case Study Questions for Term 1 exam includes The Solid State, The P block elements, Haloalkanes and Haloarenes, Biomolecules, etc. Questions for all these chapters are given in the PDF file that are available here for free to download.

Term 1 exam is about to be held in November-December this year. So, students should start their board exam preparation early. For that purpose we have provided the complete chapter wise case based questions, assertion and reason and a lot of Objective type problems for the practice purposes.

CBSE 12 Case Based Question With Answers

CBSE Case Based Questions with Answers are designed and developed for the term 1 exam which is developed by the subject matter experts. The answers are provided to help the learners to solve the problem if they are stuck at some questions and don’t know how to tackle that.

Not only answers are given but step by step explanations are given too. By taking help of those explanations students can easily get a good grasp over the concepts.

To Download case study based questions class 12 chemistry PDF visit here or download from Selfstudys.com.

To solve Class 12 Chemistry Assertion and Reason Questions read the given statement and then reason. Now, you need to verify both the assertion and reason. If both are given correctly then you have to check whether the given reason supports the statement or not.

CBSE Class 12 Marks Verification Window Last Date Today: Apply Soon, Direct Link Here

CBSE Class 12 Result 2024: Application for Verification of Marks Starts; Last Date 21st May – Check Complete Process

CBSE Class 12 Result 2024 Latest Update : Verification of Marks, Revaluation & Photocopy of Answer Sheet; Check Complete Process

CBSE Class 12th Result 2024 Out : Supplementary, Re-verification & Re-evaluation Date Released; Check Details Here

CBSE 12th Toppers List 2024: Check Toppers Name, Marks, Pass Percentage, Merit List, District & Result Full Statistics

CBSE 12th Results 2024 Out : CBSE 12th Result Declared; Check Scorecard Here from Direct Link

LPU University Admissions 2023 upto 100% Scholarship (All Pages)

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 12 Chemistry Chapter 4 - Chemical Kinetics 2024-25

Crucial Practice Problems for CBSE Class 12 Chemistry Chapter 4: Chemical Kinetics

Free PDF download of Important Questions for CBSE Class 12 Chemistry Chapter 4 - Chemical Kinetics prepared by expert Chemistry teachers from latest edition of CBSE(NCERT) books . Register online for Chemistry tuition on Vedantu.com to score more marks in CBSE board examination .

Download CBSE Class 12 Chemistry Important Questions 2024-25 PDF

Also, check CBSE Class 12 Chemistry Important Questions for other chapters:

Related Chapters

Boost Your Performance in CBSE Class 12 Chemistry Exam Chapter 4 with Important Questions

1. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds .

Ans: $\text{ Average rate of reaction }=-\dfrac{\Delta\text{R}}{\Delta \text{t}}$

$-\dfrac{{{{[{\text{R}}]}_2} - {{[{\text{R}}]}_1}}}{{{{\text{t}}_2} - {{\text{t}}_1}}}$

$ \Rightarrow - \dfrac{{0.02 - 0.03}}{{25}}{\text{}} = 4 \times {10^{ - 4}}{\text{Mmi}}{{\text{n}}^{- 1}}$

Also, it can be expressed in seconds as:

${\text{ Average rate of reaction }} = \dfrac{{4 \times {{10}^{ - 4}}}}{{60}}\; = 6.67 \times {10^{ - 6}}\;\;$

2. In a reaction, \[2A \to \] Products, the concentration of A decreases from \[{\text{0}}{\text{.5 mol }}{{\text{L}}^{{\text{ - 1}}}}\] to \[{\text{0}}{\text{.4 mol }}{{\text{L}}^{{\text{ - 1}}}}\] in 10 minutes. Calculate the rate during this interval .

Average rate = \[\dfrac{1}{2}\dfrac{{\Delta \left[ A \right]}}{{\Delta t}}\]

\[\dfrac{1}{2}\dfrac{{{{\left[ A \right]}_2} - {{\left[ A \right]}_1}}}{{{t_2} - {t_1}}}\]

= \[\dfrac{{\text{1}}}{{\text{2}}}{{ \times }}\dfrac{{{\text{0}}{\text{.4 - 0}}{\text{.5}}}}{{{\text{10}}}}\]

= $ \dfrac{\text{1}}{\text{2}}\times \dfrac{\text{1 - 0}\text{.1}}{\text{10}}$

${\text{0}}{\text{.005 mol }}{{\text{L}}^{{\text{ - 1}}}}$

$={5 \times 1}{{\text{0}}^{{\text{ - 3}}}}{\text{M mi}}{{\text{n}}^{{\text{ - 1}}}}$

3. For a reaction, \[{\text{A + B}} \to \] Product; the rate law is given by \[r{\text{ }} = {\text{ }}k{\left[ A \right]^{\dfrac{1}{2}}}{\left[ B \right]^2}\]. What is the order of the reaction ?

The order of the reaction = \[\dfrac{{\text{1}}}{{\text{2}}}{\text{ + 2 = 2}}\dfrac{{\text{1}}}{{\text{2}}}{\text{ = 2}}{\text{.5}}\]

4. The conversion of molecules X to Y follows second order kinetics. If concentration of x is increased to three times how will it affect the rate of formation of Y?

Because the reaction X Y has second-order kinetics, the rate law equation will be \[Rate{\text{ }} = {\text{ }}k{C^2}\] , with \[C{\text{ }} = {\text{ }}\left[ x \right]\] .

The rate law equation for the reaction X Y will be \[Rate{\text{ }} = {\text{ }}k{\text{ }}{C^2}\] , with \[C{\text{ }} = {\text{ }}\left[ x \right]\] because it possesses second-order kinetics. So, \[\left[ x \right] = 3C{\text{ mol }}{{\text{L}}^{{\text{ - 1}}}}\]

The rate equation is

\[Rate = K{(3C)^2}\]

= \[9(k{C^2})\]

As a result, the reaction rate will increase by 9 times.

As a result, the rate at which Y is formed will grow by 9 times.

5. A first order reaction has a rate constant \[{\text{1}}{.15 \times 1}{{\text{0}}^{{\text{ - 3}}}}{{\text{s}}^{{\text{ - 1}}}}\]. How long will \[5g\] this reactant takes to reduce to \[3g\]?

Initial amount = \[{\left[ {\text{R}} \right]_{\text{0}}}{\text{ = 5}}g\]

Final concentration = \[\left[ {\text{R}} \right]{\text{ = 3}}g\]

Rate constant = \[{\text{1}}{.15 \times 1}{{\text{0}}^{{\text{ - 3}}}}{{\text{s}}^{{\text{ - 1}}}}\]

For a first order reaction

\[t = \dfrac{{2.303}}{k}\log \dfrac{{{{\left[ R \right]}_0}}}{R}\]

\[ = \dfrac{{2.303}}{{1.15 \times {{10}^{ - 3}}}}\log \dfrac{5}{3}\]

\[ = \dfrac{{2.303}}{{1.15 \times {{10}^{ - 3}}}} \times 0.2219\]

= \[{\text{444}}{\text{.38 s}}\] or \[{\text{444 s}}\]

6. Time required to decompose \[{\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\] to half its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.

First order reaction

\[{t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k}\]

\[{t_{\dfrac{1}{2}}} = 60\min \]

\[k = \dfrac{{0.693}}{{{t_{\dfrac{1}{2}}}}}\]

\[ = \dfrac{{0.693}}{{60}}\]

\[ = 0.01155{\min ^{ - 1}}\]

\[ = 1.155{\min ^{ - 1}}\]

$k = {1.925 \times 10}^{{\text{ - 4}}}{{\text{s}}^{{\text{ - 1}}}}$

7. What will be the effect of temperature on rate constant?

A \[{10^0}\] increase in temperature almost doubles the rate constant of a process. The Arrhenius equation, on the other hand, gives the exact temperature dependency of the rate of a chemical reaction.

\[k = A{e^{ - Ea/RT}}\]

Where A stands for the Arrhenius factor, also known as the frequency factor.

T stands for temperature.

The gas constant is R.

The activation energy is referred to as \[{E_a}\] .

8. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate \[{E_a}\].

[{T_1} = 298{\text{K}}]

${T_2} = (298 + 10){\text{K}}$

We also know that when the temperature is raised by 10 degrees Celsius, the reaction rate doubles. As a result, we'll use the values \[{\text{k1 = k}}\] and \[{\text{k2 = 2k}}\] .

\[R = 8.314J{K^{ - 1}}mo{l^{ - 1}}\]

On substitution

\[\dfrac{{{k_2}}}{{{k_1}}} = \dfrac{{{E_a}}}{{2.303R}}\left[ {\dfrac{{{T_2} - {T_1}}}{{{T_1}{T_2}}}} \right]\]

\[\log \dfrac{{2k}}{k} = \dfrac{{{E_a}}}{{2.303 \times 8.314}}\left[ {\dfrac{{10}}{{298 \times 308}}} \right]\]

\[{E_a} = \dfrac{{2.303 \times 8.314 \times 298 \times 308 \times \log 2}}{{10}}\]

\[ = 52897.78{\text{ J mo}}{{\text{l}}^{{\text{ - 1}}}}\]

\[ = 52.89{\text{ kJ mo}}{{\text{l}}^{{\text{ - 1}}}}\]

9. The activation energy for the reaction \[{\text{2H}}{{\text{I}}_{(g)}} \to {{\text{H}}_{\text{2}}}{\text{ + }}{{\text{I}}_{2(g)}}\] is \[209.5{\text{ kJ mo}}{{\text{l}}^{{\text{ - 1}}}}\] at 581 k. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy.

${\text{}}{E_a} = 209.5{\text{k}}{{\text{J}}^{{\text{ - 1}}}} = 209500{\text{ J mo}}{{\text{l}}^{{\text{ - 1}}}}$

$T = 581{\text{K }}$

\[R = 8.314{\text{ J }}{{\text{k}}^{{\text{ - 1}}}}{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}\]

The percentage of reactant molecules with energy equal to or greater than activation energy is now:

\[x = {e^{Ea/RT}}\]

\[In = - {E_a}/RT{\text{ }}\]

\[\log x = - \dfrac{{{E_a}}}{{2.303RT}}{\text{ }}\]

\[\log x = \dfrac{{209500{\text{ J mo}}{{\text{l}}^{{\text{ - 1}}}}}}{{2.303 \times 8.314 \times {\text{J}}{{\text{k}}^{{\text{ - 1}}}}{\text{mo}}{{\text{l}}^{{\text{ - 1}}}} \times 581}} = 18.8323\]

\[x = Anti\log ( - 18.8323) = 1.47 \times {10^{ - 19}}\]

NCERT Exercise

1. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

A: \[{\text{3NO}}\left( g \right) \to {{\text{N}}_{\text{2}}}{\text{O}}\left( g \right)Rate{\text{ = k}}{\left[ {{\text{NO}}} \right]^{\text{2}}}\]

B: \[{{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}{\text{(}}aq{\text{) + 3I - (}}aq{\text{) + 2}}{{\text{H}}^{\text{ + }}} \to {\text{2}}{{\text{H}}_{\text{2}}}{\text{O(I) + }}{{\text{I}}_{{{\text{3}}^{\text{ - }}}}}Rate{\text{ = k}}\left[ {{{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}} \right]\left[ {{{\text{I}}^{\text{ - }}}} \right]\]

C: \[{\text{C}}{{\text{H}}_{\text{3}}}{\text{CHO(}}g{\text{)}} \to {\text{C}}{{\text{H}}_{\text{4}}}{\text{(}}g{\text{) + CO(}}g{\text{)}}Rate{\text{ = k}}{\left[ {{\text{C}}{{\text{H}}_{\text{3}}}{\text{CHO}}} \right]^{{\text{3/2}}}}\]

D: \[{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{Cl(}}g{\text{)}} \to {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(}}g{\text{) + HCl(}}g{\text{)}}Rate{\text{ = k}}\left[ {{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{Cl}}} \right]\]

Given

(i) . \[k = \dfrac{{Rate}}{{\left[ {{H_2}{O_2}} \right]\left[ {{I^ - }} \right]}}\]

Order of the reaction= 2

\[k = \dfrac{{Rate}}{{{{\left[ {NO} \right]}^2}}}\]

Therefore, Dimension of

\[k = \dfrac{{{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{{{\text{(mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{)}}}^{\text{2}}}}}\]

\[\dfrac{{{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{\text{mo}}{{\text{l}}^{\text{2}}}{\text{ }}{{\text{L}}^{{\text{ - 2}}}}}}{\text{ = L mo}}{{\text{l}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}\]

\[k = \left[ {{H_2}{O_2}} \right]\left[ {{I^ - }} \right]\]

Order of the reaction

\[k = \dfrac{{Rate}}{{\left[ {{H_2}{O_2}} \right]\left[ {{I^ - }} \right]}}\]

Dimension of

$k = \dfrac{{{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{\text{(mol}}{{\text{L}}^{{\text{ - 1}}}}{\text{)(mol}}{{\text{L}}^{{\text{ - 1}}}}{\text{)}}}} = {{\text{L}}^{{\text{ - 1}}}}{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}$

(iii) Given

\[rate{\text{ }} = {\text{ }}k{\left[ {C{H_3}CHO} \right]^{3/2}}\]

Order of the reaction will be \[\dfrac{3}{2}\]

\[k = \dfrac{{Rate}}{{{{\left[ {C{H_3}CHO} \right]}^{\dfrac{3}{2}}}}}\]

$\dfrac{{{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{{{\text{(mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{)}}}^{\dfrac{{\text{3}}}{{\text{2}}}}}}}{\text{ = }}\dfrac{{{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{\text{mo}}{{\text{l}}^{\dfrac{{\text{3}}}{{\text{2}}}}}{{\text{L}}^{\dfrac{{\text{3}}}{{\text{2}}}}}}}$

${{\text{L}}^{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{mo}}{{\text{l}}^{\dfrac{{{\text{ - 1}}}}{{\text{2}}}}}{{\text{s}}^{{\text{ - 1}}}}$

\[rate{\text{ }} = {\text{ }}k\left[ {{C_2}{H_5}Cl} \right]\]

\[1k{\text{ }} = {\text{ }}\dfrac{{Rate}}{{\left[ {{C_2}{H_5}Cl} \right]}}\]

\[\dfrac{{{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}}{{{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}}}{\text{ = }}{{\text{s}}^{{\text{ - 1}}}}\]

2. For the reaction: \[{\text{2A + B }} \to {\text{ A2B}}\] the \[rate{\text{ = k}}\left[ {\text{A}} \right]{\left[ {\text{B}} \right]^{\text{2}}}\]with \[{\text{k = 2}}{\text{.0 \times 1}}{{\text{0}}^{{\text{ - 6}}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{{\text{L}}^{\text{2}}}{{\text{s}}^{{\text{ - 1}}}}{\text{.}}\]

Calculate the reaction's beginning rate when \[\left[ {\text{A}} \right]{\text{ = 0}}{\text{.1 mol }}{{\text{L}}^{{\text{ - 1}}}}\],\[\left[ {\text{A}} \right]{\text{ = 0}}{\text{.1 mol }}{{\text{L}}^{{\text{ - 1}}}}\]Calculate the rate of reaction after \[\left[ {\text{A}} \right]\], is reduced to \[{\text{0}}{\text{.06 mol }}{{\text{L}}^{{\text{ - 1}}}}\]

The initial rate of the reaction is \[{\text{Rate = k }}\left[ {\text{A}} \right]{\text{ }}{\left[ {\text{B}} \right]^{\text{2}}}\]

= \[\left( {{\text{2}}{.0 \times 1}{{\text{0}}^{{\text{ - 6}}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{{\text{L}}^{\text{2}}}{{\text{s}}^{{\text{ - 1}}}}} \right)\left( {{\text{0}}{\text{.1mol }}{{\text{L}}^{{\text{ - 1}}}}} \right){\left( {{\text{0}}{\text{.2 mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)^{\text{2}}}\]

\[{\text{ = 8}}{.0 \times 1}{{\text{0}}^{{\text{ - 9}}}}{\text{mol}}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}\]

The concentration of A responded when \[\left[ {\text{A}} \right]\] was lowered from

\[{\text{0}}{\text{.1 mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{ }}to{\text{ 0}}{\text{.06 mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{.}}\]

\[{\text{ = }}\left( {{\text{0}}{.1 \times 0}{\text{.06}}} \right){\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{ = 0}}{\text{.04 mol }}{{\text{L}}^{{\text{ - 1}}}}\]

As a result, B concentration= \[\dfrac{{\text{1}}}{{\text{2}}}{ \times 0}{\text{.04 mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{ = 0}}{\text{.02 mol }}{{\text{L}}^{{\text{ - 1}}}}\]

After then, the concentration of B responded.

\[\left[ {\text{B}} \right]{\text{ = }}{\text{0}}{.2 \times 0.02}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{ = 0}}{\text{.18mol }}{{\text{L}}^{{\text{ - 1}}}}\]

The rate of the reaction is given by once \[\left[ {\text{A}} \right]\] is lowered to \[{\text{0}}{\text{.06 mol L - 1}}{\text{.}}\]

${20}{l}{Rate{\text{ = k }}\left[ {\text{A}} \right]{\text{ }}{{\left[ {\text{B}} \right]}^{\text{2}}}}$

${{\text{ = }}\left( {{{\text{2}}{.0 \times 1}}{{\text{0}}^{{\text{ - 6}}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{{\text{L}}^{\text{2}}}{{\text{s}}^{{\text{ - 1}}}}} \right)\left( {{\text{0}}{\text{.06mol }}{{\text{L}}^{{\text{ - 1}}}}} \right){{\left( {{\text{0}}{\text{.8mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)}^{\text{2}}}}$

${{\text{ = 3}}{{.89 \times 1}}{{\text{0}}^{{\text{ - 9}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}}$

3. The decomposition of \[{\text{N}}{{\text{H}}_{\text{3}}}\]on platinum surface is zero order reaction. What are the rates of production of \[{{\text{N}}_{\text{2}}}\] and \[{{\text{H}}_{\text{2}}}\] if \[{\text{k = 2}}{{.5 \times 1}}{{\text{0}}^{{\text{ - 4}}}}{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}{\text{L }}{{\text{s}}^{{\text{ - 1}}}}\]?

The following equation represents the breakdown of \[{\text{N}}{{\text{H}}_{\text{3}}}\] on a platinum surface. \[{\text{2N}}{{\text{H}}_{{\text{3}}(g)}}\xrightarrow{{Pt}}{\text{N + 3H + 3H}}\]

\[2\left( g \right)\] \[2\left( g \right)\] \[2\left( g \right)\]

\[Rate{\text{ }} = {\text{ }} - \dfrac{1}{2}\dfrac{{d\left[ {{\text{N}}{{\text{H}}_{\text{3}}}} \right]}}{{dt}} = \dfrac{{d\left[ {{{\text{N}}_{\text{2}}}} \right]}}{{dt}} = \dfrac{1}{3}\dfrac{{d\left[ {{{\text{H}}_{\text{2}}}} \right]}}{{dt}}\]

It is assumed, however, that the reaction is of zero order.

So, \[Rate{\text{ }} = {\text{ }} - \dfrac{1}{2}\dfrac{{d\left[ {{\text{N}}{{\text{H}}_{\text{3}}}} \right]}}{{dt}} = \dfrac{{d\left[ {{{\text{N}}_{\text{2}}}} \right]}}{{dt}} = \dfrac{1}{3}\dfrac{{d\left[ {{{\text{H}}_{\text{2}}}} \right]}}{{dt}}\]

\[{\text{ = 2}}{{ .5 \times 1}}{{\text{0}}^{{\text{ - 4}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}\]

As a result, the rate of \[{{\text{N}}_{\text{2}}}\] production is

\[\dfrac{{d\left[ {{{\text{N}}_{\text{2}}}} \right]}}{{dt}} = \dfrac{{2.5 \times {{10}^{ - 4}}}}{2}\]

\[{\text{ = 1}}{ .25 \times 1}{{\text{0}}^{{\text{ - 4}}}}{\text{mol}}{{\text{L}}^{\text{1}}}{{\text{s}}^{{\text{ - 1}}}}\]

In addition, the rate of \[{{\text{H}}_{\text{2}}}\] production is increasing.

\[\dfrac{{d\left[ {{{\text{N}}_{\text{2}}}} \right]}}{{dt}} = \dfrac{3}{2} \times 2.5 \times {10^{ - 4}}\]

\[{\text{ = 3}}{.75 \times 1}{{\text{0}}^{{\text{ - 4}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{ }}{{\text{s}}^{{\text{ - 1}}}}\]

4. The decomposition of dimethyl ether leads to the formation of \[{\text{C}}{{\text{H}}_{\text{4}}}\], \[{{\text{H}}_{\text{2}}}\] and \[{\text{CO}}\] and the reaction rate is given by\[Rate = k = {[{\text{C}}{{\text{H}}_{\text{3}}}{\text{OC}}{{\text{H}}_{\text{3}}}]^{3/2}}\]The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethy l ether, i.e

\[Rate = k = \;{({\text{PC}}{{\text{H}}_{\text{3}}}{\text{OC}}{{\text{H}}_{\text{3}}})^{3/2}}\]

It the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

In addition, the rate of \[{H_2}\] production is increasing.

\[k = \dfrac{{Rate}}{{{\text{PC}}{{\text{H}}_{\text{3}}}{\text{OC}}{{\text{H}}_{\text{3}}}}}\]

Hence, the unit of rate constants

\[k = \dfrac{{bar{{\min }^{ - 1}}}}{{ba{r^{\dfrac{3}{2}}}}}\]

\[ = ba{r^{ - 1/2}}{\min ^{ - 1}}\]

5. Mention the factors that affect the rate of a chemical reaction .

The rate of a reaction is influenced by several things.

(i) Reactant nature: The rate of the reaction is determined by the reactant's nature. Ionic compound reactions, for example, are faster than covalent compound reactions.

(ii) Reactant state: Solid reactions are sluggish, liquid reactions are quick, and gas reactions are very fast.

(iii) Temperature: The rate of reaction is heavily influenced by the temperature. Temperature raises the pace of reaction by 2-3 times for every \[{100^0}C\] increase in temperature.

\[\dfrac{{{r_T} + 10}}{{{r_T}}} = 2 - 3\]

The temperature coefficient is the name given to this proportion.

The average kinetic energy of reactant molecules increases as the temperature rises. As a result, the rate of collisions rises. The number of molecules with threshold energy grows as the temperature rises. As a result, the rate of reaction accelerates.

iv) Catalyst presence: The rate of reaction also is affected by the presence of a catalyst. Catalysts boost reaction rates by increasing reaction surface area, generating an unstable intermediate with the substrate, and providing a lower-activation-energy alternative path.

6. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is

(i) doubled

(ii) reduced to half?

Let the reactant concentration be \[\left[ {\text{A}} \right]{\text{ = a}}{\text{.}}\]

${Rate{\text{ }}of{\text{ }}reaction,{\text{ }}R = {\text{ }}k{{\left[ A \right]}^2}}$

${ = k{a^2}}$

(i) If the reactant concentration is doubled, \[\left[ {\text{A}} \right]{\text{ = a}}{\text{.}}\] , the reaction rate is

\[R = {\text{ }}k{\left( {2a} \right)^2} = {\text{ }}4k{a^2} = {\text{ }}4R\]

As a result, the reaction rate would increase by four times.

(ii) If the reactant's concentration is cut in half, \[\left[ A \right] = \dfrac{1}{2}a\] the rate of reaction will be

\[R = k{\left( {\dfrac{1}{2}a} \right)^2}\]

\[ = \dfrac{1}{4}ka\]

\[ = \dfrac{1}{4}R\]

As a result, the reaction rate would be lowered to \[{\text{ = }}\dfrac{{{{\text{1}}^{{\text{th}}}}}}{{\text{4}}}\]

7. What is the effect of temperature on the rate constant of a reaction? How can this temperature effect on rate constant be represented quantitatively?

Where k is the rate constant,

A denotes the Arrhenius factor or frequency factor,

R denotes the gas constant,

T denotes the temperature, and

\[{E_a}\] denotes the activation energy for the reaction.

\[\log \dfrac{{{k_2}}}{{{k_1}}} = \dfrac{{{E_a}}}{{2.303}}\left[ {\dfrac{{{T_2} - {T_1}}}{{{T_1}{T_2}}}} \right]\]

\[{k_1}\] = rate constant at temperature \[{T_1}\]

\[{k_1}\] = rate constant at temperature \[{T_2}\]

8. In a pseudo first order hydrolysis of ester in water, the following results were obtained:

(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.

(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester

(i) Average reaction time between 30 and 60 seconds= \[\dfrac{{d\left[ {Ester} \right]}}{{dt}}\]

\[\dfrac{{0.31 - 0.17}}{{60 - 30}} = \dfrac{{0.14}}{{30}}\]

\[{\text{ = 4}}{.67 \times 1}{{\text{0}}^{\text{ - }}}^{\text{3}}{\text{mol }}{{\text{L}}^{\text{ - }}}^{\text{1}}{{\text{s}}^{\text{ - }}}^{\text{1}}\]

(ii) pseudo first order reaction

$\text{k}=\dfrac{2.303}{\text{t}}\log \dfrac{{{[\text{ Ester }]}_{0}}}{[\text{ Ester }]} $

$\text{ When }t=30~\text{s} $

$ \text{k}=\dfrac{2.303}{30}\times \log \left( \dfrac{0.55}{0.31} \right)=1.91\times {{10}^{-2}}/\text{s} $

$ \text{ When }t=60~\text{s} $

$ \text{k}=\dfrac{2.303}{60}\times \log \left( \dfrac{0.55}{0.17} \right)=1.96\times {{10}^{-2}}/\text{s} $

$ \text{ When t}=90\,\text{s} $

$ \text{k}=\dfrac{2.303}{90}\times \log \left( \dfrac{0.55}{0.085} \right)=2.07\times {{10}^{-2}}/\text{s} $

$ \text{ Average rate constant k}=\dfrac{\text{k}1+\text{k}2+\text{k}3}{3}=1.98\times {{10}^{-2}}/\text{s} $

9. A reaction is first order in A and second order in B.

Write the differential rate equation.

How is the rate affected on increasing the concentration of three times?

How is the rate affected when the concentrations of both A and B are doubled

(i) The differential rate equation will be the following:

\[\dfrac{{d[R]\;}}{{dt}} = k[A]{[B]^2}\]

(ii) If B's concentration is three times higher, then

\[\dfrac{{d[R]\;}}{{dt}} = k[A]{[3B]^2} = {\text{ }}9.k[A]{[B]^2}\]

As a result, the reaction rate will rise by 9 times.

(iii) When both A and B concentrations are doubled,

$\dfrac{{d[R]\;}}{{dt}} = k[A]{[B]^2}$

$={k[2A][2B]^2}$

$=8.k{\text{ }}\left[ A \right]{\text{ }}{{\left[ B \right]}^2}$

As a result, the reaction rate will rise by eight times.

10. In a reaction between A and B the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:

What is the order of the reaction with respect to A and B?

Let the reaction order be x with respect to A and y with respect to B. Therefore,

\[{r_o} = {\text{ }}k{[A]^x}\;{[B]^y}\]

$ {5.07 \times {{10}^{ - 5}} = k{{\left[ {0.20} \right]}^x}{{\left[ {0.30} \right]}^y} \ldots ..\left( i \right)}$

$ {5.07 \times {{10}^{ - 5}} = {\text{ }}k{{\left[ {0.20} \right]}^x}{{\left[ {0.10} \right]}^y} \ldots .{\text{ }}\left( {ii} \right)} $

${1.43 \times {{10}^{ - 5}} = k{{\left[ {0.40} \right]}^x}{{\left[ {0.05} \right]}^y} \ldots ..\left( {iii} \right)} $

\[\dfrac{{5.07 \times {{10}^{ - 5}}}}{{5.07\; \times {{10}^{ - 5}}\;\;}} = \dfrac{{k{{[0.20]}^x}\;{{[0.30]}^y}}}{{k\; = \;{{[0.20]}^x}\;[0.30]}}\]

\[I = \dfrac{{{{\left[ {0.30} \right]}^y}}}{{{{\left[ {0.10} \right]}^y}}}\]

\[{\left[ {\dfrac{{0.30}}{{0.10}}} \right]^x}{\left[ {\dfrac{{0.30}}{{0.10}}} \right]^y}\]

We get equation (ii) by dividing equation (ii) by equation (ii).

\[\dfrac{{1.43 \times {{10}^{ - 4}}}}{{5.07\; \times {{10}^{ - 5}}\;\;}} = \dfrac{{k\;{{[0.40]}^x}{{[0.05]}^y}}}{{k\;{{[0.20]}^y}{{[0.30]}^y}}}\]

\[\dfrac{{1.43 \times {{10}^{ - 4}}}}{{5.07\; \times {{10}^{ - 5}}\;\;}} = \dfrac{{k\;{{[0.40]}^x}}}{{k\;{{[0.20]}^y}}}\]

\[0.05{]^y}\;\; = \;{[0.30]^y} = 1\;\;\]

\[2.821 = {2^x}\]

\[\log 2.821 = {\text{ }}x\log {\text{ }}2\]

\[x = \dfrac{{\;\log 2.821}}{{\log 2}}\]

\[1.5\left( {approximately} \right)\]

As a result, the reaction's order regarding A is 1.5 and zero with respect to B.

11. The following results have been obtained during the kinetic studies of the reaction :

\[2A + {\text{ }}B \to C + D\]

Determine the rate law and the rate constant for the reaction

Let the reaction order be x for reaction with respect to A and y for reaction with respect to B. As a result, the reaction rate is given by,

\[Rate = k{\left[ A \right]^x}{\left[ B \right]^y}\]

${6.0 \times {{10}^{ - 3}} = k{{\left[ {0.1} \right]}^x}{{\left[ {0.1} \right]}^y}\left( i \right)}$

${7.2 \times {{10}^{ - 2}} = k{{\left[ {0.3} \right]}^x}{{\left[ {0.2} \right]}^y}\left( {ii} \right)}$

${2.88 \times {{10}^{ - 1}} = k{{\left[ {0.3} \right]}^x}{{\left[ {0.1} \right]}^y}\left( {iii} \right)} $

$ {2.40 \times {{10}^{ - 2}} = k{{\left[ {0.4} \right]}^x}{{\left[ {0.1} \right]}^y}\left( {iv} \right)} $

When we divide equation (iv) by I we get,

\[\text{}\dfrac{{2.40 \times {{10}^{ - 2}}}}{{6.0 \times {{10}^3}}} = \dfrac{{k = \;{{[0.4]}^x}\;{{[0.1]}^y}}}{{k = \;{{[0.1]}^x}\;{{[0.1]}^y}}}{\text{}}\]

\[4 = \dfrac{{{{\left[ {0.4} \right]}^x}}}{{{{\left[ {0.1} \right]}^x}}}\]

\[4 = {\left( {\dfrac{{0.4}}{{0.1}}} \right)^x}\]

Divide (iii) by (i)

\[\text{}\dfrac{{2.88 \times {{10}^ - }^1}}{{7.2 \times {{10}^ - }^2}} = \dfrac{{k{{\left[ {0.3} \right]}^x}{{\left[ {0.4} \right]}^y}}}{{k{{\left[ {0.3} \right]}^x}{{\left[ {0.2} \right]}^y}}}\]

\[4 = {\left( {\dfrac{{0.4}}{{0.2}}} \right)^y}\]

\[4 = {2^y}\]

\[{2^2} = {2^y}\]

\[Rate{\text{ }} = {\text{ }}k{\text{ }}\left[ A \right]{\text{ }}{\left[ B \right]^2}\]

\[k = \dfrac{{Rate}}{{\left[ A \right]{{\left[ B \right]}^2}}}\]

From experiment I we understand

\[k{\text{ = }}\dfrac{{{\text{6}}{.0 \times 1}{{\text{0}}^{\text{3}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}}}{{{\text{ = }}\left( {{\text{0}}{\text{.1mol }}{{\text{L}}^{{\text{ - 1}}}}} \right){{\left( {{\text{0}}{\text{.1mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)}^{\text{2}}}}}\]

\[{\text{ = 6}}{\text{.0 }}{{\text{L}}^{\text{2}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}\]

From experiment II we understand

\[k{\text{ = }}\dfrac{{{\text{2}}.{\text{88}} \times {\text{1}}{{\text{0}}^{{\text{ - 1}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}}}{{\left( {{\text{0}}{\text{.3mol }}{{\text{L}}^{{\text{ - 1}}}}} \right){{\left( {{\text{0}}{\text{.4mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)}^{\text{2}}}}}{\text{ = 6}}{\text{.0}}{{\text{L}}^{\text{2}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}{\text{}}\]

From experiment III we understand

\[k{\text{= }}\dfrac{{{\text{2}}.{\text{40}} \times {\text{1}}{{\text{0}}^{{\text{ - 2}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}}}{{\left( {{\text{0}}{\text{.4mol }}{{\text{L}}^{{\text{ - 1}}}}} \right){{\left( {{\text{0}}{\text{.1mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)}^{\text{2}}}}}{\text{ = 6}}{\text{.0}}{{\text{L}}^{\text{2}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}{\text{}}\]

Hence, the rate constant \[k{\text{ = 6}}{\text{.0 }}{{\text{L}}^{\text{2}}}{\text{mo}}{{\text{l}}^{{\text{ - 2}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}\]

12. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:

With respect to A, the given reaction is first order, whereas with respect to B, it is zero order.

The rate of the reaction

\[Rate = {\text{ }}k{\left[ A \right]^1}{\left[ B \right]^0}\]

\[Rate = k = \left[ A \right]\]

From 1 st experiment,

${{\text{2}}{.0 \times 1}{{\text{0}}^{{\text{ - 2}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}{\text{ = }}k\left( {{\text{0}}{\text{.1mol}}{{\text{L}}^{{\text{ - 1}}}}} \right)}$

${k{\text{ = 0}}{\text{.2 mi}}{{\text{n}}^{{\text{ - 1}}}}}$

From 2 nd experiment,

${{\text{4}}{{.0 \times 1}}{{\text{0}}^{{\text{ - 2}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}{\text{ = }}k\left( {{\text{0}}{\text{.2mol }}{{\text{L}}^{{\text{ - 1}}}}} \right)}$

${\left[ A \right]{\text{ = 0}}{\text{.2 mol }}{{\text{L}}^{{\text{ - 1}}}}}$

From 3 rd experiment,

${Rate{\text{ = 0}}{\text{.2 mi}}{{\text{n}}^{{\text{ - 1}}}}{\times 0}{\text{.4 mol }}{{\text{L}}^{{\text{ - 1}}}}}$

${{\text{ = 0}}{\text{.08 mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}}$

From 4 th experiment

${{\text{2}}{.0 \times 1}{{\text{0}}^{{\text{ - 2}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{mi}}{{\text{n}}^{{\text{ - 1}}}}{\text{ = 0}}{\text{.2 mi}}{{\text{n}}^{{\text{ - 1}}}}\left[ A \right]}$

${\left[ A \right]{\text{ = 0}}{\text{.1mol }}{{\text{L}}^{{\text{ - 1}}}}}$

13. Calculate the half-life of a first order reaction from their rate constants given below:

\[\left( i \right)\;200{{\text{s}}^{{\text{ - 1}}}}\left( {ii} \right)2{\min ^{ - 1}}\left( {iii} \right)4year{s^{ - 1}}{\text{}}\]

(i) Half life

\[{\text{}}{t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k} = \dfrac{{0.693}}{{200{{\text{S}}^{ - 1}}}} = 0.346 \times {10^{ - 2}}\]

(ii) Half life

\[{\text{}}{t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k} = \dfrac{{0.693}}{{2{{\min }^{ - 1}}}} = 0.346\min {\text{}}\]

(iii) Half life

\[{\text{}}{t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k} = \dfrac{{0.693}}{{4year{s^{ - 1}}}} = 0.173years{\text{}}\]

14. The half-life for radioactive decay of 14 C is 5730 years. An archeological artifact containing wood had only 80% of the 14 C found in a living tree. Estimate the age of the sample.

The dynamics of radioactive decay are first order. As a result, the decay constant

$\text{ Decay constant k}=\dfrac{0.693}{{{\text{t}}_{1/2}}}=\dfrac{0.693}{5730\text{ year }}=1.209\times {{10}^{-4}}/\text{ years }$

The rate of counts is proportional to the number of C-14 atoms in the sample.

${{\text{N}}_{0}}=100,~\text{N}=80$

$\text{ The age of the sample t}=\dfrac{2.303}{\text{k}}\log \left( \dfrac{{{\text{N}}_{0}}}{~\text{N}} \right)$

$\text{t}=\dfrac{2.303}{1.209\times {{10}^{-4}}}\times \log \left( \dfrac{100}{80} \right)=1846\text{ years }$

Therefore, the sample age is 1846 years.

15. The experimental data for decomposition of \[{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{[ 2}}{{\text{N}}_{\text{2}}}{\text{O5}} \to {\text{4N}}{{\text{O}}_{\text{2}}}{\text{ + }}{{\text{O}}_{\text{2}}}{\text{]}}\]in gas phase at 318K are given below :

(i) Plot \[{\text{log[}}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{]}}\] against t.

(ii) Find the half-life period for the reaction.

(iii) Draw a graph between \[{\text{log[}}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{]}}\]and t.

(iv) What is the rate law?

(v) Calculate the rate constant.

(vi).Calculate the half-life period from k and compare it with(ii)

(Image will be uploaded soon)

(ii). The period that corresponds to the concentration \[\dfrac{{{\text{1}}{.630 \times 1}{{\text{0}}^{{\text{ - 2}}}}}}{{\text{2}}}{\text{mol }}{{\text{L}}^{\text{1}}}{\text{ = 0}}{.815 \times 1}{{\text{0}}^{{\text{ - 2}}}}{\text{mol }}{{\text{L}}^{ - 1}}\] is half- life.

Observing the graph, the half life is 1440s.

(iii)

(vi) The provided reaction is of first order, as evidenced by the straight-line plot of log \[{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\] v/s t. As a result, the reaction's rate law is

\[Rate = k{\text{[}}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{]}}\]

(v) From the plot \[{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\] v/s t, we get

$\ = \dfrac{{2.46 - ( - 1.79)}}{{3200 - 0}} = \dfrac{{ - 0.67}}{{3200}}$

${\text{ = 4}}{{.82 \times 1}}{{\text{0}}^{{\text{ - 4}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}$

(vi) Half life given by

$= \dfrac{{2.46 - ( - 1.79)}}{{3200 - 0}} = \dfrac{{ - 0.67}}{{3200}}$

${\text{ = 4}}{.82 \times 1}{{\text{0}}^{{\text{ - 4}}}}{\text{mol }}{{\text{L}}^{{\text{ - 1}}}}{{\text{s}}^{{\text{ - 1}}}}$

The value of \[{t_{\dfrac{1}{2}}}\] computed from k is extremely close to the value acquired from graph.

16. Rate constant for a first order reaction is 60 s -1 . How much time will it take to reduce the initial concentration of the reactant to its 1/16 th value?

$t = \dfrac{{2.303}}{k}\log \dfrac{{\left[ R \right]}}{{\left[ R \right]}}$

$ = \dfrac{{2.303}}{{60{{\text{s}}^{{\text{ - 1}}}}}}\log \dfrac{1}{1}{\text{}}$

$ = \dfrac{{2.303}}{{60{{\text{s}}^{{\text{ - 1}}}}}}\log 16$

$ = 4.62 \times {10^{ - 2}}{\text{s}}$

17. During nuclear explosion, one of the products is 90 Sr with half-life of 28.1 years. If 1 µg of 90 Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically?

$ k=\dfrac{0.693}{{{t}_{\dfrac{1}{2}}}}=\dfrac{0.693}{28.1}{{v}^{-1}} $

$ \text{Knowing} $

$ t=\dfrac{0.303}{k}\log \dfrac{\left[ R \right]}{\left[ R \right]} $

$ t=\dfrac{0.303}{\dfrac{0.693}{28.1}}\log \dfrac{1}{\left[ R \right]}10 $

$ =\dfrac{0.303}{\dfrac{0.693}{28.1}}(-108\left[ R \right])\log \left[ R \right]-\dfrac{10\times 0.303}{2.303\times 28.1}\left[ R \right] $

$ =anti\log (-0.1071)=0.7814\mu g $

Hence, 0.7814 µg of 90 Sr will remain after 10 years.

\[{\text{}}k = \dfrac{{0.693}}{{{t_{\dfrac{1}{2}}}}} = \dfrac{{0.693}}{{28.1}}{v^{ - 1}}{\text{}}\]

\[Knowing{\text{ }}t = \dfrac{{0.303}}{k}\log \dfrac{{\left[ R \right]}}{{\left[ R \right]}}{\text{ }}\]

\[60 = \dfrac{{0.303}}{{\dfrac{{0.693}}{{28.1}}}}\log \dfrac{1}{{\left[ R \right]}}{\text{ }}\]

\[\log \left[ R \right] - \dfrac{{10 \times 0.303}}{{2.303 \times 28.1}}{\text{ }}\]

\[\left[ R \right] = anti\log ( - 0.6425)\]

\[ = 0.2278\mu g\]

Thus, 0.2278µg of 90 Sr will remain after 60 years

18. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction

The time required for 99 percent completion of a first order reaction is

${t_1} = \dfrac{{2.303}}{k}\log \dfrac{{100}}{{100 - 99}}$

$= \dfrac{{2.303}}{k}\log 100$

The time required for 90 percent completion of a first order reaction is

${t_2} = \dfrac{{2.303}}{k}\log \dfrac{{100}}{{100 - 99}}$

$= \dfrac{{2.303}}{k}\log 10$

$= \dfrac{{2.303}}{k}$

${t_1} = 2{t_2}$

As a result, the time required to complete a first order reaction at 99 percent is twice the time required to complete the reaction at 90%.

19. A first order reaction takes 40 min for 30% decomposition. Calculate \[{{\text{t}}_{\dfrac{{\text{1}}}{{\text{2}}}}}\]

1 st order reaction

${t_2} = \dfrac{{2.303}}{k}\log \dfrac{{\left[ R \right]}}{{\left[ R \right]}}$

$k = \dfrac{{2.303}}{{40\min }}\log \dfrac{{100}}{{100 - 30}}$

$=\dfrac{{2.303}}{{40\min }}\log \dfrac{{10}}{7}$

$=8.918 \times {10^{ - 3}}{\min ^{ - 1}}$

\[{t_{\dfrac{1}{2}}}\] of the decomposition reaction is

${t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k} = \dfrac{{0.693}}{{8.918 \times {{10}^{ - 3}}}}\min$

$= 77.7\min$

20. For the decomposition of azoisopropane to hexane and nitrogen at 543 k, the following data are obtained .

Calculate the rate constant

The following equation represents the breakdown of azoisopropane to hexane and nitrogen at 54.3 k.

\[{{\text{(C}}{{\text{H}}_{\text{3}}}{\text{)}}_{\text{2}}}{\text{CHN = NCH(C}}{{\text{H}}_{\text{3}}}{{\text{)}}_{\text{2}}}\left( g \right) \to {{\text{N}}_{\text{2}}}\left( g \right){\text{ + }}{{\text{C}}_{\text{6}}}{{\text{H}}_{{\text{14}}}}\left( g \right)\]

At \[t = 0{P_o}\]

\[t{\text{ }} = {\text{ }}t{P_0}--p\]

Total pressure \[,\left( {Pt} \right) = \left( {{P_0} - p} \right) + p + p\]

\[Pt = {P_0} + p\]

when the value of p is substituted for the pressure of the reactant at time t

${ = Po--{\text{ }}p} $

${ = Po - {\text{ }}\left( {Pt - Po} \right)} $

$ { = 2Po - Pt} $

1st order reaction

\[k = \dfrac{{2.303}}{t}\log \dfrac{P}{{2{P_0} - {P_t}}}{\text{ }}\]

\[t = 360{\text{s }},\]

\[k = \dfrac{{2.303}}{{360}}\log \dfrac{{35.0}}{{2 \times 35.0 - 54.0}}{\text{ }}\]

\[ = 2.175 \times {10^{ - 3}}{{\text{s}}^{{\text{ - 1}}}}\]

\[when{\text{ }}t = 720{\text{s}},k = \dfrac{{2.303}}{{720}}\log \dfrac{{35.0}}{{2 \times 35.0 - 63.0}}{10^{ - 3}}{{\text{s}}^{{\text{ - 1}}}}{\text{ }}\]

Average value of rate constant

$k = \dfrac{{(2.175 \times {{10}^{ - 3}}) + (2.235 \times {{10}^{ - 3}})}}{2}{{\text{s}}^{{\text{ - 1}}}}$

$=2.20 \times {10^{ - 3}}{{\text{s}}^{{\text{ - 1}}}}$

21. The following data were obtained during the first order thermal decomposition of \[{\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\] at a constant volume

\[{\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\left( g \right) \to {\text{S}}{{\text{O}}_{\text{2}}}\left( g \right){\text{ + C}}{{\text{l}}_{\text{2}}}\left( g \right)\]

Calculate the rate of the reaction when total pressure is 0.65 atm.

The following equation represents the thermal breakdown of \[{\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\] at a constant volume.

$ { = Po--{\text{ }}p} $

$ { = Po - {\text{ }}\left( {Pt - Po} \right)} $

$ { = 2Po - Pt} $

\[{\text{}}k = \dfrac{{2.303}}{t}\log \dfrac{{{P_0}}}{{2{P_0} - {P_t}}}{\text{ }}\]

\[k = \dfrac{{2.303}}{{100s}}\log \dfrac{{0.5}}{{2 \times 0.5 - 0.6}}\]

\[when{\text{ }}t = 100{\text{s}}\]

\[K = 2.231 \times {\text{ }}{10^{ - 3}}{{\text{s}}^{{\text{ - 1}}}}\]

\[When{\text{ }}Pt = 0.65{\text{ }}atm,\]

As a result, the total pressure of \[{\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\] at time t is 0.65 atm.

$2\;{P_{{\text{SOCl}}}} = 2{\text{ }}Po - {\text{ }}Pt$

$= 2 \times 0.50 - 0.65$

$={\text{ }}0.35{\text{ }}atm$

As a result, when total pressure is 0.65 atm, the rate of equation is

${Rate = {\text{ }}k{\text{ }} = ({P_{SOCl}})}$

${ = \left( {2.33 \times {{10}^{ - 3}}{s^{ - 1}}} \right)\left( {0.354atm} \right) = 7.8{\text{ }} \times {{10}^{ - 4}}atm{s^{ - 1}}} $

22. The rate constant for the decomposition of \[{N_2}{O_5}\] at various temperatures is given below:

Draw a graph between ln k and 1/T and calculate the values of A and \[{{\text{E}}_{\text{a}}}\]. Predict the rate constant at 30 o and 50 o C.

From the given data, we get

Slope of the line

\[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = 12.301k\]

Arrhenius equation,

\[Slope = {\text{}} - \dfrac{{{E_a}}}{R}\rightarrow{\text{}}Ea = {\text{}} - slope \times R = {\text{}} - \left( { - 12.301K} \right) \times \left( {8.314J{K^{ - 1}}{\text{mo}}{{\text{l}}^{{\text{ - 1}}}}} \right) = 102.27{\text{ K J mo}}{{\text{l}}^{{\text{ - 1}}}}{\text{}}\]

\[Ink = InA - \dfrac{{{E_a}}}{{ET}}\]

\[InA = Ink + \dfrac{{{E_a}}}{{ET}}\]

Since, \[T = 273K\], \[Ink{\text{ }} = {\text{ }} - {\text{ }}7.147\]

\[InA = {\text{}} - 7.147 + \dfrac{{102.27 \times {{10}^3}}}{{8.314 \times 273}} = 37.911A{\text{ }} = {\text{ }}2.91{\text{ }} \times {\text{ }}{10^6}\]

\[T = 30 + 273K = 303K\]

\[\dfrac{I}{T} = 0.0033K = {\text{ }}3.3 \times {10^{ - 3}}K\]

At, \[\dfrac{I}{T} = 0.0033K = {\text{ }}3.3 \times {10^{ - 3}}K\]

\[In{\text{ }}k{\text{ }} = {\text{ }} - 2.8\]

\[k = {\text{ }}6.08 \times {10^{ - 2}}{s^{ - 1}}\]

\[\dfrac{I}{T} = 0.0031K = 3.1 \times {10^{ - 3}}K\]

\[In{\text{ }}k{\text{ }} = {\text{ }} - 0.5\]

\[k = {\text{ }}0.607{\text{ }}{s^{ - 1}}\]

\[\dfrac{I}{T} = 3.1 \times {10^{ - 3}}\]

\[T = 50 + 273K = 323K{\text{}}\]

23. The rate constant for the decomposition of hydrocarbons is ${\text{2}}{{.418 \times 1}}{{\text{0}}^{{\text{ - 5}}}}{{\text{s}}^{{\text{ - 1}}}}$ at 546 k. If the energy of activation is 179.9 kJ /mol, what will be the value of pre-exponential factor.

Arrhenius equation

\[K = {\text{ }}A{e^{ - E/RT}}Ink = InA - \dfrac{{{E_a}}}{{RT}}\log k = \log A\dfrac{{{E_a}}}{{2.303RT}}\]

\[ = \log {\text{ }}\left( {2.418 \times {\text{ }}{{10}^{ - 5}}{s^{ - 1}}} \right){\text{ }} + \dfrac{{179.9 \times {{10}^3}jmo{l^{ - 1}}}}{{2.303 \times 8.314JKmo{l^{ - 1}} \times 546K}}\]

\[ = \left( {0.3835{\text{ }} - 5} \right){\text{ }} + 17.2082{\text{ }} = {\text{ }}12.5917\]

\[A = 3.912 \times {10^{12}}{{\text{S}}^{{\text{ - 1}}}}\]

24. Consider a certain reaction A → Products with \[k{\text{ }} = {\text{ }}2.0{\text{ }} \times {\text{ }}{10^{ - 2}}{s^{ - 1}}\]. Calculate the concentration of A remaining after 100 s if the initial concentration of A is \[{\text{1}}{\text{.0 mol }}{{\text{L}}^{{\text{ - 1}}}}{\text{.}}\]

\[k = 2.0 \times {10^{ - 2}}{{\text{s}}^{{\text{ - 1}}}}{\text{,}}t{\text{ }} = 100{\text{ s,}}{\left[ A \right]_{\text{0}}}{\text{ = 1}}{\text{.0 mol }}{{\text{L}}^{{\text{ - 1}}}}\]

The given reaction is a first order reaction since the unit of k equals \[{s^{ - 1}}\]

\[k = \dfrac{{2.303}}{t}\log \dfrac{{\left[ A \right]}}{{\left[ A \right]}}2.0 \times {10^{ - 2}}{{\text{s}}^{{\text{ - 1}}}} = \dfrac{{2.303}}{{100s}}\log \dfrac{{1.0}}{{\left[ A \right]}}2.0 \times {10^{ - 2}}{{\text{s}}^{{\text{ - 1}}}} = \dfrac{{2.303}}{{100s}}( - \log \left[ A \right])\]

${ - \log \left[ A \right] = \dfrac{{2.0 \times {{10}^{ - 2}}100}}{{2.303}}} $

${{\text{}}[A] = anti\log \left( {\dfrac{{2.0 \times {{10}^{ - 1}} \times 100}}{{2.303}}} \right){\text{}}}$

$ = 0.135{\text{Mol}}{{\text{L}}^{ - 1}}$

As a result, the concentration of A left is \[{\text{0}}{\text{.135mol }}{{\text{L}}^{{\text{ - 1}}}}\]

25. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law with \[{{\text{t}}_{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{ = 3hours}}\]. What fraction of sample of sucrose remains after 8 hour?

$k=\dfrac{2.303}{t} \log \dfrac{[R_0]}{[R]}$

$t_{\dfrac{1}{2}} =3 \text { hours }$

$ k=\dfrac{0.693}{t_{\dfrac{1}{2}}}$

$ S o, k=\dfrac{0.693}{3}=0.231 h^{-1} $

$=0.231 h^{-1}=\dfrac{2.303}{8 h} \log \dfrac{[R]_{o}}{[R]} $

$\log \dfrac{[R]_{0}}{[R]}=\dfrac{0.231 h^{-1} \times 8 h}{2.303} $

$\dfrac{[R]_{0}}{[R]}=\text { anti } \log (0.8024) $

$\dfrac{[R]_{0}}{[R]}=6.3445 $

$\dfrac{[R]_{0}}{[R]}=0.1576 $

As a result, after 8 hours, 0.158 percent of the sucrose sample remains.

26. The decomposition of hydrocarbon follows the equation \[k{\text{ }} = {\text{ }}\left( {4.5{\text{ }} \times {\text{ }}{{10}^{11}}{s^{ - 1}}} \right){\text{ }}{e^{ - 28000}}K/T\]. Calculate \[{E_a}\]

From the given equation

\[k = {\text{ }}\left( {4.5{\text{ }} \times {{10}^{11}}{s^{ - 1}}} \right){e^{ - 28000}}K/T\;\;\;\;\left( i \right)\]

Arrhenius equation , \[k{\text{ }} = A{e^{ - E/RT}}\] \[(ii)\]

From equation (i) and (ii) we get

$\dfrac{E_{a}}{R T}=\dfrac{28000 K}{T}$

$E a=R \times 28000 K $

$=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \times 28000 k $

$=232792 \mathrm{~J} \mathrm{~mol}^{-1} $

$=232.792 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1} $

27. The rate constant for the first order decomposition of H 2 O 2 is given by the following equation: \[\log {\text{ }}k{\text{ }} = {\text{ }}14.34{\text{ }} - {\text{ }}1.25{\text{ }} \times {\text{ }}{10^4}K/T\]. Calculate \[{E_a}\] for this reaction and at what temperature will its half-period be 256 minutes?

The expression for the rate constant is as follows:

$\log \mathrm{k}=14.34-1.25 \times 10^{4} \mathrm{~K} / \mathrm{T} \ldots$..(i)

Comparing it with Arrhenius equation, we get-

$\log \mathrm{k}=\log \mathrm{A}-\dfrac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{RT}}$

Therefore, $\dfrac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}=1.25 \times 10^{4}$

$\mathrm{E}_{\mathrm{a}}=1.25 \times 10^{4} \times 2.303 \times 8.314$

The activation energy $=\mathrm{E}_{\mathrm{a}}=239339 \mathrm{~J} / \mathrm{mol}=239.339 \mathrm{~kJ} / \mathrm{mol}$

Half life period, $\mathrm{t}_{1 / 2}=256 \mathrm{~min}=256 \times 60 \mathrm{sec}$

$\mathrm{k}=\dfrac{0.693}{\mathrm{t}_{1 / 2}}$

$\mathrm{k}=\dfrac{0.693}{256 \times 60 \mathrm{sec}}$

$\mathrm{k}=4.51 \times 10^{-5} / \mathrm{s}$

Substitute in equation (i), we get-

$\log 4.51 \times 10^{-5}=14.341 .25 \times 10^{4} \mathrm{~K} / \mathrm{T}$

$-4.35=14.341 .25 \times 10^{4} \mathrm{~K} / \mathrm{T}$

$\mathrm{T}=669 \mathrm{~K}$

Hence, the temperature at which the half-life period is 256 minutes is $669 \mathrm{~K}$.

28. The decomposition of A into product has value of k as \[4.5{\text{ }} \times {\text{ }}{10^3}{s^{ - 1}}\]at 10 o C and energy of activation 60 kJ mol -1 . At what temperature would k be \[1.5 \times {\text{ }}{10^4}{s^{ - 1}}\]?

It is given that the decomposition of A into product has value of $\text{k}=4.5\times {{10}^{3}}~{{\text{s}}^{-1}}\text{ at }{{10}^{{}^\circ }}\text{C}\text{. }$

$\log \left( \dfrac{{{\text{K}}^{\prime }}}{\text{k}} \right)=\dfrac{{{\text{E}}_{\text{a}}}}{2.303\text{R}}\left[ \dfrac{{{\text{T}}^{\prime }}-\text{T}}{\text{T}{{\text{T}}^{\prime }}} \right]$

$\log \left( \dfrac{1.5\times {{10}^{4}}}{4.5\times {{10}^{3}}} \right)=\dfrac{60\times {{10}^{3}}}{2.303\times 8.314}\left[ \dfrac{{{\text{T}}^{\prime }}-283}{283~{{\text{T}}^{\prime }}} \right]$

$0.5228=3132.62\left[ \dfrac{{{\text{T}}^{\prime }}-283}{283~{{\text{T}}^{\prime }}} \right]$

${{\text{T}}^{\prime }}-283=0.0472~{{\text{T}}^{\prime }}$

${{\text{T}}^{\prime }}=297.02~\text{K}$

${{\text{T}}^{\prime }}=297.02~\text{K}-273={{24.02}^{{}^\circ }}\text{C}$

29. The time required for 10% completion of a first order reaction at 298 k is equal to that required for its 25% completion at 308 K. If the value of A is \[4 \times {\text{ }}{10^{10}}{s^{ - 1}}\], Calculate k at 318 K and \[{E_a}\]

$t=\dfrac{2.303}{k} \log \dfrac{a}{a-x}$

$a t 298 K, t=\dfrac{2.303}{k} \log \dfrac{100}{90} $

$=\dfrac{0.1054}{k} $

$ -\dfrac{2.303}{k} \log \dfrac{100}{75}$

$At 308 k=\dfrac{2.2877}{k}$

Regarding question

$=\dfrac{0.1054}{k} \log \dfrac{0.2877}{k} $

$\log \dfrac{k_{1}}{k}=2.7296$

From Arrhenius equation, we get

$\log , \log \dfrac{k_{1}}{k}=\dfrac{E_{a}}{2.303 R}\left(\dfrac{T-T}{T T^{\prime}}\right) $

$\log (2.7296)=\dfrac{E_{a}}{2.303 \times 8.314}\left(\dfrac{308-298}{298 \times 308}\right) $

$E_{a}=\dfrac{2.303 \times 8,314 \times 298 \times 308 \times \log (2.7296)}{308-298}$

$=76750.096 \mathrm{~J} \mathrm{~mol}^{-1} $

$=76.75 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$

calculate $k$ at $318 k$

$A=4 \times 10^{10} s^{-1}, T=318 K$

Again, from Arrhenius equation, we get

$\log =\log A-\dfrac{E_{a}}{2.303 R T} $

$ \log (4 \times 10)-\dfrac{76.75 \times 10^{3}}{2.303 \times 8.314 \times 318} $

$=10.6021-12.6051=-2.003 $

$k=\text { Anti } \log (-2.003)$

$=9.93 \times 10^{-3} \mathrm{~s}^{-1}$

30. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction if it does not change with temperature.

$\log , \log \dfrac{k_{2}}{k_{1}}=\dfrac{E_{a}}{2.303}\left(\dfrac{T_{2}-T_{1}}{T_{1} T_{2}}\right)$

$k_{2}=4 k_{1}$

$T_{1}=293 \mathrm{~K} $

$ T_{2}=313 \mathrm{~K} $

${\text{ So }, \log \dfrac{4 k_{2}}{k_{1}}=\dfrac{E_{a}}{2.303 \times 8.314}\left(\dfrac{313-293}{293 \times 313}\right)}$

$0.6021=\dfrac{20 \times E_{a}}{2.303 \times 8.314 \times 293 \times 313} $

$E_{a}=\dfrac{0.6021 \times 2.303 \times 8.314 \times 293 \times 313}{20} $

$=52863.00 \mathrm{~J} \mathrm{~mol}^{-1}$

$=52.86 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$

As a result, the activation energy required is $52.86 \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$

We hope, these important questions have helped you in brushing up on your concepts related to Class 12 Chemistry Chapter 4 . You must practice solving these questions regularly to be more clear with the chapter as well as the chemical formulas. Utilise your coming days smartly by following the important study materials provided above and sit for your CBSE Board exams confidently.

Important Related Links for CBSE Class 12 Chemistry

Vedantu's Important Questions of Class 12 Chemistry Chemical Kinetics offer a comprehensive and valuable resource for students studying this topic. The collection of important questions is designed to aid students in their preparation and understanding of chemical kinetics, a fundamental aspect of chemistry. By covering a wide range of concepts and problem-solving techniques, these questions help students develop a strong foundation in the subject. Vedantu's emphasis on key topics and challenging questions ensures that students are well-prepared for their Class 12 Chemistry examinations. With its user-friendly format and carefully curated content, this resource serves as an effective tool for students seeking to excel in their studies and achieve academic success.

FAQs on Important Questions for CBSE Class 12 Chemistry Chapter 4 - Chemical Kinetics 2024-25

1. What are the important topics in chemical kinetics 12?

Important Topics of Chemical Kinetics

Integrated Rate Equations.

Rate of the Chemical Reaction.

Collision Theory of the Chemical Reactions.

Factors Influencing the Rate of a Reaction.

Pseudo First Order Reaction.

Temperature Dependence of the Rate of a Reaction.

2. Which is most important chapter in chemistry class 12?

The chapter considered the most crucial in CBSE Class 12 Chemistry is Organic Chemistry. It holds significant importance for the board exam in 2024, as well as for the preparation of competitive exams like JEE and NEET, and future studies. While Organic Chemistry may seem intricate, consistent practice can make it much more manageable.

3. What is the rate of reaction in chemical kinetics notes?

In chemical kinetics notes, the rate of reaction refers to the measure of how the concentration of reactants or products changes over a specific period. It is expressed as the amount of change in concentration per unit of time. The negative sign signifies that the concentration of reactants is decreasing, while the unit for reaction rate is represented as mol $L^{-1}s^{-1}$.

4. Where can I find the free PDF downloads of Chemical Kinetics Class 12 Important Question for NCERT Chemistry?

Vedantu offers free PDF downloads of Chemical Kinetics Class 12 Important Questions for NCERT Chemistry on their official website or through our educational platforms. I recommend visiting Vedantu's website or conducting a search online using keywords like "Vedantu Chemical Kinetics Class 12 Important Questions NCERT Chemistry PDF" to find relevant resources.

5. Can I rely solely on the Chemical Kinetics Class 12 Notes for NEET Chemistry for my exam preparation?

While Vedantu's Chemical Kinetics Class 12 Important Questions for NCERT Chemistry can be a valuable resource for your exam preparation. While these Important Questions provide you with a comprehensive understanding of the chapter.

Using Vedantu's Important Questions as a foundation and supplementing them with other study materials such as textbooks, and reference books can help you grasp the concepts more effectively. Additionally, practicing a variety of questions from different sources, including previous year question papers and sample papers, will strengthen your problem-solving skills.

Remember, a well-rounded and diversified study approach will give you a better chance of success in your exams. Utilize Vedantu's Chemical Kinetics Class 12 Important Questions as a valuable tool in your preparation.

6. What is chemical kinetics?

Chemical kinetics is the field of science that studies the rate of a reaction, how it happens, and the factors that affect how fast it happens. The Greek word "kinesis," which means movement, is where the term "kinetic" comes from. Chemical reactions are classified into three categories based on their rate, these are:

A. Very fast reaction

B. Moderate or slow

C. Very slow reaction

7. Define the molecularity of the reaction in chemical kinetics?

The term "molecularity" refers to the number of reacting species—atoms, molecules, or ions that participate in an elementary reaction.It is a theoretical quantity that can only have integral value. Molecularity that is negative, null, or fractional is never possible. It plays no significance in complex reactions.

8. What is the difference between rate law and rate constant?

In a balanced chemical equation, the reaction rate is expressed in terms of the molar concentration of the reactants, with each term raised to a power that may or may not be the same as the stoichiometric coefficient of the reacting species while the rate constant is the rate of reaction per unit concentration of the reacting species.

9. What is a zero-order reaction?

A zero-order reaction is one in which the rate is unaffected by the reactant's initial concentration. It is highly uncommon and only occurs under exceptional circumstances. The rate of such reactions is equal to the rate constant. Eg,

a)Adsorption of gases into metal surfaces.

b) The dissociation of HI on the surface of gold.

10. What is the weightage of the chapter chemical kinetics in the 12th CBSE board exam?

All subjects are covered by the subject-by-subject CBSE marking scheme for the 2024–2025 school year.7 marks out of 70 marks, or ten per cent of the total, are awarded for the fourth chapter of the 12th-grade chemistry theory paper on chemical kinetics . Vedantu has also made the chapter-by-chapter weightage for each subject available for your convenience on its official website. Students can also visit the official Vedantu website for quick revision notes for this chapter.

CBSE Class 12 Chemsitry Important Questions

Cbse study materials.

New QB365-SLMS
NEET Materials
JEE Materials
Banking first yr Materials
TNPSC Materials
DIPLOMA COURSE Materials
5th Standard Materials
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

12th Chemistry Chemical Kinetics Chapter Case Study Question with Answers CBSE

By QB365 on 13 Jan, 2024

Chemical Kinetics

Chemical Kinetics Chapter Case Study Question with Answers

12th Chemistry CBSE case study questions for Chemical Kinetics - 2024

CBSE 12th Chemistry Chemical Kinetics Case Study Question & Answers

CBSE 12th Chemistry Chemical Kinetics Chapter Case Study Question with Answers

CBSE Class 12th Chemistry Sample Model Question Papers. CBSE Class 12th Chemistry Sample Case Study Questions with Answer Keys. CBSE 12th Chemistry Model Question Papers Case Study Questions CBSE 12th Chemistry CBSE Case Study Question and Answers CBSE 12th Chemistry CBSE Question Papers with Answer Keys Model Question Paper 12th Chemistry with Answer Keys Chemical Kinetics 12th CBSE Chemistry Question Papers with Answer Keys. Model Question Paper for 12th Chemistry CBSE CBSE Model Question Papers Class 12th 2024 Model Question Paper 12th Chemistry

QB365 Official Website : https://www.qb365.in/ CBSE Study Materials : https://www.qb365.in/studymaterials/ QB365 Search and Find your Answers : https://www.qb365.in/answers/ QB365 Learning App : https://play.google.com/store/apps/details?id=com.linlax.students.qb365&pcampaignid=web_share&pli=1

Related 12th Standard CBSE Chemistry Materials

12th standard cbse syllabus & materials, cbse 12th physics wave optics chapter case study question with answers, cbse 12th physics ray optics and optical instruments chapter case study question with answers, cbse 12th physics nuclei chapter case study question with answers, cbse 12th physics moving charges and magnetism chapter case study question with answers, cbse 12th physics electromagnetic induction chapter case study question with answers, cbse 12th physics atoms chapter case study question with answers, 12th physics alternating current chapter case study question with answers cbse, 12th maths vector algebra chapter case study question with answers cbse, 12th maths three dimensional geometry chapter case study question with answers cbse, 12th maths probability chapter case study question with answers cbse, 12th maths linear programming chapter case study question with answers cbse, 12th maths differential equations chapter case study question with answers cbse, 12th maths continuity and differentiability chapter case study question with answers cbse, 12th maths application of integrals chapter case study question with answers cbse, class 12th economics - non-competitive markets case study questions and answers 2022 - 2023.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

12th Standard CBSE Study Materials

12th Standard CBSE Subjects

No products in the cart.

Due to the festival holidays, please expect a delay in the Physical books order dispatch and delivery process.

Computer Science Olympiad (ICSO) Books
English Olympiad (IEO) Books
GK Olympiad (IGKO) Books
Maths Olympiad (IMO) Books
Science Olympiad (NSO) Books
Olympiads Combo Packs
SST Olympiad (ISSO) Books
Hindi Olympiad (IHO) Books
Maths Olympiad (IMO) Books – 9
Commerce Olympiad (ICO) Books
NEET Champion
NEET Previous Years Paper
NEET Sample Paper
NEET Crash Course
Online Tests
NCERT Fingertips
NEET Biology Books
NEET Physics Books
NEET Chemistry Books
Assertion & Reason
AIIMS Previous Years Paper
GK & Aptitude
JIPMER Previous Years Paper
JEE Main Guide
JEE PREVIOUS YEARS PAPER
JEE Sample Papers
JEE Crash Course
JEE Champion
JEE Mathematics Books
JEE Physics Books
JEE Chemistry Books
KCET Books – Karnataka CET
KEAM Books – Kerala Engineering Exam
WBJEE Books – West Bengal JEE
BITSAT Exam Books
MHT CET Books – Maharashtra CET
Live Classes
Recorded Classes
Monthly Magazine – Single Issue
Monthly Magazines – Subscription
Monthly Magazine: Older Volumes
Foundation Course Class 6
Foundation Course Class 7
Foundation Course Class 8
Foundation Course Class 9
Foundation Course Class 10
NCERT Solutions Class 6
NCERT Solutions Class 7
NCERT Solutions Class 8
NCERT Solutions Class 9
NCERT Solutions Class 10
NCERT Solutions Class 11
NCERT Solutions Class 12
CBSE Class 9 Books
CBSE Class 10 Reference Books
CBSE Class 10 Sample Paper Books
CBSE Class 10 Previous Year Solved Paper Books
CBSE Class 11 Books
CBSE Reference Books for Class 12
CBSE Previous Year Papers class 12 Books
CBSE Sample Papers for Class 12
Competitive Books
Olympiad Books
Govt. Exams
21 Science Crossword Puzzles
51 English Grammar Worksheets
IGKO Online Test Programme
Literature Books
Vedic Mathematics
Science Skill Development
Mathematics Skill Development
English Skill Development
Summer Programme Combo
Psychometric Online Test
General ebooks

Click on the image to zoom in

Read reviews (0)

Write a review

Score More Case Study Chapter wise Practice Questions Chemistry Class-12

₹ 125.00 ₹ 93.75 (25% Off)

Discount offer on this book in a bundle, click to view

ScoreMore Case Study Chapter-wise Practice Questions Chemistry Class-12 is curated with 800+ Chapter-wise MCQs related to Case study/ Passage based and Assertion & Reason with hints and explanations based on latest pattern of CBSE (2020-2021).

89 in stock

Your security guaranteed

Description
Table of content
Additional information
Reviews (0)

MTG ScoreMore Case Study Based Sample Questions Chemistry Class 12 is specially designed to help students get familiar with solving these new patterns of questions. The book covers 800 + sample questions for practice with detailed explanations to each question. Practising these questions will definitely help students to get an edge in their CBSE preparations.

For the academic year 2020-21 CBSE has incorporated more Objective type/MCQ based questions which will focus on measuring critical thinking ability of students.

The new pattern of questions includes Case study based questions, Passage based questions, Assertion and Reason type questions. In Case study based/ Passage based questions, students will be expected to answer questions after reading a given paragraph or a passage. Assertion and Reason type question is just another way of checking the clarity of one’s concept.

1. The Solid State
2. Solutions
3. Electrochemistry
4. Chemical Kinetics
5. Surface Chemistry
6. General Principles and Processes of Isolation of Elements*
7. The p-Block Elements
8. The d- and f-Block Elements
9. Coordination Compounds
10. Haloalkanes and Haloarenes
11. Alcohols, Phenols and Ethers
12. Aldehydes, Ketones and Carboxylic Acids
14. Biomolecules
15. Polymers*
16. Chemistry in Everyday Life*
*This chapter is not a part of the Board Examination 2020-21 syllabus

There are no reviews yet.

Your email address will not be published. Required fields are marked *

Your review *

Name *

Email *

Save my name, email, and website in this browser for the next time I comment.

Customers prefer to buy this combination offer...

Score More Case Study Chapter wise Practice Questions Combo-Phy,Chem, Bio,Maths Class-12

Total Price = ₹ 500.00

Combo Price = ₹ 375.00

Score More Case Study Chapter wise Practice Questions Biology Class-12

Score More Case Study Chapter wise Practice Questions Maths Class-12

Score More Case Study Chapter wise Practice Questions Physics Class-12

Notifications
Institutional Queries

Username or Email Address

Class Select Class Class 1 Class 2 Class 3 Class 4 Class 5 Class 6 Class 7 Class 8 Class 9 Class 10 Class 11 Class 12 Pre-Nursery

Phone number

Class Select Class Class 1 Class 2 Class 3 Class 4 Class 5 Class 6 Class 7 Class 8 Class 9 Class 10 Class 11 Class 12 Others Pre-Nursery

Country * Afghanistan Åland Islands Albania Algeria American Samoa Andorra Angola Anguilla Antarctica Antigua and Barbuda Argentina Armenia Aruba Australia Austria Azerbaijan Bahamas Bahrain Bangladesh Barbados Belarus Belau Belgium Belize Benin Bermuda Bhutan Bolivia Bonaire, Saint Eustatius and Saba Bosnia and Herzegovina Botswana Bouvet Island Brazil British Indian Ocean Territory Brunei Bulgaria Burkina Faso Burundi Cambodia Cameroon Canada Cape Verde Cayman Islands Central African Republic Chad Chile China Christmas Island Cocos (Keeling) Islands Colombia Comoros Congo (Brazzaville) Congo (Kinshasa) Cook Islands Costa Rica Croatia Cuba Curaçao Cyprus Czech Republic Denmark Djibouti Dominica Dominican Republic Ecuador Egypt El Salvador Equatorial Guinea Eritrea Estonia Eswatini Ethiopia Falkland Islands Faroe Islands Fiji Finland France French Guiana French Polynesia French Southern Territories Gabon Gambia Georgia Germany Ghana Gibraltar Greece Greenland Grenada Guadeloupe Guam Guatemala Guernsey Guinea Guinea-Bissau Guyana Haiti Heard Island and McDonald Islands Honduras Hong Kong Hungary Iceland India Indonesia Iran Iraq Ireland Isle of Man Israel Italy Ivory Coast Jamaica Japan Jersey Jordan Kazakhstan Kenya Kiribati Kuwait Kyrgyzstan Laos Latvia Lebanon Lesotho Liberia Libya Liechtenstein Lithuania Luxembourg Macao Madagascar Malawi Malaysia Maldives Mali Malta Marshall Islands Martinique Mauritania Mauritius Mayotte Mexico Micronesia Moldova Monaco Mongolia Montenegro Montserrat Morocco Mozambique Myanmar Namibia Nauru Nepal Netherlands New Caledonia New Zealand Nicaragua Niger Nigeria Niue Norfolk Island North Korea North Macedonia Northern Mariana Islands Norway Oman Pakistan Palestinian Territory Panama Papua New Guinea Paraguay Peru Philippines Pitcairn Poland Portugal Puerto Rico Qatar Reunion Romania Russia Rwanda São Tomé and Príncipe Saint Barthélemy Saint Helena Saint Kitts and Nevis Saint Lucia Saint Martin (Dutch part) Saint Martin (French part) Saint Pierre and Miquelon Saint Vincent and the Grenadines Samoa San Marino Saudi Arabia Senegal Serbia Seychelles Sierra Leone Singapore Slovakia Slovenia Solomon Islands Somalia South Africa South Georgia/Sandwich Islands South Korea South Sudan Spain Sri Lanka Sudan Suriname Svalbard and Jan Mayen Sweden Switzerland Syria Taiwan Tajikistan Tanzania Thailand Timor-Leste Togo Tokelau Tonga Trinidad and Tobago Tunisia Turkey Turkmenistan Turks and Caicos Islands Tuvalu Uganda Ukraine United Arab Emirates United Kingdom (UK) United States (US) United States (US) Minor Outlying Islands Uruguay Uzbekistan Vanuatu Vatican Venezuela Vietnam Virgin Islands (British) Virgin Islands (US) Wallis and Futuna Western Sahara Yemen Zambia Zimbabwe

Mobile number *

Email address *

Password *

Lost your password? Please enter your username or email address. You will receive a link to create a new password via email.

Username or email

Reset password

Just remembered? Log In Instead

Don’t have an account? Register with us

Case Based Questions Test: Chemical Kinetics - NEET MCQ

15 questions mcq test - case based questions test: chemical kinetics, read the passage given below and answer the following questions: the rate of a reaction, which may also be called its velocity or speed, can be defined with relation to the concentration of any of the reacting substances, or to that of any product of the reaction. if the species chosen is a reactant which has a concentration c at time t the rate is - dc/dt, while the rate with reference to a product having a concentration x at time t is dx/dt. any concentration units may be used for expressing the rate; thus, if moles per liter are employed for concentration and seconds for the time, the units for the rate are moles litre –1 sec –1 . for gas reactions pressure units are sometimes used in place of concentrations, so that legitimate units for the rate would be (mm. hg) sec –1 and atm. sec –1 the order of a reaction concerns the dependence of the rate upon the concentrations of reacting substances; thus, if the rate is found experimentally to be proportional to the ath power of the concentration of one of the reactants a, to the both power of the concentration of a second reactant b, and so forth, via., rate = k c a α c a β the over-all order of the reaction is simply n = α + β + ----- (2) such a reaction is said to be of the α th order with respect to the substance a, the β th order with respect to b. in the following questions, a statement of assertion followed by a statement of reason is given. choose the correct answer out of the following choices on the basis of the above passage. assertion: rate of reaction is a measure of change in concentration of reactant with respect to time. reason: rate of reaction is a measure of change in concentration of product with respect to time..

A. Assertion and reason both are correct statements and reason is correct explanation for assertion.
B. Assertion and reason both are correct statements but reason is not correct explanation for assertion.
C. Assertion is correct statement but reason is wrong statement.
D. Assertion is wrong statement but reason is correct statement.

Read the passage given below and answer the following questions: The rate of a reaction, which may also be called its velocity or speed, can be defined with relation to the concentration of any of the reacting substances, or to that of any product of the reaction. If the species chosen is a reactant which has a concentration c at time t the rate is - dc/dt, while the rate with reference to a product having a concentration x at time t is dx/dt. Any concentration units may be used for expressing the rate; thus, if moles per liter are employed for concentration and seconds for the time, the units for the rate are moles litre –1 sec –1 . For gas reactions pressure units are sometimes used in place of concentrations, so that legitimate units for the rate would be (mm. Hg) sec –1 and atm. sec –1 The order of a reaction concerns the dependence of the rate upon the concentrations of reacting substances; thus, if the rate is found experimentally to be proportional to the ath power of the concentration of one of the reactants A, to the both power of the concentration of a second reactant B, and so forth, via., rate = k C A α C A β the over-all order of the reaction is simply n = α + β + ----- (2) Such a reaction is said to be of the α th order with respect to the substance A, the β th order with respect to B. In the following questions, a statement of Assertion followed by a statement of Reason is given. Choose the correct answer out of the following choices on the basis of the above passage. Assertion: The unit of k is independent of order of reaction. Reason: The unit of k is moles L –1 s –1 .

Read the passage given below and answer the following questions: the rate of a reaction, which may also be called its velocity or speed, can be defined with relation to the concentration of any of the reacting substances, or to that of any product of the reaction. if the species chosen is a reactant which has a concentration c at time t the rate is - dc/dt, while the rate with reference to a product having a concentration x at time t is dx/dt. any concentration units may be used for expressing the rate; thus, if moles per liter are employed for concentration and seconds for the time, the units for the rate are moles litre –1 sec –1 . for gas reactions pressure units are sometimes used in place of concentrations, so that legitimate units for the rate would be (mm. hg) sec –1 and atm. sec –1 the order of a reaction concerns the dependence of the rate upon the concentrations of reacting substances; thus, if the rate is found experimentally to be proportional to the ath power of the concentration of one of the reactants a, to the both power of the concentration of a second reactant b, and so forth, via., rate = k c a α c a β the over-all order of the reaction is simply n = α + β + ----- (2) such a reaction is said to be of the α th order with respect to the substance a, the β th order with respect to b. in the following questions, a statement of assertion followed by a statement of reason is given. choose the correct answer out of the following choices on the basis of the above passage. assertion: for a reaction: p + 2q → products, rate = k [p] 1/2 [q] 1 so the order of reaction is 1.5 reason: order of reaction is the sum of stoichiometric coefficients of the reactants..

A. Assertion and reason both are correct statements and reason is the correct explanation for assertion.

Order of reaction may or may not be equal to the sum of stoichiometric coefficients.

Read the passage given below and answer the following questions:

The rate of a reaction, which may also be called its velocity or speed, can be defined with relation to the concentration of any of the reacting substances, or to that of any product of the reaction. If the species chosen is a reactant which has a concentration c at time t the rate is - dc/dt, while the rate with reference to a product having a concentration x at time t is dx/dt. Any concentration units may be used for expressing the rate; thus, if moles per liter are employed for concentration and seconds for the time, the units for the rate are moles litre –1 sec –1 . For gas reactions pressure units are sometimes used in place of concentrations, so that legitimate units for the rate would be (mm. Hg) sec –1 and atm. sec –1 The order of a reaction concerns the dependence of the rate upon the concentrations of reacting substances; thus, if the rate is found experimentally to be proportional to the ath power of the concentration of one of the reactants A, to the both power of the concentration of a second reactant B, and so forth, via., rate = k C A α C A β the over-all order of the reaction is simply n = α + β + ----- (2) Such a reaction is said to be of the α th order with respect to the substance A, the β th order with respect to B.

In the following questions, a statement of Assertion followed by a statement of Reason is given. Choose the correct answer out of the following choices on the basis of the above passage.

Assertion: Reactions can occur at different speeds.

Reason: Rate of reaction is also called speed of reaction.

The rate of the reaction is proportional to the concentration of the reactant. Hydrogenation of ethene results in the formation of ethane. The rate constant, k for the reaction was found to be 2.5 × 10 –15 s –1 . The concentration of the reactant reduces to one-third of the initial concentration in 5 minutes. The following questions are multiple choice questions. Choose the most appropriate answer:

Q. Find the order of reaction:

A. Zero order
B. First order
C. Second order
D. Fractional order

Q. The half-life for the reaction is:

A. 2.772 × 10 –24 s
B. 2.772 × 10 –12 s
C. 1.386 × 10 –24 s
D. 1.386 × 10 –12 s

Q. The rate law equation is:

A. Rate = k [C 2 H 6 ]
B. Rate = k [C 2 H 4 ] 2
C. Rate = k [C 2 H 4 ]
D. Rate = k [C 2 H 4 ] 2

Rate law equation, Rate = K [C 2 H 4 ]

Q. The rate constant of the reaction after 5 minutes is:

A. 0.4290 min –1
B. 0.1297 min –1
C. 0.2197 min –1
D. 0.6591 min –1

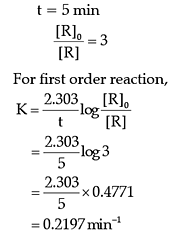
Concentration dependence of rate is called differential rate equation. Integrated differential equations give relation between directly measured experimental data i.e. concentration at different times and rate constant. The integrated rate equations are different for the reactions of different reaction orders. The first-order reaction has a rate constant 1.15 × 10 –3 s –1 .

The following questions are multiple choice questions. Choose the most appropriate answer:

Q. How long will 5g of this reactant take to reduce to 3g?

A. 222.189 s
B. 444.379 s
C. 111.095 s
D. 888.789 s

Final concentration = 3 g

Rate constant= 1.15 × 10 –3 s –1

We know that for a First order reaction

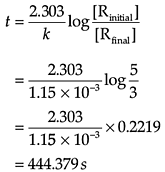
Q. Under which condition a bimolecular reaction is kinetically first order reaction:

A. When two reactants are involved.
B. When one of the reactants is in excess.
C. When one of the reactants does not involve in reaction.
D. None of these.

Q. When the rate constant has same units as the rate of reaction, the order of the reaction is:

r = k [A] 0

Unit of rate = mol L –1 s –1

Unit of k = mol L –1 s –1

Q. For a reaction,

A + H 2 O → B

The order of the reaction is:

B. Fractional order
C. Pseudo first order
D. Second order

r ∝ [A] (∵ [H 2 O] = excess)

It is called a pseudo first order reaction.

The half-life of a reaction is the time required for the concentration of reactant to decrease by half, i.e.,

[A] t = [A]/2

For first order reaction,

t 1/2 = 0.693/k

This means t 1/2 is independent of initial concentration. Figure shows that typical variation of concentration of reactant exhibiting first order kinetics. It may be noted that though the major portion of the first order kinetics may be over in a finite time, but the reaction will never cease as the concentration of reactant will be zero only at infinite time.

Q. A first order reaction has a rate constant k = 3.01 x 10 -3 /s. How long it will take to decompose half of the reactant?

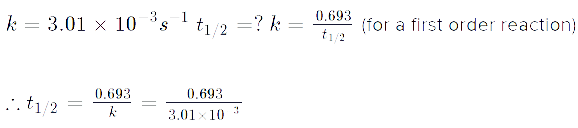
Q. For the half-life period of a first order reaction, which one of the following statements is generally false?

A. It is independent of initial concentration.
B. It is independent of temperature.
C. It decreases with the introduction of a catalyst.

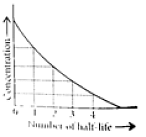
Q. The rate of a first order reaction is 0.04 mol L -1 s -1 at 10 minutes and 0.03 mol L -1 s -1 at 20 minutes after initiation. The half life of the reaction is

A. 4.408 min
B. 44.086 min
C. 24.086 min
D. 2.408 min

Substitute values in the above expression.

0.04=K[A] 10 ......(1)

0.03=K[A] 20 ......(2)

Divide equation (1) by equation (2).

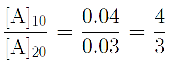
Top Courses for NEET

Important Questions for Case Based Questions Test: Chemical Kinetics

Case based questions test: chemical kinetics mcqs with answers, online tests for case based questions test: chemical kinetics, welcome back, create your account for free.

Forgot Password

Physical Chemistry

Inorganic chemistry, organic chemistry, chemical kinetics · chemistry · class 12, mcq (single correct answer).

Login | Register
Full Course
Full Course (English)
Bio Masterclass
All Courses
NCERT Ebooks
Chapter DPPs
Chapter Journey
PYQ Marked NCERT
Bridge (X- > XI)
Leaderboard

Are you sure?

This action cannot be undone. This will permanently delete All Practiced Questions.

Only bookmarked questions of selected question set or default questions are shown here. Click Here to view all bookmarked questions of the chapter

Question No.

1 (current)

Hydrogenation of vegetable ghee at 25 0 C reduces pressure of H 2 from 2 atom to 1.2 atom in 50 minute. The rate of reaction in terms of molarity per second is:

1. 1.09 x 10 -6

2. 1.09 x 10 -5

3. 1.09 x 10 -7

4. 1.09 x 10 -8

Other Reason

A hypothetical reaction, A 2 +B 2 → 2AB mechanism as given below;

A 2 ⇌ A+ A ............(Fast)

A+B 2 → AB + B ............(Slow)

A+ B → AB ............(Fast)

The order of the overall reaction is:

Following mechanism has been proposed for a reaction,

2A+B → D+E

A+B → C+D ...(Slow)

A+ C → E ...(Fast)

The rate law expression for the reaction is:

1. r = K[A] 2 [B]

2. r=K[A][B]

3. r= K[A] 2

4. r= K[A][C]

In gaseous reactions important for the understanding of the upper atmosphere H 2 O and O react bimolecularly to form two OH radicals. ∆ H for this reaction is 72kJ at 500 K and E a is 77 kJ mol -1 , then E a for the bimolecular recombination of two OH radicals to form H 2 O and O is:

1. 3 kJ mol -1

2. 4 kJ mol -1

3. 5 kJ mol -1

4. 7 kJ mol -1

For a reaction A → Product, rate law is - d [ A ] d t = K [ A ] 0 . The concentration of A left after time t when t = 1 K is:

1. [ A ] 0 e

2. [ A ] 0 × e

3. [ A ] 0 e 2

4. 1 [ A ] 0

For an exothermic chemical process occurring in two steps as;

(i) A+B → X(Slow)

(ii) X → AB (Fast)

The progress of the reaction can be best described by:

For a non-stoichiometric reaction 2A + B → C +D, the following kinetic data were obtained in three separate experiments, all at 298 K.

The rate law for the formation of C is:

1. d[C]/dt = k[ A][B]

2. d[C]/dt = k[ A] 2 [B]

3. d[C]/dt = k[ A][B] 2

4. d[C]/dt = k[ A]

For the reaction N 2 + 3H 2 → 2NH 3 , the rate d [ NH 3 ] dt = 2 x 10 -4 M s -1 . Therefore, the rate - d [ N 2 ] dt is given as:

1. 10 -4 Ms -1

2. 10 4 Ms -1

3. 10 -2 sM -1

4. 10 -4 sM -1

If 'I' is the intensity of absorbed light and 'c' is the concentration of AB for the photochemical process AB + hv→ AB *, the rate of formation of AB * is directly proportional to:

Which curve represents zero order reaction?

[email protected]
S-15, 2nd floor Uphar Cinema Market, above Red Chilli Restaurant, Green Park Extension, New Delhi, 110016

NEET Information

NEET Syllabus
NEET Application Process
NEET Seat Intake
NEET Previous Year Papers
AIIMS Previous Year Papers
NEET Course
NEET Course (English)
NEET Test Series
Terms of Use
Privacy Policy
Refund Policy

Botany Questions

Living World
Biological Classification
Plant Kingdom
Morphology of Flowering Plants
Anatomy of Flowering Plants
Cell-unit of Life
Cell Cycle and Cell Division
Transport in Plants
Mineral Nutrition
Photosynthesis in Higher Plants
Respiration in Plants
Plant Growth and Development
Reproduction in Organisms
Sexual Reproduction in Flowering Plants
Principles of Inheritance and Variation
Molecular Basis of Inheritance
Strategies for Enhancement in Food Production
Microbes in Human Welfare
Organisms and Populations
Biodiversity and Conservation
Environmental Issues

Chemistry Questions

Some Basic Concepts of Chemistry
Structure of Atom
Classification of Elements and Periodicity in Properties
Chemical Bonding and Molecular Structure
States of Matter
Thermodynamics
Equilibrium
Redox Reactions
The s-Block Elements
The p-Block Elements-XI
Organic Chemistry - Some Basic Principles and Techniques
Hydrocarbons
Environmental Chemistry
The Solid State
Electrochemistry
Chemical Kinetics
Surface Chemistry
General Principles and Processes of Isolation of Elements
The p-Block Elements-XII
The d and f Block Elements
Coordination Compounds
Haloalkanes and Haloarenes
Alcohols, Phenols and Ethers
Aldehydes, Ketones and Carboxylic Acids
Biomolecules
Chemistry in Everyday Life

Physics Questions

Units and Measurement
Mathematical Tools
Motion in A Straight Line
Motion in A Plane
Laws of Motion
Work, Energy and Power
Systems of Particles and Rotational Motion
Gravitation
Mechanical Properties of Solids
Mechanical Properties of Fluids
Thermal Properties of Matter
Kinetic Theory of Gases
Oscillations
Electric Charges and Fields
Electrostatic Potential and Capacitance
Current Electricity
Moving Charges and Magnetism
Magnetism and Matter
Electromagnetic Induction
Alternating Current
Electromagnetic Waves
Ray Optics and Optical Instruments
Wave Optics
Dual Nature of Radiation and Matter
Semiconductor Electronics

Zoology Questions

Animal Kingdom
Structural Organisation in Animals
Digestion and Absorption
Breathing and Exchange of Gases
Body Fluids and Circulation
Excretory Products and their Elimination
Locomotion and Movement
Neural Control and Coordination
Chemical Coordination and Integration
Human Reproduction
Reproductive Health
Human Health and Disease
Biotechnology Principles and Processes
Biotechnology and its Application

IMAGES

SOLUTION: Chemical kinetics Quiz Questions
SOLUTION: Chemical kinetics practice quiz soved
15 Chemical Kinetics
Quiz & Worksheet
Chemical Kinetics Practice Questions
chemical kinetics questions and answers

VIDEO

IAS Chemistry Edexcel Unit 2 Ch 6
Practice Questions of Chemical Kinetics
Chemical Kinetics
As Chemistry: Reaction Kinetics (Complete) with past paper questions
Kinetic Model of Matter Exercise 2 doubts Cambridge IG/ O level Physics 0625 0972 5054 Lesson 39f
Chemical Kinetics

COMMENTS

Chemical Kinetics Case Study Questions With Answers
Class 12 Chemistry Case Study Questions Chapter 4 Chemical Kinetics . In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Chemistry Chapter 4 Chemical Kinetics Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam ...
CBSE 12th Chemistry Chemical Kinetics Case Study Questions 2021
CBSE 12th Standard Chemistry Subject Chemical Kinetics Case Study Questions 2021. \ (t_ {1 / 2}=\frac {0.693} {k}\) this means t 1/2 is independent of initial concentration. Figure shows that typical variation of concentration of reactant exhibiting first order kinetics. It may be noted that though the major portion of the first order kinetics ...
Case Study Questions for Class 12 Chemistry Chapter 4 Chemical Kinetics
Here are the questions based on case study. Case Study Question 1: Read the passage given below and answer the following questions: The half-life of a reaction is the time required for the concentration of reactant to decrease by half, i.e., [A] t = [A]/2. For first order reaction, t 1/2 = 0.693/k.
Case Study on Chemical Kinetics Class 12 Chemistry PDF
The PDF file of the Chemical Kinetics Case Study for Class 12 Chemistry with Solutions is a very important study resource that can help students better prepare for the exam and boost conceptual learning. The solutions are in the hint manner as well as contain full examples too, refer to the link to access the Case Study on Chemical Kinetics ...
1.E: Kinetics (Practice Problems with Answers)
Explain this phenomenon. 1.E: Kinetics (Practice Problems with Answers) is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts. These are homework exercises to accompany the Textmap created for "Chemistry: The Central Science" by Brown et al.
8.3: Kinetics and the Mechanisms of Reactions
We can do a similar analysis for a reaction that might be second order in [A]: rate = k[A]2. In this case, we can manipulate the rate equation and integrate to give the equation: 1 / [A]t = kt + 1 / [A]0. Therefore, plotting 1 / [A] versus t would give a straight line, with a slope of k, the rate constant.
Case Study Questions for Class 12 Chemistry Chapter 4 Chemical Kinetics
Important Questions, MCQ's, NCERT Solutions - Class 12 Chemistry . Get here all the Important questions for Class 12 Chemistry chapter wise as free PDF download. Here you will get Extra Important Questions with answers, Numericals and Multiple Choice Questions (MCQ's) chapter wise in Printable format. Solving Chapter wise questions is one of the best ways to prepare for the examination.
Category: Case Study Based Questions for Class 12 Chemistry
Case Study Questions for Class 12 Chemistry Chapter 4 Chemical Kinetics. April 12, 2021 May 6, ... Case Study Questions for Class 9 Science Chapter 1 Matter in Our Surroundings; An Imperial Capital - Vijayanagara Assertion Reason Questions for CBSE Class 12 History Chapter 7;
4.9: Exercises on Chemical Kinetics
4.9: Exercises on Chemical Kinetics. These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here.
Case Study Question 1 on Chemical Kinetics
The kinetics of the reaction. mA + nB + pC —-> m′X + n′Y + p′Z. obey the rate expression dx/dt = k [A] m[B] n. Calculate total order and molecularity of the reaction. Ans. The total order of reaction = m + n. The molecularity of the reaction = m + n + p. Case Study Question 1 on Chemical Kinetics - Chapter 4 Read the given passages ...
Class 12 Chemistry Case Study Questions PDF Download
We have provided here Case Study questions for the Class 12 Chemistry Final Board exams. You can read these chapter-wise Case Study questions. ... Chemical Kinetics: 15: 7: 4: d -and f -Block Elements: 18: 7: 5: Coordination Compounds: 18: 7: 6: Haloalkanes and Haloarenes: 15: 6: 7: Alcohols, Phenols and Ethers: 14: 6: 8:
Chemical kinetics
Physical Chemistry (Essentials) - Class 12 3 units · 23 skills. Unit 1 Electrochemistry. Unit 2 Solid state. Unit 3. Course challenge. Test your knowledge of the skills in this course. Start Course challenge. Science. Physical Chemistry (Essentials) - Class 12.
Chemical Kinetics Questions
The study of Kinetics involves the factors affecting the rate of the chemical reactions, the mechanisms and the transitions states involved, if any. Definition: It is the area of chemistry that deals with the rate of the reactions and also with the sequence of steps in which the reaction takes place.
Important Questions for Class 12 Chemistry Chapter 4
Class 12 Chemical Kinetics Important Questions with Answers Short Answer Type Questions. Q1. State a condition under which a bimolecular reaction is kinetically a first order reaction. Answer: This is possible in case one of the reactants is taken in large excess so that its concentration changes very slightly in the reaction.
Thermodynamics Questions
Many chemical reactions exhibit the same behaviour. Q3: Write the rate equation for the reaction 2A + B → C if the order of the reaction is zero. Answer: The rate equation for the reaction 2A + B → C in the zero order reaction is, Rate = k [A] 0 [B] 0 = k. Q4: Although the reaction between H 2 (g) and O 2 (g) is highly feasible, leaving the ...
CBSE Class 12 Chemistry Case Study : Questions With Solutions
Class 12 Chemistry Case Study Questions for Term 1 exam includes The Solid State, The P block elements, Haloalkanes and Haloarenes, Biomolecules, etc. Questions for all these chapters are given in the PDF file that are available here for free to download. Term 1 exam is about to be held in November-December this year.
CBSE Class 12 Chemistry Chapter 4
Boost Your Performance in CBSE Class 12 Chemistry Exam Chapter 4 with Important Questions. 1. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds. Ans: $\text { Average rate of reaction }=-\dfrac {\Delta\text ...
12th Chemistry Chemical Kinetics Chapter Case Study Question with
12th Chemistry CBSE case study questions for Chemical Kinetics - 2024. CBSE 12th Chemistry Chemical Kinetics Case Study Question & Answers . CBSE 12th Chemistry Chemical Kinetics Chapter Case Study Question with Answers. CBSE Class 12th Chemistry Sample Model Question Papers. CBSE Class 12th Chemistry Sample Case Study Questions with Answer Keys.
Important Questions for Class 12 Chemistry Chapter 4 Chemical Kinetics
Chemical Kinetics Class 12 Important Questions Short Answer Type - II [SA-II] Question 42. A first order reaction has a rate constant of 0.0051 min-1. If we begin with 0.10 M concentration of the reactant, what concentration of reactant will remain in solution after 3 hours? (Delhi & All India 2009) Answer: Given : [R] 0 = 0.10 M, t = 3 hrs ...
Score More Case Study Chapter wise Practice Questions Chemistry Class
Discount offer on this book in a bundle, click to view. ScoreMore Case Study Chapter-wise Practice Questions Chemistry Class-12 is curated with 800+ Chapter-wise MCQs related to Case study/ Passage based and Assertion & Reason with hints and explanations based on latest pattern of CBSE (2020-2021). See Complete Description of Product. Qty: -. +.
Case Based Questions Test: Chemical Kinetics
The following questions are multiple choice questions. Choose the most appropriate answer: Q. The half-life for the reaction is: A. 2.772 × 10-24 s. B. 2.772 × 10-12 s. C. 1.386 × 10-24 s. D. 1.386 × 10-12 s. Detailed Solution for Case Based Questions Test: Chemical Kinetics - Question 6.
Chemical Kinetics · Chemistry · Class 12
Questions. Joint Entrance Examination. JEE Main. Physics Chemistry Mathematics . JEE Advanced. Physics Chemistry Mathematics . WB JEE. Physics Chemistry Mathematics . ... Chemical Kinetics · Chemistry · Class 12 Start Practice. MCQ (Single Correct Answer) CBSE 12th Chemistry Delhi Set 1 - 2023.
Chemical Kinetics Chemistry NEET Practice Questions, MCQs, Past Year
Chemical Kinetics Chemistry Practice questions, MCQs, Past Year Questions (PYQs), NCERT Questions, Question Bank, Class 11 and Class 12 Questions, NCERT Exemplar Questions and PDF Questions with answers, solutions, explanations, NCERT reference and difficulty level +91-8527521718.