add decimals practice and homework lesson 3 8

Decimals Worksheets

Thanks for visiting the Decimals Worksheets page at Math-Drills.Com where we make a POINT of helping students learn. On this page, you will find Decimals worksheets on a variety of topics including comparing and sorting decimals, adding, subtracting, multiplying and dividing decimals, and converting decimals to other number formats. To start, you will find the general use printables to be helpful in teaching the concepts of decimals and place value. More information on them is included just under the sub-title.

Further down the page, rounding, comparing and ordering decimals worksheets allow students to gain more comfort with decimals before they move on to performing operations with decimals. There are many operations with decimals worksheets throughout the page. It would be a really good idea for students to have a strong knowledge of addition, subtraction, multiplication and division before attempting these questions.

Most Popular Decimals Worksheets this Week

Grids and Charts Useful for Learning Decimals

General use decimal printables are used in a variety of contexts and assist students in completing math questions related to decimals.

The thousandths grid is a useful tool in representing decimals. Each small rectangle represents a thousandth. Each square represents a hundredth. Each row or column represents a tenth. The entire grid represents one whole. The hundredths grid can be used to model percents or decimals. The decimal place value chart is a tool used with students who are first learning place value related to decimals or for those students who have difficulty with place value when working with decimals.

• Thousandths and Hundredths Grids Thousandths Grid Hundredths Grids ( 4 on a page) Hundredths Grids ( 9 on a page) Hundredths Grids ( 20 on a page)
• Decimal Place Value Charts Decimal Place Value Chart ( Ones to Hundredths ) Decimal Place Value Chart ( Ones to Thousandths ) Decimal Place Value Chart ( Hundreds to Hundredths ) Decimal Place Value Chart ( Thousands to Thousandths ) Decimal Place Value Chart ( Hundred Thousands to Thousandths ) Decimal Place Value Chart ( Hundred Millions to Millionths )

Decimals in Expanded Form

For students who have difficulty with expanded form, try familiarizing them with the decimal place value chart, and allow them to use it when converting standard form numbers to expanded form. There are actually five ways (two more than with integers) to write expanded form for decimals, and which one you use depends on your application or preference. Here is a quick summary of the various ways using the decimal number 1.23. 1. Expanded Form using decimals: 1 + 0.2 + 0.03 2. Expanded Form using fractions: 1 + 2 ⁄ 10 + 3 ⁄ 100 3. Expanded Factors Form using decimals: (1 × 1) + (2 × 0.1) + (3 × 0.01) 4. Expanded Factors Form using fractions: (1 × 1) + (2 × 1 ⁄ 10 ) + (3 × 1 ⁄ 100 ) 5. Expanded Exponential Form: (1 × 10 0 ) + (2 × 10 -1 ) + (3 × 10 -2 )

• Converting Decimals from Standard Form to Expanded Form Using Decimals Converting Decimals from Standard to Expanded Form Using Decimals ( 3 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 4 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 5 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 6 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 7 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 8 Decimal Places) Converting Decimals from Standard to Expanded Form Using Decimals ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Form Using Fractions Converting Decimals from Standard to Expanded Form Using Fractions ( 3 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 4 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 5 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 6 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 7 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 8 Decimal Places) Converting Decimals from Standard to Expanded Form Using Fractions ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Factors Form Using Decimals Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 3 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 4 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 5 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 6 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 7 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 8 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Decimals ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Factors Form Using Fractions Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 3 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 4 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 5 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 6 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 7 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 8 Decimal Places) Converting Decimals from Standard to Expanded Factors Form Using Fractions ( 9 Decimal Places)
• Converting Decimals from Standard Form to Expanded Exponential Form Converting Decimals from Standard to Expanded Exponential Form ( 3 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 4 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 5 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 6 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 7 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 8 Decimal Places) Converting Decimals from Standard to Expanded Exponential Form ( 9 Decimal Places)
• Retro Converting Decimals from Standard Form to Expanded Form Retro Standard to Expanded Form (3 digits before decimal; 2 after) Retro Standard to Expanded Form (4 digits before decimal; 3 after) Retro Standard to Expanded Form (6 digits before decimal; 4 after) Retro Standard to Expanded Form (12 digits before decimal; 3 after)
• Retro European Format Converting Decimals from Standard Form to Expanded Form Standard to Expanded Form (3 digits before decimal; 2 after) Standard to Expanded Form (4 digits before decimal; 3 after) Standard to Expanded Form (6 digits before decimal; 4 after)

Of course, being able to convert numbers already in expanded form to standard form is also important. All five versions of decimal expanded form are included in these worksheets.

• Converting Decimals to Standard Form from Expanded Form Using Decimals Converting Decimals from Expanded Form Using Decimals to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Form Using Decimals to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Form Using Fractions Converting Decimals from Expanded Form Using Fractions to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Form Using Fractions to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Factors Form Using Decimals Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Factors Form Using Decimals to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Factors Form Using Fractions Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Factors Form Using Fractions to Standard Form ( 9 Decimal Places)
• Converting Decimals to Standard Form from Expanded Exponential Form Converting Decimals from Expanded Exponential Form to Standard Form ( 3 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 4 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 5 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 6 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 7 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 8 Decimal Places) Converting Decimals from Expanded Exponential Form to Standard Form ( 9 Decimal Places)
• Retro Converting Decimals to Standard Form from Expanded Form Retro Expanded to Standard Form (3 digits before decimal; 2 after) Retro Expanded to Standard Form (4 digits before decimal; 3 after) Retro Expanded to Standard Form (6 digits before decimal; 4 after) Retro Expanded to Standard Form (12 digits before decimal; 3 after)
• Retro European Format Converting Decimals to Standard Form from Expanded Form Retro European Format Expanded to Standard Form (3 digits before decimal; 2 after) Retro European Format Expanded to Standard Form (4 digits before decimal; 3 after) Retro European Format Expanded to Standard Form (6 digits before decimal; 4 after)

Rounding Decimals Worksheets

Rounding decimals is similar to rounding whole numbers; you have to know your place value! When learning about rounding, it is also useful to learn about truncating since it may help students to round properly. A simple strategy for rounding involves truncating, using the digits after the truncation to determine whether the new terminating digit remains the same or gets incremented, then taking action by incrementing if necessary and throwing away the rest. Here is a simple example: Round 4.567 to the nearest tenth. First, truncate the number after the tenths place 4.5|67. Next, look at the truncated part (67). Is it more than half way to 99 (i.e. 50 or more)? It is, so the decision will be to increment. Lastly, increment the tenths value by 1 to get 4.6. Of course, the situation gets a little more complicated if the terminating digit is a 9. In that case, some regrouping might be necessary. For example: Round 6.959 to the nearest tenth. Truncate: 6.9|59. Decide to increment since 59 is more than half way to 99. Incrementing results in the necessity to regroup the tenths into an extra one whole, so the result is 7.0. Watch that students do not write 6.10. You will want to correct them right away in that case. One last note: if there are three truncated digits then the question becomes is the number more than half way to 999. Likewise, for one digit; is the number more than half way to 9. And so on...

We should also mention that in some scientific and mathematical "circles," rounding is slightly different "on a 5". For example, most people would round up on a 5 such as: 6.5 --> 7; 3.555 --> 3.56; 0.60500 --> 0.61; etc. A different way to round on a 5, however, is to round to the nearest even number, so 5.5 would be rounded up to 6, but 8.5 would be rounded down to 8. The main reason for this is not to skew the results of a large number of rounding events. If you always round up on a 5, on average, you will have slightly higher results than you should. Because most pre-college students round up on a 5, that is what we have done in the worksheets that follow.

• Rounding Decimals to Whole Numbers Round Tenths to a Whole Number Round Hundredths to a Whole Number Round Thousandths to a Whole Number Round Ten Thousandths to a Whole Number Round Various Decimals to a Whole Number
• Rounding Decimals to Tenths Round Hundredths to Tenths Round Thousandths to Tenths Round Ten Thousandths to Tenths Round Various Decimals to Tenths
• Rounding Decimals to Hundredths Round Thousandths to Hundredths Round Ten Thousandths to Hundredths Round Various Decimals to Hundredths
• Rounding Decimals to Thousandths Round Ten Thousandths to Thousandths
• Rounding Decimals to Various Decimal Places Round Hundredths to Various Decimal Places Round Thousandths to Various Decimal Places Round Ten Thousandths to Various Decimal Places Round Various Decimals to Various Decimal Places
• European Format Rounding Decimals to Whole Numbers European Format Round Tenths to a Whole Number European Format Round Hundredths to a Whole Number European Format Round Thousandths to a Whole Number European Format Round Ten Thousandths to Whole Number
• European Format Rounding Decimals to Tenths European Format Round Hundredths to Tenths European Format Round Thousandths to Tenths European Format Round Ten Thousandths to Tenths
• European Format Rounding Decimals to Hundredths European Format Round Thousandths to Hundredths European Format Round Ten Thousandths to Hundredths
• European Format Rounding Decimals to Thousandths European Format Round Ten Thousandths to Thousandths

Comparing and Ordering/Sorting Decimals Worksheets.

The comparing decimals worksheets have students compare pairs of numbers and the ordering decimals worksheets have students compare a list of numbers by sorting them.

Students who have mastered comparing whole numbers should find comparing decimals to be fairly easy. The easiest strategy is to compare the numbers before the decimal (the whole number part) first and only compare the decimal parts if the whole number parts are equal. These sorts of questions allow teachers/parents to get a good idea of whether students have grasped the concept of decimals or not. For example, if a student thinks that 4.93 is greater than 8.7, then they might need a little more instruction in place value. Close numbers means that some care was taken to make the numbers look similar. For example, they could be close in value, e.g. 3.3. and 3.4 or one of the digits might be changed as in 5.86 and 6.86.

• Comparing Decimals up to Tenths Comparing Decimals up to Tenths ( Both Numbers Random ) Comparing Decimals up to Tenths ( One Digit Differs ) Comparing Decimals up to Tenths ( Both Numbers Close in Value ) Comparing Decimals up to Tenths ( Various Tricks )
• Comparing Decimals up to Hundredths Comparing Decimals up to Hundredths ( Both Numbers Random ) Comparing Decimals up to Hundredths ( One Digit Differs ) Comparing Decimals up to Hundredths ( Two Digits Swapped ) Comparing Decimals up to Hundredths ( Both Numbers Close in Value ) Comparing Decimals up to Hundredths ( One Number has an Extra Digit ) Comparing Decimals up to Hundredths ( Various Tricks )
• Comparing Decimals up to Thousandths Comparing Decimals up to Thousandths Comparing Decimals up to Thousandths ( One Digit Differs ) Comparing Decimals up to Thousandths ( Two Digits Swapped ) Comparing Decimals up to Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Thousandths ( Various Tricks )
• Comparing Decimals up to Ten Thousandths Comparing Decimals up to Ten Thousandths Comparing Decimals up to Ten Thousandths ( One Digit Differs ) Comparing Decimals up to Ten Thousandths ( Two Digits Swapped ) Comparing Decimals up to Ten Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Ten Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Ten Thousandths ( Various Tricks )
• Comparing Decimals up to Hundred Thousandths Comparing Decimals up to Hundred Thousandths Comparing Decimals up to Hundred Thousandths ( One Digit Differs ) Comparing Decimals up to Hundred Thousandths ( Two Digits Swapped ) Comparing Decimals up to Hundred Thousandths ( Both Numbers Close in Value ) Comparing Decimals up to Hundred Thousandths ( One Number has an Extra Digit ) Comparing Decimals up to Hundred Thousandths ( Various Tricks )
• European Format Comparing Decimals European Format Comparing Decimals up to Tenths European Format Comparing Decimals up to Tenths (tight) European Format Comparing Decimals up to Hundredths European Format Comparing Decimals up to Hundredths (tight) European Format Comparing Decimals up to Thousandths European Format Comparing Decimals up to Thousandths (tight)

Ordering decimals is very much like comparing decimals except there are more than two numbers. Generally, students determine the least (or greatest) decimal to start, cross it off the list then repeat the process to find the next lowest/greatest until they get to the last number. Checking the list at the end is always a good idea.

• Ordering/Sorting Decimals Ordering/Sorting Decimal Hundredths Ordering/Sorting Decimal Thousandths
• European Format Ordering/Sorting Decimals European Format Ordering/Sorting Decimal Tenths (8 per set) European Format Ordering/Sorting Decimal Hundredths (8 per set) European Format Ordering/Sorting Decimal Thousandths (8 per set) European Format Ordering/Sorting Decimal Ten Thousandths (8 per set) European Format Ordering/Sorting Decimals with Various Decimal Places(8 per set)

Converting Decimals to Fractions and Other Number Formats

There are many good reasons for converting decimals to other number formats. Dealing with a fraction in arithmetic is often easier than the equivalent decimal. Consider 0.333... which is equivalent to 1/3. Multiplying 300 by 0.333... is difficult, but multiplying 300 by 1/3 is super easy! Students should be familiar with some of the more common fraction/decimal conversions, so they can switch back and forth as needed.

• Converting Between Decimals and Fractions Converting Fractions to Terminating Decimals Converting Fractions to Terminating and Repeating Decimals Converting Terminating Decimals to Fractions Converting Terminating and Repeating Decimals to Fractions Converting Fractions to Hundredths
• Converting Between Decimals, Fraction, Percents and Ratios Converting Fractions to Decimals, Percents and Part-to-Part Ratios Converting Fractions to Decimals, Percents and Part-to-Whole Ratios Converting Decimals to Fractions, Percents and Part-to-Part Ratios Converting Decimals to Fractions, Percents and Part-to-Whole Ratios Converting Percents to Fractions, Decimals and Part-to-Part Ratios Converting Percents to Fractions, Decimals and Part-to-Whole Ratios Converting Part-to-Part Ratios to Fractions, Decimals and Percents Converting Part-to-Whole Ratios to Fractions, Decimals and Percents Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios Converting Various Fractions, Decimals, Percents and Part-to-Part Ratios with 7ths and 11ths Converting Various Fractions, Decimals, Percents and Part-to-Whole Ratios with 7ths and 11ths

Adding and Subtracting Decimals

Try the following mental addition strategy for decimals. Begin by ignoring the decimals in the addition question. Add the numbers as if they were whole numbers. For example, 3.25 + 4.98 could be viewed as 325 + 498 = 823. Use an estimate to decide where to place the decimal. In the example, 3.25 + 4.98 is approximately 3 + 5 = 8, so the decimal in the sum must go between the 8 and the 2 (i.e. 8.23)

• Adding Tenths Adding Decimal Tenths with 0 Before the Decimal (range 0.1 to 0.9) Adding Decimal Tenths with 1 Digit Before the Decimal (range 1.1 to 9.9) Adding Decimal Tenths with 2 Digits Before the Decimal (range 10.1 to 99.9)
• Adding Hundredths Adding Decimal Hundredths with 0 Before the Decimal (range 0.01 to 0.99) Adding Decimal Hundredths with 1 Digit Before the Decimal (range 1.01 to 9.99) Adding Decimal Hundredths with 2 Digits Before the Decimal (range 10.01 to 99.99)
• Adding Thousandths Adding Decimal Thousandths with 0 Before the Decimal (range 0.001 to 0.999) Adding Decimal Thousandths with 1 Digit Before the Decimal (range 1.001 to 9.999) Adding Decimal Thousandths with 2 Digits Before the Decimal (range 10.001 to 99.999)
• Adding Ten Thousandths Adding Decimal Ten Thousandths with 0 Before the Decimal (range 0.0001 to 0.9999) Adding Decimal Ten Thousandths with 1 Digit Before the Decimal (range 1.0001 to 9.9999) Adding Decimal Ten Thousandths with 2 Digits Before the Decimal (range 10.0001 to 99.9999)
• Adding Various Decimal Places Adding Various Decimal Places with 0 Before the Decimal Adding Various Decimal Places with 1 Digit Before the Decimal Adding Various Decimal Places with 2 Digits Before the Decimal Adding Various Decimal Places with Various Numbers of Digits Before the Decimal
• European Format Adding Decimals European Format Adding decimal tenths with 0 before the decimal (range 0,1 to 0,9) European Format Adding decimal tenths with 1 digit before the decimal (range 1,1 to 9,9) European Format Adding decimal hundredths with 0 before the decimal (range 0,01 to 0,99) European Format Adding decimal hundredths with 1 digit before the decimal (range 1,01 to 9,99) European Format Adding decimal thousandths with 0 before the decimal (range 0,001 to 0,999) European Format Adding decimal thousandths with 1 digit before the decimal (range 1,001 to 9,999) European Format Adding decimal ten thousandths with 0 before the decimal (range 0,0001 to 0,9999) European Format Adding decimal ten thousandths with 1 digit before the decimal (range 1,0001 to 9,9999) European Format Adding mixed decimals with Various Decimal Places European Format Adding mixed decimals with Various Decimal Places (1 to 9 before decimal)

Base ten blocks can be used for decimal subtraction. Just redefine the blocks, so the big block is a one, the flat is a tenth, the rod is a hundredth and the little cube is a thousandth. Model and subtract decimals using base ten blocks, so students can "see" how decimals really work.

• Subtracting Tenths Subtracting Decimal Tenths with No Integer Part Subtracting Decimal Tenths with an Integer Part in the Minuend Subtracting Decimal Tenths with an Integer Part in the Minuend and Subtrahend
• Subtracting Hundredths Subtracting Decimal Hundredths with No Integer Part Subtracting Decimal Hundredths with an Integer Part in the Minuend and Subtrahend Subtracting Decimal Hundredths with a Larger Integer Part in the Minuend
• Subtracting Thousandths Subtracting Decimal Thousandths with No Integer Part Subtracting Decimal Thousandths with an Integer Part in the Minuend and Subtrahend
• Subtracting Ten Thousandths Subtracting Decimal Ten Thousandths with No Integer Part Subtracting Decimal Ten Thousandths with an Integer Part in the Minuend and Subtrahend
• Subtracting Various Decimal Places Subtracting Various Decimals to Hundredths Subtracting Various Decimals to Thousandths Subtracting Various Decimals to Ten Thousandths
• European Format Subtracting Decimals European Format Decimal subtraction (range 0,1 to 0,9) European Format Decimal subtraction (range 1,1 to 9,9) European Format Decimal subtraction (range 0,01 to 0,99) European Format Decimal subtraction (range 1,01 to 9,99) European Format Decimal subtraction (range 0,001 to 0,999) European Format Decimal subtraction (range 1,001 to 9,999) European Format Decimal subtraction (range 0,0001 to 0,9999) European Format Decimal subtraction (range 1,0001 to 9,9999) European Format Decimal subtraction with Various Decimal Places European Format Decimal subtraction with Various Decimal Places (1 to 9 before decimal)

Adding and subtracting decimals is fairly straightforward when all the decimals are lined up. With the questions arranged horizontally, students are challenged to understand place value as it relates to decimals. A wonderful strategy for placing the decimal is to use estimation. For example if the question is 49.2 + 20.1, the answer without the decimal is 693. Estimate by rounding 49.2 to 50 and 20.1 to 20. 50 + 20 = 70. The decimal in 693 must be placed between the 9 and the 3 as in 69.3 to make the number close to the estimate of 70.

The above strategy will go a long way in students understanding operations with decimals, but it is also important that they have a strong foundation in place value and a proficiency with efficient strategies to be completely successful with these questions. As with any math skill, it is not wise to present this to students until they have the necessary prerequisite skills and knowledge.

• Horizontally Arranged Adding Decimals Adding Decimals to Tenths Horizontally Adding Decimals to Hundredths Horizontally Adding Decimals to Thousandths Horizontally Adding Decimals to Ten Thousandths Horizontally Adding Decimals Horizontally With Up to Two Places Before and After the Decimal Adding Decimals Horizontally With Up to Three Places Before and After the Decimal Adding Decimals Horizontally With Up to Four Places Before and After the Decimal
• Horizontally Arranged Subtracting Decimals Subtracting Decimals to Tenths Horizontally Subtracting Decimals to Hundredths Horizontally Subtracting Decimals to Thousandths Horizontally Subtracting Decimals to Ten Thousandths Horizontally Subtracting Decimals Horizontally With Up to Two Places Before and After the Decimal Subtracting Decimals Horizontally With Up to Three Places Before and After the Decimal Subtracting Decimals Horizontally With Up to Four Places Before and After the Decimal
• Horizontally Arranged Mixed Adding and Subtracting Decimals Adding and Subtracting Decimals to Tenths Horizontally Adding and Subtracting Decimals to Hundredths Horizontally Adding and Subtracting Decimals to Thousandths Horizontally Adding and Subtracting Decimals to Ten Thousandths Horizontally Adding and Subtracting Decimals Horizontally With Up to Two Places Before and After the Decimal Adding and Subtracting Decimals Horizontally With Up to Three Places Before and After the Decimal Adding and Subtracting Decimals Horizontally With Up to Four Places Before and After the Decimal

Multiplying and Dividing Decimals

Multiplying decimals by whole numbers is very much like multiplying whole numbers except there is a decimal to deal with. Although students might initially have trouble with it, through the power of rounding and estimating, they can generally get it quite quickly. Many teachers will tell students to ignore the decimal and multiply the numbers just like they would whole numbers. This is a good strategy to use. Figuring out where the decimal goes at the end can be accomplished by counting how many decimal places were in the original question and giving the answer that many decimal places. To better understand this method, students can round the two factors and multiply in their head to get an estimate then place the decimal based on their estimate. For example, multiplying 9.84 × 91, students could first round the numbers to 10 and 91 (keep 91 since multiplying by 10 is easy) then get an estimate of 910. Actually multiplying (ignoring the decimal) gets you 89544. To get that number close to 910, the decimal needs to go between the 5 and the 4, thus 895.44. Note that there are two decimal places in the factors and two decimal places in the answer, but estimating made it more understandable rather than just a method.

• Multiplying Decimals by 1-Digit Whole Numbers Multiply 2-digit tenths by 1-digit whole numbers Multiply 2-digit hundredths by 1-digit whole numbers Multiply 2-digit thousandths by 1-digit whole numbers Multiply 3-digit tenths by 1-digit whole numbers Multiply 3-digit hundredths by 1-digit whole numbers Multiply 3-digit thousandths by 1-digit whole numbers Multiply various decimals by 1-digit whole numbers
• Multiplying Decimals by 2-Digit Whole Numbers Multiplying 2-digit tenths by 2-digit whole numbers Multiplying 2-digit hundredths by 2-digit whole numbers Multiplying 3-digit tenths by 2-digit whole numbers Multiplying 3-digit hundredths by 2-digit whole numbers Multiplying 3-digit thousandths by 2-digit whole numbers Multiplying various decimals by 2-digit whole numbers
• Multiplying Decimals by Tenths Multiplying 2-digit whole by 2-digit tenths Multiplying 2-digit tenths by 2-digit tenths Multiplying 2-digit hundredths by 2-digit tenths Multiplying 3-digit whole by 2-digit tenths Multiplying 3-digit tenths by 2-digit tenths Multiplying 3-digit hundredths by 2-digit tenths Multiplying 3-digit thousandths by 2-digit tenths Multiplying various decimals by 2-digit tenths
• Multiplying Decimals by Hundredths Multiplying 2-digit whole by 2-digit hundredths Multiplying 2-digit tenths by 2-digit hundredths Multiplying 2-digit hundredths by 2-digit hundredths Multiplying 3-digit whole by 2-digit hundredths Multiplying 3-digit tenths by 2-digit hundredths Multiplying 3-digit hundredths by 2-digit hundredths Multiplying 3-digit thousandths by 2-digit hundredths Multiplying various decimals by 2-digit hundredths
• Multiplying Decimals by Various Decimal Places Multiplying 2-digit by 2-digit numbers with various decimal places Multiplying 3-digit by 2-digit numbers with various decimal places
• Decimal Long Multiplication in Various Ranges Decimal Multiplication (range 0.1 to 0.9) Decimal Multiplication (range 1.1 to 9.9) Decimal Multiplication (range 10.1 to 99.9) Decimal Multiplication (range 0.01 to 0.99) Decimal Multiplication (range 1.01 to 9.99) Decimal Multiplication (range 10.01 to 99.99) Random # Digits Random # Places
• European Format Multiplying Decimals by 2-Digit Whole Numbers European Format 2-digit whole × 2-digit hundredths European Format 2-digit tenths × 2-digit whole European Format 2-digit hundredths × 2-digit whole European Format 3-digit tenths × 2-digit whole European Format 3-digit hundredths × 2-digit whole European Format 3-digit thousandths × 2-digit whole
• European Format Multiplying Decimals by 2-Digit Tenths European Format 2-digit whole × 2-digit tenths European Format 2-digit tenths × 2-digit tenths European Format 2-digit hundredths × 2-digit tenths European Format 3-digit whole × 2-digit tenths European Format 3-digit tenths × 2-digit tenths European Format 3-digit hundredths × 2-digit tenths European Format 3-digit thousandths × 2-digit tenths
• European Format Multiplying Decimals by 2-Digit Hundredths European Format 2-digit tenths × 2-digit hundredths European Format 2-digit hundredths × 2-digit hundredths European Format 3-digit whole × 2-digit hundredths European Format 3-digit tenths × 2-digit hundredths European Format 3-digit hundredths × 2-digit hundredths European Format 3-digit thousandths × 2-digit hundredths
• European Format Multiplying Decimals by Various Decimal Places European Format 2-digit × 2-digit with various decimal places European Format 3-digit × 2-digit with various decimal places
• Dividing Decimals by Whole Numbers Divide Tenths by a Whole Number Divide Hundredths by a Whole Number Divide Thousandths by a Whole Number Divide Ten Thousandths by a Whole Number Divide Various Decimals by a Whole Number

In case you aren't familiar with dividing with a decimal divisor, the general method for completing questions is by getting rid of the decimal in the divisor. This is done by multiplying the divisor and the dividend by the same amount, usually a power of ten such as 10, 100 or 1000. For example, if the division question is 5.32/5.6, you would multiply the divisor and dividend by 10 to get the equivalent division problem, 53.2/56. Completing this division will result in the exact same quotient as the original (try it on your calculator if you don't believe us). The main reason for completing decimal division in this way is to get the decimal in the correct location when using the U.S. long division algorithm.

A much simpler strategy, in our opinion, is to initially ignore the decimals all together and use estimation to place the decimal in the quotient. In the same example as above, you would complete 532/56 = 95. If you "flexibly" round the original, you will get about 5/5 which is about 1, so the decimal in 95 must be placed to make 95 close to 1. In this case, you would place it just before the 9 to get 0.95. Combining this strategy with the one above can also help a great deal with more difficult questions. For example, 4.584184 ÷ 0.461 can first be converted the to equivalent: 4584.184 ÷ 461 (you can estimate the quotient to be around 10). Complete the division question without decimals: 4584184 ÷ 461 = 9944 then place the decimal, so that 9944 is about 10. This results in 9.944.

Dividing decimal numbers doesn't have to be too difficult, especially with the worksheets below where the decimals work out nicely. To make these worksheets, we randomly generated a divisor and a quotient first, then multiplied them together to get the dividend. Of course, you will see the quotients only on the answer page, but generating questions in this way makes every decimal division problem work out nicely.

• Decimal Long Division with Quotients That Work Out Nicely Dividing Decimals by Various Decimals with Various Sizes of Quotients Dividing Decimals by 1-Digit Tenths (e.g. 0.72 ÷ 0.8 = 0.9) Dividing Decimals by 1-Digit Tenths with Larger Quotients (e.g. 3.2 ÷ 0.5 = 6.4) Dividing Decimals by 2-Digit Tenths (e.g. 10.75 ÷ 2.5 = 4.3) Dividing Decimals by 2-Digit Tenths with Larger Quotients (e.g. 387.75 ÷ 4.7 = 82.5) Dividing Decimals by 3-Digit Tenths (e.g. 1349.46 ÷ 23.8 = 56.7) Dividing Decimals by 2-Digit Hundredths (e.g. 0.4368 ÷ 0.56 = 0.78) Dividing Decimals by 2-Digit Hundredths with Larger Quotients (e.g. 1.7277 ÷ 0.39 = 4.43) Dividing Decimals by 3-Digit Hundredths (e.g. 31.4863 ÷ 4.61 = 6.83) Dividing Decimals by 4-Digit Hundredths (e.g. 7628.1285 ÷ 99.91 = 76.35) Dividing Decimals by 3-Digit Thousandths (e.g. 0.076504 ÷ 0.292 = 0.262) Dividing Decimals by 3-Digit Thousandths with Larger Quotients (e.g. 2.875669 ÷ 0.551 = 5.219)

These worksheets would probably be used for estimating and calculator work.

• Horizontally Arranged Decimal Division Random # Digits Random # Places
• European Format Dividing Decimals with Quotients That Work Out Nicely European Format Divide Tenths by a Whole Number European Format Divide Hundredths by a Whole Number European Format Divide Thousandths by a Whole Number European Format Divide Ten Thousandths by a Whole Number European Format Divide Various Decimals by a Whole Number

In the next set of questions, the quotient does not always work out well and may have repeating decimals. The answer key shows a rounded quotient in these cases.

• European Format Dividing Decimals by Whole Numbers European Format Divide Tenths by a Whole Number European Format Divide Hundredths by a Whole Number European Format Divide Thousandths by a Whole Number European Format Divide Ten Thousandths by a Whole Number European Format Divide Various Decimals by a Whole Number
• European Format Dividing Decimals by Decimals European Format Decimal Tenth (0,1 to 9,9) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Hundredth (0,01 to 9,99) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Thousandth (0,001 to 9,999) Divided by Decimal Tenth (1,1 to 9,9) European Format Decimal Ten Thousandth (0,0001 to 9,9999) Divided by Decimal Tenth (1,1 to 9,9) European Format Various Decimal Places (0,1 to 9,9999) Divided by Decimal Tenth (1,1 to 9,9) European Format Various Decimal Places (0,1 to 9,9999) Divided by Various Decimal Places (1,1 to 9,9999)

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

• Texas Go Math
• Big Ideas Math
• Engageny Math
• McGraw Hill My Math
• enVision Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals

Clearing all math exams can be tough for students who are pursuing 5th grade but with Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals it can be easy. Because this solutions key is prepared by our highly-experienced subject experts after ample research and easy to understand the concepts too. So, students are implied to answer all the questions while practicing and cross-check the solutions through Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals.

Big Ideas Math Book 5th Grade Answer Key Chapter 3 Add and Subtract Decimals

You just need to tap on the quick links available in order to access them and learn all the topics. Bridge the Knowledge Gap taking the help of the Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals. Kick start your preparation using these resources and clear the exams with flying colors. Solutions provided in the Big Ideas Math Book 5th Grade Answer Key Chapter 3 Add and Subtract Decimals cover questions from all the Exercises, Cumulative Practice, etc.

Lesson: 1 Estimate Sum and Differences

Lesson 3.1 Estimate Sum and Differences

Estimate sum and differences homework & practice 3.1.

Lesson: 2 Use Models to Add or Subtract Decimals

Lesson 3.2 Use Models to Add or Subtract Decimals

Use models to add or subtract decimals homework & practice 3.2.

Lesson: 3 Add Decimals

Lesson 3.3 Add Decimals

Add decimals homework & practice 3.3.

Lesson: 4 Subtract Decimals

Lesson 3.4 Subtract Decimals

Subtract decimals homework & practice 3.4.

Lesson: 5 Add and Subtract Decimals

Lesson 3.5 Add and Subtract Decimals

Add and subtract decimals homework & practice 3.5.

Lesson: 6 Use Mental Maths to Add or Subtract Decimals

Lesson 3.6 Use Mental Maths to Add or Subtract Decimals

Use mental maths to add or subtract decimals homework & practice 3.6.

Lesson: 7 Problem Solving: Money

Lesson 3.7 Problem Solving: Money

Problem solving: money homework & practice 3.7.

Chapter: 3 – Add and Subtract Decimals

Add and Subtract Decimals Performance Task

Add and subtract decimals activity, add and subtract decimals chapter practice, add and subtract decimals cumulative practice, add and subtract decimals steam performance task.

Explore and Grow

Construct Arguments Compare your answers to your partner’s answers. Explain why they are the same or why they are different.

Answer: My Friend and My answers are the same in the process of addition and subtraction.

Think and Grow: Estimate Sums and Differences

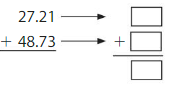
Show and Grow

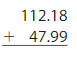
Difference of 68.8 – 29.7 = 39.1.

Apply and Grow: Practice

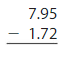
Question 9. Number Sense Descartes estimates a sum by rounding each number to the nearest ten. His estimate is 140. Which sums could he have estimated? 83.6 + 59.8 106.92 + 44.68 130.8 + 4.68 73.5 + 67.4 Answer: Descartes estimates a sum of 73.5 + 67.4 = 140.9 to be 140 by rounding each number to the nearest ten.

Explanation: First, we need to calculate the sum by rounding each number to the nearest ten: 83.6 + 59.8 = 143.4 106.92 + 44.68 = 151.6 130.8 + 4.68 = 135.48 73.5 + 67.4 = 140.9

Question 10. Precision Does rounding 209.11 – 104.53 to the nearest ten or to the nearest hundred give an estimate that is closer to the actual difference? Explain. Answer: Estimation to  the difference by rounding to nearest ten ( 209 – 105 = 104 )is closer to the actual difference ( 209.11 – 104.53 = 104.58 ).

Explanation: First, Estimate the actual difference: 209.11 – 104.53 = 104.58 Second, Estimate the difference by rounding to nearest ten: 209 – 105 = 104 Third, Estimate the difference by rounding to nearest hundred: 200 – 100 = 100

Question 11. DIG DEEPER! Newton packs a suitcase to fly on a plane. His suitcase needs to weigh less than 50.0 pounds. Should Newton overestimate or underestimate the weight of his suitcase? Explain. Answer: Newton should overestimate the weight of his suitcase because the weigh should not be more than 50.0 pounds.

Think and Grow: Modeling Real Life

Explanation: Weight of African Elephant = 5.7 Tons Weight of Hippopotamus = 2.3 Tons Difference: Weight of African Elephant – Weight of Hippopotamus = 5.7 – 2.3 = 3.4 Tons

Question 13. One cup of wild rice has 6.5 grams of protein. One cup of shredded chicken has 36.9 more grams of protein than 1 cup of wild rice. About how many grams of protein are in 1 cup of chicken? Answer: 1 cup of chicken = 43.4 grams of protein.

Explanation: One cup of wild rice = 6.5 grams One cup of shredded chicken has 36.9 more grams of protein than 1 cup of wild rice => 1 cup of chicken = 36.9 grams + 6.5 grams => 1 cup of chicken = 43.4 grams of protein.

Question 14. The speed Earth orbits the Sun is 18.5 miles per second. This speed is 3.3 miles per second slower than the speed Venus orbits the Sun. About how fast does Venus orbit the Sun? Answer: Speed of Venus orbit the Sun is 15.2 miles fast than the Earth orbit per second.

Explanation: Speed of Earth orbits the Sun = 18.5 miles This speed is 3.3 miles per second slower than the speed Venus orbits the Sun => Speed of  Venus orbit the Sun = 18.5 – 3.3 miles = 15.2 miles

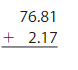
Question 7. Open-Ended Write a decimal addition problem that has an estimated sum of 35. Answer: Sum of 16.3+18.7 = 35

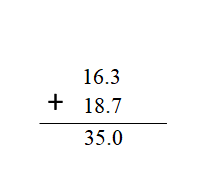
Question 8. Reasoning Describe a situation when you would estimate the difference of 25.4 and 19.8 to the nearest whole number. Answer: Estimate the difference between 25.4  and  19.8 by to round each number to the nearest whole number and then subtract the rounded numbers.

Explanation: Rounding number to nearest whole number of 25.4 = 25 Rounding number to nearest whole number of 19.8 = 20 Difference = Rounding number to nearest whole number of 25.4 – Rounding number to nearest whole number of 19.8 = 25 – 20 = 5

Question 9. Modeling Real Life Your friend participates in a 3.1-mile race. She walks for 1.4 miles of the race and runs the rest. About how many miles does your friend run? Answer: Number of miles my Friend runs = 1.7 miles.

Explanation: Number of miles the race is my Friend participates  = 3.1 mils Number of miles my Friend walks = 1.4 miles Number of miles my Friend runs = Number of miles the race is my Friend participates  – Number of miles my Friend walks =>  3.1 – 1.4 => 1.7 miles.

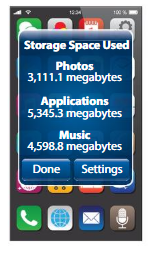
Explanation: Total storage space of Phone = 16000 megabytes Memory Storage for Photos = 3111.1 megabytes Memory Storage for Applications = 5345.3 megabytes Memory Storage for Music = 4598.8 megabytes Free Storage space = Total storage space of Phone – ( Memory Storage for Photos + Memory Storage for Applications + Memory Storage for Music) => 16000 – ( 3111.1 + 5345.3 + 4598.8 ) => 16000 – 13055.2 => 2944.8 megabytes

Review & Refresh

Find the sum. Question 11. \(\frac{2}{8}+\frac{4}{8}\) = ______ Answer: \(\frac{2}{8}+\frac{4}{8}\) = \(\frac{3}{4}\) .

Explanation: \(\frac{2}{8}+\frac{4}{8}\) = \(\frac{2+4}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 12. \(\frac{1}{2}+\frac{5}{2}\) = ______ Answer: \(\frac{1}{2}+\frac{5}{2}\) = \({3}\) .

Explanation: \(\frac{1}{2}+\frac{5}{2}\) = \(\frac{1+5}{2}\) = \(\frac{6}{2}\) = \({3}\)

Question 13. 1 + \(\frac{1}{4}\) = ______ Answer: 1 + \(\frac{1}{4}\) = \(\frac{5}{4}\) .

Explanation: 1 + \(\frac{1}{4}\) = \(\frac{4+1}{4}\) = \(\frac{5}{4}\)

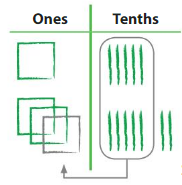
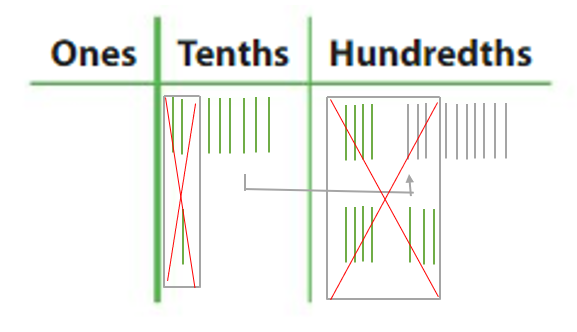
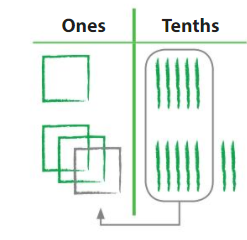
Use base ten blocks to find 1.16 – 0.89. Answer: So, 1.16 – 0.89 = 0.27

Repeated Reasoning Why can you use base ten blocks to model ones, tenths, and hundredths? Answer: Yes, we can use base ten blocks to model ones, tenths, and hundredths because they represent the numeral values in blocks which helps is east calculation and understanding.

Think and Grow: Use Models to Add or Subtract Decimals

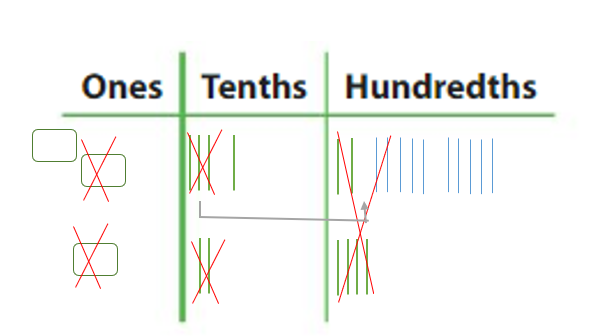
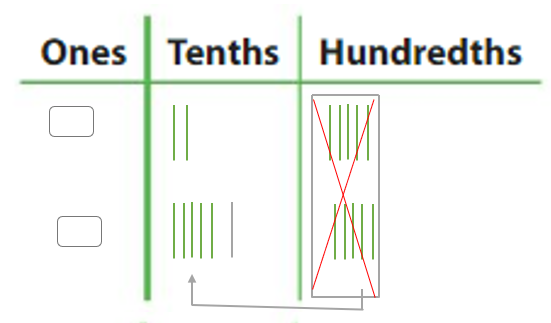
Example Find 2.42 – 1.24.

So, 2.42 – 1.24 = _____. Answer: So, 2.42 – 1.24 = 1.18

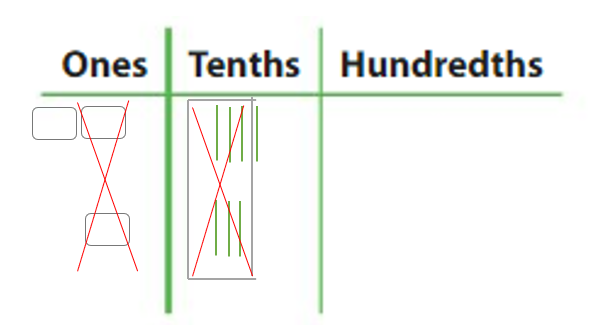
Make a quick sketch to find the sum or difference. Question 3. 1.61 + 0.22 = _____ Answer: 1.61 + 0.22 = 1.83

Question 4. 2.4 – 1.3 = _____ Answer: 2.4 – 1.3 = 1.1

Question 5. 2.2 + 0.9 = _______ Answer: 2.2 + 0.9 = 3.1

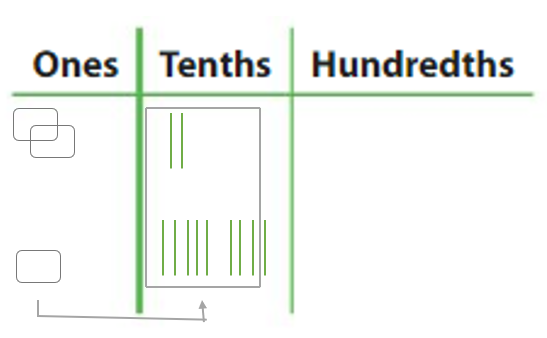
Question 6. 1.56 – 1.08 = ______ Answer: 1.56 – 1.08 = 0.48

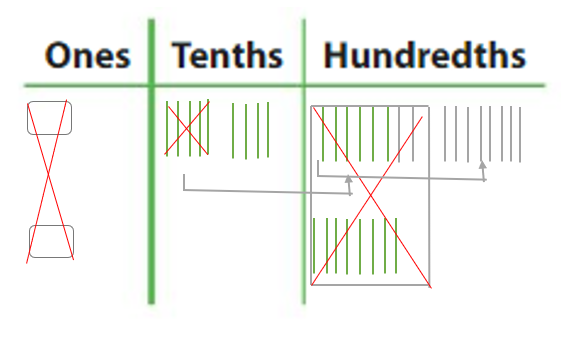
Question 7. Number Sense Newton adds two decimals that are each greater than 0.5. What can you conclude about the sum? Answer: If Newton’s adds two decimals that are each greater than 0.5 then the Sum of the decimal numbers is going to be more than 0.5.

Explanation: First Decimal Number= 1.2 Second Decimal Number = 0.8 Sum = First Decimal Number + Second Decimal Number = 1.2 + 0.8 = 2.0

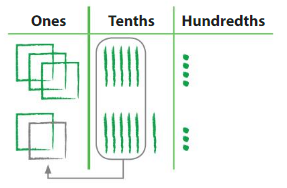
Question 9. DIG DEEPER! Use a model to find 1.31 – 0.4. Answer: 1.31 – 0.4 = 0.91.54

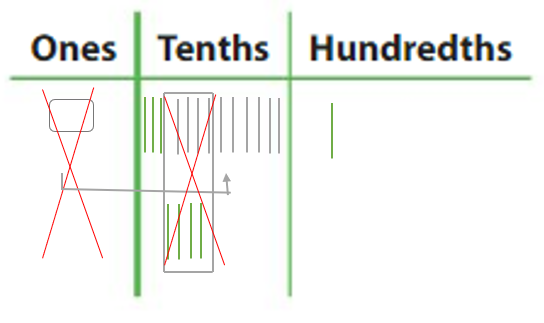
Question 10. A football player completes a 40-yard dash in 5.84 seconds. Another player completes it in 4.56 seconds. How much longer does it take the first player to complete the 40-yard dash than the second player? Answer: Time taken by the the first player to complete the 40-yard dash 1.28 seconds more than the second player.

Explanation: Time taken by the First player to complete the 40-yard dash = 5.84 seconds Time taken by the Second player to complete the 40-yard dash = 4.56 seconds Time taken by the the first player to complete the 40-yard dash than the second player = Time taken by the First player to complete the 40-yard dash – Time taken by the Second player to complete the 40-yard dash = 5.84 seconds – 4.56 seconds = 1.28 seconds.

Explanation: Length of Narwhal tusk = 4.92 feet Length of Narwhal Body = 11.48 feet Total Length of whole body Narwhal = Length of Narwhal tusk + Length of Narwhal Body = 4.92 feet + 11.48 feet = 16.40 feet.

Question 12. DIG DEEPER! An Olympic gymnast scores 6.6 points for skill. She starts with 10.0 points for execution, then loses 0.4 point for execution errors. What is the gymnast’s final score? Answer: Final score points of Olympic gymnast = 16.2.

Explanation: Score points of Olympic gymnast for skill = 6.6 Score points of Olympic gymnast for execution = 10.0 Score points lost of Olympic gymnast for execution errors = 0.4 Final score points of Olympic gymnast = Score points of Olympic gymnast for skill + Score points of Olympic gymnast for execution – Score points lost of Olympic gymnast for execution errors = 6.6 + 10.0 – 0.4 = 16.6 – 0.4 = 16.2

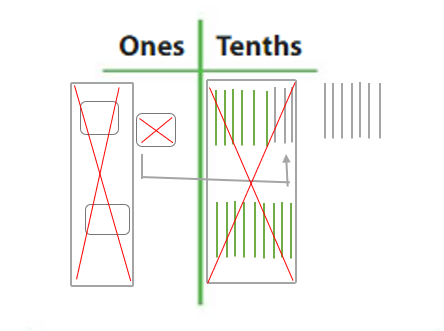
Question 3. 0.84 – 0.17 = _____ Answer: 0.84 – 0.17 = 0.67.

Question 4. 1.25 + 1.55 = _____ Answer: 1.25 + 1.55 = 2.80.

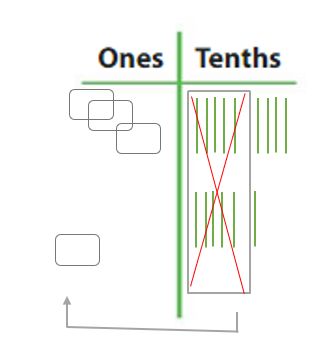
Question 5. 2.6 – 1.9 = ______ Answer: 2.6 – 1.9 = 0.7.

Question 6. 3.9 + 0.6 = ______ Answer: 3.9 + 0.6 = 4.5.

Question 8. Number Sense What is the greatest possible difference of two decimals to the hundredths place that are between 0 and 1? Answer: 0.01 is the greatest possible difference of two decimals to the hundredths place that are between 0 and 1.

Question 9. DIG DEEPER! Write a decimal addition equation that requires regrouping the tenths. Explain how you know you need to regroup to add. Answer: Find the Sum of 1.5 +2.7 = 4.2

Explanation:

Question 10. Modeling Real Life The fastest 1-mile sack race was completed in 16.68 minutes. The fastest 1-mile piggyback race was completed in 11.18 minutes. How much longer did it take to complete the sack race than the piggyback race? Answer: Time taken to complete the sack race than the piggyback race = 5.5 minutes.

Explanation: Time taken to complete fastest 1-mile sack race = 16.68 minutes Time taken to complete fastest 1-mile piggyback race  = 11.18 minutes Time taken to complete the sack race than the piggyback race = Time taken to complete fastest 1-mile sack race – Time taken to complete fastest 1-mile piggyback race = 16.68  – 11.18 = 5.5 minutes

Explanation: Number of pounds of Honey Hive A  produce = 15.25 lb. Number of pounds of Honey Hive B  produce = 20.98 lb. Total number of pounds of Honey produced Hive A and Hive B = Number of pounds of Honey Hive A  produce + Number of pounds of Honey Hive B  produce = 15.25 + 20.98 = 36.23 lb.

Explanation: Length of Rectangle = 32 yards. Width of Rectangle = 19 yards Perimeter of Rectangle = 2 (l + w) = 2( 32 + 19 ) = 2 × 51 = 102 yards.

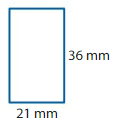
Explanation: Length of Rectangle = 36 mm Width of Rectangle = 21 mm Perimeter of Rectangle = 2 (l + w) = 2 ( 36 + 21 ) = 2 × 57 = 114 mm.

Construct Arguments +-? Answer: The adding of decimals is same as to that of adding of whole numbers because here the process we do is adding the numbers in both.

Think and Grow: Add Decimals

Check: 640.89 – 78.04 = 562.65.

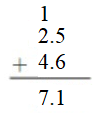
Check: 7.1 – 4.6 = 2.5.

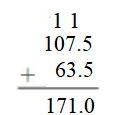
Question 12. Number Sense Which expressions have a sum greater than 24.7? 20.9 + 3.8 15.96 + 9.51 14.23 + 9.85 10.62 + 14.11 Answer: The Sum of 15.96 + 9.51= 25.74 which is  greater than 24.7.

Explanation: First, find the sum: 20.9 + 3.8 = 24.7 15.96 + 9.51 = 25.47 14.23 + 9.85 = 24.08 10.62 + 14.11 = 24.73

Question 13. YOU BE THE TEACHER Your friend finds 34.5 + 6.8 and gets a sum of 413. Without adding, explain how you know your friend’s answer is correct. Answer: My Friend’s answer is incorrect because he did not add the digits correctly .

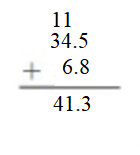
Explanation: Storage space for tale of the Monster = 3.8 megabytes Storage space for In the Game = 2.5 megabytes Total storage for tale of the Monster and In the Game = 3.8 + 2.5 = 6.3 megabytes Storage space left on the Tablet = 6.5 megabytes Storage space left after downloading the eBooks = Storage space left on the Tablet  – Total storage for tale of the Monster and In the Game = 6.5 – 6.3 = 0.2 megabytes

Question 14. A chef needs 3.75 pounds of fish for a dinner party. She catches a fish that is 2.50 pounds and another fish that is 1.75 pounds. Does she catch enough fish for her dinner party? Answer: She catches enough fish for her dinner party in fact 0.5 pounds more weight fish she catches.

Explanation: Weight of first fish = 2.50 pounds Weight of Second Fish = 1.75 pounds Weight of both Fishes = 2.50 + 1.75 = 4.25 pounds Weight of the fish needed for a dinner party = 3.75 pounds Difference: Weight of fishes caught – Weight of the fish needed for a dinner party = 4.25 – 3.75 = 0.5 pounds

Question 15. Your school’s long jump record is 5.51 meters. You jump 3.38 meters on your first attempt. Your second attempt is 1.56 meters longer than your first. Do you break your school’s record? Answer: I have broke the school record by jumping more 2.81 meters than the record distance.

Explanation: Distance long jump record in the school = 5.51 meters Distance jumped on my first attempt = 3.38 meters Your second attempt is 1.56 meters longer than your first. => Distance jumped on my second attempt = 1.56+ 3.38 meters = 4.94 meters Total distance jumped by me = Distance jumped on my first attempt + Distance jumped on my second attempt = 3.38 + 4.94 = 8.32 meters Difference: Total distance jumped by me – Distance long jump record in the school = 8.32 – 5.51 = 2.81 meters

Explanation: The melting point of aluminum = 660.32 degrees Celsius The melting point of aluminum is 403.86 degrees Celsius cooler than the melting point of gold. => Let the melting point of Gold be X => X- 403.86 = 660.32 => X = 660.32 + 403 => X = 1063.32  degrees Celsius.

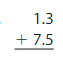
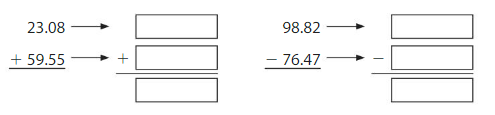
Find the sum. Check whether your answer is reasonable. Question 5. 123.98 + 47.65 = _____ Answer: 123.98 + 47.65 = 171.63. 171.63 is close to 172.

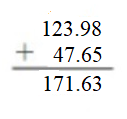
Question 6. 427.8 + 13.2 = _____ Answer: 427.8 + 13.2 = 441.0 441 is close to 441.

Question 7. Reasoning Your friend adds 46.7 and 5.4. Without calculating, is the sum greater than or less than 51? Explain. Answer: Answer is greater than 51 because the Sum of 46.7 + 5.4 = 52.1.

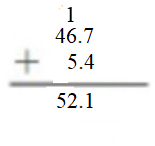
Question 8. Writing Explain why it is important to use place value to line up the numbers when adding decimals. Answer: When we add whole numbers,  in the Value (cents) column above, you line up the numbers so that the digits in the ones place-value column are aligned. In order to keep the numbers in the proper place-value column when adding decimals, align the decimal points.

Explanation: Weight of fruits for a fruit salad needed = 10.5 pounds Weight of Apples purchased = 3.8 pounds Weight of pears purchased = 6.7 pounds Total Weight of apples And Pears purchased = Weight of Apples purchased + Weight of pears purchased = 3.8  + 6.7 = 10.5 pounds => Compare: Weight of fruits for a fruit salad needed : Total Weight of apples And Pears purchased = 10.5 pounds :10.5 pounds

Question 10. Modeling Real Life A scientist has 200.59 grams of mercury. She has 135.23 fewer grams of zinc. How many grams of zinc does she have? Answer: Zinc she has is 65.36 grams.

Explanation: Mercury a Scientist has = 200.59 grams She has 135.23 fewer grams of zinc => Let the Zinc be X => X + 135.23 = 200.59 => X = 200.59 – 135.23 => X = 65.36 grams.

Find the factor pairs for the number. Question 11. 24 Answer: Factor pairs of 24 : 1 × 24 2 × 12 3 × 8 4 × 6

Question 12. 36 Answer: Factor pairs of 36 : 1 × 36 2 × 18 3 × 12 4 × 9 6 × 6

Question 13. 17 Answer: Factor pairs of 17 : 1 × 17 17 is a prime number so it has 1 and itself as factors.

Construct Arguments How is subtracting decimals similar to subtracting whole numbers? Answer: Subtracting decimals is similar to subtracting whole numbers because the process is same for both kind of numbers that is subtracting.

Think and Grow: Subtract Decimals

To subtract decimals, subtract like place values.

Check: 36.3 + 35.3 = 71.6

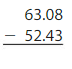
Question 7. 856.02 – 48.12 = _______ Answer: 856.02 – 48.12 = 807.90.

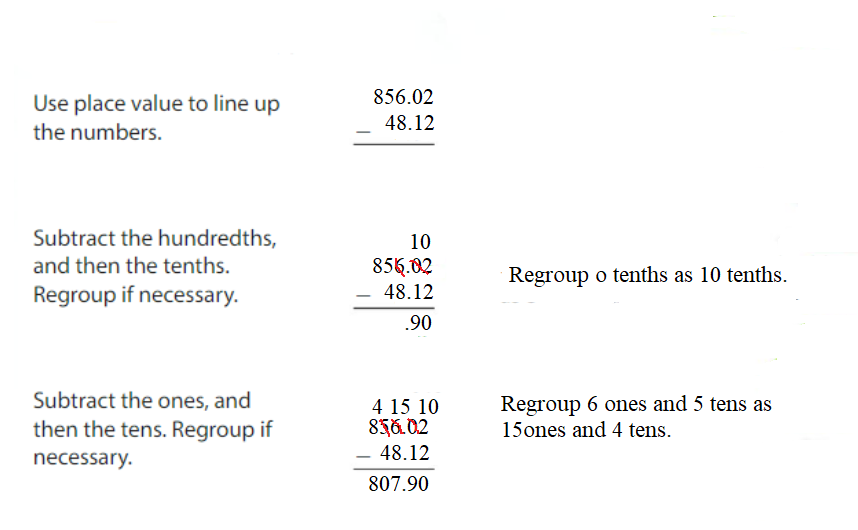
Question 8. 3.76 – 0.53 = _____ Answer: 3.76 – 0.53 = 3.23.

Question 9. 27.5 – 21.7 = ______ Answer: 27.5 – 21.7 = 5.8.

Question 10. 737.2 – 2.8 = _____ Answer: 737.2 – 2.8 = 734.4.

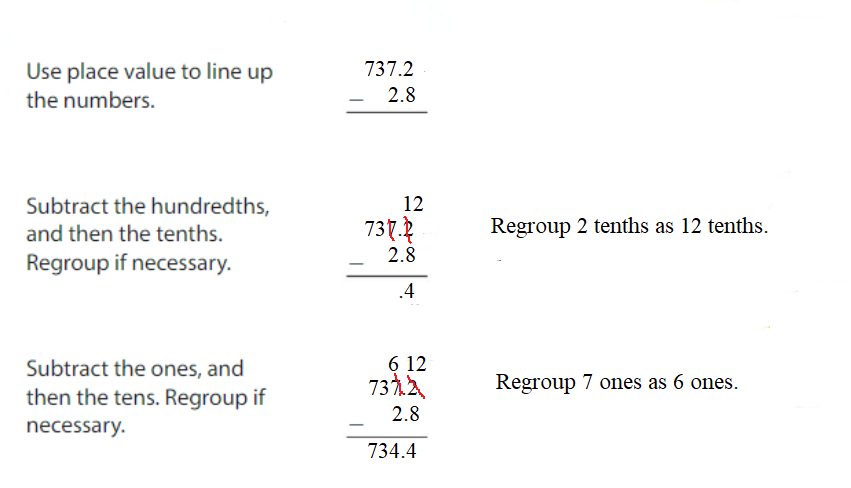
Explanation: d + 26.4 = 38.7 => d = 38.7 – 26.4 => d = 12.3 d = y + 10.1 Substitute d = 12.3 in d = y + 10.1 => d = y + 10.1 => 12.3 = y + 10.1 => y = 12.3 – 10.1 => y = 2.2

Explanation: Length of world record for the longest dog tongue = 18.58 centimeters Length of previous world record for the longest dog tongue = 11.43 centimeters Length of the record was broken = Length of world record for the longest dog tongue – Length of previous world record for the longest dog tongue = 18.58 centimeters – 11.43 centimeters = 7.15 centimeters.

Question 13. The average high summer temperature in Death Valley, California, is 46.7 degrees Celsius. The hottest temperature ever recorded is 56.7 degrees Celsius. How much greater is the hottest recorded temperature than the average high temperature? Answer: The hottest recorded temperature is greater by 10 degrees Celsius than the average high temperature.

Explanation: The average high summer temperature in Death Valley, California = 46.7 degrees Celsius The hottest temperature ever recorded = 56.7 degrees Celsius. Difference: =The hottest temperature ever recorded  – The average high summer temperature in Death Valley, California = 56.7 – 46.7 = 10 degrees Celsius

Explanation: Reading of an athlete’s fitness tracker  at noon = 2.69 miles Reading of an athlete’s fitness tracker before going to sleep=6.34 miles Reading of an athlete’s fitness tracker recorded after noon = Reading of an athlete’s fitness tracker before going to sleep – Reading of an athlete’s fitness tracker  at noon = 6.34 – 2.69 = 3.65 miles.

Question 15. DIG DEEPER! Your friend is using a pattern to knit a 139.7-centimeter-long scarf. He has already knitted 61.8 centimeters. How many centimeters of scarf does he have left to knit? Write your answer as a mixed number. Answer: Length of scarf  left to knit = 77.9/100 centimeters

Explanation: Length of long scarf pattern to knit = 139.7 centimeter Length of scarf already knitted = 61.8 centimeters Length of scarf  left to knit = Length of long scarf pattern to knit – Length of scarf already knitted = 139.7 centimeter – 61.8 centimeters = 77.9 centimeters

Find the difference. Then check your answer. Question 4. 856.02 – 48.12 = ______ Answer: 856.02 – 48.12 = 807.90 Check: 48.12 + 807.90 = 856.02

Question 5. 3.76 – 0.53 = ______ Answer: 3.76 – 0.53 = 3.23 Check: 0.53 + 3.23 = 3.76.

Question 6. 27.5 – 21.7 = ______ Answer: 27.5 – 21.7 = 5.8 Check: 21.7 + 5.8 = 27.5.

Question 7. 737.2 – 2.8 = _______ Answer: 737.2 – 2.8 = 734.4. Check: 2.8 + 734.4 = 737.2.

Question 8. Number Sense Which statements describe the difference of 134.6 and 78.9? The difference is 55.7. The difference is greater than 55. The difference is less than 55.07. Answer: The difference is 55.7 is the correct statement.

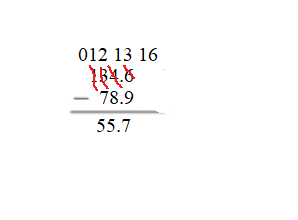
Question 10. Modeling Real Life The world record for the longest fingernails on a pair of female hands is 576.41 centimeters. The world record for the longest fingernails on a single hand is 909.60 centimeters. How much longer is the world record for the longest fingernails on a single hand than the world record for the longest fingernails on a pair of female hands? Answer: The world record for the longest fingernails on a single hand is 333.19 centimeters longer than the world record for the longest fingernails on a pair of female hands.

Explanation: Length of the world record for the longest fingernails on a pair of female hands = 576.41 centimeters. Length of the world record for the longest fingernails on a single hand = 909.60 centimeters. Difference: Length of the world record for the longest fingernails on a single hand – Length of the world record for the longest fingernails on a pair of female hands = 909.60 –  576.41 = 333.19 centimeters.

Find the product. Question 11. 80 × 10 = ______ Answer: Multiplication: 80 × 10 = 800.

Question 12. 30 × 90 = _______ Answer: Multiplication: 30 × 90 = 2700.

Question 13. 60 × 70 = _______ Answer: Multiplication: 60 × 70 = 4200.

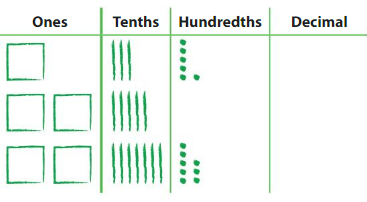
Reasoning How did you find the sum? What other ways can you find the sum? Answer: First count the figures given place values and later add the decimals values. Other ways are like counting total figures n doing the addition of them.

Think and Grow: Add and Subtract Decimals

Answer: 7.39 + 4.16 + 9.00 = 20.55. 20.55 is close to 21.

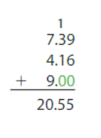
Evaluate. Check whether your answer is reasonable. Question 1. 6.84 + 2.9 + 5.22 = ______ Answer: 6.84 + 2.9 + 5.22 = 14.96 14.96 is close to 15.

Question 2. 41.55 – 14.09 + 42.4 = ______ Answer: 41.55 – 14.09 + 42.4 = 69.86. 69.86 is close to 70.

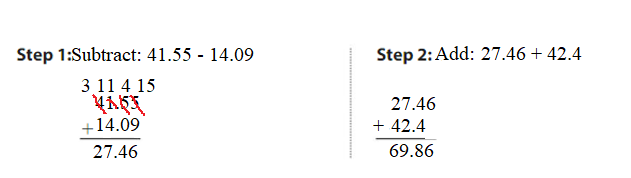
Evaluate. Check whether your answer is reasonable. Question 3. 5.3 – 1.7 – 2 = _____ Answer: 5.3 – 1.7 – 2 = 3.6 – 2 = 1.6 1.6 is close to 2.

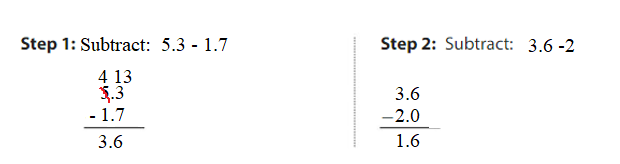
Question 4. 14.08 + 6.15 – 9.3 = ______ Answer: 14.08 + 6.15 – 9.3 = 10.93 10.93 is close to 11.

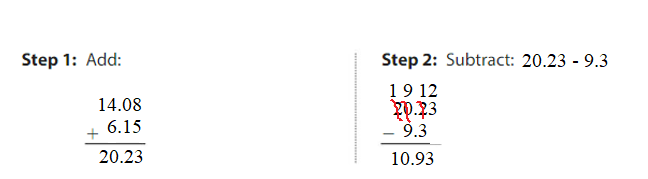
Question 5. 24.7 – 5.1 + 3.75 = _____ Answer: 24.7 – 5.1 + 3.75 = 19.6 + 3.75 = 23.35 23.35 is close to 23.

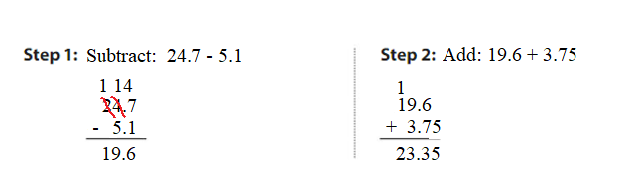
Question 6. 32.6 + 6 + 15.1 = ______ Answer: 32.6 + 6 + 15.1 = 38.6 + 15.1 = 53.7. 53.7 is close to 54.

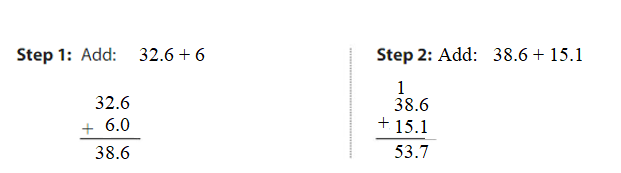
Question 7. You have $35.50. You buy a movie for $15.89 and music for $12.50. How much money do you have left? Answer: Amount left with me = $7.11.

Explanation: Total money I have = $35.50 Cost of movie purchased = $15.89 Cost of music purchased = $12.50 Total amount spent on music and movie = $15.89 + $12.50 = $28.39 Amount left with me = Total money I have – Total amount spent on music and movie = $35.50 – $28.39 = $7.11

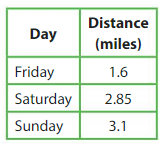
Explanation: Distance covered on Friday = 1.6 miles Distance covered on Saturday = 2.85 miles Distance covered on Sunday = 3.1 miles Total Distance covered over all = Distance covered on Friday+ Distance covered on Saturday + Distance covered on Sunday = 1.6 + 2.85 + 3.1 = 4.45 + 3.1 = 7.55 miles.

Question 9. Logic Your friend finds 5.31 + 2.8 – 1.27 and gets the answer 4.32. Is your friend’s answer reasonable? Explain. Answer: My friend answer is incorrect because the correct answer is 7 not 4.32.

Explanation: First do the adding the equation: 5.31 + 2.8 – 1.27 = 8.11 – 1.27 = 6.84 6.84 is close to 7.

Explanation: Length of the side of the river = 216.75 feet Length of the side of the river = 216.75 feet Length of the base of the river = 204 feet Perimeter  of the river = Length of the side of the river + Length of the side of the river + Length of the base of the river = 216.75 + 216.75  + 204 = 433.50 + 204 = 637.50 feet.

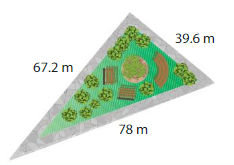
Explanation: Length of side of the park = 67.2 m Length of the base of the park = 39.6 m Length of the Height of the park = 78 m Perimeter of the park = Length of side of the park + Length of the base of the park + Length of the Height of the park = 67.2 + 39.6 + 78 = 106.8 + 78 = 184.8 m

Explanation: Weight of Bernese mountain dog = 103.33 lb. A German shepherd weighs 24.75 pounds less than the Bernese mountain dog. => 103.33 – 24.75 =.> 78.58 lb. A husky weighs 21.67 pounds less than the German shepherd. => 78.58 – 21.67 => 56.91 lb.

Question 13. DIG DEEPER! Your friend launches a water balloon 136.33 yards. Your cousin launches a balloon 15.67 yards farther than your friend and 8.33 yards farther than you. How much farther do you launch a balloon than your friend? Answer: I have launched 24 yards a balloon farther than my friend.

Explanation: Length of my friend a water balloon = 136.33 yards Your cousin launches a balloon 15.67 yards farther than your friend and 8.33 yards farther than you. =>  136.33 + 15.67 = 152 + 8.33 = 160.33 yards Difference: Your cousin launches a balloon 15.67 yards farther than your friend and 8.33 yards farther than you – Length of my friend a water balloon = 160.33 – 136.33 = 24 yards

Evaluate. Check whether your answer is reasonable. Question 1. 2.8 + 7 + 5.3 = _______ Answer: 2.8 + 7 + 5.3 = 9.8 + 5.3 = 15.1. 15.1 is close to 15.

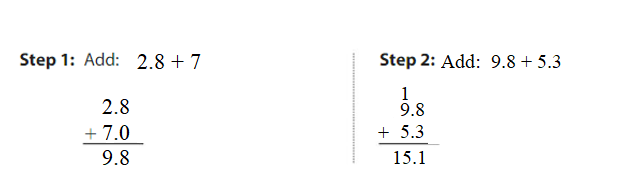
Question 2. 14.86 + 5.72 – 3 = ______ Answer: 14.86 + 5.72 – 3 = 20.58 – 3 = 17.58. 17.58 is close to 18.

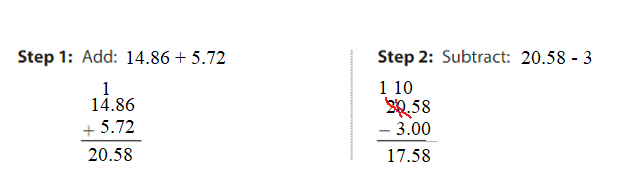
Question 3. 28.95 – 4.12 – 0.7 = ______ Answer: 28.95 – 4.12 – 0.7 = 24.83 – 0.7 = 24.13. 24.13 is close to 24.

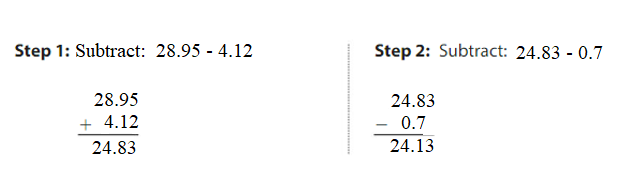
Question 4. 10.6 – 10.35 + 34.27 = _____ Answer: 10.6 – 10.35 + 34.27 = 0.25 + 34.27 = 34.52. 34.52 is close to 35.

Question 5. 19.36 + 24 + 8.5 = ______ Answer: 19.36 + 24 + 8.5 = 43.36 + 8.5 = 51.86. 51.86 is close to 52.

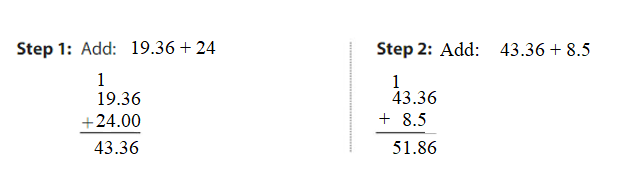
Question 6. 5 – 0.2 – 1.37 = ______ Answer: 5 – 0.2 – 1.37 = 4.8 – 1.37 = 3.43. 3.43 is close to 3.

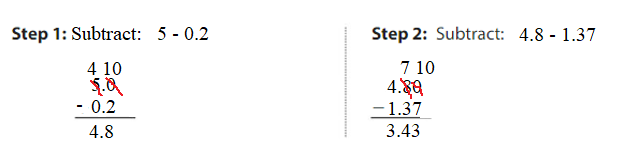
Question 7. Which One Doesn’t Belong? Which addition problem does not involve adding zeros to line up the place values? 5.39 + 1.76 + 40.9 25 + 1.8 + 6.3 18.5 + 6.2 + 0.7 12.49 + 10.8 + 0.13 Answer: The equations 25 + 1.8 + 6.3, 18.5 + 6.2 + 0.7 and 12.49 + 10.8 + 0.13 does not involve adding of zeros to line up the place values.

Explanation: First, find the sum: 5.39 + 1.76 + 40.9 = 7.15 + 40.9 = 48.05 25 + 1.8 + 6.3 = 26.8 + 6.3 =  33.1 18.5 + 6.2 + 0.7 = 24.7 + 0.7 = 25.4 12.49 + 10.8 + 0.13 = 23.29 + 0.13 = 23.42

Question 8. Logic Which expressions have an estimate greater than 10? 4.9 + 2.5 + 3.8 8.1 – 4.3 + 2.7 10.9 – 0.2 – 0.1 10.8 + 3.6 – 5.2 Answer: The Equation 4.9 + 2.5 + 3.8 and 10.9 – 0.2 – 0.1 have an estimate greater than 10.

Explanation: First, add and subtract the equation: 4.9 + 2.5 + 3.8 = 7.4 + 3.8 = 11.2 8.1 – 4.3 + 2.7 = 3.8 + 2.7 = 6.5 10.9 – 0.2 – 0.1 = 10.7 – 0.1 =10.6 10.8 + 3.6 – 5.2 = 14.4 – 5.2 = 9.2

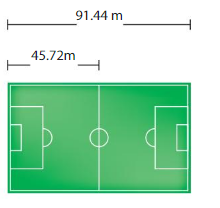
Explanation: Length of the entire soccer field = 91.44 m Length of the half soccer field = 45.72 m Length of the total run altogether = Length of the entire soccer field + Length of the half soccer field = 91.44  + 45.72 = 137.16 m

Explanation: Pumpkin A travels= 0.61 mile. Pumpkin B travels 0.28 mile farther than Pumpkin A. => 0.61 + 0.28 = 0.89 miles Pumpkin C travels 0.06 mile farther than Pumpkin B. => 0.89 + 0.06 = 0.95 miles Difference between the Pumpkin C and Pumpkin A= Pumpkin C travels – Pumpkin A travels = 0.95 – 0.61 = 0.34 miles

Explanation: No, there is no line symmetry in the given shape.

Use mental math to find each sum. 6.5 + 3.1 + 3.5 = ______ 10. 79 + 6.25 = ______ Answer: 6.5 + 3.1 + 3.5 = 13.1. 10. 79 + 6.25 = 17.04.

Explanation: Given 6.5 + 3.1 + 3.5, 6.5 and 3.5 are compatible numbers. Use addition properties to rewrite the problem. 6.5 + 3.1 + 3.5 = 3.1 + (6.5 + 3.5) Associative Property = 3.1 + 10 = 13.1

10. 79 + 6.25 = 17.04.

Reasoning Explain how you used mental math to find each. Answer: For the first one, I have rearranged the numbers  to add compatibles numbers first. Later used Associative Property to add them. Second equation directly I have added the given numbers.

Think and Grow: Use mental math to Add or Subtract Decimals

Example find 12.4 + 3.9 + 7.6. Notice that 12.4 and 7.6 are compatible numbers. Use addition properties to rewrite the problem. 12.4 + 3.9 + 7.6 = 3.9 + 12.4 + 7.6 Commutative Property = 3.9 + (12.4 + 7.6) Associative Property = 3.9 + 20 = _____ So, 12.4 + 3.9 + 7.6 = _______.

Answer: So, 12.4 + 3.9 + 7.6 = 23.9.

Explanation: Notice that 12.4 and 7.6 are compatible numbers. Use addition properties to rewrite the problem. 12.4 + 3.9 + 7.6 = 3.9 + 12.4 + 7.6 Commutative Property = 3.9 + (12.4 + 7.6) Associative Property = 3.9 + 20 = 23.9.

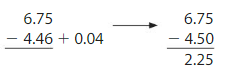
Answer: So, 6.75 – 4.46 = 2.29.

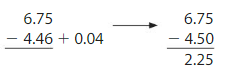
Use mental math to find the sum or difference. Question 1. 4.25 + 1.36 + 2.75 = ______ Answer: 4.25 + 1.36 + 2.75 = 8.36.

Explanation: 4.25 + 1.36 + 2.75 = ???? Notice that 4.25 and 2.75 are compatible numbers. Use addition properties to rewrite the problem. 4.25 + 1.36 + 2.75 = 1.36 + 4.25 + 2.75 Commutative Property = 1.36 + (4.25 + 2.75 )Associative Property = 1.36 + 7.00 = 8.36

Question 2. 12.78 + 5.25 = _____ Answer: 12.78 + 5.25 = 18.03.

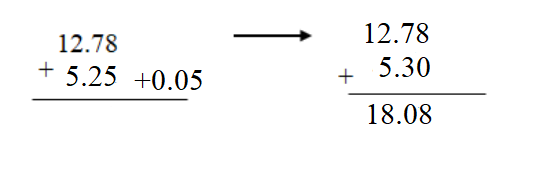
Question 3. 17.4 – 13.6 = _____ Answer: 17.4 – 13.6 = 3.8.

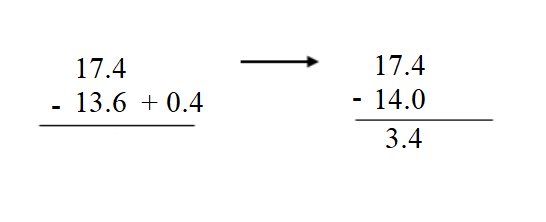
Question 4. 29.8 – 2.27 = _____ Answer: 29.8 – 2.27 = 27.53.

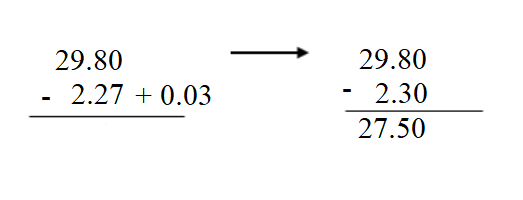
Use mental math to find the sum or difference. Question 5. 1.25 + 2.45 + 1.75 = _____ Answer: So, 1.25 + 2.45 + 1.75 = 5.45.

Explanation: 1.25 + 2.45 + 1.75 = ??? Notice that 1.25 and 1.75 are compatible numbers. Use addition properties to rewrite the problem. 1.25 + 2.45 + 1.75 =  2.45 + 1.25 + 1.75 Commutative Property = 2.45 + (1.25 + 1.75) Associative Property = 2.45 + 3.00 = 5.45.

Question 6. 8.4 + 6.15 + 2.6 = ______ Answer: So, 8.4 + 6.15 + 2.6 = 17.15.

Explanation: 8.4 + 6.15 + 2.6 = ??? Notice that 8.4 and 2.6 are compatible numbers. Use addition properties to rewrite the problem. 8.4 + 6.15 + 2.6 = 6.15 + 8.4 + 2.6 Commutative Property = 6.15 + (8.4 + 2.6)  Associative Property = 6.15 + 11.00 = 17.15

Question 7. 17.82 – 15.61 = _____ Answer: 17.82 – 15.61 = 2.21.

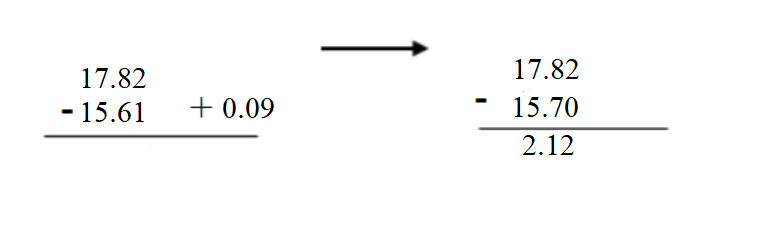
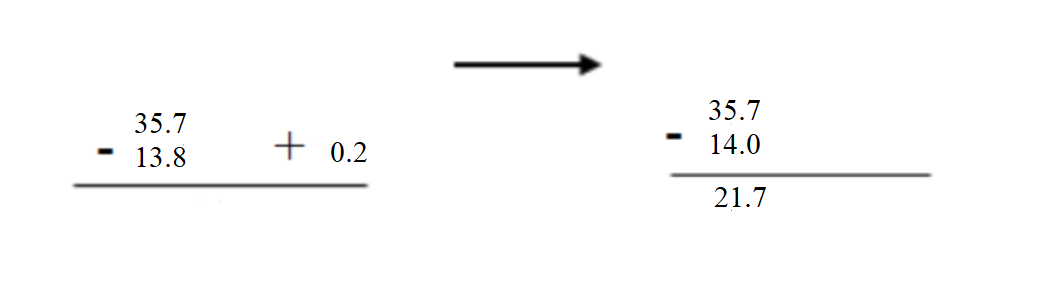
Question 8. 35.7 – 13.8 = _____ Answer: 35.7 – 13.8 = 21.9.

Question 9. Two years ago, your friend was1.25 meters tall. Today, your friend is1.48 meters tall. How many meters did your friend grow? Answer: Height my friend grew = 0.23 meters.

Explanation: Height of my Friend two years ago = 1.25 meters Height of my Friend today = 1.48 meters Height my friend grew = Height of my Friend today – Height of my Friend two years ago = 1.48 – 1.25 = 0.23 meters

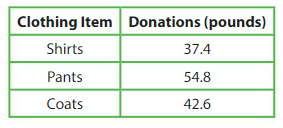
Explanation: Weight of Shirts donated = 37.4 pounds. Weight of Pants donated = 54.8 pounds. Weight of Coats donated = 42.6 pounds. Total weight of all clothing donated together = Weight of Shirts donated + Weight of Pants donated + Weight of Coats donated = 37.4 +  54.8 + 42.6 = 134.8 pounds.

Question 11. Reasoning Can you use the Commutative Property to find the difference of two decimals? Explain. Answer: Yes, we can Commutative Property to find the difference of two decimals because the methodology we doing is subtraction in between the numerals. So, there wont be any difference expect the points.

Explanation: Time taken on an average, a left-handed professional baseball player runs from home plate to first base = 4.2 seconds Time of record = 3.1 seconds Difference in the time = Time taken on an average, a left-handed professional baseball player runs from home plate to first base  – Time of record = 4.2 – 3.1 = 1.1 seconds

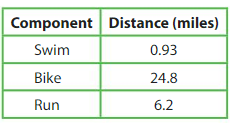
Explanation: Distance travelled to Swimming = 0.93 miles Distance travelled on Bike = 24.8 miles Distance travelled by Running = 6.2 miles Total Distance travelled on land = Distance travelled on Bike – Distance travelled by Running = 24.8  + 6.2 = 31 miles Total Distance travelled on land than in water = Total Distance travelled on land  – Distance travelled to Swimming = 31 – 0.93 = 30.07 miles

Question 15. DIG DEEPER! You paint a meter stick for a craft. You paint 30.7 centimeters blue and 67.9 centimeters green. How many millimeters are not painted? Answer: Length of meter stick not painted = 14 millimeters

Explanation: Length of blue paint painted on meter stick = 30.7 centimeters Length of green paint painted on meter stick = 67.9 centimeters Total length of meter stick painted = Length of blue paint painted on meter stick  + Length of green paint painted on meter stick = 30.7 + 67.9 = 98.6 centimeters Conversion: 1 meter = 100 centimeters Length of meter stick not painted = 100 centimeters – 98.6 centimeters = 1.4 centimeters. 1 centimeter = 10 millimeters 1.4 centimeter = ??? cross multiplication: 1.4 × 10 ÷ 1 = 14 ÷ 1 = 14 millimeters.

Use mental math to find the sum or difference Question 1. 2.73 + 2.14 = ______ Answer: 2.73 + 2.14 = 4.87.

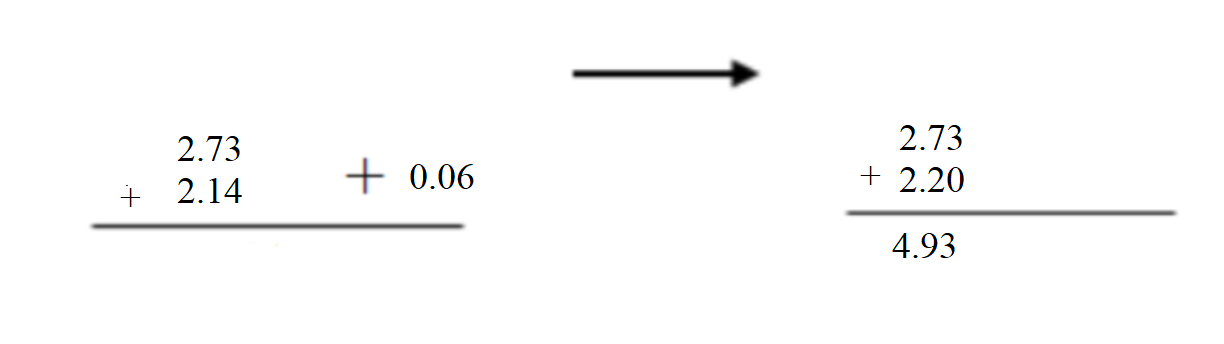
Question 2. 54.3 + 14.1 = ______ Answer: 54.3 + 14.1 = 68.40

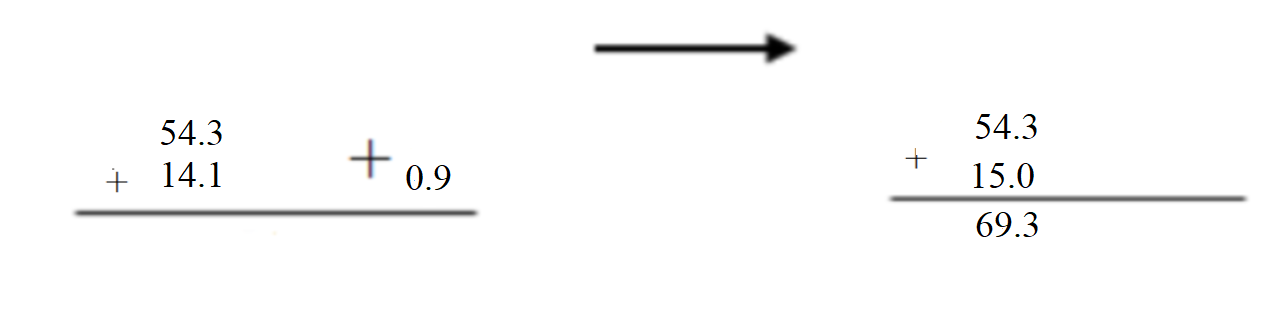
Question 3. 19.86 – 7.2 = ______ Answer:

Question 4. 41.19 – 0.58 = _______ Answer: 41.19 – 0.58 =

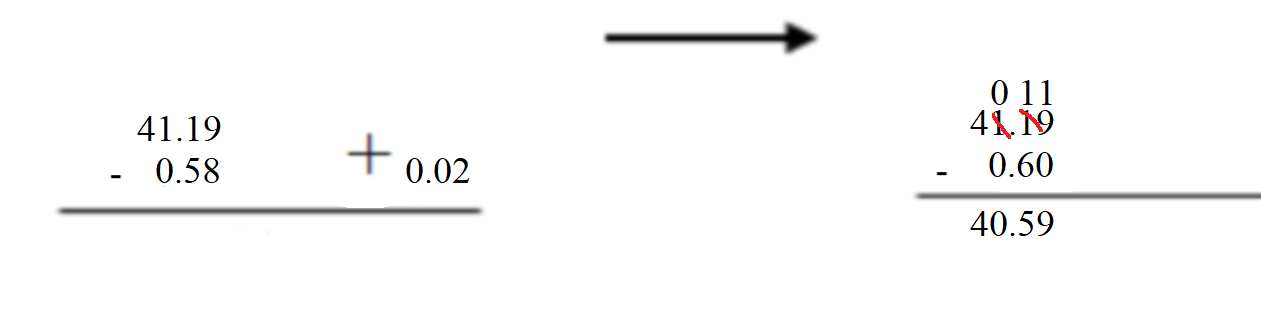
Question 5. 6.5 + 2.32 + 1.5 = _____ Answer: 6.5 + 2.32 + 1.5 = 10.32.

Explanation: Notice that 6.5 and 1.5 are compatible numbers. Use addition properties to rewrite the problem. 6.5 + 2.32 + 1.5  = 2.32 + 6.5 + 1.5 Commutative Property = 2.32 + (6.5 + 1.5)  Associative Property = 2.32 + 8.0 = 10.32.

Question 6. 2.25 – 1.15 = ______ Answer: 2.25 – 1.15 = 1.10.

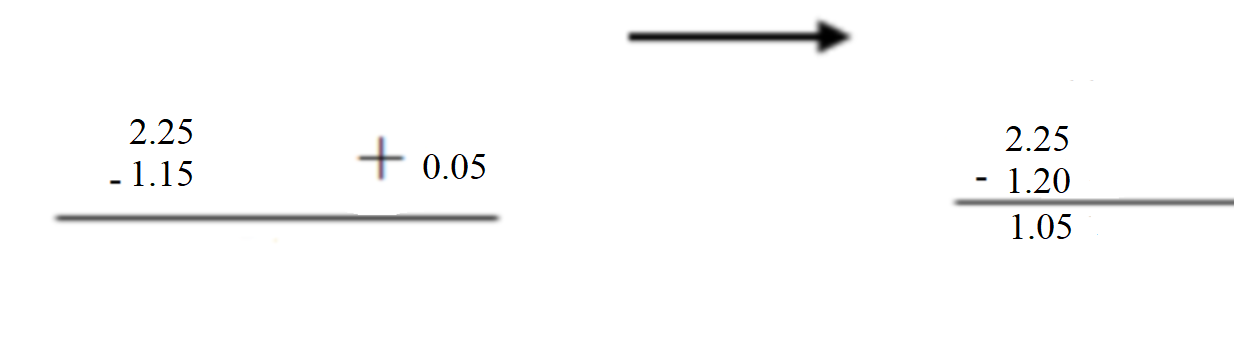
Question 8. Writing Describe a situation when you would use the Commutative Property to add decimals using mental math. Answer:

The Commutative Property of Addition states that the order of the addends does not change the sum. Let’s test the property using simple whole numbers.

4 + 5 + 9 = 18        4 + 9 + 5 = 18          5 + 4 + 9 = 18        5 + 9 + 4 = 18          9 + 5 + 4 = 18          9 + 4 + 5 = 18

As you can see, we can add the three addends (4, 5, and 9) in many different orders. The Commutative Property of Addition works also works for four, five, six addends, and it works for decimal addends, too.

Question 9. DIG DEEPER! Use mental math to find the missing number. Answer:

Explanation: Length of Albatross wingspan = 10.95 feet Length of  long Alligator = 8.89 foot Difference: Length of Albatross wingspan – Length of  long Alligator = 10.95 – 8.89 = 2.06 feet

Question 11. Modeling Real Life Your friend buys 3.5 meters of blue ribbon, 2.25 meters of red ribbon, and 3.75 meters of white ribbon. How much ribbon does she buy in all? Answer: Total Length of all ribbons = 9.50 meters.

Explanation: Length of blue ribbon = 3.5 meters Length of red ribbon = 2.25 meters Length of white ribbon = 3.75 meters Total Length of all ribbons = Length of blue ribbon + Length of red ribbon + Length of white ribbon = 3.5 + 2.25 + 3.75 = 5.75 + 3.75 = 9.50 meters

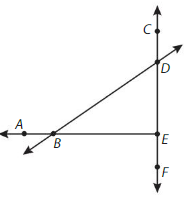
Explanation: In  geometry, a line segment is a part of a  line that is bounded by two distinct end  points , and contains every point on the line between its endpoints.

Question 13. Name two different rays. Answer: EF and AB are two different Rays.

Explanation: In geometry, a ray can be defined as a part of a  line that has a fixed starting point but no end point. It can extend infinitely in one direction.

Question 14. Name two different lines. Answer: EA and DF are different lines.

Explanation: In geometry, a line can be defined as a straight one- dimensional figure that has no thickness and extends endlessly in both directions. It is often described as the shortest distance between any two points.

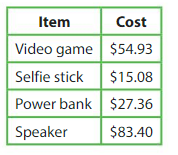
Explanation: Cost of Video game = $54.93 Cost of Selfie stick = $15.08 Cost of Power Bank = $27.36 Cost of Speaker = $83.40 Total cost of all items = Cost of Video game + Cost of Selfie stick + Cost of Power Bank + Cost of Speaker = $54.93 + $15.08 + $27.36 + $83.40 = $70.01 + $27.36 + $83.40 = $97.37 + $83.40 = $180.77.

Precision Switch papers with your partner. Check your partner’s work for reasonableness. Answer: Both the answers are reasonableness because the answers procedure is same and answers match.

Think and Grow: Problem Solving: Money

Example You have$11.83. You earn $13.75 more doing chores. Then you buy headphones for $12.39. How much money do you have left? Understand the Problem What do you know? • You have $11.83. • You earn $13.75 more. • You buy headphones for $12.39.

What do you need to find? • You need to find how much money you have left.

Make a Plan How will you solve? Write and solve an equation to find the amount of money you have left.

Explanation: Amount of money I have = $11.83 Amount of money I have earned = $13.75 Cost of Headphones = $12.39 Amount left out with me = Amount of money I have + Amount of money I have earned + Cost of Headphones = $11.83 + $13.75 – $12.39 = $25.58 – $12.39 = $13.19.

Explanation: Amount of money I have = $32.63 Amount of money earned = $28.42 Cost of Video game = $35.95 Amount of money left with me = Amount of money I have + Amount of money earned + Cost of Video game = $32.63 + $28.42 – $35.95 = $61.05 – $35.95 = $25.1.

Understand the problem. What do you know? What do you need to find? Explain. Question 2. You buy 3 cell phone games that cost $5 each and an in-game purchase for $1.69. How much money do you spend? Answer: Total Cost of money spent = $16.69

Explanation: Cost of 3 cell phones games = 3 × $5 = $15 Cost of an in-game = $1.69 Total Cost of money spent = Cost of 3 cell phones games + Cost of an in-game = $15 + $1.69 = $16.69.

Explanation: Cost of movie ticket = $4.50 Cost of a drink = $2.25 Cost of a bag of popcorn = $4.75 Total amount spent = Cost of movie ticket + Cost of a drink + Cost of a bag of popcorn = $4.50 + $2.25 + $4.75 = $6.75 + $4.75 = $11.50.

Understand the problem. Then make a plan. How will you solve? Explain. Question 4. Your friend buys a remote control car for$17.89 and some batteries for $5.49. He gives the cashier $25. How much change does he receive? Answer: Amount of change he receives = $1.62.

Explanation: Cost of remote control car = $17.89 Cost of Some batteries = $5.49 Money given to cashier = $25 Amount of change he receives = Money given to cashier- Cost of remote control car + Cost of Some batteries – = $25 – $17.89 + $5.49 = $25 – $23.38 = $1.62.

Question 5. Your cousin has $156.34 in his bank account. He withdraws $15.50 one day and $6.75 the next day.  How much money is in his bank account now? Answer: Amount left in his bank account = $134.09.

Explanation: Amount of money my cousin has in bank account = $156.34 Amount of money he withdraws one day = $15.50 Amount of money he withdraws next day = $6.75 Amount left in his bank account = Amount of money my cousin has in bank account – Amount of money he withdraws one day – Amount of money he withdraws next day = $156.34 – $15.50 – $6.75 = $156.34 – $22.25 = $134.09.

Explanation: Cost of Adult admission to open skate night = $5.75 Cost of Admission for children under 13 costs $1.50 less than adult admission => $5.75 – $1.50 => $4.25 Total admission cost for two 12-year-olds = Cost of Adult admission to open skate night  + Cost of Admission for children under 13 = $5.75 + $4.25 = $10.

Question 7. Descartes buys a book for $14.99 and a bookmark. He pays with a $20 bill and receives $3.96 in change. How much does the bookmark cost? Answer: Cost of the book mark = $1.05.

Explanation: Cost of the book and a bookmark = $14.99 Amount paid by a bill = $20 Amount of money received as change = $3.96 Cost of the book mark = Amount paid by a bill – Cost of the book and a bookmark – Amount of money received as change = $20 – $14.99 – $3.96 = $5.01 – $3.96 = $1.05.

Explanation: Cost of the coloring book = $5.99 Cost of the colored pencils = $8.99 Amount received as change = $17.42 Amount paid in two bills = $20 × 2 = $40 Cost of the pencil sharpener costs = Amount paid in two bills  – (Cost of the coloring book + Cost of the colored pencils) + Amount received as change = $40 – ( $5.99 + $8.99 ) – $17.42 = $40 – $14.98 – $17.42 = $25.02 – $17.42 = $7.6.

Explanation: Cost of a bag of dog food = $5.49 Cost of a dog’s new collar = $7.10 Amount of change he receives = $4.02 Amount paid in four bills = $5 × 4 = $20. Cost of the box of bones = Amount paid in four bills – (Cost of a bag of dog food – Cost of a dog’s new collar) – Amount of change he receives = $20 – ($5.49 + $7.10) – $4.02 = $20 – $12.59 – $4.02 = $7.41 -$4.02 = $3.39.

Explanation: Cost of the Helmet = $27.50 Cost of the Scooter = $124.99 Amount of money paid additionally = $2.49 Let the gifts cards be X. = 2Cost of the each gift cards + Amount of money paid additionally = (Cost of the Helmet + Cost of the Scooter) => 2X + $2.49 = $27.50 + $124.99 => 2X + $2.49 = $152.49 => 2X = $152.49 – $2.49 => 2X = $150.00 => X = $150.00 ÷ 2 => X = $75.

Understand the problem. What do you know? What do you need to find? Explain. Question 1. A musician buys an electronic keyboard for $89.94 and 2 books of sheet music for $7.99 each. How much does she spend in all? Answer: Total cost of money spent = $105.92.

Explanation: Cost of an electronic keyboard = $89.94 Cost of two books of sheet music = $7.99 × 2 = $15.98 Total cost of money spent = Cost of an electronic keyboard + Cost of two books of sheet music = $89.94 +  $15.98 = $105.92

Question 2. You have$28.49. You spend $14.95 at a bowling alley. You win $35.00 for setting the record score for your age group. How much money do you have now? Answer: Amount of money I have now = $48.54.

Explanation: Amount of money I have = $28.49 Amount spent at a bowling alley = $14.95 Amount of money won = $35.00 Amount of money I have now = Amount of money I have – Amount spent at a bowling alley  + Amount of money won => $28.49 – $14.95 + $35.00 => $13.54 +  $35.00 => $48.54.

Understand the problem. Then make a plan. How will you solve? Explain. Question 3. Newton wins a $50 gift card toa craft store. He uses the card to buy a scrapbook for $19.99 and a set of markers for $10.75. How much money is left on his gift card? Answer: Amount of money left on his gift card = $19.26.

Explanation: Amount of money won for a gift card to a craft store = $50 Amount of money spent to buy a scrapbook by using card = $19.99 Amount of money spent to buy a set of markers by using card = $10.75 Amount of money left on his gift card = Amount of money won for a gift card to a craft store – (Amount of money spent to buy a scrapbook by using card  + Amount of money spent to buy a set of markers by using card) = $50 – ($19.99 + $10.75) = $ 50 – $30.74 = $19.26.

Explanation: Cost of the  ballet shoes = $26.49 Cost of the tutu = $48.75 Amount given to cashier = $80 Amount of change received = Amount given to cashier – (Cost of the tutu + Cost of the ballet shoes ) = $80 – ( $ 26.49 + $48.75) = $80 – $75.24 = $4.76

Question 5. A theater director buys props for$116.20 and costumes for $494.85. He has $194.27 left. How much money did he have to start? Answer: Amount of money he  have started = $805.32.

Explanation: Cost of props = $116.20 Cost of the costumes = $494.85 Amount left with him = $194.27 Amount of money he  have started = Cost of the costumes + Cost of props + Amount left with him = $116.20 + $494.85 + $194.27 = $611.05 + $194.27 = $805.32

Question 6. Descartes uses a metal detector at a beach. He finds 3 quarters, 6 dimes,2 nickels, and 5 pennies. He drops1 quarter and 2 pennies into the water. Then he finds 4 more dimes. How much money does Descartes have now? Answer: Total amount of money Descartes have now = 163 pennies.

Explanation: Number of dimes found = 6 Number of quarters found = 3 Number of pennies found = 5 Number of nickels found = 2 Number of quarters dropped into water= 1 Number of pennies dropped into water = 2 Number of dimes found later = 4 Conversion:

Total number of quarters = Number of quarters found  – Number of quarters dropped into water => 3 – 1 = 2 Quarter into pennies => 1 Quarter = 25 pennies => 2 Quarter  = 25 × 2 = 50 pennies.

Total number of dimes = Number of dimes found  + Number of dimes found later => 6 +4 = 10 Dimes into pennies => 1 Dime = 10 pennies => 10 Dime = 10 × 10 = 100 pennies

Total number of Nickels = Number of nickels found => 2 Nickels into pennies => 1 Nickel = 5 pennies => 2 nickels = 2 × 5 = 10 pennies

Total Number of pennies = Number of pennies found – Number of pennies dropped into water => 5 – 2 =>3 pennies Total amount of money Descartes have now = Total number of quarters  + Total number of dimes + Total number of Nickels + Total Number of pennies = 50 pennies + 100 pennies + 10 pennies + 3pennies = 163 pennies.

Explanation: Cost of a ball launcher = $12.50 Number of bills he has worth $10 = 1 Number of bills he has worth $5 = 2 Number of bills he has worth $1 = 3 Number of quarters he has = 2 Conversion: Quarter into Dollars 1 Quarter = $0.25 =>2 Quarter = 0.25 × 2 = $0.50.

Amount given to cashier =  Number of bills he has worth $10 + Number of bills he has worth $5 + Number of bills he has worth $1 + Number of quarters he has => $10 + $5 + $5 + $1 + $1 + $1 + $0.50 => $23.50

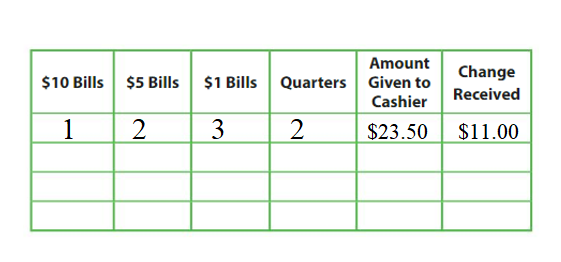
Explanation: Cost of the ultraviolet light = $13.29 Cost of the beaker = $7.99 Amount of change teacher receives= $0.77

Your science teacher pays an ultraviolet light, a beaker, and a glowing liquid kit with five $5 bills => Cost of the ultraviolet light  + Cost of the beaker  + Cost of the glowing liquid kit + Amount of change teacher receives = 5 × $5 => $13.29 + $7.99 + Cost of the glowing liquid kit + $0.77 = $25 => $22.05 + Cost of the glowing liquid kit = $25 => Cost of the glowing liquid kit = $25 – $22.05 => Cost of the glowing liquid kit = $2.95

Find the equivalent length. Question 9. 10 ft = _____ in. Answer: 10 ft = 120 in.

Explanation: Conversion: 1 feet = 12 inches => 10 feet = 10 × 12 =120 inches.

Question 10. 2 mi = ______ ft Answer: 2 mi = 10560 ft

Explanation: Conversion: 1 Mile = 5280 feet 2 mi = 5280 × 2 = 10560 ft

Question 11. \(\frac{1}{3}\) yd = ______ ft Answer: \(\frac{1}{3}\) yd = \({1}\) feet.

Explanation: Conversion: 1 Yard = 3 Feet \(\frac{1}{3}\) yd = \(\frac{1}{3}\) yd  × \({3}\) = \({1}\) feet

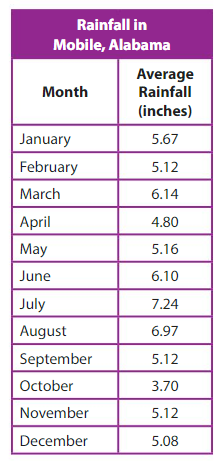
Explanation: Rainfall rate in June month = 6.10 inches Rainfall rate in July month = 7.24 inches Rainfall rate in August month = 6.97 inches Average rainfall during June, July, and August = Rainfall rate in June month + Rainfall rate in July month + Rainfall rate in August month ÷ 3 = 6.10 + 7.24  + 6.97  ÷ 3 = 20.31 ÷ 3 = 6.77 inches

Question 2. How many more inches of rainfall does the city usually get in July than in October? Answer: 3.54 inches. of Rainfall is more in the city in July  month than in October month.

Explanation: Rainfall in July month = 7.24 inches Rainfall in October month = 3.70 inches Comparison: = Rainfall in July month – Rainfall in October month = 7.24  – 3.70 = 3.54 inches.

Question 3. a. Round each rainfall amount to the nearest tenth. About how many inches of rainfall does Mobile get each year? b. How can you check whether your answer is reasonable? Answer: a)  The total Rainfall Mobile gets each year = 66.22 inches. b) We can check the answer is reasonable or not by rounding it to its nearest 10.

Explanation: a) Round each rainfall amount to the nearest tenth.

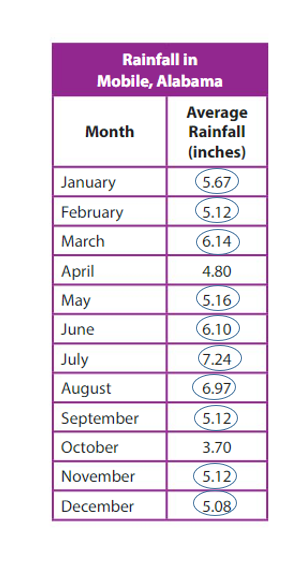
b) We can check the answer is reasonable or not by rounding it to its nearest 10. 63 is close reasonable to 66.22.

b) Seattle is known for being one of the rainiest cities in the United States, even though it usually gets less rain than Mobile each year. This means that Seattle has more frequent rain, but the light rain results in low totals than compared to rainfall in Mobile, Alabama.

Explanation: a)The average yearly amount of rainfall in Seattle, Washington, is about 3 feet. => Average Rainfall of Seattle, Washington  = 3 feet. Total Average of  Rainfall in Mobile, Alabama = 66.22 inches Difference : 1 feet = 12 inches => 3 feet = 12 × 3 = 36 inches Total Average of  Rainfall in Mobile, Alabama – Average Rainfall of Seattle, Washington = 66.22 – 36 = 30.22 inches

3.1 Estimate the Sum or Differences.

Question 3. 13.47 – 9.82 Answer: 13.47 – 9.82 = 3.65.

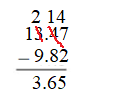
Question 4. 64.9 + 17.5 Answer: 64.9 + 17.5 = 82.4.

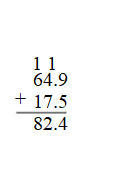
Question 5. Number Sense Descartes estimates a difference by rounding each number to the nearest whole number. His estimate is 6. Which problems could he have estimated? 97.5 – 91.8 10.3 – 4.6 23.7 – 18.1 7.2 – 0.8 Answer: His Problems of estimation to 6 are 97.5 – 91.8 and 7.2 – 0.8.

Explanation: First  round the numbers to nearest whole number later , find the difference: 97.5 – 91.8 = 98 – 92 = 6 10.3 – 4.6 = 10 – 5 = 5 23.7 – 18.1 = 23 – 18 = 5 7.2 – 0.8 = 7 – 1 = 6

3.2 Use Models to Add or Subtract Decimals

Make a quick sketch to find the sum or difference. Question 6. 0.27 + 0.19 Answer: 0.27 + 0.19 = 0.46.

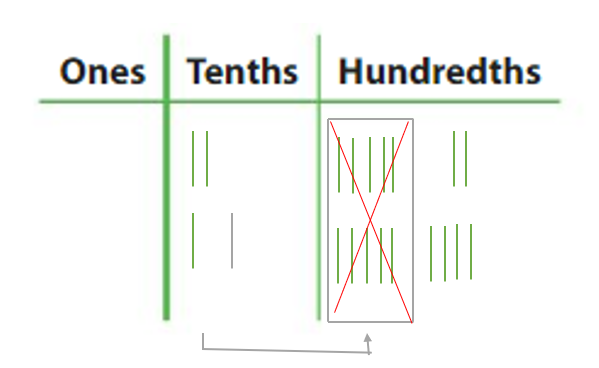
Question 7. 2.52 – 1.36 = ______ Answer: 2.52 – 1.36 = 1.16.

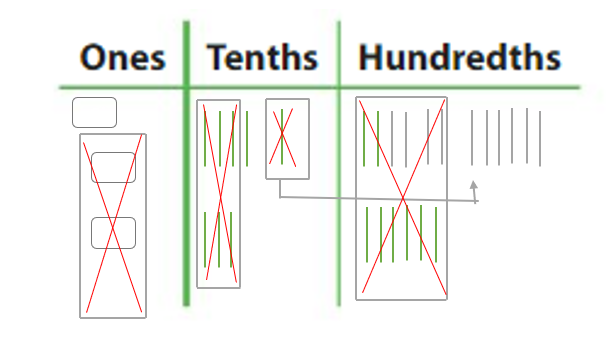
3.3 Add Decimals

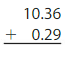
Question 10. 97.65 + 23.08 = _____ Answer: 97.65 + 23.08 = 120.73. 120.73 is reasonable.

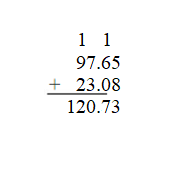
Question 11. 63.39 + 4.05 = _____ Answer: 63.39 + 4.05 = 67.44. 67.44 is a reasonable.

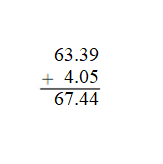
Question 12. Modeling Real Life You want to conduct an experiment. You need 0.5 cup of water and the same amount of oil. How many cups of liquid do you need for the experiment? Answer: Total number of cups required of liquid = 1 cup.

Explanation: Amount of water required = 0.5 cup Amount of oil required = 0.5 cup Total number of cups required of liquid = Amount of water required + Amount of oil required = 0.5 + 0.5 = 1 cup

3.4 Subtract Decimals

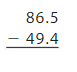
Question 15. 582.58 – 33.21 = _____ Answer: 582.58 – 33.21 = 549.37.

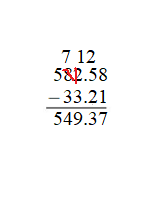
Question 16. 99.2 – 8.6 = _____ Answer: 99.2 – 8.6 = 90.6.

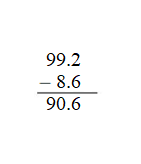
3.5 Add and Subtract Decimals

Evaluate. Check whether your answer is reasonable. Question 17. 9.28 – 5.4 – 2.75 = _____ Answer: 9.28 – 5.4 – 2.75 = 1.13. 1.13 is reasonable.

Explanation: 9.28 – 5.4 – 2.75 =  ??? 9.28 – 5.4 – 2.75 = 3.88 – 2.75 = 1.13. Check: 1.13 + 2.75 + 5.4 = 3.88 + 5.4 = 9.28.

Question 18. 2 + 18.6 – 7.9 = ______ Answer: 2 + 18.6 – 7.9 = 12.7. 12.7 is reasonable.

Explanation: 2 + 18.6 – 7.9 = ??? 2 + 18.6 – 7.9 = 20.6 – 7.9 = 12.7 Check: 12.7 + 7.9 – 18.6 = 20.6 – 18.6 = 2

Question 19. 26 – 0.8 + 13.1 = ______ Answer: 26 – 0.8 + 13.1 = 38.3 38.3 is reasonable.

Explanation: 26 – 0.8 + 13.1 = ??? 26 – 0.8 + 13.1 = 25.2 + 13.1 = 38.3

Check: 38.3 – 13.1 + 0.8 = 25.2 + 0.8 = 26

Question 20. 1.72 + 4 + 35.68 Answer: 1.72 + 4 + 35.68 = 41.4 41.4 is reasonable.

Explanation: 1.72 + 4 + 35.68 = ??? 1.72 + 4 + 35.68 = 5.72 + 35.68 = 41.4

Check: 41.4 – 35.68 -4 = 5.72 – 4 = 1.72

Explanation: Snowfall in the month of December = 27.5 Snowfall in the month of January = 30.75 Snowfall in the month of February = 12.25 Total Snowfall in all three months = Snowfall in the month of December – Snowfall in the month of January – Snowfall in the month of February = 27.5 + 30.75 + 12.25 = 58.25 + 12.25 = 70.50 inches.

3.6 Use Mental Maths to Add or Subtract Decimals

Use mental math to find the sum or difference. Question 22. 6.3 + 2.98 + 5.7 = ______ Answer: 6.3 + 2.98 + 5.7 = 14.98.

Explanation: Given 6.3 + 2.98 + 5.7 = 6.3 and 5.7 are compatible numbers. Use addition properties to rewrite the problem. 6.3 + 2.98 + 5.7 = 2.98 + (6.3 + 5.7) Associative Property = 2.98 + 12 = 14.98.

Question 23. 9.1 + 4.57 + 8.03 = _____ Answer: 9.1 + 4.57 + 8.03 = 21.7.

Explanation: Given 9.1 + 4.57 + 8.03 4.57 and 8.03 are compatible numbers. Use addition properties to rewrite the problem. 9.1 + 4.57 + 8.03 = 9.1 + (4.57 + 8.03) Associative Property = 9.1 + 12.6 = 21.7

Question 24. 25.7 – 14.9 = _____ Answer: 25.7 – 14.9 = 10.8.

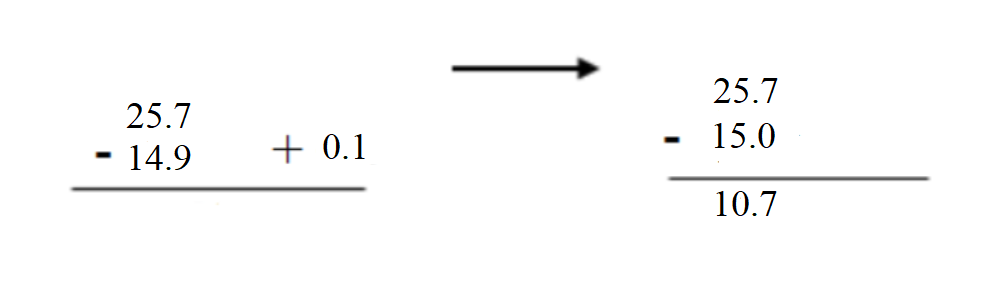
Question 25. 9.24 – 2.67 = _____ Answer: 9.24 – 2.67 = 6.57.

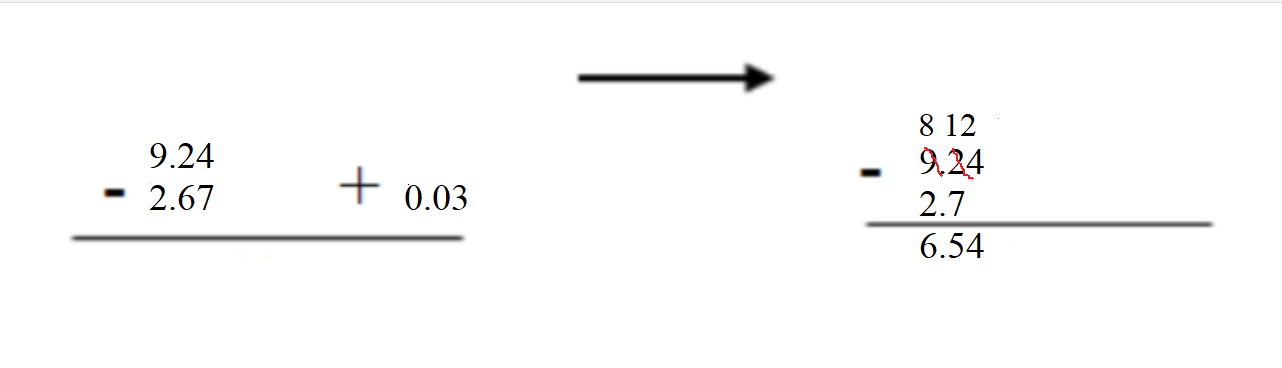
Question 26. Number Sense Use mental math to find the missing number. 9.2 + n + 2.5 = 15.8 Answer:

3.7 Problem Solving: Money

Explanation: Cost of a board game = $9.99 Cost of a pack of trading cards = $2.99 Amount of bills paid to cashier = $20 Amount of money change received = Amount of bills paid to cashier – ( Cost of a pack of trading cards + Cost of a board game  ) = $20 – ( $9.99 + $2.99 ) = $20 – $12.98 = $7.02.

Question 28. Descartes has $378.97 in his bank account. He withdraws $59.50 one day and then deposits $20.44 the next day. How much money is in his bank account now? Answer: Amount of money left in the bank account = $339.91.

Explanation: Amount of money Descartes has in his bank account= $378.97 Amount of money withdrawn = $59.50 Amount of money he deposited later = $20.44 Amount of money left in the bank account = Amount of money Descartes has in his bank account – Amount of money withdrawn +  Amount of money he deposited later = $378.97 – $59.50 + $20.44 = $319.47 + $20.44 = $339.91

Question 29. Modeling Real Life A bowling alley charges $7.50 for each person to bowl and $2.25 to rent a pair of shoes. How much does it cost you and your friend to bowl and rent shoes? Answer: Amount of money charged  for me and my friend to bowl and rent shoes = $9.75.

Explanation: Amount of money charged for each person to bowl = $7.50 Amount of money charged as rent for a pair of shoes = $2.25 Amount of money charged  for me and my friend to bowl and rent shoes = Amount of money charged for each person to bowl + Amount of money charged as rent for a pair of shoes = $7.50 + $2.25 = $9.75.

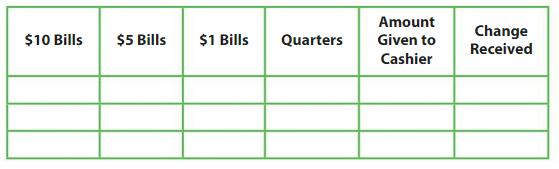
Explanation: Cost of the a magic kit = $18.75 Number of $10 bills my friend has = 2 = $10 × 2 = $ 20. Number of $5 bills my friend has = 1 = $5 × 1 = $5. Number of $1 bills my friend has = 4 = $ 1 × 4 = $ 4. Number of Quarters my friend has = 3 Conversion: 1 Quarter = 0.25 dollar => 3 Quarter = 3 × 0.25 = $0.75. Amount of money my friend has = Number of $10 bills my friend has + Number of $5 bills my friend has + Number of $1 bills my friend has + Number of Quarters my friend has = $20 + $5 + $4 + $0.75 = $ 25 + $4 + $0.75 = $29 + $0.75 = $29.75.

Question 1. Using the order of operations, which operation should you perform last to evaluate the expression? (4 × 6) + (100 ÷ 10) – (3 + 4) A. addition B. subtraction C. multiplication D. division Answer: A. addition.

Explanation: Given Equation: According to DMAS rule: First Division: => (4 × 6) + (100 ÷ 10) – (3 + 4) => (4 × 6) + 10 – (3 + 4) Second Multiplication: => (4 × 6) + 10 – (3 + 4) => 24 + 10 – (3 + 4) Third Addition: => 24 + 10 – (3 + 4) => 24 + 10 + 1 => 34 +1 => 35.

Explanation: Round all options to nearest whole number: 4.03 –  4 4.5  – 5 44.2 – 44 3.98 – 4 3.46 – 3 4.1 – 4

Answer: Total distance from A to E = 4.5 km => River Run bike trail the figure shows.

Question 4. What is 0.045 written as a fraction? A. \(\frac{45}{100}\) B. \(\frac{1,000}{45}\) C. \(\frac{45}{1,000}\) D. \(\frac{450}{1,000}\) Answer: C. \(\frac{45}{1,000}\)

Explanation: 0.045 fraction= 45 ÷ 1000.

Explanation: A recipe calls for 3 eggs. Number of recipe batches Newton makes = 5 =>Number of eggs used by Newton = 5 × 3 Number of recipe batches Descartes makes = 2 =>Number of eggs used by  Descartes = 2 × 2 Number of eggs both used = Number of eggs used by Newton + Number of eggs used by  Descartes = (5 × 3) + ( 2 × 2 ) = 15 + 4 = 19.

Question 7. What is 60.25 written in word form? A. sixty twenty-five B. sixty and twenty-five tenths C. sixty and twenty-five D. sixty and twenty-five hundredths Answer: D. sixty and twenty-five hundredths

Explanation: Number name of 60.25 = ????

Question 8. Find 55.6 – 3.97. A. 1.59 B. 51.63 C. 52.37 D. 59.57 Answer: 55.6 – 3.97 = 51.63.

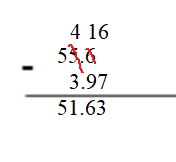
Question 9. What is the value of the expression? [21 ÷ (3 + 4)] – 2 A. 9 B. 4 R1 C. 1 D. 2 Answer: C. 1

Explanation: [21 ÷ (3 + 4)] – 2 = [21 ÷ (7)] – 2 = 3 – 2 =1

Question 11. What is the value of n? n – 9.02 = 3.85 A. 12.87 B. 5.17 C. 3.87 D. 12 Answer: n = 12.87.

Explanation: n = ?? n – 9.02 = 3.85 n = 3.85 + 9.02 n = 12.87.

Question 12. Which property is shown? 35 + (15 + 7) = (35 + 15) + 7 A. Associative Property of Addition B. Commutative Property C. Distributive Property D. Associative Property of Multiplication Answer: A. Associative Property of Addition.

Explanation: The associative property states that you can add or multiply regardless of how the numbers are grouped. 35 + (15 + 7) = (35 + 15) + 7

Explanation: First, find all sums of given Equations: 123.5 + 19.6 = 124 + 20 = 144. 87.6 + 50.4  = 88 + 50 = 138. 65.43 + 71.59 = 65 + 72 = 137. 98.03 + 34.56 = 98 + 34 = 132.

Question 14. What is five hundred four thousand, eleven written in standard form? A. 54,011 B. 54,110 C. 504,110 D. 504,011 Answer:

Explanation: First, solve the equations: 30 ÷ ( 5 × 2 ) + 5 = 30 ÷ 10 + 5 = 3 + 5 = 8. 55 – 7 ÷ 6 = 55  – 1.167 = 53.833. 4 × ( 5 – 3 ) = 4 × 2 = 8. (16 ÷ 8) + ( 3 × 2 ) = 2 + 6 = 8.

Question 16. Descartes wins a $50 gift card to a sporting goods store. He uses the card to buy two baseballs for $1.79 each, a baseball glove for $14.99, and a baseball bat for $12.25. About how much money is left on his gift card? A. $21 B. $19 C. $31 D. $18 Answer: Total amount left on his gift card= $19.18.

Explanation: Amount of gift card won for a sporting goods store = $50 Cost of the two baseballs  = $1.79 each = > 2 × 1.79 = $3.58 Cost of a baseball glove = $14.99 Cost of a baseball bat = $12.25 Total amount left on his gift card= Amount of gift card won for a sporting goods store – (Cost of the two baseballs + Cost of a baseball glove + Cost of a baseball bat ) = $50 – ( $3.58 + $14.99 + $12.25) = $50 – ( $18.57 + $12.25) = $50 – $30.82 = $19.18.

Question 17. What is the value of 4× 10 5 ? A. 45 B. 400,000 C. 40,000 D. 200 Answer: 4× 10 5    = B. 400,000.

Explanation: 4× 10 5 = 4 × 10 ×10 × 10 × 10 × 10 = 4 × 100000 = 400,000

Part B: Evaluate the expression. 9ft × 8ft >  7ft × 5ft => 72ft > 35ft

Part C: I used the order of DMAS rule. Division, Multiplication, Addition and Subtraction order of operations to evaluate the expression

Explanation: Part A: Length of the green rectangle = 9ft Width of the green rectangle = 8ft Area of the green rectangle = Length of the green rectangle × Width of the green rectangle = 9ft × 8ft = 72 ft. Length of the yellow rectangle = 7ft Width of the yellow rectangle = 5ft Area of the yellow rectangle = Length of the yellow rectangle × Width of the yellow rectangle = 7ft × 5ft = 35ft

Part C: Explain how you used order of operations to evaluate the expression. I used the order of DMAS rule. Division, Multiplication, Addition and Subtraction order of operations to evaluate the expression.

Explanation: Amount in the account at the start of the school year = $100.00 Amount in the account used for supplies = $85.89 Amount of money left in the account = Amount in the account at the start of the school year – Amount in the account used for supplies = $100.00 – $85.89 = $ 14.11

Explanation: Amount of money received in sales for the first week = forty-four dollars and thirty cents = $44.30 Amount of money received in sales for the second week = thirty-two dollars and twelve cents = $ 32.12

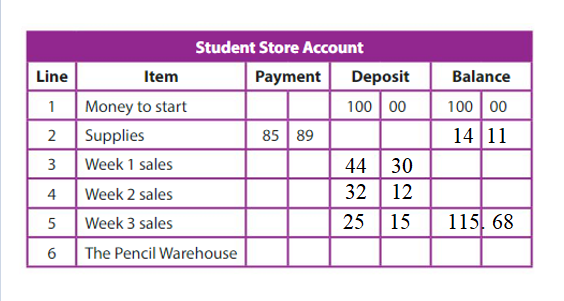
Explanation: Amount of money balance after the third week of sales = $115.68 Amount of money received in sales for the first week = forty-four dollars and thirty cents = $44.30 Amount of money received in sales for the second week = thirty-two dollars and twelve cents = $ 32.12 Amount of money left in the account = $14.11 Amount of money received in sales for the third week + Amount of money received in sales for the first week + Amount of money received in sales for the second week + Amount of money left in the account = Amount of money balance after the third week of sales = Amount of money received in sales for the third week  + $44.30 + $32.12 + $14.11 = $115.68 => Amount of money received in sales for the third week  + $76.42 + $14.11 = $115.68 => Amount of money received in sales for the third week + $90.53 = $115.68 => Amount of money received in sales for the third week  = $115.68 – $90.53 =>Amount of money received in sales for the third week  = $25.15.

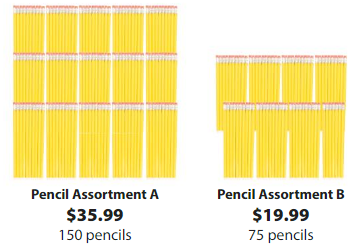
b)Cost the pencil to be sold = $0.30 because 0.06 is the profit range of 4 % out of 0.24.

c) The profit store owns from selling 100 pencils using your recommended price is $30.

d) Cost of the Notebooks and pencils = $115.24

Explanation: a) Cost of 150pencil from Pencil assortment A = $ 35.99 => Cost of each pencil from Pencil assortment A = $35.99 ÷ 150 = $ 0.2399 Cost of 75pencil from Pencil assortment B = $19.99 => Cost of each pencil from Pencil assortment B = $19.99 ÷ 75 = $0.2665

b) Cost of pencil is purchased by me = $0.24 Cost the pencil to be sold = $0.24 + $0.06 = $0.30 Because 0.06 is the profit range of 4 % out of 0.24.

c) Cost of each pencils to be sold = $0.30 Cost of 100 pencils to be sold = $0.30 × 100 = $30.

d) Total Cost of the Notebooks = $25.24 Cost of 300 pencils = $0.30 ×300 = $90 Amount of coupon used to pay = $5 Cost of the Notebooks and pencils = Total Cost of the Notebooks + Cost of 300 pencils = $25.24 + $90 = $115.24.

e) Current account balance = $115.68

Conclusion:

Hope the information provided in the above pdf is helpful for all the students in Grade 5. Download Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals for free of cost. Keep in touch with us to get the latest updates of all Grade 5 chapters.

Leave a Comment Cancel Reply

You must be logged in to post a comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 1: Decimal place value

Unit 2: add decimals, unit 3: subtract decimals, unit 4: add and subtract fractions, unit 5: multi-digit multiplication and division, unit 6: multiply fractions, unit 7: divide fractions, unit 8: multiply decimals, unit 9: divide decimals, unit 10: powers of ten, unit 11: volume, unit 12: coordinate plane, unit 13: algebraic thinking, unit 14: converting units of measure, unit 15: line plots, unit 16: properties of shapes.

• Notifications 0

• Add Friend ($5)

As a registered member you can:

• View all solutions for free
• Request more in-depth explanations for free
• Ask our tutors any math-related question for free
• Email your homework to your parent or tutor for free
• Grade 5 HMH Go Math - Answer Keys

Estimate. Then find the sum.

4.23 +6.51 Estimate    Sum:    Explanation:   6.8 +4.2     2.7 +5.37 Find the sum. 6.87 + 5.18 16.18 + 5.94 19.8 + 31.45 25.47 + 7.24 9.17 + 5.67 19.7 + 5.46 Problem Solving Marcela’s dog gained 4.1 kilograms in two months. Two months ago, the dog’s mass was 5.6 kilograms. What is the dog’s current mass?    kilograms During last week’s storm, 2.15 inches of rain fell on Monday and 1.68 inches of rain fell on Tuesday. What was the total amount of rainfall on both days?    inches Yes, email page to my online tutor. ( if you didn't add a tutor yet, you can add one here ) Thank you for doing your homework! Submit Your Question 490 COMMENTS PDF Go Math! Practice Book (TE), G5 Add Decimals possible estimates are given. Estimate. Then find the sum. Lesson 3.8 COMMON CORE STANDARD CC.5.NBT.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. 3. ... Practice Book (TE), G5 Created Date: 10/14/2015 8:30:23 PM ... Go Math 5th Grade Lesson 3.8 Add Decimals This Go Math video covers the concept of adding decimals by both the standard algorithm and by modeling a quick picture of "regrouping." Mathematical Practic... Add Decimals This lesson shows the steps to adding decimals. 5th grade GO Math: Lesson 3.8 Add Decimals pages 139-142 This video covers lesson 3.8 Add Decimals on pages 139-142 of the 5th grade GO Math textbook. Go Math Chapter 3 Chapter 3. Add and Subtract Decimals. . *Animated Math Model and Mega Math Game work only on Laptops and Desktops. . Chapter 3 Student Book. . Chapter 3 Student Practice Book. . PDF Chapter 3 Add and Subtract Decimals Chapter 3 Add and Subtract Decimals Use the GO Math! Planning Guide for correlations, ... 3.8 Practice and Homework Student Edition) 3.8 Reteach (in the Chapter Resources) 3.8 ... 1 Day LESSON 3.8 5.NBT.B.7 1 Day LESSON 3.7 5.NBT.B.7 Domain: Number and Operations in Base Ten Chapter 3 Add and Subtract Decimals Diagnostic Formative Summative Decimals Worksheets Begin by ignoring the decimals in the addition question. Add the numbers as if they were whole numbers. For example, 3.25 + 4.98 could be viewed as 325 + 498 = 823. Use an estimate to decide where to place the decimal. In the example, 3.25 + 4.98 is approximately 3 + 5 = 8, so the decimal in the sum must go between the 8 and the 2 (i.e. 8.23) Adding decimals and whole numbers (tenths) (practice) Adding decimals and whole numbers (tenths) Google Classroom. Microsoft Teams. Add. = 80 + 7.1. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere. Adding decimals with ones and tenths parts Now we're left with 8 ones and 12 tenths. To add these together, we have to make them have the same unit. If we have 12 tenths, we also have 1.2 ones. 8 ones plus 1.2 ones gives us 9.2 ones. You could also do this by changing them all to tenths. 6.3 is 63 tenths. 2.9 is 29 tenths. 63 + 29 = 92. The answer is 92 tenths, or 9.2. PDF Practice and Homework Name Lesson 3 6.8 1 4.2 2.7 1__ 5.37 11. WRITE Math Describe an addition problem that you may need to regroup hundredths to solve. Lesson 3.8 COMMON CORE STANDARD—5.NBT.B.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. Practice and Homework go math chapter 3 5th grade adding and subtracting decimals Turning Back Time. $5.00. Zip. This resource is paced with Go Math Chapter 3, which is adding and subtracting decimals. The teaching companion is filled with anchor charts, models, teacher thinking bubbles, and vocabulary for each lesson that are also included on a student journal page for quick reference. Go Math Practice Lesson 1: Investigate • Thousandths. Lesson 2: Place Value of Decimals. Lesson 3: Compare and Order Decimals. Lesson 4: Round Decimals. Lesson 5: Investigate • Decimal Addition. Lesson 6: Investigate • Decimal Subtraction. Mid-Chapter Checkpoint (lessons 1-6) Lesson 7: Estimate Decimal Sums and Differences. Lesson 8: Add Decimals. Big Ideas Math Answers Grade 5 Chapter 3 Add and Subtract Decimals Use Models to Add or Subtract Decimals Homework & Practice 3.2; Lesson: 3 Add Decimals. Lesson 3.3 Add Decimals; Add Decimals Homework & Practice 3.3; Lesson: 4 Subtract Decimals. ... Add Decimals Homework & Practice 3.3. Find the sum. Check whether your answer is reasonable. Question 1. Answer: 8.8 is close to 9. Explanation: Check: 8.8 - 1. ... 5th grade Learn fifth grade math—arithmetic with fractions and decimals, volume, unit conversion, graphing points, and more. This course is aligned with Common Core standards. Grade 5 HMH Go Math Email your homework to your parent or tutor for free; ... Chapter 3; Lesson 8: Add Decimals. Please share this page with your friends on FaceBook. Add Decimals. Estimate. Then find the sum. Question 1 (request help) Question 2 (request help) 4.23 +6.51. Estimate : Sum: (show solution) ... PDF Name Lesson 3.5 Decimal Addition Add. Draw a quick picture. 1.1 Decimal Addition 9. WRITE Math Explain why drawing a quick picture is helpful when adding decimals. Lesson 3.5 COMMON CORE STANDARD—5.NBT.B.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. Practice and Homework Lesson Plans: Go Math Grade 5 Chapter 3 Chapter 1 Place Value, Multiplication and Expression. Chapter 2 Divide Whole Numbers. Chapter 4 Multiply Decimals. Chapter 5 Divide Decimals. Chapter 6 Add & Subtract Fractions. Chapter 7 Multiply Fractions. Chapter 8 Divide Fractions. Chapter 9 Algebra: Patterns & Graphing. Chapter 10 Convert Units of Measure. Go Math 5th Grade Lesson 3.5 Decimal Addition This Go Math video Lesson 3.5 covers the topic of decimal addition. I demonstrate the importance of "regrouping" with hundredths and tenths. I attempt to mak... PDF Practice and Homework Name Lesson 3.7 Estimate Decimal Sums and Differences when adding and subtracting decimals. Estimate Decimal Sums and Differences Lesson 3.7 COMMON CORE STANDARD—5.NBT.B.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. Practice and Homework. Personal Math Trainer FOR MORE PRACTICE ... Lesson Check (5.NBT.B.7) Spiral Review (5.NBT.A.1, 5.NBT.A.3b, 5.NBT.A.4, 5 ... PDF Go Math! Practice Book (TE), G5 Problem Solving REAL WORLD 9. There are 12 students in a jewelry-making class and 8 sets of charms. What fraction of a set of charms will each student get? Each student will get of a set. P173 Each friend will get cheesecakes. Chapter 8. Lesson Check (CC.5.NF.3) 1. Eight friends share 4 bunches of grapes equally. Adding Decimals Worksheet Teaching Resources Google Paperless Practice - 5th Grade Adding Decimals {5.NBT.7}Engage your students with this interactive DIGITAL resource that works with Google Slides™. No more copies to be made, no more printer ink, and no more lost papers! With this 17-slide digital resource, your students will practice adding decimals to the hundredths place. PDF Practice and Homework Name Lesson 9.3 Equivalent Fractions and Decimals 8. Billy walks __6 10 mile to school each day. Write __6 10 as hundredths in fraction form and in decimal form. Chapter 9 511 ___50 100; 0.50 COMMON CORE STANDARD—4.NF.C.5 Understand decimal notation for fractions, and compare decimal fractions. Practice and Homework Lesson 9.3 Equivalent Fractions and Decimals 9. WRITE Math Write __5 PDF Practice and Homework Name Lesson 3.10 Patterns with Decimals add 1.32 6.56 Patterns with Decimals 7. WRITE Math Give an example of a rule describing the pattern for a sequence. Then write the terms of the sequence for your rule. Lesson 3.10 COMMON CORE STANDARD—5.NBT.B.7 Perform operations with multi-digit whole numbers and with decimals to hundredths. Practice and Homework PDF Lesson 3 Skills Practice 22 Course 1 • Chapter 2 Fractions, Decimals, and Percents Lesson 3 Skills Practice Percents and Decimals Write each percent as a decimal. The decimal is behind the number. Move it 2 places in to the left. (% is per 100) 1. 5% = 0.05 2. 8% 3. 37% 4. 12% 5. 29% 6. 54% 7. 48% 8. 79% 9. 3% 10. 6% assignment essay homework paper phd report resume speech thesis