work energy and power problem solving

Physics for You – Dare to know!

Ad blocker detected

Knowledge is free, but servers are not. Please consider supporting us by disabling your ad blocker on YouPhysics. Thanks!

Work and energy problems and solutions

When you try to solve problems of Physics in general and of Work and Energy in particular, it is important to follow a certain order . Try to be organized when you solve these problems, and you will see how it gives good results. It is worth spending a bit of time on the analysis of a problem before tackling it.

When solving problems related to Work and Energy, follow these steps:

• Read carefully the problem statement.
• Draw a picture of the physical situation described in the problem.
• Write in your notebook the givens in the problem statement.
• The first thing you need to identify when solving an energy problem is whether the mechanical energy (kinetic + potential) is conserved or not in the situation described by the problem.

The basic equation that you will have to learn to solve this type of problems is the following:

Where E C is the kinetic energy of the particle and W the work (with its sign) of each of the forces acting on it.

Then, depending on whether the forces are conservative or not, this work can be written in terms of the variation of the potential energy of the particle.

• You must choose a zero height position to calculate the gravitational potential energy.
• Do not forget to include the units in your results.
• Review the problem and check that the results you have obtained make sense.

On the following pages you will find some problems of work and energy with solutions. Try to do them before looking at the solution .

• Work and Energy - Work done by a constant force
• Work and Energy - Work done by the weight force and potential energy
• Work and Energy - The law of conservation of energy
• Work and Energy - Friction force
• Work and Energy - Energy along a roller coaster
• Work and Energy - Simple pendulum
• Work and Energy - Elastic potential energy
• Work and Energy - Bouncing ball
• Work and Energy - High diving into a pool
• Work and Energy - Vertical circular motion
• Work and Energy - Potential energy climbing the Eiffel tower
• Work and Energy - Potential energy diagram
• Work and Energy - Skier, spring and friction force
• Work and Energy - Water park
• Work and Energy - Two masses and a pulley

refers to an activity involving a force and movement in the directon of the force. A force of 20 newtons pushing an object 5 meters in the direction of the force does 100 joules of work.

is the capacity for doing work. You must have energy to accomplish work - it is like the "currency" for performing work. To do 100 joules of work, you must expend 100 joules of energy.

is the rate of doing work or the rate of using energy, which are numerically the same. If you do 100 joules of work in one second (using 100 joules of energy), the power is 100 watts.

The change in the kinetic energy of an object is equal to the net work done on the object. This fact is referred to as the Work-Energy Principle and is often a very useful tool in mechanics problem solving. It is derivable from conservation of energy and the application of the relationships for work and energy , so it is not independent of the conservation laws . It is in fact a specific application of conservation of energy. However, there are so many mechanical problems which are solved efficiently by applying this principle that it merits separate attention as a working principle.

7.2 Kinetic Energy and the Work-Energy Theorem

Learning objectives.

By the end of this section, you will be able to:

• Explain work as a transfer of energy and net work as the work done by the net force.
• Explain and apply the work-energy theorem.

Work Transfers Energy

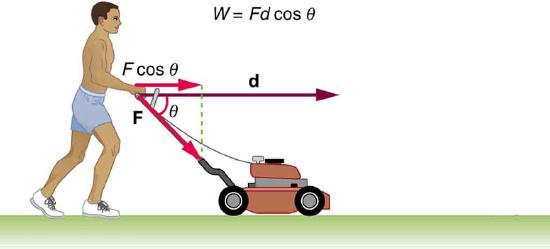
What happens to the work done on a system? Energy is transferred into the system, but in what form? Does it remain in the system or move on? The answers depend on the situation. For example, if the lawn mower in Figure 7.2 (a) is pushed just hard enough to keep it going at a constant speed, then energy put into the mower by the person is removed continuously by friction, and eventually leaves the system in the form of heat transfer. In contrast, work done on the briefcase by the person carrying it up stairs in Figure 7.2 (d) is stored in the briefcase-Earth system and can be recovered at any time, as shown in Figure 7.2 (e). In fact, the building of the pyramids in ancient Egypt is an example of storing energy in a system by doing work on the system. Some of the energy imparted to the stone blocks in lifting them during construction of the pyramids remains in the stone-Earth system and has the potential to do work.

In this section we begin the study of various types of work and forms of energy. We will find that some types of work leave the energy of a system constant, for example, whereas others change the system in some way, such as making it move. We will also develop definitions of important forms of energy, such as the energy of motion.

Net Work and the Work-Energy Theorem

We know from the study of Newton’s laws in Dynamics: Force and Newton's Laws of Motion that net force causes acceleration. We will see in this section that work done by the net force gives a system energy of motion, and in the process we will also find an expression for the energy of motion.

Let us start by considering the total, or net, work done on a system. Net work is defined to be the sum of work on an object. The net work can be written in terms of the net force on an object. F net F net . In equation form, this is W net = F net d cos θ W net = F net d cos θ where θ θ is the angle between the force vector and the displacement vector.

Figure 7.3 (a) shows a graph of force versus displacement for the component of the force in the direction of the displacement—that is, an F cos θ F cos θ vs. d d graph. In this case, F cos θ F cos θ is constant. You can see that the area under the graph is F d cos θ F d cos θ , or the work done. Figure 7.3 (b) shows a more general process where the force varies. The area under the curve is divided into strips, each having an average force ( F cos θ ) i ( ave ) ( F cos θ ) i ( ave ) . The work done is ( F cos θ ) i ( ave ) d i ( F cos θ ) i ( ave ) d i for each strip, and the total work done is the sum of the W i W i . Thus the total work done is the total area under the curve, a useful property to which we shall refer later.

Net work will be simpler to examine if we consider a one-dimensional situation where a force is used to accelerate an object in a direction parallel to its initial velocity. Such a situation occurs for the package on the roller belt conveyor system shown in Figure 7.4 .

The force of gravity and the normal force acting on the package are perpendicular to the displacement and do no work. Moreover, they are also equal in magnitude and opposite in direction so they cancel in calculating the net force. The net force arises solely from the horizontal applied force F app F app and the horizontal friction force f f . Thus, as expected, the net force is parallel to the displacement, so that θ = 0º θ = 0º and cos θ = 1 cos θ = 1 , and the net work is given by

The effect of the net force F net F net is to accelerate the package from v 0 v 0 to v v . The kinetic energy of the package increases, indicating that the net work done on the system is positive. (See Example 7.2 .) By using Newton’s second law, and doing some algebra, we can reach an interesting conclusion. Substituting F net = ma F net = ma from Newton’s second law gives

To get a relationship between net work and the speed given to a system by the net force acting on it, we take d = x − x 0 d = x − x 0 and use the equation studied in Motion Equations for Constant Acceleration in One Dimension for the change in speed over a distance d d if the acceleration has the constant value a a ; namely, v 2 = v 0 2 + 2 ad v 2 = v 0 2 + 2 ad (note that a a appears in the expression for the net work). Solving for acceleration gives a = v 2 − v 0 2 2 d a = v 2 − v 0 2 2 d . When a a is substituted into the preceding expression for W net W net , we obtain

The d d cancels, and we rearrange this to obtain

This expression is called the work-energy theorem , and it actually applies in general (even for forces that vary in direction and magnitude), although we have derived it for the special case of a constant force parallel to the displacement. The theorem implies that the net work on a system equals the change in the quantity 1 2 mv 2 1 2 mv 2 . This quantity is our first example of a form of energy.

The Work-Energy Theorem

The net work on a system equals the change in the quantity 1 2 mv 2 1 2 mv 2 .

The quantity 1 2 mv 2 1 2 mv 2 in the work-energy theorem is defined to be the translational kinetic energy (KE) of a mass m m moving at a speed v v . ( Translational kinetic energy is distinct from rotational kinetic energy, which is considered later.) In equation form, the translational kinetic energy,

is the energy associated with translational motion. Kinetic energy is a form of energy associated with the motion of a particle, single body, or system of objects moving together.

We are aware that it takes energy to get an object, like a car or the package in Figure 7.4 , up to speed, but it may be a bit surprising that kinetic energy is proportional to speed squared. This proportionality means, for example, that a car traveling at 100 km/h has four times the kinetic energy it has at 50 km/h, helping to explain why high-speed collisions are so devastating. We will now consider a series of examples to illustrate various aspects of work and energy.

Example 7.2

Calculating the kinetic energy of a package.

Suppose a 30.0-kg package on the roller belt conveyor system in Figure 7.4 is moving at 0.500 m/s. What is its kinetic energy?

Because the mass m m and speed v v are given, the kinetic energy can be calculated from its definition as given in the equation KE = 1 2 mv 2 KE = 1 2 mv 2 .

The kinetic energy is given by

Entering known values gives

which yields

Note that the unit of kinetic energy is the joule, the same as the unit of work, as mentioned when work was first defined. It is also interesting that, although this is a fairly massive package, its kinetic energy is not large at this relatively low speed. This fact is consistent with the observation that people can move packages like this without exhausting themselves.

Example 7.3

Determining the work to accelerate a package.

Suppose that you push on the 30.0-kg package in Figure 7.4 with a constant force of 120 N through a distance of 0.800 m, and that the opposing friction force averages 5.00 N.

(a) Calculate the net work done on the package. (b) Solve the same problem as in part (a), this time by finding the work done by each force that contributes to the net force.

Strategy and Concept for (a)

This is a motion in one dimension problem, because the downward force (from the weight of the package) and the normal force have equal magnitude and opposite direction, so that they cancel in calculating the net force, while the applied force, friction, and the displacement are all horizontal. (See Figure 7.4 .) As expected, the net work is the net force times distance.

Solution for (a)

The net force is the push force minus friction, or F net = 120 N – 5 . 00 N = 115 N F net = 120 N – 5 . 00 N = 115 N . Thus the net work is

Discussion for (a)

This value is the net work done on the package. The person actually does more work than this, because friction opposes the motion. Friction does negative work and removes some of the energy the person expends and converts it to thermal energy. The net work equals the sum of the work done by each individual force.

Strategy and Concept for (b)

The forces acting on the package are gravity, the normal force, the force of friction, and the applied force. The normal force and force of gravity are each perpendicular to the displacement, and therefore do no work.

Solution for (b)

The applied force does work.

The friction force and displacement are in opposite directions, so that θ = 180º θ = 180º , and the work done by friction is

So the amounts of work done by gravity, by the normal force, by the applied force, and by friction are, respectively,

The total work done as the sum of the work done by each force is then seen to be

Discussion for (b)

The calculated total work W total W total as the sum of the work by each force agrees, as expected, with the work W net W net done by the net force. The work done by a collection of forces acting on an object can be calculated by either approach.

Example 7.4

Determining speed from work and energy.

Find the speed of the package in Figure 7.4 at the end of the push, using work and energy concepts.

Here the work-energy theorem can be used, because we have just calculated the net work, W net W net , and the initial kinetic energy, 1 2 m v 0 2 1 2 m v 0 2 . These calculations allow us to find the final kinetic energy, 1 2 mv 2 1 2 mv 2 , and thus the final speed v v .

The work-energy theorem in equation form is

Solving for 1 2 mv 2 1 2 mv 2 gives

Solving for the final speed as requested and entering known values gives

Using work and energy, we not only arrive at an answer, we see that the final kinetic energy is the sum of the initial kinetic energy and the net work done on the package. This means that the work indeed adds to the energy of the package.

Example 7.5

Work and energy can reveal distance, too.

How far does the package in Figure 7.4 coast after the push, assuming friction remains constant? Use work and energy considerations.

We know that once the person stops pushing, friction will bring the package to rest. In terms of energy, friction does negative work until it has removed all of the package’s kinetic energy. The work done by friction is the force of friction times the distance traveled times the cosine of the angle between the friction force and displacement; hence, this gives us a way of finding the distance traveled after the person stops pushing.

The normal force and force of gravity cancel in calculating the net force. The horizontal friction force is then the net force, and it acts opposite to the displacement, so θ = 180º θ = 180º . To reduce the kinetic energy of the package to zero, the work W fr W fr by friction must be minus the kinetic energy that the package started with plus what the package accumulated due to the pushing. Thus W fr = − 95 . 75 J W fr = − 95 . 75 J . Furthermore, W fr = f d ′ cos θ = – f d ′ W fr = f d ′ cos θ = – f d ′ , where d ′ d ′ is the distance it takes to stop. Thus,

This is a reasonable distance for a package to coast on a relatively friction-free conveyor system. Note that the work done by friction is negative (the force is in the opposite direction of motion), so it removes the kinetic energy.

Some of the examples in this section can be solved without considering energy, but at the expense of missing out on gaining insights about what work and energy are doing in this situation. On the whole, solutions involving energy are generally shorter and easier than those using kinematics and dynamics alone.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/7-2-kinetic-energy-and-the-work-energy-theorem

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter: 11th Physics : UNIT 4 : Work, Energy and Power

Solved example problems for physics: work, energy and power, numerical problems.

1. Calculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g = 10ms -2 )

Force mg = 30 N ; height = 10 m

Work done to lift a load W = ?

W = F.S (or) mgh

W = 300 J 

Ans:  300J

2. A ball with a velocity of 5 m s -1  impinges at angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.

The impluse on the ball acts perpendicular to the smooth plane.

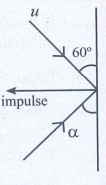
(i) The component of velocity of ball parallel to the surface.

(ii) For the component of velocity of ball perpendicular to the surface, apply law of restitution.

The component of velocity parallel to the surface will be changed.

v cos α = u cos 60°

v cos α = 5 × 1/2 = 5/2       ….(1)

According to law of restitution

v sin α = e u sin 60°

v sin α = 1/2 × 5 × √3/2 =  5 (√3/4)        ….(2)

Squaring and adding (1) and (2)

v 2 (sin 2 α + cos 2 α) = 

v = 3.3 ms -1

Ans:  v = 0.3 m  s -1

3. A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle? (Hint: Use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9?

Ans: √ 4gr ms-1

The horizontal distance, draw the point of projection to the point where the ball returns to the same level

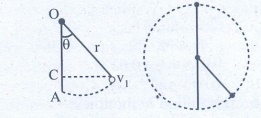
AC = OA-OC = r - rcosθ

minimum velocity = at v L = √[5 gr ]

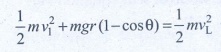
v 1 2 = v L 2 - 2gr (1 - cos θ)

v 1 2 = 5 gr - 2gr (l-cosθ)

v 1 2 = 5gr-2gr(l – 1/2)

v 1 2 = 5gr - gr => v 1 2 = 4gr

v 1 = √[4 gr ] ms -1 .

4. Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.

Momentium is censerved in both × and y direction.

In x - direction

M B V B = O + M A V A ' cosɸ ...(l)

In y - direction

O = M B V B ' - M A V A 'sinɸ  ...(2)

(2)/(1) tanɸ = V B ’/V B = 1/2

ɸ = 26.6° (or) 26° 36' [1° = 60']

Ans:  θ   = 26° 33 ′

5. A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.

Mass of the bullet m 1 = 20 g = 0.02 kg.

Mass of the pendulum m 2 = 5 kg

Centre of mass of pendulum rises to a height = h = 10 cm = 0.1 m

Speed of the bullet = u 1

Pendulum is at rest .:. u 2 = 0

Common velocity of the bullet and the pendulum after the bullet is embeded into the object = v

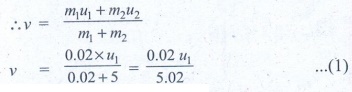
From II equation of motion

v = √[2gh] = √[2x9.8x0.1] = √[1.96] = 1.4 ms -1

Substitute the value of v in equation (1)

1.4 = 0.02 u 1 /5.02

u 1 = 5.02x1.4 / 0.02

u 1 = 351.4 ms -1

Ans:  v = 351.4m  s -1

Conceptual Questions

1. A spring which in initially in un-stretched condition, is first stretched by a length x and again by a further length x. The work done in the first case W 1  is one third of the work done in second case W 2 . True or false?

2. Which is conserved in inelastic collision? Total energy (or) Kinetic energy?

Total energy is always conserved.

But K.E. is not conserved.

3. Is there any net work done by external forces on a car moving with a constant speed along a straight road?

If a car is moving at a constant speed, then external force will be zero.

Because a = [v - u] / t

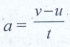
For constant speed v = u , then a =0. ( a -acceleration)

F = ma   .'. F = zero. i.e.. no external force.

W = F.S. = 0. So net work done is zero.

4. A car starts from rest and moves on a surface with uniform acceleration.

Draw  the  graph  of  kinetic  energy versus displacement. What information you can get from that graph?

5. A charged particle moves towards another charged particle. Under what conditions the total momentum and the total energy of the system conserved?

(i) Both charged particles shall be dissimilar charge, (i.e. positive and negative)

(ii) After collision the charged particles; stick together permanent.

(iii) They should move with common velocity

SOLVED EXAMPLE

2. A particle moves along X- axis from x=0 to x=8 under the influence of a force given by F= 3 x   2  - 4 x  + 5. Find the work done in the process.

3. A body of mass 10kg at rest is subjected to a force of 16N. Find the kinetic energy at the end of 10 s.

Mass m = 10 kg

Force F = 16 N

time t = 10 s

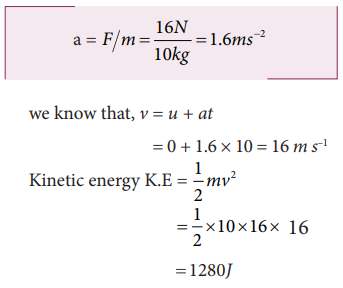
4. A body of mass 5kg is thrown up vertically with a kinetic energy of 1000 J. If acceleration due to gravity is 10 ms -2 , find the height at which the kinetic energy becomes half of the original value.

Mass m = 5kg

K.E          E = 1000J

g = 10 m s -2

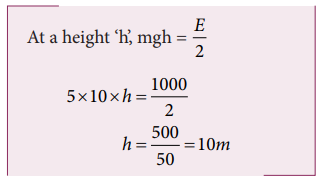
5. Two bodies of mass 60 kg and 30 kg move in the same direction along straight line with velocity 40 cm s -1  and 30 cm   s -1   respectively suffer one dimensional elastic collision. Find their velocities after collision.

Mass m 1  = 60 kg

Mass m 2  = 30 kg

V 1  =  40cm s -1

V 2  =  30c m  s -1

Likewise, 

6. A particle of mass 70 g moving at 50 cm s -1  is acted upon by a variable force as shown in the figure. What will be its speed once the force stops?

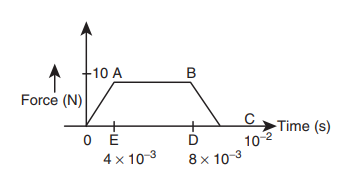
The area under the graph gives the impulse.

Impulse I = area of  ∆ OAE+ area of rectangle ABDE+ area of  ∆ DBC

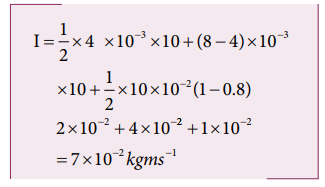
But Impulse = 2 × initial momentum of the particle= 2 × m × u

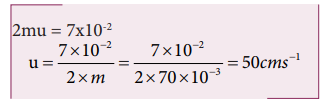
Hence the particle will reverse its direction and move with its initial speed.

7. A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical and rebounds with the speed v at an angle Φ  with an vertical. The coefficient of restitution between the particle and floor is e. What is the magnitude of v?

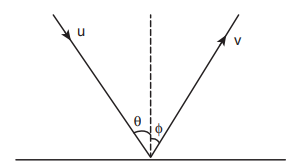
Applying component of velocities,

The x - component of velocity is

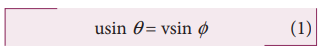
The magnitude of y – component of velocity is not same, therefore, using coefficient of restitution,

8. A particle of mass m is fixed to one end of a light spring of force constant k and un-stretched length l. It is rotated with an angular velocity  ω   in horizontal circle. What will be the length increase in the spring?

Mass spring = m Force

constant = k

Un-stretched length = l

Angular velocity = ω

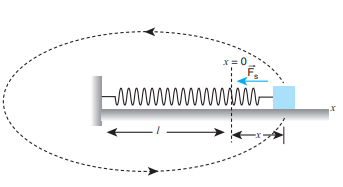
Let ‘x’ be the increase in the length of the spring.

The new length = (l+x) = r

When the spring is rotated in a horizontal circle,

Spring force = centripetal force.

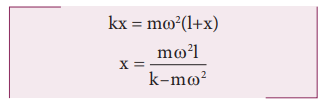
9. A gun fires 8 bullets per second into a target X. If the mass of each bullet is 3 g and its speed 600 s -1 . Then, calculate the power delivered by the bullets.

Power = work done per second = total kinetic energy of 8 bullets per second

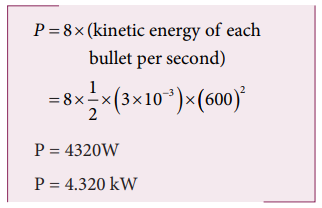
Solved Example Problems for Work

Example 4.1.

A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30 o , find the work done by the force.

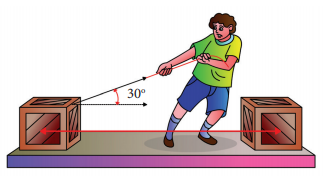
Force, F = 25 N

Displacement, dr = 15 m

Angle between F and dr, θ = 30 o

Work done ,  W  =  Fdr cos θ

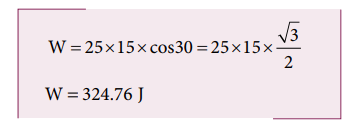
Solved Example Problems for Work done by a constant force

Example 4.2

An object of mass 2 kg falls from a height of 5 m to the ground. What is the work done by the gravitational force on the object? (Neglect air resistance; Take g = 10 m s -2 )

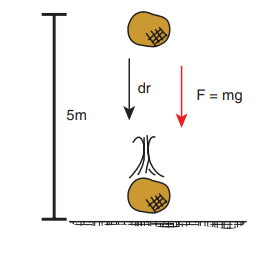
Work done by gravitational force is

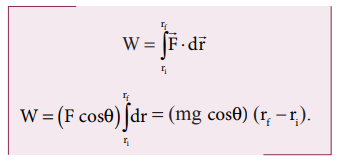
The work done by the gravitational force on the object is positive.

Example 4.3

An object of mass  m = 1 kg is sliding from top to bottom in the frictionless inclined plane of inclination angle θ = 30 o  and the length of inclined plane is 10 m as shown in the figure. Calculate the work done by gravitational force and normal force on the object. Assume acceleration due to gravity, g = 10 m s -2

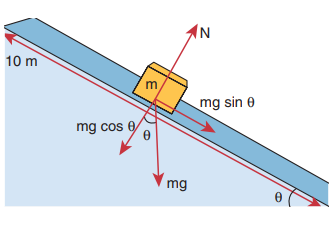
We calculated in the previous chapter that the acceleration experienced by the object in the inclined plane as g sin θ  .

According to Newton’s second law, the force acting on the mass along the inclined plane F  =  mg sin θ . Note that this force is constant throughout the motion of the mass.

The work done by the parallel component of gravitational force  (  mg sin θ )  is given by

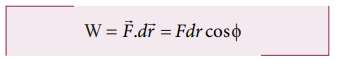
Example 4.4

If an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate

a) The work done by gravity when the  object reaches 5 m height

b) The work done by gravity when the   object comes back to Earth

c) Total work done by gravity both in  upward and downward motion and mention the physical significance of the result.

When the object goes up, the displacement points in the upward direction whereas the gravitational force acting on the object points in downward direction. Therefore, the angle between gravitational force and displacement of the object is 180°.

a. The work done by gravitational force in the upward motion.

Given that ∆r =5 m and F mg

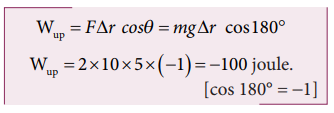
b. When the object falls back, both the gravitational force and displacement of the object are in the same direction. This implies that the angle between gravitational force and displacement of the object is 0°.

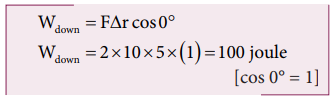
c. The total work done by gravity in the entire trip (upward and downward motion)

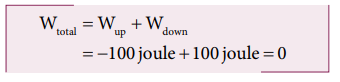
It implies that the gravity does not transfer any energy to the object. When the object is thrown upwards, the energy is transferred to the object by the external agency, which means that the object gains some energy. As soon as it comes back and hits the Earth, the energy gained by the object is transferred to the surface of the Earth (i.e., dissipated to the Earth).

Example 4.5

A weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.

a. What is the workdone by the weight lifter?

b. What is the workdone by the gravity?

c. What is the net workdone on the object?

a. When the weight lifter lifts the mass, force and displacement are in the same direction, which means that the angle between them θ = 0 0 . Therefore, the work done by the weight lifter,

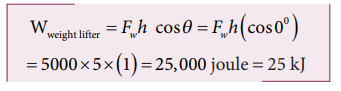
b. When the weight lifter lifts the mass, the gravity acts downwards which means that the force and displacement are in opposite direction. Therefore, the angle between them θ = 180 0

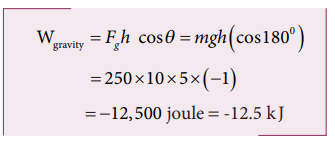
c. The net workdone (or total work done) on the object

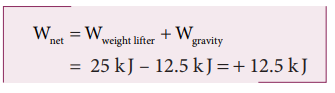
Solved Example Problems for Work done by a variable force

Example 4.6.

A variable force  F   =  k x 2  acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from  x   =  0 m to  x   =  4 m. (Assume the constant  k   = 1 N m -2 )

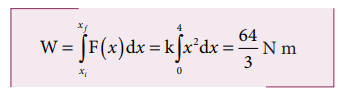
Solved Example Problems for  Kinetic energy

Example 4.7.

Two objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg m s -1 .

a. Will they have same kinetic energy?

b. Will they have same speed?

a. The kinetic energy of the mass is given by

Note that  KE 1  ≠  KE 2  i.e., even though both are having the same momentum, the kinetic energy of both masses is not the same. The kinetic energy of the heavier object has lesser kinetic energy than smaller mass. It is because the kinetic energy is inversely proportional to the mass (KE   ∝  1/m) for a given momentum.

b. As the momentum,  p  =  mv , the two objects will not have same speed.

Solved Example Problems for  Potential Energy

Example 4.8.

An object of mass 2 kg is taken to a height 5 m from the ground  g =  10ms -2  .

a. Calculate the potential energy stored in the object.

b. Where does this potential energy come from?

c. What external force must act to bring the mass to that height?

d. What is the net force that acts on the object while the object is taken to the height ‘h’?

a. The  potential energy  U   = m g h  = 2  ×  10  ×  5 = 100 J

Here the positive sign implies that the energy is stored on the mass.

b. This potential energy is transferred from external agency which applies the force on the mass.

d. From the definition of potential energy, the object must be moved at constant velocity. So the net force acting on the object is zero.

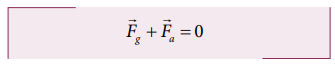
Solved Example Problems for  Elastic Potential Energy

Example 4.9

Let the two springs A and B be such that k A >k B . On which spring will more work has to be done if they are stretched by the same force?

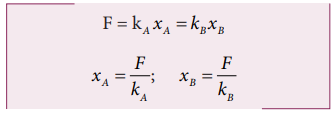
The work done on the springs are stored as potential energy in the springs.

k A >k B  implies that U B >U A  . Thus, more work is done on B than A.

Example 4.10

A body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.

a. Calculate the potential energy stored in the spring-mass system?

b. What is the work done by the spring force in this elongation?

c. Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N m -1 ).

The spring constant, k = 0.1 N m -1

The displacement,  x  = 25 cm = 0.25 m

a. The potential energy stored in the spring is given by

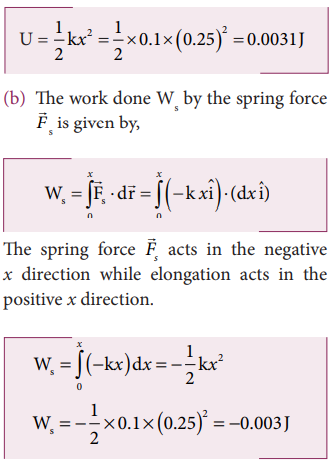
Note that the potential energy is defined through the work done by the external agency. The positive sign in the potential energy implies that the energy is transferred from the agency to the object. But the work done by the restoring force in this case is negative since restoring force is in the opposite direction to the displacement direction.

c. During compression also the potential energy stored in the object is the same.

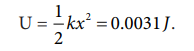
Work done by the restoring spring force during compression is given by

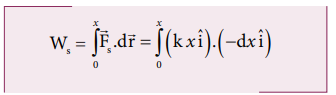
In the case of compression, the restoring spring force acts towards positive  x -axis and displacement is along negative  x  direction.

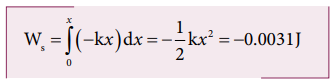
Solved Example Problems for  Conservative and nonconservative forces

Example 4.11.

Compute the work done by the gravitational force for the following cases

(As the displacement is in two dimension; unit vectors and are used)

a. Since the motion is only vertical, horizontal displacement component d x  is zero. Hence, work done by the force along path 1 (of distance h).

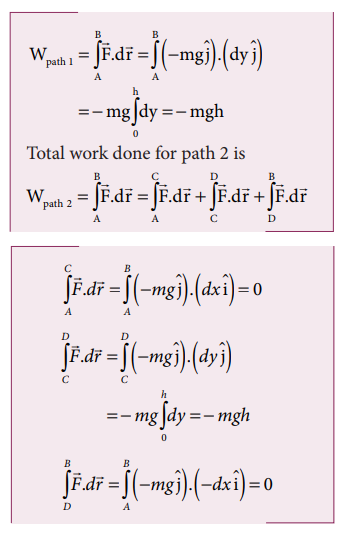
Therefore, the total work done by the force along the path 2 is

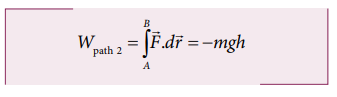
Note that the work done by the conservative force is independent of the path.

Example 4.12

Consider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 ms - 2 )

m  = 2 kg,  d  = 10 m,  F ext   = 20 N,    k   = 0.9.   When an object is in motion on the horizontal surface, it experiences two forces.

a. External force,  F ext   =  20 N

b. Kinetic friction,

f k  =μ k mg  = 0.9x(2)x10=18N.

The work done by the external force   W ext  = Fs = 20x20 =200J

The work done by the force of kinetic  friction  W k  = f k d  = (-18) x10=-180J  Here the negative sign implies that the  force of kinetic friction is  pposite to the  direction of displacement.

The total work done on the object 

W total  = Wext + W k  = 200 J – 180 J = 20 J .

Since the friction is a non-conservative force, out of 200 J given by the external force, the 180 J is lost and it can not be recovered.

Solved Example Problems for  Law of conservation of energy

Example 4.13.

An object of mass 1 kg is falling from the height  h  = 10 m. Calculate

a. The total energy of an object at  h   = 10 m

b. Potential energy of the object when it is at  h   =  4 m

c. Kinetic energy of the object when it is at  h   =  4 m

d. What will be the speed of the object when it hits the ground?

(Assume  g   = 10 m s -2 )

a. The gravitational force is a conservative force. So the total energy remains constant throughout the motion. At  h  = 10   m, the total energy E  is entirely   potential energy.

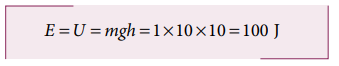
b. The potential energy of the object at  h  =   4   m is

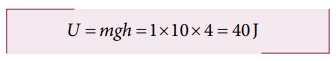
c. Since the total energy is constant throughout the motion, the kinetic energy at  h   =  4 m must be  KE  =  E  -  U  =   100   -   40   =   60J

Alternatively, the kinetic energy could also be found from velocity of the object at 4 m. At the height 4 m, the object has fallen through a height of 6 m.

The velocity after falling 6 m is calculated from the equation of motion,

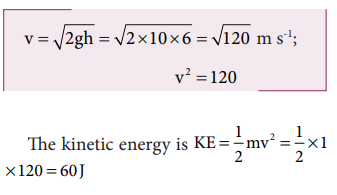
d. When the object is just about to hit the ground, the total energy is completely kinetic and the potential energy,  U   =  0.

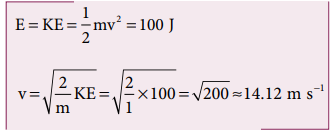
Example 4.14

A body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?

m = 100 kg, h = 10 m

Along path (1):

The minimum force  F 1  required to move the object to the height of 10 m should be equal to the gravitational force, F 1  mg = 100 x 10 = 1000 N

The distance moved along path (1) is,  = 10   m

The work done on the object along path (1) is

W = Fh = 1000 x 10 = 10,000 J

Along path (2):

In the case of the ramp, the minimum force  F 2   that we apply on the object to take it   up is not equal to  mg , it is rather equal to  mg  sin θ   . ( mg sin <  mg)  .

Here, angle θ = 30 o

Therefore, F 2   = mg sinθ = 100 × 10 ×  sin30 o  = 100 × 10 × 0.5 = 500N

Hence,  (mg sinθ < mg)

The path covered along the ramp is,

l = h/sin30 = 10/0.5 =20m

The work done on the object along path  (2) is, W = F2 l = 500 × 20 = 10,000 J

Since the gravitational force is a conservative force, the work done by gravity on the object is independent of the path taken.

In both the paths the work done by the gravitational force is 10,000 J

Along path (1): more force needs to be applied against gravity to cover lesser distance .

Along path (2): lesser force needs to be applied against the gravity to cover more distance.

As the force needs to be applied along the ramp is less, it is easier to move the object along the ramp.

Example 4.15

An object of mass m is projected from the ground with initial speed v 0 .

Find the speed at height h.

Since the gravitational force is conservative; the total energy is conserved throughout the motion.

Final values of potential energy, kinetic energy and total energy are measured at the height  h .

By law of conservation of energy, the initial and final total energies are the same.

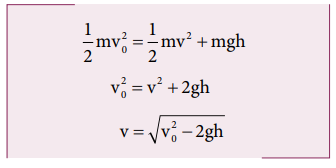
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.

Example 4.16

An object of mass 2 kg attached to a spring is moved to a distance  x   = 10 m from its equilibrium position. The spring constant  k  = 1   N m -1 and assume that the surface is   frictionless.

a. When the mass crosses the equilibrium position, what is the speed of the mass?

b. What is the force that acts on the object when the mass crosses the equilibrium position and extremum position  x  =  ±  10 m.

a. Since the spring force is a conservative force, the total energy is constant. At x  = 10   m, the total energy is purely   potential.

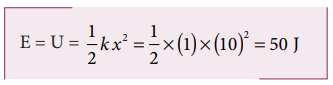
When the mass crosses the equilibrium position  x  = 0 , the potential energy

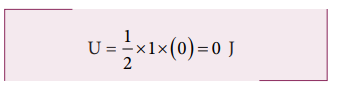
The entire energy is purely kinetic energy at this position.

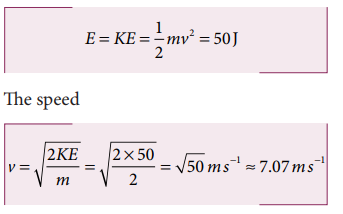
b. Since the restoring spring force is F = - kx, when the object crosses the equilibrium position, it experiences no force. Note that at equilibrium position, the object moves very fast. When the object is at  x  = +10 m (elongation), the force F = - k  x

F = - (1) (10) = - 10 N. Here the negative sign implies that the force is towards equilibrium i.e., towards negative  x -axis and when the object is at  x  = - 10 (compression), it experiences a forces F = - (1) (- 10) = +10 N. Here the positive sign implies that the force points towards positive  x -axis.

The object comes to momentary rest at  x  =  ± 10 m  even though it experiences a maximum force at both these points.

Solved Example Problems for  Motion in a vertical circle

Example 4.17.

Water in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion. (g = 10 ms -2 )

Solved Example Problems for Unit of power

Example 4.18.

Calculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).

Power, P = 75 W

Time of usage, t = 8 hour × 30 days = 240 hours

Electrical energy consumed is the product of power and time of usage.

Electrical energy = power × time of usage = P × t

Solved Example Problems for Relation between power and velocity

Example 4.19.

A vehicle of mass 1250 kg is driven with an acceleration 0.2 ms - 2  along a straight level road against an external resistive force 500 N . Calculate the power delivered by the vehicle’s engine if the velocity of the vehicle is 30 m  s - 1  .

The vehicle’s engine has to do work against resistive force and make vechile to move with an acceleration. Therefore, power delivered by the vehicle engine is

Solved Example Problems for collision

Solved Example Problems for Elastic collisions in one dimension

Example 4.20.

A lighter particle moving with a speed of 10 m s -1  collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?

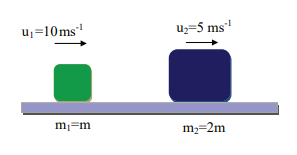
Let the mass of the fi rst body be m which  moves with an initial velocity, u 1  = 10 m s -1 .

Therefore, the mass of second body is 2m and its initial velocity is u 2  = ½ u 1  = ½(10ms -1 )

Then, the fi nal velocities of the bodies can be calculated from the equation (4.53) and equation (4.54)

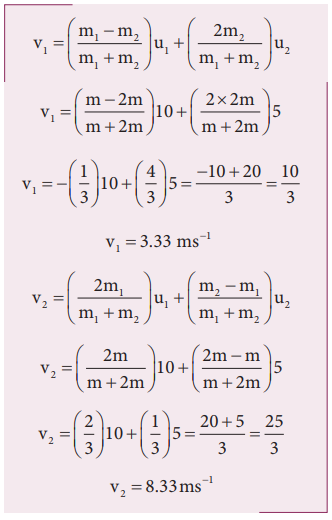
As the two speeds v 1 and v 2  are positive, they move in the same direction with the velocities, 3.33 m s −1  and 8.33 m s −1  respectively.

Solved Example Problems for Perfect inelastic collision

Example 4.21.

A bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take g = 10 ms -2 .

m 1  = 50 g = 0.05 kg; m 2  = 450 g = 0.45kg

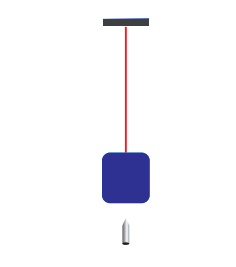
The speed of the bullet is u 1 . The second body is at rest u 2  = 0 . Let the common velocity of the bullet and the object after the bullet is embedded into the object is v.

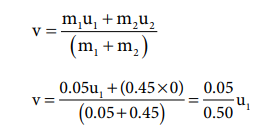
The combined velocity is the initial velocity for the vertical upward motion of the combined bullet and the object. From second equation of motion,

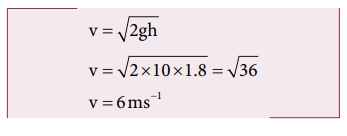
Substituting this in the above equation, the value of u 1  is

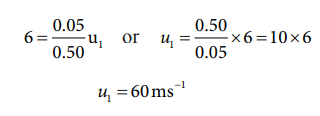
Solved Example Problems for Coefficient of restitution (e)

Example 4.22.

Show that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is

v 1 /v 2  = 1-e/1+e

From the law of conservation of linear momentum,

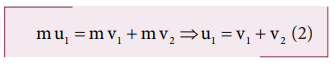
Using the equation (2) for u 1  in (1), we get

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7: Work, Energy, and Energy Resources (Exercises)

• Last updated
• Save as PDF
• Page ID 4184

Conceptual Questions

7.1: work: the scientific definition.

1. Give an example of something we think of as work in everyday circumstances that is not work in the scientific sense. Is energy transferred or changed in form in your example? If so, explain how this is accomplished without doing work.

2. Give an example of a situation in which there is a force and a displacement, but the force does no work. Explain why it does no work.

3. Describe a situation in which a force is exerted for a long time but does no work. Explain.

7.2: Kinetic Energy and the Work-Energy Theorem

4. The person in Figure does work on the lawn mower. Under what conditions would the mower gain energy? Under what conditions would it lose energy?

5. Work done on a system puts energy into it. Work done by a system removes energy from it. Give an example for each statement.

6. When solving for speed in Example, we kept only the positive root. Why?

7.3: Gravitational Potential Energy

7. In Example, we calculated the final speed of a roller coaster that descended 20 m in height and had an initial speed of 5 m/s downhill. Suppose the roller coaster had had an initial speed of 5 m/s uphill instead, and it coasted uphill, stopped, and then rolled back down to a final point 20 m below the start. We would find in that case that its final speed is the same as its initial speed. Explain in terms of conservation of energy.

8. Does the work you do on a book when you lift it onto a shelf depend on the path taken? On the time taken? On the height of the shelf? On the mass of the book?

7.4: Conservative Forces and Potential Energy

9. What is a conservative force?

10. The force exerted by a diving board is conservative, provided the internal friction is negligible. Assuming friction is negligible, describe changes in the potential energy of a diving board as a swimmer dives from it, starting just before the swimmer steps on the board until just after his feet leave it.

11. Define mechanical energy. What is the relationship of mechanical energy to nonconservative forces? What happens to mechanical energy if only conservative forces act?

12. What is the relationship of potential energy to conservative force?

7.6: Conservation of Energy

13. Consider the following scenario. A car for which friction is not negligible accelerates from rest down a hill, running out of gasoline after a short distance. The driver lets the car coast farther down the hill, then up and over a small crest. He then coasts down that hill into a gas station, where he brakes to a stop and fills the tank with gasoline. Identify the forms of energy the car has, and how they are changed and transferred in this series of events. (See Figure.)

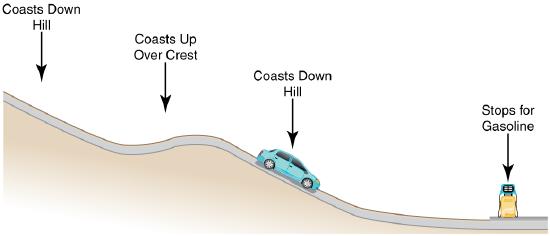
A car experiencing non-negligible friction coasts down a hill, over a small crest, then downhill again, and comes to a stop at a gas station.

14. Describe the energy transfers and transformations for a javelin, starting from the point at which an athlete picks up the javelin and ending when the javelin is stuck into the ground after being thrown.

15. Do devices with efficiencies of less than one violate the law of conservation of energy? Explain.

16. List four different forms or types of energy. Give one example of a conversion from each of these forms to another form.

17. List the energy conversions that occur when riding a bicycle.

18. Most electrical appliances are rated in watts. Does this rating depend on how long the appliance is on? (When off, it is a zero-watt device.) Explain in terms of the definition of power.

19. Explain, in terms of the definition of power, why energy consumption is sometimes listed in kilowatt-hours rather than joules. What is the relationship between these two energy units?

20. A spark of static electricity, such as that you might receive from a doorknob on a cold dry day, may carry a few hundred watts of power. Explain why you are not injured by such a spark.

7.8: Work, Energy, and Power in Humans

21. Explain why it is easier to climb a mountain on a zigzag path rather than one straight up the side. Is your increase in gravitational potential energy the same in both cases? Is your energy consumption the same in both?

22. Do you do work on the outside world when you rub your hands together to warm them? What is the efficiency of this activity?

23. Shivering is an involuntary response to lowered body temperature. What is the efficiency of the body when shivering, and is this a desirable value?

24. Discuss the relative effectiveness of dieting and exercise in losing weight, noting that most athletic activities consume food energy at a rate of 400 to 500 W, while a single cup of yogurt can contain 1360 kJ (325 kcal). Specifically, is it likely that exercise alone will be sufficient to lose weight? You may wish to consider that regular exercise may increase the metabolic rate, whereas protracted dieting may reduce it.

7.9: World Energy Use

25. What is the difference between energy conservation and the law of conservation of energy? Give some examples of each.

26. If the efficiency of a coal-fired electrical generating plant is 35%, then what do we mean when we say that energy is a conserved quantity?

Problems & Exercises

27. How much work does a supermarket checkout attendant do on a can of soup he pushes 0.600 m horizontally with a force of 5.00 N? Express your answer in joules and kilocalories.

Solution \(\displaystyle 3.00 J=7.17×10^{−4} kcal\)

28. A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.

29. (a) Calculate the work done on a 1500-kg elevator car by its cable to lift it 40.0 m at constant speed, assuming friction averages 100 N.

(b) What is the work done on the lift by the gravitational force in this process?

(c) What is the total work done on the lift?

Solution (a) \(\displaystyle 5.92×10^5J\) (b) \(\displaystyle −5.88×10^5J\) (c) The net force is zero.

30. Suppose a car travels 108 km at a speed of 30.0 m/s, and uses 2.0 gal of gasoline. Only 30% of the gasoline goes into useful work by the force that keeps the car moving at constant speed despite friction. (See [link] for the energy content of gasoline.)

(a) What is the magnitude of the force exerted to keep the car moving at constant speed?

(b) If the required force is directly proportional to speed, how many gallons will be used to drive 108 km at a speed of 28.0 m/s?

31. Calculate the work done by an 85.0-kg man who pushes a crate 4.00 m up along a ramp that makes an angle of \(\displaystyle 20.0º\) with the horizontal. (See Figure.) He exerts a force of 500 N on the crate parallel to the ramp and moves at a constant speed. Be certain to include the work he does on the crate and on his body to get up the ramp.

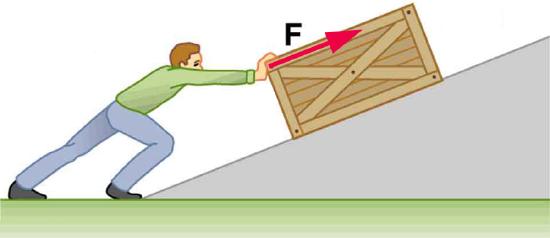
A man pushes a crate up a ramp.

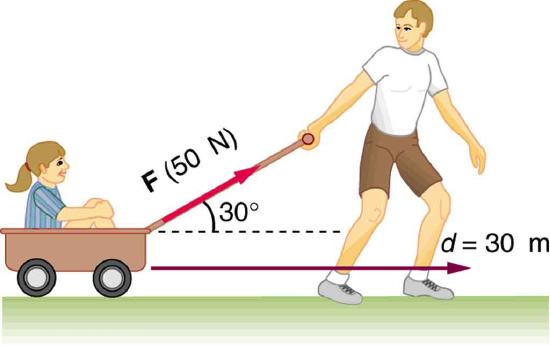
Solution \(\displaystyle 3.14×10^3J\)

32. How much work is done by the boy pulling his sister 30.0 m in a wagon as shown in Figure? Assume no friction acts on the wagon.

33. A shopper pushes a grocery cart 20.0 m at constant speed on level ground, against a 35.0 N frictional force. He pushes in a direction \(\displaystyle 25.0º\) below the horizontal.

(a) What is the work done on the cart by friction?

(b) What is the work done on the cart by the gravitational force?

(c) What is the work done on the cart by the shopper?

(d) Find the force the shopper exerts, using energy considerations.

(e) What is the total work done on the cart?

Solution (a) \(\displaystyle −700J\) (b) 0 (c) 700 J (d) 38.6 N (e) 0

34. Suppose the ski patrol lowers a rescue sled and victim, having a total mass of 90.0 kg, down a \(\displaystyle 60.0º\) slope at constant speed, as shown in Figure. The coefficient of friction between the sled and the snow is 0.100.

(a) How much work is done by friction as the sled moves 30.0 m along the hill?

(b) How much work is done by the rope on the sled in this distance?

(c) What is the work done by the gravitational force on the sled?

(d) What is the total work done?

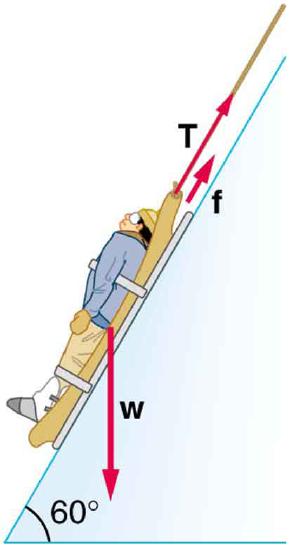
35. Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.

Solution \(\displaystyle 1/250\)

36. (a) How fast must a 3000-kg elephant move to have the same kinetic energy as a 65.0-kg sprinter running at 10.0 m/s?

(b) Discuss how the larger energies needed for the movement of larger animals would relate to metabolic rates.

37. Confirm the value given for the kinetic energy of an aircraft carrier in [link]. You will need to look up the definition of a nautical mile (1 knot = 1 nautical mile/h).

Solution \(\displaystyle 1.1×10^{10}J\)

38. (a) Calculate the force needed to bring a 950-kg car to rest from a speed of 90.0 km/h in a distance of 120 m (a fairly typical distance for a non-panic stop).

(b) Suppose instead the car hits a concrete abutment at full speed and is brought to a stop in 2.00 m. Calculate the force exerted on the car and compare it with the force found in part (a).

39. A car’s bumper is designed to withstand a 4.0-km/h (1.1-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.200 m while bringing a 900-kg car to rest from an initial speed of 1.1 m/s.

Solution \(\displaystyle 2.8×10^3N\)

40. Boxing gloves are padded to lessen the force of a blow.

(a) Calculate the force exerted by a boxing glove on an opponent’s face, if the glove and face compress 7.50 cm during a blow in which the 7.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s.

(b) Calculate the force exerted by an identical blow in the gory old days when no gloves were used and the knuckles and face would compress only 2.00 cm.

(c) Discuss the magnitude of the force with glove on. Does it seem high enough to cause damage even though it is lower than the force with no glove?

41. Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him.

Solution 102 N

42. A hydroelectric power facility (see Figure) converts the gravitational potential energy of water behind a dam to electric energy.

(a) What is the gravitational potential energy relative to the generators of a lake of volume \(\displaystyle 50.0 km^3 (mass=5.00×10^{13}kg)\), given that the lake has an average height of 40.0 m above the generators?

(b) Compare this with the energy stored in a 9-megaton fusion bomb.

Solution (a) \(\displaystyle 1.96×10^{16}J\) (b) The ratio of gravitational potential energy in the lake to the energy stored in the bomb is 0.52. That is, the energy stored in the lake is approximately half that in a 9-megaton fusion bomb.

43. (a) How much gravitational potential energy (relative to the ground on which it is built) is stored in the Great Pyramid of Cheops, given that its mass is about \(\displaystyle 7 × 10^9 kg\) and its center of mass is 36.5 m above the surrounding ground?

(b) How does this energy compare with the daily food intake of a person?

44. Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-g snake and raises it 2.5 m from the ground to a branch.

(a) How much work did the bird do on the snake?

(b) How much work did it do to raise its own center of mass to the branch?

Solution (a) 1.8 J (b) 8.6 J

45. In Example, we found that the speed of a roller coaster that had descended 20.0 m was only slightly greater when it had an initial speed of 5.00 m/s than when it started from rest. This implies that \(\displaystyle ΔPE >> KE_i\). Confirm this statement by taking the ratio of \(\displaystyle ΔPE\) to \(\displaystyle KE_i\). (Note that mass cancels.)

46. A 100-g toy car is propelled by a compressed spring that starts it moving. The car follows the curved track in Figure. Show that the final speed of the toy car is 0.687 m/s if its initial speed is 2.00 m/s and it coasts up the frictionless slope, gaining 0.180 m in altitude.

Solution \(\displaystyle v_f=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(−0.180 m)+(2.00 m/s)^2}=0.687 m/s\)

47. In a downhill ski race, surprisingly, little advantage is gained by getting a running start. (This is because the initial kinetic energy is small compared with the gain in gravitational potential energy on even small hills.) To demonstrate this, find the final speed and the time taken for a skier who skies 70.0 m along a \(\displaystyle 30º\) slope neglecting friction:

(a) Starting from rest.

(b) Starting with an initial speed of 2.50 m/s.

(c) Does the answer surprise you? Discuss why it is still advantageous to get a running start in very competitive events.

48. A \(\displaystyle 5.00×10^5-kg\) subway train is brought to a stop from a speed of 0.500 m/s in 0.400 m by a large spring bumper at the end of its track. What is the force constant \(\displaystyle k\) of the spring?

Solution \(\displaystyle 7.81×10^5N/m\)

49. A pogo stick has a spring with a force constant of \(\displaystyle 2.50×10^4N/m\), which can be compressed 12.0 cm. To what maximum height can a child jump on the stick using only the energy in the spring, if the child and stick have a total mass of 40.0 kg? Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.

7.5: Nonconservative Forces

50. A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m-high rise as shown in Figure. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.0800. (Hint: Find the distance traveled up the incline assuming a straight-line path as shown in the figure.)

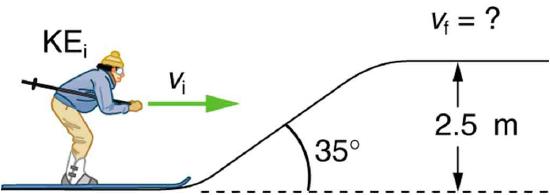
Solution 9.46 m/s

51. (a) How high a hill can a car coast up (engine disengaged) if work done by friction is negligible and its initial speed is 110 km/h?

(b) If, in actuality, a 750-kg car with an initial speed of 110 km/h is observed to coast up a hill to a height 22.0 m above its starting point, how much thermal energy was generated by friction?

(c) What is the average force of friction if the hill has a slope \(\displaystyle 2.5º\) above the horizontal?

52. Using values from Table, how many DNA molecules could be broken by the energy carried by a single electron in the beam of an old-fashioned TV tube? (These electrons were not dangerous in themselves, but they did create dangerous x rays. Later model tube TVs had shielding that absorbed x rays before they escaped and exposed viewers.)

Solution \(\displaystyle 4×10^4\) molecules

53. Using energy considerations and assuming negligible air resistance, show that a rock thrown from a bridge 20.0 m above water with an initial speed of 15.0 m/s strikes the water with a speed of 24.8 m/s independent of the direction thrown.

Solution Equating \(\displaystyle ΔPE_g\) and \(\displaystyle ΔKE\), we obtain \(\displaystyle v=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(20.0 m)+(15.0 m/s)^2}=24.8 m/s\)

54. If the energy in fusion bombs were used to supply the energy needs of the world, how many of the 9-megaton variety would be needed for a year’s supply of energy (using data from Table)? This is not as far-fetched as it may sound—there are thousands of nuclear bombs, and their energy can be trapped in underground explosions and converted to electricity, as natural geothermal energy is.

55. (a) Use of hydrogen fusion to supply energy is a dream that may be realized in the next century. Fusion would be a relatively clean and almost limitless supply of energy, as can be seen from Table. To illustrate this, calculate how many years the present energy needs of the world could be supplied by one millionth of the oceans’ hydrogen fusion energy.

(b) How does this time compare with historically significant events, such as the duration of stable economic systems?

Solution (a) \(\displaystyle 25×10^6years\) (b) This is much, much longer than human time scales.

56. The Crab Nebula (see Figure) pulsar is the remnant of a supernova that occurred in A.D. 1054. Using data from Table, calculate the approximate factor by which the power output of this astronomical object has declined since its explosion.

Solution \(\displaystyle 2×10^{−10}\)

57. Suppose a star 1000 times brighter than our Sun (that is, emitting 1000 times the power) suddenly goes supernova. Using data from Table:

(a) By what factor does its power output increase?

(b) How many times brighter than our entire Milky Way galaxy is the supernova?

(c) Based on your answers, discuss whether it should be possible to observe supernovas in distant galaxies. Note that there are on the order of \(\displaystyle 10^{11}\) observable galaxies, the average brightness of which is somewhat less than our own galaxy.

58. A person in good physical condition can put out 100 W of useful power for several hours at a stretch, perhaps by pedaling a mechanism that drives an electric generator. Neglecting any problems of generator efficiency and practical considerations such as resting time:

(a) How many people would it take to run a 4.00-kW electric clothes dryer?

(b) How many people would it take to replace a large electric power plant that generates 800 MW?

Solution (a) 40 (b) 8 million

59. What is the cost of operating a 3.00-W electric clock for a year if the cost of electricity is $0.0900 per \(\displaystyle kW⋅h\)?

60. A large household air conditioner may consume 15.0 kW of power. What is the cost of operating this air conditioner 3.00 h per day for 30.0 d if the cost of electricity is $0.110 per \(\displaystyle kW⋅h\)?

Solution $149

61. (a) What is the average power consumption in watts of an appliance that uses \(\displaystyle 5.00 kW⋅h\) of energy per day?

(b) How many joules of energy does this appliance consume in a year?

62. (a) What is the average useful power output of a person who does \(\displaystyle 6.00×10^6J\) of useful work in 8.00 h?

(b) Working at this rate, how long will it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work done to lift his body can be omitted because it is not considered useful output here.)

Solution (a) 208 W (b) 141 s

63. A 500-kg dragster accelerates from rest to a final speed of 110 m/s in 400 m (about a quarter of a mile) and encounters an average frictional force of 1200 N. What is its average power output in watts and horsepower if this takes 7.30 s?

64. (a) How long will it take an 850-kg car with a useful power output of 40.0 hp (1 hp = 746 W) to reach a speed of 15.0 m/s, neglecting friction? (b) How long will this acceleration take if the car also climbs a 3.00-m-high hill in the process?

Solution (a) 3.20 s (b) 4.04 s

65. (a) Find the useful power output of an elevator motor that lifts a 2500-kg load a height of 35.0 m in 12.0 s, if it also increases the speed from rest to 4.00 m/s. Note that the total mass of the counterbalanced system is 10,000 kg—so that only 2500 kg is raised in height, but the full 10,000 kg is accelerated.

(b) What does it cost, if electricity is $0.0900 per \(\displaystyle kW⋅h\)?

66. (a) What is the available energy content, in joules, of a battery that operates a 2.00-W electric clock for 18 months?

(b) How long can a battery that can supply \(\displaystyle 8.00×10^4J\) run a pocket calculator that consumes energy at the rate of \(\displaystyle 1.00×10^{−3}W\)?

Solution (a) \(\displaystyle 9.46×10^7J\) (b) \(\displaystyle 2.54 y\)

67. (a) How long would it take a \(\displaystyle 1.50×10^5\)-kg airplane with engines that produce 100 MW of power to reach a speed of 250 m/s and an altitude of 12.0 km if air resistance were negligible?

(b) If it actually takes 900 s, what is the power?

(c) Given this power, what is the average force of air resistance if the airplane takes 1200 s? (Hint: You must find the distance the plane travels in 1200 s assuming constant acceleration.)

68. Calculate the power output needed for a 950-kg car to climb a \(\displaystyle 2.00º\) slope at a constant 30.0 m/s while encountering wind resistance and friction totaling 600 N. Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.

Solution Identify knowns: \(\displaystyle m=950 kg\), slope angle \(\displaystyle θ=2.00º, v=3.00 m/s, f=600 N\) Identify unknowns: power \(\displaystyle P\) of the car, force \(\displaystyle F\) that car applies to road Solve for unknown: \(\displaystyle P=\frac{W}{t}=\frac{Fd}{t}=F(\frac{d}{t})=Fv,\) where \(\displaystyle F\) is parallel to the incline and must oppose the resistive forces and the force of gravity: \(\displaystyle F=f+w=600 N+mgsinθ\) Insert this into the expression for power and solve: \(\displaystyle P=(f+mgsinθ)v\) \(\displaystyle =[600 N+(950 kg)(9.80 m/s^2)sin 2º](30.0 m/s)\) \(\displaystyle =2.77×10^4W\) About 28 kW (or about 37 hp) is reasonable for a car to climb a gentle incline.

69. (a) Calculate the power per square meter reaching Earth’s upper atmosphere from the Sun. (Take the power output of the Sun to be \(\displaystyle 4.00×10^{26}W\).)

(b) Part of this is absorbed and reflected by the atmosphere, so that a maximum of \(\displaystyle 1.30 kW/m^2\) reaches Earth’s surface. Calculate the area in \(\displaystyle km^2\) of solar energy collectors needed to replace an electric power plant that generates 750 MW if the collectors convert an average of 2.00% of the maximum power into electricity. (This small conversion efficiency is due to the devices themselves, and the fact that the sun is directly overhead only briefly.) With the same assumptions, what area would be needed to meet the United States’ energy needs \(\displaystyle (1.05×10^{20}J)\)? Australia’s energy needs \(\displaystyle (5.4×10^{18}J)\)? China’s energy needs \(\displaystyle (6.3×10^{19}J)\)? (These energy consumption values are from 2006.)

70. (a) How long can you rapidly climb stairs (116/min) on the 93.0 kcal of energy in a 10.0-g pat of butter?

(b) How many flights is this if each flight has 16 stairs?

Solution (a) 9.5 min (b) 69 flights of stairs

71. (a) What is the power output in watts and horsepower of a 70.0-kg sprinter who accelerates from rest to 10.0 m/s in 3.00 s?

(b) Considering the amount of power generated, do you think a well-trained athlete could do this repetitively for long periods of time?

72. Calculate the power output in watts and horsepower of a shot-putter who takes 1.20 s to accelerate the 7.27-kg shot from rest to 14.0 m/s, while raising it 0.800 m. (Do not include the power produced to accelerate his body.)

Solution 641 W, 0.860 hp

73. (a) What is the efficiency of an out-of-condition professor who does \(\displaystyle 2.10×10^5 J\) of useful work while metabolizing 500 kcal of food energy?

(b) How many food calories would a well-conditioned athlete metabolize in doing the same work with an efficiency of 20%?

74. Energy that is not utilized for work or heat transfer is converted to the chemical energy of body fat containing about 39 kJ/g. How many grams of fat will you gain if you eat 10,000 kJ (about 2500 kcal) one day and do nothing but sit relaxed for 16.0 h and sleep for the other 8.00 h? Use data from Table for the energy consumption rates of these activities.

Solution 31 g

75. Using data from Table, calculate the daily energy needs of a person who sleeps for 7.00 h, walks for 2.00 h, attends classes for 4.00 h, cycles for 2.00 h, sits relaxed for 3.00 h, and studies for 6.00 h. (Studying consumes energy at the same rate as sitting in class.)

76. What is the efficiency of a subject on a treadmill who puts out work at the rate of 100 W while consuming oxygen at the rate of 2.00 L/min? (Hint: See Table.)

Solution 14.3%

77. Shoveling snow can be extremely taxing because the arms have such a low efficiency in this activity. Suppose a person shoveling a footpath metabolizes food at the rate of 800 W.

(a) What is her useful power output?

(b) How long will it take her to lift 3000 kg of snow 1.20 m? (This could be the amount of heavy snow on 20 m of footpath.)

(c) How much waste heat transfer in kilojoules will she generate in the process?

78. Very large forces are produced in joints when a person jumps from some height to the ground.

(a) Calculate the magnitude of the force produced if an 80.0-kg person jumps from a 0.600–m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.)

(b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force produced if the stopping distance is 0.300 m.

(c) Compare both forces with the weight of the person.

Solution (a) \(\displaystyle 3.21×10^4 N\) (b) \(\displaystyle 2.35×10^3 N\) (c) Ratio of net force to weight of person is 41.0 in part (a); 3.00 in part (b)

79. Jogging on hard surfaces with insufficiently padded shoes produces large forces in the feet and legs.

(a) Calculate the magnitude of the force needed to stop the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to include the weight of the 75.0-kg jogger’s body.)

(b) Compare this force with the weight of the jogger.

80. (a) Calculate the energy in kJ used by a 55.0-kg woman who does 50 deep knee bends in which her center of mass is lowered and raised 0.400 m. (She does work in both directions.) You may assume her efficiency is 20%.

(b) What is the average power consumption rate in watts if she does this in 3.00 min?

Solution (a) 108 kJ (b) 599 W

81. Kanellos Kanellopoulos flew 119 km from Crete to Santorini, Greece, on April 23, 1988, in the Daedalus 88, an aircraft powered by a bicycle-type drive mechanism (see Figure). His useful power output for the 234-min trip was about 350 W. Using the efficiency for cycling from [link], calculate the food energy in kilojoules he metabolized during the flight.

82. The swimmer shown in Figure exerts an average horizontal backward force of 80.0 N with his arm during each 1.80 m long stroke.

(a) What is his work output in each stroke?

(b) Calculate the power output of his arms if he does 120 strokes per minute.

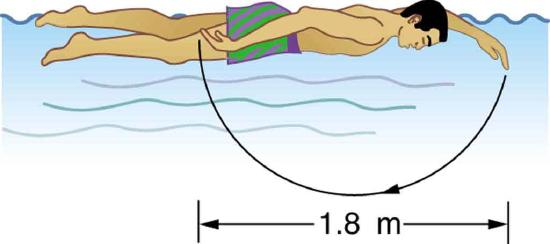
Solution (a) 144 J (b) 288 W

83. Mountain climbers carry bottled oxygen when at very high altitudes.

(a) Assuming that a mountain climber uses oxygen at twice the rate for climbing 116 stairs per minute (because of low air temperature and winds), calculate how many liters of oxygen a climber would need for 10.0 h of climbing. (These are liters at sea level.) Note that only 40% of the inhaled oxygen is utilized; the rest is exhaled.

(b) How much useful work does the climber do if he and his equipment have a mass of 90.0 kg and he gains 1000 m of altitude?

(c) What is his efficiency for the 10.0-h climb?

84. The awe-inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high, with a mass of about \(\displaystyle 7×10^9kg\). (The pyramid’s dimensions are slightly different today due to quarrying and some sagging.) Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.

(a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.

(b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps (see Figure), bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 kcal/h. What does your answer imply about how much of their work went into block-lifting, versus how much work went into friction and lifting and lowering their own bodies?

(c) Calculate the mass of food that had to be supplied each day, assuming that the average worker required 3600 kcal per day and that their diet was 5% protein, 60% carbohydrate, and 35% fat. (These proportions neglect the mass of bulk and nondigestible materials consumed.)

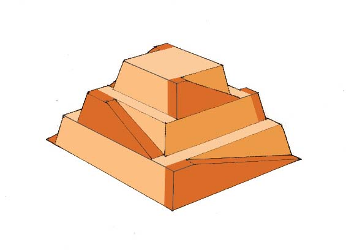
Solution (a) \(\displaystyle 2.50×10^{12} J\) (b) 2.52% (c) \(\displaystyle 1.4×10^4 kg\) (14 metric tons)

85. (a) How long can you play tennis on the 800 kJ (about 200 kcal) of energy in a candy bar?

(b) Does this seem like a long time? Discuss why exercise is necessary but may not be sufficient to cause a person to lose weight.

86. Integrated Concepts

(a) Calculate the force the woman in Figure exerts to do a push-up at constant speed, taking all data to be known to three digits.

(b) How much work does she do if her center of mass rises 0.240 m?

(c) What is her useful power output if she does 25 push-ups in 1 min? (Should work done lowering her body be included? See the discussion of useful work in Work, Energy, and Power in Humans.

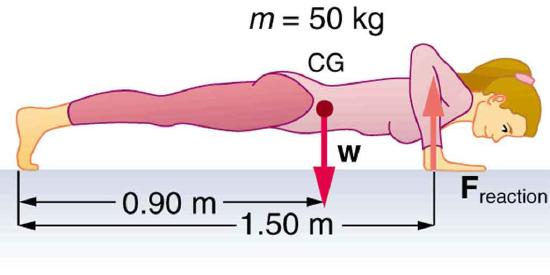
Solution (a) 294 N (b) 118 J (c) 49.0 W

87. Integrated Concepts

A 75.0-kg cross-country skier is climbing a \(\displaystyle 3.0º\) slope at a constant speed of 2.00 m/s and encounters air resistance of 25.0 N. Find his power output for work done against the gravitational force and air resistance.

(b) What average force does he exert backward on the snow to accomplish this?

(c) If he continues to exert this force and to experience the same air resistance when he reaches a level area, how long will it take him to reach a velocity of 10.0 m/s?

88. Integrated Concepts

The 70.0-kg swimmer in [link] starts a race with an initial velocity of 1.25 m/s and exerts an average force of 80.0 N backward with his arms during each 1.80 m long stroke.

(a) What is his initial acceleration if water resistance is 45.0 N?

(b) What is the subsequent average resistance force from the water during the 5.00 s it takes him to reach his top velocity of 2.50 m/s?

(c) Discuss whether water resistance seems to increase linearly with velocity.

Solution (a) \(\displaystyle 0.500 m/s^2\) (b) \(\displaystyle 62.5 N\) (c) Assuming the acceleration of the swimmer decreases linearly with time over the 5.00 s interval, the frictional force must therefore be increasing linearly with time, since \(\displaystyle f=F−ma\). If the acceleration decreases linearly with time, the velocity will contain a term dependent on time squared (\(\displaystyle t^2\)). Therefore, the water resistance will not depend linearly on the velocity.

89. Integrated Concepts

A toy gun uses a spring with a force constant of 300 N/m to propel a 10.0-g steel ball. If the spring is compressed 7.00 cm and friction is negligible:

(a) How much force is needed to compress the spring?

(b) To what maximum height can the ball be shot?

(c) At what angles above the horizontal may a child aim to hit a target 3.00 m away at the same height as the gun?

(d) What is the gun’s maximum range on level ground?

90. Integrated Concepts

(a) What force must be supplied by an elevator cable to produce an acceleration of \(\displaystyle 0.800 m/s^2\) against a 200-N frictional force, if the mass of the loaded elevator is 1500 kg?

(b) How much work is done by the cable in lifting the elevator 20.0 m?

(c) What is the final speed of the elevator if it starts from rest?

(d) How much work went into thermal energy?

Solution (a) \(\displaystyle 16.1×10^3N\) (b) \(\displaystyle 3.22×10^5J\) (c) \(\displaystyle 5.66 m/s\) (d) 4.00 kJ

91. Unreasonable Results

A car advertisement claims that its 900-kg car accelerated from rest to 30.0 m/s and drove 100 km, gaining 3.00 km in altitude, on 1.0 gal of gasoline. The average force of friction including air resistance was 700 N. Assume all values are known to three significant figures.

(a) Calculate the car’s efficiency.

(b) What is unreasonable about the result?

(c) Which premise is unreasonable, or which premises are inconsistent?

92. Unreasonable Results

Body fat is metabolized, supplying 9.30 kcal/g, when dietary intake is less than needed to fuel metabolism. The manufacturers of an exercise bicycle claim that you can lose 0.500 kg of fat per day by vigorously exercising for 2.00 h per day on their machine.

(a) How many kcal are supplied by the metabolization of 0.500 kg of fat?

(b) Calculate the kcal/min that you would have to utilize to metabolize fat at the rate of 0.500 kg in 2.00 h.

(c) What is unreasonable about the results?

(d) Which premise is unreasonable, or which premises are inconsistent?

Solution (a) \(\displaystyle 4.65×10^3kcal\) (b) 38.8 kcal/min (c) This power output is higher than the highest value on [link], which is about 35 kcal/min (corresponding to 2415 watts) for sprinting. (d) It would be impossible to maintain this power output for 2 hours (imagine sprinting for 2 hours!).

93. Construct Your Own Problem

Consider a person climbing and descending stairs. Construct a problem in which you calculate the long-term rate at which stairs can be climbed considering the mass of the person, his ability to generate power with his legs, and the height of a single stair step. Also consider why the same person can descend stairs at a faster rate for a nearly unlimited time in spite of the fact that very similar forces are exerted going down as going up. (This points to a fundamentally different process for descending versus climbing stairs.)

94. Construct Your Own Problem

Consider humans generating electricity by pedaling a device similar to a stationary bicycle. Construct a problem in which you determine the number of people it would take to replace a large electrical generation facility. Among the things to consider are the power output that is reasonable using the legs, rest time, and the need for electricity 24 hours per day. Discuss the practical implications of your results.

95. Integrated Concepts

A 105-kg basketball player crouches down 0.400 m while waiting to jump. After exerting a force on the floor through this 0.400 m, his feet leave the floor and his center of gravity rises 0.950 m above its normal standing erect position.

(a) Using energy considerations, calculate his velocity when he leaves the floor.

(b) What average force did he exert on the floor? (Do not neglect the force to support his weight as well as that to accelerate him.)

(c) What was his power output during the acceleration phase?

Solution (a) 4.32 m/s (b) \(\displaystyle 3.47×10^3N\) (c) 8.93 kW

Contributors and Attributions

Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a  Creative Commons Attribution License (by 4.0) .

Suggestions

• A Christmas Carol
• As You Like It
• Brave New World
• Don Quixote

Please wait while we process your payment

Reset Password

Your password reset email should arrive shortly..

If you don't see it, please check your spam folder. Sometimes it can end up there.

Something went wrong

Log in or create account.

•   Be between 8-15 characters.
•   Contain at least one capital letter.
•   Contain at least one number.
•   Be different from your email address.

By signing up you agree to our terms and privacy policy .

Don’t have an account? Subscribe now

Create Your Account

Sign up for your FREE 7-day trial

• Ad-free experience
• Note-taking
• Flashcards & Quizzes
• AP® English Test Prep
• Plus much more

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Already have an account? Log in

Choose Your Plan

Group Discount

$4.99 /month + tax

$24.99 /year + tax

Save over 50% with a SparkNotes PLUS Annual Plan!

Purchasing SparkNotes PLUS for a group?

Get Annual Plans at a discount when you buy 2 or more!

$24.99 $18.74   / subscription + tax

Subtotal $37.48 + tax

Save 25% on 2-49 accounts

Save 30% on 50-99 accounts

Want 100 or more? Contact us for a customized plan.

Payment Details

Payment Summary

SparkNotes Plus

 Change

You'll be billed after your free trial ends.

7-Day Free Trial

Not Applicable

Renews May 9, 2024 May 2, 2024

Discounts (applied to next billing)

SNPLUSROCKS20  |  20% Discount

This is not a valid promo code.

Discount Code (one code per order)

SparkNotes PLUS Annual Plan - Group Discount

SparkNotes Plus subscription is $4.99/month or $24.99/year as selected above. The free trial period is the first 7 days of your subscription. TO CANCEL YOUR SUBSCRIPTION AND AVOID BEING CHARGED, YOU MUST CANCEL BEFORE THE END OF THE FREE TRIAL PERIOD. You may cancel your subscription on your Subscription and Billing page or contact Customer Support at [email protected] . Your subscription will continue automatically once the free trial period is over. Free trial is available to new customers only.

For the next 7 days, you'll have access to awesome PLUS stuff like AP English test prep, No Fear Shakespeare translations and audio, a note-taking tool, personalized dashboard, & much more!

You’ve successfully purchased a group discount. Your group members can use the joining link below to redeem their group membership. You'll also receive an email with the link.

Members will be prompted to log in or create an account to redeem their group membership.

Thanks for creating a SparkNotes account! Continue to start your free trial.

We're sorry, we could not create your account. SparkNotes PLUS is not available in your country. See what countries we’re in.

There was an error creating your account. Please check your payment details and try again.

Your PLUS subscription has expired

• We’d love to have you back! Renew your subscription to regain access to all of our exclusive, ad-free study tools.
• Renew your subscription to regain access to all of our exclusive, ad-free study tools.
• Go ad-free AND get instant access to grade-boosting study tools!
• Start the school year strong with SparkNotes PLUS!
• Start the school year strong with PLUS!

Work and Power

• Study Guide

Unlock your FREE SparkNotes PLUS trial!

Unlock your free trial.

• Ad-Free experience
• Easy-to-access study notes
• AP® English test prep

A 10 kg object experiences a horizontal force which causes it to accelerate at 5 m/s 2 , moving it a distance of 20 m, horizontally. How much work is done by the force?

The magnitude of the force is given by F = ma = (10)(5) = 50 N. It acts over a distance of 20 m, in the same direction as the displacement of the object, implying that the total work done by the force is given by W = Fx = (50)(20) = 1000 Joules.

A ball is connected to a rope and swung around in uniform circular motion. The tension in the rope is measured at 10 N and the radius of the circle is 1 m. How much work is done in one revolution around the circle?

A crate is moved across a frictionless floor by a rope THAT is inclined 30 degrees above horizontal. The tension in the rope is 50 N. How much work is done in moving the crate 10 meters?

A 10 kg weight is suspended in the air by a strong cable. How much work is done, per unit time, in suspending the weight?

The crate, and thus the point of application of the force, does not move. Thus, though a force is applied, no work is done on the system.

A 5 kg block is moved up a 30 degree incline by a force of 50 N, parallel to the incline. The coefficient of kinetic friction between the block and the incline is .25. How much work is done by the 50 N force in moving the block a distance of 10 meters? What is the total work done on the block over the same distance?

Finding the work done by the 50 N force is quite simple. Since it is applied parallel to the incline, the work done is simply W = Fx = (50)(10) = 500 J.

Take a Study Break

Every Literary Reference Found in Taylor Swift's Lyrics

The 7 Most Messed-Up Short Stories We All Had to Read in School

QUIZ: Which Greek God Are You?

QUIZ: Which Bennet Sister Are You?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 5: Work and energy

About this unit.

In physics, the work goes beyond 9-5. Let's see how physicists define the term "work", and how work relates to the concepts of kinetic energy, potential energy, conservation of energy, and mechanical advantage.

Introduction to work

• Work example problems (Opens a modal)
• Work as area under curve (Opens a modal)
• Introduction to work review (Opens a modal)
• Calculating work from force vs. position graphs Get 3 of 4 questions to level up!
• Calculating work done by a force Get 3 of 4 questions to level up!

Kinetic energy

• What is kinetic energy? (Opens a modal)
• Kinetic energy review (Opens a modal)
• Using the kinetic energy equation Get 3 of 4 questions to level up!

Work-energy theorem

• Work and the work-energy principle (Opens a modal)
• Work-energy theorem review (Opens a modal)
• Calculating change in kinetic energy from a force Get 3 of 4 questions to level up!
• Velocity and mass from force vs. position graphs Get 3 of 4 questions to level up!

Spring potential energy and Hooke's law

• Intro to springs and Hooke's law (Opens a modal)
• Potential energy stored in a spring (Opens a modal)
• Spring potential energy and Hooke's law review (Opens a modal)
• Calculating spring force Get 3 of 4 questions to level up!
• Calculating elastic potential energy Get 3 of 4 questions to level up!

Gravitational potential energy and conservative forces

• Conservative forces (Opens a modal)
• Gravitational potential energy and conservative forces review (Opens a modal)
• Finding change in gravitational potential energy Get 3 of 4 questions to level up!

Conservation of energy

• Law of conservation of energy (Opens a modal)
• LOL diagrams (Opens a modal)
• Conservation of energy review (Opens a modal)
• Conservation of energy: Predict changes in energy Get 3 of 4 questions to level up!
• Conservation of energy: Numerical calculations Get 3 of 4 questions to level up!
• Power (Opens a modal)
• Power review (Opens a modal)
• Relating power and energy Get 3 of 4 questions to level up!

Explore simple machines

• Simple machines and how to use this tutorial (Opens a modal)
• Lever (Opens a modal)
• Wheel (Opens a modal)
• Pulleys (Opens a modal)

StickMan Physics

Animated Physics Lessons

Work and Power Example Solutions

Follow along with common work and power example problems and solutions. See how to solve problems when force is applied directly parallel or at an angle.

Example Work and Power Problems

1. How much work is done by the stickman that pushes a box 5 meters with a force of 12 Newtons forward?

Since the force is in the same direction as motion you plug numbers directly in and don't have to find the parallel component first.

W = (12)(5) = 60 J

2. What is the power output of the stickman that pushes the box 5 meters in 3 seconds with a constant force of 12 N?

3. How much work would be done if 12N of force was applied on an object at an angle of 25° above the horizon to move an object 5 meters horizontally.

A) Find the horizontal component of force:

adj = (cosӨ)(hyp)

adj = (cos(25°))(12)= 10.9 N

B) Find out how much work is done by this component:

W = (10.9)(5) = 54.5 J

4. What is the power output if 12N of force was applied on an object at an angle of 25° above the horizon to move an object 5 meters horizontally in 3 seconds.

Use the work from the problem above

P = 54.5/3 = 18.2 W 

• Back to the Work and Power Page
• Back to the  Stickman Physics Home Page
• For video tutorials and other physics resources check out  HoldensClass.com
• Find many of your animation resources in one place at the  StickMan Physics Gallery
• Equation Sheet

Terms and Conditions - Privacy Policy

• Work Energy Power

Work, Energy and Power

Work, Energy and Power are fundamental concepts of Physics. Work is said to be done when a force (push or pull) applied to an object causes a displacement of the object. We define the capacity to do the work as energy. Power is the work done per unit of time. This article discusses work, energy and power in detail.

What is Work?

For work to be done, a force must be exerted and there must be motion or displacement in the direction of the force. The work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force. Work has only magnitude and no direction. Hence, work is a scalar quantity.

Formula of Work

The work done by a force is defined to be the product of the component of the force in the direction of the displacement and the magnitude of this displacement.

Where W is the work done, F is the force, d is the displacement, θ is the angle between force and displacement and F cosθ is the component of force in the direction of displacement.

We understand from the work equation that if there is no displacement, there is no work done, irrespective of how large the force is. To summarize, we can say that no work is done if:

• the displacement is zero
• the force is zero
• the force and displacement are mutually perpendicular to each other.

Can the work done be negative? Watch the video and find out!

Unit of Work

The SI unit of work is Joule (J). For example, if a force of 5 newtons is applied to an object and moves 2 meters, the work done will be 10 newton-meter or 10 Joule. It should be noted that 1 J = 1 N ⋅ m = 1 kg ⋅ m 2 /s 2 .

Example of Work

An object is horizontally dragged across the surface by a 100 N force acting parallel to the surface. Find out the amount of work done by the force in moving the object through a distance of 8 m.

F = 100 N, d = 8 m

Since F and d are in the same direction, θ = 0, [θ is the angle of the force to the direction of movement], therefore

W = FdCos θ

W = 100 x 8 x Cos 0

W = 800 J [Since Cos 0 = 1]

Related Concepts

What is energy.

Energy is the ability to perform work. Energy can neither be created nor destroyed, and it can only be transformed from one form to another. The unit of Energy is the same as of Work, i.e. Joules. Energy is found in many things, and thus there are different types of energy.

All forms of energy are either kinetic or potential. The energy in motion is known as Kinetic Energy, whereas Potential Energy is the energy stored in an object and is measured by the amount of work done.

Types of Energy

Some other types of energy are given below:

• Mechanical energy
• Mechanical wave energy
• Chemical energy
• Electric energy
• Magnetic energy
• Radiant energy
• Nuclear energy
• Ionization energy
• Elastic energy
• Gravitational energy
• Thermal energy
• Heat Energy

Unit of Energy

The SI unit of energy is Joules (J), named in honour of James Prescott Joule.

Watch the video and solve NCERT exercise questions in the chapter Work and Energy Class 9

What is Power?

Power is a physical concept with several different meanings, depending on the context and the available information. We can define power as the rate of doing work, and it is the amount of energy consumed per unit of time.

Formula of Power

As discussed, power is the rate of doing work. Therefore, it can be calculated by dividing work done by time. The formula for power is given below.

Unit of Power

As power doesn’t have any direction, it is a scalar quantity. The SI unit of power is Joules per Second (J/s), which is termed as Watt. Watt can be defined as the power needed to do one joule of work in one second. The unit Watt is dedicated in honour of Sir James Watt, the developer of the steam engine.

Read the article below to learn the SI unit of power in detail.

Example of Power

First we need to calculate the work done, which requires the force necessary to lift the truck against gravity:

F = mg = 1000 x 9.81 = 9810 N.

W = Fd = 9810N x 2m = 19620 Nm = 19620 J.

The power is P = W/t = 19620J / 15s = 1308 J/s = 1308 W.

Related Concept

Work, power and energy questions.

• What is the relationship between work, energy and power?
• What happens to the energy as work is done?
• What is the difference between work, energy and power?
• Is energy transferred the same as work done?
• How does work affect an object’s energy?

How are work, energy and power related to each other?

• How are force, energy and work related?
• What is the formula of work, energy and power?
• How do you calculate energy from power?
• Can force be converted into energy?

Video Explanation of Work, Energy and Power

Here is an engaging video explanation of Work, Energy and Power and the relationship between them.

Important Resources for Work, Energy and Power

Overview of work, energy and power, watch the video and solve complete exemplar questions in the chapter work and energy class 9.

Frequently Asked Questions

Work is the energy needed to apply a force to move an object a particular distance. Power is the rate at which that work is done.

What is the unit of work?

The unit of work is Joule.

What is the unit of energy?

The unit of energy is Joule.

What is the unit of power?

The unit of power is Watt.

Is power a scalar quantity?

Power is a scalar quantity because it is a ratio of two scalar quantities.

Work, Power and Energy is one of the important topics of JEE Main and JEE Advanced, watch the video and understand the type of questions asked from this topic!

Stay tuned to BYJU’S and Fall in Love with Learning !

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Its so useful love this byju’s

Very good explanation

Excellent explaination done 5 stars to BYJU’S

it is very nice because it become easy.

very nicely done

well explained

really good platform to learn basic

Thanks a lot . It was very helpful . Lots of love for all your team .

I really love this explanation

Thank you, this explanation is very useful for this topic.

Amazing! Today was my online class test, the content given here helped me a lot. I would like to give BYJU’S five stars.

Good explanation 👍👍👍👍👍👍

Really good explanation It was very useful Thank you so much

What a nice explanation!

Very helpful

Very nice Explanations with a better understanding of concepts. Was very helpful. Provided me with all types of revision strategies before exam

Thanks so much byjus you are doing a good job,,👍

Thanks very much this information was very useful but you did not put examples of power, energy and work.

Thank u for helping, Really nice

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Exam Center
• Ticket Center
• Flash Cards
• Work and Energy

Work-Energy Theorem Problems and Solutions for High School

In this article, some problems on the work-kinetic energy theorem are presented and solved. In each answer, you can find a detailed tutorial on this topic. 

Problems on Work-Energy Theorem:

Problem (1): How much work must be done to stop a $1200-{\rm kg}$ car moving at $99\,{\rm km/h}$ in a straight path. 

Solution : The work-kinetic energy theorem states that the net work done on an object is equal to the change in the object's kinetic energy. \[W_{net}=K_2-K_1\] where $K=\frac 12 mv^2$ is the kinetic energy of an object. 

In this case, the initial and final velocities of the car are given, so $v_i=99\,{\rm km/h}$ and $v_f=0$. The wanted quantity is the net work done on the car $W_{net}=?$. Applying the work-kinetic energy theorem formula, we have \begin{align*} W_{net}&=\frac 12 m(v_2^2-v_1^2) \\\\ &=\frac 12 (1200)(0-(27.5)^2) \\\\&=453750 \quad {\rm J}\end{align*} where we converted $\rm \frac{km}{h}$ to $\rm \frac{m}{s}$ using the following formula since the SI unit of speed is ${\rm \frac ms}$ \[1\,{\rm \frac{km}{h}}=\frac{1000}{3600}\,{\rm \frac ms}\]

Problem (2): A $6-{\rm kg}$ object has a speed of $2\,{\rm m/s}$ at point A and $4\,{\rm m/s}$ later at point B. Find the total work done on the object as it moves from point A to B.

Solution : The object's mass and its velocities at two different points are given, and we are asked to find the total work done on the object. 

All these information guide us to use the work-kinetic energy theorem. Because to find the work done on an object there are two ways, either use the work formula in physics, $W=Fd\cos\theta$, or the work-energy principle. (The first method is a problem on work in physics )

In this case, neither forces acting on the object nor the distance traveled were given, so we are forced to use the work-energy theorem. \begin{align*} W_{net}&=\Delta K\\\\ &=\frac 12 mv_B^2-\frac 12 mv_A^2\\\\ &=\frac 12 (6)(4)^2-\frac 12 (6)(2)^2 \\\\&=36\quad {\rm J}\end{align*}

Problem (3): A $1650-{\rm kg}$ fast car can accelerate from 0 to $27\,{\rm m/s}$ in $2.7\,{\rm s}$.  (a) What is its acceleration? (b) What is the displacement of the car? (c) How much work was done on the car? (d) What is the average force acting on the car over this time interval?

Solution : (a) Initial $v_0=0$ and final velocity $v_f=27\,{\rm m/s}$ are given in a time interval $\Delta t=2.7\,{\rm s}$. Substituting these numerical values into the average acceleration formula, we have \[a=\frac{v_2-v_1}{\Delta t}=\frac{27-0}{2.7}=10\,{\rm m/s^2}\] (b) This is a kinematics equation problem . To solve this, we use the displacement kinematics equation, $\Delta x=\frac 12 at^2+v_0 t$, so \begin{align*} \Delta x&=\frac 12 at^2+v_0 t\\\\&=\frac 12 (10)(2.7)^2+(0)(2.7) \\\\ &=36.45\quad {\rm m}\end{align*}  (c) This part is related to the work-energy theorem problem. We use this theorem to find the total work done on the car \begin{align*} W_{net}&=\Delta K\\\\ &=\frac 12 m (v_2^2-v_1^2) \\\\&=\frac 12 (1650)(27^2-0) \\\\&=601425\quad {\rm J}\end{align*}  (d) In part (b), the distance traveled by car was found to be $d=36.45\,{\rm m}$. In part (c), the total work over this displacement is obtained, as well. 

Use the work formula $W=Fd$, and solve for $F$ to find the average force acting on the car \[F=\frac{W}{d}=\frac{601425}{36.45}=16500\,{\rm N}\]

Further practicing: Problems on speed, velocity, and acceleration with answers

Problem (4): A $12000-{\rm kg}$ truck initially moving at a constant speed of $126\,{\rm km/h}$ suddenly applies brakes and stops in $12\,{\rm m}$. How much work has been done on the truck over this distance? 

Solution : The total work done on the truck involves the work done by the friction force between the truck's tire and the road surface as well as the work done by the brakes to stop the car. 

Don't necessary to know the magnitude of these complicated forces to find the total work, instead, as we have the initial and final velocities of the truck, we can use the work-energy theorem to determine the net work done on the truck.

Before using this theorem, first convert the given ${\rm km/h}$ to ${\rm m/s}$ by multiplying it by $\frac{10}{36}$. So, the final velocity in ${\rm m/s}$ is \[126\,{\rm km/h}\times \frac{10}{36}=35\,{\rm m/s}\] Now, applying the work-kinetic energy theorem, we have \begin{align*} W_{net}&=\Delta K\\\\ &=\frac 12 mv_2^2-\frac 12 mv_1^2\\\\ &=\frac 12 (1200)(0)^2-\frac 12 (1200)(35)^2 \\\\&=735\quad {\rm kJ}\end{align*} 

Problem (5): A $4600-{\rm kg}$ bus traveling at $26.5\,{\rm m/s}$ can brake and comes to a stop in $46\,{\rm m}$. What is the force applied by the brakes?

Solution : There are two equivalent methods to solve this problem. One is using the work-energy principle, and the other is Newton's second law formula $F=ma$.  All information required to use the work-energy theorem is given, so we have \begin{align*} W_{net}&=\Delta K\\\\ &=\frac 12 mv_2^2-\frac 12 mv_1^2\\\\ &=\frac 12 (4600)(0)^2-\frac 12 (4600)(26.5)^2 \\\\&=1615175\quad {\rm J}\end{align*} This is the total work done on the bus by all forces involved. To find the magnitude of those forces we can use the definition of work, $W=Fd$. So, solving for $F$, we have \[F=\frac{W}{d}=\frac{1615175}{46}=35112.5\,{\rm N}\] We can solve this problem from the perspective of a kinematics problem. Using time-independent kinematics equation $v^2-v_0^2=2a\Delta x$, and solving for $a$, we can find the acceleration of the bus \begin{align*} a&=\frac{v^2-v_0^2}{2\Delta x}\\\\&=\frac{0-26.5^2}{2\times 46}\\\\&=7.633\quad {\rm m/s^2}\end{align*} Now, using the formula $F=ma$, the constant force exerts to the car is found to be \[F=(4600)(7.633)=35112.5\] The actual value obtained here is slightly different than the previous result, because we used the rounded value for the acceleration. You can check this out yourself.

Problem (6): A heavy truck of mass $6.5\times 10^4\,{\rm kg}$ is traveling at a constant speed of $12\,{\rm m/s}$.  (a) How much work is required to stop it? (b) What is the magnitude of the constant force needed to stop it over a displacement of $2.2\,{\rm km}$?

Solution : In all work-energy theorem problems, consider two arbitrary points having known constant velocities and compute the difference in kinetic energies. 

According to this principle, the difference in kinetic energies is equal to the total work done on the object to change the object's velocities.

(a) Kinetic energy in physics is defined as $K=\frac 12 mv^2$, so the difference in kinetic energies is determined as below \begin{align*}\Delta K&=\frac 12 m v_2^2-\frac 12 mv_1^2\\\\ &=\frac 12 (65000)(0)^2-\frac 12 (65000)(12)^2\\\\ &=4.68\quad {\rm MJ}\end{align*} where $MJ$ stands for the megajoules which is equal to $10^6\,{\rm J}$. This change in kinetic energy equals the total (net) work done on the truck by all forces acting on it. Hence, \[W_{net}=\Delta K=4.68\quad {\rm MJ}\] (b) We call all forces involved in stopping the truck, the friction force between the truck's tires and road surface, and the force that the brakes apply, as $F_{tot}$. 

In the previous part, the work done by these forces is computed. Assuming that all these forces act on the truck parallel to its displacement, so we can use the work formula $W=Fd$ to find their sum values as below \[F_{net}=\frac{W}{d}=\frac{4.68\times 10^6}{2.6\times 10^3}=1800\,{\rm m}\]   

Problem (7): A $2-{\rm kg}$ box is pushed against a slippery surface with a constant force of $50\,{\rm N}$. How far the box must be pushed, starting from rest, so that its final kinetic energy is $380\,{\rm J}$?

Solution : ''from rest'' means initial velocity is zero, $v_0=0$ so its initial kinetic energy is also zero $K_1=0$. The work-energy theorem relates the change in kinetic energy $\Delta K$ of an object to the total (net) work $W_{net}$ done on it. \[W_{net}=\Delta K=K_2-K_1=380\quad {\rm J}\] On the other hand, if we assume all forces involved are constant and parallel to the displacement, then solving the work formula $W_{net}=Fd$ for $d$, gives us the displacement of the box. Thus, \[d=\frac{W_{net}}{F}=\frac{380}{50}=7.6\quad {\rm m}\]

Problem (8): a $2200-{\rm kg}$ car starts its motion from rest at the top of a $20^\circ$ incline. An average friction force of $4000\,{\rm N}$ opposes the car coming down the incline so that the car's speed at the bottom of the path is $4.2\,{\rm m/s}$. How much distance does the car travel down along the incline?

Solution : This is an application of a work-energy problem on an incline. The car starts at rest $v_i=0$, so its initial kinetic energy is $K_i=0$. In the end, the velocity is $v_f=4.2\,{\rm m/s}$ so \[K_f=\frac 12 mv_f^2=19404\,{\rm J}\] The work-kinetic energy principle relates the change in kinetic energy of an object to the work done on all forces acting on it over a displacement $d$. \[\Delta K=\underbrace{F_{net}d}_{W_{net}}\] where we assumed that all forces act in the direction of motion.  

Assuming the car starts its motion with the engine off at the top of the inclined plane, then the only forces along the incline are the parallel component of weight, $w_{\parallel}=mg\sin\alpha$, and the friction force $f_k$ (recall these concepts from the section of the inclined plane problems ). $\alpha$ is the angle of incline. The free-body diagram of forces is shown below.

The vector sum of these forces makes the total (net) force act on the car. But what does mean by the vector sum of forces? That is the magnitude of forces along the motion minus the magnitude of forces in the opposite direction of motion. 

In this case, the car coming down the incline, so as you can see in the figure, the force $mg\sin 20^\circ$ is along the motion, and the friction force is in the opposite direction. 

Thus, adding these forces get the magnitude of total force act on the car \begin{align*} F_{net}&=mg\sin 20^\circ-f_k\\&=(2200)(10)(0.34)-4000\\&=3480\quad {\rm N}\end{align*} After such a long path to find the total force's magnitude, now we apply the work-energy theorem formula and solve for displacement $d$ \begin{align*} \Delta K&=F_{net}d\\\\ 19404-0&=3480\times d\\\\ \Rightarrow d&= 5.57\quad {\rm m}\end{align*} 

Practicing more on vectors in physics Definition of vector in physics   Definition of unit vectors in physics with solved problems Solved problems on vectors in physics

Problem (9): A $2-{\rm kg}$ crate, from rest, is pulled with a force of $66\,{\rm N}$ by a rope inclined at $32^\circ$. The crate moves through a rough floor, a distance of $10\,{\rm m}$. If an average friction force of $25\,{\rm N}$ opposes the motion, what is the speed of the box at the end of its displacement?

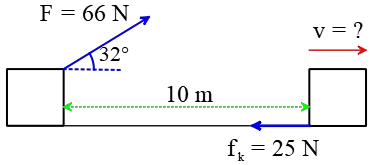
Solution : We want to solve this problem using the work-energy theorem considerations.

To use this principle, we must know the magnitude of total forces acting on the object and its initial and final velocities. 

First, draw a free body diagram, and sketch all forces acting on the crate. 

As you can see, two forces act on the crate along the motion. One is the parallel component of the pulling force $F_p$, which is obtained by resolving it, and the other is the friction force in the opposite direction of motion. 

Algebraic summing these two forces in opposite directions, get the total force acting on the crate. \begin{align*} F_{tot}&=F_{\parallel}-f_k\\\\&=F\cos\alpha-f_k\\\\&=66\cos 32^\circ-25\\\\&=31.1\quad {\rm N}\end{align*} Now, applying the work-energy principle, we have \begin{align*} \Delta K&=W_{net}\\\\K_2-K_1 &=F_{tot}d\\\\K_2-0&=31.1\times 10\\\\ \Rightarrow K_2&=311\quad {\rm J}\end{align*} The kinetic energy in the end of the path is obtained, using kinetic energy formula $K=\frac 12 mv^2$, and solving for $v$, we have \[v=\sqrt{\frac{2K}{m}}=\sqrt{\frac{2\times 311}{2}}=17.6\,{\rm m/s}\] Hence, the care at the end has a speed of about $17.6\,{\rm m/s}$. 

Problem (10): A constant force of $100\,{\rm N}$ acts on a $4\,{\rm kg}$ box on a slippery surface. Initially, the speed of the box is $20\,{\rm m/s}$ in the direction of the motion, and $3\,{\rm s}$ later its speed becomes $45\,{\rm m/s}$. Find  (a) the total work done by this external force (b) The average power delivered by the forces during time interval $3\,{\rm s}$. 

Solution : The surface is assumed slippery means the friction force can be neglected. So the only force exerted on the box is the external force $F=100\,{\rm N}$.  The box's speed at two different places is given, so its kinetic energies are also known. 

(a) The work-kinetic energy principle relates the change in kinetic energy $\Delta K=K_2-K_1$ to the total work done by forces acting on the object. \[\Delta K=W_{tot}=Fd\] So, using this principle, we have \begin{align*} W_{tot}&=K_2-K_1\\\\ &=\frac 12 mv_2^2 -\frac 12 mv_1^2\\\\ &=\frac 12 (4)(45)^2-\frac (4)(20)^2\\\\&=3250\quad {\rm J}\end{align*} (b) The power delivered by a force is defined as the ratio of the work done by this work to the time taken, so \[P=\frac{W}{t}=\frac{3250}{3}=1083.3\,{\rm W}\]

Problem (11): A $55-{\rm g}$ bullet is fired at a tree trunk. It moves at $575\,{\rm m/s}$ and penetrate the trunk a depth of $4.5\,{\rm cm}$. Find the average frictional forces that act on the bullet to stop it by applying work and energy considerations.

Solution : According to the work and energy theorem, $\Delta K=F_{net}d$, the work done on an object over a distance equals the change in kinetic energy. $F_{net}$ is the total forces that act on the object. 

When the bullet is inside the tree trunk, the frictional forces are the only forces that act on it. We call them $f$.  Applying the work-energy theorem and solving for $f$, we have \begin{align*} K_2-K_1&=fd\\\\ \frac 12 mv_2^2-\frac 12 mv_1^2 &=fd\\\\ 0-\frac 12 (0.055)(575)^2 &= f\times 4.5 \\\\ \Rightarrow \quad f&=4040\quad {\rm N}\end{align*}

Problem (12): A particle having mass $0.002\,\rm kg$ and charge $-4\,\rm \mu C$ moves from point $A$, where the electric potential is $V_A=+240\,\rm V$, to point $B$, where the electric potential is $+1200\,\rm V$. The particle has speed of $10\,\rm m/s$ at point $A$. What is the particle's speed at point $B$, assuming the only force driving the particle is the electric force?

Solution : This is related to the electric potential problems . According to the work-kinetic energy theorem, $W=\Delta K$, on the other hand, the work done on a charged particle to move it between two points with different potentials is $W=-q\Delta V$, where $\Delta V=V_2-V_1$. Combining these two expressions, we have \[\Delta K=-q\Delta V\] substituting the numerical values into the above expression and solving for the unknown speed $v_B$, we will have \begin{gather*} \frac 12 m(v_B^2-v_A^2)=-q(V_B-V_A) \\\\ \frac{(0.002)(v_B^2-10^2)}{2}=-(-4)(1200-240) \\\\ \Rightarrow \quad \boxed{v_B=1960\,\rm m/s} \end{gather*} 

Author: Dr. Ali Nemati Date Published : 9/23/2021  

© 2015 All rights reserved. by Physexams.com

Work Power Energy Exams and Problem Solutions

Work Power Energy Exam1 and Solutions

Work Power Energy Exam2 and Solutions

Work Power Energy Exam3 and Solutions

Switch language:

Solving wind’s dirty secret: innovating wind turbine blade disposal

With 800,000 tons of turbine blades disposed of in landfill annually, the wind industry has an environmental problem to solve.

• Share on Linkedin
• Share on Facebook

The disposal of wind turbine blades that have come to the end of their working lives is posing an environmental problem for an industry that is intended to help matters.

Made from fibreglass-reinforced polymer (FRP) and coated with epoxy resins, turbine blades are designed to maximise aerodynamicism whilst remaining light enough to minimise structural stress and stiff enough to achieve efficient wind capture.

Go deeper with GlobalData

Environment Sustainability in Power: Fiber-Reinforced Composite Tur...

Environment sustainability in power: floating platform wind turbines, premium insights.

The gold standard of business intelligence.

Find out more

However, the materials are problematic. Having been designed to withstand extreme weather conditions, epoxy resin is durable and therefore difficult to breakdown. The tough coating makes it near-impossible to separate the materials comprising a blade. Separating the fibres from the polymer using high temperatures results in the degradation of the plastic parts and damage to the glass fibres.

Over 317,000 onshore wind turbines are active globally, and there are another 12,000 active offshore, according to GlobalData figures. Since the first windfarm was erected in the US state of New Hampshire in 1980, over 12,600 turbines have been decommissioned. However, that number is set to grow rapidly as many near the end of their 20–30-year lifespan.

The EU’s Waste Framework Directive specifies that landfill is the “least preferred waste management option” and calls for prevention and preparation for re-use, recycling and recovery. With an estimated 800,000 tonnes of turbine blades entering landfill annually , though, there is a serious sustainability challenge to overcome.

Continuum: a mechanical solution

Although a problem for the industry, the issue of sustainable disposal of composite wind turbine blade waste has presented an opportunity for innovators. This includes Continuum, which works with machinery partner Dieffenbacher to convert fibreglass waste into construction materials.

How well do you really know your competitors?

Access the most comprehensive Company Profiles on the market, powered by GlobalData. Save hours of research. Gain competitive edge.

Your download email will arrive shortly

Not ready to buy yet? Download a free sample

We are confident about the unique quality of our Company Profiles. However, we want you to make the most beneficial decision for your business, so we offer a free sample that you can download by submitting the below form

Explaining the company’s approach to Power Technology , Martin Dronfield, CEO and interim chair of Continuum, says: “Using a 100% mechanical recycling process based around a complex series of machines, the ‘front end’ of the process mechanically strips back the end-of-life composite to small particles and constituent parts and the ‘back end’ of the process reconstructs the material with a new virgin resin and transforms it into high-performance, high-value construction panels used for building facades, concrete formwork, doors and floors and wet room wall materials.

“The panel has an CO 2 footprint of less than 70kg per tonne, whilst the Zero CO 2 emissions factory takes in 36,000 tonnes of end-of-life thermoset composite annually and produces 30,000m 3 of high-performance panelling, again annually.”

The company hopes to operate six factories across Europe by 2030, producing infinitely recyclable panels made of 92% recycled blades, with the other 8% comprised of resin. The process is powered by green electricity and produces no emissions, no waste liquids and emits no dust.

Vestas Wind Systems: a chemical solution

Vestas Wind Systems has opted for a different technique, announcing a “newly discovered chemical process” in February 2023. The method breaks down the blades to produce high quality materials, which can be repurposed to make new blades, potentially offering circularity to the industry.

In the announcement, Lisa Ekstrand, the company’s vice president and head of sustainability, said: “Once this new technology is implemented at scale, legacy blade material currently sitting in landfill, as well as blade material in active windfarms, can be disassembled and re-used. This signals a new era for the wind industry, and accelerates our journey towards achieving circularity.”

However, in a review of recycling technologies for FRP conducted in 2023, researchers pointed out that, while chemical processes “are more prone to industrial scalability thanks to the high volume of recycling material processed”, there remains an obstacle – namely “high energy consumption.”

Instead, the review favours mechanical processes for managing waste – such as those used by Continuum – noting that “among the recycling methods treated in this review, the mechanical ones, such as shredding, hammer milling, milling and grinding, are the more appreciable recycling processes to recover glass fibres.”

LM Wind Power: a preventative solution

Considering leaders in turbine blade disposal, GlobaData practice head Mohit Prasad highlights LM Wind Power as a company that “will play a central role in supporting their customers to develop fully circular wind turbines that generate less waste during their production.”

The firm addresses waste at the other end of a blade’s lifespan, aiming to eliminate waste during the manufacturing process. It reports that between 20-25% of materials purchased by wind turbine blade manufacturers are not used in the final product and notes: “Research indicates that blade manufacturing waste volumes are expected to be larger than decommissioned blade volumes in the coming decade.”

Indeed, previous estimates have found that “waste generated during manufacturing and service adds between 16% and 45% of the mass of the wind turbine blades.”

LM Wind Power is attempting to reduce this by manufacturing zero waste blades by 2030. It promises to create a circular economy by eliminating all waste – usually comprising 30% process materials (consumables, mixed with resin), 30% packaging, 15% dry glass fibre, 10% cut offs to composite materials and 15% other, it reports – from the manufacturing process and from packaging.

Polishing a clean industry

Prasad tells Power Technology that the wind turbine industry is already fairly clean, explaining: “85% to 95% of turbine’s materials are recycled. Masts, cables, gearboxes and generators are recycled and recovered. Foundations which are made of concrete are crushed to be used as filler. Nacelles and blades are generally made of fibreglass and are ground down to be used as fuel in cement factories or filler in road construction. Innovative solutions such as repurposing blades into playgrounds or bike sheds have been shown to be effective at a local level.”

However, local solutions are rapidly becoming inadequate. According to the Union of Concerned Scientists, the average blade size for an onshore wind turbine is around 164ft in length , while offshore turbines tend to be larger, with blade spans of up to 260-290ft in length . Repurposing these is not straightforward.

Yet, despite their massive size and landfill requirements, turbine blades are responsible for providing between 120,000 and 180,000 hours of electricity generation in their lifespans, making them a crucial part of the energy transition. Innovation at all stages of the lifecycle by companies such as Continuum, Vestas Wind Systems and LM Wind Power promises to clean up the sector’s waste challenge.

Sign up for our daily news round-up!

Give your business an edge with our leading industry insights.

More Relevant

Australia issues feasibility licences for six offshore wind farm projects

Us proposes 18gw offshore wind lease areas, siemens gamesa renewable energy gets grant for offshore wind turbine with hydrogen production capability, procter & gamble selected for offtake from swedish wind farm, sign up to the newsletter: in brief, your corporate email address, i would also like to subscribe to:.

Future Power Technology : Power Technology Focus (monthly)

Thematic Take (monthly)

I consent to Verdict Media Limited collecting my details provided via this form in accordance with Privacy Policy

Thank you for subscribing

View all newsletters from across the GlobalData Media network.

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Definition and Mathematics of Work
• Calculating the Amount of Work Done by Forces
• Potential Energy
• Kinetic Energy
• Mechanical Energy

Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation.

The standard metric unit of power is the Watt . As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second. For historical reasons, the horsepower is occasionally used to describe the power delivered by a machine. One horsepower is equivalent to approximately 750 Watts.

Ben's power rating is 871 Watts. He is quite a horse .

Another Formula for Power

The expression for power is work/time. And since the expression for work is force*displacement, the expression for power can be rewritten as (force*displacement)/time. Since the expression for velocity is displacement/time, the expression for power can be rewritten once more as force*velocity. This is shown below.

This new equation for power reveals that a powerful machine is both strong (big force) and fast (big velocity). A powerful car engine is strong and fast. A powerful piece of farm equipment is strong and fast. A powerful weightlifter is strong and fast. A powerful lineman on a football team is strong and fast. A machine that is strong enough to apply a big force to cause a displacement in a small mount of time (i.e., a big velocity) is a powerful machine.

Check Your Understanding

Use your understanding of work and power to answer the following questions. When finished, click the button to view the answers.

Ben and Will do the same amount of work. They apply the same force to lift the same barbell the same distance above their heads.

Yet, Ben is the most "power-full" since he does the same work in less time. Power and time are inversely proportional.

2. During a physics lab, Jack and Jill ran up a hill. Jack is twice as massive as Jill; yet Jill ascends the same distance in half the time. Who did the most work? ______________ Who delivered the most power? ______________ Explain your answers.

Jack does more work than Jill. Jack must apply twice the force to lift his twice-as-massive body up the same flight of stairs. Yet, Jill is just as "power-full" as Jack. Jill does one-half the work yet does it one-half the time. The reduction in work done is compensated for by the reduction in time.

 The tired squirrel does 0.50 Joule of work in 2.0 seconds. The power rating of this squirrel is found by

To raise her body upward at a constant speed, the student must apply a force which is equal to her weight (m•g). The work done to lift her body is

W = 102.9 J

The power is the work/time ratio which is (102.9 J) / (2 seconds) = 51.5 Watts (rounded)

5. Your household's monthly electric bill is often expressed in kilowatt-hours. One kilowatt-hour is the amount of energy delivered by the flow of l kilowatt of electricity for one hour. Use conversion factors to show how many joules of energy you get when you buy 1 kilowatt-hour of electricity.

Using conversion factors, it can be shown that 1 kilo-watt*hour is equivalent to 3.6 x 10 6 Joules . First, convert 1 kW-hr to 1000 Watt-hours. Then convert 1000 Watt-hours to 3.6 x 10 6 Watt-seconds. Since a Watt-second is equivalent to a Joule, you have found your answer.

6. An escalator is used to move 20 passengers every minute from the first floor of a department store to the second. The second floor is located 5.20 meters above the first floor. The average passenger's mass is 54.9 kg. Determine the power requirement of the escalator in order to move this number of passengers in this amount of time.

A good strategy would involve determining the work required to elevate one average passenger. Then multiply this value by 20 to determine the total work for elevating 20 passengers. Finally, the power can be determined by dividing this total work value by the time required to do the work. The solution goes as follows:

W 1 passenger = (54.9 kg • 9.8 m/s 2 ) • 5.20 m = 2798 J (rounded)

W 20 passengers = 55954 J (rounded)

P = W 20 passengers / time = (55954 J) / (60 s)

• Internal vs. External Forces