case study questions class 10 quadratic equation

• Bihar Board

GSEB SSC Result 2024

Srm university.

• TN Board Result 2024
• GSEB Board Result 2024
• Karnataka Board Result 2024
• CG Board Result 2024
• Kerala Board Result 2024
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 4 Quadratic Equations (Published by CBSE)

Cbse class 10 maths case study questions for chapter 4 - quadratic equations are released by the board. solve all these questions to perform well in your cbse class 10 maths exam 2021-22..

Check here the case study questions for CBSE Class 10 Maths Chapter 4 - Quadratic Equations. The board has published these questions to help class 10 students to understand the new format of questions. All the questions are provided with answers. Students must practice all the case study questions to prepare well for their Maths exam 2021-2022.

Case Study Questions for Class 10 Maths Chapter 4 - Quadratic Equations

CASE STUDY 1:

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400 km.

1. What will be the distance covered by Ajay’s car in two hours?

 a) 2(x + 5)km

b) (x – 5)km

c) 2(x + 10)km

d) (2x + 5)km

Answer: a) 2(x + 5)km

2. Which of the following quadratic equation describe the speed of Raj’s car?

a) x 2 – 5x – 500 = 0

b) x 2 + 4x – 400 = 0

c) x 2 + 5x – 500 = 0

d) x 2 – 4x + 400 = 0

Answer: c) x 2 + 5x – 500 = 0

3. What is the speed of Raj’s car?

a) 20 km/hour

b) 15 km/hour

c) 25 km/hour

d) 10 km/hour

Answer: a) 20 km/hour

4. How much time took Ajay to travel 400 km?

Answer: d) 16 hour

CASE STUDY 2:

The speed of a motor boat is 20 km/hr. For covering the distance of 15 km the boat took 1 hour more for upstream than downstream.

1. Let speed of the stream be x km/hr. then speed of the motorboat in upstream will be

a) 20 km/hr

b) (20 + x) km/hr

c) (20 – x) km/hr

Answer: c) (20 – x)km/hr

2. What is the relation between speed ,distance and time?

a) speed = (distance )/time

b) distance = (speed )/time

c) time = speed x distance

d) speed = distance x time

Answer: b) distance = (speed )/time

3. Which is the correct quadratic equation for the speed of the current?

a) x 2 + 30x − 200 = 0

b) x 2 + 20x − 400 = 0

c) x 2 + 30x − 400 = 0

d) x 2 − 20x − 400 = 0

Answer: c) x 2 + 30x − 400 = 0

4. What is the speed of current ?

b) 10 km/hour

c) 15 km/hour

d) 25 km/hour

Answer: b) 10 km/hour

5. How much time boat took in downstream?

a) 90 minute

b) 15 minute

c) 30 minute

d) 45 minute

Answer: d) 45 minute

Also Check:

CBSE Case Study Questions for Class 10 Maths - All Chapters

Tips to Solve Case Study Based Questions Accurately

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• gseb.org SSC Result 2024
• 10th Result 2024 Gujarat Board
• GSEB SSC 10th Result 2024
• GSEB 10th Result 2024
• GSEB SSC Toppers List 2024
• 10th Public Exam Result 2024 Tamil Nadu
• DHSE Kerala Plus Two Result 2024
• CGBSE 10th Result 2024
• CGBSE 12th Result 2024
• NDA Result 2024
• CBSE Study Material
• CBSE Class 10

Latest Education News

IIT Roorkee B. Tech Cut-Offs Dipped After Pandemic, Check Past Year Cut-Offs Here

RBSE Result 2024: Rajasthan Board Class 10, 12 Result Date And Time At rajresults.nic.in

RBSE 12th Commerce Result 2024: Rajasthan Board Class 12 Commerce Result Date And Time At rajresults.nic.in

RBSE 12th Science Result 2024: Rajasthan Board Class 12 Science Result Date And Time At rajresults.nic.in

RBSE 12th Art Result 2024: Rajasthan Board Class 12 Art Result Date And Time At rajresults.nic.in

RBSE 12th Result 2024: Rajasthan Board Class 12 Result Date And Time At rajresults.nic.in

RBSE 10th Result 2024: Rajasthan Board Class 10 Result Date And Time At rajresults.nic.in

IPL 2024 Playoffs Teams: ये है प्लेऑफ़ की प्रबल दावेदार, KKR Qualify करने वाली पहली टीम बनी

Weekly Current Affairs Questions and Answers: 06 May to 12 May 2024

Weekly Current Affairs Quiz Hindi: 06 मई से 12 मई 2024

[Today] IPL 2024 Points Table: Team Rankings and Net Run Rate

Orange Cap in IPL 2024: Top Players List with Most Runs in TATA IPL

Today’s School News Assembly Headlines (13 May):  Election 2024, Rafael Mada, HBSE Results 2024, IPL and Other News in English

Mother’s Day Speech in Hindi 2024: मदर्स डे पर छोटे और बड़े भाषण हिंदी में

Find 3 differences between the pictures of a lion on a scooter in 11 seconds!

COMEDK UGET 2024 Exam Today In 3 Shifts, Check Required Documents Here

IPL Playoffs 2024: Teams Scenario, Qualifier, Eliminator Rules, Venues and Other Details

Mother’s Day 2024: Top 11 Fun Facts You Need to Know and Share

Top 10 Weekly Current Affairs in Hindi: 06 मई से 12 मई 2024

IPL Final 2024: Date, Stadium, Venue, Tickets Price and How to Book Ticket Online

CBSE Expert

Class 10 Maths: Case Study Questions of Chapter 4 Quadratic Equations PDF

Case study Questions on the Class 10 Mathematics Chapter 4  are very important to solve for your exam. Class 10 Maths Chapter 4 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 4 Quadratic Equations

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on  Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Quadratic Equations Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 10 Maths  Chapter 4 Quadratic Equations

Case Study/Passage Based Questions

1)Formation of Quadratic Equation

Quadratic equations started around 3000 B.C. with the Babylonians. They were one of the world’s first civilizations and came up with some great ideas like agriculture, irrigation, and writing. There were many reasons why Babylonians needed to solve quadratic equations. For example to know what amount of crop you can grow on the square field. Now represent the following situations in the form of a quadratic equation.

The sum of squares of two consecutive integers is 650. (a) x 2 + 2x – 650 = 0 (b) 2x 2 +2x – 649 = 0 (c) x 2 – 2x – 650 = 0 (d) 2x 2 + 6x – 550 = 0

Answer: (b) 2×2 +2x – 649 = 0

The sum of two numbers is 15 and the sum of their reciprocals is 3/10. (a) x 2 + 10x – 150 = 0 (b) 15x 2 – x + 150 = 0 (c) x 2 – 15x + 50 = 0 (d) 3x 2 – 10x + 15 = 0

Answer: (c) x2 – 15x + 50 = 0

Two numbers differ by 3 and their product is 504. (a) 3x 2 – 504 = 0 (b) x 2 – 504x + 3 = 0 (c) 504x 2 +3 = x (d) x 2 + 3x – 504 = 0

Answer: (d) x2 + 3x – 504 = 0

A natural number whose square diminished by 84 is thrice of 8 more of a given number. (a) x 2 + 8x – 84 = 0 (b) 3x 2 – 84x + 3 = 0 (c) x 2 – 3x – 108 = 0 (d) x 2 –11x + 60 = 0

Answer: (c) x2 – 3x – 108 = 0

A natural number when increased by 12, equals 160 times its reciprocal. (a) x 2 – 12x + 160 = 0 (b) x 2 – 160x + 12 = 0 (c) 12x 2 – x – 160 = 0 (d) x 2 + 12x – 160 = 0

Answer: (d) x2 + 12x – 160 = 0

2)Nature of Roots A quadratic equation can be defined as an equation of degree 2. This means that the highest exponent of the polynomial in it is 2. The standard form of a quadratic equation is ax 2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. Every quadratic equation has two roots depending on the nature of its discriminant, D = b 2 – 4ac

Which of the following quadratic equation have no real roots? (a) –4x 2 + 7x – 4 = 0 (b) –4x 2 + 7x – 2 = 0 (c) –2x 2 +5x – 2 = 0 (d) 3x 2 + 6x + 2 = 0

Answer: (a) –4×2 + 7x – 4 = 0

Which of the following quadratic equation have rational roots? (a) x 2 + x – 1 = 0 (b) x 2 – 5x + 6 = 0 (c) 4x 2 – 3x – 2 = 0 (d) 6x 2 – x + 11 = 0

Answer: (b) x2 – 5x + 6 = 0

Which of the following quadratic equation have irrational roots? (a) 3x 2 +2x + 2 = 0 (b) 4x 2 – 7x + 3 = 0 (c) 6x 2 – 3x – 5 = 0 (d) 2x 2 +3x – 2 = 0

Answer: (c) 6×2 – 3x – 5 = 0

Which of the following quadratic equations have equal roots? (a) x 2 – 3x + 4 = 0 (b) 2x 2 – 2x + 1 = 0 (c) 5x 2 – 10x + 1 = 0 (d) 9x 2 + 6x + 1 = 0

Answer: (d) 9×2 + 6x + 1 = 0

Which of the following quadratic equations has two distinct real roots? (a) x 2 + 3x + 1 = 0 (b) –x 2 + 3x – 3 = 0 (c) 4x 2 + 8x + 4 = 0 (d) 3x 2 + 6x + 4 = 0

Answer: (a) x2 + 3x + 1 = 0

Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 4 Quadratic Equations with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 10 Maths Quadratic Equations Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

• Book Solutions
• State Boards

Case Study Questions Class 10 Maths Quadratic Equations

Case study questions class 10 maths chapter 4 quadratic equations.

CBSE Class 10 Case Study Questions Maths Quadratic Equations. Term 2 Important Case Study Questions for Class 10 Board Exam Students. Here we have arranged some Important Case Base Questions for students who are searching for Paragraph Based Questions Quadratic Equations.

At Case Study Questions there will given a Paragraph. In where some Important Questions will made on that respective Case Based Study. There will various types of marks will given 1 marks, 2 marks, 3 marks, 4 marks.

CBSE Case Study Questions Class 10 Maths Quadratic Equations

CASE STUDY 1:

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 hours more than Ajay to complete the journey of 400 km.

[ CBSE Question Bank ]

4.) How much time took Ajay to travel 400 km?

Answer – d) 16 hour

1.) What will be the distance covered by Ajay’s car in two hours?

a) 2(x +5)km

b) (x – 5)km

c) 2(x + 10)km

d) (2x + 5)km

Answer – a) 2(x +5) km

3.) What is the speed of Raj’s car?

a) 20 km/hour

b) 15 km/hour

c) 25 km/hour

d) 10 km/hour

Answer – a) 20 km/hour

CASE STUDY 2 –

Q.2) Nidhi and Riya are very close friends. Nidhi’s parents have a Maruti Alto. Riya ‘s parents have a Toyota. Both the families decided to go for a picnic to Somnath Temple in Gujarat by their own car. Nidhi’s car travels x km/h, while Riya’s car travels 5km/h more than Nidhi’s car. Nidhi’s car took 4 hours more than Riya’s car in covering 400 km.

[ KVS Raipur 2021 – 22 ]

(i) What will be the distance covered by Riya’s car in two hours? How much time took Riya to travel 400 km?

Answer- 2(x+5)km

(ii) Write the quadratic equation describe the speed of Nidhi’s car. What is the speed of Nidhi’s car?

Answer –  x 2 +5x -500= 0

We hope that above case study questions will help you for your upcoming exams. To see more click below – 

• CBSE Class 10 Maths (standard)
• CBSE Class 10 Maths (Basic)

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

We have a strong team of experienced Teachers who are here to solve all your exam preparation doubts

Essay on culture as the unifying force for the modern world, rs aggarwal class 5 solutions chapter 3, dav class 6 sst solution chapter 21 our community life, unity in diversity, dav class 6 sst solution chapter 23 our rural governance.

Sign in to your account

Username or Email Address

Remember Me

CBSE Case Study Questions for Class 10 Maths Quadratic Equation Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 10 Maths Quadratic Equation  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 10 Maths Quadratic Equation PDF

Checkout our case study questions for other chapters.

• Chapter 2: Polynomials Case Study Questions
• Chapter 3: Pair of Linear Equations in Two Variables Case Study Questions
• Chapter 5: Arithmetic Progressions Case Study Questions
• Chapter 6: Triangles Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Privacy Policy

• Neet Online Test Pack

12th Standard stateboard question papers & Study material

தமிழ் subjects.

கணினி பயன்பாடுகள்

கணினி அறிவியல்

வணிகக் கணிதம் மற்றும் புள்ளியியல்.

கணினி தொழில்நுட்பம்

கணக்குப்பதிவியல்

English Subjects

Computer Science

Business Maths and Statistics

Accountancy

Computer Applications

Computer Technology

11th Standard stateboard question papers & Study material

9th Standard stateboard question papers & Study material

Social Science

சமூக அறிவியல்

6th standard stateboard question papers & study material.

10th Standard stateboard question papers & Study material

7th Standard stateboard question papers & Study material

8th Standard stateboard question papers & Study material

கணிதம் - old

12th Standard CBSE Subject Question Paper & Study Material

Introductory Micro and Macroeconomics

Business Studies

Indian Society

Physical Education

Bio Technology

Engineering Graphics

Entrepreneurship

Hindi Elective

Home Science

Legal Studies

Political Science

11th Standard CBSE Subject Question Paper & Study Material

Mathematics

Enterprenership

Applied Mathematics

10th standard cbse subject question paper & study material.

9th Standard CBSE Subject Question Paper & Study Material

8th Standard CBSE Subject Question Paper & Study Material

7th Standard CBSE Subject Question Paper & Study Material

6th Standard CBSE Subject Question Paper & Study Material

School Exams

Tamil Nadu State Board Exams

Scholarship Exams

Study Materials , News and Scholarships

Stateboard Tamil Nadu

Free Online Tests

Educational News

Scholarships

Entrance Exams India

Video Materials

10th Standard CBSE

CBSE 10th Standard Maths Subject Quadratic Equations Case Study Questions 2021

CBSE 10th Standard Maths Subject Quadratic Equations Case Study Questions 2021 QB365 - Question Bank Software May-21 , 2021

QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get  more marks in Exams

A PHP Error was encountered

Severity: Warning

Message: in_array() expects parameter 2 to be array, null given

Filename: material/details.php

Line Number: 1436

Message: Use of undefined constant EXAM - assumed 'EXAM' (this will throw an Error in a future version of PHP)

Line Number: 1438

QB365 - Question Bank Software

Final Semester - June 2015

Case Study Questions

A quadratic equation can be defined as an equation of degree 2. This means that the highest exponent of the polynomial in it is 2. The standard form of a quadratic equation is ax 2 + bx + c = 0, where a, b, and c are real numbers and  \(a \neq 0\)   Every quadratic equation has two roots depending on the nature of its discriminant, D = b2 - 4ac.Based on the above information, answer the following questions. (i) Which of the following quadratic equation have no real roots?

(ii) Which of the following quadratic equation have rational roots?

(iii) Which of the following quadratic equation have irrational roots?

(iv) Which of the following quadratic equations have equal roots?

(v) Which of the following quadratic equations has two distinct real roots?

In our daily life we use quadratic formula as for calculating areas, determining a product's profit or formulating the speed of an object and many more. Based on the above information, answer the following questions. (i) If the roots of the quadratic equation are 2, -3, then its equation is

(ii) If one root of the quadratic equation 2x 2 + kx + 1 = 0 is -1/2, then k =

(iii) Which of the following quadratic equations, has equal and opposite roots?

(iv) Which of the following quadratic equations can be represented as (x - 2) 2 + 19 = 0?

(v) If one root of a qua drraattiic equation is  \(\frac{1+\sqrt{5}}{7}\) , then I.ts other root is

Quadratic equations started around 3000 B.C. with the Babylonians. They were one of the world's first civilisation, and came up with some great ideas like agriculture, irrigation and writing. There were many reasons why Babylonians needed to solve quadratic equations. For example to know what amount of crop you can grow on the square field; Based on the above information, represent the following questions in the form of quadratic equation. (i) The sum of squares of two consecutive integers is 650.

(ii) The sum of two numbers is 15 and the sum of their reciprocals is 3/10.

(iii) Two numbers differ by 3 and their product is 504.

(iv) A natural number whose square diminished by 84 is thrice of 8 more of given number.

(v) A natural number when increased by 12, equals 160 times its reciprocal.

Amit is preparing for his upcoming semester exam. For this, he has to practice the chapter of Quadratic Equations. So he started with factorization method. Let two linear factors of  \(a x^{2}+b x+c \text { be }(p x+q) \text { and }(r x+s)\) \(\therefore a x^{2}+b x+c=(p x+q)(r x+s)=p r x^{2}+(p s+q r) x+q s .\) Now, factorize each of the following quadratic equations and find the roots. (i) 6x 2 + x - 2 = 0

(ii) 2x 2 -+ x - 300 = 0

(iii) x 2 -  8x + 16 = 0

(iv) 6x 2 -  13x + 5 = 0

(v) 100x 2 - 20x + 1 = 0

If p(x) is a quadratic polynomial i.e., p(x) = ax 2 - + bx + c, \(a \neq 0\) , then p(x) = 0 is called a quadratic equation. Now, answer the following questions. (i) Which of the following is correct about the quadratic equation ax 2 - + bx + c = 0 ?

(ii) The degree of a quadratic equation is

(iii) Which of the following is a quadratic equation?

(iv) Which of the following is incorrect about the quadratic equation ax 2 - + bx + c = 0 ?

(v) Which of the following is not a method of finding solutions of the given quadratic equation?

*****************************************

• Previous CBSE 10th Maths Probability Chapter Case Study Question with Answers
• Next CBSE 10th Maths Statistics Chapter Case Study Question with Answers

10th Standard CBSE Maths free Online practice tests

Circles - practice test 1.

10 Questions

Arithmetic Progressions - Practice Test 1

Quadratic equations - practice test 1, reviews & comments about cbse 10th standard maths subject quadratic equations case study questions 2021.

Write your Comment

10th Standard CBSE Maths Videos

CBSE 10th Maths Sample Model Question Paper with Answer Key 2023

10th Standard CBSE Maths Usefull Links

• 10th Standard

Other 10th Standard CBSE Subjects

Other 10th Standard CBSE Maths Study material

Cbse 10th maths probability chapter case study question with answers click to view, cbse 10th maths statistics chapter case study question with answers click to view, cbse 10th maths surface areas and volumes ... click to view, cbse 10th maths areas related to circles ... click to view, cbse 10th maths circles chapter case study question with answers click to view, cbse 10th maths some applications of trigonometry ... click to view, cbse 10th maths introduction to trigonometry chapter ... click to view, cbse 10th maths coordinate geometry chapter case study question with answers click to view, cbse 10th maths triangles chapter case study question with answers click to view, cbse 10th maths arithmetic progressions chapter case ... click to view, cbse 10th maths quadratic equations chapter case study questions with answers click to view, cbse 10th maths pair of linear equation ... click to view, cbse 10th maths polynomials case study question & answers click to view, cbse 10th maths real numbers case study question & answers click to view, 10th maths model question paper 2023 click to view, register & get the solution for cbse 10th standard maths subject quadratic equations case study questions 2021.

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 10 Maths Chapter 4 Quadratic Equations

• Last modified on: 10 months ago
• Reading Time: 4 Minutes

Question 1:

Raj and Ajay are very close friends. Both the families decide to go to Ranikhet by their own cars. Raj’s car travels at a speed of x km/h while Ajay’s car travels 5 km/h faster than Raj’s car. Raj took 4 h more than Ajay to complete the journey of 400 km.

(i) What will be the distance covered by Ajay’s car in two hours? (a) 2 (x + 5) km (b) (x – 5) km (c) 2 (x + 10) km (d) (2x + 5) km

(ii) Which of the following quadratic equation describe the speed of Raj’s car? (a) x 2 − 5x − 500 = 0 (b) x 2 + 4x − 400 = 0 (c) x 2 + 5x − 500 = 0 (d) x 2 − 4x + 400 = 0

(iii) What is the speed of Raj’s car? (a) 20 km/h (b) 15 km/h (c) 25 km/h (d) 10 km/h

(iv) How much time took Ajay to travel 400 km? (a) 20 h (b) 40 h (c) 25 h (d) 16 h

(v) How much time took Raj to travel 400 km? (a) 15 h (b) 20 h (c) 18 h (d) 22 h

✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths

You may also like:

Chapter 1 Real Numbers Chapter 2 Polynomials Chapter 3 Pair of Linear Equations in Two Variables C hapter 4 Quadratic Equations Chapter 5 Arithmetic Progressions Chapter 6 Triangles Chapter 7 Coordinate Geometry Chapter 8 Introduction to Trigonometry Chapter 9 Some Applications of Trigonometry Chapter 10 Circles Chapter 11 Constructions Chapter 12 Areas Related to Circles Chapter 13 Surface Areas and Volumes Chapter 14 Statistics Chapter 15 Probability

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 4 Class 10 Quadratic Equations

Click on any of the links below to start learning from Teachoo ...

Updated for Latest NCERT for 2023-2024 Boards.

Get NCERT Solutions for all exercise questions and examples of Chapter 4 Class 10 Quadratic Equations free at Teachoo. Answers to each and every question is provided video solutions. 

In this chapter, we will learn

• What is a Quadratic Equation
• What is the Standard Form of a Quadratic Equation
• Solution of a Quadratic Equation by Factorisation ( Splitting the Middle Term method)
• Solving a Quadratic Equation by Completing the Square
• Solving a Quadratic Equation using D Formula (x = -b ± √b 2 - 4ac / 2a)
• Checking if roots are real, equal or no real roots (By Checking the value of D = b 2 - 4ac)

This chapter is divided into two parts - Serial Order Wise, Concept Wise

In Serial Order Wise, the chapter is divided into exercise questions and examples.

In Concept Wise, the chapter is divided into concepts. First the concepts are explained, and then the questions of the topic are solved - from easy to difficult.

We suggest you do the Chapter from Concept Wise - it is the Teachoo (टीचू) way of learning.

Note: When you click on a link, the first question of the exercise will open. To open other question of the exercise, go to bottom of the page. There is a list with arrows. It has all the questions with Important Questions also marked.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

Case Based Questions Test: Quadratic Equations - Class 10 MCQ

15 questions mcq test - case based questions test: quadratic equations, read the following text and answer the following questions on the basis of the same: nidhi and ria are very close friends. nidhi’s parents own a maruti alto and ria’s parents own a toyota liva. both the families decided to go for picnic to somnath temple in gujarat by their own cars. nidhi car travels x km/h when ria’s car travels 5 km/h more than nidhi’s car nidhi’s car took 4 hours more than ria’s car in covering 400 km. q. which of the following quadratic equations describe the speed of nidhi’s car.

x 2 – 5x – 500 = 0

x 2 + 4x – 400 = 0

x 2 + 5x – 500 = 0

x 2 – 4x + 400 = 0

Let Speed of Nidhi = x km/h

Time taken = t + 4 km/h

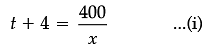
Speed of Ria = (x + 5) km/h

Time taken = t hour

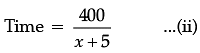
According to the question,

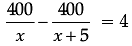
⇒ x 2 + 5x – 500 = 0

Read the following text and answer the following questions on the basis of the same: Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km. Q. How much time took Ria to travel 400 km?

⇒ x 2 + 25x – 20x – 500 = 0

⇒ x (x + 25) – 20 (x + 25) = 0

⇒ (x + 25)(x – 20) = 0 ⇒ x = – 25 (Rejected) and 20. So, x = 20 (Nidhi speed) now, 

Ria’s speed = 20 + 5 = 25 km/h

Distance = 400 km

Time = D/S = 400/25 = 16 hour

Read the following text and answer the following questions on the basis of the same: Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km. Q. What will be the distance covered by Ria’s car in two hours?

• A. 2 (x + 5) km
• B. x – 5 km
• C. 2 (x + 10) km
• D. (2x + 5)

= (x + 5) × 2 = 2(x + 5) km

Read the following text and answer the following questions on the basis of the same:

Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.

Q. What is the speed of Nidhi’s car?

⇒ (x + 25)(x – 20) = 0 ⇒ x = – 25 (Rejected) and 20

Nidhi and Ria are very close friends. Nidhi’s parents own a Maruti Alto and Ria’s parents own a Toyota Liva. Both the families decided to go for picnic to Somnath temple in Gujarat by their own cars. Nidhi car travels x km/h when Ria’s car travels 5 km/h more than Nidhi’s car Nidhi’s car took 4 hours more than Ria’s car in covering 400 km.

• D. Parabola

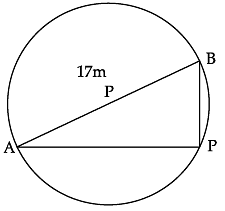
Aniket is studying in X standard. He is created a pole at on the boundary of a circular park of diameter 17 m in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7m.

x 2 + 15x – 8x – 120 = 0

x (x + 15) – 8 (x + 15) = 0

x = 8 and x = – 15 (rejected)

Q. What is the length of (AP + BP)?

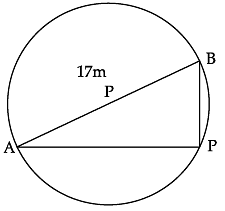
• A. x 2 + 7x – 120 = 0
• B. x 2 + 5x – 120 = 0
• C. x 2 + 7x – 120 = 0
• D. None of these

Therefore, AP = x + 7 m Now, AB = 17 m and since AB is a diameter.

Apply Pythagoras theorem,

AB 2 = AP 2 + BP 2

172 = (x + 7) 2 + x 2

289 = x 2 + 49 + 14x + x 2

x 2 + 7x – 120 = 0

A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.

Q. Represent the above equation in quadratic equation.

• A. 3x 2 + 2x + 85
• B. 3x 2 – 2x + 85
• C. 3x 2 + 2x – 85
• D. – 3x 2 + 2x + 85

3x 2 + 2x – 85

Q. Number of workers working in the industry:

x(2 + 3x) = 85

⇒ 3x 2 + 2x – 85 = 0

⇒ 3x 2 + 17x – 15x – 85 = 0

⇒ x(3x + 17) – 5(3x + 17) = 0 ⇒

⇒ (3x + 17)(x – 5) = 0

Q. If the number of workers working in the industry is x. What was the number of boxes of candles prepared by each worker on that particular day?

• C. 2(x + 3)

Q. Nature of roots of the above quadratic equation are:

• A. Real and Equal
• C. Real and Unequal

Q. How many boxes will be prepared when number of workers are increased by 2.

Number of workers when increased by 2 = x + 2

∴ Number of boxes prepared by the workers

(x + 2) = (x + 3) [2 + 3 (x + 2)

= 7 [2 + 3 × 7] [∵ x = 5]

Top Courses for Class 10

Related Content

Important Questions for Case Based Questions Test: Quadratic Equations

Case based questions test: quadratic equations mcqs with answers, online tests for case based questions test: quadratic equations, welcome back, create your account for free.

Forgot Password

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Quadratic equations

Solving equations by factorising.

• Solving quadratics by factoring: leading coefficient ≠ 1 (Opens a modal)
• Solving quadratics using structure (Opens a modal)
• Quadratics by factoring Get 3 of 4 questions to level up!
• Quadratic equations with irrational and variable coefficients Get 3 of 4 questions to level up!
• Solve equations using structure Get 3 of 4 questions to level up!

Solving equations by completing the square

• Worked example: Rewriting & solving equations by completing the square (Opens a modal)
• Worked example: completing the square (leading coefficient ≠ 1) (Opens a modal)
• Completing the square (intermediate) Get 3 of 4 questions to level up!
• Completing the square Get 3 of 4 questions to level up!

Solving equations using the quadratic formula

• The quadratic formula (Opens a modal)
• Worked example: quadratic formula (negative coefficients) (Opens a modal)
• Proof of the quadratic formula (Opens a modal)
• Quadratic formula Get 3 of 4 questions to level up!
• Equations reducible to quadratic equations (intermediate) Get 3 of 4 questions to level up!
• Equations reducible to quadratic equations (advanced) Get 3 of 4 questions to level up!

Nature of roots

• Using the quadratic formula: number of solutions (Opens a modal)
• Discriminant for types of solutions for a quadratic (Opens a modal)
• Number of solutions of quadratic equations Get 3 of 4 questions to level up!
• Equations with equal roots (intermediate) Get 3 of 4 questions to level up!
• Equations with equal roots (advanced) Get 3 of 4 questions to level up!
• Finding nature of roots Get 3 of 4 questions to level up!

Quadratic equations word problems

• Quadratic equations word problem: triangle dimensions (Opens a modal)
• Quadratic equations word problem: box dimensions (Opens a modal)
• Quadratic word problem: ball (Opens a modal)
• Word problems: Writing quadratic equations Get 3 of 4 questions to level up!
• Word problems: Solving quadratic equations Get 3 of 4 questions to level up!
• Quadratic equations word problems (basic) Get 3 of 4 questions to level up!
• Quadratic equations word problems (intermediate) Get 3 of 4 questions to level up!
• Quadratic equations word problems (advanced) Get 3 of 4 questions to level up!

• Class 10 Maths MCQs
• Chapter 4 Quadratic Equations

Class 10 Maths Chapter 4 Quadratic Equations MCQs

Class 10 Maths MCQs for Chapter 4 (Quadratic Equations) are available online here with answers. All these objective questions are prepared as per the latest CBSE syllabus (2022 – 2023) and NCERT guidelines. MCQs for Class 10 Maths Chapter 4 are prepared according to the new exam pattern. Solving these multiple-choice questions will help students to score good marks in the board exams, which they can verify with the help of detailed explanations given here. To get chapter-wise MCQs, click here . Also, find the PDF of MCQs to download here for free.

Class 10 Maths MCQs for Quadratic Equations

CBSE board has released the datasheet for the Class 10 Maths exam. It is advised for students to start revising the chapters, for the exam. Here, we have given multiple-choice questions for Chapter 4 quadratic equations, to help students to solve different types of questions, which could appear in the board exam. They can build their problem-solving capacity and boost their confidence level by practising the questions here. Get important questions for class 10 Maths here at BYJU’S.

Click here to download the PDF of additional MCQs for Practice on Quadratic equations, Chapter of Class 10 Maths along with answer key:

Download PDF

Students can also get access to Quadratic equations Class 10 Notes here.

Below are the MCQs for Quadratic Equations

1. Equation of (x+1) 2 -x 2 =0 has number of real roots equal to:

Answer: (a) 1

Explanation: (x+1) 2 -x 2 =0

X 2 +2x+1-x 2 = 0

Hence, there is one real root.

2. The roots of 100x 2 – 20x + 1 = 0 is:

(a) 1/20 and 1/20

(b) 1/10 and 1/20

(c) 1/10 and 1/10

(d) None of the above

Answer: (c) 1/10 and 1/10

Explanation: Given, 100x 2 – 20x + 1=0

100x 2 – 10x – 10x + 1 = 0

10x(10x – 1) -1(10x – 1) = 0

(10x – 1) 2 = 0

∴ (10x – 1) = 0 or (10x – 1) = 0

⇒x = 1/10 or x = 1/10

3. The sum of two numbers is 27 and product is 182. The numbers are:

(a) 12 and 13

(b) 13 and 14

(c) 12 and 15

(d) 13 and 24

Answer: (b) 13 and 14

Explanation: Let x is one number

Another number = 27 – x

Product of two numbers = 182

x(27 – x) = 182

⇒ x 2 – 27x – 182 = 0

⇒ x 2 – 13x – 14x + 182 = 0

⇒ x(x – 13) -14(x – 13) = 0

⇒ (x – 13)(x -14) = 0

⇒ x = 13 or x = 14

4. If ½ is a root of the quadratic equation x 2 -mx-5/4=0, then value of m is:

Answer: (b) -2

Explanation: Given x=½ as root of equation x 2 -mx-5/4=0.

(½) 2 – m(½) – 5/4 = 0

¼-m/2-5/4=0

5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, the other two sides of the triangle are equal to:

(a) Base=10cm and Altitude=5cm

(b) Base=12cm and Altitude=5cm

(c) Base=14cm and Altitude=10cm

(d) Base=12cm and Altitude=10cm

Answer: (b) Base=12cm and Altitude=5cm

Explanation: Let the base be x cm.

Altitude = (x – 7) cm

In a right triangle,

Base 2 + Altitude 2 = Hypotenuse 2 (From Pythagoras theorem)

∴ x 2 + (x – 7) 2 = 13 2

By solving the above equation, we get;

⇒ x = 12 or x = – 5

Since the side of the triangle cannot be negative.

Therefore, base = 12cm and altitude = 12-7 = 5cm

6. The roots of quadratic equation 2x 2 + x + 4 = 0 are:

(a) Positive and negative

(b) Both Positive

(c) Both Negative

(d) No real roots

Answer: (d) No real roots

Explanation: 2x 2 + x + 4 = 0

⇒ 2x 2 + x = -4

Dividing the equation by 2, we get

⇒ x 2 + 1/2x = -2

⇒ x 2 + 2 × x × 1/4 = -2

By adding (1/4) 2 to both sides of the equation, we get

⇒ (x) 2 + 2 × x × 1/4 + (1/4) 2 = (1/4) 2 – 2

⇒ (x + 1/4) 2 = 1/16 – 2

⇒ (x + 1/4)2 = -31/16

The square root of negative number is imaginary, therefore, there is no real root for the given equation.

Answer: (b) 3

Explanation:

Hence, we can write, √(6+x) = x

x 2 -3x+2x-6=0

x(x-3)+2(x-3)=0

(x+2) (x-3) = 0

Since, x cannot be negative, therefore, x=3

8. The sum of the reciprocals of Rehman’s ages 3 years ago and 5 years from now is 1/3. The present age of Rehman is:

Answer: (a) 7

Explanation: Let, x is the present age of Rehman

Three years ago his age = x – 3

Five years later his age = x + 5

Given, the sum of the reciprocals of Rehman’s ages 3 years ago and after 5 years is equal to 1/3.

∴ 1/x-3 + 1/x-5 = 1/3

(x+5+x-3)/(x-3)(x+5) = 1/3

(2x+2)/(x-3)(x+5) = 1/3

⇒ 3(2x + 2) = (x-3)(x+5)

⇒ 6x + 6 = x 2 + 2x – 15

⇒ x 2 – 4x – 21 = 0

⇒ x 2 – 7x + 3x – 21 = 0

⇒ x(x – 7) + 3(x – 7) = 0

⇒ (x – 7)(x + 3) = 0

⇒ x = 7, -3

We know age cannot be negative, hence the answer is 7.

9. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

(a) 30 km/hr

(b) 40 km/hr

(c) 50 km/hr

(d) 60 km/hr

Answer: (b) 40 km/hr

Explanation: Let x km/hr be the speed of train.

Time required to cover 360 km = 360/x hr.

As per the question given,

⇒ (x + 5)(360-1/x) = 360

⇒ 360 – x + 1800-5/x = 360

⇒ x 2 + 5x + 10x – 1800 = 0

⇒ x(x + 45) -40(x + 45) = 0

⇒ (x + 45)(x – 40) = 0

⇒ x = 40, -45

Negative value is not considered for speed hence the answer is 40km/hr.

10. If one root of equation 4x 2 -2x+k-4=0 is reciprocal of the other. The value of k is:

Answer: (b) 8

Explanation: If one root is reciprocal of others, then the product of roots will be:

α x 1/α = (k-4)/4

11. Which one of the following is not a quadratic equation?

(a) (x + 2) 2  = 2(x + 3) 

(b) x 2  + 3x = (–1) (1 – 3x) 2

(c) (x + 2) (x – 1) = x 2  – 2x – 3 

(d) x 3  – x 2  + 2x + 1 = (x + 1) 3

Answer: (c) (x + 2) (x – 1) = x 2  – 2x – 3 

We know that the degree of a quadratic equation is 2.

By verifying the options,

x 2  + 4x + 4 = 2x + 6

x 2  + 2x – 2 = 0

This is a quadratic equation.

x 2  + 3x = -1(1 + 9x 2  – 6x)

x 2  + 3x + 1 + 9x 2  – 6x = 0

10x 2  – 3x + 1 = 0

x 2  + x – 2 = x 2  – 2x – 3

x 2  + x – 2 – x 2  + 2x + 3 = 0

This is not a quadratic equation.

12. Which of the following equations has 2 as a root?

(a) x 2  – 4x + 5 = 0 

(b) x 2  + 3x – 12 = 0

(c) 2x 2  – 7x + 6 = 0 

(d) 3x 2  – 6x – 2 = 0

Answer: (c) 2x 2  – 7x + 6 = 0 

If 2 is a root then substituting the value 2 in place of x should satisfy the equation.

Let us verify the given options.

(a) x 2  – 4x + 5 = 0

(2) 2  – 4(2) + 5 = 1 ≠ 0

So, x = 2 is not a root of x 2  – 4x + 5 = 0

(2) 2  + 3(2) – 12 = -2 ≠ 0

So, x = 2 is not a root of x 2  + 3x – 12 = 0

(c) 2x 2  – 7x + 6 = 0

2(2) 2  – 7(2) + 6 = 0

Here, x = 2 is a root of 2x 2  – 7x + 6 = 0

13. A quadratic equation ax 2  + bx + c = 0 has no real roots, if

(a) b 2  – 4ac > 0

(b) b 2  – 4ac = 0

(c) b 2  – 4ac < 0

(d) b 2  – ac < 0

Answer: (c) b 2  – 4ac < 0

A quadratic equation ax 2  + bx + c = 0 has no real roots, if b 2  – 4ac < 0. That means, the quadratic equation contains imaginary roots.

14. The product of two consecutive positive integers is 360. To find the integers, this can be represented in the form of quadratic equation as

(a) x 2  + x + 360 = 0

(b) x 2  + x – 360 = 0

(c) 2x 2  + x – 360

(d) x 2  – 2x – 360 = 0

Answer: (b) x 2  + x – 360 = 0

Let x and (x + 1) be the two consecutive integers.

According to the given,

x(x + 1) = 360

x 2  + x = 360

x 2  + x – 360

15. The equation which has the sum of its roots as 3 is

(a) 2x 2  – 3x + 6 = 0 

(b) –x 2  + 3x – 3 = 0

(c) √2x 2  – 3/√2x + 1 = 0 

(d) 3x 2  – 3x + 3 = 0

Answer: (b) –x 2  + 3x – 3 = 0

The sum of the roots of a quadratic equation ax 2  + bx + c = 0, a ≠ 0 is given by,

Coefficient of x / coefficient of x 2  = –(b/a)

Let us verify the options.

(a) 2x 2  – 3x + 6 = 0

Sum of the roots = – b/a = -(-3/2) = 3/2

(b) -x 2  + 3x – 3 = 0

Sum of the roots = – b/a = -(3/-1) = 3

(c) √2x 2  – 3/√2x + 1=0

2x 2  – 3x + √2 = 0

Sum of the roots = – b/a = -(-3/3) = 1

16. The quadratic equation 2x 2   – √5x + 1 = 0 has

(a) two distinct real roots 

(b) two equal real roots

(c) no real roots 

(d) more than 2 real roots

Answer: (c) no real roots

2x 2  – √5x + 1 = 0

Comparing with the standard form of a quadratic equation,

a = 2, b = -√5, c = 1

b 2  – 4ac = (-√5) 2  – 4(2)(1)

= 5 – 8 

= -3 < 0

Therefore, the given equation has no real roots.

17. The equation (x + 1) 2  – 2(x + 1) = 0 has

(a) two real roots

(b) no real roots 

(c) one real root

(d) two equal roots

Answer: (a) two real roots

(x + 1) 2  – 2(x + 1) = 0

x 2  + 1 + 2x – 2x – 2 = 0

x 2  – 1 = 0

18. The quadratic formula to find the roots of a quadratic equation ax 2  + bx + c = 0 is given by

(a) [-b ± √(b 2 -ac)]/2a

(b) [-b ± √(b 2 -2ac)]/a

(c) [-b ± √(b 2 -4ac)]/4a

(d) [-b ± √(b 2 -4ac)]/2a

Answer: (d) [-b ± √(b 2 -4ac)]/2a

The quadratic formula to find the roots of a quadratic equation ax 2  + bx + c = 0 is given by [-b ± √(b 2 -4ac)]/2a.

19. The quadratic equation x 2  + 7x – 60 has

(a) two equal roots

(b) two real and unequal roots

(b) no real roots

(c) two equal complex roots

Answer: (b) two real and unequal roots

x 2  + 7x – 60 = 0

Comparing with the standard form,

a = 1, b = 7, c = -60

b 2  – 4ac = (7) 2  – 4(1)(-60) = 49 + 240 = 289 > 0

Therefore, the given quadratic equation has two real and unequal roots.

20. The maximum number of roots for a quadratic equation is equal to

Answer: (b) 2

The maximum number of roots for a quadratic equation is equal to 2 since the degree of a quadratic equation is 2.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations

NCERT Solutions Class 10 Maths Chapter 4 Quadratic Equations are provided here to help the students of CBSE class 10. Our expert teachers prepared all these solutions as per the latest CBSE syllabus and guidelines. In this chapter, we have discussed how to find the solution of a quadratic equation by – factorisation, completing the square method in details. CBSE Class 10 Maths solutions provide a detailed and step-wise explanation of each answer to the questions given in the exercises of NCERT books.

CBSE Class 10 Maths Chapter 4 Quadratic Equations Solutions

Below we have given the answers to all the questions present in Quadratic Equations in our NCERT Solutions for Class 10 Maths chapter 4. In this lesson, students are introduced to a lot of important concepts that will be useful for those who wish to pursue mathematics as a subject in their future classes. Based on these solutions, students can prepare for their upcoming Board Exams. These solutions are helpful as the syllabus covered here follows NCERT guidelines.

NCERT Solutions for Class 10 Maths Chapter 4 Exercise 4.1

NCERT Solutions for Class 10 Maths Chapter 4 Exercise 4.2

NCERT Solutions for Class 10 Maths Chapter 4 Exercise 4.3

NCERT Solutions for Class 10 Maths Chapter 4 Exercise 4.4

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.