Smart. Open. Grounded. Inventive. Read our Ideas Made to Matter.

Which program is right for you?

Through intellectual rigor and experiential learning, this full-time, two-year MBA program develops leaders who make a difference in the world.
A rigorous, hands-on program that prepares adaptive problem solvers for premier finance careers.
A 12-month program focused on applying the tools of modern data science, optimization and machine learning to solve real-world business problems.
Earn your MBA and SM in engineering with this transformative two-year program.
Combine an international MBA with a deep dive into management science. A special opportunity for partner and affiliate schools only.
A doctoral program that produces outstanding scholars who are leading in their fields of research.
Bring a business perspective to your technical and quantitative expertise with a bachelor’s degree in management, business analytics, or finance.
A joint program for mid-career professionals that integrates engineering and systems thinking. Earn your master’s degree in engineering and management.
An interdisciplinary program that combines engineering, management, and design, leading to a master’s degree in engineering and management.
Executive Programs
A full-time MBA program for mid-career leaders eager to dedicate one year of discovery for a lifetime of impact.
This 20-month MBA program equips experienced executives to enhance their impact on their organizations and the world.
Non-degree programs for senior executives and high-potential managers.
A non-degree, customizable program for mid-career professionals.
The AI Playbook: 6 steps for launching predictive AI projects
5 ‘extraordinary turnarounds’ for global well-being
Close proximity is the key to knowledge spillovers among startups
Credit: Alejandro Giraldo
Ideas Made to Matter
How to use algorithms to solve everyday problems
Kara Baskin
May 8, 2017
How can I navigate the grocery store quickly? Why doesn’t anyone like my Facebook status? How can I alphabetize my bookshelves in a hurry? Apple data visualizer and MIT System Design and Management graduate Ali Almossawi solves these common dilemmas and more in his new book, “ Bad Choices: How Algorithms Can Help You Think Smarter and Live Happier ,” a quirky, illustrated guide to algorithmic thinking.
For the uninitiated: What is an algorithm? And how can algorithms help us to think smarter?
An algorithm is a process with unambiguous steps that has a beginning and an end, and does something useful.
Algorithmic thinking is taking a step back and asking, “If it’s the case that algorithms are so useful in computing to achieve predictability, might they also be useful in everyday life, when it comes to, say, deciding between alternative ways of solving a problem or completing a task?” In all cases, we optimize for efficiency: We care about time or space.
Note the mention of “deciding between.” Computer scientists do that all the time, and I was convinced that the tools they use to evaluate competing algorithms would be of interest to a broad audience.
Why did you write this book, and who can benefit from it?
All the books I came across that tried to introduce computer science involved coding. My approach to making algorithms compelling was focusing on comparisons. I take algorithms and put them in a scene from everyday life, such as matching socks from a pile, putting books on a shelf, remembering things, driving from one point to another, or cutting an onion. These activities can be mapped to one or more fundamental algorithms, which form the basis for the field of computing and have far-reaching applications and uses.
I wrote the book with two audiences in mind. One, anyone, be it a learner or an educator, who is interested in computer science and wants an engaging and lighthearted, but not a dumbed-down, introduction to the field. Two, anyone who is already familiar with the field and wants to experience a way of explaining some of the fundamental concepts in computer science differently than how they’re taught.
I’m going to the grocery store and only have 15 minutes. What do I do?
Do you know what the grocery store looks like ahead of time? If you know what it looks like, it determines your list. How do you prioritize things on your list? Order the items in a way that allows you to avoid walking down the same aisles twice.
For me, the intriguing thing is that the grocery store is a scene from everyday life that I can use as a launch pad to talk about various related topics, like priority queues and graphs and hashing. For instance, what is the most efficient way for a machine to store a prioritized list, and what happens when the equivalent of you scratching an item from a list happens in the machine’s list? How is a store analogous to a graph (an abstraction in computer science and mathematics that defines how things are connected), and how is navigating the aisles in a store analogous to traversing a graph?
Nobody follows me on Instagram. How do I get more followers?
The concept of links and networks, which I cover in Chapter 6, is relevant here. It’s much easier to get to people whom you might be interested in and who might be interested in you if you can start within the ball of links that connects those people, rather than starting at a random spot.
You mention Instagram: There, the hashtag is one way to enter that ball of links. Tag your photos, engage with users who tag their photos with the same hashtags, and you should be on your way to stardom.
What are the secret ingredients of a successful Facebook post?
I’ve posted things on social media that have died a sad death and then posted the same thing at a later date that somehow did great. Again, if we think of it in terms that are relevant to algorithms, we’d say that the challenge with making something go viral is really getting that first spark. And to get that first spark, a person who is connected to the largest number of people who are likely to engage with that post, needs to share it.
With [my first book], “Bad Arguments,” I spent a month pouring close to $5,000 into advertising for that project with moderate results. And then one science journalist with a large audience wrote about it, and the project took off and hasn’t stopped since.
What problems do you wish you could solve via algorithm but can’t?
When we care about efficiency, thinking in terms of algorithms is useful. There are cases when that’s not the quality we want to optimize for — for instance, learning or love. I walk for several miles every day, all throughout the city, as I find it relaxing. I’ve never asked myself, “What’s the most efficient way I can traverse the streets of San Francisco?” It’s not relevant to my objective.
Algorithms are a great way of thinking about efficiency, but the question has to be, “What approach can you optimize for that objective?” That’s what worries me about self-help: Books give you a silver bullet for doing everything “right” but leave out all the nuances that make us different. What works for you might not work for me.
Which companies use algorithms well?
When you read that the overwhelming majority of the shows that users of, say, Netflix, watch are due to Netflix’s recommendation engine, you know they’re doing something right.
Related Articles

- Admiral “Amazing Grace” Hopper
Exploring the Intricacies of NP-Completeness in Computer Science
Understanding p vs np problems in computer science: a primer for beginners, understanding key theoretical frameworks in computer science: a beginner’s guide.

Learn Computer Science with Python
CS is a journey, not a destination
- Foundations
Understanding Algorithms: The Key to Problem-Solving Mastery

The world of computer science is a fascinating realm, where intricate concepts and technologies continuously shape the way we interact with machines. Among the vast array of ideas and principles, few are as fundamental and essential as algorithms. These powerful tools serve as the building blocks of computation, enabling computers to solve problems, make decisions, and process vast amounts of data efficiently.
An algorithm can be thought of as a step-by-step procedure or a set of instructions designed to solve a specific problem or accomplish a particular task. It represents a systematic approach to finding solutions and provides a structured way to tackle complex computational challenges. Algorithms are at the heart of various applications, from simple calculations to sophisticated machine learning models and complex data analysis.
Understanding algorithms and their inner workings is crucial for anyone interested in computer science. They serve as the backbone of software development, powering the creation of innovative applications across numerous domains. By comprehending the concept of algorithms, aspiring computer science enthusiasts gain a powerful toolset to approach problem-solving and gain insight into the efficiency and performance of different computational methods.
In this article, we aim to provide a clear and accessible introduction to algorithms, focusing on their importance in problem-solving and exploring common types such as searching, sorting, and recursion. By delving into these topics, readers will gain a solid foundation in algorithmic thinking and discover the underlying principles that drive the functioning of modern computing systems. Whether you’re a beginner in the world of computer science or seeking to deepen your understanding, this article will equip you with the knowledge to navigate the fascinating world of algorithms.
What are Algorithms?
At its core, an algorithm is a systematic, step-by-step procedure or set of rules designed to solve a problem or perform a specific task. It provides clear instructions that, when followed meticulously, lead to the desired outcome.
Consider an algorithm to be akin to a recipe for your favorite dish. When you decide to cook, the recipe is your go-to guide. It lists out the ingredients you need, their exact quantities, and a detailed, step-by-step explanation of the process, from how to prepare the ingredients to how to mix them, and finally, the cooking process. It even provides an order for adding the ingredients and specific times for cooking to ensure the dish turns out perfect.
In the same vein, an algorithm, within the realm of computer science, provides an explicit series of instructions to accomplish a goal. This could be a simple goal like sorting a list of numbers in ascending order, a more complex task such as searching for a specific data point in a massive dataset, or even a highly complicated task like determining the shortest path between two points on a map (think Google Maps). No matter the complexity of the problem at hand, there’s always an algorithm working tirelessly behind the scenes to solve it.
Furthermore, algorithms aren’t limited to specific programming languages. They are universal and can be implemented in any language. This is why understanding the fundamental concept of algorithms can empower you to solve problems across various programming languages.
The Importance of Algorithms
Algorithms are indisputably the backbone of all computational operations. They’re a fundamental part of the digital world that we interact with daily. When you search for something on the web, an algorithm is tirelessly working behind the scenes to sift through millions, possibly billions, of web pages to bring you the most relevant results. When you use a GPS to find the fastest route to a location, an algorithm is computing all possible paths, factoring in variables like traffic and road conditions, to provide you the optimal route.
Consider the world of social media, where algorithms curate personalized feeds based on our previous interactions, or in streaming platforms where they recommend shows and movies based on our viewing habits. Every click, every like, every search, and every interaction is processed by algorithms to serve you a seamless digital experience.
In the realm of computer science and beyond, everything revolves around problem-solving, and algorithms are our most reliable problem-solving tools. They provide a structured approach to problem-solving, breaking down complex problems into manageable steps and ensuring that every eventuality is accounted for.
Moreover, an algorithm’s efficiency is not just a matter of preference but a necessity. Given that computers have finite resources — time, memory, and computational power — the algorithms we use need to be optimized to make the best possible use of these resources. Efficient algorithms are the ones that can perform tasks more quickly, using less memory, and provide solutions to complex problems that might be infeasible with less efficient alternatives.
In the context of massive datasets (the likes of which are common in our data-driven world), the difference between a poorly designed algorithm and an efficient one could be the difference between a solution that takes years to compute and one that takes mere seconds. Therefore, understanding, designing, and implementing efficient algorithms is a critical skill for any computer scientist or software engineer.
Hence, as a computer science beginner, you are starting a journey where algorithms will be your best allies — universal keys capable of unlocking solutions to a myriad of problems, big or small.
Common Types of Algorithms: Searching and Sorting
Two of the most ubiquitous types of algorithms that beginners often encounter are searching and sorting algorithms.
Searching algorithms are designed to retrieve specific information from a data structure, like an array or a database. A simple example is the linear search, which works by checking each element in the array until it finds the one it’s looking for. Although easy to understand, this method isn’t efficient for large datasets, which is where more complex algorithms like binary search come in.
Binary search, on the other hand, is like looking up a word in the dictionary. Instead of checking each word from beginning to end, you open the dictionary in the middle and see if the word you’re looking for should be on the left or right side, thereby reducing the search space by half with each step.
Sorting algorithms, meanwhile, are designed to arrange elements in a particular order. A simple sorting algorithm is bubble sort, which works by repeatedly swapping adjacent elements if they’re in the wrong order. Again, while straightforward, it’s not efficient for larger datasets. More advanced sorting algorithms, such as quicksort or mergesort, have been designed to sort large data collections more efficiently.
Diving Deeper: Graph and Dynamic Programming Algorithms
Building upon our understanding of searching and sorting algorithms, let’s delve into two other families of algorithms often encountered in computer science: graph algorithms and dynamic programming algorithms.
A graph is a mathematical structure that models the relationship between pairs of objects. Graphs consist of vertices (or nodes) and edges (where each edge connects a pair of vertices). Graphs are commonly used to represent real-world systems such as social networks, web pages, biological networks, and more.
Graph algorithms are designed to solve problems centered around these structures. Some common graph algorithms include:
Dynamic programming is a powerful method used in optimization problems, where the main problem is broken down into simpler, overlapping subproblems. The solutions to these subproblems are stored and reused to build up the solution to the main problem, saving computational effort.
Here are two common dynamic programming problems:
Understanding these algorithm families — searching, sorting, graph, and dynamic programming algorithms — not only equips you with powerful tools to solve a variety of complex problems but also serves as a springboard to dive deeper into the rich ocean of algorithms and computer science.
Recursion: A Powerful Technique
While searching and sorting represent specific problem domains, recursion is a broad technique used in a wide range of algorithms. Recursion involves breaking down a problem into smaller, more manageable parts, and a function calling itself to solve these smaller parts.
To visualize recursion, consider the task of calculating factorial of a number. The factorial of a number n (denoted as n! ) is the product of all positive integers less than or equal to n . For instance, the factorial of 5 ( 5! ) is 5 x 4 x 3 x 2 x 1 = 120 . A recursive algorithm for finding factorial of n would involve multiplying n by the factorial of n-1 . The function keeps calling itself with a smaller value of n each time until it reaches a point where n is equal to 1, at which point it starts returning values back up the chain.
Algorithms are truly the heart of computer science, transforming raw data into valuable information and insight. Understanding their functionality and purpose is key to progressing in your computer science journey. As you continue your exploration, remember that each algorithm you encounter, no matter how complex it may seem, is simply a step-by-step procedure to solve a problem.
We’ve just scratched the surface of the fascinating world of algorithms. With time, patience, and practice, you will learn to create your own algorithms and start solving problems with confidence and efficiency.
Related Articles

Three Elegant Algorithms Every Computer Science Beginner Should Know
- 1. Micro-Worlds
- 2. Light-Bot in Java
- 3. Jeroos of Santong Island
- 4. Problem Solving and Algorithms
- 5. Creating Jeroo Methods
- 6. Conditionally Executing Actions
- 7. Repeating Actions
- 8. Handling Touch Events
- 9. Adding Text to the Screen
Problem Solving and Algorithms
Learn a basic process for developing a solution to a problem. Nothing in this chapter is unique to using a computer to solve a problem. This process can be used to solve a wide variety of problems, including ones that have nothing to do with computers.
Problems, Solutions, and Tools
I have a problem! I need to thank Aunt Kay for the birthday present she sent me. I could send a thank you note through the mail. I could call her on the telephone. I could send her an email message. I could drive to her house and thank her in person. In fact, there are many ways I could thank her, but that's not the point. The point is that I must decide how I want to solve the problem, and use the appropriate tool to implement (carry out) my plan. The postal service, the telephone, the internet, and my automobile are tools that I can use, but none of these actually solves my problem. In a similar way, a computer does not solve problems, it's just a tool that I can use to implement my plan for solving the problem.
Knowing that Aunt Kay appreciates creative and unusual things, I have decided to hire a singing messenger to deliver my thanks. In this context, the messenger is a tool, but one that needs instructions from me. I have to tell the messenger where Aunt Kay lives, what time I would like the message to be delivered, and what lyrics I want sung. A computer program is similar to my instructions to the messenger.
The story of Aunt Kay uses a familiar context to set the stage for a useful point of view concerning computers and computer programs. The following list summarizes the key aspects of this point of view.
A computer is a tool that can be used to implement a plan for solving a problem.
A computer program is a set of instructions for a computer. These instructions describe the steps that the computer must follow to implement a plan.
An algorithm is a plan for solving a problem.
A person must design an algorithm.
A person must translate an algorithm into a computer program.
This point of view sets the stage for a process that we will use to develop solutions to Jeroo problems. The basic process is important because it can be used to solve a wide variety of problems, including ones where the solution will be written in some other programming language.
An Algorithm Development Process
Every problem solution starts with a plan. That plan is called an algorithm.
There are many ways to write an algorithm. Some are very informal, some are quite formal and mathematical in nature, and some are quite graphical. The instructions for connecting a DVD player to a television are an algorithm. A mathematical formula such as πR 2 is a special case of an algorithm. The form is not particularly important as long as it provides a good way to describe and check the logic of the plan.
The development of an algorithm (a plan) is a key step in solving a problem. Once we have an algorithm, we can translate it into a computer program in some programming language. Our algorithm development process consists of five major steps.
Step 1: Obtain a description of the problem.
Step 2: analyze the problem., step 3: develop a high-level algorithm., step 4: refine the algorithm by adding more detail., step 5: review the algorithm..
This step is much more difficult than it appears. In the following discussion, the word client refers to someone who wants to find a solution to a problem, and the word developer refers to someone who finds a way to solve the problem. The developer must create an algorithm that will solve the client's problem.
The client is responsible for creating a description of the problem, but this is often the weakest part of the process. It's quite common for a problem description to suffer from one or more of the following types of defects: (1) the description relies on unstated assumptions, (2) the description is ambiguous, (3) the description is incomplete, or (4) the description has internal contradictions. These defects are seldom due to carelessness by the client. Instead, they are due to the fact that natural languages (English, French, Korean, etc.) are rather imprecise. Part of the developer's responsibility is to identify defects in the description of a problem, and to work with the client to remedy those defects.
The purpose of this step is to determine both the starting and ending points for solving the problem. This process is analogous to a mathematician determining what is given and what must be proven. A good problem description makes it easier to perform this step.
When determining the starting point, we should start by seeking answers to the following questions:
What data are available?
Where is that data?
What formulas pertain to the problem?
What rules exist for working with the data?
What relationships exist among the data values?
When determining the ending point, we need to describe the characteristics of a solution. In other words, how will we know when we're done? Asking the following questions often helps to determine the ending point.
What new facts will we have?
What items will have changed?
What changes will have been made to those items?
What things will no longer exist?
An algorithm is a plan for solving a problem, but plans come in several levels of detail. It's usually better to start with a high-level algorithm that includes the major part of a solution, but leaves the details until later. We can use an everyday example to demonstrate a high-level algorithm.
Problem: I need a send a birthday card to my brother, Mark.
Analysis: I don't have a card. I prefer to buy a card rather than make one myself.
High-level algorithm:
Go to a store that sells greeting cards Select a card Purchase a card Mail the card
This algorithm is satisfactory for daily use, but it lacks details that would have to be added were a computer to carry out the solution. These details include answers to questions such as the following.
"Which store will I visit?"
"How will I get there: walk, drive, ride my bicycle, take the bus?"
"What kind of card does Mark like: humorous, sentimental, risqué?"
These kinds of details are considered in the next step of our process.
A high-level algorithm shows the major steps that need to be followed to solve a problem. Now we need to add details to these steps, but how much detail should we add? Unfortunately, the answer to this question depends on the situation. We have to consider who (or what) is going to implement the algorithm and how much that person (or thing) already knows how to do. If someone is going to purchase Mark's birthday card on my behalf, my instructions have to be adapted to whether or not that person is familiar with the stores in the community and how well the purchaser known my brother's taste in greeting cards.
When our goal is to develop algorithms that will lead to computer programs, we need to consider the capabilities of the computer and provide enough detail so that someone else could use our algorithm to write a computer program that follows the steps in our algorithm. As with the birthday card problem, we need to adjust the level of detail to match the ability of the programmer. When in doubt, or when you are learning, it is better to have too much detail than to have too little.
Most of our examples will move from a high-level to a detailed algorithm in a single step, but this is not always reasonable. For larger, more complex problems, it is common to go through this process several times, developing intermediate level algorithms as we go. Each time, we add more detail to the previous algorithm, stopping when we see no benefit to further refinement. This technique of gradually working from a high-level to a detailed algorithm is often called stepwise refinement .
The final step is to review the algorithm. What are we looking for? First, we need to work through the algorithm step by step to determine whether or not it will solve the original problem. Once we are satisfied that the algorithm does provide a solution to the problem, we start to look for other things. The following questions are typical of ones that should be asked whenever we review an algorithm. Asking these questions and seeking their answers is a good way to develop skills that can be applied to the next problem.
Does this algorithm solve a very specific problem or does it solve a more general problem ? If it solves a very specific problem, should it be generalized?
For example, an algorithm that computes the area of a circle having radius 5.2 meters (formula π*5.2 2 ) solves a very specific problem, but an algorithm that computes the area of any circle (formula π*R 2 ) solves a more general problem.
Can this algorithm be simplified ?
One formula for computing the perimeter of a rectangle is:
length + width + length + width
A simpler formula would be:
2.0 * ( length + width )
Is this solution similar to the solution to another problem? How are they alike? How are they different?
For example, consider the following two formulae:
Rectangle area = length * width Triangle area = 0.5 * base * height
Similarities: Each computes an area. Each multiplies two measurements.
Differences: Different measurements are used. The triangle formula contains 0.5.
Hypothesis: Perhaps every area formula involves multiplying two measurements.
Example 4.1: Pick and Plant
This section contains an extended example that demonstrates the algorithm development process. To complete the algorithm, we need to know that every Jeroo can hop forward, turn left and right, pick a flower from its current location, and plant a flower at its current location.
Problem Statement (Step 1)
A Jeroo starts at (0, 0) facing East with no flowers in its pouch. There is a flower at location (3, 0). Write a program that directs the Jeroo to pick the flower and plant it at location (3, 2). After planting the flower, the Jeroo should hop one space East and stop. There are no other nets, flowers, or Jeroos on the island.
| Start | Finish |
|---|---|
Analysis of the Problem (Step 2)
The flower is exactly three spaces ahead of the jeroo.
The flower is to be planted exactly two spaces South of its current location.
The Jeroo is to finish facing East one space East of the planted flower.
There are no nets to worry about.
High-level Algorithm (Step 3)
Let's name the Jeroo Bobby. Bobby should do the following:
Get the flower Put the flower Hop East
Detailed Algorithm (Step 4)
Get the flower Hop 3 times Pick the flower Put the flower Turn right Hop 2 times Plant a flower Hop East Turn left Hop once
Review the Algorithm (Step 5)
The high-level algorithm partitioned the problem into three rather easy subproblems. This seems like a good technique.
This algorithm solves a very specific problem because the Jeroo and the flower are in very specific locations.
This algorithm is actually a solution to a slightly more general problem in which the Jeroo starts anywhere, and the flower is 3 spaces directly ahead of the Jeroo.
Java Code for "Pick and Plant"
A good programmer doesn't write a program all at once. Instead, the programmer will write and test the program in a series of builds. Each build adds to the previous one. The high-level algorithm will guide us in this process.
FIRST BUILD
To see this solution in action, create a new Greenfoot4Sofia scenario and use the Edit Palettes Jeroo menu command to make the Jeroo classes visible. Right-click on the Island class and create a new subclass with the name of your choice. This subclass will hold your new code.
The recommended first build contains three things:
The main method (here myProgram() in your island subclass).
Declaration and instantiation of every Jeroo that will be used.
The high-level algorithm in the form of comments.
The instantiation at the beginning of myProgram() places bobby at (0, 0), facing East, with no flowers.
Once the first build is working correctly, we can proceed to the others. In this case, each build will correspond to one step in the high-level algorithm. It may seem like a lot of work to use four builds for such a simple program, but doing so helps establish habits that will become invaluable as the programs become more complex.
SECOND BUILD
This build adds the logic to "get the flower", which in the detailed algorithm (step 4 above) consists of hopping 3 times and then picking the flower. The new code is indicated by comments that wouldn't appear in the original (they are just here to call attention to the additions). The blank lines help show the organization of the logic.
By taking a moment to run the work so far, you can confirm whether or not this step in the planned algorithm works as expected.
THIRD BUILD
This build adds the logic to "put the flower". New code is indicated by the comments that are provided here to mark the additions.
FOURTH BUILD (final)
Example 4.2: replace net with flower.
This section contains a second example that demonstrates the algorithm development process.
There are two Jeroos. One Jeroo starts at (0, 0) facing North with one flower in its pouch. The second starts at (0, 2) facing East with one flower in its pouch. There is a net at location (3, 2). Write a program that directs the first Jeroo to give its flower to the second one. After receiving the flower, the second Jeroo must disable the net, and plant a flower in its place. After planting the flower, the Jeroo must turn and face South. There are no other nets, flowers, or Jeroos on the island.
Jeroo_2 is exactly two spaces behind Jeroo_1.
The only net is exactly three spaces ahead of Jeroo_2.
Each Jeroo has exactly one flower.
Jeroo_2 will have two flowers after receiving one from Jeroo_1. One flower must be used to disable the net. The other flower must be planted at the location of the net, i.e. (3, 2).
Jeroo_1 will finish at (0, 1) facing South.
Jeroo_2 is to finish at (3, 2) facing South.
Each Jeroo will finish with 0 flowers in its pouch. One flower was used to disable the net, and the other was planted.
Let's name the first Jeroo Ann and the second one Andy.
Ann should do the following: Find Andy (but don't collide with him) Give a flower to Andy (he will be straight ahead) After receiving the flower, Andy should do the following: Find the net (but don't hop onto it) Disable the net Plant a flower at the location of the net Face South
Ann should do the following: Find Andy Turn around (either left or right twice) Hop (to location (0, 1)) Give a flower to Andy Give ahead Now Andy should do the following: Find the net Hop twice (to location (2, 2)) Disable the net Toss Plant a flower at the location of the net Hop (to location (3, 2)) Plant a flower Face South Turn right
The high-level algorithm helps manage the details.
This algorithm solves a very specific problem, but the specific locations are not important. The only thing that is important is the starting location of the Jeroos relative to one another and the location of the net relative to the second Jeroo's location and direction.
Java Code for "Replace Net with Flower"
As before, the code should be written incrementally as a series of builds. Four builds will be suitable for this problem. As usual, the first build will contain the main method, the declaration and instantiation of the Jeroo objects, and the high-level algorithm in the form of comments. The second build will have Ann give her flower to Andy. The third build will have Andy locate and disable the net. In the final build, Andy will place the flower and turn East.
This build creates the main method, instantiates the Jeroos, and outlines the high-level algorithm. In this example, the main method would be myProgram() contained within a subclass of Island .
This build adds the logic for Ann to locate Andy and give him a flower.
This build adds the logic for Andy to locate and disable the net.
This build adds the logic for Andy to place a flower at (3, 2) and turn South.
Solve Me First Easy Problem Solving (Basic) Max Score: 1 Success Rate: 97.78%
Simple array sum easy problem solving (basic) max score: 10 success rate: 94.51%, compare the triplets easy problem solving (basic) max score: 10 success rate: 95.81%, a very big sum easy problem solving (basic) max score: 10 success rate: 98.81%, diagonal difference easy problem solving (basic) max score: 10 success rate: 96.01%, plus minus easy problem solving (basic) max score: 10 success rate: 98.39%, staircase easy problem solving (basic) max score: 10 success rate: 98.37%, mini-max sum easy problem solving (basic) max score: 10 success rate: 94.44%, birthday cake candles easy problem solving (basic) max score: 10 success rate: 97.13%, time conversion easy problem solving (basic) max score: 15 success rate: 92.33%, cookie support is required to access hackerrank.
Seems like cookies are disabled on this browser, please enable them to open this website

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1: Algorithmic Problem Solving
- Last updated
- Save as PDF
- Page ID 46789

- Harrison Njoroge
- African Virtual University
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Unit Objectives
Upon completion of this unit the learner should be able to:
- describe an algorithm
- explain the relationship between data and algorithm
- outline the characteristics of algorithms
- apply pseudo codes and flowcharts to represent algorithms
Unit Introduction
This unit introduces learners to data structures and algorithm course. The unit is on the different data structures and their algorithms that can help implement the different data structures in the computer. The application of the different data structures is presented by using examples of algorithms and which are not confined to a particular computer programming language.
- Data: the structural representation of logical relationships between elements of data
- Algorithm: finite sequence of steps for accomplishing some computational task
- Pseudo code: an informal high-level description of the operating principle of a computer program or other algorithm
- Flow chart: diagrammatic representation illustrates a solution model to a given problem.
Learning Activities
- 1.1: Activity 1 - Introduction to Algorithms and Problem Solving In this learning activity section, the learner will be introduced to algorithms and how to write algorithms to solve tasks faced by learners or everyday problems. Examples of the algorithm are also provided with a specific application to everyday problems that the learner is familiar with. The learners will particularly learn what is an algorithm, the process of developing a solution for a given task, and finally examples of application of the algorithms are given.
- 1.2: Activity 2 - The characteristics of an algorithm This section introduces the learners to the characteristics of algorithms. These characteristics make the learner become aware of what to ensure is basic, present and mandatory for any algorithm to qualify to be one. It also exposes the learner to what to expect from an algorithm to achieve or indicate. Key expectations are: the fact that an algorithm must be exact, terminate, effective, general among others.
- 1.3: Activity 3 - Using pseudo-codes and flowcharts to represent algorithms The student will learn how to design an algorithm using either a pseudo code or flowchart. Pseudo code is a mixture of English like statements, some mathematical notations and selected keywords from a programming language. It is one of the tools used to design and develop the solution to a task or problem. Pseudo codes have different ways of representing the same thing and emphasis is on the clarity and not style.
- 1.4: Unit Summary In this unit, you have seen what an algorithm is. Based on this knowledge, you should now be able to characterize an algorithm by stating its properties. We have explored the different ways of representing an algorithm such as using human language, pseudo codes and flow chart. You should now be able to present solutions to problems in form of an algorithm.
Learn Python practically and Get Certified .
Popular Tutorials
Popular examples, reference materials, learn python interactively, dsa introduction.
- What is an algorithm?
- Data Structure and Types
- Why learn DSA?
- Asymptotic Notations
- Master Theorem
- Divide and Conquer Algorithm
Data Structures (I)
- Types of Queue
- Circular Queue
- Priority Queue
Data Structures (II)
- Linked List
- Linked List Operations
- Types of Linked List
- Heap Data Structure
- Fibonacci Heap
- Decrease Key and Delete Node Operations on a Fibonacci Heap
Tree based DSA (I)
- Tree Data Structure
- Tree Traversal
- Binary Tree
- Full Binary Tree
- Perfect Binary Tree
- Complete Binary Tree
- Balanced Binary Tree
- Binary Search Tree
Tree based DSA (II)
- Insertion in a B-tree
- Deletion from a B-tree
- Insertion on a B+ Tree
- Deletion from a B+ Tree
- Red-Black Tree
- Red-Black Tree Insertion
- Red-Black Tree Deletion
Graph based DSA
- Graph Data Structure
- Spanning Tree
- Strongly Connected Components
- Adjacency Matrix
- Adjacency List
- DFS Algorithm
- Breadth-first Search
Bellman Ford's Algorithm
Sorting and Searching Algorithms
- Bubble Sort
- Selection Sort
- Insertion Sort
- Counting Sort
- Bucket Sort
- Linear Search
- Binary Search
Greedy Algorithms
Greedy Algorithm
- Ford-Fulkerson Algorithm
- Dijkstra's Algorithm
- Kruskal's Algorithm
- Prim's Algorithm
- Huffman Coding
Dynamic Programming
- Floyd-Warshall Algorithm
- Longest Common Sequence
Other Algorithms
- Backtracking Algorithm
- Rabin-Karp Algorithm
DSA Tutorials
Merge Sort Algorithm
- Selection Sort Algorithm
What is an Algorithm?
In computer programming terms, an algorithm is a set of well-defined instructions to solve a particular problem. It takes a set of input(s) and produces the desired output. For example,
An algorithm to add two numbers:
Take two number inputs
Add numbers using the + operator
Display the result
Qualities of a Good Algorithm
- Input and output should be defined precisely.
- Each step in the algorithm should be clear and unambiguous.
- Algorithms should be most effective among many different ways to solve a problem.
- An algorithm shouldn't include computer code. Instead, the algorithm should be written in such a way that it can be used in different programming languages.
Algorithm Examples
Algorithm to add two numbers
Algorithm to find the largest among three numbers
Algorithm to find all the roots of the quadratic equation
Algorithm to find the factorial
Algorithm to check prime number
Algorithm of Fibonacci series
Algorithm 1: Add two numbers entered by the user
Algorithm 2: find the largest number among three numbers, algorithm 3: find roots of a quadratic equation ax 2 + bx + c = 0, algorithm 4: find the factorial of a number, algorithm 5: check whether a number is prime or not, algorithm 6: find the fibonacci series till the term less than 1000, table of contents.
- Qualities of Good Algorithms
- Add Two Numbers
- Find Largest Number
- Roots of Quatratic Equation
- Find Factorial of a Number
- Check Prime Number
- Find Fibonacci Series
Sorry about that.
Related Tutorials
DS & Algorithms

What is Problem Solving Algorithm?, Steps, Representation
Table of Contents
- 1 What is Problem Solving Algorithm?
- 2 Definition of Problem Solving Algorithm
- 3.1 Analysing the Problem
- 3.2 Developing an Algorithm
- 3.4 Testing and Debugging
- 4.1 Flowchart
- 4.2 Pseudo code
What is Problem Solving Algorithm?
Computers are used for solving various day-to-day problems and thus problem solving is an essential skill that a computer science student should know. It is pertinent to mention that computers themselves cannot solve a problem. Precise step-by-step instructions should be given by us to solve the problem.
Thus, the success of a computer in solving a problem depends on how correctly and precisely we define the problem, design a solution (algorithm) and implement the solution (program) using a programming language.
Thus, problem solving is the process of identifying a problem, developing an algorithm for the identified problem and finally implementing the algorithm to develop a computer program.
Definition of Problem Solving Algorithm
These are some simple definition of problem solving algorithm which given below:
Steps for Problem Solving
When problems are straightforward and easy, we can easily find the solution. But a complex problem requires a methodical approach to find the right solution. In other words, we have to apply problem solving techniques.
Problem solving begins with the precise identification of the problem and ends with a complete working solution in terms of a program or software. Key steps required for solving a problem using a computer.
For Example: Suppose while driving, a vehicle starts making a strange noise. We might not know how to solve the problem right away. First, we need to identify from where the noise is coming? In case the problem cannot be solved by us, then we need to take the vehicle to a mechanic.
The mechanic will analyse the problem to identify the source of the noise, make a plan about the work to be done and finally repair the vehicle in order to remove the noise. From the example, it is explicit that, finding the solution to a problem might consist of multiple steps.
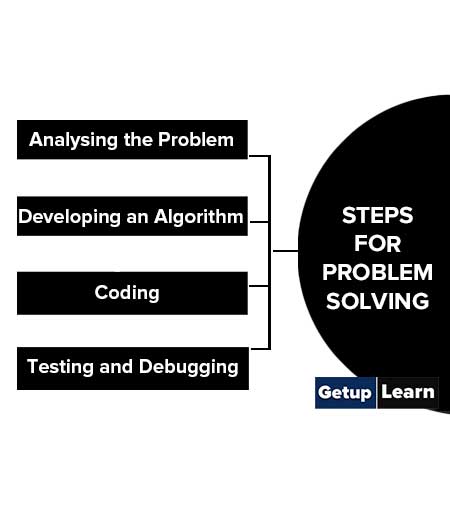
Following are Steps for Problem Solving :
Analysing the Problem
Developing an algorithm, testing and debugging.
It is important to clearly understand a problem before we begin to find the solution for it. If we are not clear as to what is to be solved, we may end up developing a program which may not solve our purpose.
Thus, we need to read and analyse the problem statement carefully in order to list the principal components of the problem and decide the core functionalities that our solution should have. By analysing a problem, we would be able to figure out what are the inputs that our program should accept and the outputs that it should produce.
It is essential to device a solution before writing a program code for a given problem. The solution is represented in natural language and is called an algorithm. We can imagine an algorithm like a very well-written recipe for a dish, with clearly defined steps that, if followed, one will end up preparing the dish.
We start with a tentative solution plan and keep on refining the algorithm until the algorithm is able to capture all the aspects of the desired solution. For a given problem, more than one algorithm is possible and we have to select the most suitable solution.
After finalising the algorithm, we need to convert the algorithm into the format which can be understood by the computer to generate the desired solution. Different high level programming languages can be used for writing a program. It is equally important to record the details of the coding procedures followed and document the solution. This is helpful when revisiting the programs at a later stage.
The program created should be tested on various parameters. The program should meet the requirements of the user. It must respond within the expected time. It should generate correct output for all possible inputs. In the presence of syntactical errors, no output will be obtained. In case the output generated is incorrect, then the program should be checked for logical errors, if any.
Software industry follows standardised testing methods like unit or component testing, integration testing, system testing, and acceptance testing while developing complex applications. This is to ensure that the software meets all the business and technical requirements and works as expected.
The errors or defects found in the testing phases are debugged or rectified and the program is again tested. This continues till all the errors are removed from the program. Once the software application has been developed, tested and delivered to the user, still problems in terms of functioning can come up and need to be resolved from time to time.
The maintenance of the solution, thus, involves fixing the problems faced by the user, answering the queries of the user and even serving the request for addition or modification of features.
Representation of Algorithms
Using their algorithmic thinking skills, the software designers or programmers analyse the problem and identify the logical steps that need to be followed to reach a solution. Once the steps are identified, the need is to write down these steps along with the required input and desired output.
There are two common methods of representing an algorithm —flowchart and pseudocode. Either of the methods can be used to represent an algorithm while keeping in mind the following:
- It showcases the logic of the problem solution, excluding any implementational details.
- It clearly reveals the flow of control during execution of the program.
A flowchart is a visual representation of an algorithm . A flowchart is a diagram made up of boxes, diamonds and other shapes, connected by arrows. Each shape represents a step of the solution process and the arrow represents the order or link among the steps.
A flow chart is a step by step diagrammatic representation of the logic paths to solve a given problem. Or A flowchart is visual or graphical representation of an algorithm .
The flowcharts are pictorial representation of the methods to b used to solve a given problem and help a great deal to analyze the problem and plan its solution in a systematic and orderly manner. A flowchart when translated in to a proper computer language, results in a complete program.
Advantages of Flowcharts:
- The flowchart shows the logic of a problem displayed in pictorial fashion which felicitates easier checking of an algorithm
- The Flowchart is good means of communication to other users. It is also a compact means of recording an algorithm solution to a problem.
- The flowchart allows the problem solver to break the problem into parts. These parts can be connected to make master chart.
- The flowchart is a permanent record of the solution which can be consulted at a later time.
Differences between Algorithm and Flowchart
| 1 | A method of representing the step-by-step logical procedure for solving a problem. | Flowchart is diagrammatic representation of an algorithm. It is constructed using different types of boxes and symbols. |
| 2 | It contains step-by-step English descriptions, each step representing a particular operation leading to solution of problem. | The flowchart employs a series of blocks and arrows, each of which represents a particular step in an algorithm. |
| 3 | These are particularly useful for small problems. | These are useful for detailed representations of complicated programs. |
| 4 | For complex programs, algorithms prove to be Inadequate. | For complex programs, Flowcharts prove to be adequate. |
Pseudo code
The Pseudo code is neither an algorithm nor a program. It is an abstract form of a program. It consists of English like statements which perform the specific operations. It is defined for an algorithm. It does not use any graphical representation.
In pseudo code , the program is represented in terms of words and phrases, but the syntax of program is not strictly followed.
Advantages of Pseudocode
- Before writing codes in a high level language, a pseudocode of a program helps in representing the basic functionality of the intended program.
- By writing the code first in a human readable language, the programmer safeguards against leaving out any important step. Besides, for non-programmers, actual programs are difficult to read and understand.
- But pseudocode helps them to review the steps to confirm that the proposed implementation is going to achieve the desire output.
Related posts:
- What is Computer System? Definition, Characteristics, Functional Units, Components
- Types of Storage Devices, Advantages, Examples
- 10 Evolution of Computing Machine, History
- Generations of Computer First To Fifth, Classification, Characteristics, Features, Examples
- What are Functions of Operating System? 6 Functions
- Advantages and Disadvantages of Operating System
- Data Representation in Computer: Number Systems, Characters, Audio, Image and Video
- What is Flowchart in Programming? Symbols, Advantages, Preparation
- Advantages and Disadvantages of Flowcharts
- What is C++ Programming Language? C++ Character Set, C++ Tokens
- What are C++ Keywords? Set of 59 keywords in C ++
- What are Data Types in C++? Types
- What are Operators in C? Different Types of Operators in C
- What are Expressions in C? Types
- What are Decision Making Statements in C? Types
Leave a Reply Cancel reply
Save my name, email, and website in this browser for the next time I comment.

EnjoyMathematics
Problem-Solving Approaches in Data Structures and Algorithms
This blog highlights some popular problem-solving strategies for solving problems in DSA. Learning to apply these strategies could be one of the best milestones for the learners in mastering data structure and algorithms.

An Incremental approach using Single and Nested loops
One of the simple ideas of our daily problem-solving activities is that we build the partial solution step by step using a loop. There is a different variation to it:
- Input-centric strategy: At each iteration step, we process one input and build the partial solution.
- Output-centric strategy: At each iteration step, we add one output to the solution and build the partial solution.
- Iterative improvement strategy: Here, we start with some easily available approximations of a solution and continuously improve upon it to reach the final solution.
Here are some approaches based on loop: Using a single loop and variables, Using nested loops and variables, Incrementing the loop by a constant (more than 1), Using the loop twice (Double traversal), Using a single loop and prefix array (or extra memory), etc.
Example problems: Insertion Sort , Finding max and min in an array , Valid mountain array , Find equilibrium index of an array , Dutch national flag problem , Sort an array in a waveform .
Decrease and Conquer Approach
This strategy is based on finding the solution to a given problem via its one sub-problem solution. Such an approach leads naturally to a recursive algorithm, which reduces the problem to a sequence of smaller input sizes. Until it becomes small enough to be solved, i.e., it reaches the recursion’s base case.
Example problems: Euclid algorithm of finding GCD , Binary Search , Josephus problem
Problem-solving using Binary Search
When an array has some order property similar to the sorted array, we can use the binary search idea to solve several searching problems efficiently in O(logn) time complexity. For doing this, we need to modify the standard binary search algorithm based on the conditions given in the problem. The core idea is simple: calculate the mid-index and iterate over the left or right half of the array.
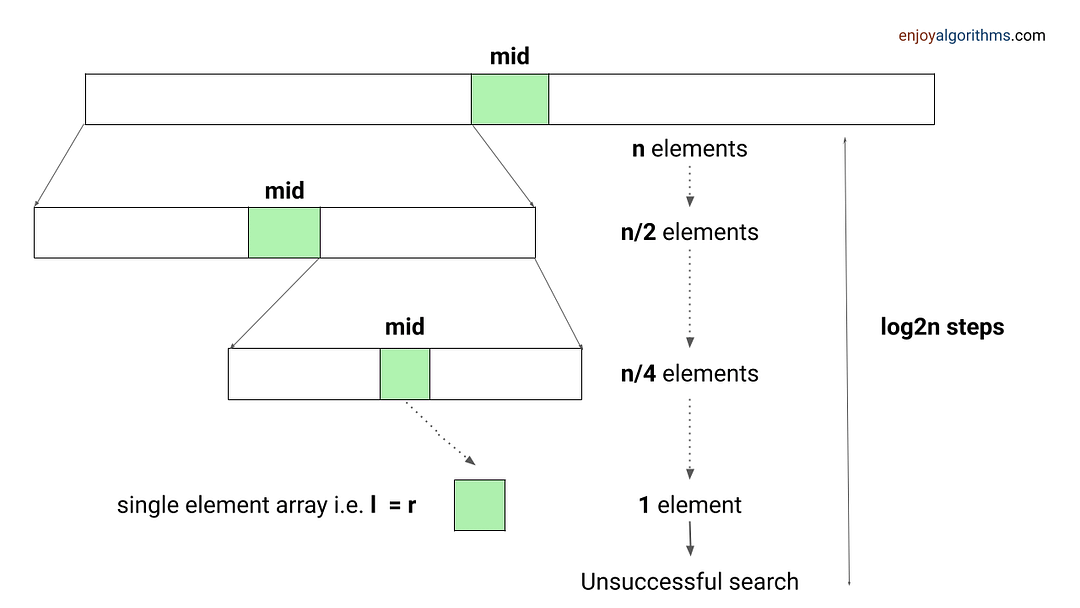
Example problems: Find Peak Element , Search a sorted 2D matrix , Find the square root of an integer , Search in Rotated Sorted Array
Divide and Conquer Approach
This strategy is about dividing a problem into more than one subproblems, solving each of them, and then, if necessary, combining their solutions to get a solution to the original problem. We solve many fundamental problems efficiently in computer science by using this strategy.
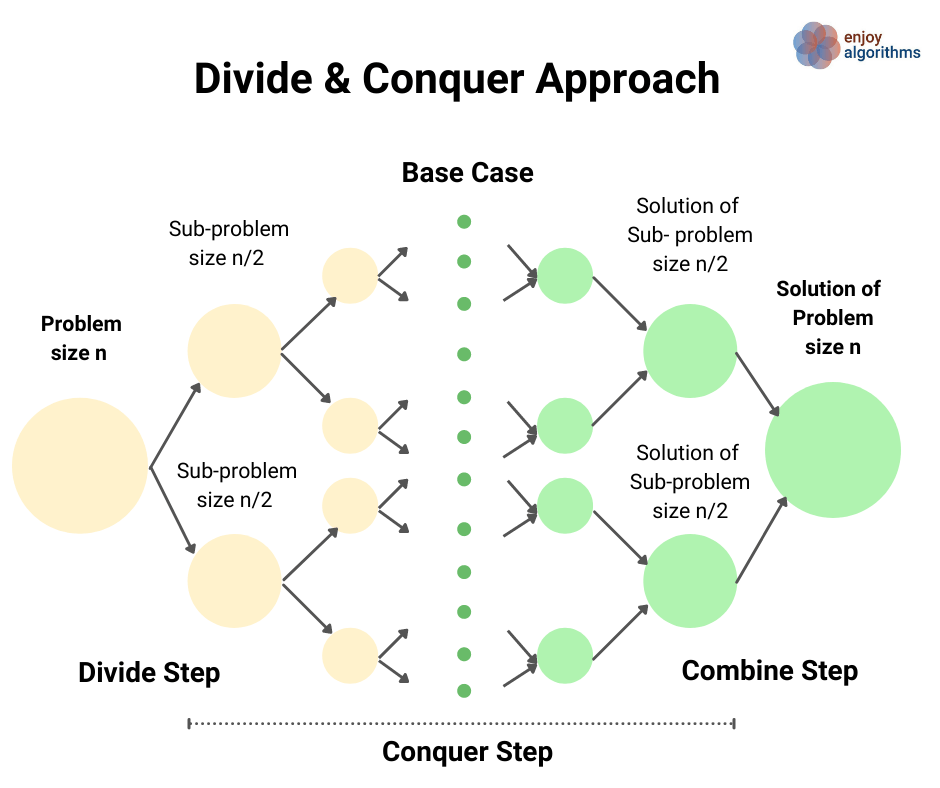
Example problems: Merge Sort , Quick Sort , Median of two sorted arrays
Two Pointers Approach
The two-pointer approach helps us optimize time and space complexity in the case of many searching problems on arrays and linked lists. Here pointers can be pairs of array indices or pointer references to an object. This approach aims to simultaneously iterate over two different input parts to perform fewer operations. There are three variations of this approach:
Pointers are moving in the same direction with the same pace: Merging two sorted arrays or linked lists, Finding the intersection of two arrays or linked lists , Checking an array is a subset of another array , etc.
Pointers are moving in the same direction at a different pace (Fast and slow pointers): Partition process in the quick sort , Remove duplicates from the sorted array , Find the middle node in a linked list , Detect loop in a linked list , Move all zeroes to the end , Remove nth node from list end , etc.
Pointers are moving in the opposite direction: Reversing an array, Check pair sum in an array , Finding triplet with zero-sum , Rainwater trapping problem , Container with most water , etc.


Sliding Window Approach
A sliding window concept is commonly used in solving array/string problems. Here, the window is a contiguous sequence of elements defined by the start and ends indices. We perform some operations on elements within the window and “slide” it in a forward direction by incrementing the left or right end.
This approach can be effective whenever the problem consists of tasks that must be performed on a contiguous block of a fixed or variable size. This could help us improve time complexity in so many problems by converting the nested loop solution into a single loop solution.
Example problems: Longest substring without repeating characters , Count distinct elements in every window , Max continuous series of 1s , Find max consecutive 1's in an array , etc.
Transform and Conquer Approach
This approach is based on transforming a coding problem into another coding problem with some particular property that makes the problem easier to solve. In other words, here we solve the problem is solved in two stages:
- Transformation stage: We transform the original problem into another easier problem to solve.
- Conquering stage: Now, we solve the transformed problem.
Example problems: Pre-sorting based algorithms (Finding the closest pair of points, checking whether all the elements in a given array are distinct, etc.)
Problem-solving using BFS and DFS Traversal
Most tree and graph problems can be solved using DFS and BFS traversal. If the problem is to search for something closer to the root (or source node), we can prefer BFS, and if we need to search for something in-depth, we can choose DFS.
Sometimes, we can use both BFS and DFS traversals when node order is not required. But in some cases, such things are not possible. We need to identify the use case of both traversals to solve the problems efficiently. For example, in binary tree problems:
- We use preorder traversal in a situation when we need to explore all the tree nodes before inspecting any leaves.
- Inorder traversal of BST generates the node's data in increasing order. So we can use inorder to solve several BST problems.
- We can use postorder traversal when we need to explore all the leaf nodes before inspecting any internal nodes.
- Sometimes, we need some specific information about some level. In this situation, BFS traversal helps us to find the output easily.
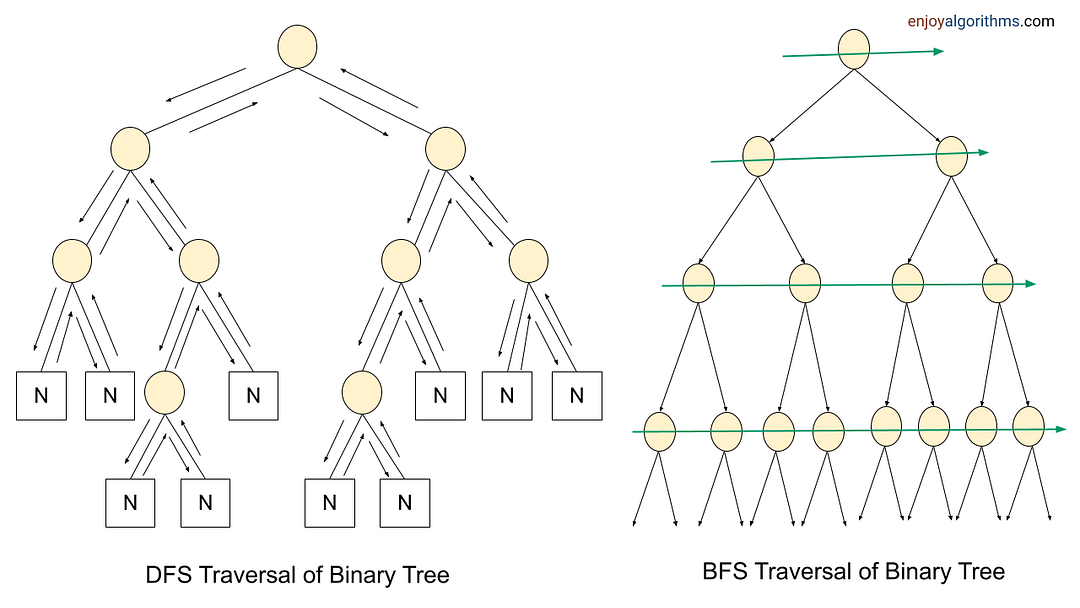
To solve tree and graph problems, sometimes we pass extra variables or pointers to the function parameters, use helper functions, use parent pointers, store some additional data inside the node, and use data structures like the stack, queue, and priority queue, etc.
Example problems: Find min depth of a binary tree , Merge two binary trees , Find the height of a binary tree , Find the absolute minimum difference in a BST , The kth largest element in a BST , Course scheduling problem , bipartite graph , Find the left view of a binary tree , etc.
Problem-solving using the Data Structures
The data structure is one of the powerful tools of problem-solving in algorithms. It helps us perform some of the critical operations efficiently and improves the time complexity of the solution. Here are some of the key insights:
- Many coding problems require an effcient way to perform the search, insert and delete operations. We can perform all these operations using the hash table in O(1) time average. It's a kind of time-memory tradeoff, where we use extra space to store elements in the hash table to improve performance.
- Sometimes we need to store data in the stack (LIFO order) or queue (FIFO order) to solve several coding problems.
- Suppose there is a requirement to continuously insert or remove maximum or minimum element (Or element with min or max priority). In that case, we can use a heap (or priority queue) to solve the problem efficiently.
- Sometimes, we store data in Trie, AVL Tree, Segment Tree, etc., to perform some critical operations efficiently.
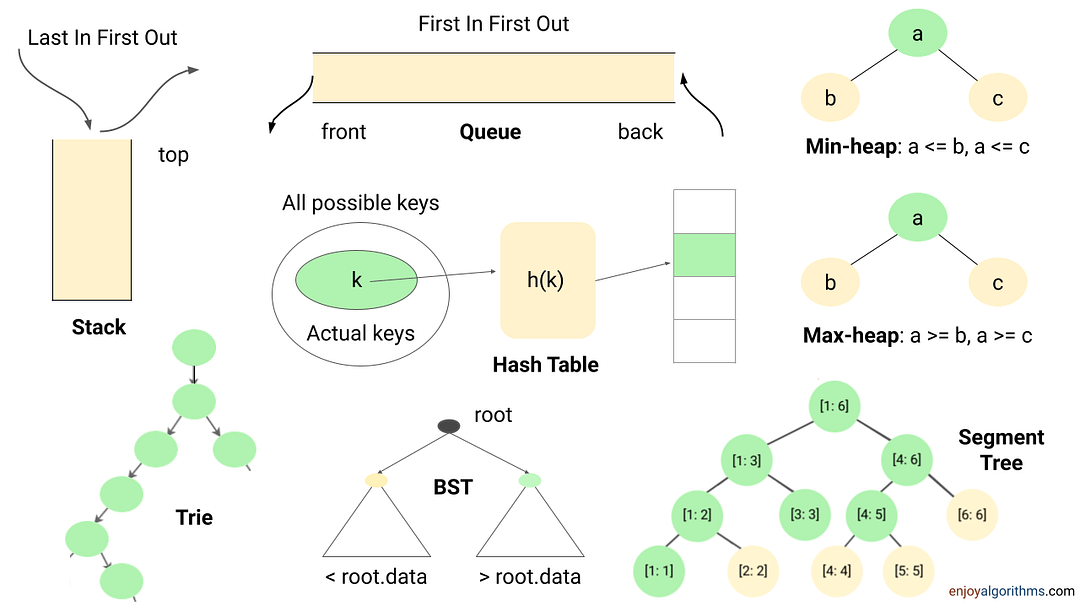
Example problems: Next greater element , Valid Parentheses , Largest rectangle in a histogram , Sliding window maximum , kth smallest element in an array , Top k frequent elements , Longest common prefix , Range sum query , Longest consecutive sequence , Check equal array , LFU cache , LRU cache , Counting sort
Dynamic Programming
Dynamic programming is one of the most popular techniques for solving problems with overlapping or repeated subproblems. Here rather than solving overlapping subproblems repeatedly, we solve each smaller subproblems only once and store the results in memory. We can solve a lot of optimization and counting problems using the idea of dynamic programming.
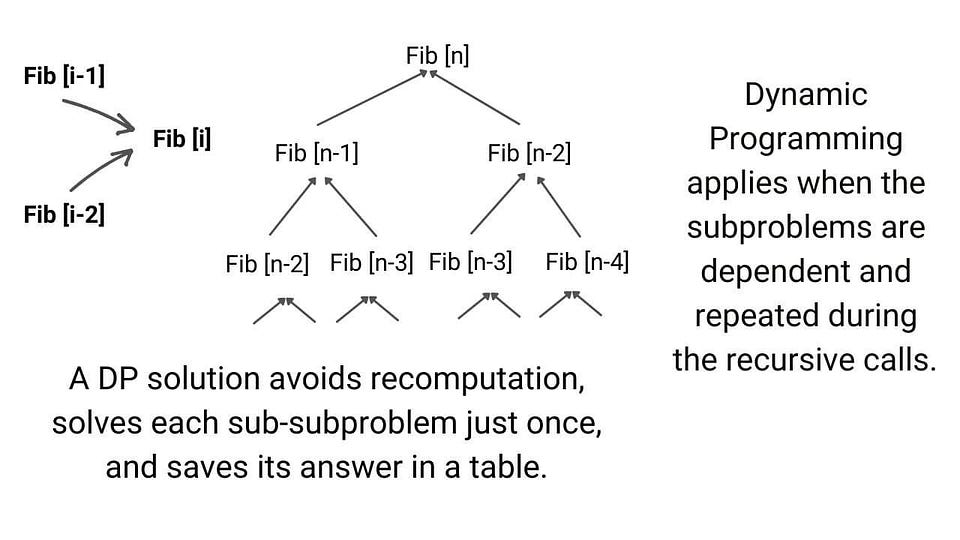
Example problems: Finding nth Fibonacci, Longest Common Subsequence , Climbing Stairs Problem , Maximum Subarray Sum , Minimum number of Jumps to reach End , Minimum Coin Change
Greedy Approach
This solves an optimization problem by expanding a partially constructed solution until a complete solution is reached. We take a greedy choice at each step and add it to the partially constructed solution. This idea produces the optimal global solution without violating the problem’s constraints.
- The greedy choice is the best alternative available at each step is made in the hope that a sequence of locally optimal choices will yield a (globally) optimal solution to the entire problem.
- This approach works in some cases but fails in others. Usually, it is not difficult to design a greedy algorithm itself, but a more difficult task is to prove that it produces an optimal solution.
Example problems: Fractional Knapsack, Dijkstra algorithm, The activity selection problem
Exhaustive Search
This strategy explores all possibilities of solutions until a solution to the problem is found. Therefore, problems are rarely offered to a person to solve the problem using this strategy.
The most important limitation of exhaustive search is its inefficiency. As a rule, the number of solution candidates that need to be processed grows at least exponentially with the problem size, making the approach inappropriate not only for a human but often for a computer as well.
But in some situations, there is a need to explore all possible solution spaces in a coding problem. For example: Find all permutations of a string , Print all subsets , etc.
Backtracking
Backtracking is an improvement over the approach of exhaustive search. It is a method for generating a solution by avoiding unnecessary possibilities of the solutions! The main idea is to build a solution one piece at a time and evaluate each partial solution as follows:
- If a partial solution can be developed further without violating the problem’s constraints, it is done by taking the first remaining valid option at the next stage. ( Think! )
- Suppose there is no valid option at the next stage, i.e., If there is a violation of the problem constraint, the algorithm backtracks to replace the partial solution’s previous stage with the following option for that stage. ( Think! )
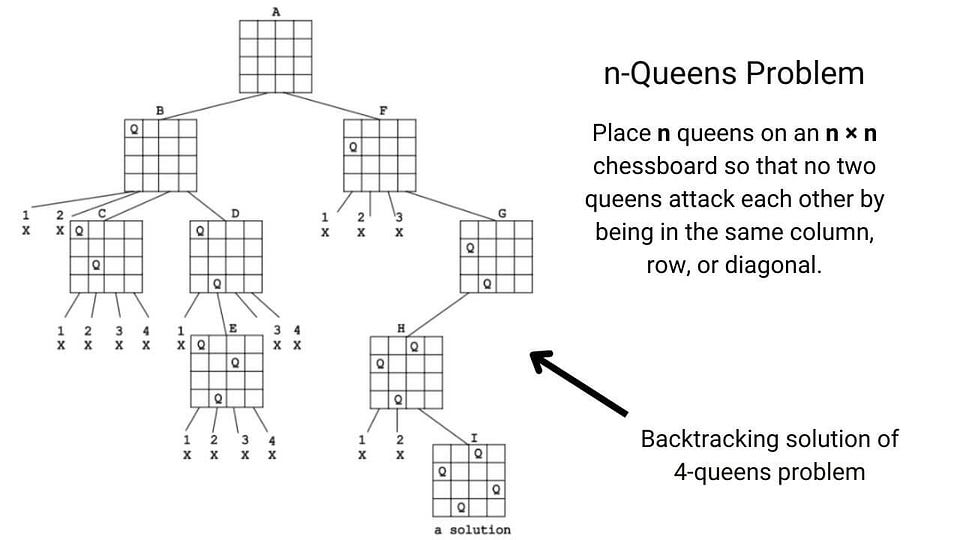
In simple words, backtracking involves undoing several wrong choices — the smaller this number, the faster the algorithm finds a solution. In the worst-case scenario, a backtracking algorithm may end up generating all the solutions as an exhaustive search, but this rarely happens!
Example problems: N-queen problem , Find all k combinations , Combination sum , Sudoku solver , etc.
Problem-solving using Bit manipulation and Numbers theory
Some of the coding problems are, by default, mathematical, but sometimes we need to identify the hidden mathematical properties inside the problem. So the idea of number theory and bit manipulation is helpful in so many cases.
Sometimes understanding the bit pattern of the input and processing data at the bit level help us design an efficient solution. The best part is that the computer performs each bit-wise operation in constant time. Even sometimes, bit manipulation can reduce the requirement of extra loops and improve the performance by a considerable margin.
Example problems: Reverse bits , Add binary string , Check the power of two , Find the missing number , etc.
Hope you enjoyed the blog. Later we will write a separate blog on each problem-solving approach. Enjoy learning, Enjoy algorithms!
More from EnjoyAlgorithms
Self-paced courses and blogs.
How to Solve an Algorithm Problem? | With Examples

If you’re stuck on an algorithm problem and not sure how to proceed, this blog post is for you! We’ll go over some general tips on solving algorithm problems, as well as a specific example of an algorithm .
Table of content:
Introduction.
- What are the 4 steps of algorithmic problem solving?
- Conclusion and References
![problem solving with algorithm [365 Toy Project: 022/365] Batman: Scarlet Part 4 - Solve the problem - Solve an Algorithm.](https://nerdleveltech.com/wp-content/uploads/365-Toy-Project-022365-Batman-Scarlet-Part-4.jpg)
What is an Algorithm?
What is an algorithm? Put simply, an algorithm is a step-by-step procedure for solving a problem. Algorithms can be written in any programming language, but they all share some common characteristics. First and foremost, algorithms are sequence tasks . That means that the steps in the algorithm must be done in order, and each step depends on the results of the previous steps. Secondly, algorithms are deterministic: given the same input data, exactly the same program will produce the same output every time. Finally, there are some measures for an algorithm to be efficient. Time and space: those two measures determine how efficient your algorithm is.

How to Solve an Algorithm Problem?
We’ll walk through some steps for solving a particular algorithm .
First, it’s important to know the basics of algorithms: every problem can be broken down into a sequence of steps that can be solved. This is known as the analysis of algorithms . Sketch out the basic structure of your algorithm on paper first or a board to avoid confusion. write some thoughts about which does what.
If a problem involves mathematical operations, conceptualizing it in terms of equations may be helpful. Break down the equation into its component parts and see if any of those particular pieces can be simplified or eliminated altogether. If so, that will lead to a solution for the whole equation.
Another strategy is to try reversing what initially seems like an impossible task. Algorithms problems often have stages were doing something one-way results in an error message or produces no useful output at all. Reverse engineer those steps and see if anything productive comes out.
What are the 4 steps of algorithmic problem-solving? and Example #1
Now that you know what an algorithm is, let’s jump into some examples and take a look at how these techniques can be put into practice…
In the following we will use the problem challenge from leetcode number #387 :
1) Understand the problem
The goal of any algorithm is to solve a problem. When solving an algorithm problem, it is important to understand the problem and the steps involved in solving it. This understanding will allow you to correctly follow the instructions and complete the task. Answer the common questions to be sure that you really understand the problem. Questions like what it does and what kind of input I’m expecting. what kind of output I should receive? Are there some exceptions I should be aware of? etc…
The goal of this challenge is to write a function that takes in a string and returns the index of the first letter in the string that does not repeat. For example, if the string is “nerd”, the function should return 0, because the first letter “n” is the first non-repeating letter in the string. If the string is “abcdefg”, the function should return 0, because the first letter “a” is the first non-repeating letter in the string.
If the string does not contain any non-repeating letters, the function should return -1. For example, if the input string is “abcabc”, the function should return -1, because no letter in the string is unique or non-repeating.
2) Break the problem down
When solving algorithms problems , breaking them down into smaller parts is usually the best way to go. Once you understand how each part works and interacts with the others, you can solve the problem more quickly.
To solve this challenge, we need to do the following:
- Iterate over the letters in the input string, and for each letter, keep track of how many times it appears in the string. We can do this using an object, dictionary, or map, where the keys are the letters in the string, and the values are the counts for each letter.
- Once we have counted the occurrences of each letter in the string, we need to find the index of the first letter that has a count of 1 (i.e. the first non-repeating letter). To do this, we can iterate over the letters in the string again, and for each letter, check if its count in the object/dictionary is 1. If it is, we return the index of the letter.
- If we reach the end of the loop without finding any value that has only 1 or non-repeating letters, we return -1 to indicate that no non-repeating letters were found.
3) Find your solution
We found one solution and the key steps in this solution are to keep track of the counts of each letter in the input string, and then to search for the first letter with a count of 1. If the count of this letter is 1 meaning that this letter only shows one time in the string. These steps can be implemented in a variety of ways, depending on the language and tools you are using to solve the challenge.
We will be demonstrating the solution with two programming languages JavaScript and Python:
The source code in JavaScript:
Here are some examples of how this function can be used:
The source code in Python :
4) Check your solution
Checking your solution again answers some questions like can I write a better code? by better I mean is the code I provided covering all cases of inputs? is it efficient? and by efficient, I mean using fewer computer resources when possible. If you’re comfortable with your answers then check if there is another solution out there for the same problem you solved, if any are found. go through them I learned a lot by doing that. Also get some feedback on your code, that way you’ll learn many ways of approaching a problem to solve it.
As we mentioned above we asked ourselves these questions but the algorithm we wrote couldn’t go through all the different cases successfully: for example, The code can’t handle the case when we handled two cases of the same character “L” and “l” in the word “Level”
So we need to address that in the following:
Now let’s revisit the code that we wrote up and see if we can come up with another solution that will cover the all different cases of a character.
The source code in JavaScript :
Now that you learned from the first example, let’s jump into another challenge and apply the same techniques we used above:
This example from leetcode problem #125 Valid Palindrome
Learn as much information as you can about the problem what is a Palindrome? Ask yourself what input you expect and what output is expected.
The Palindrome is a word, phrase, or sentence that is spelled backward as forwards. We expect a string and we can do a function that first cleans that string from any non-alphanumeric, then reverses it and compares it with the original string.
Here is a step-by-step explanation of the algorithm in plain English:
- Convert all uppercase letters in the string to lowercase. This is done so that the case of the letters in the string does not affect the outcome of the comparison.
- Remove all non-alphanumeric characters from the string. This is done because only alphanumeric characters are relevant for determining if a string is a palindrome.
- Reverse the resulting string. This is done so that we can compare the reversed string with the original string.
- Compare the reversed string with the original string. If they are the same, then the original string is a palindrome. Otherwise, it is not.
Here is an example of how this algorithm would work on the string “A man, a plan, a canal: Panama”:
- The string is converted to lowercase, so it becomes “a man, a plan, a canal: panama”.
- All non-alphanumeric characters are removed, so the string becomes “amanaplanacanalpanama”.
- The string is reversed, so it becomes “amanaplanacanalpanama”.
- The reversed string is compared with the original string, and since they are the same, the function returns true, indicating that the original string is a palindrome.
According to the steps we wrote in the previous stage, let’s put them into action and code it up.
The source code in Python:
We can make it more efficient by using the pointers method let’s break it down into a few points below:
- Create left and right pointers (will be represented by indices)
- Make each pointer move to the middle direction
- While moving to check each letter for both pointers are the same

Conclusion and references
There are many resources available to help you out, and with more practice , you’ll be able to solve many algorithm problems that come your way . This video is one of the great resources to learn about algorithms and data structures from FreeCodeCamp
It is important to keep a cool head and not get bogged down in frustration. Algorithms problems can be difficult, but with patience and perseverance, they can be solved.
When you are solving an algorithm problem, it is important to be able to check your solution against other solutions if possible to see how others approach the same problem. This is will help you to retain and understand the logic behind the different solutions so you’ll need this kind of knowledge in the future solving problems.
By following the steps outlined in this article, you will be able to solve algorithm problems with ease. Remember to keep a notebook or excel sheet with all of your solutions so that you can revisit them later on that way you will gain maximum retention of the logic.
If you want to learn more about algorithms and programming , sign up for our mailing list. We’ll send you tips, tricks, and resources to help you improve your skills.
Ahmed Radwan
Reach out if you want to join me and write articles with the nerds 🙂
How to Make Your Corporate Website Stand Out With These 10 Tips
How to write clean code and best practices, you may also like, here are some new features in javascript, top 100 problems on leetcode and its solutions – part1, learn essential javascript methods and objects.
- Smart Devices
- Programming
- Web Development
- Presentation
- Infographics
Have a language expert improve your writing
Check your paper for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Using AI tools
- What Is an Algorithm? | Definition & Examples
What Is an Algorithm? | Definition & Examples
Published on August 9, 2023 by Kassiani Nikolopoulou . Revised on August 29, 2023.
An algorithm is a set of steps for accomplishing a task or solving a problem. Typically, algorithms are executed by computers, but we also rely on algorithms in our daily lives. Each time we follow a particular step-by-step process, like making coffee in the morning or tying our shoelaces, we are in fact following an algorithm.
In the context of computer science , an algorithm is a mathematical process for solving a problem using a finite number of steps. Algorithms are a key component of any computer program and are the driving force behind various systems and applications, such as navigation systems, search engines, and music streaming services.
Instantly correct all language mistakes in your text
Upload your document to correct all your mistakes in minutes
Table of contents
What is an algorithm, how do algorithms work, examples of algorithms, other interesting articles, frequently asked questions about algorithms.
An algorithm is a sequence of instructions that a computer must perform to solve a well-defined problem. It essentially defines what the computer needs to do and how to do it. Algorithms can instruct a computer how to perform a calculation, process data, or make a decision.
The best way to understand an algorithm is to think of it as a recipe that guides you through a series of well-defined actions to achieve a specific goal. Just like a recipe produces a replicable result, algorithms ensure consistent and reliable outcomes for a wide range of tasks in the digital realm.
And just like there are numerous ways to make, for example, chocolate chip cookies by following different steps or using slightly different ingredients, different algorithms can be designed to solve the same problem, with each taking a distinct approach but achieving the same result.
Algorithms are virtually everywhere around us. Examples include the following:
- Search engines rely on algorithms to find and present relevant results as quickly as possible
- Social media platforms use algorithms to prioritize the content that we see in our feeds, taking into account factors like our past behavior, the popularity of posts, and relevance.
- With the help of algorithms, navigation apps determine the most efficient route for us to reach our destination.
- It must be correct . In other words, it should take a given problem and provide the right answer or result, even if it stops working due to an error.
- It must consist of clear, practical steps that can be completed in a limited time, whether by a person or the machine that must execute the algorithm. For example, the instructions in a cookie recipe might be considered sufficiently concrete for a human cook, but they would not be specific enough for programming an automated cookie-making machine.
- There should be no confusion about which step comes next , even if choices must be made (e.g., when using “if” statements).
- It must have a set number of steps (not an infinite number) that can be managed using loops (statements describing repeated actions or iterations).
- It must eventually reach an endpoint and not get stuck in a never-ending loop.
Check for common mistakes
Use the best grammar checker available to check for common mistakes in your text.
Fix mistakes for free
Algorithms use a set of initial data or input , process it through a series of logical steps or rules, and produce the output (i.e., the outcome, decision, or result).

If you want to make chocolate chip cookies, for instance, the input would be the ingredients and quantities, the process would be the recipe you choose to follow, and the output would be the cookies.
Algorithms are eventually expressed in a programming language that a computer can process. However, when an algorithm is being created, it will be people, not a computer, who will need to understand it. For this reason, as a first step, algorithms are written as plain instructions.
- Input: the input data is a single-digit number (e.g., 5).
- Transformation/processing: the algorithm takes the input (number 5) and performs the specific operation (i.e., multiplies the number by itself).
- Output: the result of the calculation is the square of the input number, which, in this case, would be 25 (since 5 * 5 = 25).
We could express this as an algorithm in the following way:
Algorithm: Calculate the square of a number
- Input the number (N) whose square you want to find.
- Multiply the number (N) by itself.
- Store the result of the multiplication in a variable (result).
- Output the value of the variable (result), which represents the square of the input number.
It is important to keep in mind that an algorithm is not the same as a program or code. It is the logic or plan for solving a problem represented as a simple step-by-step description. Code is the implementation of the algorithm in a specific programming language (like C++ or Python), while a program is an implementation of code that instructs a computer on how to execute an algorithm and perform a task.
Instead of telling a computer exactly what to do, some algorithms allow computers to learn on their own and improve their performance on a specific task. These machine learning algorithms use data to identify patterns and make predictions or conduct data mining to uncover hidden insights in data that can inform business decisions.
Broadly speaking, there are three different types of algorithms:
- Linear sequence algorithms follow a specific set or steps, one after the other. Just like following a recipe, each step depends on the success of the previous one.
- For example, in the context of a cookie recipe, you would include the step “if the dough is too sticky, you might need to refrigerate it.”
- For example, a looping algorithm could be used to handle the process of making multiple cookies from a single batch of dough. The algorithm would repeat a specific set of instructions to form and bake cookies until all the dough has been used.
Algorithms are fundamental tools for problem-solving in both the digital world and many real-life scenarios. Each time we try to solve a problem by breaking it down into smaller, manageable steps, we are in fact using algorithmic thinking.
- Identify which clothes are clean.
- Consider the weather forecast for the day.
- Consider the occasion for which you are getting dressed (e.g., work or school etc.).
- Consider personal preferences (e.g., style or which items match).
In mathematics, algorithms are standard methods for performing calculations or solving equations because they are efficient, reliable, and applicable to various situations.
Suppose you want to add the numbers 345 and 278. You would follow a set of steps (i.e., the standard algorithm for addition):
- Write down the numbers so the digits align.
- Start from the rightmost digits (the ones place) and add them together: 5 + 8 = 13. Write down the 3 and carry over the 1 to the next column.
- Move to the next column (the tens place) and add the digits along with the carried-over value: 4 + 7 + 1 = 12. Write down the 2 and carry over the 1 to the next column.
- Move to the leftmost column (the hundreds place) and add the digits along with the carried-over value: 3 + 2 + 1 = 6. Write down the 6.
The final result is 623

Navigation systems are another example of the use of algorithms. Such systems use algorithms to help you find the easiest and fastest route to your destination while avoiding traffic jams and roadblocks.
If you want to know more about ChatGPT, AI tools , fallacies , and research bias , make sure to check out some of our other articles with explanations and examples.
- ChatGPT vs human editor
- ChatGPT citations
- Is ChatGPT trustworthy?
- Using ChatGPT for your studies
- Sunk cost fallacy
- Straw man fallacy
- Slippery slope fallacy
- Red herring fallacy
- Ecological fallacy
- Logical fallacy
Research bias
- Implicit bias
- Framing bias
- Cognitive bias
- Optimism bias
- Hawthorne effect
- Unconscious bias
Don't submit your assignments before you do this
The academic proofreading tool has been trained on 1000s of academic texts. Making it the most accurate and reliable proofreading tool for students. Free citation check included.
Try for free
In computer science, an algorithm is a list of unambiguous instructions that specify successive steps to solve a problem or perform a task. Algorithms help computers execute tasks like playing games or sorting a list of numbers. In other words, computers use algorithms to understand what to do and give you the result you need.
Algorithms and artificial intelligence (AI) are not the same, however they are closely related.
- Artificial intelligence is a broad term describing computer systems performing tasks usually associated with human intelligence like decision-making, pattern recognition, or learning from experience.
- Algorithms are the instructions that AI uses to carry out these tasks, therefore we could say that algorithms are the building blocks of AI—even though AI involves more advanced capabilities beyond just following instructions.
Algorithms and computer programs are sometimes used interchangeably, but they refer to two distinct but interrelated concepts.
- An algorithm is a step-by-step instruction for solving a problem that is precise yet general.
- Computer programs are specific implementations of an algorithm in a specific programming language. In other words, the algorithm is the high-level description of an idea, while the program is the actual implementation of that idea.
Algorithms are valuable to us because they:
- Form the basis of much of the technology we use in our daily lives, from mobile apps to search engines.
- Power innovations in various industries that augment our abilities (e.g., AI assistants or medical diagnosis).
- Help analyze large volumes of data, discover patterns and make informed decisions in a fast and efficient way, at a scale humans are simply not able to do.
- Automate processes. By streamlining tasks, algorithms increase efficiency, reduce errors, and save valuable time.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Nikolopoulou, K. (2023, August 29). What Is an Algorithm? | Definition & Examples. Scribbr. Retrieved June 18, 2024, from https://www.scribbr.com/ai-tools/what-is-an-algorithm/
Is this article helpful?

Kassiani Nikolopoulou
Other students also liked, what is deep learning | a beginner's guide, what is data mining | definition & techniques, what is machine learning | a beginner's guide.
Kassiani Nikolopoulou (Scribbr Team)
Thanks for reading! Hope you found this article helpful. If anything is still unclear, or if you didn’t find what you were looking for here, leave a comment and we’ll see if we can help.
Still have questions?
Get unlimited documents corrected.
✔ Free APA citation check included ✔ Unlimited document corrections ✔ Specialized in correcting academic texts
Chapter: Introduction to the Design and Analysis of Algorithms
Fundamentals of Algorithmic Problem Solving
Let us start by reiterating an important point made in the introduction to this chapter:
We can consider algorithms to be procedural solutions to problems.
These solutions are not answers but specific instructions for getting answers. It is this emphasis on precisely defined constructive procedures that makes computer science distinct from other disciplines. In particular, this distinguishes it from the-oretical mathematics, whose practitioners are typically satisfied with just proving the existence of a solution to a problem and, possibly, investigating the solution’s properties.
We now list and briefly discuss a sequence of steps one typically goes through in designing and analyzing an algorithm (Figure 1.2).
Understanding the Problem
From a practical perspective, the first thing you need to do before designing an algorithm is to understand completely the problem given. Read the problem’s description carefully and ask questions if you have any doubts about the problem, do a few small examples by hand, think about special cases, and ask questions again if needed.
There are a few types of problems that arise in computing applications quite often. We review them in the next section. If the problem in question is one of them, you might be able to use a known algorithm for solving it. Of course, it helps to understand how such an algorithm works and to know its strengths and weaknesses, especially if you have to choose among several available algorithms. But often you will not find a readily available algorithm and will have to design your own. The sequence of steps outlined in this section should help you in this exciting but not always easy task.
An input to an algorithm specifies an instance of the problem the algorithm solves. It is very important to specify exactly the set of instances the algorithm needs to handle. (As an example, recall the variations in the set of instances for the three greatest common divisor algorithms discussed in the previous section.) If you fail to do this, your algorithm may work correctly for a majority of inputs but crash on some “boundary” value. Remember that a correct algorithm is not one that works most of the time, but one that works correctly for all legitimate inputs.
Do not skimp on this first step of the algorithmic problem-solving process; otherwise, you will run the risk of unnecessary rework.
Ascertaining the Capabilities of the Computational Device
Once you completely understand a problem, you need to ascertain the capabilities of the computational device the algorithm is intended for. The vast majority of
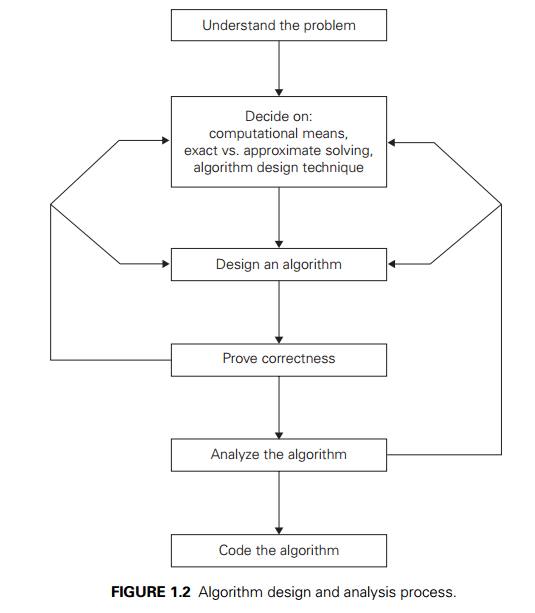
algorithms in use today are still destined to be programmed for a computer closely resembling the von Neumann machine—a computer architecture outlined by the prominent Hungarian-American mathematician John von Neumann (1903– 1957), in collaboration with A. Burks and H. Goldstine, in 1946. The essence of this architecture is captured by the so-called random-access machine ( RAM ). Its central assumption is that instructions are executed one after another, one operation at a time. Accordingly, algorithms designed to be executed on such machines are called sequential algorithms .
The central assumption of the RAM model does not hold for some newer computers that can execute operations concurrently, i.e., in parallel. Algorithms that take advantage of this capability are called parallel algorithms . Still, studying the classic techniques for design and analysis of algorithms under the RAM model remains the cornerstone of algorithmics for the foreseeable future.
Should you worry about the speed and amount of memory of a computer at your disposal? If you are designing an algorithm as a scientific exercise, the answer is a qualified no. As you will see in Section 2.1, most computer scientists prefer to study algorithms in terms independent of specification parameters for a particular computer. If you are designing an algorithm as a practical tool, the answer may depend on a problem you need to solve. Even the “slow” computers of today are almost unimaginably fast. Consequently, in many situations you need not worry about a computer being too slow for the task. There are important problems, however, that are very complex by their nature, or have to process huge volumes of data, or deal with applications where the time is critical. In such situations, it is imperative to be aware of the speed and memory available on a particular computer system.
Choosing between Exact and Approximate Problem Solving
The next principal decision is to choose between solving the problem exactly or solving it approximately. In the former case, an algorithm is called an exact algo-rithm ; in the latter case, an algorithm is called an approximation algorithm . Why would one opt for an approximation algorithm? First, there are important prob-lems that simply cannot be solved exactly for most of their instances; examples include extracting square roots, solving nonlinear equations, and evaluating def-inite integrals. Second, available algorithms for solving a problem exactly can be unacceptably slow because of the problem’s intrinsic complexity. This happens, in particular, for many problems involving a very large number of choices; you will see examples of such difficult problems in Chapters 3, 11, and 12. Third, an ap-proximation algorithm can be a part of a more sophisticated algorithm that solves a problem exactly.
Algorithm Design Techniques
Now, with all the components of the algorithmic problem solving in place, how do you design an algorithm to solve a given problem? This is the main question this book seeks to answer by teaching you several general design techniques.
What is an algorithm design technique?
An algorithm design technique (or “strategy” or “paradigm”) is a general approach to solving problems algorithmically that is applicable to a variety of problems from different areas of computing.
Check this book’s table of contents and you will see that a majority of its chapters are devoted to individual design techniques. They distill a few key ideas that have proven to be useful in designing algorithms. Learning these techniques is of utmost importance for the following reasons.
First, they provide guidance for designing algorithms for new problems, i.e., problems for which there is no known satisfactory algorithm. Therefore—to use the language of a famous proverb—learning such techniques is akin to learning to fish as opposed to being given a fish caught by somebody else. It is not true, of course, that each of these general techniques will be necessarily applicable to every problem you may encounter. But taken together, they do constitute a powerful collection of tools that you will find quite handy in your studies and work.
Second, algorithms are the cornerstone of computer science. Every science is interested in classifying its principal subject, and computer science is no exception. Algorithm design techniques make it possible to classify algorithms according to an underlying design idea; therefore, they can serve as a natural way to both categorize and study algorithms.
Designing an Algorithm and Data Structures
While the algorithm design techniques do provide a powerful set of general ap-proaches to algorithmic problem solving, designing an algorithm for a particular problem may still be a challenging task. Some design techniques can be simply inapplicable to the problem in question. Sometimes, several techniques need to be combined, and there are algorithms that are hard to pinpoint as applications of the known design techniques. Even when a particular design technique is ap-plicable, getting an algorithm often requires a nontrivial ingenuity on the part of the algorithm designer. With practice, both tasks—choosing among the general techniques and applying them—get easier, but they are rarely easy.
Of course, one should pay close attention to choosing data structures appro-priate for the operations performed by the algorithm. For example, the sieve of Eratosthenes introduced in Section 1.1 would run longer if we used a linked list instead of an array in its implementation (why?). Also note that some of the al-gorithm design techniques discussed in Chapters 6 and 7 depend intimately on structuring or restructuring data specifying a problem’s instance. Many years ago, an influential textbook proclaimed the fundamental importance of both algo-rithms and data structures for computer programming by its very title: Algorithms + Data Structures = Programs [Wir76]. In the new world of object-oriented programming, data structures remain crucially important for both design and analysis of algorithms. We review basic data structures in Section 1.4.
Methods of Specifying an Algorithm
Once you have designed an algorithm, you need to specify it in some fashion. In Section 1.1, to give you an example, Euclid’s algorithm is described in words (in a free and also a step-by-step form) and in pseudocode. These are the two options that are most widely used nowadays for specifying algorithms.
Using a natural language has an obvious appeal; however, the inherent ambi-guity of any natural language makes a succinct and clear description of algorithms surprisingly difficult. Nevertheless, being able to do this is an important skill that you should strive to develop in the process of learning algorithms.
Pseudocode is a mixture of a natural language and programming language-like constructs. Pseudocode is usually more precise than natural language, and its usage often yields more succinct algorithm descriptions. Surprisingly, computer scientists have never agreed on a single form of pseudocode, leaving textbook authors with a need to design their own “dialects.” Fortunately, these dialects are so close to each other that anyone familiar with a modern programming language should be able to understand them all.
This book’s dialect was selected to cause minimal difficulty for a reader. For the sake of simplicity, we omit declarations of variables and use indentation to show the scope of such statements as for , if , and while . As you saw in the previous section, we use an arrow “ ← ” for the assignment operation and two slashes “ // ” for comments.
In the earlier days of computing, the dominant vehicle for specifying algo-rithms was a flowchart , a method of expressing an algorithm by a collection of connected geometric shapes containing descriptions of the algorithm’s steps. This representation technique has proved to be inconvenient for all but very simple algorithms; nowadays, it can be found only in old algorithm books.
The state of the art of computing has not yet reached a point where an algorithm’s description—be it in a natural language or pseudocode—can be fed into an electronic computer directly. Instead, it needs to be converted into a computer program written in a particular computer language. We can look at such a program as yet another way of specifying the algorithm, although it is preferable to consider it as the algorithm’s implementation.
Proving an Algorithm’s Correctness
Once an algorithm has been specified, you have to prove its correctness . That is, you have to prove that the algorithm yields a required result for every legitimate input in a finite amount of time. For example, the correctness of Euclid’s algorithm for computing the greatest common divisor stems from the correctness of the equality gcd (m, n) = gcd (n, m mod n) (which, in turn, needs a proof; see Problem 7 in Exercises 1.1), the simple observation that the second integer gets smaller on every iteration of the algorithm, and the fact that the algorithm stops when the second integer becomes 0.
For some algorithms, a proof of correctness is quite easy; for others, it can be quite complex. A common technique for proving correctness is to use mathemati-cal induction because an algorithm’s iterations provide a natural sequence of steps needed for such proofs. It might be worth mentioning that although tracing the algorithm’s performance for a few specific inputs can be a very worthwhile activ-ity, it cannot prove the algorithm’s correctness conclusively. But in order to show that an algorithm is incorrect, you need just one instance of its input for which the algorithm fails.
The notion of correctness for approximation algorithms is less straightforward than it is for exact algorithms. For an approximation algorithm, we usually would like to be able to show that the error produced by the algorithm does not exceed a predefined limit. You can find examples of such investigations in Chapter 12.
Analyzing an Algorithm
We usually want our algorithms to possess several qualities. After correctness, by far the most important is efficiency . In fact, there are two kinds of algorithm efficiency: time efficiency , indicating how fast the algorithm runs, and space ef-ficiency , indicating how much extra memory it uses. A general framework and specific techniques for analyzing an algorithm’s efficiency appear in Chapter 2.
Another desirable characteristic of an algorithm is simplicity . Unlike effi-ciency, which can be precisely defined and investigated with mathematical rigor, simplicity, like beauty, is to a considerable degree in the eye of the beholder. For example, most people would agree that Euclid’s algorithm is simpler than the middle-school procedure for computing gcd (m, n) , but it is not clear whether Eu-clid’s algorithm is simpler than the consecutive integer checking algorithm. Still, simplicity is an important algorithm characteristic to strive for. Why? Because sim-pler algorithms are easier to understand and easier to program; consequently, the resulting programs usually contain fewer bugs. There is also the undeniable aes-thetic appeal of simplicity. Sometimes simpler algorithms are also more efficient than more complicated alternatives. Unfortunately, it is not always true, in which case a judicious compromise needs to be made.
Yet another desirable characteristic of an algorithm is generality . There are, in fact, two issues here: generality of the problem the algorithm solves and the set of inputs it accepts. On the first issue, note that it is sometimes easier to design an algorithm for a problem posed in more general terms. Consider, for example, the problem of determining whether two integers are relatively prime, i.e., whether their only common divisor is equal to 1. It is easier to design an algorithm for a more general problem of computing the greatest common divisor of two integers and, to solve the former problem, check whether the gcd is 1 or not. There are situations, however, where designing a more general algorithm is unnecessary or difficult or even impossible. For example, it is unnecessary to sort a list of n numbers to find its median, which is its n/ 2 th smallest element. To give another example, the standard formula for roots of a quadratic equation cannot be generalized to handle polynomials of arbitrary degrees.
As to the set of inputs, your main concern should be designing an algorithm that can handle a set of inputs that is natural for the problem at hand. For example, excluding integers equal to 1 as possible inputs for a greatest common divisor algorithm would be quite unnatural. On the other hand, although the standard formula for the roots of a quadratic equation holds for complex coefficients, we would normally not implement it on this level of generality unless this capability is explicitly required.
If you are not satisfied with the algorithm’s efficiency, simplicity, or generality, you must return to the drawing board and redesign the algorithm. In fact, even if your evaluation is positive, it is still worth searching for other algorithmic solutions. Recall the three different algorithms in the previous section for computing the greatest common divisor: generally, you should not expect to get the best algorithm on the first try. At the very least, you should try to fine-tune the algorithm you already have. For example, we made several improvements in our implementation of the sieve of Eratosthenes compared with its initial outline in Section 1.1. (Can you identify them?) You will do well if you keep in mind the following observation of Antoine de Saint-Exupery,´ the French writer, pilot, and aircraft designer: “A designer knows he has arrived at perfection not when there is no longer anything to add, but when there is no longer anything to take away.” 1
Coding an Algorithm
Most algorithms are destined to be ultimately implemented as computer pro-grams. Programming an algorithm presents both a peril and an opportunity. The peril lies in the possibility of making the transition from an algorithm to a pro-gram either incorrectly or very inefficiently. Some influential computer scientists strongly believe that unless the correctness of a computer program is proven with full mathematical rigor, the program cannot be considered correct. They have developed special techniques for doing such proofs (see [Gri81]), but the power of these techniques of formal verification is limited so far to very small programs.
As a practical matter, the validity of programs is still established by testing. Testing of computer programs is an art rather than a science, but that does not mean that there is nothing in it to learn. Look up books devoted to testing and debugging; even more important, test and debug your program thoroughly whenever you implement an algorithm.
Also note that throughout the book, we assume that inputs to algorithms belong to the specified sets and hence require no verification. When implementing algorithms as programs to be used in actual applications, you should provide such verifications.
Of course, implementing an algorithm correctly is necessary but not sufficient: you would not like to diminish your algorithm’s power by an inefficient implemen-tation. Modern compilers do provide a certain safety net in this regard, especially when they are used in their code optimization mode. Still, you need to be aware of such standard tricks as computing a loop’s invariant (an expression that does not change its value) outside the loop, collecting common subexpressions, replac-ing expensive operations by cheap ones, and so on. (See [Ker99] and [Ben00] for a good discussion of code tuning and other issues related to algorithm program-ming.) Typically, such improvements can speed up a program only by a constant factor, whereas a better algorithm can make a difference in running time by orders of magnitude. But once an algorithm is selected, a 10–50% speedup may be worth an effort.
A working program provides an additional opportunity in allowing an em-pirical analysis of the underlying algorithm. Such an analysis is based on timing the program on several inputs and then analyzing the results obtained. We dis-cuss the advantages and disadvantages of this approach to analyzing algorithms in Section 2.6.
In conclusion, let us emphasize again the main lesson of the process depicted in Figure 1.2:
As a rule, a good algorithm is a result of repeated effort and rework.
Even if you have been fortunate enough to get an algorithmic idea that seems perfect, you should still try to see whether it can be improved.
Actually, this is good news since it makes the ultimate result so much more enjoyable. (Yes, I did think of naming this book The Joy of Algorithms .) On the other hand, how does one know when to stop? In the real world, more often than not a project’s schedule or the impatience of your boss will stop you. And so it should be: perfection is expensive and in fact not always called for. Designing an algorithm is an engineering-like activity that calls for compromises among competing goals under the constraints of available resources, with the designer’s time being one of the resources.
In the academic world, the question leads to an interesting but usually difficult investigation of an algorithm’s optimality . Actually, this question is not about the efficiency of an algorithm but about the complexity of the problem it solves: What is the minimum amount of effort any algorithm will need to exert to solve the problem? For some problems, the answer to this question is known. For example, any algorithm that sorts an array by comparing values of its elements needs about n log 2 n comparisons for some arrays of size n (see Section 11.2). But for many seemingly easy problems such as integer multiplication, computer scientists do not yet have a final answer.
Another important issue of algorithmic problem solving is the question of whether or not every problem can be solved by an algorithm. We are not talking here about problems that do not have a solution, such as finding real roots of a quadratic equation with a negative discriminant. For such cases, an output indicating that the problem does not have a solution is all we can and should expect from an algorithm. Nor are we talking about ambiguously stated problems. Even some unambiguous problems that must have a simple yes or no answer are “undecidable,” i.e., unsolvable by any algorithm. An important example of such a problem appears in Section 11.3. Fortunately, a vast majority of problems in practical computing can be solved by an algorithm.
Before leaving this section, let us be sure that you do not have the misconception—possibly caused by the somewhat mechanical nature of the diagram of Figure 1.2—that designing an algorithm is a dull activity. There is nothing further from the truth: inventing (or discovering?) algorithms is a very creative and rewarding process. This book is designed to convince you that this is the case.
Exercises 1.2
Old World puzzle A peasant finds himself on a riverbank with a wolf, a goat, and a head of cabbage. He needs to transport all three to the other side of the river in his boat. However, the boat has room for only the peasant himself and one other item (either the wolf, the goat, or the cabbage). In his absence, the wolf would eat the goat, and the goat would eat the cabbage. Solve this problem for the peasant or prove it has no solution. (Note: The peasant is a vegetarian but does not like cabbage and hence can eat neither the goat nor the cabbage to help him solve the problem. And it goes without saying that the wolf is a protected species.)
New World puzzle There are four people who want to cross a rickety bridge; they all begin on the same side. You have 17 minutes to get them all across to the other side. It is night, and they have one flashlight. A maximum of two people can cross the bridge at one time. Any party that crosses, either one or two people, must have the flashlight with them. The flashlight must be walked back and forth; it cannot be thrown, for example. Person 1 takes 1 minute to cross the bridge, person 2 takes 2 minutes, person 3 takes 5 minutes, and person 4 takes 10 minutes. A pair must walk together at the rate of the slower person’s pace. (Note: According to a rumor on the Internet, interviewers at a well-known software company located near Seattle have given this problem to interviewees.)
Which of the following formulas can be considered an algorithm for comput-ing the area of a triangle whose side lengths are given positive numbers a , b , and c ?
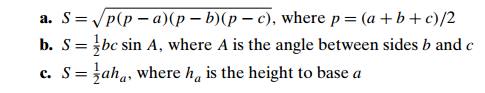
Write pseudocode for an algorithm for finding real roots of equation ax 2 + bx + c = 0 for arbitrary real coefficients a, b, and c. (You may assume the availability of the square root function sqrt (x). )
Describe the standard algorithm for finding the binary representation of a positive decimal integer
in English.
in pseudocode.
Describe the algorithm used by your favorite ATM machine in dispensing cash. (You may give your description in either English or pseudocode, which-ever you find more convenient.)
a. Can the problem of computing the number π be solved exactly?
How many instances does this problem have?
Look up an algorithm for this problem on the Internet.
Give an example of a problem other than computing the greatest common divisor for which you know more than one algorithm. Which of them is simpler? Which is more efficient?
Consider the following algorithm for finding the distance between the two closest elements in an array of numbers.
ALGORITHM MinDistance (A [0 ..n − 1] )
//Input: Array A [0 ..n − 1] of numbers
//Output: Minimum distance between two of its elements dmin ← ∞
for i ← 0 to n − 1 do
for j ← 0 to n − 1 do
if i = j and |A[i] − A[j ]| < dmin dmin ← |A[i] − A[j ]|
return dmin
Make as many improvements as you can in this algorithmic solution to the problem. If you need to, you may change the algorithm altogether; if not, improve the implementation given.
One of the most influential books on problem solving, titled How To Solve It [Pol57], was written by the Hungarian-American mathematician George Polya´ (1887–1985). Polya´ summarized his ideas in a four-point summary. Find this summary on the Internet or, better yet, in his book, and compare it with the plan outlined in Section 1.2. What do they have in common? How are they different?
Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
- Bipolar Disorder
- Therapy Center
- When To See a Therapist
- Types of Therapy
- Best Online Therapy
- Best Couples Therapy
- Best Family Therapy
- Managing Stress
- Sleep and Dreaming
- Understanding Emotions
- Self-Improvement
- Healthy Relationships
- Student Resources
- Personality Types
- Guided Meditations
- Verywell Mind Insights
- 2024 Verywell Mind 25
- Mental Health in the Classroom
- Editorial Process
- Meet Our Review Board
- Crisis Support
What Is an Algorithm in Psychology?
Definition, Examples, and Uses
Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
:max_bytes(150000):strip_icc():format(webp)/IMG_9791-89504ab694d54b66bbd72cb84ffb860e.jpg)
James Lacy, MLS, is a fact-checker and researcher.
:max_bytes(150000):strip_icc():format(webp)/James-Lacy-1000-73de2239670146618c03f8b77f02f84e.jpg)
How Does an Algorithm Work?
Examples of algorithms.
- Reasons to Use Algorithms
- Potential Pitfalls
Algorithms vs. Heuristics
When solving a problem , choosing the right approach is often the key to arriving at the best solution. In psychology, one of these problem-solving approaches is known as an algorithm. While often thought of purely as a mathematical term, the same type of process can be followed in psychology to find the correct answer when solving a problem or making a decision.
An algorithm is a defined set of step-by-step procedures that provides the correct answer to a particular problem. By following the instructions correctly, you are guaranteed to arrive at the right answer.
At a Glance
Algorithms involve following specific steps in order to reach a solution to a problem. They can be a great tool when you need an accurate solution but tend to be more time-consuming than other methods.
This article discusses how algorithms are used as an approach to problem-solving. It also covers how psychologists compare this approach to other problem-solving methods.
An algorithm is often expressed in the form of a graph, where a square represents each step. Arrows then branch off from each step to point to possible directions that you may take to solve the problem.
In some cases, you must follow a particular set of steps to solve the problem. In other instances, you might be able to follow different paths that will all lead to the same solution.
Algorithms are essential step-by-step approaches to solving a problem. Rather than guessing or using trial-and-error, this approach is more likely to guarantee a specific solution.
Using an algorithm can help you solve day-to-day problems you face, but it can also help mental health professionals find ways to help people cope with mental health problems.
For example, a therapist might use an algorithm to treat a person experiencing something like anxiety. Because the therapist knows that a particular approach is likely to be effective, they would recommend a series of specific, focused steps as part of their intervention.
There are many different examples of how algorithms can be used in daily life. Some common ones include:
- A recipe for cooking a particular dish
- The method a search engine uses to find information on the internet
- Instructions for how to assemble a bicycle
- Instructions for how to solve a Rubik's cube
- A process to determine what type of treatment is most appropriate for certain types of mental health conditions
Doctors and mental health professionals often use algorithms to diagnose mental disorders . For example, they may use a step-by-step approach when they evaluate people.
This might involve asking the individual about their symptoms and their medical history. The doctor may also conduct lab tests, physical exams, or psychological assessments.
Using this information, they then utilize the "Diagnostic and Statistical Manual of Mental Disorders" (DSM-5-TR) to make a diagnosis.
Reasons to Use Algorithms in Psychology
The upside of using an algorithm to solve a problem or make a decision is that yields the best possible answer every time. There are situations where using an algorithm can be the best approach:
When Accuracy Is Crucial
Algorithms can be particularly useful in situations when accuracy is critical. They are also a good choice when similar problems need to be frequently solved.
Computer programs can often be designed to speed up this process. Data then needs to be placed in the system so that the algorithm can be executed for the correct solution.
Artificial intelligence may also be a tool for making clinical assessments in healthcare situations.
When Each Decision Needs to Follow the Same Process
Such step-by-step approaches can be useful in situations where each decision must be made following the same process. Because the process follows a prescribed procedure, you can be sure that you will reach the correct answer each time.
Potential Pitfalls When Using Algorithms
The downside of using an algorithm to solve the problem is that this process tends to be very time-consuming.
So if you face a situation where a decision must be made very quickly, you might be better off using a different problem-solving strategy.
For example, an emergency room doctor making a decision about how to treat a patient could use an algorithm approach. However, this would be very time-consuming and treatment needs to be implemented quickly.
In this instance, the doctor would instead rely on their expertise and past experiences to very quickly choose what they feel is the right treatment approach.
Algorithms can sometimes be very complex and may only apply to specific situations. This can limit their use and make them less generalizable when working with larger populations.
Algorithms can be a great problem-solving choice when the answer needs to be 100% accurate or when each decision needs to follow the same process. A different approach might be needed if speed is the primary concern.
In psychology, algorithms are frequently contrasted with heuristics . Both can be useful when problem-solving, but it is important to understand the differences between them.
What Is a Heuristic?
A heuristic is a mental shortcut that allows people to quickly make judgments and solve problems.
These mental shortcuts are typically informed by our past experiences and allow us to act quickly. However, heuristics are really more of a rule-of-thumb; they don't always guarantee a correct solution.
So how do you determine when to use a heuristic and when to use an algorithm? When problem-solving, deciding which method to use depends on the need for either accuracy or speed.
When to Use an Algorithm
If complete accuracy is required, it is best to use an algorithm. By using an algorithm, accuracy is increased and potential mistakes are minimized.
If you are working in a situation where you absolutely need the correct or best possible answer, your best bet is to use an algorithm. When you are solving problems for your math homework, you don't want to risk your grade on a guess.
By following an algorithm, you can ensure that you will arrive at the correct answer to each problem.
When to Use a Heuristic
On the other hand, if time is an issue, then it may be best to use a heuristic. Mistakes may occur, but this approach allows for speedy decisions when time is of the essence.
Heuristics are more commonly used in everyday situations, such as figuring out the best route to get from point A to point B. While you could use an algorithm to map out every possible route and determine which one would be the fastest, that would be a very time-consuming process. Instead, your best option would be to use a route that you know has worked well in the past.
Psychologists who study problem-solving have described two main processes people utilize to reach conclusions: algorithms and heuristics. Knowing which approach to use is important because these two methods can vary in terms of speed and accuracy.
While each situation is unique, you may want to use an algorithm when being accurate is the primary concern. But if time is of the essence, then an algorithm is likely not the best choice.
Lang JM, Ford JD, Fitzgerald MM. An algorithm for determining use of trauma-focused cognitive-behavioral therapy . Psychotherapy (Chic) . 2010;47(4):554-69. doi:10.1037/a0021184
Stein DJ, Shoptaw SJ, Vigo DV, et al. Psychiatric diagnosis and treatment in the 21st century: paradigm shifts versus incremental integration . World Psychiatry . 2022;21(3):393-414. doi:10.1002/wps.20998
Bobadilla-Suarez S, Love BC. Fast or frugal, but not both: decision heuristics under time pressure . J Exp Psychol Learn Mem Cogn . 2018;44(1):24-33. doi:10.1037/xlm0000419
Giordano C, Brennan M, Mohamed B, Rashidi P, Modave F, Tighe P. Accessing artificial intelligence for clinical decision-making . Front Digit Health . 2021;3:645232. doi:10.3389/fdgth.2021.645232
By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."
Solving Edge-Weighted Maximum Clique Problem with DCA Warm-Start Quantum Approximate Optimization Algorithm
- Conference paper
- First Online: 17 June 2024
- Cite this conference paper

- Huy Phuc Nguyen Ha 29 ,
- Viet Hung Nguyen 30 &
- Anh Son Ta 29
Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 14753 ))
Included in the following conference series:
- Metaheuristics International Conference
13 Accesses
The Quantum Approximate Optimization Algorithm is a hybrid quantum-classic algorithm used for solving combinatorial optimization. However, this algorithm performs poorly when solving the constrained combinatorial optimization problem. To deal with this issue, we consider the warm-start Quantum Approximate Optimization Algorithm for solving constrained problems. This article presents a new method for improving the performance of the Quantum Approximate Optimization Algorithm, with the Difference of Convex Optimization. Our approach focuses on the warm-start version of the algorithm and uses the Difference of Convex optimization to find the warm-start parameters. To show our method’s efficiency, we do several experiments on the edge-weighted maximum clique problem and see a good result.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Gloria, T., Dacrema, M.F., Cremonesi, P.: Feature selection for classification with QAOA. In: 2022 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE (2022)
Google Scholar
Sack, S.H., Serbyn, M.: Quantum annealing initialization of the quantum approximate optimization algorithm. Quantum 5 , 491 (2021)
Article Google Scholar
Anshu, A., Metger, T.: Concentration bounds for quantum states and limitations on the QAOA from polynomial approximations. Quantum 7 , 999 (2023)
Lucas, A.: Ising formulations of many np problems. Front. Phys. 5 (2014)
Barkoutsos, P.K., et al.: Improving variational quantum optimization using CVaR. Quantum 4 , 256 (2020)
Acampora, G., Chiatto, A., Vitiello, A.: Genetic algorithms as classical optimizer for the quantum approximate optimization algorithm. Appl. Soft Comput. 142 , 110296 (2023)
Wang, Z., et al.: X y mixers: analytical and numerical results for the quantum alternating operator ansatz. Phys. RevA 101 (1), 012320 (2020)
Article MathSciNet Google Scholar
Farhi, E., Goldstone, J., Gutmann, S.: A quantum approximate optimization algo- rithm. arXiv preprint arXiv:1411.4028 (2014)
Egger, D.J., Marecek, J., Woerner, S.: Warm-starting quantum optimization. Quantum 5 , 479 (2021)
Bittel, L., Kliesch, M.: Training variational quantum algorithms is np-hard. Phys. Rev. Lett. 127 (12), 120502 (2021)
An, L.T.H., Tao, P.D.: The DC (difference of convex functions) programming and DCA revisited with DC models of real world non convex optimization problems. Ann. Oper. Res. 133 (2), 23–46 (2005)
Tao, P.D., An, L.T.H.: A DC optimization algorithm for solving the trust-region subproblem. SIAM J. Optim. 8 (2), 476–505 (1998)
Hoai An, L.T., Ta, A.S., Tao, P.D.: An efficient DCA based algorithm for power control in large scale wireless networks. Appl. Math. Comput. 318 (1), 215–226 (2018)
MathSciNet Google Scholar
Brandhofer, S., et al.: Benchmarking the performance of portfolio optimization with QAOA. Quantum Inf. Process. 22 (1), 25 (2022)
Pardalos, P.M.: Global optimization algorithms for linearly constrained indefinite quadratic problems. Comput. Math. Appl. 21 (6–7), 87–97 (1991)
An, L.T.H., Tao, P.D.: A branch and bound method via DC optimization algorithms and ellipsoidal technique for box constrained nonconvex quadratic problems. J. Global Optim. 13 (2), 171–206 (1998)
Kurowski, K., Pecyna, T., Slysz, M., Rozycki, R., Waligora, G., Wglarz, J.: Application of quantum approximate optimization algorithm to job shop scheduling problem. Eur. J. Oper. Res. 310 (2), 518–528 (2023)
Choi, J., Oh, S., Kim, J.: Quantum approximation for wireless scheduling. Appl. Sci. 10 (20), 7116 (2020)
Torta, P., Mbeng, G.B., Baldassi, C., Zecchina, R., Santoro, G.E.: Quantum approximate optimization algorithm applied to the binary perceptron. Phys. Rev. B 107 (9), 094202 (2023)
Jain, N., Coyle, B., Kashefi, E., Kumar, N.: Graph neural network initialisation of quantum approximate optimisation. Quantum 6 , 861 (2022)
Shaydulin, R., Safro, I., Larson, J.: Multistart methods for quantum approximate optimization. In: 2019 IEEE High Performance Extreme Computing Conference (HPEC), pp. 1–8. IEEE (2019)
Hadfield, S., Wang, Z., O’gorman, B., Rieffel, E.G., Venturelli, D., Biswas, R.: From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms 12 (2), 34 (2019)
Grange, C., Poss, M., Bourreau, E.: An introduction to variational quantum algorithms for combinatorial optimization problems. 4OR, 21 (3), 363–403 (2023)
Hosseinian, S., Fontes, D.B.M.M., Butenko, S.: A nonconvex quadratic optimization approach to the maximum edge weight clique problem. J. Global Optim. 72 , 219–240 (2018)
Buchheim, C., et al.: An exact algorithm for nonconvex quadratic integer minimization using ellipsoidal relaxations. SIAM J. Optim. 23 (3), 1867–1889 (2013)
Pham Dinh, T., Nguyen Canh, N., Le Thi, H.A.: An efficient combined DCA and B &B using DC/SDP relaxation for globally solving binary quadratic programs. J. Global Optim. 48 , 595–632 (2010)
Ta, A.S., Khadraoui, D., Tao, P.D., et al.: Solving partitioning-hub location- routing problem using DCA. J. Ind. Manag. Optim. 8 (1), 87–102 (2011)
Fuchs, F.G., Kolden, H.Ø., Aase, N.H., Sartor, G.: Efficient encoding of the weighted max k-cut on a quantum computer using QAOA. SN Comput. Sci. 2 (2), 89 (2021)
Kadowaki, T., Nishimori, H.: Quantum annealing in the transverse Ising model. Phys. Rev. E 58 (5), 5355 (1998)
Download references
Acknowledgement
This research is funded by Hanoi University of Science and Technology (HUST) under project number T2023-TĐ-001.
Author information
Authors and affiliations.
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Dai Co Viet, Vietnam
Huy Phuc Nguyen Ha & Anh Son Ta
Université Clermont-Auvergne, CNRS, Mines de Saint-Etienne, Clermont Auvergne INP, LIMOS, Clermont-Ferrand, France
Viet Hung Nguyen
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Anh Son Ta .
Editor information
Editors and affiliations.
Centre de Recherche, Université Bretagne Sud, Lorient, France
Marc Sevaux
Centre de Recherche, Université Bretagne Sud, LORIENT, France
Alexandru-Liviu Olteanu
Universidad Rey Juan Carlos, Móstoles, Spain
Eduardo G. Pardo
University of Macedonia, Thessaloniki, Greece
Angelo Sifaleras
Université de Technologie de Troyes, Troyes Cedex, France
Salma Makboul
Rights and permissions
Reprints and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper.
Ha, H.P.N., Nguyen, V.H., Ta, A.S. (2024). Solving Edge-Weighted Maximum Clique Problem with DCA Warm-Start Quantum Approximate Optimization Algorithm. In: Sevaux, M., Olteanu, AL., Pardo, E.G., Sifaleras, A., Makboul, S. (eds) Metaheuristics. MIC 2024. Lecture Notes in Computer Science, vol 14753 . Springer, Cham. https://doi.org/10.1007/978-3-031-62912-9_24
Download citation
DOI : https://doi.org/10.1007/978-3-031-62912-9_24
Published : 17 June 2024
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-62911-2
Online ISBN : 978-3-031-62912-9
eBook Packages : Computer Science Computer Science (R0)
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Help | Advanced Search
Quantum Physics
Title: a catalyst framework for the quantum linear system problem via the proximal point algorithm.
Abstract: Solving systems of linear equations is a fundamental problem, but it can be computationally intensive for classical algorithms in high dimensions. Existing quantum algorithms can achieve exponential speedups for the quantum linear system problem (QLSP) in terms of the problem dimension, but even such a theoretical advantage is bottlenecked by the condition number of the coefficient matrix. In this work, we propose a new quantum algorithm for QLSP inspired by the classical proximal point algorithm (PPA). Our proposed method can be viewed as a meta-algorithm that allows inverting a modified matrix via an existing \texttt{QLSP\_solver}, thereby directly approximating the solution vector instead of approximating the inverse of the coefficient matrix. By carefully choosing the step size $\eta$, the proposed algorithm can effectively precondition the linear system to mitigate the dependence on condition numbers that hindered the applicability of previous approaches.
| Subjects: | Quantum Physics (quant-ph); Data Structures and Algorithms (cs.DS); Machine Learning (cs.LG); Optimization and Control (math.OC) |
| Cite as: | [quant-ph] |
| (or [quant-ph] for this version) |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- INSPIRE HEP
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
A tent-lévy-based seagull optimization algorithm for the multi-uav collaborative task allocation problem.

Share and Cite
Zhou, Z.; Liu, H.; Dai, Y.; Qin, L. A Tent-Lévy-Based Seagull Optimization Algorithm for the Multi-UAV Collaborative Task Allocation Problem. Appl. Sci. 2024 , 14 , 5398. https://doi.org/10.3390/app14135398
Zhou Z, Liu H, Dai Y, Qin L. A Tent-Lévy-Based Seagull Optimization Algorithm for the Multi-UAV Collaborative Task Allocation Problem. Applied Sciences . 2024; 14(13):5398. https://doi.org/10.3390/app14135398
Zhou, Zhao, Huan Liu, Yongqiang Dai, and Lijing Qin. 2024. "A Tent-Lévy-Based Seagull Optimization Algorithm for the Multi-UAV Collaborative Task Allocation Problem" Applied Sciences 14, no. 13: 5398. https://doi.org/10.3390/app14135398
Article Metrics
Further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals
- Trending Now
- Foundational Courses
- Data Science
- Practice Problem
- Machine Learning
- System Design
- DevOps Tutorial
CBSE Class 11 | Problem Solving Methodologies
- CBSE Class 11 | Concepts of Programming Methodology
- NCERT Solutions Class-11 Polity Chapter-7: Federalism
- CBSE Class 11 Maths Notes
- CBSE Class 11 Revision Notes
- CBSE Class 9 Maths Revision Notes
- CBSE Class 10 Revision Notes
- CBSE Revision Notes for Class 12
- CBSE Class 8 Revision Notes
- CBSE Class 12 Economics Solved Question Paper 2020 - Set 1
- CBSE Class 8th Maths Notes
- CBSE Class 12 Economics Solved Question Paper 2020 - Set 3
- CBSE Class 12 Economics Solved Question Paper 2020 - Set 2
- CBSE Class 10 History Notes
- CBSE Class 11 | Computer Science - Python Syllabus
- CBSE Class 12 Economics Solved Question Paper 2020 (Set 58/1/2)
- CBSE Sample Papers II for Class 11 Economics with Solutions 2023-2024
- CBSE Class 12th Economics Previous Year Question Papers
- CBSE Class 12 Economics Previous Year Question Paper
- NCERT Solutions for Class 9 Maths Chapter 15 Probability
Problem Solving Process
The process of problem-solving is an activity which has its ingredients as the specification of the program and the served dish is a correct program. This activity comprises of four steps : 1. Understanding the problem: To solve any problem it is very crucial to understand the problem first. What is the desired output of the code and how that output can be generated? The obvious and essential need to generate the output is an input. The input may be singular or it may be a set of inputs. A proper relationship between the input and output must be drawn in order to solve the problem efficiently. The input set should be complete and sufficient enough to draw the output. It means all the necessary inputs required to compute the output should be present at the time of computation. However, it should be kept in mind that the programmer should ensure that the minimum number of inputs should be there. Any irrelevant input only increases the size of and memory overhead of the program. Thus Identifying the minimum number of inputs required for output is a crucial element for understanding the problem.
2. Devising the plan: Once a problem has been understood, a proper action plan has to be devised to solve it. This is called devising the plan. This step usually involves computing the result from the given set of inputs. It uses the relationship drawn between inputs and outputs in the previous step. The complexity of this step depends upon the complexity of the problem at hand.
3. Executing the plan: Once the plan has been defined, it should follow the trajectory of action while ensuring the plan’s integrity at various checkpoints. If any inconsistency is found in between, the plan needs to be revised.
4. Evaluation: The final result so obtained must be evaluated and verified to see if the problem has been solved satisfactorily.
Problem Solving Methodology(The solution for the problem)
The methodology to solve a problem is defined as the most efficient solution to the problem. Although, there can be multiple ways to crack a nut, but a methodology is one where the nut is cracked in the shortest time and with minimum effort. Clearly, a sledgehammer can never be used to crack a nut. Under problem-solving methodology, we will see a step by step solution for a problem. These steps closely resemble the software life cycle . A software life cycle involves several stages in a program’s life cycle. These steps can be used by any tyro programmer to solve a problem in the most efficient way ever. The several steps of this cycle are as follows :
Step by step solution for a problem (Software Life Cycle) 1. Problem Definition/Specification: A computer program is basically a machine language solution to a real-life problem. Because programs are generally made to solve the pragmatic problems of the outside world. In order to solve the problem, it is very necessary to define the problem to get its proper understanding. For example, suppose we are asked to write a code for “ Compute the average of three numbers”. In this case, a proper definition of the problem will include questions like : “What exactly does average mean?” “How to calculate the average?”
Once, questions like these are raised, it helps to formulate the solution of the problem in a better way. Once a problem has been defined, the program’s specifications are then listed. Problem specifications describe what the program for the problem must do. It should definitely include :
what is the input set of the program
What is the desired output of the program and in what form the output is desired?
2. Problem Analysis (Breaking down the solution into simple steps): This step of solving the problem follows a modular approach to crack the nut. The problem is divided into subproblems so that designing a solution to these subproblems gets easier. The solutions to all these individual parts are then merged to get the final solution of the original problem. It is like divide and merge approach.
Modular Approach for Programming :
The process of breaking a large problem into subproblems and then treating these individual parts as different functions is called modular programming. Each function behaves independent of another and there is minimal inter-functional communication. There are two methods to implement modular programming :
- Top Down Design : In this method, the original problem is divided into subparts. These subparts are further divided. The chain continues till we get the very fundamental subpart of the problem which can’t be further divided. Then we draw a solution for each of these fundamental parts.
- Bottom Up Design : In this style of programming, an application is written by using the pre-existing primitives of programming language. These primitives are then amalgamated with more complicated features, till the application is written. This style is just the reverse of the top-down design style.
3. Problem Designing: The design of a problem can be represented in either of the two forms :
The ways to execute any program are of three categories:
- Sequence Statements Here, all the instructions are executed in a sequence, that is, one after the another, till the program is executed.
- Selection Statements As it is self-clear from the name, in these type of statements the whole set of instructions is not executed. A selection has to be made. A selected number of instructions are executed based on some condition. If the condition holds true then some part of the instruction set is executed, otherwise, another part of the set is executed. Since this selection out of the instruction set has to be made, thus these type of instructions are called Selection Statements.
Identification of arithmetic and logical operations required for the solution : While writing the algorithm for a problem, the arithmetic and logical operations required for the solution are also usually identified. They help to write the code in an easier manner because the proper ordering of the arithmetic and logical symbols is necessary to determine the correct output. And when all this has been done in the algorithm writing step, it just makes the coding task a smoother one.
- Flow Chart : Flow charts are diagrammatic representation of the algorithm. It uses some symbols to illustrate the starting and ending of a program along with the flow of instructions involved in the program.
4. Coding: Once an algorithm is formed, it can’t be executed on the computer. Thus in this step, this algorithm has to be translated into the syntax of a particular programming language. This process is often termed as ‘coding’. Coding is one of the most important steps of the software life cycle. It is not only challenging to find a solution to a problem but to write optimized code for a solution is far more challenging.
Writing code for optimizing execution time and memory storage : A programmer writes code on his local computer. Now, suppose he writes a code which takes 5 hours to get executed. Now, this 5 hours of time is actually the idle time for the programmer. Not only it takes longer time, but it also uses the resources during that time. One of the most precious computing resources is memory. A large program is expected to utilize more memory. However, memory utilization is not a fault, but if a program is utilizing unnecessary time or memory, then it is a fault of coding. The optimized code can save both time and memory. For example, as has been discussed earlier, by using the minimum number of inputs to compute the output , one can save unnecessary memory utilization. All such techniques are very necessary to be deployed to write optimized code. The pragmatic world gives reverence not only to the solution of the problem but to the optimized solution. This art of writing the optimized code also called ‘competitive programming’.
5. Program Testing and Debugging: Program testing involves running each and every instruction of the code and check the validity of the output by a sample input. By testing a program one can also check if there’s an error in the program. If an error is detected, then program debugging is done. It is a process to locate the instruction which is causing an error in the program and then rectifying it. There are different types of error in a program : (i) Syntax Error Every programming language has its own set of rules and constructs which need to be followed to form a valid program in that particular language. If at any place in the entire code, this set of rule is violated, it results in a syntax error. Take an example in C Language
In the above program, the syntax error is in the first printf statement since the printf statement doesn’t end with a ‘;’. Now, until and unless this error is not rectified, the program will not get executed.
Once the error is rectified, one gets the desired output. Suppose the input is ‘good’ then the output is : Output:
(ii) Logical Error An error caused due to the implementation of a wrong logic in the program is called logical error. They are usually detected during the runtime. Take an example in C Language:
In the above code, the ‘for’ loop won’t get executed since n has been initialized with the value of 11 while ‘for’ loop can only print values smaller than or equal to 10. Such a code will result in incorrect output and thus errors like these are called logical errors. Once the error is rectified, one gets the desired output. Suppose n is initialised with the value ‘5’ then the output is : Output:
(iii) Runtime Error Any error which causes the unusual termination of the program is called runtime error. They are detected at the run time. Some common examples of runtime errors are : Example 1 :
If during the runtime, the user gives the input value for B as 0 then the program terminates abruptly resulting in a runtime error. The output thus appears is : Output:
Example 2 : If while executing a program, one attempts for opening an unexisting file, that is, a file which is not present in the hard disk, it also results in a runtime error.
6. Documentation : The program documentation involves :
- Problem Definition
- Problem Design
- Documentation of test perform
- History of program development
7. Program Maintenance: Once a program has been formed, to ensure its longevity, maintenance is a must. The maintenance of a program has its own costs associated with it, which may also exceed the development cost of the program in some cases. The maintenance of a program involves the following :
- Detection and Elimination of undetected errors in the existing program.
- Modification of current program to enhance its performance and adaptability.
- Enhancement of user interface
- Enriching the program with new capabilities.
- Updation of the documentation.
Control Structure- Conditional control and looping (finite and infinite)
There are codes which usually involve looping statements. Looping statements are statements in which instruction or a set of instructions is executed multiple times until a particular condition is satisfied. The while loop, for loop, do while loop, etc. form the basis of such looping structure. These statements are also called control structure because they determine or control the flow of instructions in a program. These looping structures are of two kinds :
In the above program, the ‘for’ loop gets executed only until the value of i is less than or equal to 10. As soon as the value of i becomes greater than 10, the while loop is terminated. Output:
In the above code, one can easily see that the value of n is not getting incremented. In such a case, the value of n will always remain 1 and hence the while loop will never get executed. Such loop is called an infinite loop. Output:
Please Login to comment...
Similar reads.
- School Programming
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

IMAGES
VIDEO
COMMENTS
Let's take some examples of algorithms for computer science problems. Example 1. Swap two numbers with a third variable. Step 1: Start. Step 2: Take 2 numbers as input. Step 3: Declare another variable as "temp". Step 4: Store the first variable to "temp". Step 5: Store the second variable to the First variable.
My approach to making algorithms compelling was focusing on comparisons. I take algorithms and put them in a scene from everyday life, such as matching socks from a pile, putting books on a shelf, remembering things, driving from one point to another, or cutting an onion. These activities can be mapped to one or more fundamental algorithms ...
An algorithm is a step by step process that describes how to solve a problem in a way that always gives a correct answer. When there are multiple algorithms for a particular problem (and there often are!), the best algorithm is typically the one that solves it the fastest.
Algorithms Tutorial. Algorithm is a step-by-step procedure for solving a problem or accomplishing a task. In the context of data structures and algorithms, it is a set of well-defined instructions for performing a specific computational task. Algorithms are fundamental to computer science and play a very important role in designing efficient ...
At its core, an algorithm is a systematic, step-by-step procedure or set of rules designed to solve a problem or perform a specific task. It provides clear instructions that, when followed meticulously, lead to the desired outcome. Consider an algorithm to be akin to a recipe for your favorite dish.
We've partnered with Dartmouth college professors Tom Cormen and Devin Balkcom to teach introductory computer science algorithms, including searching, sorting, recursion, and graph theory. Learn with a combination of articles, visualizations, quizzes, and coding challenges.
Algorithmic problem solving is the art of formulating efficient methods that solve problems of a mathematical nature. From the many numerical algo-rithms developed by the ancient Babylonians to the founding of graph theory by Euler, algorithmic problem solving has been a popular intellectual pursuit during the last few thousand years.
An algorithm is a plan for solving a problem. A person must design an algorithm. A person must translate an algorithm into a computer program. This point of view sets the stage for a process that we will use to develop solutions to Jeroo problems. The basic process is important because it can be used to solve a wide variety of problems ...
An algorithm is a step-by-step process used to solve a problem or reach a desired goal. It's a simple concept; you use your own algorithms for everyday tasks like deciding whether to drive or take the subway to work, or determining what you need from the grocery store. ... with computing resources used to execute multiple complex algorithms in ...
By using an example, describe how the concept of algorithms can be well presented to a group of students being introduced to it. 1.1: Activity 1 - Introduction to Algorithms and Problem Solving is shared under a CC BY-SA license and was authored, remixed, and/or curated by LibreTexts. In this learning activity section, the learner will be ...
The true test of problem solving: when one realizes that time and memory aren't infinite.
1.1: Activity 1 - Introduction to Algorithms and Problem Solving. In this learning activity section, the learner will be introduced to algorithms and how to write algorithms to solve tasks faced by learners or everyday problems. Examples of the algorithm are also provided with a specific application to everyday problems that the learner is ...
of the problem-solving process. Given a problem, a computer scientist's goal is to develop an algorithm, a step-by-step list of instructions for solving any instance of the problem that might arise. Algorithms are finite processes that if followed will solve the problem. Algorithms are solutions.
In computer programming terms, an algorithm is a set of well-defined instructions to solve a particular problem. It takes a set of input (s) and produces the desired output. For example, An algorithm to add two numbers: Take two number inputs. Add numbers using the + operator. Display the result.
Definition of Algorithm. The word Algorithm means " A set of finite rules or instructions to be followed in calculations or other problem-solving operations ". Or. " A procedure for solving a mathematical problem in a finite number of steps that frequently involves recursive operations".
A method of representing the step-by-step logical procedure for solving a problem. Flowchart is diagrammatic representation of an algorithm. It is constructed using different types of boxes and symbols. 2. It contains step-by-step English descriptions, each step representing a particular operation leading to solution of problem.
Algorithms for Coding Interviews in Python. As a developer, mastering the concepts of algorithms and being proficient in implementing them is essential to improving problem-solving skills. This course aims to equip you with an in-depth understanding of algorithms and how they can be utilized for problem-solving in Python.
This blog highlights some popular problem solving techniques for solving coding problems. Learning to apply these strategies could be one of the best milestones in mastering data structure and algorithms and cracking the coding interview. We can categorize these strategies into two categories: Iterative approach and Recursive approach.
2) Break the problem down. Here is a step-by-step explanation of the algorithm in plain English: Convert all uppercase letters in the string to lowercase. This is done so that the case of the letters in the string does not affect the outcome of the comparison. Remove all non-alphanumeric characters from the string.
An algorithm is a sequence of instructions that a computer must perform to solve a well-defined problem. It essentially defines what the computer needs to do and how to do it. Algorithms can instruct a computer how to perform a calculation, process data, or make a decision. The best way to understand an algorithm is to think of it as a recipe ...
Another important issue of algorithmic problem solving is the question of whether or not every problem can be solved by an algorithm. We are not talking here about problems that do not have a solution, such as finding real roots of a quadratic equation with a negative discriminant. For such cases, an output indicating that the problem does not ...
In psychology, one of these problem-solving approaches is known as an algorithm. While often thought of purely as a mathematical term, the same type of process can be followed in psychology to find the correct answer when solving a problem or making a decision. An algorithm is a defined set of step-by-step procedures that provides the correct ...
2.1 Introduction to QAOA. The Quantum Approximate Optimization Algorithm (QAOA) was first introduced in 2014 by Fahri [].QAOA is a hybrid classical-quantum algorithm for solving optimization problems with quadratic form \(f(x)=\sum _{i,j}Q_{ij}x_{i}x_{j}\).It is designed to run on near-term quantum computers and works by encoding the problem as a cost function minimized via the use of a series ...
Performance measure of Problem-solving Algorithms. We can evaluate an algorithm's performance with these metrics: Completeness: Is the algorithm guaranteed to find a solution if there exist one?
Solving systems of linear equations is a fundamental problem, but it can be computationally intensive for classical algorithms in high dimensions. Existing quantum algorithms can achieve exponential speedups for the quantum linear system problem (QLSP) in terms of the problem dimension, but even such a theoretical advantage is bottlenecked by the condition number of the coefficient matrix. In ...
To tackle this issue, a mathematical model for the multi-constrained multiple unmanned aerial vehicle collaborative task allocation problem is developed. To efficiently solve this model, we propose an enhanced Seagull Optimization Algorithm, which integrates the Tent chaotic mapping strategy and the Lévy flight strategy.
The problem-solving agent performs precisely by defining problems and several solutions. So we can say that problem solving is a part of artificial intelligence that encompasses a number of techniques such as a tree, B-tree, heuristic algorithms to solve a problem. We can also say that a problem-solving agent is a result-driven agent and always ...
Problem Solving Methodology(The solution for the problem) The methodology to solve a problem is defined as the most efficient solution to the problem. Although, there can be multiple ways to crack a nut, but a methodology is one where the nut is cracked in the shortest time and with minimum effort. ... Algorithm : The set of instructions ...