representation of the symmetric group order

Symmetric Group

(1)(2)(3)(1)(23)(3)(12)(123)(132)(2)(13)

(1)(2)(3)	(1)(23)	(3)(12)	(123)	(132)	(2)(13)
(1)(2)(3)	(1)(23)	(3)(12)	(123)	(132)	(2)(13)
(1)(23)	(1)(2)(3)	(132)	(2)(13)	(3)(12)	(123)
(3)(12)	(123)	(1)(2)(3)	(1)(23)	(2)(13)	(132)
(123)	(3)(12)	(2)(13)	(132)	(1)(2)(3)	(1)(23)
(132)	(2)(13)	(1)(23)	(1)(2)(3)	(123)	(3)(12)
(2)(13)	(132)	(123)	(3)(12)	(1)(23)	(1)(2)(3)

123132213231312321

123	132	213	231	312	321
123	132	213	231	312	321
132	123	312	321	213	231
213	231	123	132	321	312
231	213	321	312	123	132
312	321	132	123	231	213
321	312	231	213	132	123

Explore with Wolfram|Alpha

More things to try:

• symmetric group
• Bode plot of s/(1-s) sampling period .02
• d/dx Si(x)^2

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Symmetric Group." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/SymmetricGroup.html

Subject classifications

Math 480: Representation Theory of the Symmetric Group

Fall, 2022 prof. sara billey, course materials, interesting resources.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.3: Symmetric Groups

• Last updated
• Save as PDF
• Page ID 97998

• Northern Arizona University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Recall the groups \(S_2\) and \(S_3\) from Problems 2.5.3 and 2.2.7 . These groups act on two and three coins, respectively, that are in a row by rearranging their positions (but not flipping them over). These groups are examples of symmetric groups. In general, the symmetric group on \(n\) objects is the set of permutations that rearranges the \(n\) objects. The group operation is composition of permutations. Let’s be a little more formal.

Definition: Permutation of a set

A permutation of a set \(A\) is a function \(\sigma:A\to A\) that is both one-to-one and onto.

You should take a moment to convince yourself that the formal definition of a permutation agrees with the notion of rearranging the set of objects. The do-nothing action is the identity permutation, i.e., \(\sigma(a)=a\) for all \(a\in A\) . There are many ways to represent a permutation. One visual way is using permutation diagrams , which we will introduce via examples.

Consider the following diagrams:

Each of these diagrams represents a permutation on five objects. I’ve given the permutations the names \(\alpha\) , \(\beta\) , \(\sigma\) , and \(\gamma\) . The intention is to read the diagrams from the top down. The numbers labeling the nodes along the top are identifying position. Following an edge from the top row of nodes to the bottom row of nodes tells us what position an object moves to. It is important to remember that the numbers are referring to the position of an object, not the object itself. For example, \(\beta\) is the permutation that sends the object in the second position to the fourth position, the object in the third position to the second position, and the object in the fourth position to the third position. Moreover, the permutation \(\beta\) doesn’t do anything to the objects in positions 1 and 5.

Problem \(\PageIndex{1}\)

Describe in words what the permutations \(\sigma\) and \(\gamma\) do.

Problem \(\PageIndex{2}\)

Draw the permutation diagram for the do-nothing permutation on 5 objects. This is called the identity permutation . What does the identity permutation diagram look like in general for arbitrary \(n\) ?

Definition: Set of all Permutation

The set of all permutations on \(n\) objects is denoted by \(S_n\) .

Problem \(\PageIndex{3}\)

Draw all the permutation diagrams for the permutations in \(S_3\) .

Problem \(\PageIndex{4}\)

How many distinct permutations are there in \(S_4\) ? How about \(S_n\) for any \(n\in \mathbb{N}\) ?

If \(S_n\) is going to be a group, we need to know how to compose permutations. This is easy to do using the permutation diagrams. Consider the permutations \(\alpha\) and \(\beta\) from earlier. We can represent the composition \(\alpha \circ \beta\) via

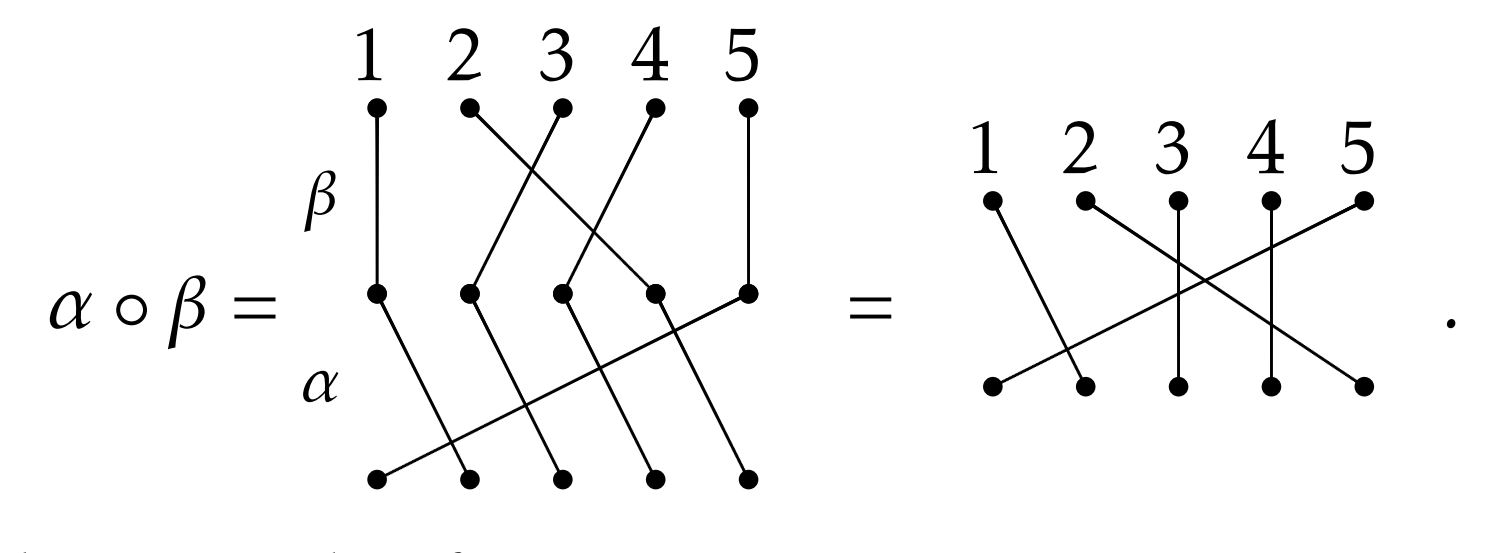
As you can see by looking at the figure, to compose two permutations, you stack the one that goes first in the composition (e.g., \(\beta\) in the example above) on top of the other and just follow the edges from the top through the middle to the bottom. If you think about how function composition works, this is very natural. The resulting permutation is determined by where we begin and where we end in the composition.

We already know that the order of composition matters for functions, and so it should matter for the composition of permutations. To make this crystal clear, let’s compose \(\alpha\) and \(\beta\) in the opposite order. We see that

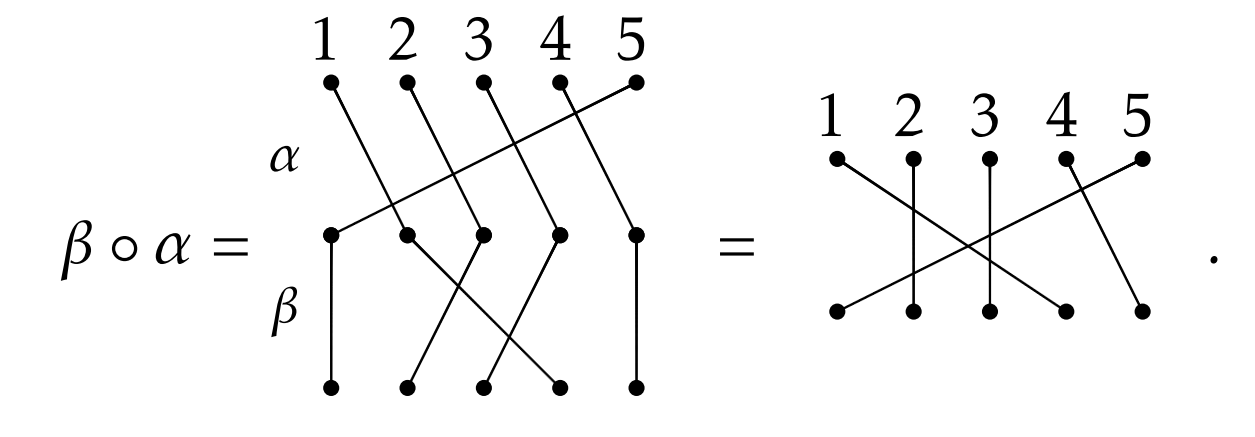
The moral of the story is that composition of permutations does not necessarily commute.

Problem \(\PageIndex{5}\)

Consider \(\alpha\) , \(\beta\) , \(\sigma\) , and \(\gamma\) from earlier. Can you find a pair of permutations that do commute? Can you identify any features about your diagrams that indicate why they commuted?

Problem \(\PageIndex{6}\)

Fix \(n\in\mathbb{N}\) . Convince yourself that any \(\rho\in S_n\) composed with the identity permutation (in either order) equals \(\rho\) .

If \(S_n\) is going to be a group, we need to know what the inverse of a permutation is.

Problem \(\PageIndex{7}\)

Given a permutation \(\rho\in S_n\) , describe a method for constructing \(\rho^{-1}\) . Briefly justify that \(\rho \circ \rho^{-1}\) will yield the identity permutation.

At this point, we have all the ingredients we need to prove that \(S_n\) forms a group under composition of permutations.

Theorem \(\PageIndex{1}\)

The set of permutations on \(n\) objects forms a group under the operation of composition. That is, \((S_n,\circ)\) is a group. Moreover, \(|S_n|=n!\) .

Note that it is standard convention to omit the composition symbol when writing down compositions in \(S_n\) . For example, we will simply write \(\alpha\beta\) to denote \(\alpha \circ \beta\) .

Permutation diagrams are fun to play with, but we need a more efficient way of encoding information. One way to do this is using cycle notation . Consider \(\alpha, \beta, \sigma\) , and \(\gamma\) in \(S_{5}\) from the previous examples. Below I have indicated what each permutation is equal to using cycle notation.

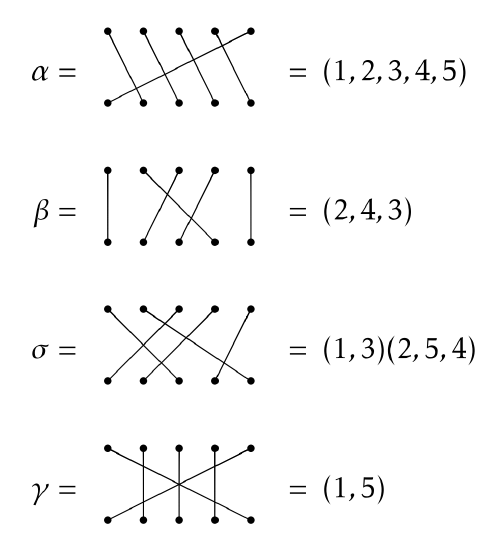
Each string of numbers enclosed by parentheses is called a cycle and if the string of numbers has length \(k\) , then we call it a \(k\) -cycle. For example, \(\alpha\) consists of a single 5-cycle, whereas \(\sigma\) consists of one 2-cycle and one 3-cycle. In the case of \(\sigma\) , we say that \(\sigma\) is the product of two disjoint cycles .

One observation that you hopefully made is that if an object in position \(i\) remains unchanged, then we don’t bother listing that number in the cycle notation. However, if we wanted to, we could use the 1-cycle \((i)\) to denote this. For example, we could write \(\beta=(1)(2,4,3)(5)\) . In particular, we could denote the identity permutation in \(S_5\) using \((1)(2)(3)(4)(5)\) . Yet, it is common to simply use \((1)\) to denote the identity in \(S_n\) for all \(n\) .

Notice that the first number we choose to write down for a given cycle is arbitrary. However, the numbers that follow are not negotiable. Typically, we would use the smallest possible number first, but this is not necessary. For example, the cycle \((2,4,7)\) could also be written as \((4,7,2)\) or \((7,2,4)\) .

Problem \(\PageIndex{8}\): \(S_3\)

Write down all 6 elements in \(S_3\) using cycle notation.

Problem \(\PageIndex{9}\): \(S_4\)

Write down all 24 elements in \(S_4\) using cycle notation.

Suppose \(\sigma\in S_n\) . Since \(\sigma\) is one-to-one and onto, it is clear that it is possible to write \(\sigma\) as a product of disjoint cycles such that each \(i\in\{1,2,\ldots, n\}\) appears exactly once.

Let’s see if we can figure out how to multiply elements of \(S_n\) using cycle notation. Consider the permutations \(\alpha=(1,3,2)\) and \(\beta=(3,4)\) in \(S_4\) . To compute the composition \(\alpha\beta=(1,3,2)(3,4)\) , let’s explore what happens in each position. Since we are doing function composition, we should work our way from right to left. Since 1 does not appear in the cycle notation for \(\beta\) , we know that \(\beta(1)=1\) (i.e., \(\beta\) maps 1 to 1). Now, we see what \(\alpha(1)=3\) . Thus, the composition \(\alpha\beta\) maps 1 to 3 (since \(\alpha\beta(1)=\alpha(\beta(1))=\alpha(1)=3\) ). Next, we should return to \(\beta\) and see what happens to 3—which is where we ended a moment ago. We see that \(\beta\) maps 3 to 4 and then \(\alpha\) maps 4 to 4 (since 4 does not appear in the cycle notation for \(\alpha\) ). So, \(\alpha\beta(3)=4\) . Continuing this way, we see that \(\beta\) maps 4 to 3 and \(\alpha\) maps 3 to 2, and so \(\alpha\beta\) maps 4 to 2. Lastly, since \(\beta(2)=2\) and \(\alpha(2)=1\) , we have \(\alpha\beta(2)=1\) . Putting this altogether, we see that \(\alpha\beta=(1,3,4,2)\) . Now, you should try a few. Things get a little trickier if the composition of two permutations results in a permutation consisting of more than a single cycle.

Problem \(\PageIndex{10}\)

Consider \(\alpha\) , \(\beta\) , \(\sigma\) , and \(\gamma\) for which we drew the permutation diagrams. Using cycle notation, compute each of the following.

• \(\alpha\gamma\)
• \(\alpha^2\)
• \(\alpha^3\)
• \(\alpha^4\)
• \(\alpha^5\)
• \(\sigma\alpha\)
• \(\alpha^{-1}\sigma^{-1}\)
• \(\beta^2\)
• \(\beta^3\)
• \(\beta\gamma\alpha\)
• \(\sigma^3\)
• \(\sigma^6\)

Problem \(\PageIndex{11}\)

Write down the group table for \(S_3\) using cycle notation.

In Problem \(\PageIndex{9}\), one of the permutations you should have written down is \((1,2)(3,4)\) . This is a product of two disjoint 2-cycles. It is worth pointing out that each cycle is a permutation in its own right. That is, \((1,2)\) and \((3,4)\) are each permutations. It just so happens that their composition does not “simplify" any further. Moreover, these two disjoint 2-cycles commute since \((1,2)(3,4)=(3,4)(1,2)\) . In fact, this phenomenon is always true.

Theorem \(\PageIndex{2}\)

Suppose \(\alpha\) and \(\beta\) are two disjoint cycles. Then \(\alpha\beta=\beta\alpha\) . That is, products of disjoint cycles commute.

Problem \(\PageIndex{12}\)

Compute the orders of all the elements in \(S_3\) . See Problem \(\PageIndex{8}\).

Problem \(\PageIndex{13}\)

Compute the orders of any twelve of the elements in \(S_4\) . See Problem \(\PageIndex{9}\).

Computing the order of a permutation is fairly easy using cycle notation once we figure out how to do it for a single cycle. In fact, you’ve probably already guessed at the following theorem.

Theorem \(\PageIndex{3}\)

If \(\alpha\in S_n\) such that \(\alpha\) consists of a single \(k\) -cycle, then \(|\alpha|=k\) .

Theorem \(\PageIndex{4}\)

Suppose \(\alpha\in S_n\) such that \(\alpha\) consists of \(m\) disjoint cycles of lengths \(k_1,\ldots, k_m\) . Then \(|\alpha|=\text{lcm}(k_1,\ldots, k_m)\) .*

Recall that \(\text{lcm}(k_1,\ldots, k_m)\) is the least common multiple of \(\{k_1,\ldots, k_m\}\) .

Problem \(\PageIndex{14}\)

Is the previous theorem true if we do not require the cycles to be disjoint? Justify your answer.

Problem \(\PageIndex{15}\)

What is the order of \((1,4,7)(2,5)(3,6,8,9)\) ?

Problem \(\PageIndex{16}\)

Draw the subgroup lattice for \(S_3\) .

Problem \(\PageIndex{17}\)

Now, using \((1,2)\) and \((1,2,3)\) as generators, draw the Cayley diagram for \(S_3\) . Look familiar?

Problem \(\PageIndex{18}\)

Consider \(S_3\) .

• Using \((1,2)\) , \((1,3)\) , and \((2,3)\) as generators, draw the Cayley diagram for \(S_3\) .
• In the previous part, we used a generating set with three elements. Is there a smaller generating set? If so, what is it?

Problem \(\PageIndex{19}\)

Recall that there are \(4!=24\) permutations in \(S_4\) .

• Pick any 12 permutations from \(S_4\) and verify that you can write them as words in the 2-cycles \((1,2), (1,3), (1,4), (2,3), (2,4),(3,4)\) . In most circumstances, your words will not consist of products of disjoint 2-cycles. For example, the permutation \((1,2,3)\) can be decomposed into \((1,2)(2,3)\) , which is a word consisting of two 2-cycles that happen to not be disjoint.
• Using your same 12 permutations, verify that you can write them as words only in the 2-cycles \((1,2),(2,3),(3,4)\) .

By the way, it might take some trial and error to come up with a way to do this. Moreover, there is more than one way to do it.

As the previous exercises hinted at, the 2-cycles play a special role in the symmetric groups. In fact, they have a special name. A transposition is a single cycle of length 2. In the special case that the transposition is of the form \((i,i+1)\) , we call it an adjacent transposition . For example, \((3,7)\) is a (non-adjacent) transposition while \((6,7)\) is an adjacent transposition.

It turns out that the set of transpositions in \(S_n\) is a generating set for \(S_n\) . In fact, the adjacent transpositions form an even smaller generating set for \(S_n\) . To get some intuition, let’s play with a few examples.

Problem \(\PageIndex{20}\)

Try to write each of the following permutations as a product of transpositions. You do not necessarily need to use adjacent transpositions.

• \((3,1,5)\)
• \((2,4,6,8)\)
• \((3,1,5)(2,4,6,8)\)
• \((1,6)(2,5,3)\)

The products you found in the previous exercise are called transposition representations of the given permutation.

Problem \(\PageIndex{21}\)

Consider the arbitrary \(k\) -cycle \((a_1,a_2,\ldots, a_k)\) from \(S_n\) (with \(k\leq n\) ). Find a way to write this permutation as a product of 2-cycles.

Problem \(\PageIndex{22}\)

Consider the arbitrary 2-cycle \((a,b)\) from \(S_n\) . Find a way to write this permutation as a product of adjacent 2-cycles.

The previous two problems imply the following theorem.

Theorem \(\PageIndex{5}\)

Consider \(S_n\) .

• Every permutation in \(S_n\) can be written as a product of transpositions.
• Every permutation in \(S_n\) can be written as a product of adjacent transpositions.

Corollary \(\PageIndex{1}\)

The set of transpositions (respectively, the set of adjacent transpositions) from \(S_n\) forms a generating set for \(S_n\) .

It is important to point out that the transposition representation of a permutation is not unique. That is, there are many words in the transpositions that will equal the same permutation. However, as we shall see in the next section, given two transposition representations for the same permutation, the number of transpositions will have the same parity (i.e., even versus odd).

Remark \(\PageIndex{1}\)

Here are two interesting facts that I will let you ponder on your own time.

• The group of rigid motion symmetries for a cube is isomorphic to \(S_4\) . To convince yourself of this fact, first prove that this group has 24 actions and then ponder the action of \(S_4\) on the four long diagonals of a cube.
• It turns out that you can generate \(S_4\) with \((1,2)\) and \((1,2,3,4)\) . Moreover, you can arrange the Cayley diagram for \(S_4\) with these generators on a truncated cube, which is depicted in Figure \(\PageIndex{5}\). Try it.

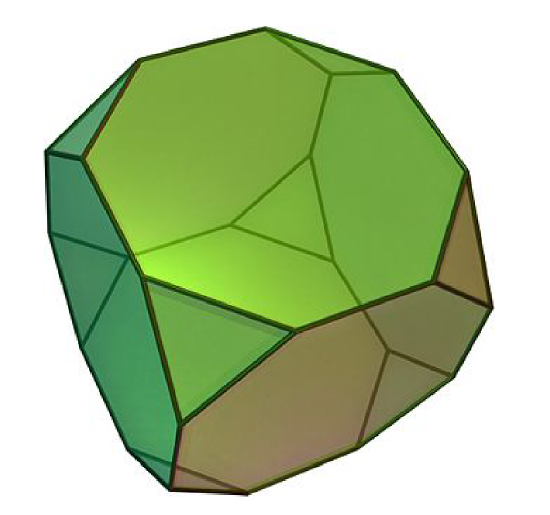
It turns out that the subgroups of symmetric groups play an important role in group theory.

Definition: Permutation Group

Every subgroup of a symmetric group is called a permutation group .

The proof of the following theorem isn’t too bad, but we’ll take it for granted. After tinkering with a few examples, you should have enough intuition to see why the theorem is true and how a possible proof might go.

Theorem \(\PageIndex{6}\): Cayley's Theorem

Every finite group is isomorphic to some permutation group. In particular, if \(G\) is a group of order \(n\) , then \(G\) is isomorphic to a subgroup of \(S_n\) .

Cayley’s Theorem guarantees that every finite group is isomorphic to a permutation group and it turns out that there is a rather simple algorithm for constructing the corresponding permutation group. I’ll briefly explain an example and then let you try a couple.

Consider the Klein four-group \(V_4=\{e,v,h,vh\}\) . Recall that \(V_4\) has the following group table.

\(\begin{array}{c|c|c|c|c} * & e & v & h & v h \\ \hline e & e & v & h & v h \\ \hline v & v & e & v h & h \\ \hline h & h & v h & e & v \\ \hline v h & v h & h & v & e \end{array}\)

If we number the elements \(e,v,h,\) and \(vh\) as \(1,2,3,\) and \(4\) , respectively, then we obtain the following table.

\(\begin{array}{c|c|c|c|c} & 1 & 2 & 3 & 4 \\ \hline 1 & 1 & 2 & 3 & 4 \\ \hline 2 & 2 & 1 & 4 & 3 \\ \hline 3 & 3 & 4 & 1 & 2 \\ \hline 4 & 4 & 3 & 2 & 1 \end{array}\)

Comparing each of the four columns to the leftmost column, we can obtain the corresponding permutations. In particular, we obtain \[\begin{aligned} e&\leftrightarrow (1)\\ v&\leftrightarrow (1,2)(3,4)\\ h&\leftrightarrow (1,3)(2,4)\\ vh&\leftrightarrow(1,4)(2,3). \end{aligned}\] Do you see where these permutations came from? The claim is that the set of permutations \(\{(1),(1,2)(3,4),(1,3)(2,4),(1,4)(2,3)\}\) is isomorphic to \(V_4\) . In this particular case, it’s fairly clear that this is true. However, it takes some work to prove that this process will always result in an isomorphic permutation group. In fact, verifying the algorithm is essentially the proof of Cayley’s Theorem.

Since there are potentially many ways to rearrange the rows and columns of a given table, it should be clear that there are potentially many isomorphisms that could result from the algorithm described above.

Here’s another way to obtain a permutation group that is isomorphic to a given group. Let’s consider \(V_4\) again. Recall that \(V_4\) is a subset of \(D_4\) , which is the symmetry group for a square. Alternatively, \(V_4\) is the symmetry group for a non-square rectangle. Label the corners of the rectangle 1, 2, 3, and 4 by starting in the upper left corner and continuing clockwise. Recall that \(v\) is the action that reflects the rectangle over the vertical midline. The result of this action is that the corners labeled by 1 and 2 switch places and the corners labeled by 3 and 4 switch places. Thus, \(v\) corresponds to the permutation \((1,2)(3,4)\) . Similarly, \(h\) swaps the corners labeled by 1 and 4 and the corners labeled by 2 and 3, and so \(h\) corresponds to the permutation \((1,4)(2,3)\) . Notice that this is not the same answer we got earlier and that’s okay as there may be many permutation representations for a given group. Lastly, \(vh\) rotates the rectangle \(180^{\circ}\) which sends ends up swapping corners labeled 1 and 3 and swapping corners labeled by 2 and 4. Therefore, \(vh\) corresponds to the permutation \((1,3)(2,4)\) .

Problem \(\PageIndex{23}\)

Consider \(D_4\) .

• Using the method outlined above, find a subgroup of \(S_8\) that is isomorphic to \(D_4\) .
• Label the corners of a square 1–4. Find a subgroup of \(S_4\) that is isomorphic to \(D_4\) by considering the natural action of \(D_4\) on the labels on the corners of the square.

Problem \(\PageIndex{24}\)

Consider \(\mathbb{Z}_6\) .

• Using the method outlined earlier, find a subgroup of \(S_6\) that is isomorphic to \(\mathbb{Z}_6\) .
• Label the corners of a regular hexagon 1–6. Find a subgroup of \(S_6\) that is isomorphic to \(\mathbb{Z}_6\) by considering the natural action of \(\mathbb{Z}_6\) on the labels on the corners of the hexagon.

Help | Advanced Search

High Energy Physics - Theory

Title: quantum corner symmetry: representations and gluing.

Abstract: The corner symmetry algebra organises the physical charges induced by gravity on codimension-$2$ corners of a manifold. In this letter, we initiate a study of the quantum properties of this group. We first describe the central extensions and how the quantum corner symmetry group arises. We then classify the Casimirs and the induced unitary irreducible representation. We finally discuss the gluing of corners, achieved identifying the maximal commuting sub-algebra. This is a concrete implementation of the gravitational constraints at the quantum level, via the entangling product.

Comments:	v1, 6 pages
Subjects:	High Energy Physics - Theory (hep-th); General Relativity and Quantum Cosmology (gr-qc)
Cite as:	[hep-th]
	(or [hep-th] for this version)

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Information

• Author Services

Initiatives

You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.

All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .

Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.

Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.

Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.

Original Submission Date Received: .

• Active Journals
• Find a Journal
• Proceedings Series
• For Authors
• For Reviewers
• For Editors
• For Librarians
• For Publishers
• For Societies
• For Conference Organizers
• Open Access Policy
• Institutional Open Access Program
• Special Issues Guidelines
• Editorial Process
• Research and Publication Ethics
• Article Processing Charges
• Testimonials
• Preprints.org
• SciProfiles
• Encyclopedia

Article Menu

• Subscribe SciFeed
• Recommended Articles
• Google Scholar
• on Google Scholar
• Table of Contents

Find support for a specific problem in the support section of our website.

Please let us know what you think of our products and services.

Visit our dedicated information section to learn more about MDPI.

JSmol Viewer

Gbvssl: contrastive semi-supervised learning based on generalized bias-variance decomposition.

1. Introduction

• We introduce a generalized bias-variance decomposition framework for studying and understanding pseudo-labeling and contrastive learning;
• We propose neighbor-enhanced pseudo-labeling and label-enhanced contrastive learning to improve pseudo-label and feature representation, respectively.
• We present a novel SSL algorithm, GBVSSL, which combines neighbor-enhanced pseudo-labeling and label-enhanced contrastive learning.
• Extensive experiments demonstrate that GBVSSL outperforms previous state-of-the-art methods on multiple SSL benchmarks and establishes a new performance benchmark on the real-world dataset Semi-INet 2021.

2. Related Work

2.1. confidence-based pseudo-labeling, 2.2. contrastive learning-based ssl, 3. generalized bias-variance decomposition, 3.1. analysis and implementation scheme for minimizing the bias h ( y , f ¯ ( x , d ) ), 3.2. analysis and implementation scheme for minimizing the variance d k l ( f ¯ ( x , d ) ∥ f ^ ( x , d ) ), 4. the proposed gbvssl method, 4.1. problem formulation, 4.2. framework, 4.3. bias minimization, 4.3.1. labeled cross-entropy, 4.3.2. neighbor-enhanced pseudo-labeling, 4.4. variance minimization, 4.4.1. similarity matrix s, 4.4.2. target adjacency matrix a, 4.4.3. label-enhanced contrastive loss, 4.5. overall loss function, 5. experimental results, 5.1. experimental setup, 5.1.1. common ssl datasets, 5.1.2. implementation details, 5.1.3. baseline methods.

Dataset	CIFAR-10			CIFAR-100			SVHN			STL-10
Model [ ]	74.34 ± 1.76	46.24 ± 1.29	13.13 ± 0.59	86.96 ± 0.80	58.80 ± 0.66	36.65 ± 0.00	67.48 ± 0.95	13.30 ± 1.12	7.16 ± 0.11	74.31 ± 0.85	55.13 ± 1.50	32.78 ± 0.40
Pseudo Label [ ]	74.61 ± 0.26	46.49 ± 2.20	15.08 ± 0.19	87.45 ± 0.85	57.74 ± 0.28	36.55 ± 0.24	64.61 ± 5.60	15.59 ± 0.95	9.40 ± 0.32	74.68 ± 0.99	55.45 ± 2.43	32.64 ± 0.71
VAT [ ]	74.66 ± 2.12	41.03 ± 1.79	10.51 ± 0.12	85.20 ± 1.40	46.84 ± 0.79	32.14 ± 0.19	74.75 ± 3.38	4.33 ± 0.12	4.11 ± 0.20	74.74 ± 0.38	56.42 ± 1.97	37.95 ± 1.12
Mean Teacher [ ]	70.09 ± 1.60	37.46 ± 3.30	8.10 ± 0.21	81.11 ± 1.44	45.17 ± 1.06	31.75 ± 0.23	36.09 ± 3.98	3.45 ± 0.03	3.27 ± 0.05	71.72 ± 1.45	56.49 ± 2.75	33.90 ± 1.37
MixMatch [ ]	38.84 ± 8.36	20.96 ± 2.45	10.25 ± 0.01	80.58 ± 3.38	47.88 ± 0.21	33.22 ± 0.06	26.61 ± 13.10	4.48 ± 0.35	5.01 ± 0.12	52.32 ± 0.91	36.34 ± 0.84	25.01 ± 0.43
ReMixMatch [ ]	8.13 ± 0.58	6.34 ± 0.22	4.65 ± 0.09	41.60 ± 1.48	25.72 ± 0.07	20.04 ± 0.13	16.43 ± 13.77	5.65 ± 0.35	5.36 ± 0.58	27.87 ± 3.85	11.14 ± 0.52	6.44 ± 0.15
FixMatch [ ]	12.66 ± 4.49	4.95 ± 0.10	4.26 ± 0.01	45.38 ± 2.07	27.71 ± 0.42	22.06 ± 0.10	3.37 ± 1.01		2.02 ± 0.03	38.19 ± 4.76	8.64 ± 0.84	5.82 ± 0.06
FlexMatch [ ]	5.29 ± 0.29	4.97 ± 0.07	4.24 ± 0.06	40.73 ± 1.44	26.17 ± 0.18	21.75 ± 0.15	8.19 ± 3.20	6.59 ± 2.29	6.72 ± 0.30	29.12 ± 5.04	9.85 ± 1.35	6.08 ± 0.34
Dash [ ]	9.29 ± 3.28	5.16 ± 0.28	4.36 ± 0.10	47.49 ± 1.05	27.47 ± 0.38	21.89 ± 0.16	5.26 ± 2.02	2.01 ± 0.01	2.08 ± 0.09	42.00 ± 4.94	10.50 ± 1.37	6.30 ± 0.49
MPL [ ]	6.93 ± 0.17	5.76 ± 0.24	4.55 ± 0.04	46.26 ± 1.84	27.71 ± 0.19	21.74 ± 0.09	-	-	-	35.76 ± 4.83	9.90 ± 0.96	6.66 ± 0.00
RelationMatch [ ]	6.87 ± 0.12		4.22 ± 0.06	45.79 ± 0.59	27.90 ± 0.15	22.18 ± 0.13	-	-	-	33.42 ± 3.92	9.55 ± 0.87	6.08 ± 0.29
CoMatch [ ]	6.51 ± 1.18	5.35 ± 0.14	4.27 ± 0.12	53.41 ± 2.36	29.78 ± 0.11	22.11 ± 0.22	8.20 ± 5.32	2.16 ± 0.04	2.01 ± 0.04		7.63 ± 0.94	5.71 ± 0.08
CCSSL [ ]	9.71 ± 2.78	5.14 ± 0.55	4.46 ± 0.20	38.81 ± 1.65	24.30 ± 0.63	19.32 ± 0.16	7.85 ± 3.6	2.12 ± 0.04	2.03 ± 0.03	17.55 ± 4.2	8.43 ± 1.1	5.77 ± 0.82
SimMatch [ ]	5.38 ± 0.01	5.36 ± 0.08	4.41 ± 0.07	39.32 ± 0.72	26.21 ± 0.37	21.50 ± 0.11	7.60 ± 2.11	2.48 ± 0.61	2.05 ± 0.05	16.98 ± 4.24	8.27 ± 0.40	5.74 ± 0.31
AdaMatch [ ]	5.09 ± 0.21	5.13 ± 0.05	4.36 ± 0.05	38.08 ± 1.35	26.66 ± 0.33	21.99 ± 0.15	6.14 ± 5.35	2.13 ± 0.04	2.02 ± 0.05	19.95 ± 5.17	8.59 ± 0.43	6.01 ± 0.02
FreeMatch [ ]		4.88 ± 0.09	4.16 ± 0.06	39.52 ± 0.01	26.22 ± 0.08	21.81 ± 0.17	10.43 ± 0.82	8.23 ± 3.22	7.56 ± 0.25	28.50 ± 5.41	9.29 ± 1.24	5.81 ± 0.32
SoftMatch [ ]	5.11 ± 0.14	4.96 ± 0.09	4.27 ± 0.05	37.60 ± 0.24	26.39 ± 0.38	21.86 ± 0.16		2.15 ± 0.07	2.09 ± 0.06	22.23 ± 3.82	9.18 ± 0.68	5.79 ± 0.15
GBVSSL	6.15 ± 0.25	4.92 ± 0.05					5.21 ± 1.05	1.99 ± 0.31		15.74 ± 3.90
Fully-Supervised	4.62 ± 0.05			19.30 ± 0.09			2.13 ± 0.02			None

5.1.4. Data Augmentation

5.2. performance on common ssl datasets, 5.3. results on semi-inat 2021 [ 42 ], 5.4. qualitative studies, 5.4.1. convergence speed, 5.4.2. mask ratio, data utilization, and pseudo-label accuracy, 5.4.3. confusion matrix, 5.4.4. t-sne visualization, 5.5. ablation experiments, 5.5.1. contrastive & class-aware & re-weighting & combination of label and pseudo-label & label propagation, 5.5.2. ratio μ of unlabeled data, 5.5.3. memory bank setup, 5.5.4. top-k selections, 5.5.5. label propagation iterations φ, 6. limitations, 7. conclusions, author contributions, data availability statement, acknowledgments, conflicts of interest.

• Yang, F.; Wu, K.; Zhang, S.; Jiang, G.; Liu, Y.; Zheng, F.; Zhang, W.; Wang, C.; Zeng, L. Class-aware contrastive semi-supervised learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14421–14430. [ Google Scholar ]
• Sohn, K.; Berthelot, D.; Carlini, N.; Zhang, Z.; Zhang, H.; Raffel, C.A.; Cubuk, E.D.; Kurakin, A.; Li, C.L. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. Adv. Neural Inf. Process. Syst. 2020 , 33 , 596–608. [ Google Scholar ]
• Zhang, B.; Wang, Y.; Hou, W.; Wu, H.; Wang, J.; Okumura, M.; Shinozaki, T. Flexmatch: Boosting semi-supervised learning with curriculum pseudo labeling. Adv. Neural Inf. Process. Syst. 2021 , 34 , 18408–18419. [ Google Scholar ]
• Berthelot, D.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Sohn, K.; Zhang, H.; Raffel, C. ReMixMatch: Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring. In Proceedings of the International Conference on Learning Representations, Online, 26 April–1 May 2020; pp. 1–13. [ Google Scholar ]
• Chen, H.; Tao, R.; Fan, Y.; Wang, Y.; Wang, J.; Schiele, B.; Xie, X.; Raj, B.; Savvides, M. Softmatch: Addressing the quantity-quality trade-off in semi-supervised learning. arXiv 2023 , arXiv:2301.10921. [ Google Scholar ]
• Li, J.; Xiong, C.; Hoi, S.C. Comatch: Semi-supervised learning with contrastive graph regularization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 9475–9484. [ Google Scholar ]
• Kim, J.; Min, Y.; Kim, D.; Lee, G.; Seo, J.; Ryoo, K.; Kim, S. Conmatch: Semi-supervised learning with confidence-guided consistency regularization. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 674–690. [ Google Scholar ]
• Zheng, M.; You, S.; Huang, L.; Wang, F.; Qian, C.; Xu, C. SimMatch: Semi-Supervised Learning with Similarity Matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 14471–14481. [ Google Scholar ]
• Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the Workshop on Challenges in Representation Learning, ICML, Atlanta, GA, USA, 16–21 June 2013; Volume 3, p. 896. [ Google Scholar ]
• Wu, Z.; Xiong, Y.; Yu, S.X.; Lin, D. Unsupervised feature learning via non-parametric instance discrimination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3733–3742. [ Google Scholar ]
• Chen, X.; Fan, H.; Girshick, R.; He, K. Improved baselines with momentum contrastive learning. arXiv 2020 , arXiv:2003.04297. [ Google Scholar ]
• He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [ Google Scholar ]
• Xie, Q.; Dai, Z.; Hovy, E.; Luong, T.; Le, Q. Unsupervised data augmentation for consistency training. Adv. Neural Inf. Process. Syst. 2020 , 33 , 6256–6268. [ Google Scholar ]
• Xu, Y.; Shang, L.; Ye, J.; Qian, Q.; Li, Y.F.; Sun, B.; Li, H.; Jin, R. Dash: Semi-supervised learning with dynamic thresholding. In Proceedings of the International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 11525–11536. [ Google Scholar ]
• Roelofs, B.; Berthelot, D.; Sohn, K.; Carlini, N.; Kurakin, A. AdaMatch: A Unified Approach to Semi-Supervised Learning and Domain Adaptation. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022; pp. 1–50. [ Google Scholar ]
• Guo, L.Z.; Li, Y.F. Class-imbalanced semi-supervised learning with adaptive thresholding. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 8082–8094. [ Google Scholar ]
• Wang, X.; Wu, Z.; Lian, L.; Yu, S.X. Debiased learning from naturally imbalanced pseudo-labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14647–14657. [ Google Scholar ]
• Wang, Y.; Chen, H.; Heng, Q.; Hou, W.; Fan, Y.; Wu, Z.; Wang, J.; Savvides, M.; Shinozaki, T.; Raj, B.; et al. Freematch: Self-adaptive thresholding for semi-supervised learning. arXiv 2022 , arXiv:2205.07246. [ Google Scholar ]
• Zhou, H.; Song, L.; Chen, J.; Zhou, Y.; Wang, G.; Yuan, J.; Zhang, Q. Rethinking soft labels for knowledge distillation: A bias-variance tradeoff perspective. In Proceedings of the International Conference on Learning Representations, Online, 3–7 May 2021; pp. 1–15. [ Google Scholar ]
• Heskes, T. Bias/variance decompositions for likelihood-based estimators. Neural Comput. 1998 , 10 , 1425–1433. [ Google Scholar ] [ CrossRef ] [ PubMed ]
• Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [ Google Scholar ]
• Zhou, D.; Bousquet, O.; Lal, T.; Weston, J.; Schölkopf, B. Learning with local and global consistency. NeurIPS 2003 , 16 , 321–328. [ Google Scholar ]
• Zbontar, J.; Jing, L.; Misra, I.; LeCun, Y.; Deny, S. Barlow twins: Self-supervised learning via redundancy reduction. In Proceedings of the International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 12310–12320. [ Google Scholar ]
• Li, S.; Han, L.; Wang, Y.; Pu, Y.; Zhu, J.; Li, J. GCL: Contrastive learning instead of graph convolution for node classification. Neurocomputing 2023 , 551 , 126491. [ Google Scholar ] [ CrossRef ]
• Cundy, C.; Ermon, S. Sequencematch: Imitation learning for autoregressive sequence modelling with backtracking. Adv. Neural Inf. Process. Syst. 2023 . [ Google Scholar ] [ CrossRef ]
• Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report, University of Toronto, Toronto, ON, Canada, 2009.
• Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 16 December 2011; Volume 2011, p. 7. [ Google Scholar ]
• Coates, A.; Ng, A.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [ Google Scholar ]
• Zagoruyko, S.; Komodakis, N. Wide residual networks. In Proceedings of the British Machine Vision Conference 2016, York, UK, 19–22 September 2016; pp. 87.1–87.12. [ Google Scholar ]
• He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [ Google Scholar ]
• Zhou, B.; Lu, J.; Liu, K.; Xu, Y.; Cheng, Z.; Niu, Y. HyperMatch: Noise-tolerant semi-supervised learning via relaxed contrastive constraint. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 24017–24026. [ Google Scholar ]
• Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [ Google Scholar ]
• Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 1–16. [ Google Scholar ]
• Kalantidis, Y.; Sariyildiz, M.B.; Pion, N.; Weinzaepfel, P.; Larlus, D. Hard negative mixing for contrastive learning. Adv. Neural Inf. Process. Syst. 2020 , 33 , 21798–21809. [ Google Scholar ]
• Wang, Y.; Chen, H.; Fan, Y.; Sun, W.; Tao, R.; Hou, W.; Wang, R.; Yang, L.; Zhou, Z.; Guo, L.Z.; et al. Usb: A unified semi-supervised learning benchmark for classification. Adv. Neural Inf. Process. Syst. 2022 , 35 , 3938–3961. [ Google Scholar ]
• Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C.A. Mixmatch: A holistic approach to semi-supervised learning. Adv. Neural Inf. Process. Syst. 2019 , 32 , 1–14. [ Google Scholar ]
• Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-supervised learning with ladder networks. Adv. Neural Inf. Process. Syst. 2015 , 28 , 3546–3554. [ Google Scholar ]
• Miyato, T.; Maeda, S.I.; Koyama, M.; Ishii, S. Virtual adversarial training: A regularization method for supervised and semi-supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018 , 41 , 1979–1993. [ Google Scholar ] [ CrossRef ] [ PubMed ]
• Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. Adv. Neural Inf. Process. Syst. 2017 , 30 , 1195–1204. [ Google Scholar ]
• Pham, H.; Dai, Z.; Xie, Q.; Le, Q.V. Meta pseudo labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11557–11568. [ Google Scholar ]
• Zhang, Y.; Yang, J.; Tan, Z.; Yuan, Y. Relationmatch: Matching in-batch relationships for semi-supervised learning. arXiv 2023 , arXiv:2305.10397. [ Google Scholar ]
• Su, J.C.; Maji, S. The semi-supervised inaturalist challenge at the fgvc8 workshop. arXiv 2021 , arXiv:2106.01364. [ Google Scholar ]

Method	Semi-iNat 2021
Supervised	19.09	35.85	34.96	57.11
MixMatch [ ]	16.89	30.83	-	-
CoMatch [ ]	20.94	38.96	38.94	61.85
FixMatch [ ]	21.41	37.65	40.3	60.05
CCSSL(MixMatch) [ ]	19.65	35.09	-	-
CCSSL(CoMatch) [ ]	24.12	43.23	39.85	63.68
CCSSL(FixMatch) [ ]	31.21	52.25	41.28	64.3
HyperMatch [ ]	33.47	-	41.57	-
GBVSSL

ss-cl	ca-cl	Re-Weight	Label-Unlabel	Label Prop	Semi-iNat 2021	CIFAR-100@2500
					21.58	72.69
√					27.86	72.45
√		√			29.66	72.82
	√				30.62	75.71
	√	√			31.49	76.09
	√		√		32.09	76.32
	√	√	√		32.91	76.57
	√	√	√	√

Ratio	CIFAR-100@10000
2	77.25	77.63
4	77.96	79.32
5		79.84
6	76.86	79.58
7	77.43

Bank Settings	Unlabeled	Labeled	Unlabeled & Labeled
Semi-iNat 2021	33.65	33.08
CIFAR-100@2500	76.32	76.69

K	8	16	32	64	128	256
Semi-iNat 2021	33.57	33.85	34.03		34.12	33.94
CIFAR-100@2500	76.66	76.54	76.86	76.82		76.75

Semi-iNat 2021	32.92	33.57		33.85
CIFAR-100@2500	76.30	76.62	76.70

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

Li, S.; Han, L.; Wang, Y.; Zhu, J. GBVSSL: Contrastive Semi-Supervised Learning Based on Generalized Bias-Variance Decomposition. Symmetry 2024 , 16 , 724. https://doi.org/10.3390/sym16060724

Li S, Han L, Wang Y, Zhu J. GBVSSL: Contrastive Semi-Supervised Learning Based on Generalized Bias-Variance Decomposition. Symmetry . 2024; 16(6):724. https://doi.org/10.3390/sym16060724

Li, Shu, Lixin Han, Yang Wang, and Jun Zhu. 2024. "GBVSSL: Contrastive Semi-Supervised Learning Based on Generalized Bias-Variance Decomposition" Symmetry 16, no. 6: 724. https://doi.org/10.3390/sym16060724

Article Metrics

Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals