unit 8 homework 5 trigonometry finding sides and angles

Snapsolve any problem by taking a picture. Try it in the Numerade app?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 1363

Learning Objectives

• Use right triangles to evaluate trigonometric functions.
• Find function values for 30°(\(\dfrac{\pi}{6}\)),45°(\(\dfrac{\pi}{4}\)),and 60°(\(\dfrac{\pi}{3}\)).
• Use equal cofunctions of complementary angles.
• Use the definitions of trigonometric functions of any angle.
• Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x -axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

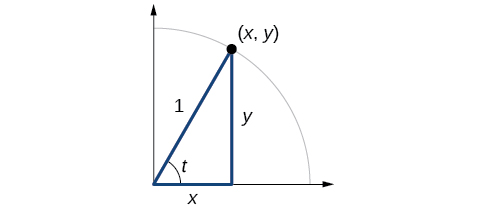
\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in Figure \(\PageIndex{2}\).

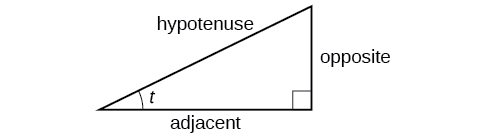
Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

• Find the sine as the ratio of the opposite side to the hypotenuse.
• Find the cosine as the ratio of the adjacent side to the hypotenuse.
• Find the tangent is the ratio of the opposite side to the adjacent side.

Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

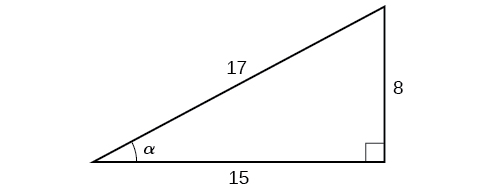
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Exercise \(\PageIndex{1}\)

Given the triangle shown in Figure \(\PageIndex{4}\), find the value of \(\sin t\).

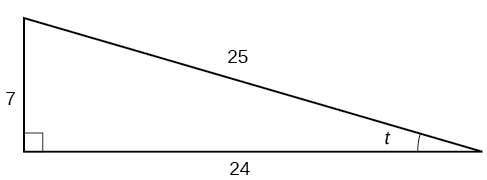
\(\frac{7}{25}\)

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

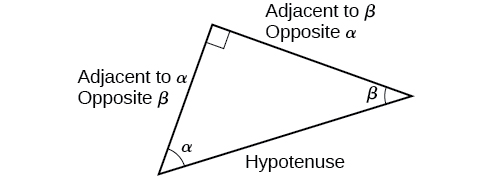
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles

• If needed, draw the right triangle and label the angle provided.
• Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
• sine as the ratio of the opposite side to the hypotenuse
• cosine as the ratio of the adjacent side to the hypotenuse
• tangent as the ratio of the opposite side to the adjacent side
• secant as the ratio of the hypotenuse to the adjacent side
• cosecant as the ratio of the hypotenuse to the opposite side
• cotangent as the ratio of the adjacent side to the opposite side

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure \(\PageIndex{6}\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).

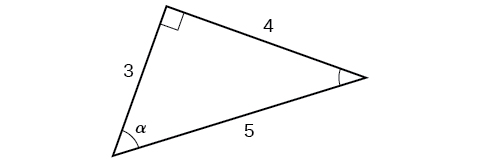
\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Exercise \(\PageIndex{2}\)

Using the triangle shown in Figure \(\PageIndex{7}\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).

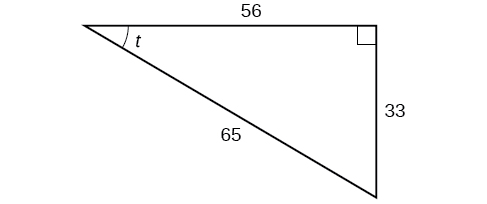
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

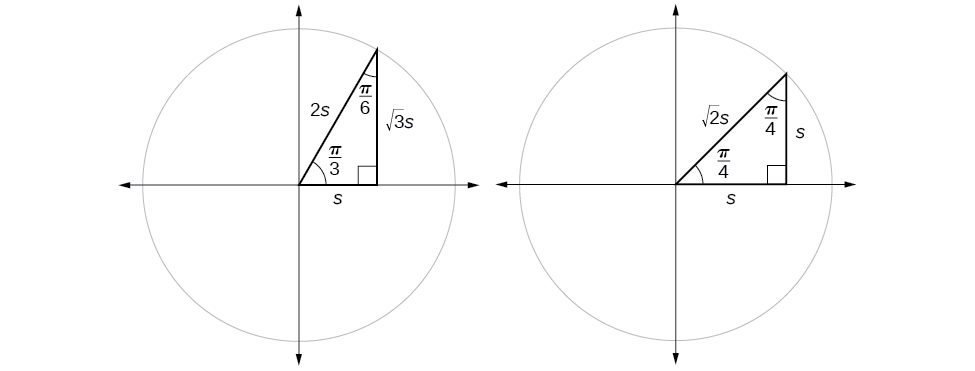
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

• Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
• Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercise \(\PageIndex{3}\)

Find the exact value of the trigonometric functions of \(\frac{π}{4}\) using side lengths.

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

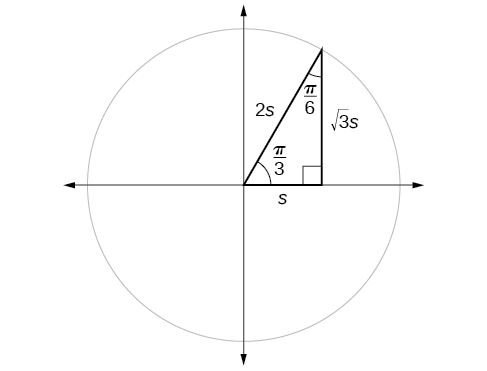
This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

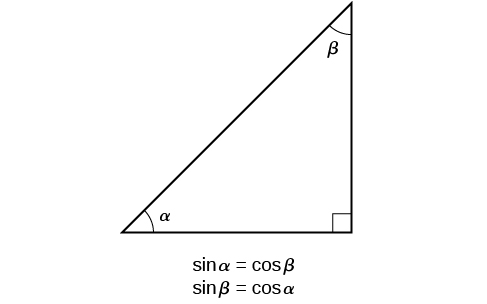
Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Exercise \(\PageIndex{4}\)

If \(\csc (\frac{π}{6})=2,\) find \( \sec (\frac{π}{3}).\)

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

how to: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure \(\PageIndex{11}\).

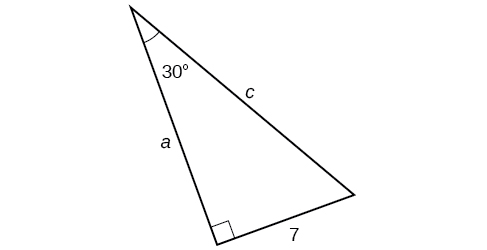
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

We rearrange to solve for \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

We can use the sine to find the hypotenuse.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Again, we rearrange to solve for \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Exercise \(\PageIndex{5}\):

A right triangle has one angle of \(\frac{π}{3}\) and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\) missing angle is \(\frac{π}{6}\)

Using Right Triangle Trigonometry to Solve Applied Problems

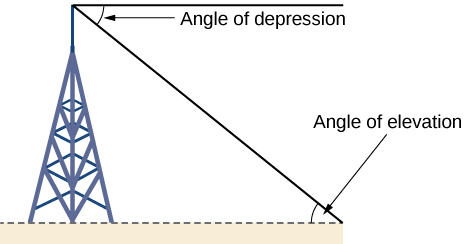
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

how to: Given a tall object, measure its height indirectly

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

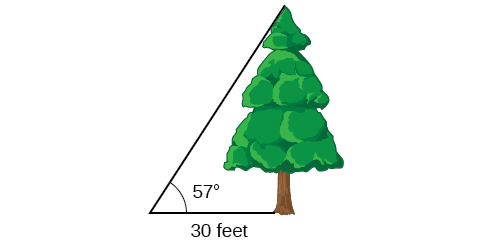
We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.

Exercise \(\PageIndex{6}\):

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of \(\frac{5π}{12}\) with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

• Finding Trig Functions on Calculator
• Finding Trig Functions Using a Right Triangle
• Relate Trig Functions to Sides of a Right Triangle
• Determine Six Trig Functions from a Triangle
• Determine Length of Right Triangle Side

Visit this website for additional practice questions from Learningpod.

Key Equations

Cofunction Identities

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example .
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See Example .
• We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See Example .
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See Example .
• We can use trigonometric functions of an angle to find unknown side lengths.
• Select the trigonometric function representing the ratio of the unknown side to the known side. See Example .
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
• The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example .

unit 8 right triangle and trigonometry homework 5 trigonometry: finding sides and angles solve for x round to the nearest tenth. plllls I will make brainlesst ​

5. x = 25.6

6. x = 11.0

7. x = 41.8°

8. x = 64.2°

9. x = 12.8°

10. x = 51.3°

Step-by-step explanation:

Let's find the x value for each triangle.

For point 5      

x: is the opposite cathetus to 52°  

20: is the adjacent cathetus to 52°  

52°: is the angle

We can find "x" with the following trigonometric function:

[tex] tan(52) = \frac{x}{20} [/tex]

[tex] x = tan(52)*20 = 25.6 [/tex]

For point 6      

x: is the hypotenuse  

5: is the opposite cathetus to the given angle  

27°: is the angle

To find "x" we need to use the trigonometric function:

[tex] sin(27) = \frac{5}{x} [/tex]

[tex]x = \frac{5}{sin(27)} = 11.0[/tex]

For point 7

x°: is the angle

6: is the hypotenuse

4: is the opposite cathetus to x°

Hence, x is:

[tex] sin(x) = \frac{4}{6} [/tex]

[tex] x = sin^{-1}(\frac{4}{6}) = 41.8 [/tex]

For point 8    

14: is the adjacent cathetus to x°

29: is the opposite cathetus to x°

To calculate "x" we need to use the trigonometric function tan(x):

[tex] tan(x) = \frac{29}{14} [/tex]

[tex] x = tan^{-1}(\frac{29}{14}) = 64.2 [/tex]

For point 9    

54: is the hypotenuse

12: is the opposite cathetus to x°

We can use sin(x) to solve for x:

[tex] sin(x) = \frac{12}{54} [/tex]

[tex] x = sin^{-1}(\frac{12}{54}) = 12.8 [/tex]

For point 10  

40: is the hypotenuse

25: is the adjacent cathetus to x°

We need to use cos(x) to solve for x:

[tex] cos(x) = \frac{25}{40} [/tex]  

[tex] x = cos^{-1}(\frac{25}{40}) = 51.3 [/tex]

I hope it helps you!

To solve the given questions, either of the trigonometric functions; sine , cosine and tangent of an angle has to be applied appropriately to either of the questions. The answers to the questions are:

5. x = 25.60

6. x = 11.00

7. x = [tex]41.8^{o}[/tex]

8. x = [tex]64.2^{o}[/tex]

9. x = [tex]12.8^{o}[/tex]

10. x = [tex]51.3^{o}[/tex]

The questions given are right angled triangles which requires the application of trigonometric functions appropriately. A right angle triangle is one that has one of its angles to be [tex]90^{o}[/tex].

So, each of the questions can be solved as follows:

5. Tan θ = [tex]\frac{opposite}{adjacent}[/tex]

Tan 52 = [tex]\frac{x}{20}[/tex]

⇒  x = Tan 52 * 20

       = 25.5988

6. Sin θ = [tex]\frac{opposite}{hypotenuse}[/tex]

Sin 27 = [tex]\frac{5}{x}[/tex]

⇒ x = [tex]\frac{5}{Sin 27}[/tex]

       = 11.0134

7. Sin θ = [tex]\frac{opposite}{hypotenuse}[/tex]

Sin x = [tex]\frac{4}{6}[/tex]

        = 0.66667

x = [tex]Sin^{-1}[/tex] 0.66667

  = [tex]41.8^{o}[/tex]

x = [tex]41.8^{o}[/tex]

8. Tan θ = [tex]\frac{opposite}{adjacent}[/tex]

Tan x = [tex]\frac{29}{14}[/tex]

          = 2.0714

x = [tex]Tan^{-1}[/tex] 2.0714

  = [tex]64.2^{o}[/tex]

x = [tex]64.2^{o}[/tex]

9. Sin θ = [tex]\frac{opposite}{hypotenuse}[/tex]

Sin x = [tex]\frac{12}{54}[/tex]

        = 0.22222

x = [tex]Sin^{-1}[/tex] 0.22222

  = [tex]12.8^{o}[/tex]

x = [tex]12.8^{o}[/tex]

10. Cos θ = [tex]\frac{adjacent}{hypotenuse}[/tex]

Cos x = [tex]\frac{25}{40}[/tex]

         = 0.625

x = [tex]Cos^{-1}[/tex] 0.625

  = [tex]51.3^{o}[/tex]

x = [tex]51.3^{o}[/tex]

Visit: https://brainly.com/question/20926900

Related Questions

Where would I start when rewriting polynomials in standard form? I have my notes but they’re still unclear to me.

standard form = combine like therms and degrees drop from left to right

In this there aren’t like therms, so:

6x^3+x^2-9x+5

therms =  each therm is seprated by a plus or a minus

in this case there are 4 therms

degree = look at the monomial with the highest degree

in this case is 3

Name = in this case there are four therms so it is a quadrinomial

Standard form denotes to arranging according to degrees or exponents

Standard form

Number of terms=4

Name Quadrinomial or Biquadratic

Can you please help me solve dis

I would say F

This is because a rectangle need to have at least one side of parallel sides that are the same length and F confirms that.

Kenney High School’s swimming pool is 25 yards long. The pool has 8 lanes, each of which is 3 yards wide. The pool is filled to a depth of 6 feet. a. What are the length and width of the pool in terms of feet? (4 points) b. How many cubic feet of water are in the pool? (3 points) c. If one cubic foot contains about 7.5 gallons, how many gallons of water are in the pool? (3 points)

Length = 75 ft

Width = 72 ft

Question b = 32,400

Water is 242,998 gallons

This is due today pls help!!!!!!!

Each value is multiplied by 1.5 so 7 times 1.5 is 10.5

10.5/3 = 3.5

To find the value of x that makes triangle DEF similar to XYZ, we have to find the scale. To do this find 2 similar sides. I chose 7.5 from XYZ and 5 from DEF. Divide 7.5 by 5 to get 1.5. 1.5 is our scale so this means we will insert 1.5 for x and get 4.5 as our answer.

On the Coordinate plane, mark all points such that y=x+3

(0, 3); (-3, 0)

ordered pairs:

y = 0 + 3 = 0 --> (0, 3)

0 = x + 3 --> x = -3 --> (-3, 0)

Brenna owns 9 T-shirts, 3 of which are red. If Brenna randomly selects a T-shirt to wear, what is the probability it will be red?

9 Shirts, 3 are Red

Probability: 3/9

Simplify: 1/3

4. If 3x − 1 = 11, the 2x = ? a. 20/3 b. 2 c. 4 d. 8 e. 72

Your answer is C

3(4)-1 = 11

3x − 1 = 11

add 1 to both sides

Divide both sides by 3

-----------------

2x = 2*4 = 8

You need to use 4/5 cups of strawberries for a single pie how many cups are needed for 2 pies i know the answer is 13/5 but how do you work that out

If the radius of a circle is 1 kilometer what is the area of the circle?

The area of the circle is [tex]1\pi[/tex] or approximately 3.14 [tex]km^2[/tex]

The formula to find the area of a circle is [tex]\pi r^2[/tex], where [tex]r[/tex] represents the radius of the circle. In this case, the area would be [tex]1^2*\pi[/tex] = [tex]\pi[/tex] ≈ 3.14 [tex]km^2[/tex].

*PLEASE PLEASE HELP I WILL MARK THE BRAINLIEST* Write an expression equivalent to 3n2 + 12n that is a product of two expressions. Enter numbers, variables, or expressions in the boxes.

3n(n + 4) = 0

3n2 + 12n factors into (3n)(n + 4n) .

Use the Pythagorean theorem to find the length of the line

This is one of my specialties so sit back, relax while I work on this for 5 mins :)

The formula is a^2 + B^2 = c^2

7^2 + 5^2 = c^2

49 + 25 = 74

8.60232526 = c

8.60232526 rounded to the nearest tenth is 8.6

So there you go. Hope it helps!!

Anyone know how to solve this?

What is the greatest common factor (GCF) of this expression?

Please answer quickly!!

hope this helps :)

Answer: 1. (5,3) 2. (3, -1) 3. (2,1) 4. (4,1)

1. Graph the system of equation in desmos.

2. Find the intersection point.

3. There's your answer.

To solve the equation: 14 = t +72 This is a(n) equation (type an math operation) In order to solve it, you need to use (type a math operation). You would _(type a math operation and a number) on both sides of the equation. The final answer is t = (type a number)

[tex]14=t+72\\14-72=t+72-72\\-58=t[/tex]

c.) Find the Surface Area of the Regular Pyramid. Surface Area: Volume: 24 yds 20 yds​

NEED HELP ASAP 50 POINTS Rhombus ABCD has a diagonal BD¯¯¯¯¯. m∠ADB=(4x−12)° m∠CDB=(3x+6)° What is the m∠ADC ? Enter your answer in the box º

Angle ADC = 7x - 6°

4x - 12 + 3x + 6 = 7x - 6

Diagonal BD of a given rhombus is angle bisector of ∠ADC, so:

Substitute the values and solve for x:

Find the value of ∠ADC:

PLEASE HELP QUICK!!!

I believe the answer is C. -10 < x <2

What is another name for the height of a pyramid? A. Length B. Width C. Altitude O D. Lateral face SUBMIT

Find another name for the height of a prism or a pyramid.

Since we know that the height of a prism or pyramid is the perpendicular distance between the two ends of a prism or pyramid.

We can find the height of the pyramid by dropping an altitude from the top of the pyramid to the base of the pyramid.

Note to moderators:

Please don't delete this answer because I'm just trying to help others.

The height of the pyramid is also called the altitude of the pyramid. Since both of these terms represent the same thing , we can use the two terms interchangeably. The correct option is C .

A pyramid geometry is defined as a three dimensional object with a polygon as its base and the triangles forms the lateral faces which meet at a point above the base called the apex . The pyramids have different parts and some of these parts have more than one name.

The height of the pyramid indicate the perpendicular distance from the base of the pyramid to the apex of the pyramid. This line segment which is perpendicular to the base and runs from the base to the apex is defined as the altitude of the pyramid.

Based on the shape of the base, the pyramids are of many types like triangular pyramid, square pyramid, etc.

Thus the correct option is C .

To know more about pyramid , visit;

https://brainly.com/question/28709442

Find the measure of the indicated angle. Need help please. I need explanation THANK YOU

Answer: Approximately 28 km

The more accurate, yet still approximate value, is roughly 27.995735464379

Round that however you need to.

=============================================================

Explanation:

As the diagram shows, the uppercase letters A,B,C represent the corner points of the triangle. They also represent the angles. The diagram says that:

The missing angle C is....

A+B+C = 180

C = 180-A-B

C = 180-59-91

which we'll use later.

Convention usually has the side lengths be lowercase letters 'a', b, and c. Those lowercase letters are opposite their uppercase counterpart. We'll have side 'a' opposite angle A, then b is opposite B, and c is opposite C. This allows us to quickly label a triangle and find the missing sides and/or angles. The phrasing "solve the triangle" basically means "find all the missing sides and angles". For this problem, we're only concerned with one side.

The diagram says that side c = 14 due to it being opposite angle C.

The goal is to find side b, which is the shorter way of saying "find AC".

-------------------------

From here, we can use the law of sines to find side b

b/sin(B) = c/sin(C)

b/sin(91) = 14/sin(30)

b = sin(91)*14/sin(30)

b = 27.995735464379 which is approximate

Side AC is roughly 28 km long.

I rounded to the nearest whole number since the "14 km" is also a whole number. Your teacher may want you to round differently.

Make sure your calculator is in degree mode.

Each of 8 ladies randomly chooses a woolen overcoat from 14 different styles. What is the probability that at least 2 ladies choose the same type of overcoat? choices ≈ 0.820 ≈ 0.918 ≈ 0.929 ≈ 0.894

Answer: 0.894

                    ≈ 0.918

Use the complement since the probability of at least 2 ladies choose the same type of overcoat is much more challenging than finding the probability that all the ladies choose a different overcoat.

P(at least 2 ladies choose the same type of overcoat) = 1 − P(all choose different)

Find the probability that they all choose a different type of overcoat.

Now use the complement to determine the probability that at least 2 ladies choose the same type of overcoat.

P(at least 2 ladies choose the same) =

1 − P(all choose different)  

≈ 1 − 0.0820  

The probability that at least 2 ladies choose the same type of overcoat is approximately 0.918 or 91.8%.

I know the answer is -2 but I need to show my work on how I got it

6x + 10 = 1x

Subtract 6x from both sides.

------------ Divide by -5

Subtract 10 from both sides

6x + 10 (-10)= 1x (-10)

6x =1x - 10

Subtract 1x from both sides

6x (-x) = 1x (-x) - 10

Divide both sides by 5

5x (/5) = -10 (/5)

Hope that helps :)

Which of the following is an equivalent ratio for the 15/24? 5/4 30/40 5/8

15/3=5 and 24/3=8

divide both by 3

Solve the expression below, when x = 8 (x - 4) + 12

Lets solve this step by step,

First we insert 8 in x's place:

(8 - 4) + 12

Now we solve:

4 + 12 = 16

Hope this Helps

I'll give brainliest PLZZZ! Solve the following problem using the elimination method: -3x + 7y = 12 x - 2y = -3

do you need to show your work or just the answer?

-3x+7y=12                                   mulitply both sides by 3 of the bottom.

-3x+7y=12                    

3x-6y=-9           < which turns into this

Then you have to sum the equations (vertically) to eliminate one variable.

Then substitute the given value of "y" into the equation

x-2 * 3=-3    then solve the equation for x      (x=3)

y=3   x=3    (3, 3)

*Check your answers.

-3*3+7*3=12

Logan has 4 2/3 cup of peanuts and 3 2/3 cup of cashews if you combine some nuts how much will he have

Answer: He will have 8 1/3 nuts

Amount of peanuts=4 2/3 cups

Amount of cashews=3 2/3 cups

Combing the nuts will give  Total amount of nuts ( peanuts and cashews)

=4 2/3  +3 2/3

pllzzzzzzzzzzzzzzzzz help

that would be 33 square feet!!!

Carlos has 38. he puts 8 apples into each bag. If he fills as many bags as possible, how many apples are left?

Answer: 6 is how many apples are left

Plz help will mark brainliest

A swimming pool is a shape of a rectangular prism. The pool is 10 feet deep. It length is 3 times it's width. The volume of the pool is 27000 cubic feet. Find the length and the width of the pool.

V = l * w * h

27000ft3 = (2w) * w * 10ft

27000ft3 = 2w^2 * 10ft

2700 = 2w^2