homework 3 free fall and graphs answer key

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.7: Free Fall

• Last updated
• Save as PDF
• Page ID 3982

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Use the kinematic equations with the variables y and g to analyze free-fall motion.
• Describe how the values of the position, velocity, and acceleration change during a free fall.
• Solve for the position, velocity, and acceleration as functions of time when an object is in a free fall.

An interesting application of Equation 3.3.2 through Equation 3.5.22 is called free fall , which describes the motion of an object falling in a gravitational field, such as near the surface of Earth or other celestial objects of planetary size. Let’s assume the body is falling in a straight line perpendicular to the surface, so its motion is one-dimensional. For example, we can estimate the depth of a vertical mine shaft by dropping a rock into it and listening for the rock to hit the bottom. But “falling,” in the context of free fall, does not necessarily imply the body is moving from a greater height to a lesser height. If a ball is thrown upward, the equations of free fall apply equally to its ascent as well as its descent.

The most remarkable and unexpected fact about falling objects is that if air resistance and friction are negligible, then in a given location all objects fall toward the center of Earth with the same constant acceleration, independent of their mass . This experimentally determined fact is unexpected because we are so accustomed to the effects of air resistance and friction that we expect light objects to fall slower than heavy ones. Until Galileo Galilei (1564–1642) proved otherwise, people believed that a heavier object has a greater acceleration in a free fall. We now know this is not the case. In the absence of air resistance, heavy objects arrive at the ground at the same time as lighter objects when dropped from the same height Figure \(\PageIndex{1}\).

In the real world, air resistance can cause a lighter object to fall slower than a heavier object of the same size. A tennis ball reaches the ground after a baseball dropped at the same time. (It might be difficult to observe the difference if the height is not large.) Air resistance opposes the motion of an object through the air, and friction between objects—such as between clothes and a laundry chute or between a stone and a pool into which it is dropped—also opposes motion between them.

For the ideal situations of these first few chapters, an object falling without air resistance or friction is defined to be in free fall . The force of gravity causes objects to fall toward the center of Earth. The acceleration of free-falling objects is therefore called acceleration due to gravity . Acceleration due to gravity is constant, which means we can apply the kinematic equations to any falling object where air resistance and friction are negligible. This opens to us a broad class of interesting situations.

Acceleration due to gravity is so important that its magnitude is given its own symbol, g. It is constant at any given location on Earth and has the average value

\[g = 9.81\; m/s^{2}\; (or\; 32.2\; ft/s^{2}) \ldotp\]

Although g varies from 9.78 m/s 2 to 9.83 m/s 2 , depending on latitude, altitude, underlying geological formations, and local topography, let’s use an average value of 9.8 m/s 2 rounded to two significant figures in this text unless specified otherwise. Neglecting these effects on the value of g as a result of position on Earth’s surface, as well as effects resulting from Earth’s rotation, we take the direction of acceleration due to gravity to be downward (toward the center of Earth). In fact, its direction defines what we call vertical. Note that whether acceleration a in the kinematic equations has the value +g or −g depends on how we define our coordinate system. If we define the upward direction as positive, then a = −g = −9.8 m/s 2 , and if we define the downward direction as positive, then a = g = 9.8 m/s 2 .

One-Dimensional Motion Involving Gravity

The best way to see the basic features of motion involving gravity is to start with the simplest situations and then progress toward more complex ones. So, we start by considering straight up-and-down motion with no air resistance or friction. These assumptions mean the velocity (if there is any) is vertical. If an object is dropped, we know the initial velocity is zero when in free fall. When the object has left contact with whatever held or threw it, the object is in free fall. When the object is thrown, it has the same initial speed in free fall as it did before it was released. When the object comes in contact with the ground or any other object, it is no longer in free fall and its acceleration of g is no longer valid. Under these circumstances, the motion is one-dimensional and has constant acceleration of magnitude g. We represent vertical displacement with the symbol y.

Kinematic Equations for Objects in Free Fall

We assume here that acceleration equals −g (with the positive direction upward).

\[v =v _{0} - gt \label{3.15}\]

\[y = y_{0} + v_{0} t - \frac{1}{2} gt^{2} \label{3.16}\]

\[v^{2} = v_{0}^{2} - 2 g(y - y_{0}) \label{3.17}\]

Problem-Solving Strategy: Free Fall

• Decide on the sign of the acceleration of gravity. In Equation \ref{3.15} through Equation \ref{3.17}, acceleration g is negative, which says the positive direction is upward and the negative direction is downward. In some problems, it may be useful to have acceleration g as positive, indicating the positive direction is downward.
• Draw a sketch of the problem. This helps visualize the physics involved.
• Record the knowns and unknowns from the problem description. This helps devise a strategy for selecting the appropriate equations to solve the problem.
• Decide which of Equation \ref{3.15} through Equation \ref{3.17} are to be used to solve for the unknowns.

Example 3.14: Free Fall of a Ball

Figure \(\PageIndex{2}\) shows the positions of a ball, at 1-s intervals, with an initial velocity of 4.9 m/s downward, that is thrown from the top of a 98-m-high building. (a) How much time elapses before the ball reaches the ground? (b) What is the velocity when it arrives at the ground?

Choose the origin at the top of the building with the positive direction upward and the negative direction downward. To find the time when the position is −98 m, we use Equation \ref{3.16}, with y 0 = 0, v 0 = −4.9 m/s, and g = 9.8 m/s 2 .

• Substitute the given values into the equation: $$y = y_{0} + v_{0} t - \frac{1}{2} gt^{2}$$ $$-98.0\; m = 0 - (4.9\; m/s)t - \frac{1}{2} (9.8\; m/s^{2}) t^{2} \ldotp$$This simplifies to $$t^{2} + t - 20 = 0 \ldotp$$This is a quadratic equation with roots t = −5.0 s and t = 4.0 s. The positive root is the one we are interested in, since time t = 0 is the time when the ball is released at the top of the building. (The time t = −5.0 s represents the fact that a ball thrown upward from the ground would have been in the air for 5.0 s when it passed by the top of the building moving downward at 4.9 m/s.)
• Using Equation \ref{3.15}, we have $$v =v _{0} - gt = -4.9\; m/s - (9.8\; m/s^{2})(4.0\; s) = -44.1\; m/s \ldotp$$

Significance

For situations when two roots are obtained from a quadratic equation in the time variable, we must look at the physical significance of both roots to determine which is correct. Since t = 0 corresponds to the time when the ball was released, the negative root would correspond to a time before the ball was released, which is not physically meaningful. When the ball hits the ground, its velocity is not immediately zero, but as soon as the ball interacts with the ground, its acceleration is not g and it accelerates with a different value over a short time to zero velocity. This problem shows how important it is to establish the correct coordinate system and to keep the signs of g in the kinematic equations consistent.

Example 3.15: Vertical Motion of a Baseball

A batter hits a baseball straight upward at home plate and the ball is caught 5.0 s after it is struck Figure \(\PageIndex{3}\). (a) What is the initial velocity of the ball? (b) What is the maximum height the ball reaches? (c) How long does it take to reach the maximum height? (d) What is the acceleration at the top of its path? (e) What is the velocity of the ball when it is caught? Assume the ball is hit and caught at the same location.

Choose a coordinate system with a positive y-axis that is straight up and with an origin that is at the spot where the ball is hit and caught.

• Equation \ref{3.16} gives $$y = y_{0} + v_{0} t - \frac{1}{2} gt^{2}$$ $$0 = 0 + v_{0} (5.0\; s)- \frac{1}{2} (9.8\; m/s^{2}) (5.0\; s)^{2} \ldotp$$which gives v 0 = 24.5 m/sec.
• At the maximum height, v = 0. With v 0 = 24.5 m/s, Equation \ref{3.17} gives $$v^{2} = v_{0}^{2} - 2 g(y - y_{0})$$ $$0 = (24.5\; m/s^{2}) - 2 (9.8\; m/s^{2})(y - 0)$$or $$y = 30.6\; m \ldotp$$
• To find the time when v = 0 , we use Equation \ref{3.15}: $$v = v_{0} - gt$$ $$0 = 24..5\; m/s - (9.8\; m/s^{2})t \ldotp$$This gives t = 2.5 s. Since the ball rises for 2.5 s, the time to fall is 2.5 s.
• The acceleration is 9.8 m/s 2 everywhere, even when the velocity is zero at the top of the path. Although the velocity is zero at the top, it is changing at the rate of 9.8 m/s 2 downward.
• The velocity at t = 5.0 s can be determined with Equation \ref{3.15}: $$\begin{split} v & = v_{0} - gt \\ & = 24.5\; m/s - 9.8\; m/s^{2} (5.0\; s) \\ & = -24.5\; m/s \ldotp \end{split}$$

The ball returns with the speed it had when it left. This is a general property of free fall for any initial velocity. We used a single equation to go from throw to catch, and did not have to break the motion into two segments, upward and downward. We are used to thinking of the effect of gravity is to create free fall downward toward Earth. It is important to understand, as illustrated in this example, that objects moving upward away from Earth are also in a state of free fall.

Exercise 3.7

A chunk of ice breaks off a glacier and falls 30.0 m before it hits the water. Assuming it falls freely (there is no air resistance), how long does it take to hit the water? Which quantity increases faster, the speed of the ice chunk or its distance traveled?

Example 3.16: Rocket Booster

A small rocket with a booster blasts off and heads straight upward. When at a height of 5.0 km and velocity of 200.0 m/s, it releases its booster. (a) What is the maximum height the booster attains? (b) What is the velocity of the booster at a height of 6.0 km? Neglect air resistance.

We need to select the coordinate system for the acceleration of gravity, which we take as negative downward. We are given the initial velocity of the booster and its height. We consider the point of release as the origin. We know the velocity is zero at the maximum position within the acceleration interval; thus, the velocity of the booster is zero at its maximum height, so we can use this information as well. From these observations, we use Equation \ref{3.17}, which gives us the maximum height of the booster. We also use Equation \ref{3.17} to give the velocity at 6.0 km. The initial velocity of the booster is 200.0 m/s.

• From Equation \ref{3.17}, \(v^{2} = v_{0}^{2} - 2 g(y - y_{0})\). With v = 0 and y 0 = 0, we can solve for y: $$y = \frac{v_{0}^{2}}{-2g} = \frac{(2.0 \times 10^{2}\; m/s)^{2}}{-2(9.8\; m/s^{2})} = 2040.8\; m \ldotp$$This solution gives the maximum height of the booster in our coordinate system, which has its origin at the point of release, so the maximum height of the booster is roughly 7.0 km.
• An altitude of 6.0 km corresponds to y = 1.0 x 10 3 m in the coordinate system we are using. The other initial conditions are y 0 = 0, and v 0 = 200.0 m/s. We have, from Equation \ref{3.17}, $$v^{2} = (200.0\; m/s)^{2} - 2(9.8\; m/s^{2})(1.0 \times 10^{3}\; m) \Rightarrow v = \pm 142.8\; m/s \ldotp$$

We have both a positive and negative solution in (b). Since our coordinate system has the positive direction upward, the +142.8 m/s corresponds to a positive upward velocity at 6000 m during the upward leg of the trajectory of the booster. The value v = −142.8 m/s corresponds to the velocity at 6000 m on the downward leg. This example is also important in that an object is given an initial velocity at the origin of our coordinate system, but the origin is at an altitude above the surface of Earth, which must be taken into account when forming the solution.

Visit this site to learn about graphing polynomials. The shape of the curve changes as the constants are adjusted. View the curves for the individual terms (for example, y = bx) to see how they add to generate the polynomial curve.

3.1 Functions and Function Notation

• ⓑ yes (Note: If two players had been tied for, say, 4th place, then the name would not have been a function of rank.)

w = f ( d ) w = f ( d )

g ( 5 ) = 1 g ( 5 ) = 1

m = 8 m = 8

y = f ( x ) = x 3 2 y = f ( x ) = x 3 2

g ( 1 ) = 8 g ( 1 ) = 8

x = 0 x = 0 or x = 2 x = 2

• ⓐ yes, because each bank account has a single balance at any given time;
• ⓑ no, because several bank account numbers may have the same balance;
• ⓒ no, because the same output may correspond to more than one input.
• ⓐ Yes, letter grade is a function of percent grade;
• ⓑ No, it is not one-to-one. There are 100 different percent numbers we could get but only about five possible letter grades, so there cannot be only one percent number that corresponds to each letter grade.

No, because it does not pass the horizontal line test.

3.2 Domain and Range

{ − 5 , 0 , 5 , 10 , 15 } { − 5 , 0 , 5 , 10 , 15 }

( − ∞ , ∞ ) ( − ∞ , ∞ )

( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ ) ( − ∞ , 1 2 ) ∪ ( 1 2 , ∞ )

[ − 5 2 , ∞ ) [ − 5 2 , ∞ )

• ⓐ values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3
• ⓑ { x | x ≤ − 2 or − 1 ≤ x < 3 } { x | x ≤ − 2 or − 1 ≤ x < 3 }
• ⓒ ( − ∞ , − 2 ] ∪ [ − 1 , 3 ) ( − ∞ , − 2 ] ∪ [ − 1 , 3 )

domain =[1950,2002] range = [47,000,000,89,000,000]

domain: ( − ∞ , 2 ] ; ( − ∞ , 2 ] ; range: ( − ∞ , 0 ] ( − ∞ , 0 ]

3.3 Rates of Change and Behavior of Graphs

$ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 $ 2.84 − $ 2.31 5 years = $ 0.53 5 years = $ 0.106 per year.

a + 7 a + 7

The local maximum appears to occur at ( − 1 , 28 ) , ( − 1 , 28 ) , and the local minimum occurs at ( 5 , − 80 ) . ( 5 , − 80 ) . The function is increasing on ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) ( − ∞ , − 1 ) ∪ ( 5 , ∞ ) and decreasing on ( − 1 , 5 ) . ( − 1 , 5 ) .

3.4 Composition of Functions

( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2 ( f g ) ( x ) = f ( x ) g ( x ) = ( x − 1 ) ( x 2 − 1 ) = x 3 − x 2 − x + 1 ( f − g ) ( x ) = f ( x ) − g ( x ) = ( x − 1 ) − ( x 2 − 1 ) = x − x 2

No, the functions are not the same.

A gravitational force is still a force, so a ( G ( r ) ) a ( G ( r ) ) makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but G ( a ( F ) ) G ( a ( F ) ) does not make sense.

f ( g ( 1 ) ) = f ( 3 ) = 3 f ( g ( 1 ) ) = f ( 3 ) = 3 and g ( f ( 4 ) ) = g ( 1 ) = 3 g ( f ( 4 ) ) = g ( 1 ) = 3

g ( f ( 2 ) ) = g ( 5 ) = 3 g ( f ( 2 ) ) = g ( 5 ) = 3

[ − 4 , 0 ) ∪ ( 0 , ∞ ) [ − 4 , 0 ) ∪ ( 0 , ∞ )

Possible answer:

g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g g ( x ) = 4 + x 2 h ( x ) = 4 3 − x f = h ∘ g

3.5 Transformation of Functions

The graphs of f ( x ) f ( x ) and g ( x ) g ( x ) are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.

g ( x ) = 1 x - 1 + 1 g ( x ) = 1 x - 1 + 1

g ( x ) = − f ( x ) g ( x ) = − f ( x )

h ( x ) = f ( − x ) h ( x ) = f ( − x )

Notice: g ( x ) = f ( − x ) g ( x ) = f ( − x ) looks the same as f ( x ) f ( x ) .

g ( x ) = 3 x - 2 g ( x ) = 3 x - 2

g ( x ) = f ( 1 3 x ) g ( x ) = f ( 1 3 x ) so using the square root function we get g ( x ) = 1 3 x g ( x ) = 1 3 x

3.6 Absolute Value Functions

using the variable p p for passing, | p − 80 | ≤ 20 | p − 80 | ≤ 20

f ( x ) = − | x + 2 | + 3 f ( x ) = − | x + 2 | + 3

x = − 1 x = − 1 or x = 2 x = 2

3.7 Inverse Functions

h ( 2 ) = 6 h ( 2 ) = 6

The domain of function f − 1 f − 1 is ( − ∞ , − 2 ) ( − ∞ , − 2 ) and the range of function f − 1 f − 1 is ( 1 , ∞ ) . ( 1 , ∞ ) .

• ⓐ f ( 60 ) = 50. f ( 60 ) = 50. In 60 minutes, 50 miles are traveled.
• ⓑ f − 1 ( 60 ) = 70. f − 1 ( 60 ) = 70. To travel 60 miles, it will take 70 minutes.

x = 3 y + 5 x = 3 y + 5

f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ] f − 1 ( x ) = ( 2 − x ) 2 ; domain of f : [ 0 , ∞ ) ; domain of f − 1 : ( − ∞ , 2 ]

3.1 Section Exercises

A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.

When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.

When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.

not a function

f ( − 3 ) = − 11 ; f ( − 3 ) = − 11 ; f ( 2 ) = − 1 ; f ( 2 ) = − 1 ; f ( − a ) = − 2 a − 5 ; f ( − a ) = − 2 a − 5 ; − f ( a ) = − 2 a + 5 ; − f ( a ) = − 2 a + 5 ; f ( a + h ) = 2 a + 2 h − 5 f ( a + h ) = 2 a + 2 h − 5

f ( − 3 ) = 5 + 5 ; f ( − 3 ) = 5 + 5 ; f ( 2 ) = 5 ; f ( 2 ) = 5 ; f ( − a ) = 2 + a + 5 ; f ( − a ) = 2 + a + 5 ; − f ( a ) = − 2 − a − 5 ; − f ( a ) = − 2 − a − 5 ; f ( a + h ) = 2 − a − h + 5 f ( a + h ) = 2 − a − h + 5

f ( − 3 ) = 2 ; f ( − 3 ) = 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( 2 ) = 1 − 3 = − 2 ; f ( − a ) = | − a − 1 | − | − a + 1 | ; f ( − a ) = | − a − 1 | − | − a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; − f ( a ) = − | a − 1 | + | a + 1 | ; f ( a + h ) = | a + h − 1 | − | a + h + 1 | f ( a + h ) = | a + h − 1 | − | a + h + 1 |

g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a g ( x ) − g ( a ) x − a = x + a + 2 , x ≠ a

a. f ( − 2 ) = 14 ; f ( − 2 ) = 14 ; b. x = 3 x = 3

a. f ( 5 ) = 10 ; f ( 5 ) = 10 ; b. x = − 1 x = − 1 or x = 4 x = 4

• ⓐ f ( t ) = 6 − 2 3 t ; f ( t ) = 6 − 2 3 t ;
• ⓑ f ( − 3 ) = 8 ; f ( − 3 ) = 8 ;
• ⓒ t = 6 t = 6
• ⓐ f ( 0 ) = 1 ; f ( 0 ) = 1 ;
• ⓑ f ( x ) = − 3 , x = − 2 f ( x ) = − 3 , x = − 2 or x = 2 x = 2

not a function so it is also not a one-to-one function

one-to- one function

function, but not one-to-one

f ( x ) = 1 , x = 2 f ( x ) = 1 , x = 2

f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2 f ( − 2 ) = 14 ; f ( − 1 ) = 11 ; f ( 0 ) = 8 ; f ( 1 ) = 5 ; f ( 2 ) = 2

f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236 f ( − 2 ) = 4 ;    f ( − 1 ) = 4.414 ; f ( 0 ) = 4.732 ; f ( 1 ) = 5 ; f ( 2 ) = 5.236

f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9 f ( − 2 ) = 1 9 ; f ( − 1 ) = 1 3 ; f ( 0 ) = 1 ; f ( 1 ) = 3 ; f ( 2 ) = 9

[ 0 , 100 ] [ 0 , 100 ]

[ − 0.001 , 0 .001 ] [ − 0.001 , 0 .001 ]

[ − 1 , 000 , 000 , 1,000,000 ] [ − 1 , 000 , 000 , 1,000,000 ]

[ 0 , 10 ] [ 0 , 10 ]

[ −0.1 , 0.1 ] [ −0.1 , 0.1 ]

[ − 100 , 100 ] [ − 100 , 100 ]

• ⓐ g ( 5000 ) = 50 ; g ( 5000 ) = 50 ;
• ⓑ The number of cubic yards of dirt required for a garden of 100 square feet is 1.
• ⓐ The height of a rocket above ground after 1 second is 200 ft.
• ⓑ The height of a rocket above ground after 2 seconds is 350 ft.

3.2 Section Exercises

The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.

There is no restriction on x x for f ( x ) = x 3 f ( x ) = x 3 because you can take the cube root of any real number. So the domain is all real numbers, ( − ∞ , ∞ ) . ( − ∞ , ∞ ) . When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x x -values are restricted for f ( x ) = x f ( x ) = x to nonnegative numbers and the domain is [ 0 , ∞ ) . [ 0 , ∞ ) .

Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x x -axis and y y -axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate − ∞ − ∞ or ∞ . ∞ . Combine the graphs to find the graph of the piecewise function.

( − ∞ , 3 ] ( − ∞ , 3 ]

( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ ) ( − ∞ , − 1 2 ) ∪ ( − 1 2 , ∞ )

( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ ) ( − ∞ , − 11 ) ∪ ( − 11 , 2 ) ∪ ( 2 , ∞ )

( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ ) ( − ∞ , − 3 ) ∪ ( − 3 , 5 ) ∪ ( 5 , ∞ )

( − ∞ , 5 ) ( − ∞ , 5 )

[ 6 , ∞ ) [ 6 , ∞ )

( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ ) ( − ∞ , − 9 ) ∪ ( − 9 , 9 ) ∪ ( 9 , ∞ )

domain: ( 2 , 8 ] , ( 2 , 8 ] , range [ 6 , 8 ) [ 6 , 8 )

domain: [ − 4 , 4], [ − 4 , 4], range: [ 0 , 2] [ 0 , 2]

domain: [ − 5 , 3 ) , [ − 5 , 3 ) , range: [ 0 , 2 ] [ 0 , 2 ]

domain: ( − ∞ , 1 ] , ( − ∞ , 1 ] , range: [ 0 , ∞ ) [ 0 , ∞ )

domain: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] ; range: [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ] [ − 6 , − 1 6 ] ∪ [ 1 6 , 6 ]

domain: [ − 3 , ∞ ) ; [ − 3 , ∞ ) ; range: [ 0 , ∞ ) [ 0 , ∞ )

domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0 f ( − 3 ) = 1 ; f ( − 2 ) = 0 ; f ( − 1 ) = 0 ; f ( 0 ) = 0

f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34 f ( − 1 ) = − 4 ; f ( 0 ) = 6 ; f ( 2 ) = 20 ; f ( 4 ) = 34

f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16 f ( − 1 ) = − 5 ; f ( 0 ) = 3 ; f ( 2 ) = 3 ; f ( 4 ) = 16

domain: ( − ∞ , 1 ) ∪ ( 1 , ∞ ) ( − ∞ , 1 ) ∪ ( 1 , ∞ )

window: [ − 0.5 , − 0.1 ] ; [ − 0.5 , − 0.1 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

window: [ 0.1 , 0.5 ] ; [ 0.1 , 0.5 ] ; range: [ 4 , 100 ] [ 4 , 100 ]

[ 0 , 8 ] [ 0 , 8 ]

Many answers. One function is f ( x ) = 1 x − 2 . f ( x ) = 1 x − 2 .

• ⓐ The fixed cost is $500.
• ⓑ The cost of making 25 items is $750.
• ⓒ The domain is [0, 100] and the range is [500, 1500].

3.3 Section Exercises

Yes, the average rate of change of all linear functions is constant.

The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.

4 ( b + 1 ) 4 ( b + 1 )

4 x + 2 h 4 x + 2 h

− 1 13 ( 13 + h ) − 1 13 ( 13 + h )

3 h 2 + 9 h + 9 3 h 2 + 9 h + 9

4 x + 2 h − 3 4 x + 2 h − 3

increasing on ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , ( − ∞ , − 2.5 ) ∪ ( 1 , ∞ ) , decreasing on ( − 2.5 , 1 ) ( − 2.5 , 1 )

increasing on ( − ∞ , 1 ) ∪ ( 3 , 4 ) , ( − ∞ , 1 ) ∪ ( 3 , 4 ) , decreasing on ( 1 , 3 ) ∪ ( 4 , ∞ ) ( 1 , 3 ) ∪ ( 4 , ∞ )

local maximum: ( − 3 , 60 ) , ( − 3 , 60 ) , local minimum: ( 3 , − 60 ) ( 3 , − 60 )

absolute maximum at approximately ( 7 , 150 ) , ( 7 , 150 ) , absolute minimum at approximately ( −7.5 , −220 ) ( −7.5 , −220 )

Local minimum at ( 3 , − 22 ) , ( 3 , − 22 ) , decreasing on ( − ∞ , 3 ) , ( − ∞ , 3 ) , increasing on ( 3 , ∞ ) ( 3 , ∞ )

Local minimum at ( − 2 , − 2 ) , ( − 2 , − 2 ) , decreasing on ( − 3 , − 2 ) , ( − 3 , − 2 ) , increasing on ( − 2 , ∞ ) ( − 2 , ∞ )

Local maximum at ( − 0.5 , 6 ) , ( − 0.5 , 6 ) , local minima at ( − 3.25 , − 47 ) ( − 3.25 , − 47 ) and ( 2.1 , − 32 ) , ( 2.1 , − 32 ) , decreasing on ( − ∞ , − 3.25 ) ( − ∞ , − 3.25 ) and ( − 0.5 , 2.1 ) , ( − 0.5 , 2.1 ) , increasing on ( − 3.25 , − 0.5 ) ( − 3.25 , − 0.5 ) and ( 2.1 , ∞ ) ( 2.1 , ∞ )

b = 5 b = 5

2.7 gallons per minute

approximately –0.6 milligrams per day

3.4 Section Exercises

Find the numbers that make the function in the denominator g g equal to zero, and check for any other domain restrictions on f f and g , g , such as an even-indexed root or zeros in the denominator.

Yes. Sample answer: Let f ( x ) = x + 1 and  g ( x ) = x − 1. f ( x ) = x + 1 and  g ( x ) = x − 1. Then f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x f ( g ( x ) ) = f ( x − 1 ) = ( x − 1 ) + 1 = x and g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . g ( f ( x ) ) = g ( x + 1 ) = ( x + 1 ) − 1 = x . So f ∘ g = g ∘ f . f ∘ g = g ∘ f .

( f + g ) ( x ) = 2 x + 6 , ( f + g ) ( x ) = 2 x + 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f − g ) ( x ) = 2 x 2 + 2 x − 6 , ( f − g ) ( x ) = 2 x 2 + 2 x − 6 , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , ( f g ) ( x ) = − x 4 − 2 x 3 + 6 x 2 + 12 x , domain: ( − ∞ , ∞ ) ( − ∞ , ∞ )

( f g ) ( x ) = x 2 + 2 x 6 − x 2 , ( f g ) ( x ) = x 2 + 2 x 6 − x 2 , domain: ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 6 ) ∪ ( − 6 , 6 ) ∪ ( 6 , ∞ )

( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , ( f + g ) ( x ) = 4 x 3 + 8 x 2 + 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , ( f − g ) ( x ) = 4 x 3 + 8 x 2 − 1 2 x , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = x + 2 , ( f g ) ( x ) = x + 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f g ) ( x ) = 4 x 3 + 8 x 2 , ( f g ) ( x ) = 4 x 3 + 8 x 2 , domain: ( − ∞ , 0 ) ∪ ( 0 , ∞ ) ( − ∞ , 0 ) ∪ ( 0 , ∞ )

( f + g ) ( x ) = 3 x 2 + x − 5 , ( f + g ) ( x ) = 3 x 2 + x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f − g ) ( x ) = 3 x 2 − x − 5 , ( f − g ) ( x ) = 3 x 2 − x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: [ 5 , ∞ ) [ 5 , ∞ )

( f g ) ( x ) = 3 x 2 x − 5 , ( f g ) ( x ) = 3 x 2 x − 5 , domain: ( 5 , ∞ ) ( 5 , ∞ )

• ⓑ f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1 f ( g ( x ) ) = 2 ( 3 x − 5 ) 2 + 1
• ⓒ f ( g ( x ) ) = 6 x 2 − 2 f ( g ( x ) ) = 6 x 2 − 2
• ⓓ ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20 ( g ∘ g ) ( x ) = 3 ( 3 x − 5 ) − 5 = 9 x − 20
• ⓔ ( f ∘ f ) ( − 2 ) = 163 ( f ∘ f ) ( − 2 ) = 163

f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7 f ( g ( x ) ) = x 2 + 3 + 2 , g ( f ( x ) ) = x + 4 x + 7

f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x f ( g ( x ) ) = x + 1 x 3 3 = x + 1 3 x , g ( f ( x ) ) = x 3 + 1 x

( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4 ( f ∘ g ) ( x ) = 1 2 x + 4 − 4 = x 2 , ( g ∘ f ) ( x ) = 2 x − 4

f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1 f ( g ( h ( x ) ) ) = ( 1 x + 3 ) 2 + 1

• ⓐ ( g ∘ f ) ( x ) = − 3 2 − 4 x ( g ∘ f ) ( x ) = − 3 2 − 4 x
• ⓑ ( − ∞ , 1 2 ) ( − ∞ , 1 2 )
• ⓐ ( 0 , 2 ) ∪ ( 2 , ∞ ) ; ( 0 , 2 ) ∪ ( 2 , ∞ ) ;
• ⓑ ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ; ( − ∞ , − 2 ) ∪ ( 2 , ∞ ) ;
• ⓒ ( 0 , ∞ ) ( 0 , ∞ )

( 1 , ∞ ) ( 1 , ∞ )

sample: f ( x ) = x 3 g ( x ) = x − 5 f ( x ) = x 3 g ( x ) = x − 5

sample: f ( x ) = 4 x g ( x ) = ( x + 2 ) 2 f ( x ) = 4 x g ( x ) = ( x + 2 ) 2

sample: f ( x ) = x 3 g ( x ) = 1 2 x − 3 f ( x ) = x 3 g ( x ) = 1 2 x − 3

sample: f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5 f ( x ) = x 4 g ( x ) = 3 x − 2 x + 5

sample: f ( x ) = x g ( x ) = 2 x + 6 f ( x ) = x g ( x ) = 2 x + 6

sample: f ( x ) = x 3 g ( x ) = ( x − 1 ) f ( x ) = x 3 g ( x ) = ( x − 1 )

sample: f ( x ) = x 3 g ( x ) = 1 x − 2 f ( x ) = x 3 g ( x ) = 1 x − 2

sample: f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 f ( x ) = x g ( x ) = 2 x − 1 3 x + 4

f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94 f ( g ( 0 ) ) = 27 , g ( f ( 0 ) ) = − 94

f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5 f ( g ( 0 ) ) = 1 5 , g ( f ( 0 ) ) = 5

18 x 2 + 60 x + 51 18 x 2 + 60 x + 51

g ∘ g ( x ) = 9 x + 20 g ∘ g ( x ) = 9 x + 20

( f ∘ g ) ( 6 ) = 6 ( f ∘ g ) ( 6 ) = 6 ; ( g ∘ f ) ( 6 ) = 6 ( g ∘ f ) ( 6 ) = 6

( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11 ( f ∘ g ) ( 11 ) = 11 , ( g ∘ f ) ( 11 ) = 11

A ( t ) = π ( 25 t + 2 ) 2 A ( t ) = π ( 25 t + 2 ) 2 and A ( 2 ) = π ( 25 4 ) 2 = 2500 π A ( 2 ) = π ( 25 4 ) 2 = 2500 π square inches

A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π A ( 5 ) = π ( 2 ( 5 ) + 1 ) 2 = 121 π square units

• ⓐ N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1 N ( T ( t ) ) = 23 ( 5 t + 1.5 ) 2 − 56 ( 5 t + 1.5 ) + 1
• ⓑ 3.38 hours

3.5 Section Exercises

A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.

A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.

For a function f , f , substitute ( − x ) ( − x ) for ( x ) ( x ) in f ( x ) . f ( x ) . Simplify. If the resulting function is the same as the original function, f ( − x ) = f ( x ) , f ( − x ) = f ( x ) , then the function is even. If the resulting function is the opposite of the original function, f ( − x ) = − f ( x ) , f ( − x ) = − f ( x ) , then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.

g ( x ) = | x - 1 | − 3 g ( x ) = | x - 1 | − 3

g ( x ) = 1 ( x + 4 ) 2 + 2 g ( x ) = 1 ( x + 4 ) 2 + 2

The graph of f ( x + 43 ) f ( x + 43 ) is a horizontal shift to the left 43 units of the graph of f . f .

The graph of f ( x - 4 ) f ( x - 4 ) is a horizontal shift to the right 4 units of the graph of f . f .

The graph of f ( x ) + 8 f ( x ) + 8 is a vertical shift up 8 units of the graph of f . f .

The graph of f ( x ) − 7 f ( x ) − 7 is a vertical shift down 7 units of the graph of f . f .

The graph of f ( x + 4 ) − 1 f ( x + 4 ) − 1 is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of f . f .

decreasing on ( − ∞ , − 3 ) ( − ∞ , − 3 ) and increasing on ( − 3 , ∞ ) ( − 3 , ∞ )

decreasing on ( 0 , ∞ ) ( 0 , ∞ )

g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1 g ( x ) = f ( x - 1 ) , h ( x ) = f ( x ) + 1

f ( x ) = | x - 3 | − 2 f ( x ) = | x - 3 | − 2

f ( x ) = x + 3 − 1 f ( x ) = x + 3 − 1

f ( x ) = ( x - 2 ) 2 f ( x ) = ( x - 2 ) 2

f ( x ) = | x + 3 | − 2 f ( x ) = | x + 3 | − 2

f ( x ) = − x f ( x ) = − x

f ( x ) = − ( x + 1 ) 2 + 2 f ( x ) = − ( x + 1 ) 2 + 2

f ( x ) = − x + 1 f ( x ) = − x + 1

The graph of g g is a vertical reflection (across the x x -axis) of the graph of f . f .

The graph of g g is a vertical stretch by a factor of 4 of the graph of f . f .

The graph of g g is a horizontal compression by a factor of 1 5 1 5 of the graph of f . f .

The graph of g g is a horizontal stretch by a factor of 3 of the graph of f . f .

The graph of g g is a horizontal reflection across the y y -axis and a vertical stretch by a factor of 3 of the graph of f . f .

g ( x ) = | − 4 x | g ( x ) = | − 4 x |

g ( x ) = 1 3 ( x + 2 ) 2 − 3 g ( x ) = 1 3 ( x + 2 ) 2 − 3

g ( x ) = 1 2 ( x - 5 ) 2 + 1 g ( x ) = 1 2 ( x - 5 ) 2 + 1

The graph of the function f ( x ) = x 2 f ( x ) = x 2 is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.

The graph of f ( x ) = | x | f ( x ) = | x | is stretched vertically by a factor of 2, shifted horizontally 4 units to the right, reflected across the horizontal axis, and then shifted vertically 3 units up.

The graph of the function f ( x ) = x 3 f ( x ) = x 3 is compressed vertically by a factor of 1 2 . 1 2 .

The graph of the function is stretched horizontally by a factor of 3 and then shifted vertically downward by 3 units.

The graph of f ( x ) = x f ( x ) = x is shifted right 4 units and then reflected across the vertical line x = 4. x = 4.

3.6 Section Exercises

Isolate the absolute value term so that the equation is of the form | A | = B . | A | = B . Form one equation by setting the expression inside the absolute value symbol, A , A , equal to the expression on the other side of the equation, B . B . Form a second equation by setting A A equal to the opposite of the expression on the other side of the equation, − B . − B . Solve each equation for the variable.

The graph of the absolute value function does not cross the x x -axis, so the graph is either completely above or completely below the x x -axis.

The distance from x to 8 can be represented using the absolute value statement: ∣ x − 8 ∣ = 4.

∣ x − 10 ∣ ≥ 15

There are no x-intercepts.

(−4, 0) and (2, 0)

( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 ) ( 0 , − 4 ) , ( 4 , 0 ) , ( − 2 , 0 )

( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 ) ( 0 , 7 ) , ( 25 , 0 ) , ( − 7 , 0 )

range: [ – 400 , 100 ] [ – 400 , 100 ]

There is no solution for a a that will keep the function from having a y y -intercept. The absolute value function always crosses the y y -intercept when x = 0. x = 0.

| p − 0.08 | ≤ 0.015 | p − 0.08 | ≤ 0.015

| x − 5.0 | ≤ 0.01 | x − 5.0 | ≤ 0.01

3.7 Section Exercises

Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that y y -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no y y -values repeat and the function is one-to-one.

Yes. For example, f ( x ) = 1 x f ( x ) = 1 x is its own inverse.

Given a function y = f ( x ) , y = f ( x ) , solve for x x in terms of y . y . Interchange the x x and y . y . Solve the new equation for y . y . The expression for y y is the inverse, y = f − 1 ( x ) . y = f − 1 ( x ) .

f − 1 ( x ) = x − 3 f − 1 ( x ) = x − 3

f − 1 ( x ) = 2 − x f − 1 ( x ) = 2 − x

f − 1 ( x ) = − 2 x x − 1 f − 1 ( x ) = − 2 x x − 1

domain of f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7 f ( x ) : [ − 7 , ∞ ) ; f − 1 ( x ) = x − 7

domain of f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5 f ( x ) : [ 0 , ∞ ) ; f − 1 ( x ) = x + 5

a. f ( g ( x ) ) = x f ( g ( x ) ) = x and g ( f ( x ) ) = x . g ( f ( x ) ) = x . b. This tells us that f f and g g are inverse functions

  f ( g ( x ) ) = x , g ( f ( x ) ) = x   f ( g ( x ) ) = x , g ( f ( x ) ) = x

not one-to-one

[ 2 , 10 ] [ 2 , 10 ]

f − 1 ( x ) = ( 1 + x ) 1 / 3 f − 1 ( x ) = ( 1 + x ) 1 / 3

f − 1 ( x ) = 5 9 ( x − 32 ) . f − 1 ( x ) = 5 9 ( x − 32 ) . Given the Fahrenheit temperature, x , x , this formula allows you to calculate the Celsius temperature.

t ( d ) = d 50 , t ( d ) = d 50 , t ( 180 ) = 180 50 . t ( 180 ) = 180 50 . The time for the car to travel 180 miles is 3.6 hours.

Review Exercises

f ( − 3 ) = − 27 ; f ( − 3 ) = − 27 ; f ( 2 ) = − 2 ; f ( 2 ) = − 2 ; f ( − a ) = − 2 a 2 − 3 a ; f ( − a ) = − 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; − f ( a ) = 2 a 2 − 3 a ; f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2 f ( a + h ) = − 2 a 2 + 3 a − 4 a h + 3 h − 2 h 2

x = − 1.8 x = − 1.8 or or  x = 1.8 or  x = 1.8

− 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64 − 64 + 80 a − 16 a 2 − 1 + a = − 16 a + 64

( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ ) ( − ∞ , − 2 ) ∪ ( − 2 , 6 ) ∪ ( 6 , ∞ )

increasing ( 2 , ∞ ) ; ( 2 , ∞ ) ; decreasing ( − ∞ , 2 ) ( − ∞ , 2 )

increasing ( − 3 , 1 ) ; ( − 3 , 1 ) ; constant ( − ∞ , − 3 ) ∪ ( 1 , ∞ ) ( − ∞ , − 3 ) ∪ ( 1 , ∞ )

local minimum ( − 2 , − 3 ) ; ( − 2 , − 3 ) ; local maximum ( 1 , 3 ) ( 1 , 3 )

( − 1.8 , 10 ) ( − 1.8 , 10 )

( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x ( f ∘ g ) ( x ) = 17 − 18 x ; ( g ∘ f ) ( x ) = − 7 − 18 x

( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2 ( f ∘ g ) ( x ) = 1 x + 2 ; ( g ∘ f ) ( x ) = 1 x + 2

( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4 ( f ∘ g ) ( x ) = 1 + x 1 + 4 x ,   x ≠ 0 ,   x ≠ − 1 4

( f ∘ g ) ( x ) = 1 x , x > 0 ( f ∘ g ) ( x ) = 1 x , x > 0

sample: g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x g ( x ) = 2 x − 1 3 x + 4 ; f ( x ) = x

f ( x ) = | x − 3 | f ( x ) = | x − 3 |

f ( x ) = 1 2 | x + 2 | + 1 f ( x ) = 1 2 | x + 2 | + 1

f ( x ) = − 3 | x − 3 | + 3 f ( x ) = − 3 | x − 3 | + 3

f − 1 ( x ) = x - 9 10 f − 1 ( x ) = x - 9 10

f − 1 ( x ) = x - 1 f − 1 ( x ) = x - 1

The function is one-to-one.

Practice Test

The relation is a function.

The graph is a parabola and the graph fails the horizontal line test.

2 a 2 − a 2 a 2 − a

− 2 ( a + b ) + 1 − 2 ( a + b ) + 1

f − 1 ( x ) = x + 5 3 f − 1 ( x ) = x + 5 3

( − ∞ , − 1.1 ) and  ( 1.1 , ∞ ) ( − ∞ , − 1.1 ) and  ( 1.1 , ∞ )

( 1.1 , − 0.9 ) ( 1.1 , − 0.9 )

f ( 2 ) = 2 f ( 2 ) = 2

f ( x ) = { | x | if x ≤ 2 3 if x > 2 f ( x ) = { | x | if x ≤ 2 3 if x > 2

x = 2 x = 2

f − 1 ( x ) = − x − 11 2 f − 1 ( x ) = − x − 11 2

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/chapter-3

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Rates of Change and Behavior of Graphs

• Last updated
• Save as PDF
• Page ID 32511

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Find the average rate of change of a function.
• Use a graph to determine where a function is increasing, decreasing, or constant.
• Use a graph to locate local maxima and local minima.
• Use a graph to locate the absolute maximum and absolute minimum.

Gasoline costs have experienced some wild fluctuations over the last several decades. Table \(\PageIndex{1}\) lists the average cost, in dollars, of a gallon of gasoline for the years 2005–2012. The cost of gasoline can be considered as a function of year.

If we were interested only in how the gasoline prices changed between 2005 and 2012, we could compute that the cost per gallon had increased from $2.31 to $3.68, an increase of $1.37. While this is interesting, it might be more useful to look at how much the price changed per year. In this section, we will investigate changes such as these.

Finding the Average Rate of Change of a Function

The price change per year is a rate of change because it describes how an output quantity changes relative to the change in the input quantity. We can see that the price of gasoline in Table \(\PageIndex{1}\) did not change by the same amount each year, so the rate of change was not constant. If we use only the beginning and ending data, we would be finding the average rate of change over the specified period of time. To find the average rate of change, we divide the change in the output value by the change in the input value.

\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]

The Greek letter \(\Delta\) (delta) signifies the change in a quantity; we read the ratio as “delta-\(y\) over delta-\(x\)” or “the change in \(y\) divided by the change in \(x\).” Occasionally we write \(\Delta f\) instead of \(\Delta y\), which still represents the change in the function’s output value resulting from a change to its input value. It does not mean we are changing the function into some other function.

In our example, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average rate of change was

\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]

On average, the price of gas increased by about 19.6¢ each year. Other examples of rates of change include:

• A population of rats increasing by 40 rats per week
• A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
• A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
• The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
• The amount of money in a college account decreasing by $4,000 per quarter

Definition: Rate of Change

A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are “output units per input units.”

The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.

\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]

Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values \(x_1\) and \(x_2\).

• Calculate the difference \(y_2−y_1=\Delta y\).
• Calculate the difference \(x_2−x_1=\Delta x\).
• Find the ratio \(\dfrac{\Delta y}{\Delta x}\).

Example \(\PageIndex{1}\): Computing an Average Rate of Change

Using the data in Table \(\PageIndex{1}\), find the average rate of change of the price of gasoline between 2007 and 2009.

In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is

\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]

Note that a decrease is expressed by a negative change or “negative increase.” A rate of change is negative when the output decreases as the input increases or when the output increases as the input decreases.

Exercise \(\PageIndex{1}\)

Using the data in Table \(\PageIndex{1}\), find the average rate of change between 2005 and 2010.

\(\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}\)

Example \(\PageIndex{2}\): Computing Average Rate of Change from a Graph

Given the function \(g(t)\) shown in Figure \(\PageIndex{1}\), find the average rate of change on the interval \([−1,2]\).

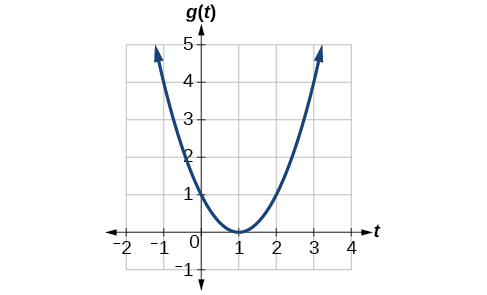
At \(t=−1\), Figure \(\PageIndex{2}\) shows \(g(−1)=4\). At \(t=2\),the graph shows \(g(2)=1\).

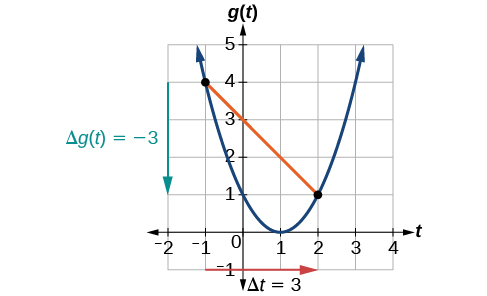
The horizontal change \(\Delta t=3\) is shown by the red arrow, and the vertical change \(\Delta g(t)=−3\) is shown by the turquoise arrow. The output changes by –3 while the input changes by 3, giving an average rate of change of

\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]

Note that the order we choose is very important. If, for example, we use \(\dfrac{y_2−y_1}{x_1−x_2}\), we will not get the correct answer. Decide which point will be 1 and which point will be 2, and keep the coordinates fixed as \((x_1,y_1)\) and \((x_2,y_2)\).

Example \(\PageIndex{3}\): Computing Average Rate of Change from a Table

After picking up a friend who lives 10 miles away, Anna records her distance from home over time. The values are shown in Table \(\PageIndex{2}\). Find her average speed over the first 6 hours.

Here, the average speed is the average rate of change. She traveled 292 miles in 6 hours, for an average speed of

\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]

The average speed is about 47 miles per hour.

Because the speed is not constant, the average speed depends on the interval chosen. For the interval \([2,3]\), the average speed is 63 miles per hour.

Example \(\PageIndex{4}\): Computing Average Rate of Change for a Function Expressed as a Formula

Compute the average rate of change of \(f(x)=x^2−\frac{1}{x}\) on the interval \([2, 4]\).

We can start by computing the function values at each endpoint of the interval.

\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]

Now we compute the average rate of change.

\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]

Exercise \(\PageIndex{2}\)

Find the average rate of change of \(f(x)=x−2\sqrt{x}\) on the interval \([1, 9]\).

\(\frac{1}{2}\)

Example \(\PageIndex{5}\): Finding the Average Rate of Change of a Force

The electrostatic force \(F\), measured in newtons, between two charged particles can be related to the distance between the particles \(d\),in centimeters, by the formula \(F(d)=\frac{2}{d^2}\). Find the average rate of change of force if the distance between the particles is increased from 2 cm to 6 cm.

We are computing the average rate of change of \(F(d)=\dfrac{2}{d^2}\) on the interval \([2,6]\).

\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]

The average rate of change is \(−\frac{1}{9}\) newton per centimeter.

Example \(\PageIndex{6}\): Finding an Average Rate of Change as an Expression

Find the average rate of change of \(g(t)=t^2+3t+1\) on the interval \([0, a]\). The answer will be an expression involving \(a\).

We use the average rate of change formula.

\(\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}\)

Exercise \(\PageIndex{3}\)

Find the average rate of change of \(f(x)=x^2+2x−8\) on the interval \([5, a]\).

Using a Graph to Determine Where a Function is Increasing, Decreasing, or Constant

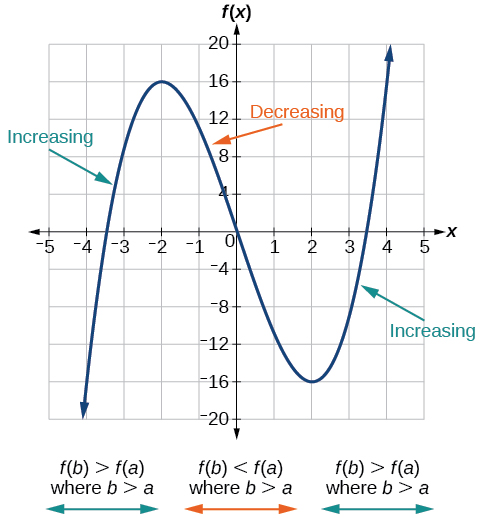
As part of exploring how functions change, we can identify intervals over which the function is changing in specific ways. We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval. The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. Figure \(\PageIndex{3}\) shows examples of increasing and decreasing intervals on a function.

While some functions are increasing (or decreasing) over their entire domain, many others are not. A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximum . If a function has more than one, we say it has local maxima. Similarly, a value of the input where a function changes from decreasing to increasing as the input variable increases is called a local minimum . The plural form is “local minima.” Together, local maxima and minima are called local extrema , or local extreme values, of the function. (The singular form is “extremum.”) Often, the term local is replaced by the term relative. In this text, we will use the term local.

Clearly, a function is neither increasing nor decreasing on an interval where it is constant. A function is also neither increasing nor decreasing at extrema. Note that we have to speak of local extrema, because any given local extremum as defined here is not necessarily the highest maximum or lowest minimum in the function’s entire domain.

For the function whose graph is shown in Figure \(\PageIndex{4}\), the local maximum is 16, and it occurs at \(x=−2\). The local minimum is −16 and it occurs at \(x=2\).

To locate the local maxima and minima from a graph, we need to observe the graph to determine where the graph attains its highest and lowest points, respectively, within an open interval. Like the summit of a roller coaster, the graph of a function is higher at a local maximum than at nearby points on both sides. The graph will also be lower at a local minimum than at neighboring points. Figure \(\PageIndex{5}\) illustrates these ideas for a local maximum.

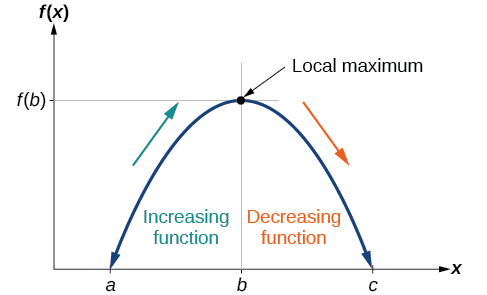
These observations lead us to a formal definition of local extrema.

Local Minima and Local Maxima

• A function \(f\) is an increasing function on an open interval if \(f(b)>f(a)\) for every \(a\), \(b\) interval where \(b>a\).
• A function \(f\) is a decreasing function on an open interval if \(f(b)<f(a)\) for every \(a\), \(b\) interval where \(b>a\).

A function \(f\) has a local maximum at a point \(b\) in an open interval \((a,c)\) if \(f(b)\) is greater than or equal to \(f(x)\) for every point \(x\) (\(x\) does not equal \(b\)) in the interval. Likewise, \(f\) has a local minimum at a point \(b\) in \((a,c)\) if \(f(b)\) is less than or equal to \(f(x)\) for every \(x\) (\(x\) does not equal \(b\)) in the interval.

Example \(\PageIndex{7}\) Finding Increasing and Decreasing Intervals on a Graph

Given the function \(p(t)\) in Figure \(\PageIndex{6}\), identify the intervals on which the function appears to be increasing.

We see that the function is not constant on any interval. The function is increasing where it slants upward as we move to the right and decreasing where it slants downward as we move to the right. The function appears to be increasing from \(t=1\) to \(t=3\) and from \(t=4\) on.

In interval notation, we would say the function appears to be increasing on the interval \((1,3)\) and the interval \((4,\infty)\).

Notice in this example that we used open intervals (intervals that do not include the endpoints), because the function is neither increasing nor decreasing at \(t=1\), \(t=3\), and \(t=4\). These points are the local extrema (two minima and a maximum).

Example \(\PageIndex{8}\): Finding Local Extrema from a Graph

Graph the function \(f(x)=\frac{2}{x}+\frac{x}{3}\). Then use the graph to estimate the local extrema of the function and to determine the intervals on which the function is increasing.

Using technology, we find that the graph of the function looks like that in Figure \(\PageIndex{7}\). It appears there is a low point, or local minimum, between \(x=2\) and \(x=3\), and a mirror-image high point, or local maximum, somewhere between \(x=−3\) and \(x=−2\)

Most graphing calculators and graphing utilities can estimate the location of maxima and minima. Figure \(\PageIndex{8}\) provides screen images from two different technologies, showing the estimate for the local maximum and minimum.

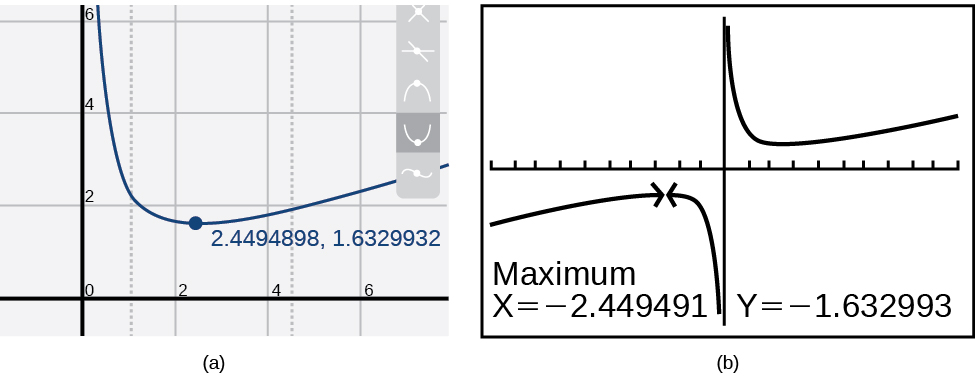
Based on these estimates, the function is increasing on the interval \((−\infty,−2.449)\) and \((2.449,\infty)\). Notice that, while we expect the extrema to be symmetric, the two different technologies agree only up to four decimals due to the differing approximation algorithms used by each. (The exact location of the extrema is at \(\pm\sqrt{6}\), but determining this requires calculus.)

Exercise \(\PageIndex{8}\)

Graph the function \(f(x)=x^3−6x^2−15x+20\) to estimate the local extrema of the function. Use these to determine the intervals on which the function is increasing and decreasing.

The local maximum appears to occur at \((−1,28)\), and the local minimum occurs at \((5,−80)\). The function is increasing on \((−\infty,−1)\cup(5,\infty)\) and decreasing on \((−1,5)\).

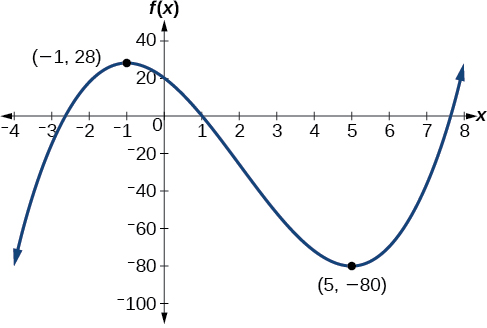
Graph of a polynomial with a local maximum at (-1, 28) and local minimum at (5, -80).

Example \(\PageIndex{9}\): Finding Local Maxima and Minima from a Graph

For the function f whose graph is shown in Figure \(\PageIndex{9}\), find all local maxima and minima.

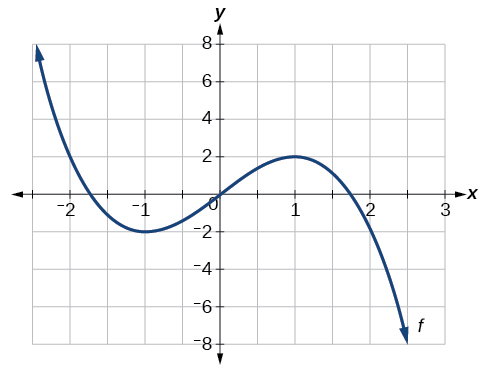
Observe the graph of \(f\). The graph attains a local maximum at \(x=1\) because it is the highest point in an open interval around \(x=1\).The local maximum is the y-coordinate at \(x=1\), which is 2.

The graph attains a local minimum at \(x=−1\) because it is the lowest point in an open interval around \(x=−1\). The local minimum is the y-coordinate at \(x=−1\), which is −2.

Analyzing the Toolkit Functions for Increasing or Decreasing Intervals

We will now return to our toolkit functions and discuss their graphical behavior in Figure \(\PageIndex{10}\), Figure \(\PageIndex{11}\), and Figure \(\PageIndex{12}\).

Use A Graph to Locate the Absolute Maximum and Absolute Minimum

There is a difference between locating the highest and lowest points on a graph in a region around an open interval (locally) and locating the highest and lowest points on the graph for the entire domain. The y-coordinates (output) at the highest and lowest points are called the absolute maximum and absolute minimum , respectively. To locate absolute maxima and minima from a graph, we need to observe the graph to determine where the graph attains it highest and lowest points on the domain of the function (Figure \(\PageIndex{13}\)).

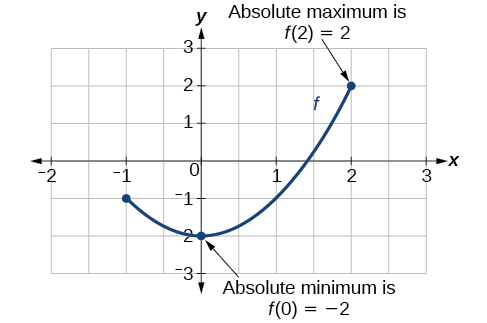
Not every function has an absolute maximum or minimum value. The toolkit function \(f(x)=x^3\) is one such function.

Absolute Maxima and Minima

• The absolute maximum of \(f\) at \(x=c\) is \(f(c)\) where \(f(c)≥f(x)\) for all \(x\) in the domain of \(f\).
• The absolute minimum of \(f\) at \(x=d\) is \(f(d)\) where \(f(d)≤f(x)\) for all \(x\) in the domain of \(f\).

Example \(\PageIndex{10}\): Finding Absolute Maxima and Minima from a Graph

For the function f shown in Figure \(\PageIndex{14}\), find all absolute maxima and minima.

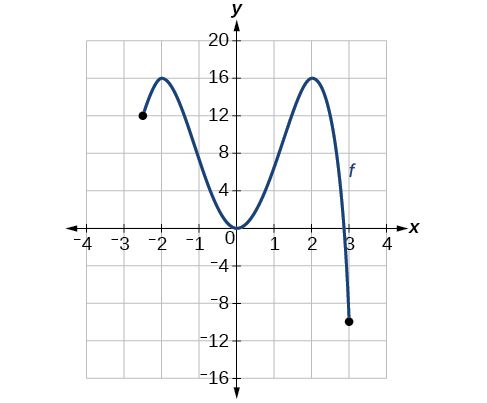
Observe the graph of \(f\). The graph attains an absolute maximum in two locations, \(x=−2\) and \(x=2\), because at these locations, the graph attains its highest point on the domain of the function. The absolute maximum is the y-coordinate at \(x=−2\) and \(x=2\), which is 16.

The graph attains an absolute minimum at x=3, because it is the lowest point on the domain of the function’s graph. The absolute minimum is the y-coordinate at x=3,which is−10.

Key Equations

• Average rate of change: \(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)

Key Concepts

• A rate of change relates a change in an output quantity to a change in an input quantity. The average rate of change is determined using only the beginning and ending data. See Example.
• Identifying points that mark the interval on a graph can be used to find the average rate of change. See Example.
• Comparing pairs of input and output values in a table can also be used to find the average rate of change. See Example.
• An average rate of change can also be computed by determining the function values at the endpoints of an interval described by a formula. See Example and Example.
• The average rate of change can sometimes be determined as an expression. See Example.
• A function is increasing where its rate of change is positive and decreasing where its rate of change is negative. See Example.
• A local maximum is where a function changes from increasing to decreasing and has an output value larger (more positive or less negative) than output values at neighboring input values.
• A local minimum is where the function changes from decreasing to increasing (as the input increases) and has an output value smaller (more negative or less positive) than output values at neighboring input values.
• Minima and maxima are also called extrema.
• We can find local extrema from a graph. See Example and Example.
• The highest and lowest points on a graph indicate the maxima and minima. See Example.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Texas Go Math Grade 5 Lesson 10.3 Answer Key Number Patterns in Graphs

Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 10.3 Answer Key Number Patterns in Graphs.

Unlock the Problem

STEP 3 Write the rule. Let n stand for number of nickels, and d stand for the number of dimes. n = __________ × ___________ Think: The relationship is multiplicative. Use multiplication to write the rule.

Answer: Step 1: Pairs that relate between Sona and Adil the number of dimes to the number of nickels are (1,2), (2,4), (3,6), (4,8), Step 2: The output is 2 times the input, Step 3: Rule: n = d X 2,

Explanation: Step 1: As the number of dimes is the input, the horizontal distance from 0 for the first point is 1 and the number of nickels is output the vertical distance for the first point is 2, So the pairs that relate between Sona and Adil the number of dimes to the number of nickels are (1,2), (2,4), (3,6), (4,8), Step 2: By seeing the pairs the relationship between the number of dimes is twice the number of nickels. so the output is two times the input. The pattern uses multiplication, Step 3: Let n stand for number of nickels, and d stand for the number of dimes. as the relationship is multiplicative. Using multiplication to write the rule as n = d X 2.

An additive pattern uses addition ¡n its rule. A multiplicative pattern uses multiplication in its rule.

Find the rule for the pattern shown in the graph.

STEP 2: Describe the relationship between the number of magazines and the weight. The output is the sum of the number of magazines and __________. The pattern uses addition.

STEP 3: Write the rule. Let w stand for total weight, and m stand for the number of magazines. w = __________ + __________ Answer: Pairs are (1,3), (2,4), (3,5), (4,6), The output total weight is the sum of the number of magazines and 2, rule is w = m + 2,

Explanation: Step 1: Number pairs that relate the number of magazines and the total weight is (1,3), (2,4), (3,5), (4,6), Step 2: By seeing the graph The output is the sum of the number of magazines and 2 the relationship between the number of magazines and the weight. The output is the sum of the number of magazines and 2 by using addition pattern and let w stand for total weight, and m stand for the number of magazines the rule is  w = m + 2.

Math Talk Mathematical Processes

Explain what the 2 stands for in w = m + 2. Answer: 2 stands for adding 2 more plus number of magazines we get the weight,

Explanation: As w = m + 2 here 2 stands we are adding 2 more to the number of magazines we will get the weight.

Share and Show

Is the pattern additive or multiplicative? Find the rule for the pattern.

Explanation: Step 1: Number pairs that relate input s and output t we see (1,3),(2,6), (3,6), Step 2:  By seeing the graph the relationship between the input and output is the output t is multiplication of 3 times with input s by using multiplication pattern rule is  t = s X 3.

Explanation: Step 1: Number pairs that relate input s and output t we see (1,4),(2,5), (3,6), Step 2:  By seeing the graph the relationship between the input and output is the output t is addition of 3 more with input s by using addition pattern rule is  t = s + 3.

Problem Solving

Question 3. H.O.T. Write Math Explain the differences between the graphs in Exercises 1 and 2. Answer: One is multiplicative pattern and other is additive pattern,

Explanation: The main difference between the graphs in Exercise 1 and 2 is the first 1 is multiplicative pattern with steeper(larger) slope and linear and seeing relations between input and output, In the second graph it is additive pattern with linear and deeper(closer) slope and seeing relations between input and output.

Question 4. Write Math Explain how you can tell whether a pattern shown in a graph is additive or multiplicative. Answer: By seeing the graph and points origin, slope is deeper or steeper, linear and relations between input and outputs,

Explanation: In additive graph it will not start from origin and slope will be deeper(closer) and it will be linear and we see the relationship between input and output, In multiplicative graph it can will start from origin and slope will be steeper(increases) and it will be linear and we see the relationship between input and output.

Explanation: Given Maryanne’s map uses a scale to show how many miles each inch on the map represents. Step 1: Number pairs that relate input  and output  is (1,0),(2,20), (3,30),(4,40), Step 2:  By seeing the graph the relationship between in for number of miles and j for number of inches on map rule is the number of miles is multiplication of 10 times with number of inches on the map using multiplication pattern rule is (actual distance) in  = j X 10 Used the pattern shown in the graph to find the rule for calculating the actual distance.

Question 6. H.O.T. If the distance on the map is 2.5 inches, how many miles is the actual distance? Explain how you calculated the actual distance. Answer: The actual distance is 25 miles,

Explanation: Given the distance on the map is 2.5inches to calculate the actual distance by using the graph and rule of question 5 we have (actual distance) in  = j X 10(where j is number of inches on the map) substituting j = 2.5 we get in = 2.5 X 10 = 25 miles the actual distance.

Question 7. H.O.T. Apply Olivia uses 1 red button for the nose and 2 blue buttons for the eyes for each rag doll she makes. Would the pattern comparing the number of nose buttons to the total number of buttons be multiplicative or additive? Explain. Answer: The number of nose buttons to total number of buttons will be multiplicative,

Explanation: Given Olivia uses 1 red button for the nose and 2 blue buttons for the eyes for each rag doll she makes. If n is the total number of buttons let r is red button for the nose and b for blue button we have 1 rag doll = 3 buttons = 1 red button + 2 blue buttons means the total number of buttons is depending upon number of red buttons and also on blue buttons which means it is multiplicative if 2 rag dolls = 3 x 2 = 6 buttons = (2 X 1r + 2 X 2b) = 2 + 4 = 6.

Daily Assessment Task

Fill in the bubble completely to show your answer. Use the graph.

Explanation: Given the graph shows the number of pounds of fish the seals at an aquarium eat each day the pattern is if p is the number of pounds of fish the seals and d is number of days Step 1: Number pairs that relate input d and output p we see (1,10),(2,20), (3,30),(4,40), Step 2:  By seeing the graph the relationship between the input and output is multiplicative of 10 times with input d is output p by using multiplicative pattern rule is  p = 10 X d which exactly matches with (C).

Explanation: Given the graph shows the relationship between the number of days and the amount of food that a bottlenose dolphin eats. If we see points on the graph Point A is day 0, Point B is day 1, Point C is day 2 and Point D is day 3, So point on the graph that shows the amount of food that the dolphin consumes in two days is Point C matches with (C).

Question 10. Multi-Step If  s is the amount of food a bottlenose dolphin cats in a day and n is the number of days, which of the following describes the rule for the pattern shown in the graph? (A) s = n + 23 (B) s = n × 23 (C) n = s × 23 (D) n = s + 23 Answer: (A) s = n + 23,

Explanation: If  s is the amount of food a bottlenose dolphin cats in a day and n is the number of days, Number pairs that relate input n and output s we see (1,23),(2,46), (3,69), the following describes the rule for the pattern shown in the graph the relationship between the input number of days n and output s is the amount of food a bottlenose dolphin cats in a day is additive of 23 more with input n is output s by using additive pattern rule is  s = n + 23 which exactly matches with (A).

Texas Test Prep

Explanation: Number pairs that relate input a and output b we see (1,5), (2,6), (3,7), (4, 8) the following describes the rule for the pattern shown in the graph the relationship between the input a and output b is additive of 4 more with input a is output b by using additive pattern rule we have b = 4 + a which exactly matches with (C).

Texas Go Math Grade 5 Lesson 10.3 Homework and Practice Answer Key

Is the pattern additive or multiplicative? Write the rule for the pattern.

Explanation: Number pairs that relate input a and output b we see (1,5), (2,6), (3,7) the following describes the rule for the pattern shown in the graph the relationship between the input a and output b are additive of 4 more with input a is output b by using additive pattern rule is b = a + 4.

Explanation: Number pairs that relate input c and output d we see (1,4), (2,8), (3,12) the following describes the rule for the pattern shown in the graph the relationship between the input c and output d is multiplicative of 4 more with input c is output d by using multiplicative pattern rule is d = c X 4.

Explanation: Number pairs that relate input e and output f we see (1,5), (2,10), (3,15) the following describes the rule for the pattern shown in the graph the relationship between the input e and output f is multiplicative of 5 more with input e is output f by using multiplicative pattern rule is f = e X 5.

Explanation: Number pairs that relate input a and output b we see (1,6), (2,7), (3,8) the following describes the rule for the pattern shown in the graph the relationship between the input g and output h is additive of 5 more with input g  is output h by using additive pattern rule is h = g + 5.

Explanation: Given Patrice rents a rowboat for several hours the pattern shown in the graph if c is for the cost and h for the number of hours is Number pairs that relate hours h and cost c we see (1,15), (2,30), (3,45) the following describes the rule for the pattern shown in the graph the relationship between the hours h and costs c is multiplicative of 15 times by using multiplicative pattern rule is c = h X $15.

Question 6. If Patrice rents the boat for 4 hours, what is the cost of the rental? Answer: The cost of the rental is $60,

Explanation: we have the rule for calculating the cost of renting the rowboat is c = h X $15, where c for the cost and h for the number of hours, so if Patrice rents the boat for 4 hours,  the cost of the rental is c= 4 X $ 15 = $60.

Lesson Check

Fill in the bubble completely to show your answer.

Explanation: Given the graph shows the relationship between the number of hours Ivana bikes and the distance she travels Step 1: Number pairs that relate hours h and number of miles m we see (1,8),(2,16), (3,24), Step 2:  By seeing the graph the relationship between the input and output is multiplicative of 8 times with input hours h is output number of miles m by using multiplicative pattern rule is  m = 8 X h so number of miles does Ivana bike in 4 hours is 8 X 4 = 32 miles which matches with (C).

Explanation: Given Rashid uses cubes to build towers. The graph shows the relationship between the number of towers t and the number of cubes c, Step 1: Number pairs that relate the number of towers t and the number of cubes  c, we see (1,12),(2,24), (3,36), Step 2:  By seeing the graph the relationship between the input and output is multiplicative of 12 times with input the number of towers t  is output  by using the number of cubes c multiplicative pattern rule is c = 12 X t therefore equation describes this relationship is (B).

Explanation: Given for every $1 Paula donates to her favorite charity, her mom donates $3, The graph shows the relationship between Paula donation as p and mom donation as m Step 1: Number pairs that relate the Paula donation as p and mom donation m we see (1,3),(2,6), (3,9), Step 2:  By seeing the graph the relationship between the input and output is multiplicative of 3 times with input Paula donation p  is output  mom donation as m by using multiplicative pattern rule is m = 3 X p therefore the amount her mom donates if Paula donates $6 is 3 X $6 = $18 matches with (A) $18, multiplicative.

Explanation: The graph shows how much time Christina spends making flower arrangements to sell. Number of baskets can she make in two hours as we know 2 hours means 2 X 60 minutes = 120 minutes, Step 1: Number pairs that relate the Christina as b means baskets and minutes as m we see as (1,15),(2,30), (3,45),(4,60), Step 2:  By seeing the graph the relationship between the input and output is multiplicative of 15 times with input baskets b  is output  minutes as m by using the multiplicative pattern rule is m = b X 15, so for 120 minutes means 120/15 = 8 baskets, which matches with (D).

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.