how to tell if a hypothesis test is two tailed

• Search Search Please fill out this field.

What Is a Two-Tailed Test?

Understanding a two-tailed test, special considerations, two-tailed vs. one-tailed test.

• Two-Tailed Test FAQs
• Corporate Finance
• Financial Analysis

What Is a Two-Tailed Test? Definition and Example

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Investopedia / Joules Garcia

A two-tailed test, in statistics, is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values. It is used in null-hypothesis testing and testing for statistical significance . If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.

Key Takeaways

• In statistics, a two-tailed test is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater or less than a range of values.
• It is used in null-hypothesis testing and testing for statistical significance.
• If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.
• By convention two-tailed tests are used to determine significance at the 5% level, meaning each side of the distribution is cut at 2.5%.

A basic concept of inferential statistics is hypothesis testing , which determines whether a claim is true or not given a population parameter. A hypothesis test that is designed to show whether the mean of a sample is significantly greater than and significantly less than the mean of a population is referred to as a two-tailed test. The two-tailed test gets its name from testing the area under both tails of a normal distribution , although the test can be used in other non-normal distributions.

A two-tailed test is designed to examine both sides of a specified data range as designated by the probability distribution involved. The probability distribution should represent the likelihood of a specified outcome based on predetermined standards. This requires the setting of a limit designating the highest (or upper) and lowest (or lower) accepted variable values included within the range. Any data point that exists above the upper limit or below the lower limit is considered out of the acceptance range and in an area referred to as the rejection range.

There is no inherent standard about the number of data points that must exist within the acceptance range. In instances where precision is required, such as in the creation of pharmaceutical drugs, a rejection rate of 0.001% or less may be instituted. In instances where precision is less critical, such as the number of food items in a product bag, a rejection rate of 5% may be appropriate.

A two-tailed test can also be used practically during certain production activities in a firm, such as with the production and packaging of candy at a particular facility. If the production facility designates 50 candies per bag as its goal, with an acceptable distribution of 45 to 55 candies, any bag found with an amount below 45 or above 55 is considered within the rejection range.

To confirm the packaging mechanisms are properly calibrated to meet the expected output, random sampling may be taken to confirm accuracy. A simple random sample takes a small, random portion of the entire population to represent the entire data set, where each member has an equal probability of being chosen.

For the packaging mechanisms to be considered accurate, an average of 50 candies per bag with an appropriate distribution is desired. Additionally, the number of bags that fall within the rejection range needs to fall within the probability distribution limit considered acceptable as an error rate. Here, the null hypothesis would be that the mean is 50 while the alternate hypothesis would be that it is not 50.

If, after conducting the two-tailed test, the z-score falls in the rejection region, meaning that the deviation is too far from the desired mean, then adjustments to the facility or associated equipment may be required to correct the error. Regular use of two-tailed testing methods can help ensure production stays within limits over the long term.

Be careful to note if a statistical test is one- or two-tailed as this will greatly influence a model's interpretation.

When a hypothesis test is set up to show that the sample mean would be only higher than the population mean, this is referred to as a  one-tailed test . A formulation of this hypothesis would be, for example, that "the returns on an investment fund would be  at least  x%." One-tailed tests could also be set up to show that the sample mean could be only less than the population mean. The key difference from a two-tailed test is that in a two-tailed test, the sample mean could be different from the population mean by being  either  higher or lower than it.

If the sample being tested falls into the one-sided critical area, the alternative hypothesis will be accepted instead of the null hypothesis. A one-tailed test is also known as a directional hypothesis or directional test.

A two-tailed test, on the other hand, is designed to examine both sides of a specified data range to test whether a sample is greater than or less than the range of values.

Example of a Two-Tailed Test

As a hypothetical example, imagine that a new  stockbroker , named XYZ, claims that their brokerage fees are lower than that of your current stockbroker, ABC) Data available from an independent research firm indicates that the mean and standard deviation of all ABC broker clients are $18 and $6, respectively.

A sample of 100 clients of ABC is taken, and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and the sample standard deviation is $6, can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?

• H 0 : Null Hypothesis: mean = 18
• H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)
• Rejection region: Z <= - Z 2.5  and Z>=Z 2.5  (assuming 5% significance level, split 2.5 each on either side).
• Z = (sample mean – mean) / (std-dev / sqrt (no. of samples)) = (18.75 – 18) / (6/(sqrt(100)) = 1.25

This calculated Z value falls between the two limits defined by: - Z 2.5  = -1.96 and Z 2.5  = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker. Therefore, the null hypothesis cannot be rejected. Alternatively, the p-value = P(Z< -1.25)+P(Z >1.25) = 2 * 0.1056 = 0.2112 = 21.12%, which is greater than 0.05 or 5%, leads to the same conclusion.

How Is a Two-Tailed Test Designed?

A two-tailed test is designed to determine whether a claim is true or not given a population parameter. It examines both sides of a specified data range as designated by the probability distribution involved. As such, the probability distribution should represent the likelihood of a specified outcome based on predetermined standards.

What Is the Difference Between a Two-Tailed and One-Tailed Test?

A two-tailed hypothesis test is designed to show whether the sample mean is significantly greater than  or  significantly less than the mean of a population. The two-tailed test gets its name from testing the area under both tails (sides) of a normal distribution. A one-tailed hypothesis test, on the other hand, is set up to show only one test; that the sample mean would be higher than the population mean, or, in a separate test, that the sample mean would be lower than the population mean.

What Is a Z-score?

A Z-score numerically describes a value's relationship to the mean of a group of values and is measured in terms of the number of standard deviations from the mean. If a Z-score is 0, it indicates that the data point's score is identical to the mean score whereas Z-scores of 1.0 and -1.0 would indicate values one standard deviation above or below the mean. In most large data sets, 99% of values have a Z-score between -3 and 3, meaning they lie within three standard deviations above and below the mean.

San Jose State University. " 6: Introduction to Null Hypothesis Significance Testing ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Study Guides
• One- and Two-Tailed Tests
• Method of Statistical Inference
• Types of Statistics
• Steps in the Process
• Making Predictions
• Comparing Results
• Probability
• Quiz: Introduction to Statistics
• What Are Statistics?
• Quiz: Bar Chart
• Quiz: Pie Chart
• Introduction to Graphic Displays
• Quiz: Dot Plot
• Quiz: Introduction to Graphic Displays
• Frequency Histogram
• Relative Frequency Histogram
• Quiz: Relative Frequency Histogram
• Frequency Polygon
• Quiz: Frequency Polygon
• Frequency Distribution
• Stem-and-Leaf
• Box Plot (Box-and-Whiskers)
• Quiz: Box Plot (Box-and-Whiskers)
• Scatter Plot
• Measures of Central Tendency
• Quiz: Measures of Central Tendency
• Measures of Variability
• Quiz: Measures of Variability
• Measurement Scales
• Quiz: Introduction to Numerical Measures
• Classic Theory
• Relative Frequency Theory
• Probability of Simple Events
• Quiz: Probability of Simple Events
• Independent Events
• Dependent Events
• Introduction to Probability
• Quiz: Introduction to Probability
• Probability of Joint Occurrences
• Quiz: Probability of Joint Occurrences
• Non-Mutually-Exclusive Outcomes
• Quiz: Non-Mutually-Exclusive Outcomes
• Double-Counting
• Conditional Probability
• Quiz: Conditional Probability
• Probability Distributions
• Quiz: Probability Distributions
• The Binomial
• Quiz: The Binomial
• Quiz: Sampling Distributions
• Random and Systematic Error
• Central Limit Theorem
• Quiz: Central Limit Theorem
• Populations, Samples, Parameters, and Statistics
• Properties of the Normal Curve
• Quiz: Populations, Samples, Parameters, and Statistics
• Sampling Distributions
• Quiz: Properties of the Normal Curve
• Normal Approximation to the Binomial
• Quiz: Normal Approximation to the Binomial
• Quiz: Stating Hypotheses
• The Test Statistic
• Quiz: The Test Statistic
• Quiz: One- and Two-Tailed Tests
• Type I and II Errors
• Quiz: Type I and II Errors
• Stating Hypotheses
• Significance
• Quiz: Significance
• Point Estimates and Confidence Intervals
• Quiz: Point Estimates and Confidence Intervals
• Estimating a Difference Score
• Quiz: Estimating a Difference Score
• Univariate Tests: An Overview
• Quiz: Univariate Tests: An Overview
• One-Sample z-test
• Quiz: One-Sample z-test
• One-Sample t-test
• Quiz: One-Sample t-test
• Two-Sample z-test for Comparing Two Means
• Quiz: Introduction to Univariate Inferential Tests
• Quiz: Two-Sample z-test for Comparing Two Means
• Two Sample t test for Comparing Two Means
• Quiz: Two-Sample t-test for Comparing Two Means
• Paired Difference t-test
• Quiz: Paired Difference t-test
• Test for a Single Population Proportion
• Quiz: Test for a Single Population Proportion
• Test for Comparing Two Proportions
• Quiz: Test for Comparing Two Proportions
• Quiz: Simple Linear Regression
• Chi-Square (X2)
• Quiz: Chi-Square (X2)
• Correlation
• Quiz: Correlation
• Simple Linear Regression
• Common Mistakes
• Statistics Tables
• Quiz: Cumulative Review A
• Quiz: Cumulative Review B
• Statistics Quizzes

In the previous example, you tested a research hypothesis that predicted not only that the sample mean would be different from the population mean but that it would be different in a specific direction—it would be lower. This test is called a directional or one‐tailed test because the region of rejection is entirely within one tail of the distribution.

Some hypotheses predict only that one value will be different from another, without additionally predicting which will be higher. The test of such a hypothesis is nondirectional or two‐tailed because an extreme test statistic in either tail of the distribution (positive or negative) will lead to the rejection of the null hypothesis of no difference.

Suppose that you suspect that a particular class's performance on a proficiency test is not representative of those people who have taken the test. The national mean score on the test is 74.

The research hypothesis is:

The mean score of the class on the test is not 74.

Or in notation: H a : μ ≠ 74

The null hypothesis is:

The mean score of the class on the test is 74.

In notation: H 0 : μ = 74

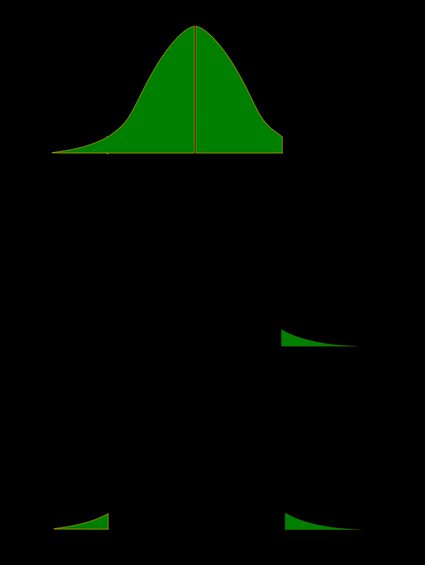
As in the last example, you decide to use a 5 percent probability level for the test. Both tests have a region of rejection, then, of 5 percent, or 0.05. In this example, however, the rejection region must be split between both tails of the distribution—0.025 in the upper tail and 0.025 in the lower tail—because your hypothesis specifies only a difference, not a direction, as shown in Figure 1(a). You will reject the null hypotheses of no difference if the class sample mean is either much higher or much lower than the population mean of 74. In the previous example, only a sample mean much lower than the population mean would have led to the rejection of the null hypothesis.

Figure 1.Comparison of (a) a two‐tailed test and (b) a one‐tailed test, at the same probability level (95 percent).

The decision of whether to use a one‐ or a two‐tailed test is important because a test statistic that falls in the region of rejection in a one‐tailed test may not do so in a two‐tailed test, even though both tests use the same probability level. Suppose the class sample mean in your example was 77, and its corresponding z ‐score was computed to be 1.80. Table 2 in "Statistics Tables" shows the critical z ‐scores for a probability of 0.025 in either tail to be –1.96 and 1.96. In order to reject the null hypothesis, the test statistic must be either smaller than –1.96 or greater than 1.96. It is not, so you cannot reject the null hypothesis. Refer to Figure 1(a).

Suppose, however, you had a reason to expect that the class would perform better on the proficiency test than the population, and you did a one‐tailed test instead. For this test, the rejection region of 0.05 would be entirely within the upper tail. The critical z ‐value for a probability of 0.05 in the upper tail is 1.65. (Remember that Table 2 in "Statistics Tables" gives areas of the curve below z ; so you look up the z ‐value for a probability of 0.95.) Your computed test statistic of z = 1.80 exceeds the critical value and falls in the region of rejection, so you reject the null hypothesis and say that your suspicion that the class was better than the population was supported. See Figure 1(b).

In practice, you should use a one‐tailed test only when you have good reason to expect that the difference will be in a particular direction. A two‐tailed test is more conservative than a one‐tailed test because a two‐tailed test takes a more extreme test statistic to reject the null hypothesis.

Previous Quiz: The Test Statistic

Next Quiz: One- and Two-Tailed Tests

• Online Quizzes for CliffsNotes Statistics QuickReview, 2nd Edition

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar

Institute for Digital Research and Education

FAQ: What are the differences between one-tailed and two-tailed tests?

When you conduct a test of statistical significance, whether it is from a correlation, an ANOVA, a regression or some other kind of test, you are given a p-value somewhere in the output.  If your test statistic is symmetrically distributed, you can select one of three alternative hypotheses. Two of these correspond to one-tailed tests and one corresponds to a two-tailed test.  However, the p-value presented is (almost always) for a two-tailed test.  But how do you choose which test?  Is the p-value appropriate for your test? And, if it is not, how can you calculate the correct p-value for your test given the p-value in your output?  

What is a two-tailed test?

First let’s start with the meaning of a two-tailed test.  If you are using a significance level of 0.05, a two-tailed test allots half of your alpha to testing the statistical significance in one direction and half of your alpha to testing statistical significance in the other direction.  This means that .025 is in each tail of the distribution of your test statistic. When using a two-tailed test, regardless of the direction of the relationship you hypothesize, you are testing for the possibility of the relationship in both directions.  For example, we may wish to compare the mean of a sample to a given value x using a t-test.  Our null hypothesis is that the mean is equal to x . A two-tailed test will test both if the mean is significantly greater than x and if the mean significantly less than x . The mean is considered significantly different from x if the test statistic is in the top 2.5% or bottom 2.5% of its probability distribution, resulting in a p-value less than 0.05.     

What is a one-tailed test?

Next, let’s discuss the meaning of a one-tailed test.  If you are using a significance level of .05, a one-tailed test allots all of your alpha to testing the statistical significance in the one direction of interest.  This means that .05 is in one tail of the distribution of your test statistic. When using a one-tailed test, you are testing for the possibility of the relationship in one direction and completely disregarding the possibility of a relationship in the other direction.  Let’s return to our example comparing the mean of a sample to a given value x using a t-test.  Our null hypothesis is that the mean is equal to x . A one-tailed test will test either if the mean is significantly greater than x or if the mean is significantly less than x , but not both. Then, depending on the chosen tail, the mean is significantly greater than or less than x if the test statistic is in the top 5% of its probability distribution or bottom 5% of its probability distribution, resulting in a p-value less than 0.05.  The one-tailed test provides more power to detect an effect in one direction by not testing the effect in the other direction. A discussion of when this is an appropriate option follows.   

When is a one-tailed test appropriate?

Because the one-tailed test provides more power to detect an effect, you may be tempted to use a one-tailed test whenever you have a hypothesis about the direction of an effect. Before doing so, consider the consequences of missing an effect in the other direction.  Imagine you have developed a new drug that you believe is an improvement over an existing drug.  You wish to maximize your ability to detect the improvement, so you opt for a one-tailed test. In doing so, you fail to test for the possibility that the new drug is less effective than the existing drug.  The consequences in this example are extreme, but they illustrate a danger of inappropriate use of a one-tailed test.

So when is a one-tailed test appropriate? If you consider the consequences of missing an effect in the untested direction and conclude that they are negligible and in no way irresponsible or unethical, then you can proceed with a one-tailed test. For example, imagine again that you have developed a new drug. It is cheaper than the existing drug and, you believe, no less effective.  In testing this drug, you are only interested in testing if it less effective than the existing drug.  You do not care if it is significantly more effective.  You only wish to show that it is not less effective. In this scenario, a one-tailed test would be appropriate. 

When is a one-tailed test NOT appropriate?

Choosing a one-tailed test for the sole purpose of attaining significance is not appropriate.  Choosing a one-tailed test after running a two-tailed test that failed to reject the null hypothesis is not appropriate, no matter how "close" to significant the two-tailed test was.  Using statistical tests inappropriately can lead to invalid results that are not replicable and highly questionable–a steep price to pay for a significance star in your results table!   

Deriving a one-tailed test from two-tailed output

The default among statistical packages performing tests is to report two-tailed p-values.  Because the most commonly used test statistic distributions (standard normal, Student’s t) are symmetric about zero, most one-tailed p-values can be derived from the two-tailed p-values.   

Below, we have the output from a two-sample t-test in Stata.  The test is comparing the mean male score to the mean female score.  The null hypothesis is that the difference in means is zero.  The two-sided alternative is that the difference in means is not zero.  There are two one-sided alternatives that one could opt to test instead: that the male score is higher than the female score (diff  > 0) or that the female score is higher than the male score (diff < 0).  In this instance, Stata presents results for all three alternatives.  Under the headings Ha: diff < 0 and Ha: diff > 0 are the results for the one-tailed tests. In the middle, under the heading Ha: diff != 0 (which means that the difference is not equal to 0), are the results for the two-tailed test. 

Two-sample t test with equal variances ------------------------------------------------------------------------------ Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- male | 91 50.12088 1.080274 10.30516 47.97473 52.26703 female | 109 54.99083 .7790686 8.133715 53.44658 56.53507 ---------+-------------------------------------------------------------------- combined | 200 52.775 .6702372 9.478586 51.45332 54.09668 ---------+-------------------------------------------------------------------- diff | -4.869947 1.304191 -7.441835 -2.298059 ------------------------------------------------------------------------------ Degrees of freedom: 198 Ho: mean(male) - mean(female) = diff = 0 Ha: diff < 0 Ha: diff != 0 Ha: diff > 0 t = -3.7341 t = -3.7341 t = -3.7341 P < t = 0.0001 P > |t| = 0.0002 P > t = 0.9999

Note that the test statistic, -3.7341, is the same for all of these tests.  The two-tailed p-value is P > |t|. This can be rewritten as P(>3.7341) + P(< -3.7341).  Because the t-distribution is symmetric about zero, these two probabilities are equal: P > |t| = 2 *  P(< -3.7341).  Thus, we can see that the two-tailed p-value is twice the one-tailed p-value for the alternative hypothesis that (diff < 0).  The other one-tailed alternative hypothesis has a p-value of P(>-3.7341) = 1-(P<-3.7341) = 1-0.0001 = 0.9999.   So, depending on the direction of the one-tailed hypothesis, its p-value is either 0.5*(two-tailed p-value) or 1-0.5*(two-tailed p-value) if the test statistic symmetrically distributed about zero. 

In this example, the two-tailed p-value suggests rejecting the null hypothesis of no difference. Had we opted for the one-tailed test of (diff > 0), we would fail to reject the null because of our choice of tails. 

The output below is from a regression analysis in Stata.  Unlike the example above, only the two-sided p-values are presented in this output.

Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 2, 197) = 46.58 Model | 7363.62077 2 3681.81039 Prob > F = 0.0000 Residual | 15572.5742 197 79.0486001 R-squared = 0.3210 -------------+------------------------------ Adj R-squared = 0.3142 Total | 22936.195 199 115.257261 Root MSE = 8.8909 ------------------------------------------------------------------------------ socst | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- science | .2191144 .0820323 2.67 0.008 .0573403 .3808885 math | .4778911 .0866945 5.51 0.000 .3069228 .6488594 _cons | 15.88534 3.850786 4.13 0.000 8.291287 23.47939 ------------------------------------------------------------------------------

For each regression coefficient, the tested null hypothesis is that the coefficient is equal to zero.  Thus, the one-tailed alternatives are that the coefficient is greater than zero and that the coefficient is less than zero. To get the p-value for the one-tailed test of the variable science having a coefficient greater than zero, you would divide the .008 by 2, yielding .004 because the effect is going in the predicted direction. This is P(>2.67). If you had made your prediction in the other direction (the opposite direction of the model effect), the p-value would have been 1 – .004 = .996.  This is P(<2.67). For all three p-values, the test statistic is 2.67. 

Your Name (required)

Your Email (must be a valid email for us to receive the report!)

Comment/Error Report (required)

How to cite this page

• © 2021 UC REGENTS

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.4: One- and Two-Tailed Tests

• Last updated
• Save as PDF
• Page ID 2148

• Rice University

Learning Objectives

• Define Type I and Type II errors
• Interpret significant and non-significant differences
• Explain why the null hypothesis should not be accepted when the effect is not significant

In the James Bond case study, Mr. Bond was given \(16\) trials on which he judged whether a martini had been shaken or stirred. He was correct on \(13\) of the trials. From the binomial distribution, we know that the probability of being correct \(13\) or more times out of \(16\) if one is only guessing is \(0.0106\). Figure \(\PageIndex{1}\) shows a graph of the binomial distribution. The red bars show the values greater than or equal to \(13\). As you can see in the figure, the probabilities are calculated for the upper tail of the distribution. A probability calculated in only one tail of the distribution is called a "one-tailed probability."

Binomial Calculator

A slightly different question can be asked of the data: "What is the probability of getting a result as extreme or more extreme than the one observed?" Since the chance expectation is \(8/16\), a result of \(3/16\) is equally as extreme as \(13/16\). Thus, to calculate this probability, we would consider both tails of the distribution. Since the binomial distribution is symmetric when \(\pi =0.5\), this probability is exactly double the probability of \(0.0106\) computed previously. Therefore, \(p = 0.0212\). A probability calculated in both tails of a distribution is called a "two-tailed probability" (see Figure \(\PageIndex{2}\)).

Should the one-tailed or the two-tailed probability be used to assess Mr. Bond's performance? That depends on the way the question is posed. If we are asking whether Mr. Bond can tell the difference between shaken or stirred martinis, then we would conclude he could if he performed either much better than chance or much worse than chance. If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which. Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability.

On the other hand, if our question is whether Mr. Bond is better than chance at determining whether a martini is shaken or stirred, we would use a one-tailed probability. What would the one-tailed probability be if Mr. Bond were correct on only \(3\) of the \(16\) trials? Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting \(3\) or more correct out of \(16\). This is a very high probability and the null hypothesis would not be rejected.

The null hypothesis for the two-tailed test is \(\pi =0.5\). By contrast, the null hypothesis for the one-tailed test is \(\pi \leq 0.5\). Accordingly, we reject the two-tailed hypothesis if the sample proportion deviates greatly from \(0.5\) in either direction. The one-tailed hypothesis is rejected only if the sample proportion is much greater than \(0.5\). The alternative hypothesis in the two-tailed test is \(\pi \neq 0.5\). In the one-tailed test it is \(\pi > 0.5\).

You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data. Statistical tests that compute one-tailed probabilities are called one-tailed tests; those that compute two-tailed probabilities are called two-tailed tests. Two-tailed tests are much more common than one-tailed tests in scientific research because an outcome signifying that something other than chance is operating is usually worth noting. One-tailed tests are appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction. For example, consider an experiment designed to test the efficacy of a treatment for the common cold. The researcher would only be interested in whether the treatment was better than a placebo control. It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless.

Some have argued that a one-tailed test is justified whenever the researcher predicts the direction of an effect. The problem with this argument is that if the effect comes out strongly in the non-predicted direction, the researcher is not justified in concluding that the effect is not zero. Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.

Hypothesis Testing for Means & Proportions

•   1  
• |   2  
• |   3  
• |   4  
• |   5  
• |   6  
• |   7  
• |   8  
• |   9  
• |   10  

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

Type i and type ii errors.

All Modules

Z score Table

t score Table

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.  

• Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);  

H 1 : Research hypothesis (investigator's belief); α =0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is a single number that summarizes the sample information.   An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

• Step 3.  Set up decision rule.  

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

• The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value.  In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
• The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.  
• The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value.   For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.  

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

• Step 4. Compute the test statistic.  

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

• Step 5. Conclusion.  

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).  

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .  

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191                 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

• Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

• Step 3. Set up decision rule.  

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05.   Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.  

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.                  

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

 The most common reason for a Type II error is a small sample size.

return to top | previous page | next page

Content ©2017. All Rights Reserved. Date last modified: November 6, 2017. Wayne W. LaMorte, MD, PhD, MPH

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved April 12, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Predictive Analytics This link opens in a new window
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

One-Tail vs Two-Tail Tests

Two-tailed Test

When testing a hypothesis, you must determine if it is a one-tailed or a two-tailed test. The most common format is a two-tailed test, meaning the critical region is located in both tails of the distribution. This is also referred to as a non-directional hypothesis.

This type of test is associated with a "neutral" alternative hypothesis. Here are some examples:

• There is a difference between the scores.
• The groups are not equal .
• There is a relationship between the variables.

One-tailed Test

The alternative option is a one-tailed test. As the name implies, the critical region lies in only one tail of the distribution. This is also called a directional  hypothesis. The image below shows a right-tailed test. A left-tailed test would be another type of one-tailed test.

This type of test is associated with a more specific alternative claim. Here are some examples:

• One group is higher than the other.
• There is a decrease in performance.
• Group A performs worse than Group B.
• << Previous: Null & Alternative Hypotheses
• Next: Alpha & Beta >>
• Last Updated: Apr 2, 2024 6:35 PM
• URL: https://resources.nu.edu/statsresources

t-test Calculator

When to use a t-test, which t-test, how to do a t-test, p-value from t-test, t-test critical values, how to use our t-test calculator, one-sample t-test, two-sample t-test, paired t-test, t-test vs z-test.

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

Black Friday

Millionaire, probability, sensitivity.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (294)
• Ecology (30)
• Everyday life (262)
• Finance (569)
• Health (440)
• Physics (509)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Statistics Made Easy

Two Sample t-test: Definition, Formula, and Example

A two sample t-test is used to determine whether or not two population means are equal.

This tutorial explains the following:

• The motivation for performing a two sample t-test.
• The formula to perform a two sample t-test.
• The assumptions that should be met to perform a two sample t-test.
• An example of how to perform a two sample t-test.

Two Sample t-test: Motivation

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. Since there are thousands of turtles in each population, it would be too time-consuming and costly to go around and weigh each individual turtle.

Instead, we might take a simple random sample of 15 turtles from each population and use the mean weight in each sample to determine if the mean weight is equal between the two populations:

However, it’s virtually guaranteed that the mean weight between the two samples will be at least a little different. The question is whether or not this difference is statistically significant . Fortunately, a two sample t-test allows us to answer this question.

Two Sample t-test: Formula

A two-sample t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

Test statistic:  ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 )

where  x 1  and  x 2 are the sample means, n 1 and n 2  are the sample sizes, and where s p is calculated as:

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)

where s 1 2  and s 2 2  are the sample variances.

If the p-value that corresponds to the test statistic t with (n 1 +n 2 -1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Two Sample t-test: Assumptions

For the results of a two sample t-test to be valid, the following assumptions should be met:

• The observations in one sample should be independent of the observations in the other sample.
• The data should be approximately normally distributed.
• The two samples should have approximately the same variance. If this assumption is not met, you should instead perform Welch’s t-test .
• The data in both samples was obtained using a random sampling method .

Two Sample t-test : Example

Suppose we want to know whether or not the mean weight between two different species of turtles is equal. To test this, will perform a two sample t-test at significance level α = 0.05 using the following steps:

Step 1: Gather the sample data.

Suppose we collect a random sample of turtles from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

Step 2: Define the hypotheses.

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

First, we will calculate the pooled standard deviation s p :

s p = √  (n 1 -1)s 1 2  +  (n 2 -1)s 2 2  /  (n 1 +n 2 -2)  = √  (40-1)18.5 2  +  (38-1)16.7 2  /  (40+38-2)  = 17.647

Next, we will calculate the test statistic  t :

t = ( x 1  –  x 2 )  /  s p (√ 1/n 1  + 1/n 2 ) =  (300-305) / 17.647(√ 1/40 + 1/38 ) =  -1.2508

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -1.2508 and degrees of freedom = n 1 +n 2 -2 = 40+38-2 = 76 is  0.21484 .

Step 5: Draw a conclusion.

Since this p-value is not less than our significance level α = 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Note:  You can also perform this entire two sample t-test by simply using the Two Sample t-test Calculator .

Additional Resources

The following tutorials explain how to perform a two-sample t-test using different statistical programs:

How to Perform a Two Sample t-test in Excel How to Perform a Two Sample t-test in SPSS How to Perform a Two Sample t-test in Stata How to Perform a Two Sample t-test in R How to Perform a Two Sample t-test in Python How to Perform a Two Sample t-test on a TI-84 Calculator

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a proportion (two tailed).

A population proportion is the share of a population that belongs to a particular category .

Hypothesis tests are used to check a claim about the size of that population proportion.

Hypothesis Testing a Proportion

The following steps are used for a hypothesis test:

• Check the conditions
• Define the claims
• Decide the significance level
• Calculate the test statistic

For example:

• Population : Nobel Prize winners
• Category : Women

And we want to check the claim:

"The share of Nobel Prize winners that are women is not 50%"

By taking a sample of 100 randomly selected Nobel Prize winners we could find that:

10 out of 100 Nobel Prize winners in the sample were women

The sample proportion is then: \(\displaystyle \frac{10}{100} = 0.1\), or 10%.

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

• The sample is randomly selected
• Being in the category
• Not being in the category
• 5 members in the category
• 5 members not in the category

In our example, we randomly selected 10 people that were women.

The rest were not women, so there are 90 in the other category.

The conditions are fulfilled in this case.

Note: It is possible to do a hypothesis test without having 5 of each category. But special adjustments need to be made.

2. Defining the Claims

We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.

The claim was:

In this case, the parameter is the proportion of Nobel Prize winners that are women (\(p\)).

The null and alternative hypothesis are then:

Null hypothesis : 50% of Nobel Prize winners were women.

Alternative hypothesis : The share of Nobel Prize winners that are women is not 50%

Which can be expressed with symbols as:

\(H_{0}\): \(p = 0.50 \)

\(H_{1}\): \(p \neq 0.50 \)

This is a ' two-tailed ' test, because the alternative hypothesis claims that the proportion is different (larger or smaller) than in the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

Advertisement

3. Deciding the Significance Level

The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

• \(\alpha = 0.1\) (10%)
• \(\alpha = 0.05\) (5%)
• \(\alpha = 0.01\) (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population proportion is:

\(\displaystyle \frac{\hat{p} - p}{\sqrt{p(1-p)}} \cdot \sqrt{n} \)

\(\hat{p}-p\) is the difference between the sample proportion (\(\hat{p}\)) and the claimed population proportion (\(p\)).

\(n\) is the sample size.

In our example:

The claimed (\(H_{0}\)) population proportion (\(p\)) was \( 0.50 \)

The sample size (\(n\)) was \(100\)

So the test statistic (TS) is then:

\(\displaystyle \frac{0.1-0.5}{\sqrt{0.5(1-0.5)}} \cdot \sqrt{100} = \frac{-0.4}{\sqrt{0.5(0.5)}} \cdot \sqrt{100} = \frac{-0.4}{\sqrt{0.25}} \cdot \sqrt{100} = \frac{-0.4}{0.5} \cdot 10 = \underline{-8}\)

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic for a proportion.

With R use the built-in math functions to calculate the test statistic for a proportion.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).

For a population proportion test, the critical value (CV) is a Z-value from a standard normal distribution .

This critical Z-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population proportion is different from 50%, the rejection region is split into both the left and right tail:

Choosing a significance level (\(\alpha\)) of 0.01, or 1%, we can find the critical Z-value from a Z-table , or with a programming language function:

Note: Because this is a two-tailed test the tail area (\(\alpha\)) needs to be split in half (divided by 2).

With Python use the Scipy Stats library norm.ppf() function find the Z-value for an \(\alpha\)/2 = 0.005 in the left tail.

With R use the built-in qnorm() function to find the Z-value for an \(\alpha\) = 0.005 in the left tail.

Using either method we can find that the critical Z-value in the left tail is \(\approx \underline{-2.5758}\)

Since a normal distribution i symmetric, we know that the critical Z-value in the right tail will be the same number, only positive: \(\underline{2.5758}\)

For a two-tailed test we need to check if the test statistic (TS) is smaller than the negative critical value (-CV), or bigger than the positive critical value (CV).

If the test statistic is smaller than the negative critical value, the test statistic is in the rejection region .

If the test statistic is bigger than the positive critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).

Here, the test statistic (TS) was \(\approx \underline{-8}\) and the critical value was \(\approx \underline{-2.5758}\)

Here is an illustration of this test in a graph:

Since the test statistic was smaller than the negative critical value we reject the null hypothesis.

This means that the sample data supports the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data supports the claim that "The share of Nobel Prize winners that are women is not 50%" at a 1% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).

The test statistic was found to be \( \approx \underline{-8} \)

For a population proportion test, the test statistic is a Z-Value from a standard normal distribution .

Because this is a two-tailed test, we need to find the P-value of a Z-value smaller than -8 and multiply it by 2 .

We can find the P-value using a Z-table , or with a programming language function:

With Python use the Scipy Stats library norm.cdf() function find the P-value of a Z-value smaller than -8 for a two tailed test:

With R use the built-in pnorm() function find the P-value of a Z-value smaller than -8 for a two tailed test:

Using either method we can find that the P-value is \(\approx \underline{1.25 \cdot 10^{-15}}\) or \(0.00000000000000125\)

This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.000000000000125%, to reject the null hypothesis.

This P-value is smaller than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is rejected at all of these significance levels.

The sample data supports the claim that "The share of Nobel Prize winners that are women is not 50%" at a 10%, 5%, and 1% significance level .

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a two-tailed tailed hypothesis test for a proportion.

Here, the sample size is 100, the occurrences are 10, and the test is for a proportion different from than 0.50.

With R use the built-in prop.test() function find the P-value for a left tailed hypothesis test for a proportion.

Here, the sample size is 100, the occurrences are 10, and the test is for a proportion different from 0.50.

Note: The conf.level in the R code is the reverse of the significance level.

Here, the significance level is 0.01, or 1%, so the conf.level is 1-0.01 = 0.99, or 99%.

Left-Tailed and Two-Tailed Tests

This was an example of a two tailed test, where the alternative hypothesis claimed that parameter is different from the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

• Right-Tailed Test
• Left-Tailed Test

COLOR PICKER

Report Error

If you want to report an error, or if you want to make a suggestion, do not hesitate to send us an e-mail:

[email protected]

Top Tutorials

Top references, top examples, get certified.