
- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators

How to Solve a Linear Function – A Step-by-Step Guide

To solve a linear function, I always begin by identifying its standard form, which is typically expressed as $y = mx + b$ . In this equation, (m) represents the slope of the line , and (b) denotes the y-intercept , where the line crosses the y-axis.
By knowing these components, I can graph the function or work with it algebraically. It’s crucial to remember that in a linear equation , the variables (x) and (y) are to the first power, indicating a constant rate of change and resulting in a straight line when graphed.
Understanding how to manipulate this equation to isolate the variable of interest is the key to finding solutions.

Whether I’m substituting values to find points on the line or reformatting the equation to point-slope or standard form depends on the context of the problem.
Encountering various linear equation word problems sharpens my skills, as they often require a tailored approach for each unique scenario.
Stay tuned, as I’m about to unveil the step-by-step process to confidently tackle any linear function that comes my way.
Steps for Solving Linear Functions
When I approach linear functions , I often think of them as a puzzle where my goal is to find the value of the variable that makes the function true. A linear function takes the form of $f(x) = mx + b$, where $m$ is the slope or rate of change , and $b$ is the y-intercept . To make things easier, I’ve broken down the process into clear steps:
Understanding Function Notation : A linear function is typically written as $f(x)$, which is equivalent to $y$. It represents the output for a given input $x$.
Identifying Key Components :
- Slope ($m$) : Determines how steep the line is on a graph.
- Y-intercept ($b$) : Where the line crosses the y-axis.
| Component | Symbol | Role in Equation |
|---|---|---|
| Slope | $m$ | Rate of change |
| Y-intercept | $b$ | Starting value of $y$ |
Writing the Equation : Start by placing the known values of the slope and y-intercept into their proper places in the equation $y = mx + b$.
Plotting the Graph : On a coordinate plane , plot the y-intercept and use the slope to find a second point. Connect these points to visualize the function as a straight line .
Solving for a Specific Value :
- If you need $y$ for a particular $x$, substitute the $x$ value into the equation and solve for $y$.
- To find an $x$ value for a given $y$, you can rearrange the equation to isolate $x$ and then substitute the $y$ value.
Remember, linear equations involving two lines can be parallel or perpendicular based on their slopes:
- Parallel lines share the same slope ($m$).
- Perpendicular lines have slopes that are negative reciprocals of each other.
The process of solving for a linear function is straightforward if you take it step by step. Just remember that you’re working with constants and a variable to find points that lie on a line, and that’s the heart of linear equations .
Applications in Real-World Contexts
In my day-to-day life, I often encounter situations where linear functions are incredibly useful.

These functions, which can be written in the form $f(x) = mx + b$, where $m$ is the slope and $b$ is the y-intercept, model relationships with a constant rate of change. Here are a few examples of how I’ve seen linear functions shine in real-world contexts:
Budgeting and Finance: For instance, if I wanted to understand how my savings account grows over time, I could use a linear function . If I start with $200 and save $50 each week, the amount of money, $M$, after $t$ weeks is represented by $M(t) = 50t + 200$.
Cooking and Recipes: When I’m cooking and need to adjust the recipe according to the number of guests, I use linear functions to scale the ingredients. If a recipe calls for 2 cups of flour for 4 cookies, the equation would look like $c = \frac{1}{2}n$, where $c$ is cups of flour and $n$ is the number of cookies.
Travel and Distance: If I go for a jog and keep a steady pace, the distance I cover can be predicted with a linear function . The distance $d$ in miles, at a constant speed $s$, after jogging for $t$ hours, would be $d(t) = st$.
These are simple applications, but they show how understanding linear functions can apply to anything from managing finances to making dinner or exercising, making this concept a valuable tool in my everyday life.
Solving linear functions can be a satisfying experience, as it sharpens my problem-solving skills and enhances my understanding of algebra.
I’ve learned that by following a methodical approach, such as using the slope-intercept form, which is denoted as $f(x) = mx + b$ , handling linear functions becomes much more straightforward.
It’s important to remember the role of $m$ , which represents the slope, and $b$, the y-intercept, in graphing these linear functions .
When I embark on solving linear equations , it’s crucial to apply systematic methods—graphing, substitution, elimination, or matrices—based on the context of the problem. Each method has its own merits, and knowing when to use each can save me time and effort.
Moreover, understanding how to interpret the solutions in real-life scenarios is an integral part of the learning process.
Whether I am predicting outcomes or determining the relationship between variables, linear functions serve as a fundamental tool in various fields, from economics to engineering.
I encourage fellow learners to practice regularly, as this will certainly fortify their abilities to solve and apply linear functions effectively. The more I engage with these concepts, the more intuitive and rewarding they become.
- Pre Calculus
- Probability
- Sets & Set Theory
- Trigonometry
Linear Equations
A linear equation is an equation for a straight line
These are all linear equations:
| y = 2x + 1 | ||
| 5x = 6 + 3y | ||
| y/2 = 3 − x |
Let us look more closely at one example:
Example: y = 2x + 1 is a linear equation:
The graph of y = 2x+1 is a straight line
- When x increases, y increases twice as fast , so we need 2x
- When x is 0, y is already 1. So +1 is also needed
- And so: y = 2x + 1
Here are some example values:
| x | y = 2x + 1 |
|---|---|
| y = 2 × (-1) + 1 = | |
| y = 2 × 0 + 1 = | |
| y = 2 × 1 + 1 = | |
| y = 2 × 2 + 1 = |
Check for yourself that those points are part of the line above!
Different Forms
There are many ways of writing linear equations, but they usually have constants (like "2" or "c") and must have simple variables (like "x" or "y").
Examples: These are linear equations:
| y = 3x − 6 | ||
| y − 2 = 3(x + 1) | ||
| y + 2x − 2 = 0 | ||
| 5x = 6 | ||
| y/2 = 3 |
But the variables (like "x" or "y") in Linear Equations do NOT have:
- Exponents (like the 2 in x 2 )
- Square roots , cube roots , etc
Examples: These are NOT linear equations:
| y − 2 = 0 | ||
| 3√x − y = 6 | ||
| x /2 = 16 |
Slope-Intercept Form
The most common form is the slope-intercept equation of a straight line :
| (or ) | |
Example: y = 2x + 1
- Slope: m = 2
- Intercept: b = 1
| You can see the effect of different values of and at |
Point-Slope Form
Another common one is the Point-Slope Form of the equation of a straight line:
Example: y − 3 = (¼)(x − 2)
It is in the form y − y 1 = m(x − x 1 ) where:
General Form
And there is also the General Form of the equation of a straight line:
| Ax + By + C = 0 |
| (A and B cannot both be 0) |
Example: 3x + 2y − 4 = 0
It is in the form Ax + By + C = 0 where:
There are other, less common forms as well.
As a Function
Sometimes a linear equation is written as a function , with f(x) instead of y :
| y = 2x − 3 |
| f(x) = 2x − 3 |
| These are the same! |
And functions are not always written using f(x):
| y = 2x − 3 |
| w(u) = 2u − 3 |
| h(z) = 2z − 3 |
| These are also the same! |
The Identity Function
There is a special linear function called the "Identity Function":
And here is its graph:
It is called "Identity" because what comes out is identical to what goes in:
| In | Out |
|---|---|
| 0 | 0 |
| 5 | 5 |
| −2 | −2 |
| ...etc | ...etc |
Constant Functions
Another special type of linear function is the Constant Function ... it is a horizontal line:
No matter what value of "x", f(x) is always equal to some constant value.
Using Linear Equations
You may like to read some of the things you can do with lines:
- Finding the Midpoint of a Line Segment
- Finding Parallel and Perpendicular Lines
- Finding the Equation of a Line from 2 Points
Solving Linear Equations
Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation. Sometimes, we may have to find the values of variables involved in a linear equation. When we are given two or more such linear equations, we can find the values of each variable by solving linear equations. There are a few methods to solve linear equations. Let us discuss each of these methods in detail.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. |
Solving Linear Equations in One Variable
A linear equation in one variable is an equation of degree one and has only one variable term. It is of the form 'ax+b = 0', where 'a' is a non zero number and 'x' is a variable. By solving linear equations in one variable, we get only one solution for the given variable. An example for this is 3x - 6 = 0. The variable 'x' has only one solution, which is calculated as 3x - 6 = 0 3x = 6 x = 6/3 x = 2
For solving linear equations with one variable, simplify the equation such that all the variable terms are brought to one side and the constant value is brought to the other side. If there are any fractional terms then find the LCM ( Least Common Multiple ) and simplify them such that the variable terms are on one side and the constant terms are on the other side. Let us work out a small example to understand this.
4x + 8 = 8x - 10. To find the value of 'x', let us simplify and bring the 'x' terms to one side and the constant terms to another side.
4x - 8x = -10 - 8 -4x = -18 4x = 18 x = 18/4 On simplifying, we get x = 9/2.
Solving Linear Equations by Substitution Method
The substitution method is one of the methods of solving linear equations. In the substitution method , we rearrange the equation such that one of the values is substituted in the second equation. Now that we are left with an equation that has only one variable, we can solve it and find the value of that variable. In the two given equations, any equation can be taken and the value of a variable can be found and substituted in another equation. For solving linear equations using the substitution method, follow the steps mentioned below. Let us understand this with an example of solving the following system of linear equations. x + y = 6 --------------(1) 2x + 4y = 20 -----------(2)
Step 1: Find the value of one of the variables using any one of the equations. In this case, let us find the value of 'x' from equation (1). x + y = 6 ---------(1) x = 6 - y Step 2: Substitute the value of the variable found in step 1 in the second linear equation. Now, let us substitute the value of 'x' in the second equation 2x + 4y = 20.
x = 6 - y Substituting the value of 'x' in 2x + 4y = 20, we get,
2(6 - y) + 4y = 20 12 - 2y + 4y = 20 12 + 2y = 20 2y = 20 - 12 2y = 8 y = 8/2 y = 4 Step 3: Now substitute the value of 'y' in either equation (1) or (2). Let us substitute the value of 'y' in equation (1).
x + y = 6 x + 4 = 6 x = 6 - 4 x = 2 Therefore, by substitution method, the linear equations are solved, and the value of x is 2 and y is 4.
Solving Linear Equations by Elimination Method
The elimination method is another way to solve a system of linear equations. Here we make an attempt to multiply either the 'x' variable term or the 'y' variable term with a constant value such that either the 'x' variable terms or the 'y' variable terms cancel out and gives us the value of the other variable. Let us understand the steps of solving linear equations by elimination method . Consider the given linear equations: 2x + y = 11 ----------- (1) x + 3y = 18 ---------- (2) Step 1: Check whether the terms are arranged in a way such that the 'x' term is followed by a 'y' term and an equal to sign and after the equal to sign the constant term should be present. The given set of linear equations are already arranged in the correct way which is ax+by=c or ax+by-c=0.
Step 2: The next step is to multiply either one or both the equations by a constant value such that it will make either the 'x' terms or the 'y' terms cancel out which would help us find the value of the other variable. Now in equation (2), let us multiply every term by the number 2 to make the coefficients of x the same in both the equations. x + 3y = 18 ---------- (2) Multiplying all the terms in equation (2) by 2, we get,
2(x) + 2(3y) = 2(18). Now equation (2) becomes, 2x + 6y = 36 -----------(2)
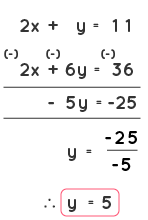
Therefore, y = 5. Step 4: Using the value obtained in step 3, find out the value of another variable by substituting the value in any of the equations. Let us substitute the value of 'y' in equation (1). We get, 2x + y = 11 2x + 5 = 11 2x = 11 - 5 2x = 6 x = 6/2 x = 3
Therefore, by solving linear equations, we get the value of x = 3 and y = 5.
Graphical Method of Solving Linear Equations
Another method for solving linear equations is by using the graph. When we are given a system of linear equations, we graph both the equations by finding values for 'y' for different values of 'x' in the coordinate system. Once it is done, we find the point of intersection of these two lines. The (x,y) values at the point of intersection give the solution for these linear equations. Let us take two linear equations and solve them using the graphical method.
x + y = 8 -------(1)
y = x + 2 --------(2)
Let us take some values for 'x' and find the values for 'y' for the equation x + y = 8. This can also be rewritten as y = 8 - x.
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 7 | 6 | 5 | 4 |
Let us take some values for 'x' and find the values for 'y' in the equation y = x + 2.
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2 | 3 | 4 | 5 | 6 |
Plotting these points on the coordinate plane, we get a graph like this.
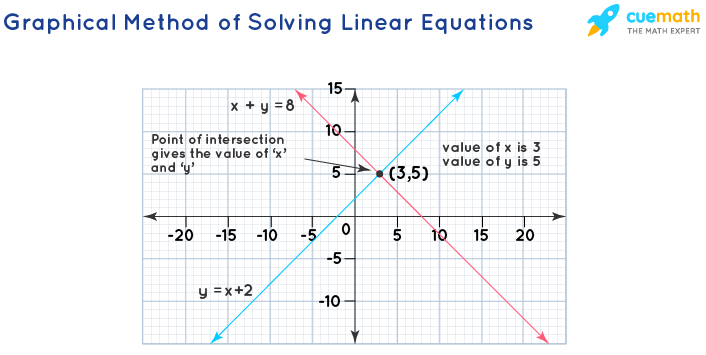
Now, we find the point of intersection of these lines to find the values of 'x' and 'y'. The two lines intersect at the point (3,5). Therefore, x = 3 and y = 5 by using the graphical method of solving linear equations .
This method is also used to find the optimal solution of linear programming problems. Let us look at one more method of solving linear equations, which is the cross multiplication method.
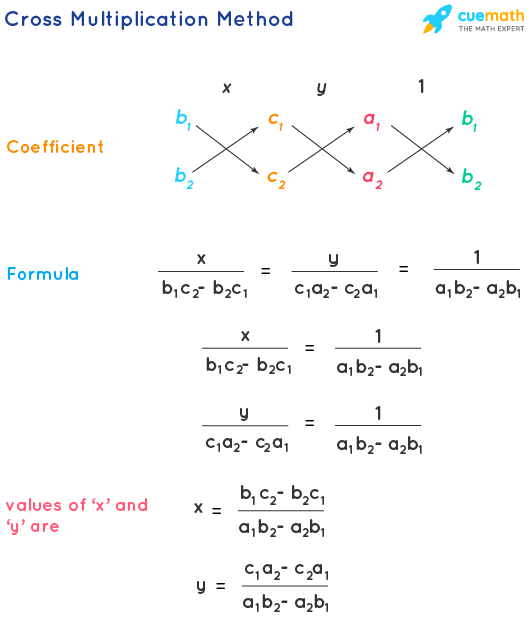
Cross Multiplication Method of Solving Linear Equations
The cross multiplication method enables us to solve linear equations by picking the coefficients of all the terms ('x' , 'y' and the constant terms) in the format shown below and apply the formula for finding the values of 'x' and 'y'.
Topics Related to Solving Linear Equations
Check the given articles related to solving linear equations.
- Linear Equations
- Application of Linear Equations
- Two-Variable Linear Equations
- Linear Equations and Half Planes
- One Variable Linear Equations and Inequations
Solving Linear Equations Examples
Example 1: Solve the following linear equations by the substitution method.
3x + y = 13 --------- (1) 2x + 3y = 18 -------- (2)
By using the substitution method of solving linear equations, let us take the first equation and find the value of 'y' and substitute it in the second equation.
From equation (1), y = 13-3x. Now, substituting the value of 'y' in equation (2), we get, 2x + 3 (13 - 3x) = 18 2x + 39 - 9x = 18 -7x + 39 = 18 -7x = 18 - 39 -7x = -21 x = -21/-7 x = 3 Now, let us substitute the value of 'x = 3' in equation (1) and find the value of 'y'. 3x + y = 13 ------- (1) 3(3) + y = 13 9 + y = 13 y = 13 - 9 y = 4
Therefore, by the substitution method, the value of x is 3 and y is 4.
Example 2: Using the elimination method of solving linear equations find the values of 'x' and 'y'.
3x + y = 21 ------ (1) 2x + 3y = 28 -------- (2)
By using the elimination method, let us make the 'y' variable to be the same in both the equations (1) and (2). To do this let us multiply all the terms of the first equation by 3. Therefore equation (1) becomes,
3(3x) + 3(y) = 63 9x + 3y = 63 ---------- (3) The second equation is, 2x + 3y = 28 Now let us cancel the 'y' terms and find the value of 'x' by subtracting equation (2) from equation (3). This is done by changing the signs of all the terms in equation (2).

Example 3: Using the cross multiplication method of solving linear equations, solve the following equations.
x + 2y - 16 = 0 --------- (1) 4x - y - 10 = 0 ---------- (2)
Compare the given equation with \(a_{1}\)x + \(b_{1}\)y + \(c_{1}\) = 0, and \(a_{2}\)x+\(b_{2}\)y+\(c_{2}\) = 0. From the given equations,
\(a_{1}\) = 1, \(a_{2}\) = 4, \(b_{1}\) = 2, \(b_{2}\) = -1, \(c_{1}\) = -16, and \(c_{2}\) = -10.
By cross multiplication method,
x = \(b_{1}\)\(c_{2}\) - \(b_{2}\)\(c_{1}\)/\(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\) y = \(c_{1}\)\(a_{2}\) - \(c_{2}\)\(a_{1}\) / \(a_{1}\)\(b_{2}\) - \(a_{2}\)\(b_{1}\)
Substituting the values in the formula we get,
x = ((2)(-10)) - ((-1)(-16)) / ((1)(-1)) - ((4)(2)) x = (-20-16)/(-1-8) x = -36/-9 x = 36/9 x = 4 y = ((-16)(4)) - ((-10)(1)) / ((1)(-1)) - ((4)(2)) y = (-64 + 10) / (-1 - 8) y = -54 / -9 y = 54/9 y = 6 Therefore, by the cross multiplication method, the value of x is 4 and y is 6.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Solving Linear Equations
Faqs on solving linear equations, what does it mean by solving linear equations.
An equation that has a degree of 1 is called a linear equation. We can have one variable linear equations , two-variable linear equations , linear equations with three variables, and more depending on the number of variables in it. Solving linear equations means finding the values of all the variables present in the equation. This can be done by substitution method, elimination method, graphical method, and the cross multiplication method . All these methods are different ways of finding the values of the variables.
How to Use the Substitution Method for Solving Linear Equations?
The substitution method of solving equations states that for a given system of linear equations, find the value of either 'x' or 'y' from any of the given equations and then substitute the value found of 'x' or 'y' in another equation so that the other unknown value can be found.
How to Use the Elimination Method for Solving Linear Equations?
In the elimination method of solving linear equations, we multiply a constant or a number with one equation or both the equations such that either the 'x' terms or the 'y' terms are the same. Then we cancel out the same term in both the equations by either adding or subtracting them and find the value of one variable (either 'x' or 'y'). After finding one of the values, we substitute the value in one of the equations and find the other unknown value.
What is the Graphical Method of Solving Linear Equations?
In the graphical method of solving linear equations, we find the value of 'y' from the given equations by putting the values of x as 0, 1, 2, 3, and so on, and plot a graph in the coordinate system for the line for various values of 'x' for both the system of linear equations. We will see that these two lines intersect at a point. This point is the solution for the given system of linear equations. If there is no intersection point between two lines, then we consider them as parallel lines , and if we found that both the lines lie on each other, those are known as coincident lines and have infinitely many solutions.
What are the Steps of Solving Linear Equations that has One Variable?
A linear equation is an equation with degree 1. To solve a linear equation that has one variable we bring the variable to one side and the constant value to the other side. Then, a non-zero number may be added, subtracted, multiplied, or divided on both sides of the equation. For example, a linear equation with one variable will be of the form 'x - 4 = 2'. To find the value of 'x', we add the constant value '4' to both sides of the equation. Therefore, the value of 'x = 6'.
What are the Steps of Solving Linear Equations having Three Variables?
To solve a system of linear equations that has three variables, we take any two equations and variables. We then take another pair of linear equations and also solve for the same variable. Now that, we have two linear equations with two variables, we can use the substitution method or elimination method, or any other method to solve the values of two unknown variables. After finding these two variables, we substitute them in any of the three equations to find the third unknown variable.
Number Line
- \frac{3}{4}x+\frac{5}{6}=5x-\frac{125}{3}
- \sqrt{2}x-\sqrt{3}=\sqrt{5}
- 7y+5-3y+1=2y+2
- \frac{x}{3}+\frac{x}{2}=10
- What is a linear equation?
- A linear equation represents a straight line on a coordinate plane. It can be written in the form: y = mx + b where m is the slope of the line and b is the y-intercept.
- How do you find the linear equation?
- To find the linear equation you need to know the slope and the y-intercept of the line. To find the slope use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points on the line. The y-intercept is the point at which x=0.
- What are the 4 methods of solving linear equations?
- There are four common methods to solve a system of linear equations: Graphing, Substitution, Elimination and Matrix.
- How do you identify a linear equation?
- Here are a few ways to identify a linear equation: Look at the degree of the equation, a linear equation is a first-degree equation. Check if the equation has two variables. Graph the equation.
- What is the most basic linear equation?
- The most basic linear equation is a first-degree equation with one variable, usually written in the form of y = mx + b, where m is the slope of the line and b is the y-intercept.
linear-equation-calculator
- High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
2.2 Linear Equations in One Variable
Learning objectives.
In this section, you will:
- Solve equations in one variable algebraically.
- Solve a rational equation.
- Find a linear equation.
- Given the equations of two lines, determine whether their graphs are parallel or perpendicular.
- Write the equation of a line parallel or perpendicular to a given line.
Caroline is a full-time college student planning a spring break vacation. To earn enough money for the trip, she has taken a part-time job at the local bank that pays $15.00/hr, and she opened a savings account with an initial deposit of $400 on January 15. She arranged for direct deposit of her payroll checks. If spring break begins March 20 and the trip will cost approximately $2,500, how many hours will she have to work to earn enough to pay for her vacation? If she can only work 4 hours per day, how many days per week will she have to work? How many weeks will it take? In this section, we will investigate problems like this and others, which generate graphs like the line in Figure 1 .
Solving Linear Equations in One Variable
A linear equation is an equation of a straight line, written in one variable. The only power of the variable is 1. Linear equations in one variable may take the form a x + b = 0 a x + b = 0 and are solved using basic algebraic operations.
We begin by classifying linear equations in one variable as one of three types: identity, conditional, or inconsistent. An identity equation is true for all values of the variable. Here is an example of an identity equation.
The solution set consists of all values that make the equation true. For this equation, the solution set is all real numbers because any real number substituted for x x will make the equation true.
A conditional equation is true for only some values of the variable. For example, if we are to solve the equation 5 x + 2 = 3 x − 6 , 5 x + 2 = 3 x − 6 , we have the following:
The solution set consists of one number: { − 4 } . { − 4 } . It is the only solution and, therefore, we have solved a conditional equation.
An inconsistent equation results in a false statement. For example, if we are to solve 5 x − 15 = 5 ( x − 4 ) , 5 x − 15 = 5 ( x − 4 ) , we have the following:
Indeed, −15 ≠ −20. −15 ≠ −20. There is no solution because this is an inconsistent equation.
Solving linear equations in one variable involves the fundamental properties of equality and basic algebraic operations. A brief review of those operations follows.
Linear Equation in One Variable
A linear equation in one variable can be written in the form
where a and b are real numbers, a ≠ 0. a ≠ 0.
Given a linear equation in one variable, use algebra to solve it.
The following steps are used to manipulate an equation and isolate the unknown variable, so that the last line reads x = _________, x = _________, if x is the unknown. There is no set order, as the steps used depend on what is given:
- We may add, subtract, multiply, or divide an equation by a number or an expression as long as we do the same thing to both sides of the equal sign. Note that we cannot divide by zero.
- Apply the distributive property as needed: a ( b + c ) = a b + a c . a ( b + c ) = a b + a c .
- Isolate the variable on one side of the equation.
- When the variable is multiplied by a coefficient in the final stage, multiply both sides of the equation by the reciprocal of the coefficient.
Solving an Equation in One Variable
Solve the following equation: 2 x + 7 = 19. 2 x + 7 = 19.
This equation can be written in the form a x + b = 0 a x + b = 0 by subtracting 19 19 from both sides. However, we may proceed to solve the equation in its original form by performing algebraic operations.
The solution is 6.
Solve the linear equation in one variable: 2 x + 1 = −9. 2 x + 1 = −9.
Solving an Equation Algebraically When the Variable Appears on Both Sides
Solve the following equation: 4 ( x −3 ) + 12 = 15 −5 ( x + 6 ) . 4 ( x −3 ) + 12 = 15 −5 ( x + 6 ) .
Apply standard algebraic properties.
This problem requires the distributive property to be applied twice, and then the properties of algebra are used to reach the final line, x = − 5 3 . x = − 5 3 .
Solve the equation in one variable: −2 ( 3 x − 1 ) + x = 14 − x . −2 ( 3 x − 1 ) + x = 14 − x .
Solving a Rational Equation
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is a considered a rational equation .
Recall that a rational number is the ratio of two numbers, such as 2 3 2 3 or 7 2 . 7 2 . A rational expression is the ratio, or quotient, of two polynomials. Here are three examples.
Rational equations have a variable in the denominator in at least one of the terms. Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).
Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Solve the rational equation: 7 2 x − 5 3 x = 22 3 . 7 2 x − 5 3 x = 22 3 .
We have three denominators; 2 x , 3 x , 2 x , 3 x , and 3. The LCD must contain 2 x , 3 x , 2 x , 3 x , and 3. An LCD of 6 x 6 x contains all three denominators. In other words, each denominator can be divided evenly into the LCD. Next, multiply both sides of the equation by the LCD 6 x . 6 x .
A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as ( x + 1 ) . ( x + 1 ) . Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are x , x , x − 1 , x − 1 , and 3 x − 3. 3 x − 3. First, factor all denominators. We then have x , x , ( x − 1 ) , ( x − 1 ) , and 3 ( x − 1 ) 3 ( x − 1 ) as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of ( x − 1 ) . ( x − 1 ) . The x x in the first denominator is separate from the x x in the ( x − 1 ) ( x − 1 ) denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the x , x , one factor of ( x − 1 ) , ( x − 1 ) , and the 3. Thus, the LCD is the following:
So, both sides of the equation would be multiplied by 3 x ( x − 1 ) . 3 x ( x − 1 ) . Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
Another example is a problem with two denominators, such as x x and x 2 + 2 x . x 2 + 2 x . Once the second denominator is factored as x 2 + 2 x = x ( x + 2 ) , x 2 + 2 x = x ( x + 2 ) , there is a common factor of x in both denominators and the LCD is x ( x + 2 ) . x ( x + 2 ) .
Sometimes we have a rational equation in the form of a proportion; that is, when one fraction equals another fraction and there are no other terms in the equation.
We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.
Multiply a ( d ) a ( d ) and b ( c ) , b ( c ) , which results in a d = b c . a d = b c .
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
Rational Equations
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.
Given a rational equation, solve it.
- Factor all denominators in the equation.
- Find and exclude values that set each denominator equal to zero.
- Find the LCD.
- Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator.
Solving a Rational Equation without Factoring
Solve the following rational equation:
We have three denominators: x , x , 2 , 2 , and 2 x . 2 x . No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is 2 x . 2 x . Only one value is excluded from a solution set, 0. Next, multiply the whole equation (both sides of the equal sign) by 2 x . 2 x .
The proposed solution is −1, which is not an excluded value, so the solution set contains one number, −1 , −1 , or { −1 } { −1 } written in set notation.
Solve the rational equation: 2 3 x = 1 4 − 1 6 x . 2 3 x = 1 4 − 1 6 x .
Solving a Rational Equation by Factoring the Denominator
Solve the following rational equation: 1 x = 1 10 − 3 4 x . 1 x = 1 10 − 3 4 x .
First find the common denominator. The three denominators in factored form are x , 10 = 2 ⋅ 5 , x , 10 = 2 ⋅ 5 , and 4 x = 2 ⋅ 2 ⋅ x . 4 x = 2 ⋅ 2 ⋅ x . The smallest expression that is divisible by each one of the denominators is 20 x . 20 x . Only x = 0 x = 0 is an excluded value. Multiply the whole equation by 20 x . 20 x .
The solution is 35 2 . 35 2 .
Solve the rational equation: − 5 2 x + 3 4 x = − 7 4 . − 5 2 x + 3 4 x = − 7 4 .
Solving Rational Equations with a Binomial in the Denominator
Solve the following rational equations and state the excluded values:
- ⓐ 3 x − 6 = 5 x 3 x − 6 = 5 x
- ⓑ x x − 3 = 5 x − 3 − 1 2 x x − 3 = 5 x − 3 − 1 2
- ⓒ x x − 2 = 5 x − 2 − 1 2 x x − 2 = 5 x − 2 − 1 2
The denominators x x and x − 6 x − 6 have nothing in common. Therefore, the LCD is the product x ( x − 6 ) . x ( x − 6 ) . However, for this problem, we can cross-multiply.
The solution is 15. The excluded values are 6 6 and 0. 0.
The LCD is 2 ( x − 3 ) . 2 ( x − 3 ) . Multiply both sides of the equation by 2 ( x − 3 ) . 2 ( x − 3 ) .
The solution is 13 3 . 13 3 . The excluded value is 3. 3.
The least common denominator is 2 ( x − 2 ) . 2 ( x − 2 ) . Multiply both sides of the equation by x ( x − 2 ) . x ( x − 2 ) .
The solution is 4. The excluded value is 2. 2.
Solve − 3 2 x + 1 = 4 3 x + 1 . − 3 2 x + 1 = 4 3 x + 1 . State the excluded values.
Solving a Rational Equation with Factored Denominators and Stating Excluded Values
Solve the rational equation after factoring the denominators: 2 x + 1 − 1 x − 1 = 2 x x 2 − 1 . 2 x + 1 − 1 x − 1 = 2 x x 2 − 1 . State the excluded values.
We must factor the denominator x 2 −1. x 2 −1. We recognize this as the difference of squares, and factor it as ( x − 1 ) ( x + 1 ) . ( x − 1 ) ( x + 1 ) . Thus, the LCD that contains each denominator is ( x − 1 ) ( x + 1 ) . ( x − 1 ) ( x + 1 ) . Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
The solution is −3. −3. The excluded values are 1 1 and −1. −1.
Solve the rational equation: 2 x − 2 + 1 x + 1 = 1 x 2 − x − 2 . 2 x − 2 + 1 x + 1 = 1 x 2 − x − 2 .
Finding a Linear Equation
Perhaps the most familiar form of a linear equation is the slope-intercept form, written as y = m x + b , y = m x + b , where m = slope m = slope and b = y -intercept . b = y -intercept . Let us begin with the slope.
The Slope of a Line
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown in Figure 2 . The lines indicate the following slopes: m = −3 , m = −3 , m = 2 , m = 2 , and m = 1 3 . m = 1 3 .
The slope of a line, m , represents the change in y over the change in x. Given two points, ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) , ( x 2 , y 2 ) , the following formula determines the slope of a line containing these points:
Finding the Slope of a Line Given Two Points
Find the slope of a line that passes through the points ( 2 , −1 ) ( 2 , −1 ) and ( −5 , 3 ) . ( −5 , 3 ) .
We substitute the y- values and the x- values into the formula.
The slope is − 4 7 . − 4 7 .
It does not matter which point is called ( x 1 , y 1 ) ( x 1 , y 1 ) or ( x 2 , y 2 ) . ( x 2 , y 2 ) . As long as we are consistent with the order of the y terms and the order of the x terms in the numerator and denominator, the calculation will yield the same result.
Find the slope of the line that passes through the points ( −2 , 6 ) ( −2 , 6 ) and ( 1 , 4 ) . ( 1 , 4 ) .
Identifying the Slope and y- intercept of a Line Given an Equation
Identify the slope and y- intercept, given the equation y = − 3 4 x − 4. y = − 3 4 x − 4.
As the line is in y = m x + b y = m x + b form, the given line has a slope of m = − 3 4 . m = − 3 4 . The y- intercept is b = −4. b = −4.
The y -intercept is the point at which the line crosses the y- axis. On the y- axis, x = 0. x = 0. We can always identify the y- intercept when the line is in slope-intercept form, as it will always equal b. Or, just substitute x = 0 x = 0 and solve for y.
The Point-Slope Formula
Given the slope and one point on a line, we can find the equation of the line using the point-slope formula.
This is an important formula, as it will be used in other areas of college algebra and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
Given one point and the slope, the point-slope formula will lead to the equation of a line:
Finding the Equation of a Line Given the Slope and One Point
Write the equation of the line with slope m = −3 m = −3 and passing through the point ( 4 , 8 ) . ( 4 , 8 ) . Write the final equation in slope-intercept form.
Using the point-slope formula, substitute −3 −3 for m and the point ( 4 , 8 ) ( 4 , 8 ) for ( x 1 , y 1 ) . ( x 1 , y 1 ) .
Note that any point on the line can be used to find the equation. If done correctly, the same final equation will be obtained.
Given m = 4 , m = 4 , find the equation of the line in slope-intercept form passing through the point ( 2 , 5 ) . ( 2 , 5 ) .
Finding the Equation of a Line Passing Through Two Given Points
Find the equation of the line passing through the points ( 3 , 4 ) ( 3 , 4 ) and ( 0 , −3 ) . ( 0 , −3 ) . Write the final equation in slope-intercept form.
First, we calculate the slope using the slope formula and two points.
Next, we use the point-slope formula with the slope of 7 3 , 7 3 , and either point. Let’s pick the point ( 3 , 4 ) ( 3 , 4 ) for ( x 1 , y 1 ) . ( x 1 , y 1 ) .
In slope-intercept form, the equation is written as y = 7 3 x − 3. y = 7 3 x − 3.
To prove that either point can be used, let us use the second point ( 0 , −3 ) ( 0 , −3 ) and see if we get the same equation.
We see that the same line will be obtained using either point. This makes sense because we used both points to calculate the slope.
Standard Form of a Line
Another way that we can represent the equation of a line is in standard form . Standard form is given as
where A , A , B , B , and C C are integers. The x- and y- terms are on one side of the equal sign and the constant term is on the other side.
Finding the Equation of a Line and Writing It in Standard Form
Find the equation of the line with m = −6 m = −6 and passing through the point ( 1 4 , −2 ) . ( 1 4 , −2 ) . Write the equation in standard form.
We begin using the point-slope formula.
From here, we multiply through by 2, as no fractions are permitted in standard form, and then move both variables to the left aside of the equal sign and move the constants to the right.
This equation is now written in standard form.
Find the equation of the line in standard form with slope m = − 1 3 m = − 1 3 and passing through the point ( 1 , 1 3 ) . ( 1 , 1 3 ) .
Vertical and Horizontal Lines
The equations of vertical and horizontal lines do not require any of the preceding formulas, although we can use the formulas to prove that the equations are correct. The equation of a vertical line is given as
where c is a constant. The slope of a vertical line is undefined, and regardless of the y- value of any point on the line, the x- coordinate of the point will be c .
Suppose that we want to find the equation of a line containing the following points: ( −3 , −5 ) , ( −3 , 1 ) , ( −3 , 3 ) , ( −3 , −5 ) , ( −3 , 1 ) , ( −3 , 3 ) , and ( −3 , 5 ) . ( −3 , 5 ) . First, we will find the slope.
Zero in the denominator means that the slope is undefined and, therefore, we cannot use the point-slope formula. However, we can plot the points. Notice that all of the x- coordinates are the same and we find a vertical line through x = −3. x = −3. See Figure 3 .
The equation of a horizontal line is given as
where c is a constant. The slope of a horizontal line is zero, and for any x- value of a point on the line, the y- coordinate will be c .
Suppose we want to find the equation of a line that contains the following set of points: ( −2 , −2 ) , ( 0 , −2 ) , ( 3 , −2 ) , ( −2 , −2 ) , ( 0 , −2 ) , ( 3 , −2 ) , and ( 5 , −2 ) . ( 5 , −2 ) . We can use the point-slope formula. First, we find the slope using any two points on the line.
Use any point for ( x 1 , y 1 ) ( x 1 , y 1 ) in the formula, or use the y -intercept.
The graph is a horizontal line through y = −2. y = −2. Notice that all of the y- coordinates are the same. See Figure 3 .
Finding the Equation of a Line Passing Through the Given Points
Find the equation of the line passing through the given points: ( 1 , −3 ) ( 1 , −3 ) and ( 1 , 4 ) . ( 1 , 4 ) .
The x- coordinate of both points is 1. Therefore, we have a vertical line, x = 1. x = 1.
Find the equation of the line passing through ( −5 , 2 ) ( −5 , 2 ) and ( 2 , 2 ) . ( 2 , 2 ) .
Determining Whether Graphs of Lines are Parallel or Perpendicular
Parallel lines have the same slope and different y- intercepts. Lines that are parallel to each other will never intersect. For example, Figure 4 shows the graphs of various lines with the same slope, m = 2. m = 2.
All of the lines shown in the graph are parallel because they have the same slope and different y- intercepts.
Lines that are perpendicular intersect to form a 90° 90° -angle. The slope of one line is the negative reciprocal of the other. We can show that two lines are perpendicular if the product of the two slopes is −1 : m 1 ⋅ m 2 = −1. −1 : m 1 ⋅ m 2 = −1. For example, Figure 5 shows the graph of two perpendicular lines. One line has a slope of 3; the other line has a slope of − 1 3 . − 1 3 .
Graphing Two Equations, and Determining Whether the Lines are Parallel, Perpendicular, or Neither
Graph the equations of the given lines, and state whether they are parallel, perpendicular, or neither: 3 y = − 4 x + 3 3 y = − 4 x + 3 and 3 x − 4 y = 8. 3 x − 4 y = 8.
The first thing we want to do is rewrite the equations so that both equations are in slope-intercept form.
First equation:
Second equation:
See the graph of both lines in Figure 6
From the graph, we can see that the lines appear perpendicular, but we must compare the slopes.
The slopes are negative reciprocals of each other, confirming that the lines are perpendicular.
Graph the two lines and determine whether they are parallel, perpendicular, or neither: 2 y − x = 10 2 y − x = 10 and 2 y = x + 4. 2 y = x + 4.
Writing the Equations of Lines Parallel or Perpendicular to a Given Line
As we have learned, determining whether two lines are parallel or perpendicular is a matter of finding the slopes. To write the equation of a line parallel or perpendicular to another line, we follow the same principles as we do for finding the equation of any line. After finding the slope, use the point-slope formula to write the equation of the new line.
Given an equation for a line, write the equation of a line parallel or perpendicular to it.
- Find the slope of the given line. The easiest way to do this is to write the equation in slope-intercept form.
- Use the slope and the given point with the point-slope formula.
- Simplify the line to slope-intercept form and compare the equation to the given line.
Writing the Equation of a Line Parallel to a Given Line Passing Through a Given Point
Write the equation of line parallel to a 5 x + 3 y = 1 5 x + 3 y = 1 and passing through the point ( 3 , 5 ) . ( 3 , 5 ) .
First, we will write the equation in slope-intercept form to find the slope.
The slope is m = − 5 3 . m = − 5 3 . The y- intercept is 1 3 , 1 3 , but that really does not enter into our problem, as the only thing we need for two lines to be parallel is the same slope. The one exception is that if the y- intercepts are the same, then the two lines are the same line. The next step is to use this slope and the given point with the point-slope formula.
The equation of the line is y = − 5 3 x + 10. y = − 5 3 x + 10. See Figure 7 .
Find the equation of the line parallel to 5 x = 7 + y 5 x = 7 + y and passing through the point ( −1 , −2 ) . ( −1 , −2 ) .
Finding the Equation of a Line Perpendicular to a Given Line Passing Through a Given Point
Find the equation of the line perpendicular to 5 x − 3 y + 4 = 0 5 x − 3 y + 4 = 0 and passing through the point ( − 4 , 1 ) . ( − 4 , 1 ) .
The first step is to write the equation in slope-intercept form.
We see that the slope is m = 5 3 . m = 5 3 . This means that the slope of the line perpendicular to the given line is the negative reciprocal, or − 3 5 . − 3 5 . Next, we use the point-slope formula with this new slope and the given point.
Access these online resources for additional instruction and practice with linear equations.
- Solving rational equations
- Equation of a line given two points
- Finding the equation of a line perpendicular to another line through a given point
- Finding the equation of a line parallel to another line through a given point
2.2 Section Exercises
What does it mean when we say that two lines are parallel?
What is the relationship between the slopes of perpendicular lines (assuming neither is horizontal nor vertical)?
How do we recognize when an equation, for example y = 4 x + 3 , y = 4 x + 3 , will be a straight line (linear) when graphed?
What does it mean when we say that a linear equation is inconsistent?
When solving the following equation:
2 x − 5 = 4 x + 1 2 x − 5 = 4 x + 1
explain why we must exclude x = 5 x = 5 and x = −1 x = −1 as possible solutions from the solution set.
For the following exercises, solve the equation for x . x .
7 x + 2 = 3 x − 9 7 x + 2 = 3 x − 9
4 x − 3 = 5 4 x − 3 = 5
3 ( x + 2 ) − 12 = 5 ( x + 1 ) 3 ( x + 2 ) − 12 = 5 ( x + 1 )
12 − 5 ( x + 3 ) = 2 x − 5 12 − 5 ( x + 3 ) = 2 x − 5
1 2 − 1 3 x = 4 3 1 2 − 1 3 x = 4 3
x 3 − 3 4 = 2 x + 3 12 x 3 − 3 4 = 2 x + 3 12
2 3 x + 1 2 = 31 6 2 3 x + 1 2 = 31 6
3 ( 2 x − 1 ) + x = 5 x + 3 3 ( 2 x − 1 ) + x = 5 x + 3
2 x 3 − 3 4 = x 6 + 21 4 2 x 3 − 3 4 = x 6 + 21 4
x + 2 4 − x − 1 3 = 2 x + 2 4 − x − 1 3 = 2
For the following exercises, solve each rational equation for x . x . State all x -values that are excluded from the solution set.
3 x − 1 3 = 1 6 3 x − 1 3 = 1 6
2 − 3 x + 4 = x + 2 x + 4 2 − 3 x + 4 = x + 2 x + 4
3 x − 2 = 1 x − 1 + 7 ( x − 1 ) ( x − 2 ) 3 x − 2 = 1 x − 1 + 7 ( x − 1 ) ( x − 2 )
3 x x − 1 + 2 = 3 x − 1 3 x x − 1 + 2 = 3 x − 1
5 x + 1 + 1 x − 3 = − 6 x 2 − 2 x − 3 5 x + 1 + 1 x − 3 = − 6 x 2 − 2 x − 3
1 x = 1 5 + 3 2 x 1 x = 1 5 + 3 2 x
For the following exercises, find the equation of the line using the point-slope formula. Write all the final equations using the slope-intercept form.
( 0 , 3 ) ( 0 , 3 ) with a slope of 2 3 2 3
( 1 , 2 ) ( 1 , 2 ) with a slope of − 4 5 − 4 5
x -intercept is 1, and ( −2 , 6 ) ( −2 , 6 )
y -intercept is 2, and ( 4 , −1 ) ( 4 , −1 )
( −3 , 10 ) ( −3 , 10 ) and ( 5 , −6 ) ( 5 , −6 )
( 1 , 3 ) and ( 5 , 5 ) ( 1 , 3 ) and ( 5 , 5 )
parallel to y = 2 x + 5 y = 2 x + 5 and passes through the point ( 4 , 3 ) ( 4 , 3 )
perpendicular to 3 y = x − 4 3 y = x − 4 and passes through the point ( −2 , 1 ) ( −2 , 1 ) .
For the following exercises, find the equation of the line using the given information.
( − 2 , 0 ) ( − 2 , 0 ) and ( −2 , 5 ) ( −2 , 5 )
( 1 , 7 ) ( 1 , 7 ) and ( 3 , 7 ) ( 3 , 7 )
The slope is undefined and it passes through the point ( 2 , 3 ) . ( 2 , 3 ) .
The slope equals zero and it passes through the point ( 1 , −4 ) . ( 1 , −4 ) .
The slope is 3 4 3 4 and it passes through the point ( 1 , 4 ) ( 1 , 4 ) .
( –1 , 3 ) ( –1 , 3 ) and ( 4 , –5 ) ( 4 , –5 )
For the following exercises, graph the pair of equations on the same axes, and state whether they are parallel, perpendicular, or neither.
y = 2 x + 7 y = − 1 2 x − 4 y = 2 x + 7 y = − 1 2 x − 4
3 x − 2 y = 5 6 y − 9 x = 6 3 x − 2 y = 5 6 y − 9 x = 6
y = 3 x + 1 4 y = 3 x + 2 y = 3 x + 1 4 y = 3 x + 2
x = 4 y = −3 x = 4 y = −3
For the following exercises, find the slope of the line that passes through the given points.
( 5 , 4 ) ( 5 , 4 ) and ( 7 , 9 ) ( 7 , 9 )
( −3 , 2 ) ( −3 , 2 ) and ( 4 , −7 ) ( 4 , −7 )
( −5 , 4 ) ( −5 , 4 ) and ( 2 , 4 ) ( 2 , 4 )
( −1 , −2 ) ( −1 , −2 ) and ( 3 , 4 ) ( 3 , 4 )
( 3 , −2 ) ( 3 , −2 ) and ( 3 , −2 ) ( 3 , −2 )
For the following exercises, find the slope of the lines that pass through each pair of points and determine whether the lines are parallel or perpendicular.
( −1 , 3 ) and ( 5 , 1 ) ( −2 , 3 ) and ( 0 , 9 ) ( −1 , 3 ) and ( 5 , 1 ) ( −2 , 3 ) and ( 0 , 9 )
( 2 , 5 ) and ( 5 , 9 ) ( −1 , −1 ) and ( 2 , 3 ) ( 2 , 5 ) and ( 5 , 9 ) ( −1 , −1 ) and ( 2 , 3 )
For the following exercises, express the equations in slope intercept form (rounding each number to the thousandths place). Enter this into a graphing calculator as Y1, then adjust the ymin and ymax values for your window to include where the y -intercept occurs. State your ymin and ymax values.
0.537 x − 2.19 y = 100 0.537 x − 2.19 y = 100
4,500 x − 200 y = 9,528 4,500 x − 200 y = 9,528
200 − 30 y x = 70 200 − 30 y x = 70
Starting with the point-slope formula y − y 1 = m ( x − x 1 ) , y − y 1 = m ( x − x 1 ) , solve this expression for x x in terms of x 1 , y , y 1 , x 1 , y , y 1 , and m m .
Starting with the standard form of an equation A x + B y = C A x + B y = C solve this expression for y y in terms of A , B , C A , B , C and x x . Then put the expression in slope-intercept form.
Use the above derived formula to put the following standard equation in slope intercept form: 7 x − 5 y = 25. 7 x − 5 y = 25.
Given that the following coordinates are the vertices of a rectangle, prove that this truly is a rectangle by showing the slopes of the sides that meet are perpendicular.
( – 1 , 1 ) , ( 2 , 0 ) , ( 3 , 3 ) ( – 1 , 1 ) , ( 2 , 0 ) , ( 3 , 3 ) and ( 0 , 4 ) ( 0 , 4 )
Find the slopes of the diagonals in the previous exercise. Are they perpendicular?

Real-World Applications
The slope for a wheelchair ramp for a home has to be 1 12 . 1 12 . If the vertical distance from the ground to the door bottom is 2.5 ft, find the distance the ramp has to extend from the home in order to comply with the needed slope.
If the profit equation for a small business selling x x number of item one and y y number of item two is p = 3 x + 4 y , p = 3 x + 4 y , find the y y value when p = $ 453 and x = 75. p = $ 453 and x = 75.
For the following exercises, use this scenario: The cost of renting a car is $45/wk plus $0.25/mi traveled during that week. An equation to represent the cost would be y = 45 + .25 x , y = 45 + .25 x , where x x is the number of miles traveled.
What is your cost if you travel 50 mi?
If your cost were $ 63.75 , $ 63.75 , how many miles were you charged for traveling?
Suppose you have a maximum of $100 to spend for the car rental. What would be the maximum number of miles you could travel?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/2-2-linear-equations-in-one-variable
© Jun 28, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

- Math Forum/Help
- Problem Solver
- College Math
- Linear Functions
Linear Functions: Problems with Solutions

| X | Y |
|---|---|
| 5 | 8 |
| 10 | 13 |
| 15 | 18 |
| 20 | 23 |
| 21 | 24 |
| 25 | 28 |
| A | B |
|---|---|
| -1 | 0 |
| -1 | 1 |
| 0 | 3 |
| 0 | 2 |
| 1 | 4 |
| 2 | 2 |
| A | B |
|---|---|
| -1 | 0 |
| -1 | 0 |
| 0 | 3 |
| 0 | 3 |
| 1 | 4 |
| 2 | 2 |
| X | Y |
|---|---|
| 5 | 10 |
| 15 | 15 |
| 20 | 25 |
| 25 | 35 |
| 25 | 24 |
| 25 | 28 |
| X | Y |
|---|---|
| 5 | 5 |
| 10 | 10 |
| 15 | 15 |
| 20 | 20 |
| 21 | 21 |
| 25 | 25 |
| X | Y |
|---|---|
| 5 | 5 |
| 10 | 5 |
| 15 | 5 |
| 20 | 5 |
| 21 | 5 |
| 25 | 5 |
*BRAND NEW* Self-paced Introduction to Counting & Probability. Enroll today!
Something appears to not have loaded correctly.
Click to refresh .
MA 26200, Fall 2024 Linear Algebra And Differential Equations
Credit Hours: 4.00. Linear algebra, elements of differential equations. Not open to students with credit in MA 26500 or 26600.
Instructor Info
| 100 | SC 239 | 1:30PM | MWF | None None | |
| 101 | PHYS 202 | 7:30AM | R | MATH 436 | |
| 102 | PHYS 202 | 8:30AM | R | MATH 436 | |
| 300 | STEW 314 | 9:30AM | MWF | MATH 640 | |
| 301 | HAMP 3153 | 4:30PM | R | MATH 436 | |
| 302 | HAMP 3153 | 3:30PM | R | MATH 436 | |
| 400 | WTHR 320 | 11:30AM | MWF | MATH 640 | |
| 401 | HAMP 3153 | 1:30PM | R | MATH 436 | |
| 402 | HAMP 3153 | 2:30PM | R | MATH 436 | |
| 403 | LILY 3118 | 7:30AM | MWF | MATH 848 | |
| 777 | PHYS 111 | 10:30AM | R | MATH 436 | |
| 888 | PHYS 111 | 11:30AM | R | MATH 436 | |
| 406 | WALC 3148 | 10:30AM | MWF | MATH 436 | |
| 407 | PHYS 110 | 7:30AM | R | MATH 436 | |
Course Materials
| Section | Type | Title | Author |
|---|---|---|---|
| ALL | SUPP | MyLab Math access for online homework - ISBN 9780136743644: MyLab Math access with Pearson eText for Differential Equations and Linear Algebra Digital Update -Access Card (18 -Weeks). ISBN 9780136791829: Differential Equations and Linear Algebra 4e Digital Update, Edwards/Penney, Loose Leaf, and MyLab Math with Pearson etext (18-weeks). ISBN 9780136791799 Differential Equations and Linear Algebra, Edwards/Penney, 4e Digital Update and MyLab Math with Pearson etext (18-weeks) Access Card. |
Important Notes
- ADA policies: please see our ADA Information page for more details
- In the event of a missed exam, see your instructor/professor as soon as possible.
- See the online course evaluation page for more information on how we collect course feedback from students
- Undergraduate
- Applied Math
- National Math Sciences Alliance
- Course Links
- Math Resource Room (MRR)
- Brightspace
- Past Courses Archive
- Past Exams Archive
- University Exam Schedules
- University Course Catalog
- University Course Schedule
- Undergraduate Advisors
- Undergraduate Plans of Study
- WIEP-WISP Tutoring Program
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067
Phone: (765) 494-1901 - FAX: (765) 494-0548 Contact Us
© 2024 Purdue University | An equal access/equal opportunity university | Copyright Complaints | DOE Degree Scorecards
Trouble with this page? Accessibility issues ? Please contact the College of Science .
Maintained by Science IT
Homework Q&A
Drag image here or click to upload
- Anatomy & Physiology
- Astrophysics
- Earth Science
- Environmental Science
- Organic Chemistry
- Precalculus
- Trigonometry
- English Grammar
- U.S. History
- World History

Math AI Solver
Use our AI math solver to solve any math homework problem online for free

Tackle Your Math Homework with Our AI Math Solver
Struggling to do your math homework? HIX Tutor’s AI Math Solver simplifies math problems. Get fast, accurate math solutions in one click with our state-of-the-art math AI solver.
Why Use HIX Tutor’s Math AI Homework Solver
Comprehensive support.
Math AI Solver can assist with math at all grade levels, ranging from elementary math to university and beyond.
Step-by-Step Solutions
Get detailed explanations for each step of the problem to gain a better understanding of your math homework.
24/7 Availability
Access our AI math solver anytime to meet your homework needs around the clock to ensure that you never miss a deadline.
Save Time and Money
Get answers to math problems in record time and save on the cost of math tutors with our free math AI solver tool.
Technologically Advanced
We offer the latest in AI math technology to ensure accurate answers to any math problems including algebra, geometry, calculus, etc.
Streamlined Learning
Our AI math problem solvers make learning all kinds of math easier by providing step-by-step guidance and answers.
Experience the Best Math AI Solver on the Market
Stuck on a difficult math question? Math AI Solver is here to assist you:
Submit Your Math Query
Type in your math question or upload the document or an image of the homework problem.
Let Math AI Solver Do Its Magic
Wait just a few moments while our advanced math homework AI tool analyzes the question and prepares an accurate solution.
Receive the Correct Answer
Receive a detailed, step-by-step solution to your math query that includes an accurate answer.
Other AI Homework Helpers
Demystify topics ranging from basic mechanics to advanced electromagnetism with detailed solutions
Chemistry AI
HIX Tutor's AI chemistry homework helper is your go-to companion to master chemistry problem-solving.
Clarify doubts, and get insights on complex processes and terminologies. Get accurate answers to hard.
HIX Tutor’s AI Math Problem Solver Features at a Glance
| ✅ Accurate AI solutions | Eliminate the risk of errors and mistakes |
|---|---|
| 📝 Rapid homework response | Get correct answers in just moments |
| 📚 Comprehensive math support | Covers maths at all grade levels |
| 📈 Ultimate math tutor | Boost your maths grade and school success |
1. What is Math AI?
A Math AI is an artificial intelligence-powered tool designed to solve complex mathematical problems efficiently and accurately. By utilizing advanced algorithms and computational power, Math AI can provide step-by-step solutions, offer insights into problem-solving strategies, and enhance our overall understanding of various mathematical concepts.
2. What math subjects does the AI math problem solver cover?
Our AI math solver tool is trained to solve a wide range of math subjects, including but not limited to, algebra, geometry, calculus, trigonometry, calculus, and more.
3. How long does this math AI take to get an answer to my math question?
HIX Tutor's math AI Solver is available 24/7 and delivers correct, step-by-step solutions to maths questions almost immediately after you submit the query.
4. What's the best Math AI solver?
HIX Tutor is the best Math AI that offers comprehensive solutions for solving complex mathematical problems. With its advanced features, such as step-by-step explanations, personalized learning paths, and interactive problem-solving tools, HIX Tutor aims to help students and professionals better understand mathematical concepts and improve their problem-solving skills.
5. How does HIX Tutor's AI for maths work?
HIX Tutor's math AI helper utilizes advanced algorithms and deep learning techniques to analyze and understand math problems. It breaks down the problem into steps, applies relevant mathematical concepts, and provides detailed explanations for each step of the solution.
6. Is HIX Tutor's mathematics AI solver accurate?
Yes, our math AI solving tool is designed to deliver accurate solutions. It has been trained on a vast dataset of mathematical problems to ensure its proficiency in providing reliable answers. However, it's important to note that while our tool strives for accuracy, occasional errors or misunderstandings may occur.
7. Is HIX Tutor's math AI solver replace the need for a maths tutor?
While our maths AI tool is designed to provide comprehensive support and step-by-step solutions, it is not intended to replace the guidance and expertise of a human maths tutor. It can be a valuable tool to supplement your learning and provide quick answers, but for in-depth understanding and tailored guidance, a maths tutor may still be beneficial in certain situations.
8. Is this math AI free to use?
Yes, you can try Math AI Solver at no cost. Once you’ve reached your free question limit, you’ll need to purchase an affordable subscription.
Discover Frequently Asked Math Questions and Their Answers
- How do you write the quadratic function #y=x^2+14x+11# in vertex form?
- How many points does #y=-2x^2+x-3# have in common with the vertex and where is the vertex in relation to the x axis?
- How do you solve #4x^4 - 16x^2 + 15 = 0#?
- How do you solve #2x^2+3x-2=0#?
- How do you solve #7(x-4)^2-2=54# using any method?
- How do you solve #x^2 + 5x + 6 = 0# algebraically?
- How do you use factoring to solve this equation #3x^2/4=27#?
- What is the vertex of # y = (1/8)(x – 5)^2 - 3#?
- How do you solve #| x^2+3x-2 | =2#?
- How do you solve #2x²+3x=5 # using the quadratic formula?
- How do you find the derivative of #y=tan(3x)# ?
- How do you differentiate #f(x)= 1/ (lnx)# using the quotient rule?
- How do you differentiate #(3+sin(x))/(3x+cos(x))#?
- What is the derivative of this function #sin^-1(x/4)#?
- What is the derivative of this function #y=sin^-1(2x)#?
- What is the derivative of this function #arcsec(x^3)#?
- What is the derivative of #y=sin(tan2x)#?
- How do you differentiate #cos(pi*x^2)#?
- What is the derivative of #f(x)=(x^2-4)ln(x^3/3-4x)#?
- What is the derivative of #y=3sin(x) - sin(3x)#?
- A triangle has corners at #(5 ,1 )#, #(2 ,9 )#, and #(4 ,3 )#. What is the area of the triangle's circumscribed circle?
- How can we find the area of irregular shapes?
- A triangle has vertices A, B, and C. Vertex A has an angle of #pi/2 #, vertex B has an angle of #( pi)/3 #, and the triangle's area is #24 #. What is the area of the triangle's incircle?
- An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(7 ,1 )# to #(8 ,5 )# and the triangle's area is #27 #, what are the possible coordinates of the triangle's third corner?
- A triangle has corners at #(7 , 9 )#, #(3 ,7 )#, and #(4 ,8 )#. What is the radius of the triangle's inscribed circle?
- Circle A has a center at #(2 ,3 )# and a radius of #1 #. Circle B has a center at #(0 ,-2 )# and a radius of #4 #. Do the circles overlap? If not, what is the smallest distance between them?
- A parallelogram has sides A, B, C, and D. Sides A and B have a length of #2 # and sides C and D have a length of # 7 #. If the angle between sides A and C is #pi/4 #, what is the area of the parallelogram?
- What is a quadrilateral that is not a parallelogram and not a trapezoid?
- Your teacher made 8 triangles he need help to identify what type triangles they are. Help him?: 1) #12, 16, 20# 2) #15, 17, 22# 3) #6, 16, 26# 4) #12, 12, 15# 5) #5,12,13# 6) #7,24,25# 7) #8,15,17# 8) #9,40,41#
- A triangle has corners A, B, and C located at #(3 ,5 )#, #(2 ,9 )#, and #(4 , 8 )#, respectively. What are the endpoints and length of the altitude going through corner C?
- What is the GCF of the set #64, 16n^2, 32n#?
- How do you write the reciprocal number of 5?
- Jeanie has a 3/4 yard piece of ribbon. She needs one 3/8 yard piece and one 1/2 yard piece. Can she cut the piece of ribbon into the two smaller pieces? Why?
- How do you find the GCF of #25k, 35j#?
- How do you write 132/100 in a mixed number?
- How do you evaluate the power #2^3#?
- How do you simplify #(4^6)^2 #?
- How do you convert 3.2 tons to pounds?
- How do you solve #\frac { 5} { 8} + \frac { 3} { 2} ( 4- \frac { 1} { 4} ) - \frac { 1} { 8}#?
- What are some acronyms for PEMDAS?
- How do you find all the asymptotes for function #y=(3x^2+2x-1)/(x^2-4 )#?
- How do you determine whether the graph of #y^2+3x=0# is symmetric with respect to the x axis, y axis or neither?
- How do you determine whether the graph of #y^2=(4x^2)/9-4# is symmetric with respect to the x axis, y axis, the line y=x or y=-x, or none of these?
- How do you find the end behavior of #-x^3+3x^2+x-3#?
- How do you find the asymptotes for #(2x^2 - x - 38) / (x^2 - 4)#?
- How do you find the asymptotes for #f(x) = (x^2) / (x^2 + 1)#?
- How do you find the vertical, horizontal and slant asymptotes of: #(3x-2) / (x+1)#?
- How do you find the Vertical, Horizontal, and Oblique Asymptote given #s(t)=(8t)/sin(t)#?
- How do you find vertical, horizontal and oblique asymptotes for #(x^3+1)/(x^2+3x)#?
- How do you find vertical, horizontal and oblique asymptotes for #y = (4x^3 + x^2 + x + 5 )/( x^2 + 3x)#?
- What is a pooled variance?
- What is the mean, mode median and range of 11, 12, 13, 12, 14, 11, 12?
- What is the z-score of sample X, if #n = 81, mu= 43, St. Dev. =90, and E[X] =57#?
- The camera club has five members, and the mathematics club has eight. There is only one member common to both clubs. In how many ways could a committee of four people be formed with at least one member from each club?
- How many permutations are there of the letter in the word baseball?
- How do you evaluate 6p4?
- What is the probability of #X= 6# successes, using the binomial formula?
- A lottery has a $100 000 first prize, a $25 000 second prize, and five $500 third prizes. A total of 50000 tickets are sold. What is the probability of winning a prize in this lottery?
- When a event is reported, the probability that is a negative event is 30%. What is the probability that 3 out of 5 reported events are negative?
- What is the median of 5, 19, 2, 28, 25?
- How do you solve this trigonometric equation?
- What is the frequency of #f(theta)= sin 3 t - cos2 t #?
- How do you evaluate #Sin(pi/2) + 6 cos(pi/3) #?
- How do you find the values of all six trigonometric functions of a right triangle ABC where C is the right angle, given a=9, b=40, c=41?
- How do you express (5*pi)/4 into degree?
- Solve for θ on the interval [90°,180°]:2tanθ +19 = 0?
- Prove that #((cos(33^@))^2-(cos(57^@))^2)/((sin(10.5^@))^2-(sin(34.5^@))^2)= -sqrt2# ?
- A triangle has sides A, B, and C. The angle between sides A and B is #(pi)/3# and the angle between sides B and C is #pi/6#. If side B has a length of 26, what is the area of the triangle?
- How do you write the following in trigonometric form and perform the operation given #(sqrt3+i)(1+i)#?
- A triangle has sides A, B, and C. The angle between sides A and B is #(2pi)/3#. If side C has a length of #32 # and the angle between sides B and C is #pi/12#, what is the length of side A?

Trust HIX Tutor’s Math AI for Reliable Math Solutions
Don’t waste hours slaving over complex equations or confusing mathematical word problems. Math AI Solver is the ultimate solution for completing math assessments quickly and efficiently. Get started now.
Koopman neural operator as a mesh-free solver of non-linear partial differential equations
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, sylvester equations and the numerical solution of partial fractional differential equations.
We develop a new matrix-based approach to the numerical solution of partial differential equations (PDE) and apply it to the numerical solution of partial fractional differential equations (PFDE). The proposed method is to discretize a given PFDE as a ...
Numerical methods for the solution of partial differential equations of fractional order
Anomalous diffusion is a possible mechanism underlying plasma transport in magnetically confined plasmas. To model this transport mechanism, fractional order space derivative operators can be used. Here, the numerical properties of partial differential ...
Solving partial differential equations by two-dimensional differential transform method
Using two-dimensional differential transform to solve Partial Differential Equations (PDE) is proposed in this study. First, the theory of two-dimensional differential transform is introduced. Second, taking two-dimensional differential transform of a ...
Information
Published in.
Academic Press Professional, Inc.
United States
Publication History
Author tags.
- Neural operator
- Koopman theory
- Partial differential equations
- Dynamic systems
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.
A time-stepping DRBEM for nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation
- Original Article
- Open access
- Published: 08 August 2024
Cite this article
You have full access to this open access article

- Mohamed Abdelsabour Fahmy 1 , 2
10 Accesses
Explore all metrics
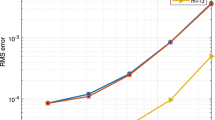
The main aim of this study is to develop a new DRBEM methodology for solving nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation. To remove domain integrals from the boundary integral equation, the DRBEM is employed. The Riemann–Liouville interpretation also discusses the time-fractional derivatives of concerns. The nonlinear, inhomogeneous, and temporal derivative terms were interpolated using the linear radial basis functions (RBFs). To attain high accuracy when solving nonlinear equations, we developed an implicit time-stepping scheme that dealt with the nonlinear term in each time step. DRBEM does not require mesh construction, making it appropriate for dealing with problems in complicated environments. Numerical results from the literature are used to demonstrate the correctness and utility of the proposed technique. The DRBEM technique and the FDM solution yield similar results. Our numerical findings further indicate the practicality of the proposed methodology.
Similar content being viewed by others
General one-dimensional model of the time-fractional diffusion-wave equation in various geometries

An efficient meshless method based on RBFs for the time fractional diffusion-wave equation
An RBF-FD Method for Numerical Solutions of 2D Diffusion-Wave and Diffusion Equations of Distributed Fractional Order
Avoid common mistakes on your manuscript.
1 Introduction
Fractional Calculus is a branch of mathematical study that deals with derivatives and integrals of non-integer orders. It has gained significant attention in various fields, including electrodynamics, viscoelasticity, image processing, control theory and biology, due to its ability to describe phenomena with complex dynamics and long-range dependencies. The development of fractional calculus can be traced back to the works of mathematicians such as Leibniz, L’Hôpital, and Laplace in the seventeenth and eighteenth centuries. However, it was not until the nineteenth century that the concept of fractional derivatives and integrals started to gain more attention. The term “fractional calculus” was first introduced by the mathematician Liouville in 1832, and later expanded upon by Riemann in 1888. However, it was not until the twentieth century that Fractional Calculus began to be systematically studied and applied in scientific and engineering disciplines. Today, Fractional Calculus plays a crucial role in modeling and analyzing systems with fractal geometry, anomalous diffusion, and non-Markovian processes, among others.
In recent years, the study of fractional calculus has also led to the development of new mathematical tools and techniques, contributing to the advancement of science and engineering. Researchers have been exploring the potential of fractional differential equations to provide more accurate models and solutions for real-world problems [ 1 , 2 , 3 , 4 ]. These equations are becoming increasingly prevalent in science and engineering to investigate a wide variety of phenomena like thermos-elasticity, quantum mechanics, continuum mechanics, chaotic synchronization, mixed convection flows, biomedicine, signal analysis, circuit systems, turbulence, and more. The integer order of differential and integral operators is local, while the fractional order of differential and integral operators is nonlocal. As a result, the next state can be identified by its prior and current states [ 5 , 6 , 7 , 8 ].
There are certain analytical methods for solving most fractional differential equations, such as Fourier and Laplace transforms, but they are rarely articulated explicitly, hence the analytical solution of the fractional differential equations is rarely presented. As a result, in the field of engineering, various numerical methods are employed to solve complex problems and analyze different engineering systems [ 9 , 10 , 11 , 12 , 13 , 14 , 15 ]. These methods include the Finite Difference Method (FDM), Finite Element Method (FEM), and the Boundary Element Method (BEM). The FDM is based on discretizing the domain into a grid and approximating derivatives using finite differences. It is commonly used in solving partial differential equations in areas such as heat conduction and fluid dynamics [ 16 , 17 , 18 , 19 , 20 ]. On the other hand, the FEM is widely used in structural analysis, heat transfer, and fluid flow problems. It divides the domain into smaller elements to simplify the computational process and is effective for complex geometries [ 21 , 22 , 23 ]. The Boundary Element Method (BEM) offers several advantages compared to FEM and FDM. BEM directly discretizes the boundary of the domain instead of the entire domain, resulting in fewer unknowns and reducing the computational cost. This makes BEM particularly efficient for problems with unbounded domains or problems with complex internal geometries. Additionally, BEM accurately captures boundary behavior and can handle problems with singularities. These advantages make BEM a valuable tool for engineering fields such as civil engineering, mechanical engineering, and biomedical engineering, particularly in areas such as potential flow problems, acoustics, and fracture mechanics [ 24 , 25 , 26 , 27 , 28 ]. Due to the nonlinearity of the bio-heat equations, solving them analytically is extremely difficult. As a result, many researchers have developed and employed a variety of numerical ways to solve them [ 29 , 30 , 31 ].
The BEM’s core concept is to convert the principal differential equation into an equivalent integral equation just on the boundary. To avoid domain integrals in the BEM formulation, the BEM generally requires a fundamental solution to the main differential equation. Domain integrals are also used to bring nonhomogeneous and nonlinear components into the BEM formulation [ 32 , 33 ]. The dual reciprocity boundary elements method (DRBEM) can discretize only the computational domain’s boundary and evaluate the solution at any needed interior location. The DRBEM does not necessitate the main equation fundamental solution; instead, it necessitates the Laplace equation fundamental solution.
In the present paper, The DRBEM methodology is proposed to solve the 2D nonlinear time fractional sub-diffusion bio-heat wave problem. To eliminate domain integrals from the boundary integral equation, the DRBEM is used. To achieve great accuracy in solving nonlinear equations, we used a time-stepping technique that dealt with the nonlinear term in each time step. Numerical data from the literature is used to demonstrate the correctness and utility of the proposed approach. The DRBEM technique and the finite difference solution produce similar results. Our numerical results further show the validity of the methods presented.
2 Formulation of the problem
Based on References [ 34 , 35 ], the nonlinear time fractional sub-diffusion bio-heat equation with initial and boundary conditions can be expressed as follows
The Riemann–Liouville fractional operators are [ 8 ]
3 DRBEM implementation
We discretize the time variable \({t}_{k}=k\tau , \tau =\frac{\mathbb{T}}{N}, k=\text{0,1},\dots ,N\) . Then the Riemann–Liouville fractional integral [ 36 ] is
By applying the DRBEM discretization to the fractional derivative of Riemann–Liouville, and integration of Eq. ( 1 ), we have
According to You [ 36 ], we obtain
Let N boundary elements and N source points to be midpoints of the boundary elements and L source points in the problem domain to implement the DRBEM Then, we use the following interpolation to approximate the inhomogeneous terms [ 37 ]:
where \({T}^{k}=T\left({x}_{1},{x}_{2},{t}_{k}\right),{Q}^{k}=Q\left({x}_{1},{x}_{2},{t}_{k}\right)\) , and \({\mu }_{i}=1+{\xi }_{i}\) is a linear radial basis functions (RBFs) and \({\xi }_{i}=\sqrt{{\left({x}_{1}-{x}_{1i}\right)}^{2}+{\left({x}_{2}-{x}_{2i}\right)}^{2}}\) for \(i=1,\dots ,N+L\)
Let \(\kappa ={\lambda }_{1}+{\lambda }_{2}\) , then using Eqs. ( 9 ) and ( 11 ), we can write Eq. ( 10 ) in a simple form as follows
Let \({\Phi }_{ir}={\mu }_{ir}\) for \(r=\text{1,2},\dots ,N+L\) . Then from ( 11 ), we have
Based on the implementation of DRBEM, we choose \({f}_{i}\) is a solution to:
where \({b}_{m}\left({t}_{k+1}\right)=b\left({x}_{1m},{x}_{2m},{t}_{k+1}\right)\)
According to [ 38 ], The particular solution \({f}_{i}\) , for linear RBFs can be written as:
Now, we employ a specific weight function, to introduce the following 2D Laplacian operator
where \({G}_{r}\left({x}_{1},{x}_{2}\right)=\frac{-1}{2\pi }\text{ln}\left(\xi \right)\)
Substituting Eq. ( 14 ) into Eq. ( 12 ), and applying the second Green’s theorem result in
The normal derivative of \({f}_{i}\) [ 38 ] is
where \({c}_{r}=\frac{1}{2\pi }{\theta }_{r}, {\theta }_{r}=\left\{\begin{array}{c}2\pi \text{for} \left({x}_{1r},{x}_{2r}\right)\in\Omega \\ \pi \text{for} \left({x}_{1r},{x}_{2r}\right)\in\Gamma \end{array}\right.\) \(r=\text{1,2},\dots ,N+L\) , and \({f}_{ir}={f}_{i}\left({x}_{1r},{x}_{2r}\right)\)
and \(n=\left({n}_{{x}_{1}},{n}_{{x}_{2}}\right)\)
For \(r\) th source point, Eq. ( 16 ) can be expressed as
According to Katsikadelis [ 39 ], Eq. ( 18 ), in terms of \(\overline{H}_{rq}\) and \({G}_{rq}\) , is
for \(r=\text{1,2},\dots ,N\) , and
Let \(q^{ * } = \frac{\partial T}{{\partial n}},{ }\hat{T}\,\,{ = }\,f\) and \(\hat{q} = \frac{\partial f}{{\partial n}}\) . In matrix form, Eq. ( 19 ) can be written as
where \(H_{ij} = \overline{H}_{ij} - \frac{1}{2}\delta_{ij} , \delta_{ij} = \left\{ {\begin{array}{*{20}c} {0 {\text{for }}i \ne j} \\ {1 {\text{for }}i = j} \\ \end{array} } \right.\)
Now, we get the following DRBEM boundary only discretization equation
By using Eq. ( 20 ) for internal nodes, we obtain
where \(\eta ={\left[{\eta }_{1},{\eta }_{2},\dots ,{\eta }_{N+L}\right]}^{T}\)
Equation ( 13 ) may be expressed as
By using Eqs. ( 11 ) and ( 24 ), we get
Combining Eqs. ( 22 ) and ( 23 ) in one equation yields the following \(N+L\) system of unknowns \(q_{1}^{*} \left( {t_{k + 1} } \right), \ldots ,q_{N}^{*} \left( {t_{k + 1} } \right)\) and \(T_{N + 1} \left( {t_{k + 1} } \right), \ldots ,T_{N + L} \left( {t_{k + 1} } \right)\) for any time steps:
Now, we introduce the following definitions
Hence from Eq. ( 26 ), we obtain \(\text{A}\overline{\text{x} }=\overline{\text{b} }\) where
and known vector \(\overline{\mathbf{b} }\) is
If g is a nonlinear function, then we obtain the nonlinear system ( 26 ). Because the computational cost of solving a nonlinear system ( 26 ) is frequently high, we will utilize the following implicit time-stepping (ITS) technique [ 40 ]:
To deal with the nonlinearity that emerges at each time step, we initially set \(\tilde{T} = {\text{T}}^{k}\) rather than \({\text{T}}^{k+1}\) . This assignment allows us to solve ( 26 ) as a linear algebraic equations system for the unknowns \({\text{T}}^{k+1}={\text{T}}^{k+\text{1,0}}\) . Recompute \(\tilde{T} = \frac{1}{2}\left( {{\text{T}}^{k + 1,0} + {\text{T}}^{k} } \right)\) . Now, using the updated \(\tilde{T}\) , system ( 26 ) is solved by computing the unknown \({\text{T}}^{k+\text{1,1}}\) and putting \(\tilde{T} = \frac{1}{2}\left( {{\text{T}}^{k + 1,1} + {\text{T}}^{k} } \right),\) until the unknown quantity converges. when the iterations—stopping condition \(\left\| {{\text{T}}^{{k + 1,{\text{l}}}} - {\text{T}}^{{k + 1,{\text{l}} - 1}} } \right\| \le \varepsilon ,\) is satisfied we can now place \({\text{T}}^{k+1}={\text{T}}^{k+1,\text{l}}\) .
4 Numerical results
There were no published results that supported the suggested technique’s conclusions. Some of the information, however, can be included as part of the planned study. As a result, we examined a special case in our research and compared our DRBEM results to the finite difference method (FDM) [ 41 ]. To evaluate the validity of the proposed DRBEM, we used the same parameters as [ 26 ].
Figures 1 – 3 show the temperature distributions for the finite difference method (FDM) and dual reciprocity boundary element method (DRBEM). Figure 1 shows the temperature distribution in the absence of heat source intensity ( \({Q}_{l}\) = 0 ) and electromagnetic heat source ( \({Q}_{r}\) = 0 ). Figure 2 shows the temperature distribution in the absence of heat source intensity ( \({Q}_{l}\) = 0 ). Figure 3 displays the temperature distribution in the absence of electromagnetic heat source ( \({Q}_{r}\) = 0 ). It is shown from these figures that the DRBEM is in excellent agreement with the FDM [ 41 ]. The computation results of the considered problem were found using MATLAB R2022a on a MacBook Pro with 2.9 GHz Core i9 processor and 16 GB RAM, 1TB SSD Storage. Based on numerical findings, the suggested DRBEM approximation is an effective solution for addressing nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation.
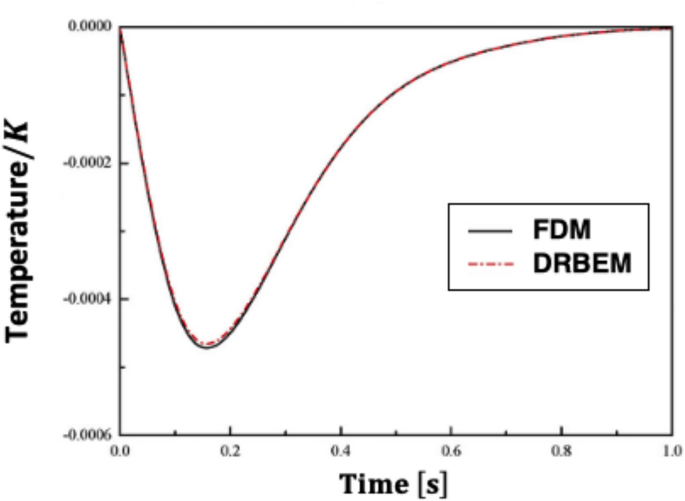
Temperature distribution in the absence of heat source intensity ( \({Q}_{l}\) = 0 ) and electromagnetic heat source ( \({Q}_{r}\) = 0 )
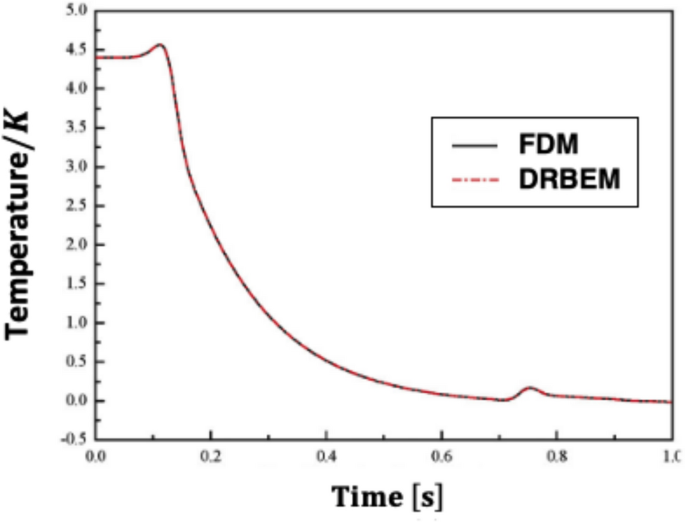
Temperature distribution in the absence of heat source intensity ( \({Q}_{l}\) = 0 )
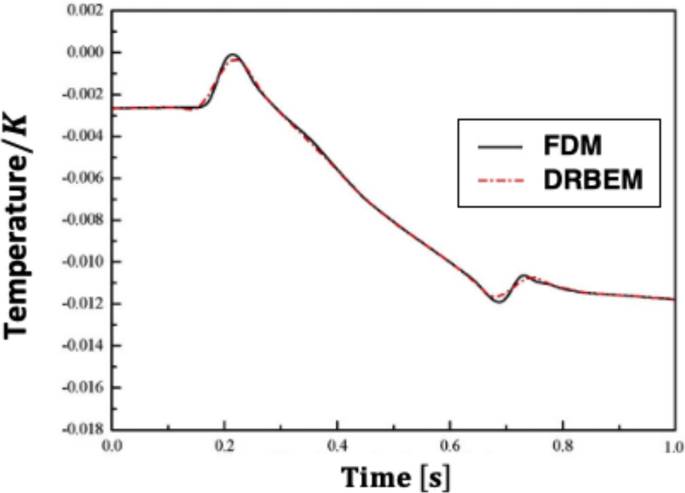
Temperature distribution in the absence of electromagnetic heat source ( \({Q}_{r}\) = 0 )
5 Conclusion
The DRBEM has been created in this research for solving the 2D nonlinear time fractional sub-diffusion bio-heat equation. The DRBEM is used to exclude domain integrals from the boundary integral equation. In the Riemann–Liouville interpretation, issues’ time-fractional derivatives are also described. The nonlinear, inhomogeneous, and temporal derivative terms were interpolated using the linear RBFs. We employed a time-stepping technique that deals with the nonlinear term in each time step to achieve excellent precision in solving nonlinear equations. DRBEM does not necessitate mesh formation, making it ideal for dealing with difficulties in complex locations. Numerical results from literature are considered to illustrate the correctness and usefulness of the provided procedure. The results of the DRBEM approach and the FDM solution are in good agreement. Our numerical results also support the viability of the provided methodology.
This study explores the physical meaning of sub-diffusion bioheat in biological systems, revealing its importance in heat transfer. Biological tissues have unique properties that affect the heat conduction equation. Many bio-heat models consider skin, deeper tissue, and the spine, while fewer consider interior body heat problems. The partial nuclear membrane’s higher temperature is termed sub-diffusive, while the inner nuclear membrane and muscle fibers are considered super-diffusive. Investigating the physical significance of bio-heat is crucial for future physics and biomedicine, as it is the origin of internationally known physics and biomedicine.
Data availability
All data generated or analyzed during this study are included in this published article.
Abbreviations
Antenna constants
Gamma function
Dirac delta function
Small number
Value of \({\mu }_{i}\) at \(r\)
Soft tissue density
Blood density
Laser pulse time characteristic
Positive constants
Soft tissue specific heat
Blood specific heat
Fundamental solution of Laplacian operator
Riemann–Liouville fractional operator
Non-Gaussian temporal profile
Total energy intensity
Thermal conductivity of soft tissue
Internal points number
Outward unit normal vector
\(=\left|\mathbf{y}-\mathbf{x}\right|\) Euclidean distance
Blood perfusion heat
Heat source intensity
Metabolic heat generation
Electromagnetic heat source
Reference metabolism
Irradiated surface absorptivity
Exact temperature
Approximate temperature
Reference temperature
Blood temperature
Blood perfusion rate
Probe position
Distance from tumor to outer surface
Mohammed MG (2021) Natural homotopy perturbation method for solving nonlinear fractional gas dynamics equations. Int J Nonlinear Anal Appl 12:813–821
Google Scholar
Jassim HK, Ahmad H, Shamaoon A, Cesarano C (2021) An efficient hybrid technique for the solution of fractional-order partial differential equations. Carpathian Math Publ 13:790–804
Article Google Scholar
Jafari H, Zayir MY, Jassim HK (2023) Analysis of fractional Navier-Stokes equations. Heat Trans 52:2859–2877
Singh J, Jassim HK, Kumar D, Dubey VP (2023) Fractal dynamics and computational analysis of local fractional Poisson equations arising in electrostatics. Commun Theor Phys 75:1–8
El-Ajou A, Arqub OA, Momani S (2015) Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: a new iterative algorithm. J Comput Phys 293:81–95
Miller KS, Ross B (1974) An Introduction the Fractional Calculus and Fractional Differential Equations. Academic Press, New York and London
Oldham KB, Spanier J (1974) The Fractional Calculus. Academic Press, New York, London
Podlubny I (1999) Fractional Differential Equations. Academic Press, San Diego
Fahmy MA, Almehmadi MM (2023) Fractional dual-phase-lag model for nonlinear viscoelastic soft tissues. Fractal Fract 7:66. https://doi.org/10.3390/fractalfract7010066
Fahmy MA (2023) A nonlinear fractional BEM model for magneto-thermo-visco-elastic ultrasound waves in temperature-dependent FGA rotating granular plates. Fractal Fract 7:214. https://doi.org/10.3390/fractalfract7030214
Mulimani M, Kumbinarasaiah S (2023) A numerical study on the nonlinear fractional Klein-Gordon equation. J Umm Al-Qura Univ Appl Sci. https://doi.org/10.1007/s43994-023-00091-0
Khatun MM, Akbar MA (2023) Analytical soliton solutions of the beta time-fractional simplified modified Camassa-Holm equation in shallow water wave propagation. J Umm Al-Qura Univ Appl Sci. https://doi.org/10.1007/s43994-023-00085-y
Fahmy MA (2023) Fractional temperature-dependent BEM for laser ultrasonic thermoelastic propagation problems of smart nanomaterials. Fractal Fract 7:536. https://doi.org/10.3390/fractalfract7070536
Fahmy MA, Alsulami MO (2023) Abouelregal AE (2023) three-temperature boundary element modeling of ultrasound wave propagation in anisotropic viscoelastic porous media. Axioms 12:473. https://doi.org/10.3390/axioms12050473
Zhuang P, Liu F, Anh V, Turner I (2008) New solution and analytical techniques of the implicit numerical methods for the anomalous sub-diffusion equation. SIAM J Numer Anal 46:1079–1095
Zeng F, Li C, Liu F, Turner I (2013) The Use of finite differencr/element approaches for solving the time-fractional subdiffusion equation. SIAM J Sci Comput 35:A2976–A3000
Cui M (2009) Compact finite difference method for the fractional diffusion equation. J Comput Phys 228:7792–7804
Article CAS Google Scholar
Dehghan M, Safarpoor M, Abbaszadeh M (2015) Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J Comput Appl Math 290:174–195
Meerschaert MM, Tadjeran C (2006) Finite difference approximation for two-sided space-fractional partial differential equations. Appl Numer Math 56:80–90
Akbar Mohebbi A, Abbaszadeh M, Dehghan M (2024) Solution of two-dimensional modified anomalous fractional sub-diffusion equation via radial basis functions (RBF) meshless method. Eng Anal Bound Elem 38:72–82. https://doi.org/10.1016/j.enganabound.2013.09.015
Burrage K, Hale N, Kay D (2012) An efficient implementation of an implicit FEM scheme for fractional-in-space reaction-diffusion equations. SIAM J Sci Comput 34:A2145–A2172
Jiang Y, Ma J (2011) High-order finite element methods for time-fractional partial differential equations. J Comput Appl Math 235:3285–3290
Liu Q, Liu F, Turner I, Anh V (2011) Finite element approximation for a modified anomalous subdiffusion equation. Appl Math Model 35:4103–4116
Katsikadelis JT (2011) The BEM for numerical solution of partial fractional differential equations. Comput Math Appl 62:891–901
Fahmy MA (2022) A computational model for nonlinear biomechanics problems of FGA biological soft tissues. Appl Sci 12:7174. https://doi.org/10.3390/app12147174
Fahmy MA (2021) A new boundary element algorithm for a general solution of nonlinear space-time fractional dual-phase-lag bio-heat transfer problems during electromagnetic radiation. Case Stud Therm Eng 25:100918. https://doi.org/10.1016/j.csite.2021.100918
Fahmy MA (2018) Boundary element algorithm for modeling and simulation of dual phase lag bioheat transfer and biomechanics of anisotropic soft tissues. Int J Appl Mech 10:1850108
Fahmy MA (2019) Boundary element modeling and simulation of biothermomechanical behavior in anisotropic laser-induced tissue hyperthermia. Eng Anal Bound Elem 101:156–164
Fahmy MA (2019) A new LRBFCM-GBEM modeling algorithm for general solution of time fractional order dual phase lag bioheat transfer problems in functionally graded tissues. Numer Heat Transf, Part A: Appl 75:616–626
Nikan O, Avazzadeh Z, Tenreiro Machado JA (2021) Numerical approach for modeling fractional heat conduction in porous medium with the generalized Cattaneo model. Appl Math Model 100:107–124. https://doi.org/10.1016/j.apm.2021.07.025
Kosztołowicz T (2023) Subdiffusion equation with fractional Caputo time derivative with respect to another function in modeling transition from ordinary subdiffusion to superdiffusion. Phys Rev E 107:064103. https://doi.org/10.1103/PhysRevE.107.064103
Article PubMed Google Scholar
Sonawane J, Sonatakke B, Takale K (2024) Numerical solution of subdiffusion bioheat equation with single phase lag. Indian J Sci Technol 17:955–966. https://doi.org/10.17485/IJST/v17i11.3220
Fathima D, Naeem M, Ali U, Ganie AH, Abdullah FA (2022) A new numerical approach for variable-order time-fractional modified subdiffusion equation via riemann-liouville fractional derivative. Symmetry 14:2462. https://doi.org/10.3390/sym14112462
Dehghan M, Safarpoor M (2016) The dual reciprocity boundary elements method for the linear and nonlinear two-dimensional time-fractional partial differential. Math Method Appl Sci 39:3979–3995. https://doi.org/10.1002/mma.3839
Abbaszadeh M, Mohebbi A (2013) A fourth-order compact solution of the two-dimensional modified anomalous fractional sub-diffusion equation with a nonlinear source term. Comput Math Appl 66:1345–1359. https://doi.org/10.1016/j.camwa.2013.08.010
Zhuang PH, Liu QX (2009) Numerical method of Rayleigh-Stokes problem for heated generalized second grade fluid with fractional derivative. Appl Math Mech 30:1533–1546
Partrigeg PW, Brebbia CA, Wrobel LC (1992) The Dual Reciprocity Boundary Element Method. Computational Mechanics Publication, Southampton
Dehghan M, Mirzaei D (2008) The dual reciprocity boundary element method (DRBEM) for two-dimensional sine-Gordon equation. Comput Method Appl Mech Eng 197:476–486
Katsikadelis JT (2002) Methods, Boundary Elements, Theory and Application. Elsevier, London
Mirzaei D, Dehghan M (2009) Implemention of meshless LBIE method to the 2D non-linear SG problem. Int J Numer Method Eng 79:1662–1682
Sonawane J, Sontakke B, Takale K (2023) Approximate solution of sub diffusion bio heat transfer equation. Baghdad Sci J 20:394–399. https://doi.org/10.21123/bsj.2023.8410
Download references
The authors did not receive support from any organization for the submitted work.
Author information
Authors and affiliations.
Adham University College, Umm Al-Qura University, 28653, Adham, Makkah, Saudi Arabia
Mohamed Abdelsabour Fahmy
Faculty of Computers and Informatics, Suez Canal, University, New Campus, Ismailia, 41522, Egypt
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Mohamed Abdelsabour Fahmy .
Ethics declarations
Conflict of interest.
The author declare no conflict of interest.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Fahmy, M.A. A time-stepping DRBEM for nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation. J.Umm Al-Qura Univ. Appll. Sci. (2024). https://doi.org/10.1007/s43994-024-00178-2
Download citation
Received : 21 January 2024
Accepted : 07 July 2024
Published : 08 August 2024
DOI : https://doi.org/10.1007/s43994-024-00178-2
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Time-stepping
- Dual reciprocity boundary elements method
- Nonlinear fractional-order
- Sub-diffusion bio-heat
- Ultrasonic wave propagation
- Electromagnetic radiation
Mathematics Subject Classification
- Find a journal
- Publish with us
- Track your research

IMAGES
COMMENTS
6. Given each set of information, find a linear equation that satisfies the given conditions, if possible. \(x\) -intercept at (6,0) and \(y\) -intercept at (0,10) 7. Find the slope of the line shown in the graph. 8. 9. 10. Does the following table represent a linear function? If so, find the linear equation that models the data.
This topic covers: - Intercepts of linear equations/functions - Slope of linear equations/functions - Slope-intercept, point-slope, & standard forms - Graphing linear equations/functions - Writing linear equations/functions - Interpreting linear equations/functions - Linear equations/functions word problems
Writing the Equation: Start by placing the known values of the slope and y-intercept into their proper places in the equation y = m x + b. Plotting the Graph: On a coordinate plane, plot the y-intercept and use the slope to find a second point. Connect these points to visualize the function as a straight line. Solving for a Specific Value:
Solving Basic Linear Equations. An equation 129 is a statement indicating that two algebraic expressions are equal. A linear equation with one variable 130, \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\).For example \(3 x - 12 = 0\) A solution 131 to a linear equation is any value that can replace the ...
Linear equations are equations that have two variables and can be plotted on a graph as a straight line. Math is Fun teaches you how to solve linear equations, how to use them in real life, and how to manipulate them algebraically. You can also learn about the slope and intercept of a line, and how to write the equation of a line from two points.
Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere. ... Linear equations word problems. Math > Algebra 1 > Forms of linear equations > Intro to slope ...
Linear equations and inequalities: Unit test; ... Two-step equations word problems Get 3 of 4 questions to level up! Multi-step equations. Learn. Why we do the same thing to both sides: Variable on both sides (Opens a modal) ... Solving proportions 2 Get 5 of 7 questions to level up!
Solving Linear Equations. Solving linear equations means finding the value of the variable(s) given in the linear equations. A linear equation is a combination of an algebraic expression and an equal to (=) symbol. It has a degree of 1 or it can be called a first-degree equation. For example, x + y = 4 is a linear equation.
It can be written in the form: y = mx + b where m is the slope of the line and b is the y-intercept. To find the linear equation you need to know the slope and the y-intercept of the line. To find the slope use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are two points on the line. The y-intercept is the point at which x=0.
Solving Linear Equations in One Variable. A linear equation is an equation of a straight line, written in one variable. The only power of the variable is 1. Linear equations in one variable may take the form a x + b = 0 a x + b = 0 and are solved using basic algebraic operations. We begin by classifying linear equations in one variable as one ...
Problem 5. Solve the equation \displaystyle x+34=82 x+34 = 82. Problem 6. Solve the linear equation 3-a=2a. Problem 7. Solve the linear equation \displaystyle 2x-20=10 2x−20 = 10. Problem 8. Solve the equation \displaystyle 20 - 2x = 18 20−2x = 18. Problem 9.
This algebra video explains how to solve linear equations. It contains plenty of examples and practice problems.Get The Full 1 Hour Video on Patreon: ...
Solution: Translating the problem into an algebraic equation gives: 2x − 5 = 13 2 x − 5 = 13. We solve this for x x. First, add 5 to both sides. 2x = 13 + 5, so that 2x = 18 2 x = 13 + 5, so that 2 x = 18. Dividing by 2 gives x = 182 = 9 x = 18 2 = 9. c) A number subtracted from 9 is equal to 2 times the number.
Slope-intercept form: y = mx + b (the typical form for linear functions) Point-slope form: {eq}y-y_1=m (x-x_1) {/eq} General form: Ax + By + C = 0. These equations would produce a straight line ...
Linear (Simple) Equations: Very Difficult Problems with Solutions. Problem 1. A number is equal to 7 times itself minus 18. Which is the number? Problem 2. A number is equal to 4 times this number less 75.
Free math problem solver answers your linear algebra homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app. Start 7-day free trial on the app. Download free on Amazon. Download free in Windows Store. Take a photo of your math problem on the app. get Go.
Equations Understand solving linear equations. • I can solve simple and multi-step equations. • I can describe how to solve equations. • I can analyze the measurements used to solve a problem and judge the level of accuracy appropriate for the solution. • I can apply equation-solving techniques to solve real-life problems. 1.1 Solving ...
Problem 2. The graph visualize an emplolyee pay based on his working hours. Determine the rate per hour. shows that if he works one hour he will be paid $40. shows that if he works 2 hours he will be paid $80. To know the payments per hour, we must measure the vertical distance between the points. Problem 3.
Linear equations 1. To solve linear equations, find the value of the variable that makes the equation true. Use the inverse of the number that multiplies the variable, and multiply or divide both sides by it. Simplify the result to get the variable value. Check your answer by plugging it back into the equation.
Art of Problem Solving AoPS Online. Math texts, online classes, and more for students in grades 5-12. Visit AoPS Online ‚ Books for Grades 5-12 ...
MyLab Math access for online homework - ISBN 9780136743644: MyLab Math access with Pearson eText for Differential Equations and Linear Algebra Digital Update -Access Card (18 -Weeks). ISBN 9780136791829: Differential Equations and Linear Algebra 4e Digital Update, Edwards/Penney, Loose Leaf, and MyLab Math with Pearson etext (18-weeks).
A Math AI is an artificial intelligence-powered tool designed to solve complex mathematical problems efficiently and accurately. By utilizing advanced algorithms and computational power, Math AI can provide step-by-step solutions, offer insights into problem-solving strategies, and enhance our overall understanding of various mathematical concepts.
For inputs, the function takes complex numbers, which are a combination of real numbers and what mathematicians call "imaginary" ones: a normal number multiplied by the square root of -1. The function seems to capture the discrepancies between Gauss's curve and the real distribution of primes.
Deep learning algorithms have been widely used to solve linear Kolmogorov partial differential equations (PDEs) in high dimensions, where the loss function is defined as a mathematical expectation. We propose to use the randomized quasi-Monte Carlo (RQMC) method instead of the Monte Carlo (MC) method for computing the loss function.
Given a word problem that includes two pairs of input and output values, use the linear function to solve a problem. Identify the input and output values. Convert the data to two coordinate pairs. Find the slope. Write the linear model. Use the model to make a prediction by evaluating the function at a given x-value.
This article proposes an efficient global algorithm for solving general linear multiplicative programming problem (GLMP). The new algorithm combines the quadratic convex relaxation problem, adaptive branching rule, region reduction technique and branch-and-bound scheme.
By approximating the Koopman operator, an infinite-dimensional operator governing all possible observations of the dynamic system, to act on the flow mapping of the dynamic system, we can equivalently learn the solution of a non-linear PDE family by solving simple linear prediction problems.
One-step inequalities: -5c ≤ 15. One-step inequality involving addition. One-step inequality word problem. Inequalities using addition and subtraction. Solving and graphing linear inequalities.
The main aim of this study is to develop a new DRBEM methodology for solving nonlinear fractional sub-diffusion bio-heat ultrasonic wave propagation problems during electromagnetic radiation. To remove domain integrals from the boundary integral equation, the DRBEM is employed. The Riemann-Liouville interpretation also discusses the time-fractional derivatives of concerns. The nonlinear ...
2 x = 6 x dividing both sides of the equation by 2. 2 x 2 = 6 2 x = 3. For. two-step linear equations. , it's easiest if we first combine the constant terms on one side of the equation and the x -terms on the other side of the equation. Then, isolate x . Two-step example. 3 x + 4 = 10 4. 3 x + 4 − 4 = 10 − 4 3 x = 6.