equations of circles algebra 2 homework

Free Printable Math Worksheets for Algebra 2

Created with infinite algebra 2, stop searching. create the worksheets you need with infinite algebra 2..

• Fast and easy to use
• Multiple-choice & free-response
• Never runs out of questions
• Multiple-version printing

Free 14-Day Trial

• Order of operations
• Evaluating expressions
• Simplifying algebraic expressions
• Multi-step equations
• Work word problems
• Distance-rate-time word problems
• Mixture word problems
• Absolute value equations
• Multi-step inequalities
• Compound inequalities
• Absolute value inequalities
• Discrete relations
• Continuous relations
• Evaluating and graphing functions
• Review of linear equations
• Graphing absolute value functions
• Graphing linear inequalities
• Direct and inverse variation
• Systems of two linear inequalities
• Systems of two equations
• Systems of two equations, word problems
• Points in three dimensions
• Systems of three equations, elimination
• Systems of three equations, substitution
• Basic matrix operations
• Matrix multiplication
• All matrix operations combined
• Matrix inverses
• Geometric transformations with matrices
• Operations with complex numbers
• Properties of complex numbers
• Rationalizing imaginary denominators
• Properties of parabolas
• Vertex form
• Graphing quadratic inequalities
• Factoring quadratic expressions
• Solving quadratic equations w/ square roots
• Solving quadratic equations by factoring
• Completing the square
• Solving equations by completing the square
• Solving equations with the quadratic formula
• The discriminant
• Naming and simple operations
• Factoring a sum/difference of cubes
• Factoring by grouping
• Factoring quadratic form
• Factoring using all techniques
• Factors and Zeros
• The Remainder Theorem
• Irrational and Imaginary Root Theorems
• Descartes' Rule of Signs
• More on factors, zeros, and dividing
• The Rational Root Theorem
• Polynomial equations
• Basic shape of graphs of polynomials
• Graphing polynomial functions
• The Binomial Theorem
• Evaluating functions
• Function operations
• Inverse functions
• Simplifying radicals
• Operations with radical expressions
• Dividing radical expressions
• Radicals and rational exponents
• Simplifying rational exponents
• Square root equations
• Rational exponent equations
• Graphing radicals
• Graphing & properties of parabolas
• Equations of parabolas
• Graphing & properties of circles
• Equations of circles
• Graphing & properties of ellipses
• Equations of ellipses
• Graphing & properties of hyperbolas
• Equations of hyperbolas
• Classifying conic sections
• Eccentricity
• Systems of quadratic equations
• Graphing simple rational functions
• Graphing general rational functions
• Simplifying rational expressions
• Multiplying / dividing rational expressions
• Adding / subtracting rational expressions
• Complex fractions
• Solving rational equations
• The meaning of logarithms
• Properties of logarithms
• The change of base formula
• Writing logs in terms of others
• Logarithmic equations
• Inverse functions and logarithms
• Exponential equations not requiring logarithms
• Exponential equations requiring logarithms
• Graphing logarithms
• Graphing exponential functions
• Discrete exponential growth and decay word problems
• Continuous exponential growth and decay word problems
• General sequences
• Arithmetic sequences
• Geometric sequences
• Comparing Arithmetic/Geometric Sequences
• General series
• Arithmetic series
• Arithmetic/Geometric Means w/ Sequences
• Finite geometric series
• Infinite geometric series
• Right triangle trig: Evaluating ratios
• Right triangle trig: Missing sides/angles
• Angles and angle measure
• Co-terminal angles and reference angles
• Arc length and sector area
• Trig ratios of general angles
• Exact trig ratios of important angles
• The Law of Sines
• The Law of Cosines
• Graphing trig functions
• Translating trig functions
• Angle Sum/Difference Identities
• Double-/Half-Angle Identities
• Sample spaces and The Counting Principle
• Independent and dependent events
• Mutualy exclusive events
• Permutations
• Combinations
• Permutations vs combinations
• Probability using permutations and combinations

Circle Equations

A circle is easy to make:

Draw a curve that is "radius" away from a central point.

All points are the same distance from the center.

In fact the definition of a circle is

Circle: The set of all points on a plane that are a fixed distance from a center.

Circle on a Graph

Let us put a circle of radius 5 on a graph:

Now let's work out exactly where all the points are.

We make a right-angled triangle:

And then use Pythagoras :

x 2 + y 2 = 5 2

There are an infinite number of those points, here are some examples:

In all cases a point on the circle follows the rule x 2 + y 2 = radius 2

We can use that idea to find a missing value

Example: x value of 2, and a radius of 5

(The ± means there are two possible values: one with + the other with − )

And here are the two points:

More General Case

Now let us put the center at (a,b)

So the circle is all the points (x,y) that are "r" away from the center (a,b) .

Now lets work out where the points are (using a right-angled triangle and Pythagoras ):

It is the same idea as before, but we need to subtract a and b :

(x−a) 2 + (y−b) 2 = r 2

And that is the "Standard Form" for the equation of a circle!

It shows all the important information at a glance: the center (a,b) and the radius r .

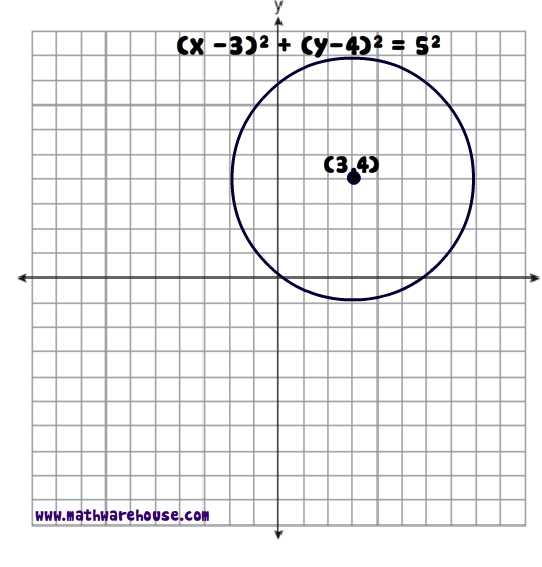
Example: A circle with center at (3,4) and a radius of 6:

Start with:

Put in (a,b) and r:

(x−3) 2 + (y−4) 2 = 6 2

We can then use our algebra skills to simplify and rearrange that equation, depending on what we need it for.

Try it Yourself

"general form".

But you may see a circle equation and not know it !

Because it may not be in the neat "Standard Form" above.

As an example, let us put some values to a, b and r and then expand it

And we end up with this:

x 2 + y 2 − 2x − 4y − 4 = 0

It is a circle equation, but "in disguise"!

So when you see something like that think "hmm ... that might be a circle!"

In fact we can write it in "General Form" by putting constants instead of the numbers:

x 2 + y 2 + Ax + By + C = 0

Note: General Form always has x 2 + y 2 for the first two terms .

Going From General Form to Standard Form

Now imagine we have an equation in General Form :

How can we get it into Standard Form like this?

The answer is to Complete the Square (read about that) twice ... once for x and once for y :

Example: x 2 + y 2 − 2x − 4y − 4 = 0

Now complete the square for x (take half of the −2, square it, and add to both sides):

(x 2 − 2x + (−1) 2 ) + (y 2 − 4y) = 4 + (−1) 2

And complete the square for y (take half of the −4, square it, and add to both sides):

(x 2 − 2x + (−1) 2 ) + (y 2 − 4y + (−2) 2 ) = 4 + (−1) 2 + (−2) 2

And we have it in Standard Form!

(Note: this used the a=1, b=2, r=3 example from before, so we got it right!)

Unit Circle

If we place the circle center at (0,0) and set the radius to 1 we get:

How to Plot a Circle by Hand

1. Plot the center (a,b)

2. Plot 4 points "radius" away from the center in the up, down, left and right direction

3. Sketch it in!

Example: Plot (x−4) 2 + (y−2) 2 = 25

The formula for a circle is (x−a) 2 + (y−b) 2 = r 2

So the center is at (4,2)

And r 2 is 25 , so the radius is √25 = 5

So we can plot:

• The Center: (4,2)
• Up: (4,2+5) = (4,7)
• Down: (4,2−5) = (4,−3)
• Left: (4−5,2) = (−1,2)
• Right: (4+5,2) = (9,2)

Now, just sketch in the circle the best we can!

How to Plot a Circle on the Computer

We need to rearrange the formula so we get "y=".

We should end up with two equations (top and bottom of circle) that can then be plotted.

So the center is at (4,2) , and the radius is √25 = 5

Rearrange to get "y=":

So when we plot these two equations we should have a circle:

• y = 2 + √[25 − (x−4) 2 ]
• y = 2 − √[25 − (x−4) 2 ]

Try plotting those functions on the Function Grapher .

It is also possible to use the Equation Grapher to do it all in one go.

Equation of Circle Worksheet (pdf)

Students will explore the equation of a circle . Specifically, students will practice writing the equation of a circle from a graph as card as graphing a circle given its equation .

Example Questions

1) Identify the coordinates of the center and the length of the radius in the circle below (x - 5) 2 + (y + 2) 2 = 4 radius: Center: (___, _____)

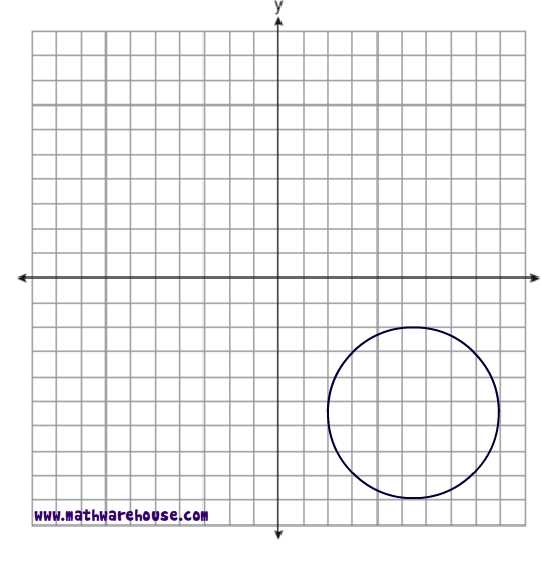
2) Graph a circle centered at (5, 1) with a radius of 5

Visual Aids

Other Details

This is a 3 part worksheet:

• Part I Model Problems
• Part II Practice Problems
• Part III Homework. Mixed questions involving the equation of a circle.
• Equation of Circle
• Interactive Equation of Circle : explore the relationship between the equation and graph of a circle by clicking and dragging..

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: The Equation of the Circle

• Last updated
• Save as PDF
• Page ID 40924

• Richard W. Beveridge
• Clatsop Community College

The equation for a circle is typically given as: \[ (x-h)^{2}+(y-k)^{2}=r^{2} \] In this equation, the point \((h, k)\) represents the center of the circle and \(r\) represents the radius of the circle. This equation is derived from the distance formula. The definition of a circle is the locus (or collection) of points that are equidistant from a given point (the center of the circle).

So, taking this definition, we can say that any point \((x, y)\) that is on the circle should be a distance of \(r\) from the center. Using the distance formula: \[ d=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}} \] Squaring both sides: \[ d^{2}=\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2} \] In this situation, the distance \(d\) is the radius of the circle, \(r .\) This distance should be the same for all points on the circle. So any point on the edge of the circle, \((x, y)\) should be a distance of \(r\) from the center of the circle, \((h, k)\) \[ (x-h)^{2}+(y-k)^{2}=r^{2} \]

Exercises \(\PageIndex{1}\)

Determine the center and radius for each circle and sketch the graph of the circle. 1) \(\quad(x-3)^{2}+(y+1)^{2}=9\) 2) \(\quad(x+4)^{2}+(y+2)^{2}=16\) 3) \(\quad(x-1)^{2}+(y-6)^{2}=20\) 4) \(\quad(x-2)^{2}+(y+5)^{2}=27\) 5) \(\quad(x+7)^{2}+(y-4)^{2}=33\) 6) \(\quad(x-5)^{2}+(y-3)^{2}=50\)

Sometimes the equation for a circle is not given in the standard form. In this situation, you need to put the equation into standard form and then determine the center and radius. In order to put the equation into standard form you will need to complete the square. Completing the square is a mathematical technique that is often useful and is the basis for how the quadratic formula is derived.

Suppose that we are given the equation of a circle that is not in standard form:

\[ x^{2}+6 x+y^{2}+10 y+25=0\]

We need to restate this relationship so that the center and radius can be easily determined from the equation. In order to do this, we need to complete the square for both the \(x\) and the \(y\) variables. There are a variety of methods for completing the square I will demonstrate one of these below.

Take the original equation and move any term that doesn't have a variable to the other side:

\[ x^{2}+6 x+y^{2}+10 y=-25\]

Then open a space after the \(6 x\) and the \(10 y:\)

The idea is that we want trinomial expressions for both \(x\) and \(y\) that are perfect squares. If we look at squaring binomial expressions, we can see that there is a pattern:

\begin{array}{l} (x+3)^{2}=(x+3)(x+3)=x^{2}+6 x+9 \\ (x+4)^{2}=(x+4)(x+4)=x^{2}+8 x+16 \\ (x+5)^{2}=(x+5)(x+5)=x^{2}+10 x+25 \\ (x+6)^{2}=(x+6)(x+6)=x^{2}+12 x+36 \end{array}

We can see that if we have \(x^{2}+6 x,\) then this would correspond to \((x+3)(x+3)\) or \((x+3)^{2}\). But there's a problem: \((x+3)^{2}\) is not equal to \(x^{2}+6 x\). It's equal to \(x^{2}+6 x+9 .\) We can't just add a 9 to the \(x^{2}+6 x,\) but we can add a 9 to both sides.

\[ x^{2}+6 x+9+y^{2}+10 y=-25+9\]

Similarly, to complete the square on the \(y,\) we see that \(y^{2}+10 y\) corresponds to \((x+5)(x+5)\) or \((x+5)^{2}\). Here, we would need to add 25 to both sides to create a perfect square.

\[ \begin{aligned} x^{2}+6 x+9+y^{2}+10 y+25 &=-25+9+25 \\ x^{2}+6 x+9+y^{2}+10 y+25 &=9 \\ (x+3)^{2}+(y+5)^{2} &=9 \end{aligned} \]

So, the center of the circle is (-3,-5) and the radius is 3 Sometimes it is not so obvious what the values of \(h\) and \(k\) should be in completing the square. Consider the equation below: \[ x^{2}+20 x+y^{2}+30 y+15=0 \] If we look back at the examples for squaring binomials, we can see the pattern that relates the coefficient of the linear term to the values for \(h\) and \(k\) \[ \begin{array}{l} (x+3)^{2}=(x+3)(x+3)=x^{2}+6 x+9 \\ (x+4)^{2}=(x+4)(x+4)=x^{2}+8 x+16 \\ (x+5)^{2}=(x+5)(x+5)=x^{2}+10 x+25 \\ (x+6)^{2}=(x+6)(x+6)=x^{2}+12 x+36 \end{array} \] Notice that the coefficient of the linear term is always double the value of the numeral in the parentheses and the constant term is always that number squared.

\[ (x+n)^{2}=(x+n)(x+n)=x^{2}+2 n x+n^{2} \] So, given the problem above, \(x^{2}+20 x+y^{2}+30 y+15=0,\) first we can move the 15 to the right hand side of the equation and then complete the squares on the \(x\) and \(y\) variables. \[ \begin{array}{c} x^{2}+20 x+y^{2}+30 y=-15 \\ (x+?)^{2}+(y+?)^{2} \\ x^{2}+20 x+100+y^{2}+30 y+225=-15+100+225 \\ (x+10)^{2}+(y+15)^{2}=310 \end{array} \] We can now see that the center of the circle is at the point (-10,-15) and the radius of the circle is \(\sqrt{310} \approx 17.6\)

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Basic (Linear)
• Biquadratic
• Logarithmic
• Exponential
• Solve For x
• Scientific Calculator
• Scientific Notation Arithmetics
• Complex Numbers
• Cartesian to Polar
• Polar to Cartesian
• System of Inequalities
• Partial Fractions
• Periodicity
• Y Intercept
• X Intercepts
• Point Slope Form
• Step Functions
• Arithmetics
• Start Point
• Area & Perimeter
• Sides & Angles
• Law of Sines
• Law of Cosines
• Width & Length
• Volume & Surface
• Edges & Diagonal
• Volume & Radius
• Surface Area
• Radius & Diameter
• Volume & Height
• Circumference
• Eccentricity
• Trigonometric Equations
• Evaluate Functions
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• circle\:(0,\:0),\:r=5
• circle\:(1,\:4),\:d=10
• c(-1,\:-4),\:d=6
• (0,\:5),\:r=8

circle-equation-calculator

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&