problem solving on arithmetic sequence

Arithmetic Sequences Problems with Solutions

Arithmetic sequences are used throughout mathematics and applied to engineering, sciences, computer sciences, biology and finance problems. A set of problems and exercises involving arithmetic sequences, along with detailed solutions are presented.

Review of Arithmetic Sequences

The formula for the n th term a n of an arithmetic sequence with a common difference d and a first term a 1 is given by \[ a_n = a_1 + (n - 1) d \] The sum s n of the first n terms of an arithmetic sequence is defined by \[ s_n = a_1 + a_2 + a_3 + ... + a_n \] and is is given by \[ s_n = \dfrac{n (a_1 + a_n)}{2} \] Arithmetic Series Online Calculator . An online calculator to calculate the sum of the terms in an arithmetic sequence.

Problems with Solutions

The first term of an arithmetic sequence is equal to 6 and the common difference is equal to 3. Find a formula for the n th term and the value of the 50 th term Solution to Problem 1: Use the value of the common difference d = 3 and the first term a 1 = 6 in the formula for the n th term given above \( a_n = a_1 + (n - 1) d \\ = 6 + 3 (n - 1) \\ = 3 n + 3 \) The 50 th term is found by setting n = 50 in the above formula. \[ a_{50} = 3 (50) + 3 = 153 \]

The first term of an arithmetic sequence is equal to 200 and the common difference is equal to -10. Find the value of the 20 th term Solution to Problem 2: Use the value of the common difference d = -10 and the first term a 1 = 200 in the formula for the n th term given above and then apply it to the 20 th term a 20 = 200 + (-10) (20 - 1 ) = 10

An arithmetic sequence has a common difference equal to 10 and its 6 th term is equal to 52. Find its 15 th term. Solution to Problem 3: We use the n th term formula for the 6 th term, which is known, to write a 6 = 52 = a 1 + 10 (6 - 1 ) The above equation allows us to calculate a 1 . a 1 = 2 Now that we know the first term and the common difference, we use the n th term formula to find the 15 th term as follows. a 15 = 2 + 10 (15 - 1) = 142

An arithmetic sequence has a its 5 th term equal to 22 and its 15 th term equal to 62. Find its 100 th term. Solution to Problem 4: We use the n th term formula for the 5 th and 15 th terms to write a 5 = a 1 + (5 - 1 ) d = 22 a 15 = a 1 + (15 - 1 ) d = 62 We obtain a system of 2 linear equations where the unknown are a 1 and d. Subtract the right and left term of the two equations to obtain 62 - 22 = 14 d - 4 d Solve for d. d = 4 Now use the value of d in one of the equations to find a 1 . a 1 + (5 - 1 ) 4 = 22 Solve for a 1 to obtain. a 1 = 6 Now that we have calculated a 1 and d we use them in the n th term formula to find the 100 th formula. a 100 = 6 + 4 (100 - 1 )= 402

Find the sum of all the integers from 1 to 1000. Solution to Problem 5: The sequence of integers starting from 1 to 1000 is given by 1 , 2 , 3 , 4 , ... , 1000 The above sequence has 1000 terms. The first term is 1 and the last term is 1000 and the common difference is equal to 1. We have the formula that gives the sum of the first n terms of an arithmetic sequence knowing the first and last term of the sequence and the number of terms (see formula above). s 1000 = 1000 (1 + 1000) / 2 = 500500

Find the sum of the first 50 even positive integers. Solution to Problem 6: The sequence of the first 50 even positive integers is given by 2 , 4 , 6 , ... The above sequence has a first term equal to 2 and a common difference d = 2. We use the n th term formula to find the 50 th term a 50 = 2 + 2 (50 - 1) = 100 We now the first term and last term and the number of terms in the sequence, we now find the sum of the first 50 terms s 50 = 50 (2 + 100) / 2 = 2550

Find the sum of all positive integers, from 5 to 1555 inclusive, that are divisible by 5. Solution to Problem 7: The first few terms of a sequence of positive integers divisible by 5 is given by 5 , 10 , 15 , ... The above sequence has a first term equal to 5 and a common difference d = 5. We need to know the rank of the term 1555. We use the formula for the n th term as follows 1555 = a 1 + (n - 1 )d Substitute a 1 and d by their values 1555 = 5 + 5(n - 1 ) Solve for n to obtain n = 311 We now know that 1555 is the 311 th term, we can use the formula for the sum as follows s 311 = 311 (5 + 1555) / 2 = 242580

Find the sum S defined by \[ S = \sum_{n=1}^{10} (2n + 1 / 2) \] Solution to Problem 8: Let us first decompose this sum as follows \( S = \sum_{n=1}^{10} (2n + 1 / 2) \) \( = 2 \sum_{n=1}^{10} n + \sum_{n=1}^{10} (1/2) \) The term ∑ n is the sum of the first 10 positive integers. The 10 first positive integers make an arirhmetic sequence with first term equal to 1, it has n = 10 terms and its 10 th term is equal to 10. This sum is obtained using the formula s n = n (a 1 + a n ) / 2 as follows 10(1+10)/2 = 55 The term ∑ (1 / 2) is the addition of a constant term 10 times and is given by 10(1/2) = 5 The sum S is given by S = 2(55) + 5 = 115

Answer the following questions related to arithmetic sequences: a) Find a 20 given that a 3 = 9 and a 8 = 24 b) Find a 30 given that the first few terms of an arithmetic sequence are given by 6,12,18,... c) Find d given that a 1 = 10 and a 20 = 466 d) Find s 30 given that a 10 = 28 and a 20 = 58 e) Find the sum S defined by \[ S = \sum_{n=1}^{20}(3n - 1 / 2) \] f) Find the sum S defined by \[ S = \sum_{n=1}^{20}0.2 n + \sum_{j=21}^{40} 0.4 j \]

Solutions to Above Exercises

a) a 20 = 60 b) a 30 = 180 c) d = 24 d) s 30 = 1335 e) 1380 f) 286

More References and links

• Geometric Sequences Problems with Solutions
• math problems with detailed solutions
• Math Tutorials and Problems

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Arithmetic Sequence Problems with Solutions – Mastering Series Challenges

JUMP TO TOPIC

Arithmetic Sequences Practice Problems and Solutions

Calculating terms in an arithmetic sequence, solving problems involving arithmetic sequences.

An arithmetic sequence is a series where each term increases by a constant amount, known as the common difference . I’ve always been fascinated by how this simple pattern appears in many mathematical problems and real-world situations alike.

Understanding this concept is fundamental for students as it not only enhances their problem-solving skills but also introduces them to the systematic approach of sequences in math .

The first term of an arithmetic sequence sets the stage, while the common difference dictates the incremental steps that each subsequent term will follow. This can be mathematically expressed as $a_n = a_1 + (n – 1)d$.

Whether I’m calculating the nth term or the sum of terms within a sequence , these formulas are the tools that uncover solutions to countless arithmetic sequence problems. Join me in unraveling the beauty and simplicity of arithmetic sequences ; together, we might just discover why they’re considered the building blocks in the world of mathematics .

When I work with arithmetic sequences , I always keep in mind that they have a unique feature: each term is derived by adding a constant value, known as the common difference , to the previous term. Let’s explore this concept through a few examples and problems.

Example 1: Finding a Term in the Sequence

Given the first term, $a_1$ of an arithmetic sequence is 5 and the common difference ( d ) is 3, what is the 10th term $a_{10}$?

Here’s how I determine it: $a_{10} = a_1 + (10 – 1)d ] [ a_{10} = 5 + 9 \times 3 ] [ a_{10} = 5 + 27 ] [ a_{10} = 32$

So, the 10th term is 32.

Sequence A: If $a_1 = 2 $and ( d = 4 ), find $a_5$.

Sequence B: For $a_3 = 7 $ and $a_7 = 19$, calculate the common difference ( d ).

I calculate $a_5$ by using the formula: $a_n = a_1 + (n – 1)d $ $ a_5 = 2 + (5 – 1) \times 4 $ $a_5 = 2 + 16 $ $a_5 = 18$

To find ( d ), I use the formula: $a_n = a_1 + (n – 1)d$ Solving for ( d ), I rearrange the terms from $a_3$ and $a_7$: $d = \frac{a_7 – a_3}{7 – 3}$ $d = \frac{19 – 7}{4}$ $d = \frac{12}{4}$ [ d = 3 ]

Here’s a quick reference table summarizing the properties of arithmetic sequences :

Remember these properties to solve any arithmetic sequence problem effectively!

In an arithmetic sequence , each term after the first is found by adding a constant, known as the common difference ( d ), to the previous term. I find that a clear understanding of the formula helps immensely:

$a_n = a_1 + (n – 1)d$

Here, $a_n$ represents the $n^{th}$term, $a_1$ is the first term, and ( n ) is the term number.

Let’s say we need to calculate the fourth and fifth terms of a sequence where the first term $a_1 $ is 8 and the common difference ( d ) is 2. The explicit formula for this sequence would be $ a_n = 8 + (n – 1)(2) $.

To calculate the fourth term $a_4 $: $a_4 = 8 + (4 – 1)(2) = 8 + 6 = 14$

For the fifth term ( a_5 ), just add the common difference to the fourth term: $a_5 = a_4 + d = 14 + 2 = 16$

Here’s a table to illustrate these calculations:

Remember, the formula provides a direct way to calculate any term in the sequence, known as the explicit or general term formula. Just insert the term number ( n ) and you’ll get the value for $a_n$. I find this methodical approach simplifies the process and avoids confusion.

When I approach arithmetic sequences , I find it helpful to remember that they’re essentially lists of numbers where each term is found by adding a constant to the previous term. This constant is called the common difference, denoted as ( d ). For example, in the sequence 3, 7, 11, 15, …, the common difference is ( d = 4 ).

To articulate the ( n )th term of an arithmetic sequence, $a_n $, I use the fundamental formula:

$a_n = a_1 + (n – 1)d $

In this expression, $a_1$ represents the first term of the sequence.

If I’m solving a specific problem—let’s call it Example 1—I might be given $a_1 = 5 $and ( d = 3 ), and asked to find $a_4 $. I’d calculate it as follows:

$a_4 = 5 + (4 – 1) \times 3 = 5 + 9 = 14$

In applications involving arithmetic series, such as financial planning or scheduling tasks over weeks, the sum of the first ( n ) terms often comes into play. To calculate this sum, ( S_n ), I rely on the formula:

$S_n = \frac{n}{2}(a_1 + a_n)$

Now, if I’m asked to work through Example 3, where I need the sum of the first 10 terms of the sequence starting with 2 and having a common difference of 5, the process looks like this:

$a_{10} = 2 + (10 – 1) \times 5 = 47$ $S_{10} = \frac{10}{2}(2 + 47) = 5 \times 49 = 245$

Linear functions and systems of equations sometimes bear a resemblance to arithmetic sequences, such as when I need to find the intersection of sequence A and sequence B. This would involve setting the nth terms equal to each other and solving the resulting linear equation.

Occasionally, arithmetic sequences can be mistaken for geometric sequences , where each term is found by multiplying by a constant. It’s important to differentiate between them based on their definitions.

For exercises, it’s beneficial to practice finding nth terms, and sums , and even constructing sequences from given scenarios. This ensures a robust understanding when faced with a variety of problems involving arithmetic sequences .

In exploring the realm of arithmetic sequences , I’ve delved into numerous problems and their corresponding solutions. The patterns in these sequences—where the difference between consecutive terms remains constant—allow for straightforward and satisfying problem-solving experiences.

For a sequence with an initial term of $a_1 $ and a common difference of ( d ), the $n^{th}$term is given by $a_n = a_1 + (n – 1)d $.

I’ve found that this formula not only assists in identifying individual terms but also in predicting future ones. Whether calculating the $50^{th}$term or determining the sum of the first several terms, the process remains consistent and is rooted in this foundational equation.

In educational settings, arithmetic sequences serve as an excellent tool for reinforcing the core concepts of algebra and functions. Complexity varies from basic to advanced problems, catering to a range of skill levels. These sequences also reflect practical real-world applications, such as financial modeling and computer algorithms, highlighting the relevance beyond classroom walls.

Through practicing these problems, the elegance and power of arithmetic sequences in mathematical analysis become increasingly apparent. They exemplify the harmony of structure and progression in mathematics —a reminder of how simple rules can generate infinitely complex and fascinating patterns.

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

9.2 Arithmetic Sequences

Learning objectives.

In this section, you will:

• Find the common difference for an arithmetic sequence.
• Write terms of an arithmetic sequence.
• Use a recursive formula for an arithmetic sequence.
• Use an explicit formula for an arithmetic sequence.

Companies often make large purchases, such as computers and vehicles, for business use. The book-value of these supplies decreases each year for tax purposes. This decrease in value is called depreciation. One method of calculating depreciation is straight-line depreciation, in which the value of the asset decreases by the same amount each year.

As an example, consider a woman who starts a small contracting business. She purchases a new truck for $25,000. After five years, she estimates that she will be able to sell the truck for $8,000. The loss in value of the truck will therefore be $17,000, which is $3,400 per year for five years. The truck will be worth $21,600 after the first year; $18,200 after two years; $14,800 after three years; $11,400 after four years; and $8,000 at the end of five years. In this section, we will consider specific kinds of sequences that will allow us to calculate depreciation, such as the truck’s value.

Finding Common Differences

The values of the truck in the example are said to form an arithmetic sequence because they change by a constant amount each year. Each term increases or decreases by the same constant value called the common difference of the sequence. For this sequence, the common difference is –3,400.

The sequence below is another example of an arithmetic sequence. In this case, the constant difference is 3. You can choose any term of the sequence , and add 3 to find the subsequent term.

Arithmetic Sequence

An arithmetic sequence is a sequence that has the property that the difference between any two consecutive terms is a constant. This constant is called the common difference . If a 1 a 1 is the first term of an arithmetic sequence and d d is the common difference, the sequence will be:

Is each sequence arithmetic? If so, find the common difference.

• ⓐ { 1 , 2 , 4 , 8 , 16 , ... } { 1 , 2 , 4 , 8 , 16 , ... }
• ⓑ { − 3 , 1 , 5 , 9 , 13 , ... } { − 3 , 1 , 5 , 9 , 13 , ... }

Subtract each term from the subsequent term to determine whether a common difference exists.

The graph of each of these sequences is shown in Figure 1 . We can see from the graphs that, although both sequences show growth, a a is not linear whereas b b is linear. Arithmetic sequences have a constant rate of change so their graphs will always be points on a line.

If we are told that a sequence is arithmetic, do we have to subtract every term from the following term to find the common difference?

No. If we know that the sequence is arithmetic, we can choose any one term in the sequence, and subtract it from the subsequent term to find the common difference.

Is the given sequence arithmetic? If so, find the common difference.

Writing Terms of Arithmetic Sequences

Now that we can recognize an arithmetic sequence, we will find the terms if we are given the first term and the common difference. The terms can be found by beginning with the first term and adding the common difference repeatedly. In addition, any term can also be found by plugging in the values of n n and d d into formula below.

Given the first term and the common difference of an arithmetic sequence, find the first several terms.

• Add the common difference to the first term to find the second term.
• Add the common difference to the second term to find the third term.
• Continue until all of the desired terms are identified.
• Write the terms separated by commas within brackets.

Write the first five terms of the arithmetic sequence with a 1 = 17 a 1 = 17 and d = − 3 d = − 3 .

Adding − 3 − 3 is the same as subtracting 3. Beginning with the first term, subtract 3 from each term to find the next term.

The first five terms are { 17 , 14 , 11 , 8 , 5 } { 17 , 14 , 11 , 8 , 5 }

As expected, the graph of the sequence consists of points on a line as shown in Figure 2 .

List the first five terms of the arithmetic sequence with a 1 = 1 a 1 = 1 and d = 5 d = 5 .

Given any first term and any other term in an arithmetic sequence, find a given term.

• Substitute the values given for a 1 , a n , n a 1 , a n , n into the formula a n = a 1 + ( n − 1 ) d a n = a 1 + ( n − 1 ) d to solve for d . d .
• Find a given term by substituting the appropriate values for a 1 , n , a 1 , n , and d d into the formula a n = a 1 + ( n − 1 ) d . a n = a 1 + ( n − 1 ) d .

Given a 1 = 8 a 1 = 8 and a 4 = 14 a 4 = 14 , find a 5 a 5 .

The sequence can be written in terms of the initial term 8 and the common difference d d .

We know the fourth term equals 14; we know the fourth term has the form a 1 + 3 d = 8 + 3 d a 1 + 3 d = 8 + 3 d .

We can find the common difference d d .

Find the fifth term by adding the common difference to the fourth term.

Notice that the common difference is added to the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. The tenth term could be found by adding the common difference to the first term nine times or by using the equation a n = a 1 + ( n − 1 ) d . a n = a 1 + ( n − 1 ) d .

Given a 3 = 7 a 3 = 7 and a 5 = 17 a 5 = 17 , find a 2 a 2 .

Using Recursive Formulas for Arithmetic Sequences

Some arithmetic sequences are defined in terms of the previous term using a recursive formula . The formula provides an algebraic rule for determining the terms of the sequence. A recursive formula allows us to find any term of an arithmetic sequence using a function of the preceding term. Each term is the sum of the previous term and the common difference. For example, if the common difference is 5, then each term is the previous term plus 5. As with any recursive formula, the first term must be given.

Recursive Formula for an Arithmetic Sequence

The recursive formula for an arithmetic sequence with common difference d d is:

Given an arithmetic sequence, write its recursive formula.

• Subtract any term from the subsequent term to find the common difference.
• State the initial term and substitute the common difference into the recursive formula for arithmetic sequences.

Writing a Recursive Formula for an Arithmetic Sequence

Write a recursive formula for the arithmetic sequence .

The first term is given as −18 −18 . The common difference can be found by subtracting the first term from the second term.

Substitute the initial term and the common difference into the recursive formula for arithmetic sequences.

We see that the common difference is the slope of the line formed when we graph the terms of the sequence, as shown in Figure 3 . The growth pattern of the sequence shows the constant difference of 11 units.

Do we have to subtract the first term from the second term to find the common difference?

No. We can subtract any term in the sequence from the subsequent term. It is, however, most common to subtract the first term from the second term because it is often the easiest method of finding the common difference.

Write a recursive formula for the arithmetic sequence.

Using Explicit Formulas for Arithmetic Sequences

We can think of an arithmetic sequence as a function on the domain of the natural numbers; it is a linear function because it has a constant rate of change. The common difference is the constant rate of change, or the slope of the function. We can construct the linear function if we know the slope and the vertical intercept.

To find the y -intercept of the function, we can subtract the common difference from the first term of the sequence. Consider the following sequence.

The common difference is − 50 − 50 , so the sequence represents a linear function with a slope of − 50 − 50 . To find the y y -intercept, we subtract − 50 − 50 from 200 : 200 − ( − 50 ) = 200 + 50 = 250 200 : 200 − ( − 50 ) = 200 + 50 = 250 . You can also find the y y -intercept by graphing the function and determining where a line that connects the points would intersect the vertical axis. The graph is shown in Figure 4 .

Recall the slope-intercept form of a line is y = m x + b . y = m x + b . When dealing with sequences, we use a n a n in place of y y and n n in place of x . x . If we know the slope and vertical intercept of the function, we can substitute them for m m and b b in the slope-intercept form of a line. Substituting − 50 − 50 for the slope and 250 250 for the vertical intercept, we get the following equation:

We do not need to find the vertical intercept to write an explicit formula for an arithmetic sequence. Another explicit formula for this sequence is a n = 200 − 50 ( n − 1 ) a n = 200 − 50 ( n − 1 ) , which simplifies to a n = − 50 n + 250. a n = − 50 n + 250.

Explicit Formula for an Arithmetic Sequence

An explicit formula for the n th n th term of an arithmetic sequence is given by

Given the first several terms for an arithmetic sequence, write an explicit formula.

• Find the common difference, a 2 − a 1 . a 2 − a 1 .
• Substitute the common difference and the first term into a n = a 1 + d ( n − 1 ) . a n = a 1 + d ( n − 1 ) .

Writing the n th Term Explicit Formula for an Arithmetic Sequence

Write an explicit formula for the arithmetic sequence.

The common difference can be found by subtracting the first term from the second term.

The common difference is 10. Substitute the common difference and the first term of the sequence into the formula and simplify.

The graph of this sequence, represented in Figure 5 , shows a slope of 10 and a vertical intercept of − 8 − 8 .

Write an explicit formula for the following arithmetic sequence.

Finding the Number of Terms in a Finite Arithmetic Sequence

Explicit formulas can be used to determine the number of terms in a finite arithmetic sequence. We need to find the common difference, and then determine how many times the common difference must be added to the first term to obtain the final term of the sequence.

Given the first three terms and the last term of a finite arithmetic sequence, find the total number of terms.

• Find the common difference d . d .
• Substitute the common difference and the first term into a n = a 1 + d ( n – 1 ) . a n = a 1 + d ( n – 1 ) .
• Substitute the last term for a n a n and solve for n . n .

Find the number of terms in the finite arithmetic sequence .

The common difference is − 7 − 7 . Substitute the common difference and the initial term of the sequence into the n th n th term formula and simplify.

Substitute − 41 − 41 for a n a n and solve for n n

There are eight terms in the sequence.

Find the number of terms in the finite arithmetic sequence.

Solving Application Problems with Arithmetic Sequences

In many application problems, it often makes sense to use an initial term of a 0 a 0 instead of a 1 . a 1 . In these problems, we alter the explicit formula slightly to account for the difference in initial terms. We use the following formula:

A five-year old child receives an allowance of $1 each week. His parents promise him an annual increase of $2 per week.

• ⓐ Write a formula for the child’s weekly allowance in a given year.
• ⓑ What will the child’s allowance be when he is 16 years old?

The situation can be modeled by an arithmetic sequence with an initial term of 1 and a common difference of 2.

Let A A be the amount of the allowance and n n be the number of years after age 5. Using the altered explicit formula for an arithmetic sequence we get:

We can find the number of years since age 5 by subtracting.

We are looking for the child’s allowance after 11 years. Substitute 11 into the formula to find the child’s allowance at age 16.

The child’s allowance at age 16 will be $23 per week.

A woman decides to go for a 10-minute run every day this week and plans to increase the time of her daily run by 4 minutes each week. Write a formula for the time of her run after n weeks. How long will her daily run be 8 weeks from today?

Access this online resource for additional instruction and practice with arithmetic sequences.

• Arithmetic Sequences

9.2 Section Exercises

What is an arithmetic sequence?

How is the common difference of an arithmetic sequence found?

How do we determine whether a sequence is arithmetic?

What are the main differences between using a recursive formula and using an explicit formula to describe an arithmetic sequence?

Describe how linear functions and arithmetic sequences are similar. How are they different?

For the following exercises, find the common difference for the arithmetic sequence provided.

{ 5 , 11 , 17 , 23 , 29 , ... } { 5 , 11 , 17 , 23 , 29 , ... }

{ 0 , 1 2 , 1 , 3 2 , 2 , ... } { 0 , 1 2 , 1 , 3 2 , 2 , ... }

For the following exercises, determine whether the sequence is arithmetic. If so find the common difference.

{ 11.4 , 9.3 , 7.2 , 5.1 , 3 , ... } { 11.4 , 9.3 , 7.2 , 5.1 , 3 , ... }

{ 4 , 16 , 64 , 256 , 1024 , ... } { 4 , 16 , 64 , 256 , 1024 , ... }

For the following exercises, write the first five terms of the arithmetic sequence given the first term and common difference.

a 1 = −25 a 1 = −25 , d = −9 d = −9

a 1 = 0 a 1 = 0 , d = 2 3 d = 2 3

For the following exercises, write the first five terms of the arithmetic series given two terms.

a 1 = 17 , a 7 = − 31 a 1 = 17 , a 7 = − 31

a 13 = − 60 , a 33 = − 160 a 13 = − 60 , a 33 = − 160

For the following exercises, find the specified term for the arithmetic sequence given the first term and common difference.

First term is 3, common difference is 4, find the 5 th term.

First term is 4, common difference is 5, find the 4 th term.

First term is 5, common difference is 6, find the 8 th term.

First term is 6, common difference is 7, find the 6 th term.

First term is 7, common difference is 8, find the 7 th term.

For the following exercises, find the first term given two terms from an arithmetic sequence.

Find the first term or a 1 a 1 of an arithmetic sequence if a 6 = 12 a 6 = 12 and a 14 = 28. a 14 = 28.

Find the first term or a 1 a 1 of an arithmetic sequence if a 7 = 21 a 7 = 21 and a 15 = 42. a 15 = 42.

Find the first term or a 1 a 1 of an arithmetic sequence if a 8 = 40 a 8 = 40 and a 23 = 115. a 23 = 115.

Find the first term or a 1 a 1 of an arithmetic sequence if a 9 = 54 a 9 = 54 and a 17 = 102. a 17 = 102.

Find the first term or a 1 a 1 of an arithmetic sequence if a 11 = 11 a 11 = 11 and a 21 = 16. a 21 = 16.

For the following exercises, find the specified term given two terms from an arithmetic sequence.

a 1 = 33 a 1 = 33 and a 7 = − 15. a 7 = − 15. Find a 4 . a 4 .

a 3 = − 17.1 a 3 = − 17.1 and a 10 = − 15.7. a 10 = − 15.7. Find a 21 . a 21 .

For the following exercises, use the recursive formula to write the first five terms of the arithmetic sequence.

a 1 = 39 ; a n = a n − 1 − 3 a 1 = 39 ; a n = a n − 1 − 3

a 1 = − 19 ; a n = a n − 1 − 1.4 a 1 = − 19 ; a n = a n − 1 − 1.4

For the following exercises, write a recursive formula for each arithmetic sequence.

a = { 40 , 60 , 80 , ... } a = { 40 , 60 , 80 , ... }

a = { 17 , 26 , 35 , ... } a = { 17 , 26 , 35 , ... }

a = { − 1 , 2 , 5 , ... } a = { − 1 , 2 , 5 , ... }

a = { 12 , 17 , 22 , ... } a = { 12 , 17 , 22 , ... }

a = { − 15 , − 7 , 1 , ... } a = { − 15 , − 7 , 1 , ... }

a = { 8.9 , 10.3 , 11.7 , ... } a = { 8.9 , 10.3 , 11.7 , ... }

a = { − 0.52 , − 1.02 , − 1.52 , ... } a = { − 0.52 , − 1.02 , − 1.52 , ... }

a = { 1 5 , 9 20 , 7 10 , ... } a = { 1 5 , 9 20 , 7 10 , ... }

a = { − 1 2 , − 5 4 , − 2 , ... } a = { − 1 2 , − 5 4 , − 2 , ... }

a = { 1 6 , − 11 12 , − 2 , ... } a = { 1 6 , − 11 12 , − 2 , ... }

For the following exercises, write a recursive formula for the given arithmetic sequence, and then find the specified term.

a = { 7 ,  4 ,  1 ,  ... } ; a = { 7 ,  4 ,  1 ,  ... } ; Find the 17 th term.

a = { 4 ,  11 ,  18 ,  ... } ; a = { 4 ,  11 ,  18 ,  ... } ; Find the 14 th term.

a = { 2 ,  6 ,  10 ,  ... } ; a = { 2 ,  6 ,  10 ,  ... } ; Find the 12 th term.

For the following exercises, use the explicit formula to write the first five terms of the arithmetic sequence.

a n = 24 − 4 n a n = 24 − 4 n

a n = 1 2 n − 1 2 a n = 1 2 n − 1 2

For the following exercises, write an explicit formula for each arithmetic sequence.

a = { 3 , 5 , 7 , ... } a = { 3 , 5 , 7 , ... }

a = { 32 , 24 , 16 , ... } a = { 32 , 24 , 16 , ... }

a = { − 5 ,  95 ,  195 ,  ... } a = { − 5 ,  95 ,  195 ,  ... }

a = { −17 ,  −217 ,  −417 , ... } a = { −17 ,  −217 ,  −417 , ... }

a = { 1.8 ,  3.6 ,  5.4 ,  ... } a = { 1.8 ,  3.6 ,  5.4 ,  ... }

a = { −18.1 , −16.2 , −14.3 , ... } a = { −18.1 , −16.2 , −14.3 , ... }

a = { 15.8 , 18.5 , 21.2 , ... } a = { 15.8 , 18.5 , 21.2 , ... }

a = { 1 3 , − 4 3 , −3 ,  ... } a = { 1 3 , − 4 3 , −3 ,  ... }

a = { 0 , 1 3 , 2 3 , ... } a = { 0 , 1 3 , 2 3 , ... }

a = { − 5 , − 10 3 , − 5 3 , … } a = { − 5 , − 10 3 , − 5 3 , … }

For the following exercises, find the number of terms in the given finite arithmetic sequence.

a = { 3 , − 4 , − 11 ,  ... , − 60 } a = { 3 , − 4 , − 11 ,  ... , − 60 }

a = { 1.2 , 1.4 , 1.6 , ... , 3.8 } a = { 1.2 , 1.4 , 1.6 , ... , 3.8 }

a = { 1 2 , 2 , 7 2 , ... , 8 } a = { 1 2 , 2 , 7 2 , ... , 8 }

For the following exercises, determine whether the graph shown represents an arithmetic sequence.

For the following exercises, use the information provided to graph the first 5 terms of the arithmetic sequence.

a 1 = 0 , d = 4 a 1 = 0 , d = 4

a 1 = 9 ; a n = a n − 1 − 10 a 1 = 9 ; a n = a n − 1 − 10

a n = − 12 + 5 n a n = − 12 + 5 n

For the following exercises, follow the steps to work with the arithmetic sequence a n = 3 n − 2 a n = 3 n − 2 using a graphing calculator:

• Select SEQ in the fourth line
• Select DOT in the fifth line
• Press [ENTER]
• n Min n Min is the first counting number for the sequence. Set n Min = 1 n Min = 1
• u ( n ) u ( n ) is the pattern for the sequence. Set u ( n ) = 3 n − 2 u ( n ) = 3 n − 2
• u ( n Min) u ( n Min) is the first number in the sequence. Set u ( n Min) = 1 u ( n Min) = 1
• Set TblStart = 1 TblStart = 1
• Set Δ Tbl = 1 Δ Tbl = 1
• Set Indpnt: Auto and Depend: Auto
• Press [2ND] then [GRAPH] to go to the TABLE

What are the first seven terms shown in the column with the heading u ( n ) ? u ( n ) ?

Use the scroll-down arrow to scroll to n = 50. n = 50. What value is given for u ( n ) ? u ( n ) ?

Press [WINDOW] . Set n Min = 1 n Min = 1 , n Max = 5 n Max = 5 , x Min = 0 x Min = 0 , x Max = 6 x Max = 6 , y Min = − 1 y Min = − 1 , and y Max = 14. y Max = 14. Then press [GRAPH] . Graph the sequence as it appears on the graphing calculator.

For the following exercises, follow the steps given above to work with the arithmetic sequence a n = 1 2 n + 5 a n = 1 2 n + 5 using a graphing calculator.

What are the first seven terms shown in the column with the heading u ( n ) u ( n ) in the TABLE feature?

Graph the sequence as it appears on the graphing calculator. Be sure to adjust the WINDOW settings as needed.

Give two examples of arithmetic sequences whose 4 th terms are 9. 9.

Give two examples of arithmetic sequences whose 10 th terms are 206. 206.

Find the 5 th term of the arithmetic sequence { 9 b , 5 b , b , … } . { 9 b , 5 b , b , … } .

Find the 11 th term of the arithmetic sequence { 3 a − 2 b , a + 2 b , − a + 6 b … } . { 3 a − 2 b , a + 2 b , − a + 6 b … } .

At which term does the sequence { 5.4 , 14.5 , 23.6 , ... } { 5.4 , 14.5 , 23.6 , ... } exceed 151?

At which term does the sequence { 17 3 , 31 6 , 14 3 , ... } { 17 3 , 31 6 , 14 3 , ... } begin to have negative values?

For which terms does the finite arithmetic sequence { 5 2 , 19 8 , 9 4 , ... , 1 8 } { 5 2 , 19 8 , 9 4 , ... , 1 8 } have integer values?

Write an arithmetic sequence using a recursive formula. Show the first 4 terms, and then find the 31 st term.

Write an arithmetic sequence using an explicit formula. Show the first 4 terms, and then find the 28 th term.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/9-2-arithmetic-sequences

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

14.3: Arithmetic Sequences

• Last updated
• Save as PDF
• Page ID 50039

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Determine if a sequence is arithmetic
• Find the general term (\(n\)th term) of an arithmetic sequence
• Find the sum of the first \(n\) terms of an arithmetic sequence

Before you get started, take this readiness quiz.

• Evaluate \(4n−1\) for the integers \(1, 2, 3\), and \(4\). If you missed this problem, review Example 1.6.
• Solve the system of equations: \(\left\{\begin{array}{l}{x+y=7} \\ {3 x+4 y=23}\end{array}\right.\). If you missed this problem, review Example 4.9.
• If \(f(n)=\frac{n}{2}(3 n+5)\), find \(f(1)+f(20)\). If you missed this problem, review Example 3.49.

Determine if a Sequence is Arithmetic

The last section introduced sequences and now we will look at two specific types of sequences that each have special properties. In this section we will look at arithmetic sequences and in the next section, geometric sequences.

An arithmetic sequence is a sequence where the difference between consecutive terms is constant. The difference between consecutive terms in an arithmetic sequence, a_{n}-a_{n-1}, is \(d\), the common difference , for \(n\) greater than or equal to two.

Definition \(\PageIndex{1}\)

An arithmetic sequence is a sequence where the difference between consecutive terms is always the same.

The difference between consecutive terms, a_{n}-a_{n-1}, is \(d\), the common difference , for \(n\) greater than or equal to two.

Example \(\PageIndex{1}\)

Determine if each sequence is arithmetic. If so, indicate the common difference.

• \(5,9,13,17,21,25, \dots\)
• \(4,9,12,17,20,25, \dots\)
• \(10,3,-4,-11,-18,-25, \dots\)

To determine if the sequence is arithmetic, we find the difference of the consecutive terms shown.

a. \(\begin{array}{cccccc}{5,} & {9,} & {13,} & {17} & {21,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-5} & {13-9} & {17-13} & {21-17} & {25-21} \\ & {4} & {4} & {4} & {4}&{4}\end{array}\)

The sequence is arithmetic. The common difference is \(d=4\).

b. \(\begin{array}{cccccc}{4,} & {9,} & {12,} & {17} & {20,} & {25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {9-4} & {12-9} & {17-12} & {20-17} & {25-20} \\ & {2} & {3} & {5} & {3}&{5}\end{array}\)

The sequence is not arithmetic as all the differences between the consecutive terms are not the same. There is no common difference.

c. \(\begin{array}{cccccc}{10,} & {3,} & {-4,} & {-11} & {-18,} & {-25, \ldots} \\ {\text { Find the difference of the consecutive terms.}} & {3-10} & {-4-3} & {-11-(-4)} & {-18-(-11)} & {-25-(-18)} \\ & {-7} & {-7} & {-7} & {-7}&{-7}\end{array}\)

The sequence is arithmetic. The common difference is \(d=-7\).

Exercise \(\PageIndex{1}\)

• \(9,20,31,42,53,64, \dots\)
• \(12,6,0,-6,-12,-18, \dots\)
• \(7,1,10,4,13,7, \dots\)
• The sequence is arithmetic with common difference \(d=11\).
• The sequence is arithmetic with common difference \(d=-6\).
• The sequence is not arithmetic as all the differences between the consecutive terms are not the same.

Exercise \(\PageIndex{2}\)

• \(-4,4,2,10,8,16, \dots\)
• \(-3,-1,1,3,5,7, \dots\)
• \(7,2,-3,-8,-13,-18, \dots\)
• The sequence is arithmetic with common difference \(d=2\).
• The sequence is arithmetic with common difference \(d=−5\).

If we know the first term, \(a_{1}\), and the common difference, \(d\), we can list a finite number of terms of the sequence.

Example \(\PageIndex{2}\)

Write the first five terms of the sequence where the first term is \(5\) and the common difference is \(d=−6\).

We start with the first term and add the common difference. Then we add the common difference to that result to get the next term, and so on.

\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {5} & {5+(-6)} & {-1+(-6)} & {-7+(-6)} & {-13+(-6)} \\ {}&{-1} & {-7} & {-13} & {-19}\end{array}\)

The sequence is \(5,-1,-7,-13,-19, \dots\)

Exercise \(\PageIndex{3}\)

Write the first five terms of the sequence where the first term is \(7\) and the common difference is \(d=−4\).

\(7,3,-1,-5,-9, \dots\)

Exercise \(\PageIndex{4}\)

Write the first five terms of the sequence where the first term is \(11\) and the common difference is \(d=−8\).

\(11,3,-5,-13,-21, \dots\)

Find the General Term (\(n\)th Term) of an Arithmetic Sequence

Just as we found a formula for the general term of a sequence, we can also find a formula for the general term of an arithmetic sequence.

Let’s write the first few terms of a sequence where the first term is \(a_{1}\) and the common difference is \(d\). We will then look for a pattern.

As we look for a pattern we see that each term starts with \(a_{1}\).

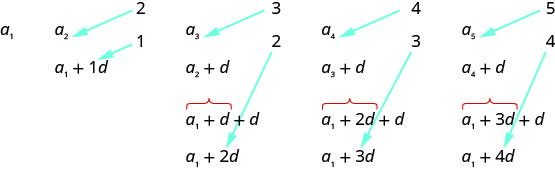
The first term adds \(0d\) to the \(a_{1}\), the second term adds \(1d\), the third term adds \(2d\), the fourth term adds \(3d\), and the fifth term adds \(4d\). The number of \(ds\) that were added to \(a_{1}\) is one less than the number of the term. This leads us to the following

\(a_{n}=a_{1}+(n-1) d\)

Definition \(\PageIndex{2}\)

The general term of an arithmetic sequence with first term \(a_{1}\) and the common difference \(d\) is

We will use this formula in the next example to find the 15 th term of a sequence.

Example \(\PageIndex{3}\)

Find the fifteenth term of a sequence where the first term is \(3\) and the common difference is \(6\).

\(\begin{array}{cc}{\text{To find the fifteenth term, }a_{15}\text{, use the formula with } a_{1}=3 \:\text{and} \:d=6.}&{a_{n}=a_{1}+(n-1) d} \\ {\text{Substitute in the values.}}&{a_{15}=3+(15-1) 6} \\{\text{Simplify.}}& {a_{15}=3+(14) 6} \\ {}&{a_{15}=87}\end{array}\)

Exercise \(\PageIndex{5}\)

Find the twenty-seventh term of a sequence where the first term is \(7\) and the common difference is \(9\).

Exercise \(\PageIndex{6}\)

Find the eighteenth term of a sequence where the first term is \(13\) and the common difference is \(−7\).

Sometimes we do not know the first term and we must use other given information to find it before we find the requested term.

Example \(\PageIndex{4}\)

Find the twelfth term of a sequence where the seventh term is \(10\) and the common difference is \(−2\). Give the formula for the general term.

To first find the first term, \(a_{1}\), use the formula with \(a_{7}=10\),\(n=7\), and \(d=−2\). Substitute in the values. Simplify.

\(a_{n}=a_{1}+(n-1) d\) \(10=a_{1}+(7-1)(-2)\) \(10=a_{1}+(6)(-2)\) \(10=a_{1}-12\) \(a_{1}=22\)

Find the twelfth term, \(a_{12}\),using the formula with \(a_{1}=22\), \(n=12\), and \(d=-2\). Substitute in the values. Simplify.

\(a_{n}=a_{1}+(n-1) d\) \(a_{12}=22+(12-1)(-2)\) \(a_{12}=22+(11)(-2)\) \(a_{12}=0\)

The twelfth term of the sequence is \(0, a_{12}=0\)

To find the general term, substitute the values into the formula.

\(a_{n}=a_{1}+(n-1) d\) \(a_{n}=22+(n-1)(-2)\) \(a_{n}=22-2 n+2\)

Answer : The general term is \(a_{n}=-2 n+24\)

Exercise \(\PageIndex{7}\)

Find the eleventh term of a sequence where the ninth term is \(8\) and the common difference is \(−3\). Give the formula for the general term.

\(a_{11}=2 .\) The general term is \(a_{n}=-3 n+35\)

Exercise \(\PageIndex{8}\)

Find the nineteenth term of a sequence where the fifth term is \(1\) and the common difference is \(−4\).Give the formula for the general term.

\(a_{19}=-55 .\) The general term is \(a_{n}=-4 n+21\)

Sometimes the information given leads us to two equations in two unknowns. We then use our methods for solving systems of equations to find the values needed.

Example \(\PageIndex{5}\)

Find the first term and common difference of a sequence where the fifth term is \(19\) and the eleventh term is \(37\). Give the formula for the general term.

Since we know two terms, we can make a system of equations using the formula for the general term.

The general term of the sequence is \(a_{n}=3n+4\).

Exercise \(\PageIndex{9}\)

Find the first term and common difference of a sequence where the fourth term is \(17\) and the thirteenth term is \(53\). Give the formula for the general term.

\(a_{1}=5, d=4 .\) The general term is \(a_{n}=4 n+1\).

Exercise \(\PageIndex{10}\)

Find the first term and common difference of a sequence where the third term is \(2\) and the twelfth term is \(−25\). Give the formula for the general term.

\(a_{1}=8, d=-3 .\) The general term is \(a_{n}=-3 n+11\).

Find the Sum of the First \(n\) Terms of an Arithmetic Sequence

As with the general sequences, it is often useful to find the sum of an arithmetic sequence. The sum, \(S_{n}\), of the first \(n\) terms of any arithmetic sequence is written as \(S_{n} =a_{1} +a_{2} +a_{3} +\ldots +a_{n}\). To find the sum by merely adding all the terms can be tedious. So we can also develop a formula to find the sum of a sequence using the first and last term of the sequence.

We can develop this new formula by first writing the sum by starting with the first term, \(a_{1}\), and keep adding a \(d\) to get the next term as:

\(S_{n}=a_{1}+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n}\).

We can also reverse the order of the terms and write the sum by starting with \(a_{n}\) and keep subtracting \(d\) to get the next term as

\(S_{n}=a_{n}+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1}\).

If we add these two expressions for the sum of the first \(n\) terms of an arithmetic sequence, we can derive a formula for the sum of the first \(n\) terms of any arithmetic series.

\(\begin{aligned} &S_{n}= a_{1} \quad+\left(a_{1}+d\right)+\left(a_{1}+2 d\right)+\ldots+a_{n} \\+&S_{n} =a_{n} \quad+\left(a_{n}-d\right)+\left(a_{n}-2 d\right)+\ldots+a_{1} \\ \hline \\ &2S_{n}=(a_{1}+a_{n})+(a_{1}+a_{n})+(a_{1}+a_{n})+\dots+(a_{1}+a_{n}) \end{aligned}\)

Because there are \(n\) sums of \((a_{1}+a_{n})\) on the right side of the equation, we rewrite the right side as \(n(a_{1}+a_{n})\).

\(2 S_{n}=n\left(a_{1}+a_{n}\right)\)

We divide by two to solve for \(S_{n}\).

\(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\)

This give us a general formula for the sum of the first \(n\) terms of an arithmetic sequence.

Definition \(\PageIndex{3}\)

The sum, \(S_{n}\), of the first \(n\) terms of an arithmetic sequence is

where \(a_{1}\) is the first term and \(a_{n}\) is the \(n\)th term.

We apply this formula in the next example where the first few terms of the sequence are given.

Example \(\PageIndex{6}\)

Find the sum of the first \(30\) terms of the arithmetic sequence: \(8, 13, 18, 23, 28, …\)

To find the sum, we will use the formula \(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). We know \(a_{1}=8, d=5\) and \(n=30\), but we need to find \(a_{n}\) in order to use the sum formula.

Find \(a_{n}\) where \(a_{1}=8, d=5\) and \(n=30\). Simplify.

\(\begin{aligned} a_{n} &=a_{1}+(n-1) d \\ a_{30} &=8+(30-1) 5 \\ a_{30} &=8+(29) 5 \\ a_{30} &=153 \end{aligned}\)

Knowing \(a_{1}=8, n=30\), and \(a_{30}=153\), use the sum formula. Substitute in the values. Simplify. Simplify.

\(\begin{aligned} S_{n} &=\frac{n}{2}\left(a_{1}+a_{n}\right) \\ S_{30} &=\frac{30}{2}(8+153) \\ S_{30} &=15(161) \\ S_{30} &=2,415 \end{aligned}\)

Exercise \(\PageIndex{11}\)

Find the sum of the first \(30\) terms of the arithmetic sequence: \(5, 9, 13, 17, 21, …\)

Exercise \(\PageIndex{12}\)

Find the sum of the first \(30\) terms of the arithmetic sequence: \(7, 10, 13, 16, 19, …\)

In the next example, we are given the general term for the sequence and are asked to find the sum of the first \(50\) terms.

Example \(\PageIndex{7}\)

Find the sum of the first \(50\) terms of the arithmetic sequence whose general term is \(a_{n}=3n−4\).

To find the sum, we will use the formula \(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). We know \(n=50\), but we need to find \(a_{1}\) and \(a_{n}\) in order to use the sum formula.

Exercise \(\PageIndex{13}\)

Find the sum of the first \(50\) terms of the arithmetic sequence whose general term is \(a_{n}=2n−5\).

Exercise \(\PageIndex{14}\)

Find the sum of the first \(50\) terms of the arithmetic sequence whose general term is \(a_{n}=4n+3\).

In the next example we are given the sum in summation notation. To add all the terms would be tedious, so we extract the information needed to use the formula to find the sum of the first \(n\) terms.

Example \(\PageIndex{8}\)

Find the sum: \(\sum_{i=1}^{25}(4 i+7)\).

To find the sum, we will use the formula \(S_{n}=\frac{n}{2}\left(a_{1}+a_{n}\right)\). We know \(n=25\), but we need to find \(a_{1}\) and \(a_{n}\) in order to use the sum formula.

Exercise \(\PageIndex{15}\)

Find the sum: \(\sum_{i=1}^{30}(6 i-4)\).

Exercise \(\PageIndex{16}\)

Find the sum: \(\sum_{i=1}^{35}(5 i-3)\).

Access these online resources for additional instruction and practice with arithmetic sequences

• Arithmetic Sequences
• Arithmetic Sequences: A Formula for the ‘n-th’ Term
• Arithmetic Series

Key Concepts

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Arithmetic Sequences? (+FREE Worksheet!)

Do you want to know how to solve Arithmetic Sequences problems? you can do it in few simple and easy steps.

Related Topics

• How to Solve Finite Geometric Series
• How to Solve Infinite Geometric Series
• How to Solve Geometric Sequences

Step by step guide to solve Arithmetic Sequences problems

• A sequence of numbers such that the difference between the consecutive terms is constant is called arithmetic sequence. For example, the sequence \(6, 8, 10, 12, 14\), … is an arithmetic sequence with common difference of \(2\).
• To find any term in an arithmetic sequence use this formula: \(\color{blue}{x_{n}=a+d(n-1)}\)
• \(a =\) the first term ,\(d =\) the common difference between terms , \(n =\) number of items

Arithmetic Sequences – Example 1:

Find the first three terms of the sequence. \(a_{17}=38,d=3\)

First, we need to find \(a_{1}\) or a. Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(a_{8}=38\), then \(n=8\). Rewrite the formula and put the values provided: \(x_{n}=a+d(n-1)→38=a+3(3-1)=a+6\), now solve for \(a\). \(38=a+6→a=38-6=32\), First three terms: \(32,35,38\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Arithmetic sequences – example 2:.

Given the first term and the common difference of an arithmetic sequence find the first five terms. \(a_{1}=18,d=2\)

Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(n=1\) then: \(x_{1}=18+2(1)→x_{1}=18\) First five terms: \(18,20,22,24,26\)

Arithmetic Sequences – Example 3:

Given the first term and the common difference of an arithmetic sequence find the first five terms. \(a_{1}=24,d=2\)

Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(n=1\) then: \(x_{1}=22+2(1)→x_{1}=24\) First five terms: \(24,26,28,30,32\)

The Best Book to Help You Ace Pre-Algebra

Pre-Algebra for Beginners The Ultimate Step by Step Guide to Preparing for the Pre-Algebra Test

Arithmetic sequences – example 4:.

Find the first five terms of the sequence. \(a_{17}=152,d=4\)

First, we need to find \(a_{1}\) or \(a\). Use arithmetic sequence formula: \(\color{blue}{x_{n}=a+d(n-1)}\) If \(a_{17}=152\), then \(n=17\). Rewrite the formula and put the values provided: \(x_{n}=a+d(n-1)→152=a+4(17-1)=a+64\), now solve for \(a\). \(152=a+64→a=152-64=88\), First five terms: \(88,92,96,100,104\)

Given the first term and the common difference of an arithmetic sequence find the first five terms and the explicit formula.

• \(\color{blue}{a_{1} = 24, d = 2}\)
• \(\color{blue}{a_{1} = –15, d = – 5}\)
• \(\color{blue}{a_{1} = 18, d = 10}\)
• \(\color{blue}{a_{1 }= –38, d = –100}\)

Download Arithmetic Sequences Worksheet

• First Five Terms \(\color{blue}{: 24, 26, 28, 30, 32, Explicit: a_{n} = 22 + 2n}\)
• First Five Terms \(\color{blue}{: –15, –20, –25, –30, –35, Explicit: a_{n} = –10 – 5n}\)
• First Five Terms \(\color{blue}{: 18, 28, 38, 48, 58, Explicit: a_{n} = 8 + 10n}\)
• First Five Terms \(\color{blue}{: –38, –138, –238, –338, –438, Explicit: a_{n} = 62 – 100n}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 4 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• How to Compare Savings Options
• 5th Grade Georgia Milestones Assessment System Math Practice Test Questions
• 7th Grade RICAS Math Worksheets: FREE & Printable
• The Ultimate 4th Grade STAAR Math Course (+FREE Worksheets)
• Unlocking Solutions: A Step-by-Step Guide to How to Solve Non-linear Equations by Substitution
• 10 Most Common ParaPro Math Questions
• Top 10 Tips You MUST Know to Retake the CLEP College Algebra
• Money and Decimals Relation: A Step-by-Step Guide
• Amounts of Money Comparison
• How to Remove Ambiguity in Infinite Limits

What people say about "How to Solve Arithmetic Sequences? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra i for beginners the ultimate step by step guide to acing algebra i, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Arithmetic Sequence

The arithmetic sequence is the sequence where the common difference remains constant between any two successive terms. Let us recall what is a sequence. A sequence is a collection of numbers that follow a pattern. For example, the sequence 1, 6, 11, 16, … is an arithmetic sequence because there is a pattern where each number is obtained by adding 5 to its previous term. We have two arithmetic sequence formulas.

• The formula for finding n th term of an arithmetic sequence
• The formula to find the sum of first n terms of an arithmetic sequence

If we want to find any term in the arithmetic sequence then we can use the arithmetic sequence formula. Let us learn the definition of an arithmetic sequence and arithmetic sequence formulas along with derivations and a lot more examples for a better understanding.

What is an Arithmetic Sequence?

An arithmetic sequence is defined in two ways. It is a "sequence where the differences between every two successive terms are the same" (or) In an arithmetic sequence, "every term is obtained by adding a fixed number (positive or negative or zero) to its previous term". The following is an arithmetic sequence as every term is obtained by adding a fixed number 4 to its previous term.

Arithmetic Sequence Example

Consider the sequence 3, 6, 9, 12, 15, .... is an arithmetic sequence because every term is obtained by adding a constant number (3) to its previous term.

• The first term, a = 3
• The common difference, d = 6 - 3 = 9 - 6 = 12 - 9 = 15 - 12 = ... = 3

Thus, an arithmetic sequence can be written as a, a + d, a + 2d, a + 3d, .... Let us verify this pattern for the above example.

a, a + d, a + 2d, a + 3d, a + 4d, ... = 3, 3 + 3, 3 + 2(3), 3 + 3(3), 3 + 4(3),... = 3, 6, 9, 12,15,....

A few more examples of an arithmetic sequence are:

• 5, 8, 11, 14, ...
• 80, 75, 70, 65, 60, ...
• π/2, π, 3π/2, 2π, ....
• -√2, -2√2, -3√2, -4√2, ...

Arithmetic Sequence Formula

The first term of an arithmetic sequence is a, its common difference is d, n is the number of terms. The general form of the AP is a, a+d, a+2d, a+3d,......up to n terms. We have different formulas associated with an arithmetic sequence used to calculate the n th term, the sum of n terms of an AP, or the common difference of a given arithmetic sequence.

The arithmetic sequence formula is given as,

• N th Term: a n = a + (n-1)d
• S n = (n/2) [2a + (n - 1)d]
• d = a n - a n-1

Nth Term of Arithmetic Sequence

The n th term of an arithmetic sequence a 1 , a 2 , a 3 , ... is given by a n = a 1 + (n - 1) d . This is also known as the general term of the arithmetic sequence. This directly follows from the understanding that the arithmetic sequence a 1 , a 2 , a 3 , ... = a 1 , a 1 + d, a 1 + 2d, a 1 + 3d,... The following table shows some arithmetic sequences along with the first term, the common difference, and the n th term.

Arithmetic Sequence Recursive Formula

The above formula for finding the n t h term of an arithmetic sequence is used to find any term of the sequence when the values of 'a 1 ' and 'd' are known. There is another formula to find the n th term which is called the " recursive formula of an arithmetic sequence " and is used to find a term (a n ) of the sequence when its previous term (a n-1 ) and 'd' are known. It says

a n = a n-1 + d

This formula just follows the definition of the arithmetic sequence.

Example: Find a 21 of an arithmetic sequence if a 19 = -72 and d = 7.

By using the recursive formula,

a 20 = a 19 + d = -72 + 7 = -65

a 21 = a 20 + d = -65 + 7 = -58

Therefore, a 21 = -58.

Arithmetic Series

The sum of the arithmetic sequence formula is used to find the sum of its first n terms. Note that the sum of terms of an arithmetic sequence is known as arithmetic series. Consider an arithmetic series in which the first term is a 1 (or 'a') and the common difference is d. The sum of its first n terms is denoted by S n . Then

• When the n th term is NOT known: S n = n/2 [2a 1 + (n-1) d]
• When the n th term is known: S n = n/2 [a 1 + a n ]

Ms. Natalie earns $200,000 per annum and her salary increases by $25,000 per annum. Then how much does she earn at the end of the first 5 years?

The amount earned by Ms. Natalie for the first year is, a = 2,00,000. The increment per annum is, d = 25,000. We have to calculate her earnings in the first 5 years. Hence n = 5. Substituting these values in the sum sum of arithmetic sequence formula,

S n = n/2 [2a 1 + (n-1) d]

⇒ S n = 5/2(2(200000) + (5 - 1)(25000))

= 5/2 (400000 +100000)

= 5/2 (500000)

She earns $1,250,000 in 5 years. We can use this formula to be more helpful for larger values of 'n'.

Sum of Arithmetic Sequence

Let us take an arithmetic sequence that has its first term to be a 1 and the common difference to be d. Then the sum of the first 'n' terms of the sequence is given by

S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + a n ... (1)

Let us write the same sum from right to left (i.e., from the n th term to the first term).

S n = a n + (a n – d) + (a n – 2d) + … + a 1 ... (2)

Adding (1) and (2), all terms with 'd' get canceled.

2S n = (a 1 + a n ) + (a 1 + a n ) + (a 1 + a n ) + … + (a 1 + a n )

2S n = n (a 1 + a n )

S n = [n(a 1 + a n )]/2

By substituting a n = a 1 + (n – 1)d into the last formula, we have

S n = n/2 [a 1 + a 1 + (n – 1)d] (or)

S n = n/2 [2a 1 + (n – 1)d]

Thus, we have derived both formulas for the sum of the arithmetic sequence.

Difference Between Arithmetic Sequence and Geometric Sequence

Here are the differences between arithmetic and geometric sequence :

Important Notes on Arithmetic Sequence:

• In arithmetic sequences, the difference between every two successive numbers is the same.
• The common difference of an arithmetic sequence a 1 , a 2 , a 3 , ... is, d = a 2 - a 1 = a 3 - a 2 = ...
• The n th term of an arithmetic sequence is a n = a 1 + (n−1)d.
• The sum of the first n terms of an arithmetic sequence is S n = n/2[2a 1 + (n − 1)d].
• The common difference between arithmetic sequences can be either positive or negative or zero.

☛ Related Topics:

• Sequence Calculator
• Series Calculator
• Arithmetic Sequence Calculator
• Geometric Sequence Calculator

Arithmetic Sequence Examples

Example 1: Find the n th term of the arithmetic sequence -5, -7/2, -2, ....

The given sequence is -5, -7/2, -2, ...

Here, the first term is a = -5, and the common difference is, d = -(7/2) - (-5) = -2 - (-7/2) = ... = 3/2.

The n th term of an arithmetic sequence is given by

a n = a 1 + (n−1)d

a n = -5 +(n - 1) (3/2)

= -5+ (3/2)n - 3/2

= 3n/2 - 13/2

Answer: The n th term of the given arithmetic sequence is, a n = 3n/2 - 13/2.

Example 2: Which term of the arithmetic sequence -3, -8, -13, -18,... is -248?

The given arithmetic sequence is -3, -8, -13, -18,...

The first term is, a = -3

The common difference is, d = -8 - (-3) = -13 - (-8) = ... = -5.

It is given that the n th term is, a n = -248.

Substitute all these values in the n th term of an arithmetic sequence formula,

a n = a 1 + (n−1)d ⇒ -248 = -3 + (-5)(n - 1) ⇒ -248 = -3 -5n + 5 ⇒ -248 = 2 - 5n ⇒ -250 = -5n ⇒ n = 50

Answer: -248 is the 50 th term of the given sequence.

Example 3: Find the sum of the arithmetic sequence -3, -8, -13, -18,.., -248.

This sequence is the same as the one that is given in Example 2 .

There we found that a = -3, d = -5, and n = 50.

So we have to find the sum of the 50 terms of the given arithmetic series.

S n = n/2[a 1 + a n ]

S 50 = [50 (-3 - 248)]/2 = -6275

Answer: The sum of the given arithmetic sequence is -6275.

go to slide go to slide go to slide

Book a Free Trial Class

Arithmetic Sequence Questions

go to slide go to slide

FAQs on Arithmetic Sequence

What is an arithmetic sequence in algebra.

An arithmetic sequence in algebra is a sequence of numbers where the difference between every two consecutive terms is the same. Generally, the arithmetic sequence is written as a, a+d, a+2d, a+3d, ..., where a is the first term and d is the common difference.

What are Arithmetic Sequence Formulas?

Here are the formulas related to an arithmetic sequence where a₁ (or a) is the first term and d is a common difference:

• The common difference, d = a n - a n-1 .
• n th term of sequence is, a n = a + (n - 1)d
• Sum of n terms of sequence is , S n = [n(a 1 + a n )]/2 (or) n/2 (2a + (n - 1)d)

What is the Definition of an Arithmetic Sequence?

A sequence of numbers in which every term (except the first term) is obtained by adding a constant number to the previous term is called an arithmetic sequence . For example, 1, 3, 5, 7, ... is an arithmetic sequence as every term is obtained by adding 2 (a constant number) to its previous term.

How to Identify An Arithmetic Sequence?

If the difference between every two consecutive terms of a sequence is the same then it is an arithmetic sequence. For example, 3, 8, 13, 18 ... is arithmetic because the consecutive terms have a fixed difference.

• 18-13 = 5 and so on.

What is the n th term of an Arithmetic Sequence?

The n th term of arithmetic sequences is given by a n = a + (n – 1) × d. Here 'a' represents the first term and 'd' represents the common difference.

What is an Arithmetic Series?

An arithmetic series is a sum of an arithmetic sequence where each term is obtained by adding a fixed number to each previous term.

What is the Arithmetic Series Formula?

The sum of the first n terms of an arithmetic sequence (arithmetic series ) with the first term 'a' and common difference 'd' is denoted by Sₙ and we have two formulas to find it.

• S n = n/2[2a + (n - 1)d]
• S n = n/2[a + a n ].

What is the Formula to Find the Common Difference in Arithmetic sequence?

The common difference of an arithmetic sequence, as its name suggests, is the difference between every two of its successive (or consecutive) terms. The formula for finding the common difference of an arithmetic sequence is, d = a n - a n-1 .

How to Find n in Arithmetic Sequence?

When we have to find the number of terms (n) in arithmetic sequences, some of the information about a, d, a n or S n might have been given in the problem. We will just substitute the given values in the formulas of a n or S n and solve it for n.

How To Find the First Term in Arithmetic sequence?

The first term of an arithmetic sequence is the number that occurs in the first position from the left. It is denoted by 'a'. If 'a' is NOT given in the problem, then some information about d (or) a n (or) S n might be given in the problem. We will just substitute the given values in the formulas of a n or S n and solve it for 'a'.

What is the Difference Between Arithmetic Sequence and Arithmetic Series?

An arithmetic sequence is a collection of numbers in which all the differences between every two consecutive numbers are equal to a constant whereas an arithmetic series is the sum of a few or more terms of an arithmetic sequence.

What are the Types of Sequences?

There are mainly 3 types of sequences in math. They are:

• Arithmetic sequence
• Geometric sequence
• Harmonic sequence

What are the Applications of Arithmetic Sequence?

Here are some applications: the salary of a person which is increased by a constant amount by each year, the rent of a taxi which charges per mile, the number of fishes in a pond that increase by a constant number each month, etc.

How to Find the n th Term in Arithmetic Sequence?

Here are the steps for finding the n th term of arithmetic sequences:

• Identify its first term, a
• Common difference , d
• Identify which term you want. i.e., n
• Substitute all these into the formula a n = a + (n – 1) × d.

How to Find the Sum of n Terms of Arithmetic Sequence?

To find the sum of the first n terms of arithmetic sequences,

• Identify its first term (a)
• Common difference (d)
• Identify which term you want (n)
• Substitute all these into the formula S n = (n/2)(2a + (n - 1)d)

Arithmetic Sequences and Sums

A Sequence is a set of things (usually numbers) that are in order.

Each number in the sequence is called a term (or sometimes "element" or "member"), read Sequences and Series for more details.

Arithmetic Sequence

In an Arithmetic Sequence the difference between one term and the next is a constant .

In other words, we just add the same value each time ... infinitely.

Example: 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number. The pattern is continued by adding 3 to the last number each time, like this:

In General we could write an arithmetic sequence like this:

{a, a+d, a+2d, a+3d, ... }

• a is the first term, and
• d is the difference between the terms (called the "common difference" )

Example (continued): 1, 4, 7, 10, 13, 16, 19, 22, 25, ...

• a = 1 (the first term)
• d = 3 (the "common difference" between terms)

And we get:

{1, 1+3, 1+2×3, 1+3×3, ... }

{1, 4, 7, 10, ... }

We can write an Arithmetic Sequence as a rule :

x n = a + d(n−1)

(We use "n−1" because d is not used in the 1st term).

Example: Write a rule, and calculate the 9th term, for this Arithmetic Sequence:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.

The values of a and d are:

• a = 3 (the first term)
• d = 5 (the "common difference")

Using the Arithmetic Sequence rule:

So the 9 th term is:

x 9 = 5× 9 − 2 = 43

Is that right? Check for yourself!

Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)

Advanced Topic : Summing an Arithmetic Series

To sum up the terms of this arithmetic sequence:

a + (a+d) + (a+2d) + (a+3d) + ...

use this formula:

What is that funny symbol? It is called Sigma Notation

And below and above it are shown the starting and ending values:

It says "Sum up n where n goes from 1 to 4. Answer= 10

Here is how to use it:

Example: Add up the first 10 terms of the arithmetic sequence:

{ 1, 4, 7, 10, 13, ... }

The values of a , d and n are:

• n = 10 (how many terms to add up)

= 5(2+9·3) = 5(29) = 145

Check: why don't you add up the terms yourself, and see if it comes to 145

Footnote: Why Does the Formula Work?

Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

First , we will call the whole sum "S" :

Next , rewrite S in reverse order:

Now add those two, term by term:

Each term is the same! And there are "n" of them so ...

Now, just divide by 2 and we get:

S = n 2 (2a + (n−1)d)

Which is our formula:

Reset password New user? Sign up

Existing user? Log in

Arithmetic and Geometric Progressions Problem Solving

Already have an account? Log in here.

Recommended Course

Algebra through puzzles.

Supercharge your algebraic intuition and problem solving skills!

• Vilakshan Gupta
• Andres Gonzalez

To solve problems on this page, you should be familiar with

• arithmetic progressions
• geometric progressions
• arithmetic-geometric progressions .

You can boost up your problem solving on arithmetic and geometric progressions through this wiki. Make sure you hit all the problems listed in this page.

Problem Solving - Basic

Problem solving - intermediate, problem solving - advanced.

This section contains basic problems based on the notions of arithmetic and geometric progressions. Starting with an example, we will head into the problems to solve.

I have an arithmetic progression such that the initial term is 5 and the common difference is 10. What is minimum value of \(n\) such that the \(n^\text{th}\) term is larger than 100? We can just start by listing out the numbers: \[ 5,15,25,35,45,55,65,75,85, 95,105. \] We can clearly see that the \(11^\text{th}\) number is larger than 100, and thus \(n=11.\) However, note that this will become impractical if the common difference becomes smaller and/or the number we are looking for becomes larger. A practical way to solve it is via applying the \(n^\text{th}\) term formula. With \(a = 5, d = 10\), we have \( T_n = a + (n-1) d > 100 \). Then \(5 + (n-1) \cdot 10 > 100 \). Solving for \(n\) yields \(n > 10.5\). So the \(11^\text{th}\) term is the smallest term that satisfies the condition. \(_\square\)

Here comes the problems for you to solve.

The average of the first 100 positive integers is \(\text{__________}.\)

If \(A, B, C, D \) are consecutive terms in an arithmetic progression, what is the value of

\[ \frac{ D^2 - A^2 } { C^2 - B^2} ? \]

Assume \( C^2 - B^2 \neq 0.\)

\[ 54+51+48+45+ \cdots\]

You are given the sum of an arithmetic progression of a finite number of terms, as shown above.

What is the minimum number of terms used to make a total value of 513?

One side of an equilateral triangle is 24 cm. The midpoints of its sides are joined to form another triangle whose midpoints, in turn, are joined to form still another triangle. This process continues indefinitely.

Find the sum of the perimeters of all these triangles that are defined above.

Once a man did a favor to a king that made the king very happy. Out of joy the king told the man to wish for anything and he would be granted. The man wanted to ask for the whole kingdom which was worth 1500 trillion dollars, but obviously that would make the king mad and he would never be granted that wish.

The man who happened to be a mathematician thought a little bit and said the following:

"Bring in a big piece of rug with an \(8\times 8\) grid in it. Starting from the top left square, put one dollar in that square. Put two dollars in the square next to it and then double of that, four dollars, in the next square and so on. When you reach the end of the first row, continue on to the next row, doubling the amount every time as you move to the next square, all the way until the \(64^\text{th}\) square at the bottom right."

The king thought for a second. The first square will take one dollar, the second two dollars, the third, four dollars, and next 8 dollars, and then 16 dollars, and then 32 dollars, 64 dollars, 128 dollars, 256 dollars, and so on. That's not too bad. I can do it.

The king agreed. What happened next?

\[1+2 \cdot 2+ 3 \cdot 2^2 + 4 \cdot 2^3 + \cdots+ 100 \cdot 2^{99}= \, ?\]

This section contains a bit harder problems than the previous section. But all these can be solved using arithmetic and geometric problems. Here we go:

Real numbers \(a_1,a_2,\ldots,a_{99}\) form an arithmetic progression.

Suppose that \[ a_2+a_5+a_8+\cdots+a_{98}=205.\] Find the value of \( \displaystyle \sum_{k=1}^{99} a_k\).

The value of \(\displaystyle \sum_{n=1}^ \infty \frac{ 2n}{ 3^n } \) can be expressed in the form \( \frac{a}{b} \), where \(a\) and \(b\) are coprime positive integers. Find \( a - b \).

Let \(a,b,c\) be positive integers such that \(\frac{b}{a}\) is an integer. If \(a,b,c\) are in geometric progression and the arithmetic mean of \(a,b,c\) is \(b+2,\) find the value of

\[\dfrac{a^2+a-14}{a+1}.\]

If an infinite GP of real numbers has second term \(x\) and sum \(4,\) where does \(x\) belong?

4 positive integers form an arithmetic progression.

If we subtract \(2,6,7\) and \(2,\) respectively, from the 4 numbers, it forms a geometric progression.

What is the sum of these 4 numbers?

Let \(a, b \in R^{+}.\)

\(a, A_{1}, A_{2}, b\) is an arithmetic progression. \(a, G_{1}, G_{2}, b\) is a geometric progression.

Which of the following must be true?

We have three numbers in an arithmetic progression, and another three numbers in a geometric progression. Adding the corresponding terms of the two series, we get \( 120 , 116 , 130 \). If the sum of all the terms in the geometric progression is \( 342 \), what is the largest term in the geometric progression?

\(\) Details and Assumptions:

• If the terms of the AP are A, B, C, and the terms of the GP are X, Y, Z, then adding the corresponding terms will give us A+X, B+Y, C+Z.

This section has problems which need advanced understanding of the notions and generally get solved on using multiple notions at a time. Let's give these problems an attempt.

\[(1-x)(1-2x)(1-4x)\cdots \left(1-2^{101}x\right)\]

What is the coefficient of \(x^{101} \) in the expansion of the above?

\[ \frac {2+6}{4^{100}} + \frac {2+2 \times 6}{4^{99}} + \frac {2+ 3 \times 6}{4^{98}} + \cdots + \frac {2+ 100 \times 6}{4} \]

Evaluate the above expression.

In JEE examination the paper consists of 90 questions. The marks are awarded in such a way that if a person gets a question correct, he gets \(+4\) marks; if he does it wrong, he gets \(-2\) marks; if he leaves the question unanswered, he gets \(0\) marks (as per 2015). Find the sum of all possible marks that a student can get in JEE.

Let \(A=\{a_1, a_2, \ldots, a_n\}\) be a set of the first \(n\) terms of an arithmetic progression. Similarly, let \(B=\{b_1, b_2, \ldots, b_n\}\) be a set of the first \(n\) terms of a geometric progression.

If a new set \(C=A+B=\{a_1+b_1, a_2+b_2, \ldots, a_n+b_n\}\) and the first four terms of \(C\) are \(\{0, 0, 1, 0\},\) what is the \(11^\text{th}\) term of \(C?\)

A linear function \(f(x)=bx+a\) has the property that \(f\big(f(x)\big)=dx+c\) is another linear function such that \(a,b,c,d\) are integers that are consecutive terms in an arithmetic sequence. Find the last three digits of the sum of all possible values of \(f(2013)\).

\[ \begin{eqnarray} &\displaystyle\sum_{n=0}^{7}\log_{3}(x_{n}) &= 308 \\ 56 \leq & \log_{3}\left ( \sum_{n=0}^{7}x_{n}\right )& \leq 57 \\ \end{eqnarray} \]

The increasing geometric sequence \(x_{0},x_{1},x_{2},\ldots\) consists entirely of integral powers of 3. If they satisfy the two conditions above, find \(\log_{3}(x_{14}).\)

Suppose \(2015\) people of different heights are arranged in a straight line from shortest to tallest such that

(i) the tops of their heads are collinear, and

(ii) for any two successive people, the horizontal distance between them is equal to the height of the shorter of the two people.

If the shortest person is \(49\) inches tall and the tallest is \(81\) inches tall, then how tall is the person at the middle of the line, (in inches)?

Given that \(a_1,a_2,a_3\) is an arithmetic progression in that order so that \(a_1+a_2+a_3=15\) and \(b_1,b_2,b_3\) is a geometric progression in that order so that \(b_1b_2b_3=27\).

If \(a_1+b_1, a_2+b_2, a_3+b_3\) are positive integers and form a geometric progression in that order, determine the maximum possible value of \(a_3\).

The answer is of the form \(\dfrac{a+b\sqrt{c}}{d}\), where \(a\), \(b\), \(c\), and \(d\) are positive integers and the fraction is in its simplest form and \(c\) is square free. Submit the value of \( a + b + c + d \).

Telescoping Series - Sum and Telescoping Series - Product

Limits of Sequences

Master concepts like these

Learn more in our Algebra through Puzzles course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

• Daily Games
• Strategy and Puzzles
• Vocabulary Games
• Junior Edition Games
• All problems
• High School Math
• MAML Problems
• Calculus Problems
• Loony Physics
• Pro Problems
• Getting Started
• Pro Control Panel
• Virtual Classroom
• Play My Favorites
• Select My Favorites

Arithmetic Sequence Problems

There are many problems we can solve if we keep in mind that the  n th term of an arithmetic sequence can be written in the following way: a n  = a 1 +(n - 1)d Where a 1  is the first term, and  d  is the common difference. For example, if we are told that the first two terms add up to the fifth term, and that the common difference is 8 less than the first term we can take this equation: a 1  + a 2  = a 5 and rewrite it as follows: a 1  + [a 1  + d] = [a 1  + 4d] This leads to a 1  = 3d. Combine this with d = a 1  - 8, and we have: a 1  = 3(a 1  - 8) or a 1  = 12. This leads to d = 4, and from this information, we can find any other term of the sequence.

Blogs on This Site

Sequences Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

Top 10 Challenges to Teaching Math and Science Using Real Problems

• Share article

Nine in ten educators believe that using a problem-solving approach to teaching math and science can be motivating for students, according to an EdWeek Research Center survey.

But that doesn’t mean it’s easy.

Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures—eats up too many precious instructional minutes.

Other challenges: About another third of educators said they weren’t given sufficient professional development in how to teach using a real-world problem-solving approach. Nearly a third say reading and writing take priority over STEM, leaving little bandwidth for this kind of instruction. About a quarter say that it’s tough to find instructional materials that embrace a problem-solving perspective.

Nearly one in five cited teachers’ lack of confidence in their own problem solving, the belief that this approach isn’t compatible with standardized tests, low parent support, and the belief that student behavior is so poor that this approach would not be feasible.

The nationally representative survey included 1,183 district leaders, school leaders, and teachers, and was conducted from March 27 to April 14. (Note: The chart below lists 11 challenges because the last two on the list—dealing with teacher preparation and student behavior—received the exact percentage of responses.)

Trying to incorporate a problem-solving approach to tackling math can require rethinking long-held beliefs about how students learn, said Elham Kazemi, a professor in the teacher education program at the University of Washington.

Most teachers were taught math using a procedural perspective when they were in school. While Kazemi believes that approach has merit, she advocates for exposing students to both types of instruction.

Many educators have “grown up around a particular model of thinking of teaching and learning as the teacher in the front of the room, imparting knowledge, showing kids how to do things,” Kazemi said.

To be sure, some teachers have figured out how to incorporate some real-world problem solving alongside more traditional methods. But it can be tough for their colleagues to learn from them because “teachers don’t have a lot of time to collaborate with one another and see each other teach,” Kazemi said.

What’s more, there are limited instructional materials emphasizing problem solving, Kazemi said.

Though that’s changing, many of the resources available have “reinforced the idea that the teacher demonstrates solutions for kids,” Kazemi said.

Molly Daley, a regional math coordinator for Education Service District 112, which serves about 30 districts near Vancouver, Wash., has heard teachers raise concerns that teaching math from a problem-solving perspective takes too long—particularly given the pressure to get through all the material students will need to perform well on state tests.

Daley believes, however, that being taught to think about math in a deeper way will help students tackle math questions on state assessments that may look different from what they’ve seen before.

“It’s myth that it’s possible to cover everything that will be on the test,” as it will appear, she said. “There’s actually no way to make sure that kids have seen every single possible thing the way it will show up. That’s kind of a losing proposition.”

But rushing through the material in a purely procedural way may actually be counterproductive, she said.

Teachers don’t want kids to “sit down at the test and say, ‘I haven’t seen this and therefore I can’t do it,’” Daley said. “I think a lot of times teachers can unintentionally foster that because they’re so urgently trying to cover everything. That’s where the kind of mindless [teaching] approaches come in.”

Teachers may think to themselves: “’OK, I’m gonna make this as simple as possible, make sure everyone knows how to follow the steps and then when they see it, they can follow it,” Daley said.

But that strategy might “take away their students’ confidence that they can figure out what to do when they don’t know what to do, which is really what you want them to be thinking when they go to approach a test,” Daley said.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

Netflix's Wednesday Season 2 Will Solve This Season 1 Problem

• More Addams Family characters like Grandmama and Uncle Fester will be part of the cast in Wednesday season 2, addressing fan concerns.
• Season 1 of Wednesday could have featured more Addams Family characters, but season 2 promises to give fans what they wanted.
• Fans can expect to see Wednesday's immediate family, Morticia and Gomez Addams, take on more active roles in Wednesday season 2.

While there are many solid Netflix series that feature great acting and intriguing storylines, season 1 of Wednesday

captured a lot of attention upon its November 2022 release. Now that season 2 of Wednesday is coming in 2025 , fans are thinking about what trouble Jenna Ortega's iconic character could get into next.

Since Jenna Ortega said Wednesday season 2 will have horror elements , fans are even more excited for what's next. Now that the Wednesday season 2 cast has been announced , one problem from season 1 is going to be addressed: the fact that the Addams Family characters weren't included enough. It seems that fans will see more of Wednesday's parents, siblings, and uncle in the second season, along with another great family member.

What Should Wednesday Season 2 Be About?

Wednesday season 2 returns in 2025 on Netflix and fans have some ideas about what should happen to Jenna Ortega's character.

Which Addams Family Characters Will Be In Wednesday Season 2?

Wednesday season 2 is solving a problem from season 1 because there will be one more Addams Family member and that Wednesday's relatives will appear in much of the show . According to Deadline , another Addams Family relative was added to the cast of Wednesday season 2: Grandmama (played by Joanna Lumley) . Fred Armisen is also coming back to play Uncle Fester. Both of these will be guest parts, so fans can expect to see them less than the other characters. But they will still hopefully be part of some funny and meaningful storylines that help show how dark and unique this family is. That is something that was missing from season 1.

Fans didn't feel they saw enough of Wednesday's immediate family in season 1. Thankfully, this problem will be solved in Wednesday season 2. Isaac Ordonez, Luis Guzmán, and Catherine Zeta-Jones are returning as Pugsley Adams, Gomez Addams, and Morticia Addams. The good news is that these three actors will be regular cast members, which will make fans happy.

When looking back on the Addams Family portrayals in movies and on TV , many viewers felt that the Addams Family characters in Wednesday season 1 felt too different. There was a lot of criticism of Wednesday in particular since she was part of a love triangle and was a little more compassionate than in the past. If the Addams Family members get more screentime, this hopefully means that there will be scenes of Wednesday's usual dynamic with her family . Fans want to see Wednesday teasing Pugsley and making her parents proud with all her dark ideas.

Who Played Grandmama In The Addams Family Movies?

• The Addams Family (1991): Judith Molina
• Addams Family Values (1993): Carol Kane
• Addams Family Reunion (1998): Alice Ghostley

It's also a smart idea to feature Grandmama, one of the most iconic and memorable Addams Family characters . She is known for making creepy cookies, coming up with spells, and generally terrorizing anyone she can. It would be fun to see Grandmama visit Wednesday at her unique boarding school Nevermore and cause some chaos. It would also be great to see Wednesday go home and see her whole family.

Fans will also be glad to see Wednesday spending time with her quirky and strange Uncle Fester again. As Fred Armisen told Netflix.com/Tudum about playing the famous character:

Its everything that I love, spooky and funny at the same time.

How Wednesday Season 1 Used The Addams Family Characters

It's fair to say that Wednesday season 1 could have featured the Addams Family characters in more scenes. While Wednesday spends a bit of time with her parents Morticia and Gomez Adams, she's mostly busy at Nevermore trying to find the Hyde Monster and learning more about her parents' history with the school.

While Uncle Fester shows up in the season 1 episode "If You Don't Woe Me By Now," he's running away since he's gotten into trouble. This storyline works since it proves his cheeky and rebellious personality but also shows that he can be charming. It's also smart since it shows how similar Wednesday and her uncle are. Hopefully Wednesday season 2 will include Uncle Fester and Wednesday investigating the new mystery together as this would be entertaining to watch.

While Wednesday's parents help her get settled at Nevermore in Wednesday season 1, Wednesday season 2 needs to answer questions and also include Morticia and Gomez Addams in more active roles. The actors did a great job playing their iconic characters and if they are given more to do, that would be more interesting. Gomez, in particular, is an impressive character because he's hilarious and charming. As Luiz Guzmán said in an interview with E! News :

"I wasn't looking to play Gomez as this goofy guy. But the words that these guys wrote were beautiful, almost poetic. But it was funny . When you convey that as an artist, it just comes across that way. They just had it right."

Jenna Ortega's 5 Best TV Roles

Jenna Ortega became famous for appearing in horror movies like X and Scream and for playing Wednesday Addams, but she has played other TV characters.

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center

We've detected unusual activity from your computer network

To continue, please click the box below to let us know you're not a robot.

Why did this happen?

Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .

For inquiries related to this message please contact our support team and provide the reference ID below.

to submit an obituary

To place an obituary, please include the information from the obituary checklist below in an email to [email protected] . There is no option to place them through our website. Feel free to contact our obituary desk at 651-228-5263 with any questions.

General Information:

• Your full name,
• Address (City, State, Zip Code),
• Phone number,
• And an alternate phone number (if any)

Obituary Specification:

• Name of Deceased,
• Obituary Text,
• A photo in a JPEG or PDF file is preferable, TIF and other files are accepted, we will contact you if there are any issues with the photo.
• Ad Run dates
• There is a discount for running more than one day, but this must be scheduled on the first run date to apply.
• If a photo is used, it must be used for both days for the discount to apply, contact us for more information.

Verification of Death:

In order to publish obituaries a name and phone number of funeral home/cremation society is required. We must contact the funeral home/cremation society handling the arrangements during their business hours to verify the death. If the body of the deceased has been donated to the University of Minnesota Anatomy Bequest Program, or a similar program, their phone number is required for verification.

Please allow enough time to contact them especially during their limited weekend hours.

A death certificate is also acceptable for this purpose but only one of these two options are necessary.

Guestbook and Outside Websites:

We are not allowed to reference other media sources with a guestbook or an obituary placed elsewhere when placing an obituary in print and online. We may place a website for a funeral home or a family email for contact instead; contact us with any questions regarding this matter.

Obituary Process:

Once your submission is completed, we will fax or email a proof for review prior to publication in the newspaper. This proof includes price and days the notice is scheduled to appear.

Please review the proof carefully. We must be notified of errors or changes before the notice appears in the Pioneer Press based on each day’s deadlines.

After publication, we will not be responsible for errors that may occur after final proofing.

All obituaries appear on TwinCities.com with a permanent online guestbook presence. If you wish to have the online presence removed, you can contact us to remove the guestbook online. Changes to an online obituary can be handled through the obituary desk. Call us with further questions.

Payment Procedure:

Pre-payment is required for all obituary notices prior to publication by the deadline specified below in our deadline schedule. Please call 651-228-5263 with your payment information after you have received the proof and approved its contents.

Credit Card: Payment accepted by phone only due to PCI (Payment Card Industry) regulations

EFT: Check by phone. Please provide your routing number and account number.

Cash: Accepted at our FRONT COUNTER Monday – Friday from 8:00AM – 3:30PM

• The minimum charge is $162 for the first 10 lines.
• Every line after the first 10 is $12.20.
• If the ad is under 10 lines it will be charged the minimum rate of $162.
• On a second run date, the lines are $8.20 per line, starting w/ the first line.
• For example: if first run date was 20 lines the cost would be $164.
• Each photo published is $125 per day.
• For example: 2 photos in the paper on 2 days would be 4 photo charges at $500.

Please follow deadline times to ensure your obituary is published on the day requested.

MEMORIAM (NON-OBITUARY) REQUEST

Unlike an obituary, Memoriam submissions are remembrances of a loved one who has passed. The rates for a memoriam differ from obituaries.

Please call or email us for more memoriam information

Please call 651-228-5280 for more information.

HOURS: Monday – Friday 8:00AM – 5:00PM (CLOSED WEEKENDS and HOLIDAYS)

Please submit your memoriam ad to [email protected] or call 651-228-5280.

Opinion | F.D. Flam: Fake scientific studies are a…

Share this:.

• Click to share on Facebook (Opens in new window)
• Click to share on Reddit (Opens in new window)
• Click to share on Twitter (Opens in new window)
• Click to print (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to share on LinkedIn (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Submit to Stumbleupon (Opens in new window)

Today's Paper

• Opinion Columnists

Opinion | F.D. Flam: Fake scientific studies are a problem that’s getting harder to solve

The issue made headlines recently when Wiley, a respected publishing house, announced it would be dropping 19 of its journals associated with a publisher they had acquired, called Hindawi, in part because they were infested with fake papers. But the problem was known before: The fraud sleuthing blog For Better Science called attention to the “fraud-positive” attitude at Wiley back in 2022. (And I covered the problem of fake research on my Follow the Science podcast back in 2021.)

These aren’t just papers with fudged data — in many cases, all the data and the text have been invented from whole cloth, generated with artificial intelligence, or plagiarized. They’re fake all the way through. The creators of these fake papers have been dubbed paper mills, and they operate by reaching out to scientists and offering to write papers with the scientists’ names at the top — for a price.

Paper mills have proliferated because of a pathology that’s afflicted many areas of science. Scientists are rewarded for the quantity of their research more than its quality. And peer review is non-functional at many journals.

In that disturbed ecosystem, parasitic companies flourish by helping scientists cheat to bolster their resumes, snag competitive academic jobs, and impress funding agencies. Ultimately that causes some precious resources get routed to cheaters and away from more worthy scientists.

Worse still, some of the fake results can seep into other articles, contaminating the state of medical knowledge, said David Sanders, a biologist at Purdue University who has been tracking scientific misconduct and the paper mill problem. For enough money, the paper mills can make a fake paper look more influential by creating other fake papers that cite it, he said. The paper mill studies can even get cited in seemingly legitimate review papers if the review authors — who are also trying for volume — don’t pay sufficient attention to what they’re reviewing.

Some paper mill papers show obvious flaws, including patently plagiarized graphs, images and text. Some are translated from English to another language and back — and that can lead to bizarre wordings, such as “lactose intolerance” becoming “lactose bigotry,” said Sanders. Still others show absurdities like an experiment in which half a sample of ovarian cancer patients was male.

Now with the help of ChatGPT, paper mills can create much more coherent, plausible papers cheaply and effortlessly. Scientific fields beset by fake papers might do better to address the roots of the problem rather than trying to chase them down.

Ivan Oransky, co-founder of the blog Retraction Watch, has been tracking problematic research for years. He said that paper mill output has been estimated to make up about 2% of papers. That may not sound big, but somewhere between 2 million and 6 million scientific papers are published every year, so 2% adds up to a lot.

Some journals are more than 50%-generated by paper mills, said Sanders. The way he described it, the paper mills find a susceptible journal and then “they completely parasitize it.”

He said he blames not just shoddy peer reviews, but a perverse system of evaluating scientific merit. “Hiring committees or grant committees don’t have the wherewithal to make an actual evaluation,” Sanders said. So scientists get rewarded based on the number of publications they author and the number of other publications that cite these.

Even many legitimate journal articles don’t advance the state of knowledge, he said, at least in the biomedical arena. Researchers might have gathered a bit of additional data for an ongoing project, which should be deposited into a data bank rather than turned into an unnecessary paper. “I would say the majority of articles that are published now make no contribution beyond the data they present,” he said. “They are not worth reading.”

The whole incentive system is warped, he said, and people are so dependent on grants for their survival that they’ll “do whatever is necessary.”

The fake papers often use a pre-existing template, he said, filling in words and data like a game of Mad Libs. Paper mill creations are more pervasive in fields where papers tend to be formulaic, like nanotechnology, computer science and an area of cancer research called microRNAs.

But some fault also lies with other scientists who cite these fake papers in review articles — which are proliferating at a rate far beyond what’s beneficial to science or society. Even when initial papers get retracted, their impact remains in the form of citations and mentions in review papers.

Eventually, the bad papers can contaminate standards of medical care, said Sanders. Some people are developing cancer diagnostics based on fake papers. He’s seen a paper mill product referenced in a thesis defense. He’s even heard from cancer patients citing a fake paper to inquire about alternative therapies.

Funding agents could help by refusing to fund work that goes into badly reviewed journals laden with fake findings. They could keep a list of approved journals that do rigorous peer review and only fund work aimed at getting published in those. Sanders said more funding should also go into fraud detection in science.

People don’t need millions of scientific papers, most of them doing little to advance our knowledge. We need more scientists to put their energy into quality control or slow, careful research. Science is a competitive field and those who make it shouldn’t be fakers.

F.D. Flam is a Bloomberg Opinion columnist covering science. She is host of the “Follow the Science” podcast.

More in Opinion

SUBSCRIBER ONLY

Opinion | serge schmemann: do not allow putin to capture another pawn in europe.

Opinion | Bill Thorness: We have always owed our soldiers more

Business | Real World Economics: The old-fashioned politics of consensus is dead

Opinion | Other voices: Trumponomics 2.0? Think ‘inflation’

Opinion | Sunday Bulletin Board: Bird people: Do you suffer from incommunipotestatum falcolumorbus?

Opinion | Eric Snoey: Wait times down. Patient satisfaction up. Why not let AI run the ER?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1   >   Unit 9

Sequences word problems.

• (Choice A)   Arithmetic sequence A Arithmetic sequence
• (Choice B)   Geometric sequence B Geometric sequence
• Your answer should be
• an integer, like 6 ‍  
• an exact decimal, like 0.75 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍