The Role of the Teacher Changes in a Problem-Solving Classroom
- Share article

How can teachers help students develop problem-solving skills when they themselves, even though confronted with an array of problems every day, may need to become better problem solvers? Our experience leads us to conclude that there is an expertise in a certain kind of problem-solving that teachers possess but that broader problem-solving skills are sometimes wanting.There are a few reasons why this happens. One reason may be that teacher preparation programs remain focused on how to teach subjects and behavior management techniques. Another reason may be that professional development opportunities offered in schools are focused elsewhere. And, another reason could be that leaders still often fail to engage their faculties in solving substantive problems within the school community.
A recent issue of Education Leadership was dedicated to the topic, “Unleashing Problem Solvers”. One theme that ran through several of the articles was the changing role of the teacher. In a positive but traditional classroom, information is shared by the teacher and the students are asked to demonstrate application of that information. A problem-solving classroom is different. A problem-solving classroom requires extraordinary planning on the part of the teacher. For problems to have relevance, students are engaged in the identification of the problem. Teachers have to become experts at creating questions that require students to reach back to information and skills already attained, while figuring out what they need to learn next in order to solve the problem. Some of us are really good at asking these kinds of questions. Others are not.
Students have to become experts at reflecting on these questions as guides resulting in a gathering of new information and skills, and answers. Teachers have to be prepared to offer lessons that bridge the gaps between the skills and information already attained and those the performance of the students demonstrate remain needed. Often it involves teams of students and they are simultaneously learning collaboration and communication skills.

Problem-Based Classrooms Require Letting Go
Opportunities for teachers to work with each other, to learn from experts, to receive feedback from observers of their work, all allow for skill development. But at the same time, there is a more challenging effort required of the teacher. Problem-based classrooms require teachers to dare to let go of control of the learning and to take hold of the role of questioner, coach, supporter, and diagnostician. In addition to the lack of training teachers have in these skills, the leaders in charge of evaluating their work also have to know what problem-solving classrooms look like and how to capture that environment in an observation, how to give feedback on the teachers’ efforts. Of course, if problem- solving is a collaborative school community process, how does that change the leader’s role? Are leaders, themselves, ready to become facilitators of the process rather than the sole problem solver? Many talk about wanting that but most get rewarded for being the problem solver.
Questions are Essential
There is a place to begin and that place is the shared understanding of what problem-based learning actually is. Because teachers traditionally plan for a time for Q and A within classes, they and their leaders may think of questions as having a correct answer. In moving into a problem-based learning design, the questions also have to be more overarching, create cognitive dissonance, and provoke the learner to search for answers. Here is why it is important to come to an understanding about the types of questions to be asked and shifting the teaching and learning practices to be one of expecting more from the learner.
Students Need Problem-Solving Skills
Problem-based learning skills are skills that prepare for a changing environment in all fields. Current educators cannot imagine some of the careers our students will have over their lifetimes. We do know that change will be part of everyone’s work. Flexibility and problem-solving are key skills. Problem- solving involves collaboration, communication, critical thinking, empathy, and integrity. If we listen to the business world, we will hear that design thinking is the way of the future.
Tim Brown, CEO of IDEO says,
Design thinking is a human-centered approach to innovation that draws from the designer’s toolkit to integrate the needs of people, the possibilities of technology, and the requirements for business success.
The only way for educators to develop these skills in students is to build lessons and units that are interdisciplinary and demand these skills. If we begin from the earliest of grades and expect more as they ascend through the grades, students will have mastered not only their subjects, but the skills that will prepare them for the world of work. How do we best prepare our students? We think problem solving is key.
A nn Myers and Jill Berkowicz are the authors of The STEM Shift (2015, Corwin) a book about leading the shift into 21st century schools. Ann and Jill welcome connecting through Twitter & Email .
Photo courtesy of Pixabay
The opinions expressed in Leadership 360 are strictly those of the author(s) and do not reflect the opinions or endorsement of Editorial Projects in Education, or any of its publications.
Sign Up for EdWeek Update
Center for Teaching
Teaching problem solving.
Print Version
Tips and Techniques
Expert vs. novice problem solvers, communicate.
- Have students identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
- If students are unable to articulate their concerns, determine where they are having trouble by asking them to identify the specific concepts or principles associated with the problem.
- In a one-on-one tutoring session, ask the student to work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
- When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)
Encourage Independence
- Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
- Have students work through problems on their own. Ask directing questions or give helpful suggestions, but provide only minimal assistance and only when needed to overcome obstacles.
- Don’t fear group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others
Be sensitive
- Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing positive reinforcement to let students know when they have mastered a new concept or skill.
Encourage Thoroughness and Patience
- Try to communicate that the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.
Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills, a teacher should be aware of principles and strategies of good problem solving in his or her discipline .
The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides
- Online Course Development Resources
- Principles & Frameworks
- Pedagogies & Strategies
- Reflecting & Assessing
- Challenges & Opportunities
- Populations & Contexts
Quick Links
- Services for Departments and Schools
- Examples of Online Instructional Modules
- Illinois Online
- Illinois Remote
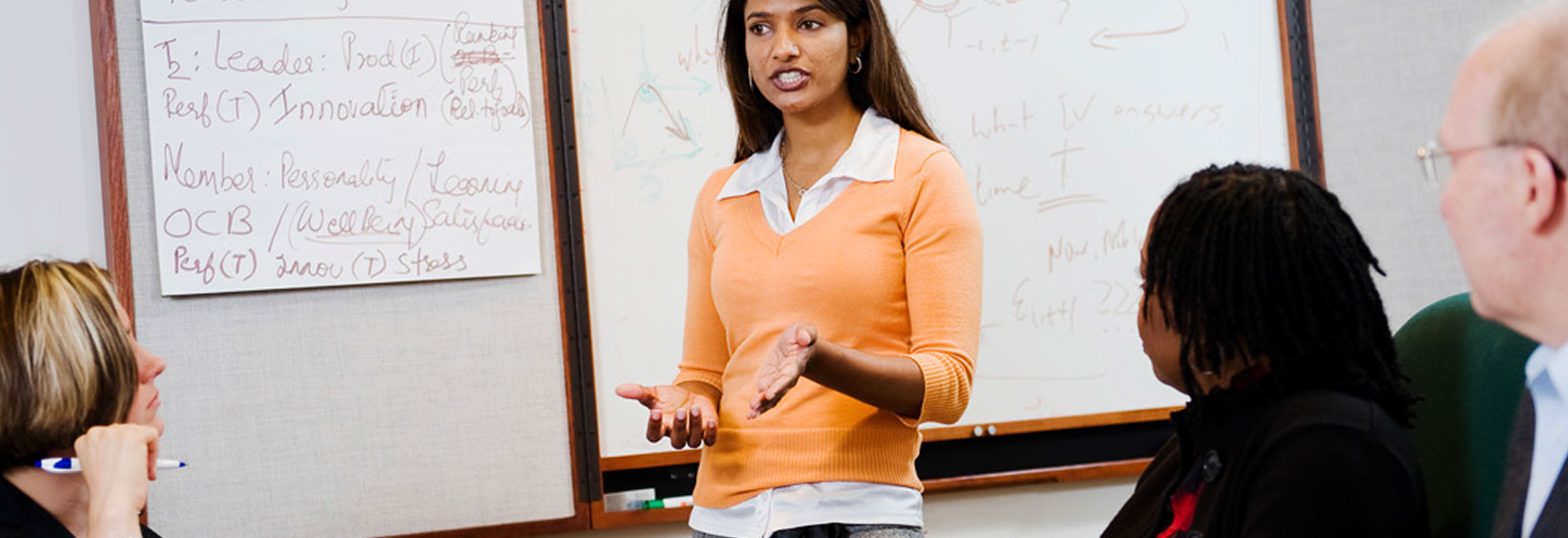
- TA Resources
- Teaching Consultation
- Teaching Portfolio Program
- Grad Academy for College Teaching
- Faculty Events
- The Art of Teaching
- 2022 Illinois Summer Teaching Institute
- Large Classes
- Leading Discussions
- Laboratory Classes
- Lecture-Based Classes
- Planning a Class Session
- Questioning Strategies
- Classroom Assessment Techniques (CATs)
- Problem-Based Learning (PBL)
- The Case Method
- Community-Based Learning: Service Learning
- Group Learning
- Just-in-Time Teaching
- Creating a Syllabus
- Motivating Students
- Dealing With Cheating
- Discouraging & Detecting Plagiarism
- Diversity & Creating an Inclusive Classroom
- Harassment & Discrimination
- Professional Conduct
- Foundations of Good Teaching
- Student Engagement
- Assessment Strategies
- Course Design
- Student Resources
- Teaching Tips
- Graduate Teacher Certificate
- Certificate in Foundations of Teaching
- Teacher Scholar Certificate
- Certificate in Technology-Enhanced Teaching
- Master Course in Online Teaching (MCOT)
- 2022 Celebration of College Teaching
- 2023 Celebration of College Teaching
- Hybrid Teaching and Learning Certificate
- 2024 Celebration of College Teaching
- Classroom Observation Etiquette
- Teaching Philosophy Statement
- Pedagogical Literature Review
- Scholarship of Teaching and Learning
- Instructor Stories
- Podcast: Teach Talk Listen Learn
- Universal Design for Learning
Sign-Up to receive Teaching and Learning news and events
Problem-Based Learning (PBL) is a teaching method in which complex real-world problems are used as the vehicle to promote student learning of concepts and principles as opposed to direct presentation of facts and concepts. In addition to course content, PBL can promote the development of critical thinking skills, problem-solving abilities, and communication skills. It can also provide opportunities for working in groups, finding and evaluating research materials, and life-long learning (Duch et al, 2001).
PBL can be incorporated into any learning situation. In the strictest definition of PBL, the approach is used over the entire semester as the primary method of teaching. However, broader definitions and uses range from including PBL in lab and design classes, to using it simply to start a single discussion. PBL can also be used to create assessment items. The main thread connecting these various uses is the real-world problem.
Any subject area can be adapted to PBL with a little creativity. While the core problems will vary among disciplines, there are some characteristics of good PBL problems that transcend fields (Duch, Groh, and Allen, 2001):
- The problem must motivate students to seek out a deeper understanding of concepts.
- The problem should require students to make reasoned decisions and to defend them.
- The problem should incorporate the content objectives in such a way as to connect it to previous courses/knowledge.
- If used for a group project, the problem needs a level of complexity to ensure that the students must work together to solve it.
- If used for a multistage project, the initial steps of the problem should be open-ended and engaging to draw students into the problem.
The problems can come from a variety of sources: newspapers, magazines, journals, books, textbooks, and television/ movies. Some are in such form that they can be used with little editing; however, others need to be rewritten to be of use. The following guidelines from The Power of Problem-Based Learning (Duch et al, 2001) are written for creating PBL problems for a class centered around the method; however, the general ideas can be applied in simpler uses of PBL:
- Choose a central idea, concept, or principle that is always taught in a given course, and then think of a typical end-of-chapter problem, assignment, or homework that is usually assigned to students to help them learn that concept. List the learning objectives that students should meet when they work through the problem.
- Think of a real-world context for the concept under consideration. Develop a storytelling aspect to an end-of-chapter problem, or research an actual case that can be adapted, adding some motivation for students to solve the problem. More complex problems will challenge students to go beyond simple plug-and-chug to solve it. Look at magazines, newspapers, and articles for ideas on the story line. Some PBL practitioners talk to professionals in the field, searching for ideas of realistic applications of the concept being taught.
- What will the first page (or stage) look like? What open-ended questions can be asked? What learning issues will be identified?
- How will the problem be structured?
- How long will the problem be? How many class periods will it take to complete?
- Will students be given information in subsequent pages (or stages) as they work through the problem?
- What resources will the students need?
- What end product will the students produce at the completion of the problem?
- Write a teacher's guide detailing the instructional plans on using the problem in the course. If the course is a medium- to large-size class, a combination of mini-lectures, whole-class discussions, and small group work with regular reporting may be necessary. The teacher's guide can indicate plans or options for cycling through the pages of the problem interspersing the various modes of learning.
- The final step is to identify key resources for students. Students need to learn to identify and utilize learning resources on their own, but it can be helpful if the instructor indicates a few good sources to get them started. Many students will want to limit their research to the Internet, so it will be important to guide them toward the library as well.
The method for distributing a PBL problem falls under three closely related teaching techniques: case studies, role-plays, and simulations. Case studies are presented to students in written form. Role-plays have students improvise scenes based on character descriptions given. Today, simulations often involve computer-based programs. Regardless of which technique is used, the heart of the method remains the same: the real-world problem.
Where can I learn more?
- PBL through the Institute for Transforming Undergraduate Education at the University of Delaware
- Duch, B. J., Groh, S. E, & Allen, D. E. (Eds.). (2001). The power of problem-based learning . Sterling, VA: Stylus.
- Grasha, A. F. (1996). Teaching with style: A practical guide to enhancing learning by understanding teaching and learning styles. Pittsburgh: Alliance Publishers.
Center for Innovation in Teaching & Learning
249 Armory Building 505 East Armory Avenue Champaign, IL 61820
217 333-1462
Email: [email protected]
Office of the Provost
- Faculty & Staff
Teaching problem solving
Strategies for teaching problem solving apply across disciplines and instructional contexts. First, introduce the problem and explain how people in your discipline generally make sense of the given information. Then, explain how to apply these approaches to solve the problem.
Introducing the problem
Explaining how people in your discipline understand and interpret these types of problems can help students develop the skills they need to understand the problem (and find a solution). After introducing how you would go about solving a problem, you could then ask students to:
- frame the problem in their own words
- define key terms and concepts
- determine statements that accurately represent the givens of a problem
- identify analogous problems
- determine what information is needed to solve the problem
Working on solutions
In the solution phase, one develops and then implements a coherent plan for solving the problem. As you help students with this phase, you might ask them to:
- identify the general model or procedure they have in mind for solving the problem
- set sub-goals for solving the problem
- identify necessary operations and steps
- draw conclusions
- carry out necessary operations
You can help students tackle a problem effectively by asking them to:
- systematically explain each step and its rationale
- explain how they would approach solving the problem
- help you solve the problem by posing questions at key points in the process
- work together in small groups (3 to 5 students) to solve the problem and then have the solution presented to the rest of the class (either by you or by a student in the group)
In all cases, the more you get the students to articulate their own understandings of the problem and potential solutions, the more you can help them develop their expertise in approaching problems in your discipline.
Why Every Educator Needs to Teach Problem-Solving Skills
Strong problem-solving skills will help students be more resilient and will increase their academic and career success .
Want to learn more about how to measure and teach students’ higher-order skills, including problem solving, critical thinking, and written communication?
Problem-solving skills are essential in school, careers, and life.
Problem-solving skills are important for every student to master. They help individuals navigate everyday life and find solutions to complex issues and challenges. These skills are especially valuable in the workplace, where employees are often required to solve problems and make decisions quickly and effectively.
Problem-solving skills are also needed for students’ personal growth and development because they help individuals overcome obstacles and achieve their goals. By developing strong problem-solving skills, students can improve their overall quality of life and become more successful in their personal and professional endeavors.
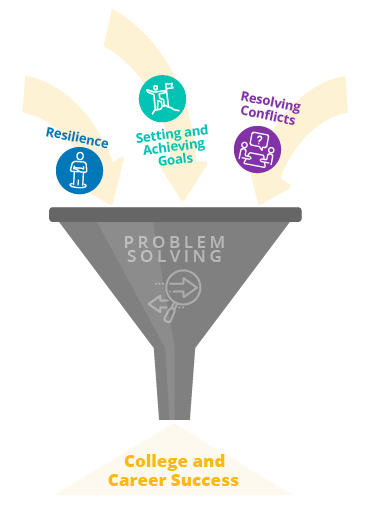
Problem-Solving Skills Help Students…
develop resilience.
Problem-solving skills are an integral part of resilience and the ability to persevere through challenges and adversity. To effectively work through and solve a problem, students must be able to think critically and creatively. Critical and creative thinking help students approach a problem objectively, analyze its components, and determine different ways to go about finding a solution.
This process in turn helps students build self-efficacy . When students are able to analyze and solve a problem, this increases their confidence, and they begin to realize the power they have to advocate for themselves and make meaningful change.
When students gain confidence in their ability to work through problems and attain their goals, they also begin to build a growth mindset . According to leading resilience researcher, Carol Dweck, “in a growth mindset, people believe that their most basic abilities can be developed through dedication and hard work—brains and talent are just the starting point. This view creates a love of learning and a resilience that is essential for great accomplishment.”
Set and Achieve Goals
Students who possess strong problem-solving skills are better equipped to set and achieve their goals. By learning how to identify problems, think critically, and develop solutions, students can become more self-sufficient and confident in their ability to achieve their goals. Additionally, problem-solving skills are used in virtually all fields, disciplines, and career paths, which makes them important for everyone. Building strong problem-solving skills will help students enhance their academic and career performance and become more competitive as they begin to seek full-time employment after graduation or pursue additional education and training.
Resolve Conflicts
In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes “thinking outside the box” and approaching a conflict by searching for different solutions. This is a very different (and more effective!) method than a more stagnant approach that focuses on placing blame or getting stuck on elements of a situation that can’t be changed.
While it’s natural to get frustrated or feel stuck when working through a conflict, students with strong problem-solving skills will be able to work through these obstacles, think more rationally, and address the situation with a more solution-oriented approach. These skills will be valuable for students in school, their careers, and throughout their lives.
Achieve Success
We are all faced with problems every day. Problems arise in our personal lives, in school and in our jobs, and in our interactions with others. Employers especially are looking for candidates with strong problem-solving skills. In today’s job market, most jobs require the ability to analyze and effectively resolve complex issues. Students with strong problem-solving skills will stand out from other applicants and will have a more desirable skill set.
In a recent opinion piece published by The Hechinger Report , Virgel Hammonds, Chief Learning Officer at KnowledgeWorks, stated “Our world presents increasingly complex challenges. Education must adapt so that it nurtures problem solvers and critical thinkers.” Yet, the “traditional K–12 education system leaves little room for students to engage in real-world problem-solving scenarios.” This is the reason that a growing number of K–12 school districts and higher education institutions are transforming their instructional approach to personalized and competency-based learning, which encourage students to make decisions, problem solve and think critically as they take ownership of and direct their educational journey.
Problem-Solving Skills Can Be Measured and Taught
Research shows that problem-solving skills can be measured and taught. One effective method is through performance-based assessments which require students to demonstrate or apply their knowledge and higher-order skills to create a response or product or do a task.
What Are Performance-Based Assessments?

With the No Child Left Behind Act (2002), the use of standardized testing became the primary way to measure student learning in the U.S. The legislative requirements of this act shifted the emphasis to standardized testing, and this led to a decline in nontraditional testing methods .
But many educators, policy makers, and parents have concerns with standardized tests. Some of the top issues include that they don’t provide feedback on how students can perform better, they don’t value creativity, they are not representative of diverse populations, and they can be disadvantageous to lower-income students.
While standardized tests are still the norm, U.S. Secretary of Education Miguel Cardona is encouraging states and districts to move away from traditional multiple choice and short response tests and instead use performance-based assessment, competency-based assessments, and other more authentic methods of measuring students abilities and skills rather than rote learning.
Performance-based assessments measure whether students can apply the skills and knowledge learned from a unit of study. Typically, a performance task challenges students to use their higher-order skills to complete a project or process. Tasks can range from an essay to a complex proposal or design.
Preview a Performance-Based Assessment
Want a closer look at how performance-based assessments work? Preview CAE’s K–12 and Higher Education assessments and see how CAE’s tools help students develop critical thinking, problem-solving, and written communication skills.
Performance-Based Assessments Help Students Build and Practice Problem-Solving Skills
In addition to effectively measuring students’ higher-order skills, including their problem-solving skills, performance-based assessments can help students practice and build these skills. Through the assessment process, students are given opportunities to practically apply their knowledge in real-world situations. By demonstrating their understanding of a topic, students are required to put what they’ve learned into practice through activities such as presentations, experiments, and simulations.
This type of problem-solving assessment tool requires students to analyze information and choose how to approach the presented problems. This process enhances their critical thinking skills and creativity, as well as their problem-solving skills. Unlike traditional assessments based on memorization or reciting facts, performance-based assessments focus on the students’ decisions and solutions, and through these tasks students learn to bridge the gap between theory and practice.
Performance-based assessments like CAE’s College and Career Readiness Assessment (CRA+) and Collegiate Learning Assessment (CLA+) provide students with in-depth reports that show them which higher-order skills they are strongest in and which they should continue to develop. This feedback helps students and their teachers plan instruction and supports to deepen their learning and improve their mastery of critical skills.

Explore CAE’s Problem-Solving Assessments
CAE offers performance-based assessments that measure student proficiency in higher-order skills including problem solving, critical thinking, and written communication.
- College and Career Readiness Assessment (CCRA+) for secondary education and
- Collegiate Learning Assessment (CLA+) for higher education.
Our solution also includes instructional materials, practice models, and professional development.
We can help you create a program to build students’ problem-solving skills that includes:
- Measuring students’ problem-solving skills through a performance-based assessment
- Using the problem-solving assessment data to inform instruction and tailor interventions
- Teaching students problem-solving skills and providing practice opportunities in real-life scenarios
- Supporting educators with quality professional development
Get started with our problem-solving assessment tools to measure and build students’ problem-solving skills today! These skills will be invaluable to students now and in the future.

Ready to Get Started?
Learn more about cae’s suite of products and let’s get started measuring and teaching students important higher-order skills like problem solving..
Teaching Problem-Solving Skills
Many instructors design opportunities for students to solve “problems”. But are their students solving true problems or merely participating in practice exercises? The former stresses critical thinking and decision making skills whereas the latter requires only the application of previously learned procedures.
Problem solving is often broadly defined as "the ability to understand the environment, identify complex problems, review related information to develop, evaluate strategies and implement solutions to build the desired outcome" (Fissore, C. et al, 2021). True problem solving is the process of applying a method – not known in advance – to a problem that is subject to a specific set of conditions and that the problem solver has not seen before, in order to obtain a satisfactory solution.
Below you will find some basic principles for teaching problem solving and one model to implement in your classroom teaching.
Principles for teaching problem solving
- Model a useful problem-solving method . Problem solving can be difficult and sometimes tedious. Show students how to be patient and persistent, and how to follow a structured method, such as Woods’ model described below. Articulate your method as you use it so students see the connections.
- Teach within a specific context . Teach problem-solving skills in the context in which they will be used by students (e.g., mole fraction calculations in a chemistry course). Use real-life problems in explanations, examples, and exams. Do not teach problem solving as an independent, abstract skill.
- Help students understand the problem . In order to solve problems, students need to define the end goal. This step is crucial to successful learning of problem-solving skills. If you succeed at helping students answer the questions “what?” and “why?”, finding the answer to “how?” will be easier.
- Take enough time . When planning a lecture/tutorial, budget enough time for: understanding the problem and defining the goal (both individually and as a class); dealing with questions from you and your students; making, finding, and fixing mistakes; and solving entire problems in a single session.
- Ask questions and make suggestions . Ask students to predict “what would happen if …” or explain why something happened. This will help them to develop analytical and deductive thinking skills. Also, ask questions and make suggestions about strategies to encourage students to reflect on the problem-solving strategies that they use.
- Link errors to misconceptions . Use errors as evidence of misconceptions, not carelessness or random guessing. Make an effort to isolate the misconception and correct it, then teach students to do this by themselves. We can all learn from mistakes.
Woods’ problem-solving model
Define the problem.
- The system . Have students identify the system under study (e.g., a metal bridge subject to certain forces) by interpreting the information provided in the problem statement. Drawing a diagram is a great way to do this.
- Known(s) and concepts . List what is known about the problem, and identify the knowledge needed to understand (and eventually) solve it.
- Unknown(s) . Once you have a list of knowns, identifying the unknown(s) becomes simpler. One unknown is generally the answer to the problem, but there may be other unknowns. Be sure that students understand what they are expected to find.
- Units and symbols . One key aspect in problem solving is teaching students how to select, interpret, and use units and symbols. Emphasize the use of units whenever applicable. Develop a habit of using appropriate units and symbols yourself at all times.
- Constraints . All problems have some stated or implied constraints. Teach students to look for the words "only", "must", "neglect", or "assume" to help identify the constraints.
- Criteria for success . Help students consider, from the beginning, what a logical type of answer would be. What characteristics will it possess? For example, a quantitative problem will require an answer in some form of numerical units (e.g., $/kg product, square cm, etc.) while an optimization problem requires an answer in the form of either a numerical maximum or minimum.
Think about it
- “Let it simmer”. Use this stage to ponder the problem. Ideally, students will develop a mental image of the problem at hand during this stage.
- Identify specific pieces of knowledge . Students need to determine by themselves the required background knowledge from illustrations, examples and problems covered in the course.
- Collect information . Encourage students to collect pertinent information such as conversion factors, constants, and tables needed to solve the problem.
Plan a solution
- Consider possible strategies . Often, the type of solution will be determined by the type of problem. Some common problem-solving strategies are: compute; simplify; use an equation; make a model, diagram, table, or chart; or work backwards.
- Choose the best strategy . Help students to choose the best strategy by reminding them again what they are required to find or calculate.
Carry out the plan
- Be patient . Most problems are not solved quickly or on the first attempt. In other cases, executing the solution may be the easiest step.
- Be persistent . If a plan does not work immediately, do not let students get discouraged. Encourage them to try a different strategy and keep trying.
Encourage students to reflect. Once a solution has been reached, students should ask themselves the following questions:
- Does the answer make sense?
- Does it fit with the criteria established in step 1?
- Did I answer the question(s)?
- What did I learn by doing this?
- Could I have done the problem another way?
If you would like support applying these tips to your own teaching, CTE staff members are here to help. View the CTE Support page to find the most relevant staff member to contact.
- Fissore, C., Marchisio, M., Roman, F., & Sacchet, M. (2021). Development of problem solving skills with Maple in higher education. In: Corless, R.M., Gerhard, J., Kotsireas, I.S. (eds) Maple in Mathematics Education and Research. MC 2020. Communications in Computer and Information Science, vol 1414. Springer, Cham. https://doi.org/10.1007/978-3-030-81698-8_15
- Foshay, R., & Kirkley, J. (1998). Principles for Teaching Problem Solving. TRO Learning Inc., Edina MN. (PDF) Principles for Teaching Problem Solving (researchgate.net)
- Hayes, J.R. (1989). The Complete Problem Solver. 2nd Edition. Hillsdale, NJ: Lawrence Erlbaum Associates.
- Woods, D.R., Wright, J.D., Hoffman, T.W., Swartman, R.K., Doig, I.D. (1975). Teaching Problem solving Skills.
- Engineering Education. Vol 1, No. 1. p. 238. Washington, DC: The American Society for Engineering Education.
Catalog search
Teaching tip categories.
- Assessment and feedback
- Blended Learning and Educational Technologies
- Career Development
- Course Design
- Course Implementation
- Inclusive Teaching and Learning
- Learning activities
- Support for Student Learning
- Support for TAs
- Learning activities ,

Problem based learning: a teacher's guide
December 10, 2021
Find out how teachers use problem-based learning models to improve engagement and drive attainment.
Main, P (2021, December 10). Problem based learning: a teacher's guide. Retrieved from https://www.structural-learning.com/post/problem-based-learning-a-teachers-guide
What is problem-based learning?
Problem-based learning (PBL) is a style of teaching that encourages students to become the drivers of their learning process . Problem-based learning involves complex learning issues from real-world problems and makes them the classroom's topic of discussion ; encouraging students to understand concepts through problem-solving skills rather than simply learning facts. When schools find time in the curriculum for this style of teaching it offers students an authentic vehicle for the integration of knowledge .
Embracing this pedagogical approach enables schools to balance subject knowledge acquisition with a skills agenda . Often used in medical education, this approach has equal significance in mainstream education where pupils can apply their knowledge to real-life problems.
PBL is not only helpful in learning course content , but it can also promote the development of problem-solving abilities , critical thinking skills , and communication skills while providing opportunities to work in groups , find and analyse research materials , and take part in life-long learning .
PBL is a student-centred teaching method in which students understand a topic by working in groups. They work out an open-ended problem , which drives the motivation to learn. These sorts of theories of teaching do require schools to invest time and resources into supporting self-directed learning. Not all curriculum knowledge is best acquired through this process, rote learning still has its place in certain situations. In this article, we will look at how we can equip our students to take more ownership of the learning process and utilise more sophisticated ways for the integration of knowledge .
Philosophical Underpinnings of PBL
Problem-Based Learning (PBL), with its roots in the philosophies of John Dewey, Maria Montessori, and Jerome Bruner, aligns closely with the social constructionist view of learning. This approach positions learners as active participants in the construction of knowledge, contrasting with traditional models of instruction where learners are seen as passive recipients of information.
Dewey, a seminal figure in progressive education, advocated for active learning and real-world problem-solving, asserting that learning is grounded in experience and interaction. In PBL, learners tackle complex, real-world problems, which mirrors Dewey's belief in the interconnectedness of education and practical life.
Montessori also endorsed learner-centric, self-directed learning, emphasizing the child's potential to construct their own learning experiences. This parallels with PBL’s emphasis on self-directed learning, where students take ownership of their learning process.
Jerome Bruner’s theories underscored the idea of learning as an active, social process. His concept of a 'spiral curriculum' – where learning is revisited in increasing complexity – can be seen reflected in the iterative problem-solving process in PBL.
Webb’s Depth of Knowledge (DOK) framework aligns with PBL as it encourages higher-order cognitive skills. The complex tasks in PBL often demand analytical and evaluative skills (Webb's DOK levels 3 and 4) as students engage with the problem, devise a solution, and reflect on their work.
The effectiveness of PBL is supported by psychological theories like the information processing theory, which highlights the role of active engagement in enhancing memory and recall. A study by Strobel and Van Barneveld (2009) found that PBL students show improved retention of knowledge, possibly due to the deep cognitive processing involved.
As cognitive scientist Daniel Willingham aptly puts it, "Memory is the residue of thought." PBL encourages learners to think critically and deeply, enhancing both learning and retention.
Here's a quick overview:
- John Dewey : Emphasized learning through experience and the importance of problem-solving.
- Maria Montessori : Advocated for child-centered, self-directed learning.
- Jerome Bruner : Underlined learning as a social process and proposed the spiral curriculum.
- Webb’s DOK : Supports PBL's encouragement of higher-order thinking skills.
- Information Processing Theory : Reinforces the notion that active engagement in PBL enhances memory and recall.
This deep-rooted philosophical and psychological framework strengthens the validity of the problem-based learning approach, confirming its beneficial role in promoting valuable cognitive skills and fostering positive student learning outcomes.

What are the characteristics of problem-based learning?
Adding a little creativity can change a topic into a problem-based learning activity. The following are some of the characteristics of a good PBL model:
- The problem encourages students to search for a deeper understanding of content knowledge;
- Students are responsible for their learning. PBL has a student-centred learning approach . Students' motivation increases when responsibility for the process and solution to the problem rests with the learner;
- The problem motivates pupils to gain desirable learning skills and to defend well-informed decisions ;
- The problem connects the content learning goals with the previous knowledge. PBL allows students to access, integrate and study information from multiple disciplines that might relate to understanding and resolving a specific problem—just as persons in the real world recollect and use the application of knowledge that they have gained from diverse sources in their life.
- In a multistage project, the first stage of the problem must be engaging and open-ended to make students interested in the problem. In the real world, problems are poorly-structured. Research suggests that well-structured problems make students less invested and less motivated in the development of the solution. The problem simulations used in problem-based contextual learning are less structured to enable students to make a free inquiry.

- In a group project, the problem must have some level of complexity that motivates students towards knowledge acquisition and to work together for finding the solution. PBL involves collaboration between learners. In professional life, most people will find themselves in employment where they would work productively and share information with others. PBL leads to the development of such essential skills . In a PBL session, the teacher would ask questions to make sure that knowledge has been shared between pupils;
- At the end of each problem or PBL, self and peer assessments are performed. The main purpose of assessments is to sharpen a variety of metacognitive processing skills and to reinforce self-reflective learning.
- Student assessments would evaluate student progress towards the objectives of problem-based learning. The learning goals of PBL are both process-based and knowledge-based. Students must be assessed on both these dimensions to ensure that they are prospering as intended from the PBL approach. Students must be able to identify and articulate what they understood and what they learned.

Why is Problem-based learning a significant skill?
Using Problem-Based Learning across a school promotes critical competence, inquiry , and knowledge application in social, behavioural and biological sciences. Practice-based learning holds a strong track record of successful learning outcomes in higher education settings such as graduates of Medical Schools.
Educational models using PBL can improve learning outcomes by teaching students how to implement theory into practice and build problem-solving skills. For example, within the field of health sciences education, PBL makes the learning process for nurses and medical students self-centred and promotes their teamwork and leadership skills. Within primary and secondary education settings, this model of teaching, with the right sort of collaborative tools , can advance the wider skills development valued in society.
At Structural Learning, we have been developing a self-assessment tool designed to monitor the progress of children. Utilising these types of teaching theories curriculum wide can help a school develop the learning behaviours our students will need in the workplace.
Curriculum wide collaborative tools include Writers Block and the Universal Thinking Framework . Along with graphic organisers, these tools enable children to collaborate and entertain different perspectives that they might not otherwise see. Putting learning in action by using the block building methodology enables children to reach their learning goals by experimenting and iterating.

How is problem-based learning different from inquiry-based learning?
The major difference between inquiry-based learning and PBL relates to the role of the teacher . In the case of inquiry-based learning, the teacher is both a provider of classroom knowledge and a facilitator of student learning (expecting/encouraging higher-order thinking). On the other hand, PBL is a deep learning approach, in which the teacher is the supporter of the learning process and expects students to have clear thinking, but the teacher is not the provider of classroom knowledge about the problem—the responsibility of providing information belongs to the learners themselves.
As well as being used systematically in medical education, this approach has significant implications for integrating learning skills into mainstream classrooms .
Using a critical thinking disposition inventory, schools can monitor the wider progress of their students as they apply their learning skills across the traditional curriculum. Authentic problems call students to apply their critical thinking abilities in new and purposeful ways. As students explain their ideas to one another, they develop communication skills that might not otherwise be nurtured.
Depending on the curriculum being delivered by a school, there may well be an emphasis on building critical thinking abilities in the classroom. Within the International Baccalaureate programs, these life-long skills are often cited in the IB learner profile . Critical thinking dispositions are highly valued in the workplace and this pedagogical approach can be used to harness these essential 21st-century skills.

What are the Benefits of Problem-Based Learning?
Student-led Problem-Based Learning is one of the most useful ways to make students drivers of their learning experience. It makes students creative, innovative, logical and open-minded. The educational practice of Problem-Based Learning also provides opportunities for self-directed and collaborative learning with others in an active learning and hands-on process. Below are the most significant benefits of problem-based learning processes:
- Self-learning: As a self-directed learning method, problem-based learning encourages children to take responsibility and initiative for their learning processes . As children use creativity and research, they develop skills that will help them in their adulthood.
- Engaging : Students don't just listen to the teacher, sit back and take notes. Problem-based learning processes encourages students to take part in learning activities, use learning resources , stay active , think outside the box and apply critical thinking skills to solve problems.
- Teamwork : Most of the problem-based learning issues involve students collaborative learning to find a solution. The educational practice of PBL builds interpersonal skills, listening and communication skills and improves the skills of collaboration and compromise.
- Intrinsic Rewards: In most problem-based learning projects, the reward is much bigger than good grades. Students gain the pride and satisfaction of finding an innovative solution, solving a riddle, or creating a tangible product.
- Transferable Skills: The acquisition of knowledge through problem-based learning strategies don't just help learners in one class or a single subject area. Students can apply these skills to a plethora of subject matter as well as in real life.
- Multiple Learning Opportunities : A PBL model offers an open-ended problem-based acquisition of knowledge, which presents a real-world problem and asks learners to come up with well-constructed responses. Students can use multiple sources such as they can access online resources, using their prior knowledge, and asking momentous questions to brainstorm and come up with solid learning outcomes. Unlike traditional approaches , there might be more than a single right way to do something, but this process motivates learners to explore potential solutions whilst staying active.

Embracing problem-based learning
Problem-based learning can be seen as a deep learning approach and when implemented effectively as part of a broad and balanced curriculum , a successful teaching strategy in education. PBL has a solid epistemological and philosophical foundation and a strong track record of success in multiple areas of study. Learners must experience problem-based learning methods and engage in positive solution-finding activities. PBL models allow learners to gain knowledge through real-world problems, which offers more strength to their understanding and helps them find the connection between classroom learning and the real world at large.
As they solve problems, students can evolve as individuals and team-mates. One word of caution, not all classroom tasks will lend themselves to this learning theory. Take spellings , for example, this is usually delivered with low-stakes quizzing through a practice-based learning model. PBL allows students to apply their knowledge creatively but they need to have a certain level of background knowledge to do this, rote learning might still have its place after all.
Key Concepts and considerations for school leaders
1. Problem Based Learning (PBL)
Problem-based learning (PBL) is an educational method that involves active student participation in solving authentic problems. Students are given a task or question that they must answer using their prior knowledge and resources. They then collaborate with each other to come up with solutions to the problem. This collaborative effort leads to deeper learning than traditional lectures or classroom instruction .
Key question: Inside a traditional curriculum , what opportunities across subject areas do you immediately see?
2. Deep Learning
Deep learning is a term used to describe the ability to learn concepts deeply. For example, if you were asked to memorize a list of numbers, you would probably remember the first five numbers easily, but the last number would be difficult to recall. However, if you were taught to understand the concept behind the numbers, you would be able to remember the last number too.
Key question: How will you make sure that students use a full range of learning styles and learning skills ?
3. Epistemology
Epistemology is the branch of philosophy that deals with the nature of knowledge . It examines the conditions under which something counts as knowledge.
Key question: As well as focusing on critical thinking dispositions, what subject knowledge should the students understand?
4. Philosophy
Philosophy is the study of general truths about human life. Philosophers examine questions such as “What makes us happy?”, “How should we live our lives?”, and “Why does anything exist?”
Key question: Are there any opportunities for embracing philosophical enquiry into the project to develop critical thinking abilities ?
5. Curriculum
A curriculum is a set of courses designed to teach specific subjects. These courses may include mathematics , science, social studies, language arts, etc.
Key question: How will subject leaders ensure that the integrity of the curriculum is maintained?
6. Broad and Balanced Curriculum
Broad and balanced curricula are those that cover a wide range of topics. Some examples of these types of curriculums include AP Biology, AP Chemistry, AP English Language, AP Physics 1, AP Psychology , AP Spanish Literature, AP Statistics, AP US History, AP World History, IB Diploma Programme, IB Primary Years Program, IB Middle Years Program, IB Diploma Programme .
Key question: Are the teachers who have identified opportunities for a problem-based curriculum?
7. Successful Teaching Strategy
Successful teaching strategies involve effective communication techniques, clear objectives, and appropriate assessments. Teachers must ensure that their lessons are well-planned and organized. They must also provide opportunities for students to interact with one another and share information.
Key question: What pedagogical approaches and teaching strategies will you use?
8. Positive Solution Finding
Positive solution finding is a type of problem-solving where students actively seek out answers rather than passively accept what others tell them.
Key question: How will you ensure your problem-based curriculum is met with a positive mindset from students and teachers?
9. Real World Application
Real-world application refers to applying what students have learned in class to situations that occur in everyday life.
Key question: Within your local school community , are there any opportunities to apply knowledge and skills to real-life problems?
10. Creativity
Creativity is the ability to think of ideas that no one else has thought of yet. Creative thinking requires divergent thinking, which means thinking in different directions.
Key question: What teaching techniques will you use to enable children to generate their own ideas ?
11. Teamwork
Teamwork is the act of working together towards a common goal. Teams often consist of two or more people who work together to achieve a shared objective.
Key question: What opportunities are there to engage students in dialogic teaching methods where they talk their way through the problem?
12. Knowledge Transfer
Knowledge transfer occurs when teachers use their expertise to help students develop skills and abilities .
Key question: Can teachers be able to track the success of the project using improvement scores?
13. Active Learning
Active learning is any form of instruction that engages students in the learning process. Examples of active learning include group discussions, role-playing, debates, presentations, and simulations .
Key question: Will there be an emphasis on learning to learn and developing independent learning skills ?
14. Student Engagement
Student engagement is the degree to which students feel motivated to participate in academic activities.
Key question: Are there any tools available to monitor student engagement during the problem-based curriculum ?

Enhance Learner Outcomes Across Your School
Download an Overview of our Support and Resources
We'll send it over now.
Please fill in the details so we can send over the resources.
What type of school are you?
We'll get you the right resource
Is your school involved in any staff development projects?
Are your colleagues running any research projects or courses?
Do you have any immediate school priorities?
Please check the ones that apply.

Download your resource
Thanks for taking the time to complete this form, submit the form to get the tool.
Classroom Practice

Problem-Based Learning (PBL)
What is Problem-Based Learning (PBL)? PBL is a student-centered approach to learning that involves groups of students working to solve a real-world problem, quite different from the direct teaching method of a teacher presenting facts and concepts about a specific subject to a classroom of students. Through PBL, students not only strengthen their teamwork, communication, and research skills, but they also sharpen their critical thinking and problem-solving abilities essential for life-long learning.
See also: Just-in-Time Teaching
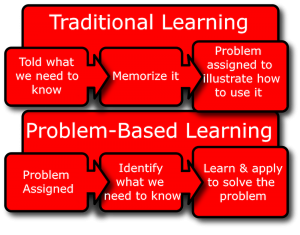
In implementing PBL, the teaching role shifts from that of the more traditional model that follows a linear, sequential pattern where the teacher presents relevant material, informs the class what needs to be done, and provides details and information for students to apply their knowledge to a given problem. With PBL, the teacher acts as a facilitator; the learning is student-driven with the aim of solving the given problem (note: the problem is established at the onset of learning opposed to being presented last in the traditional model). Also, the assignments vary in length from relatively short to an entire semester with daily instructional time structured for group work.

By working with PBL, students will:
- Become engaged with open-ended situations that assimilate the world of work
- Participate in groups to pinpoint what is known/ not known and the methods of finding information to help solve the given problem.
- Investigate a problem; through critical thinking and problem solving, brainstorm a list of unique solutions.
- Analyze the situation to see if the real problem is framed or if there are other problems that need to be solved.
How to Begin PBL
- Establish the learning outcomes (i.e., what is it that you want your students to really learn and to be able to do after completing the learning project).
- Find a real-world problem that is relevant to the students; often the problems are ones that students may encounter in their own life or future career.
- Discuss pertinent rules for working in groups to maximize learning success.
- Practice group processes: listening, involving others, assessing their work/peers.
- Explore different roles for students to accomplish the work that needs to be done and/or to see the problem from various perspectives depending on the problem (e.g., for a problem about pollution, different roles may be a mayor, business owner, parent, child, neighboring city government officials, etc.).
- Determine how the project will be evaluated and assessed. Most likely, both self-assessment and peer-assessment will factor into the assignment grade.
Designing Classroom Instruction
See also: Inclusive Teaching Strategies
- Take the curriculum and divide it into various units. Decide on the types of problems that your students will solve. These will be your objectives.
- Determine the specific problems that most likely have several answers; consider student interest.
- Arrange appropriate resources available to students; utilize other teaching personnel to support students where needed (e.g., media specialists to orientate students to electronic references).
- Decide on presentation formats to communicate learning (e.g., individual paper, group PowerPoint, an online blog, etc.) and appropriate grading mechanisms (e.g., rubric).
- Decide how to incorporate group participation (e.g., what percent, possible peer evaluation, etc.).
How to Orchestrate a PBL Activity
- Explain Problem-Based Learning to students: its rationale, daily instruction, class expectations, grading.
- Serve as a model and resource to the PBL process; work in-tandem through the first problem
- Help students secure various resources when needed.
- Supply ample class time for collaborative group work.
- Give feedback to each group after they share via the established format; critique the solution in quality and thoroughness. Reinforce to the students that the prior thinking and reasoning process in addition to the solution are important as well.
Teacher’s Role in PBL
See also: Flipped teaching
As previously mentioned, the teacher determines a problem that is interesting, relevant, and novel for the students. It also must be multi-faceted enough to engage students in doing research and finding several solutions. The problems stem from the unit curriculum and reflect possible use in future work situations.
- Determine a problem aligned with the course and your students. The problem needs to be demanding enough that the students most likely cannot solve it on their own. It also needs to teach them new skills. When sharing the problem with students, state it in a narrative complete with pertinent background information without excessive information. Allow the students to find out more details as they work on the problem.
- Place students in groups, well-mixed in diversity and skill levels, to strengthen the groups. Help students work successfully. One way is to have the students take on various roles in the group process after they self-assess their strengths and weaknesses.
- Support the students with understanding the content on a deeper level and in ways to best orchestrate the various stages of the problem-solving process.
The Role of the Students
See also: ADDIE model
The students work collaboratively on all facets of the problem to determine the best possible solution.
- Analyze the problem and the issues it presents. Break the problem down into various parts. Continue to read, discuss, and think about the problem.
- Construct a list of what is known about the problem. What do your fellow students know about the problem? Do they have any experiences related to the problem? Discuss the contributions expected from the team members. What are their strengths and weaknesses? Follow the rules of brainstorming (i.e., accept all answers without passing judgment) to generate possible solutions for the problem.
- Get agreement from the team members regarding the problem statement.
- Put the problem statement in written form.
- Solicit feedback from the teacher.
- Be open to changing the written statement based on any new learning that is found or feedback provided.
- Generate a list of possible solutions. Include relevant thoughts, ideas, and educated guesses as well as causes and possible ways to solve it. Then rank the solutions and select the solution that your group is most likely to perceive as the best in terms of meeting success.
- Include what needs to be known and done to solve the identified problems.
- Prioritize the various action steps.
- Consider how the steps impact the possible solutions.
- See if the group is in agreement with the timeline; if not, decide how to reach agreement.
- What resources are available to help (e.g., textbooks, primary/secondary sources, Internet).
- Determine research assignments per team members.
- Establish due dates.
- Determine how your group will present the problem solution and also identify the audience. Usually, in PBL, each group presents their solutions via a team presentation either to the class of other students or to those who are related to the problem.
- Both the process and the results of the learning activity need to be covered. Include the following: problem statement, questions, data gathered, data analysis, reasons for the solution(s) and/or any recommendations reflective of the data analysis.
- A well-stated problem and conclusion.
- The process undertaken by the group in solving the problem, the various options discussed, and the resources used.
- Your solution’s supporting documents, guests, interviews and their purpose to be convincing to your audience.
- In addition, be prepared for any audience comments and questions. Determine who will respond and if your team doesn’t know the answer, admit this and be open to looking into the question at a later date.
- Reflective thinking and transfer of knowledge are important components of PBL. This helps the students be more cognizant of their own learning and teaches them how to ask appropriate questions to address problems that need to be solved. It is important to look at both the individual student and the group effort/delivery throughout the entire process. From here, you can better determine what was learned and how to improve. The students should be asked how they can apply what was learned to a different situation, to their own lives, and to other course projects.
See also: Kirkpatrick Model: Four Levels of Learning Evaluation
I am a professor of Educational Technology. I have worked at several elite universities. I hold a PhD degree from the University of Illinois and a master's degree from Purdue University.
Similar Posts
Definitions of the addie model.
What is the ADDIE Model? This article attempts to explain the ADDIE model by providing different definitions. Basically, ADDIE is a conceptual framework. ADDIE is the most commonly used instructional design framework and…
Robert Gagné’s Taxonomy of Learning
Gagne classified learning outcomes into five major categories: verbal information, intellectual skills, cognitive strategies, motor skills and attitudes. What is learning to Gagné? As outlined in his 9-events of instruction, Gagne believed that learning was…
Open Source Learning Management Systems (LMS)
Learning Management Systems (LMSs) are becoming a vital part of classrooms in the 21th Century. This is a list of open source learning management systems. By open source we mean that source code of…
Adaptive Learning: What is It, What are its Benefits and How Does it Work?
People learn in many different ways. Adaptive learning has sought to address differences in ability by targeting teaching practices. The use of adaptive models, ranging from technological programs to intelligent systems, can be…
Instructional Design
What is Instructional Design The Association for Educational Communications and Technology (AECT) defines instructional design as “the theory and practice of design, development, utilization, management, and evaluation of processes and resources for learning”…
Concept Maps and How To Use Them
Concept maps help our brains take in information, mostly when there is visual information. The maps help us to see the big picture along with the connected and related data. They also help…
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- My Account Login
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Review Article
- Open access
- Published: 11 January 2023

The effectiveness of collaborative problem solving in promoting students’ critical thinking: A meta-analysis based on empirical literature
- Enwei Xu ORCID: orcid.org/0000-0001-6424-8169 1 ,
- Wei Wang 1 &
- Qingxia Wang 1
Humanities and Social Sciences Communications volume 10 , Article number: 16 ( 2023 ) Cite this article
15k Accesses
14 Citations
3 Altmetric
Metrics details
- Science, technology and society
Collaborative problem-solving has been widely embraced in the classroom instruction of critical thinking, which is regarded as the core of curriculum reform based on key competencies in the field of education as well as a key competence for learners in the 21st century. However, the effectiveness of collaborative problem-solving in promoting students’ critical thinking remains uncertain. This current research presents the major findings of a meta-analysis of 36 pieces of the literature revealed in worldwide educational periodicals during the 21st century to identify the effectiveness of collaborative problem-solving in promoting students’ critical thinking and to determine, based on evidence, whether and to what extent collaborative problem solving can result in a rise or decrease in critical thinking. The findings show that (1) collaborative problem solving is an effective teaching approach to foster students’ critical thinking, with a significant overall effect size (ES = 0.82, z = 12.78, P < 0.01, 95% CI [0.69, 0.95]); (2) in respect to the dimensions of critical thinking, collaborative problem solving can significantly and successfully enhance students’ attitudinal tendencies (ES = 1.17, z = 7.62, P < 0.01, 95% CI[0.87, 1.47]); nevertheless, it falls short in terms of improving students’ cognitive skills, having only an upper-middle impact (ES = 0.70, z = 11.55, P < 0.01, 95% CI[0.58, 0.82]); and (3) the teaching type (chi 2 = 7.20, P < 0.05), intervention duration (chi 2 = 12.18, P < 0.01), subject area (chi 2 = 13.36, P < 0.05), group size (chi 2 = 8.77, P < 0.05), and learning scaffold (chi 2 = 9.03, P < 0.01) all have an impact on critical thinking, and they can be viewed as important moderating factors that affect how critical thinking develops. On the basis of these results, recommendations are made for further study and instruction to better support students’ critical thinking in the context of collaborative problem-solving.
Similar content being viewed by others
Fostering twenty-first century skills among primary school students through math project-based learning
A meta-analysis to gauge the impact of pedagogies employed in mixed-ability high school biology classrooms

A guide to critical thinking: implications for dental education
Introduction.
Although critical thinking has a long history in research, the concept of critical thinking, which is regarded as an essential competence for learners in the 21st century, has recently attracted more attention from researchers and teaching practitioners (National Research Council, 2012 ). Critical thinking should be the core of curriculum reform based on key competencies in the field of education (Peng and Deng, 2017 ) because students with critical thinking can not only understand the meaning of knowledge but also effectively solve practical problems in real life even after knowledge is forgotten (Kek and Huijser, 2011 ). The definition of critical thinking is not universal (Ennis, 1989 ; Castle, 2009 ; Niu et al., 2013 ). In general, the definition of critical thinking is a self-aware and self-regulated thought process (Facione, 1990 ; Niu et al., 2013 ). It refers to the cognitive skills needed to interpret, analyze, synthesize, reason, and evaluate information as well as the attitudinal tendency to apply these abilities (Halpern, 2001 ). The view that critical thinking can be taught and learned through curriculum teaching has been widely supported by many researchers (e.g., Kuncel, 2011 ; Leng and Lu, 2020 ), leading to educators’ efforts to foster it among students. In the field of teaching practice, there are three types of courses for teaching critical thinking (Ennis, 1989 ). The first is an independent curriculum in which critical thinking is taught and cultivated without involving the knowledge of specific disciplines; the second is an integrated curriculum in which critical thinking is integrated into the teaching of other disciplines as a clear teaching goal; and the third is a mixed curriculum in which critical thinking is taught in parallel to the teaching of other disciplines for mixed teaching training. Furthermore, numerous measuring tools have been developed by researchers and educators to measure critical thinking in the context of teaching practice. These include standardized measurement tools, such as WGCTA, CCTST, CCTT, and CCTDI, which have been verified by repeated experiments and are considered effective and reliable by international scholars (Facione and Facione, 1992 ). In short, descriptions of critical thinking, including its two dimensions of attitudinal tendency and cognitive skills, different types of teaching courses, and standardized measurement tools provide a complex normative framework for understanding, teaching, and evaluating critical thinking.
Cultivating critical thinking in curriculum teaching can start with a problem, and one of the most popular critical thinking instructional approaches is problem-based learning (Liu et al., 2020 ). Duch et al. ( 2001 ) noted that problem-based learning in group collaboration is progressive active learning, which can improve students’ critical thinking and problem-solving skills. Collaborative problem-solving is the organic integration of collaborative learning and problem-based learning, which takes learners as the center of the learning process and uses problems with poor structure in real-world situations as the starting point for the learning process (Liang et al., 2017 ). Students learn the knowledge needed to solve problems in a collaborative group, reach a consensus on problems in the field, and form solutions through social cooperation methods, such as dialogue, interpretation, questioning, debate, negotiation, and reflection, thus promoting the development of learners’ domain knowledge and critical thinking (Cindy, 2004 ; Liang et al., 2017 ).
Collaborative problem-solving has been widely used in the teaching practice of critical thinking, and several studies have attempted to conduct a systematic review and meta-analysis of the empirical literature on critical thinking from various perspectives. However, little attention has been paid to the impact of collaborative problem-solving on critical thinking. Therefore, the best approach for developing and enhancing critical thinking throughout collaborative problem-solving is to examine how to implement critical thinking instruction; however, this issue is still unexplored, which means that many teachers are incapable of better instructing critical thinking (Leng and Lu, 2020 ; Niu et al., 2013 ). For example, Huber ( 2016 ) provided the meta-analysis findings of 71 publications on gaining critical thinking over various time frames in college with the aim of determining whether critical thinking was truly teachable. These authors found that learners significantly improve their critical thinking while in college and that critical thinking differs with factors such as teaching strategies, intervention duration, subject area, and teaching type. The usefulness of collaborative problem-solving in fostering students’ critical thinking, however, was not determined by this study, nor did it reveal whether there existed significant variations among the different elements. A meta-analysis of 31 pieces of educational literature was conducted by Liu et al. ( 2020 ) to assess the impact of problem-solving on college students’ critical thinking. These authors found that problem-solving could promote the development of critical thinking among college students and proposed establishing a reasonable group structure for problem-solving in a follow-up study to improve students’ critical thinking. Additionally, previous empirical studies have reached inconclusive and even contradictory conclusions about whether and to what extent collaborative problem-solving increases or decreases critical thinking levels. As an illustration, Yang et al. ( 2008 ) carried out an experiment on the integrated curriculum teaching of college students based on a web bulletin board with the goal of fostering participants’ critical thinking in the context of collaborative problem-solving. These authors’ research revealed that through sharing, debating, examining, and reflecting on various experiences and ideas, collaborative problem-solving can considerably enhance students’ critical thinking in real-life problem situations. In contrast, collaborative problem-solving had a positive impact on learners’ interaction and could improve learning interest and motivation but could not significantly improve students’ critical thinking when compared to traditional classroom teaching, according to research by Naber and Wyatt ( 2014 ) and Sendag and Odabasi ( 2009 ) on undergraduate and high school students, respectively.
The above studies show that there is inconsistency regarding the effectiveness of collaborative problem-solving in promoting students’ critical thinking. Therefore, it is essential to conduct a thorough and trustworthy review to detect and decide whether and to what degree collaborative problem-solving can result in a rise or decrease in critical thinking. Meta-analysis is a quantitative analysis approach that is utilized to examine quantitative data from various separate studies that are all focused on the same research topic. This approach characterizes the effectiveness of its impact by averaging the effect sizes of numerous qualitative studies in an effort to reduce the uncertainty brought on by independent research and produce more conclusive findings (Lipsey and Wilson, 2001 ).
This paper used a meta-analytic approach and carried out a meta-analysis to examine the effectiveness of collaborative problem-solving in promoting students’ critical thinking in order to make a contribution to both research and practice. The following research questions were addressed by this meta-analysis:
What is the overall effect size of collaborative problem-solving in promoting students’ critical thinking and its impact on the two dimensions of critical thinking (i.e., attitudinal tendency and cognitive skills)?
How are the disparities between the study conclusions impacted by various moderating variables if the impacts of various experimental designs in the included studies are heterogeneous?
This research followed the strict procedures (e.g., database searching, identification, screening, eligibility, merging, duplicate removal, and analysis of included studies) of Cooper’s ( 2010 ) proposed meta-analysis approach for examining quantitative data from various separate studies that are all focused on the same research topic. The relevant empirical research that appeared in worldwide educational periodicals within the 21st century was subjected to this meta-analysis using Rev-Man 5.4. The consistency of the data extracted separately by two researchers was tested using Cohen’s kappa coefficient, and a publication bias test and a heterogeneity test were run on the sample data to ascertain the quality of this meta-analysis.
Data sources and search strategies
There were three stages to the data collection process for this meta-analysis, as shown in Fig. 1 , which shows the number of articles included and eliminated during the selection process based on the statement and study eligibility criteria.
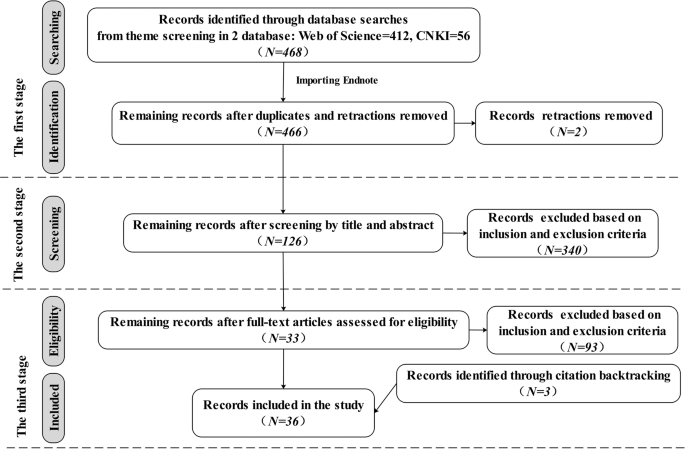
This flowchart shows the number of records identified, included and excluded in the article.
First, the databases used to systematically search for relevant articles were the journal papers of the Web of Science Core Collection and the Chinese Core source journal, as well as the Chinese Social Science Citation Index (CSSCI) source journal papers included in CNKI. These databases were selected because they are credible platforms that are sources of scholarly and peer-reviewed information with advanced search tools and contain literature relevant to the subject of our topic from reliable researchers and experts. The search string with the Boolean operator used in the Web of Science was “TS = (((“critical thinking” or “ct” and “pretest” or “posttest”) or (“critical thinking” or “ct” and “control group” or “quasi experiment” or “experiment”)) and (“collaboration” or “collaborative learning” or “CSCL”) and (“problem solving” or “problem-based learning” or “PBL”))”. The research area was “Education Educational Research”, and the search period was “January 1, 2000, to December 30, 2021”. A total of 412 papers were obtained. The search string with the Boolean operator used in the CNKI was “SU = (‘critical thinking’*‘collaboration’ + ‘critical thinking’*‘collaborative learning’ + ‘critical thinking’*‘CSCL’ + ‘critical thinking’*‘problem solving’ + ‘critical thinking’*‘problem-based learning’ + ‘critical thinking’*‘PBL’ + ‘critical thinking’*‘problem oriented’) AND FT = (‘experiment’ + ‘quasi experiment’ + ‘pretest’ + ‘posttest’ + ‘empirical study’)” (translated into Chinese when searching). A total of 56 studies were found throughout the search period of “January 2000 to December 2021”. From the databases, all duplicates and retractions were eliminated before exporting the references into Endnote, a program for managing bibliographic references. In all, 466 studies were found.
Second, the studies that matched the inclusion and exclusion criteria for the meta-analysis were chosen by two researchers after they had reviewed the abstracts and titles of the gathered articles, yielding a total of 126 studies.
Third, two researchers thoroughly reviewed each included article’s whole text in accordance with the inclusion and exclusion criteria. Meanwhile, a snowball search was performed using the references and citations of the included articles to ensure complete coverage of the articles. Ultimately, 36 articles were kept.
Two researchers worked together to carry out this entire process, and a consensus rate of almost 94.7% was reached after discussion and negotiation to clarify any emerging differences.
Eligibility criteria
Since not all the retrieved studies matched the criteria for this meta-analysis, eligibility criteria for both inclusion and exclusion were developed as follows:
The publication language of the included studies was limited to English and Chinese, and the full text could be obtained. Articles that did not meet the publication language and articles not published between 2000 and 2021 were excluded.
The research design of the included studies must be empirical and quantitative studies that can assess the effect of collaborative problem-solving on the development of critical thinking. Articles that could not identify the causal mechanisms by which collaborative problem-solving affects critical thinking, such as review articles and theoretical articles, were excluded.
The research method of the included studies must feature a randomized control experiment or a quasi-experiment, or a natural experiment, which have a higher degree of internal validity with strong experimental designs and can all plausibly provide evidence that critical thinking and collaborative problem-solving are causally related. Articles with non-experimental research methods, such as purely correlational or observational studies, were excluded.
The participants of the included studies were only students in school, including K-12 students and college students. Articles in which the participants were non-school students, such as social workers or adult learners, were excluded.
The research results of the included studies must mention definite signs that may be utilized to gauge critical thinking’s impact (e.g., sample size, mean value, or standard deviation). Articles that lacked specific measurement indicators for critical thinking and could not calculate the effect size were excluded.
Data coding design
In order to perform a meta-analysis, it is necessary to collect the most important information from the articles, codify that information’s properties, and convert descriptive data into quantitative data. Therefore, this study designed a data coding template (see Table 1 ). Ultimately, 16 coding fields were retained.
The designed data-coding template consisted of three pieces of information. Basic information about the papers was included in the descriptive information: the publishing year, author, serial number, and title of the paper.
The variable information for the experimental design had three variables: the independent variable (instruction method), the dependent variable (critical thinking), and the moderating variable (learning stage, teaching type, intervention duration, learning scaffold, group size, measuring tool, and subject area). Depending on the topic of this study, the intervention strategy, as the independent variable, was coded into collaborative and non-collaborative problem-solving. The dependent variable, critical thinking, was coded as a cognitive skill and an attitudinal tendency. And seven moderating variables were created by grouping and combining the experimental design variables discovered within the 36 studies (see Table 1 ), where learning stages were encoded as higher education, high school, middle school, and primary school or lower; teaching types were encoded as mixed courses, integrated courses, and independent courses; intervention durations were encoded as 0–1 weeks, 1–4 weeks, 4–12 weeks, and more than 12 weeks; group sizes were encoded as 2–3 persons, 4–6 persons, 7–10 persons, and more than 10 persons; learning scaffolds were encoded as teacher-supported learning scaffold, technique-supported learning scaffold, and resource-supported learning scaffold; measuring tools were encoded as standardized measurement tools (e.g., WGCTA, CCTT, CCTST, and CCTDI) and self-adapting measurement tools (e.g., modified or made by researchers); and subject areas were encoded according to the specific subjects used in the 36 included studies.
The data information contained three metrics for measuring critical thinking: sample size, average value, and standard deviation. It is vital to remember that studies with various experimental designs frequently adopt various formulas to determine the effect size. And this paper used Morris’ proposed standardized mean difference (SMD) calculation formula ( 2008 , p. 369; see Supplementary Table S3 ).
Procedure for extracting and coding data
According to the data coding template (see Table 1 ), the 36 papers’ information was retrieved by two researchers, who then entered them into Excel (see Supplementary Table S1 ). The results of each study were extracted separately in the data extraction procedure if an article contained numerous studies on critical thinking, or if a study assessed different critical thinking dimensions. For instance, Tiwari et al. ( 2010 ) used four time points, which were viewed as numerous different studies, to examine the outcomes of critical thinking, and Chen ( 2013 ) included the two outcome variables of attitudinal tendency and cognitive skills, which were regarded as two studies. After discussion and negotiation during data extraction, the two researchers’ consistency test coefficients were roughly 93.27%. Supplementary Table S2 details the key characteristics of the 36 included articles with 79 effect quantities, including descriptive information (e.g., the publishing year, author, serial number, and title of the paper), variable information (e.g., independent variables, dependent variables, and moderating variables), and data information (e.g., mean values, standard deviations, and sample size). Following that, testing for publication bias and heterogeneity was done on the sample data using the Rev-Man 5.4 software, and then the test results were used to conduct a meta-analysis.
Publication bias test
When the sample of studies included in a meta-analysis does not accurately reflect the general status of research on the relevant subject, publication bias is said to be exhibited in this research. The reliability and accuracy of the meta-analysis may be impacted by publication bias. Due to this, the meta-analysis needs to check the sample data for publication bias (Stewart et al., 2006 ). A popular method to check for publication bias is the funnel plot; and it is unlikely that there will be publishing bias when the data are equally dispersed on either side of the average effect size and targeted within the higher region. The data are equally dispersed within the higher portion of the efficient zone, consistent with the funnel plot connected with this analysis (see Fig. 2 ), indicating that publication bias is unlikely in this situation.
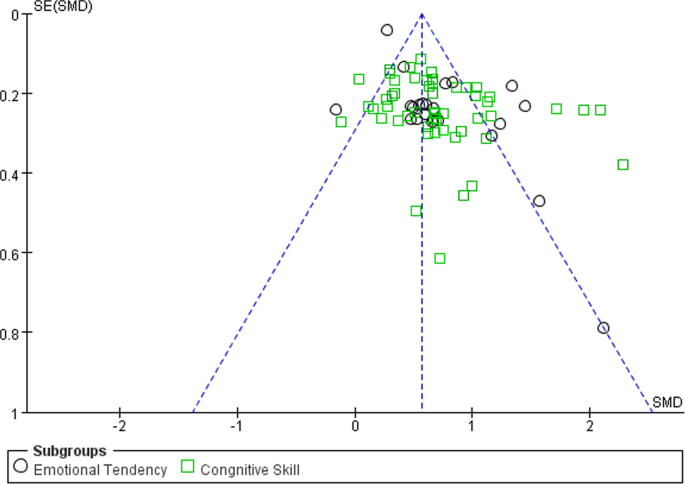
This funnel plot shows the result of publication bias of 79 effect quantities across 36 studies.
Heterogeneity test
To select the appropriate effect models for the meta-analysis, one might use the results of a heterogeneity test on the data effect sizes. In a meta-analysis, it is common practice to gauge the degree of data heterogeneity using the I 2 value, and I 2 ≥ 50% is typically understood to denote medium-high heterogeneity, which calls for the adoption of a random effect model; if not, a fixed effect model ought to be applied (Lipsey and Wilson, 2001 ). The findings of the heterogeneity test in this paper (see Table 2 ) revealed that I 2 was 86% and displayed significant heterogeneity ( P < 0.01). To ensure accuracy and reliability, the overall effect size ought to be calculated utilizing the random effect model.
The analysis of the overall effect size
This meta-analysis utilized a random effect model to examine 79 effect quantities from 36 studies after eliminating heterogeneity. In accordance with Cohen’s criterion (Cohen, 1992 ), it is abundantly clear from the analysis results, which are shown in the forest plot of the overall effect (see Fig. 3 ), that the cumulative impact size of cooperative problem-solving is 0.82, which is statistically significant ( z = 12.78, P < 0.01, 95% CI [0.69, 0.95]), and can encourage learners to practice critical thinking.
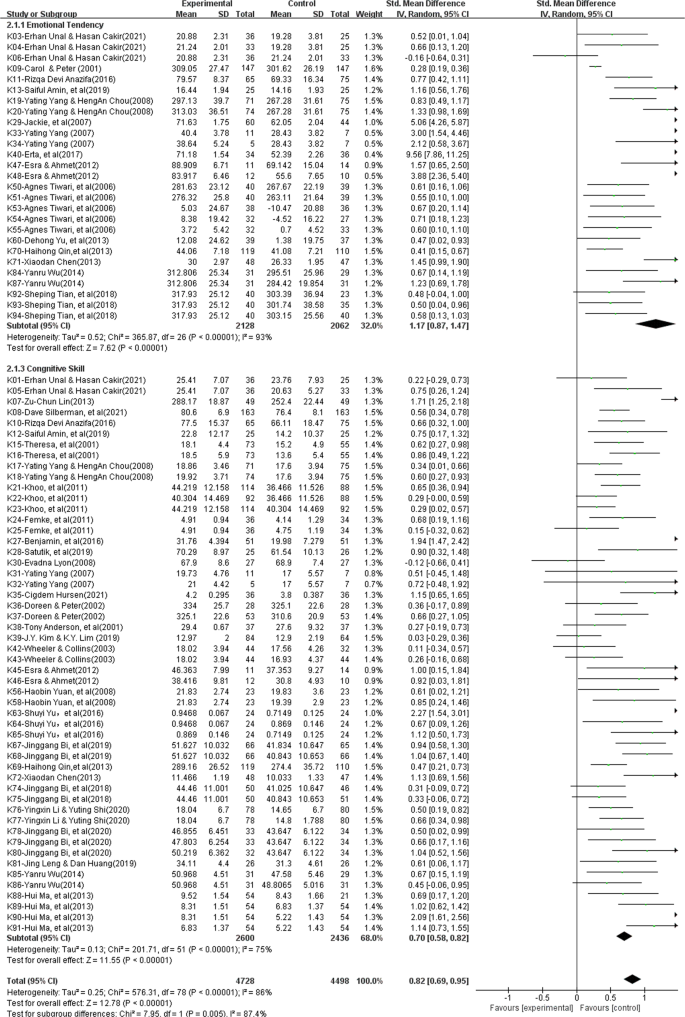
This forest plot shows the analysis result of the overall effect size across 36 studies.
In addition, this study examined two distinct dimensions of critical thinking to better understand the precise contributions that collaborative problem-solving makes to the growth of critical thinking. The findings (see Table 3 ) indicate that collaborative problem-solving improves cognitive skills (ES = 0.70) and attitudinal tendency (ES = 1.17), with significant intergroup differences (chi 2 = 7.95, P < 0.01). Although collaborative problem-solving improves both dimensions of critical thinking, it is essential to point out that the improvements in students’ attitudinal tendency are much more pronounced and have a significant comprehensive effect (ES = 1.17, z = 7.62, P < 0.01, 95% CI [0.87, 1.47]), whereas gains in learners’ cognitive skill are slightly improved and are just above average. (ES = 0.70, z = 11.55, P < 0.01, 95% CI [0.58, 0.82]).
The analysis of moderator effect size
The whole forest plot’s 79 effect quantities underwent a two-tailed test, which revealed significant heterogeneity ( I 2 = 86%, z = 12.78, P < 0.01), indicating differences between various effect sizes that may have been influenced by moderating factors other than sampling error. Therefore, exploring possible moderating factors that might produce considerable heterogeneity was done using subgroup analysis, such as the learning stage, learning scaffold, teaching type, group size, duration of the intervention, measuring tool, and the subject area included in the 36 experimental designs, in order to further explore the key factors that influence critical thinking. The findings (see Table 4 ) indicate that various moderating factors have advantageous effects on critical thinking. In this situation, the subject area (chi 2 = 13.36, P < 0.05), group size (chi 2 = 8.77, P < 0.05), intervention duration (chi 2 = 12.18, P < 0.01), learning scaffold (chi 2 = 9.03, P < 0.01), and teaching type (chi 2 = 7.20, P < 0.05) are all significant moderators that can be applied to support the cultivation of critical thinking. However, since the learning stage and the measuring tools did not significantly differ among intergroup (chi 2 = 3.15, P = 0.21 > 0.05, and chi 2 = 0.08, P = 0.78 > 0.05), we are unable to explain why these two factors are crucial in supporting the cultivation of critical thinking in the context of collaborative problem-solving. These are the precise outcomes, as follows:
Various learning stages influenced critical thinking positively, without significant intergroup differences (chi 2 = 3.15, P = 0.21 > 0.05). High school was first on the list of effect sizes (ES = 1.36, P < 0.01), then higher education (ES = 0.78, P < 0.01), and middle school (ES = 0.73, P < 0.01). These results show that, despite the learning stage’s beneficial influence on cultivating learners’ critical thinking, we are unable to explain why it is essential for cultivating critical thinking in the context of collaborative problem-solving.
Different teaching types had varying degrees of positive impact on critical thinking, with significant intergroup differences (chi 2 = 7.20, P < 0.05). The effect size was ranked as follows: mixed courses (ES = 1.34, P < 0.01), integrated courses (ES = 0.81, P < 0.01), and independent courses (ES = 0.27, P < 0.01). These results indicate that the most effective approach to cultivate critical thinking utilizing collaborative problem solving is through the teaching type of mixed courses.
Various intervention durations significantly improved critical thinking, and there were significant intergroup differences (chi 2 = 12.18, P < 0.01). The effect sizes related to this variable showed a tendency to increase with longer intervention durations. The improvement in critical thinking reached a significant level (ES = 0.85, P < 0.01) after more than 12 weeks of training. These findings indicate that the intervention duration and critical thinking’s impact are positively correlated, with a longer intervention duration having a greater effect.
Different learning scaffolds influenced critical thinking positively, with significant intergroup differences (chi 2 = 9.03, P < 0.01). The resource-supported learning scaffold (ES = 0.69, P < 0.01) acquired a medium-to-higher level of impact, the technique-supported learning scaffold (ES = 0.63, P < 0.01) also attained a medium-to-higher level of impact, and the teacher-supported learning scaffold (ES = 0.92, P < 0.01) displayed a high level of significant impact. These results show that the learning scaffold with teacher support has the greatest impact on cultivating critical thinking.
Various group sizes influenced critical thinking positively, and the intergroup differences were statistically significant (chi 2 = 8.77, P < 0.05). Critical thinking showed a general declining trend with increasing group size. The overall effect size of 2–3 people in this situation was the biggest (ES = 0.99, P < 0.01), and when the group size was greater than 7 people, the improvement in critical thinking was at the lower-middle level (ES < 0.5, P < 0.01). These results show that the impact on critical thinking is positively connected with group size, and as group size grows, so does the overall impact.
Various measuring tools influenced critical thinking positively, with significant intergroup differences (chi 2 = 0.08, P = 0.78 > 0.05). In this situation, the self-adapting measurement tools obtained an upper-medium level of effect (ES = 0.78), whereas the complete effect size of the standardized measurement tools was the largest, achieving a significant level of effect (ES = 0.84, P < 0.01). These results show that, despite the beneficial influence of the measuring tool on cultivating critical thinking, we are unable to explain why it is crucial in fostering the growth of critical thinking by utilizing the approach of collaborative problem-solving.
Different subject areas had a greater impact on critical thinking, and the intergroup differences were statistically significant (chi 2 = 13.36, P < 0.05). Mathematics had the greatest overall impact, achieving a significant level of effect (ES = 1.68, P < 0.01), followed by science (ES = 1.25, P < 0.01) and medical science (ES = 0.87, P < 0.01), both of which also achieved a significant level of effect. Programming technology was the least effective (ES = 0.39, P < 0.01), only having a medium-low degree of effect compared to education (ES = 0.72, P < 0.01) and other fields (such as language, art, and social sciences) (ES = 0.58, P < 0.01). These results suggest that scientific fields (e.g., mathematics, science) may be the most effective subject areas for cultivating critical thinking utilizing the approach of collaborative problem-solving.
The effectiveness of collaborative problem solving with regard to teaching critical thinking
According to this meta-analysis, using collaborative problem-solving as an intervention strategy in critical thinking teaching has a considerable amount of impact on cultivating learners’ critical thinking as a whole and has a favorable promotional effect on the two dimensions of critical thinking. According to certain studies, collaborative problem solving, the most frequently used critical thinking teaching strategy in curriculum instruction can considerably enhance students’ critical thinking (e.g., Liang et al., 2017 ; Liu et al., 2020 ; Cindy, 2004 ). This meta-analysis provides convergent data support for the above research views. Thus, the findings of this meta-analysis not only effectively address the first research query regarding the overall effect of cultivating critical thinking and its impact on the two dimensions of critical thinking (i.e., attitudinal tendency and cognitive skills) utilizing the approach of collaborative problem-solving, but also enhance our confidence in cultivating critical thinking by using collaborative problem-solving intervention approach in the context of classroom teaching.
Furthermore, the associated improvements in attitudinal tendency are much stronger, but the corresponding improvements in cognitive skill are only marginally better. According to certain studies, cognitive skill differs from the attitudinal tendency in classroom instruction; the cultivation and development of the former as a key ability is a process of gradual accumulation, while the latter as an attitude is affected by the context of the teaching situation (e.g., a novel and exciting teaching approach, challenging and rewarding tasks) (Halpern, 2001 ; Wei and Hong, 2022 ). Collaborative problem-solving as a teaching approach is exciting and interesting, as well as rewarding and challenging; because it takes the learners as the focus and examines problems with poor structure in real situations, and it can inspire students to fully realize their potential for problem-solving, which will significantly improve their attitudinal tendency toward solving problems (Liu et al., 2020 ). Similar to how collaborative problem-solving influences attitudinal tendency, attitudinal tendency impacts cognitive skill when attempting to solve a problem (Liu et al., 2020 ; Zhang et al., 2022 ), and stronger attitudinal tendencies are associated with improved learning achievement and cognitive ability in students (Sison, 2008 ; Zhang et al., 2022 ). It can be seen that the two specific dimensions of critical thinking as well as critical thinking as a whole are affected by collaborative problem-solving, and this study illuminates the nuanced links between cognitive skills and attitudinal tendencies with regard to these two dimensions of critical thinking. To fully develop students’ capacity for critical thinking, future empirical research should pay closer attention to cognitive skills.
The moderating effects of collaborative problem solving with regard to teaching critical thinking
In order to further explore the key factors that influence critical thinking, exploring possible moderating effects that might produce considerable heterogeneity was done using subgroup analysis. The findings show that the moderating factors, such as the teaching type, learning stage, group size, learning scaffold, duration of the intervention, measuring tool, and the subject area included in the 36 experimental designs, could all support the cultivation of collaborative problem-solving in critical thinking. Among them, the effect size differences between the learning stage and measuring tool are not significant, which does not explain why these two factors are crucial in supporting the cultivation of critical thinking utilizing the approach of collaborative problem-solving.
In terms of the learning stage, various learning stages influenced critical thinking positively without significant intergroup differences, indicating that we are unable to explain why it is crucial in fostering the growth of critical thinking.
Although high education accounts for 70.89% of all empirical studies performed by researchers, high school may be the appropriate learning stage to foster students’ critical thinking by utilizing the approach of collaborative problem-solving since it has the largest overall effect size. This phenomenon may be related to student’s cognitive development, which needs to be further studied in follow-up research.
With regard to teaching type, mixed course teaching may be the best teaching method to cultivate students’ critical thinking. Relevant studies have shown that in the actual teaching process if students are trained in thinking methods alone, the methods they learn are isolated and divorced from subject knowledge, which is not conducive to their transfer of thinking methods; therefore, if students’ thinking is trained only in subject teaching without systematic method training, it is challenging to apply to real-world circumstances (Ruggiero, 2012 ; Hu and Liu, 2015 ). Teaching critical thinking as mixed course teaching in parallel to other subject teachings can achieve the best effect on learners’ critical thinking, and explicit critical thinking instruction is more effective than less explicit critical thinking instruction (Bensley and Spero, 2014 ).
In terms of the intervention duration, with longer intervention times, the overall effect size shows an upward tendency. Thus, the intervention duration and critical thinking’s impact are positively correlated. Critical thinking, as a key competency for students in the 21st century, is difficult to get a meaningful improvement in a brief intervention duration. Instead, it could be developed over a lengthy period of time through consistent teaching and the progressive accumulation of knowledge (Halpern, 2001 ; Hu and Liu, 2015 ). Therefore, future empirical studies ought to take these restrictions into account throughout a longer period of critical thinking instruction.
With regard to group size, a group size of 2–3 persons has the highest effect size, and the comprehensive effect size decreases with increasing group size in general. This outcome is in line with some research findings; as an example, a group composed of two to four members is most appropriate for collaborative learning (Schellens and Valcke, 2006 ). However, the meta-analysis results also indicate that once the group size exceeds 7 people, small groups cannot produce better interaction and performance than large groups. This may be because the learning scaffolds of technique support, resource support, and teacher support improve the frequency and effectiveness of interaction among group members, and a collaborative group with more members may increase the diversity of views, which is helpful to cultivate critical thinking utilizing the approach of collaborative problem-solving.
With regard to the learning scaffold, the three different kinds of learning scaffolds can all enhance critical thinking. Among them, the teacher-supported learning scaffold has the largest overall effect size, demonstrating the interdependence of effective learning scaffolds and collaborative problem-solving. This outcome is in line with some research findings; as an example, a successful strategy is to encourage learners to collaborate, come up with solutions, and develop critical thinking skills by using learning scaffolds (Reiser, 2004 ; Xu et al., 2022 ); learning scaffolds can lower task complexity and unpleasant feelings while also enticing students to engage in learning activities (Wood et al., 2006 ); learning scaffolds are designed to assist students in using learning approaches more successfully to adapt the collaborative problem-solving process, and the teacher-supported learning scaffolds have the greatest influence on critical thinking in this process because they are more targeted, informative, and timely (Xu et al., 2022 ).
With respect to the measuring tool, despite the fact that standardized measurement tools (such as the WGCTA, CCTT, and CCTST) have been acknowledged as trustworthy and effective by worldwide experts, only 54.43% of the research included in this meta-analysis adopted them for assessment, and the results indicated no intergroup differences. These results suggest that not all teaching circumstances are appropriate for measuring critical thinking using standardized measurement tools. “The measuring tools for measuring thinking ability have limits in assessing learners in educational situations and should be adapted appropriately to accurately assess the changes in learners’ critical thinking.”, according to Simpson and Courtney ( 2002 , p. 91). As a result, in order to more fully and precisely gauge how learners’ critical thinking has evolved, we must properly modify standardized measuring tools based on collaborative problem-solving learning contexts.
With regard to the subject area, the comprehensive effect size of science departments (e.g., mathematics, science, medical science) is larger than that of language arts and social sciences. Some recent international education reforms have noted that critical thinking is a basic part of scientific literacy. Students with scientific literacy can prove the rationality of their judgment according to accurate evidence and reasonable standards when they face challenges or poorly structured problems (Kyndt et al., 2013 ), which makes critical thinking crucial for developing scientific understanding and applying this understanding to practical problem solving for problems related to science, technology, and society (Yore et al., 2007 ).
Suggestions for critical thinking teaching
Other than those stated in the discussion above, the following suggestions are offered for critical thinking instruction utilizing the approach of collaborative problem-solving.
First, teachers should put a special emphasis on the two core elements, which are collaboration and problem-solving, to design real problems based on collaborative situations. This meta-analysis provides evidence to support the view that collaborative problem-solving has a strong synergistic effect on promoting students’ critical thinking. Asking questions about real situations and allowing learners to take part in critical discussions on real problems during class instruction are key ways to teach critical thinking rather than simply reading speculative articles without practice (Mulnix, 2012 ). Furthermore, the improvement of students’ critical thinking is realized through cognitive conflict with other learners in the problem situation (Yang et al., 2008 ). Consequently, it is essential for teachers to put a special emphasis on the two core elements, which are collaboration and problem-solving, and design real problems and encourage students to discuss, negotiate, and argue based on collaborative problem-solving situations.
Second, teachers should design and implement mixed courses to cultivate learners’ critical thinking, utilizing the approach of collaborative problem-solving. Critical thinking can be taught through curriculum instruction (Kuncel, 2011 ; Leng and Lu, 2020 ), with the goal of cultivating learners’ critical thinking for flexible transfer and application in real problem-solving situations. This meta-analysis shows that mixed course teaching has a highly substantial impact on the cultivation and promotion of learners’ critical thinking. Therefore, teachers should design and implement mixed course teaching with real collaborative problem-solving situations in combination with the knowledge content of specific disciplines in conventional teaching, teach methods and strategies of critical thinking based on poorly structured problems to help students master critical thinking, and provide practical activities in which students can interact with each other to develop knowledge construction and critical thinking utilizing the approach of collaborative problem-solving.
Third, teachers should be more trained in critical thinking, particularly preservice teachers, and they also should be conscious of the ways in which teachers’ support for learning scaffolds can promote critical thinking. The learning scaffold supported by teachers had the greatest impact on learners’ critical thinking, in addition to being more directive, targeted, and timely (Wood et al., 2006 ). Critical thinking can only be effectively taught when teachers recognize the significance of critical thinking for students’ growth and use the proper approaches while designing instructional activities (Forawi, 2016 ). Therefore, with the intention of enabling teachers to create learning scaffolds to cultivate learners’ critical thinking utilizing the approach of collaborative problem solving, it is essential to concentrate on the teacher-supported learning scaffolds and enhance the instruction for teaching critical thinking to teachers, especially preservice teachers.
Implications and limitations
There are certain limitations in this meta-analysis, but future research can correct them. First, the search languages were restricted to English and Chinese, so it is possible that pertinent studies that were written in other languages were overlooked, resulting in an inadequate number of articles for review. Second, these data provided by the included studies are partially missing, such as whether teachers were trained in the theory and practice of critical thinking, the average age and gender of learners, and the differences in critical thinking among learners of various ages and genders. Third, as is typical for review articles, more studies were released while this meta-analysis was being done; therefore, it had a time limit. With the development of relevant research, future studies focusing on these issues are highly relevant and needed.
Conclusions
The subject of the magnitude of collaborative problem-solving’s impact on fostering students’ critical thinking, which received scant attention from other studies, was successfully addressed by this study. The question of the effectiveness of collaborative problem-solving in promoting students’ critical thinking was addressed in this study, which addressed a topic that had gotten little attention in earlier research. The following conclusions can be made:
Regarding the results obtained, collaborative problem solving is an effective teaching approach to foster learners’ critical thinking, with a significant overall effect size (ES = 0.82, z = 12.78, P < 0.01, 95% CI [0.69, 0.95]). With respect to the dimensions of critical thinking, collaborative problem-solving can significantly and effectively improve students’ attitudinal tendency, and the comprehensive effect is significant (ES = 1.17, z = 7.62, P < 0.01, 95% CI [0.87, 1.47]); nevertheless, it falls short in terms of improving students’ cognitive skills, having only an upper-middle impact (ES = 0.70, z = 11.55, P < 0.01, 95% CI [0.58, 0.82]).
As demonstrated by both the results and the discussion, there are varying degrees of beneficial effects on students’ critical thinking from all seven moderating factors, which were found across 36 studies. In this context, the teaching type (chi 2 = 7.20, P < 0.05), intervention duration (chi 2 = 12.18, P < 0.01), subject area (chi 2 = 13.36, P < 0.05), group size (chi 2 = 8.77, P < 0.05), and learning scaffold (chi 2 = 9.03, P < 0.01) all have a positive impact on critical thinking, and they can be viewed as important moderating factors that affect how critical thinking develops. Since the learning stage (chi 2 = 3.15, P = 0.21 > 0.05) and measuring tools (chi 2 = 0.08, P = 0.78 > 0.05) did not demonstrate any significant intergroup differences, we are unable to explain why these two factors are crucial in supporting the cultivation of critical thinking in the context of collaborative problem-solving.
Data availability
All data generated or analyzed during this study are included within the article and its supplementary information files, and the supplementary information files are available in the Dataverse repository: https://doi.org/10.7910/DVN/IPFJO6 .
Bensley DA, Spero RA (2014) Improving critical thinking skills and meta-cognitive monitoring through direct infusion. Think Skills Creat 12:55–68. https://doi.org/10.1016/j.tsc.2014.02.001
Article Google Scholar
Castle A (2009) Defining and assessing critical thinking skills for student radiographers. Radiography 15(1):70–76. https://doi.org/10.1016/j.radi.2007.10.007
Chen XD (2013) An empirical study on the influence of PBL teaching model on critical thinking ability of non-English majors. J PLA Foreign Lang College 36 (04):68–72
Google Scholar
Cohen A (1992) Antecedents of organizational commitment across occupational groups: a meta-analysis. J Organ Behav. https://doi.org/10.1002/job.4030130602
Cooper H (2010) Research synthesis and meta-analysis: a step-by-step approach, 4th edn. Sage, London, England
Cindy HS (2004) Problem-based learning: what and how do students learn? Educ Psychol Rev 51(1):31–39
Duch BJ, Gron SD, Allen DE (2001) The power of problem-based learning: a practical “how to” for teaching undergraduate courses in any discipline. Stylus Educ Sci 2:190–198
Ennis RH (1989) Critical thinking and subject specificity: clarification and needed research. Educ Res 18(3):4–10. https://doi.org/10.3102/0013189x018003004
Facione PA (1990) Critical thinking: a statement of expert consensus for purposes of educational assessment and instruction. Research findings and recommendations. Eric document reproduction service. https://eric.ed.gov/?id=ed315423
Facione PA, Facione NC (1992) The California Critical Thinking Dispositions Inventory (CCTDI) and the CCTDI test manual. California Academic Press, Millbrae, CA
Forawi SA (2016) Standard-based science education and critical thinking. Think Skills Creat 20:52–62. https://doi.org/10.1016/j.tsc.2016.02.005
Halpern DF (2001) Assessing the effectiveness of critical thinking instruction. J Gen Educ 50(4):270–286. https://doi.org/10.2307/27797889
Hu WP, Liu J (2015) Cultivation of pupils’ thinking ability: a five-year follow-up study. Psychol Behav Res 13(05):648–654. https://doi.org/10.3969/j.issn.1672-0628.2015.05.010
Huber K (2016) Does college teach critical thinking? A meta-analysis. Rev Educ Res 86(2):431–468. https://doi.org/10.3102/0034654315605917
Kek MYCA, Huijser H (2011) The power of problem-based learning in developing critical thinking skills: preparing students for tomorrow’s digital futures in today’s classrooms. High Educ Res Dev 30(3):329–341. https://doi.org/10.1080/07294360.2010.501074
Kuncel NR (2011) Measurement and meaning of critical thinking (Research report for the NRC 21st Century Skills Workshop). National Research Council, Washington, DC
Kyndt E, Raes E, Lismont B, Timmers F, Cascallar E, Dochy F (2013) A meta-analysis of the effects of face-to-face cooperative learning. Do recent studies falsify or verify earlier findings? Educ Res Rev 10(2):133–149. https://doi.org/10.1016/j.edurev.2013.02.002
Leng J, Lu XX (2020) Is critical thinking really teachable?—A meta-analysis based on 79 experimental or quasi experimental studies. Open Educ Res 26(06):110–118. https://doi.org/10.13966/j.cnki.kfjyyj.2020.06.011
Liang YZ, Zhu K, Zhao CL (2017) An empirical study on the depth of interaction promoted by collaborative problem solving learning activities. J E-educ Res 38(10):87–92. https://doi.org/10.13811/j.cnki.eer.2017.10.014
Lipsey M, Wilson D (2001) Practical meta-analysis. International Educational and Professional, London, pp. 92–160
Liu Z, Wu W, Jiang Q (2020) A study on the influence of problem based learning on college students’ critical thinking-based on a meta-analysis of 31 studies. Explor High Educ 03:43–49
Morris SB (2008) Estimating effect sizes from pretest-posttest-control group designs. Organ Res Methods 11(2):364–386. https://doi.org/10.1177/1094428106291059
Article ADS Google Scholar
Mulnix JW (2012) Thinking critically about critical thinking. Educ Philos Theory 44(5):464–479. https://doi.org/10.1111/j.1469-5812.2010.00673.x
Naber J, Wyatt TH (2014) The effect of reflective writing interventions on the critical thinking skills and dispositions of baccalaureate nursing students. Nurse Educ Today 34(1):67–72. https://doi.org/10.1016/j.nedt.2013.04.002
National Research Council (2012) Education for life and work: developing transferable knowledge and skills in the 21st century. The National Academies Press, Washington, DC
Niu L, Behar HLS, Garvan CW (2013) Do instructional interventions influence college students’ critical thinking skills? A meta-analysis. Educ Res Rev 9(12):114–128. https://doi.org/10.1016/j.edurev.2012.12.002
Peng ZM, Deng L (2017) Towards the core of education reform: cultivating critical thinking skills as the core of skills in the 21st century. Res Educ Dev 24:57–63. https://doi.org/10.14121/j.cnki.1008-3855.2017.24.011
Reiser BJ (2004) Scaffolding complex learning: the mechanisms of structuring and problematizing student work. J Learn Sci 13(3):273–304. https://doi.org/10.1207/s15327809jls1303_2
Ruggiero VR (2012) The art of thinking: a guide to critical and creative thought, 4th edn. Harper Collins College Publishers, New York
Schellens T, Valcke M (2006) Fostering knowledge construction in university students through asynchronous discussion groups. Comput Educ 46(4):349–370. https://doi.org/10.1016/j.compedu.2004.07.010
Sendag S, Odabasi HF (2009) Effects of an online problem based learning course on content knowledge acquisition and critical thinking skills. Comput Educ 53(1):132–141. https://doi.org/10.1016/j.compedu.2009.01.008
Sison R (2008) Investigating Pair Programming in a Software Engineering Course in an Asian Setting. 2008 15th Asia-Pacific Software Engineering Conference, pp. 325–331. https://doi.org/10.1109/APSEC.2008.61
Simpson E, Courtney M (2002) Critical thinking in nursing education: literature review. Mary Courtney 8(2):89–98
Stewart L, Tierney J, Burdett S (2006) Do systematic reviews based on individual patient data offer a means of circumventing biases associated with trial publications? Publication bias in meta-analysis. John Wiley and Sons Inc, New York, pp. 261–286
Tiwari A, Lai P, So M, Yuen K (2010) A comparison of the effects of problem-based learning and lecturing on the development of students’ critical thinking. Med Educ 40(6):547–554. https://doi.org/10.1111/j.1365-2929.2006.02481.x
Wood D, Bruner JS, Ross G (2006) The role of tutoring in problem solving. J Child Psychol Psychiatry 17(2):89–100. https://doi.org/10.1111/j.1469-7610.1976.tb00381.x
Wei T, Hong S (2022) The meaning and realization of teachable critical thinking. Educ Theory Practice 10:51–57
Xu EW, Wang W, Wang QX (2022) A meta-analysis of the effectiveness of programming teaching in promoting K-12 students’ computational thinking. Educ Inf Technol. https://doi.org/10.1007/s10639-022-11445-2
Yang YC, Newby T, Bill R (2008) Facilitating interactions through structured web-based bulletin boards: a quasi-experimental study on promoting learners’ critical thinking skills. Comput Educ 50(4):1572–1585. https://doi.org/10.1016/j.compedu.2007.04.006
Yore LD, Pimm D, Tuan HL (2007) The literacy component of mathematical and scientific literacy. Int J Sci Math Educ 5(4):559–589. https://doi.org/10.1007/s10763-007-9089-4
Zhang T, Zhang S, Gao QQ, Wang JH (2022) Research on the development of learners’ critical thinking in online peer review. Audio Visual Educ Res 6:53–60. https://doi.org/10.13811/j.cnki.eer.2022.06.08
Download references
Acknowledgements
This research was supported by the graduate scientific research and innovation project of Xinjiang Uygur Autonomous Region named “Research on in-depth learning of high school information technology courses for the cultivation of computing thinking” (No. XJ2022G190) and the independent innovation fund project for doctoral students of the College of Educational Science of Xinjiang Normal University named “Research on project-based teaching of high school information technology courses from the perspective of discipline core literacy” (No. XJNUJKYA2003).
Author information
Authors and affiliations.
College of Educational Science, Xinjiang Normal University, 830017, Urumqi, Xinjiang, China
Enwei Xu, Wei Wang & Qingxia Wang
You can also search for this author in PubMed Google Scholar
Corresponding authors
Correspondence to Enwei Xu or Wei Wang .
Ethics declarations
Competing interests.
The authors declare no competing interests.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Informed consent
Additional information.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary tables, rights and permissions.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions
About this article
Cite this article.
Xu, E., Wang, W. & Wang, Q. The effectiveness of collaborative problem solving in promoting students’ critical thinking: A meta-analysis based on empirical literature. Humanit Soc Sci Commun 10 , 16 (2023). https://doi.org/10.1057/s41599-023-01508-1
Download citation
Received : 07 August 2022
Accepted : 04 January 2023
Published : 11 January 2023
DOI : https://doi.org/10.1057/s41599-023-01508-1
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
This article is cited by
Impacts of online collaborative learning on students’ intercultural communication apprehension and intercultural communicative competence.
- Hoa Thi Hoang Chau
- Hung Phu Bui
- Quynh Thi Huong Dinh
Education and Information Technologies (2024)
Exploring the effects of digital technology on deep learning: a meta-analysis
Sustainable electricity generation and farm-grid utilization from photovoltaic aquaculture: a bibliometric analysis.
- A. A. Amusa
- M. Alhassan
International Journal of Environmental Science and Technology (2024)
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
ORIGINAL RESEARCH article
The problem-solving method: efficacy for learning and motivation in the field of physical education.

- 1 High Institute of Sport and Physical Education of Sfax, University of Sfax, Sfax, Tunisia
- 2 Research Unit of the National Sports Observatory (ONS), Tunis, Tunisia
- 3 Research Laboratory: Education, Motricity, Sport and Health, EM2S, LR19JS01, University of Sfax, Sfax, Tunisia
- 4 Department of Neuroscience, Rehabilitation, Ophthalmology, Genetics, Maternal and Child Health (DINOGMI), University of Genoa, Genoa, Italy
- 5 Centre for Intelligent Healthcare, Coventry University, Coventry, United Kingdom
- 6 Laboratory for Industrial and Applied Mathematics, Department of Mathematics and Statistics, York University, Toronto, ON, Canada
- 7 High Institute of Sport and Physical Education of Ksar Saîd, University Manouba, UMA, Manouba, Tunisia
Background: In pursuit of quality teaching and learning, teachers seek the best method to provide their students with a positive educational atmosphere and the most appropriate learning conditions.
Objectives: The purpose of this study is to compare the effects of the problem-solving method vs. the traditional method on motivation and learning during physical education courses.
Methods: Fifty-three students ( M age 15 ± 0.1 years), in their 1st year of the Tunisian secondary education system, voluntarily participated in this study, and randomly assigned to a control or experimental group. Participants in the control group were taught using the traditional methods, whereas participants in the experimental group were taught using the problem-solving method. Both groups took part in a 10-hour experiment over 5 weeks. To measure students' situational motivation, a questionnaire was used to evaluate intrinsic motivation, identified regulation, external regulation, and amotivation during the first (T0) and the last sessions (T2). Additionally, the degree of students' learning was determined via video analyses, recorded at T0, the fifth (T1), and T2.
Results: Motivational dimensions, including identified regulation and intrinsic motivation, were significantly greater (all p < 0.001) in the experimental vs. the control group. The students' motor engagement in learning situations, during which the learner, despite a degree of difficulty performs the motor activity with sufficient success, increased only in the experimental group ( p < 0.001). The waiting time in the experimental group decreased significantly at T1 and T2 vs. T0 (all p < 0.001), with lower values recorded in the experimental vs. the control group at the three-time points (all p < 0.001).
Conclusions: The problem-solving method is an efficient strategy for motor skills and performance enhancement, as well as motivation development during physical education courses.
1. Introduction
The education of children is a sensitive and poignant subject, where the wellbeing of the child in the school environment is a key issue ( Ergül and Kargin, 2014 ). For this, numerous research has sought to find solutions to the problems of the traditional method, which focuses on the teacher as an instructor, giver of knowledge, arbiter of truth, and ultimate evaluator of learning ( Ergül and Kargin, 2014 ; Cunningham and Sood, 2018 ). From this perspective, a teachers' job is to present students with a designated body of knowledge in a predetermined order ( Arvind and Kusum, 2017 ). For them, learners are seen as people with “knowledge gaps” that need to be filled with information. In this method, teaching is conceived as the act of transmitting knowledge from point A (responsible for the teacher) to point B (responsible for the students; Arvind and Kusum, 2017 ). According to Novak (2010) , in the traditional method, the teacher is the one who provokes the learning.
The traditional method focuses on lecture-based teaching as the center of instruction, emphasizing delivery of program and concept ( Johnson, 2010 ; Ilkiw et al., 2017 ; Dickinson et al., 2018 ). The student listens and takes notes, passively accepts and receives from the teacher undifferentiated and identical knowledge ( Bi et al., 2019 ). Course content and delivery are considered most important, and learners acquire knowledge through exercise and practice ( Johnson et al., 1998 ). In the traditional method, academic achievement is seen as the ability of students to demonstrate, replicate, or convey this designated body of knowledge to the teacher. It is based on a transmissive model, the teacher contenting themselves with exchanging and transmitting information to the learner. Here, only the “knowledge” and “teacher” poles of the pedagogical triangle are solicited. The teacher teaches the students, who play the role of the spectator. They receive information without participating in its creation ( Perrenoud, 2003 ). For this, researchers invented a new student-centered method with effects on improving students' graphic interpretation skills and conceptual understanding of kinematic motion represent an area of contemporary interest ( Tebabal and Kahssay, 2011 ). Indeed, in order to facilitate the process of knowledge transfer, teachers should use appropriate methods targeted to specific objectives of the school curricula.
For instance, it has been emphasized that the effectiveness of any educational process as a whole relies on the crucial role of using a well-designed pedagogical (teaching and/or learning) strategy ( Kolesnikova, 2016 ).
Alternate to a traditional method of teaching, Ergül and Kargin (2014 ), proposed the problem-solving method, which represents one of the most common student-centered learning strategies. Indeed, this method allows students to participate in the learning environment, giving them the responsibility for their own acquisition of knowledge, as well as the opportunity for the understanding and structuring of diverse information.
For Cunningham and Sood (2018) , the problem-solving method may be considered a fundamental tool for the acquisition of new knowledge, notably learning transfer. Moreover, the problem-solving method is purportedly efficient for the development of manual skills and experiential learning ( Ergül and Kargin, 2014 ), as well as the optimization of thinking ability. Additionally, the problem-solving method allows learners to participate in the learning environment, while giving them responsibility for their learning and making them understand and structure the information ( Pohan et al., 2020 ). In this context, Ali (2019) reported that, when faced with an obstacle, the student will have to invoke his/her knowledge and use his/her abilities to “break the deadlock.” He/she will therefore make the most of his/her potential, but also share and exchange with his/her colleagues ( Ali, 2019 ). Throughout the process, the student will learn new concepts and skills. The role of the teacher is paramount at the beginning of the activity, since activities will be created based on problematic situations according to the subject and the program. However, on the day of the activity, it does not have the main role, and the teacher will guide learners in difficulty and will allow them to manage themselves most of the time ( Ali, 2019 ).
The problem-solving method encourages group discussion and teamwork ( Fidan and Tuncel, 2019 ). Additionally, in this pedagogical approach, the role of the teacher is a facilitator of learning, and they take on a much more interactive and less rebarbative role ( Garrett, 2008 ).
For the teaching method to be effective, teaching should consist of an ongoing process of making desirable changes among learners using appropriate methods ( Ayeni, 2011 ; Norboev, 2021 ). To bring about positive changes in students, the methods used by teachers should be the best for the subject to be taught ( Adunola et al., 2012 ). Further, suggests that teaching methods work effectively, especially if they meet the needs of learners since each learner interprets and answers questions in a unique way. Improving problem-solving skills is a primary educational goal, as is the ability to use reasoning. To acquire this skill, students must solve problems to learn mathematics and problem-solving ( Hu, 2010 ); this encourages the students to actively participate and contribute to the activities suggested by the teacher. Without sufficient motivation, learning goals can no longer be optimally achieved, although learners may have exceptional abilities. The method of teaching employed by the teachers is decisive to achieve motivational consequences in physical education students ( Leo et al., 2022 ). Pérez-Jorge et al. (2021 ) posited that given we now live in a technological society in which children are used to receiving a large amount of stimuli, gaining and maintaining their attention and keeping them motivated at school becomes a challenge for teachers.
Fenouillet (2012) stated that academic motivation is linked to resources and methods that improve attention for school learning. Furthermore, Rolland (2009) and Bessa et al. (2021) reported a link between a learner's motivational dynamics and classroom activities. The models of learning situations, where the student is the main actor, directly refers to active teaching methods, and that there is a strong link between motivation and active teaching ( Rossa et al., 2021 ). In the same context, previous reports assert that the motivation of students in physical education is an important factor since the intra-individual motivation toward this discipline is recognized as a major determinant of physical activity for students ( Standage et al., 2012 ; Luo, 2019 ; Leo et al., 2022 ). Further, extensive research on the effectiveness of teaching methods shows that the quality of teaching often influences the performance of learners ( Norboev, 2021 ). Ayeni (2011) reported that education is a process that allows students to make changes desirable to achieve specific results. Thus, the consistency of teaching methods with student needs and learning influences student achievement. This has led several researchers to explore the impact of different teaching strategies, ranging from traditional methods to active learning techniques that can be used such as the problem-solving method ( Skinner, 1985 ; Darling-Hammond et al., 2020 ).
In the context of innovation, Blázquez (2016 ) emphasizes the importance of adopting active methods and implementing them as the main element promoting the development of skills, motivation and active participation. Pedagogical models are part of the active methods which, together with model-based practice, replace traditional teaching ( Hastie and Casey, 2014 ; Casey et al., 2021 ). Thus, many studies have identified pedagogical models as the most effective way to place students at the center of the teaching-learning process ( Metzler, 2017 ), making it possible to assess the impact of physical education on learning students ( Casey, 2014 ; Rivera-Pérez et al., 2020 ; Manninen and Campbell, 2021 ). Since each model is designed to focus on a specific program objective, each model has limitations when implemented in isolation ( Bunker and Thorpe, 1982 ; Rivera-Pérez et al., 2020 ). Therefore, focusing on developing students' social and emotional skills and capacities could help them avoid failure in physical education ( Ang and Penney, 2013 ). Thus, the current emergence of new pedagogical models goes with their hybridization with different methods, which is a wave of combinations proposed today as an innovative pedagogical strategy. The incorporation of this type of method in the current education system is becoming increasingly important because it gives students a greater role, participation, autonomy and self-regulation, and above all it improves their motivation ( Puigarnau et al., 2016 ). The teaching model of personal and social responsibility, for example, is closely related to the sports education model because both share certain approaches to responsibility ( Siedentop et al., 2011 ). One of the first studies to use these two models together was Rugby ( Gordon and Doyle, 2015 ), which found significant improvements in student behavior. Also, the recent study by Menendez and Fernandez-Rio (2017) on educational kickboxing.
Previous studies have indicated that hybridization can increase play, problem solving performance and motor skills ( Menendez and Fernandez-Rio, 2017 ; Ward et al., 2021 ) and generate positive psychosocial consequences, such as pleasure, intention to be physically active and responsibility ( Dyson and Grineski, 2001 ; Menendez and Fernandez-Rio, 2017 ).
But despite all these research results, the picture remains unclear, and it remains unknown which method is more effective in improving students' learning and motivation. Given the lack of published evidence on this topic, the aim of this study was to compare the effects of problem-solving vs. the traditional method on students' motivation and learning.
We hypothesized would that the problem-solving method would be more effective in improving students' motivation and learning better than the traditional method.
2. Materials and method
2.1. participants.
Fifty-three students, aged 15–16 ( M age 15 ± 0.1 years), in their 1st year of the Tunisian secondary education system, voluntarily participated in this study. All participants were randomly chosen. Repeating students, those who practice handball activity in civil/competitive/amateur clubs or in the high school sports association, and students who were absent, even for one session, were excluded. The first class consisted of 30 students (16 boys and 14 girls), who represented the experimental group and followed basic courses on a learning method by solving problems. The second class consisted of 23 students (10 boys and 13 girls), who represented the control group and followed the traditional teaching method. The total duration was spread over 5 weeks, or two sessions per week and each session lasted 50 min.
University research ethics board approval (CPPSUD: 0295/2021) was obtained before recruiting participants who were subsequently informed of the nature, objective, methodology, and constraints. Teacher, school director, parental/guardian, and child informed consent was obtained prior to participation in the study.
2.2. Procedure
Before the start of the experiment, the participants were familiarized with the equipment and the experimental protocol in order to ensure a good learning climate. For this and to mitigate the impact of the observer and the cameras on the students, the two researchers were involved prior to the data collection in a week of familiarization by making test recordings with the classes concerned.
An approach of a teaching cycle consisting of 10 sessions spread over 5 weeks, amounting to two sessions per week. Physical education classes were held in the morning from 8 a.m. to 9 a.m., with a single goal for each session that lasted 50 min. The cyclic programs were produced by the teacher responsible for carrying out the experiment with 18 years of service. To do this, the students had the same lessons with the same objectives, only pedagogy that differs: the experimental group worked using problem-solving pedagogy, while the control group was confronted with traditional pedagogy. The sessions took place in a handball field 40 m long and 20 m wide. Examples of training sessions using the problem-solving pedagogy and the traditional pedagogy are presented in Table 1 . In addition, a motivation questionnaire, the Situational Motivation Scale (SIMS; Guay et al., 2000 ), was administered to learners at the end of the session (i.e., in the beginning, and end of the cycle). Each student answered the questions alone and according to their own ideas. This questionnaire was taken in a classroom to prevent students from acting abnormally during the study. It lasted for a maximum of 10 min.
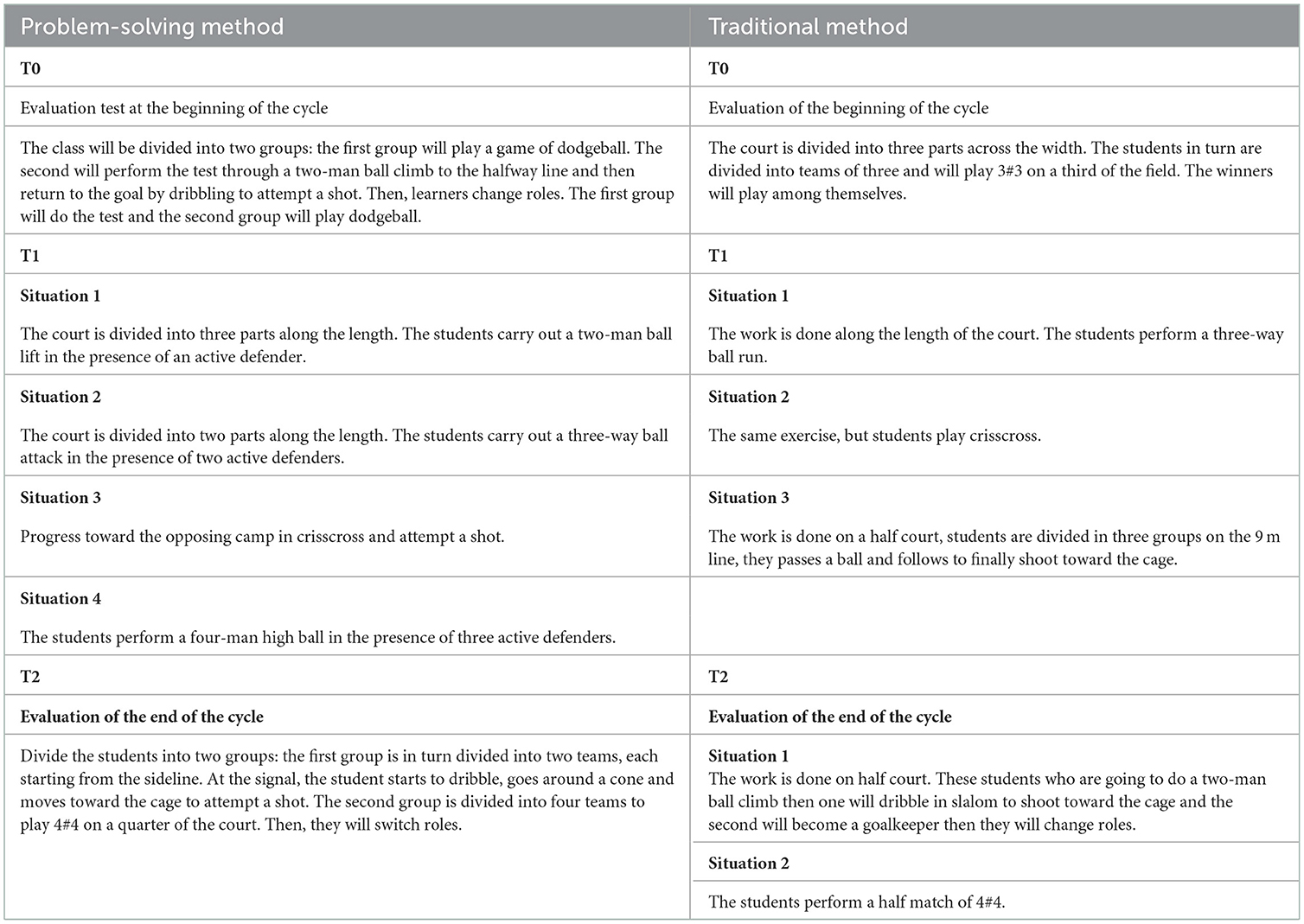
Table 1 . Example of activities for the different sessions.
Two diametrically opposed cameras were installed so to film all the movements and behaviors of each student and teacher during the three sessions [(i) test at the start of the cycle (T0), (ii) in the middle of the cycle (T1), and (iii) test at the end of the cycle (T2)]. These sessions had the same content and each consisted of four phases: the getting started, the warm-up, the work up (which consisted of three situations: first, the work was goes up the ball to two to score in the goal following a shot. Second, the same principle as the previous situation but in the presence of a defender. Finally, third, a match 7 ≠ 7), and the cooling down These recordings were analyzed using a Learning Time Analysis System grid (LTAS; Brunelle et al., 1988 ). This made it possible to measure individual learning by coding observable variables of the behavior of learners in a learning situation.
2.3. Data collection and analysis
2.3.1. the motivation questionnaire.
In this study, in order to measure the situational motivation of students, the situational motivation scale (SIMS; Guay et al., 2000 ), which used. This questionnaire assesses intrinsic motivation, identified regulation, external regulation and amotivation. SIMS has demonstrated good reliability and factor validity in the context of physical education in adolescents ( Lonsdale et al., 2011 ). The participants received exact instructions from the researchers in accordance with written instructions on how to conduct the data collection. Participants completed the SIMS anonymously at the start of a physical education class. All students had the opportunity to write down their answers without being observed and to ask questions if anything was unclear. To minimize the tendency to give socially desirable answers, they were asked to answer as honestly as possible, with the confidence that the teacher would not be able to read their answers and that their grades would not be affected by how they responded. The SIMS questionnaire was filled at T0 and T2. This scale is made up of 16 items divided into four dimensions: intrinsic motivation, identified regulation, external regulation and amotivation. Each item is rated on a 7-point Likert scale ranging from 1 (which is the weakest factor) “not at all” to 7 (which is the strongest factor) “exactly matches.”
In order to assess the internal consistency of the scales, a Cronbach alpha test was conducted ( Cronbach, 1951 ). The internal consistency of the scales was acceptable with reliability coefficients ranging from 0.719 to 0.87. The coefficient of reliability was 0.8.
In the present study, Cronbach's alphas were: intrinsic motivation = 0.790; regulation identified = 0.870; external regulation = 0.749; and amotivation = 0.719.
2.3.2. Camcorders
The audio-visual data collection was conducted using two Sony camcorders (Model; Handcam 4K) with a wireless microphone with a DJ transmitter-receiver (VHF 10HL F4 Micro HF) with a range of 80 m ( Maddeh et al., 2020 ). The collection took place over a period of 5 weeks, with three captures for each class (three sessions of 50 min for each at T0, T1, and T2). Two researchers were trained in the procedures and video capture techniques. The cameras were positioned diagonally, in order to film all the behavior of the students and teacher on the set.
2.3.3. The Learning Time Analysis System (LTAS)
To measure the degree of student learning, the analysis of videos recorded using the LTAS grid by Brunelle et al. (1988) was used, at T0, T1, and T2. This observation system with predetermined categories uses the technique of observation by small intervals (i.e., 6 s) and allows to measure individual learning by coding observable variables of their behaviors when they have been in a learning situation. This grid also permits the specification of the quantity and quality with which the participants engaged in the requested work and was graded, broadly, on two characteristics: the type of situation offered to the group by the teacher and the behavior of the target participant. The situation offered to the group was subdivided into three parts: preparatory situations; knowledge development situations, and motor development situations.
The observations and coding of behaviors are carried out “at intervals.” This technique is used extensively in research on behavior analysis. The coder observes the teaching situation and a particular student during each interval ( Brunelle et al., 1988 ). It then makes a decision concerning the characteristic of the observed behavior. The 6-s observation interval is followed by a coding interval of 6 s too. A cassette tape recorder is used to regulate the observation and recording intervals. It is recorded for this purpose with the indices “observe” and “code” at the start of each 6-s period. During each coding unit, the observer answered the following questions: What is the type of situation in which the class group finds itself? If the class group is in a learning situation proper, in what form of commitment does the observed student find himself? The abbreviations representing the various categories of behavior have been entered in the spaces which correspond to them. The coder was asked to enter a hyphen instead of the abbreviation when the same categories of behavior follow one another in consecutive intervals ( Brunelle et al., 1988 ).
During the preparatory period, the following behaviors were identified and analyzed:
- Deviant behavior: The student adopts a behavior incompatible with a listening attitude or with the smooth running of the preparatory situations.
- Waiting time: The student is waiting without listening or observing.
- Organized during: The student is involved in a complementary activity that does not represent a contribution to learning (e.g., regaining his place in a line, fetching a ball that has just left the field, replacing a piece of equipment).
During the motor development situations, the following behaviors were identified and analyzed:
- Motor engagement 1: The participant performs the motor activity with such easy that it can be inferred that their actions have little chance to engage in a learning process.
- Motor engagement 2: The participant-despite a certain degree of difficulty, performs the motor activity with sufficient success, which makes it possible to infer that they are in the process of learning.
- Motor engagement 3: The participant performs the motor activity with such difficulty that their efforts have very little chance of being part of a learning process.
2.4. Statistical analysis
Statistical tests were performed using statistical software 26.0 for windows (SPSS, Inc, Chicago, IL, USA). Data are presented in text and tables as means ± standard deviations and in figures as means and standard errors. Once the normal distribution of data was confirmed by the Shapiro-Wilk W -test, parametric tests were performed. Analysis of the results was performed using a mixed 2-way analysis of variance (ANOVA): Groups × Time with repeated measures.
For the learning parameters, the ANOVA took the following form: 2 Groups (Control Group vs. Experimental Group) × 3 Times (T0, T1, and T2).
For the dimensions of motivation, the ANOVA took the following form: 2 Groups (Control Group vs. Experimental Group) × 2 Time (T0 vs. T2).
In instances where the ANOVA showed a significant effect, a Bonferroni post-hoc test was applied in order to compare the experimental data in pairs, otherwise by an independent or paired Student's T -test. Effect sizes were calculated as partial eta-squared η p 2 to estimate the meaningfulness of significant findings, where η p 2 values of 0.01, 0.06, and 0.13 represent small, moderate, and large effect sizes, respectively ( Lakens, 2013 ). All observed differences were considered statistically significant for a probability threshold lower than p < 0.05.
Table 2 shows the results of learning variables during the preparatory and the development learning periods at T0, T1, and T2, in the control group and the experimental group.
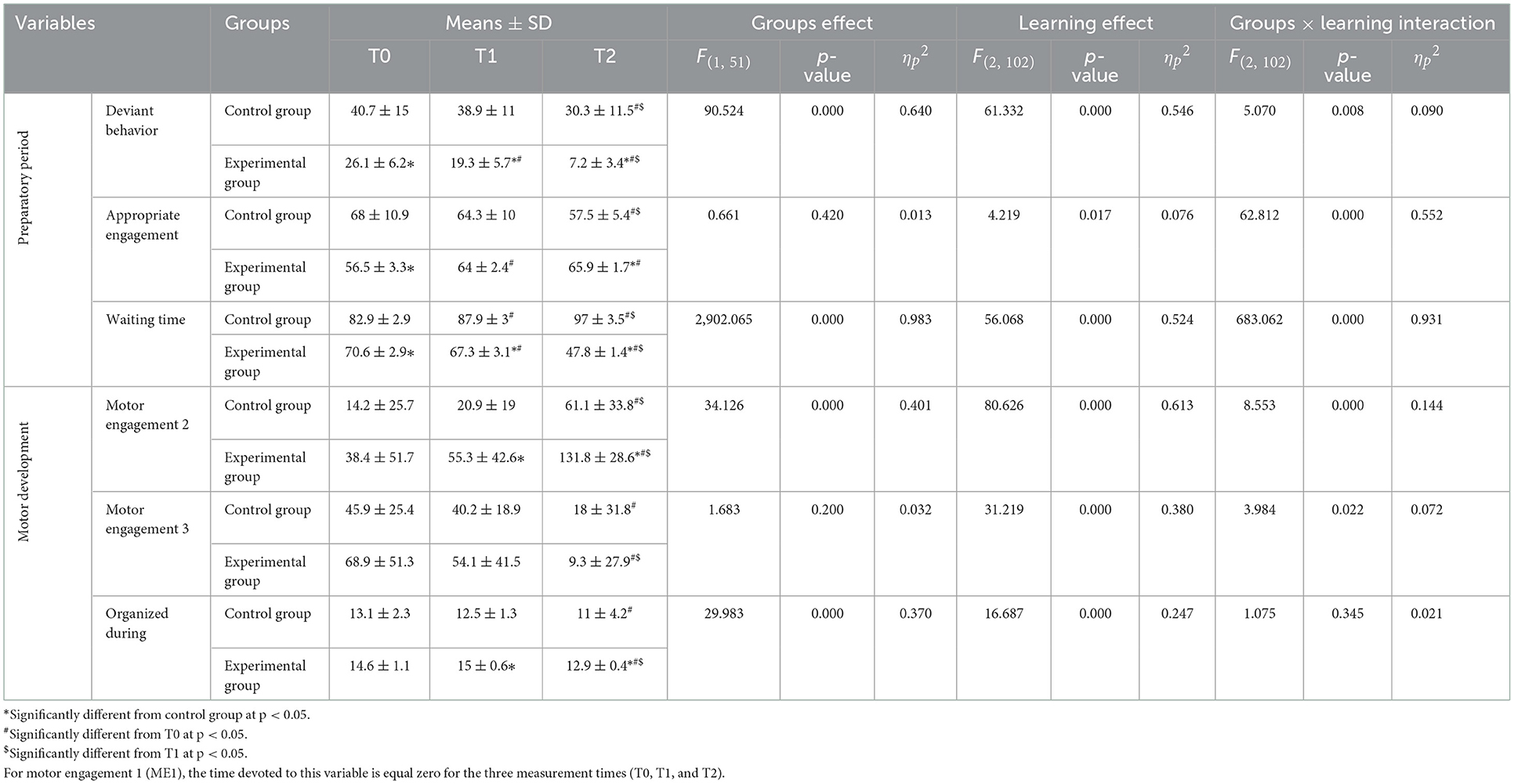
Table 2 . Comparison of learning variables using two teaching methods in physical education.
The analysis of variance of two factors with repeated measures showed a significant effect of group, learning, and group learning interaction for the deviant behavior. The post-hoc test revealed significantly less frequent deviant behaviors in the experimental than in the control group at T0, T1, and T2 (all p < 0.001). Additionally, the deviant behavior decreased significantly at T1 and T2 compared to T0 for both groups (all p < 0.001).
For appropriate engagement, there were no significant group effect, a significant learning effect, and a significant group learning interaction effect. The post-hoc test revealed that compared to T0, Appropriate engagement recorded at T1 and T2 increased significantly ( p = 0.032; p = 0.031, respectively) in the experimental group, whilst it decreased significantly in the control group ( p < 0.001). Additionally, Appropriate engagement was higher in the experimental vs. control group at T1 and T2 (all p < 0.001).
For waiting time, a significant interaction in terms of group effect, learning, and group learning was found. The post-hoc test revealed that waiting time was higher at T1 and T2 vs. T0 (all p < 0.001) in the control group. In addition, waiting time in the experimental group decreased significantly at T1 and T2 vs. T0 (all p < 0.001), with higher values recorded at T2 vs. T1 ( p = 0.025). Additionally, lower values were recorded in the experimental group vs. the control group at the three-time points (all p < 0.001).
For Motor engagement 2, a significant group, learning, and group-learning interaction effect was noted. The post-hoc test revealed that Motor engagement 2 increased significantly in both groups at T1 ( p < 0.0001) and T2 ( p < 0.0001) vs. T0 ( p = 0.045), with significantly higher values recorded in the experimental group at T1 and T2.
Regarding Motor engagement 3, a non-significant group effect was reported. Contrariwise, a significant learning effect and group learning interaction was reported ( Table 1 ). The post-hoc test revealed a significant decrease in the control group and the experimental group at T1 ( p = 0.294) at T2 ( p = 0.294) vs. T0 ( p = 0.0543). In addition, a non-significant difference between the two groups was found.
A significant group and learning effect was noted for the organized during, and a non-significant group learning interaction. For organized during, the paired Student T -test showed a significant decrease in the control group and the experimental group (all p < 0.001). The independent Student T -test revealed a non-significant difference between groups at the three-time points.
Results of the motivational dimensions in the control group and the experimental group recorded at T0 and T2 are presented in Table 3 .
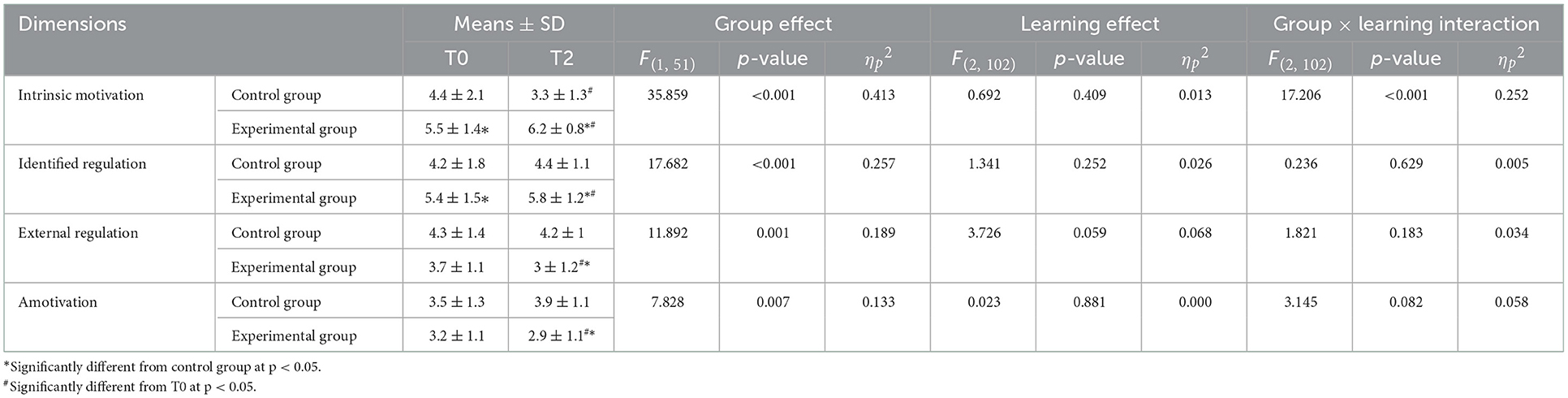
Table 3 . Comparison of the four motivational dimensions in two teaching methods in physical education.
For intrinsic motivation, a significant group effect and group learning interaction and also a non-significant learning effect was found. The post-hoc test indicated that the intrinsic motivation decreased significantly in the control group ( p = 0.029), whilst it increased in the experimental group ( p = 0.04). Additionally, the intrinsic motivation of the experimental group was higher at T0 ( p = 0.026) and T2 ( p < 0.001) compared to that of the control group.
For the identified regulation, a significant group effect, a non-significant learning effect and group learning interaction were reported. The paired Student's T -test revealed that from T0 to T1, the identified motivation increased significantly only in the experimental group ( p = 0.022), while it remained unchanged in the control group. The independent Student's T -test revealed that the identified regulation recorded in the experimental group at T0 ( p = 0.012) and T2 ( p < 0.001) was higher compared to that of the control group.
The external regulation presents a significant group effect. In addition, a non-significant learning effect and group learning interaction were reported. The paired Student's T -test showed that the external regulation decreased significantly in the experimental group ( p = 0.038), whereas it remained unchanged in the control group. Further, the independent Student's T -test revealed that the external regulation recorded at T2 was higher in the control group vs. the experimental group ( p < 0.001).
Relating to amotivation, results showed a significant group effect. Furthermore, a non-significant learning effect and group learning interaction were reported. The paired Student's T -test showed that, from T0 to T2, amotivation decreased significantly in the experimental group ( p = 0.011) and did not change in the control group. The independent Student T -test revealed that amotivation recorded at T2 was lower in the experimental compared to the control group ( p = 0.002).
4. Discussion
The main purpose of this study was to compare the effects of the problem-solving vs. traditional method on motivation and learning during physical education courses. The results revealed that the problem-solving method is more effective than the traditional method in increasing students' motivation and improving their learning. Moreover, the results showed that mean wait times and deviant behaviors decreased using the problem-solving method. Interestingly, the average time spent on appropriate engagement increased using the problem-solving method compared to the traditional method. When using the traditional method, the average wait times increased and, as a result, the time spent on appropriate engagement decreased. Then, following the decrease in deviant behaviors and waiting times, an increase in the time spent warming up was evident (i.e., appropriate engagement). Indeed, there was an improvement in engagement time using the problem-solving method and a decrease using the traditional method. On the other hand, there was a decrease in motor engagement 3 in favor of motor engagement 2. Indeed, it has been shown that the problem-solving method has been used in the learning process and allows for its improvement ( Docktor et al., 2015 ). In addition, it could also produce better quality solutions and has higher scores on conceptual and problem-solving measures. It is also a good method for the learning process to enhance students' academic performance ( Docktor et al., 2015 ; Ali, 2019 ). In contrast, the traditional method limits the ability of teachers to reach and engage all students ( Cook and Artino, 2016 ). Furthermore, it produces passive learning with an understanding of basic knowledge which is characterized by its weakness ( Goldstein, 2016 ). Taken together, it appears that the problem-solving method promotes and improves learning more than the traditional method.
It should be acknowledged that other factors, such as motivation, could influence learning. In this context, our results showed that the method of problem-solving could improve the motivation of the learners. This motivation includes several variables that change depending on the situation, namely the intrinsic motivation that pushes the learner to engage in an activity for the interest and pleasure linked to the practice of the latter ( Komarraju et al., 2009 ; Guiffrida et al., 2013 ; Chedru, 2015 ). The student, therefore, likes to learn through problem-solving and neglects that of the traditional method. These results are concordant with others ( Deci and Ryan, 1985 ; Chedru, 2015 ; Ryan and Deci, 2020 ). Regarding the three forms of extrinsic motivation: first, extrinsic motivation by an identified regulation which manifests itself in a high degree of self-determination where the learner engages in the activity because it is important for him ( Deci and Ryan, 1985 ; Chedru, 2015 ). This explains the significant difference between the two groups. Then, the motivation by external regulation which is characterized by a low degree of self-determination such as the behavior of the learner is manipulated by external circumstances such as obtaining rewards or the removal of sanctions ( Deci and Ryan, 1985 ; Chedru, 2015 ). For this, the means of this variable decreased for the experimental group which is intrinsically motivated. He does not need any reward to work and is not afraid of punishment because he is self-confident. Third, amotivation is at the opposite end of the self-determination continuum. Unmotivated students are the most likely to feel negative emotions ( Ratelle et al., 2007 ; David, 2010 ), to have low self-esteem ( Deci and Ryan, 1995 ), and who attempts to abandon their studies ( Vallerand et al., 1997 ; Blanchard et al., 2005 ). So, more students are motivated by external regulation or demotivated, less interest they show and less effort they make, and more likely they are to fail ( Grolnick et al., 1991 ; Miserandino, 1996 ; Guay et al., 2000 ; Blanchard et al., 2005 ).
It is worth noting that there is a close link between motivation and learning ( Bessa et al., 2021 ; Rossa et al., 2021 ). Indeed, when the learner's motivation is high, so will his learning. However, all this depends on the method used ( Norboev, 2021 ). For example, the method of problem-solving increase motivation more than the traditional method, as evidenced by several researchers ( Parish and Treasure, 2003 ; Artino and Stephens, 2009 ; Kim and Frick, 2011 ; Lemos and Veríssimo, 2014 ).
Given the effectiveness of the problem-solving method in improving students' learning and motivation, it should be used during physical education teaching. This could be achieved through the organization of comprehensive training programs, seminars, and workshops for teachers so to master and subsequently be able to use the problem-solving method during physical education lessons.
Despite its novelty, the present study suffers from a few limitations that should be acknowledged. First, a future study, consisting of a group taught using the mixed method would preferable so to better elucidate the true impact of this teaching and learning method. Second, no gender and/or age group comparisons were performed. This issue should be addressed in future investigations. Finally, the number of participants is limited. This may be due to working in a secondary school where the number of students in a class is limited to 30 students. Additionally, the number of participants fell to 53 after excluding certain students (exempted, absent for a session, exercising in civil clubs or member of the school association). Therefore, to account for classes of finite size, a cluster-based trial would be beneficial in the future. Moreover, future studies investigating the effect of the active method in reducing some behaviors (e.g., disruptive behaviors) and for the improvement of pupils' attention are warranted.
5. Conclusion
There was an improvement in student learning in favor of the problem-solving method. Additionally, we found that the motivation of learners who were taught using the problem-solving method was better than that of learners who were educated by the traditional method.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
University Research Ethics Board approval was obtained before recruiting participants who were subsequently informed of the nature, objective, methodology, and constraints. Teacher, school director, parental/guardian, and child informed consent was obtained prior to participation in the study. In addition, exclusion criteria included; the practice of handball activity in civil/competitive/amateur clubs or in the high school sports association. Written informed consent to participate in this study was provided by the participants' legal guardian/next of kin.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Acknowledgments
Special thanks for all students and physical education teaching staff from the 15 November 1955 Secondary School, who generously shared their time, experience, and materials for the proposes of this study.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer MJ declared a shared affiliation, with no collaboration, with the authors GE, NS, LM, and KT to the handling editor at the time of review.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adunola, O., Ed, B., and Adeniran, A. (2012). The Impact of Teachers' Teaching Methods on the Academic Performance of Primary School Pupils . Ogun: Ego Booster Books.
Google Scholar
Ali, S. S. (2019). Problem based learning: A student-centered approach. Engl. Lang. Teach . 12, 73. doi: 10.5539/elt.v12n5p73
CrossRef Full Text | Google Scholar
Ang, S. C., and Penney, D. (2013). Promoting social and emotional learning outcomes in physical education: Insights from a school-based research project in Singapore. Asia-Pac. J. Health Sport Phys. Educ . 4, 267–286. doi: 10.1080/18377122.2013.836768
Artino, A. R., and Stephens, J. M. (2009). Academic motivation and self-regulation: A comparative analysis of undergraduate and graduate students learning online. Internet. High. Educ. 12, 146–151. doi: 10.1016/j.iheduc.2009.02.001
Arvind, K., and Kusum, G. (2017). Teaching approaches, methods and strategy. Sch. Res. J. Interdiscip. Stud. 4, 6692–6697. doi: 10.21922/srjis.v4i36.10014
Ayeni, A. J. (2011). Teachers' professional development and quality assurance in Nigerian secondary schools. World J. Educ. 1, 143. doi: 10.5430/wje.v1n2p143
Bessa, C., Hastie, P., Rosado, A., and Mesquita, I. (2021). Sport education and traditional teaching: Influence on students' empowerment and self-confidence in high school physical education classes. Sustainability 13, 578. doi: 10.3390/su13020578
Bi, M., Zhao, Z., Yang, J., and Wang, Y. (2019). Comparison of case-based learning and traditional method in teaching postgraduate students of medical oncology. Med. Teach . 4, 1124–1128. doi: 10.1080/0142159X.2019.1617414
PubMed Abstract | CrossRef Full Text | Google Scholar
Blanchard, C., Pelletier, L., Otis, N., and Sharp, E. (2005). Role of self-determination and academic ability in predicting school absences and intention to drop out. J. Educ. Sci. 30, 105–123. doi: 10.7202/011772ar
Blázquez, D. (2016).Métodos de enseñanza en Educación Física. Enfoques innovadores para la enseñanza de competencias . Barcelona: Inde Publisher.
Brunelle, J., Drouin, D., Godbout, P., and Tousignant, M. (1988). Supervision of physical activity intervention. Montreal, Canada: G. Morin, Dl. Open J. Soc. Sci. 8.
Bunker, D., and Thorpe, R. (1982). A model for the teaching of games in secondary schools. Bull. Phys. Educ . 18, 5–8.
Casey, A. (2014). Models-based practice: Great white hope or white elephant? Phys. Educ. Sport Pedagog. 19, 18–34. doi: 10.1080/17408989.2012.726977
Casey, A., MacPhail, A., Larsson, H., and Quennerstedt, M. (2021). Between hope and happening: Problematizing the M and the P in models-based practice. Phys. Educ. Sport Pedagog. 26, 111–122. doi: 10.1080/17408989.2020.1789576
Chedru, M. (2015). Impact of motivation and learning styles on the academic performance of engineering students. J. Educ. Sci. 41, 457–482. doi: 10.7202/1035313ar
Cook, D. A., and Artino, A. R. (2016). Motivation to learn: An overview of contemporary theories. J. Med. Educ . 50, 997–1014. doi: 10.1111/medu.13074
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika. J. 16, 297–334. doi: 10.1007/BF02310555
Cunningham, J., and Sood, K. (2018). How effective are working memory training interventions at improving maths in schools: a study into the efficacy of working memory training in children aged 9 and 10 in a junior school?. Education 46, 174–187. doi: 10.1080/03004279.2016.1210192
Darling-Hammond, L., Flook, L., Cook-Harvey, C., Barron, B., and Osher, D. (2020). Implications for educational practice of the science of learning and development. Appl. Dev. Sci. 24, 97–140. doi: 10.1080/10888691.2018.1537791
David, A. (2010). Examining the relationship of personality and burnout in college students: The role of academic motivation. E. M. E. Rev. 1, 90–104.
Deci, E., and Ryan, R. (1985). Intrinsic motivation and self-determination in human behavior. Perspect. Soc. Psychol . 2271, 7. doi: 10.1007/978-1-4899-2271-7
Deci, E. L., and Ryan, R. M. (1995). “Human autonomy,” in Efficacy, Agency, and Self-Esteem (Boston, MA: Springer).
Dickinson, B. L., Lackey, W., Sheakley, M., Miller, L., Jevert, S., and Shattuck, B. (2018). Involving a real patient in the design and implementation of case-based learning to engage learners. Adv. Physiol. Educ. 42, 118–122. doi: 10.1152/advan.00174.2017
Docktor, J. L., Strand, N. E., Mestre, J. P., and Ross, B. H. (2015). Conceptual problem solving in high school. Phys. Rev. ST Phys. Educ. Res. 11, 20106. doi: 10.1103/PhysRevSTPER.11.020106
Dyson, B., and Grineski, S. (2001). Using cooperative learning structures in physical education. J. Phys. Educ. Recreat. Dance. 72, 28–31. doi: 10.1080/07303084.2001.10605831
Ergül, N. R., and Kargin, E. K. (2014). The effect of project based learning on students' science success. Procedia. Soc. Behav. Sci. 136, 537–541. doi: 10.1016/j.sbspro.2014.05.371
Fenouillet, F. (2012). Les théories de la motivation . Psycho Sup : Dunod.
Fidan, M., and Tuncel, M. (2019). Integrating augmented reality into problem based learning: The effects on learning achievement and attitude in physics education. Comput. Educ .142, 103635. doi: 10.1016/j.compedu.2019.103635
Garrett, T. (2008). Student-centered and teacher-centered classroom management: A case study of three elementary teachers. J. Classr. Interact. 43, 34–47.
Goldstein, O. A. (2016). Project-based learning approach to teaching physics for pre-service elementary school teacher education students. Bevins S, éditeur. Cogent. Educ. 3, 1200833. doi: 10.1080/2331186X.2016.1200833
Gordon, B., and Doyle, S. (2015). Teaching personal and social responsibility and transfer of learning: Opportunities and challenges for teachers and coaches. J. Teach. Phys. Educ. 34, 152–161. doi: 10.1123/jtpe.2013-0184
Grolnick, W. S., Ryan, R. M., and Deci, E. L. (1991). Inner resources for school achievement: Motivational mediators of children's perceptions of their parents. J. Educ. Psychol . 83, 508–517. doi: 10.1037/0022-0663.83.4.508
Guay, F., Vallerand, R. J., and Blanchard, C. (2000). On the assessment of situational intrinsic and extrinsic motivation: The Situational Motivation Scale (SIMS). Motiv. Emot . 24, 175–213. doi: 10.1023/A:1005614228250
Guiffrida, D., Lynch, M., Wall, A., and Abel, D. (2013). Do reasons for attending college affect academic outcomes? A test of a motivational model from a self-determination theory perspective. J. Coll. Stud. Dev. 54, 121–139. doi: 10.1353/csd.2013.0019
Hastie, P. A., and Casey, A. (2014). Fidelity in models-based practice research in sport pedagogy: A guide for future investigations. J. Teach. Phys. Educ . 33, 422–431. doi: 10.1123/jtpe.2013-0141
Hu, W. (2010). Creative scientific problem finding and its developmental trend. Creat. Res. J. 22, 46–52. doi: 10.1080/10400410903579551
Ilkiw, J. E., Nelson, R. W., Watson, J. L., Conley, A. J., Raybould, H. E., Chigerwe, M., et al. (2017). Curricular revision and reform: The process, what was important, and lessons learned. J. Vet. Med. Educ . 44, 480–489. doi: 10.3138/jvme.0316-068R
Johnson, A. P. (2010). Making Connections in Elementary and Middle School Social Studies. 2nd Edn. London: SAGE.
Johnson, D. W., Johnson, R. T., and Smith, K. A. (1998). Active Learning: Cooperation in the College Classroom. 2nd Edn. Edina, MN: Interaction Press.
Kim, K. J., and Frick, T. (2011). Changes in student motivation during online learning. J. Educ. Comput. 44, 23. doi: 10.2190/EC.44.1.a
Kolesnikova, I. (2016). Combined teaching method: An experimental study. World J. Educ. 6, 51–59. doi: 10.5430/wje.v6n6p51
Komarraju, M., Karau, S. J., and Schmeck, R. R. (2009). Role of the Big Five personality traits in predicting college students' academic motivation and achievement. Learn. Individ. Differ. 19, 47–52. doi: 10.1016/j.lindif.2008.07.001
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t -tests and ANOVAs. Front. Psychol . 4, 863. doi: 10.3389/fpsyg.2013.00863
Lemos, M. S., and Veríssimo, L. (2014). The relationships between intrinsic motivation, extrinsic motivation, and achievement, along elementary school. Procedia. Soc. Behav. Sci . 112, 930–938. doi: 10.1016/j.sbspro.2014.01.1251
Leo, M. F., Mouratidis, A., Pulido, J. J., López-Gajardo, M. A., and Sánchez-Oliva, D. (2022). Perceived teachers' behavior and students' engagement in physical education: the mediating role of basic psychological needs and self-determined motivation. Phys. Educ. Sport Pedagogy. 27, 59–76. doi: 10.1080/17408989.2020.1850667
Lonsdale, C., Sabiston, C., Taylor, I., and Ntoumanis, N. (2011). Measuring student motivation for physical education: Examining the psychometric properties of the Perceived Locus of Causality Questionnaire and the Situational Motivation Scale. Psychol. Sport. Exerc . 12, 284–292. doi: 10.1016/j.psychsport.2010.11.003
Luo, Y. J. (2019). The influence of problem-based learning on learning effectiveness in students' of varying learning abilities within physical education. Innov. Educ. Teach. Int. 56, 3–13. doi: 10.1080/14703297.2017.1389288
Maddeh, T., Amamou, S., Desbiens, J., and françois Souissi, N. (2020). The management of disruptive behavior of secondary school students by Tunisian trainee teachers in physical education: Effects of a training program in the prevention and management of indiscipline. J. Educ. Fac . 4, 323–344. doi: 10.34056/aujef.674931
Manninen, M., and Campbell, S. (2021). The effect of the sport education model on basic needs, intrinsic motivation and prosocial attitudes: A systematic review and multilevel meta-Analysis. Eur. Phys. Educ. Rev . 28, 76–99. doi: 10.1177/1356336X211017938
Menendez, J. I., and Fernandez-Rio, J. (2017). Hybridising sport education and teaching for personal and social responsibility to include students with disabilities. Eur. J. Spec. Needs Educ. 32, 508–524 doi: 10.1080/08856257.2016.1267943
Metzler, M. (2017). Instructional Models in Physical Education . London: Routledge.
Miserandino, M. (1996). Children who do well in school: Individual differences in perceived competence and autonomy in above-average children. J. Educ. Psychol . 88, 203–214. doi: 10.1037/0022-0663.88.2.203
Norboev, N. N. (2021). Theoretical aspects of the influence of motivation on increasing the efficiency of physical education. Curr. Res. J. Pedagog . 2, 247–252. doi: 10.37547/pedagogics-crjp-02-10-44
Novak, D. J. (2010). Learning, creating, and using knowledge: Concept maps as facilitative tools in schools and corporations. J. E-Learn. Knowl. Soc . 6, 21–30. doi: 10.20368/1971-8829/441
Parish, L. E., and Treasure, D. C. (2003). Physical activity and situational motivation in physical education: Influence of the motivational climate and perceived ability. Res. Q. Exerc. Sport. 74, 173. doi: 10.1080/02701367.2003.10609079
Pérez-Jorge, D., González-Dorta, D., Del Carmen Rodríguez-Jiménez, D., and Fariña-Hernández, L. (2021). Problem-solving teacher training, the effect of the ProyectaMates Programme in Tenerife. International Educ . 49, 777–7791. doi: 10.1080/03004279.2020.1786427
Perrenoud, P. (2003). Qu'est-ce qu'apprendre. Enfances Psy . 4, 9–17. doi: 10.3917/ep.024.0009
Pohan, A., Asmin, A., and Menanti, A. (2020). The effect of problem based learning and learning motivation of mathematical problem solving skills of class 5 students at SDN 0407 Mondang. BirLE . 3, 531–539. doi: 10.33258/birle.v3i1.850
Puigarnau, S., Camerino, O., Castañer, M., Prat, Q., and Anguera, M. T. (2016). El apoyo a la autonomía en practicantes de centros deportivos y de fitness para aumentar su motivación. Rev. Int. de Cienc. del deporte. 43, 48–64. doi: 10.5232/ricyde2016.04303
Ratelle, C. F., Guay, F., Vallerand, R. J., Larose, S., and Senécal, C. (2007). Autonomous, controlled, and amotivated types of academic motivation: A person-oriented analysis. J. Educ. Psychol. 99, 734–746. doi: 10.1037/0022-0663.99.4.734
Rivera-Pérez, S., Fernandez-Rio, J., and Gallego, D. I. (2020). Effects of an 8-week cooperative learning intervention on physical education students' task and self-approach goals, and Emotional Intelligence. Int. J. Environ. Res. Public Health . 18, 61. doi: 10.3390/ijerph18010061
Rolland, V. (2009). Motivation in the School Context . 5th Edn . Belguim: De Boeck Superior, 218.
Rossa, R., Maulidiah, R. H., and Aryni, Y. (2021). The effect of problem solving technique and motivation toward students' writing skills. J. Pena. Edukasi. 8, 43–54. doi: 10.54314/jpe.v8i1.654
Ryan, R., and Deci, E. (2020). Intrinsic and extrinsic motivation from a self-determination theory perspective: Definitions, theory, practices, and future directions. Contemp. Educ. Psychol . 61, 101860. doi: 10.1016/j.cedpsych.2020.101860
Siedentop, D., Hastie, P. A., and Van Der Mars, H. (2011). Complete Guide to Sport Education, 2nd Edn. Champaign, IL: Human Kinetics.
Skinner, B. F. (1985). Cognitive science and behaviourism. Br. J. Psychol. 76, 291–301. doi: 10.1111/j.2044-8295.1985.tb01953.x
Standage, M., Gillison, F. B., Ntoumanis, N., and Treasure, D. C. (2012). Predicting students' physical activity and health-related well-being: a prospective cross-domain investigation of motivation across school physical education and exercise settings. J. Sport. Exerc. Psychol . 34, 37–60. doi: 10.1123/jsep.34.1.37
Tebabal, A., and Kahssay, G. (2011). The effects of student-centered approach in improving students' graphical interpretation skills and conceptual understanding of kinematical motion. Lat. Am. J. Phys. Educ. 5, 9.
Vallerand, R. J., Fbrtier, M. S., and Guay, F. (1997). Self-determination and persistence in a real-life setting toward a motivational model of high school dropout. J. Pers. Soc. Psychol. 2, 1161–1176. doi: 10.1037/0022-3514.72.5.1161
Ward, P., Mitchell, M. F., van der Mars, H., and Lawson, H. A. (2021). Chapter 3: PK+12 School physical education: conditions, lessons learned, and future directions. J. Teach. Phys. Educ. 40, 363–371. doi: 10.1123/jtpe.2020-0241
Keywords: problem-solving method, traditional method, motivation, learning, students
Citation: Ezeddine G, Souissi N, Masmoudi L, Trabelsi K, Puce L, Clark CCT, Bragazzi NL and Mrayah M (2023) The problem-solving method: Efficacy for learning and motivation in the field of physical education. Front. Psychol. 13:1041252. doi: 10.3389/fpsyg.2022.1041252
Received: 10 September 2022; Accepted: 15 December 2022; Published: 25 January 2023.
Reviewed by:
Copyright © 2023 Ezeddine, Souissi, Masmoudi, Trabelsi, Puce, Clark, Bragazzi and Mrayah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

How is the problem-solving ability and scientific attitude of students in mathematics learning seen from the teacher’s perspective?
- Split-Screen
- Article contents
- Figures & tables
- Supplementary Data
- Peer Review
- Open the PDF for in another window
- Reprints and Permissions
- Cite Icon Cite
- Search Site
Nia Afrelia , Ali Mahmudi , Heri Retnawati; How is the problem-solving ability and scientific attitude of students in mathematics learning seen from the teacher’s perspective?. AIP Conf. Proc. 29 April 2024; 2622 (1): 080004. https://doi.org/10.1063/5.0133852
Download citation file:
- Ris (Zotero)
- Reference Manager
One of the main goals of learning mathematics is problem solving ability, which are important for every student to mastered. In addition, there is a domain of attitude that also supports problem-solving abilities, namely the scientific attitude. The important role of teachers is needed in training students’ problem-solving skills and scientific attitudes especially in learning mathematics. This study aims to describe how students’ mathematical problem-solving abilities and students’ scientific attitudes in the mathematics learning process based on teacher perceptions. This research is a qualitative with the type of phenomenology. Data were collected using online questionnaires and interviews with 10 mathematics teachers in Jambi province. Data analysis was carried out using the Milles & Huberman stage, which divided the steps of data analysis activities into several parts, there are data collection, data reduction, data display, and conclusion or verification. The results showed that the problem-solving ability and scientific attitude of students in learning mathematics based on the teacher’s perspective are not optimal, this happened not only because of factors from the students themselves but also exist big contribution by a teacher.
Citing articles via
Publish with us - request a quote.

Sign up for alerts
- Online ISSN 1551-7616
- Print ISSN 0094-243X
- For Researchers
- For Librarians
- For Advertisers
- Our Publishing Partners
- Physics Today
- Conference Proceedings
- Special Topics
pubs.aip.org
- Privacy Policy
- Terms of Use
Connect with AIP Publishing
This feature is available to subscribers only.
Sign In or Create an Account
You are using an outdated browser. Please upgrade your browser to improve your experience.
Issues We Care About
- Digital Divide
- Affordability
- College Readiness
- Environmental Barriers
Measuring Impact
- WGU's Success Metrics
- Policy Priorities
- Annual Report
- WGU's Story
- Careers at WGU
- Impact Blog
Revolutionizing Career Readiness: The Role of Tech in Work-Based Learning Programs
- See More Tags

This is a recap of a session from the 2024 ASU+GSV Summit. Watch the full session below.
In today's rapidly evolving job market, there's a crisis brewing: students are increasingly ill-prepared for the workforce. Entry-level positions are vanishing with the rise of AI and universities are struggling to prepare students for on-the-job success, leaving many feeling stranded and unqualified. But amidst this challenge lies an opportunity to bridge the gap between education and employment through innovative solutions like work-based learning programs.
Lack of Work-Based Learning Opportunities
According to a recent report from ECMC and VICE Media, a staggering 79% of high school students recognize the importance of on-the-job learning experiences during their postsecondary education. However, only half of them have access to career exploration programs. This glaring disparity underscores the urgent need for a shift in educational paradigms.

The Solution: Third-Party Organizations Connecting Employers and Learners
Enter tech-driven enterprises like Juvo Ventures , a pioneering early-stage venture capital firm founded in 2019. They're at the forefront of redefining career readiness by championing initiatives that connect students with real-world work experiences. Leaders like Dr. Courtney Hills McBeth , provost and chief academic officer at Western Governors University ( WGU ), and Katie Fang , founder and CEO of SchooLinks, which focuses on college and career readiness, are also leading the charge in revolutionizing traditional education models.
Dana Stephenson , co-founder and CEO of Riipen , a work-based learning platform for educators, learners and employers emphasized the importance of providing students with practical experience throughout their educational journey at the 2024 ASU+GSV Summit. He highlighted the shift away from relying solely on post-graduation employment as a launching pad for careers, advocating instead for early and continuous exposure to real-world scenarios.
Dr. Ryan Craig , managing director of Achieve Partners , stressed the need for scalable solutions that seamlessly integrate employers into the education ecosystem. “You have to make it so easy that it’s turnkey for employers,” he said, underscoring the pivotal role of intermediaries in facilitating work-based learning experiences and streamlining pathways to employment.
A Plea for Universities to Reprioritize
Dr. Hills McBeth said a key issue is focus, funding and scale, stating, “Most traditional higher ed has invested in athletics and alumni engagement and advancement offices rather than investing in employer engagement.”
WGU is changing that as a university that has prioritized student experience and career outcomes from the start. A nonprofit founded in 1997 by 19 U.S. governors, the online university supports students through job-aligned degree programs crafted with input from employers and built for career success. Organizations that hire WGU grads are reaping the rewards with a healthy 98% of employers saying WGU graduates meet or exceed their expectations.
Making it Easier for Employers to Connect with Learners
Solving the career-readiness challenge is not just about connecting students with opportunities; it's also about empowering employers, especially small and medium-sized enterprises, to actively participate in shaping the future workforce. Stephenson pointed out that many companies are eager to collaborate and engage with educational institutions to identify and nurture talent, citing the success of Juvo Ventures.
One key takeaway from this discussion is the importance of making work-based learning programs accessible and adaptable. Whether it's through shorter-duration, lower-intensity experiences or more immersive apprenticeships, flexibility is paramount to accommodating the diverse needs of students and employers alike.
More Focused State Standards
There's a growing consensus on the need for clearer, more prescriptive college and career readiness standards. Ryan Craig highlighted the current generic nature of state-level standards and calls for a more tailored approach to ensure students are equipped with the skills demanded by today's job market.
A Collaborative Effort
The revolution in career readiness isn't just about preparing students for specific jobs; it's about cultivating a mindset of adaptability, resilience, and continuous learning. By harnessing the power of technology and collaboration between states, organizations, universities, and learners, we can transform education from a passive experience into a dynamic journey that empowers individuals to thrive in an ever-changing world.
Watch the Video
Ready to Start Your Journey?
HEALTH & NURSING
Recommended Articles
Take a look at other articles from WGU. Our articles feature information on a wide variety of subjects, written with the help of subject matter experts and researchers who are well-versed in their industries. This allows us to provide articles with interesting, relevant, and accurate information.

Addressing Workforce Gaps through Adult Education

Types of Supply Chain Management Software: An In-Depth Guide

Top Qualities And Skills Of A Good Teacher

4 Jobs for People Who Like Problem-Solving

IgnitED: Rethinking Financial Aid Amid a Changing Higher Ed Landscape
The university.
- Accessibility
- Accreditation
For Students
- Student Portal
- Alumni Services
Most Visited Links
- Business Programs
- Bachelor's Degrees
- Student Experience
- Online Degrees
- Scholarships
- Financial Aid
- Diversity, Equity, and Inclusion
- Testimonials
- Student Communities

IMAGES
VIDEO
COMMENTS
A problem-solving classroom requires extraordinary planning on the part of the teacher. For problems to have relevance, students are engaged in the identification of the problem. Teachers have to ...
In PBL, students work in small collaborative groups and learn what they need to know to solve a problem. The teacher acts as a facilitator to guide the students in developing the cognitive skills required for problem solving and collaboration (Hmelo-Silver, Citation 2004).
Instructors can signpost the problem-solving skills students should develop in their courses by adapting existing problem sets to fit recommendations from the Transparency in Learning and Teaching Project (TILT). The process of increasing transparency in assignments includes communicating the assignment's purpose, task, and criteria to ...
Make students articulate their problem solving process . In a one-on-one tutoring session, ask the student to work his/her problem out loud. This slows down the thinking process, making it more accurate and allowing you to access understanding. When working with larger groups you can ask students to provide a written "two-column solution.".
Problem-Based Learning (PBL) is a teaching method in which complex real-world problems are used as the vehicle to promote student learning of concepts and principles as opposed to direct presentation of facts and concepts. In addition to course content, PBL can promote the development of critical thinking skills, problem-solving abilities, and ...
Working on solutions. In the solution phase, one develops and then implements a coherent plan for solving the problem. As you help students with this phase, you might ask them to: identify the general model or procedure they have in mind for solving the problem. set sub-goals for solving the problem. identify necessary operations and steps.
Resolve Conflicts. In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes "thinking outside the box" and approaching a conflict by searching for different solutions.
Teach problem-solving skills in the context in which they will be used by students (e.g., mole fraction calculations in a chemistry course). Use real-life problems in explanations, examples, and exams. Do not teach problem solving as an independent, abstract skill. Help students understand the problem. In order to solve problems, students need ...
learn what they need to know to solve a problem. The teacher acts as a facilitator to guide the students in developing the cognitive skills required for problem solving and collaboration (Hmelo- Silver, 2004). Many studies have confirmed that PBL improves the performance of students, not only in
The important role of collaboration in teacher learning and professional development has been recognized in many studies (e.g., Zhang, Liu, Chen, ... (2017) emphasized the importance of social and cognitive factors in promoting team problem solving and learning and argued that collaborative problem solving was essentially a social cognition ...
Problem-based learning (PBL) is a style of teaching that encourages students to become the drivers of their learning process. Problem-based learning involves complex learning issues from real-world problems and makes them the classroom's topic of discussion; encouraging students to understand concepts through problem-solving skills rather than ...
PBL is a student-centered approach to learning that involves groups of students working to solve a real-world problem, quite different from the direct teaching method of a teacher presenting facts and concepts about a specific subject to a classroom of students. Through PBL, students not only strengthen their teamwork, communication, and ...
Teachers' role within the multifaceted process of developing problem-solving skills cannot be ignored. Especially, primary school teachers hold a significant role in shaping the learning ...
2) Learning happens in a group and teacher is a facilitator. 3) All groups have to participate equally. 4) Students' learn about motivation, teamwork, problem-solving and engagement with the task. 5) Materials such as Data, photographs, articles, can be used to solve the problem.
Collaborative problem-solving has been widely embraced in the classroom instruction of critical thinking, which is regarded as the core of curriculum reform based on key competencies in the field ...
Problem-based learning (PBL) has been widely adopted in diverse fields and educational contexts to promote critical thinking and problem-solving in authentic learning situations. Its close affiliation with workplace collaboration and interdisciplinary learning contributed to its spread beyond the traditional realm of clinical education 1 to ...
Teaching and Learning Strategiesthat Enhance Problem-Solving Skills: There are two types of strategies that can overcomedifficulties in problem-solving: pedagogical strategies,which are teacher-centered methods, andmethodological strategies, which tend to be learner centered. Pedagogical Strategies
Improving problem-solving skills is a primary educational goal, as is the ability to use reasoning. To acquire this skill, students must solve problems to learn mathematics and problem-solving ; this encourages the students to actively participate and contribute to the activities suggested by the teacher. Without sufficient motivation, learning ...
2009). In the basic definitions of problem- based learning, as mentioned above, it is stated that the teacher's intervention in the process will end the problem- based learning process and the teacher should not interfere with the solution. However, in the problem-based learning process, the teacher prepares the problem or scenario,
The important role of teachers is needed in training students' problem-solving skills and scientific attitudes especially in learning mathematics. This study aims to describe how students' mathematical problem-solving abilities and students' scientific attitudes in the mathematics learning process based on teacher perceptions.
Brief. Problem solving plays an important role in mathematics and should have a prominent role in the mathematics education of K-12 students. However, knowing how to incorporate problem solving meaningfully into the mathematics curriculum is not necessarily obvious to mathematics teachers. (The term "problem solving" refers to mathematical ...
The purpose of this article is to offer teacher training and professional development recommendations in mathematics based on the findings of a federally funded 3-year intervention study that improved the problem solving of middle school students with a focus on students with learning disabilities.
The COVID-19 pandemic caused a sudden shift to virtual platforms. Physical distance and limited experience with both synchronous and asynchronous teamwork at work and school hampered problem-solving and the development of critical thinking skills. Under these circumstances, the implementation of team-based and problem-based learning (TBL, PBL, respectively) required a reevaluation of how teams ...
Attention to Problem Details: Teachers discuss learning how certain details in a problem or activity (i.e. number selection, wording) can either help or hinder student learning. Another thing I felt like I learned was the way that each part of the problem is so important and can change how the kids solve it.
problem solving is a basic ability in teaching mathematics, thus it helps individuals to develop their analytic thinking, helps students to be critical and creative, and to improve other mathematics abilities ... the role of problem-based learning on students' MPSA and MSC. The study involved 66 tenth grade students, an essay MPSA test, an ...
The problem-solving tendency questionnaire was administered before and after the teaching experiment. The purpose was to explore whether there was a difference in the problem-solving tendency of the learners in the experimental group and the control group after the virtual scenario learning model combined with multiple role experiences.
Teaching Strategies for Engaging Students. ... Role-Play Scenarios for Problem-Solving. In role-play scenarios, preschoolers can step into various roles and explore complex social interactions and problem-solving strategies. ... In conclusion, it's clear that the journey of learning and problem-solving doesn't stop at the classroom door. It ...
Teachers might incorporate games or role-playing to make lessons more engaging. The key is to find methods that work for you or your students and that can be adapted as you progress.
Even though the settings and duties differ for each, all three roles involve critical thinking and problem-solving abilities to achieve a positive outcome. If you consider yourself a goal-oriented, problem-solving enthusiast, you might feel overwhelmed at the sheer number of careers that provide opportunities for overcoming complex challenges.
Lack of Work-Based Learning Opportunities. According to a recent report from ECMC and VICE Media, a staggering 79% of high school students recognize the importance of on-the-job learning experiences during their postsecondary education. However, only half of them have access to career exploration programs.