2nd grade problem solving problems

• Home   |  
• Contact Us   |  
• Privacy Policy   |  
• Copyright   |  
• Store   |  
• 🔍 Search Site
• Online Math Learning
• Generated Sheets for +, -, x and ÷
• Mental Math
• Math Puzzles
• Place Value
• Subtraction
• Multiplication
• Venn Diagrams
• Word Problems
• Math Coloring
• Math Printables

Second Grade Math Problems

Welcome to the Second Grade Math Problems page. We have a wide selection of longer math problems requiring a wide range of math skills to solve.

These problems are also a great way of developing perseverance and getting children to try different approaches in their math.

On this webpage are our selection of longer, more in-depth problem solving sheets for 2nd grade.

Typically, there is just one problem on each page with maybe a follow up problem in some cases.

The sheets cover a wide range of Math topics, from place value and number fact knowledge to geometry and logic problems.

The following worksheets have been designed to develop a wide range of skills and problem solving techniques such as:

• making lists or tables
• drawing pictures to help solve problems
• working systematically
• logical thinking
• number fact knowledge
• persevering until all solutions have been found

An answer sheet is available for each worksheet provided, where appropriate.

These sheets can be used in many different ways:

• to challenge more able pupils
• to use as a way of developing strategies to explore more in-depth problems, such as making lists or tables
• to use as an extension activity for children who finish early
• to use as part of a Maths challenge board
• Broken Calculator Problem 1

The Broken Calculator problem is a number problem involving using an imaginary broken calculator with only the 2, 3, + and = buttons working to make different totals.

There are 2 versions of the problem sheet, one with a pre-prepared template for filling in, and a second blank version for children to show their own recording system.

• No table version
• PDF version

Anyone for an Ice Cream?

Anyone for an Ice Cream is a money activity which involves using silver coins only to make a total of 40¢ . The aim is to find all the possibilities.

• Anyone for an Ice-cream?
• Anyone for an Ice Cream? UK version
• Tyger's Coin Challenges

Tyger's Coin Challenge is a money activity. The aim is to see whether or not different amounts of money can be made from a number of coins.

• Captain Salamander's Letter

This 2nd grade math problem sheet involves working out which totals of money can be made using only 3¢ and 5¢ stamps. It is a good activity for developing perseverance and logical thinking.

• Balloon Pairs #2

Balloon Pairs is a number adding activity where the aim is to find different totals by adding the balloon numbers together. The totals are then sorted in order of size using a table.

• Balls in the Bucket Challenge #2

This challenge involves working out how different scores were made in the balls-in-the-bucket game. It is a 'finding all possibilities' type of problem.

• Birthday Girl

Birthday Girl is an activity which involves finding the correct ages of all the people in the challeges using the clues that are given.

• Climb the Mountain

This is one of our second grade math problems that involves finding all the possible paths up to the top of the mountain using the routes provided.

• Dilly's Eggs #1

Dilly's eggs is a sharing problem - drawing it out is a good strategy for tackling this problem. The aim is to find the number of eggs Dilly had using the clues provided.

• Odd Square Out

This is a good activity for developing noticing skills and recognising shapes that have been rotated or reflected.

• Parking Lots #2

Parking Lots is an activity where the aim is to find as many combinations as possible for the cars to park. Systematic working could be an area of focus for this activity.

• Pick the Cards #2

Pick the Cards is an adding game where the aim is to use combinations of numbers to reach a given total. This activity is good for adding three or four small numbers together to make a given total.

• Place It Right #2

Place It Right is a place value activity to support children with their place value learning. The aim is to make a range of 3 digit numbers with different properties.

• Share the Treasure #2

Share the Treasure is a logic acitivity where the aim is to share some treasure according to certain criteria.

• Who Chose Which Shape #2

Who Chose Which Shape is a logic problem where children have to work out which salamander chose which shape from the clues given.

Looking for some easier word problems

We have a range of easier word problems at our parent site, math-salamanders.com

The problems on this page are at a simpler level than those here.

Many of the problems, e.g. Dilly's Eggs, Pick the Cards and Share the Treasure have easier versions on this page.

Using the link below will open our main site in a new tab.

• First Grade Math Problems

Looking for some harder word problems

We have a range of more challenging word problems at our parent site, math-salamanders.com

The problems on this page are at a trickier level than those here.

Some of the problems, e.g. Place It Right and Share the Treasure have harder versions on this page.

• 3rd Grade Math Problems

Addition and Subtraction Puzzles

The puzzles in this section mainly focus on adding and subtracting numbers.

The puzzles start with adding and subtracting to 20, and progress on to harder levels and more complex puzzles.

Using the puzzles in this section will help your child to:

• develop their adding and subtracting skills;
• develop trial and improvement strategies;
• improve problem solving skills.

All the second grade math problems in this section will help your child to learn their addition and subtraction facts and become more confident with handling numbers mentally.

• Free Math Puzzles - Addition and Subtraction

Return to Math Puzzles Hub Page

Return from Second Grade Math Problems Page to Homepage

How to Print or Save these sheets

Need help with printing or saving? Follow these 3 easy steps to get your worksheets printed out perfectly!

• How to Print support

Math-Salamanders.com

Whether you are looking for a free Homeschool Math Worksheet collection, banks of useful Math resources for teaching kids, or simply wanting to improve your child's Math learning at home, there is something here at the Math Salamanders for you!

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

Grading Guide

Here is the grading guide for our worksheets.

White: the easiest level for children at their early stages in 2nd grade.

Orange: medium level of difficulty for children who are working at the expected level in 2nd grade.

Purple: this is the hardest level for children who need that extra challenge.

Visit our parent site

• Kindergarten
• First Grade

© 2012-2024 Math Salamanders Limited. All Rights Reserved.

• Home  
• Privacy Policy  
• Copyright Policy  
• Sitemap  

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Learn with the Khan Academy Kids app

Unit 1: add and subtract within 20, unit 2: place value, unit 3: add and subtract within 100, unit 4: add and subtract within 1,000, unit 5: money and time, unit 6: measurement, unit 7: data, unit 8: geometry.

50 Problems for 2 nd Graders

Practice your math skills with these 50 math problems for 2nd graders , covering addition, subtraction, place value, measurement, time, money, and geometry! Answers included.

Author Michelle Griczika

Published November 3, 2023

50 Math Problems for 2 nd Graders

Published Nov 3, 2023

Key takeaways

• Mastering addition and subtraction skills helps us solve mathematical puzzles and apply them to real-life situations.
• Understanding place value enables us to correctly read, write, and compare numbers, developing our number sense and mathematical reasoning.
• Solving measurement word problems helps us apply mathematical concepts to practical scenarios, improving our problem-solving and critical thinking abilities.
• Exploring time and money concepts allows us to understand the world around us, manage our daily routines effectively, and develop essential life skills.
• Recognizing shapes and their properties opens our eyes to the diverse world of geometry, helping us understand how objects are structured and enhancing our spatial awareness.

Table of contents

• Key Takeaways
• Addition and Subtraction
• Place Value
• Measurement Word Problems
• Time and Money

Hello, second grade mathematicians! Are you ready for some mind-boggling math challenges?

We will be going over important math skills for second graders to strengthen their understanding and knowledge.

• In second grade math , addition and subtraction skills are expanded to solve practical second grade math problems .
• Understanding place value allows us to navigate through large numbers and count objects, strengthening our number sense.
• Measurement math word problems for 2nd graders provide exciting puzzles that apply math skills to real-life scenarios, fostering problem-solving abilities and transforming us into math superstars.
• Counting money and telling time teach us essential skills for day to day life.
• Shapes are the building blocks of our surroundings. Understanding squares, triangles, and circles enables us to analyze their attributes and how they fit together.

All of these skills are necessary for 2nd grade math practice !

Unlock unlimited math questions

Put your skills to the test with fun exercises + maths games that are proven to boost ability!

Section 1: Addition and Subtraction

Section 2: Place Value

Use the greater than symbol >, less than symbol <, or equal to symbol = to answer.

Answer: <

Answer: >

Try DoodleMath for Free!

Select a year group

• Kindergarten

Measurement and data

Sample questions, section 3: measurement word problems.

Answer: 53 inches

Answer: 38 inches

Answer: 32 centimeters

Answer: 35 inches

Answer: 55 centimeters

Answer: 68 centimeters

Answer: 84 centimeters

Answer: 40 inches

Answer: 50 inches

Section 4: Time & Money

Look at the analog clock and write the digital time to the nearest five minutes:

What time is shown on the digital clock: 9:25 a.m. or 9:25 p.m.?

What time is shown on the digital clock: 1:50 a.m. or 1:50 p.m.?

Answer: $1.05

Answer: $5.08

Answer: 25 cents

Answer: 70 cents

Answer: $4.37

Section 5: Geometry

Answer: Triangle

Answer: Square

Answer: Pentagon

Answer: Hexagon

Answer: Equilateral Triangle

Answer: Trapezoid

Answer: Cube

Math practice for 2nd graders is super important because we use it every single day! For extra math practice that comes in the form of fun math games and interactive practice problems, try Doodle Learning’s math help app .

Lesson credits

Michelle Griczika

Michelle Griczika is a seasoned educator and experienced freelance writer. Her years teaching first and fifth grades coupled with her double certification in elementary and early childhood education lend depth to her understanding of diverse learning stages. Michelle enjoys running in her free time and undertaking home projects.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

Time Answer Sheet

What we offer

Quick links

All rights reserved. 

Are you a parent, teacher or student?

Get started for free!

Maths information pack

We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.

Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack

We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.

DoodleMaths

DoodleTables

DoodleEnglish

DoodleSpell

If you’d like to use Doodle’s browser version, please visit this page on a desktop.

To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

Math Word Problem Worksheets for 2nd Graders

Practicing math word problems with these worksheets in second grade will introduce kids to multi-step problems while practicing their addition and subtraction skills. Some problems will also include money questions and time. Easy and more advanced questions included in these math workbooks.

2nd Grade Math Word Problems

• Worksheets By Grade
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay

Word problems  can be challenging for students, especially second-graders, who may still be learning to read. But, you can use basic strategies that will work with nearly any student, even those who are just starting to learn written-language skills.

Instructions and Strategies

To help second-grade students learn to solve word problems, teach them to use the following steps:

• Survey the math problem:  Read the word problem to get an idea of its general nature. Talk with your students about the problem and discuss which parts are most important.
• Read the math problem:  Read the question again. This time, focus on the specific details of the problem. Which parts of the problem relate to each other?
• Ask questions about the operations involved:  Reflect again. Determine the specific math operations the problem is asking you to perform, and list them on paper in the order they are to be performed.
• Question yourself about the steps taken:  Review each step you took. Determine if your answer seems reasonable. If possible, check your answer against the book's answers to determine if you are on the right track.
• Wrap it up:  Scan through the text of the word problems you will be solving to identify any words you do not recognize. List them and determine their meanings before solving the problems. Write brief definitions of the terms for your reference during problem-solving.

Solving the Problems

After reviewing these strategies, use the following free word-problem printables to let the students practice what they've learned. There are only three worksheets because you don't want to overwhelm your second-graders when they are just learning to do word problems.

Start slowly, review the steps if needed, and give your young learners a chance to absorb the information and learn word problem-solving techniques at a relaxed pace. The printables contain terms with which young students will be familiar, such as "triangle," "square," "staircase," "dimes," "nickels," and the days of the week.

Worksheet 1

This printable includes eight math word problems that will seem quite wordy to second-graders but are actually quite simple. The problems on this worksheet include word problems phrased as questions, such as: "On Wednesday you saw 12 robins on one tree and 7 on another tree. How many robins did you see altogether?" and "Your 8 friends all have 2 wheeled bicycles, how many wheels is that altogether?" 

If students seem perplexed, read the problems aloud together with them. Explain that once you strip out the words, these are actually simple addition and multiplication problems, where the answer to the first would be: 12 robins + 7 robins=19 robins; while the answer to the second would be: 8 friends x 2 wheels (for each bike) = 16 wheels.

Worksheet 2

On this printable, students will work six questions starting with two easy problems followed by four more of increasing difficulty. Some of the questions include: "How many sides are on four triangles?" and "A man was carrying balloons but the wind blew 12 away. He has 17 balloons left. How many did he start with?"

If students need help, explain that the answer to the first would be: 4 triangles x 3 sides (for each triangle) = 12 sides; while the answer to the second would be: 17 balloons + 12 balloons (that blew away) = 29 balloons.

Worksheet 3

This final printable in the set contains slightly more difficult problems, such as this one involving money: "You have 3 quarters and your pop cost you 54 cents. How much money do you have left?"

To answer this one, have students survey the problem, then read it together as a class. Ask questions such as: "What could help us solve this problem?" If students are unsure, grab three quarters and explain that they are equal to 75 cents. The problem then ​becomes a simple subtraction problem, so wrap it up by setting up the operation numerically on the board as follows: 75 cents – 54 cents = 21 cents.

• Converting Cubic Meters to Liters
• Quiz 8th-Graders With These Math Word Problems
• Second Grade Math: Solving Word Problems
• 4th-Grade Math Word Problems
• Sixth Grade Word Problems
• Free Math Word Problem Worksheets for Fifth-Graders
• Math Word Problems for Third Graders
• 20 Free Spanish Worksheets to Help Test Your Knowledge
• First Grade Math: Word Problems
• Second Grade Christmas Math Word Problems
• Christmas Word Problem Worksheets
• Realistic Math Problems Help 6th-graders Solve Real-Life Questions
• Multiplication Word Problems With Printable Worksheets
• The Frayer Model for Math
• 7th Grade Math Worksheets
• Problem Solving in Mathematics

Grade 2 Word Problems

Free grade 2 word problems to help your students in mathematics. These free worksheets will help your students apply their knowledge to problem solve. Word Problems are often a challenge for students. They can comfortably do simple equations, but struggle to apply that knowledge to solve real life situations. It is important to do word problems daily to ensure your students get the repetition they need. Use these free worksheets to help you! They are scaled easy to hard (left to right).

Click to Preview.

Addition Word Problems

A bundle of the 3 resources.

Grade 2 & 3

A bundle of 6 Grade 2 & 3 resources. Click to Preview.

Subtraction Word Problems

3 weeks of free daily mental maths. Click to Preview.

10 weeks of daily mental maths. Click to Preview.

70 weeks of grade 2 & 3 mental maths. Click to Preview.

Grade 3 Word Problems | Draw a Picture

Word problems in grade 3 are very important. These 20 grade 3 word problems will engage students as they draw pictures to solve the questions! Drawing pictures is an effective strategy for solving problems in Mathematics. As students get older, they begin to visualize word problems. Drawing is the foundation for this! Get your students engaged in Mathematics with drawing during problem solving!

I hope you find it helpful!

Grade 4/5 Word Problem Task Cards

Daily Math Word Problems are vital to student development in Mathematics. This resource has 50 task cards, available in worksheet form with answers. Applying mathematical knowledge to solve word problems is extremely important. Some students understand how to solve equations but struggle to apply their knowledge when solving word problems. Doing daily word problems has helped my class a lot and I hope these flash cards will help yours!

Need More Grade 2 Worksheets?

For more grade 2 worksheets, check out grade 2 mental maths . There are some great worksheets there! For more 2nd grade worksheets, check out Dad Worksheets . They have a bunch of wonderful free worksheets that are helpful and easy to access. 

Privacy Policy

Terms and conditions, refund policy.

Slambo Education PTY LTD

ABN 91 195 681 869

Personification Lesson

This personification lesson includes a PowerPoint, activities and a worksheet. All ready to go to save your time!

• Grades 6-12
• School Leaders

Enter Today's Teacher Appreciation Giveaway!

Check Out These 50 Second-Grade Math Word Problems of the Day

Hunter has 47 baseball cards in his collection.

Opening your daily math lesson with a Math Word Problem of the Day is an excellent way to set the stage for learning. We all know that word problems are difficult for young learners to grasp, even when the mathematical operation portion of the problem is basic. Incorporate these second grade math word problems one day at a time at the start of your math block to build confidence, critical thinking skills, and a learning community!

Topics covered include addition, subtraction, multiplication, even/odd, three digit numbers, and time. All you need to do is post one of these second grade math word problems on your whiteboard or projector screen. Then let kids take it from there!

Want this entire set of second grade math word problems in one easy document? Get your free PowerPoint bundle by submitting your email here .

50 Second Grade Math Word Problems

1. trey has 5 squishy toys. he gets 4 more for his birthday. how many squishy toys does he have in all.

2. Stephanie brings donuts to give out to her classmates on her birthday. She brings in 8 powdered donuts, 8 glazed donuts, and 10 chocolate donuts. How many donuts did she bring in all?

3. Sara goes to the library. She is allowed to check out 10 books. She chooses 5 picture books and 3 chapter books. How many more books can she choose?

4. David plants 8 pineapple seeds, 5 strawberry seeds, and 2 blueberry seeds. How many seeds does he plant in all?

5. Paige has 10 crayons. Mike has 6 more crayons than Paige. Jon has 9 crayons. How many crayons do they have in all?

6. Jeff has 21 marbles in his collection. Eddie has 39 marbles in his collection. How many marbles do they have in all?

7. Vicki goes to the zoo and sees 8 flamingos. Next, she sees 15 ducks, before seeing 22 ibises. How many birds did she see in all?

8. Joshua sells 26 tickets to the school play. Nina sells 39 tickets to the school play. How many tickets did they sell in all?

9. The second grade goes on a field trip to the aquarium. There are 7 teachers, 62 girls, and 59 boys. How many people go on the field trip in all?

10. Some apples are in an apple orchard. 38 apples are picked. Now there are 52 left. How many apples were there to start?

11. Blake swam 18 laps on Monday. He swam 22 laps on Tuesday. He swam 27 laps on Wednesday. How many laps did he swim in all?

12. enzio reads for 25 minutes on monday. he reads for 33 minutes on tuesday. he reads for 35 minutes on wednesday. how many minutes does he read for in all.

13. Dana has 15 yummy cookies. He eats some of the cookies. Dana has 7 cookies left. How many cookies did Dana eat?

14. Eric had 12 toy cars. He gave 5 of the cars to his friend, Darren. How many toy cars does he have now?

15. Carolyn saw 15 beautiful birds in a tree. Some birds flew away. Now there are 4 birds in the tree. How many birds flew away?

16. Christina sold 32 boxes of girl scout cookies. Lea sold 44 boxes of girl scout cookies. How many more boxes did Lea sell than Christina?

17. Mimi has 23 more crayons than markers. She has 15 markers. How many crayons does she have?

18. Carrie has 36 pieces of candy. She gives 13 pieces to Tommy. How many pieces of candy does Carrie have left?

19. Dahlia has 28 dolls on a shelf. She moves some to her dollhouse. Now 15 dolls are on the shelf. How many did she move to the bed?

20. Jerry has 12 soccer balls. Bob had 17 soccer balls, but gave 8 of them to Phil. How many tennis balls do Jerry and Bob have now?

21. John has 54 pieces of candy. He eats 7 pieces on Monday. On Tuesday, he eats 11 pieces. On Wednesday, he gives 17 pieces away to friends. How many pieces of candy does he have left?

22. Maria has 29 marbles. Sam has 56 marbles. Rachel has 67 marbles. How many more marbles does Rachel have than Ella?

23. Steven buys 52 strawberries. He eats 12 of them for a snack. He eats 15 of them later that evening for dessert. How many strawberries are left?

24. Diana collects stickers. She has 48 stickers in an album. She buys 27 more stickers. She then gives 18 stickers to her friend Judy. How many stickers does she have now?

25. Hunter has 47 baseball cards in his collection. Ryan has 39 cards in his collection. How many more cards does Hunter have?

26. There are 95 people on a train. 19 people get off at the first stop. 24 people get off at the second stop. How many people are still on the train?

27. Daryl loves to collect comic books with superheroes. He has 5 comic books on his desk. He has 3 comic books in his backpack. Does Daryl have an even number or odd number of comic books?

28. Kim collects special seashells at the beach. She puts 8 shells in a pail. She puts 7 more shells in a jar. Does Kim have an even or odd number of seashells?

29. Leslie plants red peppers in her garden. Her garden has 6 rows with 5 peppers in each row. How many tomatoes are in her garden?

30. Marc puts 16 photos in an album. If there are 4 cards in each column, how many columns are there?

31. Ms. Sanders wanted to treat her class to a pizza party. There are 8 slices of pizza in each pizza pie. If she has 29 students, how many pizza pies does she need to order?

32. Four friends want to share a pumpkin pie. How could they cut the pie so each friend gets an equal share? Draw a picture to help you show your thinking.

33. Choose a three-digit number. Draw models to show the hundreds, tens, and ones to explain your thinking.

34. Liam is thinking of a number with three digits. It has 7 hundreds, 4 tens, and 6 ones. What is his number? Draw a model to explain your thinking.

35. Juliana has 257 stickers in her collection. She wants to explore this number further. First, she draws a model of the number by drawing base ten blocks. Then she writes it out in expanded form. Last, she writes it out in word form. Show how she does all three of these ways to explain 257.

36. Caleb is skip counting. He writes 160, 165, and 170 on a whiteboard. What are the next 5 numbers in his pattern?

37. The Florida Gators Football Team won their last 4 football games. They scored 25 points in the first game, 58 points in the second game, 33 points in the third game, and 77 points in the fourth game. How many points did they score in all?

38. Nolan collects Pokemon cards. He has 402 cards in his collection. He gives 25 cards to his friend Charlotte. He then gives 32 cards to his friend Maria. How many cards does he have left?

39. A school is having a bake sale. Dhomini’s mom brings 82 cupcakes. Amelia’s dad brings 75 cookies. Lorenzo’s mom brings 100 brownies. How many items are at the bake sale in all?

40. Kristella is reading a Magic Treehouse Book for her book report. She reads 24 pages on Monday. She reads 39 pages on Tuesday. She reads 37 pages on Wednesday. How many pages does she read in all?

41. Erica is reading James and the Giant Peach. The book has 144 pages. She reads 30 pages on Monday. She reads 42 pages on Tuesday. How many pages does she have left in the book?

42. Alana and her family are going to Disney World for her birthday. It is a 425 mile drive from her house. Her dad drives 127 miles before they stop for a snack. He drives another 233 miles before they stop for lunch. How many more miles do they have left until they arrive at Disney World?

43. The high school band is having a holiday concert. Peggy sells 75 tickets. Diana sells 101 tickets. Judy sells 135 tickets. How many tickets do they sell in all?

44. Mr. Axelrod’s class is tracking how many picture books they read each month. They read 329 books in March. They read 471 books in April. They read 450 books in May. How many books did they read in all?

45. The museum has 792 visitors over the weekend. 382 people visited the museum on Saturday. How many people visited the museum on Sunday?

46. Luna sells copies of the school newspaper. There are 500 copies. On Monday, she sold 122 copies. On Tuesday, she sold 198 copies. How many copies are left?

47. The second grade classes are going on a field trip to a play. Ms. Anastasio’s class has 29 students. Mr. Gordon’s class has 31 students. Mr. Fishman’s class has 33 students. Ms. McConnell’s class has 30 students. How many students go on the field trip in all?

48. Carlos is going to New York City on vacation. His plane leaves the airport at 2:30 p.m. The flight is 3 hours and 30 minutes long. What time does he land in New York City?

49. Juanita is watching the movie Harry Potter and the Sorcerer’s Stone. She starts the movie at 5 p.m. The movie is 2 hours and 32 minutes long. What time does the movie end?

50. Harry, Ron, and Hermione are on their way to Hogwarts. The train leaves the station in London at 9 a.m. It takes 7 hours to get to Hogwarts. What time do they arrive at Hogwarts?

Enjoying these second grade math word problems? Check out our second grade hub for even more resources.

Get a PPT version of these word problems.

You Might Also Like

50 Third Grade Math Word Problems of the Day

The area of Happytown is 42 square miles. Continue Reading

Copyright © 2024. All rights reserved. 5335 Gate Parkway, Jacksonville, FL 32256

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Word Problems For 2nd Grade: Develop Their Problem Solving Skills Across Single and Mixed Topics

Emma Johnson

Word problems for second grade are an important tool for improving number fluency. The key focus of math in second grade is on ensuring students are becoming more fluent with number facts and the concept of place value. Children are starting to develop more efficient written methods by this stage and are beginning to carry out calculations with increasingly larger whole numbers.

As children progress through school, they are exposed to a wider variety of problem solving questions covering a range of concepts. In second grade, these include addition, subtraction, measurement and data.  

It is important that children are regularly exposed to reasoning and problem solving questions, alongside the fluency work each lesson. It is also important to remember that all children need exposure to reasoning and problem solving questions, not just the higher attaining students who finish quickest.

We have put together a collection of 20 word problems, aimed at second grade students.

Word Problems Grade 2 Addition and Subtraction

11 grade 2 addition and subtraction questions to develop reasoning and problem solving skills.

Place value

Addition and subtraction, measurement, data representation, why are word problems important in second grade math, benefits of pairs, groups and class discussion , addition question 1, addition question 2, addition question 3, subtraction question 1, subtraction question 2, subtraction question 3, multi-step question 1, multi-step question 2, multi-step question 3, more word problems resources, second grade math word problems.

In second grade, students focus on one-step problems, covering a range of topics. At this stage the majority of word problems students are tackling will have one-step, but they may also start to be introduced to simple two-step word problems. Here is a breakdown of topics that will be covered and expectations in second grade. 

Solve number problems and practical problems involving recognizing the place value of each digit of a 3-digit number; comparing and ordering numbers up to 1,000 and identifying, representing and estimating numbers using different representations.

Solve problems, including missing number problems, using number facts, place value and more complex addition and subtraction word problems .

Solve problems involving length; adding and subtracting within money word problems involving dollar bills, quarters, dimes, nickels and pennies.

Solve-step and two-step questions (For example, ‘How many more?’ and ‘How many fewer’?) using information presented in scaled bar charts, pictograms and tables.

By second grade, children are starting to learn how to use some of the formal written methods of addition and subtraction. It is important that the link between math in school and math in real-life continues to be made. Word problems are a key element in helping students to make this link. 

How to teach problem solving in second grade

When teaching math problems to second grade, it’s important to think of ways to make them fun, engaging and something the children are able to relate to. This might include acting out the problem, using concrete resources and providing visual images, to bring the problems to life. 

Children should have plenty of opportunity to talk in pairs, groups and as a whole class, to share their understanding of what is being asked and their math strategies for problem solving . The use of manipulatives is important and all children should have access to a range of math resources when solving problems like this.

Students need to be encouraged to read word problems carefully and to make sure they understand what is being asked, before attempting to tackle the problem. This is where the use of a partner and group discussion can really help children’s understanding. Students then need to think about what they already know and how they can use this to help them answer the question. Where appropriate, students should also be encouraged to draw diagrams and pictures to help them solve the question.

Here is an example:

Mason has 24 glass jars to put flowers in.

He gives 5 to Marcy and drops 2 while carrying them inside the shop.

How many glass jars does Mason have left?

How to solve:

What do you already know?

• Mason has a total of 24 glass jars.
• We know he gives Marcy 5 jars, which means we will need to subtract 5 from 4. 
• He also dropped 2, also meaning we will need to subtract.
• In second grade, children should be building confidence with adding and subtracting within 20, and should be able to do these calculations in their heads.
• Children who aren’t able to recall quickly could use counters to represent the jars, or draw a bar model to help solve it.

How can this be drawn/represented visually?

We can draw a bar model or counters to represent this problem:

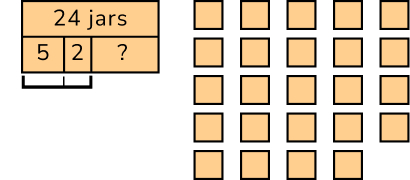
• To calculate how many jars are left, we can either use or draw 24 counters. We can then remove or cross out the 5 jars given to Marcy, and then 2 jars that were broken.
• Using the bar model, we can first subtract 5 from 24, representing the jars given to Marcy, leaving 19 jars. Then subtract 2 more from 19, to represent the two jars broken.
• Mason had 17 glass jars left. 

Addition word problems for second grade

In second grade, students are exposed to a range of addition word problems, including problems involving mental addition and addition of up to 3-digits using formal written methods.

See also: Mental math second grade

A family driving on holiday travel 146 miles from home to the first service station.

They then drive a further 175 miles to reach their destination.

How far have they traveled altogether?

Answer : 321 miles

146 + 175 = 321

Elvie is buying a can of soda from a vending machine. She has put in 2 quarters, 2 dimes, and 3 nickels. 

How much is the can of soda?

Answer : 85¢

50¢ + 20¢ + 15¢ = 85¢

Jamie scored 443 on his new online game.

Jared scored 468.

How many points did they score between them?

Answer : 911 points

443 + 468 = 911

At Third Space Learning we often tie word problems into our one-to-one online tuition. With each programme personalized to the needs of each individual student, children are able to develop their problem solving skills, math fluency and grow confidence in math.

Subtraction word problems for second grade

Subtraction word problems in second grade also need to comprise of a combination of mental calculation questions and those involving formal written subtraction up to 3-digits. Children should also be starting to estimate answers and check their calculations by using the inverse.

Ahmed collects 374 stickers.

He needs 526 stickers to fill his sticker album.

How many more stickers does he need to collect?

Answer : 152 stickers

526 – 374 = 152

 A bag of carrots weigh 360g

A bag of tomatoes weighs 235g.

How much heavier is the bag of carrots?

Answer : 125g

360 – 235 = 125

 Ahmed buys a bag of candy with 200 pieces in it.

Over 2 weeks, he eats 145 pieces. How many pieces of candy does Ahmed have left?

Answer : 55 pieces of candy

200 – 145 or count up from 145 to 200.

Multi-step word problems in second grade

When children first move into elementary school, word problems are predominantly one-step. As they become more confident they can be exposed to more word problems, requiring a second step or multi-step word problems. When first introducing two-step problems, keep the numbers used in the problems low and manageable to allow students to focus on reasoning over calculations.

Oliver had 3 bags of candies.

Each bag contained 15 candies.

Oliver’s little brother ate 17 pieces of the candy. How many pieces of candy does Oliver have left?

Answer : 9 sweets

15 + 15 + 15 = 45 

45  – 17 = 28

A teacher photocopies 95 math worksheets and 80 English worksheets in one week.

Teachers can print a maximum of 300 worksheets per week. 

How many can the teacher print for other subjects?

Answer : 125 worksheets

 95 + 80 = 175

300 – 175 = 125

A flower shop picks 19 roses and 25 daisies fresh from their garden.

A customer orders a dozen flowers for a birthday gift.

How many flowers will the flower shop have left?

Answer : 32 flowers

19 + 25 = 44 flowers (roses and daisies combined)

44 – 12 = 32 flowers

We hope that this collection of word problems for second grade becomes a useful resource in your second grade math classroom. 

For more resources, take a look at our library. Third Space Learning offers a wide array of math and word problems resources for other grades. These include worksheets , end of year assessments and a range of math games and activities for students from kindergarten through to 6th grade. 

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by former Deputy Headteacher Emma Johnson and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.

Related articles

25 Addition Word Problems For Grades 1-5 With Tips On Supporting Students’ Progress

What Is Box Method Multiplication? Explained For Elementary School Teachers, Parents And Pupils

20 Multiplication Word Problems for 3rd to 5th Grades With Tips On Supporting Students’ Progress

What Is Order Of Operations: Explained For Elementary School

Math Intervention Pack Operations and Algebraic Thinking [FREE]

Take a sneak peek behind our online tutoring with 6 intervention lessons designed by math experts while supporting your students with Operations and Algebraic Thinking.

As with our full library of lessons, each one includes questions to ask, ways to support students when they are stuck, and answers to the given questions.

Privacy Overview

Real-life word problems

Common Core Standards: Grade 2 Operations & Algebraic Thinking , Grade 2 Measurement & Data

CCSS.Math.Content.2.OA.A.1, CCSS.Math.Content.2.MD.C.8

This worksheet originally published in Math Made Easy for 3rd Grade by © Dorling Kindersley Limited .

Yes! Sign me up for updates relevant to my child's grade.

Please enter a valid email address

Thank you for signing up!

Server Issue: Please try again later. Sorry for the inconvenience

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Addition Word Problems 2nd Grade Addition Problems within 100

Welcome to our Addition Word Problems 2nd Grade Worksheets. Here you will find a wide range of free printable addition word problem worksheets, which will help your child practice solving a range of addition problems using numbers with a sum of up to 100.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Quicklinks to ...

• Addition Word Problems within 100
• Addition Word Problems within 100 with 3 addends
• Easier/Harder Addition Worksheets
• More related resources
• Addition Word Problems up to 100 Online Quiz

Addition Word Problems 2nd Grade

Addition problems within 100.

Each sheet consists of adding two or three numbers with a total of up to 100.

There is a space on each sheet for working out, so that your child can write out the problem and solve it.

We have split the worksheets up into word problems with and without regrouping.

Using these sheets will help your child to:

• add up two or three numbers within 100;
• solve addition word problems with and without regrouping.

Addition Word Problems 2nd Grade within 100

There are two versions of each sheet.

The first version (version A) contains problems where no regrouping is needed.

The second version (version B) contains similar problems but regrouping is needed to solve them.

Sheets 1A, 1B, 2A, 2B, 3A and 3B have just two addends to add up.

Sheets 4A, 4B, 5A and 5B have three addends to add together.

Addition Word Problems within 100 with 2 Addends

• Addition Word Problems within 100 Sheet 1A (no regrouping)
• PDF version
• Addition Word Problems within 100 Sheet 1B
• Addition Word Problems within 100 Sheet 2A (no regrouping)
• Addition Word Problems within 100 Sheet 2B
• Addition Word Problems within 100 Sheet 3A (no regrouping)
• Addition Word Problems within 100 Sheet 3B

Addition Word Problems within 100 with 3 Addends

• Addition Word Problems within 100 Sheet 4A (no regrouping)
• Addition Word Problems within 100 Sheet 4B
• Addition Word Problems within 100 Sheet 5A (no regrouping)
• Addition Word Problems within 100 Sheet 5B

Looking for some easier worksheets?

Take a look at our Addition word problems for first graders.

On this page, your child will learn to work out basic addition word problems with sums up to 20.

• 1st grade Addition Word Problems

Looking for some harder worksheets?

We have a range of 3-digit addition worksheets set out in columns.

• Addition Word Problems 3rd Grade (3- and 4-digits)
• 3-Digit Column Addition Worksheets

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

Addition & Subtraction Worksheets 2nd Grade

• Add and Subtract Within 20 Worksheets
• 3 Digit Addition and Subtraction Worksheets

More 2nd Grade Addition Worksheets

Here you will find some more of our 2nd Grade Addition Worksheets.

The link below will open our 2nd-grade-math-salamanders website in a new browser window.

• Addition Word Problems 2nd grade at 2nd-grade-math-salamanders.com
• Number Bonds to 20
• Math Addition Facts to 20

More 2nd Grade Math Word Problems

Here are a range of problems solving sheets for 2nd graders. Most of the sheets contain 'real-life' problems related to animal facts.

Using the sheets will help your child to:

• apply their addition, subtraction, and multiplication skills;
• apply their knowledge of rounding and place value;
• solve a range of 'real life' problems.

These sheets involve solving one or two more challenging longer problems. This link opens in a new tab.

• Second Grade Math Problems

These sheets involve solving many 'real-life' problems involving data.

• 2nd Grade Math Word Problems

These sheets involve solving a range of addition and subtraction word problems up to 100.

• 2nd Grade Addition and Subtraction Word Problems

These sheets involve solving a range of subtraction word problems up to 100.

• Subtraction Word Problems 2nd grade

These sheets involve solving a range of multiplication problems.

• Multiplication Word Problems 2nd Grade

Addition Word Problems to 100 Online Quiz

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge and skill at solving addition word problems within 100.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Second Grade Math Worksheets hub

Return to Addition Worksheets hub

Return from Addition Word Problems 2nd Grade to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Word Problems Activities for 2nd Grade

Strengthen your child's word problems skills with interactive educational resources for word problems for 2nd graders online. These learning resources include fun games and worksheets with eye-catching visuals and characters. Get started to help your 2nd grader master this concept by engaging their critical thinking.

CONTENT TYPE

• Lesson Plans
• Math (1,740)
• Number Sense (255)
• Counting (19)
• Number Representation (11)
• Represent Numbers Using Place Value Blocks (10)
• Compare and Order Numbers (80)
• Compare Numbers (65)
• Compare Numbers within 10 (2)
• Compare Objects within 10 (2)
• Compare Numbers within 20 (18)
• Compare Numbers within 100 (28)
• Use Place Value Blocks to Compare Numbers (2)
• Compare Two 2-Digit Numbers (10)
• Compare 3-Digit Numbers (9)
• Order Numbers (15)
• Order 3-Digit Numbers (10)
• Skip Counting (37)
• Skip Count by 2 (6)
• Skip Count by 5 (7)
• Skip Count by 10 (18)
• Skip Count by 100 (3)
• Even and Odd Numbers (28)
• Place Value (84)
• Read and Write Numbers (35)
• Numbers up to 100 (10)
• Expanded Form (3)
• 3-Digit Numbers in Expanded Form (3)
• Standard Form (3)
• 3-Digit Numbers in Standard Form (3)
• Unit Form (2)
• 3-Digit Numbers in Unit Form (2)
• Place Value Chart (13)
• 3-Digit Numbers on Place Value Chart (13)
• Addition (570)
• Addition Sentences (22)
• Addition Sentence within 10 (22)
• Add with Pictures (1)
• Add with Pictures within 10 (1)
• Model Addition (7)
• Addition Properties (12)
• Commutative Property of Addition (8)
• Add Using Models (8)
• Addition Strategies (178)
• Addition Strategies within 10 (28)
• Count On to Add Strategy (22)
• Add using number line (10)
• Compose and Decompose Numbers (6)
• Number Bonds (6)
• Addition Strategies within 20 (82)
• Anchor 5 and 10 (9)
• Count On Strategy (16)
• Add with 10 (10)
• Make 10 Strategy (16)
• Doubles and Near Doubles Strategy to Add (25)
• Doubles Facts (10)
• Add Three Whole Numbers (11)
• Addition Strategies within 100 (35)
• Add using multiples of 10 (19)
• Addition Strategies within 1000 (36)
• Add using multiples of 100 (25)
• Addition Facts (114)
• Fluently Add within 10 (22)
• Fluently Add within 20 (92)
• Equal Expressions (13)
• Addition Without Regrouping (168)
• Add within 100 without Regrouping (72)
• Add 2-digit number to 1-digit (17)
• Add 2-digit number to 2-digit (54)
• Add within 1000 without Regrouping (96)
• Add 10 to 3-digit numbers (15)
• Add 100 to 3-digit numbers (16)
• Add 3-digit number to 1-digit (16)
• Add 3-digit number to 2-digit (20)
• Add two 3-digit numbers (34)
• Addition With Regrouping (98)
• Add within 100 with Regrouping (51)
• Regroup and add 2-digit number to 1-digit (17)
• Regroup and add 2-digit numbers (17)
• Add within 1000 with Regrouping (47)
• Regroup ones and add (13)
• Regroup ones and tens and add (13)
• Regroup tens and add (3)
• Subtraction (496)
• Subtraction Sentences (2)
• Subtraction Sentences within 10 (2)
• Model Subtraction (9)
• Subtract using Models (7)
• Subtraction Strategies (135)
• Subtraction Strategies within 10 (7)
• Count Back Strategy within 10 (7)
• Subtraction Strategies within 20 (72)
• Count Back Strategy within 20 (32)
• Relate Addition and Subtraction within 20 (13)
• Doubles and Near Doubles Strategy to Subtract (4)
• Subtract from 10 Strategy (12)
• Subtraction Strategies within 100 (36)
• Subtract using multiples of 10 (20)
• Subtraction Strategies within 1000 (22)
• Subtract using multiples of 100 (11)
• Subtraction Facts (86)
• Fluently Subtract within 10 (7)
• Fluently Subtract within 20 (82)
• Equal Expressions in Subtraction (10)
• Subtraction Without Regrouping (157)
• Subtract within 100 without Regrouping (78)
• Subtract Multiples of 10 (14)
• Subtract within 1000 without Regrouping (79)
• Subtraction With Regrouping (86)
• Subtract within 100 with Regrouping (49)
• Subtract within 1000 with Regrouping (37)
• Multiplication (147)
• Arrays (16)
• Equal Groups (21)
• Multiplication Properties (17)
• Commutative Property (10)
• Geometry (74)
• Sides and Corners (12)
• Corners (11)
• Shapes (58)
• 2d Shapes (46)
• Identify Quadrilaterals (2)
• Trapezoids (2)
• Identify triangles (1)
• Identify polygons (1)
• Attributes of 2D shapes (11)
• Sort 2D shapes (9)
• Partition 2D Shapes (17)
• Partition into equal parts (17)
• Halves, Thirds, and Fourths (14)
• Measurement (75)
• Data Handling (23)
• Organize and Interpret Data (23)
• Organize data in bar graphs (4)
• Organize data in line plots (3)
• Organize data in picture graphs (3)
• Interpret data in bar graphs (3)
• Interpret data in line plots (6)
• Interpret data in picture graphs (4)
• Length (23)
• Measure Lengths (11)
• Measure Lengths using the ruler (9)
• Estimate Lengths (4)
• AM and PM (12)
• Analog Clock (30)
• Hour hand (12)
• Set time (10)
• Digital Clock (9)
• Time in Half Hours (15)
• Time in Hours (13)
• Time in Quarter Hours (19)
• Time to the Nearest 5 Minutes (17)
• Money (103)
• Identify Coins (10)
• Value of the Coins (10)
• Make Amounts (10)
• Counting Money (81)
• Compare Money (15)
• Count Money with Coins (34)
• Penny, Nickel, and Dime (20)
• Quarters and Half Dollar (9)
• Operations With Money (11)
• Add and Subtract Money (6)
• Word Problems (182)
• Addition and Subtraction Word Problems (159)
• Addition Word Problems (67)
• Addition Word Problems within 10 (1)
• Addition Word Problems within 20 (23)
• Addition Word Problems within 100 (34)
• Add to Compare Word Problems (15)
• Subtraction Word Problems (43)
• Subtraction Word Problems within 20 (13)
• Subtraction Word Problems within 100 (19)
• Subtract to Compare Word Problems (10)
• Multi-step Word Problems (28)
• Money Word Problems (3)
• ELA (1,471)
• Reading (989)
• Phonics (946)
• Diphthongs (25)
• Words with OI (11)
• Words with OU (11)
• Words with OW (11)
• Words with OY (11)
• Beginning Consonant Blends (14)
• SPL Blend (8)
• SQU Blend (8)
• STR Blend (7)
• Letter Sounds (26)
• Letter Sound A (1)
• Letter Sound B (1)
• Letter Sound C (1)
• Letter Sound D (1)
• Letter Sound E (1)
• Letter Sound F (1)
• Letter Sound G (1)
• Letter Sound H (1)
• Letter Sound I (1)
• Letter Sound J (1)
• Letter Sound K (1)
• Letter Sound L (1)
• Letter Sound M (1)
• Letter Sound N (1)
• Letter Sound O (1)
• Letter Sound P (1)
• Letter Sound Q (1)
• Letter Sound R (1)
• Letter Sound S (1)
• Letter Sound T (1)
• Letter Sound U (1)
• Letter Sound V (1)
• Letter Sound W (1)
• Letter Sound X (1)
• Letter Sound Y (1)
• Letter Sound Z (1)
• Vowels (69)
• Long Vowel Sounds (35)
• Long A Vowel Sound (9)
• Long E Vowel Sound (7)
• Long I Vowel Sound (6)
• Long O Vowel Sound (5)
• Long U Vowel Sound (8)
• Short Vowel Sounds (34)
• Short A Vowel Sound (8)
• Short E Vowel Sound (6)
• Short I Vowel Sound (10)
• Short O Vowel Sound (5)
• Short U Vowel Sound (5)
• Blending (175)
• CCVCC Words (36)
• Words With Diphthongs (18)
• Words With Three Letter Blends (14)
• Words With Trigraphs (28)
• Consonant Digraphs (4)
• Digraph CH (2)
• Digraph SH (2)
• Digraph TH (2)
• Digraph WH (2)
• Rhyming Words (6)
• Trigraphs (29)
• Trigraph DGE (9)
• Trigraph IGH (7)
• Trigraph SHR (8)
• Trigraph TCH (7)
• Trigraph THR (7)
• Three Letter Blends (5)
• Sight Words (581)
• Dolch Sight Words (93)
• Fry Sight Words (123)
• Silent Letter Words (11)
• Reading Skills (40)
• Cause and Effect (3)
• Inference (3)
• Identify the Main Idea (3)
• Prediction (3)
• Sequencing (3)
• Story Elements (4)
• Authors Purpose (3)
• Compare and Contrast (3)
• Central Message (3)
• Point of View (3)
• Using Illustrations (3)
• Using Text Features (3)
• Context Clues (3)
• Communication Skills (3)
• Speaking Skills (3)
• Writing (313)
• Writing Sight Words (20)
• Creative Writing (12)
• Grammar (52)
• Adverbs and Adjectives (8)
• Nouns and Pronouns (29)
• Pronouns (2)
• Punctuation (3)
• Verbs and Tenses (13)
• Vocabulary (109)
• Affixes (6)
• Figures of Speech (2)
• Alliteration (2)
• Synonyms and Antonyms (6)
• Word Puzzles (63)
• Shades of Meaning (3)
• Sorting Words into Categories (11)
• Flashcards (10)
• Phonics Flashcards (10)

Addition and Subtraction Word Problems

Solve Word Problems on Adding Three Numbers Game

Learn to solve word problems on adding three numbers through this game.

Solve 'Count On' Word Problems Game

Take the first step towards building your math castle by solving 'Count On' word problems.

Complete the Model Using Clues Worksheet

Assess your math skills by completing the model using clues in this worksheet.

Write the Equation using Clues Worksheet

Be on your way to become a mathematician by practicing to write the equation using clues.

All Word Problems Resources

Word Problems to Count by Tens Game

Shine bright in the math world by learning how to solve word problems to count by tens.

Choose the Correct Operation— Add or Subtract Worksheet

Make math practice a joyride by choosing the correct operation— Add or Subtract.

Select the Correct Model Worksheet

Pack your math practice time with fun by selecting the correct model.

Represent 'Add To' Word Problems Game

Take a deep dive into the world of math with our 'Represent 'Add To' Word Problems' game.

Represent the Scenarios Using Equations Worksheet

This downloadable worksheet is designed to represent the given scenarios using equations.

Complete the Word Problem Model Worksheet

Boost your ability to complete the word problem model by printing this playful worksheet.

Represent 'Put Together' Word Problems Game

Unearth the wisdom of mathematics by learning how to represent 'Put Together' word problems.

Addition Word Problems on Put-Together Scenarios Game

Use your skills to solve addition word problems on put-together scenarios.

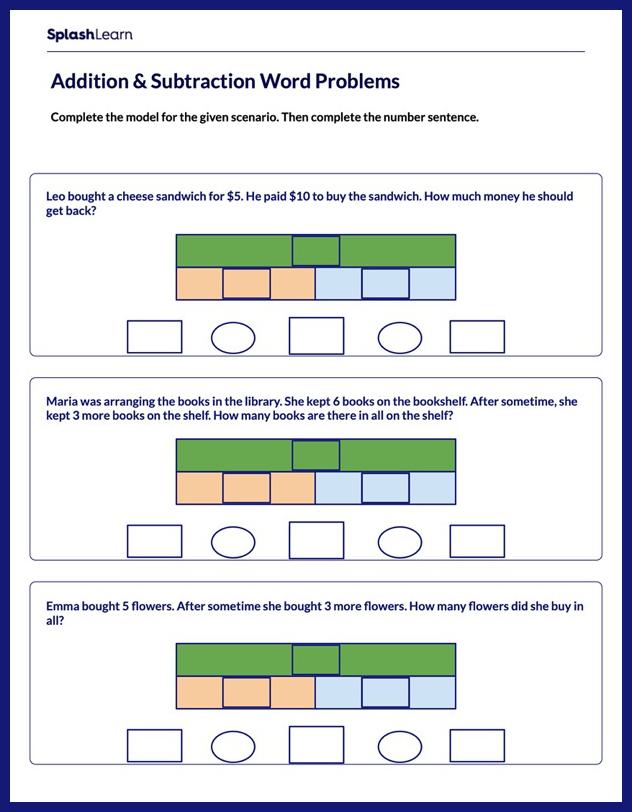
Complete the Model to Write Equations Worksheet

Be on your way to become a mathematician by practicing to complete the model to write equations.

Use Clues to Complete the Model Worksheet

Help your child revise subtraction by solving to use clues to complete the model.

Represent 'Add To' Situations Game

Dive deep into the world of addition with our 'Represent 'Add To' Situations' game.

Represent 'Put Together' Situations Game

Add more arrows to your child’s math quiver by representing 'Put Together' situations.

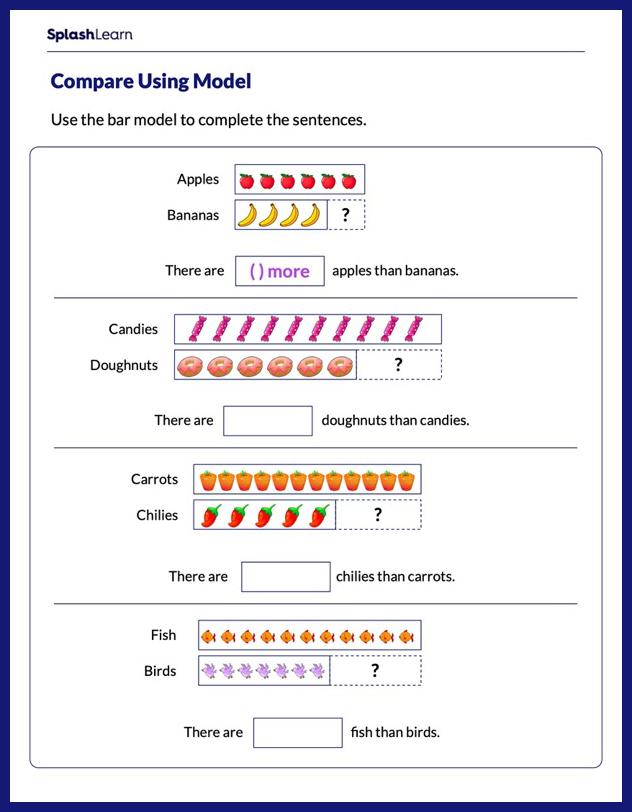
Use the Bar Model to Complete the Sentences Worksheet

Use the bar model to complete the sentences by printing this playful worksheet.

Solve Word Problems on Comparison Worksheet

Put your skills to the test by practicing to solve word problems on comparison.

Word Problems to Add Multiples of 10 Game

Learn to solve word problems to add multiples of 10.

Word Problems to Add Tens to a 2-digit number Game

Make math learning fun by solving word problems to add tens to a 2-digit number.

Complete the Bar Model Worksheet

Dive into this fun-filled printable worksheet by practicing to complete the bar model.

Complete Part-Part-Whole Model Worksheet

Learners must complete 'Part-Part-Whole' models to enhance their math skills.

Solve Word Problems on Add to Scenarios Game

Ask your little one to solve word problems on "Add to" scenarios to play this game.

Solve Word Problems on Put together Scenarios Game

Practice the superpower of addition by learning to solve word problems on "Put together" scenarios.

Select the Correct Equation Worksheet

Dive into this fun-filled printable worksheet by selecting the correct equation.

Solve Word Problems Using Bar Models Worksheet

Dive into this fun-filled printable worksheet by practicing to solve word problems using bar models.

Solve Word Problems with Add to Scenarios Game

Shine bright in the math world by learning how to solve word problems with "Add to" scenarios.

Word Problems to Subtract Multiples of 10 Game

Help your child take flight by learning how to solve word problems to subtract multiples of 10.

Use Bar Models to Compare and Solve Worksheet

This downloadable worksheet is designed to help you use bar models to compare and solve.

Represent Given Situation in a Bar Model Worksheet

In this worksheet, learners will get to represent the given situations in a bar model.

Solve Word Problems on Take From Scenarios Game

Enjoy the marvel of math-multiverse by learning to solve word problems on "Take From" scenarios.

Solve Subtraction Word Problems Game

Enjoy the marvel of mathematics by exploring how to solve subtraction word problems.

Represent Given Situation into a Bar Model Worksheet

Focus on core math skills by representing the given situation into a bar model.

Complete the Sentences Using the Bar Model Worksheet

Dive into this fun-filled printable worksheet by completing the given sentences using bar models.

Represent How Many More Scenarios Game

Shine bright in the math world by learning how to represent "How Many More" scenarios.

Solve How Many More Word Problems Game

Enter the madness of math-multiverse by exploring how to solve "How Many More" word problems.

Choose the Correct Equation for the Given Problem Worksheet

Solidify your math skills by choosing the correct equation for the given problem.

Choose the Operation for the Given Scenario Worksheet

This downloadable worksheet will help you choose the operation for the given scenario.

Solve How Many Fewer Word Problems Game

Enjoy the marvel of mathematics by exploring how to solve "How Many Fewer" word problems.

Solve Difference Unknown Scenarios Game

Kids must solve difference unknown scenarios to practice subtraction.

Complete the Equation for the Given Scenario Worksheet

Assess your math skills by completing the equation for the given scenario in this worksheet.

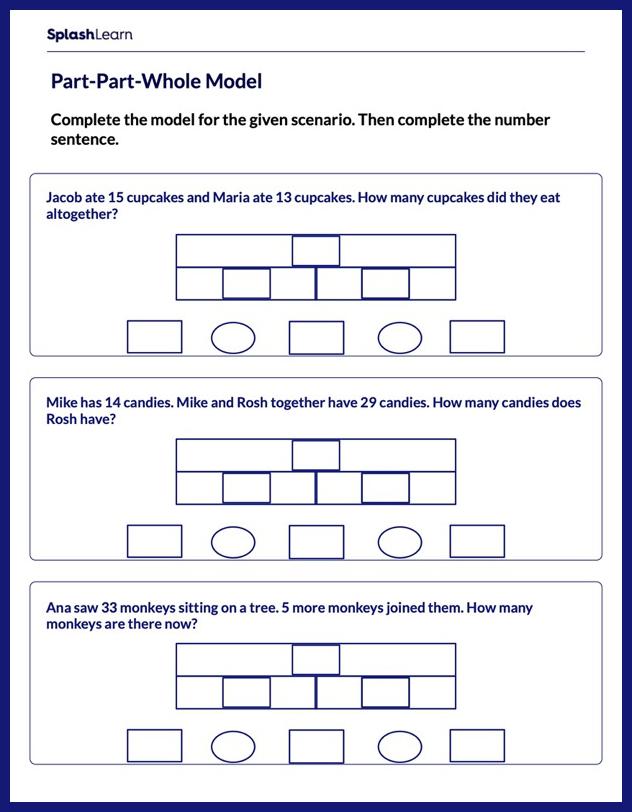
Complete the Model and Number Sentence Worksheet

Focus on core math skills by solving to complete the model and the number sentence.

Solve Scenarios with 'Difference Unknown' Game

Shine bright in the math world by learning how to solve scenarios with 'Difference Unknown'.

Add the Same Type of Coins and Compare Game

Enjoy the marvel of mathematics by exploring how to add the same type of coins and compare them.

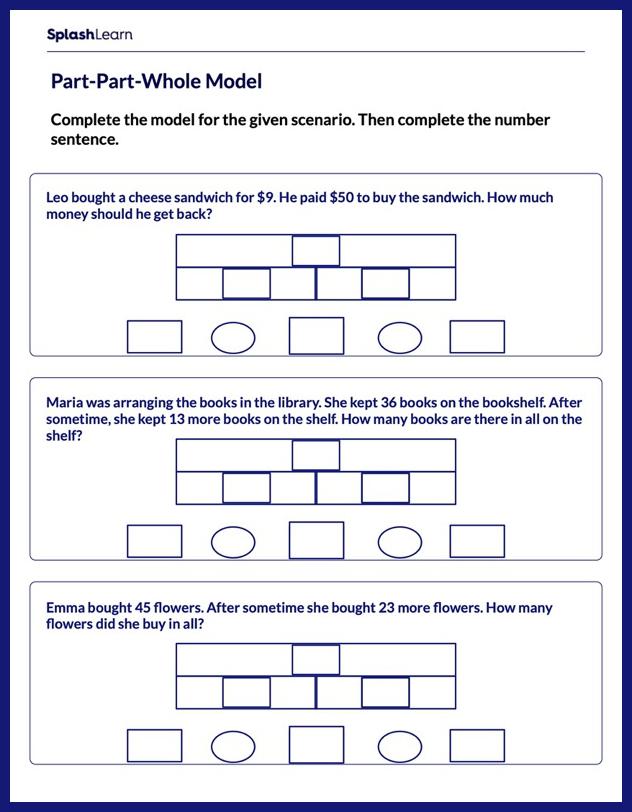
Model the Scenario and Complete the Equation Worksheet

Be on your way to become a mathematician by modeling the scenario and completing the equation.

Complete the Bar Model for the Given Information Worksheet

Pack your math practice time with fun by completing the bar model for the given information.

Add Coins of Different Types and Compare Game

Kids must add coins of different types and compare them to practice counting money.

Find the Change Game

Use your counting money skills to find the change.

Solving Comparison Word Problems Using Bar Model Worksheet

Learners must solve comparison word problems using bar models to enhance their math skills.

Solve Word Problems on Measurement Worksheet

This downloadable worksheet is designed to help you solve word problems on measurement.

Your one stop solution for all grade learning needs.

More From Forbes

How philosophy can help leaders solve wicked problems.

• Share to Facebook
• Share to Twitter
• Share to Linkedin

An old strategy can help leaders reduce the risk of the solutions backfiring.

When faced with wicked problems , political and corporate decision makers often rush to implement technological solutions. Consider the way business leaders are dealing with the global infertility problem : A 2021 study by Mercer found that , as of 2020, nearly 20% large U.S. employers offered egg freezing benefits to their employees.

However, as noted in Forbes last year, a study in the Journal of Applied Psychology found that employees may perceive egg freezing benefits as more pressure than perks, causing them to have negative reactions to the benefit as well as the organizations that offer it.

Egg freezing is not the only example of a technological solution that risks backfiring . In late 2020, Andy Jarvis , the associate director of the Alliance of Bioversity International, said, “The food system is in the mess it is right now because we introduce technologies and approaches to manage it without fully understanding all the indirect impacts the intervention can have.”

And when Geoffrey Hinton left Google last year, ending a lifetime of developing and deploying AI, he claimed that “the small but very real danger that AI will turn out to be a disaster.” So, if rushing to introduce technologies isn’t the solution to wicked problems, what is?

The Problem Behind The Problem

Throughout 2,400 years of Western civilization, philosophers have had one strategy for dealing with the big questions facing us humans. The strategy is to understand the problem behind the problem. In the case of infertility, the problem behind the problem is that women (and men) are temporal creatures. This means that we are getting older by the minute. We have limited time on this earth. And not only does women’s ability to reproduce have an expiration date, so does life for each and every one of us.

Why Is Chief Boden Leaving Chicago Fire Eamonn Walker s Exit Explained

Biden vs. trump 2024 election polls: biden leads trump by only single digits in new york, latest survey shows, here are the major allegations against sean diddy combs as cassie ventura breaks silence on attack video.

While the problem of infertility may seem to be solved with egg freezing, the problem of aging is not. No matter how early and how many eggs are put in the freezer, we are destined to run out of time. And regardless of who pays the bill for the expensive procedure, it is not the political or corporate decision makers who pay the personal price of postponing pregnancy and parenthood. ​​It is the women and men who regret that they spent their scarce time working instead of raising a family.

It’s Not About What, It’s About Who

The problem behind all the problems that have to do with rushing to implement technological solutions is that technology suppresses the existential and ethical questions we all have to ask ourselves sooner or later.

Having limited time on this earth forces us to prioritize how we spend our time, and leaders should support their employees and other stakeholders in asking these questions rather than delaying and preventing it.

To adopt the philosophers’ strategy of understanding the problem behind the problem, leaders must acknowledge that solving wicked problems is not about what, it’s about who . They can do this by asking themselves three questions.

1. Whose Problem Is This?

Wicked problems are by definition complex and tangled, and therefore have—and call for collaboration between—many stakeholders. Yet, leaders must ask themselves who depends the most on a solution. They must ask: Whose problem is this? And: Whose life will benefit, or suffer, the most if a solution is, or is not, found?

When I recently did a study among young talents from the UNLEASH community, I realized that leaders across the globe try to solve the wicked problem of climate change without asking these questions. Based in Nepal, one of the young talents participating in the study made the observation that “the indigenous groups in my country have very limited awareness about climate change because no one includes or tries to include them in the movement or advocacy work.”

His studies showed that the reason indigenous people are not included is that they have no education. But, as he explained, “they are the ones who have witnessed the impact of climate change in real life and they are also the ones who are using various strategies to cope with the impacts.” His point was that the people who suffer most from a problem are also the ones best at finding a solution. And that “if all the climate activists incorporate indigenous knowledge and use them in advocacy, the climate movement would be more impactful and meaningful.”

2. At What Level Should The Problem Be Solved?

Being accustomed to solving problems on behalf of large groups of people, political and corporate decision-makers often forget to ask themselves at what level the problem needs to be solved: Who or what needs to change for the solution to be a success? The individual? The team? The organization? Society? Humanity as a whole? Depending on the answer, leaders must focus their efforts on different things.

While individuals need time to reflect and prioritize what’s important to them, teams cannot change unless they are given the space to discuss , explore, and experiment with new ways of working. Organizational change requires different stakeholders working together to redesign the structures, technologies, processes and culture that shape collective behavior. And when a problem requires the whole of society or humanity to change, leaders must think of themselves and their organization as a tiny but crucial part of a huge ecosystem .

3. Who Do We Prevent From Solving Other Problems?

The final question takes us back to egg freezing and the issue of technology versus time. Building on the second question, leaders must ask themselves: If we make a decision to solve this problem from an organizational, societal, or humanity perspective, what decisions do we prevent individuals and teams from making? What problems do we make it harder for individuals and teams to solve themselves? And how will their limited agency affect their sense of responsibility to make the solution a success?

By asking (1) Whose problem is this? (2) At what level should the problem be solved? and (3) Who do we prevent from solving other problems? leaders give themselves and others the time they need to think through important aspects of wicked problems before deciding whether or not to implement a technological solution.

• Editorial Standards
• Reprints & Permissions

Join The Conversation

One Community. Many Voices. Create a free account to share your thoughts. 

Forbes Community Guidelines

Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.

In order to do so, please follow the posting rules in our site's  Terms of Service.   We've summarized some of those key rules below. Simply put, keep it civil.

Your post will be rejected if we notice that it seems to contain:

• False or intentionally out-of-context or misleading information
• Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
• Attacks on the identity of other commenters or the article's author
• Content that otherwise violates our site's  terms.

User accounts will be blocked if we notice or believe that users are engaged in:

• Continuous attempts to re-post comments that have been previously moderated/rejected
• Racist, sexist, homophobic or other discriminatory comments
• Attempts or tactics that put the site security at risk
• Actions that otherwise violate our site's  terms.

So, how can you be a power user?

• Stay on topic and share your insights
• Feel free to be clear and thoughtful to get your point across
• ‘Like’ or ‘Dislike’ to show your point of view.
• Protect your community.
• Use the report tool to alert us when someone breaks the rules.

Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's  Terms of Service.

Comparative study of typical neural solvers in solving math word problems

• Original Article
• Open access
• Published: 22 May 2024

Cite this article

You have full access to this open access article

• Bin He   ORCID: orcid.org/0000-0003-2088-8193 1 ,
• Xinguo Yu 1 ,
• Litian Huang 1 ,
• Hao Meng 1 ,
• Guanghua Liang 1 &
• Shengnan Chen 1  

In recent years, there has been a significant increase in the design of neural network models for solving math word problems (MWPs). These neural solvers have been designed with various architectures and evaluated on diverse datasets, posing challenges in fair and effective performance evaluation. This paper presents a comparative study of representative neural solvers, aiming to elucidate their technical features and performance variations in solving different types of MWPs. Firstly, an in-depth technical analysis is conducted from the initial deep neural solver DNS to the state-of-the-art GPT-4. To enhance the technical analysis, a unified framework is introduced, which comprises highly reusable modules decoupled from existing MWP solvers. Subsequently, a testbed is established to conveniently reproduce existing solvers and develop new solvers by combing these reusable modules, and finely regrouped datasets are provided to facilitate the comparative evaluation of the designed solvers. Then, comprehensive testing is conducted and detailed results for eight representative MWP solvers on five finely regrouped datasets are reported. The comparative analysis yields several key findings: (1) Pre-trained language model-based solvers demonstrate significant accuracy advantages across nearly all datasets, although they suffer from limitations in math equation calculation. (2) Models integrated with tree decoders exhibit strong performance in generating complex math equations. (3) Identifying and appropriately representing implicit knowledge hidden in problem texts is crucial for improving the accuracy of math equation generation. Finally, the paper also discusses the major technical challenges and potential research directions in this field. The insights gained from this analysis offer valuable guidance for future research, model development, and performance optimization in the field of math word problem solving.

Avoid common mistakes on your manuscript.

Introduction

Math Word Problem (MWP) solving has been a long-standing research problem in the field of artificial intelligence [ 1 ]. However, previous methods required hand-crafted features, making them less effective for general problem-solving. In a milestone contribution, Wang et al. [ 2 ] designed the first deep learning-based algorithm, DNS, to solve MWPs, eliminating the need for hand-crafted features. Since then, multiple neural solvers with various network cells and architectures have emerged [ 3 , 4 , 5 , 6 , 7 , 8 , 9 ], with pioneering experiments conducted on diverse datasets with varying sizes and characteristics [ 1 , 10 ]. However, the experimental results show that even MWP solvers built with similar architectures exhibit varying performance on datasets with different characteristics. Hence, a precise and impartial analysis of the existing MWP solvers has become essential to reveal the potential factors of network cells and architectures that affect the performance of neural solvers in solving different characteristics of MWPs.

Earlier MWP solvers leveraged manually designed rules or semantic parsing to map problem text into math equations, followed by an equation solver to obtain the final answer. These early efforts could only solve a limited number of problems defined in advance. Inspired by deep learning models for natural language processing [ 11 , 12 ], recent neural solvers use an Encoder-Decoder framework [ 13 ] to transform a sequence of problem sentences into another sequence of arithmetic expressions or equations. The Encoder captures the information presented by the problem text, which can be divided into two categories: sequence-based representation learning [ 5 , 14 , 15 ] and graph-based representation learning [ 6 , 16 , 17 ]. Sequence-based representation learning processes the problem text as a sequence of tokens using recurrent neural networks [ 18 , 19 ] or transformers [ 11 ], while graph-based representation learning constructs a graph from the problem text. Graph neural networks (e.g., graph transformer model [ 20 ], inductive graph learning model [ 21 ]) are then used to learn a representation for the entire graph. Mathematical expressions can be viewed as sequences of symbols or modeled as trees based on their syntactic structure, allowing Decoders to predict output expressions based on the encoding vectors produced by the encoder. By combining different types of encoders and decoders, diverse architectures of MWP solvers have been developed, including Seq2Seq-based solvers, Seq2Tree-based solvers, and Graph2Tree-based solvers.

Several reviews and surveys have been conducted to examine the progress of research in this field. For example, Mukherjee et al. [ 22 ] made a first attempt to analyze mathematical problems solving systems and approaches according to different disciplines. Zhang et al. [ 1 ] classified and analyzed different representation learning methods according to technical characteristics. Meadows et al. [ 23 ] and Lu et al. [ 24 ] conducted a literature review on the recent deep learning-based models for solving math word problems. Lan et al. [ 10 ] established a unified algorithm test platform and conducted comparative experiments on typical neural solvers. While these reviews provide valuable insights into the field of automatic math word problem solving, little comparative evaluation has been carried out to reveal the performance variations of neural solvers with different architectures in solving various types of MWPs. An initial attempt can be found in [ 10 ] which provides a collection of experimental results of the typical neural solvers on several datasets. However, no other attempts to explore the performance variations of neural solvers with different architectures in solving different types of math word problems.

While significant efforts have been made, there remains a lack of comprehensive technical analysis to compare different network structures and their impacts on final performance. This paper presents a comparative study of typical neural solvers to unveil their technical features and performance variations in solving MWPs with diverse characteristics. We initially identify the architectures of typical neural solvers, rigorously analyzing the framework of each category, notably: Seq2Seq [ 2 , 4 ], Seq2Tree [ 5 , 25 ], Graph2Tree [ 6 , 17 ] and PLM-based models [ 26 , 27 , 28 , 29 , 30 ]. We propose a four-dimensional indicator to categorize the considered datasets for precise evaluation of neural solvers’ performance in solving various characteristics of MWPs. Typical neural solvers are disassembled into highly reusable components, enabling researchers to reconstruct them and develop new solvers by replacing components with proposed ones, which benefits both model evaluation and extension. To assess the considered solvers, we establish a testbed and conduct comprehensive experiments on five popular datasets using eight representative MWP solvers, followed by a comparative analysis of the results achieved. The contributions of our work can be summarized as follows:

We provide a comprehensive and systematic analysis of deep learning-based MWP solvers, ranging from the initial deep neural solver DNS to the latest GPT-4. This is achieved through an in-depth technical analysis of network structures and neural cell types, enabling a deeper understanding of the technological evolution of MWP solvers for the research community.

To enhance the technical analysis, we introduce a unified framework consisting of reusable encoding and decoding modules decoupled from existing MWP solvers. This framework allows for the straightforward reproduction and extension of typical MWP solvers by combining these reusable modules.

We establish a testbed and provide finely regrouped datasets to facilitate objective and fair evaluations of MWP solvers. Through this testbed, we conduct comprehensive testing and report detailed results for eight representative MWP solvers on five finely regrouped datasets, specifically highlighting the performance variations of solvers with different modules in solving different types of MWPs.

We present three key findings from our experiments and discuss the major technical challenges and potential research directions in this field.

The rest of the paper is organized as follows: Sect. “ Related work ” describes related work on math word problem solving. Section “ Architecture and technical feature analysis of neural solvers ” provides a detailed analysis of the framework of typical neural solvers. A characteristic analysis of the considered datasets is presented in Sect. “ Characteristics analysis of benchmark datasets ”, and experiments and a comparative analysis are conducted in Sect. “ Experiment ”. We conclude this paper in Sect. “ Conclusion ”.

Related work

In this section, we will explore various deep learning-based approaches for solving math word problems. We will also provide an introduction to previous surveys in this field.

Deep learning-based approaches for solving MWPs

Solving MWPs has been a longstanding research focus in the field of artificial intelligence since the 1960s, as illustrated in Fig.  1 . The evolution of MWP solvers can be categorized into different stages based on the underlying technologies utilized, including rule-based approaches [ 31 ], semantic parsing-based approaches [ 16 , 32 , 33 , 34 ], etc.. More recently, neural networks inspired by deep learning models for natural language processing [ 11 , 12 ] have been designed to tackle MWPs. For instance, the Deep Neural Solver (DNS) [ 2 ] is the first deep learning algorithm capable of translating problem texts to equations without relying on manually-crafted features. This advantage has motivated extensive research on neural solvers using larger datasets, as evidenced by several studies in the literature.

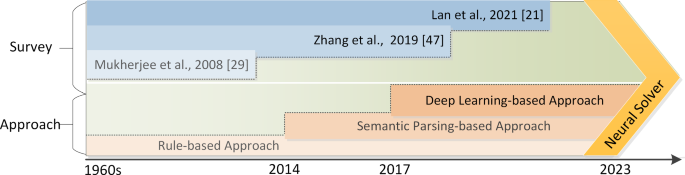
Approach evolution in solving MWPs

A significant challenge in these studies is efficiently capturing the logical relationships between natural language texts and their corresponding equations [ 1 ] which is known as problem text representation and equation representation. Inspired by translation models [ 19 ], MWP solver is typically designed as an Encoder-Decoder framework [ 1 ] as shown in Table 1 . The Encoder is responsible for learning the semantic representation and logic relationships presented explicitly or implicitly of the problem text. Researchers have tried different sequence models, leading to several representative models such as DNS [ 2 ], MathEN [ 4 ]. The Decoder, usually designed as a sequence or tree structural model, treats the math equation as a symbolic sequence consisting of numbers and operators for decoding. Several tree-structured models, such as Tree-Dec [ 25 ], GTS [ 6 ], were designed and then widely accepted for math equation decoding to enhance the math equation generation. Recently, encoder-only pre-trained models like BERT [ 35 ] and GPT [ 28 , 29 ], were included in MWP solvers to effectively represent background knowledge. In the subsequent sections, we will provide a comprehensive review from these three perspectives.

Problem text representation

To avoid sophisticated feature engineering, deep learning technologies were applied for problem text representation. In this field, Wang et al. [ 2 ] have made significant contributions by designing a customized model called Deep Neural Solver (DNS) to automatically solve MWPs. Within the DNS, the problem text and mathematical expressions are represented as sequential data, making them amenable to processing by sequence models commonly used in Natural Language Processing (NLP). Consequently, the task of solving mathematical problems is modeled as a “translation" problem within a Sequence-to-Sequence (Seq2Seq) framework. Following this pioneering work, a number of Seq2Seq models [ 4 , 5 , 13 , 36 , 37 ] for MWPs have been developed. These Seq2Seq models treat the problem text as a sequence of word tokens and utilize Recurrent Neural Networks (RNNs) such as Long-Short Term Memory (LSTM) network [ 3 ], Gated Recurrent Unit (GRU) [ 47 ], and Transformer [ 11 ] for encoding the word sequence.

To enhance the representation of the problem text, numerous optimization strategies and auxiliary techniques have been proposed. For instance, Wang et al. [ 4 ] utilized different deep neural networks for problem encoding and achieved higher accuracy compared to other Seq2Seq models. Shen et al. [ 33 ] employed a multi-head attention mechanism to capture both local and global features of the problem text. Li et al. [ 37 ] developed a group attention mechanism to extract diverse features pertaining to quantities and questions in MWPs. These efforts aim to better capture the contextual information in the problem text, thereby improving the efficiency of expression generation.

In addition to capturing the contextual information from the problem text, researchers have explored graph-based models inspired by the success of previous works [ 20 , 21 ] to capture non-sequential information, such as quantity unit relations, numerical magnitude relations, and syntactic dependency relations. These non-sequential relations are considered helpful in ensuring the logical correctness of expression generations. For instance, quantity unit relationships can help reduce illegal operations between values with different units, and numerical magnitude relationships can help reduce the occurrence of negative results from subtracting a larger number from a smaller number. Based on these assumptions, Zhang et al. propose Graph2Tree [ 6 ], which constructs a quantity cell graph and a quantity comparison graph to represent quantity unit relationships and numerical magnitude relationships, respectively. Similarly, Li et al. [ 17 ] introduce the constituency tree augmented text graph, which incorporates a constructed graph into a graph neural network [ 48 , 49 ] for encoding. The output of these graph models, combined with the output of the sequence model, is used for decoding. Additionally, knowledge-aware models [ 7 , 50 , 51 ] have been designed to improve problem representation.

Recently, Pre-trained Language Models (PLMs), and especially transformer-based language models, have shown to contain commonsense and factual knowledge [ 52 , 53 ]. To enhance the representation of problem texts, PLMs were employed for problem text encoding, aiming to reason through outside knowledge provided by the PLMs. Yu et al. [ 40 ] utilized RoBERTa [ 54 ] to capture implicit knowledge representations in input problem texts. Li et al. [ 41 ] leveraged BERT [ 35 , 55 ] for both understanding semantic patterns and representing linguistic knowledge. Liang et al. [ 26 ] employed BERT and RoBERTa for contextual number representation. These models have yielded significant improvement in terms of answer accuracy. Recently, decode-only PLMs, such GPT [ 28 ], PaLM [ 44 , 45 ] and LLaMA [ 46 ], exhibit strong reasoning abilities and their potential in solving MWPs, especially integrated with technologies of prompt [ 56 ] and chain-of-thought [ 57 ]. For instance, the latest release, GPT4-CSV [ 30 ], achieved an almost 20% increase in answer accuracy on the MATH dataset compared to GPT3.5 [ 28 ]. However, despite these improvements, issues such as actual errors and reasoning errors [ 58 ] by LLMs may lead to wrong answers even with carefully crafted prompt sequences.

Math equation representation

The representation of math equations presents another challenge in the design of MWP solvers. Initially, math equations were commonly modeled as sequences of symbols and operators, known as equation templates [ 2 ]. This allowed for direct processing by sequence models such as LSTM, GRU, etc. However, these sequence models suffer non-deterministic transduction [ 1 , 4 ] as a math word problem can have multiple correct equations. To address this issue, approaches such as MathEN [ 4 ] was proposed to normalize the duplicated equations to ensure that each problem text corresponds to a unique math equation. Chiang et al. [ 13 ] took it further by utilizing the Universal Expression Tree (UET) to represent math equations. However, these methods encode math equations using sequence models, ignoring the hierarchical structure of logical forms within math equations.

To capture the structural information, researchers have proposed tree-structured models (TreeDecoders) [ 5 , 17 , 25 ] for the iterative construction of equation trees. Liu et al. [ 25 ] developed a top-down hierarchical tree-structured decoder (Tree-Dec) inspired by Dong et al. [ 59 ]. The Tree-Dec [ 25 ] enhances a basic sequence-based LSTM decoder by incorporating tree-based information as input. This information consists of three components: parent feeding, sibling feeding, and previous token feeding, which are then processed by a global attention network. Xie et al. [ 5 ] introduced a goal-driven mechanism (GTS) for feeding tree-based information. Li et al. [ 17 ] applied a separate attention mechanism to the node representations corresponding to different node types. Additionally, Zhang et al. [ 27 ] proposed a multi-view reasoning approach that combines the top-down decomposition of TreeDecoder with the bottom-up construction of reductive reasoning [ 9 ]. Due to its exceptional ability in math equations generation, TreeDecoders has been widely adopted by subsequent MWP solvers [ 7 , 38 , 39 , 43 , 60 ]. Furthermore, several extensions of TreeDecoders have been explored, such as the generation of diverse and interpretable solutions [ 7 , 38 , 39 , 60 ].

The previous survey work

Despite the extensive research conducted in the field of MWP solving, there is a lack of comprehensive reviews. Mukherjee et al. [ 22 ] conducted a functional review of various natural language mathematical problem solvers, starting from early systems like STUDENT [ 61 ] to lately developed ROBUST [ 62 ]. The paper provides a systematic review of representative systems in domains such as math problems, physics problems, chemistry problems, and theorem proving. It highlights that these systems are generally useful for typical cases but have limitations in understanding and representing problems of diverse nature [ 22 ]. Additionally, there is a lack of unified benchmark datasets and clear evaluation strategies. However, since the publication date of the paper is early, it does not cover the current mainstream neural network-based methods, which limits its comprehensive assessment of the research field.

With the rise of machine learning-based MWP solving, Zhang et al. [ 1 ] conducted a review of these emerging works from the perspective of representation of problem texts and mathematical expressions. The paper categorizes the development of machine-answering techniques into three stages: rule-based matching, statistical learning and semantic parsing, and deep learning. The authors argue that the primary challenge in machine answering is the existence of a significant semantic gap between human-readable words and machine-understandable logic. They focus on reviewing tree-based methods [ 16 , 63 , 64 , 65 ] and deep learning-based methods [ 32 , 66 , 67 , 68 , 69 ]. The paper also reports the test results of these methods on certain datasets, aiming to provide readers with insights into the technical characteristics and classification of machine answering in the era of machine learning.

In recent literature, Meadows et al. [ 23 ] and Lu et al. [ 24 ] conducted comprehensive surveys on the emerging deep learning-based models developed for solving math word problems. These studies systematically classify and document the network architectures and training techniques utilized by these models. Furthermore, they provide a detailed analysis of the challenges faced in this field as well as the trends observed in the development of such models. Lan et al. [ 10 ] developed MWPToolkit, a unified framework and re-implementation of typical neural solvers [ 2 , 4 , 5 , 6 , 13 , 19 , 33 , 36 , 37 , 38 ]. MWPToolkit provides specified interfaces for running existing models and developing new models. However, there is a lack of technical analysis on the network structures of these neural solvers. Recently, pilot work has been conducted to compare the performance of MWP solvers based on deep learning models. Chen et al. [ 70 ] performed a comparative analysis of six representative MWP solvers to reveal their solving performance differences. Building upon this prior work, He et al. [ 71 ] further investigated the performance comparison of representation learning models in several considered MWP solvers.

This paper conducts an in-depth and comprehensive comparative analysis to reveal the technical features and performance variations of typical neural solvers when solving MWPs with different characteristics. The goal is to assist researchers in selecting more effective network units and structures for tasks with different features.

Architecture and technical feature analysis of neural solvers

The general architecture of neural solvers.

Math word problem solving is a mixed process of reasoning and calculating that can hardly be solved directly by neural networks that are designed for classification or regression tasks. Hence, most of the neural solvers take a two-step solution of expression generation and answer calculation. The former aims to translate the input problem text into a calculable math expression and then be followed by a mathematical solver to calculate the final answer. Therefore, the key challenge of solving a math word problem is to generate the target math expression.

Earlier solvers, such as DNS [ 2 ], tackle this challenge by using a seq2seq model in which math expressions are abstracted into expression templates and each template is treated as a sequence with operators and symbols. Later, to improve the capability of new expression generation, math expressions are modeled as decomposable tree structures instead of fixed structures of sequences. A milestone work of tree-structured decomposing is the Graph2Tree model proposed by Xie et al. [ 5 ] and this model is widely used in the newly developed neural solvers. Under this Graph2Tree model, the math expression generation is further divided into three sub-steps, including problem modeling, problem encoding and expression decoding as shown in Fig.  2 .

The general architecture of a neural solver for solving math word problems

Generally, a neural solver can be summarized as an Encoder-Decoder architecture of

where the problem P is consisted by a word token sequence \(V=(v_1, v_2,...,v_n)\) and each \(w_i\) denotes the token of word \(w_i\) . \(F_{encoding}(.)\) and \(F_{decoding}(.)\) are networks to obtain the problem text representation and generate math equations accordingly. The goal of building a neural solver is to train an encoding network \(F_{encoding}(.)\) for problem feather representation learning, and a decoding network \(F_{decoding}(.)\) for predicting math expressions \(ME=(e_1,e_2,...,e_m)\) to achieve the final answer. We give a detailed analysis of the architecture of mainstream encoders and decoders below separately.

Problem modeling. Problem modeling defines the pipeline of neural networks. Specifically, it models the data structure of the input and output of the solvers. For input, the problem texts are usually modeled as word sequences followed by a recursive neural network for feature learning. A huge improved work has been made which converts sequential texts into graphs, hence graph neural networks can be used for feature learning.

The output of the solvers is the target math expression which can be modeled as specially designed sequences composed of operators and number tokens. An expression vocabulary is defined which contains operators (e.g., \(+,-,\times , \div \) ), constant quantities (e.g., \( 1, \pi \) ) and numbers presented by the problem text. Based on the built vocabulary, a math expression can be abstracted as an expression template in which digits are replaced by number tokens of \(n_i\) . In recent works, target expressions are represented as expression trees. A basic expression tree contains three nodes of the root, left child and right child. The child node can be a digit or an operator that owns at most two children. By employing this tree-structured decomposing, nearly all types of expressions, even those that did not exist in the training set, can also be constructed.

Problem encoding. Problem encoding is a representation learning module to learn the features from the input problem text. According to the representation learning methods applied, problem encoding can be divided into sequence-based methods and graph-based methods.

Expression decoding. Expression decoding is to train a decoding network to convert features obtained in problem encoding into expression templates. As discussed in Problem Modeling , the expression templates can be number token sequences or trees. Hence, expression decoding can be accordingly divided into sequence-based decoding methods and tree-structured decoding methods.

Answer calculation. A number mapping operation is implemented in the stage of answer calculation after expression templates are obtained by replacing the number tokens \(n_i\) back to digits, followed by a mathematical solver to calculate the final answer.

Currently, neural solvers are designed as an Encoder-Decoder framework to accomplish the tasks of problem encoding and expression decoding. The early encoder-decoder model refers to Seq2Seq [ 2 ], that is, the Encoder takes the input problem text as a sequence, and the output expression predicted by the Decoder is also a sequence [ 65 ]. Later, researchers pointed out that the output expression can be better described as a tree structure, e.g. expression tree [ 72 ], equation tree [ 25 ], so the Seq2Tree model was proposed. The GTS, a typical Seq2Tree-based model, was proposed by Xie et al. [ 5 ], in which the output expressions are transformed as pre-order trees and a goal-driven decomposition method is proposed to generate the expression tree based on the input sequence Furthermore, several works revealed that a math word problem is not only a sequence, but also contains structured information about numeric quantities. To represent the quantity relationships, the graph structure is applied to model the quantities as nodes and relations as edges. By combining with tree-structural decoders, several Graph2Tree-based models are proposed [ 6 , 33 ] recently.

According to the network components applied in problem encoding ( Encoder ) and expression decoding ( Decoder ), neural network-based MWP solvers can be divided into four major categories: Seq2Seq, Seq2Tree, Graph2Tree and PLM-based model as shown in Table 2 .

Seq2Seq is a sequence-to-sequence framework, where both the Encoder and Decoder are sequence-based networks. The Encoder takes the sequence of word tokens as input and outputs the feature vectors, usually an embedding vector and a hidden state vector. The feature vectors are sent to the Decoder to predict the expression templates. The embedding vector is usually used to predict the current character of operators or number tokens and the hidden state vector records the contextual features of the current character. LSTM [ 3 ] and GRU [ 47 ] are two commonly used networks in building Encoders and Decoders [ 2 , 5 , 37 , 38 , 65 ]. For example, MathEN [ 65 ] leverages two LSTM networks as Encoder and Decoder , while DNS [ 2 ] employs an LSTM network and a GRU network as Encoder and Decoder separately.

Seq2Tree is an improved framework based on the Seq2Seq architecture in which the sequence-based Decoder is replaced by a tree-structured network to generate expression trees. As discussed above, the tree-structured network is a compound of prediction networks and feature networks, as well as a decision mechanism. For instance, in GTS [ 5 ], a prediction network and two feature networks are employed to merge the previous state vectors and to calculate the current state vector. In another work [ 17 ], only one feather network is used to accomplish the task of feature merging and calculation.

Graph2Tree combines the advantages of a graph-based encoder and a tree-based decoder in the process of problem encoding and expression decoding. Compared to Seq2Tree, Graph2Tree applies graphs to represent the structural relations among word tokens and digits into a network structure (e.g., graph) to enhance the feature learning during the problem encoding. Various kinds of algorithms have been proposed to construct graphs [ 6 , 7 , 17 , 39 ] by modeling the structural relations on both word token level and sentence level.

PLM-based models leverage pre-trained language models to generate intermediate MWP representation and solution. Depending on the type of PLM [ 58 ], there are two specific implementations of PLM-based models. The first implementation, represented by encoder-only PLMs like BERT [ 26 , 27 ], utilizes the PLM as an encoder to obtain the latent representation of the math word problem. This representation is then fed into a decoder, such as a Tree-based decoder, to generate the final mathematical expression. The second implementation, represented by models like GPT [ 28 , 29 , 30 ], directly employs Transformer networks for mathematical reasoning, producing the desired results without an explicit separation between encoding and decoding stages. This approach streamlines the process and enhances the efficiency of solving math word problems.

As shown in Table  2 , DNS and MahtEN are Seq2Seq models, while GTS is built as a seq2tree structure. The tree-structured decoder designed in GTS is also applied in Graph2Tree \(^1\) . Graph2Tree \(^1\) and Graph2Tree \(^2\) are two graph2tree models but differ in both graph encoding and tree decoding. In the stage of graph encoding, Graph2Tree \(^1\) uses Quantity Cell Graph and Quantity Comparison Graph to describe the quantity relationships, while Graph2Tree \(^2\) leverages Syntactic Graph to present the word dependency and the phrase structure information. In the decoding stage, a pre-order expression tree is generated in Graph2Tree \(^1\) , while Graph2Tree \(^2\) employs a hierarchical expression tree to model the output expression.

• Problem text encoding

In recent years, a trend in building MWP solvers [ 1 ] is to apply deep neural networks to capture the quantity relationships presented by problem texts explicitly and implicitly. The early MWP solvers [ 2 , 65 ] mainly use sequence-based models, such as LSTM [ 3 ], GRU [ 47 ], etc., to conduct problem representation learning, in which the problem text is regarded as an unstructured sequence. Recently, graph-based representation learning methods [ 5 , 6 , 17 ] are widely employed to enhance both structured and unstructured information learning, which attracts more and more attention of community researchers. On the other hand, several benchmark datasets with diverse characteristics were released for performance evaluation of the proposed solvers [ 10 ]. To reveal the potential effectiveness of presentation learning methods on diverse characteristics of MWPs, a comparative analysis of sequence-based and graph-based representation learning is conducted in this paper.

Sequence-based problem encoding

As a problem is mainly presented by natural language text, the sequence-based recursive neural network (RNN) models [ 3 , 47 ] are naturally taken to problem representation learning. For example, DNS [ 2 ] uses a typical Seq2Seq model for problem representation learning, where words are split into tokens inputted into a GRU module to capture quantity relations. Several follow-up works were proposed by replacing GRU with BiLSTM or BiGRU to enhance the ability of quantity relation learning [ 7 , 14 , 15 ]. To improve the semantic embedding, pre-trained language models, such as GloVe [ 17 ], BERT [ 26 ], Chinese BERT [ 55 ] and GPT [ 28 , 73 ], etc., were used to better understand the input problem texts. Besides, to capture more features between problem sentences and the goal, attention modules are employed in several works to extract local and global information. For instance, Li et al. [ 37 ] introduced a group attention that contains different attention mechanisms which achieved substantially better accuracy than baseline methods.

In a sequence-based representation learning model, every word of the problem text P is first transformed into the context representation. Given an input problem text \(P=\{ w_{1},w_{2},...,w_{n} \}\) , each word token \(w_{i}\) is vectorized into the word embedding \(w_{i}\) through word embedding techniques such as GloVe [ 17 ], BERT[ 26 ], etc. To capture the word dependency and learn the representation of each token, the sequence of word embeddings is input into the RNN whose cells can be LSTM [ 3 ], GRU [ 47 ], etc. Formally, each word embedding \(w_{i}\) of the sequence \(E=\{ w_{1},w_{2},...,w_{n} \}\) is input into the RNN one by one, and a sequence of hidden states is produced as the output.

For unidirectional encoding, the procedure of problem representation learning can be described as follows:

where \({RNN}(\cdot ,\cdot )\) denotes a recursive neural network, \(h_{i-1}^p\) denotes the previous hidden state and \(w_{i}\) denotes the current input. Repeat the above calculation from step 1 to n to obtain the final hidden state \(h_{n}\) , which is the result of the sequence-based representation learning. In practice, \({RNN}(\cdot ,\cdot )\) is usually specified as a two-layer LSTM or GRU network.

For bi-direction encoding, BiLSTM or BiGRU is applied to obtain the left vector \(\overrightarrow{h_i^p}\) and the right vector \(\overleftarrow{h_i^p}\) separately. Finally, the output hidden state \(h_i^p\) is calculated as follows:

To capture different types of features in hidden state \(h_s^p\) , attention mechanisms are employed to enhance the related features. For example, Li et at. [ 37 ] applied a multi-head attention network following a BiLSTM network. The output of the group attention \(h_a^p\) is produced by:

where Q , K and V denote the query matrix, key matrix and value matrix separately, which are all initialized as \(h_i^p\) .

The above process can be replaced by employing a pre-trained language model. As shown in Eq.  5 , a pre-trained language model PLM (.) is used to directly map the problem text, denoted as X, to a representation matrix H.

Graph-based problem encoding

To improve structural information learning, graph-based encoders were applied to represent relationships among numbers, words and sentences, etc. The structural information includes token-level information and sentence-level information. The former is also considered as local information which is constructed from the number comparison relationship (e.g., bigger, smaller), neighborhood relationship between numbers and the associated word tokens, etc. For example (as shown in Fig.  3 a), Zhang et al. [ 6 ] applied two graphs, including a quantity comparison graph and a quantity cell graph to enrich the information between related quantities. The sentence-level information, in a sense, is the global information that connects local token-level information. A commonly used sentence-level information is the syntactic structure information generated from dependency parsing. As shown in Fig.  3 b, to capture the sentence structure information, the dependency parsing and the constituency analysis [ 17 ] were applied to construct graphs. Furthermore, Wu et al. [ 50 ] proposed a mixed graph, called an edge-labeled graph, to establish the relationship between nodes at both the sentence level and problem level. Once the problem text is represented as a graph, graph networks such as GraphSAGE [ 21 ], GCN [ 74 ], can be used to learn the node embedding. One of the advantages of using graph representation learning is that external knowledge can be easily imported into the graph to improve the accuracy of problem solving [ 50 ].

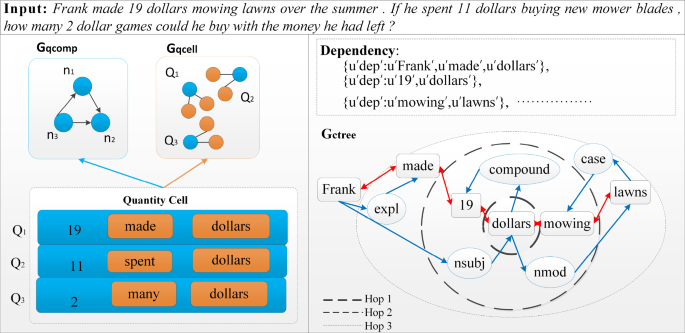
Comparison of graph-based quantity relation representation. a Quantity comparison graph and quantity cell graph designed by Zhang et al. [ 6 ]; b Constituency tree augmented text graph applied by Li et al. [ 17 ]

Different from the sequence-based representation learning methods, the graph-based representation learning methods take important structural information into consideration when encoding. Due to the fact that different researchers construct the graph using different methods, unifying these methods is more complex than unifying the sequence-based representation learning methods. Through the summary and induction of several typical works[ 6 , 7 , 16 , 17 ], we divide the procedure of sequence-based representation learning into three steps: node initialization, graph construction and graph encoding.

Graph Construction. The graph construction is a pre-process before graph encoding, which converts the problem P into a graph \(G=(V, E)\) aiming at preserving more structural information hidden in P . To this end, elements such as words and quantities are treated as nodes V , and syntactic relationships such as grammatical dependency and phrase structure are modeled as edges E .

To enrich the information during graph construction, several adjacency modeling approaches are proposed to construct graphs according to the relationships of words and numbers in P . For example, in reference [ 16 ], a Unit Dependency Graph (UDG) is constructed to represent the relationship between the numbers and the question being asked. In work [ 6 ], two graphs, including a quantity comparison graph and a quantity cell graph, are built to model the relationships between the descriptive words associated with a quantity. Syntactic constituency information is used to construct the quantity graph in [ 17 ]. Through the graph construction process, a set of graph \(\mathbb {G} =\{ G_1,G_2,...,G_K \}\) is obtained from problem P for graph encoding.

Graph encoding. After initializing the node and constructing the graph, the graph neural network is applied to obtain the output vector. The procedure can be summarized as follows:

where \(G\!N\!N(\cdot ,\cdot )\) denotes a graph neural network, such as GCN [ 74 ] or GraphSAGE [ 21 ]. The pair \((E_k,V_k)\) represents the \(k_{th}\) graph \(G_k\) in \(\mathbb {G}\) , with \(V_k\) as the node set and \(E_k\) as the edge set. Both \(V_k\) and \(E_k\) are formed during the node initialization stage. \(h_k^g\) denotes the hidden state corresponding to the input graph \(G_k\) . When more than one graph ( \(k>1\) ) is utilized, the output values \({h_k^g}_{k=1}^K\) are concatenated and projected to produce the final value H . Finally, the global graph representation \(h^g\) can be obtained:

where \(FC(\cdot )\) is a fully connected network and \(Pooling(\cdot )\) denotes pooling function.

• Math expression decoding

To achieve the final answer, vectors after problem representation learning are decoded as mathematical expressions followed by a math solver to calculate the answer. Early neural solvers, such as DNS [ 2 ], employ a typical Seq2Seq model to predict mathematical expressions. Later, to improve the generation ability of new expressions, tree-based models [ 5 ] are proposed to capture the structure information hidden in expressions.

Expression Decoder decodes the feature vectors obtained by the problem Encoder into expression templates. The decoding process is a step-by-step prediction of number tokens and operators. Therefore, recursive neural networks are naturally chosen for this task. The decoding process can be described as a conditional probability function as follows:

where x denotes vectors of input problems, \(y_t\) and \(h_t\) is the predicted character and decoder hidden state at step t separately, and \(F_{prediction}\) is a non-linear function. The key component of Eq. ( 8 ) is the computation of \(h_t\) to ensure the output expressions are mathematically correct. Hence, the default activation functions of the general RNNs need to be redesigned. According to the redesigned activation functions, expression decoding can be divided into two main categories: sequence-based decoding and tree-based decoding.

Sequence model based expression decoding

In sequence-based models, expressions are usually abstracted as a sequence of equation templates with number tokens and operators [ 2 , 37 , 65 ]. For example, the expression \(x = 5+2*3\) is described as an equation template \(x=n_1+n_3+n_2\) , \(n_i\) is the token of the i th number in problem P . In the stage of math expression generation, a decoder is designed to predict an equation template for each input problem and then expressions are generated by mapping the numbers in the input problem to the number tokens in the predicted equation template [ 2 ]. Hence, the math expression generation is transformed into a sequence prediction task and one of the core tasks of math expression generation is to design a decoder to predict the equation templates. Typical sequence models built for NLP tasks can be directly applied for building such decoders [ 47 , 72 ]. Compared to retrieval models [ 32 , 75 ], sequence-based models achieved significant improvement in solving problems requiring new equations that not existed in the training set. However, these models are usually sensitive to the length of the expressions as they generate solution expressions sequentially from left to right.

In sequence-based expression decoding, the activation function is defined according to the basic rules of arithmetic operations. For example in infix expressions, if \(y_{t-1}\) is a number, then \(y_t\) should be a non-number character. Therefore, the redesigned activation function differs according to the infix and suffix expressions used.

In infix sequence models [ 2 ], predefined rules are used to decide the type of the \(t_{th}\) character according to the \((t-1)_{th}\) character. For example, rule “If \(y_{t-1}\) in \(\{+,-,\times , \div \}\) , then \(y_t\) will not in \(\{+,-,\times , \div , ),= \}\) ” defines the following character after an operator is predicted. Similar rules are used to determine characters after “(, ), =” and numbers are predicted.

In suffix sequence models [ 36 , 37 ], two numbers will be first accessed by the RNN to determine the operator and generate a new quantity as the parent node. The representation of the parent node \(o_c\) can be calculated by a probability function like:

where \(h_l, h_r\) are the quantity representations for the previously predicted nodes, and \(W_1, W_2\) and b are trainable parameters.

Tree-structured model based expression decoding

To describe the structural relation among operators and digits, expression templates are represented as tree structures and tree-structured networks are proposed to learn the structural features of the expression trees. Compared to left-to-right sequential representation in sequence-based methods, relationships among operators and numbers are represented by tree structures, such as expression tree [ 72 ] or equation tree [ 63 ]. Strictly, the tree-structured network is not a novel network architecture but a compound of networks and a decision mechanism. For example, the previous state when predicting a left child node is the parent node state, but in a right child node prediction, both the parent node state and the left child node state are considered as the previous state [ 5 ]. Hence, a decision mechanism is designed to choose different embedding states when predicting a left and right child node. Besides, various neural cells (e.g., a prediction network and a feature network) are usually employed for current character prediction and current hidden state calculation [ 6 , 17 ].

Therefore, the tree-structured networks are decided by the structure of the expression trees and the tree-based decoding is a decomposing process of an expression tree. According to the decomposing strategy employed, tree-based decoding can be divided into two main categories: depth-first decomposing [ 5 , 6 ] and breadth-first decomposing [ 17 ].

Depth-first decomposing. As shown in Fig.  4 b, the depth-first decomposing starts from the root node and implements a pre-order operation during the prediction. As such, if an operator is predicted, then go to predict the left child until a number node is predicted, then go to predict the right child. To make full of available information, the prediction of the right child takes the information of its left sibling node and the parent information into consideration. Roy et al. [ 72 ] proposed the first approach that leverages expression trees to represent expressions. Xie et al. [ 5 ] proposed a goal-driven tree-structured neural network, which was adopted by a set of latter methods [ 6 , 14 , 15 ], to generate an expression tree.

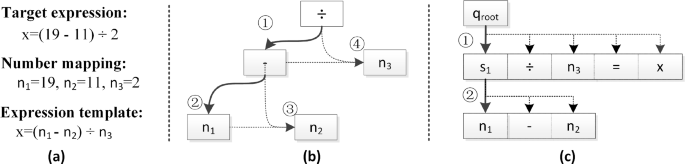
An example of tree-structured decomposing. a Input expression template; b Depth-first decomposing; c Breadth-first decomposing

Breadth-first decomposing. In breadth-first decomposing models, expressions are represented as hierarchically connected coarse equations. A coarse equation is an algebraic expression that contains both numbers and unknown variables. Compared to depth-first decomposing, an essential difference of breadth-first decomposing is that the non-leaf nodes are specified as variables. Therefore, the variable nodes are decomposable nodes that can be replaced by sub-trees. As shown in Fig.  4 (c), an example equation is firstly represented as a 1st-level coarse equation \(s_1 \div n_3(2)=x\) containing a non-leaf node \(s_1\) and four leaf nodes. Then, the non-leaf node \(s_1\) is decomposed into a sub-tree as the 2nd-level coarse equation of \(n_1(19)-n_2(11)\) . When all coarse equations are achieved then go to predict the 3rd-level coarse equations if it has, otherwise, the decomposing stops.

To start a tree generation process, the root node vector \(q_{root}\) is initialized according to the global problem representation. For each token y in the target word \(V^{dec}\) , the representation for a certain token \(\textrm{e}(y \mid P)\) , as denoted as \(h_t\) in Eq. ( 8 ), is defined as follows:

where \(\textrm{e}_{(y, op)}\) , \(\textrm{e}_{(y,u)}\) and \(\textrm{e}_{(y, con)}\) denotes the representation of operators, unknowns and quantities separately that is obtained from 3 independent embedding matrices \(M_{op}\) , \(M_{unk}\) and \(M_{con}\) . \(\bar{h}_{loc(y, P)}^{p}\) is the quantity representation from Eqs. ( 3 ) or ( 4 ). \(V^{dec}\) is the target vocabulary which consists of 4 parts: math operators \(V_{op}\) , unknowns \(V_u\) , constants \(V_{con}\) and the numbers \(n_p\) .

In order to adapt to the tree-structured expression generation, activation functions are redesigned according to the types of nodes in the expression tree. The nodes are categorized into two types: leaf nodes and non-leaf nodes. When a non-leaf node is predicted, further decomposing is needed to predict the child nodes. Otherwise, stop the current decomposing and go to predict the right child nodes. The non-leaf node differs in different representations of tree-structured expressions. In regular expression trees [ 5 , 6 ], the non-leaf nodes are operators while numbers are treated as leaf nodes. While in a heterogeneous expression tree, the non-leaf nodes are non-target variables that are represented by sub-expressions.

Based on the above discussion, the whole procedure of tree-based expression decoding can be summarized as follows [ 5 , 6 , 7 , 14 ]:

1) Tree initialization: Initialize the root tree node with the global embedding \(H_g\) and perform the first level decoding:

where the global embedding \(H_g\) is the original output of the problem Encoder .

2) Left sub-node generation: A sub-decoder is applied to derive the left sub-node. The new left child \(n_l\) is conditioned on the parent node \(n_p\) and the global embedding \(H_g\) . The token \(\hat{y}_l\) is predicted when generating the new left node:

If the generated \(\hat{y}_l \in V_{op}\) or \(\hat{y}_l \in V_{u}\) , repeat step 2). If the generated \(\hat{y}_l \in V_{con}\) or \(\hat{y}_l \in n_p\) , get into step 3).

3) Right-node generation: Different from the left sub-node generation, the right sub-node is conditioned on the left sub-node \(n_l\) , the global embedding \(H_g\) and a sub-tree embedding \(t_l\) . The right sub-node \(n_r\) and the corresponding token \(\hat{y}_r\) can be obtained as:

where the sub-tree embedding \(t_l\) is conditioned on the left sub-node token \(\hat{y}_l\) and left sub-node \(n_l\) . If the \(\hat{y}_r \in V_{op}\) or \(\hat{y}_r \in V_{u}\) , repeat step 2). If the generated \(\hat{y}_r \in V_{con}\) or \(\hat{y}_r \in n_p\) , stop decomposing and backtrack to find a new empty right sub-node position. If no new empty right nodes can be found, the generation is completed. If the empty right node position still exists, go back to step 2).

In other models [ 17 ], step 2) and 3) are combined into a sub-tree generation module in which the token embedding \(s_t\) and the corresponding token \(\hat{y}_t\) at time t are calculated as follows:

where \(st_{parent}\) stands for sub-tree node embedding from the parent layer and \(st_{sibling}\) is the sentence embedding of the sibling.

Compared to earlier sequence-based decoders which are usually retrieved models, tree-based decoders are generative models that can generate new expressions not existing in the training set. The generation ability lies in the iterative process of tree-structured decomposing as defined in Eq.  10 and the equation accuracy was greatly improved by using tree-based decoders. Detailed results can be found in Sect. “ Experiment ”.

Characteristics analysis of benchmark datasets

Widely used benchmark datasets.

Problem texts and equations are two essential items for neural solver evaluation. The problem text of each example in the dataset is a natural language stated short text that presents a fact and raises a question and the equation is a math expression(s) (e.g., an arithmetic expression, an equation or equations) that can be used to generate the final answer to the question raised by the problem text. A problem text can be stated in any language but most of the widely used datasets are stated in English [ 32 , 76 , 77 ] until Wang et al. [ 2 ] released a Chinese dataset Math23K in 2017 which contains 23,161 problems with carefully labeled equations and answers. A brief introduction of the widely accepted benchmark datasets is given as follows and the result of a statistical analysis conducted on the considered datasets is shown in Table 3 .

Alg514 is a multiple-equation dataset created by Kushman et al. [ 32 ]. It contains 514 algebra word problems from Algebra.com. In the dataset, each template corresponds to at least 6 problems (T6 setting). It only contains 28 templates in total.

Draw1K is a multiple-equation dataset created by Upadhyay et al. [ 78 ]. It contains 1000 algebra word problems also crawled and filtered from Algebra.com.

Dolphin18K is a multiple-equation dataset created by Huang et al.[ 77 ]. It contains 18,711 math word problems from Yahoo! Answers with 5,738 templates. It has much more and harder problem types than the previous datasets.

MAWPS-s is a single-equation dataset created by Koncel-Kedziorski et al. [ 76 ]. It contains 3320 arithmetic problems of different complexity compiled from different websites.

SVAMP is a single-equation dataset created by Patel et al. [ 79 ]. It contains 1000 problems with grade levels up to 4. Each problem consists of one-unknown arithmetic word problems which can be solved by expressions requiring no more than two operators.

Math23K is a single-equation dataset created by Wang et al. [ 2 ]. It contains 23, 162 Chinese math word problems crawled from the Internet. Each problem is labeled with an arithmetic expression and an answer.

HMWP is a multiple-equation dataset created by Qin et al. [ 38 ]. It contains 5491 Chinese math word problems extracted from a Chinese K12 math word problem bank.

Despite the available large-scale datasets, neural solver evaluation is still a lot trickier for the various types and characteristics of math word problems. As almost all neural solvers predict equation templates directly from the input problem text, the complexity and characteristics of the equations and the input problem texts need further study to make the evaluated results more elaborate.

Characteristics analysis

To evaluate the neural solvers, three widely used benchmark datasets include two English datasets MAWPS-s and SWAMP , and a Chinese dataset Math23k . All the selected datasets are single-equation problems as almost all solvers support the single-equation generation task. Conversely, not all solvers support the multi-equation generation task which may lead to poor comparability.

As discussed in Sect. “ Characteristics analysis of benchmark datasets ”, problem texts and expressions differ greatly in terms of scope and difficulty between different datasets. In order to reveal the performance difference of neural solvers on datasets with different characteristics, the selected benchmark datasets are categorized into several sub-sets based on four-index characteristic factors of L , H , C and S defined as follows:

Expression Length ( L ): denotes the length complexity of the output expression. L can be used as an indicator of the expression generation capability of a neural solver. According to the number of operators involved in the output expression, L is defined as a three-level indicator containing \(L_1\) , \(L_2\) and \(L_3\) . \(L_1\) level: \(l<T_0\) , \(L_2\) level: \(T_0<=l<=T_1\) , \(L_3\) level: others. Where l represents the number of operators in the output expression. \(T_0\) , \(T_1\) denote the thresholds of l at different levels of length complexity.

Expression Tree Depth ( H ): denotes the height complexity of the output expression tree. H is another generation capability indicator, especially for tree-structured neural solvers. According to the depth of the expression tree, H is defined as a two-level indicator containing \(H_1\) and \(H_2\) . \(H_2\) level: \(h < T_2\) , \(H_3\) level: others. Where h refers to the height of the expression tree, \(T_2\) is a threshold.

Implicit Condition ( C ): denotes whether implicit expressions needed to solve the problem are embedded in the problem text. \(C_{1}\) refers to problems with no implicit expression, while \(C_{2}\) refers to problems with one or more implicit expressions. C can be used as an indicator associated with the relevant information understanding of the solver.

Arithmetic Situation ( S ): denotes the situation type that a problem belongs to. The different arithmetic situation indicates different series of arithmetic operations. Based on Mayer’s work, we divide math word problems into five typical types which are Motion ( \(S_m\) ), Proportion ( \(S_p\) ), Unitary ( \(S_u\) ), InterestRate ( \(S_{ir}\) ), and Summation ( \(S_s\) ). S can be used as an indicator associated with the context understanding of the solver.

Each of the selected benchmark datasets is divided into three sub-sets of train-set (80%), valid-set (10%) and test-set (10%). These sub-sets are further characterized according to the above four indices. Tables  4 and 5 show the percentage of problems of different benchmark datasets on the four indices for training and testing separately. Compared to Math23K, expressions in MAWPS-s and SVAMP are much more simple on both factors of the expression length and expression depth. Hence, we set different thresholds for \(T_i\) to generate \(L_*\) and \(H_*\) subsets. Moreover, implicit expression and problem situation analysis are only implemented on Math23K dataset.

Experimental setup

Selected typical neural solvers: To ensure the fairness of the performance evaluation, two representative solvers were selected from each framework as shown in Table  2 . The selected solvers are listed below:

DNS [ 2 ]: The first Seq2Seq model using a deep neural network to solve math word problems. The model combines the RNN model and the similarity-based retrieval model. If the maximum similarity score returned based on the retrieval model is higher than the specified threshold, the retrieval model is then selected. Otherwise, the Seq2Seq model is selected to solve the problem.

MathEN [ 4 ]: The ensemble model that combines three Seq2Seq models uses the equation normalization method, which normalizes repeated equation templates into expression trees.

GTS [ 5 ]: A tree-structured neural model based on the Seq2Tree framework to generate expression trees in a goal-driven manner.

SAU-Solver [ 38 ]: A semantically aligned universal tree structure solver based on the Seq2Tree framework, and it generates a universal expression tree explicitly by deciding which symbol to generate according to the generated symbols’ semantics.

Graph2Tree [ 6 , 17 ]: Graph2Tree \(^1\) and Graph2Tree \(^2\) are both deep learning architectures based on the Graph2tree framework, combining the advantages of a graph-based encoder and a tree-based decoder. However, the two differ in graph encoding and tree decoding.

Bert2Tree [ 26 ]: An MWP-specific large language model with 8 pre-training objectives designed to solve the number representation issue in MWP.

GPT-4 [ 30 ]: A decoder-only large language model released by OpenAI in March, 2023.

The above selected typical solvers are evaluated in solving characteristic problems on five benchmark datasets and the detailed results can be found in Sect. “ Performance on solving characteristic problems ”.

Component Decoupling According to the discussion in Sect. “ Architecture and technical feature analysis of neural solvers ”, each solver consists of an encoder which can be decomposed into one or more basic RNN or GNN cells. To identify the contribution of these various cells during the problem solving, we decouple the above considered solvers into individual components. The decoupled components can be integrated into different solvers and can be replaced by other similar components. Components decoupled from encoders are listed as follows.

LSTM Cell : A long-short term memory network derived from sequence-based encoders for non-structural problem text encoding.

GRU Cell : A gated recurrent unit derived from sequence-based encoders for non-structural problem text encoding.

BERT Cell : A pre-trained language model used to directly map the problem text into a representation matrix for generating the solution.

GCN Cell : A graph convolution network derived from graph-based encoders for structural problem text encoding.

biGraphSAGE Cell : A bidirectional graph node embedding module derived from graph-based encoders for structural problem text encoding.

The LSTM cell and GRU cell take text sequence as input and output two text vectors including an embedding vector and a hidden state vector. The GCN cell and biGraphSAGE cell take the adjacency matrix as input and output two graph vectors. Similarly, components decoupled from decoders are listed below.

DT Cell : A depth-first decomposing tree method derived from Graph2Tree \(^1\) for math equation decoding. DT cell takes an embedding vector and a hidden vector as input and output a math equation.

BT Cell : A breadth-first decomposing tree method derived from Graph2Tree \(^2\) for math equation decoding. The BT cell takes three vectors as input, including one embedding vector and two hidden state vectors.

Hence, a super solver is developed to reproduce the selected typical solvers and design new solvers by redefining the combination of the decoupled components. The performance of newly developed solvers are shown and discussed in Sects. “ Comparative analysis of math expression decoding models ” and “ Comparative analysis of problem encoding models ” separately.

Evaluation Metrics Math word problems used for neural solver evaluation are usually composed of problem texts, equations and answers. Neural solvers take the problem texts as input and output the expression templates which are further mapped to calculable equations [ 1 ]. These generated equations are then compared with the equations labeled in datasets for algorithm performance evaluation. Besides this equation-based evaluation, answer-based evaluation is also used in cases where multiple solutions exist. The answer-based evaluation compares the answers calculated from the generated equations with labeled answers. Several commonly used evaluation metrics are introduced below, including accuracy ( \(E_{acc}\) and \(A_{acc}\) ), time cost (# Time ) and minimum GPU memory capacity (# \(\mathop {G\!\!-\!\!Mem}\) ).

Accuracy. Accuracy includes answer accuracy and equation accuracy. Answer accuracy [ 2 , 5 , 7 ] is perhaps the most common evaluation method. It simply involves calculating the percentage of final answers produced by the model that is correct. This is a good measure of the model’s overall performance, but it can be misleading if the dataset is unbalanced (e.g., if there are more easy problems than difficult ones). Equation accuracy [ 6 , 17 ] is another important measure, which refers to the accuracy of the solution that the model generates. This is typically calculated by comparing the output of the model to the correct solution to the problem, and determining whether they match. Evaluating both the solution accuracy and answer accuracy can give a more complete picture of the model’s performance on MWP solving tasks.

The Equation Accuracy ( \(E_{acc}\) ) which is computed by measuring the exact match of predicted equations and ground-truth equations as follows:

Similarly, the Answer Accuracy ( \(A_{acc}\) ) is defined as follows:

To remove extraneous parenthesis during equation matching, equations are transformed into equation trees as described in [ 17 ]. By using \(E_{acc}\) , outputs with correct answers but incorrect equations are treated as unsolved cases.

Time Cost (# Time ): denotes the time required for model training. Specifically, this article refers to the time needed for the model to complete 80 iterations with a batch size of 64.

Minimum GPU Memory Capacity (# \(\mathop {G\!\!-\!\!Mem}\) ): represents the minimum GPU memory capacity required for training the model. This metric is crucial for assessing the hardware requirements of model training, particularly for researchers with limited resources.

Hyper-parameters To improve the comparability of the experimental results, the hyper-parameters of the selected solvers and the decoupled cells are consistent with the original models. For example, the default LSTM and GRU cells are initialized as a two-layer network with 512 hidden units to accommodate the pre-trained word vector which usually has a dimension size of 300. In the biGraphSAGE cell, we set the maximum number of node hops K as \(K = 3\) and the pooling aggregator is employed. As to the optimizer, we use Adam with an initial learning rate of 0.001, and the learning rate will be halved every 20 epochs. We set the number of epochs to 80, batch size to 64, and dropout rate to 0.5. At last, we use a beam search with beam size 5 in both the sequence-based cells and tree-based cells. To alleviate the impact of the randomness of the neural network models, we conduct each experiment 5 times with different random seeds and report the average results. All these hyper-parameters have been carefully selected to balance computational efficiency with model performance.

Experimental Environment Our models run on a server with Intel i7 CPU. The GPU card is one NVIDIA GeForceRTX 3090. Codes are implemented in Python and PyTorch 1.4.0 is used for matrix operation. We use stanfordcorenlp to perform dependency parsing and token generation for Chinese datasets.

Performance comparison

Overall performance of considered solvers.

In this section, we initially present the learning curves of all considered models (excluding GPT-4) on two representative datasets (Math23k for Chinese and MAWPS-s for English).

It is evident that overfitting occurs on the MAWPS-s dataset, as shown in Fig.  5 . After 10 iterations, the models exhibit oscillations in terms of accuracy despite having low loss values. This suggests that overfitting has occurred in this case. The limited size of the MAWPS-s dataset, which contains only around 1500 training examples, is likely insufficient for effective training of most deep neural networks. On the other hand, the situation improves on the Math23K dataset. After approximately 30 iterations, both the loss and accuracy stabilize.

We have also examined the training time required for different models. As shown in Table  6 , without considering GPT-4 and fine-tuning of BERT, all models have completed training with a batch size of 64 within 4 min (# Time ), and have reached convergence in less than 80 iterations. Similarly, we have reported the minimum GPU memory capacity (# \(\mathop {G\!\!-\!\!Mem}\) ) required for training. This has been highly attractive for individual researchers as it has allowed them to quickly train the desired models locally without incurring high costs. The next step will be to evaluate the solving performance of different models.

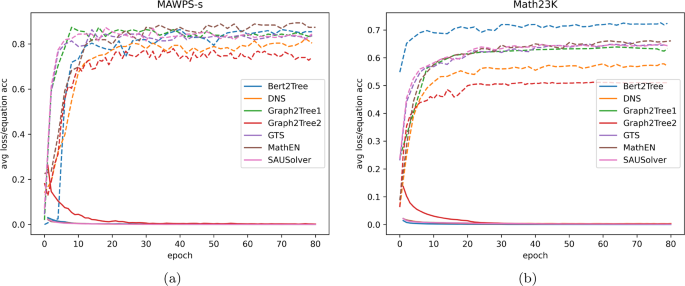
Learning curves on different datasets. a Learning curves on MAWPS-s; b Learning curves on Math23K

We provide an overall result of the considered solvers in terms of both single-equation and multi-equation tasks. We evaluate the \(E_{acc}\) and \(A_{acc}\) separately. Additionally, we report the average training time (#Time(minutes per epoch)) on Math23K.The detailed results are shown in Table  6 .

As shown in Table  6 , PLM-based models exhibit superior performance in terms of \(A_{acc}\) compared to other models. Specifically, without any additional prompts, GPT-4 achieves the best results on the MAWPS-s, SVAMP, and Draw1k datasets, with accuracies of 94.0%, 86.0%, and 42.1% respectively. On the other hand, BertTree performs well on the two Chinese datasets, Math23k and HMWP, with accuracies of 84.2% and 48.3% respectively. This demonstrates the significant advantage of PLM-based models, especially large-scale language modes such as GPT-4, in solving math word problems.

However, it is important to note that there is still room for improvement in the performance of all models, particularly in solving more complex math problems such as those in the Math23k, Draw1K, and HMWP datasets. There is still a considerable gap between the current performance levels and practical requirements. Additionally, traditional lightweight models also have their merits. For instance, models utilizing Tree-based decoders achieve leading performance in terms of \(E_{acc}\) , with 68.0%, 72.4%, 39.8%, and 39.6% on the SVAMP, Math23K, Draw1K, and HMWP datasets respectively. This highlights the potential advantages of Tree-based decoders in representing mathematical expressions. Furthermore, the resource requirements and response efficiency of large language models like GPT are also important considerations.

Among the lightweight models, Graph2Tree models demonstrate the best results on most selected datasets, particularly for multi-equation tasks on Draw1K and HMWP. This underscores the immense potential of the graph-to-tree framework in solving math word problems. However, we observed that Graph2Tree \(^2\) did not perform as well as Graph2Tree \(^1\) , underscoring the significance of careful cell selection in both problem encoding and expression decoding steps. Detailed analysis can be found in Sects. “ Comparative analysis of math expression decoding models ” and “ Comparative analysis of problem encoding models ”. Surprisingly, MathEN achieved the best performance on MAWPS-s and also outperformed other solvers in terms of \(E_{acc}\) on the Math23K dataset.

Based on the training time required per epoch on Math23K, we found that more complex models resulted in higher computational times, which is consistent with our general understanding. Among them, SAU-Solver and Graph2Tree \(^2\) had the longest training times, ranging from 3 to 4 min, while the DNS model, which only involves sequence encoding and decoding, had the shortest training time. Graph2Tree \(^1\) and GTS reported similar time costs, indicating that the added CNN unit in Graph2Tree \(^1\) has a minor impact on the computation cost of the graph-to-tree framework.

Performance on solving characteristic problems

In the following comparison, we only considered single-equation tasks for performance evaluation. This is because multi-equation tasks can be easily converted into a single-equation task by adding a special token \(<bridge>\) to convert the equations into a single tree or equation [ 10 ], without requiring any model modifications. Therefore, the performance of solvers on single-equation tasks is also useful for evaluating the performance of models on multi-equation tasks.

(1) Performance on solving problems indicated by expression length.

Table  7 presents the comparison results of \(E_{acc}\) in solving problems with varying equation lengths. Mean Accuracy Difference (MAD), denoted as \(d_{i-k}\) , is used to indicate the accuracy difference in solving problems from level \(L_{i}\) to \(L_{k}\) . Due to the difficulty of obtaining annotated standard arithmetic expressions for GPT models, we utilize the \(A_{acc}\) as a reference instead.

As depicted in Table  7 , PLM-based models have demonstrated superior performance compared to other models. Bert2Tree, in particular, has exhibited greater stability when compared to GPT-4. Specifically, its accuracy remains relatively consistent in both \(L_1\) and \(L_2\) level problems, with only a slight decrease of 17.2% in the \(L_3\) task. In contrast, GPT-4 experiences a significant decrease of 54.9% from \(L_1\) to \(L_3\) .

Graph2Tree models performed the best on SVAMP, achieving an average \(E_{acc}\) of 49.0% and 68.0%, respectively. Graph2Tree \(^1\) proved better at solving long equation problems. For example, on Math23k, it achieved state-of-the-art performance of 73.8% and 48.0% on solving \(L_2\) and \(L_3\) level problems, respectively. Similar results were obtained for both SVAMP and MAWPS-s, highlighting the potential of graph-based models in solving problems of varying length complexities.

For Seq2Tree models, GTS and SAU-Solver separately achieved an average improvement of 7.1% and 6.1%, respectively, compared to DNS on MAWPS-s. On Math23k, GTS achieved an average improvement of 7.4% compared to DNS, and SAU-Solver achieved an 8.3% improvement. The considerable improvements by the Seq2Tree models indicate their potential for equation representation learning using tree-structured decoders.

Surprisingly, MathEN achieved the highest problem-solving accuracy on the \(L_{1}\) -level task of MAWPS-s and the \(L_3\) -level task of Math23K, and also demonstrated a lower MAD value. On the other hand, DNS exhibited lower problem-solving accuracy than MathEN, and had higher MAD values, indicating that DNS is sensitive to the lengths of the expressions.

Among the four categories of solvers considered, PLM-based models demonstrated the best performance on \(L_1\) , \(L_2\) and \(L_3\) level tasks across all datasets. Notably, Graph2Tree exhibited advantages over other lightweight models specifically in handling tasks at \(L_2\) and \(L_3\) levels. Furthermore, it is worth highlighting that among the lightweight models, MathEN and SAU-Solver obtained the best results for \(L_1\) on MAWPS-s and Math23K, respectively. This could be due to the fact that \(L_1\) level tasks typically involve very simple syntax and language structure, which can be efficiently modeled by sequence-based encoders. In contrast, \(L_2\) and \(L_3\) level tasks involve more complex syntax and language structures.

Another interesting finding is that, on MAWPS-s, all models performed better at solving \(L_2\) level problems than the shorter \(L_1\) level problems except GPT-4. Further analysis showed that the average token length of \(L_1\) level problems was 26, which is significantly shorter compared to 31 and 21 on SVAMP and Math23k, respectively. It should be noted that each word is treated as a token for the English dataset MAWPS-s and SVAMP, while for the Chinese dataset Math23k, each token contains one or more words depending on the output of the applied tokenizers.

(2) Performance on solving problems indicated by expression tree height.

Table  8 shows the performances on characteristics of depth complexity. Overall, the accuracy of models decreases as the expression tree depth increases. In particular, GPT-4 achieves accuracies of 97.0% and 74.5% on the \(H_1\) and \(H_2\) subsets of MAWPS-s respectively. However, there is a significant performance drop of 30% from \(H_1\) to \(H_2\) . Similar reduction in performance is observed on Math23K. This suggests that GPT-4 is highly sensitive to the depth of the expressions.

For Graph2Tree models, an average accuracy reduction \(d_{2-1}\) by 15% and 10% for all models from \(H_1\) to \(H_2\) level problems on MAWPS-s and Mathe23K separately. \(d_{2-1}\) is an indicator of model robustness that the lower of \(d_{2-1}\) is, the more robustness of the model is. This suggests that capturing the structure information hidden in problem texts is challenging work for both sequence-based and graph-based methods.

Seq2Tree models have a 7% to 10% improvement on Math23k and MAWPS-s separately compared to DNS. SAU-Solver performs better than MathEN on MAWPS-s but worse on Math23k. Graph2Tree models perform better on Math23k than Seq2Tree models. However, Graph2Tree \(^1\) performs equal or better on \(H_2\) level problems compared to all other methods, which indicates the latency of problem learning on complexity structures. Unlike Graph2Tree \(^1\) and others, Graph2Tree \(^2\) is much more insensitive for the task of depth expression prediction. This suggests that the sentence level information might enhance the representation learning of complex expressions.

For Seq2Seq models, MathEN performs better on all datasets compared to DNS, especially on Math23k \(H_1\) level dataset which achieves the best result (69.2%). However, the accuracy reduction of MathEN by 15.6% and 12.9 from \(H_1\) to \(H_2\) level problem on MAWPS-s and Math23k separately show that MathEN is much more sensitive to expression depth than DNS.

(3) Performance on solving problems indicated by implicit condition

Table  9 demonstrates the significant advantages of PLM-based models in solving implicit condition problems. In particular, GPT-4 exhibits a 1% performance improvement on \(C_2\) compared to \(C_1\) . In terms of lightweight models, MathEN and Graph2Tree \(^1\) obtained an outstanding performance of 67.1% and 66.4% separately. For solving implicit relation problems, MathEN achieved 61.5% which is 2.3% higher than the second-highest result obtained by GTS. Meanwhile, it shows that Seq2Tree models and Graph2Tree \(^1\) method performed similarly (i.e., 59.2%, 58.6% and 58.0% separately) on solving implicit relation problems. For robustness, MathEN has the lowest \(d_{2-1}\) performance among the considered models except for the Graph2Tree \(^2\) .

(4) Performance on solving problems indicated by the arithmetic situation.

As depicted in Table  10 , PLM-based models achieve the best results across all four problem types. However, for Summation type problems ( \(S_s\) ), MathEN achieves an impressive accuracy rate of 72.2%, which is 30% higher than that of GPT-4. Among all lightweight models, MathEN exhibits outstanding performance. For example, MathEN achieved 72.2% accuracy on solving \(S_s\) type problems and GTS got 71.3% on solving Motion type problems ( \(S_m\) ). Whereas the Graph2Tree models generally performed poorly on situational problems. Since situational problems contain more complex quantity relations among various math objects. These quantity relations are usually indicated by high-level contexts which are much more challenging to obtain the required quantity relations for most sequence and graph based models. Moreover, performance differs greatly on different types of situation problems even with the same model which indicates that differentiated models are required for solving different types of situational problems.

Conclusively, the experimental results revealed the following: (1) PLM-based models have shown a significant advantage over other models in almost all tasks. However, they also suffer from a rapid decline in performance when the length and depth of expressions increase. (2) Tree-based expression decoders achieved significant improvement compared to sequence-based decoders. This demonstrates the efficiency of generative models in learning the structural information hidden in mathematical expressions, compared to traditional retrieved models. (3) For encoders, graph-based models perform similarly to sequence-based models. There may be two reasons for this observation. First, current sequence and graph-based models may have encountered a technical bottleneck. These models are trained and fine-tuned for general or specific natural language tasks that are not necessarily suitable for learning mathematical relations in sophisticated situations of math word problems containing various common sense knowledge and domain knowledge. (4) Equation normalization and ensemble models (such as MathEN) achieved outstanding performance compared to pure Seq2Seq models. Since a math word problem may have more than one equation, it is necessary to normalize duplicated equations when working with current sequence and graph-based models.

Comparative analysis of math expression decoding models

To investigate the impact of the decoding models integrated with different encoding models, we conduct a confusion test of depth-first tree decoding (DT Cell) [ 6 ] and breadth-first tree decoding (BT Cell) [ 17 ] in this section. For each decoding module, encoding modules of GRU cell [ 2 ], GCN cell [ 6 ], biGraphSAGE cell [ 17 ] and BERT [ 26 ] are connected separately to compose a full pipeline of encoding-decoding network. The test is conducted on Math23k and the corresponding result is shown in Table  11 .

As shown in Table  11 , the DT cell demonstrates significant advantages in terms of accuracy for both expression and answer when combined with any encoding model. Particularly, when using GRU, GRU+GCN, and BERT as encoders, the DT cell outperforms the BT cell by more than 10%. However, when utilizing GRU+biGraphSAGE as the encoder, the DT cell shows lower performance improvements of 6.7% and 6.5% for both \(E_{acc}\) and \(A_{acc}\) , compared to other encoder combinations. One possible reason is that the GRU+biGraphSAGE encoder incorporates heterogeneous graph information from the problem text, which has relevance to breadth-first decomposing.

Comparative analysis of problem encoding models

Experimental results obtained in Sect. “ Performance on solving characteristic problems ” show the effectiveness of tree-structured models in math expression decoding. However, the performance of models in solving different characteristic problems varies as different neural cells are applied during encoding. In this section, a further experiment is conducted to evaluate the performance of different encoding units in solving different characteristic problems.

In the following experiments, we split the encoding modules into composable neural cells from the baseline methods for problem encoding. From sequence-based encoders, LSTM and GRU cells are obtained and GCN and biGraphSAGE cells are obtained from graph-based encoders. The obtained GRU and LSTM cells are designed with 2 layers. In our experiment, both 2 and 4-layer cells are tested to evaluate the effect of cell depth in problem encoding. The above cells are implemented individually or jointly for problem encoding followed by the tree-based decoding module [ 5 ] to generate math expressions. To combine the outputs of the GCN module and the biGraphSAGE module, a multi-head attention network is used which takes the final hidden vectors of the GCN and biGraphSAGE as input and outputs a new combined hidden vector. The \(E_{acc}\) and \(A_{acc}\) results are presented in Table  12 .

In Table  12 , \(G_{qcell}\) and \(G_{qcom}\) denote the quantity cell graph and quantity comparison graph built in [ 6 ] separately as the input of the GCN network. \(G_{wcon}\) refers to the constituency graph defined in [ 17 ] and is processed by the biGraphSAGE network.

Obviously, the BERT-DT combination outperforms other combinations in almost all test items. Here, we focus on discussing the performance of lightweight model combinations.

Firstly, when selecting the number of layers for the sequence encoder, there is no significant difference in performance between 4-layer and 2-layer networks. The 2-layer GRU cell obtained the best result among all sequence-based cells. The 2-layer GRU cell performed better than the 4-layer cells and similar results were obtained by LSTM cells. Therefore, we believe that it may be not an efficient way to try to improve the problem encoding by increasing the depth of sequence-based neural networks.

Secondly, when incorporating graph information, the combination of \(G_{qcom}\) and \(G_{qcell}\) obtained the best performance. For GCN-based modules, the GCN cell with \(G_{qcom}\) information obtained outstanding results on all levels of length complexity tasks and the \(H_1\) level depth complexity task. The GCN cell performs best on \(H_2\) level task when combining the graph information of \(G_{qcell}\) and \(G_{qcom}\) . A possible reason is that the \(G_{qcell}\) is homologous to the basic text sequence while the \(G_{qcom}\) contains additional comparison information that plays an important role in guiding the math expression generation. Second, the biGraphSAGE cell with \(G_{wcon}\) got lower performance than GCN cells, partly due to the sparsity of the constituency matrix used.

Furthermore, considering the fusion of multiple features, it can be observed from Table  12 that the mixed module by combining GCN ( \(G_{qcell}\) ) and biGraphSAGE ( \(G_{wcon}\) ) achieved better performance than biGraphSAGE ( \(G_{wcon}\) ) but worse than GCN ( \(G_{qcell}\) ) individually applied. The performance is slightly improved after the \(G_{qcom}\) is added. However, the overall performance of mixed modules is worse than only GCN modules. This leads us to conclude that choosing an appropriate encoder is a key decision in hybrid information encoding.

This paper provides a comprehensive survey and performance analysis of DL-based solvers for Math Word Problems (MWPs). These solvers are categorized into four distinct groups based on their network architecture and neural cell types: Seq2Seq-based models, Seq2Tree-based models, Graph2Tree-based models, and PLM-based models.

During the training phase, it has been observed that most models exhibit overfitting issues on datasets. Figure  5 illustrates the effectiveness of the Math23K training set, which consists of 18k instances, in meeting the training requirements of most deep learning-based models. Conversely, when trained on the MAWPS-s dataset, which contains approximately 1.5 k instances, almost all models show noticeable signs of overfitting. This particular finding serves as a valuable reference point for future endeavors involving dataset construction.

In terms of overall performance, pre-trained language models outperformed other models on both single-equation tasks and multi-equation tasks. As depicted in Table  6 , GPT-4 achieves the best results on the MAWPS-s, SVAMP, and Draw-1k datasets, and the BertTree performs well on the two Chinese datasets, Math23k and HMWP. This demonstrates the significant advantage of PLM-based models, especially large-scale language modes such as GPT-4, in solving math word problems. However, there are variations in the performance of different pre-trained language models on Chinese and English datasets. Consistent findings were also reported in previous research studies [ 26 , 27 ]. For instance, in [ 26 ], it is highlighted that the adoption of the Bert2Tree model yields a 2.1% improvement in answer accuracy compared to the Graph2Tree model on the MAWPS-s dataset, while achieving a 7% improvement on the Math23k dataset. This outcome can be attributed to two factors: (1) The Chinese pre-trained model employed in this study, namely Chinese BERT with whole word masking [ 55 ], differs from the BERT-base model used for English. Thus, it is reasonable to infer that task-specific training or fine-tuning of pre-trained language models is essential to fully leverage their advantages. (2) Pre-trained language models exhibit greater proficiency in handling MWPs with intricate semantics. As evidenced by Table  3 , the average length of question texts in the Math23k and HMWP datasets is 1.5-2 times longer than that of other datasets, suggesting the presence of more complex syntactic and semantic information. Utilizing pre-trained language models allows for improved extraction and utilization of pertinent information necessary for effective problem-solving.

Meanwhile, Tables  7 and 8 show that neural solvers are sensitive to the complexity of equations (e.g., equation length, equation tree height), as well as the length of the original problem text. However, we also found that (1) the MathEN model based on the Seq2Seq framework achieved the best results on some datasets (MAWPS-s), indicating that there is room for further optimization of the Graph2Tree framework. Further work is needed to discover the main factors influencing the performance of Graph2Tree on MAWPS-s and to improve it accordingly. (2) For all solvers on MAWPS-s, the increase in expression length did not result in a decline in solving accuracy, but rather showed varying degrees of improvement, which is completely opposite to what we observed on the other two datasets. Further research is needed to explain this phenomenon.

In terms of decoding performance, models integrated with tree decoders exhibit strong performance in generating math equations. Meanwhile, the DT Cell performed much better than the BT Cell on most datasets, making it widely used. However, we believe that the BT Cell still has its special advantages, as its decoding process is more in line with human thought in arithmetic reasoning, where a task is decomposed into multiple sub-tasks, each corresponding to a certain mathematical operation semantics. Therefore, the output results of this model can be better applied in intelligent education scenario, such as step-by-step intelligent tutoring. This raises new questions for researchers on how to design models with human-like arithmetic reasoning ability and make them run efficiently.

In terms of encoding performance, implicit information representation of problem texts plays a crucial role in enhancing the performance of models. Experimental results have shown that combining structure and non-structure information can effectively enhance solver performance. However, we found that not all structure information is equally effective, and some may be more useful in improving solving performance than others. Therefore, it is necessary to design more effective mechanisms or algorithms to determine which information should be added and how the added information can be fused with current information for maximum utility.

Moreover, the emergence of large language models such as GPT has propelled MWP-solving technology to a new stage. These models can gradually improve the accuracy of MWP solvers and their remarkable reasoning abilities enable them to generate step-by-step solutions based on prompts, which is truly impressive. However, these large language models also face challenges such as large parameter sizes and usage restrictions.

Limitations

The limitations of this study are primarily attributed to the emergence of novel models and their integration with knowledge bases, which present challenges in re-implementing these algorithms. Consequently, performance comparisons with specific papers such as [ 7 , 27 ] have been considered in this study. Additionally, due to hardware constraints, we did not fine-tune the pre-trained language models, therefore, the performance of various fine-tuned models has not been reported.

Furthermore, for PLM-based models like GPT-4 [ 30 ], advanced prompts or interaction strategies were not employed in our experiments, which may result in lower accuracy. Moreover, it is worth noting that PLM-based models have the advantage of generating descriptive solution processes, but their performance evaluation in this aspect has not been conducted in this study.

In this paper, we have aimed to provide a comprehensive and analytical comparative examination of the state-of-the-art neural solvers for math word problem solving. Our objective was to serve as a reference for researchers in the design of future models by offering insights into the structure of neural solvers, their performance, and the pros and cons of the involved neural cells.

We first identify the architectures of typical neural solvers, rigorously analyzing the framework of each category, particularly the four typical categories: Seq2Seq, Seq2Tree, Graph2Tree and PLM-based models. A four-dimensional indicator is proposed to categorize the considered datasets to precisely evaluate the performance of neural solvers in solving different characteristics of MWPs. Typical neural solvers are decomposed into highly reusable components. To evaluate the considered solvers, we have established a testbed and conducted comprehensive experiments on five popular datasets using eight representative MWP solvers, followed by a comparative analysis on the achieved results.

After conducting an in-depth analysis, we found that: (1) PLM-based models consistently demonstrate significant accuracy advantages across almost all datasets, yet there remains room for improvement to meet practical demands. (2) Models integrated with tree decoders exhibit strong performance in generating math equations. The length of expressions and the depth of expression trees are important factors affecting solver performance when solving problems with different expression features. The longer the expression and the deeper the expression tree, the lower the solver performance. (3) Implicit information representation of problem texts plays a crucial role in enhancing the performance of models. While the use of multi-modal feature representation has shown promising improvements in performance, it is crucial to ensure information complementary among modalities.

Based on our findings, we have the following suggestions for future work. Firstly, there is still room to improve the performance of solvers, including problem representation learning, multi-solution generation, etc.

Secondly, to better support the potential real-world applications in education, the output of solvers should be more comprehensive. Solvers are expected to generate decomposable and interpretable solutions, rather than just simple expressions or answers. The emergence of large language models has provided ideas for addressing this issue, but it remains a challenge to ensure the validity and interpretability of the outputs for teaching and tutoring applications.

Finally, to evaluate the neural solvers more comprehensively, it is necessary to develop more diverse metrics and evaluation methods in future research. These metrics and methods should capture the performance of solvers in problem understanding, automatic addition of implicit knowledge, solution reasoning, interpretability of results, and other relevant aspects.

Data Availability

The data used in this study is available from the corresponding author upon reasonable request.

Abbreviations

Math Word Problems

Pre-trained Language Model

Tree-structural Decoder

Deep Learning

Depth-first decomposing Tree

Breadth-first decomposing Tree

Mean accuracy difference

Universal Expression Tree

Unit Dependency Graph

Explanation

Problem text

Word token of the P

Encoding network

Decoding network

The hidden vector state i

the query matrix, key matrix and value matrix separately

A graph with vertex V and edge E

trainable parameters and bias

Expression length

Expression tree depth

Implicit condition

Arithmetic situation

Equation accuracy

Math expressions

Answer accuracy

Zhang D, Wang L, Zhang L, Dai BT, Shen HT (2019) The gap of semantic parsing: a survey on automatic math word problem solvers. IEEE Trans Pattern Anal Mach Intell 42(9):2287–2305

Article   Google Scholar  

Wang Y, Liu X, Shi S (2017) Deep neural solver for math word problems. In: Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 845–854. Association for Computational Linguistics, Copenhagen, Denmark

Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J (2017) LSTM: a search space odyssey. IEEE Trans Neural Netw Learn Syst 28(10):2222–2232

Article   MathSciNet   Google Scholar  

Wang L, Wang Y, Cai D, Zhang D, Liu X (2018) Translating a math word problem to a expression tree. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pp. 1064–1069. Association for Computational Linguistics, Brussels, Belgium

Xie Z, Sun S (2019) A goal-driven tree-structured neural model for math word problems. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 5299–5305. International Joint Conferences on Artificial Intelligence Organization, Macao, China

Zhang J, Wang L, Lee RKW, Bin Y, Wang Y, Shao J, Lim EP (2020) Graph-to-tree learning for solving math word problems. In: Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pp. 3928–3937. Association for Computational Linguistics, Seattle, USA

Wu Q, Zhang Q, Wei Z (2021) An edge-enhanced hierarchical graph-to-tree network for math word problem solving. In: Findings of the Association for Computational Linguistics: EMNLP 2021, pp. 1473–1482. Association for Computational Linguistics, Punta Cana, Dominican Republic

Yang Z, Qin J, Chen J, Lin L, Liang X (2022) LogicSolver: Towards interpretable math word problem solving with logical prompt-enhanced learning. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 1–13. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Jie Z, Li J, Lu W (2022) Learning to reason deductively: Math word problem solving as complex relation extraction. In: Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics, pp. 5944–5955. Association for Computational Linguistics, Dublin, Ireland

Lan Y, Wang L, Zhang Q, Lan Y, Dai BT, Wang Y, Zhang D, Lim EP (2022) Mwptoolkit: An open-source framework for deep learning-based math word problem solvers. Proceedings of the AAAI Conference on Artificial Intelligence 36:13188–13190

Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser L, Polosukhin I (2017) Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, pp. 6000–6010. Curran Associates Inc., Red Hook, NY, USA

Lin JCW, Shao Y, Djenouri Y, Yun U (2021) ASRNN: a recurrent neural network with an attention model for sequence labeling. Knowl-Based Syst 212:106548

Chiang TR, Chen YN (2019) Semantically-aligned equation generation for solving and reasoning math word problems. In: Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologie, pp. 2656–2668. Association for Computational Linguistics, Minneapolis, Minnesota

Hong Y, Li Q, Ciao D, Haung S, Zhu SC (2021) Learning by fixing: Solving math word problems with weak supervision. In: Proceedings of the AAAI Conference on Artificial Intelligence, 35:4959–4967

Hong Y, Li Q, Gong R, Ciao D, Huang S, Zhu SC (2021) SMART: a situation model for algebra story problems via attributed grammar. In: Proceedings of the 2021 AAAI Conference on Artificial Intelligence, pp. 13009–13017. Vancouver, Canada

Roy S, Roth D (2017) Unit dependency graph and its application to arithmetic word problem solving. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, pp. 3082–3088. San Francisco, USA

Li S, Wu L, Feng S, Xu F, Xu F, Zhong S (2020) Graph-to-tree neural networks for learning structured input-output translation with applications to semantic parsing and math word problem. In: Findings of the Association for Computational Linguistics: EMNLP 2020, pp. 2841–2852. Association for Computational Linguistics, Punta Cana, Dominican Republic

Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780

Bahdanau D, Cho KH, Bengio Y (2015) Neural machine translation by jointly learning to align and translate. In: 3rd International Conference on Learning Representations. San Diego, California

Cai D, Lam W (2020) Graph transformer for graph-to-sequence learning. Proceedings of the AAAI Conference on Artificial Intelligence 34:7464–7471

Hamilton WL, Ying R, Leskovec J (2017) Inductive representation learning on large graphs. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, pp. 1025–1035. Curran Associates Inc., Red Hook, NY, USA

Mukherjee A, Garain U (2008) A review of methods for automatic understanding of natural language mathematical problems. Artificial Intell Rev 29(2):93–122

Meadows J, Freitas A (2022) A survey in mathematical language processing. arXiv:2205.15231 [cs]

Lu P, Qiu L, Yu W, Welleck S, Chang KW (2023) A survey of deep learning for mathematical reasoning. arXiv:2212.10535 [cs]

Liu Q, Guan W, Li S, Kawahara D (2019) Tree-structured decoding for solving math word problems. In: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 2370–2379. Association for Computational Linguistics, Hong Kong, China

Liang Z, Zhang J, Wang L, Qin W, Lan Y, Shao J, Zhang X (2022) MWP-BERT: Numeracy-augmented pre-training for math word problem solving. In: Findings of the Association for Computational Linguistics: NAACL 2022, pp. 997–1009. Association for Computational Linguistics, Seattle, United States

Zhang W, Shen Y, Ma Y, Cheng X, Tan Z, Nong Q, Lu W (2022) Multi-view reasoning: Consistent contrastive learning for math word problem. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 1103–1116. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, Neelakantan A, Shyam P, Sastry G, Askell A, Agarwal S, Herbert-Voss A, Krueger G, Henighan T, Child R, Ramesh A, Ziegler D, Wu J, Winter C, Hesse C, Chen M, Sigler E, Litwin M, Gray S, Chess B, Clark J, Berner C, McCandlish S, Radford A, Sutskever I, Amodei D (2020) Language models are few-shot learners. In: Advances in Neural Information Processing Systems, 33:1877–1901. Curran Associates, Inc

Radford A, Wu J, Child R, Luan D, Amodei D, Sutskever I (2019) Language models are unsupervised multitask learners. Tech. rep., OpenAI. OpenAI blog

Zhou A, Wang K, Lu Z, Shi W, Luo S, Qin Z, Lu S, Jia A, Song L, Zhan M, Li H (2023) Solving challenging math word problems using GPT-4 code interpreter with code-based self-verification. https://doi.org/10.48550/arXiv.2308.07921 . arXiv:2308.07921 [cs]

Fletcher CR (1985) Understanding and solving arithmetic word problems: a computer simulation. Behav Res Methods Instruments Comput 17(5):565–571

Kushman N, Artzi Y, Zettlemoyer L, Barzilay R (2014) Learning to automatically solve algebra word problems. In: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, pp. 271–281. Association for Computational Linguistics, Baltimore, Maryland

Shen Y, Jin C (2020) Solving math word problems with multi-encoders and multi-decoders. In: Proceedings of the 28th International Conference on Computational Linguistics, pp. 2924–2934. International Committee on Computational Linguistics, Barcelona, Spain

Liang CC, Hsu KY, Huang CT, Li CM, Miao SY, Su KY (2016) A tag-based statistical english math word problem solver with understanding, reasoning and explanation. In: Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, pp. 4254–4255. San Diego, USA

Devlin J, Chang MW, Lee K, Toutanova K (2019) BERT: Pre-training of deep bidirectional transformers for language understanding. In: Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pp. 4171–4186. Association for Computational Linguistics, Minneapolis, Minnesota

Wang L, Zhang D, Zhang J, Xu X, Gao L, Dai BT, Shen HT (2019) Template-based math word problem solvers with recursive neural networks. In: Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, pp. 7144–7151. AAAI Press, Hawaii, USA

Li J, Wang L, Zhang J, Wang Y, Dai BT, Zhang D (2019) Modeling intra-relation in math word problems with different functional multi-head attentions. In: Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pp. 6162–6167. Association for Computational Linguistics

Qin J, Lin L, Liang X, Zhang R, Lin L (2020) Semantically-aligned universal tree-structured solver for math word problems. In: Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 3780–3789. Association for Computational Linguistics, Punta Cana, Dominican Republic

Wu Q, Zhang Q, Wei Z, Huang X (2021) Math word problem solving with explicit numerical values. In: Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, pp. 5859–5869. Association for Computational Linguistics, Bangkok, Thailand

Yu W, Wen Y, Zheng F, Xiao N (2021) Improving math word problems with pre-trained knowledge and hierarchical reasoning. In: Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, pp. 3384–3394. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic

Li Z, Zhang W, Yan C, Zhou Q, Li C, Liu H, Cao Y (2022) Seeking patterns, not just memorizing procedures: Contrastive learning for solving math word problems. In: Findings of the Association for Computational Linguistics: ACL 2022, pp. 2486–2496. Association for Computational Linguistics, Dublin, Ireland

Shen J, Yin Y, Li L, Shang L, Jiang X, Zhang M, Liu Q (2021) Generate & rank: A multi-task framework for math word problems. In: Findings of the Association for Computational Linguistics: EMNLP 2021, pp. 2269–2279. Association for Computational Linguistics, Punta Cana, Dominican Republic

Shen Y, Liu Q, Mao Z, Cheng F, Kurohashi S (2022) Textual enhanced contrastive learning for solving math word problems. In: Findings of the Association for Computational Linguistics: EMNLP 2022, pp. 4297–4307. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates

Chowdhery A, Narang S, Devlin J, Bosma M, Mishra G, Roberts A, Barham P, Chung HW, Sutton C, Gehrmann S, Schuh P, Shi K, Tsvyashchenko S, Maynez J, Rao A, Barnes P, Tay Y, Shazeer N, Prabhakaran V, Reif E, Du N, Hutchinson B, Pope R, Bradbury J, Austin J, Isard M, Gur-Ari G, Yin P, Duke T, Levskaya A, Ghemawat S, Dev S, Michalewski H, Garcia X, Misra V, Robinson K, Fedus L, Zhou D, Ippolito D, Luan D, Lim H, Zoph B, Spiridonov A, Sepassi R, Dohan D, Agrawal S, Omernick M, Dai AM, Pillai TS, Pellat M, Lewkowycz A, Moreira E, Child R, Polozov O, Lee K, Zhou Z, Wang X, Saeta B, Diaz M, Firat O, Catasta M, Wei J, Meier-Hellstern K, Eck D, Dean J, Petrov S, Fiedel N (2022) PaLM: Scaling language modeling with pathways . arXiv:2204.02311 [cs]

Lewkowycz A, Andreassen A, Dohan D, Dyer E, Michalewski H, Ramasesh V, Slone A, Anil C, Schlag I, Gutman-Solo T, Wu Y, Neyshabur B, Gur-Ari G, Misra V (2022) Solving Quantitative Reasoning Problems with Language Models. In: Advances in Neural Information Processing Systems, vol. 35, pp. 3843–3857. Curran Associates, Inc

Touvron H, Lavril T, Izacard G, Martinet X, Lachaux MA, Lacroix T, Rozière B, Goyal N, Hambro E, Azhar F, Rodriguez A, Joulin A, Grave E, Lample G (2023). LLaMA: Open and efficient foundation language models https://doi.org/10.48550/arXiv.2302.13971 . arXiv:2302.13971 [cs]

Chung J, Gulcehre C, Cho K, Bengio Y (2014) Empirical evaluation of gated recurrent neural networks on sequence modeling. In: NIPS 2014 Workshop on Deep Learning, December 2014. Montreal, Canada

Ghazvini A, Abdullah SNHS, Kamru Hasan M, Bin Kasim DZA (2020) Crime spatiotemporal prediction with fused objective function in time delay neural network. IEEE Access 8:115167–115183

Djenouri Y, Srivastava G, Lin JCW (2021) Fast and accurate convolution neural network for detecting manufacturing data. IEEE Trans Ind Inform 17(4):2947–2955

Wu Q, Zhang Q, Fu J, Huang X (2020) A knowledge-aware sequence-to-tree network for math word problem solving. In: Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 7137–7146. Association for Computational Linguistics, Punta Cana, Dominican Republic

Gupta A, Kumar S, Kumar P S (2023) Solving age-word problems using domain ontology and bert. In: Proceedings of the 6th Joint International Conference on Data Science & Management of Data, pp. 95–103. ACM, New York, NY, USA

Petroni F, Rocktäschel T, Riedel S, Lewis P, Bakhtin A, Wu Y, Miller A (2019) Language models as knowledge bases? In: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), pp. 2463–2473. Association for Computational Linguistics, Hong Kong, China

Jiang Z, Xu FF, Araki J, Neubig G (2020) How can we know what language models know? Trans Assoc Comput Linguistics 8:423–438 ( Place: Cambridge, MA Publisher: MIT Press )

Liu Z, Lin W, Shi Y, Zhao J (2021) A robustly optimized bert pre-training approach with post-training. In: Proceedings of the 20th Chinese National Conference on Computational Linguistics, pp. 1218–1227. Chinese Information Processing Society of China, Huhhot, China

Cui Y, Che W, Liu T, Qin B, Yang Z, Wang S, Hu G (2019) Pre-training with whole word masking for chinese bert. IEEE/ACM Trans Audio Speech Language Process 29:3504–3514

Chen J, Pan X, Yu D, Song K, Wang X, Yu D, Chen J (2023) Skills-in-context prompting: Unlocking compositionality in large language models. https://doi.org/10.48550/arXiv.2308.00304 . arXiv:2308.00304 [cs]

Wei J, Wang X, Schuurmans D, Bosma M, ichter b, Xia F, Chi E, Le QV, Zhou D (2022) Chain-of-thought prompting elicits reasoning in large language models. In: Advances in Neural Information Processing Systems, vol. 35, pp. 24824–24837. Curran Associates, Inc

Huang X, Ruan W, Huang W, Jin G, Dong Y, Wu C, Bensalem S, Mu R, Qi Y, Zhao X, Cai K, Zhang Y, Wu S, Xu P, Wu D, Freitas A, Mustafa MA (2023) A survey of safety and trustworthiness of large language models through the lens of verification and validation. http://arxiv.org/abs/2305.11391 . arXiv:2305.11391 [cs]

Dong L, Lapata M (2016) Language to logical form with neural attention. In: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pp. 33–43. Association for Computational Linguistics, Berlin, Germany

Zhang J, Lee RKW, Lim EP, Qin W, Wang L, Shao J, Sun Q (2020) Teacher-student networks with multiple decoders for solving math word problem. In: Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, pp. 4011–4017. International Joint Conferences on Artificial Intelligence Organization, Yokohama, Japan

Bobrow DG (1964) Natural language input for a computer problem solving system. Tech. rep., Massachusetts Institute of Technology, USA

Bakman Y (2007) Robust understanding of word problems with extraneous information. arXiv General Mathematics. https://api.semanticscholar.org/CorpusID:117981901

Koncel-Kedziorski R, Hajishirzi H, Sabharwal A, Etzioni O, Ang SD (2015) Parsing algebraic word problems into equations. Trans Assoc Comput Linguistics 3:585–597 ( Place: Cambridge, MA )

Roy S, Upadhyay S, Roth D (2016) Equation parsing: Mapping sentences to grounded equations. In: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pp. 1088–1097. Association for Computational Linguistics, Austin, Texas

Wang L, Zhang D, Gao L, Song J, Guo L, Shen HT (2018) MathDQN: Solving arithmetic word problems via deep reinforcement learning. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp. 5545–5552. AAAI Press, New Orleans, USA

Hosseini MJ, Hajishirzi H, Etzioni O, Kushman N (2014) Learning to solve arithmetic word problems with verb categorization. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), pp. 523–533. Association for Computational Linguistics, Doha, Qatar

Shi S, Wang Y, Lin CY, Liu X, Rui Y (2015) Automatically solving number word problems by semantic parsing and reasoning. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 1132–1142. Lisbon, Portugal

Liang CC, Hsu KY, Huang CT, Li CM, Miao SY, Su KY (2016) A tag-based English math word problem solver with understanding, reasoning and explanation. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, pp. 67–71. Association for Computational Linguistics, San Diego, California

Upadhyay S, Chang MW, Chang KW, Yih Wt (2016) Learning from explicit and implicit supervision jointly for algebra word problems. In: Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pp. 297–306. Association for Computational Linguistics, Austin, Texas

Chen S, Zhou M, He B, Wang P, Wang Z (2022) A comparative analysis of math word problem solving on characterized datasets. In: In Proceedings of the 2022 International Conference on Intelligent Education and Intelligent Research. IEEE, Wuhan, China

He B, Chen S, Miao Z, Liang G, Pan K, Huang L (2022) Comparative analysis of problem representation learning in math word problem solving. In: In Proceedings of the 2022 International Conference on Intelligent Education and Intelligent Research. IEEE, Wuhan, China

Roy S, Roth D (2015) Solving general arithmetic word problems. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 1743–1752. Association for Computational Linguistics, Lisbon, Portugal

Yenduri G, M R, G CS, Y S, Srivastava G, Maddikunta PKR, G DR, Jhaveri RH, B P, Wang W, Vasilakos AV, Gadekallu TR (2023) Generative pre-trained transformer: A comprehensive review on enabling technologies, potential applications, emerging challenges, and future directions. arXiv:2305.10435

Zhang H, Lu G, Zhan M, Zhang B (2021) Semi-supervised classification of graph convolutional networks with laplacian rank constraints. Neural Process Lett 54(4):2645–2656

Zhou L, Dai S, Chen L (2015) Learn to solve algebra word problems using quadratic programming. In: Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 817–822. Association for Computational Linguistics, Lisbon, Portugal

Koncel-Kedziorski R, Roy S, Amini A, Kushman N, Hajishirzi H (2016) MAWPS: A math word problem repository. In: Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 1152–1157. Association for Computational Linguistics, San Diego, California

Huang D, Shi S, Lin CY, Yin J, Ma WY (2016) How well do computers solve math word problems? Large-scale dataset construction and evaluation. In: Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, pp. 887–896. Association for Computational Linguistics, Berlin, Germany

Upadhyay S, Chang MW (2017) Annotating derivations: A new evaluation strategy and dataset for algebra word problems. In: Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics, pp. 494–504. Association for Computational Linguistics, Valencia, Spain

Patel A, Bhattamishra S, Goyal N (2021) Are NLP models really able to solve simple math word problems? In: Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, pp. 2080–2094. Association for Computational Linguistics, Bangkok, Thailand

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 62007014) and the Humanities and Social Sciences Youth Fund of the Ministry of Education (No. 20YJC880024).

Author information

Authors and affiliations.

Faculty of Artificial Intelligence in Education, Central China Normal University, Wuhan, China

Bin He, Xinguo Yu, Litian Huang, Hao Meng, Guanghua Liang & Shengnan Chen

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Xinguo Yu .

Ethics declarations

Conflict of interest.

The authors declare that they have no Conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

He, B., Yu, X., Huang, L. et al. Comparative study of typical neural solvers in solving math word problems. Complex Intell. Syst. (2024). https://doi.org/10.1007/s40747-024-01454-8

Download citation

Received : 27 March 2023

Accepted : 17 April 2024

Published : 22 May 2024

DOI : https://doi.org/10.1007/s40747-024-01454-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Comparative analysis
• Deep learning model
• Math word problem solving
• Find a journal
• Publish with us
• Track your research

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 24, 2024   •   25:18 Whales Have an Alphabet
• May 23, 2024   •   34:24 I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders
• May 22, 2024   •   23:20 Biden’s Open War on Hidden Fees
• May 21, 2024   •   24:14 The Crypto Comeback
• May 20, 2024   •   31:51 Was the 401(k) a Mistake?
• May 19, 2024   •   33:23 The Sunday Read: ‘Why Did This Guy Put a Song About Me on Spotify?’
• May 17, 2024   •   51:10 The Campus Protesters Explain Themselves
• May 16, 2024   •   30:47 The Make-or-Break Testimony of Michael Cohen
• May 15, 2024   •   27:03 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand

I.C.C. Prosecutor Requests Warrants for Israeli and Hamas Leaders

The move sets up a possible showdown between the international court and israel with its biggest ally, the united states..

Hosted by Sabrina Tavernise

Featuring Patrick Kingsley

Produced by Will Reid ,  Diana Nguyen and Shannon M. Lin

Edited by Liz O. Baylen and Michael Benoist

Original music by Elisheba Ittoop

Engineered by Chris Wood

Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube

This week, Karim Khan, the top prosecutor of the International Criminal Court, requested arrest warrants for Israel’s prime minister, Benjamin Netanyahu, and the country’s defense minister, Yoav Gallant.

Patrick Kingsley, the Times’s bureau chief in Jerusalem, explains why this may set up a possible showdown between the court and Israel with its biggest ally, the United States.

On today’s episode

Patrick Kingsley , the Jerusalem bureau chief for The New York Times.

Background reading

Why did a prosecutor go public with the arrest warrant requests ?

The warrant request appeared to shore up domestic support for Mr. Netanyahu.

There are a lot of ways to listen to The Daily. Here’s how.

We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.

The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Dan Farrell, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.

Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Renan Borelli, Maddy Masiello, Isabella Anderson and Nina Lassam.

Patrick Kingsley is The Times’s Jerusalem bureau chief, leading coverage of Israel, Gaza and the West Bank. More about Patrick Kingsley

Advertisement

A .gov website belongs to an official government organization in the United States.

A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• What Associates Do
• Associates' Stories
• Promotion & Recruitment Tools
• Applying to Host an Associate

About The Public Health Associate Program

• The Public Health Associate Program (PHAP) trains early-career professionals who have a recent college degree and are interested in public health and service.
• PHAP has over 100 associates fulfilling hands-on public health workforce needs at any given time in nearly all 50 states, U.S. territories, and the District of Columbia.

Opportunities & Updates

Associate application.

The 2024 associate application period is closed. The next application period will open in early 2025.

Host Site Application

The 2024 host site application period is closed. Check back in early 2025 for the next opportunity.

PHAP is a competitive, two-year, paid training program with the Centers for Disease Control and Prevention (CDC). Associates are assigned to state, tribal, local, and territorial public health agencies and nongovernmental organizations. They work alongside other professionals across a variety of public health settings.

Associates gain hands-on experience that serves as a foundation for their public health careers. After graduating from PHAP, associates are qualified to convert non-competitively to full-time positions at CDC and the U.S. Department of Health and Human Services. Graduates also qualify to apply for positions with public health agencies and non-governmental organizations.

PHAP was established in 2007 to support CDC at the forefront of public health and train field-tested, experienced, and dedicated public health advisors. Since its inception, over 1,800 associates have participated in the program. PHAP:

• Supports associates' attainment of required performance standards while on the job.
• Increases host site capacity.
• Provides associates with the knowledge, skills, and abilities to fulfill program competencies .

Host sites orient associates to their respective agencies/organizations and train them in a wide range of public health competencies. This training fulfills standard program requirements while enhancing the associates' work performance.

PHAP offers a variety of work assignments to give associates experience to develop as public health professionals. Associates are assigned to one subject area that is selected by their host sites. These subject areas focus on the nation's most pressing public health priorities.

Associates' work assignments provide skill-building activities in:

• Analytics and Assessment
• Policy and Law
• Funding and Budgeting
• Emergency Preparedness and Response
• Community Dimensions
• Program Planning, Management, and Improvement
• Professionalism
• Communication
• Health Equity
• Public Health Infrastructure Center

Public Health Associate Program (PHAP)

The Public Health Associate Program (PHAP) is a competitive, two-year, paid training program with the Centers for Disease Control and Prevention.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Word Problems
• Time (1/2 hr)

Download & Print Only $5.30

Time word problems (1/2 hour intervals)

Elapsed time, nearest half hour.

These grade 2 word problems worksheets cover time and elapsed time.  Students are asked what time it will be or what time it was, or how many hours have elapsed between two events. Times are in half hour increments.

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More word problem worksheets

Explore all of our math word problem worksheets , from kindergarten through grade 5.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?