difference between 1 tailed and 2 tailed hypothesis

• Key Differences

Know the Differences & Comparisons

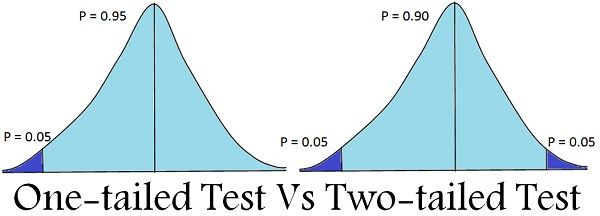
Difference Between One-tailed and Two-tailed Test

To test the hypothesis, test statistics is required, which follows a known distribution. In a test, there are two divisions of probability density curve, i.e. region of acceptance and region of rejection. the region of rejection is called as a critical region .

In the field of research and experiments, it pays to know the difference between one-tailed and two-tailed test, as they are quite commonly used in the process.

Content: One-tailed Test Vs Two-tailed Test

Comparison chart, definition of one-tailed test.

One-tailed test alludes to the significance test in which the region of rejection appears on one end of the sampling distribution. It represents that the estimated test parameter is greater or less than the critical value. When the sample tested falls in the region of rejection, i.e. either left or right side, as the case may be, it leads to the acceptance of alternative hypothesis rather than the null hypothesis. It is primarily applied in chi-square distribution; that ascertains the goodness of fit.

In this statistical hypothesis test, all the critical region, related to α , is placed in any one of the two tails. One-tailed test can be:

• Left-tailed test : When the population parameter is believed to be lower than the assumed one, the hypothesis test carried out is the left-tailed test.
• Right-tailed test : When the population parameter is supposed to be greater than the assumed one, the statistical test conducted is a right-tailed test.

Definition of Two-tailed Test

The two-tailed test is described as a hypothesis test, in which the region of rejection or say the critical area is on both the ends of the normal distribution. It determines whether the sample tested falls within or outside a certain range of values. Therefore, an alternative hypothesis is accepted in place of the null hypothesis, if the calculated value falls in either of the two tails of the probability distribution.

In this test, α is bifurcated into two equal parts, placing half on each side, i.e. it considers the possibility of both positive and negative effects. It is performed to see, whether the estimated parameter is either above or below the assumed parameter, so the extreme values, work as evidence against the null hypothesis.

Key Differences Between One-tailed and Two-tailed Test

The fundamental differences between one-tailed and two-tailed test, is explained below in points:

• One-tailed test, as the name suggest is the statistical hypothesis test, in which the alternative hypothesis has a single end. On the other hand, two-tailed test implies the hypothesis test; wherein the alternative hypothesis has dual ends.
• In the one-tailed test, the alternative hypothesis is represented directionally. Conversely, the two-tailed test is a non-directional hypothesis test.
• In a one-tailed test, the region of rejection is either on the left or right of the sampling distribution. On the contrary, the region of rejection is on both the sides of the sampling distribution.
• A one-tailed test is used to ascertain if there is any relationship between variables in a single direction, i.e. left or right. As against this, the two-tailed test is used to identify whether or not there is any relationship between variables in either direction.
• In a one-tailed test, the test parameter calculated is more or less than the critical value. Unlike, two-tailed test, the result obtained is within or outside critical value.
• When an alternative hypothesis has ‘≠’ sign, then a two-tailed test is performed. In contrast, when an alternative hypothesis has ‘> or <‘ sign, then one-tailed test is carried out.

To sum up, we can say that the basic difference between one-tailed and two-tailed test lies in the direction, i.e. in case the research hypothesis entails the direction of interrelation or difference, then one-tailed test is applied, but if the research hypothesis does not signify the direction of interaction or difference, we use two-tailed test.

You Might Also Like:

Swati Aggarwal says

April 24, 2018 at 11:47 am

Very Informative and specifically summarised. thank you.

Aurobindo says

January 20, 2019 at 8:22 am

Amazing Surbhi. I recently started following this site and I really find it very very useful. The simplicity of language, the key distinctions, range of depth covered in giving the differences. Hats off to you for your effort. Very amazing. I have definitely bookmarked this website as ‘my favorite’ and I shall keep visiting it again and again. Keep it up. Thanks.

Marian Truehill says

July 23, 2020 at 11:48 pm

This website is very useful and easy to understand for Statistics methods and concepts.

Kuje Samson says

January 11, 2023 at 5:13 am

The website is very linear to a layman statistics. I really enjoyed visiting the site

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.4: One- and Two-Tailed Tests

• Last updated
• Save as PDF
• Page ID 2148

• Rice University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Define Type I and Type II errors
• Interpret significant and non-significant differences
• Explain why the null hypothesis should not be accepted when the effect is not significant

In the James Bond case study, Mr. Bond was given \(16\) trials on which he judged whether a martini had been shaken or stirred. He was correct on \(13\) of the trials. From the binomial distribution, we know that the probability of being correct \(13\) or more times out of \(16\) if one is only guessing is \(0.0106\). Figure \(\PageIndex{1}\) shows a graph of the binomial distribution. The red bars show the values greater than or equal to \(13\). As you can see in the figure, the probabilities are calculated for the upper tail of the distribution. A probability calculated in only one tail of the distribution is called a "one-tailed probability."

Binomial Calculator

A slightly different question can be asked of the data: "What is the probability of getting a result as extreme or more extreme than the one observed?" Since the chance expectation is \(8/16\), a result of \(3/16\) is equally as extreme as \(13/16\). Thus, to calculate this probability, we would consider both tails of the distribution. Since the binomial distribution is symmetric when \(\pi =0.5\), this probability is exactly double the probability of \(0.0106\) computed previously. Therefore, \(p = 0.0212\). A probability calculated in both tails of a distribution is called a "two-tailed probability" (see Figure \(\PageIndex{2}\)).

Should the one-tailed or the two-tailed probability be used to assess Mr. Bond's performance? That depends on the way the question is posed. If we are asking whether Mr. Bond can tell the difference between shaken or stirred martinis, then we would conclude he could if he performed either much better than chance or much worse than chance. If he performed much worse than chance, we would conclude that he can tell the difference, but he does not know which is which. Therefore, since we are going to reject the null hypothesis if Mr. Bond does either very well or very poorly, we will use a two-tailed probability.

On the other hand, if our question is whether Mr. Bond is better than chance at determining whether a martini is shaken or stirred, we would use a one-tailed probability. What would the one-tailed probability be if Mr. Bond were correct on only \(3\) of the \(16\) trials? Since the one-tailed probability is the probability of the right-hand tail, it would be the probability of getting \(3\) or more correct out of \(16\). This is a very high probability and the null hypothesis would not be rejected.

The null hypothesis for the two-tailed test is \(\pi =0.5\). By contrast, the null hypothesis for the one-tailed test is \(\pi \leq 0.5\). Accordingly, we reject the two-tailed hypothesis if the sample proportion deviates greatly from \(0.5\) in either direction. The one-tailed hypothesis is rejected only if the sample proportion is much greater than \(0.5\). The alternative hypothesis in the two-tailed test is \(\pi \neq 0.5\). In the one-tailed test it is \(\pi > 0.5\).

You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data. Statistical tests that compute one-tailed probabilities are called one-tailed tests; those that compute two-tailed probabilities are called two-tailed tests. Two-tailed tests are much more common than one-tailed tests in scientific research because an outcome signifying that something other than chance is operating is usually worth noting. One-tailed tests are appropriate when it is not important to distinguish between no effect and an effect in the unexpected direction. For example, consider an experiment designed to test the efficacy of a treatment for the common cold. The researcher would only be interested in whether the treatment was better than a placebo control. It would not be worth distinguishing between the case in which the treatment was worse than a placebo and the case in which it was the same because in both cases the drug would be worthless.

Some have argued that a one-tailed test is justified whenever the researcher predicts the direction of an effect. The problem with this argument is that if the effect comes out strongly in the non-predicted direction, the researcher is not justified in concluding that the effect is not zero. Since this is unrealistic, one-tailed tests are usually viewed skeptically if justified on this basis alone.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 12.

• Hypothesis testing and p-values

One-tailed and two-tailed tests

• Z-statistics vs. T-statistics
• Small sample hypothesis test
• Large sample proportion hypothesis testing

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• The Open University
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

4 One-tailed vs two-tailed test

To gain a deeper understanding of how to conduct a hypothesis test, this section will delve into the concepts of one-tailed and two-tailed tests. These tests are vital tools in statistical hypothesis testing, and the decision of which test to employ depends on the research question and hypothesis under examination. It is crucial to give careful thought to the suitable type of test to ensure that the hypothesis is thoroughly tested and precise conclusions are derived from the data. This section will elaborate on this topic in greater detail.

To commence, complete the following activity pertaining to the formulation of null and alternative hypotheses. This exercise may be somewhat challenging, but it serves as an excellent introduction to upcoming discussions – don’t be concerned if you find it difficult!

Activity 3 Hypotheses setting

Read the following statements and then develop a null hypothesis and an alternative hypothesis.

‘It is believed that OU students need to set aside no longer than, on average, 15 hours to study an entire session of an OU course. However, a researcher believes that OU students spend longer studying an entire session of an OU course.’

H 0 : OU students spend, on average, no more than 15 hours studying an entire session of OU course.

H a : OU students spend, on average, more than 15 hours studying an entire session of OU course.

They can also be written as:

H 0 : µ ≤ 15 hours studies

H a : µ > 15 hours studies

µ is a symbol for a population mean. Remember, H 0 and H a are always opposites.

Did you identify any differences between the hypotheses you developed in Activity 1 and Activity 3? The set of hypotheses in Activity 1 has an equal (=) or not equal (≠) supposition (sign) in the statement. However, in Activity 3, the set of hypotheses has less than or equal to (≤) and greater than (>) supposition (sign) in the statement. This creates different conditions that lead to acceptance or rejection of the null hypothesis.

One-tailed and Two-tailed Tests

by Karen Grace-Martin   30 Comments

I was recently asked about when to use one and two tailed tests.

The long answer is:  Use one tailed tests when you have a specific hypothesis about the direction of your relationship.  Some examples include you hypothesize that one group mean is larger than the other; you hypothesize that the correlation is positive; you hypothesize that the proportion is below .5.

The short answer is: Never use one tailed tests.

1. Only a few statistical tests even can have one tail: z tests and t tests.  So you’re severely limited.  F tests, Chi-square tests , etc. can’t accommodate one-tailed tests because their distributions are not symmetric.  Most statistical methods, such as regression and ANOVA , are based on these tests, so you will rarely have the chance to implement them.

2. Probably because they are rare, reviewers balk at one-tailed tests.  They tend to assume that you are trying to artificially boost the power of your test.  Theoretically, however, there is nothing wrong with them when the hypothesis and the statistical test are right for them.

Reader Interactions

June 10, 2022 at 5:48 am

Dear Karen,

I am running a regression analysis, I wonder if the significance in table output for ANOVA is inherently one-tailed or two-tailed? I have a directional hypothesis, so I am wondering if I still have to divide the significance value? Thank you in advance!

June 15, 2022 at 11:08 am

It’s two-tailed. And the F tests cannot be made directional.

October 9, 2019 at 7:46 pm

Say for example I am testing a hypothesis at .05 and it is a one tailed test. I expect the treatment to have a decrease and the cut off for significance is t = -1.67 so this is a left tail test. If t value after I run the test is +2.24 is this non significant since it is not in the hypothesized direction (negative)?

August 30, 2019 at 2:13 am

does a one-tailed test always require a one-sided (directional) hypothesis, and does a two-tailed test always require a two-sided (nondirectional) hypothesis?

Asked in the other direction: Does a one-sided (directional) hypothesis always require a one-sided test, and does a two-sided (nondirectional) hypothesis always require a two-sided test?

Thanks for clarifying Claudia

September 3, 2019 at 10:11 am

Hi Claudia,

Good question. So technically, when I am talking about one-tailed test, I do mean a test of a directional hypothesis. Likewise, I mean a non-directional hypothesis when I say two-tailed test.

In z-tests and t-tests, which are symmetric distributions, these terms are indeed interchangeable. But it definitely gets more complicated once you start talking about Chi-square tests and F-tests. Both of these have 0 at the left end and all high values of the statistic in one tail. So you can’t distinguish directions for these kinds of test statistics. So you can only test nondirectional hypotheses.

May 1, 2019 at 2:30 am

I have seen textbooks reporting confidence intervals of a standard deviation using low and high values of the chi-square statistic. Is it not based on a two-sided test?

August 28, 2018 at 7:14 am

There is no need to have a specific directional hypothesis (although you would usually have one), all that is needed to justify is to have a directional claim. Most claims in published scientific research and applied research are directional, since the moment you say the difference is positive or negative you have a directional claim. The only way to avoid it is to not mention the observed difference, or to state the difference as “plus or minus X” which would be ridiculous in most contexts.

Also, you should not mistake the tailed-ness of a statistical distribution with the tailed-ness of a hypothesis. While the Chi-Square or F-distribution might only have one tail, they can still be used for inference of one-sided and two-sided hypothesis alike. One can go as far back as Fisher and find examples of that (Statistical Methods for Research Workers).

If you are interested in more detailed arguments for the use of one-sided tests see the series of articles on The One-Sided Project website at https://www.onesided.org/ .

March 2, 2018 at 1:07 am

Hello, Good Morning to all, I am working on a project of Behavior Based Safety thesis work in which I have to assess data by SPSS software. Can any one could help me because i haven’t any idea about this software

May 17, 2018 at 10:06 am

Hi Muhammad, We have a number of free resources on SPSS, but if you’re in the middle of a project we have an on-demand tutorial that will get you not just started, but able to use it: http://theanalysisinstitute.com/introspss/

August 24, 2016 at 12:08 pm

Thank you for the discussions about the power for one-sided test. I agree that we should be careful when we decide to use a one-sided test. For Chi-square test when comparing two proportions, we can use two approaches: normal-theory method (the z-test) and contingency-table approach (the Chi-square test). For the normal-theory test, it requires a large sample size with n>5 or n*proportion >10. If your proposed study satisfied this requirement, we can use normal-theory method which is z-test to compute the power for the one-sided test. If you are interested in how to compute the one-sided test power, you can refer to the textbook by Marcello Pagano and Kimberlee Gauvreau’s 2nd edition titled “Principles of Biostatistics” section 14.5 on page 330 regarding sample size estimation for one-sided hypothesis test for proportions. Thanks.

September 1, 2015 at 2:30 am

Chi-squared tests are ALWAYS one-tailed… You only reject the null hypothesis when the test statistic falls into the right tail of the chi-square distribution.

What chi-squared tests are generally NOT is “directional”. They generally do not test whether the observed values are greater than or smaller than expected, only that they differ significantly.

January 26, 2016 at 10:57 pm

If “Chi-squared tests are ALWAYS one-tailed…”, why is Karen saying in her above statement that “F tests, Chi-square tests, etc. can’t accommodate one-tailed tests”?

Sorry, but I am bit confused. Can you help?

January 27, 2016 at 11:30 am

Hi Dippies,

Perhaps better wording is “F tests, Chi-square tests, etc. can’t accommodate directional tests.” Because there is only one tail for these distributions in which to find significance, it can’t distinguish between non-directional tests (eg, H1: mu1 – mu2 not equal to 0) and directional tests (eg, H1: mu1-mu2 greater than 0). In a t-test or z-test, we can either split alpha between two tails for a non-directional test or put alpha all into one tail for a directional test. We can then see whether we’re in the right tail based on the sign of the test statistic. F’s and Chi-sq values are squared. So they’re always positive. You get the same F value regardless of the direction of the means.

October 19, 2017 at 10:29 am

Thanks for the explanation… I am wondering: what happens if I have two methods, m1 and m2, and I want to show that m1 performs better (e.g. gives a higher value) than m2? Should I still use a two-tailed test? How can I show that m1 is, in fact, better (and not just different) than m2 (assuming the test proves significant)? Thanks for any comments.

July 22, 2015 at 6:14 pm

My hypothesis says there is a positive relation between religiosity and altruistic behavior. Would a two-tailed approach using Pearson Correlation do the trick?

Some very helpful information available here! Thank you.

July 1, 2015 at 2:50 am

Hi Karen, I run paired sample t-test and it just has P-two tailed. So how to convert P-two tailed to t critical one tailed. I have t critical two tailed and df already. Thanks so much

March 20, 2015 at 2:41 pm

I have used a one-tailed test but the effect went into the opposite direction. How do I have to calculate my p-Value now. Thanks for your reply, Mirco

February 3, 2015 at 10:24 pm

F-tests are almost always one-tailed. You would convert a two-tailed test’s p-value into a one-tailed test’s p-value by *halving* the p-value, not multiplying by 2 (as recommended above).

February 6, 2015 at 5:05 pm

Thanks, Paul. Yes. I fixed the half.

While it’s true that F-tests are one-tailed, they’re not testing directional hypotheses, the way a one-tailed t or z test does.

October 29, 2014 at 11:15 pm

I trying to complete the results of my study and need to know how to convert my 1-tailed results to 2-tailed? The company that ran my stats used a 1-tailed instead of 2-tailed, which as I understand is what I should have used to show directionality. Nicole

November 3, 2014 at 4:41 pm

Hi Nicole, just double them.

September 26, 2014 at 8:13 am

Very interesting. I am reading a much celebrated book (The weakness of Civil Society in Post-Communist Europe, by Marc Howard, 2003) in polticial science at the moment containing regression analysis with one tailed coeficients. This, togheter with that they only have a N of 23 (with 5 independent variables), raise my eyebrows. The results are also quite controversial….

What would you off-hand say about that?

September 26, 2014 at 12:27 pm

Without knowing anything else, the one tailed tests of coefficients wouldn’t worry me too much except for the fact you said it’s controversial. Which means perhaps the opposite result is reasonable.

The N of 23 is more of a concern. That’s pretty small. I find results like this are not bad per se. It’s fine to consider as one possible piece of information–they are great for spurring more research. But you can’t make any conclusions based on them.

June 14, 2013 at 9:54 pm

Jst wanna thank you for your post ; it will save me on my exam tomorrow (y)

& in my course it is not always divided by 2 (p-value). It depends on the value of your t (,= 0) & if your H1:’value” is > or 0, Hasard ?

Even if i’m wrong, I want to thank you again !

January 2, 2013 at 8:16 am

how can we calculate p-value of one-tailed from two-tailed hypothesis in spss?

January 2, 2013 at 10:50 am

All you have to do is divide it by 2.

December 1, 2012 at 11:04 am

i found this issue more important please continue in such way. kind regards, nurilign.

August 27, 2010 at 12:59 pm

Thank you so much for your reply and offer to try a find a source regarding the limited utility of one-tailed tests when doing ANOVAs and regressions, as well as the advice for converting two-tailed tests to one-tailed tests.

The only problem I have is that the Pearson Correlation Coefficient output from my stats consultant does not contain the p value. In order to calculate the p value for a two-tailed test, I thought it might be possible to take the df (n-2 for two-tailed tests) and look up the significance level in the table of critical values of the correlation coefficient. Once I get those values, I would simply divide by 2 to get the one-tailed level of significance. Do you think that is a statistically sound procedure.

Thank you again for your assistance, Sue

August 25, 2010 at 11:29 am

I am currently working on my dissertation and one of my committee members suggested that I should have used a one-tailed test as I have a directional hypothesis, but I think that a two-tailed test is just as appropriate based on several of the reasons listed on the blog.

I was particularly intrigued by the statement that “F tests, chi-square tests, etc. can’t accommodate one-tailed tests because their distributions are not symmetric.” This would make a fine argument for not re-rerunning my data and was wondering if there is a reference or citation for that point. I have not been able to find that point in any of the stats texts that I own. Any help would be greatly appreciated!

August 26, 2010 at 7:23 pm

Hi Sue, Hmmm. I would think that texts that talk about the F-test would mention that it's not symmetric. You could certainly use any text that states that t-squared=F. But I'll see if I can find something that says it directly. But in any case, you don't have to rerun anything, even if you weren't using F tests. To get a one-sided p-value, just halve the two-sided p-value you have. Karen

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Privacy Overview

One-Tailed vs Two-Tailed Tests; What You Should Know

Understanding the different methods of hypothesis testing is crucial for accurate data interpretation. Among these methods, one-tailed and two-tailed tests stand out due to their specific applications and implications. 

This article discusses one-tailed vs two-tailed tests, their examples, scenarios where each test is applicable, and the pros and cons associated with one-tailed and two-tailed tests.

What is a One-Tailed Test?

One-tailed tests are used when a hypothesis predicts a specific direction of effect. They are ideal for scenarios where the interest lies in determining whether a parameter is significantly greater or less than a specific value.

This type of test evaluates whether the observed data deviates significantly from the null hypothesis (the hypothesis of no effect or no difference) but only in the specified direction.

In the context of  A/B testing , a one-tailed test is used to determine if there is a significant difference in a specific direction between two webpage versions, products, or strategies.

For example, if you conduct an A/B test to see if a new website design leads to higher user engagement compared to the current design, a one-tailed test would be used to assess if the new design increases engagement specifically, ignoring the possibility of a decrease.

This focused approach makes one-tailed tests suitable for scenarios where you expect a directional and clearly defined outcome.

Example of a One-Tailed Test in A/B Testing:

Suppose an e-commerce company wants to  increase its website’s conversion rate . The CRO team they hired hypothesizes that changing the color of the “Add to Cart” button from blue to red will lead to more clicks and, consequently, more purchases. To test this hypothesis, they set up an A/B test:

Version A (Control):   The original webpage with the blue “Add to Cart” button.

Version B (Variant):   The same webpage but with the red “Add to Cart” button.

The hypothesis predicts the red button will increase conversions. The null hypothesis (H0) states there will be no increase, or possibly a decrease, in conversions with the red button.

A one-tailed test checks for increased conversions with the red button. If the test shows statistical significance, it supports the hypothesis that the red button performs better. If not, there’s insufficient evidence to reject the null hypothesis, meaning the increase isn’t statistically significant.

Pros of one-tailed tests

Increased power.

One-tailed tests have more statistical power compared to two-tailed tests when testing the same hypothesis. They focus all statistical power in one direction of the distribution (the direction of interest), making it more likely to detect an effect in that direction.

Lower Sample Size Requirement

Due to its increased power, a one-tailed test often requires a smaller  sample size  to achieve the same level of statistical significance as a two-tailed test. This is a significant advantage in practical scenarios where collecting large samples can be time-consuming or expensive.

Specific Hypothesis Testing

One-tailed tests are tailored for specific, directional hypotheses. This means they are ideal when the hypothesis makes a specific prediction about the direction of the effect. For example, if a hypothesis states that a new marketing strategy will increase sales, a one-tailed test is appropriate because it specifically looks for an increase in sales.

Cons of one-tailed tests

Risk of missing opposite effect.

One of the main drawbacks of a one-tailed test is the risk of missing a significant effect in the opposite direction of the hypothesis. Since the test is designed to detect an effect in one specific direction, it may overlook meaningful changes that occur in the other direction.

Choosing a one-tailed test, especially after data collection, poses a risk of bias. Decisions should be based on strong theoretical grounds or prior evidence, not on a desire to achieve significant results.

Limited Insight

One-tailed tests provide less comprehensive insight compared to two-tailed tests. By focusing only on one direction, they may miss out on understanding the full spectrum of the effect being studied.

What is a Two-Tailed Test?

A two-tailed test is a statistical method used when the direction of the effect is not specified in the hypothesis; unlike a one-tailed test that looks for a significant effect in one specific direction, a two-tailed test checks for significance in both directions. 

This type of test is useful when you are interested in detecting any significant difference, regardless of whether it is positive or negative.

A/B testing uses a two-tailed test to determine whether a statistically significant difference exists between two versions (A and B) without a predetermined direction of the expected outcome.

This approach is crucial when the goal is to ascertain any significant change, whether an increase or a decrease, in a key metric due to variations in the test.

For instance, a two-tailed test is appropriate if you test two different website layouts to see which one performs better in terms of user engagement without a specific hypothesis about which layout will be superior.

Example of a Two-Tailed Test in A/B Testing:

The same ecommerce company wants to evaluate the impact of a new product description format on its website. The company is unsure whether the new format will increase or decrease customer engagement, so they conducted an A/B test again.

Version A (Control) :  The original product page with the standard description format.

Version B (Variant):   The same product page but with the new description format.

The hypothesis is: “The new format will significantly impact engagement,” without specifying the direction of this impact.

A two-tailed test is chosen to detect any significant change in engagement, whether an increase or decrease. It assesses if the new format leads to a statistically significant difference in engagement compared to the control.

If the test shows significance, it confirms the new format notably affects engagement, but further analysis is required to determine if the effect is positive or negative.

Pros of two-tailed tests

Detects effects in both directions.

The primary advantage of a two-tailed test is its ability to detect statistically significant effects in both directions. This means it can identify whether the tested variable has a positive or negative impact compared to the control.

More Conservative

A two-tailed test is considered more conservative than a one-tailed test because it divides the significance level across both ends of the distribution. This means that for a result to be considered statistically significant, it must meet a stricter criterion compared to a one-tailed test.

Cons of two-tailed tests

Reduced power.

One of the main drawbacks of a two-tailed test is its reduced statistical power compared to a one-tailed test. The power of a statistical test is its ability to detect an effect when there is one. In a two-tailed test, because the significance level is split between both tails of the distribution, it requires a stronger effect to reach  statistical significance .

Larger Sample Size Needed

Due to its reduced power, a two-tailed test often requires a larger sample size to achieve the same level of statistical significance as a one-tailed test. This can be a significant challenge in research scenarios where gathering a large amount of data is difficult, time-consuming, or expensive.

Overly General

In A/B testing, a two-tailed test can be overly general when there’s already a strong theory predicting the direction of an effect. It checks for changes in both directions, which may not be necessary if you only expect an increase or decrease.

One-Tailed vs Two-Tailed Tests: Which Should You Choose?

When deciding between a one-tailed and a two-tailed test in A/B testing, the choice hinges on your hypothesis and what you aim to discover or prove. Both tests have their place, but their applicability depends on the specific context of your research question.

Understanding the differences between these tests, their applications, and their implications is vital for accurate data interpretation and effective decision-making in various testing scenarios.

Related Posts

20 A/B Testing Mistakes To Avoid in 2024

Web Design Best Practices for Improved Conversions

• Session Recordings
• Knowledge Base

Type above and press Enter to search. Press Esc to cancel.

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Intersections & Unions
• Compound Events
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Predictive Analytics This link opens in a new window
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

One-Tail vs Two-Tail Tests

Two-tailed Test

When testing a hypothesis, you must determine if it is a one-tailed or a two-tailed test. The most common format is a two-tailed test, meaning the critical region is located in both tails of the distribution. This is also referred to as a non-directional hypothesis.

This type of test is associated with a "neutral" alternative hypothesis. Here are some examples:

• There is a difference between the scores.
• The groups are not equal .
• There is a relationship between the variables.

One-tailed Test

The alternative option is a one-tailed test. As the name implies, the critical region lies in only one tail of the distribution. This is also called a directional  hypothesis. The image below shows a right-tailed test. A left-tailed test would be another type of one-tailed test.

This type of test is associated with a more specific alternative claim. Here are some examples:

• One group is higher than the other.
• There is a decrease in performance.
• Group A performs worse than Group B.
• << Previous: Null & Alternative Hypotheses
• Next: Alpha & Beta >>
• Last Updated: Apr 19, 2024 3:09 PM
• URL: https://resources.nu.edu/statsresources

• Statistics with Python
• Data Analysis Tutorial
• Python – Data visualization tutorial
• Machine Learning Projects
• Machine Learning Interview Questions
• Machine Learning Mathematics
• Deep Learning Tutorial
• Deep Learning Project
• Deep Learning Interview Questions
• Computer Vision Tutorial
• Computer Vision Projects
• NLP Project
• NLP Interview Questions
• 100 Days of Machine Learning

Difference Between One-Tailed and Two-Tailed Tests

• Differences Between two-sample, t-test and paired t-test
• Difference Between Test E And Test C
• Difference between End-to-end Testing and Unit Testing
• Difference between JUnit and TestNG
• Difference between End-to-end Testing and Sandwich Testing
• Difference between Unit Testing and System Testing
• Difference between Volume Testing and Load Testing
• Difference between Adhoc Testing and Monkey Testing
• Difference between Tester and SDET
• Difference between Monkey Testing and Gorilla Testing
• Difference between Waterfall Testing and V-Model Testing
• Differences between Interface and Integration Testing
• Difference Between Single and Double Quotes
• Difference between Frontend Testing and Backend Testing
• Difference between GUI Testing and Usability Testing
• Difference Between Dominant and Recessive Traits
• Difference between System Testing and End-to-end Testing
• Difference between Unit Testing and Sandwich Testing
• Difference Between Pandas Head, Tail And Sample

One and Two-Tailed Tests are ways to identify the relationship between the statistical variables. For checking the relationship between variables in a single direction (Left or Right direction), we use a one-tailed test. A two-tailed test is used to check whether the relations between variables are in any direction or not.

One-Tailed Test

A one-tailed test is based on a uni-directional hypothesis where the area of rejection is on only one side of the sampling distribution. It determines whether a particular population parameter is larger or smaller than the predefined parameter. It uses one single critical value to test the data.

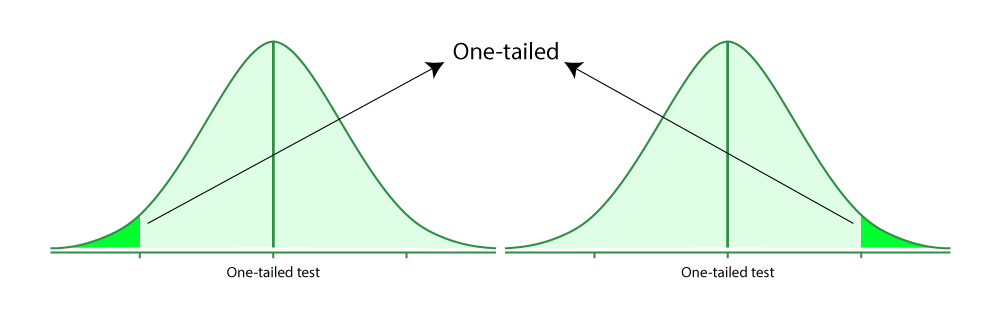
Alternative Hypothesis ( H 1​):

Test Statistic: Depending on the type of test and the distribution, the test statistic is computed ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in the critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of participants of students in coding competition on their fear level.

• H0: There is no important effect of students in coding competition on their fear level. 

The main intention is to check the decreased fear level when students participate in a coding competition.

Two-Tailed Test

A two-tailed test is also called a nondirectional hypothesis. For checking whether the sample is greater or less than a range of values, we use the two-tailed. It is used for null hypothesis testing.

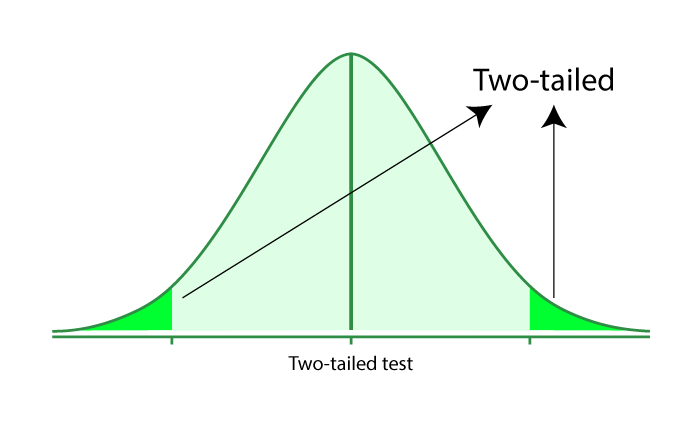
Test Statistic: Compute the test statistic as appropriate for the distribution ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in either tail of the distribution’s critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of new bill pass on the loan of farmers. 

• H0: There is no significant effect of the new bill passed on loans of farmers.

New bill passes can affect in both ways either increase or decrease the loan of farmers.

Difference Between One and Two-Tailed Test:

Please Login to comment...

Similar reads.

• ML-Statistics
• Difference Between

Improve your Coding Skills with Practice

What kind of Experience do you want to share?