introduction to geometry essay

The Importance of Geometry in Our Daily Life Essay

Introduction, importance of geometry in our life, importance of geometry in student’s life, examples of geometry in real life, visual learning of geometry.

This essay deals with the importance of geometry in our daily life. An essay includes many points to highlight the importance of geometry. It also specifies why students need to study geometry and the benefits for students in life. This essay also includes real examples of geometry in our life.

In everyday life, people are always surrounded by different spaces and different belongings, which are of different shapes. Our universe itself is consists of different planets and stars. All these have got different shapes and symbols. “To be able to understand the wonder of the world’s shape and appreciate it, we need to be able to understand and have knowledge of spatial use. In other words, the areas related to space and the position, size and shape of things in it” (10 shocking reasons why geometry is important in your life, n.d., para.2).

When one gets the idea regarding the relationship between different shapes and sizes, they can be better prepared to use those in daily lives. Here comes the importance of geometry. Geometry assists in having accurate measurements and relationships of different shapes. Geometry will increase one’s spatial understanding. It is often that people think of basic shapes and sizes always, “many people think well visually” (Shape and space in geometry, 2010, para.8). To visualize something, it is very significant that it requires an understanding of geometry. Only with the help of geometry, one can think of any kind of shape in mind before making it real.

In the workplace also use of geometry is very important. Knowledge regarding geometry is very important in order to outshine in the work. The use of geometry gives exercise for the left and right sides of the brain. The left brain is more advanced in using technical and logical activities; at the same time, the right brain is very good at visualizing. Since geometry needs both, it provides very good brain exercise. In other words, geometry uses full use of the brain. Every man-made wonders that have been created in this world are with the help of geometry. It is with the help of geometry one is able to give life for his imaginative thinking. If geometry is not used, then everything will be in one’s dream. All sorts of two and three-dimensional shapes that we see or come across are instigating in geometry. So, geometry is considered to be an unavoidable and very important part of human life.

“Geometry, the study of space and spatial relationships, is an important and essential branch of the mathematics curriculum at all grade levels. The ability to apply geometric concepts is a life skill used in many occupations” (Geometry, n.d., para.1). Geometry is “an excellent training ground for” (Finkbeiner, 1995, p.54) all the students who need to make use of tangible experiments. Doing these types of the experiment will enrich their knowledge in the subjects. Many types of the mathematical experiment can be easily understandable by the use of geometry. Not only that with the help of geometry it is very easy for the students to gain their knowledge in different types of the experiment they are doing. By studying geometry, students can apply it to their real life. When students learn geometry, it always “enhance logical reasoning” (Jordan, n.d., para.3) and the thinking capability of the student. Developing logical reasoning and deductive thinking surely increases one’s mental and mathematical ability. Development of these is very important in students as this will help in their career to achieve more and more. Not only in their career but in life also this studying of geometry will improve their thinking capacity. Understanding geometry will help students to take decisions properly and it will help them to find out solutions for problems they are facing in their life. It is “certain that geometry students adequately develop their knowledge and skills for solving” any kind of problem. (Dindyal, n.d., p.189).

Thousands of examples can be shown for the use of geometry in our life. The use of geometry is inevitable in construction works. Before the beginning of the construction, architects draw the plan of the building using geometrical figures. The use of geometry in this field is not a new trend. It has been in use since the historic period itself. “If you go back to Roman historical sites you will see such examples like the great coliseum. A great example can be seen is the famous Egyptian pyramid. Some other famous structures are Eiffel Tower which is in Italy, Chrysler in New York. If you look around your neighborhood house, you will see these shapes” (How geometry is used in construction, 2010, para.2). Geometric principles are used by architects to ensure the safety of their constructions. In most of the legendary constructions of olden and new times, we can find smart use of basic geometrical principles. The new finding in these principles reflects the developments that have taken place in the building construction field.

Geometric rules are used in the medical field for the reconstruction of our inner and outer organs. Using the geometrical principle, human movement is analyzed for applying to the fields like Robotics. In constructing and controlling the movements of robots, it is very necessary to study human nature based on certain principles. We can relate different objects in the real world using geometry. In the computerized reconstruction of the real world, these principles are used. So, the principles of geometry play a big role. It is also used in graphic designing, video game creation, etc.

Geometry has a relevant role in astronomy also. In the systematic study of space and bodies in outer space, geometric principles are used. “According to the Escher Math website, geometry allows astronomers to plan observations and reconstruct bodies in outer space such as asteroids. If gazing at the stars is something you enjoy, consider pairing your love of the night sky with your skills in geometry to become an astronomer” (Hickman, 2010, para.6).

Many studies are going on to explore the mysteries of the universe. In all the studies in this direction, geometry has an important role. Studies have proven that it is possible that secret of the nature can be found by studying the links among geometric archetypes of different objects in nature. “In nature, we find patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances” (Rawles, 2009, para.1).

From the basic principles, geometry and its applications have developed a lot. Now, it has a vast area of application. To teach ideas of geometry, advanced study tools are necessary. It is almost impossible to learn 2D and 3D concepts of geometry without proper demonstrations. “The highlights, interlaced with interactive demonstrations, are intuitively developed. By learning to recognize patterns and powerful knowledge discovery process evolved” (Inselberg, n.d., para.1).

In order to learn different patterns, influential knowledge is required. It requires the help of geometrical concept. For example, recognition of M-dimensional objects form (M-1) requires lots to understand. For representing points in the plane, it is necessary that one should have knowledge regarding indices. This requires influential geometrical algorithm. That is, in order to make these algorithms application, knowledge is prerequisite. “Applications of parallel coordinates include collision avoidance and conflict resolution algorithms for air traffic control (3 USA patents), computer vision (USA patent), data mining (USA patent) for data exploration and automatic classification, optimization, decision support and process control” (Inselberg, n.d., para.3).

Geometry has got important role in life of the people, especially students. Geometry is considered to be important part of real life. Since “world is built of shape and space, and geometry is its mathematics” (Shape and space in geometry, 2010, para.5). Geometry is very helpful for the students in order to solve many problems. With the help of geometry, many students are presently solving many problems. This helps them to understand more. Finally, many people in the world are very well in thinking visually. In order to achieve this, geometry is considered to be doorway to achieve all the results. Students who are developing strong concept or intellect in the language of geometry can always excel in advanced topics related to mathematics. Thus, geometry is very important.

10 shocking reasons why geometry is important in your life . (n.d.). Math Worksheet Center. 2010. Web.

Dindyal, J. (n.d.). Algebraic thinking in geometry at high school level: Students’ use of variables an unknowns . Google docs. 2010. Web.

Finkbeiner, D.T. (1995). Recent publications. Mathematical Association of America , p.54. Web.

Geometry . (n.d.). Much More Math. 2010. Web.

Hickman, S. (2010). What types of jobs use geometry ? eHow. Web.

How geometry is used in construction . (2010). Peerpapers.com. Web.

Inselberg, A. (n.d.). Parallel coordinates: Visual multidimensional geometry and its applications . 2010. Web.

Jordan, M. (n.d.). Why homework is important ? Much More Math. 2010. Web.

Rawles, B.A. (2009). The geometry code: Symbolic wisdom of natural laws within us . Elysian Publishing. Web.

Shape and space in geometry . (2010). Annenberg Media. Web.

• Chicago (A-D)
• Chicago (N-B)

IvyPanda. (2021, December 8). The Importance of Geometry in Our Daily Life. https://ivypanda.com/essays/the-importance-of-geometry-in-our-daily-life/

"The Importance of Geometry in Our Daily Life." IvyPanda , 8 Dec. 2021, ivypanda.com/essays/the-importance-of-geometry-in-our-daily-life/.

IvyPanda . (2021) 'The Importance of Geometry in Our Daily Life'. 8 December.

IvyPanda . 2021. "The Importance of Geometry in Our Daily Life." December 8, 2021. https://ivypanda.com/essays/the-importance-of-geometry-in-our-daily-life/.

1. IvyPanda . "The Importance of Geometry in Our Daily Life." December 8, 2021. https://ivypanda.com/essays/the-importance-of-geometry-in-our-daily-life/.

Bibliography

IvyPanda . "The Importance of Geometry in Our Daily Life." December 8, 2021. https://ivypanda.com/essays/the-importance-of-geometry-in-our-daily-life/.

• Encoding Object Affordances and Geometrical Features
• Significance and Agency of Geometry
• Technology in Classrooms: Learning and Teaching Geometry
• Geometry, Space, Manipulative, and Technology
• Concept of Learning Geometry in School
• History and Geometric Pattern of Muqarnas
• Geometry in High School: Issues and Solutions
• Geometry of Islamic Art and Application on Architecture
• Earth Measurement and Origin of Geometry
• Modernity' Influences on Islamic Architecture and Geometry
• Math Difficulties: Equal Educational Opportunities
• Exponential and Logarithmic Functions
• Pythagorean Theorem: History, Formula, and Proof
• Women Mathematicians: Maria Agnesi, Sophie Germain
• Mathematical Patterns and Nature. Number Systems

• Even more »

Account Options

• Try the new Google Books
• Advanced Book Search
• Psychology Press
• Barnes&Noble.com
• Books-A-Million
• All sellers  »

Selected pages

Other editions - View all

Common terms and phrases, references to this book, about the author  (1996), bibliographic information.

• Search Menu
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Urban Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Archaeology
• Greek and Roman Papyrology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Agriculture
• History of Education
• History of Emotions
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Variation
• Language Families
• Language Evolution
• Language Reference
• Lexicography
• Linguistic Theories
• Linguistic Typology
• Linguistic Anthropology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Modernism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Culture
• Music and Media
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Lifestyle, Home, and Garden
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Oncology
• Medical Toxicology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Medical Ethics
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Neuroscience
• Cognitive Psychology
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business History
• Business Ethics
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic Methodology
• Economic History
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Theory
• Political Behaviour
• Political Economy
• Political Institutions
• Politics and Law
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Developmental and Physical Disabilities Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

Geometry: A Very Short Introduction

Author webpage

• Cite Icon Cite
• Permissions Icon Permissions

Geometry: A Very Short Introduction discusses the fundaments of Euclidean and non-Euclidean geometries. This topic includes curved spaces, projective geometry in Renaissance art, and the geometry of spacetime inside a black hole. The study of geometry is at least 2,500 years old, and within it is the concept of mathematical proof or deductive reasoning from a set of axioms. Geometry remained a very active area of research in mathematics, with links to science and art. The subject of geometry includes examples of mathematical objects, such as Platonic solids, or theorems like the Pythagorean theorem, as well as general principles.

Signed in as

Institutional accounts.

• Google Scholar Indexing
• GoogleCrawler [DO NOT DELETE]

Personal account

• Sign in with email/username & password
• Get email alerts
• Save searches
• Purchase content
• Activate your purchase/trial code

Institutional access

• Sign in with a library card Sign in with username/password Recommend to your librarian
• Institutional account management
• Get help with access

Access to content on Oxford Academic is often provided through institutional subscriptions and purchases. If you are a member of an institution with an active account, you may be able to access content in one of the following ways:

IP based access

Typically, access is provided across an institutional network to a range of IP addresses. This authentication occurs automatically, and it is not possible to sign out of an IP authenticated account.

Sign in through your institution

Choose this option to get remote access when outside your institution. Shibboleth/Open Athens technology is used to provide single sign-on between your institution’s website and Oxford Academic.

• Click Sign in through your institution.
• Select your institution from the list provided, which will take you to your institution's website to sign in.
• When on the institution site, please use the credentials provided by your institution. Do not use an Oxford Academic personal account.
• Following successful sign in, you will be returned to Oxford Academic.

If your institution is not listed or you cannot sign in to your institution’s website, please contact your librarian or administrator.

Sign in with a library card

Enter your library card number to sign in. If you cannot sign in, please contact your librarian.

Society Members

Society member access to a journal is achieved in one of the following ways:

Sign in through society site

Many societies offer single sign-on between the society website and Oxford Academic. If you see ‘Sign in through society site’ in the sign in pane within a journal:

• Click Sign in through society site.
• When on the society site, please use the credentials provided by that society. Do not use an Oxford Academic personal account.

If you do not have a society account or have forgotten your username or password, please contact your society.

Sign in using a personal account

Some societies use Oxford Academic personal accounts to provide access to their members. See below.

A personal account can be used to get email alerts, save searches, purchase content, and activate subscriptions.

Some societies use Oxford Academic personal accounts to provide access to their members.

Viewing your signed in accounts

Click the account icon in the top right to:

• View your signed in personal account and access account management features.
• View the institutional accounts that are providing access.

Signed in but can't access content

Oxford Academic is home to a wide variety of products. The institutional subscription may not cover the content that you are trying to access. If you believe you should have access to that content, please contact your librarian.

For librarians and administrators, your personal account also provides access to institutional account management. Here you will find options to view and activate subscriptions, manage institutional settings and access options, access usage statistics, and more.

Our books are available by subscription or purchase to libraries and institutions.

External resource

• In the OUP print catalogue
• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Rights and permissions
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Finite Geometries

• Last updated
• Save as PDF
• Page ID 89842

• Mark A. Fitch
• University of Alaska Anchorage

Definition: Intersect

Two lines intersect if and only if they share a point.

Definition: Parallel

Two lines are parallel if and only if they do not intersect.

Definition: Four Point Geometry

The four point geometry is defined by the following axioms and definitions.

• There exist exactly four points.
• Any two distinct points have exactly one line on both of them.
• Each line is on exactly two points.

Explore the four point geometry as follows.

• Draw and label four points.
• Use axiom 2 to draw as many lines as possible.
• How many lines exist in this geometry?
• Find a pair of parallel lines.
• Can you find three lines that are pairwise parallel?
• Can you find a point that is on three lines?

Introduction to Coordinate Geometry

Recall that a plane is a flat surface that goes on forever in both directions. If we were to place a point on the plane, coordinate geometry gives us a way to describe exactly where it is by using two numbers.

What are coordinates?

To introduce the idea, consider the grid above. The columns of the grid are lettered A,B,C etc. The rows are numbered 1,2,3 etc from the top. We can see that the X is in box D3; that is, column D, row 3.

D and 3 are called the coordinates of the box. It has two parts: the row and the column. There are many boxes in each row and many boxes in each column. But by having both we can find one single box, where the row and column intersect.

--> The Coordinate Plane

In coordinate geometry, points are placed on the "coordinate plane" as shown below. It has two scales - one running across the plane called the "x axis " and another a right angles to it called the y axis . (These can be thought of as similar to the column and row in the paragraph above.) The point where the axes cross is called the origin and is where both x and y are zero.

On the x-axis, values to the right are positive and those to the left are negative. On the y-axis, values above the origin are positive and those below are negative.

A point's location on the plane is given by two numbers,the first tells where it is on the x-axis and the second which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates". Note that the order is important; the x coordinate is always the first one of the pair.

For a more in-depth explanation of the coordinate plane see The Coordinate Plane . For more on the coordinates of a point see Coordinates of a Point

Things you can do in Coordinate Geometry

• Determine the distance between them
• Find the midpoint, slope and equation of a line segment
• Determine if lines are parallel or perpendicular
• Find the area and perimeter of a polygon defined by the points
• Transform a shape by moving, rotating and reflecting it.
• Define the equations of curves, circles and ellipses.

Other Coordinate Geometry topics

• Introduction to coordinate geometry
• The coordinate plane
• The origin of the plane
• Axis definition
• Coordinates of a point
• Distance between two points
• Introduction to Lines in Coordinate Geometry
• Line (Coordinate Geometry)
• Ray (Coordinate Geometry)
• Segment (Coordinate Geometry)
• Midpoint Theorem
• Distance from a point to a line
• - When line is horizontal or vertical
• - Using two line equations
• - Using trigonometry
• - Using a formula
• Intersecting lines
• Cirumscribed rectangle (bounding box)
• Area of a triangle (formula method)
• Area of a triangle (box method)
• Centroid of a triangle
• Incenter of a triangle
• Area of a polygon
• Algorithm to find the area of a polygon
• Area of a polygon (calculator)
• Definition and properties, diagonals
• Area and perimeter
• Definition and properties, altitude, median
• Parallelogram
• Definition and properties, altitude, diagonals
• Print blank graph paper

• Math Article
• Coordinate Geometry

Co-ordinate Geometry

Coordinate Geometry is considered to be one of the most interesting concepts of mathematics. Coordinate Geometry (or the analytic geometry ) describes the link between geometry and algebra through graphs involving curves and lines. It provides geometric aspects in Algebra and enables them to solve geometric problems. It is a part of geometry where the position of points on the plane is described using an ordered pair of numbers. Here, the concepts of coordinate geometry (also known as Cartesian geometry) are explained along with its formulas and their derivations.

Introduction to Coordinate Geometry

Coordinate geometry (or analytic geometry) is defined as the study of geometry using the coordinate points. Using coordinate geometry, it is possible to find the distance between two points, dividing lines in m:n ratio, finding the mid-point of a line, calculating the area of a triangle in the Cartesian plane, etc. There are certain terms in Cartesian geometry that should be properly understood. These terms include:

What is a Co-ordinate and a Co-ordinate Plane?

You must be familiar with plotting graphs on a plane, from the tables of numbers for both linear and non-linear equations. The number line which is also known as a Cartesian plane is divided into four quadrants by two axes perpendicular to each other, labelled as the x-axis ( horizontal line ) and the y-axis( vertical line ).

The four quadrants along with their respective values are represented in the graph below-

• Quadrant 1 : (+x, +y)
• Quadrant 2 : (-x, +y)
• Quadrant 3 : (-x, -y)
• Quadrant 4 : (+x, -y)

The point at which the axes intersect is known as the origin . The location of any point on a plane is expressed by a pair of values (x, y) and these pairs are known as the coordinates .

The figure below shows the Cartesian plane with coordinates (4,2). If the coordinates are identified, the distance between the two points and the interval’s midpoint that is connecting the points can be computed.

Coordinate Geometry Fig. 1: Cartesian Plane

Equation of a Line in Cartesian Plane

Equation of a line can be represented in many ways, few of which is given below-

(i) General Form

The general form of a line is given as Ax + By + C = 0.

(ii) Slope intercept Form 

Let x, y be the coordinate of a point through which a line passes, m be the slope of a line, and c be the y-intercept, then the equation of a line is given by:

(iii) Intercept Form of a Line

Consider a and b be the x-intercept and y-intercept respectively, of a line, then the equation of a line is represented as-

Slope of a Line: 

Consider the general form of a line Ax + By + C = 0, the slope can be found by converting this form to the slope-intercept form.

Ax + By + C = 0

⇒ By = − Ax – C

Comparing the above equation with y = mx + c,

Thus, we can directly find the slope of a line from the general equation of a line.

Coordinate Geometry Formulas and Theorems

Distance formula: to calculate distance between two points.

Let the two points be A and B, having coordinates to be (x 1 , y 1 ) and (x 2 , y 2 ), respectively.

Thus, the distance between two points is given as-

Coordinate Geometry Fig. 2: Distance Formula

Midpoint Theorem: To Find Mid-point of a Line Connecting Two Points

Consider the same points A and B, which have coordinates (x 1 , y 1 ) and (x 2 , y 2 ), respectively. Let M(x,y) be the midpoint of lying on the line connecting these two points A and B. The coordinates of point M is given as-

Angle Formula: To Find The Angle Between Two Lines

Consider two lines A and B, having their slopes m 1 and m 2, respectively.

Let “θ” be the angle between these two lines, then the angle between them can be represented as-

Special Cases:

• Case 1:  When the two lines are parallel to each other,

m 1 = m 2 = m

Substituting the value in the equation above,

• Case 2:  When the two lines are perpendicular to each other,

m 1 . m 2 = -1

Substituting the value in the original equation,

\(\begin{array}{l}\large \tan \theta = \frac{m_{1} – m_{2}}{1 + (-1)} = \frac{m_{1} – m_{2}}{0}\end{array} \) which is undefined.

Section Formula: To Find a Point Which Divides a Line into m:n Ratio

Consider a line A and B having coordinates (x 1 , y 1 ) and (x 2 , y 2 ), respectively. Let P be a point that which divides the line in the ratio m:n, then the coordinates of the coordinates of the point P is given as-

• When the ratio m:n is internal:
• When the ratio m:n is external:

Students can follow the link provided to learn more about the section formula  along its proof and solved examples.

Area of a Triangle in Cartesian Plane

The area of a triangle In coordinate geometry whose vertices are (x 1 , y 1 ), (x 2 , y 2 ) and (x 3 , y 3 ) is

If the area of a triangle whose vertices are (x 1 , y 1 ),(x 2 , y 2 ) and (x 3 , y 3 ) is zero, then the three points are collinear.

• Important:  Click here to Download  Co-ordinate Geometry pdf

Examples Based On Coordinate Geometry Concepts

Examples 1: Find the distance between points M (4,5) and N (-3,8).

Applying the distance formula we have,

Example 2: Find the equation of a line parallel to 3x+4y = 5 and passing through points (1,1).

For a line parallel to the given line, the slope will be of the same magnitude.

Thus the equation of a line will be represented as 3x+4y=k

Substituting the given points in this new equation, we have

k = 3 × 1 + 4 × 1 = 3 + 4 = 7

Therefore the equation is 3x + 4y = 7

Coordinate Geometry Questions For Practice

• Calculate the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
• Find the area of the triangle having vertices at A, B, and C which are at points (2, 3), (–1, 0), and (2, – 4), respectively. Also, mention the type of triangle.
• A point A is equidistant from B(3, 8) and C(-10, x). Find the value for x and the distance BC.

Video Lesson on Coordinate Geometry Toughest Problems

Continue Learning

Frequently asked questions, what is abscissa and ordinates in coordinate geometry.

The abscissa and ordinate is used to represent the position of a point on a graph. The horizontal value or the X axis value is the abscissa while the vertical value i.e. the Y axis value is the ordinate. For example, in an ordered pair (2, 3), 2 is abscissa and 3 is ordinate.

What is a Cartesian Plane?

A Cartesian plane is a plane which is formed by two perpendicular lines known as the x-axis (horizontal axis) and the y-axis (vertical axis). The exact position of a point in Cartesian plane can be determined using the ordered pair (x, y).

Why do we Need Coordinate Geometry?

Coordinate geometry has various applications in real life. Some of the areas where coordinate geometry is an integral part include.

• In digital devices like computers, mobile phones, etc. to locate the position of cursor or finger.
• In aviation to determine the position and location of airplanes accurately.
• In maps and in navigation (GPS).
• To map geographical locations using latitudes and longitudes.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Very good tuition

Awesome!!! You are blowing my mind.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Login Get started

Geometry: An Introduction to Triangles

• SchoolTutoring Academy
• September 28, 2012
• No Comments

A triangle is a closed curve which is formed by 3 line segments. The line segments by which the triangle is formed are called sides of the triangle. The points of intersections of the sides of the triangle are called the vertices of the triangle. The angles formed at the vertices are called the angles of the triangle.

So, in a triangle, there are 3 sides, 3 vertices and 3 angles.

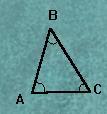
Here, we will name this triangle as ΔABC where,

Sides : AB, BC, CA

Vertices:   A, B, C

Angles: ∠BAC, ∠ABC , ∠BCA.

Parts of the triangle:

There is some terminology associated with the triangles.

Base : Its is the bottom side of the triangle.

Base angles : Two angles which touch the base.

Vertex of the triangle : The angle which is opposite to the base

Legs : The two sides which are not bases.

Types of triangles:

The triangles are classified based on sides and angles.

Based on sides, the triangles are classified as follows.

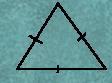
a)      Equilateral triangle:

A triangle in which all three sides (angles) are equal.

b)      Isosceles triangle:

A triangle in which any two sides (angles) are equal.

c)      Scalene triangle:

A triangle in which no two sides (angles) are equal.

Based on the angles the triangles are classified as follows.

a)      Acute angled triangle:

Any triangle in which all the angles are less than 90 0 .

b)      Obtuse angled triangle:

Any triangle with one of the angles greater than 90 0 .

c)      Right angled triangle:

A triangle in which one of the angles is equal to 90 0 .

Do you also need help with your Study Skills? Take a look at our Study Skills tutoring services.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Prince-Edward-Island visit: Tutoring in Prince-Edward-Island.

Geometry: Relations of Lines

Geometry: congruent triangles.

Perceptrons : An Introduction to Computational Geometry

Marvin Minsky (1927–2016) was Toshiba Professor of Media Arts and Sciences and Donner Professor of Electrical Engineering and Computer Science at MIT. He was a cofounder of the MIT Media Lab and a consultant for the One Laptop Per Child project.

The late Seymour A. Papert was a Professor in MIT's AI Lab (1960–1980s) and MIT's Media Lab (1985–2000) and the author of Mindstorms: Children, Computers, and Powerful Ideas .

The first systematic study of parallelism in computation by two pioneers in the field.

Reissue of the 1988 Expanded Edition with a new foreword by Léon Bottou

In 1969, ten years after the discovery of the perceptron—which showed that a machine could be taught to perform certain tasks using examples—Marvin Minsky and Seymour Papert published Perceptrons, their analysis of the computational capabilities of perceptrons for specific tasks. As Léon Bottou writes in his foreword to this edition, “Their rigorous work and brilliant technique does not make the perceptron look very good.” Perhaps as a result, research turned away from the perceptron. Then the pendulum swung back, and machine learning became the fastest-growing field in computer science. Minsky and Papert's insistence on its theoretical foundations is newly relevant.

Perceptrons —the first systematic study of parallelism in computation—marked a historic turn in artificial intelligence, returning to the idea that intelligence might emerge from the activity of networks of neuron-like entities. Minsky and Papert provided mathematical analysis that showed the limitations of a class of computing machines that could be considered as models of the brain. Minsky and Papert added a new chapter in 1987 in which they discuss the state of parallel computers, and note a central theoretical challenge: reaching a deeper understanding of how “objects” or “agents” with individuality can emerge in a network. Progress in this area would link connectionism with what the authors have called “society theories of mind.”

• Permissions
• Cite Icon Cite

Perceptrons : An Introduction to Computational Geometry By: Marvin Minsky, Seymour A. Papert https://doi.org/10.7551/mitpress/11301.001.0001 ISBN (electronic): 9780262343930 Publisher: The MIT Press Published: 2017

Download citation file:

• Ris (Zotero)
• Reference Manager

Table of Contents

• [ Front Matter ] Doi: https://doi.org/10.7551/mitpress/11301.003.0023 Open the PDF Link PDF for [ Front Matter ] in another window
• Foreword By Léon Bottou Léon Bottou Search for other works by this author on: This Site Google Scholar Doi: https://doi.org/10.7551/mitpress/11301.003.0001 Open the PDF Link PDF for Foreword in another window
• Prologue: A View from 1988 Doi: https://doi.org/10.7551/mitpress/11301.003.0002 Open the PDF Link PDF for Prologue: A View from 1988 in another window
• Introduction Doi: https://doi.org/10.7551/mitpress/11301.003.0003 Open the PDF Link PDF for Introduction in another window
• [ Opening ] Doi: https://doi.org/10.7551/mitpress/11301.003.0024 Open the PDF Link PDF for [ Opening ] in another window
• 1: Theory of Linear Boolean Inequalities Doi: https://doi.org/10.7551/mitpress/11301.003.0005 Open the PDF Link PDF for 1: Theory of Linear Boolean Inequalities in another window
• 2: Group Invariance of Boolean Inequalities Doi: https://doi.org/10.7551/mitpress/11301.003.0006 Open the PDF Link PDF for 2: Group Invariance of Boolean Inequalities in another window
• 3: Parity and One-in-a-box Predicates Doi: https://doi.org/10.7551/mitpress/11301.003.0007 Open the PDF Link PDF for 3: Parity and One-in-a-box Predicates in another window
• 4: The "And/Or" Theorem Doi: https://doi.org/10.7551/mitpress/11301.003.0008 Open the PDF Link PDF for 4: The "And/Or" Theorem in another window
• [ Opening ] Doi: https://doi.org/10.7551/mitpress/11301.003.0025 Open the PDF Link PDF for [ Opening ] in another window
• 5: 𝜓CONNECTED: A Geometric Property with Unbounded Order Doi: https://doi.org/10.7551/mitpress/11301.003.0010 Open the PDF Link PDF for 5: 𝜓CONNECTED: A Geometric Property with Unbounded Order in another window
• 6: Geometric Patterns of Small Order: Spectra and Context Doi: https://doi.org/10.7551/mitpress/11301.003.0011 Open the PDF Link PDF for 6: Geometric Patterns of Small Order: Spectra and Context in another window
• 7: Stratification and Normalization Doi: https://doi.org/10.7551/mitpress/11301.003.0012 Open the PDF Link PDF for 7: Stratification and Normalization in another window
• 8: The Diameter-Limited Perceptron Doi: https://doi.org/10.7551/mitpress/11301.003.0013 Open the PDF Link PDF for 8: The Diameter-Limited Perceptron in another window
• 9: Geometric Predicates and Serial Algorithms Doi: https://doi.org/10.7551/mitpress/11301.003.0014 Open the PDF Link PDF for 9: Geometric Predicates and Serial Algorithms in another window
• [ Opening ] Doi: https://doi.org/10.7551/mitpress/11301.003.0026 Open the PDF Link PDF for [ Opening ] in another window
• 10: Magnitude of the Coefficients Doi: https://doi.org/10.7551/mitpress/11301.003.0016 Open the PDF Link PDF for 10: Magnitude of the Coefficients in another window
• 11: Learning Doi: https://doi.org/10.7551/mitpress/11301.003.0017 Open the PDF Link PDF for 11: Learning in another window
• 12: Linear Separation and Learning Doi: https://doi.org/10.7551/mitpress/11301.003.0018 Open the PDF Link PDF for 12: Linear Separation and Learning in another window
• 13: Perceptrons and Pattern Recognition Doi: https://doi.org/10.7551/mitpress/11301.003.0019 Open the PDF Link PDF for 13: Perceptrons and Pattern Recognition in another window
• Epilogue: The New Connectionism Doi: https://doi.org/10.7551/mitpress/11301.003.0020 Open the PDF Link PDF for Epilogue: The New Connectionism in another window
• Bibliographic Notes Doi: https://doi.org/10.7551/mitpress/11301.003.0021 Open the PDF Link PDF for Bibliographic Notes in another window
• Index Doi: https://doi.org/10.7551/mitpress/11301.003.0022 Open the PDF Link PDF for Index in another window
• Open Access

A product of The MIT Press

Mit press direct.

• About MIT Press Direct

Information

• Accessibility
• For Authors
• For Customers
• For Librarians
• Direct to Open
• Media Inquiries
• Rights and Permissions
• For Advertisers
• About the MIT Press
• The MIT Press Reader
• MIT Press Blog
• Seasonal Catalogs
• MIT Press Home
• Give to the MIT Press
• Direct Service Desk
• Terms of Use
• Privacy Statement
• Crossref Member
• COUNTER Member  
• The MIT Press colophon is registered in the U.S. Patent and Trademark Office

This Feature Is Available To Subscribers Only

Sign In or Create an Account

Grade 7 Mathematics Module: Basic Concepts and Terms in Geometry

This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson.

Each SLM is composed of different parts. Each part shall guide you step-by-step as you discover and understand the lesson prepared for you.

Pre-tests are provided to measure your prior knowledge on lessons in each SLM. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. At the end of each module, you need to answer the post-test to self-check your learning. Answer keys are provided for each activity and test. We trust that you will be honest in using these.

Please use this module with care. Do not put unnecessary marks on any part of this SLM. Use a separate sheet of paper in answering the exercises and tests. And read the instructions carefully before performing each task.

This module was designed and written with you in mind. It is here to help you master Basic Concepts and Terms in Geometry. The scope of this module permits it to be used in many different learning situations. The language used recognizes the diverse vocabulary level of students. The lessons are arranged to follow the standard sequence of the course. But the order in which you read them can be changed to correspond with the textbook you are now using.

After going through this module, you are expected to:

• represent point, line and plane using concrete and pictorial models ; and
• illustrate subsets of a line.

Grade 7 Mathematics Quarter 3 Self-Learning Module: Basic Concepts and Terms in Geometry

Can't find what you're looking for.

We are here to help - please use the search box below.

Leave a Comment Cancel reply