problem solving involving inverse matrix

7.7 Solving Systems with Inverses

Learning objectives.

In this section, you will:

• Find the inverse of a matrix.
• Solve a system of linear equations using an inverse matrix.

Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?

There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.

Finding the Inverse of a Matrix

We know that the multiplicative inverse of a real number a a is a −1 , a −1 , and a a −1 = a −1 a = ( 1 a ) a = 1. a a −1 = a −1 a = ( 1 a ) a = 1. For example, 2 −1 = 1 2 2 −1 = 1 2 and ( 1 2 ) 2 = 1. ( 1 2 ) 2 = 1. The multiplicative inverse of a matrix is similar in concept, except that the product of matrix A A and its inverse A −1 A −1 equals the identity matrix . The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by I n I n where n n represents the dimension of the matrix. [link] and the following equations.

The identity matrix acts as a 1 in matrix algebra. For example, A I = I A = A . A I = I A = A .

A matrix that has a multiplicative inverse has the properties

A matrix that has a multiplicative inverse is called an invertible matrix . Only a square matrix may have a multiplicative inverse, as the reversibility, A A −1 = A −1 A = I , A A −1 = A −1 A = I , is a requirement. Not all square matrices have an inverse, but if A A is invertible, then A −1 A −1 is unique. We will look at two methods for finding the inverse of a 2 × 2 2 × 2 matrix and a third method that can be used on both 2 × 2 2 × 2 and 3 × 3 3 × 3 matrices.

The Identity Matrix and Multiplicative Inverse

The identity matrix , I n , I n , is a square matrix containing ones down the main diagonal and zeros everywhere else.

If A A is an n × n n × n matrix and B B is an n × n n × n matrix such that A B = B A = I n , A B = B A = I n , then B = A −1 , B = A −1 , the multiplicative inverse of a matrix A . A .

Showing That the Identity Matrix Acts as a 1

Given matrix A , show that A I = I A = A . A I = I A = A .

Use matrix multiplication to show that the product of A A and the identity is equal to the product of the identity and A.

Given two matrices, show that one is the multiplicative inverse of the other.

• Given matrix A A of order n × n n × n and matrix B B of order n × n n × n multiply A B . A B .
• If A B = I , A B = I , then find the product B A . B A . If B A = I , B A = I , then B = A −1 B = A −1 and A = B −1 . A = B −1 .

Showing That Matrix A Is the Multiplicative Inverse of Matrix B

Show that the given matrices are multiplicative inverses of each other.

Multiply A B A B and B A . B A . If both products equal the identity, then the two matrices are inverses of each other.

A A and B B are inverses of each other.

Show that the following two matrices are inverses of each other.

Finding the Multiplicative Inverse Using Matrix Multiplication

We can now determine whether two matrices are inverses, but how would we find the inverse of a given matrix? Since we know that the product of a matrix and its inverse is the identity matrix, we can find the inverse of a matrix by setting up an equation using matrix multiplication .

Use matrix multiplication to find the inverse of the given matrix.

For this method, we multiply A A by a matrix containing unknown constants and set it equal to the identity.

Find the product of the two matrices on the left side of the equal sign.

Next, set up a system of equations with the entry in row 1, column 1 of the new matrix equal to the first entry of the identity, 1. Set the entry in row 2, column 1 of the new matrix equal to the corresponding entry of the identity, which is 0.

Using row operations, multiply and add as follows: ( −2 ) R 1 + R 2 → R 2 . ( −2 ) R 1 + R 2 → R 2 . Add the equations, and solve for c . c .

Back-substitute to solve for a . a .

Write another system of equations setting the entry in row 1, column 2 of the new matrix equal to the corresponding entry of the identity, 0. Set the entry in row 2, column 2 equal to the corresponding entry of the identity.

Using row operations, multiply and add as follows: ( −2 ) R 1 + R 2 = R 2 . ( −2 ) R 1 + R 2 = R 2 . Add the two equations and solve for d . d .

Once more, back-substitute and solve for b . b .

Finding the Multiplicative Inverse by Augmenting with the Identity

Another way to find the multiplicative inverse is by augmenting with the identity. When matrix A A is transformed into I , I , the augmented matrix I I transforms into A −1 . A −1 .

For example, given

augment A A with the identity

Perform row operations with the goal of turning A A into the identity.

• Switch row 1 and row 2. [ 5 3 2 1 | 0 1 1 0 ] [ 5 3 2 1 | 0 1 1 0 ]
• Multiply row 2 by −2 −2 and add to row 1. [ 1 1 2 1 | −2 1 1 0 ] [ 1 1 2 1 | −2 1 1 0 ]
• Multiply row 1 by −2 −2 and add to row 2. [ 1 1 0 −1 | −2 1 5 −2 ] [ 1 1 0 −1 | −2 1 5 −2 ]
• Add row 2 to row 1. [ 1 0 0 −1 | 3 −1 5 −2 ] [ 1 0 0 −1 | 3 −1 5 −2 ]
• Multiply row 2 by −1. −1. [ 1 0 0 1 | 3 −1 −5 2 ] [ 1 0 0 1 | 3 −1 −5 2 ]

The matrix we have found is A −1 . A −1 .

Finding the Multiplicative Inverse of 2×2 Matrices Using a Formula

When we need to find the multiplicative inverse of a 2 × 2 2 × 2 matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.

If A A is a 2 × 2 2 × 2 matrix, such as

the multiplicative inverse of A A is given by the formula

where a d − b c ≠ 0. a d − b c ≠ 0. If a d − b c = 0 , a d − b c = 0 , then A A has no inverse.

Using the Formula to Find the Multiplicative Inverse of Matrix A

Use the formula to find the multiplicative inverse of

Using the formula, we have

We can check that our formula works by using one of the other methods to calculate the inverse. Let’s augment A A with the identity.

• Multiply row 1 by −2 −2 and add to row 2. [ 1 −2 0 1 | 1 0 −2 1 ] [ 1 −2 0 1 | 1 0 −2 1 ]
• Multiply row 1 by 2 and add to row 1. [ 1 0 0 1 | −3 2 −2 1 ] [ 1 0 0 1 | −3 2 −2 1 ]

So, we have verified our original solution.

Use the formula to find the inverse of matrix A . A . Verify your answer by augmenting with the identity matrix.

Finding the Inverse of the Matrix, If It Exists

Find the inverse, if it exists, of the given matrix.

We will use the method of augmenting with the identity.

• Switch row 1 and row 2. [ 1 3 3 2 | 0 1 1 0 ] [ 1 3 3 2 | 0 1 1 0 ]
• Multiply row 1 by −3 and add it to row 2. [ 1 2 0 0 | 1 0 −3 1 ] [ 1 2 0 0 | 1 0 −3 1 ]
• There is nothing further we can do. The zeros in row 2 indicate that this matrix has no inverse.

Finding the Multiplicative Inverse of 3×3 Matrices

Unfortunately, we do not have a formula similar to the one for a 2 × 2 2 × 2 matrix to find the inverse of a 3 × 3 3 × 3 matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.

Given a 3 × 3 3 × 3 matrix

augment A A with the identity matrix

To begin, we write the augmented matrix with the identity on the right and A A on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.

Given a 3 × 3 3 × 3 matrix, find the inverse

• Write the original matrix augmented with the identity matrix on the right.
• Use elementary row operations so that the identity appears on the left.
• What is obtained on the right is the inverse of the original matrix.
• Use matrix multiplication to show that A A −1 = I A A −1 = I and A −1 A = I . A −1 A = I .

Finding the Inverse of a 3 × 3 Matrix

Given the 3 × 3 3 × 3 matrix A , A , find the inverse.

Augment A A with the identity matrix, and then begin row operations until the identity matrix replaces A . A . The matrix on the right will be the inverse of A . A .

To prove that B = A −1 , B = A −1 , let’s multiply the two matrices together to see if the product equals the identity, if A A −1 = I A A −1 = I and A −1 A = I . A −1 A = I .

Find the inverse of the 3 × 3 3 × 3 matrix.

Solving a System of Linear Equations Using the Inverse of a Matrix

Solving a system of linear equations using the inverse of a matrix requires the definition of two new matrices: X X is the matrix representing the variables of the system, and B B is the matrix representing the constants. Using matrix multiplication , we may define a system of equations with the same number of equations as variables as

To solve a system of linear equations using an inverse matrix , let A A be the coefficient matrix , let X X be the variable matrix, and let B B be the constant matrix. Thus, we want to solve a system A X = B . A X = B . For example, look at the following system of equations.

From this system, the coefficient matrix is

The variable matrix is

And the constant matrix is

Then A X = B A X = B looks like

Recall the discussion earlier in this section regarding multiplying a real number by its inverse, ( 2 −1 ) 2 = ( 1 2 ) 2 = 1. ( 2 −1 ) 2 = ( 1 2 ) 2 = 1. To solve a single linear equation a x = b a x = b for x , x , we would simply multiply both sides of the equation by the multiplicative inverse (reciprocal) of a . a . Thus,

The only difference between a solving a linear equation and a system of equations written in matrix form is that finding the inverse of a matrix is more complicated, and matrix multiplication is a longer process. However, the goal is the same—to isolate the variable.

We will investigate this idea in detail, but it is helpful to begin with a 2 × 2 2 × 2 system and then move on to a 3 × 3 3 × 3 system.

Solving a System of Equations Using the Inverse of a Matrix

Given a system of equations, write the coefficient matrix A , A , the variable matrix X , X , and the constant matrix B . B . Then

Multiply both sides by the inverse of A A to obtain the solution.

If the coefficient matrix does not have an inverse, does that mean the system has no solution?

No, if the coefficient matrix is not invertible, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions.

Solving a 2 × 2 System Using the Inverse of a Matrix

Solve the given system of equations using the inverse of a matrix.

Write the system in terms of a coefficient matrix, a variable matrix, and a constant matrix.

First, we need to calculate A −1 . A −1 . Using the formula to calculate the inverse of a 2 by 2 matrix, we have:

Now we are ready to solve. Multiply both sides of the equation by A −1 . A −1 .

The solution is ( −1 , 1 ) . ( −1 , 1 ) .

Can we solve for X X by finding the product B A −1 ? B A −1 ?

No, recall that matrix multiplication is not commutative, so A −1 B ≠ B A −1 . A −1 B ≠ B A −1 . Consider our steps for solving the matrix equation.

Notice in the first step we multiplied both sides of the equation by A −1 , A −1 , but the A −1 A −1 was to the left of A A on the left side and to the left of B B on the right side. Because matrix multiplication is not commutative, order matters.

Solving a 3 × 3 System Using the Inverse of a Matrix

Solve the following system using the inverse of a matrix.

Write the equation A X = B . A X = B .

First, we will find the inverse of A A by augmenting with the identity.

Multiply row 1 by 1 5 . 1 5 .

Multiply row 1 by 4 and add to row 2.

Add row 1 to row 3.

Multiply row 2 by −3 and add to row 1.

Multiply row 3 by 5.

Multiply row 3 by 1 5 1 5 and add to row 1.

Multiply row 3 by − 19 5 − 19 5 and add to row 2.

Multiply both sides of the equation by A −1 . A −1 . We want A −1 A X = A −1 B : A −1 A X = A −1 B :

The solution is ( 1 , 2 , 0 ) . ( 1 , 2 , 0 ) .

Solve the system using the inverse of the coefficient matrix.

Given a system of equations, solve with matrix inverses using a calculator.

• Save the coefficient matrix and the constant matrix as matrix variables [ A ] [ A ] and [ B ] . [ B ] .
• Enter the multiplication into the calculator, calling up each matrix variable as needed.
• If the coefficient matrix is invertible, the calculator will present the solution matrix; if the coefficient matrix is not invertible, the calculator will present an error message.

Using a Calculator to Solve a System of Equations with Matrix Inverses

Solve the system of equations with matrix inverses using a calculator

On the matrix page of the calculator, enter the coefficient matrix as the matrix variable [ A ] , [ A ] , and enter the constant matrix as the matrix variable [ B ] . [ B ] .

On the home screen of the calculator, type in the multiplication to solve for X , X , calling up each matrix variable as needed.

Evaluate the expression.

Access these online resources for additional instruction and practice with solving systems with inverses.

• The Identity Matrix
• Determining Inverse Matrices
• Using a Matrix Equation to Solve a System of Equations

7.7 Section Exercises

In a previous section, we showed that matrix multiplication is not commutative, that is, A B ≠ B A A B ≠ B A in most cases. Can you explain why matrix multiplication is commutative for matrix inverses, that is, A −1 A = A A −1 ? A −1 A = A A −1 ?

Does every 2 × 2 2 × 2 matrix have an inverse? Explain why or why not. Explain what condition is necessary for an inverse to exist.

Can you explain whether a 2 × 2 2 × 2 matrix with an entire row of zeros can have an inverse?

Can a matrix with an entire column of zeros have an inverse? Explain why or why not.

Can a matrix with zeros on the diagonal have an inverse? If so, find an example. If not, prove why not. For simplicity, assume a 2 × 2 2 × 2 matrix.

In the following exercises, show that matrix A A is the inverse of matrix B . B .

A = [ 1 0 −1 1 ] , B = [ 1 0 1 1 ] A = [ 1 0 −1 1 ] , B = [ 1 0 1 1 ]

A = [ 1 2 3 4 ] , B = [ −2 1 3 2 − 1 2 ] A = [ 1 2 3 4 ] , B = [ −2 1 3 2 − 1 2 ]

A = [ 4 5 7 0 ] , B = [ 0 1 7 1 5 − 4 35 ] A = [ 4 5 7 0 ] , B = [ 0 1 7 1 5 − 4 35 ]

A = [ −2 1 2 3 −1 ] , B = [ −2 −1 −6 −4 ] A = [ −2 1 2 3 −1 ] , B = [ −2 −1 −6 −4 ]

A = [ 1 0 1 0 1 −1 0 1 1 ] , B = 1 2 [ 2 1 −1 0 1 1 0 −1 1 ] A = [ 1 0 1 0 1 −1 0 1 1 ] , B = 1 2 [ 2 1 −1 0 1 1 0 −1 1 ]

A = [ 1 2 3 4 0 2 1 6 9 ] , B = 1 4 [ 6 0 −2 17 −3 −5 −12 2 4 ] A = [ 1 2 3 4 0 2 1 6 9 ] , B = 1 4 [ 6 0 −2 17 −3 −5 −12 2 4 ]

A = [ 3 8 2 1 1 1 5 6 12 ] , B = 1 36 [ −6 84 −6 7 −26 1 −1 −22 5 ] A = [ 3 8 2 1 1 1 5 6 12 ] , B = 1 36 [ −6 84 −6 7 −26 1 −1 −22 5 ]

For the following exercises, find the multiplicative inverse of each matrix, if it exists.

[ 3 −2 1 9 ] [ 3 −2 1 9 ]

[ −2 2 3 1 ] [ −2 2 3 1 ]

[ −3 7 9 2 ] [ −3 7 9 2 ]

[ −4 −3 −5 8 ] [ −4 −3 −5 8 ]

[ 1 1 2 2 ] [ 1 1 2 2 ]

[ 0 1 1 0 ] [ 0 1 1 0 ]

[ 0.5 1.5 1 −0.5 ] [ 0.5 1.5 1 −0.5 ]

[ 1 0 6 −2 1 7 3 0 2 ] [ 1 0 6 −2 1 7 3 0 2 ]

[ 0 1 −3 4 1 0 1 0 5 ] [ 0 1 −3 4 1 0 1 0 5 ]

[ 1 2 −1 −3 4 1 −2 −4 −5 ] [ 1 2 −1 −3 4 1 −2 −4 −5 ]

[ 1 9 −3 2 5 6 4 −2 7 ] [ 1 9 −3 2 5 6 4 −2 7 ]

[ 1 −2 3 −4 8 −12 1 4 2 ] [ 1 −2 3 −4 8 −12 1 4 2 ]

[ 1 2 1 2 1 2 1 3 1 4 1 5 1 6 1 7 1 8 ] [ 1 2 1 2 1 2 1 3 1 4 1 5 1 6 1 7 1 8 ]

[ 1 2 3 4 5 6 7 8 9 ] [ 1 2 3 4 5 6 7 8 9 ]

For the following exercises, solve the system using the inverse of a 2 × 2 2 × 2 matrix.

5 x − 6 y = − 61 4 x + 3 y = − 2 5 x − 6 y = − 61 4 x + 3 y = − 2

8 x + 4 y = −100 3 x −4 y = 1 8 x + 4 y = −100 3 x −4 y = 1

3 x −2 y = 6 − x + 5 y = −2 3 x −2 y = 6 − x + 5 y = −2

5 x −4 y = −5 4 x + y = 2.3 5 x −4 y = −5 4 x + y = 2.3

−3 x −4 y = 9 12 x + 4 y = −6 −3 x −4 y = 9 12 x + 4 y = −6

−2 x + 3 y = 3 10 − x + 5 y = 1 2 −2 x + 3 y = 3 10 − x + 5 y = 1 2

8 5 x − 4 5 y = 2 5 − 8 5 x + 1 5 y = 7 10 8 5 x − 4 5 y = 2 5 − 8 5 x + 1 5 y = 7 10

1 2 x + 1 5 y = − 1 4 1 2 x − 3 5 y = − 9 4 1 2 x + 1 5 y = − 1 4 1 2 x − 3 5 y = − 9 4

For the following exercises, solve a system using the inverse of a 3 × 3 3 × 3 matrix.

3 x −2 y + 5 z = 21 5 x + 4 y = 37 x −2 y −5 z = 5 3 x −2 y + 5 z = 21 5 x + 4 y = 37 x −2 y −5 z = 5

4 x + 4 y + 4 z = 40 2 x − 3 y + 4 z = −12 − x + 3 y + 4 z = 9 4 x + 4 y + 4 z = 40 2 x − 3 y + 4 z = −12 − x + 3 y + 4 z = 9

6 x − 5 y − z = 31 − x + 2 y + z = −6 3 x + 3 y + 2 z = 13 6 x − 5 y − z = 31 − x + 2 y + z = −6 3 x + 3 y + 2 z = 13

6 x −5 y + 2 z = −4 2 x + 5 y − z = 12 2 x + 5 y + z = 12 6 x −5 y + 2 z = −4 2 x + 5 y − z = 12 2 x + 5 y + z = 12

4 x −2 y + 3 z = −12 2 x + 2 y −9 z = 33 6 y −4 z = 1 4 x −2 y + 3 z = −12 2 x + 2 y −9 z = 33 6 y −4 z = 1

1 10 x − 1 5 y + 4 z = −41 2 1 5 x −20 y + 2 5 z = −101 3 10 x + 4 y − 3 10 z = 23 1 10 x − 1 5 y + 4 z = −41 2 1 5 x −20 y + 2 5 z = −101 3 10 x + 4 y − 3 10 z = 23

1 2 x − 1 5 y + 1 5 z = 31 100 − 3 4 x − 1 4 y + 1 2 z = 7 40 − 4 5 x − 1 2 y + 3 2 z = 1 4 1 2 x − 1 5 y + 1 5 z = 31 100 − 3 4 x − 1 4 y + 1 2 z = 7 40 − 4 5 x − 1 2 y + 3 2 z = 1 4

0.1 x + 0.2 y + 0.3 z = −1.4 0.1 x −0.2 y + 0.3 z = 0.6 0.4 y + 0.9 z = −2 0.1 x + 0.2 y + 0.3 z = −1.4 0.1 x −0.2 y + 0.3 z = 0.6 0.4 y + 0.9 z = −2

For the following exercises, use a calculator to solve the system of equations with matrix inverses.

2 x − y = −3 − x + 2 y = 2.3 2 x − y = −3 − x + 2 y = 2.3

− 1 2 x − 3 2 y = − 43 20 5 2 x + 11 5 y = 31 4 − 1 2 x − 3 2 y = − 43 20 5 2 x + 11 5 y = 31 4

12.3 x −2 y −2.5 z = 2 36.9 x + 7 y −7.5 z = −7 8 y −5 z = −10 12.3 x −2 y −2.5 z = 2 36.9 x + 7 y −7.5 z = −7 8 y −5 z = −10

0.5 x −3 y + 6 z = −0.8 0.7 x −2 y = −0.06 0.5 x + 4 y + 5 z = 0 0.5 x −3 y + 6 z = −0.8 0.7 x −2 y = −0.06 0.5 x + 4 y + 5 z = 0

For the following exercises, find the inverse of the given matrix.

[ 1 0 1 0 0 1 0 1 0 1 1 0 0 0 1 1 ] [ 1 0 1 0 0 1 0 1 0 1 1 0 0 0 1 1 ]

[ − 1 0 2 5 0 0 0 2 0 2 − 1 0 1 − 3 0 1 ] [ − 1 0 2 5 0 0 0 2 0 2 − 1 0 1 − 3 0 1 ]

[ 1 − 2 3 0 0 1 0 2 1 4 − 2 3 − 5 0 1 1 ] [ 1 − 2 3 0 0 1 0 2 1 4 − 2 3 − 5 0 1 1 ]

[ 1 2 0 2 3 0 2 1 0 0 0 0 3 0 1 0 2 0 0 1 0 0 1 2 0 ] [ 1 2 0 2 3 0 2 1 0 0 0 0 3 0 1 0 2 0 0 1 0 0 1 2 0 ]

[ 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 1 1 1 1 1 ] [ 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 1 1 1 1 1 ]

Real-World Applications

For the following exercises, write a system of equations that represents the situation. Then, solve the system using the inverse of a matrix.

2,400 tickets were sold for a basketball game. If the prices for floor 1 and floor 2 were different, and the total amount of money brought in is $64,000, how much was the price of each ticket?

In the previous exercise, if you were told there were 400 more tickets sold for floor 2 than floor 1, how much was the price of each ticket?

A food drive collected two different types of canned goods, green beans and kidney beans. The total number of collected cans was 350 and the total weight of all donated food was 348 lb, 12 oz. If the green bean cans weigh 2 oz less than the kidney bean cans, how many of each can was donated?

Students were asked to bring their favorite fruit to class. 95% of the fruits consisted of banana, apple, and oranges. If oranges were twice as popular as bananas, and apples were 5% less popular than bananas, what are the percentages of each individual fruit?

A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at $1 and the chocolate chip cookies at $0.75. They raised $700 and sold 850 items. How many brownies and how many cookies were sold?

A clothing store needs to order new inventory. It has three different types of hats for sale: straw hats, beanies, and cowboy hats. The straw hat is priced at $13.99, the beanie at $7.99, and the cowboy hat at $14.49. If 100 hats were sold this past quarter, $1,119 was taken in by sales, and the amount of beanies sold was 10 more than cowboy hats, how many of each should the clothing store order to replace those already sold?

Anna, Ashley, and Andrea weigh a combined 370 lb. If Andrea weighs 20 lb more than Ashley, and Anna weighs 1.5 times as much as Ashley, how much does each girl weigh?

Three roommates shared a package of 12 ice cream bars, but no one remembers who ate how many. If Tom ate twice as many ice cream bars as Joe, and Albert ate three less than Tom, how many ice cream bars did each roommate eat?

A farmer constructed a chicken coop out of chicken wire, wood, and plywood. The chicken wire cost $2 per square foot, the wood $10 per square foot, and the plywood $5 per square foot. The farmer spent a total of $51, and the total amount of materials used was 14 ft 2 . 14 ft 2 . He used 3 ft 2 3 ft 2 more chicken wire than plywood. How much of each material in did the farmer use?

Jay has lemon, orange, and pomegranate trees in his backyard. An orange weighs 8 oz, a lemon 5 oz, and a pomegranate 11 oz. Jay picked 142 pieces of fruit weighing a total of 70 lb, 10 oz. He picked 15.5 times more oranges than pomegranates. How many of each fruit did Jay pick?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra/pages/7-7-solving-systems-with-inverses

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Inverse Matrix Questions

Inverse matrix questions and solutions are given here to help students learn how to find the inverse of different matrices using different formulas and techniques. As we know, matrices are one of the most scoring concepts for students. Finding the inverse matrix is simple for 2×2 matrices. However, we can easily find the inverse matrix for 3×3 and 4×4 matrices using some simple rules. In this article, you will learn how to find the inverse of a given matrix using a suitable method.

What is an inverse matrix?

Suppose A is a non-singular square matrix of order n×n, and there is a matrix B of the same order, such that AB = BA = I, then B is called the inverse matrix of A, and I is the identity matrix.

Inverse matrix formula for 2×2 matrix

|A| = ad – bc

Therefore, A -1 = adjA/|A|

That means,

Inverse matrix formula for 3×3 or n×n matrix

Step 1: Find the determinant of the given matrix, say A.

Step 2: Find the cofactor matrix C ij = (-1) i+j det (M ij ), where M ij is the (i,j)th minor matrix after removing the ith row and the jth column.

Step 3: Find the transpose of the cofactor matrix to get the adj A.

Step 4: A -1 = adj A/det(A)

Learn more about the inverse matrix here.

Inverse Matrix Questions and Answers

1. Find the inverse of the matrix \(\begin{array}{l}A=\begin{bmatrix}2 & 3 \\1 & 2 \\\end{bmatrix}\end{array} \) .

Let us find the determinant of A.

Here, |A| ≠ 0, so the inverse of A exists.

Now, A -1 = adjA/|A|

2. What is the inverse of the matrix \(\begin{array}{l}A=\begin{bmatrix}1 & 2 \\-3 & 0 \\\end{bmatrix}\end{array} \) ?

Let us calculate the determinant of A.

As we know, A -1 = adjA/|A|

3. If \(\begin{array}{l}A=\begin{bmatrix}cos\ \theta & sin\ \theta \\-sin\ \theta & cos\ \theta \\\end{bmatrix}\end{array} \) and A -1 = A T , find the value of θ.

Also, given that,

⇒ AA -1 = AA T

From the above,

cos 2 θ + sin 2 θ = 1

This is one of the trigonometric identities and is true for all real values of θ.

4. Calculate the inverse of the matrix \(\begin{array}{l}A=\begin{bmatrix}2 & 4 & -6 \\7 & 3 & 5 \\1 & -2 & 4 \\\end{bmatrix}\end{array} \) .

First, find the determinant of matrix A.

= 2(12 + 10) – 4(28 – 5) – 6(-14 – 3)

= 2(22) – 4(23) – 6(-17)

= 44 – 92 + 102

Thus, the inverse matrix exists.

5. If \(\begin{array}{l}A=\begin{bmatrix}2 & 1 \\7 & 2 \\\end{bmatrix}\end{array} \) , show that (A -1 ) -1 = A.

Here, matrix A is non-singular.

Let A -1 = B

= (-⅔)(-⅔) – (⅓)(7/3)

= (4/9) – (7/9)

= (4 – 7)/9

That means B -1 = (A -1 ) -1 = A

6. Find x, y, z if \(\begin{array}{l}A=\begin{bmatrix}0 & 2y & z \\x & y & -z \\x & -y & z \\\end{bmatrix}\end{array} \) satisfies A T = A -1 .

⇒ AA T = AA -1

⇒ AA T = I {since A -1 A = AA -1 = I}

By performing multiplication on the LHS, we get:

By equating the corresponding elements, we have:

4y 2 + z 2 = 1 …(1)

x 2 + y 2 + z 2 = 1 …(2)

2y 2 – z 2 = 0 …(3)

Adding equations (1) and (3), we get:

4y 2 + z 2 + 2y 2 – z 2 = 1 + 0

⇒ y = ±1/√6

Substituting the value of y in equation (3), we get:

z 2 = 2(1/6)

⇒ z = ±1/√3

Substituting the values of y and z in equation (2), we get:

x 2 = 1 – y 2 – z 2

x 2 = 1 – (1/6) – (1/3)

x 2 = (6 – 1 – 2)/6

⇒ x = ±1/√2

Therefore, x = ±1/√2, y = ±1/√6 and z = ±1/√3.

7. Find the value of x for which the matrix \(\begin{array}{l}A=\begin{bmatrix}2 & 0 & 10 \\ 0 & x+7 & -3 \\0 & 4 & x \\\end{bmatrix}\end{array} \) is invertible.

Let us find the determinant of the given matrix.

= 2[(x + 7)x – (-3)(4)] – 0 + 10(0 – 0)

= 2(x 2 + 7x + 12)

We know that a matrix is invertible if and only if its determinant is not equal to 0.

Let |A| = 0

2(x 2 + 7x + 12) = 0

⇒ x 2 + 7x + 12 = 0

⇒ x 2 + 3x + 4x + 12 = 0

⇒ x(x + 3) + 4(x + 3) = 0

⇒ (x + 3)(x + 4) = 0

⇒ x + 3 = 0, x + 4 = 0

⇒ x = -3, x = -4

Thus, for x = -3 and -4, the given matrix is invertible.

8. Find the inverse of \(\begin{array}{l}A=\begin{bmatrix}1 & 2 & 3 \\2 & 4 & 5 \\3 & 5 & 6 \\\end{bmatrix}\end{array} \) using row operations.

Let us write the augmented matrix [A | I ] such that I is a square matrix of the order same as A.

R 3 → R 3 – 3R 1

R 2 → R 2 – 2R 1

Now, interchange R 2 and R 3 .

R 2 → (-1).R 2 and R 3 → (-1).R 3

R 2 → R 2 – 3R 3

R 1 → R 1 – 2R 2

R 1 → R 1 – 3R 3

This is of the form [ I | B].

Here, B is the inverse of A.

9. Determine the formula for the inverse of matrix \(\begin{array}{l}A=\begin{bmatrix}p & 0 & 0 & 0 \\0 & q & 0 & 0 \\0 & 0 & r & 0 \\0 & 0 & 0 & s \\\end{bmatrix}\end{array} \) , where p, q, r, s ≠ 0.

Let us write the augmented matrix [A | I ].

R 1 → (1/p) R 1

R 2 → (1/q) R 2

R 3 → (1/r) R 3

R 4 → (1/s) R 4

Hence, the inverse of A is:

10. If A is 3 × 3 invertible matrix, then show that for any scalar k (non-zero), kA is invertible and (kA) –1 = (1/k)A –1 .

= [k (1/k)] (A A -1 )

= 1. (AA -1 )

= I {since AA -1 = A -1 A = I}

That means kA is the inverse of (1/k)A -1 .

Therefore, (kA) -1 = (1/k) A -1

Practice Questions on Inverse Matrix

• Find the inverse of the matrix \(\begin{array}{l}A=\begin{bmatrix}3 & 5 \\-2 & 4 \\\end{bmatrix}\end{array} \) .
• If \(\begin{array}{l}A=\begin{bmatrix}2 & 1 & 1\\1 & 2 & 1\\1 & 1 & 2\\\end{bmatrix}\end{array} \) , find A -1 exists.
• Using elementary row operations, find the inverse of the matrix \(\begin{array}{l}\begin{bmatrix}-4 & 8 & 4\\-1 & 2 & 1\\-3 & 6 & 3\\\end{bmatrix}\end{array} \) .
• Calculate the inverse matrix for \(\begin{array}{l}B=\begin{bmatrix}4+3i & -i \\i &4-3i \\\end{bmatrix}\end{array} \) .
• What is the inverse of the matrix \(\begin{array}{l}A=\begin{bmatrix}1 & 0 & 1 & 2 \\-1 & 1 & 2 & 0 \\-2 & 0 & 1 & 2 \\0 & 0 & 0 & 1 \\\end{bmatrix}\end{array} \) ?

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 7.

• Inverse matrix introduction
• Invertible matrices and determinants
• Invertible matrices and transformations

Inverse matrices and matrix equations

• Determine invertible matrices

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Problems in Mathematics

• Inverse Matrices
• An $n\times n$ matrix $A$ is said to be invertible if there exists an $n\times n$ matrix $B$ such that $AB=BA=I$. Such a matrix $B$ is unique and called the inverse matrix of $A$, denoted by $A^{-1}$

Let $A, B$ be $n\times n$ matrices.

• $A$ is invertible if and only if $\rref([ A \mid I_n])=[ I_n \mid A’]$ for some $n\times n$ matrix $A’$. In this case, $A’=A^{-1}$.
• $A$ is invertible if and only if $A$ is nonsingular.
• If $A, B$ are invertible, then $(AB)^{-1}=B^{-1}A^{-1}$
• A $2\times 2$ matrix $A=\begin{bmatrix} a & b\\ c& d \end{bmatrix}$ is invertible if and only if the determinant $\det(A)=ad-bc \neq 0$. If $A$ is invertible, then the inverse matrix is given by $A^{-1}=\frac{1}{\det(A)}\begin{bmatrix} d & -b\\ -c& a \end{bmatrix}$.
• If $A$ is invertible, then $A^{\trans}$ is invertible and $(A^{\trans})^{-1}=(A^{-1})^{\trans}$.
• For each of the following $3\times 3$ matrices $A$, determine whether $A$ is invertible and find the inverse $A^{-1}$ if exists by computing the augmented matrix $[A|I]$, where $I$ is the $3\times 3$ identity matrix. (a) $A=\begin{bmatrix} 1 & 3 & -2 \\ 2 &3 &0 \\ 0 & 1 & -1 \end{bmatrix}$ (b) $A=\begin{bmatrix} 1 & 0 & 2 \\ -1 &-3 &2 \\ 3 & 6 & -2 \end{bmatrix}$.
• Let A be the matrix \[\begin{bmatrix} 1 & -1 & 0 \\ 0 &1 &-1 \\ 0 & 0 & 1 \end{bmatrix}.\] Is the matrix $A$ invertible? If not, then explain why it isn’t invertible. If so, then find the inverse. ( The Ohio State University )
• Find the inverse matrix of \[A=\begin{bmatrix} 1 & 1 & 2 \\ 0 &0 &1 \\ 1 & 0 & 1 \end{bmatrix}\] if it exists. If you think there is no inverse matrix of $A$, then give a reason. ( The Ohio State University )
• Let $A$ be the following $3\times 3$ upper triangular matrix. \[A=\begin{bmatrix} 1 & x & y \\ 0 &1 &z \\ 0 & 0 & 1 \end{bmatrix},\] where $x, y, z$ are some real numbers. Determine whether the matrix $A$ is invertible or not. If it is invertible, then find the inverse matrix $A^{-1}$.
• For which choice(s) of the constant $k$ is the following matrix invertible? \[A=\begin{bmatrix} 1 & 1 & 1 \\ 1 &2 &k \\ 1 & 4 & k^2 \end{bmatrix}.\] ( Johns Hopkins University )
• Suppose that $M, P$ are two $n \times n$ non-singular matrix. Prove that there is a matrix $N$ such that $MN = P$.
• Let $A$ be an $n \times n$ matrix satisfying $A^2+c_1A+c_0I=O$, where $c_0, c_1$ are scalars, $I$ is the $n\times n$ identity matrix, and $O$ is the $n\times n$ zero matrix. Prove that if $c_0\neq 0$, then the matrix $A$ is invertible (nonsingular). How about the converse? Namely, is it true that if $c_0=0$, then the matrix $A$ is not invertible?
• A square matrix $A$ is called idempotent if $A^2=A$. Show that a square invertible idempotent matrix is the identity matrix.
• Find the inverse matrix of $A=\begin{bmatrix} 1 & 0 & 1 \\ 1 &0 &0 \\ 2 & 1 & 1 \end{bmatrix}$ if it exists. If you think there is no inverse matrix of $A$, then give a reason. See (a)
• Find a nonsingular $2\times 2$ matrix $A$ such that $A^3=A^2B-3A^2$, where $B=\begin{bmatrix} 4 & 1\\ 2& 6 \end{bmatrix}$. Verify that the matrix $A$ you obtained is actually a nonsingular matrix. See (b)
• Determine whether there exists a nonsingular matrix $A$ if $A^2=AB+2A$, where $B$ is the following matrix. If such a nonsingular matrix $A$ exists, find the inverse matrix $A^{-1}$. (a) \[B=\begin{bmatrix} -1 & 1 & -1 \\ 0 &-1 &0 \\ 1 & 2 & -2 \end{bmatrix}\] (b) \[B=\begin{bmatrix} -1 & 1 & -1 \\ 0 &-1 &0 \\ 2 & 1 & -4 \end{bmatrix}.\]
• Determine whether there exists a nonsingular matrix $A$ if $A^4=ABA^2+2A^3$, where $B$ is the following matrix. $B=\begin{bmatrix} -1 & 1 & -1 \\ 0 &-1 &0 \\ 2 & 1 & -4 \end{bmatrix}.$ If such a nonsingular matrix $A$ exists, find the inverse matrix $A^{-1}$. ( The Ohio State University, Linear Algebra Final Exam Problem )
• Let $A, B, C$ be the following $3\times 3$ matrices. \[A=\begin{bmatrix} 1 & 2 & 3 \\ 4 &5 &6 \\ 7 & 8 & 9 \end{bmatrix}, B=\begin{bmatrix} 1 & 0 & 1 \\ 0 &3 &0 \\ 1 & 0 & 5 \end{bmatrix}, C=\begin{bmatrix} -1 & 0\ & 1 \\ 0 &5 &6 \\ 3 & 0 & 1 \end{bmatrix}.\] Then compute and simplify the following expression. \[(A^{\trans}-B)^{\trans}+C(B^{-1}C)^{-1}.\] ( The Ohio State University )
• Let $A$ be the coefficient matrix of the system of linear equations \begin{align*} -x_1-2x_2&=1\\ 2x_1+3x_2&=-1. \end{align*} (a) Solve the system by finding the inverse matrix $A^{-1}$. (b) Let $\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$ be the solution of the system obtained in part (a). Calculate and simplify \[A^{2017}\mathbf{x}.\] ( The Ohio State University )
• (a) Let $A$ be a $6\times 6$ matrix and suppose that $A$ can be written as $A=BC$, where $B$ is a $6\times 5$ matrix and $C$ is a $5\times 6$ matrix. Prove that the matrix $A$ cannot be invertible. (b) Let $A$ be a $2\times 2$ matrix and suppose that $A$ can be written as $A=BC$, where $B$ is a $ 2\times 3$ matrix and $C$ is a $3\times 2$ matrix. Can the matrix $A$ be invertible?
• For a real number $a$, consider $2\times 2$ matrices $A, P, Q$ satisfying the following five conditions. (1) $A=aP+(a+1)Q$, (2) $P^2=P$, (3) $Q^2=Q$, (4) $PQ=O$, (5) $QP=O$, where $O$ is the $2\times 2$ zero matrix. Then do the following problems. (a) Prove that $(P+Q)A=A$. (b) Suppose $a$ is a positive real number and let $A=\begin{bmatrix} a & 0\\ 1& a+1 \end{bmatrix}$. Then find all matrices $P, Q$ satisfying conditions (1)-(5). (c) Let $n$ be an integer greater than $1$. For any integer $k$, $2\leq k \leq n$, we define the matrix $A_k=\begin{bmatrix} k & 0\\ 1& k+1 \end{bmatrix}$. Then calculate and simplify the matrix product $A_nA_{n-1}A_{n-2}\cdots A_2$. ( Tokyo University Entrance Exam 2007 )
• Let $\mathbf{v}$ be a nonzero vector in $\R^n$. Then the dot product $\mathbf{v}\cdot \mathbf{v}=\mathbf{v}^{\trans}\mathbf{v}\neq 0$. Set $a:=\frac{2}{\mathbf{v}^{\trans}\mathbf{v}}$ and define the $n\times n$ matrix $A$ by $A=I-a\mathbf{v}\mathbf{v}^{\trans}$, where $I$ is the $n\times n$ identity matrix. Prove that $A$ is a symmetric matrix and $AA=I$. Conclude that the inverse matrix is $A^{-1}=A$.
• Consider the system of linear equations \begin{align*} x_1&= 2, \\ -2x_1 + x_2 &= 3, \\ 5x_1-4x_2 +x_3 &= 2 \end{align*} (a) Find the coefficient matrix and its inverse matrix. (b) Using the inverse matrix, solve the system of linear equations. ( The Ohio State University )
• Consider the following system of linear equations \begin{align*} 2x+3y+z&=-1\\ 3x+3y+z&=1\\ 2x+4y+z&=-2. \end{align*} (a) Find the coefficient matrix $A$ for this system. (b) Find the inverse matrix of the coefficient matrix found in (a) (c) Solve the system using the inverse matrix $A^{-1}$.
• Consider the matrix \[A=\begin{bmatrix} 1 & 2 & 1 \\ 2 &5 &4 \\ 1 & 1 & 0 \end{bmatrix}.\] (a) Calculate the inverse matrix $A^{-1}$. If you think the matrix $A$ is not invertible, then explain why. (b)  Are the vectors \[ \mathbf{A}_1=\begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}, \mathbf{A}_2=\begin{bmatrix} 2 \\ 5 \\ 1 \end{bmatrix}, \text{ and } \mathbf{A}_3=\begin{bmatrix} 1 \\ 4 \\ 0 \end{bmatrix}\] linearly independent? (c)  Write the vector $\mathbf{b}=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$ as a linear combination of $\mathbf{A}_1$, $\mathbf{A}_2$, and $\mathbf{A}_3$. ( The Ohio State University, Linear Algebra Exam )
• A $2 \times 2$ matrix $A$ satisfies $\tr(A^2)=5$ and $\tr(A)=3$. Find $\det(A)$. See (a)
• Suppose that a real matrix $A$ maps each of the following vectors \[\mathbf{x}_1=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, \mathbf{x}_2=\begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}, \mathbf{x}_3=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \] into the vectors \[\mathbf{y}_1=\begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}, \mathbf{y}_2=\begin{bmatrix} -1 \\ 0 \\ 3 \end{bmatrix}, \mathbf{y}_3=\begin{bmatrix} 3 \\ 1 \\ 1 \end{bmatrix},\] respectively. That is, $A\mathbf{x}_i=\mathbf{y}_i$ for $i=1,2,3$. Find the matrix $A$. ( Kyoto University Exam )
• Let $A$ and $B$ are $n \times n$ matrices with real entries. Assume that $A+B$ is invertible. Then show that \[A(A+B)^{-1}B=B(A+B)^{-1}A.\] ( University of California, Berkeley Qualifying Exam )
• Let $A$ be an $n\times n$ invertible matrix. Prove that the inverse matrix of $A$ is uniques.
• Let $\mathbf{u}$ and $\mathbf{v}$ be vectors in $\R^n$, and let $I$ be the $n \times n$ identity matrix. Suppose that the inner product of $\mathbf{u}$ and $\mathbf{v}$ satisfies \[\mathbf{v}^{\trans}\mathbf{u}\neq -1.\] Define the matrix \[A=I+\mathbf{u}\mathbf{v}^{\trans}.\] Prove that $A$ is invertible and the inverse matrix is given by the formula \[A^{-1}=I-a\mathbf{u}\mathbf{v}^{\trans},\] where \[a=\frac{1}{1+\mathbf{v}^{\trans}\mathbf{u}}.\] This formula is called the Sherman-Woodberry formula .
• Let $A$ be a singular $2\times 2$ matrix such that $\tr(A)\neq -1$ and let $I$ be the $2\times 2$ identity matrix. Then prove that the inverse matrix of the matrix $I+A$ is given by the following formula: \[(I+A)^{-1}=I-\frac{1}{1+\tr(A)}A.\] Using the formula, calculate the inverse matrix of $\begin{bmatrix} 2 & 1\\ 1& 2 \end{bmatrix}$.
• Let $A=\begin{bmatrix} a & 0\\ 0& b \end{bmatrix}$. Show that (a) $A^n=\begin{bmatrix} a^n & 0\\ 0& b^n \end{bmatrix}$ for any $n \in \N$. (b) Let $B=S^{-1}AS$, where $S$ be an invertible $2 \times 2$ matrix. Show that $B^n=S^{-1}A^n S$ for any $n \in \N$
• Let $A$ be an $n\times n$ invertible matrix. Then prove the transpose $A^{\trans}$ is also invertible and that the inverse matrix of the transpose $A^{\trans}$ is the transpose of the inverse matrix $A^{-1}$. Namely, show that $(A^{\trans})^{-1}=(A^{-1})^{\trans}$.
• A square matrix $A$ is called nilpotent if there exists a positive integer $k$ such that $A^k=O$, where $O$ is the zero matrix. (a) If $A$ is a nilpotent $n \times n$ matrix and $B$ is an $n\times n$ matrix such that $AB=BA$. Show that the product $AB$ is nilpotent. (b) Let $P$ be an invertible $n \times n$ matrix and let $N$ be a nilpotent $n\times n$ matrix. Is the product $PN$ nilpotent? If so, prove it. If not, give a counterexample.
• (a) Show that if $A$ is invertible, then $A$ is nonsingular. (b) Let $A, B, C$ be $n\times n$ matrices such that $AB=C$. Prove that if either $A$ or $B$ is singular, then so is $C$. (c) Show that if $A$ is nonsingular, then $A$ is invertible.
• A square matrix $A$ is called nilpotent if some power of $A$ is the zero matrix. Namely, $A$ is nilpotent if there exists a positive integer $k$ such that $A^k=O$, where $O$ is the zero matrix. Suppose that $A$ is a nilpotent matrix and let $B$ be an invertible matrix of the same size as $A$. Is the matrix $B-A$ invertible? If so prove it. Otherwise, give a counterexample.
• Let $A$ be an $n\times n$ matrix. The $(i, j)$ cofactor $C_{ij}$ of $A$ is defined to be $C_{ij}=(-1)^{ij}\det(M_{ij})$, where $M_{ij}$ is the $(i,j)$ minor matrix obtained from $A$ removing the $i$-th row and $j$-th column. Then consider the $n\times n$ matrix $C=(C_{ij})$, and define the $n\times n$ matrix $\Adj(A)=C^{\trans}$. The matrix $\Adj(A)$ is called the adjoint matrix of $A$. When $A$ is invertible, then its inverse can be obtained by the formula \[A^{-1}=\frac{1}{\det(A)}\Adj(A).\] For each of the following matrices, determine whether it is invertible, and if so, then find the invertible matrix using the above formula. (a) $A=\begin{bmatrix} 1 & 5 & 2 \\ 0 &-1 &2 \\ 0 & 0 & 1 \end{bmatrix}$. (b) $B=\begin{bmatrix} 1 & 0 & 2 \\ 0 &1 &4 \\ 3 & 0 & 1 \end{bmatrix}$.
• Let $A$ be a real symmetric matrix whose diagonal entries are all positive real numbers. Is it true that the all of the diagonal entries of the inverse matrix $A^{-1}$ are also positive? If so, prove it. Otherwise, give a counterexample.
• Let $A$ be an $n\times n$ nonsingular matrix with integer entries. Prove that the inverse matrix $A^{-1}$ contains only integer entries if and only if $\det(A)=\pm 1$.
• Introduction to Matrices
• Elementary Row Operations
• Gaussian-Jordan Elimination
• Solutions of Systems of Linear Equations
• Linear Combination and Linear Independence
• Nonsingular Matrices
• Subspaces in $\R^n$
• Bases and Dimension of Subspaces in $\R^n$
• General Vector Spaces
• Subspaces in General Vector Spaces
• Linearly Independency of General Vectors
• Bases and Coordinate Vectors
• Dimensions of General Vector Spaces
• Linear Transformation from $\R^n$ to $\R^m$
• Linear Transformation Between Vector Spaces
• Orthogonal Bases
• Determinants of Matrices
• Computations of Determinants
• Introduction to Eigenvalues and Eigenvectors
• Eigenvectors and Eigenspaces
• Diagonalization of Matrices
• The Cayley-Hamilton Theorem
• Dot Products and Length of Vectors
• Eigenvalues and Eigenvectors of Linear Transformations
• Jordan Canonical Form

• School Guide
• Class 12 Syllabus
• Class 12 Revision Notes
• Maths Notes Class 12
• Physics Notes Class 12
• Chemistry Notes Class 12
• Biology Notes Class 12
• NCERT Solutions Class 12 Maths
• RD Sharma Solutions Class 12
• Algebra From Basics to Advanced : Definition, Branches, Examples

Basics of Algebra

• What is a variable in algebra?
• Algebraic Expressions in Math: Definition, Example and Equation
• Like and Unlike Terms
• Mathematical Operations on Algebraic Expressions - Algebraic Expressions and Identities | Class 8 Maths

Algebraic Expression

• Algebra | Set -1
• Algebraic Identities
• Factorization of Polynomial
• Division of Algebraic Expressions

Polynomials

• Polynomials - Definition, Standard Form, Types, Identities, Zeroes
• Types of Polynomials
• Zeros of Polynomial
• Geometrical meaning of the Zeroes of a Polynomial
• Multiplying Polynomials
• Dividing Polynomials - Long Division Algorithm
• Division Algorithm for Polynomials
• Division Algorithm Problems and Solutions
• Remainder Theorem
• Factor Theorem
• Algebraic Identities of Polynomials
• Factoring Polynomials
• Relationship between Zeroes and Coefficients of a Polynomial

Linear Equations

• Linear Equations in One Variable
• Solve Linear Equations with Variable on both Sides
• Graphical Methods of Solving Pair of Linear Equations in Two Variables
• Reducing Equations to Simpler Form | Class 8 Maths
• Linear Equation in Two Variables
• Graph of Linear Equations in Two Variables
• Equations of Lines Parallel to the x-axis and y-axis
• Pair of Linear Equations in Two Variables
• Number of Solutions to a System of Equations Algebraically
• Solve the Linear Equation using Substitution Method
• Cross Multiplication Method
• Equations Reducible to Linear Form

Quadratic Equations

• Quadratic Equations - Roots, Solution, Formula and Examples
• Solving Quadratic Equations
• Roots of Quadratic Equation

Cubic Equations

• Cubic Equation Formula
• Solving Cubic Equations

Sequence and Series

• Arithmetic Progression
• Arithmetic Series
• Arithmetic Sequence
• Geometric Progression
• Geometric Series
• Representation of a Set
• Types Of Sets
• Universal Sets
• Venn Diagram
• Operations on Sets
• Union of Sets
• Cartesian Product of Sets

Relations and Functions

• Relation and Function
• What is a Function?
• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition
• Domain and Range of a Function
• Piecewise Function
• Linear Function
• Exponential Functions | Definition, Formula, Examples
• Six Trigonometric Functions
• Inverse Trigonometric Functions
• Increasing and Decreasing Functions

Matrices and Determinants

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication: How to Multiply Matrices, Methods, Examples
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices

Inverse of a Matrix

• Invertible Matrix
• Determinant of a Matrix
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants
• Vector Algebra
• Vector Addition
• Vector Operations
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Magnitude of a Vector
• Direction Cosines and Direction Ratios
• Resultant Vector Formula
• Vector Projection Formula
• Orthogonal and Orthonormal Vectors in Linear Algebra
• Distance Formula in Coordinate Geometry
• Direction of a Vector Formula
• Section Formula - Vector Algebra
• Angle between Two Vectors Formula
• Program to find equation of a plane passing through 3 points
• Cartesian Plane
• What is a plane in geometry?
• Boolean Algebra
• Properties of Boolean Algebra
• Boolean Algebraic Theorems

The inverse of Matrix is the matrix that on multiplying with the original matrix results in an identity matrix. For any matrix A, its inverse is denoted as A -1 .

Let’s learn about the Matrix Inverse in detail, including its definition, formula, methods on how to find the inverse of a matrix, and examples.

Table of Content

Matrix Inverse

Terms related to matrix inverse, how to find inverse of matrix, inverse of a matrix formula, inverse matrix method, inverse of 2×2 matrix example, determinant of inverse matrix, properties of inverse of matrix, matrix inverse solved examples.

The inverse of a matrix is another matrix that, when multiplied by the given matrix, yields the multiplicative identity .

For matrix A and its inverse of A -1 , the identity property holds.

A.A -1 = A -1 A = I

where I is the identity matrix.

The terminology listed below can help you grasp the inverse of a matrix more clearly and easily.

Singular Matrix

A matrix whose value of the determinant is zero is called a singular matrix, i.e. any matrix A is called a singular matrix if |A| = 0. Inverse of a singular matrix does not exist.

Non-Singular Matrix

A matrix whose value of the determinant is non-zero is called a non-singular matrix, i.e. any matrix A is called a non-singular matrix if |A| ≠ 0. Inverse of a non-singular matrix exists.

• Identity Matrix

A square matrix in which all the elements are zero except for the principal diagonal elements is called the identity matrix. It is represented using I. It is the identity element of the matrix as for any matrix A,

An example of an Identity matrix is,

I 3×3 = [Tex] \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1 \\\end{bmatrix}[/Tex]

This is an identity matrix of order 3×3.\

Read More :

There are Two-ways to find the Inverse of a matrix in mathematics:

• Using Matrix Formula
• Using Inverse Matrix Methods

The inverse of matrix A, that is A -1 is calculated using the inverse of matrix formula, which involves dividing the adjoint of a matrix by its determinant.

[Tex]A^{-1}=\frac{\text{Adj A}}{|A|}   [/Tex]

• adj A = adjoint of the matrix A, and 
• |A| = determinant of the matrix A.

Note : This formula only works on Square matrices.

To find inverse of matrix using inverse of a matrix formula, follow these steps.

Step 1: Determine the minors of all A elements.

Step 2: Next, compute the cofactors of all elements and build the cofactor matrix by substituting the elements of A with their respective cofactors.

Step 3: Take the transpose of A’s cofactor matrix to find its adjoint (written as adj A).

Step 4: Multiply adj A by the reciprocal of the determinant of A.

Now, for any non-singular square matrix A,

A -1 = 1 / |A| × Adj (A)

Example: Find the inverse of the matrix  [Tex]A=\left[\begin{array}{ccc}4 & 3 & 8\\6 & 2 & 5\\1 & 5 & 9\end{array}\right]            [/Tex]  using the formula.

We have,  [Tex]A=\left[\begin{array}{ccc}4 & 3 & 8\\6 & 2 & 5\\1 & 5 & 9\end{array}\right] [/Tex] Find the adjoint of matrix A by computing the cofactors of each element and then getting the cofactor matrix’s transpose. adj A =  [Tex]\left[\begin{array}{ccc}-7 & -49 & 28\\13 & 28 & -17\\-1 & 28 & -10\end{array}\right] [/Tex] Find the value of determinant of the matrix. |A| = 4(18–25) – 3(54–5) + 8(30–2) ⇒ |A| = 49 So, the inverse of the matrix is, A –1 =  [Tex]\frac{1}{49}\left[\begin{array}{ccc}-7 & -49 & 28\\13 & 28 & -17\\-1 & 28 & -10\end{array}\right] [/Tex] ⇒ A –1 =  [Tex]\left[\begin{array}{ccc}- \frac{1}{7} & \frac{13}{49} & – \frac{1}{49}\\-1 & \frac{4}{7} & \frac{4}{7}\\\frac{4}{7} & – \frac{17}{49} & – \frac{10}{49}\end{array}\right] [/Tex]

There are two Inverse matrix methods to find matrix inverse:

• Determinant Method
• Elementary Transformation Method

Method 1: Determinant Method

The most important method for finding the matrix inverse is using a determinant.

The inverse matrix is also found using the following equation:

A -1 = adj(A) / det(A)

• adj(A) is the adjoint of a matrix A, and
• det(A) is the determinant of a matrix A.

For finding the adjoint of a matrix A the cofactor matrix of A is required. Then adjoint (A) is the transpose of the Cofactor matrix of A i.e.,

adj (A) = [C ij ] T

• For the cofactor of a matrix i.e., C ij , we can use the following formula:

C ij = (-1) i+j det (M ij )

where M ij refers to the (i, j) th minor matrix when i th row and j th column is removed.

Method 2: Elementary Transformation Method

Follow the steps below to find an Inverse matrix by elementary transformation method.

Step 1 : Write the given matrix as A = IA, where I is the identity matrix of the order same as A.

Step 2 : Use the sequence of either row operations or column operations till the identity matrix is achieved on the LHS also use similar elementary operations on the RHS such that we get I = BA. Thus, the matrix B on RHS is the inverse of matrix A.

Step 3 : Make sure we either use Row Operation or Column Operation while performing elementary operations.

We can easily find the inverse of the 2 × 2 Matrix using the elementary operation. Let’s understand this with the help of an example.

Example: Find the inverse of the 2 × 2, A =   [Tex]     [/Tex]  using the elementary operation.

Given: A = IA [Tex]\begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix}~=~\begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}~×~\begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix} [/Tex] Now, R 1 ⇢ R 1 /2 [Tex]\begin{bmatrix}1 & 1/2\\ 1 & 2\end{bmatrix}~=~\begin{bmatrix}1/2 & 0\\ 0 & 1\end{bmatrix}~×~A [/Tex] R 2 ⇢ R 2 – R 1 [Tex]\begin{bmatrix}1 & 1/2\\ 0 & 3/2\end{bmatrix}~=~\begin{bmatrix}1/2 & 0\\ -1/2 & 1\end{bmatrix}~×~A [/Tex] R 2 ⇢ R 2 × 2/3 [Tex]\begin{bmatrix}1 & 1/2\\ 0 & 1\end{bmatrix}~=~\begin{bmatrix}1/2 & 0\\-1/3 & 2/3\end{bmatrix}~×~A [/Tex] R 1 ⇢ R 1 – R 2 /2 [Tex]\begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}~=~\begin{bmatrix}2/3 & -1/6\\ -1/3 & 2/3\end{bmatrix}~×~A [/Tex] Thus, the inverse of the matrix A =  [Tex] \begin{bmatrix}2 & 1\\ 1 & 2\end{bmatrix}   [/Tex]  is A -1 =  [Tex]\begin{bmatrix}2/3 & -1/6\\ -1/3 & 2/3\end{bmatrix} [/Tex]

Inverse of the 2×2 matrix can also be calculated using the shortcut method apart from the method discussed above. Let’s consider an example to understand the shortcut method to calculate the inverse of 2 × 2 Matrix.

For given matrix A =  [Tex]\begin{bmatrix}a & b\\ c & d\end{bmatrix} [/Tex] We know, |A| = (ad – bc) and adj A =  [Tex]\begin{bmatrix}d & -b\\ -c & a\end{bmatrix} [/Tex] then using the formula for inverse A -1 =  (1 / |A|) × Adj A ⇒ A -1 =  [Tex][1 / (ad – bc)] × \begin{bmatrix}d & -b\\ -c & a\end{bmatrix} [/Tex] Thus, the inverse of the 2 × 2 matrix is calculated.

Inverse of 3X3 Matrix Example

Let us take any 3×3 Matrix A =  [Tex]\begin{bmatrix}a & b & c\\ l & m & n\\ p & q & r\end{bmatrix} [/Tex]

The inverse of 3×3 matrix is calculated using the inverse matrix formula , 

A -1 = (1 / |A|) × Adj A

Determinant of inverse matrix is the reciprocal of the determinant of the original matrix. i.e., 

det(A -1 ) = 1 / det(A)

The proof of the above statement is discussed below:

det(A × B) = det (A) × det(B)  (already know) ⇒ A × A -1 = I  (by Inverse matrix property) ⇒ det(A × A -1 ) = det(I) ⇒ det(A) × det(A -1 ) = det(I)     [ but, det(I) = 1] ⇒ det(A) × det(A -1 ) = 1 ⇒ det(A -1 ) = 1 / det(A) Hence, Proved.

Inverse matrix has the following properties:

• For any non-singular matrix A, (A -1 ) -1 = A
• For any two non-singular matrices A and B, (AB) -1 = B -1 A -1
• Inverse of a non-singular matrix exists, for a singular matrix, the inverse does not exist.
• For any nonsingular A, (A T ) -1 = (A -1 ) T
• Matrices: Properties and Formulas
• Mathematical Operation on Matrices
• Determinant of Matrix
• How to find the Determinant of Matrix?

Let’s solve some example questions on Inverse of Matrix.

Example 1: Find the inverse of the matrix  [Tex]\bold{A=\left[\begin{array}{ccc}2 & 3 & 1\\1 & 1 & 2\\2 & 3 & 4\end{array}\right]      }      [/Tex]  using the formula.

We have, [Tex]A=\left[\begin{array}{ccc}2 & 3 & 1\\1 & 1 & 2\\2 & 3 & 4\end{array}\right] [/Tex] Find the adjoint of matrix A by computing the cofactors of each element and then getting the cofactor matrix’s transpose. adj A =  [Tex]\left[\begin{array}{ccc}-2 & -9 & 5\\0 & 6 & -3\\1 & 0 & -1\end{array}\right] [/Tex] Find the value of determinant of the matrix. |A| = 2(4–6) – 3(4–4) + 1(3–2) = –3 So, the inverse of the matrix is, A –1 =  [Tex]\frac{1}{-3}\left[\begin{array}{ccc}-2 & -9 & 5\\0 & 6 & -3\\1 & 0 & -1\end{array}\right] [/Tex]       =  [Tex]\left[\begin{array}{ccc}\frac{2}{3} & 3 & – \frac{5}{3}\\0 & -2 & 1\\- \frac{1}{3} & 0 & \frac{1}{3}\end{array}\right] [/Tex]

Example 2: Find the inverse of the matrix A=\bold{ using the formula.} [Tex]\left[\begin{array}{ccc}6 & 2 & 3\\0 & 0 & 4\\2 & 0 & 0\end{array}\right]       [/Tex]

We have, A= [Tex]\left[\begin{array}{ccc}6 & 2 & 3\\0 & 0 & 4\\2 & 0 & 0\end{array}\right] [/Tex] Find the adjoint of matrix A by computing the cofactors of each element and then getting the cofactor matrix’s transpose. adj A =  [Tex]\left[\begin{array}{ccc}0 & 0 & 8\\8 & -6 & -24\\0 & 4 & 0\end{array}\right] [/Tex] Find the value of determinant of the matrix. |A| = 6(0–4) – 2(0–8) + 3(0–0)      = 16 So, the inverse of the matrix is, A –1 =  [Tex]\frac{1}{16}\left[\begin{array}{ccc}0 & 0 & 8\\8 & -6 & -24\\0 & 4 & 0\end{array}\right] [/Tex]       =  [Tex]\left[\begin{array}{ccc}0 & 0 & \frac{1}{2}\\\frac{1}{2} & – \frac{3}{8} & – \frac{3}{2}\\0 & \frac{1}{4} & 0\end{array}\right] [/Tex]

Example 3: Find the inverse of the matrix A= [Tex]\bold{\left[\begin{array}{ccc}1 & 2 & 3\\0 & 1 & 4\\0 & 0 & 1\end{array}\right]      }      [/Tex]  using the formula.

We have, A= [Tex]\left[\begin{array}{ccc}1 & 2 & 3\\0 & 1 & 4\\0 & 0 & 1\end{array}\right] [/Tex] Find the adjoint of matrix A by computing the cofactors of each element and then getting the cofactor matrix’s transpose. adj A =  [Tex]\left[\begin{array}{ccc}1 & -2 & 5\\0 & 1 & -4\\0 & 0 & 1\end{array}\right] [/Tex] Find the value of determinant of the matrix. |A| = 1(1–0) – 2(0–0) + 3(0–0) = 1 So, the inverse of the matrix is, A –1 =  [Tex]\frac{1}{1}\left[\begin{array}{ccc}1 & -2 & 5\\0 & 1 & -4\\0 & 0 & 1\end{array}\right] [/Tex] =  [Tex]\left[\begin{array}{ccc}1 & -2 & 5\\0 & 1 & -4\\0 & 0 & 1\end{array}\right] [/Tex]

Example 4: Find the inverse of the matrix A= [Tex]\bold{\left[\begin{array}{ccc}1 & 2 & 3\\2 & 1 & 4\\3 & 4 & 1\end{array}\right]      }      [/Tex]  using the formula.

We have, A= [Tex]\left[\begin{array}{ccc}1 & 2 & 3\\2 & 1 & 4\\3 & 4 & 1\end{array}\right] [/Tex] Find the adjoint of matrix A by computing the cofactors of each element and then getting the cofactor matrix’s transpose. adj A =  [Tex]\left[\begin{array}{ccc}-15 & 10 & 5\\10 & -8 & 2\\5 & 2 & -3\end{array}\right] [/Tex] Find the value of determinant of the matrix. |A| = 1(1–16) – 2(2–12) + 3(8–3) = 20 So, the inverse of the matrix is, A –1 =  [Tex]\frac{1}{20}\left[\begin{array}{ccc}-15 & 10 & 5\\10 & -8 & 2\\5 & 2 & -3\end{array}\right] [/Tex]       =  [Tex]\left[\begin{array}{ccc}- \frac{3}{4} & \frac{1}{2} & \frac{1}{4}\\\frac{1}{2} & – \frac{2}{5} & \frac{1}{10}\\\frac{1}{4} & \frac{1}{10} & – \frac{3}{20}\end{array}\right] [/Tex]

Frequently Asked Questions on Inverse of Matrix

What is inverse of matrix.

Reciprocal of a matrix is called the Inverse of a matrix. Only square matrices with non-zero determinants are invertible. Suppose for any square matrix A with inverse matrix B their product is always an identity matrix (I) of the same order. [A]×[B] = [I]

What is Matrix?

Matrix is a rectangular array of numbers that are divided into a defined number of rows and columns. The number of rows and columns in a matrix is referred to as its dimension or order.

What is the Inverse of 2×2 Matrix?

For any matrix A or order 3×3 its inverse is found using the formula, A -1 = (1 / |A|) × Adj A

What is the Inverse of 3×3 Matrix?

The inverse of any square 3×3 matrix (say A) is the matrix of the same order denoted by A -1 such that their product is an Identity matrix of order 3×3. [A] 3×3 × [A -1 ] 3×3 = [I] 3×3

Are Adjoint and Inverse of Matrix the same?

No, the adjoint of a matrix and the inverse of a matrix are not the same. 

How to use the Inverse of Matrix?

The inverse of a matrix is used for solving algebraic expressions in matrix form. For example, to solve AX = B, where A is the coefficient matrix, X is the variable matrix and B is the constant matrix. Here the variable matrix is found using the inverse operation as, X = A -1 B

What are Invertible Matrices?

The matrices whose inverse exist are called invertible. Invertible matrices are matrices that have a non-zero determinant.

Why does Inverse of 2 × 3 Matrix not exist?

The inverse of only a square matrix exists. As the 2 × 3 matrix is not a square matrix but rather a rectangular matrix thus, its inverse does not exist. Similarly, the 2 × 1 matrix is also not a square matrix but rather a rectangular matrix thus, its inverse does not exist.

What is Inverse of Identity Matrix?

The inverse of an identity matrix is the identity matrix itself. This is because the identity matrix, denoted as I (or I n for an n × n matrix), is the only matrix for which every element along the main diagonal is 1 and all other elements are 0. When we multiply an identity matrix by itself (or its inverse), we get the identity matrix again.

Please Login to comment...

Similar reads.

• Maths-Class-12
• Mathematics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.8: Solving Systems with Inverses

• Last updated
• Save as PDF
• Page ID 114083

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

In this section, you will:

• Find the inverse of a matrix.
• Solve a system of linear equations using an inverse matrix.

Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?

There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.

Finding the Inverse of a Matrix

We know that the multiplicative inverse of a real number aa is a−1,a−1, and aa−1=a−1a=(1a)a=1.aa−1=a−1a=(1a)a=1. For example, 2−1=122−1=12 and (12)2=1.(12)2=1. The multiplicative inverse of a matrix is similar in concept, except that the product of matrix AA and its inverse A−1A−1 equals the identity matrix. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by InIn where nn represents the dimension of the matrix. [link] and the following equations.

I2=[1001]I2=[ 1001 ]

I3=⎡⎣⎢100010001⎤⎦⎥I3=[ 100010001 ]

The identity matrix acts as a 1 in matrix algebra. For example, AI=IA=A.AI=IA=A.

A matrix that has a multiplicative inverse has the properties

AA−1=IA−1A=IAA−1=IA−1A=I

A matrix that has a multiplicative inverse is called an invertible matrix. Only a square matrix may have a multiplicative inverse, as the reversibility, AA−1=A−1A=I,AA−1=A−1A=I, is a requirement. Not all square matrices have an inverse, but if AA is invertible, then A−1A−1 is unique. We will look at two methods for finding the inverse of a 2×22×2 matrix and a third method that can be used on both 2×22×2 and 3×33×3 matrices.

THE IDENTITY MATRIX AND MULTIPLICATIVE INVERSE

The identity matrix , In,In, is a square matrix containing ones down the main diagonal and zeros everywhere else.

I2=[1001]I3=⎡⎣⎢100010001⎤⎦⎥ 2×2 3×3I2=[ 1001 ]I3=[ 100010001 ] 2×2 3×3

If AA is an n×nn×n matrix and BB is an n×nn×n matrix such that AB=BA=In,AB=BA=In, then B=A−1,B=A−1, the multiplicative inverse of a matrix A.A.

Showing That the Identity Matrix Acts as a 1

Given matrix A , show that AI=IA=A.AI=IA=A.

A=[3−245]A=[ 34−25 ]

Given two matrices, show that one is the multiplicative inverse of the other.

• Given matrix AA of order n×nn×n and matrix BB of order n×nn×n multiply AB.AB.
• If AB=I,AB=I, then find the product BA.BA. If BA=I,BA=I, then B=A−1B=A−1 and A=B−1.A=B−1.

Showing That Matrix A Is the Multiplicative Inverse of Matrix B

Show that the given matrices are multiplicative inverses of each other.

A=[1−25−9],B=[−92−51]A=[ 15−2−9 ],B=[ −9−521 ]

Show that the following two matrices are inverses of each other.

A=[1−14−3],B=[−31−41]A=[ 14−1−3 ],B=[ −3−411 ]

Finding the Multiplicative Inverse Using Matrix Multiplication

We can now determine whether two matrices are inverses, but how would we find the inverse of a given matrix? Since we know that the product of a matrix and its inverse is the identity matrix, we can find the inverse of a matrix by setting up an equation using matrix multiplication.

Use matrix multiplication to find the inverse of the given matrix.

A=[12−2−3]A=[ 1−22−3 ]

Finding the Multiplicative Inverse by Augmenting with the Identity

Another way to find the multiplicative inverse is by augmenting with the identity. When matrix AA is transformed into I,I, the augmented matrix II transforms into A−1.A−1.

For example, given

A=[2513]A=[ 2153 ]

augment AA with the identity

[2513∣∣∣1001][ 2153|1001 ]

Perform row operations with the goal of turning AA into the identity.

[5231∣∣∣0110][ 5321|0110 ]

[1211∣∣∣−2110][ 1121|−2110 ]

[101−1∣∣∣−251−2][ 110−1|−215−2 ]

[100−1∣∣∣35−1−2][ 100−1|3−15−2 ]

[1001∣∣∣3−5−12][ 1001|3−1−52 ]

The matrix we have found is A−1.A−1.

A−1=[3−5−12]A−1=[ 3−1−52 ]

Finding the Multiplicative Inverse of 2×2 Matrices Using a Formula

When we need to find the multiplicative inverse of a 2×22×2 matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.

If AA is a 2×22×2 matrix, such as

A=[acbd]A=[ abcd ]

the multiplicative inverse of AA is given by the formula

A−1=1ad−bc[d−c−ba]A−1=1ad−bc[ d−b−ca ]

where ad−bc≠0.ad−bc≠0. If ad−bc=0,ad−bc=0, then AA has no inverse.

Using the Formula to Find the Multiplicative Inverse of Matrix A

Use the formula to find the multiplicative inverse of

We can check that our formula works by using one of the other methods to calculate the inverse. Let’s augment AA with the identity.

[12−2−3∣∣∣1001][ 1−22−3|1001 ]

[10−21∣∣∣1−201][ 1−201|10−21 ]

[1001∣∣∣−3−221][ 1001|−32−21 ]

So, we have verified our original solution.

A−1=[−3−221]A−1=[ −32−21 ]

Use the formula to find the inverse of matrix A.A. Verify your answer by augmenting with the identity matrix.

A=[12−13]A=[ 1−123 ]

Finding the Inverse of the Matrix, If It Exists

Find the inverse, if it exists, of the given matrix.

A=[3162]A=[ 3612 ]

Finding the Multiplicative Inverse of 3×3 Matrices

Unfortunately, we do not have a formula similar to the one for a 2×22×2 matrix to find the inverse of a 3×33×3 matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.

Given a 3×33×3 matrix

A=⎡⎣⎢232334111⎤⎦⎥A=[ 231331241 ]

augment AA with the identity matrix

A∣∣∣∣I=⎡⎣⎢232334111 ∣∣∣∣ 100010001⎤⎦⎥A|I=[ 231331241 | 100010001 ]

To begin, we write the augmented matrix with the identity on the right and AA on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.

Given a 3×33×3 matrix, find the inverse

• Write the original matrix augmented with the identity matrix on the right.
• Use elementary row operations so that the identity appears on the left.
• What is obtained on the right is the inverse of the original matrix.
• Use matrix multiplication to show that AA−1=IAA−1=I and A−1A=I.A−1A=I.

Finding the Inverse of a 3 × 3 Matrix

Given the 3×33×3 matrix A,A, find the inverse.

To prove that B=A−1,B=A−1, let’s multiply the two matrices together to see if the product equals the identity, if AA−1=IAA−1=I and A−1A=I.A−1A=I.

AA−1=⎡⎣⎢232334111⎤⎦⎥ ⎡⎣⎢−1−1610−201−3⎤⎦⎥=⎡⎣⎢2(−1)+3(−1)+1(6)3(−1)+3(−1)+1(6)2(−1)+4(−1)+1(6)2(1)+3(0)+1(−2)3(1)+3(0)+1(−2)2(1)+4(0)+1(−2)2(0)+3(1)+1(−3)3(0)+3(1)+1(−3)2(0)+4(1)+1(−3)⎤⎦⎥=⎡⎣⎢100010001⎤⎦⎥AA−1=[ 231331241 ] [ −110−1016−2−3 ]=[ 2(−1)+3(−1)+1(6)2(1)+3(0)+1(−2)2(0)+3(1)+1(−3)3(−1)+3(−1)+1(6)3(1)+3(0)+1(−2)3(0)+3(1)+1(−3)2(−1)+4(−1)+1(6)2(1)+4(0)+1(−2)2(0)+4(1)+1(−3) ]=[ 100010001 ]

A−1A=⎡⎣⎢−1−1610−201−3⎤⎦⎥ ⎡⎣⎢232334111⎤⎦⎥=⎡⎣⎢−1(2)+1(3)+0(2)−1(2)+0(3)+1(2)6(2)+−2(3)+−3(2)−1(3)+1(3)+0(4)−1(3)+0(3)+1(4)6(3)+−2(3)+−3(4)−1(1)+1(1)+0(1)−1(1)+0(1)+1(1)6(1)+−2(1)+−3(1)⎤⎦⎥=⎡⎣⎢100010001⎤⎦⎥A−1A=[ −110−1016−2−3 ] [ 231331241 ]=[ −1(2)+1(3)+0(2)−1(3)+1(3)+0(4)−1(1)+1(1)+0(1)−1(2)+0(3)+1(2)−1(3)+0(3)+1(4)−1(1)+0(1)+1(1)6(2)+−2(3)+−3(2)6(3)+−2(3)+−3(4)6(1)+−2(1)+−3(1) ]=[ 100010001 ]

Find the inverse of the 3×33×3 matrix.

A=⎡⎣⎢2−10−1711311−7−2⎤⎦⎥A=[ 2−1711−111−703−2 ]

Solving a System of Linear Equations Using the Inverse of a Matrix

Solving a system of linear equations using the inverse of a matrix requires the definition of two new matrices: XX is the matrix representing the variables of the system, and BB is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as

To solve a system of linear equations using an inverse matrix, let AA be the coefficient matrix, let XX be the variable matrix, and let BB be the constant matrix. Thus, we want to solve a system AX=B.AX=B. For example, look at the following system of equations.

a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2

From this system, the coefficient matrix is

A=[a1a2b1b2]A=[ a1b1a2b2 ]

The variable matrix is

X=[xy]X=[ xy ]

And the constant matrix is

B=[c1c2]B=[ c1c2 ]

Then AX=BAX=B looks like

[a1a2b1b2] [xy]=[c1c2][ a1b1a2b2 ] [ xy ]=[ c1c2 ]

Recall the discussion earlier in this section regarding multiplying a real number by its inverse, (2−1)2=(12)2=1.(2−1)2=(12)2=1. To solve a single linear equation ax=bax=b for x,x, we would simply multiply both sides of the equation by the multiplicative inverse (reciprocal) of a.a. Thus,

ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1)b x=(a−1)b ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1)b x=(a−1)b

The only difference between a solving a linear equation and a system of equations written in matrix form is that finding the inverse of a matrix is more complicated, and matrix multiplication is a longer process. However, the goal is the same—to isolate the variable.

We will investigate this idea in detail, but it is helpful to begin with a 2×22×2 system and then move on to a 3×33×3 system.

SOLVING A SYSTEM OF EQUATIONS USING THE INVERSE OF A MATRIX

Given a system of equations, write the coefficient matrix A,A, the variable matrix X,X, and the constant matrix B.B. Then

Multiply both sides by the inverse of AA to obtain the solution.

(A−1)AX=(A−1)B[(A−1)A]X=(A−1)BIX=(A−1)BX=(A−1)B(A−1)AX=(A−1)B[ (A−1)A ]X=(A−1)BIX=(A−1)BX=(A−1)B

If the coefficient matrix does not have an inverse, does that mean the system has no solution?

No, if the coefficient matrix is not invertible, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions.

Solving a 2 × 2 System Using the Inverse of a Matrix

Solve the given system of equations using the inverse of a matrix.

3x+8y=54x+11y=73x+8y=54x+11y=7

Can we solve for XX by finding the product BA−1?BA−1?

No, recall that matrix multiplication is not commutative, so A−1B≠BA−1.A−1B≠BA−1. Consider our steps for solving the matrix equation.

Notice in the first step we multiplied both sides of the equation by A−1,A−1, but the A−1A−1 was to the left of AA on the left side and to the left of BB on the right side. Because matrix multiplication is not commutative, order matters.

Solving a 3 × 3 System Using the Inverse of a Matrix

Solve the following system using the inverse of a matrix.

5x+15y+56z=35−4x−11y−41z=−26−x−3y−11z=−75x+15y+56z=35−4x−11y−41z=−26−x−3y−11z=−7

Solve the system using the inverse of the coefficient matrix.

2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2 2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2

Given a system of equations, solve with matrix inverses using a calculator.

• Save the coefficient matrix and the constant matrix as matrix variables [A][ A ] and [B].[ B ].
• Enter the multiplication into the calculator, calling up each matrix variable as needed.
• If the coefficient matrix is invertible, the calculator will present the solution matrix; if the coefficient matrix is not invertible, the calculator will present an error message.

Using a Calculator to Solve a System of Equations with Matrix Inverses

Solve the system of equations with matrix inverses using a calculator

2x+3y+z=323x+3y+z=−272x+4y+z=−22x+3y+z=323x+3y+z=−272x+4y+z=−2

Access these online resources for additional instruction and practice with solving systems with inverses.

• The Identity Matrix
• Determining Inverse Matrices
• Using a Matrix Equation to Solve a System of Equations

9.7 Section Exercises

In a previous section, we showed that matrix multiplication is not commutative, that is, AB≠BAAB≠BA in most cases. Can you explain why matrix multiplication is commutative for matrix inverses, that is, A−1A=AA−1?A−1A=AA−1?

Does every 2×22×2 matrix have an inverse? Explain why or why not. Explain what condition is necessary for an inverse to exist.

Can you explain whether a 2×22×2 matrix with an entire row of zeros can have an inverse?

Can a matrix with an entire column of zeros have an inverse? Explain why or why not.

Can a matrix with zeros on the diagonal have an inverse? If so, find an example. If not, prove why not. For simplicity, assume a 2×22×2 matrix.

In the following exercises, show that matrix AA is the inverse of matrix B.B.

A=[1−101],B=[1101]A=[ 10−11 ],B=[ 1011 ]

A=[1324],B=[−2321−12]A=[ 1234 ],B=[ −2132−12 ]

A=[4750],B=[01517−435]A=[ 4570 ],B=[ 01715−435 ]

A=[−2312−1],B=[−2−6−1−4]A=[ −2123−1 ],B=[ −2−1−6−4 ]

A=⎡⎣⎢1000111−11⎤⎦⎥,B=12⎡⎣⎢20011−1−111⎤⎦⎥A=[ 10101−1011 ],B=12[ 21−10110−11 ]

A=⎡⎣⎢141206329⎤⎦⎥,B=14⎡⎣⎢617−120−32−2−54⎤⎦⎥A=[ 123402169 ],B=14[ 60−217−3−5−1224 ]

A=⎡⎣⎢3158162112⎤⎦⎥,B=136⎡⎣⎢−67−184−26−22−615⎤⎦⎥A=[ 3821115612 ],B=136[ −684−67−261−1−225 ]

For the following exercises, find the multiplicative inverse of each matrix, if it exists.

[31−29][ 3−219 ]

[−2321][ −2231 ]

[−3972][ −3792 ]

[−4−5−38][ −4−3−58 ]

[1212][ 1122 ]

[0110][ 0110 ]

[0.511.5−0.5][ 0.51.51−0.5 ]

⎡⎣⎢1−23010672⎤⎦⎥[ 106−217302 ]

⎡⎣⎢041110−305⎤⎦⎥[ 01−3410105 ]

⎡⎣⎢1−3−224−4−11−5⎤⎦⎥[ 12−1−341−2−4−5 ]

⎡⎣⎢12495−2−367⎤⎦⎥[ 19−32564−27 ]

⎡⎣⎢1−41−2843−122⎤⎦⎥[ 1−23−48−12142 ]

⎡⎣⎢⎢121316121417121518⎤⎦⎥⎥[ 121212131415161718 ]

⎡⎣⎢147258369⎤⎦⎥[ 123456789 ]

For the following exercises, solve the system using the inverse of a 2×22×2 matrix.

5x−6y=−614x+3y=−25x−6y=−614x+3y=−2

8x+4y=−1003x−4y=18x+4y=−1003x−4y=1

3x−2y=6−x+5y=−23x−2y=6−x+5y=−2

5x−4y=−54x+y=2.35x−4y=−54x+y=2.3

−3x−4y=912x+4y=−6−3x−4y=912x+4y=−6

−2x+3y=310−x+5y=12−2x+3y=310−x+5y=12

85x−45y=25−85x+15y=71085x−45y=25−85x+15y=710

12x+15y=−1412x−35y=−9412x+15y=−1412x−35y=−94

For the following exercises, solve a system using the inverse of a 3×33×3 matrix.

3x−2y+5z=215x+4y=37x−2y−5z=53x−2y+5z=215x+4y=37x−2y−5z=5

4x+4y+4z=402x−3y+4z=−12−x+3y+4z=94x+4y+4z=402x−3y+4z=−12−x+3y+4z=9

6x−5y−z=31−x+2y+z=−63x+3y+2z=136x−5y−z=31−x+2y+z=−63x+3y+2z=13

6x−5y+2z=−42x+5y−z=122x+5y+z=126x−5y+2z=−42x+5y−z=122x+5y+z=12

4x−2y+3z=−122x+2y−9z=336y−4z=14x−2y+3z=−122x+2y−9z=336y−4z=1

110x−15y+4z=−41215x−20y+25z=−101310x+4y−310z=23110x−15y+4z=−41215x−20y+25z=−101310x+4y−310z=23

12x−15y+15z=31100−34x−14y+12z=740−45x−12y+32z=1412x−15y+15z=31100−34x−14y+12z=740−45x−12y+32z=14

0.1x+0.2y+0.3z=−1.40.1x−0.2y+0.3z=0.60.4y+0.9z=−20.1x+0.2y+0.3z=−1.40.1x−0.2y+0.3z=0.60.4y+0.9z=−2

For the following exercises, use a calculator to solve the system of equations with matrix inverses.

2x−y=−3−x+2y=2.32x−y=−3−x+2y=2.3

−12x−32y=−432052x+115y=314−12x−32y=−432052x+115y=314

12.3x−2y−2.5z=236.9x+7y−7.5z=−78y−5z=−1012.3x−2y−2.5z=236.9x+7y−7.5z=−78y−5z=−10

0.5x−3y+6z=−0.80.7x−2y=−0.060.5x+4y+5z=00.5x−3y+6z=−0.80.7x−2y=−0.060.5x+4y+5z=0

For the following exercises, find the inverse of the given matrix.

⎡⎣⎢⎢⎢⎢1000011010110101⎤⎦⎥⎥⎥⎥[ 1010010101100011 ]

⎡⎣⎢⎢⎢⎢−1001002−320−105201⎤⎦⎥⎥⎥⎥[ −1025000202−101−301 ]

⎡⎣⎢⎢⎢⎢101−5−214030−210231⎤⎦⎥⎥⎥⎥[ 1−230010214−23−5011 ]

⎡⎣⎢⎢⎢⎢⎢⎢1000022020013012000230110⎤⎦⎥⎥⎥⎥⎥⎥[ 1202302100003010200100120 ]

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢100001010001001001000101000011000001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥[ 100000010000001000000100000010111111 ]

Real-World Applications

For the following exercises, write a system of equations that represents the situation. Then, solve the system using the inverse of a matrix.

2,400 tickets were sold for a basketball game. If the prices for floor 1 and floor 2 were different, and the total amount of money brought in is $64,000, how much was the price of each ticket?

In the previous exercise, if you were told there were 400 more tickets sold for floor 2 than floor 1, how much was the price of each ticket?

A food drive collected two different types of canned goods, green beans and kidney beans. The total number of collected cans was 350 and the total weight of all donated food was 348 lb, 12 oz. If the green bean cans weigh 2 oz less than the kidney bean cans, how many of each can was donated?

Students were asked to bring their favorite fruit to class. 95% of the fruits consisted of banana, apple, and oranges. If oranges were twice as popular as bananas, and apples were 5% less popular than bananas, what are the percentages of each individual fruit?

A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at $1 and the chocolate chip cookies at $0.75. They raised $700 and sold 850 items. How many brownies and how many cookies were sold?

A clothing store needs to order new inventory. It has three different types of hats for sale: straw hats, beanies, and cowboy hats. The straw hat is priced at $13.99, the beanie at $7.99, and the cowboy hat at $14.49. If 100 hats were sold this past quarter, $1,119 was taken in by sales, and the amount of beanies sold was 10 more than cowboy hats, how many of each should the clothing store order to replace those already sold?

Anna, Ashley, and Andrea weigh a combined 370 lb. If Andrea weighs 20 lb more than Ashley, and Anna weighs 1.5 times as much as Ashley, how much does each girl weigh?

Three roommates shared a package of 12 ice cream bars, but no one remembers who ate how many. If Tom ate twice as many ice cream bars as Joe, and Albert ate three less than Tom, how many ice cream bars did each roommate eat?

A farmer constructed a chicken coop out of chicken wire, wood, and plywood. The chicken wire cost $2 per square foot, the wood $10 per square foot, and the plywood $5 per square foot. The farmer spent a total of $51, and the total amount of materials used was 14ft2.14ft2. He used 3 ft23 ft2 more chicken wire than plywood. How much of each material in did the farmer use?

Jay has lemon, orange, and pomegranate trees in his backyard. An orange weighs 8 oz, a lemon 5 oz, and a pomegranate 11 oz. Jay picked 142 pieces of fruit weighing a total of 70 lb, 10 oz. He picked 15.5 times more oranges than pomegranates. How many of each fruit did Jay pick?

Chapter 2 Matrices

2.4 Solving Systems with Inverses

Learning Objectives

By the end of this section, you will be able to:

• Use the formula for [latex]2\times2[/latex] matrices
• Use augmenting for [latex]2\times2[/latex] and [latex]3\times 3[/latex] matrices
• Use the inverse to solve a system of equations

Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?

There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.

Finding the Inverse of a Matrix

The multiplicative inverse of a real number [latex]a[/latex] is [latex]a^{-1}[/latex], where the product is 1: [latex]aa^{-1}=a^{-1}a=(\frac{1}{a})a=1[/latex]. For example, [latex]2^{-1}=\frac{1}{2}[/latex] and [latex](\frac{1}{2})2=1[/latex]. The multiplicative inverse of a matrix is similar in concept, except that the product of matrix [latex]A[/latex]   and its inverse [latex]A^{-1}[/latex] equals the identity matrix . The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by [latex]I_n[/latex] where [latex]n[/latex]   represents the dimension of the matrix.  Shown below are the identity matrices for a [latex]2\times2[/latex] matrix and a [latex]3\times3[/latex] matrix, respectively.

[latex]I_2=\begin{bmatrix} 1&0\\0&1\end{bmatrix}[/latex], [latex]I_3=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}[/latex]

The identity matrix acts as a 1 in matrix algebra. For example, [latex]AI=IA=A[/latex]

A matrix that has a multiplicative inverse has the properties

[latex]\begin{array}{rcl} AA^{-1} & = & I\\ A^{-1}A & = & I\\ \end{array}[/latex]

A matrix that has a multiplicative inverse is called an invertible matrix. Only a square matrix may have a multiplicative inverse, as the reversibility, [latex]AA^{-1}=A^{-1}A=I[/latex], is a requirement. Not all square matrices have an inverse, but if [latex]A[/latex]    is invertible, then [latex]A^{-1}[/latex] is unique. We will look at two methods for finding the inverse of a [latex]2\times2[/latex] matrix and a third method that can be used on both [latex]2\times2[/latex] and [latex]3\times3[/latex] matrices.

The Identity Matrix and Multiplicative Inverse

The identity matrix , [latex]I_n[/latex],   is a square matrix containing ones down the main diagonal and zeros everywhere else.

[latex]\begin{array}{rcc}I_2&=&\begin{bmatrix} 1&0\\0&1\end{bmatrix}\\& & 2\times2\end{array}[/latex] [latex]\begin{array}{rcc}I_3&=&\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\\& & 3\times3\end{array}[/latex]

If [latex]A[/latex]   is an [latex]n\times n[/latex] matrix and [latex]B[/latex]   is an [latex]n\times n[/latex] matrix such that [latex]AB=BA=I_n[/latex] then [latex]B=A^{-1}[/latex], the multiplicative inverse of a matrix [latex]A[/latex].

Given matrix [latex]A[/latex] , show that [latex]AI=IA=A[/latex].

[latex]A=\begin{bmatrix} 3&4\\-2&5\end{bmatrix}[/latex]

Use matrix multiplication to show that the product of  and the identity is equal to the product of the identity and A.

[latex]AI=\begin{bmatrix} 3&4\\-2&5\end{bmatrix}\begin{bmatrix} 1&0\\0&1\end{bmatrix}=\begin{bmatrix} 3\cdot1+4\cdot0&3\cdot0+4\cdot1\\-2\cdot1+5\cdot0&-2\cdot0+5\cdot1\end{bmatrix}=\begin{bmatrix} 3&4\\-2&5\end{bmatrix}[/latex]

[latex]IA=\begin{bmatrix} 1&0\\0&1\end{bmatrix}\begin{bmatrix} 3&4\\-2&5\end{bmatrix}=\begin{bmatrix} 1\cdot3+0\cdot-2&1\cdot4+0\cdot5\\0\cdot3+1\cdot-2&0\cdot4+1\cdot5\end{bmatrix}=\begin{bmatrix} 3&4\\-2&5\end{bmatrix}[/latex]

To work this problem using the matrix calculator, click here .

Given two matrices, show that one is the multiplicative inverse of the other.

• Given matrix [latex]A[/latex] of order [latex]n\times n[/latex] and matrix [latex]B[/latex] of order [latex]n\times n[/latex] multiply [latex]AB[/latex].
• If [latex]AB=I[/latex] then find the product [latex]BA[/latex]. If [latex]BA=I[/latex] then [latex]B=A^{-1}[/latex] and [latex]A=B^{-1}[/latex].

Show that the given matrices are multiplicative inverses of each other.

[latex]A=\begin{bmatrix} 1&5\\-2&-9\end{bmatrix}[/latex], [latex]B=\begin{bmatrix} -9&-5\\2&1\end{bmatrix}[/latex]

Multiply [latex]AB[/latex] and [latex]BA[/latex] If both products equal the identity, then the two matrices are inverses of each other.

[latex]\begin{array}{rcl}AB&=&\begin{bmatrix} 1&5\\-2&-9\end{bmatrix}\begin{bmatrix} -9&-5\\2&1\end{bmatrix}\\ &=&\begin{bmatrix} 1\cdot-9+5\cdot2&1\cdot-5+5\cdot1\\-2\cdot-9-9\cdot2&-2\cdot-5+-9\cdot1\end{bmatrix}\\ &=&\begin{bmatrix} 1&0\\0&1\end{bmatrix}\\ \end{array}[/latex]

[latex]\begin{array}{rcl}BA&=&\begin{bmatrix} -9&-5\\2&1\end{bmatrix}\begin{bmatrix} 1&5\\-2&-9\end{bmatrix}\\ &=&\begin{bmatrix} -9\cdot1-5\cdot-2&-9\cdot5-5\cdot-9\\2\cdot1+1\cdot-2&2\cdot-5+1\cdot-9\end{bmatrix}\\ &=&\begin{bmatrix} 1&0\\0&1\end{bmatrix} \end{array}[/latex]

[latex]A[/latex] and [latex]B[/latex]are inverses of each other.

Show that the following two matrices are inverses of each other.

[latex]A=\begin{bmatrix} 1&4\\-1&-3\end{bmatrix}[/latex], [latex]B=\begin{bmatrix} -3&-4\\1&1\end{bmatrix}[/latex]

[latex]AB=\begin{bmatrix} 1&0\\0&1\end{bmatrix}=BA[/latex]

Finding the Multiplicative Inverse by Augmenting with the Identity

One way to find the multiplicative inverse is by augmenting with the identity. When matrix [latex]A[/latex] is transformed into [latex]I[/latex], the augmented matrix [latex]I[/latex] transforms into [latex]A^{-1}[/latex].

Given [latex]A=\begin{bmatrix}2&1\\5&3\end{bmatrix}[/latex], augment [latex]A[/latex]   with the identity [latex]\left[ \begin{array}{cc|cc}2&1&1&0\\5&3&0&1\end{array}\right][/latex].

Perform row operations with the goal of turning   into the identity.

Switch row 1 and row 2.

[latex]\left[ \begin{array}{cc|cc}5&3&0&1\\2&1&1&0\end{array}\right][/latex]

Multiply row 2 by –2 and add to row 1.

[latex]\left[ \begin{array}{cc|cc}1&1&-2&1\\2&1&1&0\end{array}\right][/latex]

Multiply row 1 by –2 and add to row 2.

[latex]\left[ \begin{array}{cc|cc}1&1&-2&1\\0&-1&5&-2\end{array}\right][/latex]

Add row 2 to row 1.

[latex]\left[ \begin{array}{cc|cc}1&0&3&-1\\0&-1&5&-2\end{array}\right][/latex]

Multiply row 2 by –1.

[latex]\left[ \begin{array}{cc|cc}1&0&3&-1\\0&1&-5&2\end{array}\right][/latex]

The matrix we have found is [latex]A^{-1}[/latex].

[latex]A^{-1}=\begin{bmatrix}3&-1\\-5&2\end{bmatrix}[/latex]

Finding the Multiplicative Inverse of [latex]2\times2[/latex] Matrices Using a Formula

When we need to find the multiplicative inverse of a  matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.

Formula for the Inverse of a 2 by 2 Matrix

If [latex]A[/latex]   is a [latex]2\times2[/latex] matrix, such as [latex]A=\begin{bmatrix}a&b\\c&d\end{bmatrix}[/latex]

the multiplicative inverse of A is given by the formula

[latex]A^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d&-b\\-c&a\end{bmatrix}[/latex]

where [latex]ad-bc\neq0[/latex]. If [latex]ad-bc=0[/latex] then [latex]A[/latex] has no inverse.

Use the formula to find the multiplicative inverse of

[latex]A=\begin{bmatrix}2&1\\5&3\end{bmatrix}[/latex]  

Using the formula, we have

[latex]\begin{array}{rcl}A^{-1}&=&\frac{1}{(2)(3)-(5)(1)}\begin{bmatrix}3&-1\\-5&2\end{bmatrix}\\ &=&\frac{1}{1}\begin{bmatrix}3&-1\\-5&2\end{bmatrix}\\ &=&\begin{bmatrix}3&-1\\-5&2\end{bmatrix}\\ \end{array}[/latex]

Notice this matches the inverse we found above by augmenting with the identity matrix.

Use the formula to find the inverse of matrix [latex]A=\begin{bmatrix}1&-1\\2&3\end{bmatrix}[/latex].

Verify your answer by augmenting with the identity matrix.

[latex]A^{-1}=\begin{bmatrix}\frac{3}{5}&\frac{1}{5}\\-\frac{2}{5}&\frac{1}{5}\end{bmatrix}[/latex]

Find the inverse, if it exists, of the given matrix: [latex]A=\begin{bmatrix} 3&6\\1&2\end{bmatrix}[/latex].

We will use the method of augmenting with the identity.

[latex]\left[ \begin{array}{cc|cc}3&6&1&0\\1&2&0&1\end{array}\right][/latex]

[latex]\left[ \begin{array}{cc|cc}1&2&0&1\\3&6&1&0\end{array}\right][/latex]

Multiply row 1 by [latex]-3[/latex] and add it to row 2.

[latex]\left[ \begin{array}{cc|cc}1&2&0&1\\0&0&1&-3\end{array}\right][/latex]

There is nothing further we can do. The zeros in row 2 indicate that this matrix has no inverse.

Finding the Multiplicative Inverse of  Matrices

Unfortunately, we do not have a formula similar to the one for a [latex]2\times2[/latex] matrix to find the inverse of a [latex]3\times3[/latex] matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.

Given a [latex]3\times3[/latex]   matrix

[latex]A=\begin{bmatrix}2&3&1\\3&3&1\\2&4&1\end{bmatrix}[/latex]

augment [latex]A[/latex] with the identity matrix

[latex]A|I=\left[\begin{array}{ccc|ccc}2&3&1&1&0&0\\3&3&1&0&1&0\\2&4&1&0&0&1\end{array}\right][/latex]

To begin, we write the augmented matrix with the identity on the right and [latex]A[/latex]   on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.

Given a 3 by 3 matrix, find the inverse

• Write the original matrix augmented with the identity matrix on the right.
• Use elementary row operations so that the identity appears on the left.
• What is obtained on the right is the inverse of the original matrix.
• Use matrix multiplication to show that [latex]AA^{-1}=I[/latex] and [latex]A^{-1}A=I[/latex].

Given the [latex]3\times3[/latex] matrix [latex]A[/latex], find the inverse.

Augment [latex]A[/latex]   with the identity matrix, and then begin row operations until the identity matrix replaces [latex]A[/latex]. The matrix on the right will be the inverse of [latex]A[/latex].

[latex]A=\left[\begin{array}{ccc|ccc}2&3&1&1&0&0\\3&3&1&0&1&0\\2&4&1&0&0&1\end{array}\right] \xrightarrow[ ]{ \text {Interchange }R_2 \text{ and } R_1} \left[\begin{array}{ccc|ccc}3&3&1&0&1&0\\2&3&1&1&0&0\\2&4&1&0&0&1\end{array}\right][/latex]

[latex]-R_2+R_1=R_1 \longrightarrow \left[ \begin{array}{ccc|ccc}1&0&0&-1&1&0\\2&3&1&1&0&0\\2&4&1&0&0&1 \end{array} \right][/latex]

[latex]-R_2+R_3=R_3 \longrightarrow \left[ \begin{array}{ccc|ccc}1&0&0&-1&1&0\\2&3&1&1&0&0\\0&1&0&-1&0&1 \end{array} \right][/latex]

[latex]R_1\leftrightarrow R_2 \longrightarrow \left[ \begin{array}{ccc|ccc}1&0&0&-1&1&0\\0&1&0&-1&0&1\\2&3&1&1&0&0 \end{array} \right][/latex]

[latex]-2R_1+R_3=R_3 \longrightarrow \left[ \begin{array}{ccc|ccc}1&0&0&-1&1&0\\0&1&0&-1&0&1\\0&3&1&3&-2&0 \end{array} \right][/latex]

[latex]-3R_2+R_3=R_3 \longrightarrow \left[ \begin{array}{ccc|ccc}1&0&0&-1&1&0\\0&1&0&-1&0&1\\0&0&1&6&-2&-3 \end{array} \right][/latex]

[latex]A^{-1}=B=\begin{bmatrix}-1&1&0\\-1&0&1\\6&-2&-3\end{bmatrix}[/latex]

To prove that [latex]B=A^{-1}[/latex] let’s multiply the two matrices together to see if the product equals the identity, if [latex]AA^{-1}=I[/latex] and [latex]A^{-1}A=I[/latex].

[latex]\begin{array}{rcl}AA^{-1}&=&\begin{bmatrix}2&3&1\\3&3&1\\2&4&1\end{bmatrix}\begin{bmatrix}-1&1&0\\-1&0&1\\6&-2&-3\end{bmatrix}\\ &=&\begin{bmatrix}2(-1)+3(-1)+1(6)&2(1)+3(0)+1(-2)&2(0)+3(1)+1(-3)\\3(-1)+3(-1)+1(6)&3(1)+3(0)+1(-2)&3(0)+3(1)+1(-3)\\2(-1)+4(-1)+1(6)&2(1)+4(0)+1(-2)&2(0)+4(1)+1(-3)\end{bmatrix}\\ &=&\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\end{array}[/latex]

[latex]\begin{array}{rcl}A^{-1}A&=&\begin{bmatrix}-1&1&0\\-1&0&1\\6&-2&-3\end{bmatrix}\begin{bmatrix}2&3&1\\3&3&1\\2&4&1\end{bmatrix}\\ &=&\begin{bmatrix}-1(2)+1(3)+0(2)&-1(3)+1(3)+0(4)&-1(1)+1(1)+0(1)\\-1(2)+0(3)+1(2)&-1(3)+0(3)+1(4)&-1(1)+0(1)+1(1)\\6(2)+(-2)(3)+(-3)(2)&6(3)+(-2)(3)+(-3)(4)&6(1)+(-2)(1)+(-3)(1)\end{bmatrix}\\ &=&\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\end{array}[/latex]

Find the inverse of the  matrix.

[latex]A=\begin{bmatrix}2&-17&11\\-1&11&-7\\0&3&-2\end{bmatrix}[/latex]

[latex]A^{-1}=\begin{bmatrix}1&1&2\\2&4&-3\\3&6&-5\end{bmatrix}[/latex]

Solving a System of Linear Equations Using the Inverse of a Matrix

Solving a system of linear equations using the inverse of a matrix requires the definition of two new matrices: [latex]X[/latex] is the matrix representing the variables of the system, and [latex]B[/latex]   is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as

[latex]AX=B[/latex]

To solve a system of linear equations using an inverse matrix, let [latex]A[/latex]   be the coefficient matrix, let [latex]X[/latex] be the variable matrix, and let [latex]B[/latex]   be the constant matrix. Thus, we want to solve a system [latex]AX=B[/latex]. For example, look at the following system of equations.

[latex]\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end {cases}[/latex]

From this system, the coefficient matrix is

[latex]A=\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}[/latex]

The variable matrix is

[latex]X=\begin{bmatrix}x\\y\end{bmatrix}[/latex]

And the constant matrix is

[latex]B=\begin{bmatrix}c_1\\c_2\end{bmatrix}[/latex]

Then [latex]AX=B[/latex] looks like

[latex]\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}c_1\\c_2\end{bmatrix}[/latex]

Solving this system of equations written in matrix form is similar to solving a linear equation, except there is no matrix “division” so instead we need to use the inverse. The goal is the same—to isolate the variable.  We will investigate this idea in detail, but it is helpful to begin with a [latex]2\times2[/latex] system and then move on to a [latex]3\times3[/latex] system.

Solving a System of Equations Using the Inverse of a Matrix

Given a system of equations, write the coefficient matrix [latex]A[/latex], the variable matrix [latex]X[/latex], and the constant matrix [latex]B[/latex]. Then

Multiply both sides by the inverse of  to obtain the solution.

[latex]\begin{array}{rcl}(A^{-1})AX&=&(A^{-1})B\\ [(A^{-1})A]X&=&(A^{-1})B\\ IX&=&(A^{-1})B\\ X&=&(A^{-1})B\\ \end{array}[/latex]

Important:  If the coefficient matrix does not have an inverse, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions.

Solve the given system of equations using the inverse of a matrix.

[latex]\begin{cases}3x+8y=5\\4x+11y=7\end {cases}[/latex]

  Write the system in terms of a coefficient matrix, a variable matrix, and a constant matrix.

[latex]A=\begin{bmatrix}3&8\\4&11\end{bmatrix}[/latex], [latex]X=\begin{bmatrix}x\\y\end{bmatrix}[/latex], [latex]B=\begin{bmatrix}5\\7\end{bmatrix}[/latex]

[latex]\begin{bmatrix}3&8\\4&11\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}5\\7\end{bmatrix}[/latex]

Using the formula to calculate [latex]A^{-1}[/latex], we have:

[latex]\begin{array}{rcl}A^{-1}&=&\frac{1}{(ad-bc)}\begin{bmatrix}d&-b\\-c&a\end{bmatrix}\\ &=&\frac{1}{3(11)-8(4)}\begin{bmatrix}11&-8\\-4&3\end{bmatrix}\\ &=&\frac{1}{1}\begin{bmatrix}11&-8\\-4&3\end{bmatrix}\\ A^{-1}&=&\begin{bmatrix}11&-8\\-4&3\end{bmatrix}\\ \end{array}[/latex]

Now we are ready to solve. Multiply both sides of the equation by [latex]A^{-1}[/latex].

[latex]\begin{array}{rcl}(A^{-1})AX&=&(A^{-1})B\\ \begin{bmatrix}11&-8\\-4&3\end{bmatrix}\begin{bmatrix}3&8\\4&11\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}&=&\begin{bmatrix}11&-8\\-4&3\end{bmatrix}\begin{bmatrix}5\\7\end{bmatrix}\\ \begin{bmatrix}1&0\\0&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}&=&\begin{bmatrix}11(5)+(-8)(7)\\-4(5)+3(7)\end{bmatrix}\\ \begin{bmatrix}x\\y\end{bmatrix}&=&\begin{bmatrix}-1\\1\end{bmatrix}\\ \end{array}[/latex].

The solution is [latex](-1,1)[/latex].

Note that you cannot solve for [latex]X[/latex] by finding the product [latex]BA^{-1}[/latex].  Recall that matrix multiplication is not commutative, so [latex]A^{-1}B\neq A^{-1}[/latex]. Consider our steps for solving the matrix equation.

Notice in the first step we multiplied both sides of the equation by [latex]A^{-1}[/latex], but the [latex]A^{-1}[/latex] was to the left of [latex]A[/latex] on the left side and to the left of [latex]B[/latex] on the right side. Because matrix multiplication is not commutative, order matters.

Solve the following system using the inverse of a matrix.

[latex]\begin{cases}5x+15y+56z=35\\-4x-11y-41z=-26\\-x-3y-11z=-7\end {cases}[/latex]

  Write the equation [latex]AX=B[/latex].

[latex]\begin{bmatrix}5&15&56\\-4&-11&-41\\-1&-3&-11\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}35\\-26\\-7\end{bmatrix}[/latex]

First, we will find the inverse of [latex]A[/latex] by augmenting with the identity.

[latex]\left[ \begin{array}{ccc|ccc}5&15&56&1&0&0\\-4&-11&-41&0&1&0\\-1&-3&-11&0&0&1\end{array}\right][/latex]

Multiply row 1 by [latex]\frac{1}{5}[/latex].

[latex]\left[ \begin{array}{ccc|ccc}1&3&\frac{56}{5}&\frac{1}{5}&0&0\\-4&-11&-41&0&1&0\\-1&-3&-11&0&0&1\end{array}\right][/latex]

Multiply row 1 by 4 and add to row 2.

[latex]\left[ \begin{array}{ccc|ccc}1&3&\frac{56}{5}&\frac{1}{5}&0&0\\0&1&\frac{19}{5}&\frac{4}{5}&1&0\\-1&-3&-11&0&0&1\end{array}\right][/latex]

Add row 1 to row 3.

[latex]\left[ \begin{array}{ccc|ccc}1&3&\frac{56}{5}&\frac{1}{5}&0&0\\0&1&\frac{19}{5}&\frac{4}{5}&1&0\\0&0&\frac{1}{5}&\frac{1}{5}&0&1\end{array}\right][/latex]

Multiply row 2 by −3 and add to row 1.

[latex]\left[ \begin{array}{ccc|ccc}1&3&-\frac{1}{5}&-\frac{11}{5}&-3&0\\0&1&\frac{19}{5}&\frac{4}{5}&1&0\\0&0&\frac{1}{5}&\frac{1}{5}&0&1\end{array}\right][/latex]

Multiply row 3 by 5.

[latex]\left[ \begin{array}{ccc|ccc}1&3&-\frac{1}{5}&-\frac{11}{5}&-3&0\\0&1&\frac{19}{5}&\frac{4}{5}&1&0\\0&0&1&1&0&5\end{array}\right][/latex]

Multiply row 3 by [latex]\frac{1}{5}[/latex] and add to row 1.

[latex]\left[ \begin{array}{ccc|ccc}1&0&0&-2&-3&1\\0&1&\frac{19}{5}&\frac{4}{5}&1&0\\0&0&1&1&0&5\end{array}\right][/latex]

Multiply row 3 by [latex]-\frac{19}{5}[/latex]  and add to row 2.

[latex]\left[ \begin{array}{ccc|ccc}1&0&0&-2&-3&1\\0&1&0&-3&1&-19\\0&0&1&1&0&5\end{array}\right][/latex]

[latex]A^{-1}=\begin{bmatrix}-2&-3&1\\-3&1&-19\\1&0&5\end{bmatrix}[/latex]

Multiply both sides of the equation by [latex]A^{-1}[/latex]. We want [latex]A^{-1}AX=A^{-1}B[/latex]:

[latex]\begin{bmatrix}-2&-3&1\\-3&1&-19\\1&0&5\end{bmatrix}\begin{bmatrix}5&15&56\\-4&-11&-41\\-1&-3&-11\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}-2&-3&1\\-3&1&-19\\1&0&5\end{bmatrix}\begin{bmatrix}35\\-26\\-7\end{bmatrix}[/latex]

[latex]A^{-1}B=\begin{bmatrix}70+78-7\\-105-26+133\\35+0-35\end{bmatrix}=\begin{bmatrix}1\\2\\0\end{bmatrix}[/latex]

The solution is [latex](1,2,0)[/latex].

Solve the system using the inverse of the coefficient matrix.

[latex]\begin{cases}2x-17y+11z=0\\-x+11y-7z=8\\3y-2z=-2\end {cases}[/latex]

[latex]X=\begin{bmatrix}1\\2\\0\end{bmatrix}[/latex], so [latex]x=4[/latex], [latex]y=38[/latex], [latex]z=58[/latex]

Systems of equations in many variables can get very complex, but solving using matrices can easily be handled by calculators or computers.

Given a system of equations, solve with matrix inverses using a calculator.

• Save the coefficient matrix and the constant matrix as matrix variables [latex][A][/latex] and [latex][B][/latex].
• Enter the multiplication into the calculator, calling up each matrix variable as needed.
• If the coefficient matrix is invertible, the calculator will present the solution matrix; if the coefficient matrix is not invertible, the calculator will present an error message.

A matrix whose product with another matrix results in the identity matrix; also called the inverse of a matrix

A square matrix containing ones down the main diagonal and zeros everywhere else; the identity matrix acts as a 1 in matrix algebra

Finite Mathematics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

MULTIPLICATIVE INVERSES OF MATRICES

In this section multiplicative identity elements and multiplicative inverses are introduced and used to solve matrix equations. This leads to another method for solving systems of equations. IDENTITY MATRICES The identity property for real numbers says that a * I = a and I * a = a for any real number a. If there is to be a multiplicative identity matrix I, such that:

 AI = A and  IA = A,

for any matrix A, then A and I must be square matrices of the same size. Otherwise it would not be possible to find both products. For example, let A be the 2 X 2 matrix and let

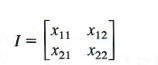
Check that with this definition of I, both Al = A and IA = A.  

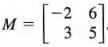
Verify that MI = M and IM = M

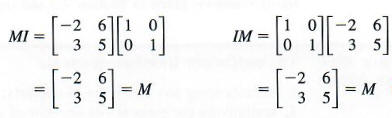
The 2 X 2 identity matrix found above suggests the following generalization: n x n IDENTITY MATRIX

For any value of n there is an n X n identity matrix having l's down the diagonal and 0's elsewhere. The n x n identity matrix is given by l where:

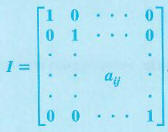
Here aij = 1 when i = j (the diagonal elements) and aaj = 0 otherwise.

Example 2 - STATING AND VERIFYING THE 3 X 3 IDENTITY MATRIX Let K =

By the definition of matrix multiplication,  

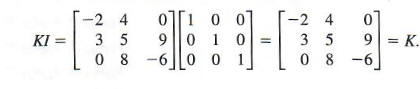
Recall that l/a can also be written a^(-1). In the rest of this section, a method is developed for finding a multiplicative inverse for square matrices. The multiplicative inverse of a matrix A is written A^(-1). This matrix must satisfy the statements

The multiplicative inverse of a matrix can be found using the matrix row transformations given in the previous tutorial and repeated here for convenience.

MATRIX ROW TRANSFORMATIONS

The matrix row transformations are:

interchanging any two rows of a matrix;

multiplying the elements of any row of a matrix by the same nonzero scalar k; and

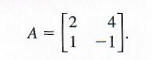
Let the unknown inverse matrix be

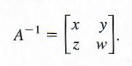
By the definition of matrix inverse, AA^(-1) = 1, or

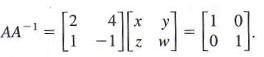
Setting corresponding elements equal gives the system of equations

Since equations (1) and (3) involve only x and z, while equations (2) and (4) involve only y and w, these four equations lead to two systems of equations, 2x + 4z = 1 x-z=0

2y + 4w = 0 y-w=1. Writing the two systems as augmented matrices gives

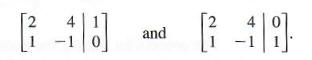
The numbers in the first column to the right of the vertical bar give the values of x and z. The second column gives the values of y and w. That is,

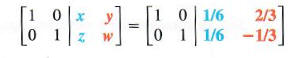
To check, multiply A by A^(-1). The result should be I

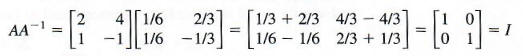
Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Browse Course Material

Course info.

• Prof. Gilbert Strang

Departments

• Mathematics

As Taught In

• Linear Algebra

Learning Resource Types

Problem solving: powers of a matrix.

• Download video
• Download transcript

Study Guides > Precalculus II

Solving systems with inverses, learning objectives.

• Find the inverse of a matrix.
• Solve a system of linear equations using an inverse matrix.

Finding the Inverse of a Matrix

A general note: the identity matrix and multiplicative inverse, example 1: showing that the identity matrix acts as a 1, how to: given two matrices, show that one is the multiplicative inverse of the other..

• Given matrix [latex]A[/latex] of order [latex]n\times n[/latex] and matrix [latex]B[/latex] of order [latex]n\times n[/latex] multiply [latex]AB[/latex].
• If [latex]AB=I[/latex], then find the product [latex]BA[/latex]. If [latex]BA=I[/latex], then [latex]B={A}^{-1}[/latex] and [latex]A={B}^{-1}[/latex].

Example 2: Showing That Matrix A Is the Multiplicative Inverse of Matrix B

Finding the multiplicative inverse using matrix multiplication, example 3: finding the multiplicative inverse using matrix multiplication, finding the multiplicative inverse by augmenting with the identity.

• Switch row 1 and row 2. [latex]\left[\begin{array}{rr}\hfill 5& \hfill 3\\ \hfill 2& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 0& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right][/latex]
• Multiply row 2 by [latex]-2[/latex] and add to row 1. [latex]\left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 2& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right][/latex]
• Multiply row 1 by [latex]-2[/latex] and add to row 2. [latex]\left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 0& \hfill -1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 5& \hfill -2\end{array}\right][/latex]
• Add row 2 to row 1. [latex]\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill -1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 3& \hfill -1\\ \hfill 5& \hfill -2\end{array}\right][/latex]
• Multiply row 2 by [latex]-1[/latex]. [latex]\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1\end{array}\text{ }|\text{ }\begin{array}{rr}\hfill 3& \hfill -1\\ \hfill -5& \hfill 2\end{array}\right][/latex]

Finding the Multiplicative Inverse of 2×2 Matrices Using a Formula

Example 4: using the formula to find the multiplicative inverse of matrix a, analysis of the solution.

• Multiply row 1 by [latex]-2[/latex] and add to row 2. [latex]\left[\begin{array}{cc}1& -2\\ 0& 1\end{array}|\begin{array}{cc}1& 0\\ -2& 1\end{array}\right][/latex]
• Multiply row 1 by 2 and add to row 1. [latex]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}|\begin{array}{cc}-3& 2\\ -2& 1\end{array}\right][/latex]

Example 5: Finding the Inverse of the Matrix, If It Exists

• Switch row 1 and row 2. [latex]\left[\begin{array}{cc}1& 3\\ 3& 6\text{ }\end{array}\text{ }\text{ }\text{ }|\begin{array}{cc}0& 1\\ 1& 0\end{array}\right][/latex]
• Multiply row 1 by −3 and add it to row 2. [latex]\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}|\begin{array}{cc}1& 0\\ -3& 1\end{array}\right][/latex]
• There is nothing further we can do. The zeros in row 2 indicate that this matrix has no inverse.

Finding the Multiplicative Inverse of 3×3 Matrices

How to: given a [latex]3\times 3[/latex] matrix, find the inverse.

• Write the original matrix augmented with the identity matrix on the right.
• Use elementary row operations so that the identity appears on the left.
• What is obtained on the right is the inverse of the original matrix.
• Use matrix multiplication to show that [latex]A{A}^{-1}=I[/latex] and [latex]{A}^{-1}A=I[/latex].

Example 6: Finding the Inverse of a 3 × 3 Matrix

 solving a system of linear equations using the inverse of a matrix, a general note: solving a system of equations using the inverse of a matrix, if the coefficient matrix does not have an inverse, does that mean the system has no solution, example 7: solving a 2 × 2 system using the inverse of a matrix, can we solve for [latex]x[/latex] by finding the product [latex]b{a}^{-1}[/latex], example 8: solving a 3 × 3 system using the inverse of a matrix, how to: given a system of equations, solve with matrix inverses using a calculator..

• Save the coefficient matrix and the constant matrix as matrix variables [latex]\left[A\right][/latex] and [latex]\left[B\right][/latex].
• Enter the multiplication into the calculator, calling up each matrix variable as needed.
• If the coefficient matrix is invertible, the calculator will present the solution matrix; if the coefficient matrix is not invertible, the calculator will present an error message.

Example 9: Using a Calculator to Solve a System of Equations with Matrix Inverses

Key equations, key concepts.

• An identity matrix has the property [latex]AI=IA=A[/latex].
• An invertible matrix has the property [latex]A{A}^{-1}={A}^{-1}A=I[/latex].
• Use matrix multiplication and the identity to find the inverse of a [latex]2\times 2[/latex] matrix.
• The multiplicative inverse can be found using a formula.
• Another method of finding the inverse is by augmenting with the identity.
• We can augment a [latex]3\times 3[/latex] matrix with the identity on the right and use row operations to turn the original matrix into the identity, and the matrix on the right becomes the inverse.
• Write the system of equations as [latex]AX=B[/latex], and multiply both sides by the inverse of [latex]A:{A}^{-1}AX={A}^{-1}B[/latex].
• We can also use a calculator to solve a system of equations with matrix inverses.

Section Exercises

Licenses & attributions, cc licensed content, specific attribution.

• Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Solving Systems with Inverses

Introduction to solving systems with inverses, learning objectives.

By the end of this section, you will be able to:

• Find the inverse of a matrix.
• Solve a system of linear equations using an inverse matrix.

Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?

There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.

• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution