Hypothesis Testing - Chi Squared Test
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health


Introduction
This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.
The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.
Learning Objectives
After completing this module, the student will be able to:
- Perform chi-square tests by hand
- Appropriately interpret results of chi-square tests
- Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples
Tests with One Sample, Discrete Outcome
Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.
In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response
Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0
We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.
When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.
The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.
A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:
|
|
|
|
|
|
| Number of Students | 255 | 125 | 90 | 470 |
Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.
In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance.
The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.
H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15, or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15
H 1 : H 0 is false. α =0.05
Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.
- Step 2. Select the appropriate test statistic.
The test statistic is:
We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.
- Step 3. Set up decision rule.
The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.
- Step 4. Compute the test statistic.
We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.
|
|
|
|
|
|
|---|---|---|---|---|
|
| 255 | 125 | 90 | 470 |
|
| 470(0.60) =282 | 470(0.25) =117.5 | 470(0.15) =70.5 | 470 |
Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:
- Step 5. Conclusion.
We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15. The p-value is p < 0.005.
In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?
Consider the following:
|
|
|
|
|
|
|---|---|---|---|---|
|
| 255 | 125 | 90 | 470 |
|
| 282 | 117.5 | 70.5 | 470 |
If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?
The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:
|
|
|
|
|
30 |
|
|---|---|---|---|---|---|
|
| 20 | 932 | 1374 | 1000 | 3326 |
- Step 1. Set up hypotheses and determine level of significance.
H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23 or equivalently
H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23
H 1 : H 0 is false. α=0.05
The formula for the test statistic is:
We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.
Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.
We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.
|
|
|
|
|
30 |
|
|---|---|---|---|---|---|
|
| 20 | 932 | 1374 | 1000 | 3326 |
|
| 66.5 | 1297.1 | 1197.4 | 765.0 | 3326 |
The test statistic is computed as follows:
We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.
Again, the χ 2 goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?
In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.
In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.
The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?
We presented the following approach to the test using a Z statistic.
- Step 1. Set up hypotheses and determine level of significance
H 0 : p = 0.75
H 1 : p ≠ 0.75 α=0.05
We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used
This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:
We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).
We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:
|
| Saw a Dentist in Past 12 Months | Did Not See a Dentist in Past 12 Months | Total |
|---|---|---|---|
| # of Participants | 64 | 61 | 125 |
H 0 : p 1 =0.75, p 2 =0.25 or equivalently H 0 : Distribution of responses is 0.75, 0.25
We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.
Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)
|
|
|
|
|
|---|---|---|---|
|
| 64 | 61 | 125 |
|
| 93.75 | 31.25 | 125 |
(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)
We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 ! In statistics, there are often several approaches that can be used to test hypotheses.
Tests for Two or More Independent Samples, Discrete Outcome
Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.
The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.
The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.
Test Statistic for Testing H 0 : Distribution of outcome is independent of groups
and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).
Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table. r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.
The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.
Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| N |
In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.
The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:
Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).
The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:
P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).
The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.
|
|
|
|
|
|
|---|---|---|---|---|
|
| 10 | 8 | 7 | 25 |
|
| 22 | 15 | 13 | 50 |
|
| 30 | 28 | 17 | 75 |
|
| 62 | 51 | 37 | 150 |
The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:
P(Group 1 and Response 1) = P(Group 1) P(Response 1),
P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.
Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4. We could do the same for Group 2 and Response 1:
P(Group 2 and Response 1) = P(Group 2) P(Response 1),
P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.
The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.
Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:
Expected Cell Frequency = (Row Total * Column Total)/N.
The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.
In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.
|
|
|
|
|
|
|---|---|---|---|---|
|
| 32 | 30 | 28 | 90 |
|
| 74 | 64 | 42 | 180 |
|
| 110 | 25 | 15 | 150 |
|
| 39 | 6 | 5 | 50 |
|
| 255 | 125 | 90 | 470 |
Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.
H 0 : Living arrangement and exercise are independent
H 1 : H 0 is false. α=0.05
The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.
- Step 2. Select the appropriate test statistic.
The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.
The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table. The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.
We now compute the expected frequencies using the formula,
Expected Frequency = (Row Total * Column Total)/N.
The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.
|
|
|
|
|
|
|---|---|---|---|---|
|
| 32 (48.8) | 30 (23.9) | 28 (17.2) | 90 |
|
| 74 (97.7) | 64 (47.9) | 42 (34.5) | 180 |
|
| 110 (81.4) | 25 (39.9) | 15 (28.7) | 150 |
|
| 39 (27.1) | 6 (13.3) | 5 (9.6) | 50 |
|
| 255 | 125 | 90 | 470 |
Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.
Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.
We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.
Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data.
Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.
|
|
|
|
|
|---|---|---|---|
|
| 36% | 33% | 31% |
|
| 41% | 36% | 23% |
|
| 73% | 17% | 10% |
|
| 78% | 12% | 10% |
|
| 54% | 27% | 19% |
From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).
Test Yourself
Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.
|
|
|
|
|
|---|---|---|---|
| 0-4 | 21 | 20 | 16 |
| 5-6 | 135 | 71 | 35 |
| 7-10 | 158 | 62 | 35 |
Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.
In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.
In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.
A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.
|
|
|
|
|
|---|---|---|---|
|
| 50 | 23 | 0.46 |
|
| 50 | 11 | 0.22 |
We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows.
H 0 : p 1 = p 2
H 1 : p 1 ≠ p 2 α=0.05
Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.
We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:
In this example, we have
Therefore, the sample size is adequate, so the following formula can be used:
Reject H 0 if Z < -1.960 or if Z > 1.960.
We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:
We now substitute to compute the test statistic.
- Step 5. Conclusion.
We now conduct the same test using the chi-square test of independence.
H 0 : Treatment and outcome (meaningful reduction in pain) are independent
H 1 : H 0 is false. α=0.05
The formula for the test statistic is:
For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)
We now compute the expected frequencies using:
The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.
|
|
|
|
|
|---|---|---|---|
|
| 23 (17.0) | 27 (33.0) | 50 |
|
| 11 (17.0) | 39 (33.0) | 50 |
|
| 34 | 66 | 100 |
A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.
(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)
Chi-Squared Tests in R
The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.
Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores
We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.
H 0 : Apgar scores and patient outcome are independent of one another.
H A : Apgar scores and patient outcome are not independent.
Chi-squared = 14.3
Since 14.3 is greater than 9.49, we reject H 0.
There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

LEARN STATISTICS EASILY
Learn Data Analysis Now!

Understanding the Null Hypothesis in Chi-Square
The null hypothesis in chi square testing suggests no significant difference between a study’s observed and expected frequencies. It assumes any observed difference is due to chance and not because of a meaningful statistical relationship.
Introduction
The chi-square test is a valuable tool in statistical analysis. It’s a non-parametric test applied when the data are qualitative or categorical. This test helps to establish whether there is a significant association between 2 categorical variables in a sample population.
Central to any chi-square test is the concept of the null hypothesis. In the context of chi-square, the null hypothesis assumes no significant difference exists between the categories’ observed and expected frequencies. Any difference seen is likely due to chance or random error rather than a meaningful statistical difference.
- The chi-square null hypothesis assumes no significant difference between observed and expected frequencies.
- Failing to reject the null hypothesis doesn’t prove it true, only that data lacks strong evidence against it.
- A p-value < the significance level indicates a significant association between variables.
Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.
Understanding the Concept of Null Hypothesis in Chi Square
The null hypothesis in chi-square tests is essentially a statement of no effect or no relationship. When it comes to categorical data, it indicates that the distribution of categories for one variable is not affected by the distribution of categories of the other variable.
For example, if we compare the preference for different types of fruit among men and women, the null hypothesis would state that the preference is independent of gender. The alternative hypothesis, on the other hand, would suggest a dependency between the two.
Steps to Formulate the Null Hypothesis in Chi-Square Tests
Formulating the null hypothesis is a critical step in any chi-square test. First, identify the variables being tested. Then, once the variables are determined, the null hypothesis can be formulated to state no association between them.
Next, collect your data. This data must be frequencies or counts of categories, not percentages or averages. Once the data is collected, you can calculate the expected frequency for each category under the null hypothesis.
Finally, use the chi-square formula to calculate the chi-square statistic. This will help determine whether to reject or fail to reject the null hypothesis.
| Step | Description |
|---|---|
| 1. Identify Variables | Determine the variables being tested in your study. |
| 2. State the Null Hypothesis | Formulate the null hypothesis to state that there is no association between the variables. |
| 3. Collect Data | Gather your data. Remember, this must be frequencies or counts of categories, not percentages or averages. |
| 4. Calculate Expected Frequencies | Under the null hypothesis, calculate the expected frequency for each category. |
| 5. Compute Chi Square Statistic | Use the chi square formula to calculate the chi square statistic. This will help determine whether to reject or fail to reject the null hypothesis. |
Practical Example and Case Study
Consider a study evaluating whether smoking status is independent of a lung cancer diagnosis. The null hypothesis would state that smoking status (smoker or non-smoker) is independent of cancer diagnosis (yes or no).
If we find a p-value less than our significance level (typically 0.05) after conducting the chi-square test, we would reject the null hypothesis and conclude that smoking status is not independent of lung cancer diagnosis, suggesting a significant association between the two.
Observed Table
| Smoking Status | Cancer Diagnosis | No Cancer Diagnosis |
|---|---|---|
| Smoker | 70 | 30 |
| Non-Smoker | 20 | 80 |
Expected Table
| Smoking Status | Cancer Diagnosis | No Cancer Diagnosis |
|---|---|---|
| Smoker | 50 | 50 |
| Non-Smoker | 40 | 60 |
Common Misunderstandings and Pitfalls
One common misunderstanding is the interpretation of failing to reject the null hypothesis. It’s important to remember that failing to reject the null does not prove it true. Instead, it merely suggests that our data do not provide strong enough evidence against it.
Another pitfall is applying the chi-square test to inappropriate data. The chi-square test requires categorical or nominal data. Applying it to ordinal or continuous data without proper binning or categorization can lead to incorrect results.
The null hypothesis in chi-square testing is a powerful tool in statistical analysis. It provides a means to differentiate between observed variations due to random chance versus those that may signify a significant effect or relationship. As we continue to generate more data in various fields, the importance of understanding and correctly applying chi-square tests and the concept of the null hypothesis grows.
Recommended Articles
Interested in diving deeper into statistics? Explore our range of statistical analysis and data science articles to broaden your understanding. Visit our blog now!
- Simple Null Hypothesis – an overview (External Link)
- Chi-Square Calculator: Enhance Your Data Analysis Skills
- Effect Size for Chi-Square Tests: Unveiling its Significance
- What is the Difference Between the T-Test vs. Chi-Square Test?
- Understanding the Assumptions for Chi-Square Test of Independence
How to Report Chi-Square Test Results in APA Style: A Step-By-Step Guide
Frequently asked questions (faqs).
It’s a statistical test used to determine if there’s a significant association between two categorical variables.
The null hypothesis suggests no significant difference between observed and expected frequencies exists. The alternative hypothesis suggests a significant difference.
No, we never “accept” the null hypothesis. We only fail to reject it if the data doesn’t provide strong evidence against it.
Rejecting the null hypothesis implies a significant difference between observed and expected frequencies, suggesting an association between variables.
Chi-Square tests are appropriate for categorical or nominal data.
The significance level, often 0.05, is the probability threshold below which the null hypothesis can be rejected.
A p-value < the significance level indicates a significant association between variables, leading to rejecting the null hypothesis.
Using the Chi-Square test for improper data, like ordinal or continuous data, without proper categorization can lead to incorrect results.
Identify the variables, state their independence, collect data, calculate expected frequencies, and apply the Chi-Square formula.
Understanding the null hypothesis is essential for correctly interpreting and applying Chi-Square tests, helping to make informed decisions based on data.
Similar Posts
Chebyshev’s Theorem Calculator: A Tool for Unlocking Statistical Insights
Explore Chebyshev’s Theorem Calculator to unlock statistical insights and enhance your data analysis with precision and clarity.

What Makes a Variable Qualitative or Quantitative?
Explore the critical distinctions between Qualitative vs Quantitative variables, their research significance, and common misunderstandings.

This is a concise guide on how to report Chi-Square Test results in APA style, including significance, p-value, and effect size.

Florence Nightingale: How Data Visualization in the Form of Pie Charts Saved Lives
Discover how Florence Nightingale used data visualization and pie charts to revolutionize healthcare during the Crimean War.

How To Lie With Statistics?
Is It Possible To Lie With Statistics? Of Course, It Is! But, How? There Are Several Techniques Presented Here — Never Fall For Such Lies!

Principal Component Analysis: Transforming Data into Truthful Insights
This comprehensive guide explores how Principal Component Analysis transforms complex data into insightful, truthful information.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Statistics
Course: ap®︎/college statistics > unit 12, chi-square statistic for hypothesis testing.
- Chi-square goodness-of-fit example
- Expected counts in a goodness-of-fit test
- Conditions for a goodness-of-fit test
- Test statistic and P-value in a goodness-of-fit test
- Conclusions in a goodness-of-fit test
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
8. The Chi squared tests
The χ²tests.

H : proportion of flavors of candy are the same
H : proportions of flavors are not the same
H : proportion of people who buy snacks is independent of the movie type
H : proportion of people who buy snacks is different for different types of movies
Number of categories minus 1
Number of categories for first variable minus 1, multiplied by number of categories for second variable minus 1
How to perform a Chi-square test
For both the Chi-square goodness of fit test and the Chi-square test of independence , you perform the same analysis steps, listed below. Visit the pages for each type of test to see these steps in action.
- Define your null and alternative hypotheses before collecting your data.
- Decide on the alpha value. This involves deciding the risk you are willing to take of drawing the wrong conclusion. For example, suppose you set α=0.05 when testing for independence. Here, you have decided on a 5% risk of concluding the two variables are independent when in reality they are not.
- Check the data for errors.
- Check the assumptions for the test. (Visit the pages for each test type for more detail on assumptions.)
- Perform the test and draw your conclusion.
Both Chi-square tests in the table above involve calculating a test statistic. The basic idea behind the tests is that you compare the actual data values with what would be expected if the null hypothesis is true. The test statistic involves finding the squared difference between actual and expected data values, and dividing that difference by the expected data values. You do this for each data point and add up the values.
Then, you compare the test statistic to a theoretical value from the Chi-square distribution . The theoretical value depends on both the alpha value and the degrees of freedom for your data. Visit the pages for each test type for detailed examples.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Chi-Square Test of Independence and an Example
By Jim Frost 87 Comments
The Chi-square test of independence determines whether there is a statistically significant relationship between categorical variables . It is a hypothesis test that answers the question—do the values of one categorical variable depend on the value of other categorical variables? This test is also known as the chi-square test of association.

In this post, I’ll show you how the Chi-square test of independence works. Then, I’ll show you how to perform the analysis and interpret the results by working through the example. I’ll use this test to determine whether wearing the dreaded red shirt in Star Trek is the kiss of death!
If you need a primer on the basics, read my hypothesis testing overview .
Overview of the Chi-Square Test of Independence
The Chi-square test of association evaluates relationships between categorical variables. Like any statistical hypothesis test , the Chi-square test has both a null hypothesis and an alternative hypothesis.
- Null hypothesis: There are no relationships between the categorical variables. If you know the value of one variable, it does not help you predict the value of another variable.
- Alternative hypothesis: There are relationships between the categorical variables. Knowing the value of one variable does help you predict the value of another variable.
The Chi-square test of association works by comparing the distribution that you observe to the distribution that you expect if there is no relationship between the categorical variables. In the Chi-square context, the word “expected” is equivalent to what you’d expect if the null hypothesis is true. If your observed distribution is sufficiently different than the expected distribution (no relationship), you can reject the null hypothesis and infer that the variables are related.
For a Chi-square test, a p-value that is less than or equal to your significance level indicates there is sufficient evidence to conclude that the observed distribution is not the same as the expected distribution. You can conclude that a relationship exists between the categorical variables.
When you have smaller sample sizes, you might need to use Fisher’s exact test instead of the chi-square version. To learn more, read my post, Fisher’s Exact Test: Using and Interpreting .
Star Trek Fatalities by Uniform Colors
We’ll perform a Chi-square test of independence to determine whether there is a statistically significant association between shirt color and deaths. We need to use this test because these variables are both categorical variables. Shirt color can be only blue, gold, or red. Fatalities can be only dead or alive.
The color of the uniform represents each crewmember’s work area. We will statistically assess whether there is a connection between uniform color and the fatality rate. Believe it or not, there are “real” data about the crew from authoritative sources and the show portrayed the deaths onscreen. The table below shows how many crewmembers are in each area and how many have died.
| Blue | Science and Medical | 136 | 7 |
| Gold | Command and Helm | 55 | 9 |
| Red | Operations, Engineering, and Security | 239 | 24 |
| Ship’s total | All | 430 | 40 |
Tip: Because the chi-square test of association assesses the relationship between categorical variables, bar charts are a great way to graph the data. Use clustering or stacking to compare subgroups within the categories.

Related post : Bar Charts: Using, Examples, and Interpreting
Performing the Chi-Square Test of Independence for Uniform Color and Fatalities
For our example, we will determine whether the observed counts of deaths by uniform color are different from the distribution that we’d expect if there is no association between the two variables.
The table below shows how I’ve entered the data into the worksheet. You can also download the CSV dataset for StarTrekFatalities .
| Blue | Dead | 7 |
| Blue | Alive | 129 |
| Gold | Dead | 9 |
| Gold | Alive | 46 |
| Red | Dead | 24 |
| Red | Alive | 215 |
You can use the dataset to perform the analysis in your preferred statistical software. The Chi-squared test of independence results are below. As an aside, I use this example in my post about degrees of freedom in statistics . Learn why there are two degrees of freedom for the table below.
In our statistical results, both p-values are less than 0.05. We can reject the null hypothesis and conclude there is a relationship between shirt color and deaths. The next step is to define that relationship.
Describing the relationship between categorical variables involves comparing the observed count to the expected count in each cell of the Dead column. I’ve annotated this comparison in the statistical output above.
Statisticians refer to this type of table as a contingency table. To learn more about them and how to use them to calculate probabilities, read my post Using Contingency Tables to Calculate Probabilities .
Related post : Chi-Square Table
Graphical Results for the Chi-Square Test of Association
Additionally, you can use bar charts to graph each cell’s contribution to the Chi-square statistic, which is below.
Surprise! It’s the blue and gold uniforms that contribute the most to the Chi-square statistic and produce the statistical significance! Red shirts add almost nothing. In the statistical output, the comparison of observed counts to expected counts shows that blue shirts die less frequently than expected, gold shirts die more often than expected, and red shirts die at the expected rate.
The graph below reiterates these conclusions by displaying fatality percentages by uniform color along with the overall death rate.
The Chi-square test indicates that red shirts don’t die more frequently than expected. Hold on. There’s more to this story!
Time for a bonus lesson and a bonus analysis in this blog post!
2 Proportions test to compare Security Red-Shirts to Non-Security Red-Shirts
The bonus lesson is that it is vital to include the genuinely pertinent variables in the analysis. Perhaps the color of the shirt is not the critical variable but rather the crewmember’s work area. Crewmembers in Security, Engineering, and Operations all wear red shirts. Maybe only security guards have a higher death rate?
We can test this theory using the 2 Proportions test. We’ll compare the fatality rates of red-shirts in security to red-shirts who are not in security.
The summary data are below. In the table, the events represent the counts of deaths, while the trials are the number of personnel.
| Events | Trials | |
| Security | 18 | 90 |
| Not security | 6 | 149 |
The p-value of 0.000 signifies that the difference between the two proportions is statistically significant. Security has a mortality rate of 20% while the other red-shirts are only at 4%.
Security officers have the highest mortality rate on the ship, closely followed by the gold-shirts. Red-shirts that are not in security have a fatality rate similar to the blue-shirts.
As it turns out, it’s not the color of the shirt that affects fatality rates; it’s the duty area. That makes more sense.
Risk by Work Area Summary
The Chi-square test of independence and the 2 Proportions test both indicate that the death rate varies by work area on the U.S.S. Enterprise. Doctors, scientists, engineers, and those in ship operations are the safest with about a 5% fatality rate. Crewmembers that are in command or security have death rates that exceed 15%!
Share this:

Reader Interactions
February 6, 2024 at 9:55 pm
Hi Jim. I am using R to calclate a chi sqaure of independence. I have an value of 1.486444 with a P value greater than 0.05. My question is how do I interpet the value of 1.48644? Is this a strong association between two variables or a weak association?
February 6, 2024 at 10:19 pm
You really just look at the p-value. If you assess the chi-square value, you need as the chi-square value in conjunction with a chi-square distribution with the correct degrees of freedom and use that to calculate the probability. But the p-value does that for you!
In your case, the p-value is greater than your significance level. So, you fail to reject the null hypothesis. You have insufficient evidence to conclude that an association exists between your variables.
Also, it’s important to note that this test doesn’t indicate the strength of association. It only tells you whether your sample data provide sufficient evidence to conclude that an association exists in the population. Unfortunately, you can’t conclude that an association exists.
September 1, 2022 at 5:01 am
Thank you this was such a helpful article.
I’m not sure if you check these comments anymore, yet if you do I did have a quick question for you. I was trying to follow along in SPSS to reproduce your example and I managed to do most of it. I put your data in, used Weight Cases by Frequency of Deaths, and then was able to do the Chi Square analysis that achieved the exact same results as yours.
Unfortunately, I am totally stuck on the next part where you do the 2 graphs, especially the Percentage of Fatalities by Shirt Color. The math makes sense – it’s just e.g., Gold deaths / (Gold deaths + Gold Alive). However, I cannot seem to figure out how to create a bar chart like that in SPSS!? I’ve tried every combination of variables and settings I can think of in the Chart Builder and no luck. I’ve also tried the Compute Variable option with various formulas to create a new column with the death percentages by shirt color but can’t find a way to sum the frequencies.. The best I can get is using an IF statement so it only calculates on the rows with a Death statistic and then I can get the first part: Frequency / ???, but can’t sum the 2 frequencies of Deaths & Alive per shirt colour to calculate the figure properly. And I’m not sure what other things I can try.
So basically I’m totally stuck at the moment. If by some chance you see this, is there any chance you might please be able to help me figure out how to do that Percentage of Fatalities by Shirt Color bar graph in SPSS? The only way I can see at the moment is to manually type the calculated figures into a new dataset and graph it. That would work but doesn’t seem a very practical way of doing things if this was a large dataset instead of a small example one. Hence I’m assuming this must be a better way of doing this?
Thank you in advance for any help you can give me.
September 1, 2022 at 3:38 pm
Yes, I definitely check these comments!
Unfortunately, I don’t have much experience using SPSS, so I’ll be of limited help with that. There must be some way to do that in SPSS though. Worst case scenario, calculate the percentages by hand or in Excel and then enter them into SPSS and graph them. That shouldn’t be necessary but would work in a pinch.
Perhaps someone with more SPSS experience can provide some tips?
September 18, 2021 at 6:09 pm
Hi. This comment relates to Warren’s post. The null hypothesis is that there is no statistically significant relationship between “Uniform color” and “Status”. During the summing used to calculate the Chi-squared statistic, each of the (6) contributions are included. (3 Uniform colors x 2 status possibilities) The “Alive” column gives the small contributions that bring the total contribution from 5.6129 up to 6.189. Any reasoning specific to the “Dead” column only begins after the 2-dimensional Chi-squared calculation has been completed.
September 19, 2021 at 12:38 am
Hi Bill, thanks for your clarifications. I got confused with whom you were replying!
September 17, 2021 at 5:53 pm
The chi-square formula is: χ2 = ∑(Oi – Ei)2/Ei, where Oi = observed value (actual value) and Ei = expected value.
September 17, 2021 at 5:56 pm
Hi Bill, thanks. I do cover the formula and example calculations in my other post on the topic, How Chi-Squared Works .
September 16, 2021 at 6:24 pm
Why is the Pearson Chi Square statistic not equal to the sum of the contributions to Chi-Square? I get 5.6129. The p-value for that Chi-Squre statistic is .0604 which is NOT significant in this century OR the 24th.
September 14, 2021 at 8:25 am
Thank you JIm, Excellent concept teaching!
July 15, 2021 at 1:05 pm
Thank you so much for the Star Trek example! As a long-time Trek fan and Stats student, I absolutely love the debunking of the red shirt theory!
July 19, 2021 at 10:19 pm
I’m so glad you liked my example. I’m a life-long Trek fan as well! I found the red shirt question to be interesting. One the one hand, part of the answer of the answer is that red shirts comprise just over 50% of the crew, so of course they’ll have more deaths. And then on the other hand, it’s only certain red shirts that actually have an elevated risk, those in security.
May 16, 2021 at 1:42 pm
Got this response from the gentleman who did the calculation using a Chi Square. Would you mind commenting? “The numbers reported are nominate (counting) numbers not ordinate (measurement) numbers. As such chi-square analysis must be used to statistically compare outcomes. Two-sample student t-tests cannot be used for ordinate numbers. Correlations are also not usually used for ordinate numbers and most importantly correlations do NOT show cause and effect.”
May 16, 2021 at 3:13 pm
I agree with the first comment. However, please note that I recommended the 2-sample proportions test and the other person is mentioning the 2-sample t-test. Very different tests! And, I agree that the t-test is not appropriate for the Pfizer data. Basically, he’s saying you have categorical data and the t-test is for continuous data. That’s all correct. And that’s why I recommended the the proportions test.
As for the other part about “correlations do NOT show cause and effect.” That’s not quite correct. More accurately, you’d say that correlations do not NECESSARILY imply causation. Sometimes they do and sometimes they don’t imply causation. It depends on the context in which the data were collected. Correlations DO suggest causation when you use a randomized controlled trial (RCT) for the experiment and data collection, which is exactly what Pfizer did. Consequently, the Pfizer data DO suggest that the vaccine caused a reduction in the proportion of COVID infections in the vaccine group compared to the control group (no vaccine). RCTs are intentionally designed so you can draw causal inferences, which is why the FDA requires them for vaccine and other medical trials.
If you’re interested, I’ve written an article about why randomized controlled trials allow you to make causal inferences .
May 16, 2021 at 12:41 pm
Mr. Jim Frost…You are Da Man!! Thank you!! Yes, this is the same document I have been looking at, just did not know how to interpret Table 9. Sorry, never intended to ask you for medical advice, just wanted to understand the statistics and feel confident that the calculations were performed correctly. You have made my day! Now just a purely statistics question, assuming I have not worn out your patience with my dumb questions…Can you explain the criteria used to determine when a Chi Square should be used versus a 2-samples proportions test? I think I saw a comment from someone on your website stating that the Chi Sqaure is often misused in the medical field. Fascinating, fascinating field you are in. Thank you so much for sharing your knowledge and expertise.
May 16, 2021 at 3:00 pm
You bet! That’s why I’m here . . . to educate and clarify statistics and statistical analyses!
The chi-squared test of independence (or association) and the two-sample proportions test are related. The main difference is that the chi-squared test is more general while the 2-sample proportions test is more specific. And, it happens that the proportions test it more targeted at specifically the type of data you have.
The chi-squared test handles two categorical variables where each one can have two or more values. And, it tests whether there is an association between the categorical variables. However, it does not provide an estimate of the effect size or a CI. If you used the chi-squared test with the Pfizer data, you’d presumably obtain significant results and know that an association exists, but not the nature or strength of that association.
The two proportions test also works with categorical data but you must have two variables that each have two levels. In other words, you’re dealing with binary data and, hence, the binomial distribution. The Pfizer data you had fits this exactly. One of the variables is experimental group: control or vaccine. The other variable is COVID status: infected or not infected. Where it really shines in comparison to the chi-squared test is that it gives you an effect size and a CI for the effect size. Proportions and percentages are basically the same thing, but displayed differently: 0.75 vs. 75%.
What you’re interested in answering is whether the percentage (or proportion) of infections amongst those in the vaccinated group is significantly different than the percentage of infections for those in control group. And, that’s the exact question that the proportions test answers. Basically, it provides a more germane answer to that question.
With the Pfizer data, the answer is yes, those in the vaccinated group have a significantly lower proportion of infections than those in the control group (no vaccine). Additionally, you’ll see the proportion for each group listed, and the effect size is the difference between the proportion, which you can find on a separate line, along with the CI of the difference.
Compare that more specific and helpful answer to the one that chi-squared provides: yes, there’s an association between vaccinations and infections. Both are correct but because the proportions test is more applicable to the specific data at hand, it gives a more useful answer.
I see you have an additional comment with questions, so I’m off to that one!
May 15, 2021 at 1:00 pm
Hi Jim, So sorry if my response came off as anything but appreciative of your input. I tried to duplicate your results in your Flu Vaccine article using the 2 Proportion test as you recommended. I was able to duplicate your Estimate for Difference of -0.01942, but I could not duplicate your value for Z, so clearly I am not doing the calculation correctly – even when using Z calculators. So since I couldn’t duplicate your correct results for your flu example, I did not have confidence to proceed to Moderna. I was able to calculate effectiveness (the hazard ratio that is widely reported), but as I have reviewed the EUA documents presented to the FDA in December 2020, I know that there is no regression analysis, and most importantly, no data to show an antibody response produced by the vaccine. So they are not showing the vaccine was successful in producing an immune response, just giving simplistic proportions of how many got covid and how many didn’t. And as they did not even factor in the number of people who had had covid prior to vaccine, I just cant understand how these numbers have any significance at all. I mention the PCR test because it too is under an EUA, and has severe limitations. I would think that those limitations would be statistically significant, as are the symptoms which can indicate any bacterial or viral infection. And you state “I’m sure you can find a journal article or documentation that shows the thorough results if you’re interested”. Clearly I am VERY interested, as I love my parents more than life itself, and have seen the VAERS data, and I don’t want them to be the next statistic. But I CANT find the thorough results that you say are so easy to find. If I could I would not be trying to learn to perform statistical calculations. So I went out on a limb, as you are a fellow trekky and seem like a super nice guy, sharing your expertise with others, and thought you might be able to help me understand the statistics so I can help my parents make an informed choice. We are at a point that children and pregnant women are getting these vaccines. Unhealthy, elderly people in nursing homes (all the people excluded in the trials) are getting these vaccines. I simply ask the question…..do these vaccines provide more protection than NOT getting the vaccine? The ENTIRE POPULATION is being forced to get these vaccines. And you tell me “I’m sure you can find a journal article or documentation that shows the thorough results if you’re interested.” I can only ask…how are you NOT interested? This is the most important statistical question of our lifetime, and of your children’s and granchildren’s lifetime. And I find that no physician or statistician able or willing to answer these questions. Respectfully, Chris
May 15, 2021 at 11:00 pm
No worries. On my website, I’m just discussing the statistical nature of Moderna’s study. Of course, everyone is free to make their own determination and decide accordingly.
You’re obviously free to question the methods and analysis, but as a statistician, I’m satisfied that Moderna performed an appropriate clinical trial and followed that up with a rigorous and appropriate statistical analysis. In my opinion, they have demonstrated that their vaccine is safe and effective. The only caveat is that we don’t have long-term safety data because not enough time has gone by. However, most side effects for vaccines show up in the first 45 days. That timeframe occurred during the trial and all side effects were recorded.
However, I’m not going to get into a debate about whether anyone should get the vaccine or not. I run a statistics website and that’s the aspect I’m focusing on. There are other places to debate the merits of being vaccinated.
May 14, 2021 at 8:05 pm
Hi Jim, thanks for the reply. I have to admit the detail of all the statistical methods you mention are over my head, but by scanning the document it appears you did not actually calculate the vaccine’s efficacy, just stated how the analysis should be done. I am referring to comments like “To analyze the COVID-19 vaccine data, statisticians will use a stratified Cox proportional hazard regression model to assess the magnitude of the difference between treatment and control groups using a one-sided 0.025 significance level”. And “The full data and analyses are currently unavailable, but we can evaluate their interim analysis report. Moderna (and Pfizer) are still assessing the data and will present their analyses to Federal agencies in December 2020.” I am looking at the December 2020 reports that both Pfizer and Moderna presented to the FDA, and I see no “stratified Cox proportional hazard regression model”, just the simplistic hazard ratio you mention in your paper. I don’t see how that shows the results are statistically significant and not chance. Also the PCR test does not confirm disease, just presence of virus (dead or alive) and virus presence doesnt indicate disease. And the symptoms are symptoms of any viral or bacterial infection, or cancer. Just sort of suprised to see no statistical analysis in the December 2020 reports. Was hoping you had done the heavy lifting…lol
May 14, 2021 at 11:38 pm
Hi Christine,
You had asked if Chi-square would work for your data and my response was no, but here are two methods that would. No, I didn’t analyze the Moderna data myself. I don’t have access to their complete data that would allow me to replicate their results. However, in my post, I did calculate the effectiveness, which you can do using the numbers I had, but not the significance.
Based on the data you indicated you had, I’d recommend the two-sample proportions test that I illustrate in the flu vaccine post. That won’t replicate the more complex analyses but is doable with the data that you have.
The Cox proportional hazard regression model analyzes the hazard ratio. The hazard ratio is the outcome measure in this context. They’re tied together and it’s the regression analysis that indicate significance. I’d imagine you’d have to read a thorough report to get the nitty gritty details. I got the details of their analysis straight from Moderna.
I’m not sure what your point with the PCR test. But, I’m just reporting how they did their analysis.
Moderna, Pfizer, and the others have done the “heavy lifting.” When I wrote the post about the COVID vaccination, it was before it was approved for emergency use. By this point, I’m sure you can find a journal article or documentation that shows the thorough results if you’re interested.
May 14, 2021 at 2:56 pm
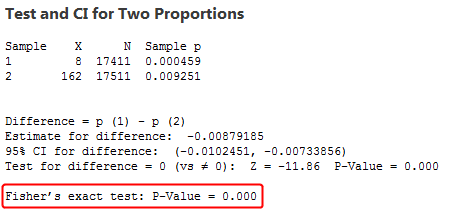
Hi Jim, my parents are looking into getting the Pfizer vaccine, and I was wondering if I could use a chi square analysis to see if its statistically effective. From the EUA document, 17411 people got the Pfizer vaccine, and of those people – 8 got covid, and 17403 did not. Of the control group of 17511 that did not get the vaccine, 162 got covid, and 17349 did not. My calculations show this is not statistically significant, but wasn’t sure if I did my calculation correctly, or if I can even use a chi square for this data. Can you help? PS. As a Trekky family, I love your analysis…but we all know its the new guy with a speaking part that gets axed…lol
May 14, 2021 at 3:28 pm
There are several ways you can analyze the effectiveness. I write about how they assessed the Moderna vaccine’s effectiveness , which uses a special type of regression analysis.
The other approach is to use a two-sample proportions test. I don’t write about that in the COVID context but I show how it works for flu vaccinations . The same ideas apply to COVID vaccinations. You’re dealing comparing the proportion of infections in the control group to the treatment group. Hence, a two-sample proportions test.
A chi-square analysis won’t get you where you want to go. It would tell you if there is an association, but it’s not going to tell you the effect size.
I’d read those two posts that I wrote. They’ll give you a good insight for possible ways to analyze the data. I also show how they calculate effectiveness for both the COVID and flu shots!
I hope that helps!
April 9, 2021 at 2:49 am
thank you so much for your response and advice! I will probably go for the logistic regression then 🙂
All the best for you!
April 10, 2021 at 12:39 am
You’re very welcome! Best of luck with your study! 🙂
April 7, 2021 at 4:18 am
thank you so much for your quick response! This actually helps me a lot and I also already thought about doing a binary logistic regression. However, my supervisor wanted me to use a chi-square test, as he thinks it is easier to perform and less work. So now I am struggling to decide, which option would be more feasible.
Coming back to the chi-square test – could I create a new variable which differentiates between the four experimental conditions and use this as a new ID? Or can I use the DV to weight the frequencies in the chi-square test? – I did that once in a analysis using a continuous DV as weight. Yet, I am not sure if or how that works with a binary variable. Do you have an idea what would work best in the case of a chi-square test?
Thank you so much!!
April 8, 2021 at 11:25 pm
You’re very welcome!
I don’t think either binary logistic regression or chi-square are more less work than the other. However, Chi-square won’t give you the answers you want. You can’t do interaction effects with chi-square. You won’t get nice odds ratios which are a much more intuitive way to interpret the results than chi-square, at least in my opinion. With chi-square, you don’t get a p-value/significance for each variable, just the overall analysis. With logistic regression, you get p-values for each variable and the interaction term if you include it.
I think you can do chi-square analyses with more than one independent variable. You’d essentially have a three dimensional table rather than a two-dimensional table. I’ve never done that myself so I don’t have much advice to offer you there. But, I strongly recommend using logistic regression. You’ll get results that are more useful.
April 6, 2021 at 10:59 am
thank you so much for this helpful post!
April 6, 2021 at 5:36 am
thank you for this very helpful post. Currently, I am working on my master’s thesis and I am struggling with identifying the right way to test my hypothesis as in my case I have three dummy variables (2 independent and 1 dependent).
The experiment was on the topic advice taking. It was a 2×2 between sample design manipulating the source of advice to be a human (0) or an algorithm (1) and the task to be easy (0) or difficult (1). Then, I measured whether the participants followed (1) or not followed (0) the advice. Now, I want to test if there is an interaction effect. In the easy task I expect that the participants rather follow the human advice and in the difficult task the participants rather follow the algorithmic advice.
I want to test this using a chi-square independence test, but I am not sure how to do that with three variables. Should I rather use the variable “Follow/Notfollow” as a weight or should I combine two of the variables so that I have a new variable with four categories, e.g. Easy.Human, Easy.Algorithm, Difficult.Human, Difficult.Algorithm or Human.Follow, Human.NotFollow, Algorithm.Follow, Algorithm.NotFollow
I am not sure, if this is scientifically correct. I would highly appreciate your help and your advice.
Thank you so much in advance! Best, Anni
April 7, 2021 at 1:58 am
I think using binary logistic regression would be your best bet. You can use your dummy DV with that type. And have two dummy IVs also works. You can also include an interaction term, which isn’t possible in chi-square tests. This model would tell you whether source of advice, difficulty of task, and their interaction relate to the probability of participants following the advice.
March 29, 2021 at 12:43 pm
Hi Jim, I want to thank you for all the content that you have posted online. It has been very helpful for me to apply simple principles of statistics at work. I wanted your thoughts on how to approach the following problem, which appeared to be slightly different from the examples that you shared above. We have two groups – test group (exposed to an ad for brand A) and control group (not exposed to any ads for brand A). We asked both groups a qn: Have you heard of brand A? The possible answers were a Y/N. We then did a t-test to determine if the answers were significantly different for the test and control groups (they were) We asked both groups a follow-up qn as well: How likely are you to buy any of the following brands in the next 3 months? The options were as follows (any one could be picked. B,C & D are competing brands with A) 1.A 2.B 3.C 4.D We wanted to check if the responses we received from both groups were statistically different. Based on my reading, it seemed like the Chi-Square test was the right one to run here. However, I wasn’t too sure what the categorical variables would be in this case and how we could run the Chi-square test here. Would like to get our inputs on how to approach this. Thanks
March 29, 2021 at 2:53 pm
For the first question, I’d typically recommend a 2-sample proportions test. You have two groups and the outcome variable is binary, which is good for proportions. Using a 2-sample proportions test will tell you whether the proportion of individuals who have heard of Brand A differs by the two groups (ads and no ads). You could use the chi-squared test of independence for this case but I recommend the proportions test because it’s designed specifically for this scenario. The procedure can also estimate the effect size and a CI for the effect size (depending on your software). A t-test is not appropriate for these data.
For the next question, yes, the chi-square test is good choice as long as they can only pick one of the options. Maybe, which brand are you most likely to purchase in the next several months. The categories must be mutually exclusive to use chi-square. One variable could be exposed to ad with yes and no as levels. The other would be the purchase question with A, B, C, D as levels. That gives you a 2 X 4 table for your chi-squared test of independence.
March 29, 2021 at 5:08 am
I don’t see the relationship between the table of shirt color and status and the tabulated statistics. Sam
March 29, 2021 at 3:39 pm
I show the relationship several ways in this post. The key is to understand how the actual counts compare to the expected counts. The analysis calculates the expected counts under the assumption that there is no relationship between the variables. Consequently, when there are differences between the actual and expected accounts, a relationship potentially exists.
In the Tabulated Statistics output, I circle and explain how the actual counts compare to the expected counts. Blue uniforms have fewer deaths than expected while Gold uniforms have more deaths than expected. Red uniforms equal the expect amount, although I explore that in more detail later in the post. You can also see these relationships in the graph titled Percentage of Fatalities.
Overall, the results show the relationship between uniform color and deaths and the p-value indicates that this relationship is statistically significant.
February 20, 2021 at 8:51 am
Suppose you have two variables that checking out books and means to get to the central library. How might you formulate null hypothesis and alternative hypothesis for the independence test? please answer anyone
February 21, 2021 at 3:15 pm
In this case, the null hypothesis states that there is no relationship between means to get to the library and checking out a book. The alternative hypothesis states that there is a relationship between them.
November 18, 2020 at 12:39 pm
Hi there I’m just wondering if it would be appropriate to use a Chi square test in the following scenario; – A data set of 1000 individuals – Calculate Score A for all 1000 individuals; results are continuous numerical data eg. 2.13, 3.16, which then allow individuals to be placed in categories; low risk (3.86) -Calculate Score B for the same 1000 individuals; results are discrete numerical data eg. 1, 6, 26 ,4 which the allow individuals to be placed in categories; low risk (26). – I then want to compared the two scoring systems A & B ; to see if (1) the individuals are scoring similarly on both scores (2) I have reason to believe one of the scores overestimates the risk, I’d like tot test this.
Thank you, I haven’t been able to find any similar examples and its stressing me out 🙁
November 13, 2020 at 1:53 pm
Would you be able to advise?
My organization is sending out 6 different emails to employees, in which they have to click on a link in the email. We want to see if one variation in language might get a higher click rate rate for the link. So we have 6 between subjects conditions, and the response can either be a ‘clicked on the link’ or ‘NOT clicked on the link’.
Is this a Chi-Square of Independence test? Also, how would I know where the difference lies, if the test is significant? (i.e., what is the non-parametric equivalent of running an ANOVA and followup pairwise comparisons?
Thanks Jim!
October 15, 2020 at 11:05 pm
I am working on the press coverage of civil military relations in Pakistani press from 2008 to 2018, I want to check that whether is a difference of coverage between two tenures ie 2008 to 2013 and 2013 to 2018. Secondly I want to check the difference of coverage between two types of newspapers ie english newspapers and urdu newspapers. furthermore I also want to check the category wise difference of coverage from the tenure 2008 to 2018.
I have divided my data into three different distributions, 1 is pro civilian, 2 is pro military and 3 is neutral.
October 4, 2020 at 4:07 am
Hi thank you so much for this. I would like to ask, if the study Is about whether factors such as pricing, marketing, and brand affects the intention of the buyer to purchase the product. Can I use Chi-test for the statistic treatment? and if it is not can I ask what statistical treatment would you suggest? Thank you so much again.
October 3, 2020 at 2:51 pm
Jim, Thank you for the post. You displayed a lot of creativity linking the two lessons to Star Trek. Your website and ebook offerings are very inspiring to me. Bill
October 4, 2020 at 12:53 am
Thanks so much, Bill. I really appreciate the kind words and I’m happy that the website and ebooks have been helpful!
September 29, 2020 at 7:10 am
Thank-you for your explanation. I am trying to help my son with his final school year investigation. He has raw data which he collected from 21 people of varying experience. They all threw a rugby ball at a target and the accuracy, time of ball in the air and experience (rated from 1-5) were all recorded. He has calculated the speed and the displacement, and used correlation to compare speed versus accuracy and experience versus accuracy. He needs to incrementally increase the difficulty of maths he uses in his analysis and he was thinking of the Chi Square test as a next step, however from your explanation above the current form of his data would not be suitable for this test. Is there a way of re-arranging the data so that we can use the Chi Square test? Thanks!
September 30, 2020 at 4:33 pm
Hi Rhonwen,
The chi-squared test of independence looks for correlation between categorical variables. From your description, I’m not seeing a good pair of categorical variables to test for correlation. To me, the next step for this data appears to be regression analysis.
September 12, 2020 at 5:37 pm
Thank you for the detailed teaching! I think this explains chi square much better than other websites I have found today. Do you mind sharing which software you use to get Expected Count and contribution to Chi square? Thank you for your help.
August 22, 2020 at 1:06 pm
Good day jim! I was wondering what kind of data analysis should i use if i am going to have a research on knowledge, attitude and practices? Looking forward to your reply! Thank you!
June 25, 2020 at 8:43 am
Very informative and easy to understand it. Thank you so much sir
June 2, 2020 at 11:03 am
Hi I wanted to know how the significance probability can be calculated if the significance level wasn’t given. Thank you
June 3, 2020 at 7:39 pm
Hi, you don’t need to know the significance level to be able to calculate the p-value. For calculating the p-value, you must know the null hypothesis, which we do for this example.
However, I do use a significance level of 0.05 for this example, making the results statistically significant.
May 26, 2020 at 5:55 am
What summary statistics can I use to describe the graph of a categorical data? Good presentation by the way. Very Insightful
May 26, 2020 at 8:39 pm
Hi Michael,
For categorical data like the type in this example, which is in a two-way contingency table, you’d often use counts or percentages. A bar chart is often a good choice for graphing counts or percentages by multiple categories. I show an example of graphing data for contingency tables in my Introduction to Statistics ebook .
May 25, 2020 at 10:27 am
Thank you for your answer. I saw online that bar graphs can be used to visualise the data (I guess it would be the percentage of death in my case) with 95% Ci intervals for the error bar. Is this also applicable if I only have a 2×2 contingency table? If not, what could be my error bar?
May 26, 2020 at 8:59 pm
Hi John, you can obtain CIs for proportions, which is basically a percentage. And, bar charts are often good for graphing contingency tables.
May 24, 2020 at 9:34 am
Hi! So I am working on this little project where I am trying to find a relationship between sex and mortality brought by this disease so my variables are: sex (male or female) and status (dead or alive). I am new to statistics so I do not know much. Is there any way to check the normality of categorical data? There is a part wherein our data must be based on data normality but I am not sure it this applies to categorical data. Thank you for your answer!
May 24, 2020 at 4:23 pm
The normal distribution is for continuous data. You have discrete data values–two binary variables to be precise. So, the normal distribution is not applicable to your data.
May 21, 2020 at 11:26 pm
Hi Jim, this was really helpful. I am in the midst of my proposal on a research to determine the association between burnout and physical activity among anaesthesia trainees.
They are both categorial variable physical activity – 3 categories: high, moderate, low burnout – 2 categories: high and low
How do I calculate my sample size for my study?
May 22, 2020 at 2:13 pm
Hi Jaishree,
I suggest you download a free sample size and power calculation program called G*Power . Then do the following:
- In G*Power, under Test Family, choose, χ². Under Statistical test, choose Goodness-of-fit tests: Contingency tables.
- In Effect size w, you’ll need to enter a value. 0.1 = weak. 0.3 medium, and 0.5 large. That’s based on subject area knowledge.
- In β/α ratio, that’s the ratio of the Type II error rate/Type I error rate. They have a default value of 1, but that seems too low. 2-3 might be more appropriate but you can try different values to see how this affects the results.
- Then you need to enter your sample size and DF. Read my post about Degrees of Freedom , which includes a section about calculating it for chi-square tests.
- Click Calculate.
Experiment and adjust values to see how that changes the output. You want to find a sample size that produces sufficient power while incorporating your best estimates of the other parameters (effect size, etc.).
May 16, 2020 at 10:55 am
Learned so much from this post!! This was such a clear example that it is the first time for me that some statistic tests really make sense to me. Thank you so much for sharing your knowledge, Jim!!
May 5, 2020 at 11:46 am
the information that you have given here has been so useful to me – really understand it much better now. So, thank you very much! Just a quick question, how did you graph the contribution to chi-square statistics? Only, I’ve been using stata to do some data analysis and I’m not sure how it is that I would be able to create a graph like that for my own data. Any insight into that, that you can give would be extremely useful.
May 6, 2020 at 1:30 am
I used Minitab statistical software for the graphs. I think graphs often bring the data to life more than just a table of numbers.
March 20, 2020 at 2:38 pm
I have the results of two Exit Satisfaction Surveys related to two cohorts (graduates of 2017-18 and graduates of 2018-19). The information I received was just the “number” of ratings on each of the 5 points on the Likert Scale (e.g., 122 respondents Strongly Agreed to a given item). I changed the raw ratings into percentages for comparison, e.g., for Part A of the Survey (Proficiency and Knowledge in my major field), I calculated the minimum and maximum percentages on the Strongly Agree point and did the same for other points on the scale. My questions are (1) can I report the range of percentages on each point on the scale for each item or is it better to report an overall agreement/disagreement? and (2) what’s the best statistics to compare the satisfaction of the two cohorts in the same survey? The 2017-18 cohorts included 126, and the 2018-19 cohort included 296 graduates.
I checked out your Introduction to Statistics book that I purchased, but I couldn’t decide about the appropriate statistics for the analysis of each of the surveys as well as comparison of both cohorts.
My sincere thanks in advance for your time and advice,
All the best, Ellie
March 20, 2020 at 7:30 am
Thank you for an excellent post! I am myself will soon perform a Chi-square test of independence on survey responses with two variables, and now think it might be good to start with a 2 proportion test (is a Z-test with 2 proportions what you use in this example?). Since you don’t discuss whether the Star Trek data meets the assumptions of the two tests you use, I wonder if they share approximately the same assumptions? I have already made certain that my data may be used with the Chi-square (my data is by the way not necessarily normally distributed, and has unkown mean and variance), can I therefore be comfortable with using a 2 proportions Z-test too? I hope you have the time to help me out here!
February 18, 2020 at 8:53 am
Excellent post. Btw, is it similar to what they called Test of Association that uses contingency table? The way they compute for the expected value is (row total × column total)/(sample total) . And to check if there is a relationship between two variable, check if the calculate chi-squared value is greater that the critical value of the chi-squared. Is it just the same?
February 20, 2020 at 11:09 am
Hi Hephzibah,
Yes, they’re the same test–test of independence and test of association. I’ll add something to that effect to the article to make that more clear.
January 6, 2020 at 9:24 am
Jim, thanks for creating and publishing this great content. In the initial chi-square test for independence we determined that shirt color does have a relationship with death rate. The Pearson ch-square measurement is 6.189, is this number meaningful? How do we interpret this in plain english?
January 6, 2020 at 3:09 pm
There’s really no direct interpretation of the chi-square value. That’s the test statistic, similar to the t-value in t-tests and the F-value in F-tests. These values are placed in the chi-square probability distribution that has the specified degrees of freedom (df=2 for this example). By placing the value into the probability distribution, the procedure can calculate probabilities, such as the p-value. I’ve been meaning to write a post that shows how this works for chi-squared tests. I show how this works for t-tests and F-tests for one-way ANOVA . Read those to get an idea of the process. Of course, for this chi-squared test uses chi-squared as the test statistic and probability distribution.
I’ll write a post soon about how this test works, both in terms of calculating the chi-square value itself and then using it in the probability distribution.
January 5, 2020 at 7:28 am
Would Chi-squared test be the statistical test of choice, for comparing the incidence rates of disease X between two states? Many thanks.
January 6, 2020 at 1:20 am
Hi Michaela,
It sounds like you’d need to use a two-sample proportions test. I show an example of this test using real data in my post about the effective of flu vaccinations . The reason you’d need to use a proportions test is because your observed data are presumably binary (diseased/not diseased).
You could use the chi-squared test, but I think for your case the results are easier to understand using a two-sample proportions test.
June 3, 2019 at 6:57 pm
Lets say the expected salary for a position is 20,000 dollars. In our observed salary we have various figures a little above and below 20,000 and we want to do a hypothesis test. These salaries are ratio, so does that mean we cannot use Chi Square? Do we have to convert? How? In fact, when you run a chi square on the salary data Chi Square turns out to be very high, sort of off the Chi Square Critical Value chart.
June 3, 2019 at 10:28 pm
Chi-square analysis requires two or more categorical (nominal) variables. Salary is a continuous (ratio) variable. Consequently, you can’t use chi-square.
If you have the one continuous variable of salary and you want to determine whether the difference between the mean salary and $20,000 is statistically significant or not, you’d need to use a one-sample t-test. My post about the different forms of t-tests should be helpful for you.
April 13, 2019 at 4:23 am
I don’t know how to thank you for your detailed informative reply. And I am happy that a specialist like you found this study interesting yoohoo 🙂
As to your comment on how we (me and my graduate student whose thesis I am directing) tracked the errors from Sample writing 1 to 5 for each participant, We did it manually through a close content analysis. I had no idea of a better alternative since going through 25 pieces of writing samples needed meticulous comparison for each participant. I advised my student to tabulate the number, frequency, and type of errors for each participant separately so we could keep track of their (lack of) improvement depending on the participant’s proficiency level.
Do you have any suggestion to make it more rigorous?
Very many thanks, Ellie
April 10, 2019 at 11:52 am
Hi, Jim. I first decided to choose chi-square to analyze my data but now I am thinking of poisson regression since my dependent variable is ‘count.’. I want to see if there is any significant difference between Grade 10 students’ perceptions of their writing problems and the frequency of their writing errors in the five paragraphs they wrote. Here is the detailed situation:
1. Five sample paragraphs were collected from 5 students at 5 proficiency levels based on their total marks in English final exam in the previous semester (from Outstanding to Poor). 2. The students participated in an interview and expressed their perceptions of their problem areas in writing. 3. The students submitted their paragraphs every 2 weeks during the semester. 4. The paragraphs were marked based on the school’s marking rubrics. 5. Errors were categorized under five components (e.g., grammar, word choice, etc.). 6. Paragraphs were compared for measuring the students’ improvement by counting errors manually in each and every paragraph. 7. The students’ errors were also compared to their perceived problem areas to study the extent of their awareness of their writing problems. This comparison showed that students were not aware of a major part of their errors while their perceived errors were not necessarily observed in their writing samples. 8. Comparison of Paragraphs 1 and 5 for each student showed decrease in the number of errors in some language components while some errors still persisted. 9. I’m also interested to see if proficiency level has any impact on students’ perceptions of their real problem areas and the frequency of their errors in each language category.
My question is which test should be used to answer Qs 7 and 8? As to Q9, one of the dependent variables is count and the other one is nominal. One correlation I’m thinking is eta squared (interval-nominal) but for the proficiency-frequency I’m not sure.
My sincere apologies for this long query and many thanks for any clues to the right stats.
April 11, 2019 at 12:25 am
That sounds like a very interesting study!
I think that you’re correct to use some form of regression rather than chi-square. The chi-squared test of independence doesn’t work with counts within an observation. Chi-squared looks at the multiple characteristics of an observations and essentially places in a basket for that combination. For example, you have a red shirt/dead basket and a red-shirt/alive basket. The procedure looks at each observation and places it into one of the baskets. Then it counts the observations in each basket.
What you have are counts (of errors) within each observation. You want to understand that IVs that relate to those counts. That’s a regression thing. Now, what form of regression. Because it involves counts, Poisson regression is a good possibility. You might also read up on negative binomial regression, which is related. Sometimes you can have count data that doesn’t meet certain requirements of the Poisson distribution, but you can use Negative Binomial regression. For more information, look on page 321-322 of my ebook that you just bought! 🙂 I talk a bit about regression with counts.
And, there’s a chance that you might be able to use OLS regression. That depends on how you’re handling the multiple assessments and the average number of errors. The Poisson distribution begins to approximate the normal distribution at around a mean of 25-ish. If the number of errors tend to fall around here or higher, OLS might be the ticket! If you’re summing multiple observations together, that might help in this regard.
I don’t understand the design of how you’re tracking changing the number of errors over time, and how you’ll model that. You might included lagged values of errors to explain current errors, along with other possible IVs.
I found point number 7 to be really interesting. Is it that the blind spot allows the error to persist in greater numbers and that awareness of errors had reduced numbers of those types? Your interpretation of that should be very interesting!
Oh, and for the nominal dependent variable, use nominal logistic regression (p. 319-320)!
I hope this helps!
March 27, 2019 at 11:53 am
Thanks for your clear posts, Could you please give some insight like in T test and F test, how can we calculate a chi- square test statistic value and how to convert to p value?
March 29, 2019 at 12:26 am
I have that exact topic in mind for a future blog post! I’ll write one up similar to the t-test and F-test posts in the near future. It’s too much to do in the comments section, but soon an entire post for it! I’ll aim for sometime in the next couple of months. Stay tuned!
November 16, 2018 at 1:47 pm
This was great. 🙂
September 21, 2018 at 10:47 am
thanks i have learnt alot
February 5, 2018 at 4:26 pm
Hello, Thanks for the nice tutorial. Can you please explain how the ‘Expected count’ is being calculated in the table “tabulated statistics: Uniform color, Status” ?
February 5, 2018 at 10:25 pm
Hi Shihab, that’s an excellent question!
You calculate the expected value for each cell by first multiplying the column proportion by the row proportion that are associated with each cell. This calculation produces the expected proportion for that cell. Then, you take the expected proportion and multiply it by the total number of observations to obtain the expected count. Let’s work through an example!
I’ll calculate the expected value for wearing a Blue uniform and being Alive. That’s the top-left cell in the statistical output.
At the bottom of the Alive column, we see that 90.7% of all observations are alive. So, 0.907 is the proportion for the Alive column. The output doesn’t display the proportion for the Blue row, but we can calculate that easily. We can see that there are 136 total counts in the Blue row and there are 430 total crew members. Hence, the proportion for the Blue row is 136/430 = 0.31627.
Next, we multiply 0.907 * 0.31627 = 0.28685689. That’s the expected proportion that should fall in that Blue/Alive cell.
Now, we multiply that proportion by the total number of observations to obtain the expected count for that cell: 0.28685689 * 430 = 123.348
You can see in the statistical output that has been rounded up to 123.35.
You simply repeat that procedure for the rest of the cells.
January 18, 2018 at 2:29 pm
very nice, thanks
January 1, 2018 at 8:51 am
Amazing post!! In the tabulated statistics section, you ran a Pearson Chi Square and a Likelihood Ratio Chi Square test. Are both of these necessary and do BOTH have to fall below the significance level for the null to be rejected? I’m assuming so. I don’t know what the difference is between these two tests but I will look it up. That was the only part that lost me:)
January 2, 2018 at 11:16 am
Thanks again, Jessica! I really appreciate your kind words!
When the two p-values are in agreement (e.g., both significant or insignificant), that’s easy. Fortunately, in my experience, these two p-values usually do agree. And, as the sample size increases, the agreement between them also increases.
I’ve looked into what to do when they disagree and have not found any clear answers. This paper suggests that as long as all expected frequencies are at least 5, use the Pearson Chi-Square test. When it is less than 5, the article recommends an adjusted Chi-square test, which is neither of the displayed tests!
These tests are most likely to disagree when you have borderline results to begin with (near your significance level), and particularly when you have a small sample. Either of these conditions alone make the results questionable. If these tests disagree, I’d take it as a big warning sign that more research is required!
December 8, 2017 at 6:58 am
December 8, 2017 at 11:10 am
December 7, 2017 at 8:18 am
A good presentation. My experience with researchers in health sciences and clinical studies is that very often people do not bother about the hypotheses (null and alternate) but run after a p-value, more so with Chi-Square test of independence!! Your narration is excellent.
December 7, 2017 at 4:08 am
Helpful post. I can understand now
December 6, 2017 at 9:47 pm
Excellent Example, Thank you.
December 6, 2017 at 11:24 pm
You’re very welcome. I’m glad it was helpful!
Comments and Questions Cancel reply
Null Hypothesis In Chi Square
Unraveling the null hypothesis in chi-square analysis.
In the vast landscape of statistical analysis, where numbers dance and patterns emerge, the chi-square test stands as a stalwart, helping researchers discern the significance of observed data. At its heart lies a critical concept: the null hypothesis. Let us embark on a journey to demystify this cornerstone of chi-square analysis, exploring its essence, implications, and applications.

Null Hypothesis in Chi-Square:
Unveiling the Essence
At its core, the null hypothesis in chi-square analysis posits that there is no significant difference between the observed and expected frequencies of a categorical variable. In simpler terms, it suggests that any deviation between what we expect to observe and what we actually observe is due to chance alone, rather than any true effect or relationship.
This hypothesis serves as the null point against which researchers gauge the validity of their findings. It embodies skepticism, challenging researchers to substantiate any claims of association or difference in frequencies within their data. By subjecting their hypotheses to rigorous scrutiny, researchers ensure that their conclusions are grounded in empirical evidence rather than mere conjecture.
Understanding Chi-Square Analysis
In essence, chi-square analysis compares observed frequencies in different categories to the frequencies we would expect to see if there were no association between the variables being studied. It quantifies the extent of deviation from expected frequencies, providing researchers with a measure of the likelihood that such deviation occurred purely by chance.
Embracing the Null Hypothesis:
Within the realm of chi-square analysis, the null hypothesis serves as both a guiding principle and a formidable adversary. Its assertion of no significant difference challenges researchers to scrutinize their data rigorously, employing statistical tools to discern genuine patterns from random fluctuations.
When conducting a chi-square test, researchers formulate two hypotheses: the null hypothesis (H₀) and the alternative hypothesis (H₁). The null hypothesis posits no relationship or difference between variables, while the alternative hypothesis suggests the presence of such a relationship or difference.
In the context of chi-square analysis, the null hypothesis typically takes the form: “There is no significant difference between the observed and expected frequencies of the categorical variable.” Conversely, the alternative hypothesis might propose that a relationship exists, such as: “There is a significant difference between the observed and expected frequencies of the categorical variable.”
Interpreting Chi-Square Results:
Once the chi-square test is conducted, researchers turn their attention to the p-value—a numerical measure that quantifies the strength of evidence against the null hypothesis. A low p-value suggests that the observed deviation from expected frequencies is unlikely to occur purely by chance, leading researchers to reject the null hypothesis in favor of the alternative.
Applications and Extensions:
Beyond the Basics
In the realm of chi-square analysis, the null hypothesis serves as a beacon of skepticism, challenging researchers to scrutinize their findings with precision and diligence. By subjecting their hypotheses to rigorous testing, researchers ensure that their conclusions are anchored in empirical evidence rather than mere speculation.
As we navigate the intricate landscape of statistical analysis, let us heed the call of the null hypothesis, embracing its skepticism as a cornerstone of scientific inquiry. In doing so, we honor the pursuit of truth and uphold the integrity of empirical research for generations to come.

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
8.1 - the chi-square test of independence.
How do we test the independence of two categorical variables? It will be done using the Chi-Square Test of Independence.
As with all prior statistical tests we need to define null and alternative hypotheses. Also, as we have learned, the null hypothesis is what is assumed to be true until we have evidence to go against it. In this lesson, we are interested in researching if two categorical variables are related or associated (i.e., dependent). Therefore, until we have evidence to suggest that they are, we must assume that they are not. This is the motivation behind the hypothesis for the Chi-Square Test of Independence:
- \(H_0\): In the population, the two categorical variables are independent.
- \(H_a\): In the population, the two categorical variables are dependent.
Note! There are several ways to phrase these hypotheses. Instead of using the words "independent" and "dependent" one could say "there is no relationship between the two categorical variables" versus "there is a relationship between the two categorical variables." Or "there is no association between the two categorical variables" versus "there is an association between the two variables." The important part is that the null hypothesis refers to the two categorical variables not being related while the alternative is trying to show that they are related.
Once we have gathered our data, we summarize the data in the two-way contingency table. This table represents the observed counts and is called the Observed Counts Table or simply the Observed Table. The contingency table on the introduction page to this lesson represented the observed counts of the party affiliation and opinion for those surveyed.
The question becomes, "How would this table look if the two variables were not related?" That is, under the null hypothesis that the two variables are independent, what would we expect our data to look like?
Consider the following table:
| Success | Failure | Total | |
|---|---|---|---|
| Group 1 | A | B | A+B |
| Group 2 | C | D | C+D |
| Total | A+C | B+D | A+B+C+D |
The total count is \(A+B+C+D\). Let's focus on one cell, say Group 1 and Success with observed count A. If we go back to our probability lesson, let \(G_1\) denote the event 'Group 1' and \(S\) denote the event 'Success.' Then,
\(P(G_1)=\dfrac{A+B}{A+B+C+D}\) and \(P(S)=\dfrac{A+C}{A+B+C+D}\).
Recall that if two events are independent, then their intersection is the product of their respective probabilities. In other words, if \(G_1\) and \(S\) are independent, then...
\begin{align} P(G_1\cap S)&=P(G_1)P(S)\\&=\left(\dfrac{A+B}{A+B+C+D}\right)\left(\dfrac{A+C}{A+B+C+D}\right)\\[10pt] &=\dfrac{(A+B)(A+C)}{(A+B+C+D)^2}\end{align}
If we considered counts instead of probabilities, then we get the count by multiplying the probability by the total count. In other words...
\begin{align} \text{Expected count for cell with A} &=P(G_1)P(S)\ x\ (\text{total count}) \\ &= \left(\dfrac{(A+B)(A+C)}{(A+B+C+D)^2}\right)(A+B+C+D)\\[10pt]&=\mathbf{\dfrac{(A+B)(A+C)}{A+B+C+D}} \end{align}
This is the count we would expect to see if the two variables were independent (i.e. assuming the null hypothesis is true).
The expected count for each cell under the null hypothesis is:
\(E=\dfrac{\text{(row total)}(\text{column total})}{\text{total sample size}}\)
Example 8-1: Political Affiliation and Opinion Section
To demonstrate, we will use the Party Affiliation and Opinion on Tax Reform example.
Observed Table:
| favor | indifferent | opposed | total | |
|---|---|---|---|---|
| democrat | 138 | 83 | 64 | 285 |
| republican | 64 | 67 | 84 | 215 |
| total | 202 | 150 | 148 | 500 |
Find the expected counts for all of the cells.
We need to find what is called the Expected Counts Table or simply the Expected Table. This table displays what the counts would be for our sample data if there were no association between the variables.
Calculating Expected Counts from Observed Counts
| favor | indifferent | opposed | total | |
|---|---|---|---|---|
| democrat | \(\frac{285(202)}{500}=115.14\) | \(\frac{285(150)}{500}=85.5\) | \(\frac{285(148)}{500}=84.36\) | 285 |
| republican | \(\frac{215(202)}{500}=86.86\) | \(\frac{215(150)}{500}=64.5\) | \(\frac{215(148)}{500}=63.64\) | 215 |
| total | 202 | 150 | 148 | 500 |
Chi-Square Test Statistic Section
To better understand what these expected counts represent, first recall that the expected counts table is designed to reflect what the sample data counts would be if the two variables were independent. Taking what we know of independent events, we would be saying that the sample counts should show similarity in opinions of tax reform between democrats and republicans. If you find the proportion of each cell by taking a cell's expected count divided by its row total, you will discover that in the expected table each opinion proportion is the same for democrats and republicans. That is, from the expected counts, 0.404 of the democrats and 0.404 of the republicans favor the bill; 0.3 of the democrats and 0.3 of the republicans are indifferent; and 0.296 of the democrats and 0.296 of the republicans are opposed.
The statistical question becomes, "Are the observed counts so different from the expected counts that we can conclude a relationship exists between the two variables?" To conduct this test we compute a Chi-Square test statistic where we compare each cell's observed count to its respective expected count.
In a summary table, we have \(r\times c=rc\) cells. Let \(O_1, O_2, …, O_{rc}\) denote the observed counts for each cell and \(E_1, E_2, …, E_{rc}\) denote the respective expected counts for each cell.
The Chi-Square test statistic is calculated as follows:
\(\chi^{2*}=\frac{(O_1-E_1)^2}{E_1}+\frac{(O_2-E_2)^2}{E_2}+...+\frac{(O_{rc}-E_{rc})^2}{E_{rc}}=\overset{rc}{ \underset{i=1}{\sum}}\frac{(O_i-E_i)^2}{E_i}\)
Under the null hypothesis and certain conditions (discussed below), the test statistic follows a Chi-Square distribution with degrees of freedom equal to \((r-1)(c-1)\), where \(r\) is the number of rows and \(c\) is the number of columns. We leave out the mathematical details to show why this test statistic is used and why it follows a Chi-Square distribution.
As we have done with other statistical tests, we make our decision by either comparing the value of the test statistic to a critical value (rejection region approach) or by finding the probability of getting this test statistic value or one more extreme (p-value approach).
The critical value for our Chi-Square test is \(\chi^2_{\alpha}\) with degree of freedom =\((r - 1) (c -1)\), while the p-value is found by \(P(\chi^2>\chi^{2*})\) with degrees of freedom =\((r - 1)(c - 1)\).
Example 8-1 Cont'd: Chi-Square Section
Let's apply the Chi-Square Test of Independence to our example where we have a random sample of 500 U.S. adults who are questioned regarding their political affiliation and opinion on a tax reform bill. We will test if the political affiliation and their opinion on a tax reform bill are dependent at a 5% level of significance. Calculate the test statistic.
- Using Minitab
The contingency table ( political_affiliation.csv ) is given below. Each cell contains the observed count and the expected count in parentheses. For example, there were 138 democrats who favored the tax bill. The expected count under the null hypothesis is 115.14. Therefore, the cell is displayed as 138 (115.14).
| favor | indifferent | opposed | total | |
|---|---|---|---|---|
| democrat | 138 (115.14) | 83 (85.5) | 64 (84.36) | 285 |
| republican | 64 (86.86) | 67 (64.50) | 84 (63.64) | 215 |
| total | 202 | 150 | 148 | 500 |
Calculating the test statistic by hand:
\begin{multline} \chi^{2*}=\dfrac{(138−115.14)^2}{115.14}+\dfrac{(83−85.50)^2}{85.50}+\dfrac{(64−84.36)^2}{84.36}+\\ \dfrac{(64−86.86)^2}{86.86}+\dfrac{(67−64.50)^2}{64.50}+\dfrac{(84−63.64)^2}{63.64}=22.152\end{multline}
...with degrees for freedom equal to \((2 - 1)(3 - 1) = 2\).
Minitab: Chi-Square Test of Independence
To perform the Chi-Square test in Minitab...
- Choose Stat > Tables > Chi-Square Test for Association
- If you have summarized data (i.e., observed count) from the drop-down box 'Summarized data in a two-way table.' Select and enter the columns that contain the observed counts, otherwise, if you have the raw data use 'Raw data' (categorical variables). Note that if using the raw data your data will need to consist of two columns: one with the explanatory variable data (goes in the 'row' field) and the response variable data (goes in the 'column' field).
- Labeling (Optional) When using the summarized data you can label the rows and columns if you have the variable labels in columns of the worksheet. For example, if we have a column with the two political party affiliations and a column with the three opinion choices we could use these columns to label the output.
- Click the Statistics tab. Keep checked the four boxes already checked, but also check the box for 'Each cell's contribution to the chi-square.' Click OK .
Note! If you have the observed counts in a table, you can copy/paste them into Minitab. For instance, you can copy the entire observed counts table (excluding the totals!) for our example and paste these into Minitab starting with the first empty cell of a column.
The following is the Minitab output for this example.
Cell Contents: Count, Expected count, Contribution to Chi-Square
| favor | indifferent | opposed | All | |
|---|---|---|---|---|
| 1 | 138 115.14 4.5836 | 83 85.50 0.0731 | 64 84.36 4.9138 | 285 |
| 2 | 64 86.86 6.0163 | 67 64.50 0.0969 | 84 63.64 6.5137 | 215 |
| All | 202 | 150 | 148 | 500 |
Pearson Chi-Sq = 4.5386 + 0.073 + 4.914 + 6.016 + 0.097 + 6.5137 = 22.152 DF = 2, P-Value = 0.000
Likelihood Ratio Chi-Square
The Chi-Square test statistic is 22.152 and calculated by summing all the individual cell's Chi-Square contributions:
\(4.584 + 0.073 + 4.914 + 6.016 + 0.097 + 6.532 = 22.152\)
The p-value is found by \(P(X^2>22.152)\) with degrees of freedom =\((2-1)(3-1) = 2\).
Minitab calculates this p-value to be less than 0.001 and reports it as 0.000. Given this p-value of 0.000 is less than the alpha of 0.05, we reject the null hypothesis that political affiliation and their opinion on a tax reform bill are independent. We conclude that there is evidence that the two variables are dependent (i.e., that there is an association between the two variables).
Conditions for Using the Chi-Square Test Section
Exercise caution when there are small expected counts. Minitab will give a count of the number of cells that have expected frequencies less than five. Some statisticians hesitate to use the Chi-Square test if more than 20% of the cells have expected frequencies below five, especially if the p-value is small and these cells give a large contribution to the total Chi-Square value.
Example 8-2: Tire Quality Section
The operations manager of a company that manufactures tires wants to determine whether there are any differences in the quality of work among the three daily shifts. She randomly selects 496 tires and carefully inspects them. Each tire is either classified as perfect, satisfactory, or defective, and the shift that produced it is also recorded. The two categorical variables of interest are the shift and condition of the tire produced. The data ( shift_quality.txt ) can be summarized by the accompanying two-way table. Does the data provide sufficient evidence at the 5% significance level to infer that there are differences in quality among the three shifts?
| Perfect | Satisfactory | Defective | Total | |
|---|---|---|---|---|
| Shift 1 | 106 | 124 | 1 | 231 |
| Shift 2 | 67 | 85 | 1 | 153 |
| Shift 3 | 37 | 72 | 3 | 112 |
| Total | 210 | 281 | 5 | 496 |
Chi-Square Test
| C1 | C2 | C3 | Total | |
| 1 | 106 97.80 | 124 130.87 | 1 2.33 | 231 |
| 2 | 67 64.78 | 85 86.68 | 1 1.54 | 153 |
| 3 | 37 47.42 | 72 63.45 | 3 1.13 | 112 |
| Total | 210 | 281 | 5 | 496 |
Chi-Sq = 8.647 DF = 4, P-Value = 0.071
Note that there are 3 cells with expected counts less than 5.0.
In the above example, we don't have a significant result at a 5% significance level since the p-value (0.071) is greater than 0.05. Even if we did have a significant result, we still could not trust the result, because there are 3 (33.3% of) cells with expected counts < 5.0
Sometimes researchers will categorize quantitative data (e.g., take height measurements and categorize as 'below average,' 'average,' and 'above average.') Doing so results in a loss of information - one cannot do the reverse of taking the categories and reproducing the raw quantitative measurements. Instead of categorizing, the data should be analyzed using quantitative methods.
Try it! Section
A food services manager for a baseball park wants to know if there is a relationship between gender (male or female) and the preferred condiment on a hot dog. The following table summarizes the results. Test the hypothesis with a significance level of 10%.
| Condiment | |||||
|---|---|---|---|---|---|
| Gender | Ketchup | Mustard | Relish | Total | |
| Male | 15 | 23 | 10 | 48 | |
| Female | 25 | 19 | 8 | 52 | |
| Total | 40 | 42 | 18 | 100 | |
The hypotheses are:
- \(H_0\): Gender and condiments are independent
- \(H_a\): Gender and condiments are not independent
We need to expected counts table:
| Condiment | |||||
|---|---|---|---|---|---|
| Gender | Ketchup | Mustard | Relish | Total | |
| Male | 15 (19.2) | 23 (20.16) | 10 (8.64) | 48 | |
| Female | 25 (20.8) | 19 (21.84) | 8 (9.36) | 52 | |
| Total | 40 | 42 | 18 | 100 | |
None of the expected counts in the table are less than 5. Therefore, we can proceed with the Chi-Square test.
The test statistic is:
\(\chi^{2*}=\frac{(15-19.2)^2}{19.2}+\frac{(23-20.16)^2}{20.16}+...+\frac{(8-9.36)^2}{9.36}=2.95\)
The p-value is found by \(P(\chi^2>\chi^{2*})=P(\chi^2>2.95)\) with (3-1)(2-1)=2 degrees of freedom. Using a table or software, we find the p-value to be 0.2288.
With a p-value greater than 10%, we can conclude that there is not enough evidence in the data to suggest that gender and preferred condiment are related.
- Math Article
- Chi Square Test
Chi-Square Test

A chi-squared test (symbolically represented as χ 2 ) is basically a data analysis on the basis of observations of a random set of variables. Usually, it is a comparison of two statistical data sets. This test was introduced by Karl Pearson in 1900 for categorical data analysis and distribution . So it was mentioned as Pearson’s chi-squared test .
The chi-square test is used to estimate how likely the observations that are made would be, by considering the assumption of the null hypothesis as true.
A hypothesis is a consideration that a given condition or statement might be true, which we can test afterwards. Chi-squared tests are usually created from a sum of squared falsities or errors over the sample variance.
Chi-Square Distribution
When we consider, the null speculation is true, the sampling distribution of the test statistic is called as chi-squared distribution . The chi-squared test helps to determine whether there is a notable difference between the normal frequencies and the observed frequencies in one or more classes or categories. It gives the probability of independent variables.
Note: Chi-squared test is applicable only for categorical data, such as men and women falling under the categories of Gender, Age, Height, etc.
Finding P-Value
P stands for probability here. To calculate the p-value, the chi-square test is used in statistics. The different values of p indicates the different hypothesis interpretation, are given below:
- P≤ 0.05; Hypothesis rejected
- P>.05; Hypothesis Accepted
Probability is all about chance or risk or uncertainty. It is the possibility of the outcome of the sample or the occurrence of an event. But when we talk about statistics, it is more about how we handle various data using different techniques. It helps to represent complicated data or bulk data in a very easy and understandable way. It describes the collection, analysis, interpretation, presentation, and organization of data. The concept of both probability and statistics is related to the chi-squared test.
Also, read:
The following are the important properties of the chi-square test:
- Two times the number of degrees of freedom is equal to the variance.
- The number of degree of freedom is equal to the mean distribution
- The chi-square distribution curve approaches the normal distribution when the degree of freedom increases.
The chi-squared test is done to check if there is any difference between the observed value and expected value. The formula for chi-square can be written as;
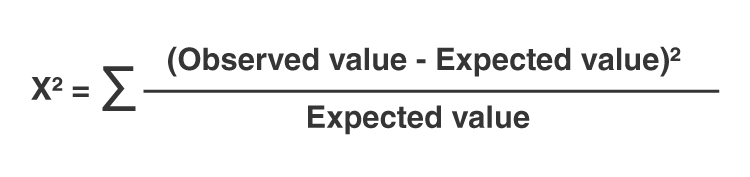
χ 2 = ∑(O i – E i ) 2 /E i
where O i is the observed value and E i is the expected value.
Chi-Square Test of Independence
The chi-square test of independence also known as the chi-square test of association which is used to determine the association between the categorical variables. It is considered as a non-parametric test . It is mostly used to test statistical independence.
The chi-square test of independence is not appropriate when the categorical variables represent the pre-test and post-test observations. For this test, the data must meet the following requirements:
- Two categorical variables
- Relatively large sample size
- Categories of variables (two or more)
- Independence of observations
Example of Categorical Data
Let us take an example of a categorical data where there is a society of 1000 residents with four neighbourhoods, P, Q, R and S. A random sample of 650 residents of the society is taken whose occupations are doctors, engineers and teachers. The null hypothesis is that each person’s neighbourhood of residency is independent of the person’s professional division. The data are categorised as:
| Categories | P | Q | R | S | Total |
| Doctors | 90 | 60 | 104 | 95 | 349 |
| Engineers | 30 | 50 | 51 | 20 | 151 |
| Teachers | 30 | 40 | 45 | 35 | 150 |
| Total | 150 | 150 | 200 | 150 | 650 |
Assume the sample living in neighbourhood P, 150, to estimate what proportion of the whole 1,000 people live in neighbourhood P. In the same way, we take 349/650 to calculate what ratio of the 1,000 are doctors. By the supposition of independence under the hypothesis, we should “expect” the number of doctors in neighbourhood P is;
150 x 349/650 ≈ 80.54
So by the chi-square test formula for that particular cell in the table, we get;
(Observed – Expected) 2 /Expected Value = (90-80.54) 2 /80.54 ≈ 1.11
Some of the exciting facts about the Chi-square test are given below:
The Chi-square statistic can only be used on numbers. We cannot use them for data in terms of percentages, proportions, means or similar statistical contents. Suppose, if we have 20% of 400 people, we need to convert it to a number, i.e. 80, before running a test statistic.
A chi-square test will give us a p-value. The p-value will tell us whether our test results are significant or not.
However, to perform a chi-square test and get the p-value, we require two pieces of information:
(1) Degrees of freedom. That’s just the number of categories minus 1.
(2) The alpha level(α). You or the researcher chooses this. The usual alpha level is 0.05 (5%), but you could also have other levels like 0.01 or 0.10.
In elementary statistics, we usually get questions along with the degrees of freedom(DF) and the alpha level. Thus, we don’t usually have to figure out what they are. To get the degrees of freedom, count the categories and subtract 1.
The chi-square distribution table with three probability levels is provided here. The statistic here is used to examine whether distributions of certain variables vary from one another. The categorical variable will produce data in the categories and numerical variables will produce data in numerical form.
The distribution of χ 2 with (r-1)(c-1) degrees of freedom(DF) , is represented in the table given below. Here, r represents the number of rows in the two-way table and c represents the number of columns.
|
| |||
| 3.84 | 6.64 | 10.83 | |
| 5.99 | 9.21 | 13.82 | |
| 7.82 | 11.35 | 16.27 | |
| 9.49 | 13.28 | 18.47 | |
| 11.07 | 15.09 | 20.52 | |
| 12.59 | 16.81 | 22.46 | |
| 14.07 | 18.48 | 24.32 | |
| 15.51 | 20.09 | 26.13 | |
| 16.92 | 21.67 | 27.88 | |
| 18.31 | 23.21 | 29.59 | |
| 19.68 | 24.73 | 31.26 | |
| 21.03 | 26.22 | 32.91 | |
| 22.36 | 27.69 | 34.53 | |
| 23.69 | 29.14 | 36.12 | |
| 25.00 | 30.58 | 37.70 | |
| 26.30 | 32.00 | 39.25 | |
| 27.59 | 33.41 | 40.79 | |
| 28.87 | 34.81 | 42.31 | |
| 30.14 | 36.19 | 43.82 | |
| 31.41 | 37.57 | 45.32 | |
| 32.67 | 38.93 | 46.80 | |
| 33.92 | 40.29 | 48.27 | |
| 35.17 | 41.64 | 49.73 | |
| 36.42 | 42.98 | 51.18 | |
| 37.65 | 44.31 | 52.62 | |
| 38.89 | 45.64 | 54.05 | |
| 40.11 | 46.96 | 55.48 | |
| 41.34 | 48.28 | 56.89 | |
| 42.56 | 49.59 | 58.30 | |
| 43.77 | 50.89 | 59.70 | |
| 44.99 | 52.19 | 61.10 | |
| 46.19 | 53.49 | 62.49 | |
| 47.40 | 54.78 | 63.87 | |
| 48.60 | 56.06 | 65.25 | |
| 49.80 | 57.34 | 66.62 | |
| 51.00 | 58.62 | 67.99 | |
| 52.19 | 59.89 | 69.35 | |
| 53.38 | 61.16 | 70.71 | |
| 54.57 | 62.43 | 72.06 | |
| 55.76 | 63.69 | 73.41 | |
| 56.94 | 64.95 | 74.75 | |
| 58.12 | 66.21 | 76.09 | |
| 59.30 | 67.46 | 77.42 | |
| 60.48 | 68.71 | 78.75 | |
| 61.66 | 69.96 | 80.08 | |
| 62.83 | 71.20 | 81.40 | |
| 64.00 | 72.44 | 82.72 | |
| 65.17 | 73.68 | 84.03 | |
| 66.34 | 74.92 | 85.35 | |
| 67.51 | 76.15 | 86.66 | |
| 68.67 | 77.39 | 87.97 | |
| 69.83 | 78.62 | 89.27 | |
| 70.99 | 79.84 | 90.57 | |
| 72.15 | 81.07 | 91.88 | |
| 73.31 | 82.29 | 93.17 | |
| 74.47 | 83.52 | 94.47 | |
| 75.62 | 84.73 | 95.75 | |
| 76.78 | 85.95 | 97.03 | |
| 77.93 | 87.17 | 98.34 | |
| 79.08 | 88.38 | 99.62 | |
| 80.23 | 89.59 | 100.88 | |
| 81.38 | 90.80 | 102.15 | |
| 82.53 | 92.01 | 103.46 | |
| 83.68 | 93.22 | 104.72 | |
| 84.82 | 94.42 | 105.97 | |
| 85.97 | 95.63 | 107.26 | |
| 87.11 | 96.83 | 108.54 | |
| 88.25 | 98.03 | 109.79 | |
| 89.39 | 99.23 | 111.06 | |
| 90.53 | 100.42 | 112.31 | |
| 91.67 | 101.62 | 113.56 | |
| 92.81 | 102.82 | 114.84 | |
| 93.95 | 104.01 | 116.08 | |
| 95.08 | 105.20 | 117.35 | |
| 96.22 | 106.39 | 118.60 | |
| 97.35 | 107.58 | 119.85 | |
| 98.49 | 108.77 | 121.11 | |
| 99.62 | 109.96 | 122.36 | |
| 100.75 | 111.15 | 123.60 | |
| 101.88 | 112.33 | 124.84 | |
| 103.01 | 113.51 | 126.09 | |
| 104.14 | 114.70 | 127.33 | |
| 105.27 | 115.88 | 128.57 | |
| 106.40 | 117.06 | 129.80 | |
| 107.52 | 118.24 | 131.04 | |
| 108.65 | 119.41 | 132.28 | |
| 109.77 | 120.59 | 133.51 | |
| 110.90 | 121.77 | 134.74 | |
| 112.02 | 122.94 | 135.96 | |
| 113.15 | 124.12 | 137.19 | |
| 114.27 | 125.29 | 138.45 | |
| 115.39 | 126.46 | 139.66 | |
| 116.51 | 127.63 | 140.90 | |
| 117.63 | 128.80 | 142.12 | |
| 118.75 | 129.97 | 143.32 | |
| 119.87 | 131.14 | 144.55 | |
| 120.99 | 132.31 | 145.78 | |
| 122.11 | 133.47 | 146.99 | |
| 123.23 | 134.64 | 148.21 | |
| 124.34 | 135.81 | 149.48 | |
Solved Problem
A survey on cars had conducted in 2011 and determined that 60% of car owners have only one car, 28% have two cars, and 12% have three or more. Supposing that you have decided to conduct your own survey and have collected the data below, determine whether your data supports the results of the study.
Use a significance level of 0.05. Also, given that, out of 129 car owners, 73 had one car and 38 had two cars.
Let us state the null and alternative hypotheses.
H 0 : The proportion of car owners with one, two or three cars is 0.60, 0.28 and 0.12 respectively.
H 1 : The proportion of car owners with one, two or three cars does not match the proposed model.
A Chi-Square goodness of fit test is appropriate because we are examining the distribution of a single categorical variable.
Let’s tabulate the given information and calculate the required values.
| Observed (O ) | Expected (E ) | O – E | (O – E ) | (O – E ) /E | |
| One car | 73 | 0.60 × 129 = 77.4 | -4.4 | 19.36 | 0.2501 |
| Two cars | 38 | 0.28 × 129 = 36.1 | 1.9 | 3.61 | 0.1 |
| Three or more cars | 18 | 0.12 × 129 = 15.5 | 2.5 | 6.25 | 0.4032 |
| Total | 129 | 0.7533 |
Therefore, χ 2 = ∑(O i – E i ) 2 /E i = 0.7533
Let’s compare it to the chi-square value for the significance level 0.05.
The degrees for freedom = 3 – 1 = 2
Using the table, the critical value for a 0.05 significance level with df = 2 is 5.99.
That means that 95 times out of 100, a survey that agrees with a sample will have a χ 2 value of 5.99 or less.
The Chi-square statistic is only 0.7533, so we will accept the null hypothesis.

Frequently Asked Questions – FAQs
What is the chi-square test write its formula, how do you calculate chi squared, what is a chi-square test used for, how do you interpret a chi-square test, what is a good chi-square value.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

4.3.2: Introduction to Goodness-of-Fit Chi-Square
- Last updated
- Save as PDF
- Page ID 44956

- Michelle Oja
- Taft College
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
The firs t of our two \(\chi^{2}\) tests, the Goodness of Fit test, assesses the distribution of frequencies into different categories of one quantitative variable against any specific distribution. Usually this is equal frequency distributions because that's what we would expect to get if categorization was completely random, but it can also be a specific distribution. For example, if Dr. MO wanted to compare a specific class's frequency of each ethnicity to a specific distribution, it would make more sense to compare her class to the ethnic demographics of the college rather than an assumption that all of the ethnic groups would have the same number of students in the target class.
Hypotheses for Chi-Square
All \(\chi^{2}\) tests, including the goodness-of-fit test, are non-parametric. This means that there is no population parameter we are estimating or testing against; we are working only with our sample data. This makes it more difficult to have mathematical statements for \(\chi^{2}\) hypotheses (symbols showing which group is bigger or whatever). The next section will walk through the mathematical hypotheses. For now, we will learn how to still state our hypotheses verbally.
Research Hypothesis
The research hypothesis is that we expect a pattern of difference, and then we explain that pattern of difference.
Using Dr. MO's sample class, she works at a college that is designated as a Hispanic-Serving Institution (HSI), so we would expect a pattern of difference such that there will be more students who are Hispanic in her class than students from any other ethnic group.
Null Hypotheses
For goodness-of-fit \(\chi^{2}\) tests, our null hypothesis is often that there is an equal number of observations in each category. That is, there is no pattern of difference between the frequencies in each category. Unless we're looking at the situation above in which we have a distribution of frequencies that we are comparing our sample to, the null hypothesis is that each group will be the same size.
Degrees of Freedom and the \(\chi^{2}\) table
Our degrees of freedom for the \(\chi^{2}\) test are based on the number of categories we have in our variable, not on the number of people or observations like it was for our other tests. Luckily, they are still as simple to calculate:
\[d f=k-1 \nonumber\]
Do you remember what "k" stood for when we discussed ANOVAs?
Exercise \(\PageIndex{1}\)
What does "k" stand for?
The letter "k" usually stands for the number of groups. In Chi-Square, this would be the number of different categories.
So for our pet preference example, we have 3 categories, so we have 2 degrees of freedom. Our degrees of freedom, along with our significance level (still defaulted to \(α = 0.05\)) are used to find our critical values in the \(\chi^{2}\) table, which is next, or can be found through the Common Critical Value Tables at the end of this book.
Back to blog home
How to test your hypothesis (with statistics), the statsig team.
Navigating the realm of data-driven decisions, the role of hypothesis testing cannot be overstated. It serves as a crucial tool that helps you make informed choices by validating your assumptions with statistical rigor.
Diving into the metrics can often seem daunting, but understanding the basics of hypothesis testing empowers you to leverage data effectively. This guide aims to demystify the process and equip you with the knowledge to apply it confidently in your projects.
Understanding Hypothesis Testing Fundamentals
At its core, a hypothesis is an assumption you make about a particular parameter in your data set, crafted to test its validity through statistical analysis. This is not just a guess; it's a statement that suggests a potential outcome based on observed data patterns.
The foundation of hypothesis testing lies in two critical concepts:
Null hypothesis (H0) : This hypothesis posits that there is no effect or no difference in the data. It serves as a default position that indicates any observed effect is due to sampling error.
Alternative hypothesis (H1) : Contrary to the null, this hypothesis suggests that there is indeed an effect or a difference.
To give you a clearer picture:
Suppose you want to test if a new feature on your app increases user engagement. The null hypothesis would state that the feature does not change engagement, while the alternative hypothesis would assert that it does.
In practice, you would collect data on user engagement, apply a hypothesis testing statistics calculator to analyze this data, and determine whether to reject the null hypothesis or fail to reject it (note that "fail to reject" does not necessarily mean "accept"). This decision is usually based on a p-value, which quantifies the probability of obtaining a result at least as extreme as the one observed, under the assumption that the null hypothesis is correct.
Selecting the right statistical test
Choosing the right statistical test is pivotal; it hinges on your data type and the questions at hand. For instance, a t-test is optimal for comparing the means of two groups when you assume a normal distribution. This test helps you decide if differences in group means are statistically significant.
When your study involves more than two groups, ANOVA (Analysis of Variance) is the go-to method. It evaluates differences across group means to ascertain variability within samples. If your data consists of categories, the chi-squared test evaluates whether distributions of categorical variables differ from each other.
Criteria for test selection:
T-test : Use when comparing two groups under normal distribution.
ANOVA : Apply when comparing three or more groups.
Chi-squared : Best for categorical data analysis.
Each test serves a specific purpose, tailored to the nature of your data and research objectives. By selecting the appropriate test, you enhance the reliability of your conclusions, ensuring that your decisions are data-driven.
Sample size and power considerations
Calculating the right sample size is crucial for the reliability of your hypothesis testing. A larger sample size decreases the margin of error and boosts the confidence level. This makes your results more dependable and robust.
Statistical power is the likelihood of correctly rejecting the null hypothesis when it is indeed false. Several factors influence this power:
Sample size : Larger samples increase power.
Effect size : Bigger effects are easier to detect.
Significance level : Lower levels demand stronger evidence.
Understanding these elements helps you design more effective tests. With the right balance, you maximize the chance of detecting true effects, making your insights actionable. Always consider these factors when planning your experiments to ensure meaningful and accurate outcomes.
Implementing the test: Steps and procedures
Setting up and executing a statistical test involves several clear steps. First, define your hypotheses and decide on the appropriate statistical test based on your data type. Next, gather your data through reliable collection methods, ensuring accuracy and relevance.
Handling data anomalies is part of the process. Identify outliers and decide whether to exclude them based on their impact on your results. Utilize software tools like R, Python, or specialized statistical software to analyze the data.
Interpreting the results is crucial. Focus on the p-value; it helps determine the statistical significance of your test results. A low p-value (typically less than 0.05) suggests that you can reject the null hypothesis.
Remember, while p-values indicate whether an effect exists, they don't measure its size or importance. Always complement p-value analysis with confidence intervals and effect size measures to fully understand your test outcomes. This approach ensures you make informed decisions based on comprehensive data analysis.
Common Mistakes and Misinterpretations
P-hacking stands out as a notable pitfall in hypothesis testing. Researchers might cycle through various methods or subsets until they find a p-value that supports their desired outcome. This practice risks producing results that do not accurately reflect the true nature of the data.
Misunderstandings about p-values are widespread. Remember, a significant p-value does not imply causation. It also does not indicate the magnitude of an effect, merely that the effect is unlikely to be due to chance.
Always approach p-values with a critical eye. Appreciate their role in hypothesis testing but understand their limitations. They are tools for decision making, not definitive proofs. For a deeper understanding, you might find it helpful to read about how hypothesis testing is akin to a game of flipping coins, or explore further explanations on the nuances of p-values in hypothesis testing .
Statsig for startups
Statsig offers a generous program for early-stage startups who are scaling fast and need a sophisticated experimentation platform.
Build fast?
Try statsig today.

Recent Posts
How to add feature flags to next.js.
In this tutorial, we show how to setup Next.JS Product Analytics with the Statsig SDKs. We'll use Next.JS App Router, Statsig for product analytics, and also share how to deploy this app with Vercel.
Go from 0 to 1 with Statsig's free suite of data tools for startups
Statsig has four data tools that are ideal for earlier stage companies: Web Analytics, Session Replay, Sidecar (low-code website experimentation), and Product Analytics.
The Marketers go-to tech stack for website optimization
Boost your site's conversions with Statsig's Web Analytics, low code experimentation Sidecar, and Session Replay. Optimize efficiently with deep insights and testing tools.
Experiment scorecards: Essentials and best practices
An experiment scorecard is more than just a collection of numbers; it's a narrative of your experiment's journey from hypothesis to conclusion.
What's the difference between Statsig and PostHog?
Statsig and PostHog both offer suites of tools that help builders be more data-driven in how they develop products, but how do they differ?
Intro to product analytics
Product analytics reveals user interactions, driving informed decisions, enhancing UX, and boosting business outcomes.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Chi-Square (Χ²) Table | Examples & Downloadable Table
Chi-Square (Χ²) Table | Examples & Downloadable Table
Published on May 31, 2022 by Shaun Turney . Revised on June 21, 2023.
The chi-square (Χ 2 ) distribution table is a reference table that lists chi-square critical values . A chi-square critical value is a threshold for statistical significance for certain hypothesis tests and defines confidence intervals for certain parameters.
Chi-square critical values are calculated from chi-square distributions . They’re difficult to calculate by hand, which is why most people use a reference table or statistical software instead.
Download chi-square table (PDF)
Table of contents
When to use a chi-square distribution table, chi-square distribution table (right-tail probabilities), how to use the table, left-tailed and two-tailed probabilities, practice questions, other interesting articles, frequently asked questions about chi-square tables.
You will need a chi-square critical value if you want to:
- Calculate a confidence interval for a population variance or standard deviation
- Test whether the variance or standard deviation of a population is equal to a certain value (test of a single variance)
- Test whether the frequency distribution of a categorical variable is different from your expectations ( chi-square goodness of fit test )
- Test whether two categorical variables are related to each other ( chi-square test of independence )
- Test whether the proportions of two closely related variables are equal ( McNemar’s test )
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

Use the table below to find the chi-square critical value for your chi-square test or confidence interval or download the chi-square distribution table (PDF) .
The table provides the right-tail probabilities. If you need the left-tail probabilities, you’ll need to make a small additional calculation .
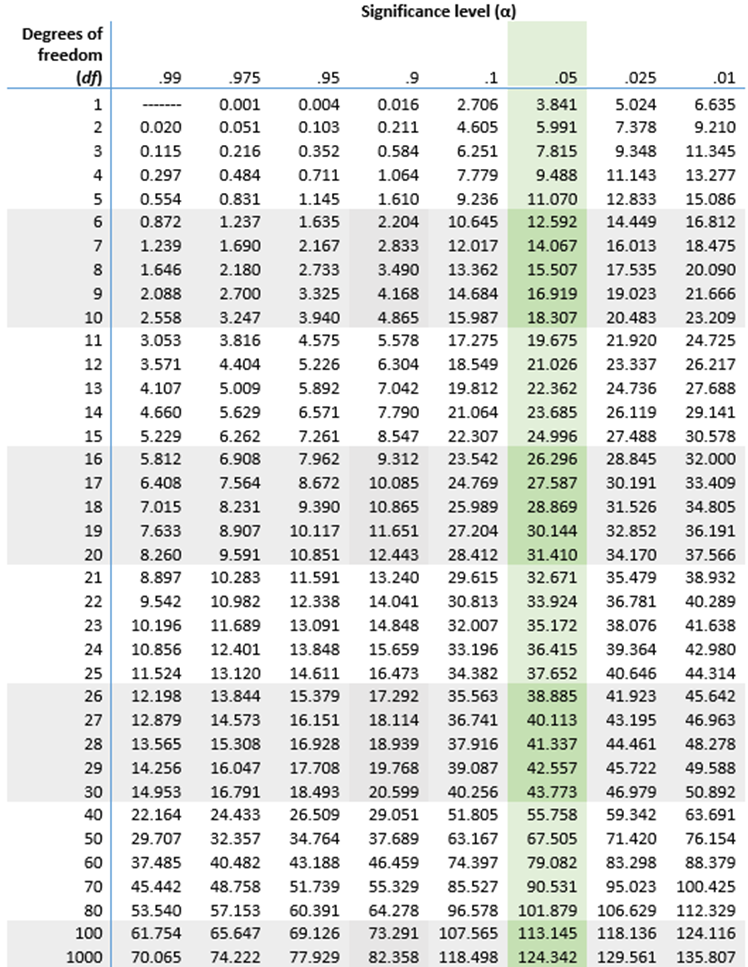
To find the chi-square critical value for your hypothesis test or confidence interval, follow the three steps below.
The team wants to use a chi-square goodness of fit test to test the null hypothesis ( H 0 ) that the four entrances are used equally often by the population.
Step 1: Calculate the degrees of freedom
There isn’t just one chi-square distribution —there are many, and their shapes differ depending on a parameter called “degrees of freedom” (also referred to as df or k ). Each row of the chi-square distribution table represents a chi-square distribution with a different df.
You need to use the distribution with the correct df for your test or confidence interval. The table below gives equations to calculate df for several common procedures:
| Test or procedure | Degrees of freedom ( ) equation |
|---|---|
| Test of a single variance Confidence interval for variance or standard deviation | = sample size − 1 |
| = number of groups − 1 | |
| = (number of variable 1 groups − 1) * (number of variable 2 groups − 1) | |
| = 1 |
df = number of groups − 1
Step 2: Choose a significance level
The columns of the chi-square distribution table indicate the significance level of the critical value. By convention, the significance level (α) is almost always .05, so the column for .05 is highlighted in the table.
In rare situations, you may want to increase α to decrease your Type II error rate or decrease α to decrease your Type I error rate.
To calculate a confidence interval, choose the significance level based on your desired confidence level :
α = 1 − confidence level
The most common confidence level is 95% (.95), which corresponds to α = .05.
Step 3: Find the critical value in the table
You now have the two numbers you need to find your critical value in the chi-square distribution table:
- The degrees of freedom ( df ) are listed along the left-hand side of the table. Find the table row corresponding to the degrees of freedom you calculated.
- The significance levels (α) are listed along the top of the table. Find the column corresponding to your chosen significance level.
- The table cell where the row and column meet is your critical value.
The security team can now compare this chi-square critical value to the Pearson’s chi-square they calculated for their sample. If the critical value is larger than the sample’s chi-square, they can reject the null hypothesis.
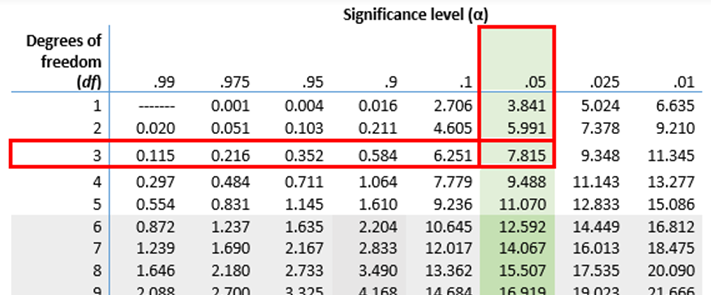
The table provided here gives the right-tail probabilities. You should use this table for most chi-square tests, including the chi-square goodness of fit test and the chi-square test of independence, and McNemar’s test.
If you want to perform a two-tailed or left-tailed test, you’ll need to make a small additional calculation.
Left-tailed tests
The most common left-tailed test is the test of a single variance when determining whether a population’s variance or standard deviation is less than a certain value.
To find the critical value for a left-tailed probability in the table above, simply use the table column for 1 − α.
You pride yourself on making every cookie the same size, so you decide to randomly sample 25 of your cookies to see if their standard deviation is less than 0.2 inches.
This is a left-tailed test because you want to know if the standard deviation is less than a certain value. You look up the left-tailed probability in the right-tailed table by subtracting one from your significance level : 1 − α = 1 − .05 = 0.95.
The critical value for df = 25 − 1 = 24 and α = .95 is 13.848.
Two-tailed tests
The most common left-tailed test is the test of a single variance when determining whether a population’s variance or standard deviation is equal to a certain value.
They find in a medical textbook that the standard deviation of head diameter of six-month-old babies is 1 inch, but they want to confirm this number themselves. They randomly sample 20 six-month-old babies and measure their heads.
This is a two-tailed test because they want to know if the standard deviation is equal to a certain value. They should look up the two critical values in the columns for:
The critical value for df = 20 − 1 = 19 and α = .025 is 32.852. The critical value for df = 19 and α = .975 is 8.907.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Student’s t table
- Student’s t distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
You can use the qchisq() function to find a chi-square critical value in R.
For example, to calculate the chi-square critical value for a test with df = 22 and α = .05:
qchisq(p = .05, df = 22, lower.tail = FALSE)
You can use the CHISQ.INV.RT() function to find a chi-square critical value in Excel.
For example, to calculate the chi-square critical value for a test with df = 22 and α = .05, click any blank cell and type:
=CHISQ.INV.RT(0.05,22)
A chi-square distribution is a continuous probability distribution . The shape of a chi-square distribution depends on its degrees of freedom , k . The mean of a chi-square distribution is equal to its degrees of freedom ( k ) and the variance is 2 k . The range is 0 to ∞.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 21). Chi-Square (Χ²) Table | Examples & Downloadable Table. Scribbr. Retrieved June 11, 2024, from https://www.scribbr.com/statistics/chi-square-distribution-table/
Is this article helpful?

Shaun Turney
Other students also liked, chi-square (χ²) tests | types, formula & examples, chi-square (χ²) distributions | definition & examples, hypothesis testing | a step-by-step guide with easy examples, what is your plagiarism score.

Statistics Made Easy
Chi-Square Test of Independence in R (With Examples)
A Chi-Square Test of Independence is used to determine whether or not there is a significant association between two categorical variables .
This tutorial explains how to perform a Chi-Square Test of Independence in R.
Example: Chi-Square Test of Independence in R
Suppose we want to know whether or not gender is associated with political party preference. We take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:
| 120 | 90 | 40 | 250 | |
| 110 | 95 | 45 | 250 | |
| 230 | 185 | 85 | 500 |
Use the following steps to perform a Chi-Square Test of Independence in R to determine if gender is associated with political party preference.
Step 1: Create the data.
First, we will create a table to hold our data:
Step 2: Perform the Chi-Square Test of Independence.
Next, we can perform the Chi-Square Test of Independence using the chisq.test() function:
The way to interpret the output is as follows:
- Chi-Square Test Statistic: 0.86404
- Degrees of freedom: 2 (calculated as #rows-1 * #columns-1)
- p-value: 0.6492
Recall that the Chi-Square Test of Independence uses the following null and alternative hypotheses:
- H 0 : (null hypothesis) The two variables are independent.
- H 1 : (alternative hypothesis) The two variables are not independent.
Since the p-value (0.6492) of the test is not less than 0.05, we fail to reject the null hypothesis. This means we do not have sufficient evidence to say that there is an association between gender and political party preference.
In other words, gender and political party preference are independent.
Additional Resources
An Introduction to the Chi-Square Test of Independence Chi-Square Test of Independence Calculator How to Calculate the P-Value of a Chi-Square Statistic in R How to Find the Chi-Square Critical Value in R
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
One Reply to “Chi-Square Test of Independence in R (With Examples)”
Leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
P-Value And Statistical Significance: What It Is & Why It Matters
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Learn about our Editorial Process
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.
Hypothesis testing
When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.
The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.
The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.
The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).
What a p-value tells you
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).
The level of statistical significance is often expressed as a p-value between 0 and 1.
The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.
Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.
Example: Test Statistic and p-Value
Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.
P-value interpretation
The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.
A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.
A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.
This suggests the effect under study likely represents a real relationship rather than just random chance.
For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.
It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).
Therefore, we reject the null hypothesis and accept the alternative hypothesis.
Example: Statistical Significance
Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.
What does a p-value of 0.001 mean?
A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.
Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.
Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.
A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.
This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.
Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.
One-Tailed Test

Two-Tailed Test
How do you calculate the p-value ?
Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.
Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.
These tables help you understand how often you would expect to see your test statistic under the null hypothesis.
Understanding the Statistical Test:
Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.
For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.
Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.
This factor is particularly important to consider when comparing results across different analyses.
Example: Choosing a Statistical Test
If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.
How to report
A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).
Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).
Example: Reporting the results
In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).
The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:
“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.
The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)
- Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
- Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
- p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
- The opposite of significant is “nonsignificant,” not “insignificant.”
Why is the p -value not enough?
A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.
However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).
To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .
When do you reject the null hypothesis?
In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.
Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.
The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.
What does p-value of 0.05 mean?
If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.
Are all p-values below 0.05 considered statistically significant?
No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.
A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.
Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.
How does sample size affect the interpretation of p-values?
Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.
With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.
Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.
Can a non-significant p-value indicate that there is no effect or difference in the data?
No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.
There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.
Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.
Can P values be exactly zero?
While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001
Further Information
- P-values and significance tests (Kahn Academy)
- Hypothesis testing and p-values (Kahn Academy)
- Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
- Criticism of using the “ p “< 0.05”.
- Publication manual of the American Psychological Association
- Statistics for Psychology Book Download
Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.
Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.
Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.
Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.
Related Articles

Exploratory Data Analysis

Research Methodology , Statistics
What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples
Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research
Should we believe innocent looks or statistics? Explaining P-Value
Published June 6, 2024
Should you believe innocent looks or statistics? I hope you side with statistics after reading this blog. Otherwise it would mean I have failed as an educator. Well, one day I came home and found my dogs near a bunch of chewed books. To be fair, I didn’t catch them red-handed, but it was “obvious” that they were the ones who chewed the books. Evidence is out there. Apart from innocent looks, they sounded smart and the picture below says it all, doesn’t it?

This situation reminded me of my statistics course where I taught concepts like hypothesis testing, statistical significance and p-value. In hypothesis testing, we reach a statistical significance when we get a small p-value relative to a pre-determined alpha value. The standard for confirming statistical significance is a p-value smaller than 0.05, although smaller or larger p-values are also used.
The small p-value means that the null hypothesis is unlikely given the observed data. To be clear, the p-value does not tell us about the probability that the hypothesis is true or false. Rather, it tells us how unusual the data is assuming the null hypothesis is true. Therefore, rejecting the null hypothesis doesn’t necessarily mean that the alternative hypothesis is correct. It only suggests that we have sufficient evidence to reject the null hypothesis.
Now, let’s break this down in the case of dogs chewing books. My mom loves the dogs, and she argues that dogs are innocent. We might view this as a null hypothesis. But what about catching them near a pile of the chewed books? Let’s accept this as an alternative hypothesis. Then, we will get the following scenario:
H0: My dogs don’t chew books. 🡺 Null hypothesis
H1: My dogs chew books. 🡺Alternative hypothesis
In our scenario, the p-value is the probability of finding dogs standing by the chewed books under the assumption that the dogs don’t chew books (null hypothesis). What is the chance of finding dogs near the chewed books if the assumption that my dogs don’t chew books is true? Very small, right? (Well unless my door was open, and the neighbor’s dogs had access to my house; this is Type I error. Or if we believe in conspiracy theories that the Martians secretly came and did that while I wasn’t at home).
Indeed, we should conclude that the p-value is very small here since it is less likely to find dogs standing by the chewed books if the dogs don’t really chew books. Think of finding dogs near chewed books as data. We test our alternative hypothesis against this data. We would more likely reject the null hypothesis and confirm the alternative hypothesis that the dogs actually chew the books.
Conceptually, the p-value is the probability or proportion of obtaining test results at least as extreme as the result actually observed, assuming that the null hypothesis is true. In this analogy, we made our decision qualitatively. Statistical tests provide a number, which is compared against a previously determined alpha value. For example, if we set the alpha value to 0.05 and then get a p-value smaller than the alpha value, then we reject the null hypothesis and conclude that the results are significant.
P-value approach stands at the core of statistical significance testing. It is widely used in academic research. Whether it is elementary statistics tests such as t-tests, chi-square tests, and ANOVA or advanced regression analysis and many others, almost all statistical tests provide us with p-value, which tells us how much our research findings are just by chance. If we find this randomness very low, we should then have confidence that the results are because of hypothesized independent variables. However, you might find p-value less useful in terms of predicting outcomes, a situation that some call “perils of policy by p-value”. It is for this reason that private sector relies less on p-value approach as investors care more about prediction. But this is the topic of another blog.
Namig Abassov, Digital Humanities Data Analyst
Questions about Data Science and Analytics? Reach out to us at [email protected]
Critical Value Calculator
Use this calculator for critical values to easily convert a significance level to its corresponding Z value, T score, F-score, or Chi-square value. Outputs the critical region as well. The tool supports one-tailed and two-tailed significance tests / probability values.
Related calculators
- Using the critical value calculator
- What is a critical value?
- T critical value calculation
- Z critical value calculation
- F critical value calculation
Using the critical value calculator
If you want to perform a statistical test of significance (a.k.a. significance test, statistical significance test), determining the value of the test statistic corresponding to the desired significance level is necessary. You need to know the desired error probability ( p-value threshold , common values are 0.05, 0.01, 0.001) corresponding to the significance level of the test. If you know the significance level in percentages, simply subtract it from 100%. For example, 95% significance results in a probability of 100%-95% = 5% = 0.05 .
Then you need to know the shape of the error distribution of the statistic of interest (not to be mistaken with the distribution of the underlying data!) . Our critical value calculator supports statistics which are either:
- Z -distributed (normally distributed, e.g. absolute difference of means)
- T -distributed (Student's T distribution, usually appropriate for small sample sizes, equivalent to the normal for sample sizes over 30)
- X 2 -distributed ( Chi square distribution, often used in goodness-of-fit tests, but also for tests of homogeneity or independence)
- F -distributed (Fisher-Snedecor distribution), usually used in analysis of variance (ANOVA)
Then, for distributions other than the normal one (Z), you need to know the degrees of freedom . For the F statistic there are two separate degrees of freedom - one for the numerator and one for the denominator.
Finally, to determine a critical region, one needs to know whether they are testing a point null versus a composite alternative (on both sides) or a composite null versus (covering one side of the distribution) a composite alternative (covering the other). Basically, it comes down to whether the inference is going to contain claims regarding the direction of the effect or not. Should one want to claim anything about the direction of the effect, the corresponding null hypothesis is direction as well (one-sided hypothesis).
Depending on the type of test - one-tailed or two-tailed, the calculator will output the critical value or values and the corresponding critical region. For one-sided tests it will output both possible regions, whereas for a two-sided test it will output the union of the two critical regions on the opposite sides of the distribution.
What is a critical value?
A critical value (or values) is a point on the support of an error distribution which bounds a critical region from above or below. If the statistics falls below or above a critical value (depending on the type of hypothesis, but it has to fall inside the critical region) then a test is declared statistically significant at the corresponding significance level. For example, in a two-tailed Z test with critical values -1.96 and 1.96 (corresponding to 0.05 significance level) the critical regions are from -∞ to -1.96 and from 1.96 to +∞. Therefore, if the statistic falls below -1.96 or above 1.96, the null hypothesis test is statistically significant.
You can think of the critical value as a cutoff point beyond which events are considered rare enough to count as evidence against the specified null hypothesis. It is a value achieved by a distance function with probability equal to or greater than the significance level under the specified null hypothesis. In an error-probabilistic framework, a proper distance function based on a test statistic takes the generic form [1] :
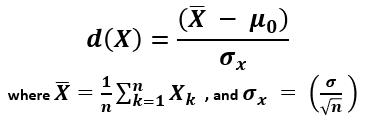
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).
Here is how it looks in practice when the error is normally distributed (Z distribution) with a one-tailed null and alternative hypotheses and a significance level α set to 0.05:

And here is the same significance level when applied to a point null and a two-tailed alternative hypothesis:
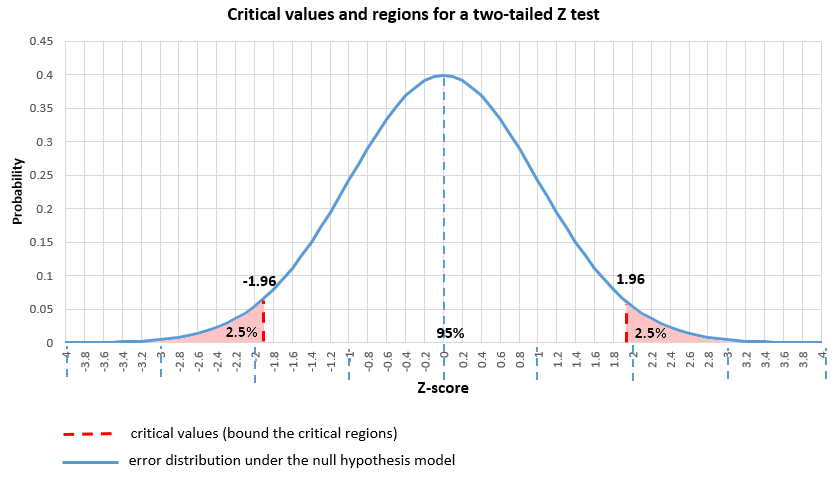
The distance function would vary depending on the distribution of the error: Z, T, F, or Chi-square (X 2 ). The calculation of a particular critical value based on a supplied probability and error distribution is simply a matter of calculating the inverse cumulative probability density function (inverse CPDF) of the respective distribution. This can be a difficult task, most notably for the T distribution [2] .
T critical value calculation
The T-distribution is often preferred in the social sciences, psychiatry, economics, and other sciences where low sample sizes are a common occurrence. Certain clinical studies also fall under this umbrella. This stems from the fact that for sample sizes over 30 it is practically equivalent to the normal distribution which is easier to work with. It was proposed by William Gosset, a.k.a. Student, in 1908 [3] , which is why it is also referred to as "Student's T distribution".
To find the critical t value, one needs to compute the inverse cumulative PDF of the T distribution. To do that, the significance level and the degrees of freedom need to be known. The degrees of freedom represent the number of values in the final calculation of a statistic that are free to vary whilst the statistic remains fixed at a certain value.
It should be noted that there is not, in fact, a single T-distribution, but there are infinitely many T-distributions, each with a different level of degrees of freedom. Below are some key values of the T-distribution with 1 degree of freedom, assuming a one-tailed T test is to be performed. These are often used as critical values to define rejection regions in hypothesis testing.
| Probability value | Degrees of Freedom | T critical value |
|---|---|---|
| 0.2000 | 1 | 1.3764 |
| 0.1000 | 1 | 3.0777 |
| 0.0500 | 1 | 6.3138 |
| 0.0250 | 1 | 12.7062 |
| 0.0200 | 1 | 15.8946 |
| 0.0100 | 1 | 31.8205 |
| 0.0010 | 1 | 318.3088 |
| 0.0005 | 1 | 636.6193 |
Z critical value calculation
The Z-score is a statistic showing how many standard deviations away from the normal, usually the mean, a given observation is. It is often called just a standard score, z-value, normal score, and standardized variable. A Z critical value is just a particular cutoff in the error distribution of a normally-distributed statistic.
Z critical values are computed by using the inverse cumulative probability density function of the standard normal distribution with a mean (μ) of zero and standard deviation (σ) of one. Below are some commonly encountered probability values (significance levels) and their corresponding Z values for the critical region, assuming a one-tailed hypothesis .
| Probability value | Z critical value |
|---|---|
| 0.2000 | 0.8416 |
| 0.1000 | 1.2816 |
| 0.0500 | 1.6449 |
| 0.0250 | 1.9600 |
| 0.0200 | 2.0537 |
| 0.0100 | 2.3263 |
| 0.0010 | 3.0902 |
| 0.0005 | 3.2905 |
The critical region defined by each of these would span from the Z value to plus infinity for the right-tailed case, and from minus infinity to minus the Z critical value in the left-tailed case. Our calculator for critical value will both find the critical z value(s) and output the corresponding critical regions for you.
Chi Square (Χ 2 ) critical value calculation
Chi square distributed errors are commonly encountered in goodness-of-fit tests and homogeneity tests, but also in tests for independence in contingency tables. Since the distribution is based on the squares of scores, it only contains positive values. Calculating the inverse cumulative PDF of the distribution is required in order to convert a desired probability (significance) to a chi square critical value.
Just like the T and F distributions, there is a different chi square distribution corresponding to different degrees of freedom. Hence, to calculate a Χ 2 critical value one needs to supply the degrees of freedom for the statistic of interest.
F critical value calculation
F distributed errors are commonly encountered in analysis of variance (ANOVA), which is very common in the social sciences. The distribution, also referred to as the Fisher-Snedecor distribution, only contains positive values, similar to the Χ 2 one. Similar to the T distribution, there is no single F-distribution to speak of. A different F distribution is defined for each pair of degrees of freedom - one for the numerator and one for the denominator.
Calculating the inverse cumulative PDF of the F distribution specified by the two degrees of freedom is required in order to convert a desired probability (significance) to a critical value. There is no simple solution to find a critical value of f and while there are tables, using a calculator is the preferred approach nowadays.
References
1 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.
2 Shaw T.W. (2006) – "Sampling Student's T distribution – use of the inverse cumulative distribution function", Journal of Computational Finance 9(4):37-73, DOI:10.21314/JCF.2006.150
3 "Student" [William Sealy Gosset] (1908) - "The probable error of a mean", Biometrika 6(1):1–25. DOI:10.1093/biomet/6.1.1
Cite this calculator & page
If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Critical Value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/critical-value-calculator.php URL [Accessed Date: 11 Jun, 2024].
Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

Statistical calculators

IMAGES
VIDEO
COMMENTS
We then determine the appropriate test statistic for the hypothesis test. The formula for the test statistic is given below. Test Statistic for Testing H0: p1 = p 10 , p2 = p 20 , ..., pk = p k0. We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1.
A chi-square test of independence is a nonparametric hypothesis test used to find out whether two categorical variables are related to each other. ... Null hypothesis (H 0): Whether a household recycles and the type of intervention they receive are not related in the population; ...
A Chi-Square test of independence uses the following null and alternative hypotheses: H0: (null hypothesis) The two variables are independent. H1: (alternative hypothesis) The two variables are not independent. (i.e. they are associated) We use the following formula to calculate the Chi-Square test statistic X2: X2 = Σ (O-E)2 / E.
Find the critical chi-square value in a chi-square critical value table or using statistical software. Compare the chi-square value to the critical value to determine which is larger. Decide whether to reject the null hypothesis.
The null hypothesis in chi-square testing is a powerful tool in statistical analysis. It provides a means to differentiate between observed variations due to random chance versus those that may signify a significant effect or relationship. As we continue to generate more data in various fields, the importance of understanding and correctly ...
Watch a video that explains how to use the chi-square statistic to test hypotheses about categorical data with an example.
The Chi-square test is a statistical method used to determine if there's a significant association between two categorical variables in a sample.
The null hypothesis will never be proven true; you just fail to reject it. ... The chi square test is one type of hypothesis test. But why did this specific type of test (chi square) have to be ...
She therefore erects the null hypothesis that there is no difference between the two distributions. This is what is tested by the chi squared (χ²) test (pronounced with a hard ch as in "sky"). By default, all χ² tests are two sided.
Chi-squared tests of independence assess relationships for categorical variables. Calculate expected values, chi-square, degrees of freedom, and p-values.
Paul Andersen shows you how to calculate the ch-squared value to test your null hypothesis. He explains the importance of the critical value and defines the...
The chi-square goodness of fit test is a hypothesis test. It allows you to draw conclusions about the distribution of a population based on a sample. Using the chi-square goodness of fit test, you can test whether the goodness of fit is "good enough" to conclude that the population follows the distribution. With the chi-square goodness of ...
A Chi-square test is a hypothesis testing method. Two common Chi-square tests involve checking if observed frequencies in one or more categories match expected frequencies.
The Chi-square test of independence determines whether there is a statistically significant relationship between categorical variables.It is a hypothesis test that answers the question—do the values of one categorical variable depend on the value of other categorical variables?
The final step of the chi-square test of significance is to determine if the value of the chi-square test statistic is large enough to reject the null hypothesis. Statistical software makes this determination much easier. For the purpose of this analysis, only the Pearson Chi-Square statistic is needed.
Unraveling the Null Hypothesis in Chi-Square Analysis. In the vast landscape of statistical analysis, where numbers dance and patterns emerge, the chi-square test stands as a stalwart, helping researchers discern the significance of observed data. At its heart lies a critical concept: the null hypothesis.
It will be done using the Chi-Square Test of Independence. As with all prior statistical tests we need to define null and alternative hypotheses. Also, as we have learned, the null hypothesis is what is assumed to be true until we have evidence to go against it. In this lesson, we are interested in researching if two categorical variables are ...
The Chi-Square test statistic is 1.118 and the corresponding two-sided p-value is .572. Recall the hypotheses used for a Chi-Square Test of Independence: H 0: The two variables are independent. H A: The two variables are not independent, i.e. they are associated. In this particular example, our null hypothesis is that gender and political party ...
If your chi-square calculated value is less than the chi-square critical value, then you "fail to reject" your null hypothesis. Figure 5. Finding the probability value for a chi-square of 1.2335 with 1 degree of freedom .
A Chi-Square goodness of fit test uses the following null and alternative hypotheses: H 0 : (null hypothesis) A variable follows a hypothesized distribution. H 1 : (alternative hypothesis) A variable does not follow a hypothesized distribution.
Chi-Square test is a statistical hypothesis for a given set of categorical data. Learn its p-value, distribution, formula, example for categorical variables, properties, degree of freedom table here at BYJU'S.
Hypotheses for Chi-Square. Research Hypothesis; Null Hypotheses; Degrees of Freedom and the \(\chi^{2}\) table. Exercise \(\PageIndex{1}\) The first of our two \(\chi^{2}\) tests, the Goodness of Fit test, assesses the distribution of frequencies into different categories of one quantitative variable against any specific distribution.Usually this is equal frequency distributions because that's ...
The null hypothesis would state that the feature does not change engagement, while the alternative hypothesis would assert that it does. ... Chi-squared: Best for categorical data analysis. Each test serves a specific purpose, tailored to the nature of your data and research objectives. By selecting the appropriate test, you enhance the ...
The chi-square (Χ2) distribution table is a reference table that lists chi-square critical values. A chi-square critical value is a threshold for statistical significance for certain hypothesis tests and defines confidence intervals for certain parameters. Chi-square critical values are calculated from chi-square distributions.
The final step is to interpret the results of your chi-square test. If you rejected the null hypothesis, you might conclude that there is a statistically significant association between the variables.
This tutorial explains how to perform a Chi-Square test of Independence in R, including an example.
The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01. ... For example, you might use a t-test to compare means, a chi-squared test for categorical data, ...
The standard for confirming statistical significance is a p-value smaller than 0.05, although smaller or larger p-values are also used. The small p-value means that the null hypothesis is unlikely given the observed data. To be clear, the p-value does not tell us about the probability that the hypothesis is true or false.
It is a special case of Gamma distribution, very known for its applications in hypothesis testing and confidence intervals. If we have a set of normally distributed and independent random variables, we compute the square value for each random variable and we sum every squared value, the final random value follows a chi-squared distribution ...
Z, T, Chi-Square, and F critical values and regions. Easy to use critical value calculator for converting a probability value (alpha threshold, a.k.a. significance level) to a Z value, T value, Chi-Square value, or F value using the inverse cumulative probability density function (inverse cumulative PDF) of the respective distribution. Calculate the score corresponding to a given significance ...