look for patterns in problem solving

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Problem Solving by Finding a Pattern

One important math concept that children begin to learn and apply in elementary school is reading and using a table. This is essential knowledge, because we encounter tables of data all the time in our everyday lives! But it’s not just important that kids can read and answer questions based on information in a table, it’s also important that they know how to create their own table and then use it to solve problems, find patterns, graph equations, and so on. And while some may think of these as two different things, I think problem solving by making a table and finding a pattern go hand in hand!

This is such a useful math problem solving strategy! Kids can get so overwhelmed by math word problems, but helping them organize the information in a table and then find a pattern can make things easier!

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :

Finding Patterns in Math Problems:

So when should kids use problem solving by finding a pattern ? Well, when the problem gives a set of data, or a pattern that is continuing and can be arranged in a table, it’s good to consider looking for the pattern and determining the “rule” of the pattern.

As I mentioned when I discussed problem solving by making a list , finding a pattern can be immensely helpful and save a lot of time when working on a word problem. Sometimes, however, a student may not recognize the pattern right away, or may get bogged down with all the details of the question.

Setting up a table and filling in the information given in the question is a great way to organize things and provide a visual so that the “rule” of the pattern can be determined. The “rule” can then be used to find the answer to the question. This removes the tedious work of completing a table, which is especially nice if a lot of computation is involved.

But a table is also great for kids who struggle with math, because it gives them a way to get to the solution even if they have a hard time finding the pattern, or aren’t confident that they are using the “rule” correctly.

Because even though using a known pattern can save you time, and eliminate the need to fill out the entire table, it’s not necessary. A student who is unsure could simply continue filling out their table until they reach the solution they’re looking for.

Helping students learn how to set up a table is also helpful because they can use it to organize information (much like making a list) even if there isn’t a pattern to be found, because it can be done in a systematic way, ensuring that nothing is left out.

If your students are just learning how to read and create tables, I would suggest having them circle their answer in the table to show that they understood the question and knew where in the table to find the answer.

If you have older students, encourage them to find a pattern in the table and explain it in words , and then also with mathematical symbols and/or an equation. This will help them form connections and increase number sense. It will also help them see how to use their “rule” or equation to solve the given question as well as make predictions about the data.

It’s also important for students to consider whether or not their pattern will continue predictably . In some instances, the pattern may look one way for the first few entries, then change, so this is important to consider as the problems get more challenging.

There are tons of examples of problems where creating a table and finding a pattern is a useful strategy, but here’s just one example for you:

Ben decides to prepare for a marathon by running ten minutes a day, six days a week. Each week, he increases his time running by two minutes per day. How many minutes will he run in week 8?

Included in the table is the week number (we’re looking at weeks 1-8), as well as the number of minutes per day and the total minutes for the week. The first step is to fill in the first couple of weeks by calculating the total time.

Making a table and finding a pattern is an excellent math problem solving strategy! This is a great example!

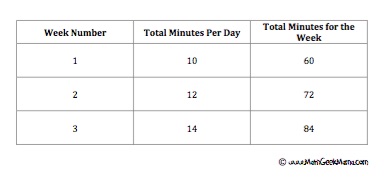
Once you’ve found weeks 1-3, you may see a pattern and be able to calculate the total minutes for week 8. For example, in this case, the total number of minutes increases by 12 each week, meaning in week 8 he will run for 144 minutes.

If not, however, simply continue with the table until you get to week 8, and then you will have your answer.

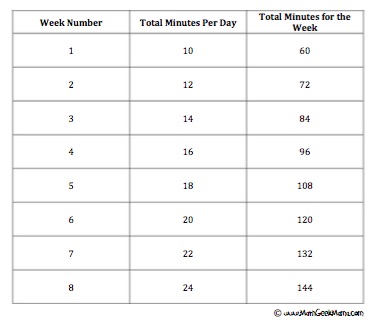
I think it is especially important to make it clear to students that it is perfectly acceptable to complete the entire table (or continue a given table) if they don’t see or don’t know how to use the pattern to solve the problem.

I was working with a student once and she was given a table, but was then asked a question about information not included in that table . She was able to tell me the pattern she saw, but wasn’t able to correctly use the “rule” to find the answer. I insisted that she simply extend the table until she found what she needed. Then I showed her how to use the “rule” of the pattern to get the same answer.

I hope you find this helpful! Looking for and finding patterns is such an essential part of mathematics education! If you’re looking for more ideas for exploring patterns with younger kids, check out this post for making patterns with Skittles candy .

And of course, don’t miss the other posts in this Math Problem Solving Series:

Problem Solving by Solving an Easier Problem
Problem Solving by Drawing a Picture
Problem Solving by Working Backwards
Problem Solving by Making a List

One Comment

I had so much trouble spotting patterns when I was in school. Fortunately for her, my daughter rocks at it! This technique will be helpful for her when she’s a bit older! #ThoughtfulSpot

Comments are closed.

August Math Problem of the Day Calendar

${FREE} Mental Math Challenge for Kids: Exercise Your Brain!$

{FREE} Mental Math Challenge for Kids: Exercise Your Brain!

Subtracting Mixed Numbers Printable Board Game {FREE}

DIY Mancala Game Board! {Learning Math Through Play!}

February Math Problem of the Day {FREE Printable!}

Math Myths Debunked: Math is Just a Set of Rules to Memorize

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Pattern Problem Solving: Teach Students to Find a Pattern in Math Problems

Pattern analysis is a critical 21st century skill.

Need more tips and tricks for teaching math? You can find them in our math resources center .

Pattern problem solving

In this article, we’ll delve into the concept of pattern problem solving, a fundamental mathematical strategy that involves the identification of repeated sequences or elements to solve complex problems.

This method is instrumental in enhancing logical thinking and mathematical comprehension among students. Let's explore how this works, why it's important, and how to teach this critical skill effectively.

Math teacher teaches problem solving. pattern problem solving.

What is pattern problem solving?

Pattern problem solving is a mathematical strategy in which students look for patterns in data to solve a problem. To find a pattern, students search for repeated items, numbers, or series of events.

The following problem can be solved by finding the pattern:

There are 1000 lockers in a high school with 1000 students. The first student opens all 1000 lockers; next, the second student closes lockers 2, 4, 6, 8, 10, and so on up to locker 1000; the third student changes the state (opens lockers that are closed, closes lockers that are open) of lockers 3, 6, 9, 12, 15, and so on; the fourth student changes the state of lockers 4, 8, 12, 16, and so on. This continues until every student has had a turn. How many lockers will be open at the end?

For the answer, visit The Locker Problem from the Math Doctors

Why is pattern problem solving important?

Pattern problem solving is an important strategy for students as it encourages them to observe and understand patterns in data, which is a critical aspect of mathematical and logical thinking.

This strategy allows students to predict future data points or behaviors based on existing patterns. It helps students understand the inherent structure of data sets and mathematical problems, making them easier to solve.

Pattern recognition also aids in the understanding of multiplication facts, for example, recognizing that 4 x 7 is the same as 7 x 4. Overall, pattern problem solving fosters analytical thinking, problem-solving skills, and a deeper understanding of mathematics.

Boy solves math problem in class. pattern problem solving.

How to teach students to find the pattern in a math problem (using an example)

In the upcoming section, we will break down the steps on how to find a pattern in a math problem effectively. We will use a practical example to illustrate each step and provide helpful teaching tips throughout the process.

The goal is to offer a clear and comprehensible guide for educators teaching students about pattern problem solving in math.

Sample question: If you build a four-sided pyramid using basketballs and don't count the bottom as a side, how many balls will there be in a pyramid that has six layers?

Helpful teaching tip: Use cooperative learning groups to find solutions to the above problem. Cooperative learning groups help students verbalize their thinking, brainstorm ideas, discuss options, and justify their positions. After finding a solution, each group can present it to the class, explaining how they reached their solution and why they think it is correct. Or, students can explain their solutions in writing, and the teacher can display the solutions. Then students can circulate around the room to read each group's solution.

1. Ensure students understand the problem

Demonstrate that the first step to solving a problem is understanding it. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words.

Sometimes you can solve a problem simply through pattern recognition, but more often you must extend the pattern to find the solution. Making a number table will help you see the pattern more clearly.

In this problem, students understand:

The top layer will have one basketball. I need to find how many balls there will be in each layer of a pyramid, from the first to the sixth. I need to find how many basketballs will be in the entire pyramid.

2. Choose a pattern problem solving strategy

To successfully find a pattern, you need to be sure that the pattern will continue.

Have students give reasons why they think the pattern is predictable and not based on probability. Problems that are solved most easily by finding a pattern include those that ask students to extend a sequence of numbers or to make a prediction based on data.

In this problem, students may also choose to make a table or draw a picture to organize and represent their thinking.

3. Solve the problem

Start with the top layer of the pyramid, one basketball. Determine how many balls must be under that ball to make the next layer or a pyramid. Let students use manipulatives if needed— they can use manipulatives of any kind, from coins to cubes to golf balls. Let students also draw pictures to help solve the problem, if needed.

If your students are in groups, you may want to have each group use a different manipulative and then compare their solutions. This will help you understand if different manipulatives affect the solution.

Helpful teaching tip: If students are younger, solve this problem with only three layers.

If it helps to visualize the pyramid, use manipulatives to create the third layer. Record the number and look for a pattern. The second layer adds 3 basketballs and the next adds 5 basketballs. Each time you add a new layer, the number of basketballs needed to create that layer increases by 2.

1 1 + 3 = 4 4 + 5 = 9

Continue until six layers are recorded. Once a pattern is found, students might not need to use manipulatives. 9 + 7 = 16

16 + 9 = 25 25 + 11 = 36

Then add the basketballs used to make all six layers.

The answer is 91 balls .

Look at the list to see if there is another pattern. The number of balls used in each level is the square of the layer number. So the 10th layer would have 10 x 10 = 100 balls .

4. Check your students' answers

Read the problem again to be sure the question was answered:

Yes, I found the total number of basketballs in the six-layer pyramid.

Also check the math to be sure it’s correct:

1 + 4 + 9 + 16 + 25 +36 = 91

Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem:

Finding a pattern was a good way to solve this problem because the pattern was predictable.

5. Explain

Students should be able to explain the process they went through to find their answers. Students must be able to talk or write about their thinking. Demonstrate how to write a paragraph describing the steps they took and the decisions they made throughout.

I started with the first layer. I used blocks to make the pyramid and made a list of the number of blocks I used. Then I created a table to record the number of balls in each layer. I made four layers, then saw a pattern. I saw that or each layer, the number of balls used was the number of the layer multiplied by itself. I finished the pattern without the blocks, by multiplying the number of balls that would be in layers 5 and 6. Then I added up each layer. 1 + 4 + 9 + 16 + 25 +36 = 91. I got a total of 91 basketballs

How can you stretch this pattern problem solving strategy?

Find the pattern math problem solving. pattern problem solving.

Math problems can be simple, with few criteria needed to solve them, or they can be multidimensional, requiring charts or tables to organize students' thinking and to record patterns.

In using patterns, it is important for students to find out if the pattern will continue predictably. Have students determine if there is a reason for the pattern to continue, and be sure students use logic when finding patterns to solve problems.

For example, if it rains on Sunday, snows on Monday, rains on Tuesday, and snows on Wednesday, will it rain on Thursday?
Another example: If Lauren won the first and third game of chess, and Walter won the second and fourth game, who will win the fifth game?
Another example: If a plant grew 13 centimeters in the first week and 10 centimeters in the second week, how many centimeters will it grow in the third week?

Because these are questions of probability or nature, be sure students understand why patterns can't be used to find these answers.

Featured Middle School Resources

History of Earth Day Reading Passage and Quiz

Related Resources

Problem Solving: Make a Table Math Strategy

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.3: Problem Solving Strategies

Last updated
Save as PDF
Page ID 82975

Michelle Manes
University of Hawaii

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.

Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.

How to Solve It

George Pólya was a great champion in the field of teaching effective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985. [1]

$George_Pólya_ca_1973.jpg$

George Pólya, circa 1973

Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 ( http://creativecommons.org/licenses/by/2.0 )], via Wikimedia Commons ↵

In 1945, Pólya published the short book How to Solve It , which gave a four-step method for solving mathematical problems:

First, you have to understand the problem.
After understanding, then make a plan.
Carry out the plan.
Look back on your work. How could it be better?

This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.

Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!

We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:

What if the picture was different?
What if the numbers were simpler?
What if I just made up some numbers?

You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.

This brings us to the most important problem solving strategy of all:

Problem Solving Strategy 2 (Try Something!).

If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.

And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.

Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?

Think/Pair/Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.

Problem Solving Strategy 3 (Draw a Picture).

Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?

Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?

After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.

Problem Solving Strategy 4 (Make Up Numbers).

Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!

You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.

Watch the solution only after you tried this strategy for yourself.

If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!

(Squares on a Chess Board)

How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)

Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!

Think / Pair / Share

It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”

Problem Solving Strategy 5 (Try a Simpler Problem).

Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?

Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).

Problem Solving Strategy 6 (Work Systematically).

If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.

For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:

Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate).

Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!

For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.

Problem Solving Strategy 8 (Look for and Explain Patterns).

Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.

If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:

Describe all of the patterns you see in the table.
Can you explain and justify any of the patterns you see? How can you be sure they will continue?
What calculation would you do to find the total number of squares on a 100 × 100 chess board?

(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)

(Broken Clock)

This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. ( Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)

$index-12_1-300x282-1.png$

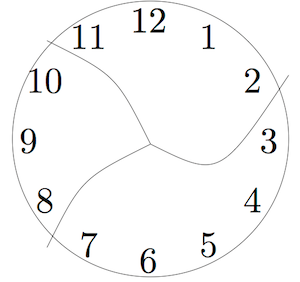
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)

Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?

Problem Solving Strategy 9 (Find the Math, Remove the Context).

Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.

In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:

What is the sum of all the numbers on the clock’s face?
Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
How do I know when I am done? When should I stop looking?

Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.

Problem Solving Strategy 10 (Check Your Assumptions).

When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?

In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:

$index-13_1-300x296.png$

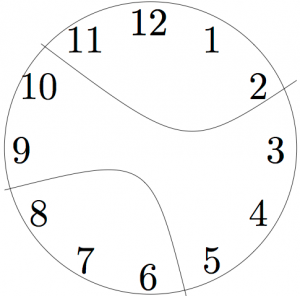
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.

PRINT TO PLAY
DIGITAL GAMES

Problem-Solving Strategies

October 16, 2019

There are many different ways to solve a math problem, and equipping students with problem-solving strategies is just as important as teaching computation and algorithms. Problem-solving strategies help students visualize the problem or present the given information in a way that can lead them to the solution. Solving word problems using strategies works great as a number talks activity and helps to revise many skills.

Problem-solving strategies

1. create a diagram/picture, 2. guess and check., 3. make a table or a list., 4. logical reasoning., 5. find a pattern, 6. work backward, 1. create a diagram/draw a picture.

Creating a diagram helps students visualize the problem and reach the solution. A diagram can be a picture with labels, or a representation of the problem with objects that can be manipulated. Role-playing and acting out the problem like a story can help get to the solution.

Alice spent 3/4 of her babysitting money on comic books. She is left with $6. How much money did she make from babysitting?

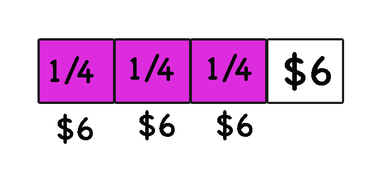
2. Guess and check

Teach students the same strategy research mathematicians use.

With this strategy, students solve problems by making a reasonable guess depending on the information given. Then they check to see if the answer is correct and they improve it accordingly. By repeating this process, a student can arrive at a correct answer that has been checked. It is recommended that the students keep a record of their guesses by making a chart, a table or a list. This is a flexible strategy that works for many types of problems. When students are stuck, guessing and checking helps them start and explore the problem. However, there is a trap. Exactly because it is such a simple strategy to use, some students find it difficult to consider other strategies. As problems get more complicated, other strategies become more important and more effective.

Find two numbers that have sum 11 and product 24.

Try/guess 5 and 6 the product is 30 too high

adjust to 4 and 7 with product 28 still high

adjust again 3 and 8 product 24

3. Make a table or a list

Carefully organize the information on a table or list according to the problem information. It might be a table of numbers, a table with ticks and crosses to solve a logic problem or a list of possible answers. Seeing the given information sorted out on a table or a list will help find patterns and lead to the correct solution.

To make sure you are listing all the information correctly read the problem carefully.

Find the common factors of 24, 30 and 18

Logical reasoning is the process of using logical, systemic steps to arrive at a conclusion based on given facts and mathematic principles. Read and understand the problem. Then find the information that helps you start solving the problem. Continue with each piece of information and write possible answers.

Thomas, Helen, Bill, and Mary have cats that are black, brown, white, or gray. The cats’ names are Buddy, Lucky, Fifi, and Moo. Buddy is brown. Thoma’s cat, Lucky, is not gray. Helen’s cat is white but is not named Moo. The gray cat belongs to Bill. Which cat belongs to each student, and what is its color?

A table or list is useful in solving logic problems.

Since Lucky is not gray it can be black or brown. However, Buddy is brown so Lucky has to be black.

Buddy is brown so it cannot be Helen’s cat. Helen’s cat cannot be Moo, Buddy or Lucky, so it is Fifi.

Therefore, Moo is Bill’s cat and Buddy is Mary’s cat.

5. Find a pattern.

Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the “find a pattern” problem-solving strategy. Data can be organized in a table or a list to reveal the pattern and help discover the “rule” of the pattern.

The “rule” can then be used to find the answer to the question and complete the table/list.

Shannon’s Pizzeria made 5 pizzas on Sunday, 10 pizzas on Monday, 20 pizzas on Tuesday, and 40 pizzas on Wednesday. If this pattern continues, how many pizzas will the pizzeria make on Saturday?

6. Working backward

Problems that can be solved with this strategy are the ones that list a series of events or a sequence of steps .

In this strategy, the students must start with the solution and work back to the beginning. Each operation must be reversed to get back to the beginning. So if working forwards requires addition, when students work backward they will need to subtract. And if they multiply working forwards, they must divide when working backward.

Mom bought a box of candy. Mary took 5 of them, Nick took 4 of them and 31 were given out on Halloween night. The next morning they found 8 pieces of candy in the box. How many candy pieces were in the box when mom bought it.

For this problem, we know that the final number of candy was 8, so if we work backward to “put back” the candy that was taken from the box we can reach the number of candy pieces that were in the box, to begin with.

The candy was taken away so we will normally subtract them. However, to get back to the original number of candy we need to work backward and do the opposite, which is to add them.

8 candy pieces were left + the 31 given out + plus the ones Mary took + the ones Nick took

8+31+5+4= 48 Answer: The box came with 48 pieces of candy.

Selecting the best strategy for a problem comes with practice and often problems will require the use of more than one strategies.

Print and digital activities

I have created a collection of print and digital activity cards and worksheets with word problems (print and google slides) to solve using the strategies above. The collection includes 70 problems (5 challenge ones) and their solution s and explanations.

sample below

How to use the activity cards

Allow the students to use manipulatives to solve the problems. (counters, shapes, lego blocks, Cuisenaire blocks, base 10 blocks, clocks) They can use manipulatives to create a picture and visualize the problem. They can use counters for the guess and check strategy. Discuss which strategy/strategies are better for solving each problem. Discuss the different ways. Use the activities as warm-ups, number talks, initiate discussions, group work, challenge, escape rooms, and more.

Ask your students to write their own problems using the problems in this resource, and more, as examples. Start with a simple type. Students learn a lot when trying to compose a problem. They can share the problem with their partner or the whole class. Make a collection of problems to share with another class.

For the google slides the students can use text boxes to explain their thinking with words, add shapes and lines to create diagrams, and add (insert) tables and diagrams.

Many of the problems can be solved faster by using algebraic expressions. However, since I created this resource for grades 4 and up I chose to show simple conceptual ways of solving the problems using the strategies above. You can suggest different ways of solving the problems based on the grade level.

Find the free and premium versions of the resource below. The premium version includes 70 problems (challenge problems included) and their solutions

There are 2 versions of the resource

70 google slides with explanations + 70 printable task cards

70 google slides with explanations + 11 worksheets

Multiplying fractions/mixed numbers/simplifying

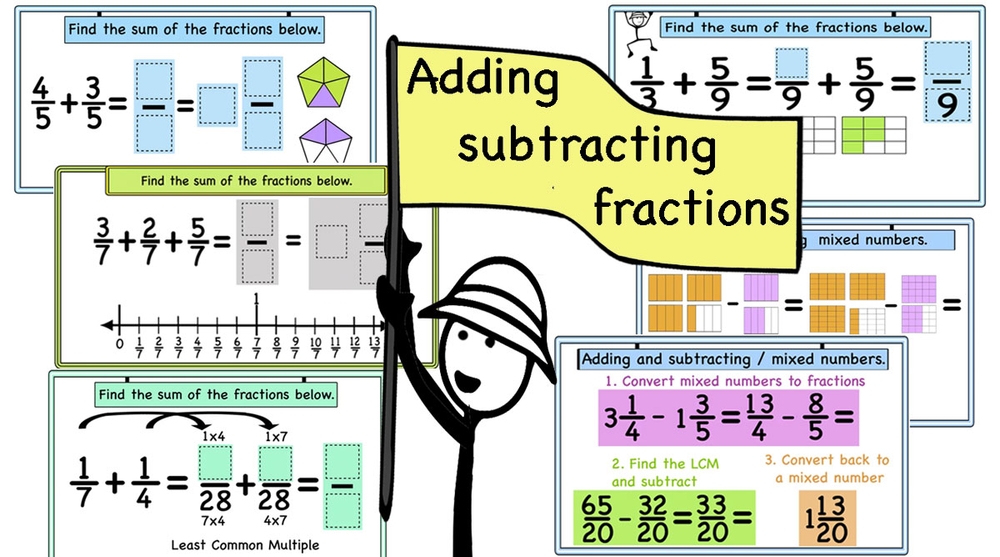
Adding and subtracting fractions

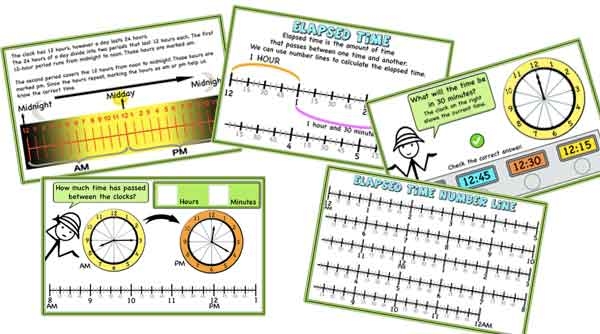
AM/PM, 24-hour clock, Elapsed Time – ideas, games, and activities

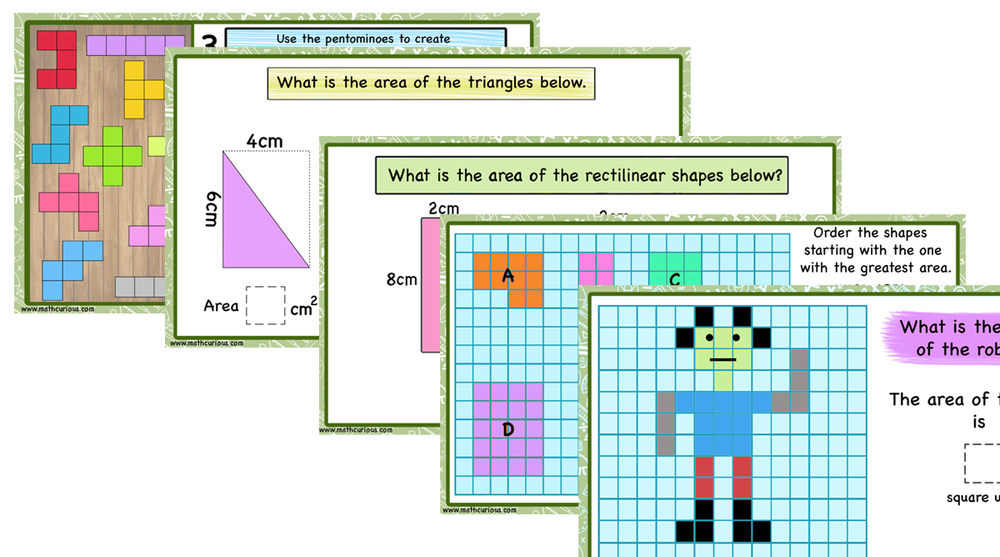
Teaching area, ideas, games, print, and digital activities

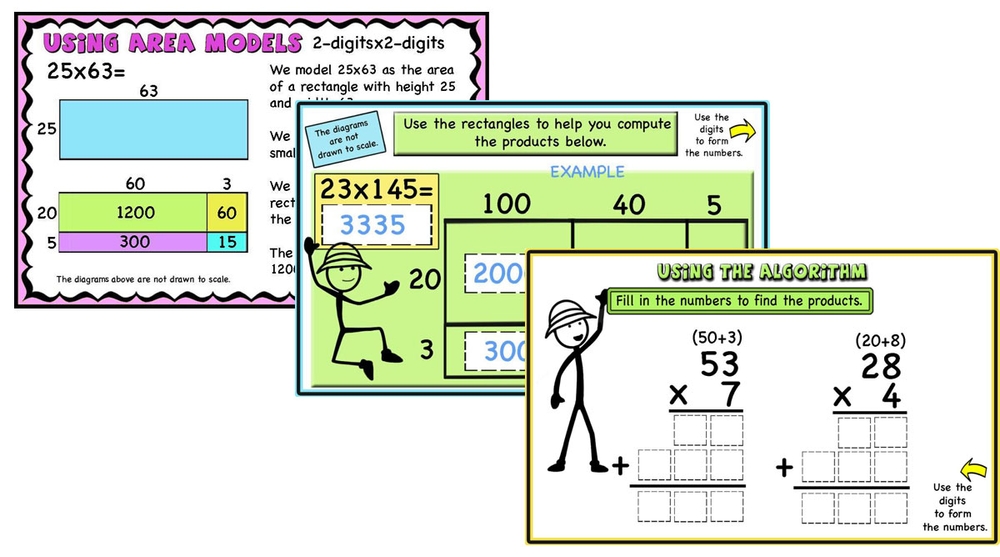
Multi-Digit Multiplication, Area model, Partial Products algorithm, Puzzles, Word problems

Place Value – Representing and adding 2/3 digit numbers with manipulatives

Multiplication Mission – arrays, properties, multiples, factors, division

Fractions Games and activities – Equivalence, make 1, compare, add, subtract, like, unlike

Diving into Division -Teaching division conceptually

Expressions with arrays

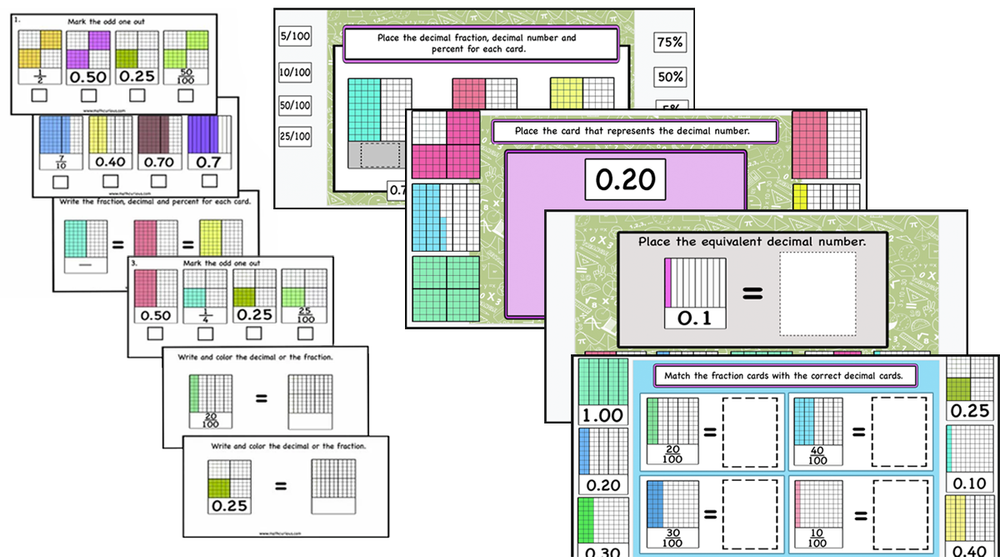
Decimals, Decimal fractions, Percentages – print and digital

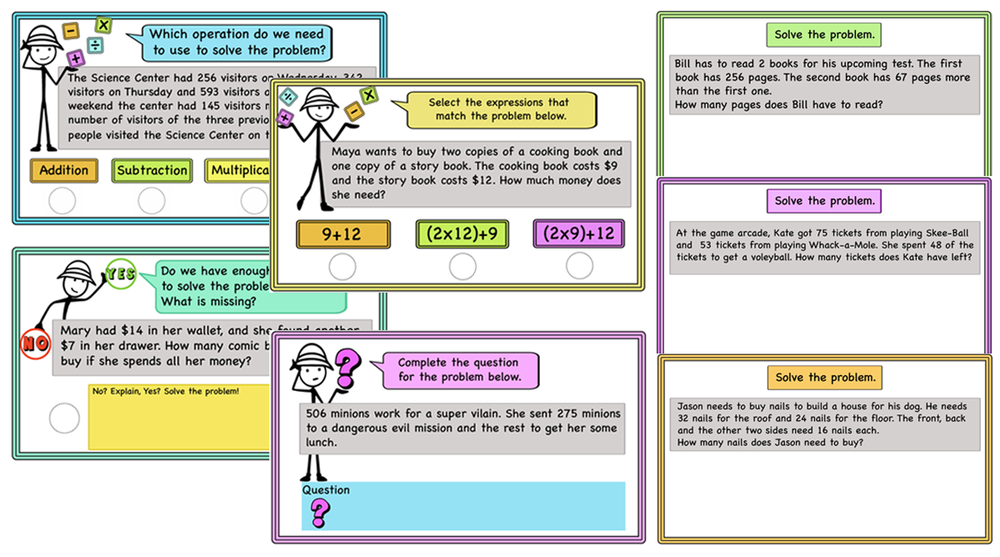
Solving Word Problems- Math talks-Strategies, Ideas and Activities-print and digital

Check out our best selling card games now available at amazon.com and amazon.ca.

Chicken Escape

A multiplayer card game that makes mental math practice fun! Chicken Escape is a fast-paced multiplayer card game. While playing…

Dragon Times – A math Adventure card game

Dragon Times is an educational fantasy card game that aims to motivate children to practice multiplication and division facts while…

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 3rd grade > Unit 8

Finding patterns in numbers.

Recognizing number patterns
Math patterns
Intro to even and odd numbers
Patterns with multiplying even and odd numbers
Patterns with even and odd
Patterns in hundreds chart
Patterns in multiplication tables
Arithmetic patterns and problem solving: FAQ

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Pre-Algebra

Math Review of Equivalent Sentences

More problem-solving strategies: identify subgoals.

Math Problem Solving Strategies

In these lessons, we will learn some math problem solving strategies for example, Verbal Model (or Logical Reasoning), Algebraic Model, Block Model (or Singapore Math), Guess & Check Model and Find a Pattern Model.

Related Pages Solving Word Problems Using Block Models Heuristic Approach to Problem-Solving Algebra Lessons

Problem Solving Strategies

The strategies used in solving word problems:

What do you know?
What do you need to know?
Draw a diagram/picture

Solution Strategies Label Variables Verbal Model or Logical Reasoning Algebraic Model - Translate Verbal Model to Algebraic Model Solve and Check.

Solving Word Problems

Step 1: Identify (What is being asked?) Step 2: Strategize Step 3: Write the equation(s) Step 4: Answer the question Step 5: Check

Problem Solving Strategy: Guess And Check

Using the guess and check problem solving strategy to help solve math word problems.

Example: Jamie spent $40 for an outfit. She paid for the items using $10, $5 and $1 bills. If she gave the clerk 10 bills in all, how many of each bill did she use?

Problem Solving : Make A Table And Look For A Pattern

Identify - What is the question?
Plan - What strategy will I use to solve the problem?
Solve - Carry out your plan.
Verify - Does my answer make sense?

Example: Marcus ran a lemonade stand for 5 days. On the first day, he made $5. Every day after that he made $2 more than the previous day. How much money did Marcus made in all after 5 days?

Find A Pattern Model (Intermediate)

In this lesson, we will look at some intermediate examples of Find a Pattern method of problem-solving strategy.

Example: The figure shows a series of rectangles where each rectangle is bounded by 10 dots. a) How many dots are required for 7 rectangles? b) If the figure has 73 dots, how many rectangles would there be?

a) The number of dots required for 7 rectangles is 52.

b) If the figure has 73 dots, there would be 10 rectangles.

Example: Each triangle in the figure below has 3 dots. Study the pattern and find the number of dots for 7 layers of triangles.

The number of dots for 7 layers of triangles is 36.

Example: The table below shows numbers placed into groups I, II, III, IV, V and VI. In which groups would the following numbers belong? a) 25 b) 46 c) 269

Solution: The pattern is: The remainder when the number is divided by 6 determines the group. a) 25 ÷ 6 = 4 remainder 1 (Group I) b) 46 ÷ 6 = 7 remainder 4 (Group IV) c) 269 ÷ 6 = 44 remainder 5 (Group V)

Example: The following figures were formed using matchsticks.

a) Based on the above series of figures, complete the table below.

b) How many triangles are there if the figure in the series has 9 squares?

c) How many matchsticks would be used in the figure in the series with 11 squares?

b) The pattern is +2 for each additional square. 18 + 2 = 20 If the figure in the series has 9 squares, there would be 20 triangles.

c) The pattern is + 7 for each additional square 61 + (3 x 7) = 82 If the figure in the series has 11 squares, there would be 82 matchsticks.

Example: Seven ex-schoolmates had a gathering. Each one of them shook hands with all others once. How many handshakes were there?

Total = 6 + 5 + 4 + 3 + 2 + 1 = 21 handshakes.

The following video shows more examples of using problem solving strategies and models. Question 1: Approximate your average speed given some information Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home that is 16 feet wide. The width of your pictures are 2, 3 and 4 feet. You want space between your pictures to be the same and the space to the left and right to be 6 inches more than between the pictures. How would you place the pictures?

The following are some other examples of problem solving strategies.

Explore it/Act it/Try it (EAT) Method (Basic) Explore it/Act it/Try it (EAT) Method (Intermediate) Explore it/Act it/Try it (EAT) Method (Advanced)

Finding A Pattern (Basic) Finding A Pattern (Intermediate) Finding A Pattern (Advanced)

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Upgrade Your Browser

Your browser is more than six years old. Please take a few minutes to upgrade to a newer browser so you can experience this website and the rest of the Internet more fully.

Problems into Patterns

To thrive in complexity you have to adapt—quickly and often! You can’t afford to wait for deep analysis or complete data. You don’t have time to take things apart, fix each piece, and put them back together. Even if you could, complex systems are massively entangled and emergent, so fixing parts may not fix the whole.

Newton described a powerful problem-solving method. 1) Define the problem. 2) Name all the parts. 3) Understand the parts. 4) Find the right answer and take the right action. That is great when things are simple. The problem is that most of your real problems are not simple. They have open boundaries, multiple causes, and messy interdependencies. So, even if you had time for Newton’s method—which you don’t—the system and the problem will transform itself before you finish step 1.

When you see your challenge as a “problem,” you automatically look for parts to fix, root causes, and definitive answers. When conditions are right, that works—great! When it doesn’t work, you need a backup strategy.

In these turbulent times, you need another problem-solving approach. One that is fast and flexible, and at the same time allows for uncertainty, massive interdependency, and multiple measures of success. You need to see your challenge as a “pattern.” When you do, you are free to move into Adaptive Action and Inquiry. You need Pattern Logic.

Pattern Logic allows you to see into complex situations without taking them apart. It helps you understand history and possible futures. It welcomes diverse perspectives and parallel explanations. It directly informs action, because you can use what you see to do what you can to get what you never got before.

In HSD we have lots of Pattern Logic models and methods to help you see, understand, and influence patterns in complexity. The CDE Model is the most general. Same and Different is the most simple. The Landscape Diagram is useful for managing systemic change. The Difference Matrix and Generative Engagement balance the energy in relationships. Four Truths and Conflict Circles open dialogue in the middle of conflict. You can find many more useful tools on our website . All of them leverage the power of Pattern Logic to inform perception, sense making, and action when traditional problem solving fails you.

This may sound radical, but it is amazingly simple. These examples may help you see the power and possibilities of Pattern Logic.

If you see employee engagement as a problem, you run surveys, identify gaps, and plan for action. If you see it through Pattern Logic you ask:

WHAT places is engagement the greatest? What are they saying in that place about why they’re engaged? What do others say about engagement?
SO WHAT lessons can we learn from the patterns of why people are engaged, what they say about their engagement, and what unengaged people are saying?
NOW WHAT is a single, immediate, wise action that will encourage these same patterns in other parts of the organization?

If you see vaccine distribution as a problem, you try to fix weak links in the supply chain and convert resistant populations. If you see it through the lens of Pattern Logic you ask:

WHAT infrastructure already exists in our system that can be repurposed?
SO WHAT will allow us to build additional capacity for future epi- or pandemics at the same time as we respond today?
NOW WHAT will inspire and enable people and processes to use their local knowledge to make decisions that benefit the larger system?

If you see failing customer service as a problem, you retrain the bad and reward the good service providers. If you see it in Pattern Logic, you ask:

WHAT do customers really need and appreciate?
SO WHAT patterns do we see in what they say? So what are constant features of those patterns and what reasonable variations would build on them?
NOW WHAT continuous feedback methods will help service providers stay within acceptable boundaries?

If you see culture change as a problem, you convince leaders and managers to change their behavior. If you see culture as a pattern, you ask:

WHAT behaviors am I seeing in general? What are contradictions? What has surprised me? What do I wonder? What patterns do we want to see?
SO WHAT tensions or competing perspectives exist currently. What other tensions can help us see the underlying differences between what we have and what we want?
NOW WHAT is a change in policy, procedure, practice, or people that will leverage those tensions and provide impetus to shift the system into a new cultural pattern?

If you see racism as a problem, you point out privilege and police what people say. If you see it as a pattern, you ask:

WHAT do people in marginalized groups need to feel safe and productive in our community?
SO WHAT are we doing today—individually and collectively, through policy and procedure—that constrains their safety and productivity?
NOW WHAT can I/we do to change expectations and behaviors to create safety and increase patterns of safety and productivity around here?

Adaptive Action, Inquiry, and Pattern Logic may be simple, but they are not easy. They require intention, attention, and practice. Here are some guides you may find useful as you develop Pattern Logic muscles for yourself and your team.

Sometimes you need to depend on Newton to solve simple problems. Even within the most complex patterns, you will find solvable problems. When you do, use more traditional approaches to solve them as quickly and efficiently as you can.
The more complex the pattern, the more information you need about what people are saying and doing to see it well, understand it in useful ways, and to influence it effectively.
Various constraints in the system—time, access, funding, agreement—will affect how explicit you can be about using Pattern Logic. Always consider what is fit for function, given current circumstances and opportunities.
No one can do someone else’s Adaptive Action. When you speculate about how someone else might shift a problematic pattern, you are wasting your time and energy. Focus on the patterns you and your colleagues can influence.
The pattern-shifting process of Adaptive Action never ends. Each action transforms the current pattern to create the next one. In that moment, current becomes past, future becomes current, and you begin the next cycle of seeing, understanding, and influencing patterns in complex systems.
There is no “perfect” analysis of a pattern in a complex system. Some will be more true and useful than others, but you will never know ahead of time what will be the best. Make your best guess based on what you know, watch what happens, and whatever happens, begin your next pattern-shifting cycle of Adaptive Action.

We believe effective leaders and problem solvers use Pattern Logic intuitively. Over time, trial and error has taught them the power of patterns, and they use Adaptive Action and Inquiry implicitly. But even they benefit from an explicit process and practical discipline of human systems dynamics. For the rest of us, Pattern Logic can unleash a new way to engage with the world. We build comfort and capacity for complexity when we change problems to be solved into patterns to be shifted. Join us as we continue to teach and learn these practices in our HSD community.

Glenda Eoyang, PhD, HSDP [email protected]

Please enable JavaScript to get a reCAPTCHA challenge. Learn more about ReCAPTCHA .

Patterns Questions

Patterns questions and answers are given here to help students understand how to solve patterns questions using simple techniques. Solving different pattern questions will be beneficial for a quick understanding of the logic in patterns. In this article, you will learn how to solve patterns in maths with detailed explanations.

What are Patterns in Mathematics?

In mathematics, a pattern is a sequence of numbers that are formed in a particular way. Every pattern contains a specific rule. For example, the sequence of even numbers is a pattern since each number is obtained by adding 2 to the previous number.

i.e., 2, 4, 6, 8, 10, 12, 14,….

Here, 2 + 2 = 4

8 + 2 = 10 and so on.

Also, check:

Number patterns in Whole numbers
Algebra as pattern

A pattern can be of numbers or figures, which means we can also observe patterns in a sequence of similar figures. Let’s have a look at the solved problems on the various number and figure patterns.

Patterns Questions and Answers

1. Identify the pattern for the following sequence and find the next number.

2, 3, 5, 8, 12, 17, 23, ____.

2, 3, 5, 8, 12, 17, 23, ____

The pattern involved in the given sequence is:

12 + 5 = 17

17 + 6 = 23

23 + 7 = 30

Therefore, the next number of the given sequence is 30.

2. Observe the below figure and identify the missing part.

Consider the question figure, where the design in each part will be obtained by rotating the previous design by 90 degrees in the clockwise direction.

So, the missing part will be option (b).

Hence, the complete figure is:

3. Write the next three numbers of the following sequence.

173, 155, 137, 119, 101

The pattern in the given sequence is:

173 – 18 = 155

155 – 18 = 137

137 – 18 = 119

119 – 18 = 101

So, the next three numbers can be written as:

101 – 18 = 83

83 – 18 = 65

65 – 18 = 47

Thus, the sequence is 173, 155, 137, 119, 101, 83, 65, 47.

4. Observe the following figure and choose the correct option.

Each part of the square box contains a triangle inscribed in the circle in the given figure. Also, the triangle in the next circle is the vertical image of the previous one.

Similarly, in the second row, the triangle in the missing part will be an image of the previous one.

Thus, the missing part is option (a).

5. What is the formula for the pattern for this sequence?

11, 21, 31, 41, 51, 61, 71

The numbers in this sequence are written as:

11 + 10 = 21, 21 + 10 = 31, 31 + 10 = 41, and so on.

This can also be expressed as:

11 = 10 + 1 = 10 × 1 + 1

21 = 20 + 1 = 10 × 2 + 1

31 = 30 + 1 = 10 × 3 + 1

41 = 40 + 1 = 10 × 4 + 1 and so on.

From this, we can write the formula for the above pattern as: 10n + 1, where n = 1, 2, 3, etc.

6. Find the pattern in the sequence and write the next two numbers.

10, 17, 36, 73, 134,…

Given sequence is:

10 = 1 3 + 9

17 = 2 3 + 9

36 = 3 3 + 9

73 = 4 3 + 9

134 = 5 3 + 9

So, the next number = 6 3 + 9 = 216 + 9 = 225

Again, the next number = 7 3 + 9 = 343 + 9 = 352

Therefore, the sequence is:

10, 17, 36, 73, 134, 225, 352.

7. Observe the pattern given below. Find the missing number.

In the given figure, we can observe that the sum of the four numbers is equal to the number written in the middle of the shape.

That means,

11 + 22 + 33 + 44 = 110

16 + 24 + 32 + 40 = 112

? + 23 + 34 + 12 = 114

? = 114 – 23 – 34 – 12 = 45

Therefore, the missing number is 45.

8. What is the next number of the following sequence?

20, 18, 21, 16, 23, 12, 25, 8, 27, 4, 33, ?

Given sequence:

20, 18, 21, 16, 23, 12, 25, 8, 27, 4, 33

Let us find the difference between two consecutive numbers of the sequence to identify the pattern.

18 – 20 = -2

21 – 18 = 3

16 – 21 = -5

23 – 16 = 7

12 – 23 = -11

25 – 12 = 13

8 – 25 = -17

27 – 8 = 19

4 – 27 = -23

33 – 4 = 29

Here, we can see that the differences are the prime numbers.

So, the number number = 33 – 31 = 2

9. Estimate the next number of the following sequence.

1, 2, 6, 15, 31, ?

Let’s write the difference between consecutive numbers.

2 – 1 = 1

6 – 2 = 4

15 – 6 = 9

31 – 15 = 16

Here, 1 = 1 2 , 4 = 2 2 , 9 = 3 2 , 16 = 4 2 .

Thus, the next number of the sequence will be obtained by adding 5 2 , i.e. 25, to the previous number.

Therefore, 31 + 5 2 = 31 + 25 = 56.

10. What will be the next number of the given sequence?

1, 5, 12, 22, 35, ?

Let’s write the difference between consecutive numbers.

5 – 1 = 4

12 – 5 = 7

22 – 12 = 10

35 – 22 = 13

The difference between these numbers follows a pattern that 3 is odd to the previous difference.

So, the next number will be obtained by adding 13 + 3, i.e. 16 to 35.

Hence, the next number = 35 + 16 = 51.

Practice Problems on Patterns

Find the correct number to complete the pattern given below.

20, 21, 23, 26, 30, 35, 41, ___.

Find the next number in the sequence, 12, 21, 23, 32, 34, 43.
Write the missing numbers in the following.

Register with BYJU'S & Download Free PDFs

Look for Patterns problem solving 5

Loading ad...

lbchambless

problem solving with patterns

Google Classroom
Microsoft Teams
Download PDF

DEV Community

Posted on Nov 2, 2023

20 Essential Coding Patterns to Ace Your Next Coding Interview

Navigating through coding interviews requires more than just a good grasp of algorithms and data structures; it demands a strategic approach and a keen eye for patterns. In todays competitive world of tech job interviews, understanding and mastering coding patterns can significantly enhance your problem-solving skills and boost your performance.

Coding patterns, or as we like to call them, are recurring techniques that provide a structured approach to solving complex problems . Think of them as the building blocks of algorithms, helping you to break down problems into more manageable parts.

In this blog, we will explore 20 essential coding patterns that are pivotal for acing coding interviews. We will delve into the pros and cons of each pattern, providing you with a balanced view to help you make informed decisions during your interviews. And to top it off, we will equip you with real problem examples from the Grokking the Coding Interview course. I'm the author of this course, feel free to reach out to me if you have questions.

Let's go through each pattern one by one.

1. Two Pointers

Description.

The Two Pointers technique is a clever strategy used in algorithm design, particularly when dealing with arrays or linked lists. Imagine you have two fingers, and you place each at different ends or positions of an array. These ‘fingers’ or pointers then traverse through the array, helping you to compare, search, or even manipulate the data efficiently.

Ordered Data Structures : This pattern shines when applied to ordered arrays or lists, allowing for intelligent, position-based decisions that can significantly optimize the algorithm.
Efficiency : By reducing the need for nested loops, the Two Pointers technique helps in achieving linear time complexity, making your algorithm faster and more efficient.

Pros and Cons

Efficiency : Achieves O(n) time complexity for problems that might otherwise require O(n^2).
Simplicity : Once mastered, it provides a straightforward and elegant solution.
Applicability : Mainly beneficial for problems involving sequences or intervals.
Initial Complexity : It might take some time to get the hang of this pattern and understand where and how to move the pointers.

Example Problems from Grokking the Coding Interview

Pair with Target Sum : Find a pair in an array that adds up to a specific target sum.
Squaring a Sorted Array : Given a sorted array, create a new array containing squares of all the numbers of the input array in the sorted order.
Triplet Sum to Zero : Given an array of unsorted numbers, find all unique triplets in it that add up to zero.

2. Island (Matrix Traversal) Pattern

The Island pattern, also known as Matrix Traversal, is a technique used to navigate through a 2D array or matrix. The primary goal is to identify and process contiguous groups of elements, often referred to as ‘islands’. This pattern is particularly useful when you need to explore and manipulate grid-based data.

Grid-Based Problems : Excelling in problems where you need to traverse a grid to find connected components or regions.
Contiguous Elements : Ideal for situations where you need to group together adjacent elements that share a common property.
Comprehensive : Provides a thorough way to explore all the elements in a grid.
Versatile : Can be used to solve a variety of problems related to 2D arrays.
Complexity : Can be more complex to implement compared to linear data structure traversal.
Space Overhead : May require additional space for recursion or queue/stack for breadth-first/depth-first traversal.
Number of Islands : Count the number of islands in a given 2D matrix.
Biggest Island : Find the largest island in terms of area or number of cells.
Flood Fill : Change the color of an image represented by a 2D array.

3. Fast & Slow Pointers

The Fast & Slow Pointers technique involves two pointers traversing through a data structure at different speeds. This ingenious approach is particularly useful in identifying cycles, finding middle elements, and solving various other problems related to linked lists and arrays.

Cycle Detection : Perfect for identifying cycles in a linked list or array, which is a common interview question.
Finding Middle Elements : Efficiently find the middle element of a linked list without knowing the length beforehand.
Problem-Specific Solutions : Solve specific problems like finding the start of a cycle in a linked list.
Space Efficiency : Achieves solutions without the need for extra space, adhering to O(1) space complexity.
Versatility : Applicable to a variety of problems, making it a versatile pattern to know.
Initial Complexity : Understanding how to move the pointers and at what speed can be tricky at first.
Specificity : While versatile, it is mostly beneficial for problems related to linked lists and certain array problems.
LinkedList Cycle : Determine if a linked list has a cycle.
Middle of the LinkedList : Find the middle node of a linked list.
Palindrome LinkedList : Check if a linked list is a palindrome.

4. Sliding Window

The Sliding Window pattern involves creating a ‘window’ over a portion of data and sliding it across to solve problems efficiently. This technique is particularly useful for array or list-based problems where you need to find or calculate something among all the contiguous subarrays or sublists of a given size.

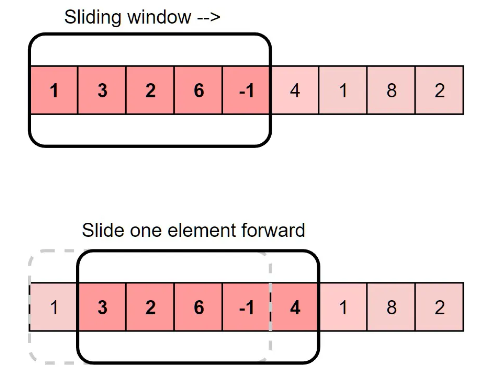
Contiguous Subarrays : Ideal for problems that require you to deal with contiguous subarrays or sublists.
Variable Sized Window : Can be adapted for problems where the window size is not fixed and needs to be adjusted based on certain conditions.
Efficiency : Provides a way to reduce time complexity from O(n^2) to O(n) for specific problems.
Versatility : Can be used for a variety of problems, including maximum sum subarray, smallest subarray with a given sum, and longest substring with K distinct characters.
Initial Complexity : Understanding how to adjust the window size and when to slide the window can be challenging initially.
Specificity : Mainly beneficial for problems involving contiguous subarrays or sublists.
Maximum Sum Subarray of Size K : Given an array of positive numbers and a positive number ‘k’, find the maximum sum of any contiguous subarray of size ‘k’.
Fruits Into Baskets : Given an array of characters where each character represents a fruit tree, you are given two baskets, and your goal is to put maximum number of fruits in each basket.
Longest Substring with K Distinct Characters : Given a string, find the length of the longest substring in it with no more than K distinct characters.

5. Merge Intervals

The Merge Intervals pattern is a powerful technique used to deal with overlapping intervals or ranges. It involves sorting and then merging intervals based on specific conditions. This pattern is incredibly useful for time-based problems, scheduling, and range manipulation.

Overlapping Intervals : Perfect for problems where you need to merge overlapping intervals or find if an interval overlaps with any other.
Interval Scheduling : Useful for problems that involve scheduling based on time intervals.
Clarity : Provides a clear and systematic way to deal with overlapping intervals.
Efficiency : Helps in reducing the problem complexity and achieving optimal solutions.
Sorting Overhead : Requires the intervals to be sorted beforehand, which could add to the time complexity.
Specificity : Mainly beneficial for problems involving intervals and ranges.
Merge Intervals : Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.
Insert Interval : Given a list of non-overlapping intervals sorted by their start time, insert a given interval at the correct position and merge all necessary intervals to produce a list that has only mutually exclusive intervals.
Intervals Intersection : Given two lists of intervals, find the intersection of these two lists. Each list consists of disjoint intervals sorted on their start time.

6. Cyclic Sort

Cyclic Sort is a unique and intuitive sorting algorithm, particularly well-suited for problems where you are given a range of numbers and asked to sort them. The beauty of this pattern lies in its ability to sort the numbers in-place, utilizing the fact that the numbers are consecutive or have a specific range.

Consecutive Numbers : Ideal for scenarios where you have an array of numbers in a specific range, and you need to sort them or find missing/duplicate numbers.
In-Place Sorting : Provides a way to sort the numbers without using any extra space.
Space Efficiency : Achieves sorting without the need for additional space, adhering to O(1) space complexity.
Time Efficiency : Offers a linear time complexity solution for specific range-based sorting problems.
Limited Applicability : Best suited for problems involving numbers in a specific range and may not be applicable for other types of sorting problems.
Initial Learning Curve : Understanding the cyclic sort pattern and knowing when to apply it can take some time.
Find the Missing Number : Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one that is missing from the array.
Find all Duplicates : Find all the duplicate numbers (without using extra space and in O(n) runtime).
Duplicates In Array : Given an array of integers, 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.

7. In-place Reversal of a Linked List

The In-place Reversal of a Linked List pattern is a technique used to reverse the elements of a linked list without using additional memory. This is achieved by manipulating the pointers of the nodes in the linked list to reverse their direction.

Memory Efficiency : Since no additional data structures are used, this pattern is memory efficient.
Reversing Sub-lists : Can be extended to reverse sub-lists within a linked list, providing versatility in solving more complex problems.
Space Efficiency : Achieves in-place reversal, ensuring O(1) space complexity.
Versatility : Can be used to solve various problems related to linked lists, including reversing sub-lists and finding palindromes.
Pointer Manipulation : Requires careful manipulation of pointers, which can be error-prone.
Initial Learning Curve : Understanding how to reverse the pointers without losing the rest of the linked list can be challenging initially.
Reverse a LinkedList : Given the head of a Singly LinkedList, reverse the LinkedList.
Reverse a Sub-list : Given the head of a LinkedList and two positions ‘p’ and ‘q’, reverse the LinkedList from position ‘p’ to ‘q’.
Reverse Every K-element Sub-list : Given the head of a LinkedList and a number ‘k’, reverse every ‘k’ sized sub-list starting from the head.

8. Tree Breadth First Search

The Tree Breadth First Search (BFS) pattern involves traversing a tree level by level, ensuring that you visit all the nodes at the current depth before moving on to the nodes at the next depth level. This is usually implemented using a queue.

Level Order Traversal : Ideal for problems that require you to traverse a tree in level order or when you need to perform operations on nodes at the same depth.
Minimum Depth : Useful for finding the minimum depth of a tree, as you can stop the traversal once you find the first leaf node.
Complete Traversal : Ensures that every node in the tree is visited.
Level Order Information : Provides information about the depth or level of each node.
Space Overhead : Requires additional space for the queue, which can be as large as the number of nodes at the largest level.
Not as Efficient for Depth-Related Queries : For problems that depend on depth information, a depth-first search might be more efficient.
Binary Tree Level Order Traversal : Traverse a tree in level order and return the values of the nodes at each level.
Reverse Level Order Traversal : Traverse a tree in reverse level order.
Zigzag Traversal : Traverse a tree in a zigzag order.

9. Tree Depth First Search

The Tree Depth First Search (DFS) pattern involves traversing a tree in a depth-first manner, meaning you go as deep as possible down one branch before backing up and exploring other branches. This is typically implemented using recursion or a stack.

Path Finding : Ideal for problems where you need to find a path or check the existence of a path with certain properties.
Complex Tree Traversals : Useful for more complex tree traversal problems where you need to maintain state or perform operations as you traverse.
Space Efficiency : For a balanced tree, DFS uses less space than BFS.
Simplicity : Recursive implementations can be more straightforward and concise.
Can Be Less Efficient for Wide Trees : For very wide trees, DFS can use more space than BFS.
May Not Find the Shortest Path : If you're looking for the shortest path in an unweighted tree, BFS is generally a better choice.
Binary Tree Path Sum : Given a binary tree and a number ‘S’, find if the tree has a path from root-to-leaf such that the sum of all the node values of that path equals ‘S’.
All Paths for a Sum : Find all root-to-leaf paths in a binary tree that have a sum equal to a given number.
Count Paths for a Sum : Find the number of paths in a tree that sum up to a given value.

10. Two Heaps

The Two Heaps pattern involves using two priority queues (heaps) to maintain a running balance or median of a set of numbers. One heap keeps track of the smaller half of the numbers, and the other keeps track of the larger half.

Running Median : Perfect for problems where you need to find the median of a set of numbers as new numbers are added.
Balanced Partition : Useful for problems where you need to maintain a balanced partition of numbers.
Efficiency : Provides a way to efficiently find the median or maintain balance in O(log N) time.
Dynamic : Can handle dynamic datasets where numbers are added over time.
Complexity : Implementation can be more complex due to the need to balance the two heaps.
Space Overhead : Requires additional space to store the numbers in the heaps.
Find the Median of a Number Stream : Design a class to calculate the median of a number stream.
Sliding Window Median : Find the median of all subarrays of size ‘K’ in the array.
Maximize Capital : Given a set of investment projects with their respective profits, we need to find the most profitable projects. We are given an initial capital and are allowed to invest only in a fixed number of projects. Our goal is to choose projects that give us the maximum profit.

11. Subsets

The Subsets pattern involves dealing with problems that require generating all possible combinations or subsets of a set. This pattern is particularly useful when you need to explore all the different ways to combine elements, which is a common scenario in many coding problems.

Combinatorial Problems : Ideal for problems where you need to generate all possible combinations of elements.
Exhaustive Search : Useful when you need to perform an exhaustive search over all possible subsets of a set.
Comprehensive : Ensures that you consider all possible combinations of elements.
Versatile : Can be used to solve a variety of problems, including generating power sets, combinations, and permutations.
Time Complexity : Can lead to exponential time complexity, as the number of subsets of a set is 2^N.
Space Complexity : Requires additional space to store all the subsets.
Subsets : Given a set with distinct elements, find all of its distinct subsets.
Subsets With Duplicates : Given a set of numbers that might contain duplicates, find all of its distinct subsets.
Permutations : Given a set of distinct numbers, find all of its permutations.

12. Modified Binary Search

The Modified Binary Search pattern involves adapting the classic binary search algorithm to solve various problems, often related to searching in a sorted array or finding the boundary of a condition.

Sorted Arrays : Perfect for problems involving searching or making decisions based on sorted arrays.
Finding Boundaries : Useful for finding the start or end of a condition in a sorted array.
Efficiency : Provides a logarithmic time complexity solution for searching problems, making it highly efficient.
Versatility : Can be adapted to solve a wide range of problems beyond simple searching.
Applicability : Mainly beneficial for problems involving sorted arrays or conditions with clear boundaries.
Implementation Nuances : Requires careful implementation to handle edge cases and avoid infinite loops.
Order-agnostic Binary Search : Given a sorted array of numbers, find the index of a given number. The array could be sorted in ascending or descending order.
Ceiling of a Number : Given an array of numbers sorted in ascending order, find the ceiling of a given number. The ceiling of a number is the smallest number in the given array greater than or equal to the given number.
Next Letter : Given an array of lowercase letters sorted in ascending order, find the smallest letter in the given array greater than a given ‘key’.

13. Bitwise XOR

The Bitwise XOR pattern involves using the XOR bitwise operator to solve problems, often related to finding missing numbers or duplicate numbers in an array. XOR is a binary operator that returns 1 when the two bits are different and 0 when they are the same.

Finding Missing or Duplicate Numbers : Ideal for problems where you need to find a missing number or duplicate numbers in an array.
Bit Manipulation : Useful for problems that require manipulation of bits to achieve the desired result.
Efficiency : Provides a constant space solution for certain problems, making it highly efficient.
Simplicity : Once understood, the XOR operator can be used to create elegant and simple solutions.
Specificity : Mainly beneficial for problems involving finding missing or duplicate numbers.
Learning Curve : Understanding how the XOR operator works and when to use it can take some time.
Single Number : In a non-empty array of integers, every number appears twice except for one, find that single number.
Two Single Numbers : In a non-empty array of numbers, every number appears exactly twice except two numbers that appear only once. Find the two numbers that appear only once.
Complement of Base 10 Number : For a given positive number N in base-10, return the complement of its binary representation as a base-10 integer.

14. Top 'K' Elements

The Top 'K' Elements pattern involves finding the 'K' largest or smallest elements in an array or stream of data. This pattern is particularly useful when dealing with large datasets and you need to maintain a subset of the data based on certain criteria.

Priority Queue : Utilizes a min-heap or max-heap to efficiently keep track of the 'K' largest or smallest elements.
Streaming Data : Ideal for scenarios where the data is streaming in, and you need to maintain the 'K' largest or smallest elements at any given time.
Efficiency : Provides a way to find the 'K' largest or smallest elements in O(N log K) time.
Space Efficiency : Only requires O(K) space, regardless of the size of the dataset.
Limited to 'K' Elements : Only maintains information about the top 'K' elements, not the entire dataset.
Heap Maintenance : Requires careful maintenance of the heap to ensure efficiency.
Top 'K' Numbers : Given an unsorted array of numbers, find the ‘K’ largest numbers in it.
Kth Smallest Number : Given an unsorted array of numbers, find the Kth smallest number in it.
‘K’ Closest Points to the Origin : Given an array of points in the a 2D plane, find ‘K’ closest points to the origin.

15. K-way Merge

The K-way Merge pattern involves merging multiple sorted arrays or lists into a single sorted list. This pattern is highly useful in scenarios where you have multiple sorted datasets that you need to combine and maintain the sorted order.

Multiple Sorted Arrays : Ideal for merging multiple sorted arrays or lists.
External Sorting : Useful in external sorting, where the data to be sorted does not fit into memory and is stored in sorted chunks.
Efficiency : Provides a way to merge multiple sorted arrays in O(N log K) time, where ‘N’ is the total number of elements across all arrays, and ‘K’ is the number of arrays.
Space Efficiency : Only requires O(K) space for the priority queue.
Dependent on Sorting : The efficiency of this pattern depends on the arrays being sorted.
Priority Queue Overhead : Requires maintenance of a priority queue, which adds to the complexity.
Merge K Sorted Lists : Given an array of ‘K’ sorted LinkedLists, merge them into one sorted list.
Kth Smallest Number in M Sorted Lists : Given ‘M’ sorted arrays, find the K’th smallest number among all the arrays.
Find the Smallest Range Covering Elements from K Lists : Given ‘M’ sorted arrays, find the smallest range that includes at least one number from each of the ‘M’ lists.

16. Topological Sort

Topological Sort is a pattern used for linearly ordering the vertices of a directed graph in such a way that for every directed edge (U, V), vertex U comes before V. This pattern is particularly useful in scenarios where you have a set of tasks and some tasks depend on others.

Task Scheduling : Ideal for problems where tasks need to be scheduled in a specific order, respecting their dependencies.
Course Scheduling : Useful in scenarios like course scheduling where some courses have prerequisites.
Clarity : Provides a clear and systematic way to order tasks or vertices.
Detecting Cycles : Helps in detecting cycles in a directed graph, which is important for understanding if a valid ordering is possible.
Applicability : Mainly beneficial for problems involving directed graphs and ordering of vertices.
Complexity : Implementation can be complex, especially for beginners.
Topological Sort : Given a directed graph, find the topological ordering of its vertices.
Tasks Scheduling : Find if it is possible to schedule all the tasks.
Tasks Scheduling Order : Find the order of tasks we should pick to finish all tasks.

A Trie, also known as a prefix tree, is a tree-like data structure used to store a dynamic set of strings, where the keys are usually strings. It is particularly useful for retrieval of a key in a dataset of strings, which makes it highly efficient for solving word-based problems.

Autocomplete : Ideal for implementing autocomplete functionality in search engines or text editors.
Spell Checker : Useful for building spell checkers in word processors.
IP Routing : Used in IP routing to store and search routes.
Efficiency : Provides fast retrieval of strings and is more efficient than hash tables or sets when it comes to string keys.
Prefix Searching : Excellent for problems that require prefix searching or matching.
Space Overhead : Can use more space compared to other data structures when the dataset is sparse.
Complexity : Implementation can be complex, especially when handling deletion of words from the Trie.
Insert into and Search in a Trie : Implement insertion and search in a Trie.
Longest Common Prefix : Find the longest common prefix of a set of strings.
Word Search : Given a 2D board and a word, find if the word exists in the grid.

18. Backtracking

Backtracking is a general algorithmic technique that considers searching through all the possible configurations of a search space in order to solve computational problems. It is particularly useful for optimization problems and when a complete search of the solution space is required. The main idea is to explore each possibility until the solution is found or all possibilities have been exhausted.

Combinatorial Problems : Ideal for solving problems that require generating all possible configurations like permutations, combinations, and subsets.
Puzzle Solving : Useful for solving puzzles such as Sudoku, crossword puzzles, and the N-Queens problem.
Completeness : Ensures that the entire solution space is explored, guaranteeing that the optimal solution will be found if it exists.
Space Efficiency : Uses less memory as it only needs to store the current state and the decision stack.
Time Complexity : Can lead to exponential time complexity, as it explores all possible configurations.
Optimization Required : May require additional optimizations like pruning to be practical for larger instances.
Subsets : Given a set of numbers, find all of its subsets.
N-Queens : Place N queens on an N×N chessboard so that no two queens threaten each other.

19. Monotonic Stack

A Monotonic Stack is a specialized data structure that maintains elements in a sorted order while supporting stack operations. It is particularly useful for problems where you need to find the next greater or smaller element in an array or when you need to maintain a running maximum or minimum value efficiently.

Next Greater Element : Ideal for finding the next greater element for each element in an array.
Maximum Area Histogram : Useful for problems like finding the largest rectangular area under a histogram.
Efficiency : Provides a way to solve certain problems in linear time, making it highly efficient.
Simplicity : Once understood, the monotonic stack can lead to concise and elegant solutions.
Specificity : Mainly beneficial for problems involving finding the next greater or smaller element and related problems.
Learning Curve : Understanding how and when to use a monotonic stack can take some time.

Example Problems

Next Greater Element : Given an array, find the next greater element for each element in the array.
Maximum Area Histogram : Given a histogram, find the largest rectangular area under the histogram.
Largest Rectangle in Histogram : Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

20. 0/1 Knapsack (Dynamic Programming)

The 0/1 Knapsack problem is a classic optimization problem that falls under the category of Dynamic Programming. In this problem, you are given a set of items, each with a weight and a value, and a knapsack with a maximum capacity. The goal is to determine the maximum value that can be accommodated in the knapsack without exceeding its capacity. The "0/1" part of the name reflects the fact that you can't break an item, you either take it or leave it.

Resource Allocation : Ideal for problems where you need to optimally allocate limited resources to maximize profit or minimize cost.
Budgeting : Useful for budgeting scenarios where you need to choose a subset of projects or investments to maximize return.
Optimality : Ensures that the optimal solution is found, provided that the problem satisfies the principle of optimality.
Generality : Can be adapted to solve a wide variety of optimization problems.
Time and Space Complexity : The naive implementation has a time and space complexity of O(nW), where n is the number of items and W is the capacity of the knapsack. This can be prohibitive for large inputs.
Requires Integer Weights and Values : The classic 0/1 Knapsack problem requires weights and values to be integers.
0/1 Knapsack : Given the weights and profits of ‘N’ items, put these items in a knapsack which has a capacity ‘C’. The goal is to get the maximum profit out of the items in the knapsack.
Equal Subset Sum Partition : Given a set of positive numbers, find if we can partition it into two subsets such that the sum of elements in both subsets is equal.
Subset Sum : Given a set of positive numbers, determine if there exists a subset in the set whose sum is equal to a given number ‘S’.

Mastering these patterns is definitely not about memorizing solutions; it’s about understanding the underlying principles and learning how to apply them to a wide array of problems. The versatility of these patterns ensures that you are well-equipped to handle different challenges, making you a formidable candidate in any coding interview.

Remember, practice is key. The more problems you solve using these patterns, the more proficient you will become in recognizing problem types and applying the appropriate patterns. So, keep practicing, stay persistent, and you will find yourself excelling in coding interviews, ready to tackle any problem that comes your way.

Want to read more about coding patterns:

Don’t Just LeetCode; Follow the Coding Patterns Instead
Top LeetCode Patterns for FAANG Coding Interviews
Grokking Dynamic Programming Patterns for Coding Interviews

Top comments (3)

Templates let you quickly answer FAQs or store snippets for re-use.

Joined Mar 15, 2024

Please add the correct link "In-place Reversal of a Linked List" onwards. FYI @arslan_ah

Location India
Work Team lead
Joined Jul 23, 2019

Joined Nov 7, 2023

after 6, most of the link are wrong

Are you sure you want to hide this comment? It will become hidden in your post, but will still be visible via the comment's permalink .

Hide child comments as well

For further actions, you may consider blocking this person and/or reporting abuse

Spec Coder: Your Powerful AI Co-pilot for Supercharged Coding in Visual Studio Code

Harish Kumar - Jun 3

Functional Programming in Python: A New Way to Think About Problem-Solving

Manav Codaty - Jun 3

Annotations in Java Spring

Akriti Keswani - Jun 3

Exploring .NET 9 Preview 4: All You Need To Know 🥳

ByteHide - Jun 3

We're a place where coders share, stay up-to-date and grow their careers.

Supported by

A.I.’s Black Boxes Just Got a Little Less Mysterious

Researchers at the A.I. company Anthropic claim to have found clues about the inner workings of large language models, possibly helping to prevent their misuse and to curb their potential threats.

Share full article

A woman works into an office with the name Anthropic on a glass door.

By Kevin Roose

Reporting from San Francisco

One of the weirder, more unnerving things about today’s leading artificial intelligence systems is that nobody — not even the people who build them — really knows how the systems work.

That’s because large language models, the type of A.I. systems that power ChatGPT and other popular chatbots, are not programmed line by line by human engineers, as conventional computer programs are.

Instead, these systems essentially learn on their own, by ingesting vast amounts of data and identifying patterns and relationships in language, then using that knowledge to predict the next words in a sequence.

One consequence of building A.I. systems this way is that it’s difficult to reverse-engineer them or to fix problems by identifying specific bugs in the code. Right now, if a user types “Which American city has the best food?” and a chatbot responds with “Tokyo,” there’s no real way of understanding why the model made that error, or why the next person who asks may receive a different answer.

And when large language models do misbehave or go off the rails, nobody can really explain why. (I encountered this problem last year when a Bing chatbot acted in an unhinged way during an interaction with me. Not even top executives at Microsoft could tell me with any certainty what had gone wrong.)

The inscrutability of large language models is not just an annoyance but a major reason some researchers fear that powerful A.I. systems could eventually become a threat to humanity.

After all, if we can’t understand what’s happening inside these models, how will we know if they can be used to create novel bioweapons, spread political propaganda or write malicious computer code for cyberattacks? If powerful A.I. systems start to disobey or deceive us, how can we stop them if we can’t understand what’s causing that behavior in the first place?

To address these problems, a small subfield of A.I. research known as “mechanistic interpretability” has spent years trying to peer inside the guts of A.I. language models. The work has been slow going, and progress has been incremental.

There has also been growing resistance to the idea that A.I. systems pose much risk at all. Last week, two senior safety researchers at OpenAI, the maker of ChatGPT, left the company amid conflict with executives about whether the company was doing enough to make its products safe.

But this week, a team of researchers at the A.I. company Anthropic announced what they called a major breakthrough — one they hope will give us the ability to understand more about how A.I. language models actually work, and to possibly prevent them from becoming harmful.

The team summarized its findings in a blog post called “ Mapping the Mind of a Large Language Model .”

The researchers looked inside one of Anthropic’s A.I. models — Claude 3 Sonnet, a version of the company’s Claude 3 language model — and used a technique known as “dictionary learning” to uncover patterns in how combinations of neurons, the mathematical units inside the A.I. model, were activated when Claude was prompted to talk about certain topics. They identified roughly 10 million of these patterns, which they call “features.”

They found that one feature, for example, was active whenever Claude was asked to talk about San Francisco. Other features were active whenever topics like immunology or specific scientific terms, such as the chemical element lithium, were mentioned. And some features were linked to more abstract concepts, like deception or gender bias.

They also found that manually turning certain features on or off could change how the A.I. system behaved, or could get the system to even break its own rules.

For example, they discovered that if they forced a feature linked to the concept of sycophancy to activate more strongly, Claude would respond with flowery, over-the-top praise for the user, including in situations where flattery was inappropriate.

Chris Olah, who led the Anthropic interpretability research team, said in an interview that these findings could allow A.I. companies to control their models more effectively.

“We’re discovering features that may shed light on concerns about bias, safety risks and autonomy,” he said. “I’m feeling really excited that we might be able to turn these controversial questions that people argue about into things we can actually have more productive discourse on.”

Other researchers have found similar phenomena in small- and medium-size language models. But Anthropic’s team is among the first to apply these techniques to a full-size model.

Jacob Andreas, an associate professor of computer science at M.I.T., who reviewed a summary of Anthropic’s research, characterized it as a hopeful sign that large-scale interpretability might be possible.

“In the same way that understanding basic things about how people work has helped us cure diseases, understanding how these models work will both let us recognize when things are about to go wrong and let us build better tools for controlling them,” he said.

Mr. Olah, the Anthropic research leader, cautioned that while the new findings represented important progress, A.I. interpretability was still far from a solved problem.

For starters, he said, the largest A.I. models most likely contain billions of features representing distinct concepts — many more than the 10 million or so features that Anthropic’s team claims to have discovered. Finding them all would require enormous amounts of computing power and would be too costly for all but the richest A.I. companies to attempt.

Even if researchers were to identify every feature in a large A.I. model, they would still need more information to understand the full inner workings of the model. There is also no guarantee that A.I. companies would act to make their systems safer.

Still, Mr. Olah said, even prying open these A.I. black boxes a little bit could allow companies, regulators and the general public to feel more confident that these systems can be controlled.

“There are lots of other challenges ahead of us, but the thing that seemed scariest no longer seems like a roadblock,” he said.

Kevin Roose is a Times technology columnist and a host of the podcast " Hard Fork ." More about Kevin Roose

Explore Our Coverage of Artificial Intelligence

News and Analysis

Google appears to have rolled back its new A.I. Overviews after the technology produced a litany of untruths and errors.

OpenAI said that it has begun training a new flagship A.I. model that would succeed the GPT-4 technology that drives its popular online chatbot, ChatGPT.

Elon Musk’s A.I. company, xAI, said that it had raised $6 billion , helping to close the funding gap with OpenAI, Anthropic and other rivals.

The Age of A.I.

After some trying years during which Mark Zuckerberg could do little right, many developers and technologists have embraced the Meta chief as their champion of “open-source” A.I.

D’Youville University in Buffalo had an A.I. robot speak at its commencement . Not everyone was happy about it.

A new program, backed by Cornell Tech, M.I.T. and U.C.L.A., helps prepare lower-income, Latina and Black female computing majors for A.I. careers.

IMAGES

7.6
Problem Solving
PPT
Look for a Pattern Strategy
Problem Solving
lesson 6 problem solving look for a pattern

VIDEO

Problem Solving Strategy : Look for a Pattern
How to Find a Pattern when Solving Problems
Problem solving
How to Solve a Problem in Four Steps: The IDEA Model
Types of Problem Solving
How to Find a Pattern when Solving Problems

COMMENTS

Math Strategies: Problem Solving by Finding a Pattern
One of the most useful strategies in math is problem solving by finding a pattern. Teach kids to make a table, find a pattern, and solve the problem! One of the most useful strategies in math is problem solving by finding a pattern. ... In some instances, the pattern may look one way for the first few entries, then change, so this is important ...
Pattern Problem Solving: Math (Grades 2-8)
Pattern problem solving is a mathematical strategy in which students look for patterns in data to solve a problem. To find a pattern, students search for repeated items, numbers, or series of events. The following problem can be solved by finding the pattern: There are 1000 lockers in a high school with 1000 students.
Problem Solving (Look for a Pattern)
This foundations of math video explains the four-step process of problem solving: understanding the problem, devising a plan, carrying out the plan, and loo...
Arithmetic patterns and problem solving
Patterns in arithmetic. Math isn't just about numbers - it's about patterns, too! In this unit, you'll figure out how to spot patterns in different types of problems and learn cool strategies to solve them. You'll tackle word problems, master estimation, and learn to write expressions like a pro.
Module 1: Problem Solving Strategies
Make a table and look for a pattern: Procedure: Make a table reflecting the data in the problem. If done in an orderly way, such a table will often reveal patterns and relationships that suggest how the problem can be solved. ... Problem Solving Strategy 3 (Using a variable to find the sum of a sequence.) Gauss's strategy for sequences. last ...
Finding Patterns (video lessons, examples and solutions)
Here we will look at some advanced examples of "Find a Pattern" method of problem solving strategy. Example: Each hexagon below is surrounded by 12 dots. a) Find the number of dots for a pattern with 6 hexagons in the first column. b) Find the pattern of hexagons with 229 dots. Solution:
Welcome to CK-12 Foundation
Develop and use the strategy "look for a pattern." Plan and compare alternative approaches to solving a problem. Solve real-world problems using the above strategies as part of a plan. Introduction. In this section, we will apply the problem-solving plan you learned about in the last section to solve several real-world problems.
1.3: Problem Solving Strategies
Problem Solving Strategy 8 (Look for and Explain Patterns). Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand!
Find a Pattern
Elementary Math Problem Solving - Find a PatternIn this video, we explore one of eight problem-solving strategies for the primary math student. Students are ...
Get ready for patterns and problem solving
Practice. Let's build a solid foundation of addition and subtraction word problems so that we'll be ready for patterns and problem solving in third grade. In this unit, you will tackle word problems from every angle—adding, subtracting, number lines, and even 2-step word problems!
PDF LOOK FOR PATTERNS
LOOK FOR PATTERNS When students use this problem-solving strategy, they are required to analyze patterns in data and make predictions and generalizations based on their analysis. They then must check the generalization against the information in the problem and possibly make a prediction from, or extension of, the given information.
Problem-Solving Strategies
5. Find a pattern. Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the "find a pattern" problem-solving strategy.
Finding patterns in numbers (video)
Transcript. This video discusses how to identify patterns in number sequences. By analyzing three different sequences, the speaker demonstrates that patterns can involve adding a certain amount to each number, or multiplying each number by a certain amount. It's important to ensure the pattern remains consistent throughout the sequence. Questions.
More Problem-Solving Strategies: Look for a Pattern
Step 1: Make a Table. The first step to look for a pattern is to make a table showing the relationships that are there. For example, suppose the problem were to find the next three numbers in the series 2, 4, 6, 8. They are related in a simple way, such that 2 +2 is 4 +2 is 6 +2 is 8. In order to extend the pattern, 8 +2 is 10, +2 is 12 +2 is 14.
Math Problem Solving Strategies
The following video shows more examples of using problem solving strategies and models. Question 2: The table shows the number of seats in each of the first four rows in an auditorium. The remaining ten rows follow the same pattern. Find the number of seats in the last row. Question 3: You are hanging three pictures in the wall of your home ...
Look for a Pattern
A pattern is something that repeats itself. When you find a pattern in a problem, you can identify what comes next by continuing the pattern. Usually, you can find a pattern by making a table and therefore, these strategies are often used together. At Laura's birthday party, Laura and her guests open a piñata. The first child receives 9 pieces ...
How to Find a Pattern when Solving Problems
Learn how to look for patterns in a word problem to help you find a solution.We hope you are enjoying this video! For more in-depth learning, check out Miaca...
PDF Problem Solving • Shape Patterns
Problem Solving • Shape Patterns Use the strategy act it out to solve pattern problems. What might be the next three figures in the pattern below? ... model the and act out the problem. Solve the Problem Look for a group of figures that repeats and circle that group. The repeating group is , , , , .
Problems into Patterns
Newton described a powerful problem-solving method. 1) Define the problem. 2) Name all the parts. 3) Understand the parts. 4) Find the right answer and take the right action. That is great when things are simple. The problem is that most of your real problems are not simple. They have open boundaries, multiple causes, and messy ...
Patterns Questions with Solutions
Algebra as pattern; A pattern can be of numbers or figures, which means we can also observe patterns in a sequence of similar figures. Let's have a look at the solved problems on the various number and figure patterns. Patterns Questions and Answers. 1. Identify the pattern for the following sequence and find the next number.
Look for Patterns problem solving 5 worksheet
Look for Patterns problem solving 5 Look for Patterns problem solving 5. Loading ad... lbchambless Member for 4 years 2 months Age: 9-12. Level: 5. Language: English (en) ID: 71391. 27/03/2020. Country code: US. Country: United States. School subject: Math ...
20 Essential Coding Patterns to Ace Your Next Coding Interview
Example Problems from Grokking the Coding Interview. Number of Islands: Count the number of islands in a given 2D matrix. Biggest Island: Find the largest island in terms of area or number of cells. Flood Fill: Change the color of an image represented by a 2D array. 3.
A.I.'s Black Boxes Just Got a Little Less Mysterious
A new program, backed by Cornell Tech, M.I.T. and U.C.L.A., helps prepare lower-income, Latina and Black female computing majors for A.I. careers. Researchers at the A.I. company Anthropic claim ...