what does an alternative hypothesis mean in psychology

Alternative Hypothesis

An alternative hypothesis is a competing explanation or theory that challenges the main hypothesis. It offers an alternative perspective to explain a phenomenon.

Related terms

Null Hypothesis : The null hypothesis assumes no significant relationship or difference between variables.

Multiple Hypotheses : Multiple hypotheses refer to having more than one possible explanation for a phenomenon.

Independent Variable : The independent variable is a factor that researchers manipulate in an experiment to determine its effect on the dependent variable.

" Alternative Hypothesis " appears in:

Subjects ( 1 ).

AP Statistics

Practice Questions ( 2 )

Which alternative hypothesis could best explain the neurodevelopmental origin of schizophrenia beyond the dopamine hypothesis?

Which alternative hypothesis counters the social exchange theory that equates interpersonal attraction to rewards minus costs?

Are you a college student?

Study guides for the entire semester

200k practice questions

Glossary of 50k key terms - memorize important vocab

About Fiveable

Code of Conduct

Terms of Use

Privacy Policy

CCPA Privacy Policy

AP Score Calculators

Study Guides

Practice Quizzes

Cram Events

Crisis Text Line

Help Center

Stay Connected

© 2024 Fiveable Inc. All rights reserved.

AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.

Research Methods In Psychology

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

Research methods in psychology are systematic procedures used to observe, describe, predict, and explain behavior and mental processes. They include experiments, surveys, case studies, and naturalistic observations, ensuring data collection is objective and reliable to understand and explain psychological phenomena.

Hypotheses are statements about the prediction of the results, that can be verified or disproved by some investigation.

There are four types of hypotheses :

• Null Hypotheses (H0 ) – these predict that no difference will be found in the results between the conditions. Typically these are written ‘There will be no difference…’
• Alternative Hypotheses (Ha or H1) – these predict that there will be a significant difference in the results between the two conditions. This is also known as the experimental hypothesis.
• One-tailed (directional) hypotheses – these state the specific direction the researcher expects the results to move in, e.g. higher, lower, more, less. In a correlation study, the predicted direction of the correlation can be either positive or negative.
• Two-tailed (non-directional) hypotheses – these state that a difference will be found between the conditions of the independent variable but does not state the direction of a difference or relationship. Typically these are always written ‘There will be a difference ….’

All research has an alternative hypothesis (either a one-tailed or two-tailed) and a corresponding null hypothesis.

Once the research is conducted and results are found, psychologists must accept one hypothesis and reject the other. 

So, if a difference is found, the Psychologist would accept the alternative hypothesis and reject the null.  The opposite applies if no difference is found.

Sampling techniques

Sampling is the process of selecting a representative group from the population under study.

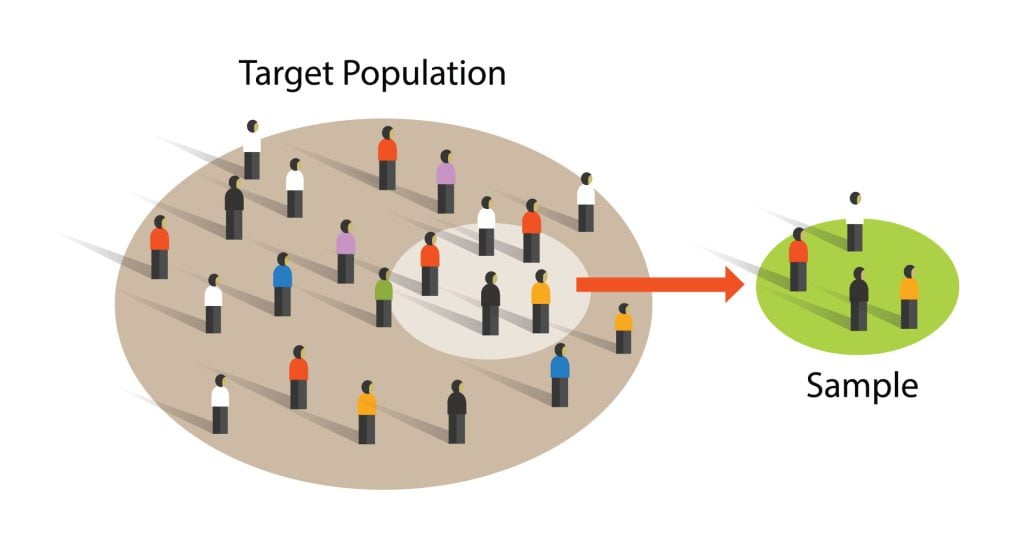
A sample is the participants you select from a target population (the group you are interested in) to make generalizations about.

Representative means the extent to which a sample mirrors a researcher’s target population and reflects its characteristics.

Generalisability means the extent to which their findings can be applied to the larger population of which their sample was a part.

• Volunteer sample : where participants pick themselves through newspaper adverts, noticeboards or online.
• Opportunity sampling : also known as convenience sampling , uses people who are available at the time the study is carried out and willing to take part. It is based on convenience.
• Random sampling : when every person in the target population has an equal chance of being selected. An example of random sampling would be picking names out of a hat.
• Systematic sampling : when a system is used to select participants. Picking every Nth person from all possible participants. N = the number of people in the research population / the number of people needed for the sample.
• Stratified sampling : when you identify the subgroups and select participants in proportion to their occurrences.
• Snowball sampling : when researchers find a few participants, and then ask them to find participants themselves and so on.
• Quota sampling : when researchers will be told to ensure the sample fits certain quotas, for example they might be told to find 90 participants, with 30 of them being unemployed.

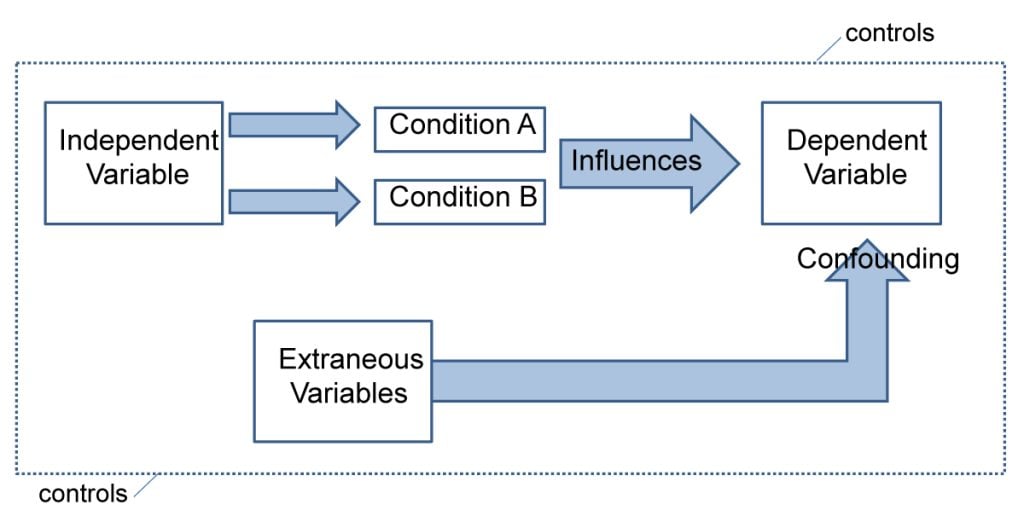
Experiments always have an independent and dependent variable .

• The independent variable is the one the experimenter manipulates (the thing that changes between the conditions the participants are placed into). It is assumed to have a direct effect on the dependent variable.
• The dependent variable is the thing being measured, or the results of the experiment.

Operationalization of variables means making them measurable/quantifiable. We must use operationalization to ensure that variables are in a form that can be easily tested.

For instance, we can’t really measure ‘happiness’, but we can measure how many times a person smiles within a two-hour period. 

By operationalizing variables, we make it easy for someone else to replicate our research. Remember, this is important because we can check if our findings are reliable.

Extraneous variables are all variables which are not independent variable but could affect the results of the experiment.

It can be a natural characteristic of the participant, such as intelligence levels, gender, or age for example, or it could be a situational feature of the environment such as lighting or noise.

Demand characteristics are a type of extraneous variable that occurs if the participants work out the aims of the research study, they may begin to behave in a certain way.

For example, in Milgram’s research , critics argued that participants worked out that the shocks were not real and they administered them as they thought this was what was required of them. 

Extraneous variables must be controlled so that they do not affect (confound) the results.

Randomly allocating participants to their conditions or using a matched pairs experimental design can help to reduce participant variables. 

Situational variables are controlled by using standardized procedures, ensuring every participant in a given condition is treated in the same way

Experimental Design

Experimental design refers to how participants are allocated to each condition of the independent variable, such as a control or experimental group.

• Independent design ( between-groups design ): each participant is selected for only one group. With the independent design, the most common way of deciding which participants go into which group is by means of randomization. 
• Matched participants design : each participant is selected for only one group, but the participants in the two groups are matched for some relevant factor or factors (e.g. ability; sex; age).
• Repeated measures design ( within groups) : each participant appears in both groups, so that there are exactly the same participants in each group.
• The main problem with the repeated measures design is that there may well be order effects. Their experiences during the experiment may change the participants in various ways.
• They may perform better when they appear in the second group because they have gained useful information about the experiment or about the task. On the other hand, they may perform less well on the second occasion because of tiredness or boredom.
• Counterbalancing is the best way of preventing order effects from disrupting the findings of an experiment, and involves ensuring that each condition is equally likely to be used first and second by the participants.

If we wish to compare two groups with respect to a given independent variable, it is essential to make sure that the two groups do not differ in any other important way. 

Experimental Methods

All experimental methods involve an iv (independent variable) and dv (dependent variable)..

• Field experiments are conducted in the everyday (natural) environment of the participants. The experimenter still manipulates the IV, but in a real-life setting. It may be possible to control extraneous variables, though such control is more difficult than in a lab experiment.
• Natural experiments are when a naturally occurring IV is investigated that isn’t deliberately manipulated, it exists anyway. Participants are not randomly allocated, and the natural event may only occur rarely.

Case studies are in-depth investigations of a person, group, event, or community. It uses information from a range of sources, such as from the person concerned and also from their family and friends.

Many techniques may be used such as interviews, psychological tests, observations and experiments. Case studies are generally longitudinal: in other words, they follow the individual or group over an extended period of time. 

Case studies are widely used in psychology and among the best-known ones carried out were by Sigmund Freud . He conducted very detailed investigations into the private lives of his patients in an attempt to both understand and help them overcome their illnesses.

Case studies provide rich qualitative data and have high levels of ecological validity. However, it is difficult to generalize from individual cases as each one has unique characteristics.

Correlational Studies

Correlation means association; it is a measure of the extent to which two variables are related. One of the variables can be regarded as the predictor variable with the other one as the outcome variable.

Correlational studies typically involve obtaining two different measures from a group of participants, and then assessing the degree of association between the measures. 

The predictor variable can be seen as occurring before the outcome variable in some sense. It is called the predictor variable, because it forms the basis for predicting the value of the outcome variable.

Relationships between variables can be displayed on a graph or as a numerical score called a correlation coefficient.

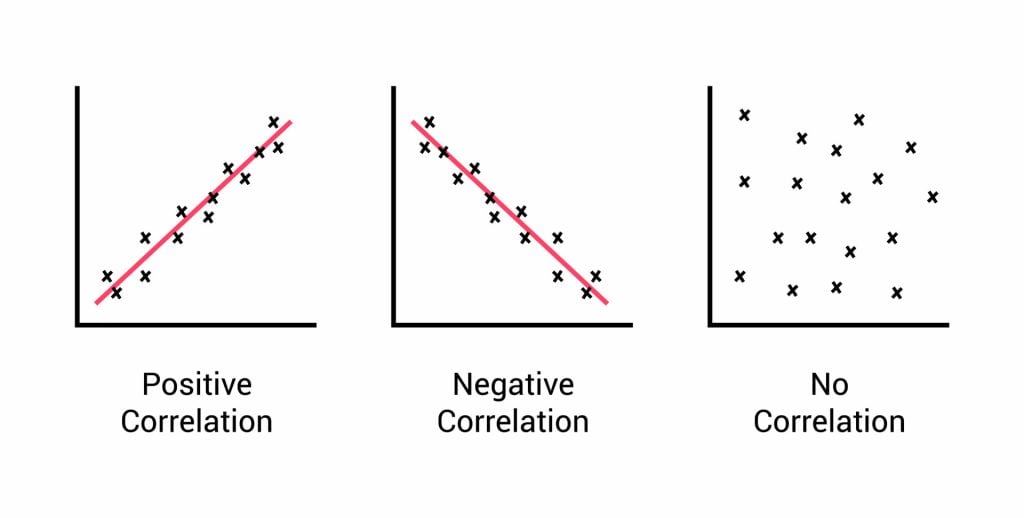
• If an increase in one variable tends to be associated with an increase in the other, then this is known as a positive correlation .
• If an increase in one variable tends to be associated with a decrease in the other, then this is known as a negative correlation .
• A zero correlation occurs when there is no relationship between variables.

After looking at the scattergraph, if we want to be sure that a significant relationship does exist between the two variables, a statistical test of correlation can be conducted, such as Spearman’s rho.

The test will give us a score, called a correlation coefficient . This is a value between 0 and 1, and the closer to 1 the score is, the stronger the relationship between the variables. This value can be both positive e.g. 0.63, or negative -0.63.

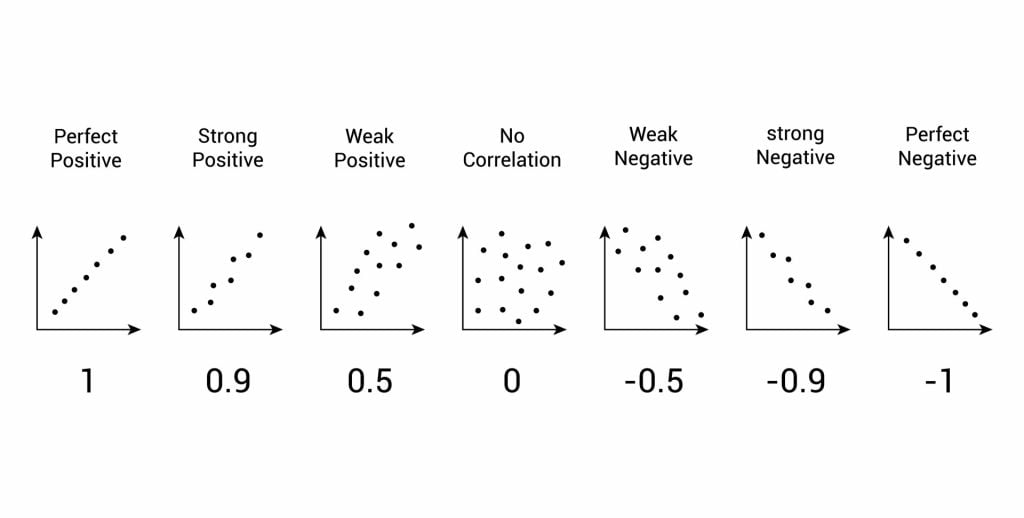
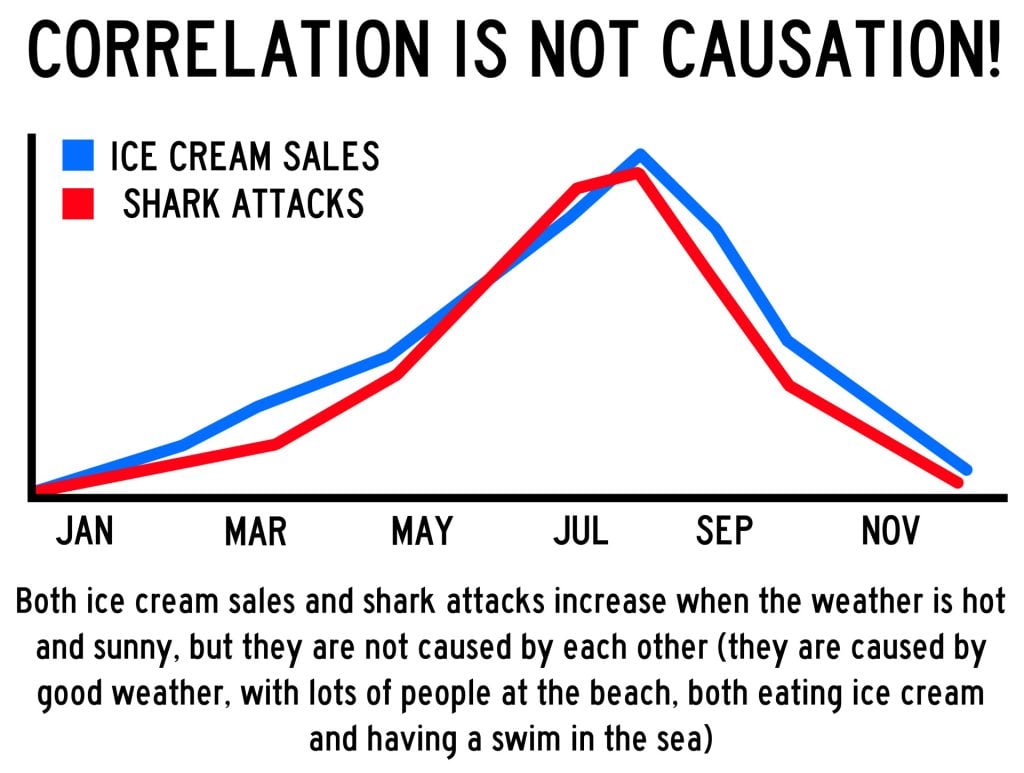
A correlation between variables, however, does not automatically mean that the change in one variable is the cause of the change in the values of the other variable. A correlation only shows if there is a relationship between variables.

Correlation does not always prove causation, as a third variable may be involved. 

Interview Methods

Interviews are commonly divided into two types: structured and unstructured.

A fixed, predetermined set of questions is put to every participant in the same order and in the same way. 

Responses are recorded on a questionnaire, and the researcher presets the order and wording of questions, and sometimes the range of alternative answers.

The interviewer stays within their role and maintains social distance from the interviewee.

There are no set questions, and the participant can raise whatever topics he/she feels are relevant and ask them in their own way. Questions are posed about participants’ answers to the subject

Unstructured interviews are most useful in qualitative research to analyze attitudes and values.

Though they rarely provide a valid basis for generalization, their main advantage is that they enable the researcher to probe social actors’ subjective point of view. 

Questionnaire Method

Questionnaires can be thought of as a kind of written interview. They can be carried out face to face, by telephone, or post.

The choice of questions is important because of the need to avoid bias or ambiguity in the questions, ‘leading’ the respondent or causing offense.

• Open questions are designed to encourage a full, meaningful answer using the subject’s own knowledge and feelings. They provide insights into feelings, opinions, and understanding. Example: “How do you feel about that situation?”
• Closed questions can be answered with a simple “yes” or “no” or specific information, limiting the depth of response. They are useful for gathering specific facts or confirming details. Example: “Do you feel anxious in crowds?”

Its other practical advantages are that it is cheaper than face-to-face interviews and can be used to contact many respondents scattered over a wide area relatively quickly.

Observations

There are different types of observation methods :

• Covert observation is where the researcher doesn’t tell the participants they are being observed until after the study is complete. There could be ethical problems or deception and consent with this particular observation method.
• Overt observation is where a researcher tells the participants they are being observed and what they are being observed for.
• Controlled : behavior is observed under controlled laboratory conditions (e.g., Bandura’s Bobo doll study).
• Natural : Here, spontaneous behavior is recorded in a natural setting.
• Participant : Here, the observer has direct contact with the group of people they are observing. The researcher becomes a member of the group they are researching.  
• Non-participant (aka “fly on the wall): The researcher does not have direct contact with the people being observed. The observation of participants’ behavior is from a distance

Pilot Study

A pilot  study is a small scale preliminary study conducted in order to evaluate the feasibility of the key s teps in a future, full-scale project.

A pilot study is an initial run-through of the procedures to be used in an investigation; it involves selecting a few people and trying out the study on them. It is possible to save time, and in some cases, money, by identifying any flaws in the procedures designed by the researcher.

A pilot study can help the researcher spot any ambiguities (i.e. unusual things) or confusion in the information given to participants or problems with the task devised.

Sometimes the task is too hard, and the researcher may get a floor effect, because none of the participants can score at all or can complete the task – all performances are low.

The opposite effect is a ceiling effect, when the task is so easy that all achieve virtually full marks or top performances and are “hitting the ceiling”.

Research Design

In cross-sectional research , a researcher compares multiple segments of the population at the same time

Sometimes, we want to see how people change over time, as in studies of human development and lifespan. Longitudinal research is a research design in which data-gathering is administered repeatedly over an extended period of time.

In cohort studies , the participants must share a common factor or characteristic such as age, demographic, or occupation. A cohort study is a type of longitudinal study in which researchers monitor and observe a chosen population over an extended period.

Triangulation means using more than one research method to improve the study’s validity.

Reliability

Reliability is a measure of consistency, if a particular measurement is repeated and the same result is obtained then it is described as being reliable.

• Test-retest reliability :  assessing the same person on two different occasions which shows the extent to which the test produces the same answers.
• Inter-observer reliability : the extent to which there is an agreement between two or more observers.

Meta-Analysis

A meta-analysis is a systematic review that involves identifying an aim and then searching for research studies that have addressed similar aims/hypotheses.

This is done by looking through various databases, and then decisions are made about what studies are to be included/excluded.

Strengths: Increases the conclusions’ validity as they’re based on a wider range.

Weaknesses: Research designs in studies can vary, so they are not truly comparable.

Peer Review

A researcher submits an article to a journal. The choice of the journal may be determined by the journal’s audience or prestige.

The journal selects two or more appropriate experts (psychologists working in a similar field) to peer review the article without payment. The peer reviewers assess: the methods and designs used, originality of the findings, the validity of the original research findings and its content, structure and language.

Feedback from the reviewer determines whether the article is accepted. The article may be: Accepted as it is, accepted with revisions, sent back to the author to revise and re-submit or rejected without the possibility of submission.

The editor makes the final decision whether to accept or reject the research report based on the reviewers comments/ recommendations.

Peer review is important because it prevent faulty data from entering the public domain, it provides a way of checking the validity of findings and the quality of the methodology and is used to assess the research rating of university departments.

Peer reviews may be an ideal, whereas in practice there are lots of problems. For example, it slows publication down and may prevent unusual, new work being published. Some reviewers might use it as an opportunity to prevent competing researchers from publishing work.

Some people doubt whether peer review can really prevent the publication of fraudulent research.

The advent of the internet means that a lot of research and academic comment is being published without official peer reviews than before, though systems are evolving on the internet where everyone really has a chance to offer their opinions and police the quality of research.

Types of Data

• Quantitative data is numerical data e.g. reaction time or number of mistakes. It represents how much or how long, how many there are of something. A tally of behavioral categories and closed questions in a questionnaire collect quantitative data.
• Qualitative data is virtually any type of information that can be observed and recorded that is not numerical in nature and can be in the form of written or verbal communication. Open questions in questionnaires and accounts from observational studies collect qualitative data.
• Primary data is first-hand data collected for the purpose of the investigation.
• Secondary data is information that has been collected by someone other than the person who is conducting the research e.g. taken from journals, books or articles.

Validity means how well a piece of research actually measures what it sets out to, or how well it reflects the reality it claims to represent.

Validity is whether the observed effect is genuine and represents what is actually out there in the world.

• Concurrent validity is the extent to which a psychological measure relates to an existing similar measure and obtains close results. For example, a new intelligence test compared to an established test.
• Face validity : does the test measure what it’s supposed to measure ‘on the face of it’. This is done by ‘eyeballing’ the measuring or by passing it to an expert to check.
• Ecological validit y is the extent to which findings from a research study can be generalized to other settings / real life.
• Temporal validity is the extent to which findings from a research study can be generalized to other historical times.

Features of Science

• Paradigm – A set of shared assumptions and agreed methods within a scientific discipline.
• Paradigm shift – The result of the scientific revolution: a significant change in the dominant unifying theory within a scientific discipline.
• Objectivity – When all sources of personal bias are minimised so not to distort or influence the research process.
• Empirical method – Scientific approaches that are based on the gathering of evidence through direct observation and experience.
• Replicability – The extent to which scientific procedures and findings can be repeated by other researchers.
• Falsifiability – The principle that a theory cannot be considered scientific unless it admits the possibility of being proved untrue.

Statistical Testing

A significant result is one where there is a low probability that chance factors were responsible for any observed difference, correlation, or association in the variables tested.

If our test is significant, we can reject our null hypothesis and accept our alternative hypothesis.

If our test is not significant, we can accept our null hypothesis and reject our alternative hypothesis. A null hypothesis is a statement of no effect.

In Psychology, we use p < 0.05 (as it strikes a balance between making a type I and II error) but p < 0.01 is used in tests that could cause harm like introducing a new drug.

A type I error is when the null hypothesis is rejected when it should have been accepted (happens when a lenient significance level is used, an error of optimism).

A type II error is when the null hypothesis is accepted when it should have been rejected (happens when a stringent significance level is used, an error of pessimism).

Ethical Issues

• Informed consent is when participants are able to make an informed judgment about whether to take part. It causes them to guess the aims of the study and change their behavior.
• To deal with it, we can gain presumptive consent or ask them to formally indicate their agreement to participate but it may invalidate the purpose of the study and it is not guaranteed that the participants would understand.
• Deception should only be used when it is approved by an ethics committee, as it involves deliberately misleading or withholding information. Participants should be fully debriefed after the study but debriefing can’t turn the clock back.
• All participants should be informed at the beginning that they have the right to withdraw if they ever feel distressed or uncomfortable.
• It causes bias as the ones that stayed are obedient and some may not withdraw as they may have been given incentives or feel like they’re spoiling the study. Researchers can offer the right to withdraw data after participation.
• Participants should all have protection from harm . The researcher should avoid risks greater than those experienced in everyday life and they should stop the study if any harm is suspected. However, the harm may not be apparent at the time of the study.
• Confidentiality concerns the communication of personal information. The researchers should not record any names but use numbers or false names though it may not be possible as it is sometimes possible to work out who the researchers were.

Related Articles

Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

A-Level Psychology

A-level Psychology AQA Revision Notes

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.4: The Alternative Hypothesis

• Last updated
• Save as PDF
• Page ID 195833

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

9 Chapter 9 Hypothesis testing

The first unit was designed to prepare you for hypothesis testing. In the first chapter we discussed the three major goals of statistics:

• Describe: connects to unit 1 with descriptive statistics and graphing
• Decide: connects to unit 1 knowing your data and hypothesis testing
• Predict: connects to hypothesis testing and unit 3

The remaining chapters will cover many different kinds of hypothesis tests connected to different inferential statistics. Needless to say, hypothesis testing is the central topic of this course. This lesson is important but that does not mean the same thing as difficult. There is a lot of new language we will learn about when conducting a hypothesis test. Some of the components of a hypothesis test are the topics we are already familiar with:

• Test statistics
• Probability
• Distribution of sample means

Hypothesis testing is an inferential procedure that uses data from a sample to draw a general conclusion about a population. It is a formal approach and a statistical method that uses sample data to evaluate hypotheses about a population. When interpreting a research question and statistical results, a natural question arises as to whether the finding could have occurred by chance. Hypothesis testing is a statistical procedure for testing whether chance (random events) is a reasonable explanation of an experimental finding. Once you have mastered the material in this lesson you will be used to solving hypothesis testing problems and the rest of the course will seem much easier. In this chapter, we will introduce the ideas behind the use of statistics to make decisions – in particular, decisions about whether a particular hypothesis is supported by the data.

Logic and Purpose of Hypothesis Testing

The statistician Ronald Fisher explained the concept of hypothesis testing with a story of a lady tasting tea. Fisher was a statistician from London and is noted as the first person to formalize the process of hypothesis testing. His elegantly simple “Lady Tasting Tea” experiment demonstrated the logic of the hypothesis test.

Figure 1. A depiction of the lady tasting tea Photo Credit

Fisher would often have afternoon tea during his studies. He usually took tea with a woman who claimed to be a tea expert. In particular, she told Fisher that she could tell which was poured first in the teacup, the milk or the tea, simply by tasting the cup. Fisher, being a scientist, decided to put this rather bizarre claim to the test. The lady accepted his challenge. Fisher brought her 8 cups of tea in succession; 4 cups would be prepared with the milk added first, and 4 with the tea added first. The cups would be presented in a random order unknown to the lady.

The lady would take a sip of each cup as it was presented and report which ingredient she believed was poured first. Using the laws of probability, Fisher determined the chances of her guessing all 8 cups correctly was 1/70, or about 1.4%. In other words, if the lady was indeed guessing there was a 1.4% chance of her getting all 8 cups correct. On the day of the experiment, Fisher had 8 cups prepared just as he had requested. The lady drank each cup and made her decisions for each one.

After the experiment, it was revealed that the lady got all 8 cups correct! Remember, had she been truly guessing, the chance of getting this result was 1.4%. Since this probability was so low , Fisher instead concluded that the lady could indeed differentiate between the milk or the tea being poured first. Fisher’s original hypothesis that she was just guessing was demonstrated to be false and was therefore rejected. The alternative hypothesis, that the lady could truly tell the cups apart, was then accepted as true.

This story demonstrates many components of hypothesis testing in a very simple way. For example, Fisher started with a hypothesis that the lady was guessing. He then determined that if she was indeed guessing, the probability of guessing all 8 right was very small, just 1.4%. Since that probability was so tiny, when she did get all 8 cups right, Fisher determined it was extremely unlikely she was guessing. A more reasonable conclusion was that the lady had the skill to tell the cups apart.

In hypothesis testing, we will always set up a particular hypothesis that we want to demonstrate to be true. We then use probability to determine the likelihood of our hypothesis is correct. If it appears our original hypothesis was wrong, we reject it and accept the alternative hypothesis. The alternative hypothesis is usually the opposite of our original hypothesis. In Fisher’s case, his original hypothesis was that the lady was guessing. His alternative hypothesis was the lady was not guessing.

This result does not prove that he does; it could be he was just lucky and guessed right 13 out of 16 times. But how plausible is the explanation that he was just lucky? To assess its plausibility, we determine the probability that someone who was just guessing would be correct 13/16 times or more. This probability can be computed to be 0.0106. This is a pretty low probability, and therefore someone would have to be very lucky to be correct 13 or more times out of 16 if they were just guessing. A low probability gives us more confidence there is evidence Bond can tell whether the drink was shaken or stirred. There is also still a chance that Mr. Bond was very lucky (more on this later!). The hypothesis that he was guessing is not proven false, but considerable doubt is cast on it. Therefore, there is strong evidence that Mr. Bond can tell whether a drink was shaken or stirred.

You may notice some patterns here:

• We have 2 hypotheses: the original (researcher prediction) and the alternative
• We collect data
• We determine how likley or unlikely the original hypothesis is to occur based on probability.
• We determine if we have enough evidence to support the original hypothesis and draw conclusions.

Now let’s being in some specific terminology:

Null hypothesis : In general, the null hypothesis, written H 0 (“H-naught”), is the idea that nothing is going on: there is no effect of our treatment, no relation between our variables, and no difference in our sample mean from what we expected about the population mean. The null hypothesis indicates that an apparent effect is due to chance. This is always our baseline starting assumption, and it is what we (typically) seek to reject . For mathematical notation, one uses =).

Alternative hypothesis : If the null hypothesis is rejected, then we will need some other explanation, which we call the alternative hypothesis, H A or H 1 . The alternative hypothesis is simply the reverse of the null hypothesis. Thus, our alternative hypothesis is the mathematical way of stating our research question.  In general, the alternative hypothesis (also called the research hypothesis)is there is an effect of treatment, the relation between variables, or differences in a sample mean compared to a population mean. The alternative hypothesis essentially shows evidence the findings are not due to chance.  It is also called the research hypothesis as this is the most common outcome a researcher is looking for: evidence of change, differences, or relationships. There are three options for setting up the alternative hypothesis, depending on where we expect the difference to lie. The alternative hypothesis always involves some kind of inequality (≠not equal, >, or <).

• If we expect a specific direction of change/differences/relationships, which we call a directional hypothesis , then our alternative hypothesis takes the form based on the research question itself.  One would expect a decrease in depression from taking an anti-depressant as a specific directional hypothesis.  Or the direction could be larger, where for example, one might expect an increase in exam scores after completing a student success exam preparation module.  The directional hypothesis (2 directions) makes up 2 of the 3 alternative hypothesis options.  The other alternative is to state there are differences/changes, or a relationship but not predict the direction.  We use a non-directional alternative hypothesis  (typically see ≠ for mathematical notation).

Probability value (p-value) : the probability of a certain outcome assuming a certain state of the world. In statistics, it is conventional to refer to possible states of the world as hypotheses since they are hypothesized states of the world. Using this terminology, the probability value is the probability of an outcome given the hypothesis. It is not the probability of the hypothesis given the outcome. It is very important to understand precisely what the probability values mean. In the James Bond example, the computed probability of 0.0106 is the probability he would be correct on 13 or more taste tests (out of 16) if he were just guessing. It is easy to mistake this probability of 0.0106 as the probability he cannot tell the difference. This is not at all what it means. The probability of 0.0106 is the probability of a certain outcome (13 or more out of 16) assuming a certain state of the world (James Bond was only guessing).

A low probability value casts doubt on the null hypothesis. How low must the probability value be in order to conclude that the null hypothesis is false? Although there is clearly no right or wrong answer to this question, it is conventional to conclude the null hypothesis is false if the probability value is less than 0.05 (p < .05). More conservative researchers conclude the null hypothesis is false only if the probability value is less than 0.01 (p<.01). When a researcher concludes that the null hypothesis is false, the researcher is said to have rejected the null hypothesis. The probability value below which the null hypothesis is rejected is called the α level or simply α (“alpha”). It is also called the significance level . If α is not explicitly specified, assume that α = 0.05.

Decision-making is part of the process and we have some language that goes along with that. Importantly, null hypothesis testing operates under the assumption that the null hypothesis is true unless the evidence shows otherwise. We (typically) seek to reject the null hypothesis, giving us evidence to support the alternative hypothesis .  If the probability of the outcome given the hypothesis is sufficiently low, we have evidence that the null hypothesis is false. Note that all probability calculations for all hypothesis tests center on the null hypothesis. In the James Bond example, the null hypothesis is that he cannot tell the difference between shaken and stirred martinis. The probability value is low that one is able to identify 13 of 16 martinis as shaken or stirred (0.0106), thus providing evidence that he can tell the difference. Note that we have not computed the probability that he can tell the difference.

The specific type of hypothesis testing reviewed is specifically known as null hypothesis statistical testing (NHST). We can break the process of null hypothesis testing down into a number of steps a researcher would use.

• Formulate a hypothesis that embodies our prediction ( before seeing the data )
• Specify null and alternative hypotheses
• Collect some data relevant to the hypothesis
• Compute a test statistic
• Identify the criteria probability (or compute the probability of the observed value of that statistic) assuming that the null hypothesis is true
• Drawing conclusions. Assess the “statistical significance” of the result

Steps in hypothesis testing

Step 1: formulate a hypothesis of interest.

The researchers hypothesized that physicians spend less time with obese patients. The researchers hypothesis derived from an identified population. In creating a research hypothesis, we also have to decide whether we want to test a directional or non-directional hypotheses. Researchers typically will select a non-directional hypothesis for a more conservative approach, particularly when the outcome is unknown (more about why this is later).

Step 2: Specify the null and alternative hypotheses

Can you set up the null and alternative hypotheses for the Physician’s Reaction Experiment?

Step 3: Determine the alpha level.

For this course, alpha will be given to you as .05 or .01.  Researchers will decide on alpha and then determine the associated test statistic based from the sample. Researchers in the Physician Reaction study might set the alpha at .05 and identify the test statistics associated with the .05 for the sample size.  Researchers might take extra precautions to be more confident in their findings (more on this later).

Step 4: Collect some data

For this course, the data will be given to you.  Researchers collect the data and then start to summarize it using descriptive statistics. The mean time physicians reported that they would spend with obese patients was 24.7 minutes as compared to a mean of 31.4 minutes for normal-weight patients.

Step 5: Compute a test statistic

We next want to use the data to compute a statistic that will ultimately let us decide whether the null hypothesis is rejected or not. We can think of the test statistic as providing a measure of the size of the effect compared to the variability in the data. In general, this test statistic will have a probability distribution associated with it, because that allows us to determine how likely our observed value of the statistic is under the null hypothesis.

To assess the plausibility of the hypothesis that the difference in mean times is due to chance, we compute the probability of getting a difference as large or larger than the observed difference (31.4 – 24.7 = 6.7 minutes) if the difference were, in fact, due solely to chance.

Step 6: Determine the probability of the observed result under the null hypothesis 

Using methods presented in later chapters, this probability associated with the observed differences between the two groups for the Physician’s Reaction was computed to be 0.0057. Since this is such a low probability, we have confidence that the difference in times is due to the patient’s weight (obese or not) (and is not due to chance). We can then reject the null hypothesis (there are no differences or differences seen are due to chance).

Keep in mind that the null hypothesis is typically the opposite of the researcher’s hypothesis. In the Physicians’ Reactions study, the researchers hypothesized that physicians would expect to spend less time with obese patients. The null hypothesis that the two types of patients are treated identically as part of the researcher’s control of other variables. If the null hypothesis were true, a difference as large or larger than the sample difference of 6.7 minutes would be very unlikely to occur. Therefore, the researchers rejected the null hypothesis of no difference and concluded that in the population, physicians intend to spend less time with obese patients.

This is the step where NHST starts to violate our intuition. Rather than determining the likelihood that the null hypothesis is true given the data, we instead determine the likelihood under the null hypothesis of observing a statistic at least as extreme as one that we have observed — because we started out by assuming that the null hypothesis is true! To do this, we need to know the expected probability distribution for the statistic under the null hypothesis, so that we can ask how likely the result would be under that distribution. This will be determined from a table we use for reference or calculated in a statistical analysis program. Note that when I say “how likely the result would be”, what I really mean is “how likely the observed result or one more extreme would be”. We need to add this caveat as we are trying to determine how weird our result would be if the null hypothesis were true, and any result that is more extreme will be even more weird, so we want to count all of those weirder possibilities when we compute the probability of our result under the null hypothesis.

Let’s review some considerations for Null hypothesis statistical testing (NHST)!

Null hypothesis statistical testing (NHST) is commonly used in many fields. If you pick up almost any scientific or biomedical research publication, you will see NHST being used to test hypotheses, and in their introductory psychology textbook, Gerrig & Zimbardo (2002) referred to NHST as the “backbone of psychological research”. Thus, learning how to use and interpret the results from hypothesis testing is essential to understand the results from many fields of research.

It is also important for you to know, however, that NHST is flawed, and that many statisticians and researchers think that it has been the cause of serious problems in science, which we will discuss in further in this unit. NHST is also widely misunderstood, largely because it violates our intuitions about how statistical hypothesis testing should work. Let’s look at an example to see this.

There is great interest in the use of body-worn cameras by police officers, which are thought to reduce the use of force and improve officer behavior. However, in order to establish this we need experimental evidence, and it has become increasingly common for governments to use randomized controlled trials to test such ideas. A randomized controlled trial of the effectiveness of body-worn cameras was performed by the Washington, DC government and DC Metropolitan Police Department in 2015-2016. Officers were randomly assigned to wear a body-worn camera or not, and their behavior was then tracked over time to determine whether the cameras resulted in less use of force and fewer civilian complaints about officer behavior.

Before we get to the results, let’s ask how you would think the statistical analysis might work. Let’s say we want to specifically test the hypothesis of whether the use of force is decreased by the wearing of cameras. The randomized controlled trial provides us with the data to test the hypothesis – namely, the rates of use of force by officers assigned to either the camera or control groups. The next obvious step is to look at the data and determine whether they provide convincing evidence for or against this hypothesis. That is: What is the likelihood that body-worn cameras reduce the use of force, given the data and everything else we know?

It turns out that this is not how null hypothesis testing works. Instead, we first take our hypothesis of interest (i.e. that body-worn cameras reduce use of force), and flip it on its head, creating a null hypothesis – in this case, the null hypothesis would be that cameras do not reduce use of force. Importantly, we then assume that the null hypothesis is true. We then look at the data, and determine how likely the data would be if the null hypothesis were true. If the data are sufficiently unlikely under the null hypothesis that we can reject the null in favor of the alternative hypothesis which is our hypothesis of interest. If there is not sufficient evidence to reject the null, then we say that we retain (or “fail to reject”) the null, sticking with our initial assumption that the null is true.

Understanding some of the concepts of NHST, particularly the notorious “p-value”, is invariably challenging the first time one encounters them, because they are so counter-intuitive. As we will see later, there are other approaches that provide a much more intuitive way to address hypothesis testing (but have their own complexities).

Step 7: Assess the “statistical significance” of the result. Draw conclusions.

The next step is to determine whether the p-value that results from the previous step is small enough that we are willing to reject the null hypothesis and conclude instead that the alternative is true. In the Physicians Reactions study, the probability value is 0.0057. Therefore, the effect of obesity is statistically significant and the null hypothesis that obesity makes no difference is rejected. It is very important to keep in mind that statistical significance means only that the null hypothesis of exactly no effect is rejected; it does not mean that the effect is important, which is what “significant” usually means. When an effect is significant, you can have confidence the effect is not exactly zero. Finding that an effect is significant does not tell you about how large or important the effect is.

How much evidence do we require and what considerations are needed to better understand the significance of the findings? This is one of the most controversial questions in statistics, in part because it requires a subjective judgment – there is no “correct” answer.

What does a statistically significant result mean?

There is a great deal of confusion about what p-values actually mean (Gigerenzer, 2004). Let’s say that we do an experiment comparing the means between conditions, and we find a difference with a p-value of .01. There are a number of possible interpretations that one might entertain.

Does it mean that the probability of the null hypothesis being true is .01? No. Remember that in null hypothesis testing, the p-value is the probability of the data given the null hypothesis. It does not warrant conclusions about the probability of the null hypothesis given the data.

Does it mean that the probability that you are making the wrong decision is .01? No. Remember as above that p-values are probabilities of data under the null, not probabilities of hypotheses.

Does it mean that if you ran the study again, you would obtain the same result 99% of the time? No. The p-value is a statement about the likelihood of a particular dataset under the null; it does not allow us to make inferences about the likelihood of future events such as replication.

Does it mean that you have found a practially important effect? No. There is an essential distinction between statistical significance and practical significance . As an example, let’s say that we performed a randomized controlled trial to examine the effect of a particular diet on body weight, and we find a statistically significant effect at p<.05. What this doesn’t tell us is how much weight was actually lost, which we refer to as the effect size (to be discussed in more detail). If we think about a study of weight loss, then we probably don’t think that the loss of one ounce (i.e. the weight of a few potato chips) is practically significant. Let’s look at our ability to detect a significant difference of 1 ounce as the sample size increases.

A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context and is often referred to as the effect size .

Many differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

Be aware that the term effect size can be misleading because it suggests a causal relationship—that the difference between the two means is an “effect” of being in one group or condition as opposed to another. In other words, simply calling the difference an “effect size” does not make the relationship a causal one.

Figure 1 shows how the proportion of significant results increases as the sample size increases, such that with a very large sample size (about 262,000 total subjects), we will find a significant result in more than 90% of studies when there is a 1 ounce difference in weight loss between the diets. While these are statistically significant, most physicians would not consider a weight loss of one ounce to be practically or clinically significant. We will explore this relationship in more detail when we return to the concept of statistical power in Chapter X, but it should already be clear from this example that statistical significance is not necessarily indicative of practical significance.

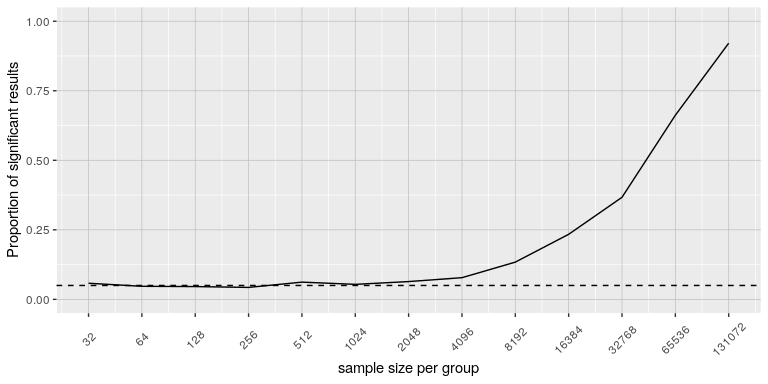
Figure 1: The proportion of significant results for a very small change (1 ounce, which is about .001 standard deviations) as a function of sample size.

Challenges with using p-values

Historically, the most common answer to this question has been that we should reject the null hypothesis if the p-value is less than 0.05. This comes from the writings of Ronald Fisher, who has been referred to as “the single most important figure in 20th century statistics” (Efron, 1998 ) :

“If P is between .1 and .9 there is certainly no reason to suspect the hypothesis tested. If it is below .02 it is strongly indicated that the hypothesis fails to account for the whole of the facts. We shall not often be astray if we draw a conventional line at .05 … it is convenient to draw the line at about the level at which we can say: Either there is something in the treatment, or a coincidence has occurred such as does not occur more than once in twenty trials” (Fisher, 1925 )

Fisher never intended p<0.05p < 0.05 to be a fixed rule:

“no scientific worker has a fixed level of significance at which from year to year, and in all circumstances, he rejects hypotheses; he rather gives his mind to each particular case in the light of his evidence and his ideas” (Fisher, 1956 )

Instead, it is likely that p < .05 became a ritual due to the reliance upon tables of p-values that were used before computing made it easy to compute p values for arbitrary values of a statistic. All of the tables had an entry for 0.05, making it easy to determine whether one’s statistic exceeded the value needed to reach that level of significance. Although we use tables in this class, statistical software examines the specific probability value for the calculated statistic.

Assessing Error Rate: Type I and Type II Error

Although there are challenges with p-values for decision making, we will examine a way we can think about hypothesis testing in terms of its error rate.  This was proposed by Jerzy Neyman and Egon Pearson:

“no test based upon a theory of probability can by itself provide any valuable evidence of the truth or falsehood of a hypothesis. But we may look at the purpose of tests from another viewpoint. Without hoping to know whether each separate hypothesis is true or false, we may search for rules to govern our behaviour with regard to them, in following which we insure that, in the long run of experience, we shall not often be wrong” (Neyman & Pearson, 1933 )

That is: We can’t know which specific decisions are right or wrong, but if we follow the rules, we can at least know how often our decisions will be wrong in the long run.

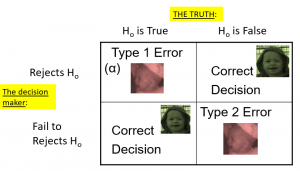
To understand the decision-making framework that Neyman and Pearson developed, we first need to discuss statistical decision-making in terms of the kinds of outcomes that can occur. There are two possible states of reality (H0 is true, or H0 is false), and two possible decisions (reject H0, or retain H0). There are two ways in which we can make a correct decision:

• We can reject H0 when it is false (in the language of signal detection theory, we call this a hit )
• We can retain H0 when it is true (somewhat confusingly in this context, this is called a correct rejection )

There are also two kinds of errors we can make:

• We can reject H0 when it is actually true (we call this a false alarm , or Type I error ), Type I error  means that we have concluded that there is a relationship in the population when in fact there is not. Type I errors occur because even when there is no relationship in the population, sampling error alone will occasionally produce an extreme result.
• We can retain H0 when it is actually false (we call this a miss , or Type II error ). Type II error  means that we have concluded that there is no relationship in the population when in fact there is.

Summing up, when you perform a hypothesis test, there are four possible outcomes depending on the actual truth (or falseness) of the null hypothesis H0 and the decision to reject or not. The outcomes are summarized in the following table:

Table 1. The four possible outcomes in hypothesis testing.

• The decision is not to reject H0 when H0 is true (correct decision).
• The decision is to reject H0 when H0 is true (incorrect decision known as a Type I error ).
• The decision is not to reject H0 when, in fact, H0 is false (incorrect decision known as a Type II error ).
• The decision is to reject H0 when H0 is false ( correct decision ).

Neyman and Pearson coined two terms to describe the probability of these two types of errors in the long run:

• P(Type I error) = αalpha
• P(Type II error) = βbeta

That is, if we set αalpha to .05, then in the long run we should make a Type I error 5% of the time. The 𝞪 (alpha) , is associated with the p-value for the level of significance. Again it’s common to set αalpha as .05. In fact, when the null hypothesis is true and α is .05, we will mistakenly reject the null hypothesis 5% of the time. (This is why α is sometimes referred to as the “Type I error rate.”) In principle, it is possible to reduce the chance of a Type I error by setting α to something less than .05. Setting it to .01, for example, would mean that if the null hypothesis is true, then there is only a 1% chance of mistakenly rejecting it. But making it harder to reject true null hypotheses also makes it harder to reject false ones and therefore increases the chance of a Type II error.

In practice, Type II errors occur primarily because the research design lacks adequate statistical power to detect the relationship (e.g., the sample is too small).  Statistical power is the complement of Type II error. We will have more to say about statistical power shortly. The standard value for an acceptable level of β (beta) is .2 – that is, we are willing to accept that 20% of the time we will fail to detect a true effect when it truly exists. It is possible to reduce the chance of a Type II error by setting α to something greater than .05 (e.g., .10). But making it easier to reject false null hypotheses also makes it easier to reject true ones and therefore increases the chance of a Type I error. This provides some insight into why the convention is to set α to .05. There is some agreement among researchers that level of α keeps the rates of both Type I and Type II errors at acceptable levels.

The possibility of committing Type I and Type II errors has several important implications for interpreting the results of our own and others’ research. One is that we should be cautious about interpreting the results of any individual study because there is a chance that it reflects a Type I or Type II error. This is why researchers consider it important to replicate their studies. Each time researchers replicate a study and find a similar result, they rightly become more confident that the result represents a real phenomenon and not just a Type I or Type II error.

Test Statistic Assumptions

Last consideration we will revisit with each test statistic (e.g., t-test, z-test and ANOVA) in the coming chapters.  There are four main assumptions. These assumptions are often taken for granted in using prescribed data for the course.  In the real world, these assumptions would need to be examined, often tested using statistical software.

• Assumption of random sampling. A sample is random when each person (or animal) point in your population has an equal chance of being included in the sample; therefore selection of any individual happens by chance, rather than by choice. This reduces the chance that differences in materials, characteristics or conditions may bias results. Remember that random samples are more likely to be representative of the population so researchers can be more confident interpreting the results. Note: there is no test that statistical software can perform which assures random sampling has occurred but following good sampling techniques helps to ensure your samples are random.
• Assumption of Independence. Statistical independence is a critical assumption for many statistical tests including the 2-sample t-test and ANOVA. It is assumed that observations are independent of each other often but often this assumption. Is not met. Independence means the value of one observation does not influence or affect the value of other observations. Independent data items are not connected with one another in any way (unless you account for it in your study). Even the smallest dependence in your data can turn into heavily biased results (which may be undetectable) if you violate this assumption. Note: there is no test statistical software can perform that assures independence of the data because this should be addressed during the research planning phase. Using a non-parametric test is often recommended if a researcher is concerned this assumption has been violated.
• Assumption of Normality. Normality assumes that the continuous variables (dependent variable) used in the analysis are normally distributed. Normal distributions are symmetric around the center (the mean) and form a bell-shaped distribution. Normality is violated when sample data are skewed. With large enough sample sizes (n > 30) the violation of the normality assumption should not cause major problems (remember the central limit theorem) but there is a feature in most statistical software that can alert researchers to an assumption violation.
• Assumption of Equal Variance. Variance refers to the spread or of scores from the mean. Many statistical tests assume that although different samples can come from populations with different means, they have the same variance. Equality of variance (i.e., homogeneity of variance) is violated when variances across different groups or samples are significantly different. Note: there is a feature in most statistical software to test for this.

We will use 4 main steps for hypothesis testing:

• Usually the hypotheses concern population parameters and predict the characteristics that a sample should have
• Null: Null hypothesis (H0) states that there is no difference, no effect or no change between population means and sample means. There is no difference.
• Alternative: Alternative hypothesis (H1 or HA) states that there is a difference or a change between the population and sample. It is the opposite of the null hypothesis.
• Set criteria for a decision. In this step we must determine the boundary of our distribution at which the null hypothesis will be rejected. Researchers usually use either a 5% (.05) cutoff or 1% (.01) critical boundary. Recall from our earlier story about Ronald Fisher that the lower the probability the more confident the was that the Tea Lady was not guessing.  We will apply this to z in the next chapter.
• Compare sample and population to decide if the hypothesis has support
• When a researcher uses hypothesis testing, the individual is making a decision about whether the data collected is sufficient to state that the population parameters are significantly different.

Further considerations

The probability value is the probability of a result as extreme or more extreme given that the null hypothesis is true. It is the probability of the data given the null hypothesis. It is not the probability that the null hypothesis is false.

A low probability value indicates that the sample outcome (or one more extreme) would be very unlikely if the null hypothesis were true. We will learn more about assessing effect size later in this unit.

3.  A non-significant outcome means that the data do not conclusively demonstrate that the null hypothesis is false. There is always a chance of error and 4 outcomes associated with hypothesis testing.

• It is important to take into account the assumptions for each test statistic.

Learning objectives

Having read the chapter, you should be able to:

• Identify the components of a hypothesis test, including the parameter of interest, the null and alternative hypotheses, and the test statistic.
• State the hypotheses and identify appropriate critical areas depending on how hypotheses are set up.
• Describe the proper interpretations of a p-value as well as common misinterpretations.
• Distinguish between the two types of error in hypothesis testing, and the factors that determine them.
• Describe the main criticisms of null hypothesis statistical testing
• Identify the purpose of effect size and power.

Exercises – Ch. 9

• In your own words, explain what the null hypothesis is.
• What are Type I and Type II Errors?
• Why do we phrase null and alternative hypotheses with population parameters and not sample means?
• If our null hypothesis is “H0: μ = 40”, what are the three possible alternative hypotheses?
• Why do we state our hypotheses and decision criteria before we collect our data?
• When and why do you calculate an effect size?

Answers to Odd- Numbered Exercises – Ch. 9

1. Your answer should include mention of the baseline assumption of no difference between the sample and the population.

3. Alpha is the significance level. It is the criteria we use when decided to reject or fail to reject the null hypothesis, corresponding to a given proportion of the area under the normal distribution and a probability of finding extreme scores assuming the null hypothesis is true.

5. μ > 40; μ < 40; μ ≠ 40

7. We calculate effect size to determine the strength of the finding.  Effect size should always be calculated when the we have rejected the null hypothesis.  Effect size can be calculated for non-significant findings as a possible indicator of Type II error.

Introduction to Statistics for Psychology Copyright © 2021 by Alisa Beyer is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

How to Write a Great Hypothesis

Hypothesis Definition, Format, Examples, and Tips

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Amy Morin, LCSW, is a psychotherapist and international bestselling author. Her books, including "13 Things Mentally Strong People Don't Do," have been translated into more than 40 languages. Her TEDx talk,  "The Secret of Becoming Mentally Strong," is one of the most viewed talks of all time.

Verywell / Alex Dos Diaz

• The Scientific Method

Hypothesis Format

Falsifiability of a hypothesis.

• Operationalization

Hypothesis Types

Hypotheses examples.

• Collecting Data

A hypothesis is a tentative statement about the relationship between two or more variables. It is a specific, testable prediction about what you expect to happen in a study. It is a preliminary answer to your question that helps guide the research process.

Consider a study designed to examine the relationship between sleep deprivation and test performance. The hypothesis might be: "This study is designed to assess the hypothesis that sleep-deprived people will perform worse on a test than individuals who are not sleep-deprived."

At a Glance

A hypothesis is crucial to scientific research because it offers a clear direction for what the researchers are looking to find. This allows them to design experiments to test their predictions and add to our scientific knowledge about the world. This article explores how a hypothesis is used in psychology research, how to write a good hypothesis, and the different types of hypotheses you might use.

The Hypothesis in the Scientific Method

In the scientific method , whether it involves research in psychology, biology, or some other area, a hypothesis represents what the researchers think will happen in an experiment. The scientific method involves the following steps:

• Forming a question
• Performing background research
• Creating a hypothesis
• Designing an experiment
• Collecting data
• Analyzing the results
• Drawing conclusions
• Communicating the results

The hypothesis is a prediction, but it involves more than a guess. Most of the time, the hypothesis begins with a question which is then explored through background research. At this point, researchers then begin to develop a testable hypothesis.

Unless you are creating an exploratory study, your hypothesis should always explain what you  expect  to happen.

In a study exploring the effects of a particular drug, the hypothesis might be that researchers expect the drug to have some type of effect on the symptoms of a specific illness. In psychology, the hypothesis might focus on how a certain aspect of the environment might influence a particular behavior.

Remember, a hypothesis does not have to be correct. While the hypothesis predicts what the researchers expect to see, the goal of the research is to determine whether this guess is right or wrong. When conducting an experiment, researchers might explore numerous factors to determine which ones might contribute to the ultimate outcome.

In many cases, researchers may find that the results of an experiment  do not  support the original hypothesis. When writing up these results, the researchers might suggest other options that should be explored in future studies.

In many cases, researchers might draw a hypothesis from a specific theory or build on previous research. For example, prior research has shown that stress can impact the immune system. So a researcher might hypothesize: "People with high-stress levels will be more likely to contract a common cold after being exposed to the virus than people who have low-stress levels."

In other instances, researchers might look at commonly held beliefs or folk wisdom. "Birds of a feather flock together" is one example of folk adage that a psychologist might try to investigate. The researcher might pose a specific hypothesis that "People tend to select romantic partners who are similar to them in interests and educational level."

Elements of a Good Hypothesis

So how do you write a good hypothesis? When trying to come up with a hypothesis for your research or experiments, ask yourself the following questions:

• Is your hypothesis based on your research on a topic?
• Can your hypothesis be tested?
• Does your hypothesis include independent and dependent variables?

Before you come up with a specific hypothesis, spend some time doing background research. Once you have completed a literature review, start thinking about potential questions you still have. Pay attention to the discussion section in the  journal articles you read . Many authors will suggest questions that still need to be explored.

How to Formulate a Good Hypothesis

To form a hypothesis, you should take these steps:

• Collect as many observations about a topic or problem as you can.
• Evaluate these observations and look for possible causes of the problem.
• Create a list of possible explanations that you might want to explore.
• After you have developed some possible hypotheses, think of ways that you could confirm or disprove each hypothesis through experimentation. This is known as falsifiability.

In the scientific method ,  falsifiability is an important part of any valid hypothesis. In order to test a claim scientifically, it must be possible that the claim could be proven false.

Students sometimes confuse the idea of falsifiability with the idea that it means that something is false, which is not the case. What falsifiability means is that  if  something was false, then it is possible to demonstrate that it is false.

One of the hallmarks of pseudoscience is that it makes claims that cannot be refuted or proven false.

The Importance of Operational Definitions

A variable is a factor or element that can be changed and manipulated in ways that are observable and measurable. However, the researcher must also define how the variable will be manipulated and measured in the study.

Operational definitions are specific definitions for all relevant factors in a study. This process helps make vague or ambiguous concepts detailed and measurable.

For example, a researcher might operationally define the variable " test anxiety " as the results of a self-report measure of anxiety experienced during an exam. A "study habits" variable might be defined by the amount of studying that actually occurs as measured by time.

These precise descriptions are important because many things can be measured in various ways. Clearly defining these variables and how they are measured helps ensure that other researchers can replicate your results.

Replicability

One of the basic principles of any type of scientific research is that the results must be replicable.

Replication means repeating an experiment in the same way to produce the same results. By clearly detailing the specifics of how the variables were measured and manipulated, other researchers can better understand the results and repeat the study if needed.

Some variables are more difficult than others to define. For example, how would you operationally define a variable such as aggression ? For obvious ethical reasons, researchers cannot create a situation in which a person behaves aggressively toward others.

To measure this variable, the researcher must devise a measurement that assesses aggressive behavior without harming others. The researcher might utilize a simulated task to measure aggressiveness in this situation.

Hypothesis Checklist

• Does your hypothesis focus on something that you can actually test?
• Does your hypothesis include both an independent and dependent variable?
• Can you manipulate the variables?
• Can your hypothesis be tested without violating ethical standards?

The hypothesis you use will depend on what you are investigating and hoping to find. Some of the main types of hypotheses that you might use include:

• Simple hypothesis : This type of hypothesis suggests there is a relationship between one independent variable and one dependent variable.
• Complex hypothesis : This type suggests a relationship between three or more variables, such as two independent and dependent variables.
• Null hypothesis : This hypothesis suggests no relationship exists between two or more variables.
• Alternative hypothesis : This hypothesis states the opposite of the null hypothesis.
• Statistical hypothesis : This hypothesis uses statistical analysis to evaluate a representative population sample and then generalizes the findings to the larger group.
• Logical hypothesis : This hypothesis assumes a relationship between variables without collecting data or evidence.

A hypothesis often follows a basic format of "If {this happens} then {this will happen}." One way to structure your hypothesis is to describe what will happen to the  dependent variable  if you change the  independent variable .

The basic format might be: "If {these changes are made to a certain independent variable}, then we will observe {a change in a specific dependent variable}."

A few examples of simple hypotheses:

• "Students who eat breakfast will perform better on a math exam than students who do not eat breakfast."
• "Students who experience test anxiety before an English exam will get lower scores than students who do not experience test anxiety."​
• "Motorists who talk on the phone while driving will be more likely to make errors on a driving course than those who do not talk on the phone."
• "Children who receive a new reading intervention will have higher reading scores than students who do not receive the intervention."

Examples of a complex hypothesis include:

• "People with high-sugar diets and sedentary activity levels are more likely to develop depression."
• "Younger people who are regularly exposed to green, outdoor areas have better subjective well-being than older adults who have limited exposure to green spaces."

Examples of a null hypothesis include:

• "There is no difference in anxiety levels between people who take St. John's wort supplements and those who do not."
• "There is no difference in scores on a memory recall task between children and adults."
• "There is no difference in aggression levels between children who play first-person shooter games and those who do not."

Examples of an alternative hypothesis:

• "People who take St. John's wort supplements will have less anxiety than those who do not."
• "Adults will perform better on a memory task than children."
• "Children who play first-person shooter games will show higher levels of aggression than children who do not." 

Collecting Data on Your Hypothesis

Once a researcher has formed a testable hypothesis, the next step is to select a research design and start collecting data. The research method depends largely on exactly what they are studying. There are two basic types of research methods: descriptive research and experimental research.

Descriptive Research Methods

Descriptive research such as  case studies ,  naturalistic observations , and surveys are often used when  conducting an experiment is difficult or impossible. These methods are best used to describe different aspects of a behavior or psychological phenomenon.

Once a researcher has collected data using descriptive methods, a  correlational study  can examine how the variables are related. This research method might be used to investigate a hypothesis that is difficult to test experimentally.

Experimental Research Methods

Experimental methods  are used to demonstrate causal relationships between variables. In an experiment, the researcher systematically manipulates a variable of interest (known as the independent variable) and measures the effect on another variable (known as the dependent variable).

Unlike correlational studies, which can only be used to determine if there is a relationship between two variables, experimental methods can be used to determine the actual nature of the relationship—whether changes in one variable actually  cause  another to change.

The hypothesis is a critical part of any scientific exploration. It represents what researchers expect to find in a study or experiment. In situations where the hypothesis is unsupported by the research, the research still has value. Such research helps us better understand how different aspects of the natural world relate to one another. It also helps us develop new hypotheses that can then be tested in the future.

Thompson WH, Skau S. On the scope of scientific hypotheses .  R Soc Open Sci . 2023;10(8):230607. doi:10.1098/rsos.230607

Taran S, Adhikari NKJ, Fan E. Falsifiability in medicine: what clinicians can learn from Karl Popper [published correction appears in Intensive Care Med. 2021 Jun 17;:].  Intensive Care Med . 2021;47(9):1054-1056. doi:10.1007/s00134-021-06432-z

Eyler AA. Research Methods for Public Health . 1st ed. Springer Publishing Company; 2020. doi:10.1891/9780826182067.0004

Nosek BA, Errington TM. What is replication ?  PLoS Biol . 2020;18(3):e3000691. doi:10.1371/journal.pbio.3000691

Aggarwal R, Ranganathan P. Study designs: Part 2 - Descriptive studies .  Perspect Clin Res . 2019;10(1):34-36. doi:10.4103/picr.PICR_154_18

Nevid J. Psychology: Concepts and Applications. Wadworth, 2013.

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 31 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

psychologyrocks

Hypotheses; directional and non-directional, what is the difference between an experimental and an alternative hypothesis.

Nothing much! If the study is a laboratory experiment then we can call the hypothesis “an experimental hypothesis”, where we make a prediction about how the IV causes an effect on the DV. If we have a non-experimental design, i.e. we are not able to manipulate the IV as in a natural or quasi-experiment , or if some other research method has been used, then we call it an “alternativehypothesis”, alternative to the null.

Directional hypothesis: A directional (or one tailed hypothesis) states which way you think the results are going to go, for example in an experimental study we might say…”Participants who have been deprived of sleep for 24 hours will have more cold symptoms in the following week after exposure to a virus than participants who have not been sleep deprived”; the hypothesis compares the two groups/conditions and states which one will ….have more/less, be quicker/slower, etc.

If we had a correlational study, the directional hypothesis would state whether we expect a positive or a negative correlation, we are stating how the two variables will be related to each other, e.g. there will be a positive correlation between the number of stressful life events experienced in the last year and the number of coughs and colds suffered, whereby the more life events you have suffered the more coughs and cold you will have had”. The directional hypothesis can also state a negative correlation, e.g. the higher the number of face-book friends, the lower the life satisfaction score “

Non-directional hypothesis: A non-directional (or two tailed hypothesis) simply states that there will be a difference between the two groups/conditions but does not say which will be greater/smaller, quicker/slower etc. Using our example above we would say “There will be a difference between the number of cold symptoms experienced in the following week after exposure to a virus for those participants who have been sleep deprived for 24 hours compared with those who have not been sleep deprived for 24 hours.”

When the study is correlational, we simply state that variables will be correlated but do not state whether the relationship will be positive or negative, e.g. there will be a significant correlation between variable A and variable B.

Null hypothesis The null hypothesis states that the alternative or experimental hypothesis is NOT the case, if your experimental hypothesis was directional you would say…

Participants who have been deprived of sleep for 24 hours will NOT have more cold symptoms in the following week after exposure to a virus than participants who have not been sleep deprived and any difference that does arise will be due to chance alone.

or with a directional correlational hypothesis….

There will NOT be a positive correlation between the number of stress life events experienced in the last year and the number of coughs and colds suffered, whereby the more life events you have suffered the more coughs and cold you will have had”

With a non-directional or  two tailed hypothesis…

There will be NO difference between the number of cold symptoms experienced in the following week after exposure to a virus for those participants who have been sleep deprived for 24 hours compared with those who have not been sleep deprived for 24 hours.

or for a correlational …

there will be NO correlation between variable A and variable B.

When it comes to conducting an inferential stats test, if you have a directional hypothesis , you must do a one tailed test to find out whether your observed value is significant. If you have a non-directional hypothesis , you must do a two tailed test .

Exam Techniques/Advice

• Remember, a decent hypothesis will contain two variables, in the case of an experimental hypothesis there will be an IV and a DV; in a correlational hypothesis there will be two co-variables
• both variables need to be fully operationalised to score the marks, that is you need to be very clear and specific about what you mean by your IV and your DV; if someone wanted to repeat your study, they should be able to look at your hypothesis and know exactly what to change between the two groups/conditions and exactly what to measure (including any units/explanation of rating scales etc, e.g. “where 1 is low and 7 is high”)
• double check the question, did it ask for a directional or non-directional hypothesis?
• if you were asked for a null hypothesis, make sure you always include the phrase “and any difference/correlation (is your study experimental or correlational?) that does arise will be due to chance alone”

Practice Questions:

• Mr Faraz wants to compare the levels of attendance between his psychology group and those of Mr Simon, who teaches a different psychology group. Which of the following is a suitable directional (one tailed) hypothesis for Mr Faraz’s investigation?

A There will be a difference in the levels of attendance between the two psychology groups.

B Students’ level of attendance will be higher in Mr Faraz’s group than Mr Simon’s group.

C Any difference in the levels of attendance between the two psychology groups is due to chance.

D The level of attendance of the students will depend upon who is teaching the groups.

2. Tracy works for the local council. The council is thinking about reducing the number of people it employs to pick up litter from the street. Tracy has been asked to carry out a study to see if having the streets cleaned at less regular intervals will affect the amount of litter the public will drop. She studies a street to compare how much litter is dropped at two different times, once when it has just been cleaned and once after it has not been cleaned for a month.

Write a fully operationalised non-directional (two-tailed) hypothesis for Tracy’s study. (2)

3. Jamila is conducting a practical investigation to look at gender differences in carrying out visuo-spatial tasks. She decides to give males and females a jigsaw puzzle and will time them to see who completes it the fastest. She uses a random sample of pupils from a local school to get her participants.

(a) Write a fully operationalised directional (one tailed) hypothesis for Jamila’s study. (2) (b) Outline one strength and one weakness of the random sampling method. You may refer to Jamila’s use of this type of sampling in your answer. (4)

4. Which of the following is a non-directional (two tailed) hypothesis?

A There is a difference in driving ability with men being better drivers than women

B Women are better at concentrating on more than one thing at a time than men

C Women spend more time doing the cooking and cleaning than men

D There is a difference in the number of men and women who participate in sports

Revision Activity

writing-hypotheses-revision-sheet

Quizizz link for teachers: https://quizizz.com/admin/quiz/5bf03f51add785001bc5a09e

Share this:

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.4: The Alternative Hypothesis

• Last updated
• Save as PDF
• Page ID 14493

• Foster et al.
• University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

If the null hypothesis is rejected, then we will need some other explanation, which we call the alternative hypothesis, \(H_A\) or \(H_1\). The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a directional hypothesis, then our alternative hypothesis takes the form:

\[\mathrm{H}_{\mathrm{A}}: \mu>7.47 \quad \text { or } \quad \mathrm{H}_{\mathrm{A}}: \mu<7.47 \nonumber \]

based on the research question itself. We should only use a directional hypothesis if we have good reason, based on prior observations or research, to suspect a particular direction. When we do not know the direction, such as when we are entering a new area of research, we use a non-directional alternative:

\[\mathrm{H}_{\mathrm{A}}: \mu \neq 7.47 \nonumber \]

We will set different criteria for rejecting the null hypothesis based on the directionality (greater than, less than, or not equal to) of the alternative. To understand why, we need to see where our criteria come from and how they relate to \(z\)-scores and distributions.

Writing hypotheses in words

As we alluded to in the null hypothesis section, we can write our hypotheses in word statements (in addition to the statements with symbols). These statements should be specific enough to the particular experiment or situation being referred to. That is, don't make them generic enough so that they would apply to any hypothesis test that you would conduct. 

Examples for how to write null and alternate hypotheses in words for directional and non-directional situations are given throughout the chapters. 

Contributors and Attributions

Foster et al.  (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)

• Privacy Policy

Home » What is a Hypothesis – Types, Examples and Writing Guide

What is a Hypothesis – Types, Examples and Writing Guide

Table of Contents

Definition:

Hypothesis is an educated guess or proposed explanation for a phenomenon, based on some initial observations or data. It is a tentative statement that can be tested and potentially proven or disproven through further investigation and experimentation.

Hypothesis is often used in scientific research to guide the design of experiments and the collection and analysis of data. It is an essential element of the scientific method, as it allows researchers to make predictions about the outcome of their experiments and to test those predictions to determine their accuracy.

Types of Hypothesis

Types of Hypothesis are as follows:

Research Hypothesis

A research hypothesis is a statement that predicts a relationship between variables. It is usually formulated as a specific statement that can be tested through research, and it is often used in scientific research to guide the design of experiments.

Null Hypothesis

The null hypothesis is a statement that assumes there is no significant difference or relationship between variables. It is often used as a starting point for testing the research hypothesis, and if the results of the study reject the null hypothesis, it suggests that there is a significant difference or relationship between variables.

Alternative Hypothesis

An alternative hypothesis is a statement that assumes there is a significant difference or relationship between variables. It is often used as an alternative to the null hypothesis and is tested against the null hypothesis to determine which statement is more accurate.

Directional Hypothesis

A directional hypothesis is a statement that predicts the direction of the relationship between variables. For example, a researcher might predict that increasing the amount of exercise will result in a decrease in body weight.

Non-directional Hypothesis

A non-directional hypothesis is a statement that predicts the relationship between variables but does not specify the direction. For example, a researcher might predict that there is a relationship between the amount of exercise and body weight, but they do not specify whether increasing or decreasing exercise will affect body weight.

Statistical Hypothesis

A statistical hypothesis is a statement that assumes a particular statistical model or distribution for the data. It is often used in statistical analysis to test the significance of a particular result.

Composite Hypothesis

A composite hypothesis is a statement that assumes more than one condition or outcome. It can be divided into several sub-hypotheses, each of which represents a different possible outcome.

Empirical Hypothesis

An empirical hypothesis is a statement that is based on observed phenomena or data. It is often used in scientific research to develop theories or models that explain the observed phenomena.

Simple Hypothesis

A simple hypothesis is a statement that assumes only one outcome or condition. It is often used in scientific research to test a single variable or factor.

Complex Hypothesis

A complex hypothesis is a statement that assumes multiple outcomes or conditions. It is often used in scientific research to test the effects of multiple variables or factors on a particular outcome.

Applications of Hypothesis

Hypotheses are used in various fields to guide research and make predictions about the outcomes of experiments or observations. Here are some examples of how hypotheses are applied in different fields:

• Science : In scientific research, hypotheses are used to test the validity of theories and models that explain natural phenomena. For example, a hypothesis might be formulated to test the effects of a particular variable on a natural system, such as the effects of climate change on an ecosystem.
• Medicine : In medical research, hypotheses are used to test the effectiveness of treatments and therapies for specific conditions. For example, a hypothesis might be formulated to test the effects of a new drug on a particular disease.
• Psychology : In psychology, hypotheses are used to test theories and models of human behavior and cognition. For example, a hypothesis might be formulated to test the effects of a particular stimulus on the brain or behavior.
• Sociology : In sociology, hypotheses are used to test theories and models of social phenomena, such as the effects of social structures or institutions on human behavior. For example, a hypothesis might be formulated to test the effects of income inequality on crime rates.
• Business : In business research, hypotheses are used to test the validity of theories and models that explain business phenomena, such as consumer behavior or market trends. For example, a hypothesis might be formulated to test the effects of a new marketing campaign on consumer buying behavior.
• Engineering : In engineering, hypotheses are used to test the effectiveness of new technologies or designs. For example, a hypothesis might be formulated to test the efficiency of a new solar panel design.

How to write a Hypothesis

Here are the steps to follow when writing a hypothesis:

Identify the Research Question

The first step is to identify the research question that you want to answer through your study. This question should be clear, specific, and focused. It should be something that can be investigated empirically and that has some relevance or significance in the field.

Conduct a Literature Review

Before writing your hypothesis, it’s essential to conduct a thorough literature review to understand what is already known about the topic. This will help you to identify the research gap and formulate a hypothesis that builds on existing knowledge.

Determine the Variables

The next step is to identify the variables involved in the research question. A variable is any characteristic or factor that can vary or change. There are two types of variables: independent and dependent. The independent variable is the one that is manipulated or changed by the researcher, while the dependent variable is the one that is measured or observed as a result of the independent variable.

Formulate the Hypothesis

Based on the research question and the variables involved, you can now formulate your hypothesis. A hypothesis should be a clear and concise statement that predicts the relationship between the variables. It should be testable through empirical research and based on existing theory or evidence.

Write the Null Hypothesis

The null hypothesis is the opposite of the alternative hypothesis, which is the hypothesis that you are testing. The null hypothesis states that there is no significant difference or relationship between the variables. It is important to write the null hypothesis because it allows you to compare your results with what would be expected by chance.

Refine the Hypothesis

After formulating the hypothesis, it’s important to refine it and make it more precise. This may involve clarifying the variables, specifying the direction of the relationship, or making the hypothesis more testable.

Examples of Hypothesis

Here are a few examples of hypotheses in different fields:

• Psychology : “Increased exposure to violent video games leads to increased aggressive behavior in adolescents.”
• Biology : “Higher levels of carbon dioxide in the atmosphere will lead to increased plant growth.”
• Sociology : “Individuals who grow up in households with higher socioeconomic status will have higher levels of education and income as adults.”
• Education : “Implementing a new teaching method will result in higher student achievement scores.”
• Marketing : “Customers who receive a personalized email will be more likely to make a purchase than those who receive a generic email.”
• Physics : “An increase in temperature will cause an increase in the volume of a gas, assuming all other variables remain constant.”
• Medicine : “Consuming a diet high in saturated fats will increase the risk of developing heart disease.”

Purpose of Hypothesis

The purpose of a hypothesis is to provide a testable explanation for an observed phenomenon or a prediction of a future outcome based on existing knowledge or theories. A hypothesis is an essential part of the scientific method and helps to guide the research process by providing a clear focus for investigation. It enables scientists to design experiments or studies to gather evidence and data that can support or refute the proposed explanation or prediction.

The formulation of a hypothesis is based on existing knowledge, observations, and theories, and it should be specific, testable, and falsifiable. A specific hypothesis helps to define the research question, which is important in the research process as it guides the selection of an appropriate research design and methodology. Testability of the hypothesis means that it can be proven or disproven through empirical data collection and analysis. Falsifiability means that the hypothesis should be formulated in such a way that it can be proven wrong if it is incorrect.

In addition to guiding the research process, the testing of hypotheses can lead to new discoveries and advancements in scientific knowledge. When a hypothesis is supported by the data, it can be used to develop new theories or models to explain the observed phenomenon. When a hypothesis is not supported by the data, it can help to refine existing theories or prompt the development of new hypotheses to explain the phenomenon.

When to use Hypothesis

Here are some common situations in which hypotheses are used:

• In scientific research , hypotheses are used to guide the design of experiments and to help researchers make predictions about the outcomes of those experiments.
• In social science research , hypotheses are used to test theories about human behavior, social relationships, and other phenomena.
• I n business , hypotheses can be used to guide decisions about marketing, product development, and other areas. For example, a hypothesis might be that a new product will sell well in a particular market, and this hypothesis can be tested through market research.

Characteristics of Hypothesis

Here are some common characteristics of a hypothesis:

• Testable : A hypothesis must be able to be tested through observation or experimentation. This means that it must be possible to collect data that will either support or refute the hypothesis.
• Falsifiable : A hypothesis must be able to be proven false if it is not supported by the data. If a hypothesis cannot be falsified, then it is not a scientific hypothesis.
• Clear and concise : A hypothesis should be stated in a clear and concise manner so that it can be easily understood and tested.
• Based on existing knowledge : A hypothesis should be based on existing knowledge and research in the field. It should not be based on personal beliefs or opinions.
• Specific : A hypothesis should be specific in terms of the variables being tested and the predicted outcome. This will help to ensure that the research is focused and well-designed.
• Tentative: A hypothesis is a tentative statement or assumption that requires further testing and evidence to be confirmed or refuted. It is not a final conclusion or assertion.
• Relevant : A hypothesis should be relevant to the research question or problem being studied. It should address a gap in knowledge or provide a new perspective on the issue.

Advantages of Hypothesis

Hypotheses have several advantages in scientific research and experimentation:

• Guides research: A hypothesis provides a clear and specific direction for research. It helps to focus the research question, select appropriate methods and variables, and interpret the results.
• Predictive powe r: A hypothesis makes predictions about the outcome of research, which can be tested through experimentation. This allows researchers to evaluate the validity of the hypothesis and make new discoveries.
• Facilitates communication: A hypothesis provides a common language and framework for scientists to communicate with one another about their research. This helps to facilitate the exchange of ideas and promotes collaboration.
• Efficient use of resources: A hypothesis helps researchers to use their time, resources, and funding efficiently by directing them towards specific research questions and methods that are most likely to yield results.
• Provides a basis for further research: A hypothesis that is supported by data provides a basis for further research and exploration. It can lead to new hypotheses, theories, and discoveries.
• Increases objectivity: A hypothesis can help to increase objectivity in research by providing a clear and specific framework for testing and interpreting results. This can reduce bias and increase the reliability of research findings.

Limitations of Hypothesis

Some Limitations of the Hypothesis are as follows:

• Limited to observable phenomena: Hypotheses are limited to observable phenomena and cannot account for unobservable or intangible factors. This means that some research questions may not be amenable to hypothesis testing.
• May be inaccurate or incomplete: Hypotheses are based on existing knowledge and research, which may be incomplete or inaccurate. This can lead to flawed hypotheses and erroneous conclusions.
• May be biased: Hypotheses may be biased by the researcher’s own beliefs, values, or assumptions. This can lead to selective interpretation of data and a lack of objectivity in research.
• Cannot prove causation: A hypothesis can only show a correlation between variables, but it cannot prove causation. This requires further experimentation and analysis.
• Limited to specific contexts: Hypotheses are limited to specific contexts and may not be generalizable to other situations or populations. This means that results may not be applicable in other contexts or may require further testing.
• May be affected by chance : Hypotheses may be affected by chance or random variation, which can obscure or distort the true relationship between variables.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Data Collection – Methods Types and Examples

Delimitations in Research – Types, Examples and...

Research Process – Steps, Examples and Tips

Research Design – Types, Methods and Examples

Institutional Review Board – Application Sample...

Evaluating Research – Process, Examples and...

Statistics Made Easy

What is an Alternative Hypothesis in Statistics?

Often in statistics we want to test whether or not some assumption is true about a population parameter .

For example, we might assume that the mean weight of a certain population of turtle is 300 pounds.

To determine if this assumption is true, we’ll go out and collect a sample of turtles and weigh each of them. Using this sample data, we’ll conduct a hypothesis test .

The first step in a hypothesis test is to define the  null and  alternative hypotheses .

These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

These two hypotheses are defined as follows:

Null hypothesis (H 0 ): The sample data is consistent with the prevailing belief about the population parameter.

Alternative hypothesis (H A ): The sample data suggests that the assumption made in the null hypothesis is not true. In other words, there is some non-random cause influencing the data.

Types of Alternative Hypotheses

There are two types of alternative hypotheses:

A  one-tailed hypothesis involves making a “greater than” or “less than ” statement. For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches.

The null and alternative hypotheses in this case would be:

• Null hypothesis: µ ≥ 70 inches
• Alternative hypothesis: µ < 70 inches

A  two-tailed hypothesis involves making an “equal to” or “not equal to” statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches.

• Null hypothesis: µ = 70 inches
• Alternative hypothesis: µ ≠ 70 inches

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Examples of Alternative Hypotheses

The following examples illustrate how to define the null and alternative hypotheses for different research problems.

Example 1: A biologist wants to test if the mean weight of a certain population of turtle is different from the widely-accepted mean weight of 300 pounds.

The null and alternative hypothesis for this research study would be:

• Null hypothesis: µ = 300 pounds
• Alternative hypothesis: µ ≠ 300 pounds

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight of this population of turtles is different from 300 pounds.

Example 2: An engineer wants to test whether a new battery can produce higher mean watts than the current industry standard of 50 watts.

• Null hypothesis: µ ≤ 50 watts
• Alternative hypothesis: µ > 50 watts

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean watts produced by the new battery is greater than the current industry standard of 50 watts.

Example 3: A botanist wants to know if a new gardening method produces less waste than the standard gardening method that produces 20 pounds of waste.

• Null hypothesis: µ ≥ 20 pounds
• Alternative hypothesis: µ < 20 pounds

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight produced by this new gardening method is less than 20 pounds.

When to Reject the Null Hypothesis

Whenever we conduct a hypothesis test, we use sample data to calculate a test-statistic and a corresponding p-value.

If the p-value is less than some significance level (common choices are 0.10, 0.05, and 0.01), then we reject the null hypothesis.

This means we have sufficient evidence from the sample data to say that the assumption made by the null hypothesis is not true.

If the p-value is  not less than some significance level, then we fail to reject the null hypothesis.

This means our sample data did not provide us with evidence that the assumption made by the null hypothesis was not true.

Additional Resource:   An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Aims And Hypotheses, Directional And Non-Directional

March 7, 2021 - paper 2 psychology in context | research methods.

• Back to Paper 2 - Research Methods

In Psychology, hypotheses are predictions made by the researcher about the outcome of a study. The research can chose to make a specific prediction about what they feel will happen in their research (a directional hypothesis) or they can make a ‘general,’ ‘less specific’ prediction about the outcome of their research (a non-directional hypothesis). The type of prediction that a researcher makes is usually dependent on whether or not any previous research has also investigated their research aim.

Variables Recap:

The  independent variable  (IV)  is the variable that psychologists  manipulate/change  to see if changing this variable has an effect on the  depen dent variable  (DV).

The  dependent variable (DV)  is the variable that the psychologists  measures  (to see if the IV has had an effect).

It is important that the only variable that is changed in research is the  independent variable (IV),   all other variables have to be kept constant across the control condition and the experimental conditions. Only then will researchers be able to observe the true effects of  just  the independent variable (IV) on the dependent variable (DV).

Research/Experimental Aim(S):

An aim is a clear and precise statement of the purpose of the study. It is a statement of why a research study is taking place. This should include what is being studied and what the study is trying to achieve. (e.g. “This study aims to investigate the effects of alcohol on reaction times”.

It is important that aims created in research are realistic and ethical.

Hypotheses:

This is a testable statement that predicts what the researcher expects to happen in their research. The research study itself is therefore a means of testing whether or not the hypothesis is supported by the findings. If the findings do support the hypothesis then the hypothesis can be retained (i.e., accepted), but if not, then it must be rejected.

Three Different Hypotheses:

We're not around right now. But you can send us an email and we'll get back to you, asap.

Start typing and press Enter to search

Cookie Policy - Terms and Conditions - Privacy Policy

In this post

Before carrying out their research, most psychologists will make a prediction about what will happen. This is known as a hypothesis, which is a statement regarding what the psychologist believes will or should happen at the end of the study. For example, a psychologist may predict that children who listen to music whilst revising will do better in their exams than those children who do not.

There are two types of hypotheses, which are null hypotheses and alternative hypotheses, both of which we will look at now in more detail.

What is a null hypothesis?

A null hypothesis predicts that there will be no pattern or trend in results. In other words, it predicts no difference and no correlation . (A correlation is a relationship between two or more things.)

Before starting their research, psychologists usually have both a null and an alternative hypothesis and their aim is to find out which one is correct. Once they have identified which one is correct they will reject the other, as this one will not be supported by their research findings.

What is an alternative hypothesis?

Unlike a null hypothesis, an alternative hypothesis predicts that there will be a difference or a correlation between two or more things. In other words, an alternative hypothesis predicts some kind of pattern or trend in results. Have a look at the following alternative hypotheses, which are based around the core studies within this course:

• Participants will be able to accurately recall more information at the start and end of a list than in the middle
• Children whose efforts are praised are more likely to grow up with a growth mindset than those who are praised personally
• Children are more likely to behave aggressively when they witnessed an aggressive adult role model
• Children under the age of eight are more likely to be egocentric than those who are over the age of eight.

It will help you in the exam, if you are asked to write some form of hypothesis, if you begin a null hypothesis with “there will be no…” and an alternative hypothesis with “there will be a…”. There are usually two marks available for writing a hypothesis correctly. One mark will be for knowing whether it is predicting a different or a correlation or not and the other mark will be for stating the rest of the hypothesis, i.e. the variables, which must be done in a clear and accurate way.

Interested in a Psychology GCSE?

We offer the Edexcel GCSE in Psychology through our online campus.

Learn more about our Psychology GCSE courses

Read another one of our posts

Understanding dementia: types, symptoms, and care needs.

A Comprehensive Guide to Health and Social Care Training

Understanding and Supporting Mental Health Conditions

The Role of Diet in Managing Chronic Diseases

Effective Communication Skills in Health and Social Care

Understanding Animal Training – Positive Reinforcement Techniques

Key Skills for Successful Care Home Management

Save your cart?

Introduction to Hypothesis Testing (Psychology)

Contents Toggle Main Menu 1 What is a Hypothesis test? 2 The Null and Alternative Hypotheses 3 The Structure of a Hypothesis Test 3.1 Summary of Steps for a Hypothesis Test 4 P -Values 5 Parametric and Non-Parametric Hypothesis Tests 6 One and two tailed tests 7 Type I and Type II Errors 8 See Also 9 Worksheets

What is a Hypothesis test?

A statistical hypothesis is an unproven statement which can be tested. A hypothesis test is used to test whether this statement is true.

The Null and Alternative Hypotheses

• The null hypothesis $H_0$, is where you assume that the observations are statistically independent i.e. no difference in the populations you are testing. If the null hypothesis is true, it suggests that any changes witnessed in an experiment are because of random chance and not because of changes made to variables in the experiment. For example, serotonin levels have no effect on ability to cope with stress. See also Null and alternative hypotheses .
• The alternative hypothesis $H_1$, is a theory that the observations are related (not independent) in some way. We only adopt the alternative hypothesis if we have rejected the null hypothesis. For example, serotonin levels affect a person's ability to cope with stress. You do not necessarily have to specify in what way they are related but can do (see one and two tailed tests for more information).

The Structure of a Hypothesis Test

• The first step of a hypothesis test is to state the null hypothesis $H_0$ and the alternative hypothesis $H_1$ . The null hypothesis is the statement or claim being made (which we are trying to disprove) and the alternative hypothesis is the hypothesis that we are trying to prove and which is accepted if we have sufficient evidence to reject the null hypothesis.

For example, consider a person in court who is charged with murder. The jury needs to decide whether the person in innocent (the null hypothesis) or guilty (the alternative hypothesis). As usual, we assume the person is innocent unless the jury can provide sufficient evidence that the person is guilty. Similarly, we assume that $H_0$ is true unless we can provide sufficient evidence that it is false and that $H_1$ is true, in which case we reject $H_0$ and accept $H_1$.

To decide if we have sufficient evidence against the null hypothesis to reject it (in favour of the alternative hypothesis), we must first decide upon a significance level . The significance level is the probability of rejecting the null hypothesis when it the null hypothesis is true and is denoted by $\alpha$. The $5\%$ significance level is a common choice for statistical test.

The next step is to collect data and calculate the test statistic and associated $p$-value using the data. Assuming that the null hypothesis is true, the $p$-value is the probability of obtaining a sample statistic equal to or more extreme than the observed test statistic.

Next we must compare the $p$-value with the chosen significance level. If $p \lt \alpha$ then we reject $H_0$ and accept $H_1$. The lower $p$, the more evidence we have against $H_0$ and so the more confidence we can have that $H_0$ is false. If $p \geq \alpha$ then we do not have sufficient evidence to reject the $H_0$ and so must accept it.

Alternatively, we can compare our test statistic with the appropriate critical value for the chosen significance level. We can look up critical values in distribution tables (see worked examples below). If our test statistic is:

• positive and greater than the critical value, then we have sufficient evidence to reject the null hypothesis and accept the alternative hypothesis.
• positive and lower than or equal to the critical value, we must accept the null hypothesis.
• negative and lower than the critical value, then we have sufficient evidence to reject the null hypothesis and accept the alternative hypothesis.
• negative and greater than or equal to the critical value, we must accept the null hypothesis.

For either method:

Significant difference found: Reject the null hypothesis No significant difference found: Accept the null hypothesis

Finally, we must interpret our results and come to a conclusion. Returning to the example of the person in court, if the result of our hypothesis test indicated that we should accept $H_1$ and reject $H_0$, our conclusion would be that the jury should declare the person guilty of murder.

Summary of Steps for a Hypothesis Test

• Specify the null and the alternative hypothesis
• Decide upon the significance level.
• Comparing the $p$-value to the significance level $\alpha$, or
• Comparing the test statistic to the critical value.
• Interpret your results and draw a conclusion

P -Values"> P -Values

The $p$ -value is the probability of the test statistic (e.g. t -value or Chi-Square value) occurring given the null hypothesis is true. Since it is a probability, the $p$-value is a number between $0$ and $1$.

• Typically $p \leq 0.05$ shows that there is strong evidence for $H_1$ so we can accept it and reject $H_0$. Any $p$-value less than $0.05$ is significant and $p$-values less than $0.01$ are very significant .
• Typically $ p > 0.05$ shows that there is poor evidence for $H_1$ so we reject it and accept $H_0$.
• The smaller the $p$-value the more evidence there is supporting the hypothesis.
• The rule for accepting and rejecting the hypothesis is:

\begin{align} \text {Significant difference found} &= \textbf{Reject}\text{ the null hypothesis}\\ \text {No Significant difference found} &= \textbf{Accept}\text{ the null hypothesis}\\ \end{align}

• Note : The significance level is not always $0.05$. It can differ depending on the application and is often subjective (different people will have different opinions on what values are appropriate). For example, if lives are at stake then the $p$-value must be very small for safety reasons.
• See $P$-values for further detail on this topic.

Parametric and Non-Parametric Hypothesis Tests

There are parametric and non-parametric hypothesis tests.

• A parametric hypothesis assumes that the data follows a Normal probability distribution (with equal variances if we are working with more than one set of data) . A parametric hypothesis test is a statement about the parameters of this distribution (typically the mean). This can be seen in more detail in the Parametric Hypotheses Tests section .
• A non-parametric test assumes that the data does not follow any distribution and usually bases its calculations on the median . Note that although we assume the data does not follow a particular distribution it may do anyway. This can be seen in more detail in the Non-Parametric Hypotheses Tests section .

One and two tailed tests

Whether a test is One-tailed or Two-tailed is appropriate depends upon the alternative hypothesis $H_1$.

• One-tailed tests are used when the alternative hypothesis states that the parameter of interest is either bigger or smaller than the value stated in the null hypothesis. For example, the null hypothesis might state that the average weight of chocolate bars produced by a chocolate factory in Slough is 35g (as is printed on the wrapper), while the alternative hypothesis might state that the average weight of the chocolate bars is in fact lower than 35g.
• Two-tailed tests are used when the hypothesis states that the parameter of interest differs from the null hypothesis but does not specify in which direction. In the above example, a Two-tailed alternative hypothesis would be that the average weight of the chocolate bars is not equal to 35g.

Type I and Type II Errors

• A Type I error is made if we reject the null hypothesis when it is true (so should have been accepted). Returning to the example of the person in court, a Type I error would be made if the jury declared the person guilty when they are in fact innocent. The probability of making a Type I error is equal to the significance level $\alpha$.
• A Type II error is made if we accept the null hypothesis when it is false i.e. we should have rejected the null hypothesis and accepted the alternative hypothesis. This would occur if the jury declared the person innocent when they are in fact guilty.

For more information about the topics covered here see hypothesis testing .

• Introduction to hypothesis testing
• Binomial tests

• Gottesman & Shields AO1 AO3
• Kety AO1 AO3
• Evolutionary Psychology AO1 AO2 AO3
• Drugs & the Brain AO1 AO2 AO3
• Brendgen AO1 AO3
• Development (Maturation) AO1 AO2 AO3
• Aggression & Freud AO1 AO2 AO3
• Development & Freud AO1 AO2 AO3
• Individual Differences & Freud AO1 AO2 AO3
• Raine AO1 AO3
• Biological Key Question AO1 AO2
• Baddeley AO1 AO3
• Multi Store Model AO1 AO2 AO3
• Reconstructive Memory AO1 AO2 AO3
• Schmolck AO1 AO3
• Tulving's Long Term Memory AO1 AO2 AO3
• Working Memory AO1 AO2 AO3
• Cognitive Key Question AO1 AO2
• Bandura AO3
• Becker AO1 AO3
• Classical Conditioning AO1 AO2 AO3
• Operant Conditioning AO1 AO2 AO3
• Pavlov AO1 AO3
• Social Learning AO1 AO2 AO3
• Systematic Desensitisation
• Watson & Rayner AO1 AO3
• Learning Key Question AO1 AO2
• Agency Theory AO1 AO2 AO3
• Burger AO1 AO3
• Situational Factors AO1 AO2 AO3
• Milgram AO3
• Realistic Conflict Theory AO1 AO2 AO3
• Social Impact Theory AO1 AO2 AO3
• Social Identity Theory AO1 AO2 AO3
• Social Key Question AO1 AO2
• Biological Explanation AO1 AO2
• Non-Biological Explanation AO1 AO2
• Biological Treatment AO1 AO2
• Psychological Treatment AO1 AO2
• Diagnosing Abnormality AO1 AO2 AO3
• Diagnostic Manuals AO1 AO2 AO3
• Carlsson AO1 AO3
• Kroenke AO1 AO3
• HCPC Guidelines AO1 AO2 AO3
• Rosenhan AO1 AO3
• Non-biological Explanation AO1 AO2
• Biological Treatments AO1 AO2
• Clinical Key Question AO1 AO2
• Social Control AO2 AO3
• Ethics AO1 AO2 AO3
• Personality AO1 AO2 AO3
• Mental Health Differences AO1 AO2 AO3
• Differences in Obedience & Prejudice AO1 AO2 AO3
• Loftus study AO1 AO2 AO3
• Nature vs Nurture AO1 AO2 AO3
• Scientific Status AO1 AO2
• Animal Studies AO1 AO2 AO3
• Bradshaw AO1 AO3
• Scoville & Milner AO1 AO3
• Content Analyses AO1 AO2 AO3
• Experimental Method AO1 AO2 AO3
• Experimental Variables AO1 AO2
• Hypotheses AO1 AO2
• Chi-Squared Test AO1 AO2
• Mann-Whitney U Test AO1 AO2
• Spearman's Rho AO1 AO2
• Wilcoxon Test AO1 AO2
• Longitudinal Design AO1 AO2 AO3
• Quantitative Data & Analysis AO1 AO2 AO3
• Research Design AO1 AO2 AO3
• Sampling AO1 AO2 AO3
• Brown et al. AO1 AO3