what is predictor variable in research

Predictor Variable

Understanding Predictor Variables in Statistical Modeling

In the realm of statistical analysis and machine learning , a predictor variable plays a pivotal role. It is a variable that is used to forecast or predict the outcome of another variable, which is typically referred to as the response or dependent variable. Predictor variables are the features or factors that are believed to influence the dependent variable, and they are used in a variety of statistical models, including linear regression , logistic regression , and various machine learning algorithms.

What is a Predictor Variable?

A predictor variable, also known as an independent variable, is an input or factor that is used to predict the value of a dependent variable. It is the aspect of an experiment or data set that is manipulated or measured to determine its effects on the dependent variable. In a statistical model, the predictor variable is the variable that is being used to explain the variability in the dependent variable or to predict future values of the dependent variable.

Types of Predictor Variables

Predictor variables can be of various types, including:

These are variables that represent quantitative data and can be measured on a numerical scale. They can be further classified into discrete variables (countable, like the number of children in a family) and continuous variables (measurable, like height or weight).

• Categorical Variables : These represent qualitative data and describe categories or groups to which data points belong, such as gender, color, or type of car.
• Ordinal Variables : These are categorical variables that have a clear order or ranking, like socioeconomic status (low, middle, high) or education level (high school, bachelor's, master's, PhD).
• Binary Variables : These are a special type of categorical variable with only two categories or levels, such as yes/no, true/false, or 0/1.

Role of Predictor Variables in Modeling

In statistical modeling, predictor variables are used to build a model that describes the relationship between the predictors and the dependent variable. This model can then be used for various purposes:

• Prediction: Estimating the value of the dependent variable for new data points based on the values of the predictor variables.
• Inference: Understanding the nature of the relationship between the predictor and dependent variables, such as determining which predictors are significant or how changes in predictors affect the dependent variable.

Choosing Predictor Variables

The selection of predictor variables is a critical step in the modeling process. The choice of predictors can significantly affect the model's performance and the accuracy of its predictions. Factors to consider when selecting predictor variables include:

• Relevance: The variable should have a theoretical or empirical justification for its inclusion in the model.
• Data Quality: The variable should be measured accurately and reliably.
• Availability: The variable should be available for all observations in the dataset and for future data points where predictions will be made.
• Non-collinearity: Predictors should not be too highly correlated with each other, as this can lead to multicollinearity issues in the model.

Challenges with Predictor Variables

While predictor variables are essential for building statistical models, there are several challenges that analysts may encounter, including:

• Overfitting: Including too many predictor variables can lead to a model that fits the training data too closely and performs poorly on new data.
• Underfitting: Conversely, including too few predictor variables can result in a model that does not capture the complexity of the data and fails to make accurate predictions.
• Confounding Variables: These are variables that influence both the predictor and the dependent variable, potentially leading to incorrect conclusions about the relationship between the two.

Predictor variables are the backbone of statistical modeling and machine learning. They provide the means to understand and predict the behavior of a dependent variable. The careful selection and analysis of predictor variables are crucial for developing robust models that can offer valuable insights and accurate predictions.

The world's most comprehensive data science & artificial intelligence glossary

Please sign up or login with your details

Generation Overview

AI Generator calls

AI Video Generator calls

AI Chat messages

Genius Mode messages

Genius Mode images

AD-free experience

Private images

• Includes 500 AI Image generations, 1750 AI Chat Messages, 30 AI Video generations, 60 Genius Mode Messages and 60 Genius Mode Images per month. If you go over any of these limits, you will be charged an extra $5 for that group.
• For example: if you go over 500 AI images, but stay within the limits for AI Chat and Genius Mode, you'll be charged $5 per additional 500 AI Image generations.
• Includes 100 AI Image generations and 300 AI Chat Messages. If you go over any of these limits, you will have to pay as you go.
• For example: if you go over 100 AI images, but stay within the limits for AI Chat, you'll have to reload on credits to generate more images. Choose from $5 - $1000. You'll only pay for what you use.

Out of credits

Refill your membership to continue using DeepAI

Share your generations with friends

Understanding Predictor Variables – What Are They and How Do They Impact Your Data Analysis?

Introduction.

Data analysis is a crucial aspect of any research or decision-making process. It involves examining and interpreting data to uncover meaningful insights and patterns. One important factor in data analysis is understanding predictor variables. In this blog post, we will explore what predictor variables are and their significance in data analysis.

What are predictor variables?

Predictor variables, also known as independent variables or features, are the variables that are used to predict or explain the outcome variable in a statistical model. These variables are chosen based on their potential influence on the outcome, and their relationship helps in understanding the factors that contribute to the observed results. For instance, if we want to predict the sales of a product, we may consider variables such as price, advertising expenditure, and customer reviews as predictor variables. By analyzing the relationship between these variables and sales, we can understand which factors are significant in explaining the variations in sales.

Examples of commonly used predictor variables

There are several instances where predictor variables play a significant role. Some commonly used predictor variables include: – Age: In healthcare research, age is often considered as a predictor variable to understand its impact on various health outcomes. – Education level: When analyzing factors affecting job satisfaction, education level can be a crucial predictor variable. – Weather conditions: When studying the impact of weather on consumer behavior, variables like temperature, humidity, and precipitation can act as predictor variables.

Role of predictor variables in statistical modeling

Predictor variables form the backbone of statistical modeling. They are used to build models that explain the relationship between the independent variables and the outcome variable. This relationship helps in predicting future outcomes or understanding the factors that contribute to the observed results. Statistical models, such as linear regression models or logistic regression models, use predictor variables to estimate how changes in these variables affect the outcome variable. By analyzing the coefficients associated with the predictor variables, we can determine the direction and magnitude of their impact on the outcome.

Types of predictor variables

Predictor variables can be categorized into different types based on the nature of the variables and the analysis techniques used.

Continuous predictor variables

Continuous predictor variables are measured on a continuous scale, meaning they can take any value within a given range. Examples of continuous predictor variables include age, temperature, income, and time spent on a task. When analyzing continuous predictor variables, it is essential to consider their distribution and relationships with the outcome variable. Techniques such as correlation analysis, scatter plots, and regression models can be used to understand the relationship and assess the significance of these variables.

Categorical predictor variables

Categorical predictor variables are variables that take distinct categories or classes. Examples of categorical variables include gender, education level (e.g., high school, college, or postgraduate), or product type (e.g., A, B, or C). Analyzing categorical predictor variables involves techniques such as chi-square tests, one-way analysis of variance (ANOVA), or logistic regression. These techniques help examine the relationship between the categories of the variable and the outcome variable.

Interaction predictor variables

Interaction predictor variables represent the combined effect of two or more predictor variables on the outcome variable. They capture the synergistic or contrasting relationships among the variables. For example, if we want to understand the impact of price and brand recognition on purchase intention, we may include an interaction term between these two variables. This allows us to examine whether the effect of price on purchase intention differs based on different levels of brand recognition. Interaction predictor variables are essential in capturing complex relationships and improving the predictive power of statistical models.

How do predictor variables impact data analysis?

Predictor variables have a significant impact on data analysis and statistical modeling. They influence the results, interpretations, and predictions derived from the analysis.

Influence on statistical models and predictions

The choice and inclusion of predictor variables in statistical models determine how well the model can predict the outcome variable. By including relevant predictor variables and understanding their relationship with the outcome, we can build models that accurately represent the underlying patterns in the data. For example, in a linear regression model predicting housing prices, variables such as square footage, number of bedrooms, and location can significantly impact the model’s predictive power. These predictor variables provide valuable insights into the factors affecting housing prices and help make more accurate predictions.

Significance testing and the impact of predictor variables

In data analysis, significance testing is performed to determine the strength and significance of the relationship between predictor variables and the outcome variable. By assessing the p-values associated with the predictor variables, we can determine if their impact on the outcome is statistically significant. Significance testing helps identify the predictor variables that have a meaningful impact, allowing us to focus on the most relevant features in our analysis. It informs decision-making, as variables with high significance provide more confidence in their influence on the outcome.

Relationship between predictor variables and outcome variables

By analyzing the relationship between predictor variables and outcome variables, we can gain deeper insights into the underlying mechanisms and patterns in the data. Understanding these relationships is crucial for hypothesis testing, identifying trends, and making informed decisions based on the analysis. For example, in a marketing campaign analysis, predictor variables such as advertising expenditure and social media engagement can help understand their impact on sales. Analyzing the relationship between these variables and sales can guide marketers in optimizing their strategies and allocating resources more effectively.

Best practices for using predictor variables in data analysis

To ensure accurate and meaningful data analysis, it is important to follow best practices when working with predictor variables.

Carefully selecting predictor variables based on research goals

It is crucial to select predictor variables based on the research goals or the specific questions being addressed. Including irrelevant or redundant variables can introduce noise and reduce the predictive power or interpretability of the model. By clearly defining the research objectives, researchers can select predictor variables that align with the research question and have a logical and plausible relationship with the outcome variable.

Assessing multicollinearity among predictor variables

Multicollinearity refers to the correlation or interdependence among predictor variables. When predictor variables are highly correlated, it can cause instability in the model estimates and hinder the interpretation of individual variables’ effects on the outcome. To address multicollinearity, researchers can perform correlation analysis or variance inflation factor (VIF) analysis to identify variables that exhibit strong correlations. Removing highly correlated variables or combining them into composite variables can help mitigate the issue and improve the model’s accuracy.

Techniques for feature selection and model refinement

Feature selection is the process of identifying the most relevant predictor variables for the analysis. It involves evaluating the predictive power and significance of each variable and selecting the subset of variables that contribute the most to the model’s accuracy. Techniques such as stepwise regression, lasso regression, or random forest variable importance can help in feature selection. By iteratively evaluating and refining the model, researchers can build models that include the most important predictor variables and improve the overall performance and interpretability of the analysis.

In conclusion, predictor variables are essential components of data analysis and statistical modeling. They are used to predict or explain the outcome variable and provide valuable insights into the factors contributing to observed results. Understanding different types of predictor variables, their impact on data analysis, and best practices for their inclusion and handling can significantly improve the accuracy and interpretability of the analysis. By incorporating predictor variables effectively, researchers can make informed decisions, predict future outcomes, and gain a deeper understanding of complex relationships within the data.

Related posts:

• The Ultimate Guide – What Are Predictor Variables and How Do They Impact Data Analysis?
• Understanding the Predictor Variable – A Comprehensive Guide to its Definition and Importance
• The Ultimate Guide – What Is a Predictor Variable and How Does It Impact Data Analysis?
• Calculating Linear Regression Coefficient in Python
• Getting Started with Linear Regression in Python

• Privacy Policy

Home » Variables in Research – Definition, Types and Examples

Variables in Research – Definition, Types and Examples

Table of Contents

Variables in Research

Definition:

In Research, Variables refer to characteristics or attributes that can be measured, manipulated, or controlled. They are the factors that researchers observe or manipulate to understand the relationship between them and the outcomes of interest.

Types of Variables in Research

Types of Variables in Research are as follows:

Independent Variable

This is the variable that is manipulated by the researcher. It is also known as the predictor variable, as it is used to predict changes in the dependent variable. Examples of independent variables include age, gender, dosage, and treatment type.

Dependent Variable

This is the variable that is measured or observed to determine the effects of the independent variable. It is also known as the outcome variable, as it is the variable that is affected by the independent variable. Examples of dependent variables include blood pressure, test scores, and reaction time.

Confounding Variable

This is a variable that can affect the relationship between the independent variable and the dependent variable. It is a variable that is not being studied but could impact the results of the study. For example, in a study on the effects of a new drug on a disease, a confounding variable could be the patient’s age, as older patients may have more severe symptoms.

Mediating Variable

This is a variable that explains the relationship between the independent variable and the dependent variable. It is a variable that comes in between the independent and dependent variables and is affected by the independent variable, which then affects the dependent variable. For example, in a study on the relationship between exercise and weight loss, the mediating variable could be metabolism, as exercise can increase metabolism, which can then lead to weight loss.

Moderator Variable

This is a variable that affects the strength or direction of the relationship between the independent variable and the dependent variable. It is a variable that influences the effect of the independent variable on the dependent variable. For example, in a study on the effects of caffeine on cognitive performance, the moderator variable could be age, as older adults may be more sensitive to the effects of caffeine than younger adults.

Control Variable

This is a variable that is held constant or controlled by the researcher to ensure that it does not affect the relationship between the independent variable and the dependent variable. Control variables are important to ensure that any observed effects are due to the independent variable and not to other factors. For example, in a study on the effects of a new teaching method on student performance, the control variables could include class size, teacher experience, and student demographics.

Continuous Variable

This is a variable that can take on any value within a certain range. Continuous variables can be measured on a scale and are often used in statistical analyses. Examples of continuous variables include height, weight, and temperature.

Categorical Variable

This is a variable that can take on a limited number of values or categories. Categorical variables can be nominal or ordinal. Nominal variables have no inherent order, while ordinal variables have a natural order. Examples of categorical variables include gender, race, and educational level.

Discrete Variable

This is a variable that can only take on specific values. Discrete variables are often used in counting or frequency analyses. Examples of discrete variables include the number of siblings a person has, the number of times a person exercises in a week, and the number of students in a classroom.

Dummy Variable

This is a variable that takes on only two values, typically 0 and 1, and is used to represent categorical variables in statistical analyses. Dummy variables are often used when a categorical variable cannot be used directly in an analysis. For example, in a study on the effects of gender on income, a dummy variable could be created, with 0 representing female and 1 representing male.

Extraneous Variable

This is a variable that has no relationship with the independent or dependent variable but can affect the outcome of the study. Extraneous variables can lead to erroneous conclusions and can be controlled through random assignment or statistical techniques.

Latent Variable

This is a variable that cannot be directly observed or measured, but is inferred from other variables. Latent variables are often used in psychological or social research to represent constructs such as personality traits, attitudes, or beliefs.

Moderator-mediator Variable

This is a variable that acts both as a moderator and a mediator. It can moderate the relationship between the independent and dependent variables and also mediate the relationship between the independent and dependent variables. Moderator-mediator variables are often used in complex statistical analyses.

Variables Analysis Methods

There are different methods to analyze variables in research, including:

• Descriptive statistics: This involves analyzing and summarizing data using measures such as mean, median, mode, range, standard deviation, and frequency distribution. Descriptive statistics are useful for understanding the basic characteristics of a data set.
• Inferential statistics : This involves making inferences about a population based on sample data. Inferential statistics use techniques such as hypothesis testing, confidence intervals, and regression analysis to draw conclusions from data.
• Correlation analysis: This involves examining the relationship between two or more variables. Correlation analysis can determine the strength and direction of the relationship between variables, and can be used to make predictions about future outcomes.
• Regression analysis: This involves examining the relationship between an independent variable and a dependent variable. Regression analysis can be used to predict the value of the dependent variable based on the value of the independent variable, and can also determine the significance of the relationship between the two variables.
• Factor analysis: This involves identifying patterns and relationships among a large number of variables. Factor analysis can be used to reduce the complexity of a data set and identify underlying factors or dimensions.
• Cluster analysis: This involves grouping data into clusters based on similarities between variables. Cluster analysis can be used to identify patterns or segments within a data set, and can be useful for market segmentation or customer profiling.
• Multivariate analysis : This involves analyzing multiple variables simultaneously. Multivariate analysis can be used to understand complex relationships between variables, and can be useful in fields such as social science, finance, and marketing.

Examples of Variables

• Age : This is a continuous variable that represents the age of an individual in years.
• Gender : This is a categorical variable that represents the biological sex of an individual and can take on values such as male and female.
• Education level: This is a categorical variable that represents the level of education completed by an individual and can take on values such as high school, college, and graduate school.
• Income : This is a continuous variable that represents the amount of money earned by an individual in a year.
• Weight : This is a continuous variable that represents the weight of an individual in kilograms or pounds.
• Ethnicity : This is a categorical variable that represents the ethnic background of an individual and can take on values such as Hispanic, African American, and Asian.
• Time spent on social media : This is a continuous variable that represents the amount of time an individual spends on social media in minutes or hours per day.
• Marital status: This is a categorical variable that represents the marital status of an individual and can take on values such as married, divorced, and single.
• Blood pressure : This is a continuous variable that represents the force of blood against the walls of arteries in millimeters of mercury.
• Job satisfaction : This is a continuous variable that represents an individual’s level of satisfaction with their job and can be measured using a Likert scale.

Applications of Variables

Variables are used in many different applications across various fields. Here are some examples:

• Scientific research: Variables are used in scientific research to understand the relationships between different factors and to make predictions about future outcomes. For example, scientists may study the effects of different variables on plant growth or the impact of environmental factors on animal behavior.
• Business and marketing: Variables are used in business and marketing to understand customer behavior and to make decisions about product development and marketing strategies. For example, businesses may study variables such as consumer preferences, spending habits, and market trends to identify opportunities for growth.
• Healthcare : Variables are used in healthcare to monitor patient health and to make treatment decisions. For example, doctors may use variables such as blood pressure, heart rate, and cholesterol levels to diagnose and treat cardiovascular disease.
• Education : Variables are used in education to measure student performance and to evaluate the effectiveness of teaching strategies. For example, teachers may use variables such as test scores, attendance, and class participation to assess student learning.
• Social sciences : Variables are used in social sciences to study human behavior and to understand the factors that influence social interactions. For example, sociologists may study variables such as income, education level, and family structure to examine patterns of social inequality.

Purpose of Variables

Variables serve several purposes in research, including:

• To provide a way of measuring and quantifying concepts: Variables help researchers measure and quantify abstract concepts such as attitudes, behaviors, and perceptions. By assigning numerical values to these concepts, researchers can analyze and compare data to draw meaningful conclusions.
• To help explain relationships between different factors: Variables help researchers identify and explain relationships between different factors. By analyzing how changes in one variable affect another variable, researchers can gain insight into the complex interplay between different factors.
• To make predictions about future outcomes : Variables help researchers make predictions about future outcomes based on past observations. By analyzing patterns and relationships between different variables, researchers can make informed predictions about how different factors may affect future outcomes.
• To test hypotheses: Variables help researchers test hypotheses and theories. By collecting and analyzing data on different variables, researchers can test whether their predictions are accurate and whether their hypotheses are supported by the evidence.

Characteristics of Variables

Characteristics of Variables are as follows:

• Measurement : Variables can be measured using different scales, such as nominal, ordinal, interval, or ratio scales. The scale used to measure a variable can affect the type of statistical analysis that can be applied.
• Range : Variables have a range of values that they can take on. The range can be finite, such as the number of students in a class, or infinite, such as the range of possible values for a continuous variable like temperature.
• Variability : Variables can have different levels of variability, which refers to the degree to which the values of the variable differ from each other. Highly variable variables have a wide range of values, while low variability variables have values that are more similar to each other.
• Validity and reliability : Variables should be both valid and reliable to ensure accurate and consistent measurement. Validity refers to the extent to which a variable measures what it is intended to measure, while reliability refers to the consistency of the measurement over time.
• Directionality: Some variables have directionality, meaning that the relationship between the variables is not symmetrical. For example, in a study of the relationship between smoking and lung cancer, smoking is the independent variable and lung cancer is the dependent variable.

Advantages of Variables

Here are some of the advantages of using variables in research:

• Control : Variables allow researchers to control the effects of external factors that could influence the outcome of the study. By manipulating and controlling variables, researchers can isolate the effects of specific factors and measure their impact on the outcome.
• Replicability : Variables make it possible for other researchers to replicate the study and test its findings. By defining and measuring variables consistently, other researchers can conduct similar studies to validate the original findings.
• Accuracy : Variables make it possible to measure phenomena accurately and objectively. By defining and measuring variables precisely, researchers can reduce bias and increase the accuracy of their findings.
• Generalizability : Variables allow researchers to generalize their findings to larger populations. By selecting variables that are representative of the population, researchers can draw conclusions that are applicable to a broader range of individuals.
• Clarity : Variables help researchers to communicate their findings more clearly and effectively. By defining and categorizing variables, researchers can organize and present their findings in a way that is easily understandable to others.

Disadvantages of Variables

Here are some of the main disadvantages of using variables in research:

• Simplification : Variables may oversimplify the complexity of real-world phenomena. By breaking down a phenomenon into variables, researchers may lose important information and context, which can affect the accuracy and generalizability of their findings.
• Measurement error : Variables rely on accurate and precise measurement, and measurement error can affect the reliability and validity of research findings. The use of subjective or poorly defined variables can also introduce measurement error into the study.
• Confounding variables : Confounding variables are factors that are not measured but that affect the relationship between the variables of interest. If confounding variables are not accounted for, they can distort or obscure the relationship between the variables of interest.
• Limited scope: Variables are defined by the researcher, and the scope of the study is therefore limited by the researcher’s choice of variables. This can lead to a narrow focus that overlooks important aspects of the phenomenon being studied.
• Ethical concerns: The selection and measurement of variables may raise ethical concerns, especially in studies involving human subjects. For example, using variables that are related to sensitive topics, such as race or sexuality, may raise concerns about privacy and discrimination.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Control Variable – Definition, Types and Examples

Moderating Variable – Definition, Analysis...

Categorical Variable – Definition, Types and...

Independent Variable – Definition, Types and...

Ratio Variable – Definition, Purpose and Examples

Ordinal Variable – Definition, Purpose and...

Types of Variable

All experiments examine some kind of variable(s). A variable is not only something that we measure, but also something that we can manipulate and something we can control for. To understand the characteristics of variables and how we use them in research, this guide is divided into three main sections. First, we illustrate the role of dependent and independent variables. Second, we discuss the difference between experimental and non-experimental research. Finally, we explain how variables can be characterised as either categorical or continuous.

Dependent and Independent Variables

An independent variable, sometimes called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, sometimes called an outcome variable.

Imagine that a tutor asks 100 students to complete a maths test. The tutor wants to know why some students perform better than others. Whilst the tutor does not know the answer to this, she thinks that it might be because of two reasons: (1) some students spend more time revising for their test; and (2) some students are naturally more intelligent than others. As such, the tutor decides to investigate the effect of revision time and intelligence on the test performance of the 100 students. The dependent and independent variables for the study are:

Dependent Variable: Test Mark (measured from 0 to 100)

Independent Variables: Revision time (measured in hours) Intelligence (measured using IQ score)

The dependent variable is simply that, a variable that is dependent on an independent variable(s). For example, in our case the test mark that a student achieves is dependent on revision time and intelligence. Whilst revision time and intelligence (the independent variables) may (or may not) cause a change in the test mark (the dependent variable), the reverse is implausible; in other words, whilst the number of hours a student spends revising and the higher a student's IQ score may (or may not) change the test mark that a student achieves, a change in a student's test mark has no bearing on whether a student revises more or is more intelligent (this simply doesn't make sense).

Therefore, the aim of the tutor's investigation is to examine whether these independent variables - revision time and IQ - result in a change in the dependent variable, the students' test scores. However, it is also worth noting that whilst this is the main aim of the experiment, the tutor may also be interested to know if the independent variables - revision time and IQ - are also connected in some way.

In the section on experimental and non-experimental research that follows, we find out a little more about the nature of independent and dependent variables.

Experimental and Non-Experimental Research

• Experimental research : In experimental research, the aim is to manipulate an independent variable(s) and then examine the effect that this change has on a dependent variable(s). Since it is possible to manipulate the independent variable(s), experimental research has the advantage of enabling a researcher to identify a cause and effect between variables. For example, take our example of 100 students completing a maths exam where the dependent variable was the exam mark (measured from 0 to 100), and the independent variables were revision time (measured in hours) and intelligence (measured using IQ score). Here, it would be possible to use an experimental design and manipulate the revision time of the students. The tutor could divide the students into two groups, each made up of 50 students. In "group one", the tutor could ask the students not to do any revision. Alternately, "group two" could be asked to do 20 hours of revision in the two weeks prior to the test. The tutor could then compare the marks that the students achieved.
• Non-experimental research : In non-experimental research, the researcher does not manipulate the independent variable(s). This is not to say that it is impossible to do so, but it will either be impractical or unethical to do so. For example, a researcher may be interested in the effect of illegal, recreational drug use (the independent variable(s)) on certain types of behaviour (the dependent variable(s)). However, whilst possible, it would be unethical to ask individuals to take illegal drugs in order to study what effect this had on certain behaviours. As such, a researcher could ask both drug and non-drug users to complete a questionnaire that had been constructed to indicate the extent to which they exhibited certain behaviours. Whilst it is not possible to identify the cause and effect between the variables, we can still examine the association or relationship between them. In addition to understanding the difference between dependent and independent variables, and experimental and non-experimental research, it is also important to understand the different characteristics amongst variables. This is discussed next.

Categorical and Continuous Variables

Categorical variables are also known as discrete or qualitative variables. Categorical variables can be further categorized as either nominal , ordinal or dichotomous .

• Nominal variables are variables that have two or more categories, but which do not have an intrinsic order. For example, a real estate agent could classify their types of property into distinct categories such as houses, condos, co-ops or bungalows. So "type of property" is a nominal variable with 4 categories called houses, condos, co-ops and bungalows. Of note, the different categories of a nominal variable can also be referred to as groups or levels of the nominal variable. Another example of a nominal variable would be classifying where people live in the USA by state. In this case there will be many more levels of the nominal variable (50 in fact).
• Dichotomous variables are nominal variables which have only two categories or levels. For example, if we were looking at gender, we would most probably categorize somebody as either "male" or "female". This is an example of a dichotomous variable (and also a nominal variable). Another example might be if we asked a person if they owned a mobile phone. Here, we may categorise mobile phone ownership as either "Yes" or "No". In the real estate agent example, if type of property had been classified as either residential or commercial then "type of property" would be a dichotomous variable.
• Ordinal variables are variables that have two or more categories just like nominal variables only the categories can also be ordered or ranked. So if you asked someone if they liked the policies of the Democratic Party and they could answer either "Not very much", "They are OK" or "Yes, a lot" then you have an ordinal variable. Why? Because you have 3 categories, namely "Not very much", "They are OK" and "Yes, a lot" and you can rank them from the most positive (Yes, a lot), to the middle response (They are OK), to the least positive (Not very much). However, whilst we can rank the levels, we cannot place a "value" to them; we cannot say that "They are OK" is twice as positive as "Not very much" for example.

Continuous variables are also known as quantitative variables. Continuous variables can be further categorized as either interval or ratio variables.

• Interval variables are variables for which their central characteristic is that they can be measured along a continuum and they have a numerical value (for example, temperature measured in degrees Celsius or Fahrenheit). So the difference between 20°C and 30°C is the same as 30°C to 40°C. However, temperature measured in degrees Celsius or Fahrenheit is NOT a ratio variable.
• Ratio variables are interval variables, but with the added condition that 0 (zero) of the measurement indicates that there is none of that variable. So, temperature measured in degrees Celsius or Fahrenheit is not a ratio variable because 0°C does not mean there is no temperature. However, temperature measured in Kelvin is a ratio variable as 0 Kelvin (often called absolute zero) indicates that there is no temperature whatsoever. Other examples of ratio variables include height, mass, distance and many more. The name "ratio" reflects the fact that you can use the ratio of measurements. So, for example, a distance of ten metres is twice the distance of 5 metres.

Ambiguities in classifying a type of variable

In some cases, the measurement scale for data is ordinal, but the variable is treated as continuous. For example, a Likert scale that contains five values - strongly agree, agree, neither agree nor disagree, disagree, and strongly disagree - is ordinal. However, where a Likert scale contains seven or more value - strongly agree, moderately agree, agree, neither agree nor disagree, disagree, moderately disagree, and strongly disagree - the underlying scale is sometimes treated as continuous (although where you should do this is a cause of great dispute).

It is worth noting that how we categorise variables is somewhat of a choice. Whilst we categorised gender as a dichotomous variable (you are either male or female), social scientists may disagree with this, arguing that gender is a more complex variable involving more than two distinctions, but also including measurement levels like genderqueer, intersex and transgender. At the same time, some researchers would argue that a Likert scale, even with seven values, should never be treated as a continuous variable.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 31 January 2022

The clinician’s guide to interpreting a regression analysis

• Sofia Bzovsky 1 ,
• Mark R. Phillips   ORCID: orcid.org/0000-0003-0923-261X 2 ,
• Robyn H. Guymer   ORCID: orcid.org/0000-0002-9441-4356 3 , 4 ,
• Charles C. Wykoff 5 , 6 ,
• Lehana Thabane   ORCID: orcid.org/0000-0003-0355-9734 2 , 7 ,
• Mohit Bhandari   ORCID: orcid.org/0000-0001-9608-4808 1 , 2 &
• Varun Chaudhary   ORCID: orcid.org/0000-0002-9988-4146 1 , 2

on behalf of the R.E.T.I.N.A. study group

Eye volume  36 ,  pages 1715–1717 ( 2022 ) Cite this article

20k Accesses

9 Citations

1 Altmetric

Metrics details

• Outcomes research

Introduction

When researchers are conducting clinical studies to investigate factors associated with, or treatments for disease and conditions to improve patient care and clinical practice, statistical evaluation of the data is often necessary. Regression analysis is an important statistical method that is commonly used to determine the relationship between several factors and disease outcomes or to identify relevant prognostic factors for diseases [ 1 ].

This editorial will acquaint readers with the basic principles of and an approach to interpreting results from two types of regression analyses widely used in ophthalmology: linear, and logistic regression.

Linear regression analysis

Linear regression is used to quantify a linear relationship or association between a continuous response/outcome variable or dependent variable with at least one independent or explanatory variable by fitting a linear equation to observed data [ 1 ]. The variable that the equation solves for, which is the outcome or response of interest, is called the dependent variable [ 1 ]. The variable that is used to explain the value of the dependent variable is called the predictor, explanatory, or independent variable [ 1 ].

In a linear regression model, the dependent variable must be continuous (e.g. intraocular pressure or visual acuity), whereas, the independent variable may be either continuous (e.g. age), binary (e.g. sex), categorical (e.g. age-related macular degeneration stage or diabetic retinopathy severity scale score), or a combination of these [ 1 ].

When investigating the effect or association of a single independent variable on a continuous dependent variable, this type of analysis is called a simple linear regression [ 2 ]. In many circumstances though, a single independent variable may not be enough to adequately explain the dependent variable. Often it is necessary to control for confounders and in these situations, one can perform a multivariable linear regression to study the effect or association with multiple independent variables on the dependent variable [ 1 , 2 ]. When incorporating numerous independent variables, the regression model estimates the effect or contribution of each independent variable while holding the values of all other independent variables constant [ 3 ].

When interpreting the results of a linear regression, there are a few key outputs for each independent variable included in the model:

Estimated regression coefficient—The estimated regression coefficient indicates the direction and strength of the relationship or association between the independent and dependent variables [ 4 ]. Specifically, the regression coefficient describes the change in the dependent variable for each one-unit change in the independent variable, if continuous [ 4 ]. For instance, if examining the relationship between a continuous predictor variable and intra-ocular pressure (dependent variable), a regression coefficient of 2 means that for every one-unit increase in the predictor, there is a two-unit increase in intra-ocular pressure. If the independent variable is binary or categorical, then the one-unit change represents switching from one category to the reference category [ 4 ]. For instance, if examining the relationship between a binary predictor variable, such as sex, where ‘female’ is set as the reference category, and intra-ocular pressure (dependent variable), a regression coefficient of 2 means that, on average, males have an intra-ocular pressure that is 2 mm Hg higher than females.

Confidence Interval (CI)—The CI, typically set at 95%, is a measure of the precision of the coefficient estimate of the independent variable [ 4 ]. A large CI indicates a low level of precision, whereas a small CI indicates a higher precision [ 5 ].

P value—The p value for the regression coefficient indicates whether the relationship between the independent and dependent variables is statistically significant [ 6 ].

Logistic regression analysis

As with linear regression, logistic regression is used to estimate the association between one or more independent variables with a dependent variable [ 7 ]. However, the distinguishing feature in logistic regression is that the dependent variable (outcome) must be binary (or dichotomous), meaning that the variable can only take two different values or levels, such as ‘1 versus 0’ or ‘yes versus no’ [ 2 , 7 ]. The effect size of predictor variables on the dependent variable is best explained using an odds ratio (OR) [ 2 ]. ORs are used to compare the relative odds of the occurrence of the outcome of interest, given exposure to the variable of interest [ 5 ]. An OR equal to 1 means that the odds of the event in one group are the same as the odds of the event in another group; there is no difference [ 8 ]. An OR > 1 implies that one group has a higher odds of having the event compared with the reference group, whereas an OR < 1 means that one group has a lower odds of having an event compared with the reference group [ 8 ]. When interpreting the results of a logistic regression, the key outputs include the OR, CI, and p-value for each independent variable included in the model.

Clinical example

Sen et al. investigated the association between several factors (independent variables) and visual acuity outcomes (dependent variable) in patients receiving anti-vascular endothelial growth factor therapy for macular oedema (DMO) by means of both linear and logistic regression [ 9 ]. Multivariable linear regression demonstrated that age (Estimate −0.33, 95% CI − 0.48 to −0.19, p  < 0.001) was significantly associated with best-corrected visual acuity (BCVA) at 100 weeks at alpha = 0.05 significance level [ 9 ]. The regression coefficient of −0.33 means that the BCVA at 100 weeks decreases by 0.33 with each additional year of older age.

Multivariable logistic regression also demonstrated that age and ellipsoid zone status were statistically significant associated with achieving a BCVA letter score >70 letters at 100 weeks at the alpha = 0.05 significance level. Patients ≥75 years of age were at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those <50 years of age, since the OR is less than 1 (OR 0.96, 95% CI 0.94 to 0.98, p  = 0.001) [ 9 ]. Similarly, patients between the ages of 50–74 years were also at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those <50 years of age, since the OR is less than 1 (OR 0.15, 95% CI 0.04 to 0.48, p  = 0.001) [ 9 ]. As well, those with a not intact ellipsoid zone were at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those with an intact ellipsoid zone (OR 0.20, 95% CI 0.07 to 0.56; p  = 0.002). On the other hand, patients with an ungradable/questionable ellipsoid zone were at an increased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those with an intact ellipsoid zone, since the OR is greater than 1 (OR 2.26, 95% CI 1.14 to 4.48; p  = 0.02) [ 9 ].

The narrower the CI, the more precise the estimate is; and the smaller the p value (relative to alpha = 0.05), the greater the evidence against the null hypothesis of no effect or association.

Simply put, linear and logistic regression are useful tools for appreciating the relationship between predictor/explanatory and outcome variables for continuous and dichotomous outcomes, respectively, that can be applied in clinical practice, such as to gain an understanding of risk factors associated with a disease of interest.

Schneider A, Hommel G, Blettner M. Linear Regression. Anal Dtsch Ärztebl Int. 2010;107:776–82.

Google Scholar  

Bender R. Introduction to the use of regression models in epidemiology. In: Verma M, editor. Cancer epidemiology. Methods in molecular biology. Humana Press; 2009:179–95.

Schober P, Vetter TR. Confounding in observational research. Anesth Analg. 2020;130:635.

Article   Google Scholar  

Schober P, Vetter TR. Linear regression in medical research. Anesth Analg. 2021;132:108–9.

Szumilas M. Explaining odds ratios. J Can Acad Child Adolesc Psychiatry. 2010;19:227–9.

Thiese MS, Ronna B, Ott U. P value interpretations and considerations. J Thorac Dis. 2016;8:E928–31.

Schober P, Vetter TR. Logistic regression in medical research. Anesth Analg. 2021;132:365–6.

Zabor EC, Reddy CA, Tendulkar RD, Patil S. Logistic regression in clinical studies. Int J Radiat Oncol Biol Phys. 2022;112:271–7.

Sen P, Gurudas S, Ramu J, Patrao N, Chandra S, Rasheed R, et al. Predictors of visual acuity outcomes after anti-vascular endothelial growth factor treatment for macular edema secondary to central retinal vein occlusion. Ophthalmol Retin. 2021;5:1115–24.

Download references

R.E.T.I.N.A. study group

Varun Chaudhary 1,2 , Mohit Bhandari 1,2 , Charles C. Wykoff 5,6 , Sobha Sivaprasad 8 , Lehana Thabane 2,7 , Peter Kaiser 9 , David Sarraf 10 , Sophie J. Bakri 11 , Sunir J. Garg 12 , Rishi P. Singh 13,14 , Frank G. Holz 15 , Tien Y. Wong 16,17 , and Robyn H. Guymer 3,4

Author information

Authors and affiliations.

Department of Surgery, McMaster University, Hamilton, ON, Canada

Sofia Bzovsky, Mohit Bhandari & Varun Chaudhary

Department of Health Research Methods, Evidence & Impact, McMaster University, Hamilton, ON, Canada

Mark R. Phillips, Lehana Thabane, Mohit Bhandari & Varun Chaudhary

Centre for Eye Research Australia, Royal Victorian Eye and Ear Hospital, East Melbourne, VIC, Australia

Robyn H. Guymer

Department of Surgery, (Ophthalmology), The University of Melbourne, Melbourne, VIC, Australia

Retina Consultants of Texas (Retina Consultants of America), Houston, TX, USA

Charles C. Wykoff

Blanton Eye Institute, Houston Methodist Hospital, Houston, TX, USA

Biostatistics Unit, St. Joseph’s Healthcare Hamilton, Hamilton, ON, Canada

Lehana Thabane

NIHR Moorfields Biomedical Research Centre, Moorfields Eye Hospital, London, UK

Sobha Sivaprasad

Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Peter Kaiser

Retinal Disorders and Ophthalmic Genetics, Stein Eye Institute, University of California, Los Angeles, CA, USA

David Sarraf

Department of Ophthalmology, Mayo Clinic, Rochester, MN, USA

Sophie J. Bakri

The Retina Service at Wills Eye Hospital, Philadelphia, PA, USA

Sunir J. Garg

Center for Ophthalmic Bioinformatics, Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Rishi P. Singh

Cleveland Clinic Lerner College of Medicine, Cleveland, OH, USA

Department of Ophthalmology, University of Bonn, Bonn, Germany

Frank G. Holz

Singapore Eye Research Institute, Singapore, Singapore

Tien Y. Wong

Singapore National Eye Centre, Duke-NUD Medical School, Singapore, Singapore

You can also search for this author in PubMed   Google Scholar

• Varun Chaudhary
• , Mohit Bhandari
• , Charles C. Wykoff
• , Sobha Sivaprasad
• , Lehana Thabane
• , Peter Kaiser
• , David Sarraf
• , Sophie J. Bakri
• , Sunir J. Garg
• , Rishi P. Singh
• , Frank G. Holz
• , Tien Y. Wong
•  & Robyn H. Guymer

Contributions

SB was responsible for writing, critical review and feedback on manuscript. MRP was responsible for conception of idea, critical review and feedback on manuscript. RHG was responsible for critical review and feedback on manuscript. CCW was responsible for critical review and feedback on manuscript. LT was responsible for critical review and feedback on manuscript. MB was responsible for conception of idea, critical review and feedback on manuscript. VC was responsible for conception of idea, critical review and feedback on manuscript.

Corresponding author

Correspondence to Varun Chaudhary .

Ethics declarations

Competing interests.

SB: Nothing to disclose. MRP: Nothing to disclose. RHG: Advisory boards: Bayer, Novartis, Apellis, Roche, Genentech Inc.—unrelated to this study. CCW: Consultant: Acuela, Adverum Biotechnologies, Inc, Aerpio, Alimera Sciences, Allegro Ophthalmics, LLC, Allergan, Apellis Pharmaceuticals, Bayer AG, Chengdu Kanghong Pharmaceuticals Group Co, Ltd, Clearside Biomedical, DORC (Dutch Ophthalmic Research Center), EyePoint Pharmaceuticals, Gentech/Roche, GyroscopeTx, IVERIC bio, Kodiak Sciences Inc, Novartis AG, ONL Therapeutics, Oxurion NV, PolyPhotonix, Recens Medical, Regeron Pharmaceuticals, Inc, REGENXBIO Inc, Santen Pharmaceutical Co, Ltd, and Takeda Pharmaceutical Company Limited; Research funds: Adverum Biotechnologies, Inc, Aerie Pharmaceuticals, Inc, Aerpio, Alimera Sciences, Allergan, Apellis Pharmaceuticals, Chengdu Kanghong Pharmaceutical Group Co, Ltd, Clearside Biomedical, Gemini Therapeutics, Genentech/Roche, Graybug Vision, Inc, GyroscopeTx, Ionis Pharmaceuticals, IVERIC bio, Kodiak Sciences Inc, Neurotech LLC, Novartis AG, Opthea, Outlook Therapeutics, Inc, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Samsung Pharm Co, Ltd, Santen Pharmaceutical Co, Ltd, and Xbrane Biopharma AB—unrelated to this study. LT: Nothing to disclose. MB: Research funds: Pendopharm, Bioventus, Acumed—unrelated to this study. VC: Advisory Board Member: Alcon, Roche, Bayer, Novartis; Grants: Bayer, Novartis—unrelated to this study.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Bzovsky, S., Phillips, M.R., Guymer, R.H. et al. The clinician’s guide to interpreting a regression analysis. Eye 36 , 1715–1717 (2022). https://doi.org/10.1038/s41433-022-01949-z

Download citation

Received : 08 January 2022

Revised : 17 January 2022

Accepted : 18 January 2022

Published : 31 January 2022

Issue Date : September 2022

DOI : https://doi.org/10.1038/s41433-022-01949-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Factors affecting patient satisfaction at a plastic surgery outpatient department at a tertiary centre in south africa.

• Chrysis Sofianos

BMC Health Services Research (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• 8.2 - The Basics of Indicator Variables

A " binary predictor " is a variable that takes on only two possible values. Here are a few common examples of binary predictor variables that you are likely to encounter in your own research:

• Gender (male, female)
• Smoking status (smoker, nonsmoker)
• Treatment (yes, no)
• Health status (diseased, healthy)
• Company status (private, public)

Example : On average, do smoking mothers have babies with lower birth weight?

In the previous section, we briefly investigated data ( birthsmokers.txt ) on a random sample of n = 32 births that allow researchers (Daniel, 1999) to answer the above research question. The researchers collected the following data:

• Response ( y ): birth weight ( Weight ) in grams of baby
• Potential predictor ( x 1 ): length of gestation ( Gest ) in weeks
• Potential predictor ( x 2 ): Smoking status of mother (smoker or non-smoker)

In order to include a qualitative variable in a regression model, we have to " code " the variable, that is, assign a unique number to each of the possible categories. A common coding scheme is to use what's called a " zero-one indicator variable ." Using such a variable here, we code the binary predictor Smoking as:

• x i 2 = 1, if mother i smokes
• x i 2 = 0, if mother i does not smoke

In doing so, we use the tradition of assigning the value of 1 to those having the characteristic of interest and 0 to those not having the characteristic. Tradition is less important, though, than making sure you keep track of your coding scheme so that you can properly draw conclusions. Incidentally, other terms sometimes used instead of " zero-one indicator variable " are " dummy variable " or " binary variable ".

A scatter plot of the data in which blue circles represent the data on non-smoking mothers (x 2 =0) and red circles represent the data on smoking mothers (x 2 =1):

suggests that there might be two distinct linear trends in the data — one for smoking mothers and one for non-smoking mothers. Therefore, a first order model with one binary and one quantitative predictor appears to be a natural model to formulate for these data. That is:

\[y_i=(\beta_0+\beta_1x_{i1}+\beta_2x_{i2})+\epsilon_i\] 

• y i is birth weight of baby i in grams
• x i 1 is the length of gestation of baby i in weeks
• x i 2 = 1, if the mother smoked during pregnancy, and x i 2 = 0, if she did not

and the independent error terms ε i follow a normal distribution with mean 0 and equal variance σ 2 .

How does a model containing a (0,1) indicator variable for two groups yield two distinct response functions? In short, this screencast below, illustrates how the mean response function:

\[\mu_Y=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}\]

yields one regression function for non-smoking mothers ( x i 2 = 0):

\[\mu_Y=\beta_0+\beta_1x_{i1}\]

and one regression function for smoking mothers ( x i 2 = 1):

\[\mu_Y=(\beta_0+\beta_2)+\beta_1x_{i1}\]

Note that the two formulated regression functions have the same slope ( β 1 ) but different intercepts ( β 0 and β 0 + β 2 ) — mathematical characteristics that, based on the above scatter plot, appear to summarize the trend in the data well.

Now, given that we generally use regression models to answer research questions, we need to figure out how each of the parameters in our model enlightens us about our research problem! The fundamental principle is that you can determine the meaning of any regression coefficient by seeing what effect changing the value of the predictor has on the mean response μ Y . Here's the interpretation of the regression coefficients in a regression model with one (0, 1) binary indicator variable and one quantitative predictor:

• β 1 represents the change in the mean response μ Y for each additional unit increase in the quantitative predictor x 1 ... for both groups. 

• β 2 represents how much higher (or lower) the mean response function of the second group is than that of the first group... for any value of x 1 . 

Upon fitting our formulated regression model to our data, statistical software output tells us:

Unfortunately, this output doesn't precede the phrase "regression equation" with the adjective "estimated" in order to emphasize that we've only obtained an estimate of the actual unknown population regression function. But anyway — if we set Smoking once equal to 0 and once equal to 1 — we obtain, as hoped, two distinct estimated lines:

Now, let's use our model and analysis to answer the following research question: Is there a significant difference in mean birth weights for the two groups, after taking into account length of gestation? As is always the case, the first thing we need to do is to "translate" the research question into an appropriate statistical procedure. We can show that if the slope parameter β 2 is 0, there is no difference in the means of the two groups — for any length of gestation. That is, we can answer our research question by testing the null hypothesis H 0 : β 2 = 0 against the alternative H A : β 2 ≠ 0.

Well, that's easy enough! The software output:

reports that the P -value is < 0.001. At just about any significance level, we can reject the null hypothesis H 0 : β 2 = 0 in favor of the alternative hypothesis H A : β 2 ≠ 0. There is sufficient evidence to conclude that there is a statistically significant difference in the mean birth weight of all babies of smoking mothers and the mean birth weight of babies of all non-smoking mothers, after taking into account length of gestation.

A 95% confidence interval for β 2 tells us the magnitude of the difference. A 95% t -multiplier with n - p = 32-3 = 29 degrees of freedom is t (0.025, 29) = 2.0452. Therefore, a 95% confidence interval for β 2 is:

-244.54 ± 2.0452(41.98) or (-330.4, -158.7).

We can be 95% confident that the mean birth weight of smoking mothers is between 158.7 and 330.4 grams less than the mean birth weight of non-smoking mothers, for a fixed length of gestation. It is up to the researchers to debate whether or not the difference is a meaningful difference.

\(\mu_Y|(x_{i1}=x+1) = \beta_0+\beta_1(x+1)\) \(\mu_Y|(x_{i1}=x) = \beta_0+\beta_1 x\)

Take the difference,

\(\mu_Y|(x_{i1}=x+1) - \mu_Y|(x_{i1}=x) = \beta_0+\beta_1(x+1) - (\beta_0+\beta_1 x) = \beta_1\)

Start Here!

• Welcome to STAT 462!
• Search Course Materials
• Lesson 1: Statistical Inference Foundations
• Lesson 2: Simple Linear Regression (SLR) Model
• Lesson 3: SLR Evaluation
• Lesson 4: SLR Assumptions, Estimation & Prediction
• Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation
• Lesson 6: MLR Assumptions, Estimation & Prediction
• Lesson 7: Transformations & Interactions
• 8.1 - Example on Birth Weight and Smoking
• 8.3 - Two Separate Advantages
• 8.4 - Coding Qualitative Variables
• 8.5 - Additive Effects
• 8.6 - Interaction Effects
• 8.7 - Leaving an Important Interaction Out of a Model
• 8.8 - Further Categorical Predictor Examples
• Lesson 9: Influential Points
• Lesson 10: Regression Pitfalls
• Lesson 11: Model Building
• Lesson 12: Logistic, Poisson & Nonlinear Regression
• Website for Applied Regression Modeling, 2nd edition
• Notation Used in this Course
• R Software Help
• Minitab Software Help

Copyright © 2018 The Pennsylvania State University Privacy and Legal Statements Contact the Department of Statistics Online Programs

Machine Learning 101: Criterion vs Predictor (With Coded Examples)

• February 22, 2024
• General , Supervised Learning

In data science, there are many different ways to slice the pie. While many refer to independent and dependent variables differently, they usually mean the same thing.

Your predictor variables are your independent variables, and with these, you’ll (hopefully) be able to predict your criterion variable (dependent variable).

In the rest of this 3-minute guide , we’ll go over a deep-dive into criterion vs. predictor variables , what each of these means, and supply you with some code at the bottom to show you how to split each of these out in the python coding language .

This one is embarrassing to mess up, but don’t worry; we’ve got your back.

What is a criterion variable?

Simply, a criterion variable is a variable we’re trying to predict. Many machine learning projects refer to this as Y or as our target variable .

The best way to identify your criterion variable is to identify the variable that you care about.

In a business context, this will be the variable that most closely resembles the problem you’re trying to solve.

For example, if your boss wants to build a model that can predict future sales of your company’s product, the criterion variable is the variable that most closely resembles sales.

It’s worth noting that a criterion variable could be a relationship of multiple variables (Or something much more complicated ).

Let’s say your boss wants you to do a research study for your company and needs you to look at the average amount spent per stock in the last six days.

You open your data and have these variables:

In this scenario, we’ll have to find a way to combine our two variables to get the outcome that we need.

Now that we’ve combined our two variables, the result we get is our official criterion variable.

This new variable will help us explain our solution, and we can describe the correlation and relationship between the other predictor variables in-depth.

What is a Predictor variable?

A predictor variable is a variable used to predict another variable’s value, and these values can be utilized in both classification and regression. In most machine learning and statistics projects, there will be many predictor variables, as accuracy usually increases with more data.

For example, if you want to predict the price of a house, the predictor variables might be the size of the house, the number of bedrooms, the number of bathrooms, and the location.

The predictor variable sometimes is referred to as the independent variable. Since we know in machine learning projects, there is generally more than one predictor variable; these are sometimes referred to as “X.”

Once our target ( criterion variable ) is split from our independent variables ( predictor variables ), many data scientists will refer to this batch of predictor variables as just variables.

What is the difference between a criterion variable and a predictor variable?

The main difference between a criterion variable and a predictor variable is that a predictor variable is used to find the values of the criterion variable. While there can be many predictor variables in a project, there is usually only a single criterion variable.

One of the most critical steps in any project design or machine learning project is understanding the business context and how that relates to selecting the correct criterion variable.

What do a Criterion Variable and Predictor Variable Look Like in a Machine Learning Project?

Since we now know that predictor variables are variables used to predict the value of a criterion variable, we can discuss the different types of predictor variables that exist.

There are two main types of predictor variables: categorical and quantitative.

Categorical predictor variables are those that can be divided into groups or categories. For example, a categorical predictor variable could be color, with the categories: red, blue, and green.

Quantitative predictor variables are those that can be quantified or measured. For example, a quantitative predictor variable could be age, with the values being the ages of different individuals.

Python Example of Criterion and Predictor Variables

Your boss wants you to build the most accurate model you can to predict what someone’s salary (in dollars) will be.

Your boss has provided you with the dataset below:

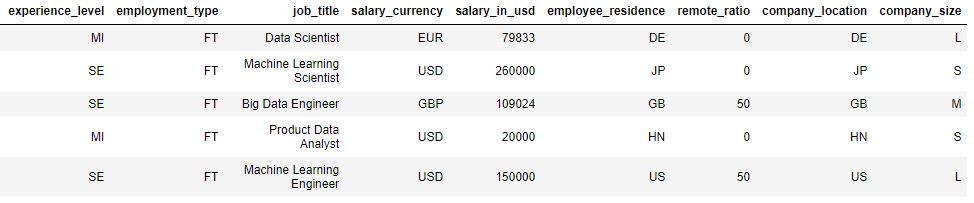
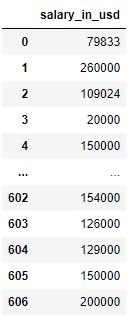
You quickly notice that a good criterion variable would be salary_in_usd, and you split that out from the rest of the data.

Our Criterion Variable:

Our Predictor Variables (Mix of Quantitative and Categorical)

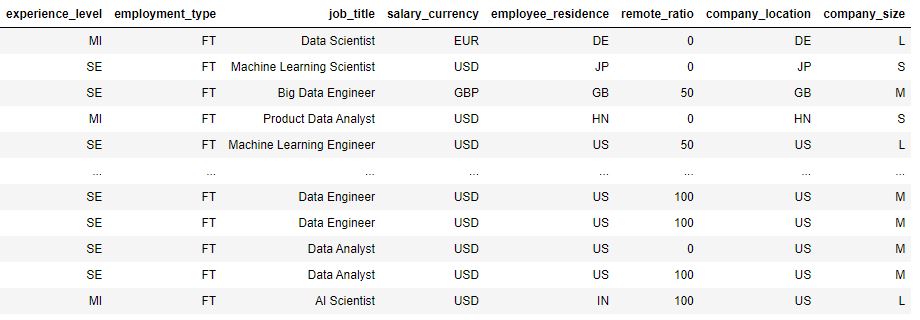
Now that you have your datasets, you’re ready to start modeling!

Do Criterion Variables Exist in Unsupervised Learning?

Criterion variables do not exist in unsupervised learning. Since unsupervised learning does not have labeled data, we do not have a dependent variable (criterion variable). These projects will only have predictor variables that we use to try to draw insights.

Other Articles in our Machine Learning 101 Series

We have many quick guides that go over some of the fundamental parts of machine learning. Some of those guides include:

• Reverse Standardization : Now that you can split your data correctly, use this guide to build your first model.
• CountVectorizer vs. TFIDFVectorizer : Two classical NLP algorithms; you’ll need correct data splitting here to take these two on.
• Welch’s T-Test : Do you know the difference between the student’s t-test and welch’s t-test? Don’t worry, we explain it in-depth here.
• Parameter Versus Variable : Commonly misunderstood – these two aren’t the same thing. This article will break down the difference.
• Feature Selection With SelectKBest Using Scikit-Learn : Feature selection is tough; we make it easy for both regression and classification in this guide.
• Normal Distribution vs. Uniform Distribution : Now that you know the difference between your variables, you can now start to understand the different distributions these variables can have.
• Heatmaps In Python : Visualizing data is key in data science; this post will teach eight different libraries to plot heatmaps.
• Gini Index vs. Entropy : Learn how decision trees make splitting decisions. These two are the workhouse of top-performing tree-based methods.
• Recent Posts

• Make Your Software More Green with Renewable Energy [Discover the Game-Changing Tips] - May 12, 2024
• How to Price a Software Development Project [Must-See Tips] - May 11, 2024
• TurboTax Online vs. Software: Which is Better? [Find Out Now!] - May 11, 2024

Trending now

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.4: The “Role” of Variables- Predictors and Outcomes

• Last updated
• Save as PDF
• Page ID 3947

• Danielle Navarro
• University of New South Wales

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Okay, I’ve got one last piece of terminology that I need to explain to you before moving away from variables. Normally, when we do some research we end up with lots of different variables. Then, when we analyse our data we usually try to explain some of the variables in terms of some of the other variables. It’s important to keep the two roles “thing doing the explaining” and “thing being explained” distinct. So let’s be clear about this now. Firstly, we might as well get used to the idea of using mathematical symbols to describe variables, since it’s going to happen over and over again. Let’s denote the “to be explained” variable Y , and denote the variables “doing the explaining” as X1, X2, etc.

Now, when we doing an analysis, we have different names for X and Y , since they play different roles in the analysis. The classical names for these roles are independent variable (IV) and dependent variable (DV). The IV is the variable that you use to do the explaining (i.e., X) and the DV is the variable being explained (i.e., Y ). The logic behind these names goes like this: if there really is a relationship between X and Y then we can say that Y depends on X, and if we have designed our study “properly” then X isn’t dependent on anything else. However, I personally find those names horrible: they’re hard to remember and they’re highly misleading, because (a) the IV is never actually “independent of everything else” and (b) if there’s no relationship, then the DV doesn’t actually depend on the IV. And in fact, because I’m not the only person who thinks that IV and DV are just awful names, there are a number of alternatives that I find more appealing. The terms that I’ll use in these notes are predictors and outcomes. The idea here is that what you’re trying to do is use X (the predictors) to make guesses about Y (the outcomes). 4 This is summarised in Table 2.2.

4 Annoyingly, though, there’s a lot of different names used out there. I won’t list all of them – there would be no point in doing that – other than to note that R often uses “response variable” where I’ve used “outcome”, and a traditionalist would use “dependent variable”. Sigh. This sort of terminological confusion is very common, I’m afraid.

13 Predictor and Outcome Variable Examples

A predictor variable is used to predict the occurrence and/or level of another variable, called the outcome variable.

A researcher will measure both variables in a scientific study and then use statistical software to determine if the predictor variable is associated with the outcome variable. If there is a strong correlation, we say the predictor variable has high predictive validity .

This methodology is often used in epidemiological research. Researchers will measure both variables in a given population and then determine the degree of association between the predictor and outcome variable.

This allows scientists to examine the connection between many meaningful variables, such as exercise and health or personality type and depression, just to give a few examples.

Although this type of research can provide significant insights that help us understand a phenomenon, we cannot say that the predictor valuable causes the outcome variable.

In order to use the term ‘cause and effect’, the researcher must be able to control and manipulate the level of a variable and then observe the changes in the other variable.

Definition of Predictor and Outcome Variables

In reality, many variables usually affect the outcome variable. So, researchers will measure numerous predictor variables in the population under study and then determine the degree of association that each one has with the outcome variable.

It sounds a bit complicated, but fortunately, the use of a statistical technique called multiple regression analysis simplifies the process.

As long as the variables are measured accurately and the population size is large, the software will be able to determine which of the predictor variables are associated with the outcome variable and the degree of association.

Not all predictors will have an equal influence on the outcome variable. Some may have a very small impact, some may have a substantial impact, and others may have no impact at all.

Predictor and outcome are not to be confused with independent and dependent variables .

Examples of Predictor and Outcome Variables

1. diet and health.

Does the food you eat have any impact on your physical health? This is a question that a lot of people want to know the answer to.

Many of us have very poor diets, with lots of fast food and salty snacks. Other people, however, almost never make a run through the drive-thru, and consume mostly fruits and veggies.

Thankfully, epidemiological research can give us a relatively straightforward answer. First, researchers measure the quality of diet of each person in a large population.

So, they will track how much fast food and fruits and veggies people consume. There are a lot of different ways to measure this.

Secondly, researchers will measure some aspects of health. This could involve checking cholesterol levels, for example. There are a lot of different ways to measure health. The final step is to input all of the data into the statistical software program and perform the regression analysis to see the results.

Quality of diet is the predictor variable, and health is the outcome variable.

2. Noise Pollution and IQ

One scientist speculates that living in a noisy environment will affect a person’s ability to concentrate, which will then affect their mental acuity and subsequent cognitive development .

So, they decide to conduct a study examining the relationship between noise pollution and IQ.

First, they travel through lots of different neighborhoods and use a sound level meter to assess noise pollution. Some neighborhoods are in the suburbs, and some are near busy highways or construction sites.

Next, they collect data on SAT scores of the children living in those neighborhoods.

They then conduct a regression analysis to determine the connection between the sound level meter data and the SAT scores.

In this example, the predictor variable is the sound levels, and the outcome variable is the SAT scores.

Surprisingly, the results revealed an inverse relationship between noise and SAT scores. That is, the more noise in the environment the higher the SAT score. Any idea why?

3. Family Income and Achievement Test Scores

In this study, sociologists conducted a study examining the relationship between how much income a family has and the achievement test scores of their children.

The researchers collected data from schools on the achievement test scores of hundreds of students and then estimated the household income of the families based on the occupation of the parents.

The results revealed a strong relationship between family income and test scores, such that the higher the family income, the higher the test score of the child.

In this example, family income is the predictor variable, and test score is the outcome variable.

4. Parental Utterances and Children’s Vocabulary

A team of child psychologist is interested in the impact of how much parents talk to their child and that child’s verbal skills.

So, they design a study that involves observing families in the home environment. They randomly choose 50 families to study that live nearby.

A research assistant visits each family, records, and later counts the number of utterances spoken by the mother directed at their only child.

On a different occasion, a second research assistant administers a verbal skills test to every child. Yes, this type of study takes a lot of time.

The regression analysis reveals a direct relationship between the number of utterances from the mother and the child’s verbal skills test score. The more utterances, the higher the score.

In this example, the predictor variable is the number of utterances directed at the child, and the outcome variable is the child’s verbal skills test score.

5. Video Games and Aggressiveness

The debate about the effects of TV violence and video games has been raging for nearly 70 years. There have been hundreds, maybe even thousands of studies conducted on the issue.

One type of study involves assessing how frequently a group of people play certain video games and then tracking their level of aggressiveness over a period of time.

Of course, there are other factors involved in whether a person is aggressive or not, so the researchers might assess those variables as well.

In this type of study, the predictor variable is the frequency of playing video games, and the outcome variable is the level of aggressiveness.

6. Chemicals in Food Products and Puberty

In many countries, farmers may inject various antibiotics and growth hormones into their cattle to ward off infection and increase body mass and milk production.

Unfortunately, those chemicals do not disappear once the food hits the supermarket shelves. Some parents, educators, and food scientists began to notice an association between these agricultural practices and the onset of puberty in young children.

Numerous scientific studies were conducted examining the relationship between these practices and puberty.

So, the researchers studied the relationship between the predictor variable (chemicals in food) and the outcome variable (onset of puberty).

7. Full Moon and Craziness

Who hasn’t heard that a full moon brings out the crazies? A lot of people have theorized that when the moon is full, people get a little bit wild and uninhibited.

That can lead to people doing things they would not normally do.

To put this theory to the test, a group of criminologists decides to examine the police records of numerous large cities and compare that with the lunar cycle.

The researchers input all of the data into a stats program to examine the degree of association between police incidents and the moon.

In this study, the lunar cycle is the predictor variable, and contravention of the law is the outcome variable.  

8. Testosterone and Leadership Style

There are many types of leadership styles. Some leaders are very people-oriented and try to help their employees prosper and feel good about their jobs.

Other leaders are more task-driven and prefer to clearly define objectives, set deadlines, and push their staff to work hard.

To examine the relationship between leadership style and testosterone, a researcher first administers a questionnaire to hundreds of employees in several types of companies. The questionnaire asks the employees to describe the leadership style of their primary supervisor.

At the same time, the researcher also collects data on the testosterone levels of those supervisors and matches them with the questionnaire data.

By examining the association between the two, it will be possible to determine if there is a link between leadership style and testosterone.

The predictor variable is testosterone, and the outcome variable is leadership style.  

9. Personality Type and Driver Safety

A national bus company wants to hire the safest drivers possible. Fewer accidents mean passengers will be safe and their insurance rates will be lower. 

So, the HR staff begin collecting data on the safety records of their drivers over the last 3 years. At the same time, they administer a personality inventory that assesses Type A and Type B personalities.

The Type A personality is intense, impatient, and highly competitive. The Type B personality is easygoing and relaxed. People have varying levels of each type.

The HR department wants to know if there is a relationship between personality type (A or B) and accidents among their drivers.

The predictor variable is personality type, and the outcome variable is the number of accidents.

10. Vitamins and Health

Americans take a lot of vitamins. However, there is some debate about whether vitamins actually do anything to improve health.

There are so many factors that affect health, will taking a daily supplement really count?

So, a group of small vitamin companies pull their resources and hire an outside consulting firm to conduct a large-scale scientific study.

The firm randomly selects thousands of people from throughout the country to participate in the study. The people selected come from a wide range of SES backgrounds, ethnicities, and ages.

Each person is asked to go to a nearby hospital and have a basic health screening that includes cholesterol and blood pressure. They also respond to a questionnaire that asks if they take a multi-vitamin, how many and how often.

The consulting firm then compares the degree of association between multi-vitamins and health.

Multi-vitamin use is the predictor variable, and health is the outcome variable.

11. Automobiles and Climate Change

A group of climatologists has received funding from the EU to conduct a large-scale study on climate change.

The researchers collect data on a wide range of variables that are suspected of affecting the climate. Some of those variables include automobile production, industrial output, size of cattle herds, and deforestation, just to name a few.

The researchers proceed by gathering the data beginning with the 1970s all the way to the current year. They also collect data on yearly temperature fluctuations.

Once all the data is collected, it is put into a stats program, and a few minutes later, the results are revealed.

In this example, there are many predictor variables, such as automobile production, and one primary outcome variable (yearly temperature fluctuations).

12. Smartphone Use and Eye Strain

If you’ve ever noticed, people spend a lot of time looking at their smartphones.

When they are reading, when they are waiting in line, in bed at night, and even when walking from point A to point B.

Many optometrists are concerned that all of this screen time is doing harm to people’s eyesight. So, they decide to conduct a study.

Fortunately, they all work for a nationwide optometry company with offices located in Wal-Marts.

When patients come into their office, they give each one a standard eye exam. They also put a question on the in-take form asking each person to estimate how many hours a day they spend looking at their smartphone screen. 

Then they examine the relation between screen-time usage and the results of the eye exams.

In this study, the predictor variable is screen-time, and the outcome variable is the eye-exam results.

13. Soil Composition and Agricultural Yields

Although farming looks easy, it can be a very scientific enterprise. Agriculturalists study the composition of soil to help determine what type of food will grow best.

Today, they know a lot about which soil nutrients affect the growth of different plant varieties because there have been decades of studies.

The research involves collecting soil samples, measuring crop yields, and then examining the association between the two.

For example, scientists will measure the pH levels, mineral composition, as well as water and air content over many acres of land and relate that to the amount harvested of a particular crop (e.g., corn).

In this example, there are numerous predictor variables, all of which have some effect on crop growth, which is the outcome variable.

Even though there are so many variables to consider, the regression analysis will be able to tell us how important each one is in predicting the outcome variable.

There can be a lot of reasons why something happens. More often than not, nothing happens as a result of just one factor. Our physical health, climate change, and a person’s level of aggressiveness are all the result of numerous factors.

Fortunately for science, there is a brilliant way of determining which factors are connected to a phenomenon and how strong is each and every one of them.

By collecting data on a predictor variable (or variables) and then examining the association with the outcome variable, we can gain valuable insights into just about any subject matter we wish to study.

Ferguson, C. J., & Kilburn, J. (2010). Much ado about nothing: The misestimation and overinterpretation of violent video game effects in Eastern and Western nations: Comment on Anderson et al. (2010). Psychological Bulletin, 136 (2), 174–178. https://doi.org/10.1037/a0018566

Ferguson, C. J., San Miguel, C., Garza, A., & Jerabeck, J. M. (2012). A longitudinal test of video game violence influences on dating and aggression: A 3-year longitudinal study of adolescents, Journal of Psychiatric Research, 46 (2), 141-146. https://doi.org/10.1016/j.jpsychires.2011.10.014

Gordon, R. (2015). Regression Analysis for the Social Sciences (2 nd ed). New York: Routledge.

Hoff, E. (2003). The specificity of environmental influence: Socioeconomic status affects early vocabulary development via maternal speech. Child Development, 74 (5), 1368–1378.

Lopez-Rodriguez, D., Franssen, D., Heger, S., & Parent, AS. (2011). Endocrine-disrupting chemicals and their effects on puberty. Best Practice & Research Clinical Endocrinology & Metabolism, 35 (5), 101579. https://doi.org/10.1016/j.beem.2021.101579

Man, A., Li, H., & Xia, N. (2020). Impact of lifestyles (Diet and Exercise) on vascular health: Oxidative stress and endothelial function. Oxidative Medicine and Cellular Longevity , 1496462. https://doi.org/10.1155/2020/1496462

Thompson, R., Smith, R. B., Karim, Y. B., Shen, C., Drummond, K., Teng, C., & Toledano, M. B. (2022). Noise pollution and human cognition: An updated systematic review and meta-analysis of recent evidence. Environment International , 158 , 106905.

Dave Cornell (PhD)

Dr. Cornell has worked in education for more than 20 years. His work has involved designing teacher certification for Trinity College in London and in-service training for state governments in the United States. He has trained kindergarten teachers in 8 countries and helped businessmen and women open baby centers and kindergartens in 3 countries.

• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 25 Positive Punishment Examples
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 25 Dissociation Examples (Psychology)
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ 15 Zone of Proximal Development Examples
• Dave Cornell (PhD) https://helpfulprofessor.com/author/dave-cornell-phd/ Perception Checking: 15 Examples and Definition

Chris Drew (PhD)

This article was peer-reviewed and edited by Chris Drew (PhD). The review process on Helpful Professor involves having a PhD level expert fact check, edit, and contribute to articles. Reviewers ensure all content reflects expert academic consensus and is backed up with reference to academic studies. Dr. Drew has published over 20 academic articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education and holds a PhD in Education from ACU.

• Chris Drew (PhD) #molongui-disabled-link 25 Positive Punishment Examples
• Chris Drew (PhD) #molongui-disabled-link 25 Dissociation Examples (Psychology)
• Chris Drew (PhD) #molongui-disabled-link 15 Zone of Proximal Development Examples
• Chris Drew (PhD) #molongui-disabled-link Perception Checking: 15 Examples and Definition

1 thought on “13 Predictor and Outcome Variable Examples”

If I want to undertake an interventional study where I measure the Knowledge, attitudes and practices of adolescents in 3 key sexual and reproductive areas. And their parents’ acceptance of ASRH education for their children, and their misconceptions of ASRH. And then I introduce both children and parents to ASRH education. Then I do an end line to look for improvement in the adolescent’s KAP in those 3 areas, and an increased acceptance of ASRH education among parents, what is my predictor variable and outcome variable?

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

• Open access
• Published: 09 May 2024

Development and validation of a predictive model for the risk of sarcopenia in the older adults in China

• Qiugui Li 1   na1 ,
• Hongtao Cheng 1   na1 ,
• Wenjiao Cen 1 ,
• Tao Yang 2 &
• Shengru Tao 3  

European Journal of Medical Research volume  29 , Article number:  278 ( 2024 ) Cite this article

53 Accesses

Metrics details

Sarcopenia is a progressive age-related disease that can cause a range of adverse health outcomes in older adults, and older adults with severe sarcopenia are also at increased short-term mortality risk. The aim of this study was to construct and validate a risk prediction model for sarcopenia in Chinese older adults.

This study used data from the 2015 China Health and Retirement Longitudinal Study (CHARLS), a high-quality micro-level data representative of households and individuals aged 45 years and older adults in China. The study analyzed 65 indicators, including sociodemographic indicators, health-related indicators, and biochemical indicators.

3454 older adults enrolled in the CHARLS database in 2015 were included in the final analysis. A total of 997 (28.8%) had phenotypes of sarcopenia. Multivariate logistic regression analysis showed that sex, Body Mass Index (BMI), Mean Systolic Blood Pressure (MSBP), Mean Diastolic Blood Pressure (MDBP) and pain were predictive factors for sarcopenia in older adults. These factors were used to construct a nomogram model, which showed good consistency and accuracy. The AUC value of the prediction model in the training set was 0.77 (95% CI = 0.75–0.79); the AUC value in the validation set was 0.76 (95% CI = 0.73–0.79). Hosmer–Lemeshow test values were P  = 0.5041 and P  = 0.2668 (both P  > 0.05). Calibration curves showed significant agreement between the nomogram model and actual observations. ROC and DCA showed that the nomograms had good predictive properties.

Conclusions

The constructed sarcopenia risk prediction model, incorporating factors such as sex, BMI, MSBP, MDBP, and pain, demonstrates promising predictive capabilities. This model offers valuable insights for clinical practitioners, aiding in early screening and targeted interventions for sarcopenia in Chinese older adults.

With the rapid development of China’s economy, the country has gradually transitioned into an aging society. According to the findings of the seventh census conducted in 2020, China’s population aged 60 and above is projected to exceed 260 million, accounting for 18.7% of the total population. Within this demographic, those aged 65 and above are expected to surpass 190 million, making up 13.5% of the total population [ 1 ]. The increasing number of older adults will significantly escalate expenditures within the social security system, imposing a considerable financial burden on the government. Among the various health-related factors contributing to disability in older adults, sarcopenia and cognitive impairment have attracted significant academic and clinical attention [ 2 ]. Currently, China’s focus on sarcopenia has started relatively late, with general hospitals showing evident specialization and insufficient understanding of sarcopenia, which has yet to be categorized into a specific field.

Sarcopenia was traditionally defined by a reduction in muscle mass, but current research highlights the significance of muscle strength and its impact on physical function [ 3 ]. Since 2016, the World Health Organization has officially recognized sarcopenia as a disease and a pressing public health concern in aging populations [ 4 , 5 , 6 ]. The loss of skeletal muscle mass is central to sarcopenia and can lead to physical dysfunction [ 7 ]. Studies indicate that sarcopenia affects over a quarter of older adults in Chinese communities [ 8 ], with a global incidence among individuals over 60 ranging from 10 to 27% [ 9 ]. Various factors contribute to the onset of sarcopenia, including age, nutrition intake, physical inactivity, diseases, and iatrogenic factors [ 10 ]. Risk factors such as aging, malnutrition, smoking, and low BMI have been identified [ 11 , 12 ], with higher prevalence observed in patients with chronic obstructive pulmonary disease [ 13 ], chronic heart failure [ 14 ] and chronic liver disease [ 15 ]. Furthermore, sarcopenia is associated with adverse outcomes like falls, functional decline, frailty, and mortality [ 16 , 17 ].

Although there are a number of sarcopenia risk prediction models, they all have some limitations. For example, some models have small sample sizes, which may limit their generalizability and applicability to different older adults [ 18 ]. Additionally, some models rely on predictor variables that are difficult and time-consuming to collect, limiting their usefulness in real-world clinical applications [ 19 ]. Furthermore, there are models that do not capture all risk factors for sarcopenia, which may affect their predictive accuracy [ 20 ]. These limitations underscore the need for further research to develop more comprehensive and practical prediction models for sarcopenia.

In contrast to foreign studies primarily focused on disease-specific correlations with sarcopenia, research in our country is predominantly centered on current situations and influencing factors. Key factors such as age, exercise habits, number of diseases, malnutrition, risk of falls, and fatigue are identified as easily inducible factors for sarcopenia. This study aims to identify and incorporate these factors into the construction of a sarcopenia risk prediction model, providing valuable insights for early screening and intervention by clinical medical staff.

Data source

We utilized data from the China Health and Retirement Longitudinal Study (CHARLS), publicly accessible at http://charls.pku.edu.cn . CHARLS is an ongoing longitudinal survey encompassing families and individuals aged 45 and older across 150 counties and 450 communities (villages) within 28 provinces, autonomous regions, and municipalities nationwide. Its comprehensive content spans demographic, economic, health, pension, and other pertinent information. Approval for this project was granted by the Biomedical Ethics Committee of Peking University (Beijing, China) (IRB00001052-11015), with our study adhering strictly to the principles outlined in the Declaration of Helsinki, and obtaining informed consent from all participants. Our analysis specifically focused on CHARLS2015 data, wherein after excluding subjects with missing data, a total of 3454 participants were ultimately included in our study cohort. Notably, our research targeted individuals aged 60 and above. The flowchart of the study is outlined in Fig.  1 .

Flowchart of the study

Data extraction

Assessment of symptoms of sarcopenia.

Sarcopenia was evaluated according to the criteria recommended by the AWGS2019 [ 7 ], which encompass muscle strength, physical performance and appendicular skeletal muscle mass (ASM). Handgrip strength (unit: kg) was assessed in both the dominant and non-dominant hand using the YuejianTM WL-1000 dynamometer. Participants were instructed to squeeze the handle as firmly as possible for 3 s. Measurements were taken twice for each hand, with a minimum interval of 15 s between trials. The recorded value represents the average of the maximum grip strength from both hands. The thresholds for low grip strength established by AWGS are < 28 kg for men and < 18 kg for women [ 21 ]. Physical performance decline, as per AWGS criteria, is defined as 5 times sitting time > 12 s or 6-m walking speed < 1 m/s [ 22 ]. ASM measurements were derived using validated anthropometric equations specifically developed for the Chinese population [ 23 , 24 ]. The study demonstrated strong concordance between the ASM equation and Dual-Energy X-ray Absorptiometry (DXA) [ 23 , 24 ]. In our study cohort, the cutoff for low muscle mass was determined based on sex-specific criteria, equating to a minimum of 20% of height-adjusted muscle mass (ASM/Ht 2 ) [ 23 , 24 , 25 , 26 ]. Height and weight were recorded in centimeters and kilograms, respectively. Regarding sex, a value of 1 represents male and a value of 2 represents female. Consequently, individuals with ASM/Ht 2  < 5.69 kg/m 2 for females and ASM/Ht 2  < 6.88 kg/m 2 for males were classified as having low muscle mass. The ASM equation utilized is:

Sarcopenia manifests through a blend of diminished muscle strength, impaired physical performance, or decreased appendicular skeletal muscle mass. Diagnosis typically hinges on identifying low muscle strength, either alone or accompanied by reduced appendicular skeletal muscle mass. Individuals displaying low muscle strength, compromised physical performance, and diminished appendicular skeletal muscle mass were classified as having severe sarcopenia. For the purposes of this study, participants were segregated into two main groups: those with sarcopenia and those without.

Assessment of depressive symptoms

Depressive symptoms were assessed with a 10-item stream using the Center for Epidemiologic Studies Depression Scale (CES-D) to assess depressive mood and behavior. CESD pay attention to the individual's situation in the past week and rate it as “Rarely or none of the time (< 1 day)”, “Some or a little of the time (1-2 days)”, “Occasionally or a moderate amount of the time (3-4 days)”, and “Most or all of the time (5-7 days)” according to the frequency of symptoms, and assign 0, 1, 2, and 3 points, respectively, with higher scores representing individuals with more severe depressive symptoms. In this study, according to the research results of ROBERTS and his colleagues [ 27 ], CESD ≥ 16 is considered to have depressive symptoms, and < 16 is considered to have no depressive symptoms.

Assessment of cognitive function

CHARLS measures cognitive function in three parts: Telephone Interview for Cognitive Status (TICS), Word Recall, and Picture Drawing. The higher the score, the better the cognitive function. The TICS requires the subject to correctly name the year, month, day, day of the week, and season, and each correct answer is worth 1 point; the subject is required to correctly calculate 100-7, and each correct answer is worth 1 point, and the scores of the two parts are added together, the total score is 0–10 points, which mainly evaluates the subject’s orientation, calculation ability and attention. Word recall: the researchers read 10 words and asked the subjects to recall the 10 words in a short time and after answering several other questions, each correct recall of a word was recorded as 1 point, and the average score of the two words recalled was taken. A total score of 0–10 points was used to assess episodic memory ability. Picture drawing: the researcher provides a picture of two overlapping five-pointed stars and asks the subjects to draw the figure on a white piece of paper. If they can draw a similar figure, they get 1 point, and if they cannot, they get 0 points. It is used to evaluate the subject's visuospatial ability.

Assessment of activities of daily living

Activities of daily living include physical self-maintenance scale (PSMS) and instrumental activities of daily living (IADL). PSMS evaluates essential tasks like dressing, bathing, eating, getting out of bed, going to the toilet, controlling bowel and urine. Meanwhile, IADL assesses more complex activities such as shopping, cooking, doing housework, taking medicine, managing money and making phone calls. According to the degree, it is divided into “No, I don’t have any difficulty”, “I have difficulty but can still do it”, “Yes, I have difficulty and need help” and “I cannot do it”. These options correspond to scores of 1, 2, 3, and 4, respectively, indicating higher scores reflect greater impairment in the skill.

Socio-demographic information

Socio-demographics include sex, age, marital status, education level, address and residence. Sex is defined as male and female. Education level was divided into no schooling, primary school, junior high school and above. Marital status was defined as married if the subject was currently married and living with a spouse; unmarried if the subject was currently separated, divorced, widowed, or never married. Address is divided into “Family house”, “Nursing home” and “Other”. Residence is divided into “The center of city/town”, “Combination zone between urban and rural areas”, “Village” and “Special area”.

Health-related information

Within the health-related data examined as potential risk factors, a broad spectrum of conditions and indicators were included. These encompassed physical disabilities, neurological impairments such as brain damage, sensory deficits like blindness, deafness and muteness, as well as prevalent medical conditions including hypertension, dyslipidemia, diabetes, cancer and various chronic diseases affecting organs such as the lungs, liver, heart and kidneys. Mental health aspects such as emotional disturbances, memory-related ailments, and joint diseases or rheumatism were also considered. Other factors such as asthma, pain (specifically chronic pain), history of surgeries like cataract or hip fracture, usage of assistive devices like hearing aids, dental health indicators like tooth loss and lifestyle habits like smoking status, alcohol consumption, and social activity levels were evaluated. Additionally, variables related to accidents, falls, vision and hearing impairments and subjective health assessments were included. Specifically, aspects like distant vision, near vision, hearing ability and self-assessment of health status were categorized as “good”, “fair” or “poor”, while the remaining variables were dichotomized as “yes” or “no”. These variables can be directly obtained from the CHARLS questionnaire.

Statistical methods

In this study, data from the CHARLS database in 2015 were selected for analysis. Continuous variables were expressed as medians and interquartile ranges, and rank sum tests were used to compare between groups; categorical variables were expressed as percentages, and χ 2 tests or Fisher's exact tests were used to compare between groups. First, the data set is randomly divided into training set ( n  = 2417) and verification set ( n  = 1037) according to the ratio of 7:3. During this process, we set a random seed to ensure the randomization and repeatability of the sampling [ 28 ].

Utilizing a nomogram to depict the risk of sarcopenia among the older adults in China, we employed Least Absolute Selection and Shrinkage Operator (LASSO) regression analysis to construct and validate the model. We chose LASSO regression due to its capability to manage high-dimensional datasets with multicollinearity, effectively selecting variables and improving model interpretability. In contrast to Rigid and Elastic Net models, LASSO provides greater flexibility in variable selection and sparsity, making it the preferred choice for our specific research objectives and dataset characteristics. This choice ultimately leads to a more accurate and concise model. The primary R packages utilized in this study include: “mice”, “tableone”, “glmnet”, “rms”, “pROC” and “rmda”. First, LASSO regression analysis was performed on the training set data to select predictors of sarcopenia in Chinese older adults [ 29 , 30 ]. Then, the tuning parameter (λ) suitable for LASSO regression analysis was determined by tenfold cross-validation, and the most significant features were screened using the LASSO algorithm. Finally, the selected predictors were included in the multivariate logistic regression analysis and the predictors with P -value < 0.05 were included in the nomogram model. The maximum missing value of all extracted variables does not exceed 20%, and multiple imputation is used to handle missing data [ 31 ].

In this study, the area under the receiver operating characteristic curve (AUROC) was used to determine the discriminative ability of the model. Calibration curves are used to determine the degree of agreement between predicted probabilities and observed results. Clinical validity was assessed by decision curve analysis (DCA). All data in this study were analyzed using R software (version 4.1.0). All tests were two-tailed and P  < 0.05 was considered statistically significant.

General information and clinical characteristics of the older adults

A total of 3454 older adult subjects (aged 60 years and older) were enrolled in this study, and the screening process for specific subjects is shown in Fig.  1 . The general information and clinical characteristics of the subjects are listed in Table  1 . There were 1708 men (49.4%) and 1746 women (50.6%). More detailed information is provided in a separate document (see supplement information).

Prevalence and associated variables of sarcopenia

The prevalence of sarcopenia was 28.8% (997/3454). There were significant differences in sex, BMI, and MDBP between the two groups of older adults ( P  < 0.05). According to clinical experience [ 32 , 33 ], pain and MSBP were included in the model, and significant differences were found between the two groups of older adults. In the older adults, 2417 (70%) and 1037 (30%) were randomly assigned to the training and validation sets, respectively. The comparison of training and validation sets in the supplement information shows no significant difference between the two groups ( P  > 0.05).

LASSO logistic regression

In this investigation, non-zero coefficients were identified as potential predictors of frailty through the LASSO regression model (Fig.  2 A and Fig.  2 B). Subsequently, these underlying factors linked with sarcopenia were incorporated into multiple logistic regression models utilizing the ‘rms’ package within the ‘R’ software environment. Ultimately, it was found that sex ( P  < 0.001), BMI ( P  < 0.001), MSBP ( P  < 0.001), MDBP ( P  < 0.001) and pain ( P  = 0.015) were correlated with sarcopenia in the older adults (Table  2 ).

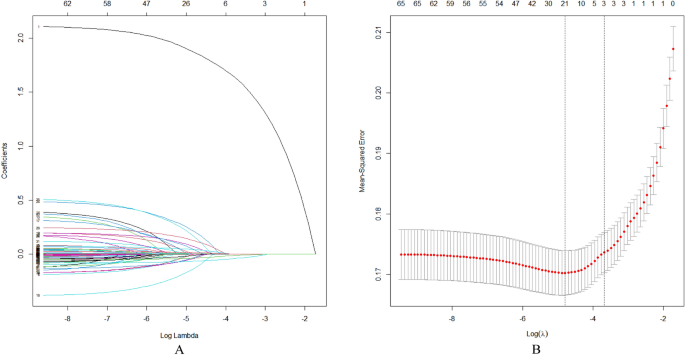
Demographic and clinical feature selection using the LASSO regression model. A According to the logarithmic (lambda) sequence, a coefficient profile was generated, and non-zero coefficients were produced by the optimal lambda. B The optimal parameter (lambda) in the LASSO model was selected via tenfold cross-validation using minimum criteria. The partial likelihood deviation (binomial deviation) curve relative to log (lambda) was plotted. A virtual vertical line at the optimal value was drawn using one SE of minimum criterion (the 1-SE criterion)

Developing predictive models

Based on tenfold cross-validation, LASSO regression analysis was used to screen the best predictors of the model. Multiple logistic regression was used to build the prediction model. The variance inflation factor (VIF) test was performed, and the VIF values of all variables were < 4. Without covariance, the model fits well. The predictive model consists of variables with a P -value of less than 0.05 in a multivariate logistic regression. These variables included sex, BMI, MSBP, MDBP, pain as predictors. The prediction model adopts nomogram, which can be used to quantitatively predict the risk of sarcopenia in the older adults (Fig.  3 ).

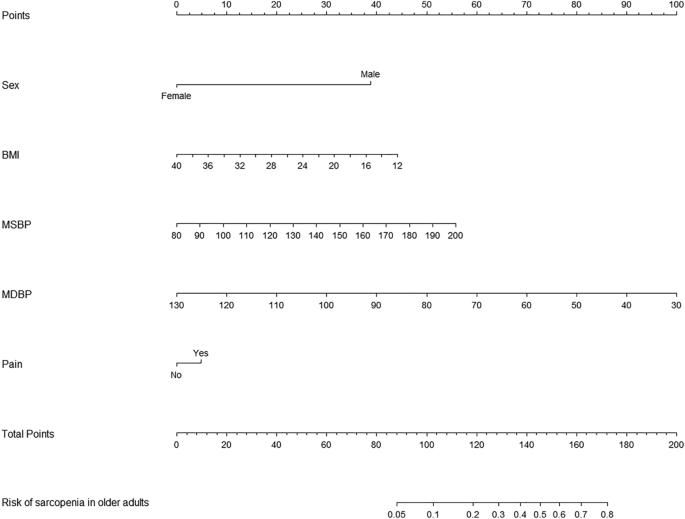
A nomogram for predicting sarcopenia in the older adults in China

Validating predictive models

AUC (area under curve) is a statistical metric that measures the performance of a classifier, specifically indicating the probability that a randomly chosen positive sample will rank higher than a randomly chosen negative sample. It is commonly utilized to assess the effectiveness of machine learning models. AUC values were computed to evaluate the discriminative power of the prediction model, by examining the incidence of sarcopenia among older adults in both the training and validation datasets. As shown in Fig.  4 A, B, the AUC value of the predictive model in the training set was 0.77 (95% CI = 0.75–0.7901); the AUC value in the validation set was 0.76 (95% CI = 0.7287–0.7904). These data suggest that the nomogram has good discriminative power and predictive value, correctly identifying sarcopenic and non-sarcopenic patients.

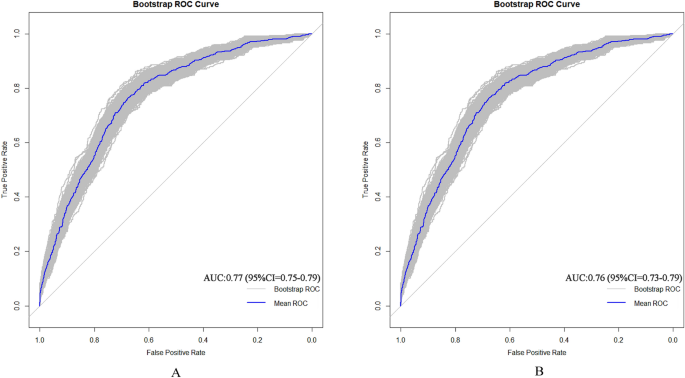
A Nomogram ROC curves generated from the training dataset. B Nomogram ROC curves generated using the validation dataset

Correcting the predictive model

Calibration plots and the Hosmer–Lemeshow goodness-of-fit test were used to evaluate the model plots ( P  > 0.05 indicated that the model fit was very good). The test results show that the model fits both the training set ( χ 2  = 7.305, df  = 8, p  = 0.5041) and the validation set ( χ 2  = 9.9748, df  = 8, p  = 0.2668) well. The calibration plots of the training and validation sets based on the multivariate logistic regression model are shown in Fig.  5 A, B. The calibration curves of the modality maps showed that the predicted probability of sarcopenia for the training set (Fig.  5 A) and the validation set (Fig.  5 B) were highly consistent with the actual probability of sarcopenia.

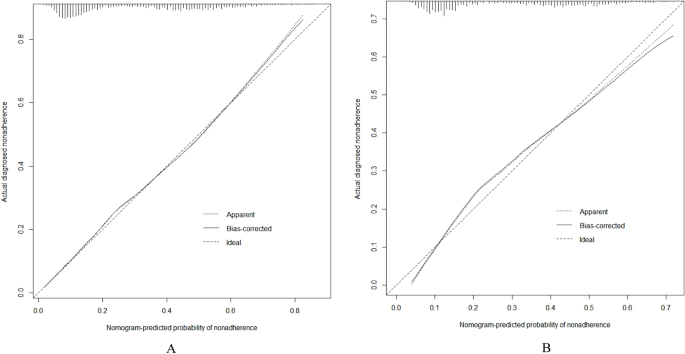
A Calibration plots for training dataset. B Calibration plots for validation dataset

Clinical validity assessment

The DCA method was used to evaluate the clinical validity of the model, and the results are shown in Figs.  6 A, B. From the decision curve, the net benefit of the prediction model on the internal validation set is significantly higher than that of the two extreme cases, indicating that the nomogram model has better net benefit and prediction accuracy.

A DCA curves for training data set. B DCA curves for validation data set

This study reveals that the prevalence of sarcopenia among the older adults in China stands at 28.8%, aligning with the findings reported by Cruz-Jentoft and his colleagues [ 34 ], which ranged from 1 to 29%. Sarcopenia can lead to reduced mobility, increased disability, falls, and risk of death [ 35 , 36 ]. Therefore, identification of high-risk individuals is critical to preventing sarcopenia and its associated adverse outcomes.

This study shows that sex is a predictor of sarcopenia, and the results show that sarcopenia is related to sex, and the male population suffers from sarcopenia more often, which is consistent with previous research findings [ 37 , 38 ]. The reason for the analysis may be that sarcopenia is caused by genetic inheritance or gene mutation. Since the disease-causing gene is located on the sex chromosome, and men have only one chromosome, one gene mutation is enough to cause the disease; women have two chromosomes, so two copies of muscular dystrophy can only be caused by a mutation in the gene. It is rare for a woman to inherit two disease-causing genes on her chromosomes, so men are more likely to have muscular dystrophy than women [ 39 ].Whether it is genetic or a mutation, there is currently no way to change the gene. The only way to control it is to delay development, improve symptoms, increase muscle strength, and prolong life through medication.

Our study revealed that BMI serves as a predictor of sarcopenia, with a lower BMI indicating a higher risk of sarcopenia, consistent with findings reported by Wu LC and colleagues [ 40 ]. This suggests a potential association between higher BMI and improved prognosis among older adults. However, it is important to note that while higher BMI may confer certain benefits, such as reduced risk of sarcopenia, it can also contribute to metabolic syndrome, posing physiological challenges for older individuals. Moreover, metabolic disorders associated with obesity may exacerbate malnutrition, perpetuating a detrimental cycle. A meta-analysis encompassing 26 studies [ 41 ] underscored the significant impact of different training modalities on muscle strength and physical performance in older adults with sarcopenia. Similarly, a systematic review [ 42 ] highlighted the positive effects of appropriate physical activity in enhancing muscle strength and flexibility, averting muscle atrophy and degeneration, and promoting blood circulation and metabolism, thereby fostering overall health in older adults aged 60 years and above [ 43 ]. Furthermore, the role of supplements in enhancing muscle mass and preventing metabolic syndrome onset is noteworthy. Selenium and magnesium, investigated in randomized controlled trials and dietary observational studies [ 44 , 45 ], have shown potential associations with improved physical activity and muscle performance in older adults. Additionally, randomized controlled trials [ 46 ] have consistently demonstrated the efficacy of omega-3 fatty acids in preserving muscle mass and mitigating age-related muscle loss. In addressing the role of supplements, it is pertinent to mention Beta-hydroxy-beta-methylbutyrate (HMB), a metabolite of the essential amino acid leucine, which has garnered attention for its potential benefits in muscle health. Several studies have explored the effects of HMB supplementation on muscle mass preservation and physical function in older adults [ 47 , 48 ]. These findings suggest that HMB may serve as a valuable adjunct to nutritional interventions and muscle training in mitigating the risk of sarcopenia among older adults. Therefore, early nutritional intervention and muscle training should be offered to older adults at risk for sarcopenia to reduce the risk of sarcopenia.

At the same time, this study also found that blood pressure is closely related to the occurrence of sarcopenia. High systolic blood pressure may reflect the stiffness of the blood vessels, which may reduce the ability of blood to flow to the muscles, resulting in an inadequate supply of nutrients to the muscles, thus increasing muscle loss. Low diastolic blood pressure may indicate that the heart is not pumping enough blood to the body during diastole, which may also affect the supply of nutrients to the muscles [ 49 ]. Both high systolic blood pressure and low diastolic blood pressure can be signs of physical decline in the older adults, and physical decline is closely related to sarcopenia. Therefore, in the future, in addition to paying attention to heart, brain and kidney complications, hypertensive patients should also pay attention to muscle loss.

In addition, this study shows that chronic pain, particularly chronic low back pain, is also associated with sarcopenia, which has a critical impact on spinal health because maintaining spinal function requires the involvement of strong lower back muscles. On the one hand, the decrease in muscle quantity and quality reduces muscle tolerance to exercise and makes muscles more susceptible to fatigue, which reduces their ability to maintain overall spinal stability. Spinal instability greatly increases the incidence of chronic low back pain. On the other hand, the decline in the function of the trunk muscles, especially the dorsi extensors, leads to a weakening of the muscles' suspension force on the spine, making it difficult for the body to maintain a normal upright posture, resulting in a severe forward tilt of the body. Leaning forward increases the work of the posterior muscles, fatigues the muscle tissue, and makes it impossible to keep the body upright, creating a vicious cycle that affects the patient's quality of life [ 50 ]. Therefore, the prevention and treatment of sarcopenia is a very important and urgent issue for spinal health in older adults.

The nomogram, constructed through multifactorial regression analysis, amalgamates various predictive indicators to represent the relationships between variables in the predictive model using scaled line segments on a common plane according to a predetermined ratio. It serves as a tool to forecast the probability of a clinical outcome event by summing the scores assigned to each predictor to derive a total score. Widely employed across diverse clinical domains, the nomogram stands as a common predictive model utilized in research endeavors. To further bolster the credibility of our findings, we recognize the importance of engaging with previous studies that have developed and validated nomograms, as this interaction could enhance the robustness of our research outcomes. In this study, we identified sex, BMI, MSBP, MDBP and pain as the main factors predicting sarcopenia in Chinese older adults. Our prediction model, constructed based on these five factors influencing sarcopenia development, exhibited good discrimination, calibration, and clinical validity. This suggests that the prediction model holds value for effectively identifying high-risk older adults with sarcopenia. The nomogram specifically quantifies the hazard ratio in terms of scores, allowing for the calculation of the probability of a certain outcome through simple calculations. It provides individualized risk assessment for each person, enhancing relevance and accuracy.

Therefore, the establishment of a prediction model for sarcopenia in older adults constitutes a novel achievement of this study. Nomograms, as efficient and accurate assessment tools, can assist clinical medical staff in objectively screening older adults at risk of sarcopenia, thereby providing a theoretical basis and starting point for formulating early prevention and intervention measures. Their clinical applicability is robust, aiding in the identification of patients at high risk for sarcopenia, enabling the implementation of early intervention plans, and facilitating individual health management in older adults.

This study has several limitations. Firstly, the absence of age-specific analysis based on different age groups is a notable gap. Sarcopenia, which involves a decrease in muscle mass due to age-related hormonal changes, would have benefited from a more granular examination across age brackets. Secondly, the CHARLS database lacked some potential predictors, such as dietary habits and nutritional status, limiting the scope of our analysis. Thirdly, the nomogram developed in this study is specific to data from China, and its generalizability to other regions and countries remains to be determined through external validation. Additionally, while pain was identified as an important factor in sarcopenia, the study did not delve into the specifics of pain, such as its location, intensity, and duration, which could have provided deeper insights. Furthermore, patients with impaired cognitive function were not excluded, and in some cases, family members assisted with self-reporting, potentially introducing biases into the results. Given these limitations, future research should aim to conduct prospective studies, incorporate more comprehensive predictor variables, and externally validate the model to enhance its generalizability and accuracy.

Our sarcopenia risk prediction model based on CHARLS data provides a reliable and accurate tool for Chinese older adults. This model can help clinicians to identify high-risk patients earlier and take timely preventive and interventional measures to improve the quality of life and health outcomes of the older adults.

Availability of data and materials

The datasets generated during and/or analyzed during the current study are available in the CHARLS repository, http://charls.pku.edu.cn .

Ren R, Qi J, Lin S, et al. The China alzheimer report 2022. General Psychiatry. 2022;35(1): e100751.

Article   PubMed   PubMed Central   Google Scholar  

Liu YZZ, Rao K, Wang S. Blue book of elderly health: annual report on elderly health in China (2018). China: Social Science Academic Press; 2019.

Google Scholar  

Damluji AA, Alfaraidhy M, Alhajri N, et al. Sarcopenia and cardiovascular diseases. Circulation. 2023;147(20):1534–53.

Cruz-Jentoft AJ, Sayer AA. Sarcopenia. Lancet (London, England). 2019;393(10191):2636–46.

Article   PubMed   Google Scholar  

Bauer J, Morley JE, Schols A, et al. Sarcopenia: a time for action. An SCWD position paper. J Cachexia Sarcopenia Muscle. 2019;10(5):956–61.

Anker SD, Morley JE, von Haehling S. Welcome to the ICD-10 code for sarcopenia. J Cachexia Sarcopenia Muscle. 2016;7(5):512–4.

Chen LK, Woo J, Assantachai P, et al. Asian working group for sarcopenia: 2019 consensus update on sarcopenia diagnosis and treatment. J Am Med Directors Assoc. 2020;21(3):300-7.e2.

Article   Google Scholar  

Xu W, Chen T, Cai Y, et al. Sarcopenia in community-dwelling oldest old is associated with disability and poor physical function. J Nutr Health Aging. 2020;24(23):339–45.

Article   CAS   PubMed   Google Scholar  

Petermann-Rocha F, Balntzi V, Gray SR, et al. Global prevalence of sarcopenia and severe sarcopenia: a systematic review and meta-analysis. J Cachexia Sarcopenia Muscle. 2022;13(1):86–99.

Cesari M, Kuchel GA. Role of sarcopenia definition and diagnosis in clinical care: moving from risk assessment to mechanism-guided interventions. J Am Geriatr Soc. 2020;68(7):1406–9.

Shimokata H, Ando F. Sarcopenia and its risk factors in epidemiological study. Nihon Ronen Igakkai zasshi Japanese journal of geriatrics. 2012;49(6):721–5.

PubMed   Google Scholar  

Dodds RM, Granic A, Davies K, et al. Prevalence and incidence of sarcopenia in the very old: findings from the Newcastle 85+ Study. J Cachexia Sarcopenia Muscle. 2017;8(2):229–37.

Bone AE, Hepgul N, Kon S, et al. Sarcopenia and frailty in chronic respiratory disease. Chron Respir Dis. 2017;14(1):85–99.

Springer J, Springer JI, Anker SD. Muscle wasting and sarcopenia in heart failure and beyond: update 2017. ESC Heart Failure. 2017;4(4):492–8.

Bhanji RA, Narayanan P, Allen AM, et al. Sarcopenia in hiding: the risk and consequence of underestimating muscle dysfunction in nonalcoholic steatohepatitis. Hepatology (Baltimore, MD). 2017;66(6):2055–65.

Cruz-Jentoft AJ, Bahat G, Bauer J, et al. Sarcopenia: revised European consensus on definition and diagnosis. Age Ageing. 2019;48(1):16–31.

Gao K, Cao LF, Ma WZ, et al. Association between sarcopenia and cardiovascular disease among middle-aged and older adults: findings from the China health and retirement longitudinal study. EClinicalMedicine. 2022;44: 101264.

Cai G, Ying J, Pan M, et al. Development of a risk prediction nomogram for sarcopenia in hemodialysis patients. BMC Nephrol. 2022;23(1):319.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Yin G, Qin J, Wang Z, et al. A nomogram to predict the risk of sarcopenia in older people. Medicine. 2023;102(16): e33581.

Mo YH, Su YD, Dong X, et al. Development and validation of a nomogram for predicting sarcopenia in community-dwelling older adults. J Am Med Dir Assoc. 2022;23(5):715-21.e5.

Zhao Y, Hu Y, Smith JP, et al. Cohort profile: the China Health and Retirement Longitudinal Study (CHARLS). Int J Epidemiol. 2014;43(1):61–8.

Chen LK, Woo J, Assantachai P, et al. Asian working group for sarcopenia: 2019 consensus update on sarcopenia diagnosis and treatment. J Am Med Dir Assoc. 2020;21(3):300-7.e2.

Wen X, Wang M, Jiang CM, et al. Anthropometric equation for estimation of appendicular skeletal muscle mass in Chinese adults. Asia Pac J Clin Nutr. 2011;20(4):551–6.

Yang M, Hu X, Wang H, et al. Sarcopenia predicts readmission and mortality in elderly patients in acute care wards: a prospective study. J Cachexia Sarcopenia Muscle. 2017;8(2):251–8.

Alexandre Tda S, Duarte YA, Santos JL, et al. Sarcopenia according to the European Working Group on Sarcopenia in Older People (EWGSOP) versus dynapenia as a risk factor for mortality in the elderly. J Nutr Health Aging. 2014;18(8):751–6.

Wu X, Li X, Xu M, et al. Sarcopenia prevalence and associated factors among older Chinese population: Findings from the China Health and Retirement Longitudinal Study. PLoS ONE. 2021;16(3): e0247617.

Roberts RE, Rhoades HM, Vernon SW. Using the CES-D scale to screen for depression and anxiety: effects of language and ethnic status. Psychiatry Res. 1990;31(1):69–83.

Wu WT, Li YJ, Feng AZ, et al. Data mining in clinical big data: the frequently used databases, steps, and methodological models. Mil Med Res. 2021;8(1):44.

PubMed   PubMed Central   Google Scholar  

Lyu J, Li Z, Wei H, et al. A potent risk model for predicting new-onset acute coronary syndrome in patients with type 2 diabetes mellitus in Northwest China. Acta Diabetol. 2020;57(6):705–13.

Morris TP, White IR, Royston P. Tuning multiple imputation by predictive mean matching and local residual draws. BMC Med Res Methodol. 2014;14:75.

Xue QL. The frailty syndrome: definition and natural history. Clin Geriatr Med. 2011;27(1):1–15.

Chen J, Wang X, Xu Z. Sarcopenia and chronic pain in the elderly: a systematic review and meta-analysis. J Pain Res. 2023;16:3569–81.

Du Y, Oh C, No J. Associations between sarcopenia and metabolic risk factors: a systematic review and meta-analysis. J Obes Metab Syndr. 2018;27(3):175–85.

Cruz-Jentoft AJ, Landi F, Schneider SM, et al. Prevalence of and interventions for sarcopenia in ageing adults: a systematic review. Report of the International Sarcopenia Initiative (EWGSOP and IWGS). Age Ageing. 2014;43(6):748–59.

Papadopoulou SK. Sarcopenia: a contemporary health problem among older adult populations. Nutrients. 2020;12(5):1293.

Senior HE, Henwood TR, Beller EM, et al. Prevalence and risk factors of sarcopenia among adults living in nursing homes. Maturitas. 2015;82(4):418–23.

Gao Q, Hu K, Yan C, et al. Associated factors of sarcopenia in community-dwelling older adults: a systematic review and meta-analysis. Nutrients. 2021;13(12):4291.

Bouchard DR, Dionne IJ, Brochu M. Sarcopenic/obesity and physical capacity in older men and women: data from the Nutrition as a Determinant of Successful Aging (NuAge)-the Quebec longitudinal Study. Obesity (Silver Spring, Md). 2009;17(11):2082–8.

Laurent MR, Dedeyne L, Dupont J, et al. Age-related bone loss and sarcopenia in men. Maturitas. 2019;122:51–6.

Wu LC, Kao HH, Chen HJ, et al. Preliminary screening for sarcopenia and related risk factors among the elderly. Medicine. 2021;100(19): e25946.

Lu L, Mao L, Feng Y, et al. Effects of different exercise training modes on muscle strength and physical performance in older people with sarcopenia: a systematic review and meta-analysis. BMC Geriatr. 2021;21(1):708.

Montero-Fernández N, Serra-Rexach JA. Role of exercise on sarcopenia in the elderly. Eur J Phys Rehabil Med. 2013;49(1):131–43.

Beaudart C, Dawson A, Shaw SC, et al. Nutrition and physical activity in the prevention and treatment of sarcopenia: systematic review. Osteoporosis Int. 2017;28(6):1817–33.

Article   CAS   Google Scholar  

Rederstorff M, Krol A, Lescure A. Understanding the importance of selenium and selenoproteins in muscle function. CMLS. 2006;63(1):52–9.

Brown MR, Cohen HJ, Lyons JM, et al. Proximal muscle weakness and selenium deficiency associated with long term parenteral nutrition. Am J Clin Nutr. 1986;43(4):549–54.

Lalia AZ, Dasari S, Robinson MM, et al. Influence of omega-3 fatty acids on skeletal muscle protein metabolism and mitochondrial bioenergetics in older adults. Aging. 2017;9(4):1096–129.

Yang C, Song Y, Li T, et al. Effects of beta-hydroxy-beta-methylbutyrate supplementation on older adults with sarcopenia: a randomized, double-blind, placebo-controlled study. J Nutr Health Aging. 2023;27(5):329–39.

Landi F, Calvani R, Picca A, et al. Beta-hydroxy-beta-methylbutyrate and sarcopenia: from biological plausibility to clinical evidence. Curr Opin Clin Nutr Metab Care. 2019;22(1):37–43.

Zhang XZ, Xie WQ, Chen L, et al. Blood flow restriction training for the intervention of sarcopenia: current stage and future perspective. Front Med. 2022;9: 894996.

Lin T, Dai M, Xu P, et al. Prevalence of sarcopenia in pain patients and correlation between the two conditions: a systematic review and meta-analysis. J Am Med Directors Assoc. 2022;23(5):902.e1-e20.

Download references

Acknowledgements

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

No funding.

Author information

Qiugui Li and Hongtao Cheng equally contributed to this work.

Authors and Affiliations

School of Nursing, Jinan University, Guangzhou, Guangdong, China

Qiugui Li, Hongtao Cheng & Wenjiao Cen

Department of Neurosurgery, The First Affiliated Hospital of Jinan University, Guangzhou, Guangdong, China

Department of Healthcare-Associated Infection Management, The First Affiliated Hospital of Jinan University, Guangzhou, Guangdong, China

Shengru Tao

You can also search for this author in PubMed   Google Scholar

Contributions

Qiugui Li, Hongtao Cheng: raise questions, screen variables, analyze data, write papers; Wenjiao Cen: screen variables; Tao Yang, Shengru Tao: Revise the thesis.

Corresponding author

Correspondence to Shengru Tao .

Ethics declarations

Ethics approval and consent to participate.

This is a retrospective study based on CHARLS database. The patient's information has been hidden before the study. The original CHARLS was approved by the Ethical Review Committee of Peking University (IRB00001052–11015), and all participants signed the informed consent at the time of participation. This research followed the guidance of the Declaration of Helsinki.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary material 1. comparison between variables in the training and validation datasets, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Li, Q., Cheng, H., Cen, W. et al. Development and validation of a predictive model for the risk of sarcopenia in the older adults in China. Eur J Med Res 29 , 278 (2024). https://doi.org/10.1186/s40001-024-01873-w

Download citation

Received : 30 January 2024

Accepted : 26 April 2024

Published : 09 May 2024

DOI : https://doi.org/10.1186/s40001-024-01873-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Predictive model

European Journal of Medical Research

ISSN: 2047-783X

• Submission enquiries: [email protected]
• General enquiries: [email protected]