Learning Objectives
By the end of this section, you will be able to:
- Represent the work done by any force
- Evaluate the work done for various forces
In physics, work is done on an object when energy is transferred to the object. In other words, work is done when a force acts on something that undergoes a displacement from one position to another. Forces can vary as a function of position, and displacements can be along various paths between two points. We first define the increment of work dW done by a force F → F → acting through an infinitesimal displacement d r → d r → as the dot product of these two vectors:
Then, we can add up the contributions for infinitesimal displacements, along a path between two positions, to get the total work.

Work Done by a Force
The work done by a force is the integral of the force with respect to displacement along the path of the displacement:
The vectors involved in the definition of the work done by a force acting on a particle are illustrated in Figure 7.2 . While in general, Equation 7.2 requires mathematics beyond the scope of this text, in many simple situations this integral becomes a familiar integral in one variable. We will examine several such examples and restrict our discussion to these cases.
We choose to express the dot product in terms of the magnitudes of the vectors and the cosine of the angle between them, because the meaning of the dot product for work can be put into words more directly in terms of magnitudes and angles. We could equally well have expressed the dot product in terms of the various components introduced in Vectors . In two dimensions, these were the x - and y -components in Cartesian coordinates, or the r - and φ φ -components in polar coordinates; in three dimensions, it was just x -, y -, and z -components. Which choice is more convenient depends on the situation. In words, you can express Equation 7.1 for the work done by a force acting over a displacement as a product of one component acting parallel to the other component. From the properties of vectors, it doesn’t matter if you take the component of the force parallel to the displacement or the component of the displacement parallel to the force—you get the same result either way.
Recall that the magnitude of a force times the cosine of the angle the force makes with a given direction is the component of the force in the given direction. The components of a vector can be positive, negative, or zero, depending on whether the angle between the vector and the component-direction is between 0 ° 0 ° and 90 ° 90 ° or 90 ° 90 ° and 180 ° 180 ° , or is equal to 90 ° 90 ° . As a result, the work done by a force can be positive, negative, or zero, depending on whether the force is generally in the direction of the displacement, generally opposite to the displacement, or perpendicular to the displacement. The maximum work is done by a given force when it is along the direction of the displacement ( cos θ = ± 1 cos θ = ± 1 ), and zero work is done when the force is perpendicular to the displacement ( cos θ = 0 cos θ = 0 ).
The units of work are units of force multiplied by units of length, which in the SI system is newtons times meters, N · m. N · m. This combination is called a joule , for historical reasons that we will mention later, and is abbreviated as J. In the English system, still used in the United States, the unit of force is the pound (lb) and the unit of distance is the foot (ft), so the unit of work is the foot-pound ( ft · lb ) . ( ft · lb ) .
Work Done by Constant Forces and Contact Forces
The simplest work to evaluate is that done by a force that is constant in magnitude and direction. In this case, we can factor out the force; the remaining integral is just the total displacement, which only depends on the end points A and B , but not on the path between them:
Figure 7.3 (a) shows a person exerting a constant force F → F → along the handle of a lawn mower, which makes an angle θ θ with the horizontal. The horizontal displacement of the lawn mower, over which the force acts, is d → . d → . The work done on the lawn mower is W = F → · d → = F d cos θ W = F → · d → = F d cos θ , which the figure also illustrates as the horizontal component of the force times the magnitude of the displacement.
Figure 7.3 (b) shows a person holding a briefcase. The person must exert an upward force, equal in magnitude to the weight of the briefcase, but this force does no work, because the displacement over which it acts is zero.
In Figure 7.3 (c), where the person in (b) is walking horizontally with constant speed, the work done by the person on the briefcase is still zero, but now because the angle between the force exerted and the displacement is 90 ° 90 ° ( F → F → perpendicular to d → d → ) and cos 90 ° = 0 cos 90 ° = 0 .
Example 7.1
Calculating the work you do to push a lawn mower.
Substituting the known values gives
Significance
When you mow the grass, other forces act on the lawn mower besides the force you exert—namely, the contact force of the ground and the gravitational force of Earth. Let’s consider the work done by these forces in general. For an object moving on a surface, the displacement d r → d r → is tangent to the surface. The part of the contact force on the object that is perpendicular to the surface is the normal force N → . N → . Since the cosine of the angle between the normal and the tangent to a surface is zero, we have
The normal force never does work under these circumstances. (Note that if the displacement d r → d r → did have a relative component perpendicular to the surface, the object would either leave the surface or break through it, and there would no longer be any normal contact force. However, if the object is more than a particle, and has an internal structure, the normal contact force can do work on it, for example, by displacing it or deforming its shape. This will be mentioned in the next chapter.)
The part of the contact force on the object that is parallel to the surface is friction, f → . f → . For this object sliding along the surface, kinetic friction f → k f → k is opposite to d r → , d r → , relative to the surface, so the work done by kinetic friction is negative. If the magnitude of f → k f → k is constant (as it would be if all the other forces on the object were constant), then the work done by friction is
where | l A B | | l A B | is the path length on the surface. The force of static friction does no work in the reference frame between two surfaces because there is never displacement between the surfaces. As an external force, static friction can do work. Static friction can keep someone from sliding off a sled when the sled is moving and perform positive work on the person. If you’re driving your car at the speed limit on a straight, level stretch of highway, the negative work done by air resistance is balanced by the positive work done by the static friction of the road on the drive wheels. You can pull the rug out from under an object in such a way that it slides backward relative to the rug, but forward relative to the floor. In this case, kinetic friction exerted by the rug on the object could be in the same direction as the displacement of the object, relative to the floor, and do positive work. The bottom line is that you need to analyze each particular case to determine the work done by the forces, whether positive, negative or zero.
Example 7.2
Moving a couch.
- The work done by friction i W = − ( 0.6 ) ( 1 kN ) ( 3 m + 1 m ) = − 2.4 kJ . W = − ( 0.6 ) ( 1 kN ) ( 3 m + 1 m ) = − 2.4 kJ .
- The length of the path along the hypotenuse is 10 m 10 m , so the total work done against friction is W = ( 0.6 ) ( 1 kN ) ( 3 m + 1 m + 1 0 m ) = 4.3 kJ . W = ( 0.6 ) ( 1 kN ) ( 3 m + 1 m + 1 0 m ) = 4.3 kJ .
Check Your Understanding 7.1
Can kinetic friction ever be a constant force for all paths?
The other force on the lawn mower mentioned above was Earth’s gravitational force, or the weight of the mower. Near the surface of Earth, the gravitational force on an object of mass m has a constant magnitude, mg , and constant direction, vertically down. Therefore, the work done by gravity on an object is the dot product of its weight and its displacement. In many cases, it is convenient to express the dot product for gravitational work in terms of the x -, y -, and z -components of the vectors. A typical coordinate system has the x -axis horizontal and the y -axis vertically up. Then the gravitational force is − m g j ^ , − m g j ^ , so the work done by gravity, over any path from A to B , is
The work done by a constant force of gravity on an object depends only on the object’s weight and the difference in height through which the object is displaced. Gravity does negative work on an object that moves upward ( y B > y A y B > y A ), or, in other words, you must do positive work against gravity to lift an object upward. Alternately, gravity does positive work on an object that moves downward ( y B < y A y B < y A ), or you do negative work against gravity to “lift” an object downward, controlling its descent so it doesn’t drop to the ground. (“Lift” is used as opposed to “drop”.)
Example 7.3
Shelving a book.
- Since the book starts on the shelf and is lifted down y B − y A = − 1 m y B − y A = − 1 m , we have W = − ( 20 N ) ( − 1 m ) = 20 J . W = − ( 20 N ) ( − 1 m ) = 20 J .
- There is zero difference in height for any path that begins and ends at the same place on the shelf, so W = 0 . W = 0 .
Check Your Understanding 7.2
Can Earth’s gravity ever be a constant force for all paths?
Work Done by Forces that Vary
In general, forces may vary in magnitude and direction at points in space, and paths between two points may be curved. The infinitesimal work done by a variable force can be expressed in terms of the components of the force and the displacement along the path,
Here, the components of the force are functions of position along the path, and the displacements depend on the equations of the path. (Although we chose to illustrate dW in Cartesian coordinates, other coordinates are better suited to some situations.) Equation 7.2 defines the total work as a line integral, or the limit of a sum of infinitesimal amounts of work. The physical concept of work is straightforward: you calculate the work for tiny displacements and add them up. Sometimes the mathematics can seem complicated, but the following example demonstrates how cleanly they can operate.
Example 7.4
Work done by a variable force over a curved path.
Then, the integral for the work is just a definite integral of a function of x .
The integral of x 2 x 2 is x 3 / 3 , x 3 / 3 , so
Check Your Understanding 7.3
Find the work done by the same force in Example 7.4 over a cubic path, y = ( 0.25 m −2 ) x 3 y = ( 0.25 m −2 ) x 3 , between the same points A = ( 0 , 0 ) A = ( 0 , 0 ) and B = ( 2 m, 2 m ) . B = ( 2 m, 2 m ) .
One very important and widely applicable variable force is the force exerted by a perfectly elastic spring, which satisfies Hooke’s law F → = − k Δ x → , F → = − k Δ x → , where k is the spring constant, and Δ x → = x → − x → eq Δ x → = x → − x → eq is the displacement from the spring’s unstretched (equilibrium) position ( Newton’s Laws of Motion ). Note that the unstretched position is only the same as the equilibrium position if no other forces are acting (or, if they are, they cancel one another). Forces between molecules, or in any system undergoing small displacements from a stable equilibrium, behave approximately like a spring force.
To calculate the work done by a spring force, we can choose the x -axis along the length of the spring, in the direction of increasing length, as in Figure 7.7 , with the origin at the equilibrium position x eq = 0 . x eq = 0 . (Then positive x corresponds to a stretch and negative x to a compression.) With this choice of coordinates, the spring force has only an x -component, F x = − k x F x = − k x , and the work done when x changes from x A x A to x B x B is
Notice that W A B W A B depends only on the starting and ending points, A and B , and is independent of the actual path between them, as long as it starts at A and ends at B. That is, the actual path could involve going back and forth before ending.
Another interesting thing to notice about Equation 7.5 is that, for this one-dimensional case, you can readily see the correspondence between the work done by a force and the area under the curve of the force versus its displacement. Recall that, in general, a one-dimensional integral is the limit of the sum of infinitesimals, f ( x ) d x f ( x ) d x , representing the area of strips, as shown in Figure 7.8 . In Equation 7.5 , since F = − k x F = − k x is a straight line with slope − k − k , when plotted versus x , the “area” under the line is just an algebraic combination of triangular “areas,” where “areas” above the x -axis are positive and those below are negative, as shown in Figure 7.9 . The magnitude of one of these “areas” is just one-half the triangle’s base, along the x -axis, times the triangle’s height, along the force axis. (There are quotation marks around “area” because this base-height product has the units of work, rather than square meters.)
Example 7.5
Work done by a spring force.
For part (a), x A = 0 x A = 0 and x B = 6 cm x B = 6 cm ; for part (b), x B = 6 cm x B = 6 cm and x B = 12 cm x B = 12 cm . In part (a), the work is given and you can solve for the spring constant; in part (b), you can use the value of k , from part (a), to solve for the work.
- W = 0.54 J = 1 2 k [ ( 6 cm ) 2 − 0 ] W = 0.54 J = 1 2 k [ ( 6 cm ) 2 − 0 ] , so k = 3 N/cm . k = 3 N/cm .
- W = 1 2 ( 3 N/cm ) [ ( 12 cm ) 2 − ( 6 cm ) 2 ] = 1.62 J . W = 1 2 ( 3 N/cm ) [ ( 12 cm ) 2 − ( 6 cm ) 2 ] = 1.62 J .
Check Your Understanding 7.4
The spring in Example 7.5 is compressed 6 cm from its equilibrium length. (a) Does the spring force do positive or negative work and (b) what is the magnitude?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Authors: William Moebs, Samuel J. Ling, Jeff Sanny
- Publisher/website: OpenStax
- Book title: University Physics Volume 1
- Publication date: Sep 19, 2016
- Location: Houston, Texas
- Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- Section URL: https://openstax.org/books/university-physics-volume-1/pages/7-1-work
© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

StickMan Physics
Animated Physics Lessons
Work and Power Example Solutions
Follow along with common work and power example problems and solutions. See how to solve problems when force is applied directly parallel or at an angle.
Example Work and Power Problems
1. How much work is done by the stickman that pushes a box 5 meters with a force of 12 Newtons forward?
Since the force is in the same direction as motion you plug numbers directly in and don't have to find the parallel component first.
W = (12)(5) = 60 J
2. What is the power output of the stickman that pushes the box 5 meters in 3 seconds with a constant force of 12 N?
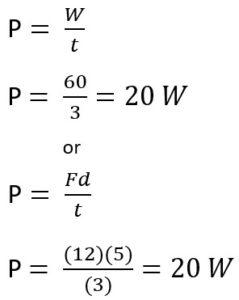
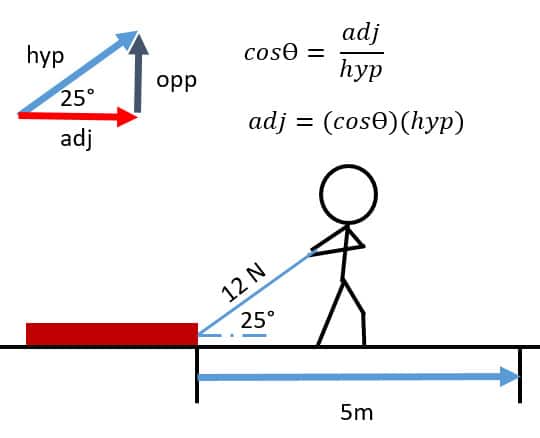
3. How much work would be done if 12N of force was applied on an object at an angle of 25° above the horizon to move an object 5 meters horizontally.
A) Find the horizontal component of force:
adj = (cosӨ)(hyp)
adj = (cos(25°))(12)= 10.9 N
B) Find out how much work is done by this component:
W = (10.9)(5) = 54.5 J
4. What is the power output if 12N of force was applied on an object at an angle of 25° above the horizon to move an object 5 meters horizontally in 3 seconds.
Use the work from the problem above
P = 54.5/3 = 18.2 W
- Back to the Work and Power Page
- Back to the Stickman Physics Home Page
- For video tutorials and other physics resources check out HoldensClass.com
- Find many of your animation resources in one place at the StickMan Physics Gallery
- Equation Sheet
Terms and Conditions - Privacy Policy
- Write something.
- Write something else.
- Write something different.
- Write something completely different.
- the acceleration of the bullet in the rifle
- the force of the propellant on the bullet in the rifle
- the work done on the bullet while it is in the barrel
- the horizontal acceleration of the bullet as it flies through the air
- the force of aerodynamic drag on the bullet
- the work done by aerodynamic drag on the bullet
- How far did the block move during this part of the experiment?
- How much work was done on the block during this part of the experiment?
- coefficient of static friction for wood on wood
- coefficient of kinetic friction for wood on wood
- Draw a free body diagram showing all the forces acting on the model rocket.
- the weight of the rocket
- the net force on the rocket while the engine was running
- the acceleration of the rocket while the engine was running
- the distance traveled by the rocket while the engine was running
- the speed of the rocket when the engine stopped
- the work done by the engine on the rocket
- Draw a free body diagram showing all the forces acting on the model rocket after the engine shut down.
- What is the acceleration of the rocket after the engine shut down?
- What maximum height above the ground did the rocket reach?
- How much work did gravity do on the rocket from launch until it reached its maximum height?
- If your answers to part g. and part k. are not equal (to within 2 or 3 significant digits), you've made a mistake somewhere. If they are equal, you've probably done it correctly (probably).
- the weight of the car
- the force of the tires pushing the car up the ramp
- the distance the car traveled up the ramp
- the increase in height of the car
- the work done by the engine pushing the car up the ramp
- Draw a free body diagram showing all the forces acting on the lawnmower. Do not resolve any of the forces into components. Do indicate their directions, however.
- the gravitational force of the Earth
- the normal force of the ground
- the force applied by the homeowner
- the force of friction from the ground
- What does the area under this curve represent?
- Calculate its cumulative value at 200 m intervals. Compile your results in a table like the one below.
| interval ending at | 0.0 km | 0.2 km | 0.4 km | 0.6 km | 0.8 km | 1.0 km |
|---|---|---|---|---|---|---|
| interval area | ||||||
| cumulative area |
- Sketch a graph of this quantity with respect to displacement.
statistical
- Use the given data to create a force-displacement graph.
- Determine the work done on the projectile as a function of its displacement.
- Compute the launch speed of the projectile.
Data adapted from Kampen, Kaczmarczik, and Rath; 2006 .

- Exam Center
- Ticket Center
- Flash Cards
- Work and Energy
Physics Work Problems for High Schools
In this tutorial, we want to practice some problems on work in physics. All these questions are easy and helpful for your high school homework.
Work Problems: Constant Force
Problem (1): A constant force of 1200 N is required to push a car along a straight line. A person displaces the car by 45 m. How much work is done by the person?
Solution : If a constant force $F$ acts on an object over a distance of $d$, and $F$ is parallel to $d$, then the work done by force $F$ is the product of the force times distance.
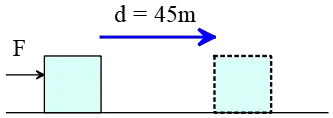
In this case, a force of $1200\,{\rm N}$ displaces the car $45\,{\rm m}$. The pushing force is parallel to the displacement. So, the work done by the person is equal to \[W=Fd=1200\times 45=54000\,{\rm J}\] The SI unit of work is the joule, ${\rm J}$.
Problem (2): You lift a book of mass $2\,{\rm kg}$ at constant speed straight upward a distance of $2\,{\rm m}$. How much work is done during this lifting by you?
Solution : The force you apply to lift the book must be balanced with the book's weight. So, the exerted force on the book is \[F=mg=2\times 10=20\quad{\rm N}\] The book is lifted 2 meters vertically. The force and displacement are both parallel to each other, so the work done by the person is the product of them. \[W=Fd=20\times 2=40\quad {\rm J}\]
Problem (3): A force of $F=20\,{\rm N}$ at an angle of $37^\circ$ is applied to a 3-kg object initially at rest. The object has displaced a distance of $25\,{\rm m}$ over a frictionless horizontal table. Determine the work done by (a) The applied force (b) The normal force exerted by the table (c) The force of gravity
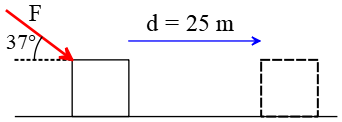
Solution : In this problem, the force makes an angle with the displacement. In such cases, we should use the work formula $W=Fd\cos\theta$ where $\theta$ is the angle between force $F$ and displacement. To this object, an external force $F$, normal force $F_N$, and a gravity force $w=mg$ are applied.
(a) Using vector decompositions, the component of the force parallel to the displacement is found to be $F_{\parallel}=F\cos \theta$. Thus, the product of this component parallel to the displacement times the magnitude of displacement gives us the work done by external force $F$ as below \begin{align*} W_F&=\underbrace{F\cos\theta}_{F_{\parallel}}d\\\\ &=(20\times \cos 37^\circ)(25)\\\\&=400\quad {\rm J}\end{align*} (b) Now, we want to find the work done by the normal force. But let's define what the normal force is.
In physics, ''normal'' means perpendicular. When an object is in contact with a surface, a contact force is exerted on the object. The component of the contact force perpendicular to the surface is called the normal force.
Thus, by definition, the normal force is always perpendicular to the displacement. So, the angle between $F_N$ and displacement $d$ is $90^\circ$. Hence, the work done by the normal force is determined to be \[W_N=F_N d\cos\theta=(30)(25)\cos 90^\circ=0\] (c) The weight of the object is the same as the force of gravity. This force applies to the object vertically downward, and the displacement of the object is horizontal. So, again, the angle between these two vectors is $\theta=90^\circ$. Hence, the work done by the force of gravity is zero.
Problem (4): A person pulls a crate using a force of $56\,{\rm N}$ which makes an angle of $25^\circ$ with the horizontal. The floor is frictionless. How much work does he do in pulling the crate over a horizontal distance of $200\,{\rm m}$?
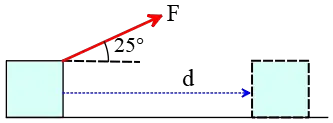
Solution : The component of the external force parallel to the displacement does work on an object over a distance of $d$. In all work problems in physics, this force component parallel to the displacement is found by the formula $F_{\parallel}=F\cos \theta$. Thus, the work done by this force is computed as below \begin{align*} W&=F_{\parallel}d\\&=(F\cos\theta)d\\&=(56\cos 25^\circ)(200) \\&=10080\quad {\rm J}\end{align*} We could use the work formula from the beginning $W=Fd\cos\theta$ where $\theta$ is the angle between $F$ and $d$.
Problem (5): A worker pushes a cart with a force of $45\,{\rm N}$ directed at an angle of $32^\circ$ below the horizontal. The cart moves at a constant speed. (a) Find the work done by the worker as the cart moves a straight distance of $50\,{\rm m}$. (b) What is the net work done on the cart?
Solution :(a) All information to find the work done by the worker is given, so we have \begin{align*} W&=Fd\cos\theta\\&=(45)(50) \cos 32^\circ\\&=1912.5\quad {\rm J}\end{align*} (b) ''net'' means "total". In all work problems in physics, there are two equivalent methods to find the net work. Identify all forces that are applied to the cart, find their resultant force, and then compute the work done by this net force over a specific distance.
Or compute all works done on the object across a distance individually, then sum them algebraically.
Usually, the second method is easier. We take this approach here.
The cart moves in a straight horizontal path. All forces apply on it are, the worker force $F$, the normal force $F_N$, and the force of gravity or its weight $F_g=mg$. The work done by normal and gravity forces in a horizontal displacement is always zero since the angle between these forces and the displacement is $90^\circ$. So, $W_N=W_g=0$. Hence, the net (total) work done on the object is \[W_{total}=W_N+W_g+W_F=1912.5\,{\rm J}\]
Problem (6): A $1200-{\rm kg}$ box is at rest on a rough floor. How much work is required to move it $5\,{\rm m}$ at a constant speed (a) along the floor against a $230\,{\rm N}$ friction force, (b) vertically?
Solution : In this problem, we want to displace a box $5\,{\rm m}$ horizontally and vertically. In the horizontal direction, there is also kinetic friction.
(a) At constant speed , means there is no acceleration in the course of displacement, so according to Newton's second law $\Sigma F=ma$, the net force on the box must be zero. To meet this condition, the external force $F_p$ applied by a person must cancel out the friction force $f_k$. So, \[F_p=f_k=230\quad {\rm N}\] The force $F_p$ and displacement are both parallel, so their product get the work done by $F_p$ \[W_p=F_p d=230\times 5=1150\quad {\rm J}\] (b) In the vertical path, two forces act on the box. One is the external lifting force, and the other is the force of gravity. Since the box is moving at constant speed vertically, there is no acceleration, and thus this lifting external force $F_p$ must be balanced with the weight of the box. \[F_p=F_g=mg=(1200)(10)=12000\,{\rm J}\] Assume the box is moved vertically upward. In this case, the lifting force and displacement are parallel, so the angle between them is zero $\theta=0$, and the work done by this force is \[W_p=F_p d\cos 0=12000\times 5=60\,{\rm kJ}\] On the other side, the weight force, or force of gravity $F_g=mg$ is always downward, so the angle between the box's weight and upward displacement is $180^\circ$. So, the work done by the weight of the box is \begin{align*}W_g&=F_g d\cos 180^\circ \\\\ &=(1200)(10)(5)(-1) \\\\ &=-60\,{\rm kJ}\end{align*} In such cases where the angle between $F$ and $d$ is $180^\circ$, they are called antiparallel.
Problem (7): A 40-kg crate is pushed using a force of 150 N at a distance of $6\,{\rm m}$ on a rough surface. The crate moves at a constant speed. Find (a) the work done by the external force on the crate. (b) The coefficient of kinetic friction between the crate and the floor?
Solution : (a) the crate is moved horizontally through a distance of $6\,{\rm m}$ by a force parallel to its displacement. So, the work done by this external force is \[W_p=F_p d \cos\theta=(150)(6)\cos 0=900\,{\rm J}\] where subscript $p$ denotes the person or any external agent.
(b) According to the definition of the kinetic friction force formula, $f_k=\mu_k F_N$, to find the coefficient of kinetic friction $\mu_k$, we must have both the friction force and normal force $F_N$.
In the question, we are told that the crate moves at a constant speed, so there is no acceleration, and thus, the net force applied to it must be zero.
When the friction force, which opposes the motion, is equal to the external force $F_p$, then this condition is satisfied. So, \[f_k=F_p=150\,{\rm N}\] On the other side, the crate is not lifted off the floor, so there is no motion vertically.
Balancing all forces applied vertically, the weight force and the normal force $F_N$, we can find the normal force $F_N$ as below \begin{gather*} F_N-F_g=0\\ F_N=F_g\\ \Rightarrow F_N=mg=40\times 10=400\quad {\rm N}\end{gather*} Therefore, the coefficient of kinetic friction is found to be \[f_k=\frac{f_k}{F_N}=\frac{150}{400}=0.375\]
Practice these questions to understand friction force Problems on the coefficient of friction
Problem (8): A 18-kg packing box is pulled at constant speed by a rope inclined at $20^\circ$. The box moves a distance of 20 m over a rough horizontal surface. Assume the coefficient of kinetic friction between the box and the surface to be $0.5$. (a) Find the tension in the rope? (b) How much work is done by the rope on the box?
Solution : The aim of this problem is to find the work done by the tension in the rope. The magnitude of the tension in the rope is not given. So, we must first find it.
(a) We are told the box moves at a constant speed, so, as previously mentioned, the net force on the box must be zero to produce no acceleration. But what forces are acting horizontally on the box? The horizontal component of tension in the rope, $T_{\parallel}=T\cos\theta$, and the kinetic friction force $f_k$ in the opposite direction of motion are the forces acting on the box horizontally.
If these two forces are equal in magnitude but opposite in direction, then their resultant (net) becomes zero, and consequently, the box will move at a constant speed. \begin{align*} f_k&=T_{\parallel}\\\mu_k F_N&=T\cos\theta\quad (I) \end{align*} The forces in the vertical direction must also cancel each other since there is no motion vertically. As you can see in the figure, we have \[F_N=T\sin\theta+F_g\] Substituting this into the relation (I), rearranging and solving for $T$, yields \begin{gather*} \mu_k (T\sin\theta+mg)=T\cos\theta \\\\ \Rightarrow T=\frac{\mu_k mg}{\cos\theta-\mu_k\sin\theta}\end{gather*} Substituting the numerical values into the above expression, we find the tension in the rope. \[T=\frac{(0.5)(18)(10)}{\cos 20^\circ-(0.5) \sin20^\circ}=117\quad {\rm N}\] (b) The only force that causes the box to move some distance is the horizontal component of the tension in the rope, $T_{\parallel}=T\cos\theta$. So, the work done by the tension in the rope is \begin{align*} W&=T_{\parallel}d\\ &=(117)( \cos 20^\circ)(20) \\&=2199\quad {\rm J}\end{align*}
Problem (9): A table of mass 40 kg is accelerated from rest at a constant rate of $2\,{\rm m/s^2}$ for $4\,{\rm s}$ by a constant force. What is the net work done on the table?
Solution : This is a combination of a kinematics problem and a physics work problem. Here, first, we must find the distance over which the box is displaced. The given information is: initial speed $v_0=0$, acceleration $2\,{\rm m/s^2}$, time taken $t=4\,{\rm s}$. Using this data, we can find the total displacement by applying the kinematics equation $\Delta x=\frac 12 at^2+v_0t$, \begin{align*} \Delta x&=\frac 12 at^2+v_0t\\\\&=\frac 12 (2)(4)^2+0(4)\\\\&=16\quad {\rm m}\end{align*} So, this constant force causes the table to move a distance of 16 meters across the surface. To find the work done, we need a force, as well. The force is mass times acceleration, $F=ma$, so we have \[F=ma=40\times 2=80\,{\rm N}\] Now that we have both the force and displacement, the net work done on the table is the product of force along the displacement times the magnitude of displacement \[W=80\times 16=128\quad {\rm J}\]
Work problems in a uniform circular motion
Problem (10): A 5-kg object is held at the end of a string and undergoes uniform circular motion around a circle of radius $5\,{\rm m}$. If the tangential speed of the object around the circle is $15\,{\rm m/s}$, how much work was done on the object by the centripetal force?
Solution : Here, an object moves around a circle, so we encounter a uniform circular motion problem .
In such motions around a curve or circle, that force in the radial direction exerting on the object is called the centripetal force.
On the other hand, a movement around a circle is tangent to the path at any instant of time. Thus, we conclude that in any uniform circular motion, a force is applied to the whirling object that is perpendicular to its motion at any moment of time.
So, the angle between the centripetal force and displacement at any instant is always zero, $\theta=0$. Using the work formula $W=Fd\cos\theta$, we find that the work done by the centripetal force is always zero.
This is another example of zero work in physics.
Work problems on an incline
Problem (11): A $5-{\rm kg}$ box, initially at rest, slides $2.5\,{\rm m}$ down a ramp of angle $30^\circ$. The coefficient of friction between the box and the incline is $\mu_k=0.435$. Determine (a) the work done by the gravity force, (b) the work done by the frictional force, and (c) the work done by the normal force exerted by the surface.
Solution : This part is related to problems on inclined plane surfaces . The forces acting on a box on an inclined plane are shown in the figure. As you can see, the forces along the direction of motion are the parallel component of the weight $W_{\parallel}$, and the friction force $f_k$.
(a) In the figure, you realize that the angle between the object's weight (the same as the force of gravity) and downward displacement $d$ is zero, $\theta=30^\circ$.
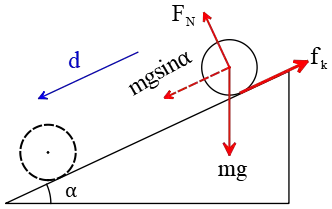
So, the work done by the force of gravity on the box is found using work formula as below \begin{align*} W&=Fd\cos\theta\\&=(mg)(d) \cos 30^\circ\\&=(5\times 10)(2.5) \cos 30^\circ\\&=108.25\quad {\rm J}\end{align*} (b) To find the work done by friction, we need to know its magnitude. From the kinetic friction force formula, $f_k=\mu_k F_N$, we must determine, first, the normal force acting on the box.
There is no motion in the direction perpendicular to the incline, so the resultant of forces acting in this direction must be zero. Equating the same direction forces, we will have \[F_N=mg\sin\alpha=(5)(10) \sin 30^\circ=25\,{\rm N}\] Substituting this into the above equation for kinetic friction, we can find its magnitude as \[f_k=\mu_k F_N=(0.435)(25)=10.875\,{\rm N}\] The friction force and the displacement of the box down the ramp are parallel, i.e., $\theta=0$. The work done by friction is \begin{align*} W_f&=f_kd\cos\theta \\\\ &=(10.875)(2.5) \cos 0\\\\ &=27.1875\,{\rm J}\end{align*} (c) By definition, the normal force is the same contact force that is applied to the object from the surface perpendicularly. On the other hand, the object moves along the incline, so its displacement is perpendicular to the normal force, $\theta=90^\circ$. Hence, the work done by the normal force is zero. \[W_N=F_N d\cos\theta=F_N d\cos 90^\circ=0\]
Problem (12): We want to push a $950-{\rm kg}$ heavy object 650 m up along a $7^\circ$ incline at a constant speed. How much work do we do over this distance? Ignore friction.
Solution : When it comes to constant speed in all work problems in physics, you must remember that all forces in the same direction must be equal to the opposing forces. This condition ensures that there is no acceleration in the motion.
In this case, all forces acting on the object are: the pushing force along the incline upward $F_p$, and the parallel component of the force of gravity (weight) along the incline downward, $W_{\parallel}=mg\sin\alpha$. Thus, we can find the pushing force as \begin{align*}F_p&=mg\sin 7^\circ\\\\ &=(950)(10) \sin 7^\circ \\\\& =1159\quad {\rm N}\end{align*} In the question, we are told that the object is moving up the incline, so the angle between its displacement and upward pushing force is zero, $\theta=0$. Hence, the work done by the person to push the object along the incline upward is \begin{align*} W_p&=F_p d\cos\theta\\&=1159\times 650 \cos 0\\&=753350\quad{\rm J}\end{align*}
Problem (13): Consider an electron moving at a constant speed of $1.1\times 10^6\,\rm m/s$ in a straight line. How much energy is required to stop this electron? (Take the electron's mass, $m_e=9.11\times 10^{-31}\,\rm kg$.
Solution : In this problem on work, we cannot use the work formula directly, since none of the work variables, i.e., $F$, $d$, $\theta$, are given except the velocity. In these cases, we have a problem on the work-energy theorem .
According to this rule, the net work done over a distance by a constant force on an object of mass $m$ equals the change in its kinetic energy \[W_{net}=\underbrace{\frac 12 mv_f^2-\frac 12 mv_i^2}_{\Delta K}\] Substituting the numerical values given in this problem, we get the required work to stop this fast-moving electron. \begin{align*}W_{net}&=\frac 12 m(v_f^2-v_i^2) \\\\ &=\frac 12 (9.11\times 10^{-31}) \left(0^2-(1.1\times 10^6)^2 \right) \\\\ &=-5.5\times 10^{-19}\,\rm J\end{align*} where we set the final velocity $v_f=0$ since the electron is to stop.
Problem (14): How much power is needed to lift a $25-\rm kg$ weight $1\,\rm m$ in $1\,\rm s$?
Solution : The power in physics is defined as the ratio of work done on an object to the time taken $P=\frac{W}{t}$. The SI unit of power is the watt ($W$).
In this problem, first, we must find the amount of work done in lifting the object as much as $1,\rm m$ vertically. The only force involved in this situation is the downward weight force. Thus, \[W=(mg)h=(25\times 10)(1)=250\,{\rm J}\] This amount of work has been done in a time interval of $1\,\rm s$. Hence, the power is calculated as below \[P=\frac{W}{t}=\frac{250}{1}=250\,\rm W\]
Problem (15): A particle having charge $-3.6\,\rm nC$ is released from rest in a uniform electric field $E$ moves a distance of $5\,\rm cm$ through it. The electric potential difference between those two points is $\Delta V=+400\,\rm V$. What work was done by the electric force on the particle?
Solution : The work done by the electric force on a charged particle is calculated by $W_E=qEd$, where $E$ is the magnitude of the electric field and $d$ is the amount of distance traveled through $E$. But in this case, the electric field strength is not given, and we cannot use this formula.
We can see this as a problem on electric potential . Recall that the work done by the electric force on a charge to move it between two points with different potentials is given by $W=-q\Delta V$. Substituting the given numerical values into this, we will have \begin{align*} W&=-q\Delta V \\&=-(-3.6)(+400) \\&=\boxed{1440\,\rm J} \end{align*}
Here, we learned how to calculate the work done by a constant force in physics by solving a couple of example problems.
Overall, the work done by a constant force is the product of the horizontal component of the force times the displacement between the initial and final points.
In addition, power, a related quantity to work in physics, is also defined as the rate at which work is done.
Author : Dr. Ali Nemati Date Published : 9/20/2021
© 2015 All rights reserved. by Physexams.com

HIGH SCHOOL
- ACT Tutoring
- SAT Tutoring
- PSAT Tutoring
- ASPIRE Tutoring
- SHSAT Tutoring
- STAAR Tutoring
GRADUATE SCHOOL
- MCAT Tutoring
- GRE Tutoring
- LSAT Tutoring
- GMAT Tutoring
- AIMS Tutoring
- HSPT Tutoring
- ISAT Tutoring
- SSAT Tutoring
Search 50+ Tests
Loading Page
math tutoring
- Elementary Math
- Pre-Calculus
- Trigonometry
science tutoring
Foreign languages.
- Mandarin Chinese
elementary tutoring
- Computer Science
Search 350+ Subjects
- Video Overview
- Tutor Selection Process
- Online Tutoring
- Mobile Tutoring
- Instant Tutoring
- How We Operate
- Our Guarantee
- Impact of Tutoring
- Reviews & Testimonials
- About Varsity Tutors
High School Physics : Calculating Work
Study concepts, example questions & explanations for high school physics, all high school physics resources, example questions, example question #1 : calculating work.

In this case, there is only one force acting upon the object: the force due to gravity. Plug in our given information for the distance to solve for the work done by gravity.

Remember, since the object will be moving downward, the distance should be negative.

The work done is positive because the distance and the force act in the same direction.
Example Question #2 : Calculating Work

Work is a force times a distance:

We know the distance that the book needs to travel, but we need to sovle for the lifting force required to move it.
There are two forces acting upon the book: the lifting force and gravity. Since the book is moving with a constant velocity, that means the net force will be zero. Mathemetically, that would look like this:

We can expand the right side of the equation using Newton's second law:

Use the given mass and value of gravity to solve for the lifting force.

Now that we have the force and the distance, we can solve for the work to lift the book.

This problem can also be solved using energy. Work is equal to the change in potential energy:

Example Question #11 : Work

The relationship between work, force, and distance is:

We are given the force on the toy and the work done. Using these values, we can find the distance. Note that the mass is not relevant for this question.

The relationship between work, force and distance is:

We are given the value for the force and the distance that the toy travels. Using these values, we can find the work done by the cat. Note that the mass of the toy is not relevant for this calculation.

Example Question #7 : Calculating Work

We are given the value for the work done by the cat and the distance that the toy travels. Using these values, we can find the force on the toy. Note that the mass of the toy is not relevant for this calculation.

The formula for work is:

Given the values for force and distance, we can calculate the work done.
Note that no work is done by the force of gravity or the weight of the box, since the vertical position does not change.

Work is the product of force times a distance:

We are given the work and the distance traveled, allowing us to solve for the force. The mass of the cabinet is not necessary information.

Example Question #10 : Calculating Work

None of these

Use the data given to calculate the kinetic energy of the rocket at the two different velocities. Then find the amount of work done using the following equation:

Kinetic energy of the rocket at the two velocities:

The change in the kinetic energy at the two velocities:

Report an issue with this question
If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.
DMCA Complaint
If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.
Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.
Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.
Please follow these steps to file a notice:
You must include the following:
A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.
Send your complaint to our designated agent at:
Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105
Or fill out the form below:
Contact Information
Complaint details.

| Email address: | |
| Your name: | |
| Feedback: |
Work done by force – problems and solutions
1. A person pulls a block 2 m along a horizontal surface by a constant force F = 20 N. Determine the work done by force F acting on the block.
Angle (θ ) = 0
W = F d cos θ = (20)(2)(cos 0) = (20)(2)(1) = 40 Joule
The horizontal force (F x ) = F cos 30 o = (10)(0.5√3) = 5√3 N
W = F d = w h = m g h
W = work, F = force, d = distance, w = weight , h = height, m = mass, g = acceleration due to gravity.
Weight (w) = m g = (1 kg)(10 m/s 2 ) = 10 kg m/s 2 = 10 N
k = F / x = w / x = m g / x
W = – (250)(0.0004)
The minus sign indicates that the direction of spring force is opposite with the direction of object displacement.
Work done by force F :
W 2 = F k d = (2)(2)(cos 180) = (2)(2)(-1) = -4 Joule
W net = 20 – 4
Wanted: Work (W)
Force (F) = 200 Newton
W = (200 Newton)(2 meters)
8 . The driver of the sedan wants to park his car exactly 0.5 m in front of the truck which is at 10 m from the sedan’s position. What is the work required by the sedan?
Force (F) = 50 Newton
W = 475 Joule
Displacement (s) = 4 meters
W = F s = (120 Newton)(4 meters) = 480 N m = 480 Joule
11. Based on figure below, if work done by net force is 375 Joule, determine object’s displacement.
12. The activities below w hich do not do work is …
The equation of work :
B ased on the above formula, work done by force and there is a displacement.
Displacement = 0 so work = 0.
W = F d = (350 Newton)(6 meters) = 2100 Newton-meters = 2100 Joule
W = F s = (14 Newton)(8 meters) = 112 Newton meters = 112 Joule
Displacement of hammer before hits the wood (d) = 40 cm = 0.4 meters
W = F d = (2000 N)(0.6 m) = 1200 Nm = 1200 Joule
Share this:
Leave a comment cancel reply, discover more from physics.
Chapter: 11th Physics : UNIT 4 : Work, Energy and Power
Solved example problems for physics: work, energy and power, numerical problems.
1. Calculate the work done by a force of 30 N in lifting a load of 2kg to a height of 10m (g = 10ms -2 )
Force mg = 30 N ; height = 10 m
Work done to lift a load W = ?
W = F.S (or) mgh
W = 300 J
Ans: 300J
2. A ball with a velocity of 5 m s -1 impinges at angle of 60˚ with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.
The impluse on the ball acts perpendicular to the smooth plane.
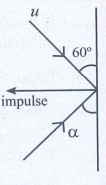
(i) The component of velocity of ball parallel to the surface.
(ii) For the component of velocity of ball perpendicular to the surface, apply law of restitution.
The component of velocity parallel to the surface will be changed.
v cos α = u cos 60°
v cos α = 5 × 1/2 = 5/2 ….(1)
According to law of restitution
v sin α = e u sin 60°
v sin α = 1/2 × 5 × √3/2 = 5 (√3/4) ….(2)
Squaring and adding (1) and (2)
v 2 (sin 2 α + cos 2 α) =

v = 3.3 ms -1
Ans: v = 0.3 m s -1
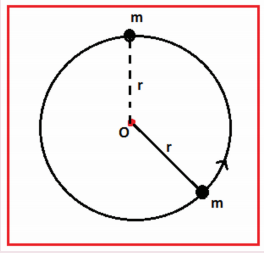
3. A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure. What initial speed must be given to the object to reach the top of the circle? (Hint: Use law of conservation of energy). Is this speed less or greater than speed obtained in the section 4.2.9?
Ans: √ 4gr ms-1
The horizontal distance, draw the point of projection to the point where the ball returns to the same level
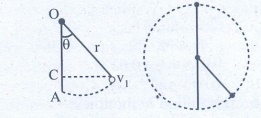
AC = OA-OC = r - rcosθ
minimum velocity = at v L = √[5 gr ]
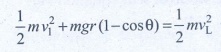
v 1 2 = v L 2 - 2gr (1 - cos θ)
v 1 2 = 5 gr - 2gr (l-cosθ)
v 1 2 = 5gr-2gr(l – 1/2)
v 1 2 = 5gr - gr => v 1 2 = 4gr
v 1 = √[4 gr ] ms -1 .
4. Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.
Momentium is censerved in both × and y direction.
In x - direction
M B V B = O + M A V A ' cosɸ ...(l)
In y - direction
O = M B V B ' - M A V A 'sinɸ ...(2)
(2)/(1) tanɸ = V B ’/V B = 1/2
ɸ = 26.6° (or) 26° 36' [1° = 60']
Ans: θ = 26° 33 ′
5. A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Mass of the bullet m 1 = 20 g = 0.02 kg.
Mass of the pendulum m 2 = 5 kg
Centre of mass of pendulum rises to a height = h = 10 cm = 0.1 m
Speed of the bullet = u 1
Pendulum is at rest .:. u 2 = 0
Common velocity of the bullet and the pendulum after the bullet is embeded into the object = v
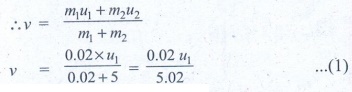
From II equation of motion
v = √[2gh] = √[2x9.8x0.1] = √[1.96] = 1.4 ms -1
Substitute the value of v in equation (1)
1.4 = 0.02 u 1 /5.02
u 1 = 5.02x1.4 / 0.02
u 1 = 351.4 ms -1
Ans: v = 351.4m s -1
Conceptual Questions
1. A spring which in initially in un-stretched condition, is first stretched by a length x and again by a further length x. The work done in the first case W 1 is one third of the work done in second case W 2 . True or false?

2. Which is conserved in inelastic collision? Total energy (or) Kinetic energy?
Total energy is always conserved.
But K.E. is not conserved.
3. Is there any net work done by external forces on a car moving with a constant speed along a straight road?
If a car is moving at a constant speed, then external force will be zero.
Because a = [v - u] / t
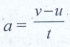
For constant speed v = u , then a =0. ( a -acceleration)
F = ma .'. F = zero. i.e.. no external force.
W = F.S. = 0. So net work done is zero.
4. A car starts from rest and moves on a surface with uniform acceleration.
Draw the graph of kinetic energy versus displacement. What information you can get from that graph?

5. A charged particle moves towards another charged particle. Under what conditions the total momentum and the total energy of the system conserved?
(i) Both charged particles shall be dissimilar charge, (i.e. positive and negative)
(ii) After collision the charged particles; stick together permanent.
(iii) They should move with common velocity
SOLVED EXAMPLE

2. A particle moves along X- axis from x=0 to x=8 under the influence of a force given by F= 3 x 2 - 4 x + 5. Find the work done in the process.

3. A body of mass 10kg at rest is subjected to a force of 16N. Find the kinetic energy at the end of 10 s.
Mass m = 10 kg
Force F = 16 N
time t = 10 s
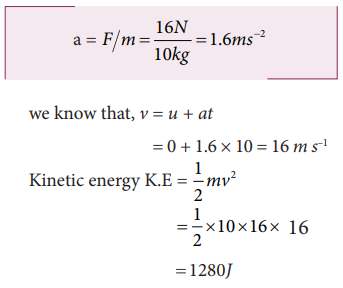
4. A body of mass 5kg is thrown up vertically with a kinetic energy of 1000 J. If acceleration due to gravity is 10 ms -2 , find the height at which the kinetic energy becomes half of the original value.
Mass m = 5kg
K.E E = 1000J
g = 10 m s -2
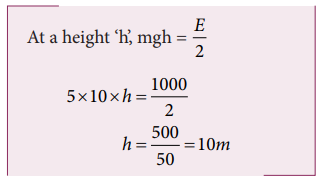
5. Two bodies of mass 60 kg and 30 kg move in the same direction along straight line with velocity 40 cm s -1 and 30 cm s -1 respectively suffer one dimensional elastic collision. Find their velocities after collision.
Mass m 1 = 60 kg
Mass m 2 = 30 kg
V 1 = 40cm s -1
V 2 = 30c m s -1

Likewise,

6. A particle of mass 70 g moving at 50 cm s -1 is acted upon by a variable force as shown in the figure. What will be its speed once the force stops?
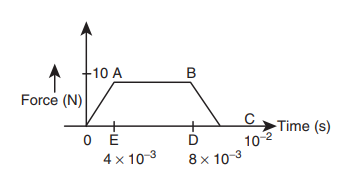
The area under the graph gives the impulse.
Impulse I = area of ∆ OAE+ area of rectangle ABDE+ area of ∆ DBC
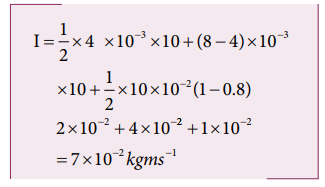
But Impulse = 2 × initial momentum of the particle= 2 × m × u
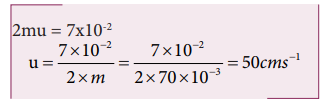
Hence the particle will reverse its direction and move with its initial speed.
7. A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical and rebounds with the speed v at an angle Φ with an vertical. The coefficient of restitution between the particle and floor is e. What is the magnitude of v?
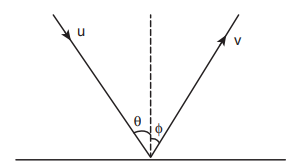
Applying component of velocities,

The x - component of velocity is
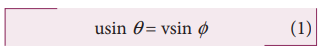
The magnitude of y – component of velocity is not same, therefore, using coefficient of restitution,

8. A particle of mass m is fixed to one end of a light spring of force constant k and un-stretched length l. It is rotated with an angular velocity ω in horizontal circle. What will be the length increase in the spring?
Mass spring = m Force
constant = k
Un-stretched length = l
Angular velocity = ω
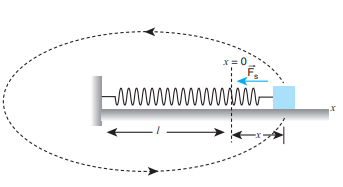
Let ‘x’ be the increase in the length of the spring.
The new length = (l+x) = r
When the spring is rotated in a horizontal circle,
Spring force = centripetal force.
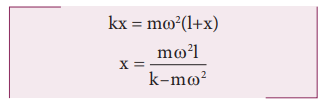
9. A gun fires 8 bullets per second into a target X. If the mass of each bullet is 3 g and its speed 600 s -1 . Then, calculate the power delivered by the bullets.
Power = work done per second = total kinetic energy of 8 bullets per second
Solved Example Problems for Work
Example 4.1.
A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30 o , find the work done by the force.
Force, F = 25 N
Displacement, dr = 15 m
Angle between F and dr, θ = 30 o
Work done , W = Fdr cos θ
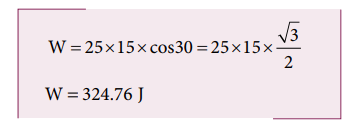
Solved Example Problems for Work done by a constant force
Example 4.2
An object of mass 2 kg falls from a height of 5 m to the ground. What is the work done by the gravitational force on the object? (Neglect air resistance; Take g = 10 m s -2 )
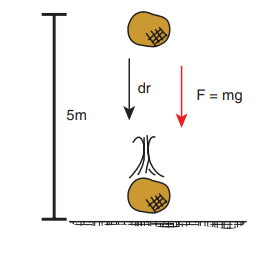
Work done by gravitational force is
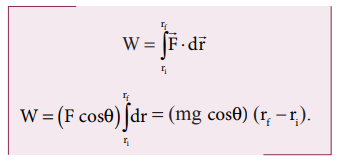
The work done by the gravitational force on the object is positive.
Example 4.3
An object of mass m = 1 kg is sliding from top to bottom in the frictionless inclined plane of inclination angle θ = 30 o and the length of inclined plane is 10 m as shown in the figure. Calculate the work done by gravitational force and normal force on the object. Assume acceleration due to gravity, g = 10 m s -2
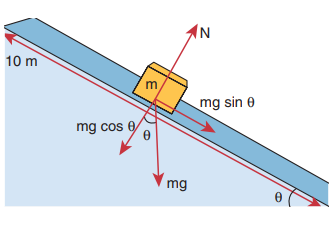
We calculated in the previous chapter that the acceleration experienced by the object in the inclined plane as g sin θ .
According to Newton’s second law, the force acting on the mass along the inclined plane F = mg sin θ . Note that this force is constant throughout the motion of the mass.
The work done by the parallel component of gravitational force ( mg sin θ ) is given by
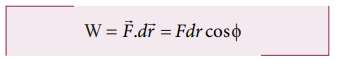
Example 4.4
If an object of mass 2 kg is thrown up from the ground reaches a height of 5 m and falls back to the Earth (neglect the air resistance). Calculate
a) The work done by gravity when the object reaches 5 m height
b) The work done by gravity when the object comes back to Earth
c) Total work done by gravity both in upward and downward motion and mention the physical significance of the result.
When the object goes up, the displacement points in the upward direction whereas the gravitational force acting on the object points in downward direction. Therefore, the angle between gravitational force and displacement of the object is 180°.
a. The work done by gravitational force in the upward motion.
Given that ∆r =5 m and F mg
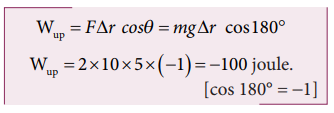
b. When the object falls back, both the gravitational force and displacement of the object are in the same direction. This implies that the angle between gravitational force and displacement of the object is 0°.
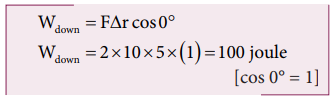
c. The total work done by gravity in the entire trip (upward and downward motion)
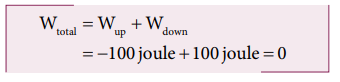
It implies that the gravity does not transfer any energy to the object. When the object is thrown upwards, the energy is transferred to the object by the external agency, which means that the object gains some energy. As soon as it comes back and hits the Earth, the energy gained by the object is transferred to the surface of the Earth (i.e., dissipated to the Earth).
Example 4.5
A weight lifter lifts a mass of 250 kg with a force 5000 N to the height of 5 m.
a. What is the workdone by the weight lifter?
b. What is the workdone by the gravity?
c. What is the net workdone on the object?
a. When the weight lifter lifts the mass, force and displacement are in the same direction, which means that the angle between them θ = 0 0 . Therefore, the work done by the weight lifter,
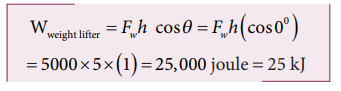
b. When the weight lifter lifts the mass, the gravity acts downwards which means that the force and displacement are in opposite direction. Therefore, the angle between them θ = 180 0
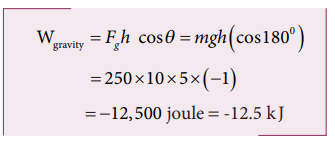
c. The net workdone (or total work done) on the object
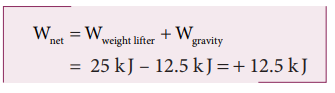
Solved Example Problems for Work done by a variable force
Example 4.6.
A variable force F = k x 2 acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x = 0 m to x = 4 m. (Assume the constant k = 1 N m -2 )
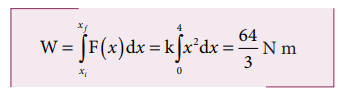
Solved Example Problems for Kinetic energy
Example 4.7.
Two objects of masses 2 kg and 4 kg are moving with the same momentum of 20 kg m s -1 .
a. Will they have same kinetic energy?
b. Will they have same speed?
a. The kinetic energy of the mass is given by

Note that KE 1 ≠ KE 2 i.e., even though both are having the same momentum, the kinetic energy of both masses is not the same. The kinetic energy of the heavier object has lesser kinetic energy than smaller mass. It is because the kinetic energy is inversely proportional to the mass (KE ∝ 1/m) for a given momentum.
b. As the momentum, p = mv , the two objects will not have same speed.
Solved Example Problems for Potential Energy
Example 4.8.
An object of mass 2 kg is taken to a height 5 m from the ground g = 10ms -2 .
a. Calculate the potential energy stored in the object.
b. Where does this potential energy come from?
c. What external force must act to bring the mass to that height?
d. What is the net force that acts on the object while the object is taken to the height ‘h’?
a. The potential energy U = m g h = 2 × 10 × 5 = 100 J
Here the positive sign implies that the energy is stored on the mass.
b. This potential energy is transferred from external agency which applies the force on the mass.

d. From the definition of potential energy, the object must be moved at constant velocity. So the net force acting on the object is zero.
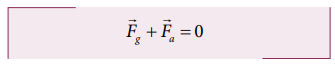
Solved Example Problems for Elastic Potential Energy
Example 4.9
Let the two springs A and B be such that k A >k B . On which spring will more work has to be done if they are stretched by the same force?
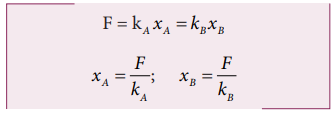
The work done on the springs are stored as potential energy in the springs.

k A >k B implies that U B >U A . Thus, more work is done on B than A.
Example 4.10
A body of mass m is attached to the spring which is elongated to 25 cm by an applied force from its equilibrium position.
a. Calculate the potential energy stored in the spring-mass system?
b. What is the work done by the spring force in this elongation?
c. Suppose the spring is compressed to the same 25 cm, calculate the potential energy stored and also the work done by the spring force during compression. (The spring constant, k = 0.1 N m -1 ).
The spring constant, k = 0.1 N m -1
The displacement, x = 25 cm = 0.25 m
a. The potential energy stored in the spring is given by
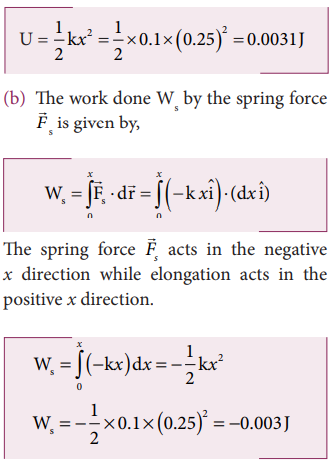
Note that the potential energy is defined through the work done by the external agency. The positive sign in the potential energy implies that the energy is transferred from the agency to the object. But the work done by the restoring force in this case is negative since restoring force is in the opposite direction to the displacement direction.
c. During compression also the potential energy stored in the object is the same.
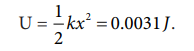
Work done by the restoring spring force during compression is given by
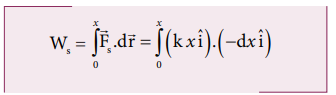
In the case of compression, the restoring spring force acts towards positive x -axis and displacement is along negative x direction.
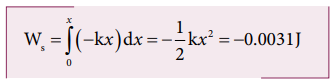
Solved Example Problems for Conservative and nonconservative forces
Example 4.11.
Compute the work done by the gravitational force for the following cases

(As the displacement is in two dimension; unit vectors and are used)
a. Since the motion is only vertical, horizontal displacement component d x is zero. Hence, work done by the force along path 1 (of distance h).
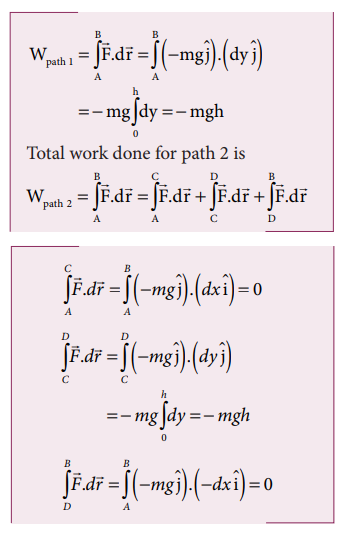
Therefore, the total work done by the force along the path 2 is
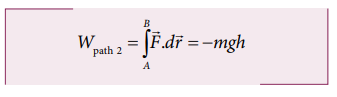
Note that the work done by the conservative force is independent of the path.
Example 4.12
Consider an object of mass 2 kg moved by an external force 20 N in a surface having coefficient of kinetic friction 0.9 to a distance 10 m. What is the work done by the external force and kinetic friction ? Comment on the result. (Assume g = 10 ms - 2 )
m = 2 kg, d = 10 m, F ext = 20 N, k = 0.9. When an object is in motion on the horizontal surface, it experiences two forces.
a. External force, F ext = 20 N
b. Kinetic friction,
f k =μ k mg = 0.9x(2)x10=18N.
The work done by the external force W ext = Fs = 20x20 =200J
The work done by the force of kinetic friction W k = f k d = (-18) x10=-180J Here the negative sign implies that the force of kinetic friction is pposite to the direction of displacement.
The total work done on the object
W total = Wext + W k = 200 J – 180 J = 20 J .
Since the friction is a non-conservative force, out of 200 J given by the external force, the 180 J is lost and it can not be recovered.
Solved Example Problems for Law of conservation of energy
Example 4.13.
An object of mass 1 kg is falling from the height h = 10 m. Calculate
a. The total energy of an object at h = 10 m
b. Potential energy of the object when it is at h = 4 m
c. Kinetic energy of the object when it is at h = 4 m
d. What will be the speed of the object when it hits the ground?
(Assume g = 10 m s -2 )
a. The gravitational force is a conservative force. So the total energy remains constant throughout the motion. At h = 10 m, the total energy E is entirely potential energy.
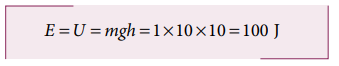
b. The potential energy of the object at h = 4 m is
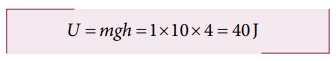
c. Since the total energy is constant throughout the motion, the kinetic energy at h = 4 m must be KE = E - U = 100 - 40 = 60J
Alternatively, the kinetic energy could also be found from velocity of the object at 4 m. At the height 4 m, the object has fallen through a height of 6 m.
The velocity after falling 6 m is calculated from the equation of motion,
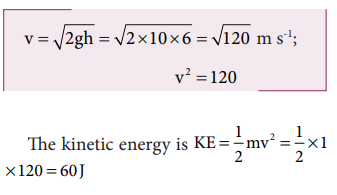
d. When the object is just about to hit the ground, the total energy is completely kinetic and the potential energy, U = 0.
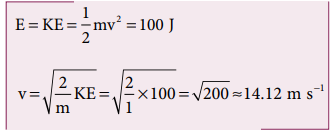
Example 4.14
A body of mass 100 kg is lifted to a height 10 m from the ground in two different ways as shown in the figure. What is the work done by the gravity in both the cases? Why is it easier to take the object through a ramp?

m = 100 kg, h = 10 m
Along path (1):
The minimum force F 1 required to move the object to the height of 10 m should be equal to the gravitational force, F 1 mg = 100 x 10 = 1000 N
The distance moved along path (1) is, = 10 m
The work done on the object along path (1) is
W = Fh = 1000 x 10 = 10,000 J
Along path (2):
In the case of the ramp, the minimum force F 2 that we apply on the object to take it up is not equal to mg , it is rather equal to mg sin θ . ( mg sin < mg) .
Here, angle θ = 30 o
Therefore, F 2 = mg sinθ = 100 × 10 × sin30 o = 100 × 10 × 0.5 = 500N
Hence, (mg sinθ < mg)
The path covered along the ramp is,
l = h/sin30 = 10/0.5 =20m
The work done on the object along path (2) is, W = F2 l = 500 × 20 = 10,000 J
Since the gravitational force is a conservative force, the work done by gravity on the object is independent of the path taken.
In both the paths the work done by the gravitational force is 10,000 J
Along path (1): more force needs to be applied against gravity to cover lesser distance .
Along path (2): lesser force needs to be applied against the gravity to cover more distance.
As the force needs to be applied along the ramp is less, it is easier to move the object along the ramp.
Example 4.15
An object of mass m is projected from the ground with initial speed v 0 .
Find the speed at height h.
Since the gravitational force is conservative; the total energy is conserved throughout the motion.

Final values of potential energy, kinetic energy and total energy are measured at the height h .
By law of conservation of energy, the initial and final total energies are the same.
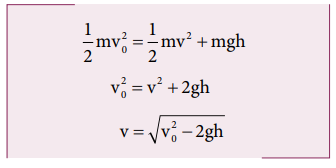
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.
Example 4.16
An object of mass 2 kg attached to a spring is moved to a distance x = 10 m from its equilibrium position. The spring constant k = 1 N m -1 and assume that the surface is frictionless.
a. When the mass crosses the equilibrium position, what is the speed of the mass?
b. What is the force that acts on the object when the mass crosses the equilibrium position and extremum position x = ± 10 m.
a. Since the spring force is a conservative force, the total energy is constant. At x = 10 m, the total energy is purely potential.
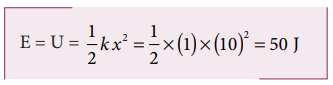
When the mass crosses the equilibrium position x = 0 , the potential energy
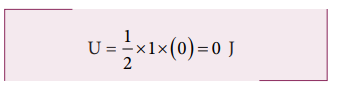
The entire energy is purely kinetic energy at this position.
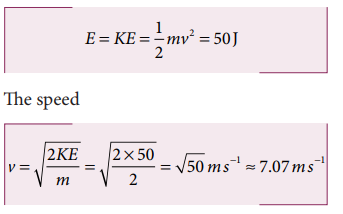
b. Since the restoring spring force is F = - kx, when the object crosses the equilibrium position, it experiences no force. Note that at equilibrium position, the object moves very fast. When the object is at x = +10 m (elongation), the force F = - k x
F = - (1) (10) = - 10 N. Here the negative sign implies that the force is towards equilibrium i.e., towards negative x -axis and when the object is at x = - 10 (compression), it experiences a forces F = - (1) (- 10) = +10 N. Here the positive sign implies that the force points towards positive x -axis.
The object comes to momentary rest at x = ± 10 m even though it experiences a maximum force at both these points.
Solved Example Problems for Motion in a vertical circle
Example 4.17.
Water in a bucket tied with rope is whirled around in a vertical circle of radius 0.5 m. Calculate the minimum velocity at the lowest point so that the water does not spill from it in the course of motion. (g = 10 ms -2 )

Solved Example Problems for Unit of power
Example 4.18.
Calculate the energy consumed in electrical units when a 75 W fan is used for 8 hours daily for one month (30 days).
Power, P = 75 W
Time of usage, t = 8 hour × 30 days = 240 hours
Electrical energy consumed is the product of power and time of usage.
Electrical energy = power × time of usage = P × t

Solved Example Problems for Relation between power and velocity
Example 4.19.
A vehicle of mass 1250 kg is driven with an acceleration 0.2 ms - 2 along a straight level road against an external resistive force 500 N . Calculate the power delivered by the vehicle’s engine if the velocity of the vehicle is 30 m s - 1 .
The vehicle’s engine has to do work against resistive force and make vechile to move with an acceleration. Therefore, power delivered by the vehicle engine is
Solved Example Problems for collision
Solved Example Problems for Elastic collisions in one dimension
Example 4.20.
A lighter particle moving with a speed of 10 m s -1 collides with an object of double its mass moving in the same direction with half its speed. Assume that the collision is a one dimensional elastic collision. What will be the speed of both particles after the collision?
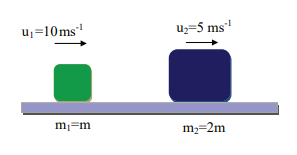
Let the mass of the fi rst body be m which moves with an initial velocity, u 1 = 10 m s -1 .
Therefore, the mass of second body is 2m and its initial velocity is u 2 = ½ u 1 = ½(10ms -1 )
Then, the fi nal velocities of the bodies can be calculated from the equation (4.53) and equation (4.54)
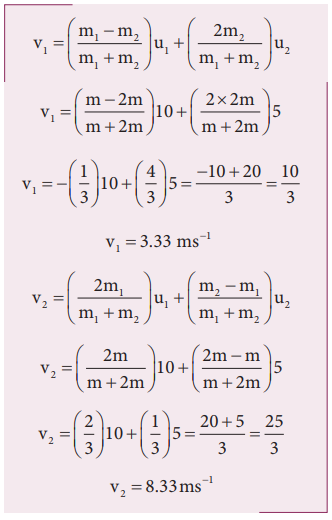
As the two speeds v 1 and v 2 are positive, they move in the same direction with the velocities, 3.33 m s −1 and 8.33 m s −1 respectively.
Solved Example Problems for Perfect inelastic collision
Example 4.21.
A bullet of mass 50 g is fired from below into a suspended object of mass 450 g. The object rises through a height of 1.8 m with bullet remaining inside the object. Find the speed of the bullet. Take g = 10 ms -2 .
m 1 = 50 g = 0.05 kg; m 2 = 450 g = 0.45kg
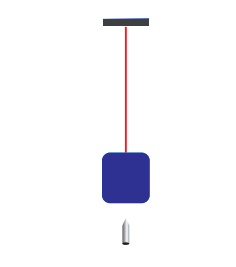
The speed of the bullet is u 1 . The second body is at rest u 2 = 0 . Let the common velocity of the bullet and the object after the bullet is embedded into the object is v.
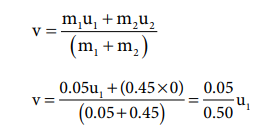
The combined velocity is the initial velocity for the vertical upward motion of the combined bullet and the object. From second equation of motion,
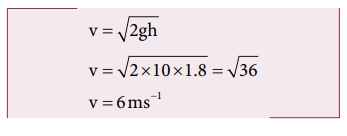
Substituting this in the above equation, the value of u 1 is
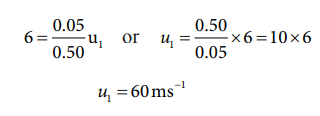
Solved Example Problems for Coefficient of restitution (e)
Example 4.22.
Show that the ratio of velocities of equal masses in an inelastic collision when one of the masses is stationary is
v 1 /v 2 = 1-e/1+e

From the law of conservation of linear momentum,
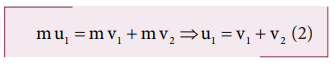
Using the equation (2) for u 1 in (1), we get

Related Topics
Privacy Policy , Terms and Conditions , DMCA Policy and Compliant
Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.
What is the 3-body problem, and is it really unsolvable?
The three-body problem is a physics conundrum that has boggled scientists since Isaac Newton's day. But what is it, why is it so hard to solve and is the sci-fi series of the same name really possible?

A rocket launch. Our nearest stellar neighbor. A Netflix show. All of these things have something in common: They must contend with the "three-body problem." But exactly what is this thorny physics conundrum?
The three-body problem describes a system containing three bodies that exert gravitational forces on one another. While it may sound simple, it's a notoriously tricky problem and "the first real worry of Newton," Billy Quarles , a planetary dynamicist at Valdosta State University in Georgia, told Live Science.
In a system of only two bodies, like a planet and a star, calculating how they'll move around each other is fairly straightforward: Most of the time, those two objects will orbit roughly in a circle around their center of mass, and they'll come back to where they started each time. But add a third body, like another star, and things get a lot more complicated. The third body attracts the two orbiting each other, pulling them out of their predictable paths .
The motion of the three bodies depends on their starting state — their positions, velocities and masses. If even one of those variables changes, the resulting motion could be completely different.
"I think of it as if you're walking on a mountain ridge," Shane Ross , an applied mathematician at Virginia Tech, told Live Science. "With one small change, you could either fall to the right or you could fall to the left. Those are two very close initial positions, and they could lead to very different states."
There aren't enough constraints on the motions of the bodies to solve the three-body problem with equations, Ross said.
Related: Cosmic 'superbubbles' might be throwing entire galaxies into chaos, theoretical study hints

Sign up for the Live Science daily newsletter now
Get the world’s most fascinating discoveries delivered straight to your inbox.
But some solutions to the three-body problem have been found. For example, if the starting conditions are just right, three bodies of equal mass could chase one another in a figure-eight pattern. Such tidy solutions are the exception, however, when it comes to real systems in space.
Certain conditions can make the three-body problem easier to parse. Consider Tatooine , Luke Skywalker's fictional home world from "Star Wars" — a single planet orbiting two suns. Those two stars and the planet make up a three-body system. But if the planet is far enough away and orbiting both stars together, it's possible to simplify the problem.

"When it's the Tatooine case, as long as you're far enough away from the central binary, then you think of this object as just being a really fat star," Quarles said. The planet doesn't exert much force on the stars because it's so much less massive, so the system becomes similar to the more easily solvable two-body problem. So far, scientists have found more than a dozen Tatooine-like exoplanets , Quarles told Live Science.
But often, the orbits of the three bodies never truly stabilize, and the three-body problem gets "solved" with a bang. The gravitational forces could cause two of the three bodies to collide, or they could fling one of the bodies out of the system forever — a possible source of "rogue planets" that don't orbit any star , Quarles said. In fact, three-body chaos may be so common in space that scientists estimate there may be 20 times as many rogue planets as there are stars in our galaxy.
When all else fails, scientists can use computers to approximate the motions of bodies in an individual three-body system. That makes it possible to predict the motion of a rocket launched into orbit around Earth, or to predict the fate of a planet in a system with multiple stars.
— 'Mathematically perfect' star system being investigated for potential alien technology
— How common are Tatooine worlds?
— Mathematicians find 12,000 new solutions to 'unsolvable' 3-body problem
With all this tumult, you might wonder if anything could survive on a planet like the one featured in Netflix's "3 Body Problem," which — spoiler alert — is trapped in a chaotic orbit around three stars in the Alpha Centauri system , our solar system 's nearest neighbor.
"I don't think in that type of situation, that's a stable environment for life to evolve," Ross said. That's one aspect of the show that remains firmly in the realm of science fiction.
Skyler Ware is a freelance science journalist covering chemistry, biology, paleontology and Earth science. She was a 2023 AAAS Mass Media Science and Engineering Fellow at Science News. Her work has also appeared in Science News Explores, ZME Science and Chembites, among others. Skyler has a Ph.D. in chemistry from Caltech.
Earth's upper atmosphere could hold a missing piece of the universe, new study hints
32 fun and random facts about Albert Einstein
'Physics itself disappears': How theoretical physicist Thomas Hertog helped Stephen Hawking produce his final, most radical theory of everything
Number Line
- \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
- \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
- \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
- \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
- \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
- How do you solve word problems?
- To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
- How do you identify word problems in math?
- Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
- Is there a calculator that can solve word problems?
- Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
- What is an age problem?
- An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.
| 🌐 Languages | EN, ES, PT & more |
|---|---|
| 🏆 Practice | Improve your math skills |
| 😍 Step by step | In depth solution steps |
| ⭐️ Rating | based on 20924 reviews |
word-problems-calculator
- High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...
Please add a message.
Message received. Thanks for the feedback.
share this!
January 29, 2024
This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
How does a 'reverse sprinkler' work? Researchers solve decades-old physics puzzle
by James Devitt, New York University

For decades scientists have been trying to solve Feynman's Sprinkler Problem: How does a sprinkler running in reverse—in which the water flows into the device rather than out of it—work? Through a series of experiments, a team of mathematicians has figured out how flowing fluids exert forces and move structures, thereby revealing the answer to this long-standing mystery.
"Our study solves the problem by combining precision lab experiments with mathematical modeling that explains how a reverse sprinkler operates," explains Leif Ristroph, associate professor at New York University's Courant Institute of Mathematical Sciences and senior author of the paper appearing in the journal Physical Review Letters .
"We found that the reverse sprinkler spins in the 'reverse' or opposite direction when taking in water as it does when ejecting it, and the cause is subtle and surprising."
"The regular or 'forward' sprinkler is similar to a rocket, since it propels itself by shooting out jets," adds Ristroph. "But the reverse sprinkler is mysterious since the water being sucked in doesn't look at all like jets. We discovered that the secret is hidden inside the sprinkler, where there are indeed jets that explain the observed motions."
The research answers one of the oldest and most difficult problems in the physics of fluids. And while Ristroph recognizes there is modest utility in understanding the workings of a reverse sprinkler—"There is no need to 'unwater' lawns," he says—the findings teach us about the underlying physics and whether we can improve the methods needed to engineer devices that use flowing fluids to control motions and forces.
"We now have a much better understanding about situations in which fluid flow through structures can induce motion," notes Brennan Sprinkle, an assistant professor at Colorado School of Mines and one of the paper's co-authors. "We think these methods we used in our experiments will be useful for many practical applications involving devices that respond to flowing air or water."
The Feynman sprinkler problem is typically framed as a thought experiment about a type of lawn sprinkler that spins when fluid, such as water, is expelled out of its S-shaped tubes or "arms." The question asks what happens if fluid is sucked in through the arms: Does the device rotate, in what direction, and why?
The problem is associated with pioneers in physics, from Ernst Mach, who posed the problem in the 1880s, to the Nobel laureate Richard Feynman, who worked on and popularized it from the 1960s through 1980s. It has since spawned numerous studies that debate the outcome and the underlying physics—and to this day it is presented as an open problem in physics and in fluid mechanics textbooks.
In setting out to solve the reverse sprinkler problem, Ristroph, Sprinkle, and their co-authors, Kaizhe Wang, an NYU doctoral student at the time of the study, and Mingxuan Zuo, an NYU graduate student, custom manufactured sprinkler devices and immersed them in water in an apparatus that pushes in or pulls out water at controllable rates.
To let the device spin freely in response to the flow, the researchers built a new type of ultra-low-friction rotary bearing. They also designed the sprinkler in a way that enabled them to observe and measure how the water flows outside, inside, and through it.
"This has never been done before and was key to solving the problem," Ristroph explains.
To better observe the reverse sprinkler process, the researchers added dyes and microparticles in the water, illuminated with lasers, and captured the flows using high-speed cameras.
The results showed that a reverse sprinkler rotates much more slowly than does a conventional one—about 50 times slower—but the mechanisms are fundamentally similar.
A conventional forward sprinkler acts like a rotating version of a rocket powered by water jetting out of the arms. A reverse sprinkler acts as an "inside-out rocket," with its jets shooting inside the chamber where the arms meet. The researchers found that the two internal jets collide but they do not meet exactly head on, and their math model showed how this subtle effect produces forces that rotate the sprinkler in reverse.
The team sees the breakthrough as potentially beneficial to harnessing climate-friendly energy sources.
"There are ample and sustainable sources of energy flowing around us—wind in our atmosphere as well as waves and currents in our oceans and rivers," says Ristroph. "Figuring out how to harvest this energy is a major challenge and will require us to better understand the physics of fluids."
Journal information: Physical Review Letters
Provided by New York University
Explore further
Feedback to editors

Millions of insects migrate through 30-meter Pyrenees pass
4 hours ago

Study finds human-caused nitrous oxide emissions grew 40% from 1980–2020, greatly accelerating climate change
5 hours ago

Wind from black holes may influence development of surrounding galaxies

Machine learning speeds up climate model simulations at finer resolutions, making them usable on local levels
6 hours ago

Coastal research shows flood risk for several Alaska communities

Combined X-ray surveys and supercomputer simulations track 12 billion years of cosmic black-hole growth
7 hours ago

Scientists spot more Milky Way-like galaxies in early universe, advancing our understanding of how galaxies were formed

Human bodies mostly recover from space, tourist mission shows

Unlocking the future of sustainable mining through carbon sequestration

Scientists engineer yellow-seeded camelina with high oil output
8 hours ago
Relevant PhysicsForums posts
How to calculate electron temperature of arc plasma, researchers finds experimental evidence for a graviton-like particle, could you use the moon to reflect sunlight onto a solar sail.
Jun 10, 2024
List of Verdet Constants?
May 31, 2024
Discussion about least squares method
May 29, 2024
Does energy exist?
More from Other Physics Topics
Related Stories

Study tests viability of Tesla's 100-year old patented device
May 17, 2021

To uncover new fluid flow laws, researchers turn to drinking straws
Mar 23, 2023

Did nature have a hand in the formation of the Great Sphinx?
Oct 31, 2023

How do birds breathe better? Researchers' discovery will throw you for a loop
Mar 16, 2021
Researchers uncover the science behind blowing bubbles
Aug 28, 2018

Scientists uncover how the shape of melting ice depends on water temperature
Jan 31, 2022
Recommended for you

Thermoelectric effect between two liquid materials observed for the first time
14 hours ago

High-precision timing data determine upper limit for photon mass
13 hours ago

New study reveals brain's fractal-like structure near phase transition, a finding that may be universal across species

New insights on the role of nucleon exchange in nuclear fusion

Cutting-edge mathematics provides new tool for particle collision puzzle
Jun 7, 2024

QUIET: A place to study qubits shielded from the effects of cosmic rays
Let us know if there is a problem with our content.
Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).
Please select the most appropriate category to facilitate processing of your request
Thank you for taking time to provide your feedback to the editors.
Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.
E-mail the story
Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.
Newsletter sign up
Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.
More information Privacy policy
Donate and enjoy an ad-free experience
We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.
E-mail newsletter
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations
Graph your math problems
Practice, practice, practice

Get math help in your language
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
High school physics
New high school physics course coming soon, unit 1: one-dimensional motion, unit 2: forces and newton's laws of motion, unit 3: two-dimensional motion, unit 4: uniform circular motion and gravitation, unit 5: work and energy, unit 6: linear momentum and collisions, unit 7: torque and angular momentum, unit 8: simple harmonic motion, unit 9: waves, unit 10: sound, unit 11: static electricity, unit 12: dc circuits.
Help | Advanced Search
Quantum Physics
Title: solving the zeh problem about the density operator with higher-order statistics.
Abstract: Since a 1932 work from von Neumann, it is generally considered that if two statistical mixtures are represented by the same density operator \r{ho}, they should in fact be considered as the same mixture. In a 1970 paper, Zeh, considering this result to be a consequence of what he called the measurement axiom, introduced a thought experiment with neutron spins and showed that in that experiment the density operator could not tell the whole story. Since then, no consensus has emerged yet, and controversies on the subject still presently develop. In this paper, stimulated by our previous works in the field of Quantum Information Processing, we show that the two mixtures imagined by Zeh, with the same \r{ho}, should however be distinguished. We show that this result suppresses a restriction unduly installed on statistical mixtures, but does not affect the general use of \r{ho}, e.g. in quantum statistical mechanics, and the von Neumann entropy keeps its own interest and even helps clarifying this confusing consequence of the measurement axiom. In order to avoid any ambiguity, the identification of the introduction of this postulate, which von Neumann rather suggested to be a general property, is given in an appendix where it is shown that Zeh was right when he spoke of a measurement axiom and identified his problem. The use and content of a density operator is also discussed in another physical case which we are led to call the Landau-Feynman situation, and which implies the concept of entanglement rather than the one of mixed states.
| Subjects: | Quantum Physics (quant-ph) |
| Cite as: | [quant-ph] |
| (or [quant-ph] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- INSPIRE HEP
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
Numbers, Facts and Trends Shaping Your World
Read our research on:
Full Topic List
Regions & Countries
- Publications
- Our Methods
- Short Reads
- Tools & Resources
Read Our Research On:
Americans’ Dismal Views of the Nation’s Politics
1. the biggest problems and greatest strengths of the u.s. political system, table of contents.
- The impact of partisan polarization
- Persistent concerns over money in politics
- Views of the parties and possible changes to the two-party system
- Other important findings
- Explore chapters of this report
- In their own words: Americans on the political system’s biggest problems
- In their own words: Americans on the political system’s biggest strengths
- Are there clear solutions to the nation’s problems?
- Evaluations of the political system
- Trust in the federal government
- Feelings toward the federal government
- The relationship between the federal and state governments
- Americans’ ratings of their House member, governor and local officials
- Party favorability ratings
- Most characterize their party positively
- Quality of the parties’ ideas
- Influence in congressional decision-making
- Views on limiting the role of money in politics
- Views on what kinds of activities can change the country for the better
- How much can voting affect the future direction of the country?
- Views of members of Congress
- In their own words: Americans’ views of the major problems with today’s elected officials
- How much do elected officials care about people like me?
- What motivates people to run for office?
- Quality of recent political candidates
- In elections, is there usually at least one candidate who shares your views?
- What the public sees as most important in political candidates
- Impressions of the people who will be running for president in 2024
- Views about presidential campaigns
- How much of an impact does who is president have on your life?
- Whose priorities should the president focus on?
- How different are the Republican and Democratic parties?
- Views of how well the parties represent people’s interests
- What if there were more political parties?
- Would more parties make solving problems easier or harder?
- How likely is it that an independent candidate will become president?
- Americans who feel unrepresented by the parties have highly negative views of the political system
- Views of the Electoral College
- Should the size of the U.S. House of Representatives change?
- Senate seats and population size
- Younger adults more supportive of structural changes
- Politics in a single word or phrase: An outpouring of negative sentiments
- Negative emotions prevail when Americans think about politics
- Americans say the tone of political debate in the country has worsened
- Which political topics get too much – and too little – attention?
- Majority of Americans find it stressful to talk politics with people they disagree with
- Acknowledgments
The public sees a number of specific problems with American politics. Partisan fighting, the high cost of political campaigns, and the outsize influence of special interests and lobbyists are each seen as characteristic of the U.S. political system by at least 84% of Americans.
Yet 63% also say that “ordinary Americans care about making the political system work well” is a good description of U.S. politics today. Still, when asked to describe a strength of the political system in their own words, more than half either say “nothing” (22%) or decline to give an answer (34%).
Americans view negative statements as better descriptions of the political system than positive ones
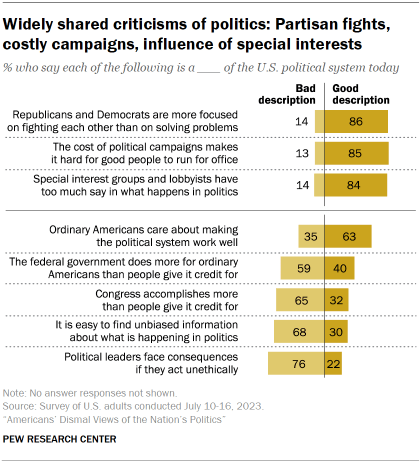
More than eight-in-ten adults say that each of the following is at least a somewhat good description of the U.S. political system today:
- Republicans and Democrats are more focused on fighting each other than on solving problems (86%);
- The cost of political campaigns makes it hard for good people to run for office (85%);
- Special interest groups and lobbyists have too much say in what happens in politics (84%).
About six-in-ten (63%) think ordinary Americans want to make the political system work well. This is the rare positive sentiment that a majority views as a good descriptor of the political system.
Fewer than half of adults hold the view that the government deserves more credit than it gets: Majorities say that “the federal government does more for ordinary Americans than people give it credit for” (59%) and “Congress accomplishes more than people give it credit for” (65%) are both bad descriptions of the political system.
Nearly seven-in-ten adults express frustration with the availability of unbiased information about politics: 68% say the statement “it is easy to find unbiased information about what is happening in politics” is not a good description of the political system.
And just 22% of Americans say that political leaders facing consequences for acting unethically is a good description of the political system. They are more than three times as likely to say that this is a bad description (76% say this).
Many critiques of the political system are bipartisan
Partisans have similar views of many of the descriptions of the political system included in the survey.
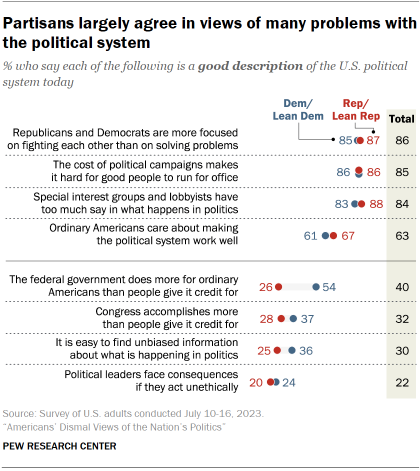
Overwhelming majorities in both parties think there is too much partisan fighting, campaigns cost too much, and lobbyists and special interests have too much say in politics. And just 24% of Democrats and Democratic-leaning independents and 20% of Republicans and Republican leaners say that political leaders face consequences if they act unethically.
The widest partisan gap is over a description of the federal government. Democrats are roughly twice as likely as Republicans to say “the federal government does more for ordinary Americans than people give it credit for” (54% vs. 26%).
There is a narrower gap in views of Congress’ accomplishments: 37% of Democrats and 28% of Republicans say it accomplishes more than people give it credit for.
Democrats are also more likely to say, “It is easy to find unbiased information about what is happening in politics” (36% of Democrats and 25% of Republicans say this is a good description of the political system today), while Republicans are slightly more likely than Democrats to view ordinary Americans as wanting to make the political system work well (67% of Republicans and 61% of Democrats say this is a good description).
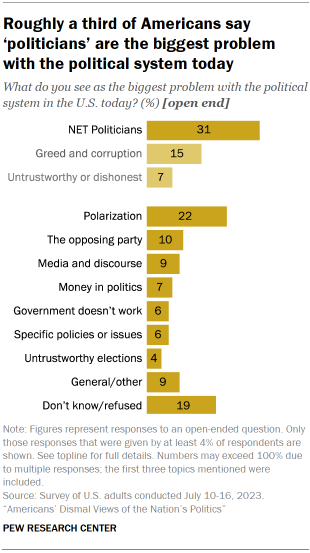
When asked to describe in their own words the biggest problem with the political system in the U.S. today, Americans point to a wide range of factors.
Negative characteristics attributed to politicians and political leaders are a common complaint: 31% of U.S. adults say politicians are the biggest problem with the system, including 15% who point to greed or corruption and 7% who cite dishonesty or a lack of trustworthiness.
The biggest problem, according to one woman in her 50s, is that politicians are “hiding the truth and fulfilling their own agendas.” Similarly, a man in his 30s says, “They don’t work for the people. They are too corrupt and busy filling their pockets.”
Explore more voices: The political system’s biggest problems
What do you see as the biggest problem with the political system in the U.S. today?
“An almost total lack of credibility and trust. Coupled with a media that’s so biased, that they’ve lost all objectivity.” –Man, 70s
“Lying about intentions or not following through with what elected officials said they would do.” –Woman, 20s
“Blind faith in political figures.” –Woman, 50s
“Our elected officials would rather play political games than serve the needs of their constituents.” –Woman, 50s
“Same politicians in office too long.” –Woman, 30s
“Extremism on both sides exploited by the mainstream media for ratings. It is making it impossible for both parties to work together.” –Man, 30s
“It has become too polarized. No one is willing to compromise or be moderate.” –Woman, 40s
“Too much money in politics coming from large corporations and special interest.” –Man, 30s
“The people have no say in important matters, we have NO representation at all. Our lawmakers are isolated and could care less what we want.” –Man, 60s
About two-in-ten adults cite deep divisions between the parties as the biggest problem with the U.S. political system, with respondents describing a lack of cooperation between the parties or among elected leaders in Washington.
“Both of the political parties are so busy trying to stop the other party, they are wasting their opportunities to solve the problems faced by our nation,” in the view of one man in his 70s.
Even as some blame polarization, others (10% of respondents) identify the other party as the system’s biggest problem. Some Republicans say that the biggest problem is “Democrats” while some Democrats simply say “Republicans.”
Smaller but substantial shares of adults name the media and political discourse (9%), the influence of money in politics (7%), government’s perceived failures (6%), specific policy areas and issues (6%) or problems with elections and voting (4%) as the biggest problem with the political system today.
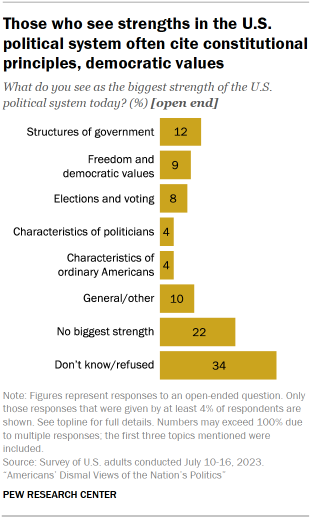
Far fewer adults name a specific strength of the political system today when asked to describe the system’s biggest strength in their own words. More than half either say that the system lacks a biggest strength (22%) or decline to answer (34%). As one woman in her 60s writes, “I’m not seeing any strengths!”
Among those who do identify strengths of the U.S. political system, the structure of political institutions and the principles that define the constitutional order are named most frequently (by 12% of respondents). Many respondents specifically point to the Constitution itself or refer to the separation of powers or the checks and balances created by the Constitution.
A man in his 20s believes that the “separation of powers and federalism work pretty well,” while one in his 30s writes that the system’s greatest strength is “the checks and balances to make sure that monumental changes aren’t made unilaterally.”
Explore more voices: The political system’s biggest strengths
What do you see as the biggest strength of the U.S. political system today?
“Everyone getting a say; democracy.” –Woman, 40s
“The right to have your opinions heard.” –Man, 60s
“In spite of our differences, we are still a democracy, and I believe there are people within our government who still care and are interested in the betterment of our country.” –Woman, 50s
“The freedom of speech and religion” –Woman, 50s
“If we have fair, honest elections we can vote out the corruption and/or incompetent politicians.” –Man, 70s
“The Constitution.” –Man, 50s
“The checks and balances to control the power of any office. The voice of the people and the options to remove an official from office.” –Man, 60s
“New, younger voices in government.” –Woman, 40s
“If we can’t get more bipartisanship we’ll become weaker. Our biggest strength is our working together.” –Woman, 60s
“The way that every two years the people get to make their voice heard.” –Man, 30s
About one-in-ten (9%) refer to individual freedoms and related democratic values, while a similar share (8%) discuss the right to vote and the existence of free elections. A woman in her 70s echoes many similar comments when she points to “the possibility of change in upcoming elections.”
However, even some of the descriptions of positive characteristics of the system are couched in respondents’ doubts about the way the system is working today. One woman in her 50s adds a qualification to what she views as the system’s biggest strength, saying, “Theoretically every voter has a say.”
Smaller shares of the public point to the positive characteristics of some politicians (4%) or the positive characteristics of the American people (4%) as reasons for optimism.
The public remains roughly evenly split over whether there are clear solutions to the biggest issues facing the country. Half of Americans today say there are clear solutions to most of the big issues facing the country, while about as many (48%) say most big issues don’t have clear solutions.
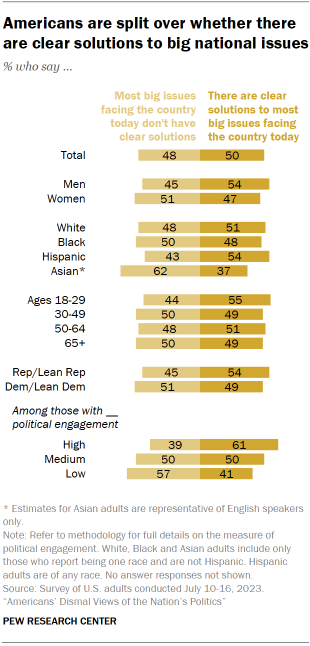
There are relatively modest demographic and political differences in perceptions of whether the solutions to the nations’ problems are clear or not.
While both men and women are relatively divided on this question, women are 6 percentage points more likely to think the big issues facing the country don’t have clear solutions.
Race and ethnicity
While 43% of Hispanic adults and about half of Black (50%) and White (48%) adults say there aren’t clear solutions for most big issues, that rises to 62% among Asian adults.
Age differences on this question are modest, but those under 30 are slightly more likely than those 30 and older to say most big issues have clear solutions.
Partisanship and political engagement
Both Republicans and Democrats are relatively split on this question, though Republicans are slightly more likely to say there are clear solutions to most big issues.
Those with higher levels of political engagement are more likely to say there are clear solutions to most big issues facing the country.
About six-in-ten adults with high levels of political engagement (61%) say there are clear solutions to big issues today, compared with half of those with medium levels of engagement and 41% of those with lower engagement.
Sign up for our weekly newsletter
Fresh data delivery Saturday mornings
Sign up for The Briefing
Weekly updates on the world of news & information
- Election 2024
- Election System & Voting Process
- Federal Government
- National Conditions
- Political Animosity
- Political Discourse
- Political Parties
- Political Polarization
- State & Local Government
- Trust in Government
- Trust, Facts & Democracy
In GOP Contest, Trump Supporters Stand Out for Dislike of Compromise
What americans know about their government, congress has long struggled to pass spending bills on time, how the gop won the turnout battle and a narrow victory in last year’s midterms, narrow majorities in u.s. house have become more common but haven’t always led to gridlock, most popular, report materials.
1615 L St. NW, Suite 800 Washington, DC 20036 USA (+1) 202-419-4300 | Main (+1) 202-857-8562 | Fax (+1) 202-419-4372 | Media Inquiries
Research Topics
- Email Newsletters
ABOUT PEW RESEARCH CENTER Pew Research Center is a nonpartisan fact tank that informs the public about the issues, attitudes and trends shaping the world. It conducts public opinion polling, demographic research, media content analysis and other empirical social science research. Pew Research Center does not take policy positions. It is a subsidiary of The Pew Charitable Trusts .
© 2024 Pew Research Center
- TPC and eLearning
- What's NEW at TPC?
- Read Watch Interact
- Practice Review Test
- Teacher-Tools
- Subscription Selection
- Seat Calculator
- Ad Free Account
- Edit Profile Settings
- Classes (Version 2)
- Student Progress Edit
- Task Properties
- Export Student Progress
- Task, Activities, and Scores
- Metric Conversions Questions
- Metric System Questions
- Metric Estimation Questions
- Significant Digits Questions
- Proportional Reasoning
- Acceleration
- Distance-Displacement
- Dots and Graphs
- Graph That Motion
- Match That Graph
- Name That Motion
- Motion Diagrams
- Pos'n Time Graphs Numerical
- Pos'n Time Graphs Conceptual
- Up And Down - Questions
- Balanced vs. Unbalanced Forces
- Change of State
- Force and Motion
- Mass and Weight
- Match That Free-Body Diagram
- Net Force (and Acceleration) Ranking Tasks
- Newton's Second Law
- Normal Force Card Sort
- Recognizing Forces
- Air Resistance and Skydiving
- Solve It! with Newton's Second Law
- Which One Doesn't Belong?
- Component Addition Questions
- Head-to-Tail Vector Addition
- Projectile Mathematics
- Trajectory - Angle Launched Projectiles
- Trajectory - Horizontally Launched Projectiles
- Vector Addition
- Vector Direction
- Which One Doesn't Belong? Projectile Motion
- Forces in 2-Dimensions
- Being Impulsive About Momentum
- Explosions - Law Breakers
- Hit and Stick Collisions - Law Breakers
- Case Studies: Impulse and Force
- Impulse-Momentum Change Table
- Keeping Track of Momentum - Hit and Stick
- Keeping Track of Momentum - Hit and Bounce
- What's Up (and Down) with KE and PE?
- Energy Conservation Questions
- Energy Dissipation Questions
- Energy Ranking Tasks
- LOL Charts (a.k.a., Energy Bar Charts)
- Match That Bar Chart
- Words and Charts Questions
- Name That Energy
- Stepping Up with PE and KE Questions
- Case Studies - Circular Motion
- Circular Logic
- Forces and Free-Body Diagrams in Circular Motion
- Gravitational Field Strength
- Universal Gravitation
- Angular Position and Displacement
- Linear and Angular Velocity
- Angular Acceleration
- Rotational Inertia
- Balanced vs. Unbalanced Torques
- Getting a Handle on Torque
- Torque-ing About Rotation
- Properties of Matter
- Fluid Pressure
- Buoyant Force
- Sinking, Floating, and Hanging
- Pascal's Principle
- Flow Velocity
- Bernoulli's Principle
- Balloon Interactions
- Charge and Charging
- Charge Interactions
- Charging by Induction
- Conductors and Insulators
- Coulombs Law
- Electric Field
- Electric Field Intensity
- Polarization
- Case Studies: Electric Power
- Know Your Potential
- Light Bulb Anatomy
- I = ∆V/R Equations as a Guide to Thinking
- Parallel Circuits - ∆V = I•R Calculations
- Resistance Ranking Tasks
- Series Circuits - ∆V = I•R Calculations
- Series vs. Parallel Circuits
- Equivalent Resistance
- Period and Frequency of a Pendulum
- Pendulum Motion: Velocity and Force
- Energy of a Pendulum
- Period and Frequency of a Mass on a Spring
- Horizontal Springs: Velocity and Force
- Vertical Springs: Velocity and Force
- Energy of a Mass on a Spring
- Decibel Scale
- Frequency and Period
- Closed-End Air Columns
- Name That Harmonic: Strings
- Rocking the Boat
- Wave Basics
- Matching Pairs: Wave Characteristics
- Wave Interference
- Waves - Case Studies
- Color Addition and Subtraction
- Color Filters
- If This, Then That: Color Subtraction
- Light Intensity
- Color Pigments
- Converging Lenses
- Curved Mirror Images
- Law of Reflection
- Refraction and Lenses
- Total Internal Reflection
- Who Can See Who?
- Formulas and Atom Counting
- Atomic Models
- Bond Polarity
- Entropy Questions
- Cell Voltage Questions
- Heat of Formation Questions
- Reduction Potential Questions
- Oxidation States Questions
- Measuring the Quantity of Heat
- Hess's Law
- Oxidation-Reduction Questions
- Galvanic Cells Questions
- Thermal Stoichiometry
- Molecular Polarity
- Quantum Mechanics
- Balancing Chemical Equations
- Bronsted-Lowry Model of Acids and Bases
- Classification of Matter
- Collision Model of Reaction Rates
- Density Ranking Tasks
- Dissociation Reactions
- Complete Electron Configurations
- Elemental Measures
- Enthalpy Change Questions
- Equilibrium Concept
- Equilibrium Constant Expression
- Equilibrium Calculations - Questions
- Equilibrium ICE Table
- Intermolecular Forces Questions
- Ionic Bonding
- Lewis Electron Dot Structures
- Limiting Reactants
- Line Spectra Questions
- Mass Stoichiometry
- Measurement and Numbers
- Metals, Nonmetals, and Metalloids
- Metric Estimations
- Metric System
- Molarity Ranking Tasks
- Mole Conversions
- Name That Element
- Names to Formulas
- Names to Formulas 2
- Nuclear Decay
- Particles, Words, and Formulas
- Periodic Trends
- Precipitation Reactions and Net Ionic Equations
- Pressure Concepts
- Pressure-Temperature Gas Law
- Pressure-Volume Gas Law
- Chemical Reaction Types
- Significant Digits and Measurement
- States Of Matter Exercise
- Stoichiometry Law Breakers
- Stoichiometry - Math Relationships
- Subatomic Particles
- Spontaneity and Driving Forces
- Gibbs Free Energy
- Volume-Temperature Gas Law
- Acid-Base Properties
- Energy and Chemical Reactions
- Chemical and Physical Properties
- Valence Shell Electron Pair Repulsion Theory
- Writing Balanced Chemical Equations
- Mission CG1
- Mission CG10
- Mission CG2
- Mission CG3
- Mission CG4
- Mission CG5
- Mission CG6
- Mission CG7
- Mission CG8
- Mission CG9
- Mission EC1
- Mission EC10
- Mission EC11
- Mission EC12
- Mission EC2
- Mission EC3
- Mission EC4
- Mission EC5
- Mission EC6
- Mission EC7
- Mission EC8
- Mission EC9
- Mission RL1
- Mission RL2
- Mission RL3
- Mission RL4
- Mission RL5
- Mission RL6
- Mission KG7
- Mission RL8
- Mission KG9
- Mission RL10
- Mission RL11
- Mission RM1
- Mission RM2
- Mission RM3
- Mission RM4
- Mission RM5
- Mission RM6
- Mission RM8
- Mission RM10
- Mission LC1
- Mission RM11
- Mission LC2
- Mission LC3
- Mission LC4
- Mission LC5
- Mission LC6
- Mission LC8
- Mission SM1
- Mission SM2
- Mission SM3
- Mission SM4
- Mission SM5
- Mission SM6
- Mission SM8
- Mission SM10
- Mission KG10
- Mission SM11
- Mission KG2
- Mission KG3
- Mission KG4
- Mission KG5
- Mission KG6
- Mission KG8
- Mission KG11
- Mission F2D1
- Mission F2D2
- Mission F2D3
- Mission F2D4
- Mission F2D5
- Mission F2D6
- Mission KC1
- Mission KC2
- Mission KC3
- Mission KC4
- Mission KC5
- Mission KC6
- Mission KC7
- Mission KC8
- Mission AAA
- Mission SM9
- Mission LC7
- Mission LC9
- Mission NL1
- Mission NL2
- Mission NL3
- Mission NL4
- Mission NL5
- Mission NL6
- Mission NL7
- Mission NL8
- Mission NL9
- Mission NL10
- Mission NL11
- Mission NL12
- Mission MC1
- Mission MC10
- Mission MC2
- Mission MC3
- Mission MC4
- Mission MC5
- Mission MC6
- Mission MC7
- Mission MC8
- Mission MC9
- Mission RM7
- Mission RM9
- Mission RL7
- Mission RL9
- Mission SM7
- Mission SE1
- Mission SE10
- Mission SE11
- Mission SE12
- Mission SE2
- Mission SE3
- Mission SE4
- Mission SE5
- Mission SE6
- Mission SE7
- Mission SE8
- Mission SE9
- Mission VP1
- Mission VP10
- Mission VP2
- Mission VP3
- Mission VP4
- Mission VP5
- Mission VP6
- Mission VP7
- Mission VP8
- Mission VP9
- Mission WM1
- Mission WM2
- Mission WM3
- Mission WM4
- Mission WM5
- Mission WM6
- Mission WM7
- Mission WM8
- Mission WE1
- Mission WE10
- Mission WE2
- Mission WE3
- Mission WE4
- Mission WE5
- Mission WE6
- Mission WE7
- Mission WE8
- Mission WE9
- Vector Walk Interactive
- Name That Motion Interactive
- Kinematic Graphing 1 Concept Checker
- Kinematic Graphing 2 Concept Checker
- Graph That Motion Interactive
- Two Stage Rocket Interactive
- Rocket Sled Concept Checker
- Force Concept Checker
- Free-Body Diagrams Concept Checker
- Free-Body Diagrams The Sequel Concept Checker
- Skydiving Concept Checker
- Elevator Ride Concept Checker
- Vector Addition Concept Checker
- Vector Walk in Two Dimensions Interactive
- Name That Vector Interactive
- River Boat Simulator Concept Checker
- Projectile Simulator 2 Concept Checker
- Projectile Simulator 3 Concept Checker
- Hit the Target Interactive
- Turd the Target 1 Interactive
- Turd the Target 2 Interactive
- Balance It Interactive
- Go For The Gold Interactive
- Egg Drop Concept Checker
- Fish Catch Concept Checker
- Exploding Carts Concept Checker
- Collision Carts - Inelastic Collisions Concept Checker
- Its All Uphill Concept Checker
- Stopping Distance Concept Checker
- Chart That Motion Interactive
- Roller Coaster Model Concept Checker
- Uniform Circular Motion Concept Checker
- Horizontal Circle Simulation Concept Checker
- Vertical Circle Simulation Concept Checker
- Race Track Concept Checker
- Gravitational Fields Concept Checker
- Orbital Motion Concept Checker
- Angular Acceleration Concept Checker
- Balance Beam Concept Checker
- Torque Balancer Concept Checker
- Aluminum Can Polarization Concept Checker
- Charging Concept Checker
- Name That Charge Simulation
- Coulomb's Law Concept Checker
- Electric Field Lines Concept Checker
- Put the Charge in the Goal Concept Checker
- Circuit Builder Concept Checker (Series Circuits)
- Circuit Builder Concept Checker (Parallel Circuits)
- Circuit Builder Concept Checker (∆V-I-R)
- Circuit Builder Concept Checker (Voltage Drop)
- Equivalent Resistance Interactive
- Pendulum Motion Simulation Concept Checker
- Mass on a Spring Simulation Concept Checker
- Particle Wave Simulation Concept Checker
- Boundary Behavior Simulation Concept Checker
- Slinky Wave Simulator Concept Checker
- Simple Wave Simulator Concept Checker
- Wave Addition Simulation Concept Checker
- Standing Wave Maker Simulation Concept Checker
- Color Addition Concept Checker
- Painting With CMY Concept Checker
- Stage Lighting Concept Checker
- Filtering Away Concept Checker
- InterferencePatterns Concept Checker
- Young's Experiment Interactive
- Plane Mirror Images Interactive
- Who Can See Who Concept Checker
- Optics Bench (Mirrors) Concept Checker
- Name That Image (Mirrors) Interactive
- Refraction Concept Checker
- Total Internal Reflection Concept Checker
- Optics Bench (Lenses) Concept Checker
- Kinematics Preview
- Velocity Time Graphs Preview
- Moving Cart on an Inclined Plane Preview
- Stopping Distance Preview
- Cart, Bricks, and Bands Preview
- Fan Cart Study Preview
- Friction Preview
- Coffee Filter Lab Preview
- Friction, Speed, and Stopping Distance Preview
- Up and Down Preview
- Projectile Range Preview
- Ballistics Preview
- Juggling Preview
- Marshmallow Launcher Preview
- Air Bag Safety Preview
- Colliding Carts Preview
- Collisions Preview
- Engineering Safer Helmets Preview
- Push the Plow Preview
- Its All Uphill Preview
- Energy on an Incline Preview
- Modeling Roller Coasters Preview
- Hot Wheels Stopping Distance Preview
- Ball Bat Collision Preview
- Energy in Fields Preview
- Weightlessness Training Preview
- Roller Coaster Loops Preview
- Universal Gravitation Preview
- Keplers Laws Preview
- Kepler's Third Law Preview
- Charge Interactions Preview
- Sticky Tape Experiments Preview
- Wire Gauge Preview
- Voltage, Current, and Resistance Preview
- Light Bulb Resistance Preview
- Series and Parallel Circuits Preview
- Thermal Equilibrium Preview
- Linear Expansion Preview
- Heating Curves Preview
- Electricity and Magnetism - Part 1 Preview
- Electricity and Magnetism - Part 2 Preview
- Vibrating Mass on a Spring Preview
- Period of a Pendulum Preview
- Wave Speed Preview
- Slinky-Experiments Preview
- Standing Waves in a Rope Preview
- Sound as a Pressure Wave Preview
- DeciBel Scale Preview
- DeciBels, Phons, and Sones Preview
- Sound of Music Preview
- Shedding Light on Light Bulbs Preview
- Models of Light Preview
- Electromagnetic Radiation Preview
- Electromagnetic Spectrum Preview
- EM Wave Communication Preview
- Digitized Data Preview
- Light Intensity Preview
- Concave Mirrors Preview
- Object Image Relations Preview
- Snells Law Preview
- Reflection vs. Transmission Preview
- Magnification Lab Preview
- Reactivity Preview
- Ions and the Periodic Table Preview
- Periodic Trends Preview
- Chemical Reactions Preview
- Intermolecular Forces Preview
- Melting Points and Boiling Points Preview
- Bond Energy and Reactions Preview
- Reaction Rates Preview
- Ammonia Factory Preview
- Stoichiometry Preview
- Nuclear Chemistry Preview
- Gaining Teacher Access
- Algebra Based Physics Course
- Teacher Notes
- Tasks and Classes
- Tasks - Classic
- Subscription
- Subscription Locator
- 1-D Kinematics
- Newton's Laws
- Vectors - Motion and Forces in Two Dimensions
- Momentum and Its Conservation
- Work and Energy
- Circular Motion and Satellite Motion
- Thermal Physics
- Static Electricity
- Electric Circuits
- Vibrations and Waves
- Sound Waves and Music
- Light and Color
- Reflection and Mirrors
- About the Physics Interactives
- Task Tracker
- Usage Policy
- Newtons Laws
- Vectors and Projectiles
- Forces in 2D
- Momentum and Collisions
- Circular and Satellite Motion
- Balance and Rotation
- Electromagnetism
- Waves and Sound
- Atomic Physics
- Forces in Two Dimensions
- Work, Energy, and Power
- Circular Motion and Gravitation
- Sound Waves
- 1-Dimensional Kinematics
- Circular, Satellite, and Rotational Motion
- Einstein's Theory of Special Relativity
- Waves, Sound and Light
- QuickTime Movies
- About the Concept Builders
- Pricing For Schools
- Directions for Version 2
- Measurement and Units
- Relationships and Graphs
- Rotation and Balance
- Vibrational Motion
- Reflection and Refraction
- Teacher Accounts
- Task Tracker Directions
- Kinematic Concepts
- Kinematic Graphing
- Wave Motion
- Sound and Music
- About CalcPad
- 1D Kinematics
- Vectors and Forces in 2D
- Simple Harmonic Motion
- Rotational Kinematics
- Rotation and Torque
- Rotational Dynamics
- Electric Fields, Potential, and Capacitance
- Transient RC Circuits
- Light Waves
- Units and Measurement
- Stoichiometry
- Molarity and Solutions
- Thermal Chemistry
- Acids and Bases
- Kinetics and Equilibrium
- Solution Equilibria
- Oxidation-Reduction
- Nuclear Chemistry
- Newton's Laws of Motion
- Work and Energy Packet
- Static Electricity Review
- NGSS Alignments
- 1D-Kinematics
- Projectiles
- Circular Motion
- Magnetism and Electromagnetism
- Graphing Practice
- About the ACT
- ACT Preparation
- For Teachers
- Other Resources
- Solutions Guide
- Solutions Guide Digital Download
- Motion in One Dimension
- Work, Energy and Power
- Algebra Based Physics
- Honors Physics
- Other Tools
- Frequently Asked Questions
- Purchasing the Download
- Purchasing the CD
- Purchasing the Digital Download
- About the NGSS Corner
- NGSS Search
- Force and Motion DCIs - High School
- Energy DCIs - High School
- Wave Applications DCIs - High School
- Force and Motion PEs - High School
- Energy PEs - High School
- Wave Applications PEs - High School
- Crosscutting Concepts
- The Practices
- Physics Topics
- NGSS Corner: Activity List
- NGSS Corner: Infographics
- About the Toolkits
- Position-Velocity-Acceleration
- Position-Time Graphs
- Velocity-Time Graphs
- Newton's First Law
- Newton's Second Law
- Newton's Third Law
- Terminal Velocity
- Projectile Motion
- Forces in 2 Dimensions
- Impulse and Momentum Change
- Momentum Conservation
- Work-Energy Fundamentals
- Work-Energy Relationship
- Roller Coaster Physics
- Satellite Motion
- Electric Fields
- Circuit Concepts
- Series Circuits
- Parallel Circuits
- Describing-Waves
- Wave Behavior Toolkit
- Standing Wave Patterns
- Resonating Air Columns
- Wave Model of Light
- Plane Mirrors
- Curved Mirrors
- Teacher Guide
- Using Lab Notebooks
- Current Electricity
- Light Waves and Color
- Reflection and Ray Model of Light
- Refraction and Ray Model of Light
- Classes (Legacy)
- Teacher Resources
- HomeSchool Course
- Subscriptions

- Newton's Laws
- Einstein's Theory of Special Relativity
- About Concept Checkers
- School Pricing
- Newton's Laws of Motion
- Newton's First Law
- Newton's Third Law
Mechanics: Work, Energy and Power
Work, energy and power: audio guided solution, audio guided solution, habits of an effective problem solver.
- Read the problem carefully and develop a mental picture of the physical situation. If necessary, sketch a simple diagram of the physical situation to help you visualize it.
- Identify the known and unknown quantities in an organized manner. Equate given values to the symbols used to represent the corresponding quantity - e.g., v o = 0 m/s; a = 4.2 m/s/s; v f = 22.9 m/s; d = ???.
- Use physics formulas and conceptual reasoning to plot a strategy for solving for the unknown quantity.
- Identify the appropriate formula(s) to use.
- Perform substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read About It!
Get more information on the topic of Work, Energy and Power at The Physics Classroom Tutorial .
- Sample Work Calculations
Return to Problem Set
Return to Overview
View Audio Guided Solution for Problem:

IMAGES
VIDEO
COMMENTS
Problem 2: Hans Full is pulling on a rope to drag his backpack to school across the ice. He pulls upwards and rightwards with a force of 22.9 Newtons at an angle of 35 degrees above the horizontal to drag his backpack a horizontal distance of 129 meters to the right. Determine the work (in Joules) done upon the backpack.
Watch this video to learn how to solve work example problems in physics, such as calculating the work done by a force, the kinetic energy of a moving object, and the power output of a machine. This video is part of the Khan Academy's work and energy tutorial, which offers free online courses on various topics.
The first thing you need to identify when solving an energy problem is whether the mechanical energy (kinetic + potential) is conserved or not in the situation described by the problem. The basic equation that you will have to learn to solve this type of problems is the following: Where E C is the kinetic energy of the particle and W the work ...
The measurement of work and energy with the same unit reinforces the idea that work and energy are related and can be converted into one another. 1.0 J = 1.0 N∙m, the units of force multiplied by distance. 1.0 N = 1.0 kg∙m/s 2, so 1.0 J = 1.0 kg∙m 2 /s 2. Analyzing the units of the term (1/2)mv 2 will produce the same units for joules.
In physics, work is done on an object when energy is transferred to the object. In other words, work is done when a force acts on something that undergoes a displacement from one position to another. ... We can solve this problem by substituting the given values into the definition of work done on an object by a constant force, stated in the ...
Intro to springs and Hooke's law. What is Hooke's Law? Potential energy stored in a spring. What is elastic potential energy? Spring potential energy example (mistake in math) LOL diagrams. Vertical springs and energy conservation. This unit is part of the Physics library. Browse videos, articles, and exercises by topic.
Example Work and Power Problems. 1. How much work is done by the stickman that pushes a box 5 meters with a force of 12 Newtons forward? W = (F) (d) Since the force is in the same direction as motion you plug numbers directly in and don't have to find the parallel component first. W = (12) (5) = 60 J. 2.
The amount of energy transferred by a force is called the work done by that force. The formula to find the work done by a particular force on an object is W equals F d cosine theta. W refers to the work done by the force F. In other words, W is telling you the amount of energy that the force F is giving to the object.
the work done by aerodynamic drag on the bullet. A group of students are performing an experiment to measure the coefficient of friction between a wood block and a wood plank. One of the students pulls on the block with a force that increases from 0.000 N to 4.135 N in 0.5 seconds.
Here, we learned how to calculate the work done by a constant force in physics by solving a couple of example problems. Overall, the work done by a constant force is the product of the horizontal component of the force times the displacement between the initial and final points. In addition, power, a related quantity to work in physics, is also ...
of work will they have accomplished? 12. If 68 Joules of work were necessary to move a 4 Newton crate, how far was the crate moved? 13. How much work is done in holding a 15 N sack of potatoes while waiting in line at the grocery store for 3 minutes.
How do you solve Work problems in Physics? This lesson is part of our unit on Energy and Conservation of Energy for Physics classes and as a foundation for ...
Correct answer: Explanation: The formula for work is , work equals force times distance. In this case, there is only one force acting upon the object: the force due to gravity. Plug in our given information for the distance to solve for the work done by gravity. Remember, since the object will be moving downward, the distance should be negative.
A person pulls a block 2 m along a horizontal surface by a constant force F = 20 N. Determine the work done by force F acting on the block. Known : Force (F) = 20 N. Displacement (s) = 2 m. Angle (θ) = 0. Wanted : Work (W) Solution : W = F d cos θ = (20) (2) (cos 0) = (20) (2) (1) = 40 Joule. See also Rotational dynamics - problems and ...
What is work in physics? We all do lots of work: homework, working on projects or working at a job. But in physics work has a very specific meaning. This vid...
Solved Example Problems for Work. Example 4.1. A box is pulled with a force of 25 N to produce a displacement of 15 m. If the angle between the force and displacement is 30o, find the work done by the force. Solution. Force, F = 25 N. Displacement, dr = 15 m. Angle between F and dr, θ = 30o.
An example problem, its solution, and annotations on the process of solving the problem. The solutions to the problems from past exams will help you see what a good solution looks like. But seeing the solution alone may not illustrate the general method that could be used to solve other problems.
The three-body problem is a physics conundrum that has boggled scientists since Isaac Newton's day. But what is it, why is it so hard to solve and is the sci-fi series of the same name really ...
In solving work problems, one must always be aware of this definition - theta is the angle between the force and the displacement which it causes. If the force is in the same direction as the displacement, then the angle is 0 degrees. ... An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of ...
An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.
The problem is associated with pioneers in physics, from Ernst Mach, who posed the problem in the 1880s, to the Nobel laureate Richard Feynman, who worked on and popularized it from the 1960s ...
Free math problem solver answers your physics homework questions with step-by-step explanations. Mathway. Visit Mathway on the web. Start 7-day free trial on the app ... Download free on Amazon. Download free in Windows Store. get Go. Physics. Basic Math. Pre-Algebra. Algebra. Trigonometry. Precalculus. Calculus. Statistics. Finite Math. Linear ...
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
Find troubleshooting steps for problems such as your Creative Cloud desktop app not showing available Photoshop updates, you cannot activate Photoshop or it is appearing in trial mode, Photoshop is not recognizing your camera's raw files, you are experiencing image rendering issues or slow performance, Photoshop is crashing, or some tool, font, or plug-in is not working properly.
This algebra-based course covers the main topics in high school introductory and honors physics, including motion, force, work, energy, momentum, collisions, torque, waves, sound, static electricity, and circuits. ... Solving freefall problems using kinematic formulas; One-dimensional motion: Quiz 2; One-dimensional motion: Unit test;
Solving the Zeh problem about the density operator with higher-order statistics. Since a 1932 work from von Neumann, it is generally considered that if two statistical mixtures are represented by the same density operator \r {ho}, they should in fact be considered as the same mixture. In a 1970 paper, Zeh, considering this result to be a ...
1. The biggest problems and greatest strengths of the U.S. political system. The public sees a number of specific problems with American politics. Partisan fighting, the high cost of political campaigns, and the outsize influence of special interests and lobbyists are each seen as characteristic of the U.S. political system by at least 84% of ...
Use physics formulas and conceptual reasoning to plot a strategy for solving for the unknown quantity. Identify the appropriate formula(s) to use. Perform substitutions and algebraic manipulations in order to solve for the unknown quantity. Read About It! Get more information on the topic of Work, Energy and Power at The Physics Classroom ...