Word Problems on Fraction
In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers.
1. 4/7 of a number is 84. Find the number. Solution: According to the problem, 4/7 of a number = 84 Number = 84 × 7/4 [Here we need to multiply 84 by the reciprocal of 4/7]
= 21 × 7 = 147 Therefore, the number is 147.
2. Rachel took \(\frac{1}{2}\) hour to paint a table and \(\frac{1}{3}\) hour to paint a chair. How much time did she take in all?
| Time taken to paint a table = \(\frac{1}{2}\) hour Time taken to paint a chair = \(\frac{1}{3}\) hour Total time taken = \(\frac{1}{2}\) hour + \(\frac{1}{3}\) hour = \(\frac{5}{6}\) hour | \(\frac{1}{2}\) + \(\frac{1}{3}\) L.C.M. of 2, 3 is 6. = \(\frac{3}{6}\) + \(\frac{2}{6}\) \(\frac{1 × 3}{2 × 3}\) = \(\frac{3}{6}\) \(\frac{1 × 2}{3 × 2}\) = \(\frac{2}{6}\) |
3. If 3\(\frac{1}{2}\) m of wire is cut from a piece of 10 m long wire, how much of wire is left?
Total length of the wire = 10 m
Fraction of the wire cut out = 3\(\frac{1}{2}\) m = \(\frac{7}{2}\) m
Length of the wire left = 10 m – 3\(\frac{1}{2}\) m
= [\(\frac{10}{1}\) - \(\frac{7}{2}\)] m, [L.C.M. of 1, 2 is 2]
= [\(\frac{20}{2}\) - \(\frac{7}{2}\)] m, [\(\frac{10}{1}\) × \(\frac{2}{2}\)]
= [\(\frac{20 - 7}{2}\)] m
= \(\frac{13}{2}\) m
= 6\(\frac{1}{2}\) m
4. One half of the students in a school are girls, 3/5 of these girls are studying in lower classes. What fraction of girls are studying in lower classes?
Fraction of girls studying in school = 1/2
Fraction of girls studying in lower classes = 3/5 of 1/2
= 3/5 × 1/2
= (3 × 1)/(5 × 2)
= 3/10
Therefore, 3/10 of girls studying in lower classes.
5. Maddy reads three-fifth of 75 pages of his lesson. How many more pages he need to complete the lesson? Solution: Maddy reads = 3/5 of 75 = 3/5 × 75
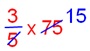
= 45 pages. Maddy has to read = 75 – 45. = 30 pages. Therefore, Maddy has to read 30 more pages. 6. A herd of cows gives 4 litres of milk each day. But each cow gives one-third of total milk each day. They give 24 litres milk in six days. How many cows are there in the herd? Solution: A herd of cows gives 4 litres of milk each day. Each cow gives one-third of total milk each day = 1/3 of 4 Therefore, each cow gives 4/3 of milk each day. Total no. of cows = 4 ÷ 4/3 = 4 × ¾ = 3 Therefore there are 3 cows in the herd.
Questions and Answers on Word problems on Fractions:
1. Shelly walked \(\frac{1}{3}\) km. Kelly walked \(\frac{4}{15}\) km. Who walked farther? How much farther did one walk than the other?
2. A frog took three jumps. The first jump was \(\frac{2}{3}\) m long, the second was \(\frac{5}{6}\) m long and the third was \(\frac{1}{3}\) m long. How far did the frog jump in all?
3. A vessel contains 1\(\frac{1}{2}\) l of milk. John drinks \(\frac{1}{4}\) l of milk; Joe drinks \(\frac{1}{2}\) l of milk. How much of milk is left in the vessel?
● Multiplication is Repeated Addition.
● Multiplication of Fractional Number by a Whole Number.
● Multiplication of a Fraction by Fraction.
● Properties of Multiplication of Fractional Numbers.
● Multiplicative Inverse.
● Worksheet on Multiplication on Fraction.
● Division of a Fraction by a Whole Number.
● Division of a Fractional Number.
● Division of a Whole Number by a Fraction.
● Properties of Fractional Division.
● Worksheet on Division of Fractions.
● Simplification of Fractions.
● Worksheet on Simplification of Fractions.
● Word Problems on Fraction.
● Worksheet on Word Problems on Fractions.
5th Grade Numbers
5th Grade Math Problems
From Word Problems on Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments
|
What’s this? | Facebook X Pinterest WhatsApp Messenger |
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Line-segment, ray and line | definition of in line-segment | symbol.
Jun 14, 24 04:36 PM
What are Parallel Lines in Geometry? | Two Parallel Lines | Examples
Jun 14, 24 02:44 PM

Intersecting Lines | What Are Intersecting Lines? | Definition
Jun 14, 24 01:26 PM
Definition of Points, Lines and Shapes in Geometry | Types & Examples
Jun 14, 24 09:45 AM
Subtracting Integers | Subtraction of Integers |Fundamental Operations
Jun 13, 24 04:32 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Fractions Questions and Problems with Solutions
Questions and problems with solutions on fractions are presented. Detailed solutions to the examples are also included. In order to master the concepts and skills of fractions, you need a thorough understanding (NOT memorizing) of the rules and properties and lot of practice and patience. I hope the examples, questions, problems in the links below will help you.
- Fractions and Mixed Numbers , define fractions and mixed numbers, and introduce important vocabulary.
- Evaluate Fractions of Quantities .
- Fractions Rules including questions with Solutions
- Properties of Fractions
- Complex Fractions with Variables
- Equivalent Fractions examples and questions with solutions.
- Reduce Fractions examples and questions with solutions.
- Reduce Fractions Calculator
- Simplify Fractions , examples and questions including solutions.
- Factor Fractions , examples with questions including solutions.
- Adding Fractions. Add fractions with same denominator or different denominator. Several examples with detailed solutions and exercises.
- Multiply Fractions. Multiply a fraction by another fraction or a number by a fraction. Examples with solutions and exercises.
- Divide Fractions. Divide a fraction by a fraction, a fraction by a number of a number by a fraction. Several examples with solutions and exercises with answers.
Fractions Per Grade
- Fractions and Mixed Numbers , questions and problems with solutions for grade 7
- Fractions and Mixed Numbers , questions and problems with solutions for grade 6
- Fractions , questions for grade 5 and their solutions
- Fractions , questions for grade 4 their answers.
Fractions Calculators
- Fractions Calculator including reducing, adding and multiplying fractions.
- Add Mixed Numbers Calculator
Solving Word Problems by Adding and Subtracting Fractions and Mixed Numbers
Learn how to solve fraction word problems with examples and interactive exercises.
Example 1: Rachel rode her bike for one-fifth of a mile on Monday and two-fifths of a mile on Tuesday. How many miles did she ride altogether?
Analysis: To solve this problem, we will add two fractions with like denominators.
Solution:
Answer: Rachel rode her bike for three-fifths of a mile altogether.
Analysis: To solve this problem, we will subtract two fractions with unlike denominators.
Answer: Stefanie swam one-third of a lap farther in the morning.
Analysis: To solve this problem, we will add three fractions with unlike denominators. Note that the first is an improper fraction.
Answer: It took Nick three and one-fourth hours to complete his homework altogether.

Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having like denominators.
Answer: Diego and his friends ate six pizzas in all.
Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having like denominators.
Answer: The Cocozzelli family took one-half more days to drive home.
Analysis: To solve this problem, we will add two mixed numbers, with the fractional parts having unlike denominators.
Answer: The warehouse has 21 and one-half meters of tape in all.
Analysis: To solve this problem, we will subtract two mixed numbers, with the fractional parts having unlike denominators.
Answer: The electrician needs to cut 13 sixteenths cm of wire.
Analysis: To solve this problem, we will subtract a mixed number from a whole number.
Answer: The carpenter needs to cut four and seven-twelfths feet of wood.
Summary: In this lesson we learned how to solve word problems involving addition and subtraction of fractions and mixed numbers. We used the following skills to solve these problems:
- Add fractions with like denominators.
- Subtract fractions with like denominators.
- Find the LCD.
- Add fractions with unlike denominators.
- Subtract fractions with unlike denominators.
- Add mixed numbers with like denominators.
- Subtract mixed numbers with like denominators.
- Add mixed numbers with unlike denominators.
- Subtract mixed numbers with unlike denominators.
Directions: Subtract the mixed numbers in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the fraction three-fourths, enter 3/4 into the form. To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| RESULTS BOX: |
Fraction Word Problems (Difficult)
Here are some examples of more difficult fraction word problems. We will illustrate how block models (tape diagrams) can be used to help you to visualize the fraction word problems in terms of the information given and the data that needs to be found.
Related Pages Fraction Word Problems Singapore Math Lessons Fraction Problems Using Algebra Algebra Word Problems
Block modeling (also known as tape diagrams or bar models) are widely used in Singapore Math and the Common Core to help students visualize and understand math word problems.
Example: 2/9 of the people on a restaurant are adults. If there are 95 more children than adults, how many children are there in the restaurant?
Solution: Draw a diagram with 9 equal parts: 2 parts to represent the adults and 7 parts to represent the children.
5 units = 95 1 unit = 95 ÷ 5 = 19 7 units = 7 × 19 = 133
Answer: There are 133 children in the restaurant.
Example: Gary and Henry brought an equal amount of money for shopping. Gary spent $95 and Henry spent $350. After that Henry had 4/7 of what Gary had left. How much money did Gary have left after shopping?
350 – 95 = 255 3 units = 255 1 unit = 255 ÷ 3 = 85 7 units = 85 × 7 = 595
Answer: Gary has $595 after shopping.
Example: 1/9 of the shirts sold at Peter’s shop are striped. 5/8 of the remainder are printed. The rest of the shirts are plain colored shirts. If Peter’s shop has 81 plain colored shirts, how many more printed shirts than plain colored shirts does the shop have?
Solution: Draw a diagram with 9 parts. One part represents striped shirts. Out of the remaining 8 parts: 5 parts represent the printed shirts and 3 parts represent plain colored shirts.
3 units = 81 1 unit = 81 ÷ 3 = 27 Printed shirts have 2 parts more than plain shirts. 2 units = 27 × 2 = 54
Answer: Peter’s shop has 54 more printed colored shirts than plain shirts.
Solve a problem involving fractions of fractions and fractions of remaining parts
Example: 1/4 of my trail mix recipe is raisins and the rest is nuts. 3/5 of the nuts are peanuts and the rest are almonds. What fraction of my trail mix is almonds?
How to solve fraction word problem that involves addition, subtraction and multiplication using a tape diagram or block model
Example: Jenny’s mom says she has an hour before it’s bedtime. Jenny spends 3/5 of the hour texting a friend and 3/8 of the remaining time brushing her teeth and putting on her pajamas. She spends the rest of the time reading her book. How long did Jenny read?
How to solve a four step fraction word problem using tape diagrams?
Example: In an auditorium, 1/6 of the students are fifth graders, 1/3 are fourth graders, and 1/4 of the remaining students are second graders. If there are 96 students in the auditorium, how many second graders are there?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: 5th grade > Unit 6
- Multiplying fractions word problem: muffins
- Multiplying fractions word problem: laundry
- Multiplying fractions word problem: bike
Multiply fractions word problems
- Multiply fractions: FAQ
- Your answer should be
- a proper fraction, like 1 / 2 or 6 / 10
- an improper fraction, like 10 / 7 or 14 / 8

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

4.9: Solving Equations with Fractions
- Last updated
- Save as PDF
- Page ID 24084

- David Arnold
- College of the Redwoods
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Undoing Subtraction
We can still add the same amount to both sides of an equation without changing the solution.
Solve for x : \(x - \frac{5}{6} = \frac{1}{3}\).
To “undo” subtracting 5/6, add 5/6 to both sides of the equation and simplify.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x - \frac{5}{6} + \frac{5}{6} = \frac{1}{3} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Add } \frac{5}{6} \text{ to both sides.}} \\ x = \frac{1 \cdot 2}{3 \cdot 2} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 6.}} \\ x = \frac{2}{6} + \frac{5}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
It is perfectly acceptable to leave your answer as an improper fraction. If you desire, or if you are instructed to do so, you can change your answer to a mixed fraction (7 divided by 6 is 1 with a remainder of 1). That is \(x = 1 \frac{1}{6}\).
Checking the Solution
Substitute 7/6 for x in the original equation and simplify.
\[ \begin{aligned} x - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{7}{6} - \frac{5}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Substitute 7/6 for } x.} \\ \frac{2}{6} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Subtract.}} \\ \frac{1}{3} = \frac{1}{3} ~ & \textcolor{red}{ \text{ Reduce.}} \end{aligned}\nonumber \]
Because the last statement is true, we conclude that 7/6 is a solution of the equation x − 5/6 = 1/3.
Undoing Addition
You can still subtract the same amount from both sides of an equation without changing the solution.
Solve for x : \(x + \frac{2}{3} = - \frac{3}{5}\).
To “undo” adding 2/3, subtract 2/3 from both sides of the equation and simplify.
\[ \begin{aligned} x + \frac{2}{3} = - \frac{3}{5} ~ & \textcolor{red}{ \text{ Original equation.}} \\ x + \frac{2}{3} - \frac{2}{3} = - \frac{3}{5} - \frac{2}{3} ~ & \textcolor{red}{ \text{ Subtract } \frac{2}{3} \text{ from both sides.}} \\ x = - \frac{3 \cdot 3}{5 \cdot 3} - \frac{2 \cdot 5}{3 \cdot 5} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 15.}} \\ x = - \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify.}} \\ x = - \frac{19}{15} ~ & \textcolor{red}{ \text{ Subtract.}} \end{aligned}\nonumber \]
Readers are encouraged to check this solution in the original equation.
Solve for x : \(x + \frac{3}{4} = - \frac{1}{2}\)
Undoing Multiplication
We “undo” multiplication by dividing. For example, to solve the equation 2 x = 6, we would divide both sides of the equation by 2. In similar fashion, we could divide both sides of the equation
\[ \frac{3}{5} x = \frac{4}{10}\nonumber \]
by 3/5. However, it is more efficient to take advantage of reciprocals. For convenience, we remind readers of the Multiplicative Inverse Property .
Multiplicative Inverse Property
Let a / b be any fraction. The number b / a is called the multiplicative inverse or reciprocal of a / b . The product of reciprocals is 1.
\[ \frac{a}{b} \cdot \frac{b}{a} = 1.\nonumber \]
Let’s put our knowledge of reciprocals to work.
Solve for x : \(\frac{3}{5}x = \frac{4}{10}\).
To “undo” multiplying by 3/5, multiply both sides by the reciprocal 5/3 and simplify.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{5}{3} \left( \frac{3}{5} x \right) = \frac{5}{3} \left( \frac{4}{10} \right) & ~ \textcolor{red}{ \text{ Multiply both sides by 5/3.}} \\ \left( \frac{5}{3} \cdot \frac{3}{5} \right) x = \frac{20}{30} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, multiply.} \end{array}} \\ 1x = \frac{2}{3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } \frac{5}{3} \cdot \frac{3}{5} = 1. \\ \text{ On the right, reduce: } \frac{20}{30} = \frac{2}{3}. \end{array}} \\ x = \frac{2}{3} ~ & \textcolor{red}{ \text{ On the left, } 1x = x.} \end{aligned}\nonumber \]
Substitute 2/3 for x in the original equation and simplify.
\[ \begin{aligned} \frac{3}{5} x = \frac{4}{10} ~ & \textcolor{red}{ \text{ Original equation.}} \\ \frac{3}{5} \left( \frac{2}{3} \right) = \frac{4}{10} ~ & \textcolor{red}{ \text{ Substitute 2/3 for }x.} \\ \frac{6}{15} = \frac{4}{10} ~ & \textcolor{red}{ \text{ Multiply numerators; multiply denominators.}} \\ \frac{2}{5} = \frac{2}{5} ~ & \textcolor{red}{ \text{ Reduce both sides to lowest terms.}} \end{aligned}\nonumber \]
Because this last statement is true, we conclude that 2/3 is a solution of the equation (3/5) x = 4/10.
Solve for y : \( \frac{2}{3} y = \frac{4}{5}\)
Solve for x : \(- \frac{8}{9} x = \frac{5}{18}\).
To “undo” multiplying by −8/9, multiply both sides by the reciprocal −9/8 and simplify.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ - \frac{9}{8} \left( - \frac{8}{9} x \right) = - \frac{9}{8} \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by } -9/8.} \\ \left[ - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) \right] x = - \frac{3 \cdot 3}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot 3 \cdot 3} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, use the associative property to regroup.} \\ \text{ On the right, prime factor.} \end{array}} 1x = \frac{ \cancel{3} \cdot \cancel{3}}{2 \cdot 2 \cdot 2} \cdot \frac{5}{2 \cdot \cancel{3} \cdot \cancel{3}} ~ & \textcolor{red}{ \begin{array}{l} \text{ On the left, } - \frac{9}{8} \cdot \left( - \frac{8}{9} \right) = 1. \\ \text{ On the right, cancel common factors.} \end{array}} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ On the left, } 1x = x. \text{ Multiply on the right.}} \end{aligned}\nonumber \]
Solve for z: \(− \frac{2}{7} z = \frac{4}{21}\)
Clearing Fractions from the Equation
Although the technique demonstrated in the previous examples is a solid mathematical technique, working with fractions in an equation is not always the most efficient use of your time.
To clear all fractions from an equation, multiply both sides of the equation by the least common denominator of the fractions that appear in the equation.
Let’s put this idea to work.
In Example 1, we were asked to solve the following equation for x :
\[x - \frac{5}{6} = \frac{1}{3}.\nonumber \]
Take a moment to review the solution technique in Example 1. We will now solve this equation by first clearing all fractions from the equation.
Multiply both sides of the equation by the least common denominator for the fractions appearing in the equation.
\[ \begin{aligned} x - \frac{5}{6}= \frac{1}{3} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 6 \left( x - \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 6.}} \\ 6x - 6 \left( \frac{5}{6} \right) = 6 \left( \frac{1}{3} \right) ~ & \textcolor{red}{ \text{ Distribute the 6.}} \\ 6x-5 = 2 ~ & \textcolor{red}{ \text{ On each side, multiply first.}} \\ ~ & \textcolor{red}{6 \left( \frac{5}{6} \right) = 5 \text{ and } 6 \left( \frac{1}{3} \right) = 2.} \end{aligned}\nonumber \]
Note that the equation is now entirely clear of fractions, making it a much simpler equation to solve.
\[ \begin{aligned} 6x - 5 + 5 = 2 + 5 ~ & \textcolor{red}{ \text{ Add 5 to both sides.}} \\ 6x = 7 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{6x}{6} = \frac{7}{6} ~ & \textcolor{red}{ \text{ Divide both sides by 6.}} \\ x = \frac{7}{6} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Note that this is the same solution found in Example 1.
Solve for t : \(t - \frac{2}{7} = - \frac{1}{4}\)
In Example 4, we were asked to solve the following equation for x .
\[- \frac{8}{9}x = \frac{5}{18}\nonumber \]
Take a moment to review the solution in Example 4. We will now solve this equation by first clearing all fractions from the equation.
Multiply both sides of the equation by the least common denominator for the fractions that appear in the equation.
\[ \begin{aligned} - \frac{8}{9} x = \frac{5}{18} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 18 \left( - \frac{8}{9} x \right) = 18 \left( \frac{5}{18} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 18.}} \\ -16x=5 ~ & \textcolor{red}{ \text{ On each side, cancel and multiply.}} \\ ~ & \textcolor{red}{ 18 \left( - \frac{8}{9} \right) = -16 \text{ and } 18 \left( \frac{5}{18} \right) = 5.} \end{aligned}\nonumber \]
Note that the equation is now entirely free of fractions. Continuing,
\[ \begin{aligned} \frac{-16x}{-16} = \frac{5}{-16} ~ & \textcolor{red}{ \text{ Divide both sides by } -16.} \\ x = - \frac{5}{16} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Note that this is the same as the solution found in Example 4.
Solve for u :
\[ - \frac{7}{9} u = \frac{14}{27}\nonumber \]
Solve for x : \(\frac{2}{3}x + \frac{3}{4} = \frac{1}{2}\).
\[ \begin{aligned} \frac{2}{3} x + \frac{3}{4} = \frac{1}{2} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 12 \left( \frac{2}{3} x + \frac{3}{4} = \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 12.}} \\ 12 \left( \frac{2}{3}x \right) + 12 \left( \frac{3}{4} \right) = 12 \left( \frac{1}{2} \right) ~ & \textcolor{red}{ \text{ On the left, distribute 12.}} \\ 8x + 9 = 6 ~ & \textcolor{red}{ \text{ Multiply: } 12 \left( \frac{2}{3} x \right) = 8x, ~ 12 \left( \frac{3}{4} \right) = 9,} \\ ~ & \textcolor{red}{ \text{ and } 12 \left( \frac{1}{2} \right) = 6.} \end{aligned}\nonumber \]
Note that the equation is now entirely free of fractions. We need to isolate the terms containing x on one side of the equation.
\[ \begin{aligned} 8x + 9 - 9 = 6 - 9 ~ & \textcolor{red}{ \text{ Subtract 9 from both sides.}} \\ 8x = - 3 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{8x}{8} = \frac{-3}{8} ~ & \textcolor{red}{ \text{ Divide both sides by 8.}} \\ x = - \frac{3}{8} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Solve for r : \(\frac{3}{4} r + \frac{2}{3} = \frac{1}{2}\)
Solve for x : \( \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8}.\)
Multiply both sides of the equation by the least common denominator for the fractions in the equation.
\[ \begin{aligned} \frac{2}{3} - \frac{3x}{4} = \frac{x}{2} - \frac{1}{8} ~ & \textcolor{red}{ \text{ Original equation.}} \\ 24 \left( \frac{2}{3} - \frac{3x}{4} \right) = 24 \left( \frac{x}{2} - \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 24.}} \\ 24 \left( \frac{2}{3} \right) - 24 \left( \frac{3x}{4} \right) = 24 \left( \frac{x}{2} \right) - 24 \left( \frac{1}{8} \right) ~ & \textcolor{red}{ \text{ On both sides, distribute 24.}} \\ 16 - 18x = 12x - 3 ~ & \textcolor{red}{ \text{ Left: } 24 \left( \frac{2}{3} \right) = 16, ~ 24 \left( \frac{3x}{4} \right) = 18x.} \\ ~ & \textcolor{red}{ \text{ Right: } 24 \left( \frac{x}{2} \right) = 12x, ~ 24 \left( \frac{1}{8} \right) = 3.} \end{aligned}\nonumber \]
\[ \begin{aligned} 16 - 18x - 12x = 12x - 3 - 12x ~ & \textcolor{red}{ \text{ Subtract } 12x \text{ from both sides.}} \\ 16 - 30x = -3 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } -18x - 12x = -30x. \\ \text{ Right: } 12x - 12x = 0. \end{aligned}} \\ 16 - 30x - 16 = -3 - 16 ~ & \textcolor{red}{ \text{ Subtract 16 from both sides.}} \\ -30x = -19 ~ & \textcolor{red}{ \begin{aligned} \text{ Left: } 16-16=0. \\ \text{ Right: } -3 - 16 = -19. \end{aligned}} \\ \frac{-30x}{-30} = \frac{-19}{-30} ~ & \textcolor{red}{ \text{ Divide both sides by } -30.} \\ x = \frac{19}{30} ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
Solve for s : \( \frac{3}{2} - \frac{2s}{5} = \frac{s}{3} - \frac{1}{5}\).
Add texts here. Do not delete this text first.
Applications
Let’s look at some applications that involve equations containing fractions. For convenience, we repeat the Requirements for Word Problem Solutions .
Requirements for Word Problem Solutions
- Statements such as “Let P represent the perimeter of the rectangle.”
- Labeling unknown values with variables in a table.
- Labeling unknown quantities in a sketch or diagram.
- Set up an Equation . Every solution to a word problem must include a carefully crafted equation that accurately describes the constraints in the problem statement.
- Solve the Equation . You must always solve the equation set up in the previous step.
- Answer the Question . This step is easily overlooked. For example, the problem might ask for Jane’s age, but your equation’s solution gives the age of Jane’s sister Liz. Make sure you answer the original question asked in the problem. Your solution should be written in a sentence with appropriate units. 5. Look Back. It is important to note that this step does not imply that you should simply check your solution in your equation. After all, it’s possible that your equation incorrectly models the problem’s situation, so you could have a valid solution to an incorrect equation. The important question is: “Does your answer make sense based on the words in the original problem statement.”
In the third quarter of a basketball game, announcers informed the crowd that attendance for the game was 12,250. If this is two-thirds of the capacity, find the full seating capacity for the basketball arena.
We follow the Requirements for Word Problem Solutions .
1. Set up a Variable Dictionary . Let F represent the full seating capacity. Note: It is much better to use a variable that “sounds like” the quantity that it represents. In this case, letting F represent the full seating capacity is much more descriptive than using x to represent the full seating capacity.
2. Set up an Equation . Two-thirds of the full seating capacity is 12,250.
\[ \begin{aligned} \colorbox{cyan}{Two-thirds} & \text{ of } & \colorbox{cyan}{Full Seating Capacity} & \text{ is } & 12,250 \\ \frac{2}{3} & \cdot & F & = & 12,250 \end{aligned}\nonumber \]
Hence, the equation is
\[ \frac{2}{3} F = 12250.\nonumber \]
3. Solve the Equation . Multiply both sides by 3 to clear fractions, then solve.
\[ \begin{aligned} \frac{2}{3} F = 12250 ~ & \textcolor{red}{ \text{ Original equation.}} \\ 3 \left( \frac{2}{3} F \right) = 3(12250) ~ & \textcolor{red}{ \text{ Multiply both sides by 3.}} \\ 2F = 36750 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ \frac{2F}{2} = \frac{36750}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ F = 18375 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \end{aligned}\nonumber \]
4. Answer the Question . The full seating capacity is 18,375.
5. Look Back . The words of the problem state that 2/3 of the seating capacity is 12,250. Let’s take two-thirds of our answer and see what we get.
\[ \begin{aligned} \frac{2}{3} \cdot 18375 & = \frac{2}{3} \cdot \frac{18375}{1} \\ & = \frac{2}{3} \cdot \frac{3 \cdot 6125}{1} \\ & = \frac{2}{ \cancel{3}} \cdot \frac{ \cancel{3} \cdot 6125}{1} \\ & = 12250 \end{aligned}\nonumber \]
This is the correct attendance, so our solution is correct.
Attendance for the Celtics game was 9,510. If this is 3/4 of capacity, what is the capacity of the Celtics’ arena?
The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
1. Set up a Variable Dictionary . Our variable dictionary will take the form of a well labeled diagram.
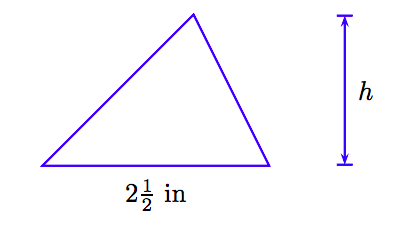
2. Set up an Equation . The area A of a triangle with base b and height h is
\[A = \frac{1}{2} bh.\nonumber \]
Substitute A = 20 and b = \(2 \frac{1}{2}\).
\[20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h.\nonumber \]
3. Solve the Equation . Change the mixed fraction to an improper fraction, then simplify.
\[ \begin{aligned} 20 = \frac{1}{2} \left( 2 \frac{1}{2} \right) h ~ & \textcolor{red}{ \text{ Original equation.}} \\ 20 = \frac{1}{2} \left( \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Mixed to improper: } 2 \frac{1}{2} = \frac{5}{2}.} \\ 20 = \left( \frac{1}{2} \cdot \frac{5}{2} \right) h ~ & \textcolor{red}{ \text{ Associative property.}} \\ 20 = \frac{5}{4} h ~ & \textcolor{red}{ \text{ Multiply: } \frac{1}{2} \cdot \frac{5}{2} = \frac{5}{4}.} \end{aligned}\nonumber \]
Now, multiply both sides by 4/5 and solve.
\[ \begin{aligned} \frac{4}{5} (20) = \frac{4}{5} \left( \frac{5}{4} h \right) ~ & \textcolor{red}{ \text{ Multiply both sides by 4/5.}} \\ 16 = h ~ & \textcolor{red}{ \text{ Simplify: } \frac{4}{5} (20) = 16} \\ ~ & \textcolor{red}{ \text{ and } \frac{4}{5} \cdot \frac{5}{4} = 1.} \end{aligned}\nonumber \]
4. Answer the Question . The height of the triangle is 16 inches.
5. Look Back . If the height is 16 inches and the base is \(2 \frac{1}{2}\) inches, then the area is
\[ \begin{aligned} A & = \frac{1}{2} \left( 2 \frac{1}{2} \right) (16) \\ & = \frac{1}{2} \cdot \frac{5}{2} \cdot \frac{16}{1} \\ & = \frac{5 \cdot 16}{2 \cdot 2} \\ & = \frac{(5) \cdot (2 \cdot 2 \cdot 2 \cdot 2)}{(2) \cdot (2)} \\ & = \frac{5 \cdot \cancel{2} \cdot \cancel{2} \cdot 2 \cot 2}{ \cancel{2} \cdot \cancel{2}} & = 20 \end{aligned}\nonumber \]
This is the correct area (20 square inches), so our solution is correct.
The area of a triangle is 161 square feet. If the base of the triangle measures \(40 \frac{1}{4}\) feet, find the height of the triangle.
1. Is 1/4 a solution of the equation \(x + \frac{5}{8} = \frac{5}{8}\)?
2. Is 1/4 a solution of the equation \(x + \frac{1}{3} = \frac{5}{12}\)?
3. Is −8/15 a solution of the equation \(\frac{1}{4} x = − \frac{1}{15}\)?
4. Is −18/7 a solution of the equation \(− \frac{3}{8} x = \frac{25}{28}\)?
5. Is 1/2 a solution of the equation \(x + \frac{4}{9} = \frac{17}{18}\)?
6. Is 1/3 a solution of the equation \(x + \frac{3}{4} = \frac{13}{12}\)?
7. Is 3/8 a solution of the equation \(x − \frac{5}{9} = − \frac{13}{72}\)?
8. Is 1/2 a solution of the equation \(x − \frac{3}{5} = − \frac{1}{10}\)?
9. Is 2/7 a solution of the equation \(x − \frac{4}{9} = − \frac{8}{63}\)?
10. Is 1/9 a solution of the equation \(x − \frac{4}{7} = − \frac{31}{63}\)?
11. Is 8/5 a solution of the equation \( \frac{11}{14}x = \frac{44}{35}\)?
12. Is 16/9 a solution of the equation \(\frac{13}{18} x = \frac{104}{81}\)?
In Exercises 13-24, solve the equation and simplify your answer.
13. \(2x − 3=6x + 7\)
14. \(9x − 8 = −9x − 3\)
15. \(−7x +4=3x\)
16. \(6x +9= −6x\)
17. \(−2x = 9x − 4\)
18. \(−6x = −9x + 8\)
19. \(−8x = 7x − 7\)
20. \(−6x = 5x + 4\)
21. \(−7x +8=2x\)
22. \(−x − 7=3x\)
23. \(−9x +4=4x − 6\)
24. \(−2x +4= x − 7\)
In Exercises 25-48, solve the equation and simplify your answer.
25. \(x + \frac{3}{2 = \frac{1}{2}\)
26. \(x − \frac{3}{4} = \frac{1}{4}\)
27. \(− \frac{9}{5} x = \frac{1}{2}\)
28. \(\frac{7}{3} x = − \frac{7}{2}\)
29. \(\frac{3}{8} x = \frac{8}{7}\)
30. \(− \frac{1}{9} x = − \frac{3}{5}\)
31. \(\frac{2}{5} x = − \frac{1}{6}\)
32. \(\frac{1}{6} x = \frac{2}{9}\)
33. \(− \frac{3}{2} x = \frac{8}{7}\)
34. \(− \frac{3}{2} x = − \frac{7}{5}\)
35. \(x + \frac{3}{4} = \frac{5}{9}\)
36. \(x − \frac{1}{9} = − \frac{3}{2}\)
37. \(x − \frac{4}{7} = \frac{7}{8}\)
38. \(x + \frac{4}{9} = − \frac{3}{4}\)
39. \(x + \frac{8}{9} = \frac{2}{3}\)
40. \(x − \frac{5}{6} = \frac{1}{4}\)
41. \(x + \frac{5}{2} = − \frac{9}{8}\)
42. \(x + \frac{1}{2} = \frac{5}{3}\)
43. \(− \frac{8}{5} x = \frac{7}{9}\)
44. \(− \frac{3}{2} x = − \frac{5}{9}\)
45. \(x − \frac{1}{4} = − \frac{1}{8}\)
46. \(x − \frac{9}{2} = − \frac{7}{2}\)
47. \(− \frac{1}{4} x = \frac{1}{2}\)
48. \(− \frac{8}{9} x = − \frac{8}{3}\)
In Exercises 49-72, solve the equation and simplify your answer.
49. \(− \frac{7}{3} x − \frac{2}{3} = \frac{3}{4} x + \frac{2}{3}\)
50. \(\frac{1}{2} x − \frac{1}{2} = \frac{3}{2} x + \frac{3}{4}\)
51. \(− \frac{7}{2} x − \frac{5}{4} = \frac{4}{5}\)
52. \(− \frac{7}{6} x + \frac{5}{6} = − \frac{8}{9}\)
53. \(− \frac{9}{7} x + \frac{9}{2} = − \frac{5}{2}\)
54. \(\frac{5}{9} x − \frac{7}{2} = \frac{1}{4}\)
55. \(\frac{1}{4} x − \frac{4}{3} = − \frac{2}{3}\)
56. \(\frac{8}{7} x + \frac{3}{7} = \frac{5}{3}\)
57. \(\frac{5}{3} x + \frac{3}{2} = − \frac{1}{4}\)
58. \(\frac{1}{2} x − \frac{8}{3} = − \frac{2}{5}\)
59. \(− \frac{1}{3} x + \frac{4}{5} = − \frac{9}{5} x − \frac{5}{6}\)
60. \(− \frac{2}{9} x − \frac{3}{5} = \frac{4}{5} x − \frac{3}{2}\)
61. \(− \frac{4}{9} x − \frac{8}{9} = \frac{1}{2} x − \frac{1}{2}\)
62. \(− \frac{5}{4} x − \frac{5}{3} = \frac{8}{7} x + \frac{7}{3}\)
63. \(\frac{1}{2} x − \frac{1}{8} = − \frac{1}{8} x + \frac{5}{7}\)
64. \(− \frac{3}{2} x + \frac{8}{3} = \frac{7}{9} x − \frac{1}{2}\)
65. \(− \frac{3}{7} x − \frac{1}{3} = − \frac{1}{9}\)
66. \(\frac{2}{3} x + \frac{2}{9} = − \frac{9}{5}\)
67. \(− \frac{3}{4} x + \frac{2}{7} = \frac{8}{7} x − \frac{1}{3}\)
68. \(\frac{1}{2} x + \frac{1}{3} = − \frac{5}{2} x − \frac{1}{4}\)
69. \(− \frac{3}{4} x − \frac{2}{3} = − \frac{2}{3} x − \frac{1}{2}\)
70. \(\frac{1}{3} x − \frac{5}{7} = \frac{3}{2} x + \frac{4}{3}\)
71. \(− \frac{5}{2} x + \frac{9}{5} = \frac{5}{8}\)
72. \(\frac{9}{4} x + \frac{4}{3} = − \frac{1}{6}\)
73. At a local soccer game, announcers informed the crowd that attendance for the game was 4,302. If this is 2/9 of the capacity, find the full seating capacity for the soccer stadium.
74. At a local basketball game, announcers informed the crowd that attendance for the game was 5,394. If this is 2/7 of the capacity, find the full seating capacity for the basketball stadium.
75. The area of a triangle is 51 square inches. If the length of the base is \(8 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
76. The area of a triangle is 20 square inches. If the length of the base is \(2 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
77. The area of a triangle is 18 square inches. If the length of the base is \(4 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
78. The area of a triangle is 44 square inches. If the length of the base is \(5 \frac{1}{2}\) inches, find the height (altitude) of the triangle.
79. At a local hockey game, announcers informed the crowd that attendance for the game was 4,536. If this is 2/11 of the capacity, find the full seating capacity for the hockey stadium.
80. At a local soccer game, announcers informed the crowd that attendance for the game was 6,970. If this is 2/7 of the capacity, find the full seating capacity for the soccer stadium.
81. Pirates . About one-third of the world’s pirate attacks in 2008 occurred off the Somali coast. If there were 111 pirate attacks off the Somali coast, estimate the number of pirate attacks worldwide in 2008.
82. Nuclear arsenal . The U.S. and Russia agreed to cut nuclear arsenals of long-range nuclear weapons by about a third, down to 1, 550. How many long-range nuclear weapons are there now? Associated Press-Times-Standard 04/04/10 Nuclear heartland anxious about missile cuts.
83. Seed vault . The Svalbard Global Seed Vault has amassed half a million seed samples, and now houses at least one-third of the world’s crop seeds. Estimate the total number of world’s crop seeds. Associated Press-Times-Standard 03/15/10 Norway doomsday seed vault hits half-million mark.
84. Freight train . The three and one-half mile long Union Pacific train is about 2 1 2 times the length of a typical freight train. How long is a typical freight train? Associated Press-Times-Standard 01/13/10 Unusally long train raises safety concerns.
13. \(− \frac{5}{2}\)
15. \(\frac{2}{5}\)
17. \(\frac{4}{11}\)
19. \(\frac{7}{15}\)
21. \(\frac{8}{9}\)
23. \(\frac{10}{13}\)
25. \(−1\)
27. \(− \frac{5}{18}\)
29. \(\frac{64}{21}\)
31. \(− \frac{5}{12}\)
33. \(− \frac{16}{21}\)
35. \(− \frac{7}{36}\)
37. \(\frac{81}{56}\)
39. \(− \frac{2}{9}\)
41. \(− \frac{29}{8}\)
43. \(− \frac{35}{72}\)
45. \(\frac{1}{8}\)
47. \(−2\)
49. \(− \frac{16}{37}\)
51. \(− \frac{41}{70}\)
53. \(\frac{49}{9}\)
55. \(\frac{8}{3}\)
57. \(− \frac{21}{20}\)
59. \(− \frac{49}{44}\)
61. \(− \frac{7}{17}\)
63. \(\frac{47}{35}\)
65. \(− \frac{14}{27}\)
67. \(\frac{52}{159}\)
69. \(− 2\)
71. \(\frac{47}{100}\)
81. There were about 333 pirate attacks worldwide.
83. 1,500,000

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs
- Word Problems
- Add/subtract fractions

Download & Print From only $2.60
Add & subtract fractions word problems
Like & unlike denominators.
Below are our grade 5 math word problem worksheet on adding and subtracting fractions. The problems include both like and unlike denominators , and may include more than two terms.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
More word problem worksheets
Explore all of our math word problem worksheets , from kindergarten through grade 5.
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.
- Forgot Password?

Fraction Word Problems: Addition, Subtraction, and Mixed Numbers
In today’s post, we’re going to see how to solve some of the problems that we’ve introduced in Smartick: fraction word problems. They appear during the word problems section at the end of the daily session.
We’re going to look at how to solve problems involving addition and subtraction of fractions, including mixed fractions (the ones that are made up of a whole number and a fraction).
Try and solve the fraction word problems by yourself first, before you look for the solutions and their respective explanations below.
Fraction Word Problems
Problem nº 1.

Problem nº 2

Problem nº 3

Solution to Problem nº 1
This is an example of a problem involving the addition of a whole number and a fraction.

The simplest way to show the number of cookies I ate is to write it as a mixed number. And the data given in the word problem gives us the result: 9 biscuits and 5 / 6 of a biscuit = 9 5 / 6 biscuits.
Solution to Problem nº 2
In this example, we have to subtract two fractions with the same denominator.

To calculate how full the gas tank is, we have to subtract both fractions. Since we are given fractions, the best way to present the solution is in the form of a fraction. Additionally, we’re dealing with two fractions with the same denominator, so we just have to subtract the numerators of both fractions to get the result. 8 / 10 – 4 / 10 = 4 / 10
Solution to Problem nº 3
This problem requires us to subtract a mixed number and a fraction.

To solve this problem, we need to subtract the number of episodes that were downloaded this morning from the total number of episodes that are now downloaded.
To do this, we need to change the mixed number into a fraction: the 5 becomes 60 / 12 (5 x 12 = 60) and we add it to the fraction 60 / 12 + 8 / 12 = 68 / 12 .
We’ve converted the mixed number 5 8 / 12 to 68 / 12 . Now we just have to subtract the number of episodes that were downloaded yesterday ( 7 / 12 ), 68 / 12 – 7 / 12 = 61 / 12 .
Hopefully, you didn’t need the explanations and were able to solve them yourself without any help!
Fraction Video Tutorials
In the following video tutorials, you can learn a bit more about fractions. And if you would like to learn more math concepts, check out Smartick’s Youtube channel !
Simplifying Fractions
Simplification Using the GCD
Equivalent Fractions
If you would like to practice more fraction word problems like these and others, log in to Smartick and enjoy learning math.
Learn More:
- Word Problems with Fractions
- What Is a Fraction? Learn Everything There Is to Know!
- Using Mixed Numbers to Represent Improper Fractions
- Learning How to Subtract Fractions
- Learn How to Subtract Fractions
- 15 fun minutes a day
- Adapts to your child’s level
- Millions of students since 2009

- Recent Posts
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024
- Pythagorean Theorem: Definition, Proofs and an Example of Practical Application - 02/29/2024
Add a new public comment to the blog: Cancel reply
The comments that you write here are moderated and can be seen by other users. For private inquiries please write to [email protected]
Your personal details will not be shown publicly.
I have read and accepted the Privacy and Cookies Policy
It is really great. It helps me a lot. Thank you

for World Environment Day with code NATURE30

Share this article

Table of Contents
Latest updates.

1 Million Means: 1 Million in Rupees, Lakhs and Crores

Ways To Improve Learning Outcomes: Learn Tips & Tricks

The Three States of Matter: Solids, Liquids, and Gases

Types of Motion: Introduction, Parameters, Examples

Understanding Frequency Polygon: Detailed Explanation

Uses of Silica Gel in Packaging?

Visual Learning Style for Students: Pros and Cons

Air Pollution: Know the Causes, Effects & More

Sexual Reproduction in Flowering Plants

Integers Introduction: Check Detailed Explanation
Tag cloud :.
- entrance exams
- engineering
- ssc cgl 2024
- Written By Keerthi Kulkarni
- Last Modified 22-06-2023
Word Problems on Fractions: Types & Solved Examples
Word Problems on Fractions: A fraction is a mathematical expression for a portion of a whole. Each portion acquired when we divide the entire whole into parts is referred to as a fraction. When we divide a pizza into parts, for example, each slice represents a fraction of the whole pizza. Fractions are subjected to a variety of operations, including addition, subtraction, multiplication, and division. Fractions are used in many real-life situations.
This article will outline how to construct and solve fraction word problems. Students will come across fraction word problems with answers, fraction problem solving and dividing fractions word problems. It is advisable to practice all the problems thoroughly before attempting the exam. Keep reading to know more about word problems on fractions,, definition, types, solved examples and many more
Definition of Fractions
A fraction is a number that is used to expresses a part per whole. Each part obtained when we divide the whole into several parts is called the fraction.
Example: When we cut an apple into two-part, then each part represents the fraction \(\left(\frac{1}{2}\right)\) of the apple.

A fraction consists mainly of two parts, one is the numerator, and the other one is the denominator. The upper part or topmost part of the fraction is called the numerator, and the bottom part or below part is called the denominator.

We have mainly three types of fractions: proper fractions, improper fractions, and mixed fractions. They are categorised by the relationship between the numerator and denominator of the fractions.

Word Problems on Fractions
The fraction problem solving consist of a few sentences describing a real-life scenario where a mathematical calculation of fraction formulas are used to solve a problem.
Example: Keerthi took one piece of pizza, which is cut into a total of four pieces. Find the fraction of the pizza taken by Keerthi? The fraction of pizza taken by Keerthi \(=\frac{1}{4}\)
Some of the word problems on fractions that uses fraction formula are listed below:
- Word problems on simplification of fractions
- Word problems on addition and subtraction of fractions
- Word problems on multiplication of fractions
- Word problems on dividing fractions
- Word problems on fractions, percentages, decimals.
Word Problems on Simplifications of Fractions
A fraction in which the numerator and the denominator have no common factor other than “one” is said to be the simplest form of fractions.
Example: Divya took \(8\) apples from the bucket of \(24\) apples. Find the fraction of apples taken by the Divya? The fraction of apples taken by Divya \(=\frac{8}{24}\) and its simplest form is \(\frac{1}{3}\)
Word Problems on Addition of Fractions
To add the like fractions (Fractions with the same denominators), keep the denominator the same and add the numerator values of the given fractions.
To add the unlike fractions (fractions with different denominators), convert the denominators of the given fractions equal to L.C.M of their denominators. Now add the numerator value and take the denominator of the resultant as L.C.M.
Example: Sahana bought \(\frac{1}{4} \mathrm{~kg}\) of apples and \(\frac{1}{2} \mathrm{~kg}\) of oranges from the shop. Total how many fruits she bought? The total fruits bought by Sahana \(=\frac{1}{2}+\frac{1}{4}=\frac{1 \times 2+1}{4}=\frac{3}{4} \mathrm{~kg}\)
Word Problems on Subtraction of Fractions
To subtract the like fractions (Fractions with the same denominators), keep the denominator the same and find the difference of the numerator values of the given fractions.
To subtract the unlike fractions (fractions with different denominators), convert the denominators of the given fractions equal to L.C.M of their denominators. Now find the difference of the numerator value and take the denominator of the resultant as L.C.M.
Example: Keerthi travelled \(\frac{2}{5} \mathrm{~km}\) to school. While returning home, she stopped at her friend’s house at a distance of \(\frac{1}{3} \mathrm{~km}\). Find the remaining distance? The remaining distance needs to be travelled \(=\frac{2}{5}-\frac{1}{3}=\frac{(2 \times 3)-(1 \times 5)}{5 \times 3}=\frac{6-5}{15}=\frac{1}{15} \mathrm{~km}\)
Word Problems on Multiplication of Fractions
To multiply the two or more fractions, find the product of numerators of the given fractions and the product of the denominators of the given fractions separately.
Example: Keerthi had \(Rs.10000\), and she had donated \(\frac{1}{10}\) of the money to the Oldage home. How much amount did she donate? The amount Keerthi donated \(=\frac{1}{10} \times Rs.10000= Rs. 1000\)
Word Problems on Division of Fractions
The division of fractions is nothing but multiplying the first fraction with the reciprocal of the second fraction. The reciprocal of the fraction is a fraction obtained by interchanging the numerator and denominator.
Example: The area of the rectangle is \(\frac{15}{4} \mathrm{~cm}^{2}\), whose length is \(\frac{5}{2} \mathrm{~cm}\). Find the width of the rectangle? We know that area of rectangle \(= \text {length} \times \text {bredath}\) And, breadth \(=\frac{\text { area }}{\text { length }}=\frac{15}{\frac{4}{2}}=\frac{15}{4} \times \frac{2}{5}=\frac{3}{2} \mathrm{~cm}\).
Word Problems on Conversion of Fractions to Percentage
We know that percentages are also fractions with the denominator equals to hundred. To convert the given fraction to a percentage, multiply it with hundred and to convert any percentage value to a fraction, divide with hundred.
Example: Keerthi ate \(\frac{2}{5}\) of the pizza. How much percentage of pizza is eaten by Keerthi? The percentage of pizza ate by Keerthi \(=\frac{2}{5} \times 100 \%=40 \%\).
Word Problems on Conversion of Fractions to Decimals
Decimal numbers are the numbers (quotient) obtained by dividing the fraction’s numerator with the given fraction’s denominator. To convert the given decimal to the fractional value by writing the given number without decimals and making the denominator equal to \(1\) followed by the zeroes and number of zeroes equal to the number of decimal places.
Example: Keerthi got \(\frac{1}{10}\) of the price of a T.V. as a discount. Find the discount in decimal. The part of the discount received by a Keerthi as a discount \(=\frac{1}{10}=0.1\)
Solved Examples – Word Problems on Fractions
Q.1. In February \(2021\) , a school was working only three-fourths of the total number of days in the month and the remaining number of days given as holidays. How many days did the school work in the month of February? Ans: The year \(2021\) is a non-leap year. We know that a non-leap has \(28\) days in February month. So, the total number of days \(=28\). Given, the school was working only three-fourths of the total number of days in the month. The number of days school working in February month \(=\frac{3}{4}\) of \(28\). \(=\frac{3}{4} \times 28=21\) days Hence, the school working for \(21\) days in the month of February for the year \(2021\).
Q.2. Keerthi needs \(1 \frac{1}{2}\) cups of sugar for baking a cake. She decided to make \(6\) cakes for her friends. How many cups of sugar did she need for making the \(6\) cakes? Ans: Given, Keerthi needs \(1 \frac{1}{2}\) cup of sugar to make a cake. The total cups of sugar required to make 6 cakes is calculated by multiplying the sugar needed for one cake with the number of cakes that needs to be prepared by Keerthi and is given by \(1 \frac{1}{2} \times 6\) Convert the above-mixed fraction to an improper fraction by multiplying the denominator with the whole and add to the numerator keeping the same denominator as \(1 \frac{1}{2}=\frac{(\text { whole×denominator })+\text { numerator })}{\text { denominator }}=\frac{(1 \times 2)+1}{2}=\frac{3}{2}\) The total cups of sugar needed for making \(6\) cakes \(=\frac{3}{2} \times 6=9\) Hence, Keerthi needs \(9\) cups of sugar to make \(6\) cakes.
Q.3. An oil container contains \(7 \frac{1}{2}\) litres of oil which are poured into \(2 \frac{1}{2}\) litres bottles. How many bottles are needed to fill \(7 \frac{1}{2}\) litres of oil? Ans: Given, a container holds total oil of \(7 \frac{1}{2}\) litres, and the total amount held by each bottle is \(2 \frac{1}{2}\) litres. Consider the number of bottles required is \(x\). From the given question, the total oil in the container is equal to the product of oil in each bottle and the number of bottles required. \(\Rightarrow 7 \frac{1}{2}=x \times 2 \frac{1}{2}\) \(\Rightarrow \frac{15}{2}=x \times \frac{5}{2}\) \(\Rightarrow 15=5 x\) \(\Rightarrow x=\frac{15}{5}=3\) Therefore, \(3\) bottles are required to fill the total oil in the container.
Q.4. A square garden has the area \(\frac{36}{25} \,\text {sq.ft}\). Find the side of the square garden. Ans: Given the area of the square garden is \(\frac{36}{25} \,\text {sq.ft}\). Let the length of the side of the square garden is \(a\) fts. We know that area of the square \( = {\rm{side}} \times {\rm{side}} = {a^2}\) Thus, \(a^{2}=\frac{36}{25}\) \(\Rightarrow a=\sqrt{\frac{36}{25}}=\frac{\sqrt{36}}{\sqrt{25}}=\frac{6}{5}\) feet. Hence, the length of the side of the square garden is \(\frac{6}{5}\) feet.
Q.5. At a party, total \(280\) ice-creams are prepared. Four-seventh of them is eaten by the children. Find the ice-creams eaten by the children. Ans: Total ice-creams prepared \(=280\) Number of ice-creams eaten by children \(=\frac{4}{7}\) of \(280=\frac{4}{7} \times 280=160\) Hence, children ate \(160\) ice-creams.
In mathematics, a fraction is used to represent a piece of something larger. It depicts the whole’s equal pieces. The numerator and denominator are the two elements of a fraction. The numerator is the number at the top, while the denominator is the number at the bottom. The numerator specifies the number of equal parts taken, whereas the denominator specifies the total number of equal parts in the total.
In this article, we have studied the definitions of fractions, different types of fractions. We also studied the word problems on fractions and their operations. This article gives the word problems on fractions, addition and subtraction of fractions, multiplication of fractions, division of fractions, the simplest form of fractions, conversion of fractions to percentage, decimals etc., with the help of solved examples.
FAQs on Word Problems on Fractions
Here are some of most commonly asked questions on word problems on fractions.
Q.1: How do you solve word problems with fractions?
Ans: To solve word problems with fractions, first, read and write the given data. Write the mathematical form by given data and perform the operations on fractions according to the data.
Q.2: How do you write a fraction division in word problems?
Ans: The fraction division can be written as keeping the first fraction as it is and multiplying it with the reciprocal of the second fraction.
Q.3: How do you know when to divide or multiply fractions in a word problem?
Ans: To find the product, we need to multiply and to find any one of the quantities, we need to divide.
Q.4: What is an example of a fraction word problem?
Ans: Keerthi ate 40% of the pizza. How much is part of the pizza eaten by Keerthi.
Q.5: What is a fraction?
Ans: A fraction is a number that is used to express a part per whole.
Learn About Conversion Of Fractions
We hope this detailed article on Word Problem on Fractions helps you in your preparation. If you get stuck do let us know in the comments section below and we will get back to you at the earliest.
Stay tuned to Embibe to learn more important concepts
Related Articles
1 Million Means: 1 million in numerical is represented as 10,00,000. The Indian equivalent of a million is ten lakh rupees. It is not a...
Ways To Improve Learning Outcomes: With the development of technology, students may now rely on strategies to enhance learning outcomes. No matter how knowledgeable a...
The Three States of Matter: Anything with mass and occupied space is called ‘Matter’. Matters of different kinds surround us. There are some we can...
Motion is the change of a body's position or orientation over time. The motion of humans and animals illustrates how everything in the cosmos is...
Understanding Frequency Polygon: Students who are struggling with understanding Frequency Polygon can check out the details here. A graphical representation of data distribution helps understand...
When you receive your order of clothes or leather shoes or silver jewellery from any online shoppe, you must have noticed a small packet containing...
Visual Learning Style: We as humans possess the power to remember those which we have caught visually in our memory and that too for a...
Air Pollution: In the past, the air we inhaled was pure and clean. But as industrialisation grows and the number of harmful chemicals in the...
In biology, flowering plants are known by the name angiosperms. Male and female reproductive organs can be found in the same plant in flowering plants....
Integers Introduction: To score well in the exam, students must check out the Integers introduction and understand them thoroughly. The collection of negative numbers and whole...

Human Respiratory System – Detailed Explanation
Human Respiratory System: Students preparing for the NEET and Biology-related exams must have an idea about the human respiratory system. It is a network of tissues...
Place Value of Numbers: Detailed Explanation
Place Value of Numbers: Students must understand the concept of the place value of numbers to score high in the exam. In mathematics, place value...
The Leaf: Types, Structures, Parts
The Leaf: Students who want to understand everything about the leaf can check out the detailed explanation provided by Embibe experts. Plants have a crucial role...
Factors Affecting Respiration: Definition, Diagrams with Examples
In plants, respiration can be regarded as the reversal of the photosynthetic process. Like photosynthesis, respiration involves gas exchange with the environment. Unlike photosynthesis, respiration...
General Terms Related to Spherical Mirrors
General terms related to spherical mirrors: A mirror with the shape of a portion cut out of a spherical surface or substance is known as a...
Number System: Types, Conversion and Properties
Number System: Numbers are highly significant and play an essential role in Mathematics that will come up in further classes. In lower grades, we learned how...
Types of Respiration
Every living organism has to "breathe" to survive. The process by which the living organisms use their food to get energy is called respiration. It...
Animal Cell: Definition, Diagram, Types of Animal Cells
Animal Cell: An animal cell is a eukaryotic cell with membrane-bound cell organelles without a cell wall. We all know that the cell is the fundamental...
Conversion of Percentages: Conversion Method & Examples
Conversion of Percentages: To differentiate and explain the size of quantities, the terms fractions and percent are used interchangeably. Some may find it difficult to...
Arc of a Circle: Definition, Properties, and Examples
Arc of a circle: A circle is the set of all points in the plane that are a fixed distance called the radius from a fixed point...
Ammonia (NH3): Preparation, Structure, Properties and Uses
Ammonia, a colourless gas with a distinct odour, is a chemical building block and a significant component in producing many everyday items. It is found...
CGPA to Percentage: Calculator for Conversion, Formula, & More
CGPA to Percentage: The average grade point of a student is calculated using their cumulative grades across all subjects, omitting any supplemental coursework. Many colleges,...
Uses of Ether – Properties, Nomenclature, Uses, Disadvantages
Uses of Ether: Ether is an organic compound containing an oxygen atom and an ether group connected to two alkyl/aryl groups. It is formed by the...
General and Middle Terms: Definitions, Formula, Independent Term, Examples
General and Middle terms: The binomial theorem helps us find the power of a binomial without going through the tedious multiplication process. Further, the use...
Mutually Exclusive Events: Definition, Formulas, Solved Examples
Mutually Exclusive Events: In the theory of probability, two events are said to be mutually exclusive events if they cannot occur simultaneously or at the...
Geometry: Definition, Shapes, Structure, Examples
Geometry is a branch of mathematics that is largely concerned with the forms and sizes of objects, their relative positions, and the qualities of space....
Bohr’s Model of Hydrogen Atom: Expressions for Radius, Energy
Rutherford’s Atom Model was undoubtedly a breakthrough in atomic studies. However, it was not wholly correct. The great Danish physicist Niels Bohr (1885–1962) made immediate...

39 Insightful Publications

Embibe Is A Global Innovator

Innovator Of The Year Education Forever

Interpretable And Explainable AI

Revolutionizing Education Forever

Best AI Platform For Education

Enabling Teachers Everywhere

Decoding Performance

Leading AI Powered Learning Solution Provider

Auto Generation Of Tests

Disrupting Education In India

Problem Sequencing Using DKT

Help Students Ace India's Toughest Exams

Best Education AI Platform

Unlocking AI Through Saas

Fixing Student’s Behaviour With Data Analytics

Leveraging Intelligence To Deliver Results

Brave New World Of Applied AI

You Can Score Higher

Harnessing AI In Education

Personalized Ed-tech With AI

Exciting AI Platform, Personalizing Education

Disruptor Award For Maximum Business Impact

Top 20 AI Influencers In India

Proud Owner Of 9 Patents

Innovation in AR/VR/MR

Best Animated Frames Award 2024
Trending Searches
Previous year question papers, sample papers.
Unleash Your True Potential With Personalised Learning on EMBIBE

Ace Your Exam With Personalised Learning on EMBIBE
Enter mobile number.
By signing up, you agree to our Privacy Policy and Terms & Conditions
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Inverse operations
Solve equations with fractions
Here you will learn about how to solve equations with fractions, including solving equations with one or more operations. You will also learn about solving equations with fractions where the unknown is the denominator of a fraction.
Students will first learn how to solve equations with fractions in 7th grade as part of their work with expressions and equations and expand that knowledge in 8th grade.
What are equations with fractions?
Equations with fractions involve solving equations where the unknown variable is part of the numerator and/or denominator of a fraction.
The numerator (top number) in a fraction is divided by the denominator (bottom number).
To solve equations with fractions, you will use the “balancing method” to apply the inverse operation to both sides of the equation in order to work out the value of the unknown variable.
The inverse operation of addition is subtraction.
The inverse operation of subtraction is addition.
The inverse operation of multiplication is division.
The inverse operation of division is multiplication.
For example,
\begin{aligned} \cfrac{2x+3}{5} \, &= 7\\ \colorbox{#cec8ef}{$\times \, 5$} \; & \;\; \colorbox{#cec8ef}{$\times \, 5$} \\\\ 2x+3&=35 \\ \colorbox{#cec8ef}{$-\,3$} \; & \;\; \colorbox{#cec8ef}{$- \, 3$} \\\\ 2x & = 32 \\ \colorbox{#cec8ef}{$\div \, 2$} & \; \; \; \colorbox{#cec8ef}{$\div \, 2$}\\\\ x & = 16 \end{aligned}

Common Core State Standards
How does this relate to 7th grade and 8th grade math?
- Grade 7: Expressions and Equations (7.EE.A.1) Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
- Grade 8: Expressions and Equations (8.EE.C.7) Solve linear equations in one variable.
- Grade 8: Expressions and Equations (8.EE.C.7b) Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.
How to solve equations with fractions
In order to solve equations with fractions:
Identify the operations that are being applied to the unknown variable.
- Apply the inverse operations, one at a time, to both sides of the equation .
- When you have the variable on one side, you have the final answer.
- Check the answer by substituting the answer back into the original equation .
![example of problem solving involving fractions [FREE] Solve Equations with Fractions Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/02/Grade-6-to-8-Solve-Equations-with-Fractions-Worksheet-listing-image.png)
[FREE] Solve Equations with Fractions Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of solving equations with fractions. 15 questions with answers to identify areas of strength and support!
Solve equations with fractions examples
Example 1: equations with one operation.
Solve for x \text{: } \cfrac{x}{5}=4 .
The unknown is x.
Looking at the left hand side of the equation, the x is divided by 5.
\cfrac{x}{5}
2 Apply the inverse operations, one at a time, to both sides of the equation.
The inverse of “dividing by 5 ” is “multiplying by 5 ”.
You will multiply both sides of the equation by 5.

3 When you have the variable on one side, you have the final answer.
The final answer is x=20.
4 Check the answer by substituting the answer back into the original equation.
You can check the answer by substituting the answer back into the original equation.
\cfrac{20}{5}=20\div5=4
Example 2: equations with one operation
Solve for x \text{: } \cfrac{x}{3}=8 .
Looking at the left hand side of the equation, the x is divided by 3.
\cfrac{x}{3}
Apply the inverse operations, one at a time, to both sides of the equation.
The inverse of “dividing by 3 ” is “multiplying by 3 ”.
You will multiply both sides of the equation by 3.
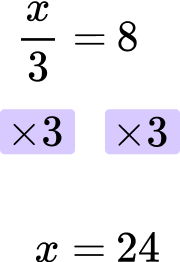
Write the final answer, checking that it is correct.
The final answer is x=24.
\cfrac{24}{3}=24\div3=8
Example 3: equations with two operations
Solve for x \text{: } \cfrac{x \, + \, 1}{2}=7 .
Looking at the left hand side of the equation, 1 is added to x and then divided by 2 (the denominator of the fraction).
\cfrac{x \, + \, 1}{2}
First, clear the fraction by multiplying both sides of the equation by 2.
Then, subtract 1 from both sides.
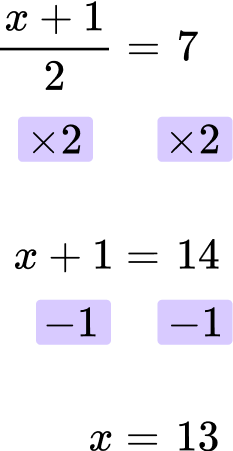
The final answer is x=13.
\cfrac{13 \, +1 \, }{2}=\cfrac{14}{2}=14\div2=7
Example 4: equations with two operations
Solve for x \text{: } \cfrac{x}{4}-2=3 .
Looking at the left hand side of the equation, x is divided by 4 and then 2 is subtracted.
\cfrac{x}{4}-2
First, add 2 to both sides of the equation.
Then, multiply both sides of the equation by 4.
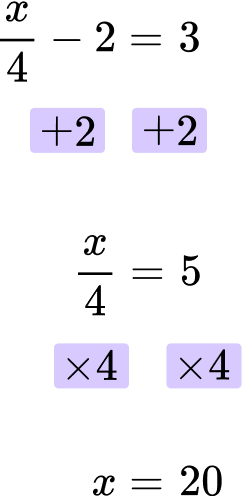
\cfrac{20}{4}-2=20\div4-2=5-2=3
Example 5: equations with three operations
Solve for x \text{: } \cfrac{3x}{5}+1=7 .
Looking at the left hand side of the equation, x is multiplied by 3, then divided by 5 , and then 1 is added.
\cfrac{3x}{5}+1
First, subtract 1 from both sides of the equation.
Then, multiply both sides of the equation by 5.
Finally, divide both sides by 3.
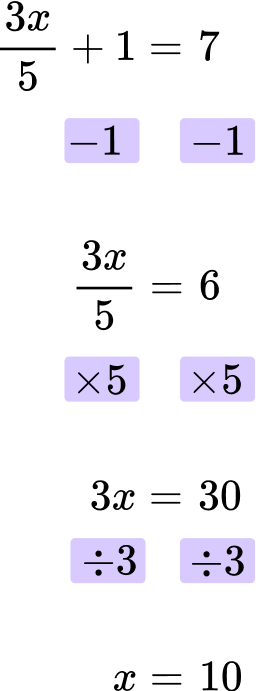
The final answer is x=10.
\cfrac{3 \, \times \, 10}{5}+1=\cfrac{30}{5}+1=6+1=7
Example 6: equations with three operations
Solve for x \text{: } \cfrac{2x-1}{7}=3 .
Looking at the left hand side of the equation, x is multiplied by 2, then 1 is subtracted, and the last operation is divided by 7 (the denominator).
\cfrac{2x-1}{7}
First, multiply both sides of the equation by 7.
Next, add 1 to both sides.
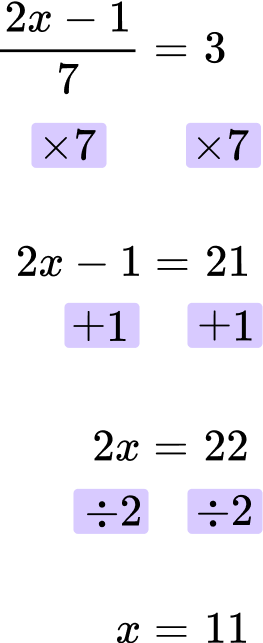
The final answer is x=11.
\cfrac{2 \, \times \, 11-1}{7}=\cfrac{22-1}{7}=\cfrac{21}{7}=3
Example 7: equations with the unknown as the denominator
Solve for x \text{: } \cfrac{24}{x}=6 .
Looking at the left hand side of the equation, x is the denominator. 24 is divided by x.
\cfrac{24}{x}
You need to multiply both sides of the equation by x.
Then, you can divide both sides by 6.
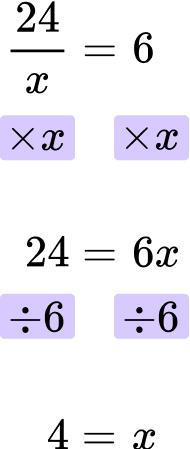
The final answer is x=4.
\cfrac{24}{4}=24\div4=6
Example 8: equations with the unknown as the denominator
Solve for x \text{: } \cfrac{18}{x}-6=3 .
Looking at the left hand side of the equation, x is the denominator. 18 is divided by x , and then 6 is subtracted.
\cfrac{18}{x}-6
First, add 6 to both sides of the equation.
Then, multiply both sides of the equation by x.
Finally, divide both sides by 9.
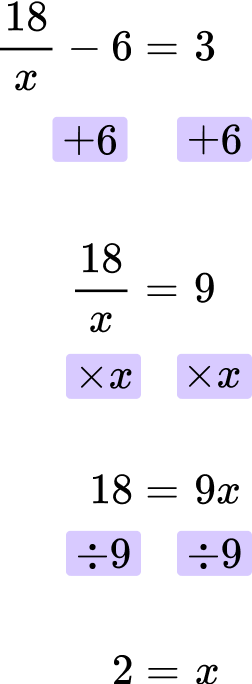
The final answer is x=2.
\cfrac{18}{2}-6=9-6=3
Teaching tips for solving equations with fractions
- When students first start working through practice problems and word problems, provide step-by-step instructions to assist them with solving linear equations.
- Introduce solving equations with fractions with one-step problems, then two-step problems, before introducing multi-step problems.
- Students will need lots of practice with solving linear equations. These standards provide the foundation for work with future linear equations in Algebra I and II.
- Provide opportunities for students to explain their thinking through writing. Ensure that they are using key vocabulary, such as, absolute value, coefficient, equation, common factors, inequalities, simplify, etc.
Easy mistakes to make
- The solution to an equation can be any type of number The unknowns do not have to be integers (whole numbers and their negative opposites). The solutions can be fractions or decimals. They can also be positive or negative numbers.
- The unknown of an equation can be on either side of the equation The unknown, represented by a letter, is often on the left hand side of the equations; however, it doesn’t have to be. It could also be on the right hand side of an equation.

- Lowest common denominator (LCD) It is common to get confused between solving equations involving fractions and adding and subtracting fractions. When adding and subtracting, you need to work out the lowest/least common denominator (sometimes called the least common multiple or LCM). When you solve equations involving fractions, multiply both sides of the equation by the denominator of the fraction.
Related math equations lessons
- Math equations
- Rearranging equations
- How to find the equation of a line
- Substitution
- Linear equations
- Writing linear equations
- Solving equations
- Identity math
- One step equations
Practice solve equations with fractions questions
1. Solve: \cfrac{x}{6}=3

You will multiply both sides of the equation by 6, because the inverse of “dividing by 6 ” is “multiplying by 6 ”.
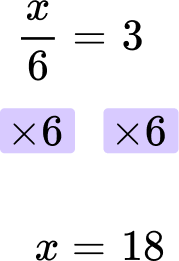
The final answer is x = 18.
\cfrac{18}{6}=18 \div 6=3
2. Solve: \cfrac{x \, + \, 4}{2}=7
Then subtract 4 from both sides.
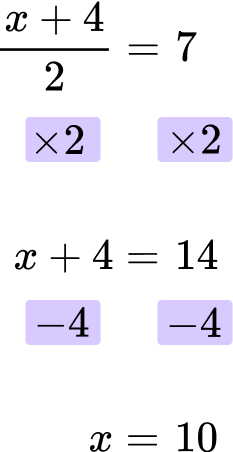
The final answer is x = 10.
\cfrac{10 \, + \, 4}{2}=\cfrac{14}{2}=14 \div 2=7
3. Solve: \cfrac{x}{8}-5=1
First, add 5 to both sides of the equation.
Then multiply both sides of the equation by 8.
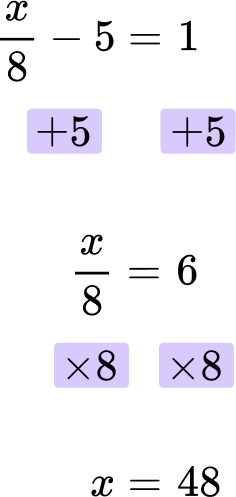
The final answer is x = 48.
\cfrac{48}{8}-5=48 \div 8-5=1
4. Solve: \cfrac{3x \, + \, 2}{4}=2
First, multiply both sides of the equation by 4.
Next, subtract 2 from both sides.
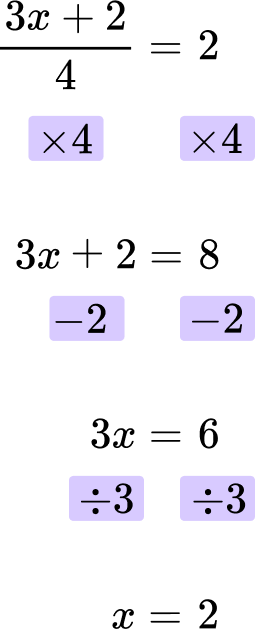
The final answer is x = 2.
\cfrac{3 \, \times \, 2+2}{4}=\cfrac{6 \, + \, 2}{4}=\cfrac{8}{4}=8 \div 4=2
5. Solve: \cfrac{4x}{7}-2=6
Then multiply both sides of the equation by 7.
Finally, divide both sides by 4.
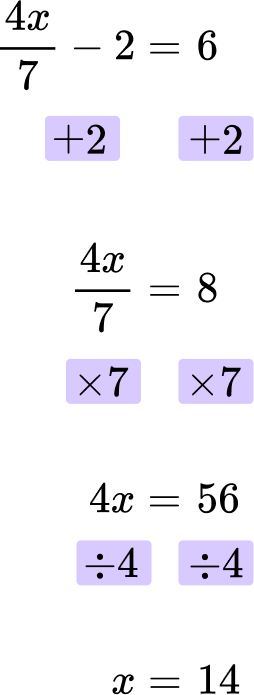
The final answer is x = 14.
\cfrac{4 \, \times \, 14}{7}-2=\cfrac{56}{7}-2=56 \div 7-2=6
6. Solve: \cfrac{42}{x}=7
Then you divide both sides by 7.
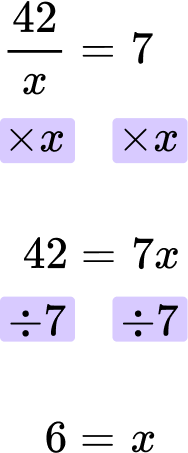
The final answer is x = 6.
\cfrac{42}{6}=42 \div 6=7
Solve equations with fractions FAQs
Yes, you still follow the order of operations when solving equations with fractions. You will start with any operations in the numerator and follow PEMDAS (parenthesis, exponents, multiply/divide, add/subtract), followed by any operations in the denominator. Then you will solve the rest of the equation as usual.
The next lessons are
- Inequalities
- Types of graphs
- Math formulas
- Coordinate plane
- Number patterns
- Algebraic expressions
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview
Singapore math support and resources
Solving Fraction Word Problems Through Visualization
Through visualization, algebra-type word problems can be solved without formally introducing algebra. Here is a typical example of a non-routine word problem from a 4th grade Singapore Math workbook involving fractions:
⅓ of Amy’s money is equal to ½ of Bob’s money. Amy has $40 more than Bob. How much does Amy have?
A good visualization tool to solve such a problem is the bar model. For example,

Without explicitly representing any values with variables, students can easily visualize the problem and are able to understand there are 5 equal units involved. The extra unit that Amy has is exactly $40. So, since Amy has 3 of these units, she has 3 x $40 = $120.
Recognizing problems visually also makes them think algebraically. Without realizing it, students would be working with algebra through interesting word problems.
Related Resources

For more related resources, please refer to our Bar Models page.
Leave a Comment Cancel Reply
Your email address will not be published. Required fields are marked *
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Word Problems on Fraction with Solutions | Fraction Word Problems with Answers
Are you feeling difficulty in solving the word problems on fractions? Here you will get plenty of information on how to solve word problems and the method used to solve them. You can apply this related knowledge to the problems you encounter on fractions. By going through the article you can also check the solved examples for a better understanding of the concept.
- Simplification of Fractions
- Worksheet on Simplification of Fractions
- Types of Fractions
What are Fractions?
A fractional number is considered as the ratio between two numbers. Fractions are defined by \(\frac {a}{b} \) a is called the numerator which means the equal number of parts that are counted. b is called the denominator which means a number of parts in the whole.
Fraction Word Problems with Answers
Problem 1: Mickey has read three-fifth of his 75 pages book. How many more pages he needs to read to complete his book? Solution: Let us write the given information, Mickey has read \(\frac {3}{5} \) of a 75 page book. Which can be written as \(\frac {3}{5} \) * 75 \(\frac {3}{5} \) * 75 = 45 So, Mickey has completed reading 45 pages from his book. Now to find the number of pages he needs to read to complete his book Total number of pages = 75 Number of pages Mickey has completed reading = 45 Number of pages he needs to read to complete his book = (75 – 45) = 30pages Number of pages mickey needs to read to complete his book = 30 pages.
Problem 2: Minnie has Rs. 675. She gave \(\frac {13}{15} \) of the amount to Daisy. Then Daisy spent \(\frac {9}{15} \) of the amount given to her. How much amount is Daisy left with? Solution: Amount Minnie gave to Daisy = \(\frac {13}{15} \) of 675 Which can be written as \(\frac {13}{15} \) * 675 \(\frac {13}{15} \) * 675 = Rs.585 Amount Daisy spent = \(\frac {9}{15} \) of 585 Which can be written as \(\frac {9}{15} \) * 585 \(\frac {9}{15} \) * 585 = 351 Amount Daisy is left with = Amount Minnie gave to Daisy – Amount Daisy spent Rs 585 – Rs 351 = Rs 234 Amount left with Daisy left = Rs 234
Problem 3: Tom bought \(\frac {1}{5} \)L milk on Monday and \(\frac {2}{5} \)L on Tuesday. How much milk did he buy in two days? Solution: Milk bought on Monday = \(\frac {1}{5} \)L Milk bought on Tuesday = \(\frac {2}{5} \)L Total milk he bought = \(\frac {1}{5} \)L + \(\frac {2}{5} \)L \(\frac {1}{5} \)L + \(\frac {2}{5} \)L = \(\frac {1 + 2}{5} \)L = \(\frac {3}{5} \)L Milk bought by Tom in two days = \(\frac {3}{5} \)L
Problem 4: Jerry bought \(\frac {5}{7} \)Kg of cheese and used \(\frac {1}{7} \)Kg. How much cheese is left? Solution: Cheese bought = \(\frac {5}{7} \)Kg Cheese used = \(\frac {1}{7} \)Kg Cheese left = Cheese bought – Cheese used \(\frac {5}{7} \)Kg – \(\frac {1}{7} \)Kg = \(\frac {5 – 1}{7} \)Kg \(\frac {4}{7} \)Kg Cheese left with Jerry = \(\frac {4}{7} \)Kg
Problem 5: Jaggu bought \(\frac {4}{7} \)Kg banana on Monday and \(\frac {2}{7} \)Kg of apple on Tuesday. What is the total quantity of fruits Jaggu bought? Solution: Quantity of bananas bought by Jaggu on Monday = \(\frac {4}{7} \)Kg Quantity of apples bought by Jaggu on Tuesday = \(\frac {2}{7} \)Kg The total quantity of fruits Jaggu bought = Quantity of bananas + Quantity of apples \(\frac {4}{7} \)Kg + \(\frac {2}{7} \)Kg = \(\frac {4 + 2}{7} \)Kg \(\frac {6}{7} \)Kg The total quantity of fruits Jaggu bought = \(\frac {6}{7} \)Kg
Problem 6: Ben bought \(\frac {4}{7} \)m cloth at the rate of Rs 140 per meter. How much amount did he pay? Solution: Cost per meter = Rs 140 Length of cloth ben bought =\(\frac {4}{7} \)m Amount Ben paid = Length of cloth ben bought * Cost per meter \(\frac {4}{7} \)m * Rs 140 = \(\frac {4 * 140}{7} \) \(\frac {4 * 140}{7} \) = \(\frac {560}{7} \) = Rs 80 Amount paid by Ben = Rs 80
Problem 7: What is the difference between \(\frac {3}{5} \) of 5000 and \(\frac {5}{8} \) of 4000 Solution: First, we need to find what is \(\frac {3}{5} \) of 5000 and \(\frac {5}{8} \) of 4000 \(\frac {3}{5} \) of 5000 = \(\frac {3}{5} \) * 5000 = 3000 \(\frac {5}{8} \) of 4000 = \(\frac {5}{8} \) * 4000 = 2500 Now, difference between \(\frac {3}{5} \) of 5000 and \(\frac {5}{8} \) of 4000 = (3000 – 2500) = 500 The difference between \(\frac {3}{5} \) of 5000 and \(\frac {5}{8} \) of 4000 = 500
Problem 8: Jane spent \(\frac {1}{5} \) of her pockey money on food and \(\frac {3}{4} \) on books, how much did she spend alltogether? Solution: Amount spent on food = \(\frac {1}{5} \) Amount spent on books = \(\frac {3}{4} \) Total amount spent = Amount spent on food + Amount spent on books \(\frac {1}{5} \) + \(\frac {3}{4} \) = ( \(\frac {1}{5} \) * \(\frac {4}{4} \) ) + ( \(\frac {3}{4} \) + \(\frac {5}{5} \) ) = \(\frac {4}{20} \) + \(\frac {15}{20} \) = \(\frac {19}{20} \) Amount spent by Jane = \(\frac {19}{20} \)
Problem 9: In a high school contest, Ross jumped 3\(\frac {8}{9} \)m and Joye jumped 4\(\frac {1}{3} \)m. Who jumped more height and by how much more? Solution: Height Ross jumped = 3\(\frac {8}{9} \)m Height Joey jumped = 4\(\frac {1}{3} \)m The given numbers are mixed fractional numbers let’s convert them to improper fractional numbers So, 3\(\frac {8}{9} \)m = \(\frac {35}{9} \)m 4\(\frac {1}{3} \)m = \(\frac {13}{3} \)m This means, Ross jumed \(\frac {35}{9} \)m and Joey jumped \(\frac {13}{3} \)m Now to know who jumped more height we need to compare these numbers by cross multiplication \(\frac {35}{9} \) * \(\frac {13}{3} \) = \(\frac {35 * 3}{9 * 13} \) = \(\frac {105}{117} \) We know 117 > 105 so, \(\frac {13}{3} \) > \(\frac {35}{9} \) This means Joey jumped more height To know by how more Joey jumped than Ross we need to subtract \(\frac {13}{3} \) from \(\frac {35}{9} \) LCM is 9 So,( \(\frac {13}{3} \) * \(\frac {3}{3} \) ) – \(\frac {35}{9} \) = \(\frac {39}{9} \) – \(\frac {35}{9} \) = \(\frac {39 – 35}{9} \) = \(\frac {4}{9} \) Joey jumed \(\frac {4}{9} \) more than Ross.
Problem 10: Bunny bought 2\(\frac {2}{5} \)kg of strawberry, 2kg of blackberry and 1\(\frac {2}{5} \)kg of blueberry. What is the total weight of berries Bunny bought? Solution: Weight of strawberry = 2\(\frac {2}{5} \)kg Weight of blackberry = 2kg Weight of blueberry = 1\(\frac {2}{5} \)kg We can see that weights of berries are in mixed fractional form and whole number form Now, let’s convert them to fractional numbers so that we can add them and find the weight of the berries 2\(\frac {2}{5} \)kg =\(\frac {12}{5} \)kg 2kg = \(\frac {2}{1} \)kg 1\(\frac {2}{5} \)kg = \(\frac {7}{5} \)kg Total weight of berries = Sum of (strawberry + blackberry + blueberry) = \(\frac {12}{5} \) + \(\frac {2}{1} \) + \(\frac {7}{5} \) LCM is 5 = \(\frac {12}{5} \) + (\(\frac {2}{1} \) + \(\frac {5}{5} \)) + \(\frac {7}{5} \) = \(\frac {12}{5} \) + \(\frac {10}{5} \) + \(\frac {7}{5} \) = \(\frac {12 + 10 + 7}{5} \) = \(\frac {29}{5} \) \(\frac {12}{5} \) is a improper fractional number so let us convert it in to mixed fractional number \(\frac {29}{5} \) = 5\(\frac {4}{5} \) The total weight of berries = 5\(\frac {4}{5} \)kg
Problem 11: Mickey bought \(\frac {7}{8} \)kg of noddels and Minnie bought \(\frac {6}{8} \)kg of noddels. What is the total quantity of noddels they have? Solution: Weight of noddles Mickey bought = \(\frac {7}{8} \)kg Weight of noddels Minnie bought = \(\frac {6}{8} \)kg Total weight of noddels = Weight of noddles Mickey bought +Weight of noddels Minnie bought = \(\frac {7}{8} \)kg + \(\frac {6}{8} \)kg = \(\frac {7 +6}{8} \)kg = \(\frac {13}{8} \)kg This is an improper fractional number so it can be converted to a mixed fractional number \(\frac {13}{8} \)kg = 1\(\frac {5}{8} \)kg The total quantity of noddles Mickey and Minnie have = 1\(\frac {5}{8} \)kg
Problem 12: Kitty’s mother bought 1\(\frac {3}{4} \)kg of cookies and her father bought 1\(\frac {1}{2} \)kg of cookies. What is the total weight of cookies that Kitty has? Solution: Weight of cookies bought by Kitty’s mother = 1\(\frac {3}{4} \)kg Weight of cookies bought by Kitty’s father = 1\(\frac {1}{2} \)kg To know the total weight of cookies we have to add them We can’t add mixed fractional numbers so let us convert them into improper fractional numbers 1\(\frac {3}{4} \)kg = \(\frac {7}{4} \)kg 1\(\frac {1}{2} \)kg = \(\frac {3}{2} \)kg Now we can add these two fractional numbers \(\frac {7}{4} \)kg + \(\frac {3}{2} \)kg LCM= 4 = \(\frac {1*7 + 2*3}{4} \) = \(\frac {7 + 6}{4} \) = \(\frac {13}{4} \) \(\frac {13}{4} \) is an improper fractional number So we have to convert it into a mixed fractional number \(\frac {13}{4} \) = 3\(\frac {1}{4} \) The total quantity of cookies Kitty have = 3\(\frac {1}{4} \)kg
Leave a Comment Cancel Reply
You must be logged in to post a comment.
WORD PROBLEMS INVOLVING OPERATIONS WITH FRACTIONS
Problem 1 :
Mary poured 5/8 liter of apple juice equally in to 5 glasses. How much of apple juice was there in each glass?
(A) 1/8 liter (B) 1/5 liter (C) 1/6 liter
Original quantity of apple juice = 5/8 liter
Number of glasses to be divide = 5
Quantity of apple juice in each glass = (5/8) ÷ 5
Here we can consider 5 as 5/1
= (5/8) ÷ (5/1)
= (5/8) ⋅ (1/5)
= 1/8
So 1/8 liter apple juice will get each glass.
Problem 2 :
John cuts lead strips to make stained-glass windows. He has a 3 ¾ foot strip of lead and cuts into 5 equal pieces. How long is each piece of lead?
(A) 1/6 feet (B) 3/4 feet (C) 2/3 feet
Original length of the lead strip = 3 ¾ foot
Length of each lead strip = 3 ¾ foot ÷ 5
= 15/4 ÷ 5
= (15/4) ⋅ (1/5)
= 3/4
The required length of each piece of lead is ¾ feet.
Problem 3 :
Mrs.Mathew divided ¾ kg of grapes equally among 6 children. How many kilograms of grapes did each child get?
(A) 1/8 kg (B) 3 /11 kg ( C) 2/3 kg
Quantity of grapes that Mrs.Mathew had = 3/4 kg
Number of children is be divided = 6
Quantity of grapes that e ach children will get
= (original quantity of grapes)/(Number of children)
= (3/4) ÷ 6
= (3/4) ⋅ (1/6)
= 1/8 kg
That is each child will get 1/8 kg of grapes.
Problem 4 :
The perimeter of square piece of paper is 3/4 m. What is the length of its side?
(A) 1/15 m (B) 3 /16 m ( C) 2/3 m
Perimeter of square piece = 3/4 m
Perimeter of any square = 4a
4a = 3/4 m
The length of four sides = 3/4 m
length of one side = (3/4) ÷ 4
= (3/4) ⋅ (1/4)
The length of each side of a square is 3/16 m.
Problem 5 :
The product of two fractions is 30 1/3. One of them is 5 2/3. Find the other?
(A) 91/17 (B) 15/19 (C) 25/97
Let x be the required fraction.
One of the fraction = 5 2/3 = 17/3
Product of two fractions = 30 1/3 = 91/3
(17/3) ⋅ x = 91/3
x = 91/3 ÷ (17/3)
x = (91/3) ⋅ (3/17)
x = 91/17
So, the required fraction is 91/17.
Problem 6 :
How many pieces of wood each 1/5 m long can be cut from a piece 3 m long ?
(A) 18 pieces (B) 11 pieces (C) 15 pieces
Length of the given wood = 3 m
Length of each piece = (1/5) m
Length of each pieces which has been cut
= Length of wood/(measurement of wood piece)
= 3 / (1/5)
That is, 3 m wood can be cut into 15 equal parts.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Sat math videos (part 7 - calculator).
Jun 13, 24 03:21 AM
SAT Math Videos - Part 8 (Calculator)
Jun 13, 24 02:35 AM
Velocity and Acceleration
Jun 13, 24 02:12 AM
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
- Member login
Adding fractions word problems
Have a great basic math word problem.
Share it here with a very detailed solution!
Enter Your Title
|
Entering your basic math word problem is easy to do. Just type!... |
|
Do you have a picture to add? Great! Click the button and find it on your computer. Then select it. |
Add a Picture/Graphic Caption (optional)
Click here to upload more images (optional)
Author Information (optional)
To receive credit as the author, enter your information below.
|
|
|
|
|
Submit Your Contribution
- Check box to agree to these submission guidelines .
- I am at least 16 years of age.
- I understand and accept the privacy policy .
- I understand that you will display my submission on your website.
(You can preview and edit on the next page)
What Other Visitors Have Said
Click below to see contributions from other visitors to this page...
Click here to write your own.
Subtracting fractions word problems
Recent Articles
How to divide any number by 5 in 2 seconds.
Feb 28, 24 11:07 AM
Math Trick to Square Numbers from 50 to 59
Feb 23, 24 04:46 AM
Sum of Consecutive Odd Numbers
Feb 22, 24 10:07 AM
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.

IMAGES
VIDEO
COMMENTS
Fraction word problems are math word problems involving fractions that require students to use problem-solving skills within the context of a real-world situation. To solve a fraction word problem, you must understand the context of the word problem, what the unknown information is, and what operation is needed to solve it.
The solution to this problem is an irreducible fraction (a fraction which cannot be simplified). Therefore, there is nothing left to do. Word problems with fractions: involving two fractions. In these problems, we should remember how to carry out operations with fractions. Carefully read the following problem and the steps we have taken to ...
Here are some examples and solutions of fraction word problems. The first example is a one-step word problem. The second example shows how blocks can be used to help illustrate the problem. The third example is a two-step word problem. More examples and solutions using the bar modeling method to solve fraction word problems are shown in the videos.
Solving Word Problems Involving Fractions - Example problems with step by step solution. SOLVING WORD PROBLEMS INVOLVING FRACTIONS. Problem 1 : ... So, the marks scored in the subjects math and English are 180 and 60. Problem 3 : If 1/8 of a pencil is black, 1/2 of the remaining is white and the remaining 3 1/2 cm is blue, find the total length ...
How to solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, by using visual fraction models or equations to represent the problem. Examples and step by step solutions. Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers, Common Core Grade 5, 5.nf.2
Solution: Step 1: Assign variables : Let x = number. Step 2: Solve the equation. Isolate variable x. Answer: The number is 21. Example: The numerator of a fraction is 3 less than the denominator. When both the numerator and denominator are increased by 4, the fraction is increased by fraction.
Here are four situations that involve and . Before calculating, decide if each answer is greater than 1 or less than 1. Write a multiplication equation or division equation for the situation. Answer the question. Show your reasoning. Draw a tape diagram, if needed. There was. 3 4. liter of water in Andre's water bottle.
Fraction Word Problems - Examples and Worked Solutions of Word Problems, to solve a word problem that involves adding fractions with unlike denominators, Solve a problem involving fractions of fractions and fractions of remaining parts, using bar models or tape diagrams, with video lessons, examples and step-by-step solutions.
In word problems on fraction we will solve different types of problems on multiplication of fractional numbers and division of fractional numbers. 1. 4/7 of a number is 84. Find the number. Solution: According to the problem, 4/7 of a number = 84. Number = 84 × 7/4.
Questions and problems with solutions on fractions are presented. Detailed solutions to the examples are also included. In order to master the concepts and skills of fractions, you need a thorough understanding (NOT memorizing) of the rules and properties and lot of practice and patience. I hope the examples, questions, problems in the links ...
Identify your areas for growth in these lessons: Dividing fractions by fractions. Dividing fractions word problems. Start quiz. Unit test. Test your understanding of Fractions with these NaN questions. Start test. In this topic, we will explore fractions conceptually and add, subtract, multiply, and divide fractions.
Analysis: To solve this problem, we will divide the first mixed number by the second. First, we will convert each mixed number into an improper fraction. Solution: Answer: The warehouse will have 2 and 2/25 pieces of tape. Summary: In this lesson we learned how to solve word problems involving multiplication and division of fractions and mixed ...
Fraction Word Problems - using block models (tape diagrams), Solve a problem involving fractions of fractions and fractions of remaining parts, how to solve a four step fraction word problem using tape diagrams, grade 5, grade 6, grade 7, with video lessons, examples and step-by-step solutions.
Lesson 6: Multiplying fractions word problems. Multiplying fractions word problem: muffins. Multiplying fractions word problem: laundry. Multiplying fractions word problem: bike. ... Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit ...
How do you solve equations with fractions? This webpage from Mathematics LibreTexts explains the steps and rules for solving equations with fractions, using examples and exercises. You will learn how to simplify, clear, and check your solutions. Whether you need a review or a challenge, this webpage can help you master equations with fractions.
Like & unlike denominators. Below are our grade 5 math word problem worksheet on adding and subtracting fractions. The problems include both like and unlike denominators, and may include more than two terms. Worksheet #1 Worksheet #2 Worksheet #3 Worksheet #4. Worksheet #5 Worksheet #6.
Problem nº 1. Problem nº 2. Problem nº 3. Solution to Problem nº 1. This is an example of a problem involving the addition of a whole number and a fraction. The simplest way to show the number of cookies I ate is to write it as a mixed number. And the data given in the word problem gives us the result: 9 biscuits and 5 / 6 of a biscuit = 9 ...
This fraction word problem requires subtraction. Solution: The fact that the problem is asking how much more black pepper the recipe needs is an indication that 3/4 is bigger than 1/4. However, it does not hurt to check! 3/4 - 1/4 = 2/4 = 1/2. The black pepper is 1/2 of a teaspoon more than the red pepper. Example #2:
Word Problems on Conversion of Fractions to Percentage. We know that percentages are also fractions with the denominator equals to hundred. To convert the given fraction to a percentage, multiply it with hundred and to convert any percentage value to a fraction, divide with hundred. Example: Keerthi ate 2 5 of the pizza.
Example 1: equations with one operation. Solve for x \text {: } \cfrac {x} {5}=4 x: 5x = 4. Identify the operations that are being applied to the unknown variable. The unknown is x. x. Looking at the left hand side of the equation, the x x is divided by 5. 5. \cfrac {x} {5} 5x. 2 Apply the inverse operations, one at a time, to both sides of the ...
Leave a Comment / Fractions / By teachmath. Through visualization, algebra-type word problems can be solved without formally introducing algebra. Here is a typical example of a non-routine word problem from a 4th grade Singapore Math workbook involving fractions: ⅓ of Amy's money is equal to ½ of Bob's money. Amy has $40 more than Bob.
Step 1: Identify the fractions that will be divided. Our two fractions in this case are the {eq}\frac23 {/eq} cup of milkshake and the {eq}\frac45 {/eq} of a serving. Step 2: Identify whether we ...
What are Fractions? A fractional number is considered as the ratio between two numbers. Fractions are defined by \(\frac {a}{b} \) a is called the numerator which means the equal number of parts that are counted. b is called the denominator which means a number of parts in the whole. Fraction Word Problems with Answers. Problem 1:
WORD PROBLEMS INVOLVING OPERATIONS WITH FRACTIONS. Problem 1 : Mary poured 5/8 liter of apple juice equally in to 5 glasses. How much of apple juice was there in each glass? (A) 1/8 liter (B) 1/5 liter (C) 1/6 liter. Solution : Original quantity of apple juice = 5/8 liter. Number of glasses to be divide = 5.
Solution. This word problem requires addition of fractions. Choosing a common denominator of 4, we get. 1/2 + 3/4 = 2/4 + 3/4 = 5/4. So, John walked a total of 5/4 miles. Example #2: Mary is preparing a final exam. She study 3/2 hours on Friday, 6/4 hours on Saturday, and 2/3 hours on Sunday. How many hours she studied over the weekend.
Step 2: For the addition and subtraction of fractions, all fractions must have the same denominator. If your fractions already have the same denominator, you can skip to Step 3. The fractions 3 20 ...