chi square hypothesis test calculator

• Salary & Income Tax Calculators
• Mortgage Calculators
• Retirement Calculators
• Depreciation Calculators
• Statistics and Analysis Calculators
• Date and Time Calculators
• Contractor Calculators
• Budget & Savings Calculators
• Loan Calculators
• Forex Calculators
• Real Function Calculators
• Engineering Calculators
• Tax Calculators
• Volume Calculators
• 2D Shape Calculators
• 3D Shape Calculators
• Logistics Calculators
• HRM Calculators
• Sales & Investments Calculators
• Grade & GPA Calculators
• Conversion Calculators
• Ratio Calculators
• Sports & Health Calculators
• Other Calculators

Chi-Square Calculator

You can use this chi-square calculator as part of a statistical analysis test to determine if there is a significant difference between observed and expected frequencies.

To use the calculator, simply input the true and expected values (on separate lines) and click on the "Calculate" button to generate the results.

Observed Values

Expected Values

Use this tool to calculate the p-value for a given chi-square value and degrees of freedom.

Chi-square Value:

Degrees of Freedom:

P-value Type: Right Tail Left Tail

What is a Chi-square Test?

A chi-square test is a popular statistical analysis tool that is employed to identify the extent to which an observed frequency differs from the expected frequency.

Let's look at an example.

Let's say you are a college professor. The 100 students you teach complete a test that is graded on a scale ranging from 2 (lowest possible grade) through to 5 (highest possible grade). In advance of the test, you expect 25% of the students to achieve a 5, 45% to achieve a 4, 20% to achieve a 3, and 10% to get a 2.

After the test, you grade the papers. You can then use the chi-square test to determine the extent to which your predicted grades differed from the actual grades.

How to Calculate a Chi-square

The chi-square value is determined using the formula below:

X 2 = (observed value - expected value) 2 / expected value

Returning to our example, before the test, you had anticipated that 25% of the students in the class would achieve a score of 5. As such, you expected 25 of the 100 students would achieve a grade 5. However, in reality, 30 students achieved a score of 5. As such, the chi-square calculation is as follows:

X 2 = (30 - 25) 2 / 25 = (5) 2 / 25 = 25 / 25 = 1

An In-depth Example of the Chi-square Calculator

Let's take a more in-depth look at the paper grading example.

The grade distribution for the 100 students you tested were as follows: 30 received a 5, 25 received a 4, 40 received a 3, and 5 received a 2.

• a.) We can now determine how many students were expected to receive each grade per the forecast distribution.
• Grade 2: 0.10 * 100 = 10
• Grade 3: 0.20 * 100 = 20
• Grade 4: 0.45 * 100 = 45
• Grade 5: 0.25 * 100 = 25
• b.) We can use this information to determine the chi-square value for each grade.
• Grade 2: X 2 = (5 - 10) 2 / 10 = 2.5
• Grade 3: X 2 = (40 - 20) 2 / 20 = 20
• Grade 4: X 2 = (25 - 45) 2 / 45 = 8.89
• Grade 5: X 2 = (30 - 25) 2 / 25 = 1
• c.) Finally, we can sum the chi-square values: X 2 = 2.5 + 20 + 8.89 + 1 = 32.39

You may also be interested in our P-Value Calculator or T-Value Calculator

• Currently 4.67/5

Rating: 4.7 /5 (438 votes)

Chi-Square Calculator

Use this Chi Square calculator to easily test contingency tables of categorical variables for independence or for a goodness-of-fit test. Can be used as a Chi-Square goodness-of-fit calculator , as a Chi-Square test of independence calculator or as a test of homogeneity. Supports unlimited numbers of rows and columns (groups and categories): 2x2, 3x3, 4x4, 5x5, 2x3, 2x4 and arbitrary N x M contingency tables. Outputs Χ 2 and p-value.

Related calculators

• Using the Chi-Square calculator

As a Chi-Square Test of Independence or Homogeneity

As a chi-square test of goodness-of-fit.

• What is a "Chi Squared test"?
• Chi-Square Formula
• Types of Chi-Square tests

Chi-Square Test of Independence

Chi-square test of homogeneity, chi-square goodness-of-fit test, comparing the three types of chi-square tests, other tests,     using the chi-square calculator.

The above easy to use tool can function in two main modes: as a goodness-of-fit test and as a test of independence / homogeneity. These modes apply to different situations covered in detail below. The mode of operation can be selected from the radio button below the data input field in the Chi Square calculator interface.

Copy/paste the data from a spreadsheet file into the data input field of the calculator or input it manually by using space ( ) as a column separator and new line as a row separator. The data in all cells should be entered as counts (whole numbers, integers). For example, if you have this data in Excel:

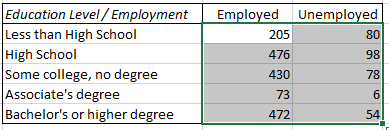
simply copy and paste the numerical cells into the calculator's input field above. Click here to see how this example works. If the sample data is known to be independent the result can be treated as a test of homogeneity. If the data is based on two categorical variables measured from the same population the result can be interpreted as a test of independence between the variables.

Make sure to select the appropriate type of test "Chi-Square test of Goodness-of-fit".

    What is a "Chi Squared test"?

A Chi-Squared test is any statistical test in which the sampling distribution of the parameter is Χ 2 -distributed under the null hypothesis and thus refers to a whole host of different kinds of tests that rely on this distribution. In its original version it was developed by Karl Pearson in 1900 as a goodness of fit test: testing whether a particular set of observed data fits a frequency distribution from the Pearson family of distributions (Pearson's Chi-Squared test). Pearson in 1904 expanded its application to a test of independence between the rows and columns of a contingency table of categorical variables [1] . It was further expanded by R. Fisher in 1922-24.

The statistical model behind the tests requires that the variables are the result of simple random sampling and are thus independent and identically distributed (ID) (under the null hypothesis). Consequently, the test can be used as a test for independence or a test for homogeneity (identity of distributions). In certain restricted situations it can also function as a test for the difference in variances. This, however, also means that if one wants to test non-IID data a different test should be chosen.

As with most statistical tests it performs poorly with very low sample size, in particular: because the Χ 2 assumption might not hold well for the data at hand. For a simple 2 by 2 contingency table the requirement is that each cell has a value larger than 5. For larger tables no more than 20% of all cells should have values under 5. Our chi-square calculator will check for some of these conditions and issue warnings where appropriate.

    Chi-Square Formula

The formula is the same regardless if you are doing a test of goodness-of-fit, test of independence or of homogeneity . Despite the formula behind all three tests being the same, however, all three have different null hypotheses and interpretations (see below). The Chi-Square formula is simply:

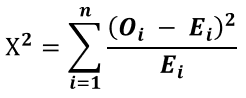
where n is the number of cells in the table and O i and E i are the observed and expected values of each cell. The resulting Χ 2 statistic's cumulative distribution function is calculated from a chi-square distribution with (r - 1) · (c - 1) degrees of freedom (r - number of rows, c - number of columns).

    Types of Chi-Square tests

Here we examine the three applications of the Chi Square test: as a test of independence, as a test of homogeneity (identical distribution) and as a goodness-of-fit test.

When using the calculator as a test for independence obtaining a small p-value is to be interpreted as evidence that the two (or more) groups are not independent. Note that if there are more than two variables you cannot say which ones are independent and which are not: it might be all of them or just some of them.

This test refers to testing if two or more variables share the same probability distribution and is also supported by this online Chi Square calculator. The test of homogeneity is used to determine whether two or more independent samples differ in their distributions on a single variable of interest: comparing two or more groups on a categorical outcome. For example, one can compare the educational levels of groups of people from different cities in a country to determine if the proportions between the groups are essentially the same or if there is a statistically significant difference. The null hypothesis H 0 is that the proportions between the groups are the same while the alternative H 1 is that they are different.

Note that upon observing a low p-value one can only say that at least one proportion is different from at least one other proportion, but we cannot say which. Further procedures such as Sheffe, Holm or Dunn-Bonferroni need to be deployed to select a suitable critical value for the further tests to identify pairwise significant differences.

When technically feasible, randomization is often used to produce independent samples.

The goodness-of-fit test can be used to assess how well a certain frequency distribution matches an expected (or known) distribution . The null hypothesis H 0 is that the data follows a specified distribution while the alternative H 1 is that it does not follow that distribution. Rejecting the null means the sample differs from the population on the variable of interest.

For example, if we know that a fair dice should produce each number with a frequency of 1/6 then we can roll a dice 1,000 times, record how many times we observed a given number and then check it against the ideal dice distribution to see if it is fair. If the observations we get are 168 ones, 170 twos, 160 threes, 163 fours, 173 fives and 166 sixes, do we have evidence the dice is rigged? Load example data in the calculator to perform the calculation.

Another example is in population surveys where a representative survey across a certain demographic dimension or geographic locale is required. Knowing the age distribution of the whole population from a recent census or birth & death registries, you can compare the frequencies in your sample to those of the entire population. With a big enough sample the test will be sensitive enough to pick any substantial discrepancy between your sample and the population you are trying to represent.

Yet another application is found in online A/B testing where a Chi-Square goodness-of-fit test is the statistical basis for performing an SRM check . It is used to detect various departures from the assumed statistical model such as randomizer bias, issues with experiment triggering, tracking, log processing, and so on.

This table offers a quick reference to the differences between the three main uses of the Χ 2 test and should be useful to anyone using our X 2 calculator for any purpose.

Under certain conditions the X 2 test can be used as a test for the difference in variances. When both marginal distributions are fixed the Chi-Square test can also be used as a test of unrelated classification.

    References

1 Franke T.M. (2012) – "The Chi-Square Test: Often Used and More Often Misinterpreted", American Journal of Evaluation , 33:448 DOI: 10.1177/1098214011426594

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Chi-Square Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/chi-square-calculator.php URL [Accessed Date: 21 May, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

     Statistical calculators

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

Compare observed and expected frequencies

This calculator compares observed and expected frequencies within (up to 20) categories using the chi-square test. Enter the names of the categories into the first column, then enter the actual counts observed and expected for each group. Learn more about chi-square in the description below the calculator.

View the results

What is chi-square.

A chi-square test compares count data in different groups to their expected counts within each group. "Subjects" in the experiment can be individuals, events, items, or anything else so long as it can be counted.

It is a flexible method where the researcher must determine the expected counts for each group. The expected counts can be that they are equal, are based on previous research, follow some statistical distribution, or something else entirely.

The key is that its focus is on count data. If you are analyzing rates or percentages, then chi-square is not the appropriate tool.

How to use the chi-square table calculator

Enter the label (optional), actual counts of observed subjects (or events), and expected counts for each category on a separate line. Labels for each category are not used in calculation but are often helpful to organize the input data.

Important: Expected frequencies (like observed) should be entered as counts. Decimals in the expected count are acceptable so long as they do not represent percentages (for 15% of 250 total individuals, enter 37.5).

Example experiment setup

Suppose you have 605 subjects in total spread across five categories and observe the counts for each below:

• Group A: 200
• Group B: 102
• Group C: 50
• Group D: 153
• Group E: 100

We can compare the counts that we observe to the expected distribution to see if there is evidence that our sample as a whole is different from the hypothesized distribution.

How do I find the expected frequencies?

Chi-square calculators require you to enter the expected frequencies in each group so that it knows what it is comparing against.

Here is an example of how to calculate expected frequencies . One common assumption is that all groups are equal (e.g. 605 / 5 = 121 expected per group). This calculator allows for more flexible options beyond just that, and decimals are acceptable so long as the expected frequencies add up to the total number of observations.

A specific use-case of chi-square is analyzing contingency tables. With contingency tables, the expected counts are determined using the assumption that the factors are not-related. This contingency table calculator includes an option to do a Yates' correction .

Performing a chi-square test ? We can help.

Sign up for more information on how to perform this and other common statistical analyses.

How to calculate chi-square by hand

Chi-square is not as complicated as some statistical tests and is sometimes done by hand. You can use the formula below, entering the observed (O) and expected (E) frequencies for each group. By summing up the calculated values for each of the categories, we can calculate the chi-square test statistic as shown below:

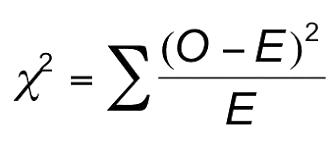
Once you have calculated the test statistic, you would need to use a computer or a chi-square table to find the approximate P value.

While this can be done by hand, there are several opportunities for human error, which is why we recommend this calculator (or Prism for more advanced analysis).

Assumptions of chi-square

While chi-square is one of the more flexible tests in statistics, it has the following assumptions:

• Analyzing counts (not percentages)
• Large number of subjects in each category (usually greater than 5)
• Comparing to a theoretical distribution

See more details in our analysis checklist .

Related tests and calculators

Chi-square test for contingency tables.

Chi-square tests are also used to analyze contingency tables . If you have a 2x2 contingency table, use this calculator . The difference is that with contingency tables, the expected counts are calculated behind the scenes with the assumption that the variables are not associated.

Binomial test

If you have only two categories, use this binomial test calculator instead. Chi-square can give P values that are too low in this case, but the binomial test will calculate it exactly.

Chi-square test vs t-test

Chi-square tests if the observed counts in each category varies from its expected "theoretical" population, whereas t-tests evaluate whether two sample means (or one sample mean and a fixed value) are statistically equivalent.

Interpreting results

The chi-square p value tests if the observed counts are consistent with the expected counts. You would interpret chi-square value figures below your significance threshold (often 0.05) as "evidence that the data were not sampled from the distribution you expected". If a P value is greater than your significance threshold, there is no evidence that the observed values were different from the expected, theoretical distribution.

Note that P values are easy to misinterpret , but large P values are not evidence that no difference exists; it could be that you don't have enough data to detect a difference.

This calculator performs a two-tailed chi-square test and assumes a P value significance threshold of 0.05.

The results page also includes the chi-squared statistic and its degrees of freedom. Notice the category names are not involved at all in the interpretation. See this example for help with interpreting a chi-square P value.

Graphing chi-square results

This calculator does not create a graphic of the chi-square results. A grouped bar chart is commonly used to visualize the difference between observed and expected counts, and is one of the many custom graphics offered with Prism .

Ready for more advanced analyses?

Start your 30 day free trial of Prism and get access to:

• Step by step guides on how to perform the most common analysis
• Sample data to save you time
• More tips on how Prism can help your research

With Prism, in a matter of minutes you learn how to go from entering data to performing statistical analyses and generating high-quality graphs.

Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required.

Chi square calculator

What is the chi-square test.

Before you use our chi square calculator we want you to be informed about the chi-square test. It is a statistical hypothesis test used to see if a data set fits a particular distribution. Calculating chi-square can be done in two ways. One method is by finding the expected frequencies and the other way is by calculation of degrees of freedom and critical value.

The hypotheses for this research are:

Null Hypothesis: The distributions of the data set fit a normal distribution.

Alternative Hypothesis: The distributions of the data set do not fit a normal distribution.

The chi-square test is used to test whether or not there is a significant difference between two types of categorical variables in sample size, and it gives a value for each variable type. This test is used to find whether the expected frequency in each category of one variable matches with the observed frequency in a different variable, and if so, which category is more probable.

Calculating chi-square using a total number of frequencies:

1) Find the degrees of freedom for this research question by taking (r-1)(c-1), where r is for the number of rows of data and c is for the number of columns. In this case df = (4-1)(3-1)= 4

Click here to use chi square calculator for free

2) Find the critical value by going to an online table or a more comprehensive chart with degrees of freedom under “5” and find the closest chi-square value, or, alternatively use online software to calculate the critical value.

3) Calculate chi-square using the total number of frequencies by using the formula where Oi is observed items in category i, Ei is the expected frequency of category i. This is then compared to what standard deviation they are from one another, if they are far enough away then it is considered significant.

Calculating chi-square using observed and expected frequencies:

2) Find the critical value by going to an online table or a more comprehensive chart with degrees of freedom under “4” and find the closest chi-square value, or, alternatively use online software to calculate the critical value.

3) Calculate chi-square using observed and expected frequencies by using the formula where Oi is observed items in category i, Ei is the expected frequency of category i. This then needs to be compared to what standard deviation they are from one another, if they are far enough away then it is considered significant.

Click here to use our T Distribution Table

Non-parametric methods like the chi-square test help researchers with social science data sets due to the fact that the variables can have more than two outcomes. It is a great statistic for categorical variables because it calculates the probabilities of both variables compared to each other and uses this to see how significant they are.

An example used for a chi-square test is comparing smoking habits between men and women using gender as a variable with two possible outcomes:

Male and female. Using a chi-square test, the researcher would look at how many men smoke compared to women, and then see if there’s a correlation between gender and smoking habits, which is what the alternative hypothesis states.

Since technology has advanced with programs such as SPSS making it easier for researchers to calculate data sets.

If you want to round numbers for free click here

• By IIT Bombay Learn HTML Java Tutorial Django Tutorial PHP Tutorial
• On-Demand (Videos) Core Python Certification Complete Python Certification Course Online Create Own Cryptocurrency C Programming Online
• Live Courses (1:1 Live Sesions) Coding For Kids Online C Programming Complete Python For Kids Online Essential Python For Kids Online Complete C++ Programming For Kids
• For Kids Coding For Kids Online C Programming Essential Python For Kids Online Complete Python For Kids Online C Programming For Kids Complete C++ Programming For Kids

EVM - Cryptocurrency

Cryptocurrency

Chi-Square Calculator

Presenting the newtum-powered chi-square statistical tool.

Discover the precision of Newtum's Chi-Square Calculator. This tool simplifies your statistical analysis, offering a quick and accurate way to perform chi-square tests and interpret data with confidence.

Understanding the Statistical Significance Tool

The Chi-Square Calculator is a statistical tool used to determine the significance of an observed association between categorical variables. It helps in hypothesis testing and data analysis.

Decoding the Chi-Square Test Formula

Grasp the essentials of the chi-square test formula and its critical role in statistical research. Understanding this formula is key to accurate data interpretation.

• State the hypothesis for your analysis.
• Input observed frequencies into the calculator.
• Automatically calculate expected frequencies.
• Compute the chi-square statistic value.
• Compare to critical values for significance.

Step-by-Step Guide to Using the Chi-Square Calculator

Our Chi-Square Calculator is incredibly user-friendly. Follow the simple instructions below to effortlessly analyze your data and obtain results in no time.

• Enter your data into the designated fields.
• Click the 'Calculate' button for results.
• Review the chi-square test outcome.
• Interpret the results to make data-driven decisions.

Explore the Superior Features of Our Chi-Square Calculator

• User-Friendly Interface: Navigate with ease.
• Instant Results: Get answers in seconds.
• Data Security: Your data never leaves your device.
• Accessibility Across Devices: Use on any device.
• No Installation Needed: Access directly online.
• Examples for Clarity: Understand with practical examples.
• Transparent Process: Clear computation steps.
• Educational Resource: Enhance your statistical knowledge.
• Responsive Customer Support: Get help when needed.
• Regular Updates: Stay up-to-date with the latest features.
• Privacy Assurance: No servers mean total privacy.
• Efficient Data Analysis: Quick and reliable.
• Language Accessibility: Use in multiple languages.
• Engaging and Informative Content: Learn as you use.
• Fun and Interactive Learning: Enjoy statistical analysis.
• Shareable Results: Easily share findings.
• Responsive Design: Optimal on all screen sizes.
• Educational Platform Integration: A seamless learning tool.
• Comprehensive Documentation: Detailed user guidance.

Applications and Uses of the Chi-Square Calculator

• Analyze contingency tables for independence.
• Test hypotheses in scientific research.
• Examine data in market research studies.
• Evaluate outcomes in medical trials.
• Determine goodness of fit for observed frequencies.

Applying the Chi-Square Formula: Practical Examples

Example 1: If the observed frequency of an event is 'x' and the expected frequency is 'y', the chi-square calculator will determine the significance of the discrepancy.

Example 2: Consider a study with an expected outcome ratio of 1:1. If the actual observed ratio deviates, inputting these values into the calculator will reveal whether the variation is due to chance or indicates a statistically significant difference.

Securing Your Statistical Analysis with Our Chi-Square Calculator

Conclude your statistical analysis with peace of mind using our Chi-Square Calculator. Since all computations are performed on your local device, your data remains private and secure. There's no server processing, ensuring that sensitive information never leaves your computer. This secure, client-side operation doesn't compromise on functionality or accuracy, making our tool the preferred choice for confidential and precise statistical analysis.

Frequently Asked Questions: Chi-Square Calculator Insights

Frequently asked questions about the chi-square calculator.

• What is a chi-square test?
• When should I use a chi-square calculator?
• How does the chi-square calculator ensure data security?
• Can I use the chi-square calculator on different devices?
• Does the chi-square calculator provide instant results?

People also viewed

104, Building No. 5, Sector 3, Millennium Business Park, Mahape, Navi Mumbai - 400710

• Core Python Certification
• Create Own Cryptocurrency
• Python for Kids
• Learn HTML (IIT)
• Learn PHP(IIT)
• Java Tutorial (IIT)
• Django Tutorial (IIT)
• C Prog. for Kids
• Python For Kids Online
• C++ for Kids
• Verify Certificate
• Book Free Demo
• Online Compiler
• Generate Genesis Block

Copyright © 2024 Newtum. All Right Reserved.

• Privacy policy
• Terms & Conditions

Descriptive Statistics

Hypothesis test, chi-square test calculator.

In the captivating arena of statistics, the chi-square test emerges as one of the most popular tools to examine categorical data. This non-parametric test can be invaluable when you wish to explore associations between two categorical variables. But manual calculations can be tedious and error-prone. Enter the Chi-Square Test Calculator — a nifty tool that makes categorical data analysis both efficient and accurate. Let's delve deeper into the wonders of the chi-square test and the prowess of our calculator.

The Essence of the Chi-Square Test

The chi-square test, at its foundation, assesses whether there's a significant association between two categorical variables in a contingency table. For instance, it can determine if there's a correlation between a person's gender and their choice of beverage, or between a student's major and their preferred extracurricular activity.

Why Use the Chi-Square Test Calculator?

• Streamlined Interface: No need to get lost in the sea of numbers. Our calculator's design ensures that even beginners can input data with ease and retrieve results instantly.
• Precise Computation: Manual chi-square tests can be tricky, but the calculator eliminates human errors, delivering accurate results every time.
• Comprehensive Analysis: The calculator doesn’t just spit out a chi-square value. It provides crucial associated metrics, such as degrees of freedom and the p-value, enabling robust data interpretation.
• Visualization Tools: For those who appreciate graphical insights, the calculator offers visual representations of the data, enhancing comprehension.

Harnessing the Chi-Square Test Calculator

• Data Input: Start by entering the observed frequencies for each category in your contingency table.
• Execute the Test: Once your data is populated, hit 'Calculate.' The tool will compute the chi-square statistic, degrees of freedom, and p-value.
• Interpretation: A p-value typically less than 0.05 suggests that the observed frequencies significantly differ from what would be expected under the null hypothesis, indicating an association between the variables.

The Chi-Square Test in Action

From healthcare to market research, the chi-square test has diverse applications:

• Medicine: Is there a significant relationship between a particular treatment and recovery outcomes?
• Education: Do students' study habits correlate with their final grades?
• Business: Does brand loyalty vary significantly between different age groups?

With the Chi-Square Test Calculator, these questions can be answered promptly and decisively.

Wrapping Up

In the vast statistical universe, the Chi-Square Test Calculator shines as a beacon for those navigating categorical data. Whether you’re a seasoned researcher, a student grappling with data for a project, or a curious individual exploring patterns, our tool makes the chi-square test a seamless experience. Delve into the intricacies of categorical data and let our calculator be your guide on this analytical journey!

Chi-Square Calculator

The results are in! And the groups have different numbers

• But is that just random chance?
• Or have you found something significant?

The Chi-Square Test  gives us a "p" value to help us decide.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

37: Chi-Square Test For Independence Calculator

• Last updated
• Save as PDF
• Page ID 8625

• Larry Green
• Lake Tahoe Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\(\chi^{2}\) test for independence calculator

Enter in the observed values and hit Calculate and the \(\chi^{2}\) test statistic and the p-value will be calculated for you.  Leave blank the last rows and columns that don't have data values.

Back to the Calculator Menu

Chi-Square (Χ²) Test & How To Calculate Formula Equation

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Chi-square (χ2) is used to test hypotheses about the distribution of observations into categories with no inherent ranking.

What Is a Chi-Square Statistic?

The Chi-square test (pronounced Kai) looks at the pattern of observations and will tell us if certain combinations of the categories occur more frequently than we would expect by chance, given the total number of times each category occurred.

It looks for an association between the variables. We cannot use a correlation coefficient to look for the patterns in this data because the categories often do not form a continuum.

There are three main types of Chi-square tests, tests of goodness of fit, the test of independence, and the test for homogeneity. All three tests rely on the same formula to compute a test statistic.

These tests function by deciphering relationships between observed sets of data and theoretical or “expected” sets of data that align with the null hypothesis.

What is a Contingency Table?

Contingency tables (also known as two-way tables) are grids in which Chi-square data is organized and displayed. They provide a basic picture of the interrelation between two variables and can help find interactions between them.

In contingency tables, one variable and each of its categories are listed vertically, and the other variable and each of its categories are listed horizontally.

Additionally, including column and row totals, also known as “marginal frequencies,” will help facilitate the Chi-square testing process.

In order for the Chi-square test to be considered trustworthy, each cell of your expected contingency table must have a value of at least five.

Each Chi-square test will have one contingency table representing observed counts (see Fig. 1) and one contingency table representing expected counts (see Fig. 2).

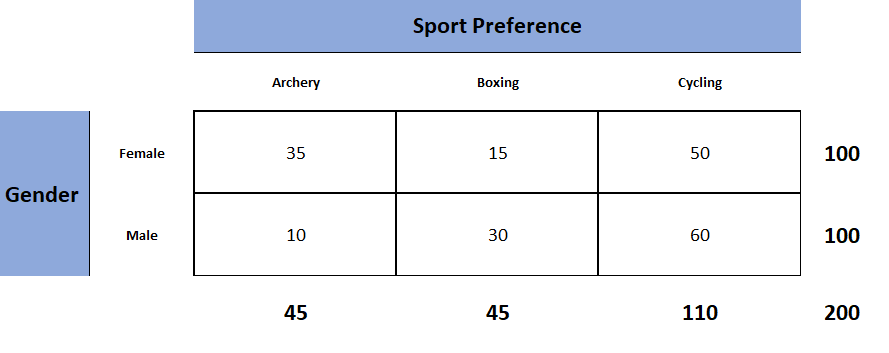
Figure 1. Observed table (which contains the observed counts).

To obtain the expected frequencies for any cell in any cross-tabulation in which the two variables are assumed independent, multiply the row and column totals for that cell and divide the product by the total number of cases in the table.

Figure 2. Expected table (what we expect the two-way table to look like if the two categorical variables are independent).

To decide if our calculated value for χ2 is significant, we also need to work out the degrees of freedom for our contingency table using the following formula: df= (rows – 1) x (columns – 1).

Formula Calculation

Calculate the chi-square statistic (χ2) by completing the following steps:

• Calculate the expected frequencies and the observed frequencies.
• For each observed number in the table, subtract the corresponding expected number (O — E).
• Square the difference (O —E)².
• Divide the squares obtained for each cell in the table by the expected number for that cell (O – E)² / E.
• Sum all the values for (O – E)² / E. This is the chi-square statistic.
• Calculate the degrees of freedom for the contingency table using the following formula; df= (rows – 1) x (columns – 1).

Once we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we can use the χ2 table (often at the back of a statistics book) to check if our value for χ2 is higher than the critical value given in the table. If it is, then our result is significant at the level given.

Interpretation

The chi-square statistic tells you how much difference exists between the observed count in each table cell to the counts you would expect if there were no relationship at all in the population.

Small Chi-Square Statistic: If the chi-square statistic is small and the p-value is large (usually greater than 0.05), this often indicates that the observed frequencies in the sample are close to what would be expected under the null hypothesis.

The null hypothesis usually states no association between the variables being studied or that the observed distribution fits the expected distribution.

In theory, if the observed and expected values were equal (no difference), then the chi-square statistic would be zero — but this is unlikely to happen in real life.

Large Chi-Square Statistic : If the chi-square statistic is large and the p-value is small (usually less than 0.05), then the conclusion is often that the data does not fit the model well, i.e., the observed and expected values are significantly different. This often leads to the rejection of the null hypothesis.

How to Report

To report a chi-square output in an APA-style results section, always rely on the following template:

χ2 ( degrees of freedom , N = sample size ) = chi-square statistic value , p = p value .

In the case of the above example, the results would be written as follows:

A chi-square test of independence showed that there was a significant association between gender and post-graduation education plans, χ2 (4, N = 101) = 54.50, p < .001.

APA Style Rules

• Do not use a zero before a decimal when the statistic cannot be greater than 1 (proportion, correlation, level of statistical significance).
• Report exact p values to two or three decimals (e.g., p = .006, p = .03).
• However, report p values less than .001 as “ p < .001.”
• Put a space before and after a mathematical operator (e.g., minus, plus, greater than, less than, equals sign).
• Do not repeat statistics in both the text and a table or figure.

p -value Interpretation

You test whether a given χ2 is statistically significant by testing it against a table of chi-square distributions , according to the number of degrees of freedom for your sample, which is the number of categories minus 1. The chi-square assumes that you have at least 5 observations per category.

If you are using SPSS then you will have an expected p -value.

For a chi-square test, a p-value that is less than or equal to the .05 significance level indicates that the observed values are different to the expected values.

Thus, low p-values (p< .05) indicate a likely difference between the theoretical population and the collected sample. You can conclude that a relationship exists between the categorical variables.

Remember that p -values do not indicate the odds that the null hypothesis is true but rather provide the probability that one would obtain the sample distribution observed (or a more extreme distribution) if the null hypothesis was true.

A level of confidence necessary to accept the null hypothesis can never be reached. Therefore, conclusions must choose to either fail to reject the null or accept the alternative hypothesis, depending on the calculated p-value.

The four steps below show you how to analyze your data using a chi-square goodness-of-fit test in SPSS (when you have hypothesized that you have equal expected proportions).

Step 1 : Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… on the top menu as shown below:

Step 2 : Move the variable indicating categories into the “Test Variable List:” box.

Step 3 : If you want to test the hypothesis that all categories are equally likely, click “OK.”

Step 4 : Specify the expected count for each category by first clicking the “Values” button under “Expected Values.”

Step 5 : Then, in the box to the right of “Values,” enter the expected count for category one and click the “Add” button. Now enter the expected count for category two and click “Add.” Continue in this way until all expected counts have been entered.

Step 6 : Then click “OK.”

The four steps below show you how to analyze your data using a chi-square test of independence in SPSS Statistics.

Step 1 : Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).

Step 2 : Select the variables you want to compare using the chi-square test. Click one variable in the left window and then click the arrow at the top to move the variable. Select the row variable and the column variable.

Step 3 : Click Statistics (a new pop-up window will appear). Check Chi-square, then click Continue.

Step 4 : (Optional) Check the box for Display clustered bar charts.

Step 5 : Click OK.

Goodness-of-Fit Test

The Chi-square goodness of fit test is used to compare a randomly collected sample containing a single, categorical variable to a larger population.

This test is most commonly used to compare a random sample to the population from which it was potentially collected.

The test begins with the creation of a null and alternative hypothesis. In this case, the hypotheses are as follows:

Null Hypothesis (Ho) : The null hypothesis (Ho) is that the observed frequencies are the same (except for chance variation) as the expected frequencies. The collected data is consistent with the population distribution.

Alternative Hypothesis (Ha) : The collected data is not consistent with the population distribution.

The next step is to create a contingency table that represents how the data would be distributed if the null hypothesis were exactly correct.

The sample’s overall deviation from this theoretical/expected data will allow us to draw a conclusion, with a more severe deviation resulting in smaller p-values.

Test for Independence

The Chi-square test for independence looks for an association between two categorical variables within the same population.

Unlike the goodness of fit test, the test for independence does not compare a single observed variable to a theoretical population but rather two variables within a sample set to one another.

The hypotheses for a Chi-square test of independence are as follows:

Null Hypothesis (Ho) : There is no association between the two categorical variables in the population of interest.

Alternative Hypothesis (Ha) : There is no association between the two categorical variables in the population of interest.

The next step is to create a contingency table of expected values that reflects how a data set that perfectly aligns the null hypothesis would appear.

The simplest way to do this is to calculate the marginal frequencies of each row and column; the expected frequency of each cell is equal to the marginal frequency of the row and column that corresponds to a given cell in the observed contingency table divided by the total sample size.

Test for Homogeneity

The Chi-square test for homogeneity is organized and executed exactly the same as the test for independence.

The main difference to remember between the two is that the test for independence looks for an association between two categorical variables within the same population, while the test for homogeneity determines if the distribution of a variable is the same in each of several populations (thus allocating population itself as the second categorical variable).

Null Hypothesis (Ho) : There is no difference in the distribution of a categorical variable for several populations or treatments.

Alternative Hypothesis (Ha) : There is a difference in the distribution of a categorical variable for several populations or treatments.

The difference between these two tests can be a bit tricky to determine, especially in the practical applications of a Chi-square test. A reliable rule of thumb is to determine how the data was collected.

If the data consists of only one random sample with the observations classified according to two categorical variables, it is a test for independence. If the data consists of more than one independent random sample, it is a test for homogeneity.

What is the chi-square test?

The Chi-square test is a non-parametric statistical test used to determine if there’s a significant association between two or more categorical variables in a sample.

It works by comparing the observed frequencies in each category of a cross-tabulation with the frequencies expected under the null hypothesis, which assumes there is no relationship between the variables.

This test is often used in fields like biology, marketing, sociology, and psychology for hypothesis testing.

What does chi-square tell you?

The Chi-square test informs whether there is a significant association between two categorical variables. Suppose the calculated Chi-square value is above the critical value from the Chi-square distribution.

In that case, it suggests a significant relationship between the variables, rejecting the null hypothesis of no association.

How to calculate chi-square?

To calculate the Chi-square statistic, follow these steps:

1. Create a contingency table of observed frequencies for each category.

2. Calculate expected frequencies for each category under the null hypothesis.

3. Compute the Chi-square statistic using the formula: Χ² = Σ [ (O_i – E_i)² / E_i ], where O_i is the observed frequency and E_i is the expected frequency.

4. Compare the calculated statistic with the critical value from the Chi-square distribution to draw a conclusion.

Related Articles

Exploratory Data Analysis

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Convergent Validity: Definition and Examples

Content Validity in Research: Definition & Examples

Construct Validity In Psychology Research

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 12, chi-square statistic for hypothesis testing.

• Chi-square goodness-of-fit example
• Expected counts in a goodness-of-fit test
• Conditions for a goodness-of-fit test
• Test statistic and P-value in a goodness-of-fit test
• Conclusions in a goodness-of-fit test

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

P Value from Chi-Square Calculator

This calculator is designed to generate a p -value from a chi-square score. If you need to derive a chi-square score from raw data, you should use our chi-square calculator (which will additionally calculate the p -value for you).

The calculator below should be self-explanatory, but just in case it's not: your chi-square score goes in the chi-square score box, you stick your degrees of freedom in the DF box ( df = ( N Columns -1 )*( N Rows -1 ) for chi-square test for independence), select your significance level, then press the button.

Enter your values above, then press "Calculate".

Chi-Square Calculators

This site features a number of different chi-square calculators which you might find helpful.

Chi-Square Calculator for 2 x 2 Contingency Table Chi-Square Calculator for 5 x 5 (or less) Contingency Table Chi-Square Calculator for Goodness of Fit Fisher Exact Test Calculator for 2 x 2 Contingency Table

Hypothesis Testing - Chi Squared Test

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific tests considered here are called chi-square tests and are appropriate when the outcome is discrete (dichotomous, ordinal or categorical). For example, in some clinical trials the outcome is a classification such as hypertensive, pre-hypertensive or normotensive. We could use the same classification in an observational study such as the Framingham Heart Study to compare men and women in terms of their blood pressure status - again using the classification of hypertensive, pre-hypertensive or normotensive status.  

The technique to analyze a discrete outcome uses what is called a chi-square test. Specifically, the test statistic follows a chi-square probability distribution. We will consider chi-square tests here with one, two and more than two independent comparison groups.

Learning Objectives

After completing this module, the student will be able to:

• Perform chi-square tests by hand
• Appropriately interpret results of chi-square tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

Tests with One Sample, Discrete Outcome

Here we consider hypothesis testing with a discrete outcome variable in a single population. Discrete variables are variables that take on more than two distinct responses or categories and the responses can be ordered or unordered (i.e., the outcome can be ordinal or categorical). The procedure we describe here can be used for dichotomous (exactly 2 response options), ordinal or categorical discrete outcomes and the objective is to compare the distribution of responses, or the proportions of participants in each response category, to a known distribution. The known distribution is derived from another study or report and it is again important in setting up the hypotheses that the comparator distribution specified in the null hypothesis is a fair comparison. The comparator is sometimes called an external or a historical control.   

In one sample tests for a discrete outcome, we set up our hypotheses against an appropriate comparator. We select a sample and compute descriptive statistics on the sample data. Specifically, we compute the sample size (n) and the proportions of participants in each response

Test Statistic for Testing H 0 : p 1 = p 10 , p 2 = p 20 , ..., p k = p k0

We find the critical value in a table of probabilities for the chi-square distribution with degrees of freedom (df) = k-1. In the test statistic, O = observed frequency and E=expected frequency in each of the response categories. The observed frequencies are those observed in the sample and the expected frequencies are computed as described below. χ 2 (chi-square) is another probability distribution and ranges from 0 to ∞. The test above statistic formula above is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories.  

When we conduct a χ 2 test, we compare the observed frequencies in each response category to the frequencies we would expect if the null hypothesis were true. These expected frequencies are determined by allocating the sample to the response categories according to the distribution specified in H 0 . This is done by multiplying the observed sample size (n) by the proportions specified in the null hypothesis (p 10 , p 20 , ..., p k0 ). To ensure that the sample size is appropriate for the use of the test statistic above, we need to ensure that the following: min(np 10 , n p 20 , ..., n p k0 ) > 5.  

The test of hypothesis with a discrete outcome measured in a single sample, where the goal is to assess whether the distribution of responses follows a known distribution, is called the χ 2 goodness-of-fit test. As the name indicates, the idea is to assess whether the pattern or distribution of responses in the sample "fits" a specified population (external or historical) distribution. In the next example we illustrate the test. As we work through the example, we provide additional details related to the use of this new test statistic.  

A University conducted a survey of its recent graduates to collect demographic and health information for future planning purposes as well as to assess students' satisfaction with their undergraduate experiences. The survey revealed that a substantial proportion of students were not engaging in regular exercise, many felt their nutrition was poor and a substantial number were smoking. In response to a question on regular exercise, 60% of all graduates reported getting no regular exercise, 25% reported exercising sporadically and 15% reported exercising regularly as undergraduates. The next year the University launched a health promotion campaign on campus in an attempt to increase health behaviors among undergraduates. The program included modules on exercise, nutrition and smoking cessation. To evaluate the impact of the program, the University again surveyed graduates and asked the same questions. The survey was completed by 470 graduates and the following data were collected on the exercise question:

Based on the data, is there evidence of a shift in the distribution of responses to the exercise question following the implementation of the health promotion campaign on campus? Run the test at a 5% level of significance.

In this example, we have one sample and a discrete (ordinal) outcome variable (with three response options). We specifically want to compare the distribution of responses in the sample to the distribution reported the previous year (i.e., 60%, 25%, 15% reporting no, sporadic and regular exercise, respectively). We now run the test using the five-step approach.  

• Step 1. Set up hypotheses and determine level of significance.

The null hypothesis again represents the "no change" or "no difference" situation. If the health promotion campaign has no impact then we expect the distribution of responses to the exercise question to be the same as that measured prior to the implementation of the program.

H 0 : p 1 =0.60, p 2 =0.25, p 3 =0.15,  or equivalently H 0 : Distribution of responses is 0.60, 0.25, 0.15  

H 1 :   H 0 is false.          α =0.05

Notice that the research hypothesis is written in words rather than in symbols. The research hypothesis as stated captures any difference in the distribution of responses from that specified in the null hypothesis. We do not specify a specific alternative distribution, instead we are testing whether the sample data "fit" the distribution in H 0 or not. With the χ 2 goodness-of-fit test there is no upper or lower tailed version of the test.

• Step 2. Select the appropriate test statistic.  

The test statistic is:

We must first assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=470 and the proportions specified in the null hypothesis are 0.60, 0.25 and 0.15. Thus, min( 470(0.65), 470(0.25), 470(0.15))=min(282, 117.5, 70.5)=70.5. The sample size is more than adequate so the formula can be used.

• Step 3. Set up decision rule.  

The decision rule for the χ 2 test depends on the level of significance and the degrees of freedom, defined as degrees of freedom (df) = k-1 (where k is the number of response categories). If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. Critical values can be found in a table of probabilities for the χ 2 distribution. Here we have df=k-1=3-1=2 and a 5% level of significance. The appropriate critical value is 5.99, and the decision rule is as follows: Reject H 0 if χ 2 > 5.99.

• Step 4. Compute the test statistic.  

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) and the expected frequencies into the formula for the test statistic identified in Step 2. The computations can be organized as follows.

Notice that the expected frequencies are taken to one decimal place and that the sum of the observed frequencies is equal to the sum of the expected frequencies. The test statistic is computed as follows:

• Step 5. Conclusion.  

We reject H 0 because 8.46 > 5.99. We have statistically significant evidence at α=0.05 to show that H 0 is false, or that the distribution of responses is not 0.60, 0.25, 0.15.  The p-value is p < 0.005.  

In the χ 2 goodness-of-fit test, we conclude that either the distribution specified in H 0 is false (when we reject H 0 ) or that we do not have sufficient evidence to show that the distribution specified in H 0 is false (when we fail to reject H 0 ). Here, we reject H 0 and concluded that the distribution of responses to the exercise question following the implementation of the health promotion campaign was not the same as the distribution prior. The test itself does not provide details of how the distribution has shifted. A comparison of the observed and expected frequencies will provide some insight into the shift (when the null hypothesis is rejected). Does it appear that the health promotion campaign was effective?  

Consider the following: 

If the null hypothesis were true (i.e., no change from the prior year) we would have expected more students to fall in the "No Regular Exercise" category and fewer in the "Regular Exercise" categories. In the sample, 255/470 = 54% reported no regular exercise and 90/470=19% reported regular exercise. Thus, there is a shift toward more regular exercise following the implementation of the health promotion campaign. There is evidence of a statistical difference, is this a meaningful difference? Is there room for improvement?

The National Center for Health Statistics (NCHS) provided data on the distribution of weight (in categories) among Americans in 2002. The distribution was based on specific values of body mass index (BMI) computed as weight in kilograms over height in meters squared. Underweight was defined as BMI< 18.5, Normal weight as BMI between 18.5 and 24.9, overweight as BMI between 25 and 29.9 and obese as BMI of 30 or greater. Americans in 2002 were distributed as follows: 2% Underweight, 39% Normal Weight, 36% Overweight, and 23% Obese. Suppose we want to assess whether the distribution of BMI is different in the Framingham Offspring sample. Using data from the n=3,326 participants who attended the seventh examination of the Offspring in the Framingham Heart Study we created the BMI categories as defined and observed the following:

• Step 1.  Set up hypotheses and determine level of significance.

H 0 : p 1 =0.02, p 2 =0.39, p 3 =0.36, p 4 =0.23     or equivalently

H 0 : Distribution of responses is 0.02, 0.39, 0.36, 0.23

H 1 :   H 0 is false.        α=0.05

The formula for the test statistic is:

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ..., n p k ) > 5. The sample size here is n=3,326 and the proportions specified in the null hypothesis are 0.02, 0.39, 0.36 and 0.23. Thus, min( 3326(0.02), 3326(0.39), 3326(0.36), 3326(0.23))=min(66.5, 1297.1, 1197.4, 765.0)=66.5. The sample size is more than adequate, so the formula can be used.

Here we have df=k-1=4-1=3 and a 5% level of significance. The appropriate critical value is 7.81 and the decision rule is as follows: Reject H 0 if χ 2 > 7.81.

We now compute the expected frequencies using the sample size and the proportions specified in the null hypothesis. We then substitute the sample data (observed frequencies) into the formula for the test statistic identified in Step 2. We organize the computations in the following table.

The test statistic is computed as follows:

We reject H 0 because 233.53 > 7.81. We have statistically significant evidence at α=0.05 to show that H 0 is false or that the distribution of BMI in Framingham is different from the national data reported in 2002, p < 0.005.  

Again, the χ 2   goodness-of-fit test allows us to assess whether the distribution of responses "fits" a specified distribution. Here we show that the distribution of BMI in the Framingham Offspring Study is different from the national distribution. To understand the nature of the difference we can compare observed and expected frequencies or observed and expected proportions (or percentages). The frequencies are large because of the large sample size, the observed percentages of patients in the Framingham sample are as follows: 0.6% underweight, 28% normal weight, 41% overweight and 30% obese. In the Framingham Offspring sample there are higher percentages of overweight and obese persons (41% and 30% in Framingham as compared to 36% and 23% in the national data), and lower proportions of underweight and normal weight persons (0.6% and 28% in Framingham as compared to 2% and 39% in the national data). Are these meaningful differences?

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable in a single population. We presented a test using a test statistic Z to test whether an observed (sample) proportion differed significantly from a historical or external comparator. The chi-square goodness-of-fit test can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square goodness-of-fit test.

The NCHS report indicated that in 2002, 75% of children aged 2 to 17 saw a dentist in the past year. An investigator wants to assess whether use of dental services is similar in children living in the city of Boston. A sample of 125 children aged 2 to 17 living in Boston are surveyed and 64 reported seeing a dentist over the past 12 months. Is there a significant difference in use of dental services between children living in Boston and the national data?

We presented the following approach to the test using a Z statistic. 

• Step 1. Set up hypotheses and determine level of significance

H 0 : p = 0.75

H 1 : p ≠ 0.75                               α=0.05

We must first check that the sample size is adequate. Specifically, we need to check min(np 0 , n(1-p 0 )) = min( 125(0.75), 125(1-0.75))=min(94, 31)=31. The sample size is more than adequate so the following formula can be used

This is a two-tailed test, using a Z statistic and a 5% level of significance. Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. The sample proportion is:

We reject H 0 because -6.15 < -1.960. We have statistically significant evidence at a =0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data. (p < 0.0001).  

We now conduct the same test using the chi-square goodness-of-fit test. First, we summarize our sample data as follows:

H 0 : p 1 =0.75, p 2 =0.25     or equivalently H 0 : Distribution of responses is 0.75, 0.25 

We must assess whether the sample size is adequate. Specifically, we need to check min(np 0 , np 1, ...,np k >) > 5. The sample size here is n=125 and the proportions specified in the null hypothesis are 0.75, 0.25. Thus, min( 125(0.75), 125(0.25))=min(93.75, 31.25)=31.25. The sample size is more than adequate so the formula can be used.

Here we have df=k-1=2-1=1 and a 5% level of significance. The appropriate critical value is 3.84, and the decision rule is as follows: Reject H 0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

(Note that (-6.15) 2 = 37.8, where -6.15 was the value of the Z statistic in the test for proportions shown above.)

We reject H 0 because 37.8 > 3.84. We have statistically significant evidence at α=0.05 to show that there is a statistically significant difference in the use of dental service by children living in Boston as compared to the national data.  (p < 0.0001). This is the same conclusion we reached when we conducted the test using the Z test above. With a dichotomous outcome, Z 2 = χ 2 !   In statistics, there are often several approaches that can be used to test hypotheses. 

Tests for Two or More Independent Samples, Discrete Outcome

Here we extend that application of the chi-square test to the case with two or more independent comparison groups. Specifically, the outcome of interest is discrete with two or more responses and the responses can be ordered or unordered (i.e., the outcome can be dichotomous, ordinal or categorical). We now consider the situation where there are two or more independent comparison groups and the goal of the analysis is to compare the distribution of responses to the discrete outcome variable among several independent comparison groups.  

The test is called the χ 2 test of independence and the null hypothesis is that there is no difference in the distribution of responses to the outcome across comparison groups. This is often stated as follows: The outcome variable and the grouping variable (e.g., the comparison treatments or comparison groups) are independent (hence the name of the test). Independence here implies homogeneity in the distribution of the outcome among comparison groups.    

The null hypothesis in the χ 2 test of independence is often stated in words as: H 0 : The distribution of the outcome is independent of the groups. The alternative or research hypothesis is that there is a difference in the distribution of responses to the outcome variable among the comparison groups (i.e., that the distribution of responses "depends" on the group). In order to test the hypothesis, we measure the discrete outcome variable in each participant in each comparison group. The data of interest are the observed frequencies (or number of participants in each response category in each group). The formula for the test statistic for the χ 2 test of independence is given below.

Test Statistic for Testing H 0 : Distribution of outcome is independent of groups

and we find the critical value in a table of probabilities for the chi-square distribution with df=(r-1)*(c-1).

Here O = observed frequency, E=expected frequency in each of the response categories in each group, r = the number of rows in the two-way table and c = the number of columns in the two-way table.   r and c correspond to the number of comparison groups and the number of response options in the outcome (see below for more details). The observed frequencies are the sample data and the expected frequencies are computed as described below. The test statistic is appropriate for large samples, defined as expected frequencies of at least 5 in each of the response categories in each group.  

The data for the χ 2 test of independence are organized in a two-way table. The outcome and grouping variable are shown in the rows and columns of the table. The sample table below illustrates the data layout. The table entries (blank below) are the numbers of participants in each group responding to each response category of the outcome variable.

Table - Possible outcomes are are listed in the columns; The groups being compared are listed in rows.

In the table above, the grouping variable is shown in the rows of the table; r denotes the number of independent groups. The outcome variable is shown in the columns of the table; c denotes the number of response options in the outcome variable. Each combination of a row (group) and column (response) is called a cell of the table. The table has r*c cells and is sometimes called an r x c ("r by c") table. For example, if there are 4 groups and 5 categories in the outcome variable, the data are organized in a 4 X 5 table. The row and column totals are shown along the right-hand margin and the bottom of the table, respectively. The total sample size, N, can be computed by summing the row totals or the column totals. Similar to ANOVA, N does not refer to a population size here but rather to the total sample size in the analysis. The sample data can be organized into a table like the above. The numbers of participants within each group who select each response option are shown in the cells of the table and these are the observed frequencies used in the test statistic.

The test statistic for the χ 2 test of independence involves comparing observed (sample data) and expected frequencies in each cell of the table. The expected frequencies are computed assuming that the null hypothesis is true. The null hypothesis states that the two variables (the grouping variable and the outcome) are independent. The definition of independence is as follows:

 Two events, A and B, are independent if P(A|B) = P(A), or equivalently, if P(A and B) = P(A) P(B).

The second statement indicates that if two events, A and B, are independent then the probability of their intersection can be computed by multiplying the probability of each individual event. To conduct the χ 2 test of independence, we need to compute expected frequencies in each cell of the table. Expected frequencies are computed by assuming that the grouping variable and outcome are independent (i.e., under the null hypothesis). Thus, if the null hypothesis is true, using the definition of independence:

P(Group 1 and Response Option 1) = P(Group 1) P(Response Option 1).

 The above states that the probability that an individual is in Group 1 and their outcome is Response Option 1 is computed by multiplying the probability that person is in Group 1 by the probability that a person is in Response Option 1. To conduct the χ 2 test of independence, we need expected frequencies and not expected probabilities . To convert the above probability to a frequency, we multiply by N. Consider the following small example.

The data shown above are measured in a sample of size N=150. The frequencies in the cells of the table are the observed frequencies. If Group and Response are independent, then we can compute the probability that a person in the sample is in Group 1 and Response category 1 using:

P(Group 1 and Response 1) = P(Group 1) P(Response 1),

P(Group 1 and Response 1) = (25/150) (62/150) = 0.069.

Thus if Group and Response are independent we would expect 6.9% of the sample to be in the top left cell of the table (Group 1 and Response 1). The expected frequency is 150(0.069) = 10.4.   We could do the same for Group 2 and Response 1:

P(Group 2 and Response 1) = P(Group 2) P(Response 1),

P(Group 2 and Response 1) = (50/150) (62/150) = 0.138.

The expected frequency in Group 2 and Response 1 is 150(0.138) = 20.7.

Thus, the formula for determining the expected cell frequencies in the χ 2 test of independence is as follows:

Expected Cell Frequency = (Row Total * Column Total)/N.

The above computes the expected frequency in one step rather than computing the expected probability first and then converting to a frequency.  

In a prior example we evaluated data from a survey of university graduates which assessed, among other things, how frequently they exercised. The survey was completed by 470 graduates. In the prior example we used the χ 2 goodness-of-fit test to assess whether there was a shift in the distribution of responses to the exercise question following the implementation of a health promotion campaign on campus. We specifically considered one sample (all students) and compared the observed distribution to the distribution of responses the prior year (a historical control). Suppose we now wish to assess whether there is a relationship between exercise on campus and students' living arrangements. As part of the same survey, graduates were asked where they lived their senior year. The response options were dormitory, on-campus apartment, off-campus apartment, and at home (i.e., commuted to and from the university). The data are shown below.

Based on the data, is there a relationship between exercise and student's living arrangement? Do you think where a person lives affect their exercise status? Here we have four independent comparison groups (living arrangement) and a discrete (ordinal) outcome variable with three response options. We specifically want to test whether living arrangement and exercise are independent. We will run the test using the five-step approach.  

H 0 : Living arrangement and exercise are independent

H 1 : H 0 is false.                α=0.05

The null and research hypotheses are written in words rather than in symbols. The research hypothesis is that the grouping variable (living arrangement) and the outcome variable (exercise) are dependent or related.   

• Step 2.  Select the appropriate test statistic.  

The condition for appropriate use of the above test statistic is that each expected frequency is at least 5. In Step 4 we will compute the expected frequencies and we will ensure that the condition is met.

The decision rule depends on the level of significance and the degrees of freedom, defined as df = (r-1)(c-1), where r and c are the numbers of rows and columns in the two-way data table.   The row variable is the living arrangement and there are 4 arrangements considered, thus r=4. The column variable is exercise and 3 responses are considered, thus c=3. For this test, df=(4-1)(3-1)=3(2)=6. Again, with χ 2 tests there are no upper, lower or two-tailed tests. If the null hypothesis is true, the observed and expected frequencies will be close in value and the χ 2 statistic will be close to zero. If the null hypothesis is false, then the χ 2 statistic will be large. The rejection region for the χ 2 test of independence is always in the upper (right-hand) tail of the distribution. For df=6 and a 5% level of significance, the appropriate critical value is 12.59 and the decision rule is as follows: Reject H 0 if c 2 > 12.59.

We now compute the expected frequencies using the formula,

Expected Frequency = (Row Total * Column Total)/N.

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency.   The expected frequencies are shown in parentheses.

Notice that the expected frequencies are taken to one decimal place and that the sums of the observed frequencies are equal to the sums of the expected frequencies in each row and column of the table.  

Recall in Step 2 a condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 9.6) and therefore it is appropriate to use the test statistic.

We reject H 0 because 60.5 > 12.59. We have statistically significant evidence at a =0.05 to show that H 0 is false or that living arrangement and exercise are not independent (i.e., they are dependent or related), p < 0.005.  

Again, the χ 2 test of independence is used to test whether the distribution of the outcome variable is similar across the comparison groups. Here we rejected H 0 and concluded that the distribution of exercise is not independent of living arrangement, or that there is a relationship between living arrangement and exercise. The test provides an overall assessment of statistical significance. When the null hypothesis is rejected, it is important to review the sample data to understand the nature of the relationship. Consider again the sample data. 

Because there are different numbers of students in each living situation, it makes the comparisons of exercise patterns difficult on the basis of the frequencies alone. The following table displays the percentages of students in each exercise category by living arrangement. The percentages sum to 100% in each row of the table. For comparison purposes, percentages are also shown for the total sample along the bottom row of the table.

From the above, it is clear that higher percentages of students living in dormitories and in on-campus apartments reported regular exercise (31% and 23%) as compared to students living in off-campus apartments and at home (10% each).  

Test Yourself

 Pancreaticoduodenectomy (PD) is a procedure that is associated with considerable morbidity. A study was recently conducted on 553 patients who had a successful PD between January 2000 and December 2010 to determine whether their Surgical Apgar Score (SAS) is related to 30-day perioperative morbidity and mortality. The table below gives the number of patients experiencing no, minor, or major morbidity by SAS category.  

Question: What would be an appropriate statistical test to examine whether there is an association between Surgical Apgar Score and patient outcome? Using 14.13 as the value of the test statistic for these data, carry out the appropriate test at a 5% level of significance. Show all parts of your test.

In the module on hypothesis testing for means and proportions, we discussed hypothesis testing applications with a dichotomous outcome variable and two independent comparison groups. We presented a test using a test statistic Z to test for equality of independent proportions. The chi-square test of independence can also be used with a dichotomous outcome and the results are mathematically equivalent.  

In the prior module, we considered the following example. Here we show the equivalence to the chi-square test of independence.

A randomized trial is designed to evaluate the effectiveness of a newly developed pain reliever designed to reduce pain in patients following joint replacement surgery. The trial compares the new pain reliever to the pain reliever currently in use (called the standard of care). A total of 100 patients undergoing joint replacement surgery agreed to participate in the trial. Patients were randomly assigned to receive either the new pain reliever or the standard pain reliever following surgery and were blind to the treatment assignment. Before receiving the assigned treatment, patients were asked to rate their pain on a scale of 0-10 with higher scores indicative of more pain. Each patient was then given the assigned treatment and after 30 minutes was again asked to rate their pain on the same scale. The primary outcome was a reduction in pain of 3 or more scale points (defined by clinicians as a clinically meaningful reduction). The following data were observed in the trial.

We tested whether there was a significant difference in the proportions of patients reporting a meaningful reduction (i.e., a reduction of 3 or more scale points) using a Z statistic, as follows. 

H 0 : p 1 = p 2    

H 1 : p 1 ≠ p 2                             α=0.05

Here the new or experimental pain reliever is group 1 and the standard pain reliever is group 2.

We must first check that the sample size is adequate. Specifically, we need to ensure that we have at least 5 successes and 5 failures in each comparison group or that:

In this example, we have

Therefore, the sample size is adequate, so the following formula can be used:

Reject H 0 if Z < -1.960 or if Z > 1.960.

We now substitute the sample data into the formula for the test statistic identified in Step 2. We first compute the overall proportion of successes:

We now substitute to compute the test statistic.

• Step 5.  Conclusion.  

We now conduct the same test using the chi-square test of independence.  

H 0 : Treatment and outcome (meaningful reduction in pain) are independent

H 1 :   H 0 is false.         α=0.05

The formula for the test statistic is:  

For this test, df=(2-1)(2-1)=1. At a 5% level of significance, the appropriate critical value is 3.84 and the decision rule is as follows: Reject H0 if χ 2 > 3.84. (Note that 1.96 2 = 3.84, where 1.96 was the critical value used in the Z test for proportions shown above.)

We now compute the expected frequencies using:

The computations can be organized in a two-way table. The top number in each cell of the table is the observed frequency and the bottom number is the expected frequency. The expected frequencies are shown in parentheses.

A condition for the appropriate use of the test statistic was that each expected frequency is at least 5. This is true for this sample (the smallest expected frequency is 22.0) and therefore it is appropriate to use the test statistic.

(Note that (2.53) 2 = 6.4, where 2.53 was the value of the Z statistic in the test for proportions shown above.)

Chi-Squared Tests in R

The video below by Mike Marin demonstrates how to perform chi-squared tests in the R programming language.

Answer to Problem on Pancreaticoduodenectomy and Surgical Apgar Scores

We have 3 independent comparison groups (Surgical Apgar Score) and a categorical outcome variable (morbidity/mortality). We can run a Chi-Squared test of independence.

H 0 : Apgar scores and patient outcome are independent of one another.

H A : Apgar scores and patient outcome are not independent.

Chi-squared = 14.3

Since 14.3 is greater than 9.49, we reject H 0.

There is an association between Apgar scores and patient outcome. The lowest Apgar score group (0 to 4) experienced the highest percentage of major morbidity or mortality (16 out of 57=28%) compared to the other Apgar score groups.

Chi-Square test for One Pop. Variance

Instructions: This calculator conducts a Chi-Square test for one population variance (\(\sigma^2\)). Please select the null and alternative hypotheses, type the hypothesized variance, the significance level, the sample variance, and the sample size, and the results of the Chi-Square test will be presented for you:

Chi-Square test for One Population Variance

More about the Chi-Square test for one variance so you can better understand the results provided by this solver: A Chi-Square test for one population variance is a hypothesis that attempts to make a claim about the population variance (\(\sigma^2\)) based on sample information.

Main Properties of the Chi-Square Distribution

The test, as every other well formed hypothesis test, has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population variance which represents the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis.

The main properties of a one sample Chi-Square test for one population variance are:

• The distribution of the test statistic is the Chi-Square distribution, with n-1 degrees of freedom
• The Chi-Square distribution is one of the most important distributions in statistics, together with the normal distribution and the F-distribution
• Depending on our knowledge about the "no effect" situation, the Chi-Square test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

Can you use Chi-square for one variable?

Absolutely! The Chi-Square statistics is a very versatile statistics, that can be used for a one-way situation (one variable) for example for testing for one variance, or for a goodness of fit test .

But it can also be used for a two-way situation (two variables) for example for a Chi-Square test of independence .

How do you do hypothesis test for single population variance?

The sample variance \(s^2\) has some very interesting distributional properties. In fact, based on how the variance is constructed, we can think of the variance as the sum of pieces that have a standard normal distribution but they are squared.

Without getting into much detail, the sum of squared standard normal distributions is tightly related to the Chi-Square distribution, as we will see in the next section.

What is the Chi-Square Formula?

The formula for a Chi-Square statistic for testing for one population variance is

The null hypothesis is rejected when the Chi-Square statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

To compute critical values directly, please go to our Chi-Square critical values calculator

Related Calculators

log in to your account

Reset password.

“extremely user friendly”

“truly amazing!”

“so easy to use!”

Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net