- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
- Probability and Statistics

How to Find the Perfect Sample Size for Your Research Study
Last Updated: April 26, 2024 Fact Checked
Determining Key Values
- Standard Sample Size Formula
- Large or Unknown Population Formula
- Slovin's Formula
Calculator, Practice Problems, and Answers
This article was reviewed by Joseph Meyer . Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 434,156 times.
Scientific studies often rely on surveys distributed among a sample of some total population. Your sample will need to include a certain number of people, however, if you want it to accurately reflect the conditions of the overall population it's meant to represent. To calculate your necessary sample size, you'll need to determine several set values and plug them into an appropriate formula.

- Precision has a greater statistical impact when you work with a smaller group. For instance, if you wish to perform a survey among members of a local organization or employees of a small business, the population size should be accurate within a dozen or so people. [1] X Research source
- Larger surveys allow for a greater deviance in the actual population. For example, if your demographic includes everyone living in the United States, you could estimate the size to roughly 320 million people, even though the actual value may vary by hundreds of thousands.

- The margin of error is a percentage the indicates how close your sample results will be to the true value of the overall population discussed in your study.
- Smaller margin of errors will result in more accurate answers, but choosing a smaller margin of error will also require a larger sample.
- In this example, the margin of error essentially indicates that, if the entire population were asked the same poll question, you are “confident” that somewhere between 30% (35 - 5) and 40% (35 + 5) would agree with option A .

- In other words, choosing a confidence level of 95% allows you to claim that you 95% certain that your results accurately fall within your chosen margin of error.
- A larger confidence level indicates a greater degree of accuracy, but it will also require a larger sample. The most common confidence levels are 90% confident, 95% confident, and 99% confident.
- Setting a confidence level of 95% for the example stated in the margin of error step would mean that you are 95% certain that 30% to 40% of the total concerned population would agree with option A of your survey.

- Plainly stated, if 99% of your survey responses answer "Yes" and only 1% answer "No," the sample probably represents the overall population very accurately.
- On the other hand, if 45% answer "Yes" and 55% answer "No," there is a greater chance of error.
- Since this value is difficult to determine you give the actual survey, most researchers set this value at 0.5 (50%). This is the worst case scenario percentage, so sticking with this value will guarantee that your calculated sample size is large enough to accurately represent the overall population within your confidence interval and confidence level.

- You can calculate z-scores by hand, look for an online calculator, or find your z-score on a z-score table. Each of these methods can be fairly complex, however.
- 80% confidence => 1.28 z-score
- 85% confidence => 1.44 z-score
- 90% confidence => 1.65 z-score
- 95% confidence => 1.96 z-score
- 99% confidence => 2.58 z-score
Using the Standard Formula

- N = population size
- z = z-score
- e = margin of error
- p = standard of deviation

- Example: Determine the ideal survey size for a population size of 425 people. Use a 99% confidence level, a 50% standard of deviation, and a 5% margin of error.
- For 99% confidence, you would have a z-score of 2.58.

- = [2.58 2 * 0.5(1-0.5)] / 0.05 2 / 1 + [2.58 2 * 0.5(1-0.5)] / 0.05 2 * 425 ]
- = [6.6564 * 0.25] / 0.0025 / 1 + [6.6564 * 0.25] / 1.0625 ]
- = 665 / 2.5663
- = 259.39 (final answer)
Creating a Formula for Unknown or Very Large Populations

- Note that this equation is merely the top half of the full formula.

- Example: Determine the necessary survey size for an unknown population with a 90% confidence level, 50% standard of deviation, a 3% margin of error.
- For 90% confidence, use the z-score would be 1.65.

- = [1.65 2 * 0.5(1-0.5)] / 0.03 2
- = [2.7225 * 0.25] / 0.0009
- = 0.6806 / 0.0009
- = 756.22 (final answer)
Using Slovin's Formula

- Note that this is the least accurate formula and, as such, the least ideal. You should only use this if circumstances prevent you from determining an appropriate standard of deviation and/or confidence level (thereby preventing you from determining your z-score, as well).

- Example: Calculate the necessary survey size for a population of 240, allowing for a 4% margin of error.

- = 240 / (1 + 240 * 0.04 2 )
- = 240 / (1 + 240 * 0.0016)
- = 240 / (1 + 0.384}
- = 240 / (1.384)
- = 173.41 (final answer)

Community Q&A
You Might Also Like

- ↑ https://www.khanacademy.org/math/ap-statistics/gathering-data-ap/sampling-observational-studies/e/identifying-population-sample
- ↑ https://www.khanacademy.org/math/statistics-probability/confidence-intervals-one-sample/estimating-population-proportion/v/margin-of-error-1
- ↑ https://www.khanacademy.org/math/ap-statistics/xfb5d8e68:inference-categorical-proportions/introduction-confidence-intervals/a/interpreting-confidence-levels-and-confidence-intervals
- ↑ https://www.mathsisfun.com/data/standard-deviation-formulas.html
- ↑ https://www.mathsisfun.com/data/standard-deviation.html
- ↑ https://prudencexd.weebly.com/
- ↑ https://www.mathsisfun.com/data/sampling.html
About This Article

To calculate sample size, first find the population size, or number of people taking your study, and margin of error, which is the amount of error you'll allow in your results. Then, calculate your confidence level, which is how confident you are in percentage terms that your results will fall within your margin of error, and z-score, a constant value linked to your confidence level. Next, specify your standard of deviation, which is the amount of variation you expect in your results. Finally, plug your variables into the standard formula to figure out the sample size. To learn how to create a formula for unknown populations, read on! Did this summary help you? Yes No
- Send fan mail to authors
Reader Success Stories
Muhammad Abu-Salih
Apr 5, 2016
Did this article help you?

Akaninyene Akpan
Sep 9, 2017
Aug 19, 2017
Mar 28, 2023
Takele Teklu
Jun 29, 2020

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
wikiHow Tech Help Pro:
Level up your tech skills and stay ahead of the curve
Sample Size Calculator
Find out the sample size.
This calculator computes the minimum number of necessary samples to meet the desired statistical constraints.
| Confidence Level: | ||
| Margin of Error: | ||
| Population Proportion: | Use 50% if not sure | |
| Population Size: | Leave blank if unlimited population size. | |
Find Out the Margin of Error
This calculator gives out the margin of error or confidence interval of observation or survey.
| Confidence Level: | ||
| Sample Size: | ||
| Population Proportion: | ||
| Population Size: | Leave blank if unlimited population size. | |
Related Standard Deviation Calculator | Probability Calculator
In statistics, information is often inferred about a population by studying a finite number of individuals from that population, i.e. the population is sampled, and it is assumed that characteristics of the sample are representative of the overall population. For the following, it is assumed that there is a population of individuals where some proportion, p , of the population is distinguishable from the other 1-p in some way; e.g., p may be the proportion of individuals who have brown hair, while the remaining 1-p have black, blond, red, etc. Thus, to estimate p in the population, a sample of n individuals could be taken from the population, and the sample proportion, p̂ , calculated for sampled individuals who have brown hair. Unfortunately, unless the full population is sampled, the estimate p̂ most likely won't equal the true value p , since p̂ suffers from sampling noise, i.e. it depends on the particular individuals that were sampled. However, sampling statistics can be used to calculate what are called confidence intervals, which are an indication of how close the estimate p̂ is to the true value p .
Statistics of a Random Sample
The uncertainty in a given random sample (namely that is expected that the proportion estimate, p̂ , is a good, but not perfect, approximation for the true proportion p ) can be summarized by saying that the estimate p̂ is normally distributed with mean p and variance p(1-p)/n . For an explanation of why the sample estimate is normally distributed, study the Central Limit Theorem . As defined below, confidence level, confidence intervals, and sample sizes are all calculated with respect to this sampling distribution. In short, the confidence interval gives an interval around p in which an estimate p̂ is "likely" to be. The confidence level gives just how "likely" this is – e.g., a 95% confidence level indicates that it is expected that an estimate p̂ lies in the confidence interval for 95% of the random samples that could be taken. The confidence interval depends on the sample size, n (the variance of the sample distribution is inversely proportional to n , meaning that the estimate gets closer to the true proportion as n increases); thus, an acceptable error rate in the estimate can also be set, called the margin of error, ε , and solved for the sample size required for the chosen confidence interval to be smaller than e ; a calculation known as "sample size calculation."
Confidence Level
The confidence level is a measure of certainty regarding how accurately a sample reflects the population being studied within a chosen confidence interval. The most commonly used confidence levels are 90%, 95%, and 99%, which each have their own corresponding z-scores (which can be found using an equation or widely available tables like the one provided below) based on the chosen confidence level. Note that using z-scores assumes that the sampling distribution is normally distributed, as described above in "Statistics of a Random Sample." Given that an experiment or survey is repeated many times, the confidence level essentially indicates the percentage of the time that the resulting interval found from repeated tests will contain the true result.
| Confidence Level | z-score (±) |
| 0.70 | 1.04 |
| 0.75 | 1.15 |
| 0.80 | 1.28 |
| 0.85 | 1.44 |
| 0.92 | 1.75 |
| 0.95 | 1.96 |
| 0.96 | 2.05 |
| 0.98 | 2.33 |
| 0.99 | 2.58 |
| 0.999 | 3.29 |
| 0.9999 | 3.89 |
| 0.99999 | 4.42 |
Confidence Interval
In statistics, a confidence interval is an estimated range of likely values for a population parameter, for example, 40 ± 2 or 40 ± 5%. Taking the commonly used 95% confidence level as an example, if the same population were sampled multiple times, and interval estimates made on each occasion, in approximately 95% of the cases, the true population parameter would be contained within the interval. Note that the 95% probability refers to the reliability of the estimation procedure and not to a specific interval. Once an interval is calculated, it either contains or does not contain the population parameter of interest. Some factors that affect the width of a confidence interval include: size of the sample, confidence level, and variability within the sample.
There are different equations that can be used to calculate confidence intervals depending on factors such as whether the standard deviation is known or smaller samples (n<30) are involved, among others. The calculator provided on this page calculates the confidence interval for a proportion and uses the following equations:
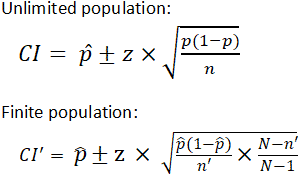
| where is z score is the population proportion and are sample size is the population size |
Within statistics, a population is a set of events or elements that have some relevance regarding a given question or experiment. It can refer to an existing group of objects, systems, or even a hypothetical group of objects. Most commonly, however, population is used to refer to a group of people, whether they are the number of employees in a company, number of people within a certain age group of some geographic area, or number of students in a university's library at any given time.
It is important to note that the equation needs to be adjusted when considering a finite population, as shown above. The (N-n)/(N-1) term in the finite population equation is referred to as the finite population correction factor, and is necessary because it cannot be assumed that all individuals in a sample are independent. For example, if the study population involves 10 people in a room with ages ranging from 1 to 100, and one of those chosen has an age of 100, the next person chosen is more likely to have a lower age. The finite population correction factor accounts for factors such as these. Refer below for an example of calculating a confidence interval with an unlimited population.
EX: Given that 120 people work at Company Q, 85 of which drink coffee daily, find the 99% confidence interval of the true proportion of people who drink coffee at Company Q on a daily basis.
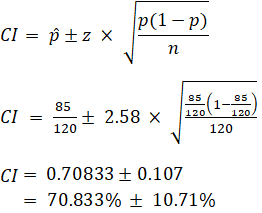
Sample Size Calculation
Sample size is a statistical concept that involves determining the number of observations or replicates (the repetition of an experimental condition used to estimate the variability of a phenomenon) that should be included in a statistical sample. It is an important aspect of any empirical study requiring that inferences be made about a population based on a sample. Essentially, sample sizes are used to represent parts of a population chosen for any given survey or experiment. To carry out this calculation, set the margin of error, ε , or the maximum distance desired for the sample estimate to deviate from the true value. To do this, use the confidence interval equation above, but set the term to the right of the ± sign equal to the margin of error, and solve for the resulting equation for sample size, n . The equation for calculating sample size is shown below.

| where is the z score is the margin of error is the population size is the population proportion |
EX: Determine the sample size necessary to estimate the proportion of people shopping at a supermarket in the U.S. that identify as vegan with 95% confidence, and a margin of error of 5%. Assume a population proportion of 0.5, and unlimited population size. Remember that z for a 95% confidence level is 1.96. Refer to the table provided in the confidence level section for z scores of a range of confidence levels.
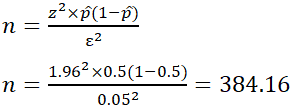
Thus, for the case above, a sample size of at least 385 people would be necessary. In the above example, some studies estimate that approximately 6% of the U.S. population identify as vegan, so rather than assuming 0.5 for p̂ , 0.06 would be used. If it was known that 40 out of 500 people that entered a particular supermarket on a given day were vegan, p̂ would then be 0.08.
| Search | |

How to Determine Sample Size for a Research Study
Frankline kibuacha | apr. 06, 2021 | 3 min. read.

This article will discuss considerations to put in place when determining your sample size and how to calculate the sample size.
Confidence Interval and Confidence Level
As we have noted before, when selecting a sample there are multiple factors that can impact the reliability and validity of results, including sampling and non-sampling errors . When thinking about sample size, the two measures of error that are almost always synonymous with sample sizes are the confidence interval and the confidence level.
Confidence Interval (Margin of Error)
Confidence intervals measure the degree of uncertainty or certainty in a sampling method and how much uncertainty there is with any particular statistic. In simple terms, the confidence interval tells you how confident you can be that the results from a study reflect what you would expect to find if it were possible to survey the entire population being studied. The confidence interval is usually a plus or minus (±) figure. For example, if your confidence interval is 6 and 60% percent of your sample picks an answer, you can be confident that if you had asked the entire population, between 54% (60-6) and 66% (60+6) would have picked that answer.
Confidence Level
The confidence level refers to the percentage of probability, or certainty that the confidence interval would contain the true population parameter when you draw a random sample many times. It is expressed as a percentage and represents how often the percentage of the population who would pick an answer lies within the confidence interval. For example, a 99% confidence level means that should you repeat an experiment or survey over and over again, 99 percent of the time, your results will match the results you get from a population.
The larger your sample size, the more confident you can be that their answers truly reflect the population. In other words, the larger your sample for a given confidence level, the smaller your confidence interval.
Standard Deviation
Another critical measure when determining the sample size is the standard deviation, which measures a data set’s distribution from its mean. In calculating the sample size, the standard deviation is useful in estimating how much the responses you receive will vary from each other and from the mean number, and the standard deviation of a sample can be used to approximate the standard deviation of a population.
The higher the distribution or variability, the greater the standard deviation and the greater the magnitude of the deviation. For example, once you have already sent out your survey, how much variance do you expect in your responses? That variation in responses is the standard deviation.
Population Size

As demonstrated through the calculation below, a sample size of about 385 will give you a sufficient sample size to draw assumptions of nearly any population size at the 95% confidence level with a 5% margin of error, which is why samples of 400 and 500 are often used in research. However, if you are looking to draw comparisons between different sub-groups, for example, provinces within a country, a larger sample size is required. GeoPoll typically recommends a sample size of 400 per country as the minimum viable sample for a research project, 800 per country for conducting a study with analysis by a second-level breakdown such as females versus males, and 1200+ per country for doing third-level breakdowns such as males aged 18-24 in Nairobi.
How to Calculate Sample Size
As we have defined all the necessary terms, let us briefly learn how to determine the sample size using a sample calculation formula known as Andrew Fisher’s Formula.
- Determine the population size (if known).
- Determine the confidence interval.
- Determine the confidence level.
- Determine the standard deviation ( a standard deviation of 0.5 is a safe choice where the figure is unknown )
- Convert the confidence level into a Z-Score. This table shows the z-scores for the most common confidence levels:
| 80% | 1.28 | |
| 85% | 1.44 | |
| 90% | 1.65 | |
| 95% | 1.96 | |
| 99% | 2.58 | |
- Put these figures into the sample size formula to get your sample size.

Here is an example calculation:
Say you choose to work with a 95% confidence level, a standard deviation of 0.5, and a confidence interval (margin of error) of ± 5%, you just need to substitute the values in the formula:
((1.96)2 x .5(.5)) / (.05)2
(3.8416 x .25) / .0025
.9604 / .0025
Your sample size should be 385.
Fortunately, there are several available online tools to help you with this calculation. Here’s an online sample calculator from Easy Calculation. Just put in the confidence level, population size, the confidence interval, and the perfect sample size is calculated for you.
GeoPoll’s Sampling Techniques
With the largest mobile panel in Africa, Asia, and Latin America, and reliable mobile technologies, GeoPoll develops unique samples that accurately represent any population. See our country coverage here , or contact our team to discuss your upcoming project.
Related Posts
Sample Frame and Sample Error
Probability and Non-Probability Samples
How GeoPoll Conducts Nationally Representative Surveys
- Tags market research , Market Research Methods , sample size , survey methodology
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Sample Size Essentials: The Foundation of Reliable Statistics
By Jim Frost Leave a Comment
What is Sample Size?
Sample size is the number of observations or data points collected in a study. It is a crucial element in any statistical analysis because it is the foundation for drawing inferences and conclusions about a larger population .

Imagine you’re tasting a new brand of cookies. Sampling just one cookie might not give you a true sense of the overall flavor—what if you picked the only burnt one? Similarly, in statistics, the sample size determines how well your study represents the larger group. A larger sample size can mean the difference between a snapshot and a panorama, providing a clearer, more accurate picture of the reality you’re studying.
In this blog post, learn why adequate sample sizes are not just a statistical nicety but a fundamental component of trustworthy research. However, large sample sizes can’t fix all problems. By understanding the impact of sample size on your results, you can make informed decisions about your research design and have more confidence in your findings .
Benefits of a Large Sample Size
A large sample size can significantly enhance the reliability and validity of study results. We’re primarily looking at how well representative samples reflect the populations from which the researchers drew them. Here are several key benefits.
Increased Precision
Larger samples tend to yield more precise estimates of the population parameters . Larger samples reduce the effect of random fluctuations in the data, narrowing the margin of error around the estimated values.
Estimate precision refers to how closely the results obtained from a sample align with the actual population values. A larger sample size tends to yield more precise estimates because it reduces the effect of random variability within the sample. The more data points you have, the smaller the margin of error and the closer you are to capturing the correct value of the population parameter.
For example, estimating the average height of adults using a larger sample tends to give an estimate closer to the actual average than using a smaller sample.
Learn more about Statistics vs. Parameters , Margin of Error , and Confidence Intervals .
Greater Statistical Power
The power of a statistical test is its capability to detect an effect if there is one, such as a difference between groups or a correlation between variables. Larger samples increase the likelihood of detecting actual effects.
Statistical power is the probability that a study will detect an effect when one exists. The sample size directly influences it; a larger sample size increases statistical power . Studies with more data are more likely to detect existing differences or relationships.
For instance, in testing whether a new drug is more effective than an existing one, a larger sample can more reliably detect small but real improvements in efficacy .
Better Generalizability
With a larger sample, there is a higher chance that the sample adequately represents the diversity of the population, improving the generalizability of the findings to the population.
Consider a national survey gauging public opinion on a policy. A larger sample captures a broader range of demographic groups and opinions.
Learn more about Representative Samples .
Reduced Impact of Outliers
In a large sample, outliers have less impact on the overall results because many observations dilute their influence. The numerous data points stabilize the averages and other statistical estimates, making them more representative of the general population.
If measuring income levels within a region, a few very high incomes will distort the average less in a larger sample than in a smaller one .
Learn more about 5 Ways to Identify Outliers .
The Limits of Larger Sample Sizes: A Cautionary Note
While larger sample sizes offer numerous advantages, such as increased precision and statistical power, it’s important to understand their limitations. They are not a panacea for all research challenges. Crucially, larger sample sizes do not automatically correct for biases in sampling methods , other forms of bias, or fundamental errors in study design. Ignoring these issues can lead to misleading conclusions, regardless of how many data points are collected.
Sampling Bias
Even a large sample is misleading if it’s not representative of the population. For instance, if a study on employee satisfaction only includes responses from headquarters staff but not remote workers, increasing the number of respondents won’t address the inherent bias in missing a significant segment of the workforce.
Learn more about Sampling Bias: Definition & Examples .
Other Forms of Bias
Biases related to data collection methods, survey question phrasing, or data analyst subjectivity can still skew results. If the underlying issues are not addressed, a larger sample size might magnify these biases instead of mitigating them.
Errors in Study Design
Simply adding more data points will not overcome a flawed experimental design . For example, increasing the sample size will not clarify the causal relationships if the design doesn’t control a confounding variable .
Large Sample Sizes are Expensive!
Additionally, it is possible to have too large a sample size. Larger sizes come with their own challenges, such as higher costs and logistical complexities. You get to a point of diminishing returns where you have a very large sample that will detect such small effects that they’re meaningless in a practical sense.
The takeaway here is that researchers must exercise caution and not rely solely on a large sample size to safeguard the reliability and validity of their results. An adequate amount of data must be paired with an appropriate sampling method, a robust study design, and meticulous execution to truly understand and accurately represent the phenomena being studied .
Sample Size Calculation
Statisticians have devised quantitative ways to find a good sample size. You want a large enough sample to have a reasonable chance of detecting a meaningful effect when it exists but not too large to be overly expensive.
In general, these methods focus on using the population’s variability . More variable populations require larger samples to assess them. Let’s go back to the cookie example to see why.
If all cookies in a population are identical (zero variability), you only need to sample one cookie to know what the average cookie is like for the entire population. However, suppose there’s a little variability because some cookies are cooked perfectly while others are overcooked. You’ll need a larger sample size to understand the ratio of the perfect to overcooked cookies.
Now, instead of just those two types, you have an entire range of how much they are over and undercooked. And some use sweeter chocolate chips than others. You’ll need an even larger sample to understand the increased variability and know what an average cookie is really like.

Power and sample size analysis quantifies the population’s variability. Hence, you’ll often need a variability estimate to perform this type of analysis. These calculations also frequently factor in the smallest practically meaningful effect size you want to detect, so you’ll use a manageable sample size.
To learn more about determining how to find a sample size, read my following articles :
- How to Calculate Sample Size
- What is Power in Statistics?
Sample Size Summary
Understanding the implications of sample size is fundamental to conducting robust statistical analysis. While larger samples provide more reliable and precise estimates, smaller samples can compromise the validity of statistical inferences.
Always remember that the breadth of your sample profoundly influences the strength of your conclusions. So, whether conducting a simple survey or a complex experimental study, consider your sample size carefully. Your research’s integrity depends on it.
Consequently, the effort to achieve an adequate sample size is a worthwhile investment in the precision and credibility of your research .
Share this:

Reader Interactions
Comments and questions cancel reply.
Sample Size in Statistics (How to Find it): Excel, Cochran’s Formula, General Tips
- What is a Sample Size?
- Part One: General Tips.
Cochran’s Sample Size Formula
- Yamane’s Sample Size Formula
- Known Confidence Interval and Width ( unknown population standard deviation).
- Known Confidence Interval and Width ( known population standard deviation).
Find a sample size to estimate a population mean
- Use Excel to find a sample size.
What is a “Sample Size”?
A sample size is a part of the population chosen for a survey or experiment. For example, you might take a survey of dog owner’s brand preferences. You won’t want to survey all the millions of dog owners in the country (either because it’s too expensive or time consuming), so you take a sample size. That may be several thousand owners. The sample size is a representation of all dog owner’s brand preferences. If you choose your sample wisely, it will be a good representation.
When Error can Creep in
When you only survey a small sample of the population, uncertainty creeps in to your statistics. If you can only survey a certain percentage of the true population, you can never be 100% sure that your statistics are a complete and accurate representation of the population. This uncertainty is called sampling error and is usually measured by a confidence interval . For example, you might state that your results are at a 90% confidence level. That means if you were to repeat your survey over and over, 90% of the time your would get the same results.

Back to top
How to Find a Sample Size in Statistics
A sample is a percentage of the total population in statistics. You can use the data from a sample to make inferences about a population as a whole. For example, the standard deviation of a sample can be used to approximate the standard deviation of a population. Finding a sample size can be one of the most challenging tasks in statistics and depends upon many factors including the size of your original population.
General Tips
Step 1: Conduct a census if you have a small population. A “small” population will depend on your budget and time constraints. For example, it may take a day to take a census of a student body at a small private university of 1,000 students but you may not have the time to survey 10,000 students at a large state university.
Step 2: Use a sample size from a similar study. Chances are, your type of study has already been undertaken by someone else. You’ll need access to academic databases to search for a study (usually your school or college will have access). A pitfall: you’ll be relying on someone else correctly calculating the sample size. Any errors they have made in their calculations will transfer over to your study.
Step 3: Use a table to find your sample size. If you have a fairly generic study, then there is probably a table for it. For example, if you have a clinical study , you may be able to use a table published in Machin et. al’s Sample Size Tables for Clinical Studies, Third Edition .
Step 4: Use a sample size calculator. Various calculators are available online, some simple, some more complex and specialized. For example, this calculator is for group- or cluster-randomized trials (GRTs) .
Step 5: Use a formula . There are many different formulas you can use, depending on what you know (or don’t know) about your population. If you know some parameters about your population (like a known standard deviation), you can use the techniques below. If you don’t know much about your population, use Slovin’s formula. . Back to top
The Cochran formula allows you to calculate an ideal sample size given a desired level of precision , desired confidence level , and the estimated proportion of the attribute present in the population.
Cochran’s formula is considered especially appropriate in situations with large populations. A sample of any given size provides more information about a smaller population than a larger one, so there’s a ‘correction’ through which the number given by Cochran’s formula can be reduced if the whole population is relatively small.
The Cochran formula is:
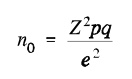
- e is the desired level of precision (i.e. the margin of error ),
- p is the (estimated) proportion of the population which has the attribute in question,
- q is 1 – p.
The z-value is found in a Z table .
Cochran’s Formula Example
Suppose we are doing a study on the inhabitants of a large town, and want to find out how many households serve breakfast in the mornings. We don’t have much information on the subject to begin with, so we’re going to assume that half of the families serve breakfast: this gives us maximum variability. So p = 0.5. Now let’s say we want 95% confidence, and at least 5 percent—plus or minus—precision. A 95 % confidence level gives us Z values of 1.96, per the normal tables, so we get
((1.96) 2 (0.5) (0.5)) / (0.05) 2 = 385.
So a random sample of 385 households in our target population should be enough to give us the confidence levels we need.
Modification for the Cochran Formula for Sample Size Calculation In Smaller Populations
If the population we’re studying is small, we can modify the sample size we calculated in the above formula by using this equation:
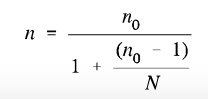
385 / (1 + ( 384 / 1000 )) = 278
So for this smaller population, all we need are 278 households in our sample; a substantially smaller sample size.
Yamane’s Formula
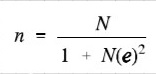
- e = precision level
- N = population size.
How to Find a Sample Size Given a Confidence Level and Width (unknown population standard deviation)
Part two shows you how to find a sample size for a given confidence level and width (e.g. 95% CL, 6% wide) for an unknown population standard deviation .
Example question : 41% of Jacksonville residents said that they had been in a hurricane. How many adults should be surveyed to estimate the true proportion of adults who have been in a hurricane, with a 95% confidence interval 6% wide?
Step 1: Using the data given in the question, figure out the following variables:
- z a/2 : Divide the confidence level by two, and look that area up in the z-table : .95 / 2 = 0.475 The closest z-score for 0.475 is 1.96 .
- E ( margin of error ): Divide the given width by 2. 6% / 2 = 0.06 / 2 = 0.03
Step 3: Divide Z a/2 by E . 1.96 / .03 = 65.3333333
Step 4: Square Step 3 : 65.3333333 × 65.3333333 = 4268.44444
Step 5: Multiply Step 2 by Step 4: 0.2419 × 4268.44444 = 1,032.53671 = 1,033 people to survey . Back to top
How to Find a Sample Size Given a Confidence Level and Width (known population standard deviation)
Part 3 shows you how to determine the appropriate sample size for a given confidence level and width , given that you know the population standard deviation .
Example question: Suppose we want to know the average age of an Florida State College student, plus or minus 0.5 years. We’d like to be 99% confident about our result. From a previous study, we know that the standard deviation for the population is 2.9.
Step 1: Find z a/2 by dividing the confidence level by two, and looking that area up in the z-table : .99/2 = 0.495. The closest z-score for 0.495 is 2.58 .
Step 2: Multiply step 1 by the standard deviation. 2.58 * 2.9 = 7.482
Step 3: Divide Step 2 by the margin of error. Our margin of error (from the question), is 0.5. 7.482/0.5 = 14.96
Step 4: Square Step 3. 14.96 * 14.96 = 223.8016

How to find a sample size in Excel.

How to use Excel Sampling to find a Sample
If you have a set of data and you know your sample size, you can use Excel’s Data Analysis toolpak to select either a periodic sample or a random sample. A random sample is just that — randomly selected from your data set. A periodic sample (also called a systematic sample ) is where Excel chooses the nth data item to include in your sample. For example, if you wanted to choose every 5th number from the following list: 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, Excel would return 8 and 13 (the 5th and 10th numbers in order).
If you don’t know what sample size you need, calculate it before using the Data Analysis tool (using the methods outlined at the top of this article). The Data Analysis tool can help you extract a sample, but it can’t help you decide on the size . Why? There are many “human” factors that go into selecting a sample size including budget, prior research (you can use a sample size from previous research) and tables constructed from previous research.
How to use Excel Sampling to find a Sample: Steps
Step 1: Enter your data items into Excel. You can enter your data into rows or columns. Ensure the rows and columns are even; for example, enter data into column A to cell 12 and column B to cell 12.
Step 2: Click “Data” and then click “Data Analysis.” If you don’t see Data Analysis on your toolbar, load the Data Analysis Toolpak .
Step 3: Click “Sampling” and then click “OK.”
Step 4: Click in the Input Range box and then select your entire data set.
Step 5: Click either “Periodic Sampling” or “Random Sampling.” If you choose periodic, enter the nth number (i.e. every 5) and if you choose random sampling, enter the sample size.
Step 6: Choose an output range. For example, click the “New Worksheet” button and Excel will return the sample in a new worksheet.
Step 7: Click “OK.”
That’s it!
Check out our YouTube channel for more Excel tips and help! Back to top
Related Articles
Ways to Reduce Sample Size. Effective Sample Size. . Unequal sample size.
Bartlett, J. et al. (2001). Organizational Research: Determining Appropriate Sample Size in Survey Research. Retrieved January 15, 2018 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.486.8295&rep=rep1&type=pdf. Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, 2000. Israel, G. (n.d.) Determining Sample Size. University of Florida IFAS Extension. Article posted on Tarleton State University website. Retrieved January 13, 2018 from https://www.tarleton.edu/academicassessment/documents/Samplesize.pdf.
Sample Size Calculator
Table of contents
If you're conducting research and wonder how many measurements you need so that it is statistically significant , this sample size calculator is here to help you. All you need to do is ask yourself these three questions before you use it:
- How accurate should your result be? (margin of error)
- What level of confidence do you need? (confidence level)
- What is your initial estimate ? (proportion estimate)
Read on to learn how to calculate the sample size using this tool, and what do all the variables in the sample size calculation formula mean.
Sample size calculation formula
The equation that our sample size calculator uses is:
- Z Z Z — The z-score associated with the confidence level you chose. Our statistical significance calculator calculates this value automatically, but if you want to learn how to calculate it by hand, take a look at the instructions of our confidence interval calculator .
- M E \mathrm{ME} ME — Margin of error, also known as the confidence interval . It tells you that you can be sure (with a probability of confidence level, for example, 95%), that the real value doesn't differ from the one that you obtained by more than this percentage. You can learn more about it at our margin of error calculator .
- p p p — Your initial proportion estimate. For example, if you are conducting a survey among students trying to find out how many of them read more than 5 books last year, you may know a result of a previous survey — 40%. If you have no such estimate, use the conservative value of 50%.
- n 1 n_1 n 1 — Required sample size.
If your population is finite — for example, you are conducting a survey among students of only one faculty — you need to include a correction in the following form:
- N N N — Total population size.
- n 2 n_2 n 2 — Size of the sample taken from the whole population that will make your research statistically significant.
How to calculate sample size: an example
We will analyze a survey case step-by-step so you can get a clear picture of how to use our sample size calculator . You are planning to conduct a survey to find out what is the proportion of students on your campus who regularly eat their lunch at the campus canteen.
Decide how accurate you want your result to be. Let's say that it is important for the canteen to know the result, with a margin of error of 2 % 2\% 2% maximum.
Decide on your confidence level . We can assume you want to be 99 % 99\% 99% sure that your result is correct.
Do you have an initial proportion guess ? Let's say you accessed a similar survey from 10 years ago, and the proportion was equal to 30 % 30\% 30% . You can assume it as your initial estimate.
Is the total population of students so high that you can assume it's infinite ? Probably not. You need to find the current data for the number of students on the campus — let's assume it is 25 , 000 25,000 25 , 000 .
All you need to do now is input all this data into our sample size calculator. It finds the sample size required for the result to be statistically significant is 3 , 051 3,051 3 , 051 . You need to ask that many students the same question… Are you sure you can't settle for a 95 % 95\% 95% confidence level? 😀
Other useful tools beyond the sample size calculator
Now that you know how to calculate sample size, you can go beyond and use it to calculate other statistics of interest in your research:
Sampling error calculator : sample size is the most influential feature when predicting the sampling error. Use it to calculate the error of your sample.
Normal probability calculator for sampling distributions : use your sample size, along with the population mean and standard deviation, to find the probability that your sample mean falls within a specific range.
Sampling distribution of the sample proportion calculator : use your sample size and the population proportion to find the probability that your sample proportion falls within a specific range.
.css-17jgrqx.css-17jgrqx{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-17jgrqx.css-17jgrqx:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-17jgrqx .js-external-link-button.link-like,.css-17jgrqx .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-17jgrqx .js-external-link-button.link-like:hover,.css-17jgrqx .js-external-link-anchor:hover,.css-17jgrqx .js-external-link-button.link-like:active,.css-17jgrqx .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-17jgrqx .js-external-link-button.link-like:focus-visible,.css-17jgrqx .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-17jgrqx p,.css-17jgrqx div{margin:0;display:block;}.css-17jgrqx pre{margin:0;display:block;}.css-17jgrqx pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-17jgrqx pre:not(:first-child){padding-top:8px;}.css-17jgrqx ul,.css-17jgrqx ol{display:block margin:0;padding-left:20px;}.css-17jgrqx ul li,.css-17jgrqx ol li{padding-top:8px;}.css-17jgrqx ul ul,.css-17jgrqx ol ul,.css-17jgrqx ul ol,.css-17jgrqx ol ol{padding-top:0;}.css-17jgrqx ul:not(:first-child),.css-17jgrqx ol:not(:first-child){padding-top:4px;} .css-jdoljy{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-jdoljy code,.css-jdoljy kbd,.css-jdoljy pre,.css-jdoljy samp{font-family:monospace;}.css-jdoljy code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-jdoljy figcaption,.css-jdoljy caption{text-align:center;}.css-jdoljy figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-jdoljy h3{font-size:1.75rem;}.css-jdoljy h4{font-size:1.5rem;}.css-jdoljy .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-jdoljy .mathBlock .katex{font-size:24px;text-align:left;}.css-jdoljy .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-jdoljy .videoBlock,.css-jdoljy .imageBlock{margin-bottom:16px;}.css-jdoljy .imageBlock__image-align--left,.css-jdoljy .videoBlock__video-align--left{float:left;}.css-jdoljy .imageBlock__image-align--right,.css-jdoljy .videoBlock__video-align--right{float:right;}.css-jdoljy .imageBlock__image-align--center,.css-jdoljy .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-jdoljy .imageBlock__image-align--none,.css-jdoljy .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-jdoljy .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-jdoljy .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-jdoljy .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-jdoljy .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-jdoljy .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-jdoljy .katex .katex-version::after{content:'0.13.13';}.css-jdoljy .katex .katex-mathml{position:absolute;clip:rect(1px, 1px, 1px, 1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-jdoljy .katex .katex-html>.newline{display:block;}.css-jdoljy .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-jdoljy .katex .strut{display:inline-block;}.css-jdoljy .katex .textbf{font-weight:bold;}.css-jdoljy .katex .textit{font-style:italic;}.css-jdoljy .katex .textrm{font-family:KaTeX_Main;}.css-jdoljy .katex .textsf{font-family:KaTeX_SansSerif;}.css-jdoljy .katex .texttt{font-family:KaTeX_Typewriter;}.css-jdoljy .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-jdoljy .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-jdoljy .katex .mathrm{font-style:normal;}.css-jdoljy .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-jdoljy .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-jdoljy .katex .amsrm{font-family:KaTeX_AMS;}.css-jdoljy .katex .mathbb,.css-jdoljy .katex .textbb{font-family:KaTeX_AMS;}.css-jdoljy .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-jdoljy .katex .mathfrak,.css-jdoljy .katex .textfrak{font-family:KaTeX_Fraktur;}.css-jdoljy .katex .mathtt{font-family:KaTeX_Typewriter;}.css-jdoljy .katex .mathscr,.css-jdoljy .katex .textscr{font-family:KaTeX_Script;}.css-jdoljy .katex .mathsf,.css-jdoljy .katex .textsf{font-family:KaTeX_SansSerif;}.css-jdoljy .katex .mathboldsf,.css-jdoljy .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-jdoljy .katex .mathitsf,.css-jdoljy .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-jdoljy .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-jdoljy .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-jdoljy .katex .vlist-r{display:table-row;}.css-jdoljy .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-jdoljy .katex .vlist>span{display:block;height:0;position:relative;}.css-jdoljy .katex .vlist>span>span{display:inline-block;}.css-jdoljy .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-jdoljy .katex .vlist-t2{margin-right:-2px;}.css-jdoljy .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-jdoljy .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-jdoljy .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-jdoljy .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-jdoljy .katex .msupsub{text-align:left;}.css-jdoljy .katex .mfrac>span>span{text-align:center;}.css-jdoljy .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-jdoljy .katex .mfrac .frac-line,.css-jdoljy .katex .overline .overline-line,.css-jdoljy .katex .underline .underline-line,.css-jdoljy .katex .hline,.css-jdoljy .katex .hdashline,.css-jdoljy .katex .rule{min-height:1px;}.css-jdoljy .katex .mspace{display:inline-block;}.css-jdoljy .katex .llap,.css-jdoljy .katex .rlap,.css-jdoljy .katex .clap{width:0;position:relative;}.css-jdoljy .katex .llap>.inner,.css-jdoljy .katex .rlap>.inner,.css-jdoljy .katex .clap>.inner{position:absolute;}.css-jdoljy .katex .llap>.fix,.css-jdoljy .katex .rlap>.fix,.css-jdoljy .katex .clap>.fix{display:inline-block;}.css-jdoljy .katex .llap>.inner{right:0;}.css-jdoljy .katex .rlap>.inner,.css-jdoljy .katex .clap>.inner{left:0;}.css-jdoljy .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-jdoljy .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-jdoljy .katex .overline .overline-line,.css-jdoljy .katex .underline .underline-line,.css-jdoljy .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-jdoljy .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-jdoljy .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-jdoljy .katex .sizing.reset-size1.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-jdoljy .katex .sizing.reset-size1.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-jdoljy .katex .sizing.reset-size1.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-jdoljy .katex .sizing.reset-size1.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-jdoljy .katex .sizing.reset-size1.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-jdoljy .katex .sizing.reset-size1.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-jdoljy .katex .sizing.reset-size1.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-jdoljy .katex .sizing.reset-size1.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-jdoljy .katex .sizing.reset-size1.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-jdoljy .katex .sizing.reset-size1.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-jdoljy .katex .sizing.reset-size1.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-jdoljy .katex .sizing.reset-size2.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-jdoljy .katex .sizing.reset-size2.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-jdoljy .katex .sizing.reset-size2.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-jdoljy .katex .sizing.reset-size2.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-jdoljy .katex .sizing.reset-size2.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-jdoljy .katex .sizing.reset-size2.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-jdoljy .katex .sizing.reset-size2.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-jdoljy .katex .sizing.reset-size2.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-jdoljy .katex .sizing.reset-size2.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-jdoljy .katex .sizing.reset-size2.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-jdoljy .katex .sizing.reset-size2.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-jdoljy .katex .sizing.reset-size3.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-jdoljy .katex .sizing.reset-size3.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-jdoljy .katex .sizing.reset-size3.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-jdoljy .katex .sizing.reset-size3.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-jdoljy .katex .sizing.reset-size3.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-jdoljy .katex .sizing.reset-size3.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-jdoljy .katex .sizing.reset-size3.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-jdoljy .katex .sizing.reset-size3.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-jdoljy .katex .sizing.reset-size3.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-jdoljy .katex .sizing.reset-size3.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-jdoljy .katex .sizing.reset-size3.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-jdoljy .katex .sizing.reset-size4.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-jdoljy .katex .sizing.reset-size4.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-jdoljy .katex .sizing.reset-size4.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-jdoljy .katex .sizing.reset-size4.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-jdoljy .katex .sizing.reset-size4.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-jdoljy .katex .sizing.reset-size4.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-jdoljy .katex .sizing.reset-size4.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-jdoljy .katex .sizing.reset-size4.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-jdoljy .katex .sizing.reset-size4.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-jdoljy .katex .sizing.reset-size4.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-jdoljy .katex .sizing.reset-size4.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-jdoljy .katex .sizing.reset-size5.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-jdoljy .katex .sizing.reset-size5.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-jdoljy .katex .sizing.reset-size5.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-jdoljy .katex .sizing.reset-size5.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-jdoljy .katex .sizing.reset-size5.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-jdoljy .katex .sizing.reset-size5.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-jdoljy .katex .sizing.reset-size5.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-jdoljy .katex .sizing.reset-size5.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-jdoljy .katex .sizing.reset-size5.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-jdoljy .katex .sizing.reset-size5.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-jdoljy .katex .sizing.reset-size5.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-jdoljy .katex .sizing.reset-size6.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-jdoljy .katex .sizing.reset-size6.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-jdoljy .katex .sizing.reset-size6.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-jdoljy .katex .sizing.reset-size6.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-jdoljy .katex .sizing.reset-size6.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-jdoljy .katex .sizing.reset-size6.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-jdoljy .katex .sizing.reset-size6.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-jdoljy .katex .sizing.reset-size6.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-jdoljy .katex .sizing.reset-size6.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-jdoljy .katex .sizing.reset-size6.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-jdoljy .katex .sizing.reset-size6.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-jdoljy .katex .sizing.reset-size7.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-jdoljy .katex .sizing.reset-size7.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-jdoljy .katex .sizing.reset-size7.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-jdoljy .katex .sizing.reset-size7.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-jdoljy .katex .sizing.reset-size7.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-jdoljy .katex .sizing.reset-size7.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-jdoljy .katex .sizing.reset-size7.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-jdoljy .katex .sizing.reset-size7.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-jdoljy .katex .sizing.reset-size7.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-jdoljy .katex .sizing.reset-size7.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-jdoljy .katex .sizing.reset-size7.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-jdoljy .katex .sizing.reset-size8.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-jdoljy .katex .sizing.reset-size8.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-jdoljy .katex .sizing.reset-size8.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-jdoljy .katex .sizing.reset-size8.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-jdoljy .katex .sizing.reset-size8.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-jdoljy .katex .sizing.reset-size8.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-jdoljy .katex .sizing.reset-size8.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-jdoljy .katex .sizing.reset-size8.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-jdoljy .katex .sizing.reset-size8.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-jdoljy .katex .sizing.reset-size8.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-jdoljy .katex .sizing.reset-size8.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-jdoljy .katex .sizing.reset-size9.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-jdoljy .katex .sizing.reset-size9.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-jdoljy .katex .sizing.reset-size9.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-jdoljy .katex .sizing.reset-size9.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-jdoljy .katex .sizing.reset-size9.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-jdoljy .katex .sizing.reset-size9.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-jdoljy .katex .sizing.reset-size9.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-jdoljy .katex .sizing.reset-size9.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-jdoljy .katex .sizing.reset-size9.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-jdoljy .katex .sizing.reset-size9.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-jdoljy .katex .sizing.reset-size9.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-jdoljy .katex .sizing.reset-size10.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-jdoljy .katex .sizing.reset-size10.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-jdoljy .katex .sizing.reset-size10.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-jdoljy .katex .sizing.reset-size10.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-jdoljy .katex .sizing.reset-size10.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-jdoljy .katex .sizing.reset-size10.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-jdoljy .katex .sizing.reset-size10.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-jdoljy .katex .sizing.reset-size10.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-jdoljy .katex .sizing.reset-size10.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-jdoljy .katex .sizing.reset-size10.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-jdoljy .katex .sizing.reset-size10.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-jdoljy .katex .sizing.reset-size11.size1,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-jdoljy .katex .sizing.reset-size11.size2,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-jdoljy .katex .sizing.reset-size11.size3,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-jdoljy .katex .sizing.reset-size11.size4,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-jdoljy .katex .sizing.reset-size11.size5,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-jdoljy .katex .sizing.reset-size11.size6,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-jdoljy .katex .sizing.reset-size11.size7,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-jdoljy .katex .sizing.reset-size11.size8,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-jdoljy .katex .sizing.reset-size11.size9,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-jdoljy .katex .sizing.reset-size11.size10,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-jdoljy .katex .sizing.reset-size11.size11,.css-jdoljy .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-jdoljy .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-jdoljy .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-jdoljy .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-jdoljy .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-jdoljy .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-jdoljy .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-jdoljy .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-jdoljy .katex .delimcenter{position:relative;}.css-jdoljy .katex .op-symbol{position:relative;}.css-jdoljy .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-jdoljy .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-jdoljy .katex .op-limits>.vlist-t{text-align:center;}.css-jdoljy .katex .accent>.vlist-t{text-align:center;}.css-jdoljy .katex .accent .accent-body{position:relative;}.css-jdoljy .katex .accent .accent-body:not(.accent-full){width:0;}.css-jdoljy .katex .overlay{display:block;}.css-jdoljy .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-jdoljy .katex .mtable .arraycolsep{display:inline-block;}.css-jdoljy .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-jdoljy .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-jdoljy .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-jdoljy .katex .svg-align{text-align:left;}.css-jdoljy .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-jdoljy .katex svg path{stroke:none;}.css-jdoljy .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-jdoljy .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-jdoljy .katex .stretchy::before,.css-jdoljy .katex .stretchy::after{content:'';}.css-jdoljy .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-jdoljy .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-jdoljy .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-jdoljy .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-jdoljy .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-jdoljy .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-jdoljy .katex .x-arrow-pad{padding:0 0.5em;}.css-jdoljy .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-jdoljy .katex .x-arrow,.css-jdoljy .katex .mover,.css-jdoljy .katex .munder{text-align:center;}.css-jdoljy .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-jdoljy .katex .fbox,.css-jdoljy .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-jdoljy .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-jdoljy .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-jdoljy .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-jdoljy .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-jdoljy .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-jdoljy .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-jdoljy .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-jdoljy .katex .mtr-glue{width:50%;}.css-jdoljy .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-jdoljy .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-jdoljy .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-jdoljy .katex-display{display:block;margin:1em 0;text-align:center;}.css-jdoljy .katex-display>.katex{display:block;white-space:nowrap;}.css-jdoljy .katex-display>.katex>.katex-html{display:block;position:relative;}.css-jdoljy .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-jdoljy .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-jdoljy .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-jdoljy body{counter-reset:katexEqnNo mmlEqnNo;}.css-jdoljy table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-jdoljy .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-jdoljy .tableBlock thead,.css-jdoljy .tableBlock thead th{border-bottom:1px solid #333!important;}.css-jdoljy .tableBlock th,.css-jdoljy .tableBlock td{padding:10px;text-align:left;}.css-jdoljy .tableBlock th{font-weight:bold!important;}.css-jdoljy .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-jdoljy .tableBlock caption>p{margin:0;}.css-jdoljy .tableBlock th>p,.css-jdoljy .tableBlock td>p{margin:0;}.css-jdoljy .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-jdoljy .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-jdoljy .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-jdoljy .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-jdoljy .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-jdoljy .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-jdoljy .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-jdoljy .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-jdoljy .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-jdoljy .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-jdoljy .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-jdoljy .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-jdoljy .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-jdoljy .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-jdoljy .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-jdoljy .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-jdoljy .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-jdoljy .tableBlock [data-text-align='center']{text-align:center;}.css-jdoljy .tableBlock [data-text-align='left']{text-align:left;}.css-jdoljy .tableBlock [data-text-align='right']{text-align:right;}.css-jdoljy .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-jdoljy .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-jdoljy .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-jdoljy .tableBlock__font-size--xxsmall{font-size:10px;}.css-jdoljy .tableBlock__font-size--xsmall{font-size:12px;}.css-jdoljy .tableBlock__font-size--small{font-size:14px;}.css-jdoljy .tableBlock__font-size--large{font-size:18px;}.css-jdoljy .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-jdoljy .tableBlock__border--bordered td,.css-jdoljy .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-jdoljy .tableBlock__border--borderless tbody+tbody,.css-jdoljy .tableBlock__border--borderless td,.css-jdoljy .tableBlock__border--borderless th,.css-jdoljy .tableBlock__border--borderless tr,.css-jdoljy .tableBlock__border--borderless thead,.css-jdoljy .tableBlock__border--borderless thead th{border:0!important;}.css-jdoljy .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-jdoljy .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-jdoljy .tableBlock__table-compactl th,.css-jdoljy .tableBlock__table-compact td{padding:3px!important;}.css-jdoljy .tableBlock__full-size{width:100%;}.css-jdoljy .textBlock{margin-bottom:16px;}.css-jdoljy .textBlock__text-formatting--finePrint{font-size:12px;}.css-jdoljy .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-jdoljy .textBlock__text-infoBox p{margin:0;}.css-jdoljy .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-jdoljy .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-jdoljy .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-jdoljy .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-jdoljy .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-jdoljy .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-jdoljy .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-jdoljy .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-jdoljy.css-jdoljy{color:#2B3148;background-color:transparent;font-family:"Roboto","Helvetica","Arial",sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-jdoljy.css-jdoljy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-jdoljy .js-external-link-button.link-like,.css-jdoljy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-jdoljy .js-external-link-button.link-like:hover,.css-jdoljy .js-external-link-anchor:hover,.css-jdoljy .js-external-link-button.link-like:active,.css-jdoljy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-jdoljy .js-external-link-button.link-like:focus-visible,.css-jdoljy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-jdoljy p,.css-jdoljy div{margin:0;display:block;}.css-jdoljy pre{margin:0;display:block;}.css-jdoljy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-jdoljy pre:not(:first-child){padding-top:8px;}.css-jdoljy ul,.css-jdoljy ol{display:block margin:0;padding-left:20px;}.css-jdoljy ul li,.css-jdoljy ol li{padding-top:8px;}.css-jdoljy ul ul,.css-jdoljy ol ul,.css-jdoljy ul ol,.css-jdoljy ol ol{padding-top:0;}.css-jdoljy ul:not(:first-child),.css-jdoljy ol:not(:first-child){padding-top:4px;} Statistical parameters
Confidence level
Margin of error
Proportion estimate
Your initial estimate of the result you will obtain.
Sample size
Correction for finite population
- Skip to main content
- Skip to primary sidebar
- Skip to footer
- QuestionPro

- Solutions Industries Gaming Automotive Sports and events Education Government Travel & Hospitality Financial Services Healthcare Cannabis Technology Use Case NPS+ Communities Audience Contactless surveys Mobile LivePolls Member Experience GDPR Positive People Science 360 Feedback Surveys
- Resources Blog eBooks Survey Templates Case Studies Training Help center
Home Audience
Sample Size Determination: Definition, Formula, and Example

Are you ready to survey your research target? Research surveys help you gain insights from your target audience. The data you collect gives you insights to meet customer needs, leading to increased sales and customer loyalty. Sample size calculation and determination are imperative to the researcher to determine the right number of respondents, keeping in mind the research study’s quality.
So, how should you do the sample size determination? How do you know who should get your survey? How do you decide on the number of the target audience?
Sending out too many surveys can be expensive without giving you a definitive advantage over a smaller sample. But if you send out too few, you won’t have enough data to draw accurate conclusions.
Knowing how to calculate and determine the appropriate sample size accurately can give you an edge over your competitors. Let’s take a look at what a good sample includes. Also, let’s look at the sample size calculation formula so you can determine the perfect sample size for your next survey.
What is Sample Size?
‘Sample size’ is a market research term used for defining the number of individuals included in conducting research. Researchers choose their sample based on demographics, such as age, gender questions , or physical location. It can be vague or specific.
For example, you may want to know what people within the 18-25 age range think of your product. Or, you may only require your sample to live in the United States, giving you a wide population range. The total number of individuals in a particular sample is the sample size.
What is sample size determination?
Sample size determination is the process of choosing the right number of observations or people from a larger group to use in a sample. The goal of figuring out the sample size is to ensure that the sample is big enough to give statistically valid results and accurate estimates of population parameters but small enough to be manageable and cost-effective.
In many research studies, getting information from every member of the population of interest is not possible or useful. Instead, researchers choose a sample of people or events that is representative of the whole to study. How accurate and precise the results are can depend a lot on the size of the sample.
Choosing the statistically significant sample size depends on a number of things, such as the size of the population, how precise you want your estimates to be, how confident you want to be in the results, how different the population is likely to be, and how much money and time you have for the study. Statistics are often used to figure out how big a sample should be for a certain type of study and research question.
Figuring out the sample size is important in ensuring that research findings and conclusions are valid and reliable.
Why do you need to determine the sample size?
Let’s say you are a market researcher in the US and want to send out a survey or questionnaire . The survey aims to understand your audience’s feelings toward a new cell phone you are about to launch. You want to know what people in the US think about the new product to predict the phone’s success or failure before launch.
Hypothetically, you choose the population of New York, which is 8.49 million. You use a sample size determination formula to select a sample of 500 individuals that fit into the consumer panel requirement. You can use the responses to help you determine how your audience will react to the new product.
However, determining a sample size requires more than just throwing your survey at as many people as possible. If your estimated sample sizes are too big, it could waste resources, time, and money. A sample size that’s too small doesn’t allow you to gain maximum insights, leading to inconclusive results.
LEARN ABOUT: Survey Sample Sizes
What are the terms used around the sample size?
Before we jump into sample size determination, let’s take a look at the terms you should know:
1. Population size:
Population size is how many people fit your demographic. For example, you want to get information on doctors residing in North America. Your population size is the total number of doctors in North America.
Don’t worry! Your population size doesn’t always have to be that big. Smaller population sizes can still give you accurate results as long as you know who you’re trying to represent.
2. Confidence level:
The confidence level tells you how sure you can be that your data is accurate. It is expressed as a percentage and aligned to the confidence interval. For example, if your confidence level is 90%, your results will most likely be 90% accurate.
3. The margin of error (confidence interval):
There’s no way to be 100% accurate when it comes to surveys. Confidence intervals tell you how far off from the population means you’re willing to allow your data to fall.
A margin of error describes how close you can reasonably expect a survey result to fall relative to the real population value. Remember, if you need help with this information, use our margin of error calculator .
4. Standard deviation:
Standard deviation is the measure of the dispersion of a data set from its mean. It measures the absolute variability of a distribution. The higher the dispersion or variability, the greater the standard deviation and the greater the magnitude of the deviation.
For example, you have already sent out your survey. How much variance do you expect in your responses? That variation in response is the standard deviation.
Sample size calculation formula – sample size determination
With all the necessary terms defined, it’s time to learn how to determine sample size using a sample calculation formula.
Your confidence level corresponds to a Z-score. This is a constant value needed for this equation. Here are the z-scores for the most common confidence levels:
90% – Z Score = 1.645
95% – Z Score = 1.96
99% – Z Score = 2.576
If you choose a different confidence level, various online tools can help you find your score.
Necessary Sample Size = (Z-score)2 * StdDev*(1-StdDev) / (margin of error)2
Here is an example of how the math works, assuming you chose a 90% confidence level, .6 standard deviation, and a margin of error (confidence interval) of +/- 4%.
((1.64)2 x .6(.6)) / (.04)2
( 2.68x .0.36) / .0016
.9648 / .0016
603 respondents are needed, and that becomes your sample size.
Free Sample Size Calculator
How is a sample size determined?
Determining the right sample size for your survey is one of the most common questions researchers ask when they begin a market research study. Luckily, sample size determination isn’t as hard to calculate as you might remember from an old high school statistics class.
Before calculating your sample size, ensure you have these things in place:
Goals and objectives:
What do you hope to do with the survey? Are you planning on projecting the results onto a whole demographic or population? Do you want to see what a specific group thinks? Are you trying to make a big decision or just setting a direction?
Calculating sample size is critical if you’re projecting your survey results on a larger population. You’ll want to make sure that it’s balanced and reflects the community as a whole. The sample size isn’t as critical if you’re trying to get a feel for preferences.
For example, you’re surveying homeowners across the US on the cost of cooling their homes in the summer. A homeowner in the South probably spends much more money cooling their home in the humid heat than someone in Denver, where the climate is dry and cool.
For the most accurate results, you’ll need to get responses from people in all US areas and environments. If you only collect responses from one extreme, such as the warm South, your results will be skewed.
Precision level:
How close do you want the survey results to mimic the true value if everyone responded? Again, if this survey determines how you’re going to spend millions of dollars, then your sample size determination should be exact.
The more accurate you need to be, the larger the sample you want to have, and the more your sample will have to represent the overall population. If your population is small, say, 200 people, you may want to survey the entire population rather than cut it down with a sample.
Confidence level:
Think of confidence from the perspective of risk. How much risk are you willing to take on? This is where your Confidence Interval numbers become important. How confident do you want to be — 98% confident, 95% confident?
Understand that the confidence percentage you choose greatly impacts the number of completions you’ll need for accuracy. This can increase the survey’s length and how many responses you need, which means increased costs for your survey.
Knowing the actual numbers and amounts behind percentages can help make more sense of your correct sample size needs vs. survey costs.
For example, you want to be 99% confident. After using the sample size determination formula, you find you need to collect an additional 1000 respondents.
This, in turn, means you’ll be paying for samples or keeping your survey running for an extra week or two. You have to determine if the increased accuracy is more important than the cost.
Population variability:
What variability exists in your population? In other words, how similar or different is the population?
If you are surveying consumers on a broad topic, you may have lots of variations. You’ll need a larger sample size to get the most accurate picture of the population.
However, if you’re surveying a population with similar characteristics, your variability will be less, and you can sample fewer people. More variability equals more samples, and less variability equals fewer samples. If you’re not sure, you can start with 50% variability.
Response rate:
You want everyone to respond to your survey. Unfortunately, every survey comes with targeted respondents who either never open the study or drop out halfway. Your response rate will depend on your population’s engagement with your product, service organization, or brand.
The higher the response rate, the higher your population’s engagement level. Your base sample size is the number of responses you must get for a successful survey.
Consider your audience:
Besides the variability within your population, you need to ensure your sample doesn’t include people who won’t benefit from the results. One of the biggest mistakes you can make in sample size determination is forgetting to consider your actual audience.
For example, you don’t want to send a survey asking about the quality of local apartment amenities to a group of homeowners.
Select your respondents
Focus on your survey’s objectives:
You may start with general demographics and characteristics, but can you narrow those characteristics down even more? Narrowing down your audience makes getting a more accurate result from a small sample size easier.
For example, you want to know how people will react to new automobile technology. Your current population includes anyone who owns a car in a particular market.
However, you know your target audience is people who drive cars that are less than five years old. You can remove anyone with an older vehicle from your sample because they’re unlikely to purchase your product.
Once you know what you hope to gain from your survey and what variables exist within your population, you can decide how to calculate sample size. Using the formula for determining sample size is a great starting point to get accurate results.
After calculating the sample size, you’ll want to find reliable customer survey software to help you accurately collect survey responses and turn them into analyzed reports.
LEARN MORE: Population vs Sample
In sample size determination, statistical analysis plan needs careful consideration of the level of significance, effect size, and sample size.
Researchers must reconcile statistical significance with practical and ethical factors like practicality and cost. A well-designed study with a sufficient sample size can improve the odds of obtaining statistically significant results.
To meet the goal of your survey, you may have to try a few methods to increase the response rate, such as:
- Increase the list of people who receive the survey.
- To reach a wider audience, use multiple distribution channels, such as SMS, website, and email surveys.
- Send reminders to survey participants to complete the survey.
- Offer incentives for completing the survey, such as an entry into a prize drawing or a discount on the respondent’s next order.
- Consider your survey structure and find ways to simplify your questions. The less work someone has to do to complete the survey, the more likely they will finish it.
- Longer surveys tend to have lower response rates due to the length of time it takes to complete the survey. In this case, you can reduce the number of questions in your survey to increase responses.
QuestionPro’s sample size calculator makes it easy to find the right sample size for your research based on your desired level of confidence, your margin of error, and the size of the population.
FREE TRIAL LEARN MORE
Frequently Asked Questions (FAQ)
The four ways to determine sample size are: 1. Power analysis 2. Convenience sampling, 3. Random sampling , 4. Stratified sampling
The three factors that determine sample size are: 1. Effect size, 2. Level of significance 3. Power
Using statistical techniques like power analysis, the minimal detectable effect size, or the sample size formula while taking into account the study’s goals and practical limitations is the best way to calculate the sample size.
The sample size is important because it affects how precise and accurate the results of a study are and how well researchers can spot real effects or relationships between variables.
The sample size is the number of observations or study participants chosen to be representative of a larger group
MORE LIKE THIS

QuestionPro Thrive: A Space to Visualize & Share the Future of Technology
Jun 18, 2024

Relationship NPS Fails to Understand Customer Experiences — Tuesday CX

CX Platform: Top 13 CX Platforms to Drive Customer Success
Jun 17, 2024

How to Know Whether Your Employee Initiatives are Working
Other categories.
- Academic Research
- Artificial Intelligence
- Assessments
- Brand Awareness
- Case Studies
- Communities
- Consumer Insights
- Customer effort score
- Customer Engagement
- Customer Experience
- Customer Loyalty
- Customer Research
- Customer Satisfaction
- Employee Benefits
- Employee Engagement
- Employee Retention
- Friday Five
- General Data Protection Regulation
- Insights Hub
- Life@QuestionPro
- Market Research
- Mobile diaries
- Mobile Surveys
- New Features
- Online Communities
- Question Types
- Questionnaire
- QuestionPro Products
- Release Notes
- Research Tools and Apps
- Revenue at Risk
- Survey Templates
- Training Tips
- Tuesday CX Thoughts (TCXT)
- Uncategorized
- Video Learning Series
- What’s Coming Up
- Workforce Intelligence

Making Smart Companies Smarter since 1991
How to determine the best statistics sample size for your research.
Knowing how to determine the correct statistics sample size is critical for meaningful research outcomes. This article will guide you through the importance of sample size, the methods to calculate it, and the essential factors that influence it.
Key Takeaways
- An appropriate sample size is crucial for achieving statistically significant and reliable research results, balancing accuracy and practicality.
- Key factors influencing sample size calculation include population size, margin of error, and confidence level, which combine to determine the necessary sample size for robust data representation.
- Various tools and best practices, including online calculators and statistical software, can assist researchers in accurately determining the ideal sample size while considering study goals, cost-efficiency, and potential non-responses.
Sampling illuminates a select group like a spotlight in a vast theater, narrating a story that represents the entire audience. The art and science of choosing the right sample size—a number that can confidently speak for a larger population—are paramount in the realm of research. Whether it’s tasting a spoonful of soup to judge the whole pot or polling a random sample of voters to predict an election, the chosen sample holds the key to unlocking statistically significant insights.
Understanding Sample Size in Statistics

What gives sample size such weight in the field of research? It’s the fulcrum upon which the balance of accuracy and reliability rests. From the classrooms of academia to the boardrooms of market research, ensuring that your study’s sample size is robust enough to represent a population is the cornerstone of extracting meaningful and statistically significant results.
Understanding the nuances of sample size calculation empowers you to elevate your study from simple data collection to informed decision-making.
Definition of Sample Size
So, what exactly is this crucial concept known as sample size? It is the subset of a larger group, the chosen few who bear the responsibility of representing the collective traits, behaviors, or opinions of the entire population. Whether it’s individuals, observations, or data points, the sample size is the lens through which researchers view the broader universe of their study. And like any well-crafted lens, the clarity of the image it provides is paramount to the accuracy of the insights drawn.
Why Sample Size Matters
Overlooking the importance of an appropriate sample size risk false conclusions, mirages of non-existent trends, or oversights of pivotal truths. An adequately sized sample size serves as the foundation for statistical significance, narrowing the margin of error and bolstering the confidence in the results. It’s the difference between a guess and an educated estimate, between a shaky hypothesis and robust evidence.
The size of your sample dictates the precision of your estimates and the power of your statistical tests—making it a guardian against the randomness of chance.
Key Factors Influencing Sample Size Calculation

Identifying the ideal sample size for your study isn’t guesswork but a meticulous process influenced by various factors. These key variables—population size, margin of error, confidence level, and more—interlock to form a precise mathematical framework guiding researchers to the number that will best serve their study’s goals.
The interplay between these elements is subtle yet powerful, as small adjustments can lead to significant changes in the required size of your sample.
Population Size
The larger the population size of your study, the more samples you need to collect. A larger population whispers the need for a larger sample size to ensure the echoes of your findings reverberate with reliability. Yet, as you’ll see, this is but one piece of the puzzle in the grand scheme of sample size calculation.
Margin of Error
The margin of error signifies uncertainty, acknowledging that our estimates are educated approximations, not pinpoint accuracies. As this margin decreases, the need for a larger sample size ascends, tightening the reins on variability and enhancing the precision of our estimates. It’s a delicate balancing act: striving for a smaller margin of error without inflating the resource cost of data collection to unsustainable heights.
Confidence Level
The confidence level signifies certainty, statistically assuring that the sample’s story likely holds true for the larger population. Higher confidence levels require larger samples, as they demand more evidence to back up their claims of representation.
It’s a measure of how firmly your study can stand behind its findings, a testament to the trustworthiness of the insights drawn from the data.
How to Calculate Sample Size

With the stage set and the actors of target population size, margin of error, and confidence level ready, how then do we direct the play to calculate the ideal sample size? The script is written in the language of statistics—a formulaic approach that considers these factors and translates them into a concrete number.
By adhering to this mathematical approach, researchers can determine a minimum sample size that ideally meets their study’s requirements, thus effectively helping them determine sample size.
Sample Size Formula
The sample size formula guides our calculation, standing as a beacon amidst numerous variables. These formulas are the brainchildren of statisticians who have distilled the essence of sample size calculation into equations such as Slovin’s and Fisher’s.
By plugging in values for population size, margin of error, and desired confidence level, these formulas yield the sample size needed to navigate the waters of statistical research with precision and confidence.
Using Z-Scores in Sample Size Calculation
Z-scores, statistical indicators, measure the deviation of our data points from the mean, which is closely related to the concept of standard deviation. They are integral to the sample size calculation, as they define the confidence level for survey results. A higher z-score indicates a greater need for accuracy, thereby nudging the required sample size upward.
It’s the statistical equivalent of adjusting the focus on a microscope, ensuring that the final image is as sharp and clear as possible.
Example Calculation
Let’s illustrate this with an example. Suppose we seek to understand the proportion of U.S. supermarket shoppers who identify as vegan. Aiming for a 95% confidence level and a margin of error of 5%, the formula tells us that we need at least 385 individuals to survey. This is the number that statistically stands up to scrutiny, ensuring that the voices we hear resonate with the collective chorus of the vegan community.
Tools for Calculating Sample Size

In the digital age, advanced tools can simplify the process of sample size calculation. From the simple to the complex, a range of calculators and software is at the researcher’s disposal, each promising to streamline the journey to the optimal sample size. Whether you’re a seasoned statistician or a newcomer to the field, these tools are invaluable allies in the pursuit of statistical precision. Some of the popular tools for sample size calculation include:
- Sample Size Calculator by Creative Research Systems
- Sample Size Calculator by Raosoft
- Sample Size Calculator by SurveyMonkey
These tools can help you determine the appropriate sample size for your research study, ensuring that your results are statistically significant and reliable.
Online Sample Size Calculators
Online sample size calculators are reliable tools for time-pressed researchers. By inputting key parameters like confidence level, population size, and margin of error, these calculators churn out the minimum number of samples required in mere moments.
For example, Qualtrics offers an easy-to-use calculator that transforms the complex into the accessible, supporting researchers as they determine their ideal survey sample size.
Statistical Software
For a more hands-on approach, statistical software like R or SPSS offer advanced tools for sample size calculation. These programs can handle a plethora of variables and cater to a variety of research designs, offering functions that stretch beyond the capabilities of basic calculators.
With these programs, the possibilities are as vast as the data sets they analyze, offering a high degree of customization and precision in the calculation process.
Best Practices for Determining Sample Size
Determining the best sample size is not just a matter of mathematical prowess; it’s also an art that requires an understanding of the study’s context and constraints. Best practices balance cost, accuracy, and study objectives, ensuring the chosen sample size reflects thoughtful consideration and research integrity, not just a numerical value.
Balancing Cost and Accuracy
Cost and accuracy often pull researchers in opposite directions. The push for precise results beckons for a larger sample size, while budget constraints demand frugality. The challenge lies in finding the sweet spot where the cost of data collection aligns with the need for reliable results.
An oversized sample may drain resources, while a sample too small risks the integrity of the study. It’s about making informed choices that respect both the sanctity of data and the realities of research funding.
Considering Study Goals
The study’s objectives should guide every researcher in determining the sample size. What are the goals of the research? What insights are sought? The sample size must be tailored to answer these questions effectively, ensuring that the findings are not just statistically sound but also meaningful and actionable.
Whether it’s capturing the nuances of qualitative data or the precision of quantitative metrics, the sample size must be a fit-for-purpose tool in the researcher’s kit.
Accounting for Non-Responses
Every researcher is familiar with the issue of non-responses, the silent gaps in the data collected. To mitigate this, prudent sample size planning includes a buffer—an estimation of the likely dropout rate, which adjusts the required number upward to compensate. This foresight ensures that the final sample size retains its representativeness and reliability, reflecting a true cross-section of the population despite the inevitable no-shows.
Common Mistakes in Sample Size Calculation

Even experienced researchers can fall into traps when calculating sample size. Common missteps—whether it’s underestimating the number needed, neglecting variability, or ignoring population diversity—can skew results and compromise the integrity of the study.
Awareness of these potential blunders is the first step towards avoiding them and ensuring the robustness of research outcomes.
Underestimating Sample Size
Underestimating sample size is a costly mistake that can obscure the actual effects and complicate interpretation. A sample size too small to detect significant effects is akin to a flashlight too dim to navigate the darkness—it leaves researchers stumbling towards false conclusions and missed opportunities for discovery.
Ignoring Variability
Variability enriches data, adding nuances to findings and depth to conclusions. Ignoring this diversity can lead to an underestimation of sample size, resulting in a bland and underpowered study.
It’s essential to consider the range of responses, the highs and lows, the outliers and the averages, to ensure that your sample size is robust enough to capture the full spectrum of your population’s characteristics.
Overlooking Population Diversity
In order to accurately portray the population, it’s crucial to consider diversity. A sample that mirrors the rich tapestry of the broader population ensures that findings are not only statistically valid but also culturally and contextually relevant.
Neglecting this diversity can lead to a skewed sample that fails to represent the nuances and variations within the population, thereby undermining the generalizability of the study’s results.
Applications of Sample Size in Different Fields
Although the principles of determining sample size are universal, their application varies dramatically across different study fields. From the granular focus of market research to the broad-scale implications of public health studies, understanding the context-specific nuances of sample size is pivotal.
Each field comes with its own set of challenges and requirements, making the ability to adapt sample size calculation strategies to the unique demands of each area a valuable skill for researchers.
Market Research
In the competitive field of market research, the sample size can be the determinant of a product’s success or failure. A well-calculated sample size can unveil the deepest insights into consumer behavior, preferences, and trends, guiding businesses towards informed decisions and strategic growth.
While not all surveys require the rigorousness of a statistically significant sample size, such as those for customer feedback, the need for accuracy remains critical when the stakes are high, and the market landscape is rapidly changing.
Healthcare Studies
Given the significant implications for life and health, accurate sample size calculations in healthcare studies are of ethical importance. Whether it’s evaluating the efficacy of a new treatment or gauging patient satisfaction, the sample size must be carefully calibrated to ensure that the results are reliable and can inform clinical decisions and policy-making.
Educational Research
Educational research greatly benefits from statistically significant sample sizes, forming the basis for meaningful changes based on feedback from students and faculty. By ensuring that the sample represents the diversity of the student body, educational institutions can make data-driven decisions that enhance the learning experience and foster an environment conducive to academic success.
As we draw the curtain on our exploration of sample size in research, it’s clear that the journey to determining the right number is both an art and a science. It requires a blend of statistical knowledge, practical understanding of research goals, and an appreciation of the field of study. By adhering to best practices, avoiding common mistakes, and leveraging the right tools, researchers can ensure that their findings are robust, reliable, and reflective of the population they seek to understand. May this guide serve as a compass in your research endeavors, leading you to the treasure trove of accurate and actionable insights.
Frequently Asked Questions
Why is sample size important in research.
Having an appropriate sample size is crucial in research because it impacts the accuracy of the findings, the statistical power, and the ability to generalize the results to the broader population, ultimately reducing the margin of error and increasing confidence in the outcomes.

How does population size affect sample size?
As population size increases, the sample size needed for representative and reliable research findings also increases, but there is a point where further population increase has a diminishing effect on the required sample size.
What is a margin of error and how does it impact sample size?
A smaller margin of error requires a larger sample size to achieve the desired precision in the estimates. This is because the margin of error represents the range within which the true value in the population is expected to fall.
Can I use an online calculator to determine sample size?
Yes, you can use online sample size calculators to estimate the appropriate sample size based on input parameters such as confidence level, population size, and margin of error.
What are common mistakes to avoid in sample size calculation?
To ensure accuracy and representativeness, common mistakes to avoid in sample size calculation include underestimating the needed sample size, ignoring data variability, and overlooking population diversity. Proper consideration of these factors is crucial for the validity of study results.
Popular searches
- How to Get Participants For Your Study
- How to Do Segmentation?
- Conjoint Preference Share Simulator
- MaxDiff Analysis
- Likert Scales
- Reliability & Validity
Request consultation
Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.
Looking for an online survey platform?
Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.
Catherine Chipeta
Source real human respondents swiftly and at scale through Conjointly.
Monthly newsletter
Get the latest updates about market research, automated tools, product testing and pricing techniques.
How many respondents do you need? Use our sample size calculator to get the right sample size for your next survey. We also answer frequently asked questions on sample size and provide suggestions to improve your surveys in this handy guide.
Conjointly's Respondent Recruitment Solutions
What is a sample and why sample size matters.
Researching the entire population is often not feasible due to many constraints. Instead, sampling is used, which is more practical for analysis and generates results more promptly.
A sample is a subset of individuals selected from the target population to estimate the characteristics of the population. Sample size is important because it determines the accuracy and quality of your survey results. It is especially important in market research as robust data is the key to unlocking meaningful and actionable insights about your target audience .
Want to identify the number of responses required for your survey quickly? Just use our sample size calculator.
If you want to learn more about the theories behind the calculator and sample size, we also compiled everything you need to know in this guide.
Sample Size Calculator
Four important components of sample size calculation.
Here are four key components you’ll need to understand in calculating your minimum sample size:
1. Population size
The population size is the total number of people in the population (target audience) you are looking to survey. For example, if you were surveying the general population of a city with 30,000 residents, the population size for your study is 30,000.
When surveying small populations, a finite population correction is used. You can use 100,000 with caution if you do not know the exact size of a large population; the sample size remains quite static over 100,000.
Get quality-assured responses directly from Conjointly
Reliable market research starts with quality sample. With access to millions of consumers from broad communities to deep-profiled niche markets, Conjointly provides numerous options to delivers quality respondents straight into your survey, starting at only $0.90 per response.
2. Confidence level
The confidence level indicates the probability that your confidence interval contains the true population value, if you were to repeat your study with a random sample selection .
For example, with a confidence level of 95%, your study could be repeated several times and your population would fall within the confidence interval on 95% of these occurrences.
The accuracy of your results is determined by how high your confidence interval is. You should also note that as your confidence level increases, so does your required sample size.
Conjointly’s default confidence level is 90% as it is most useful in business settings. However, you can easily adjust the confidence levels in your Conjointly reports.
3. Confidence interval (Margin of error)
The confidence interval is a range of values that are likely to contain your population value and is expressed in percentage points. For example, a confidence interval of ±2% means that your true population will lie either 2 percentage points above or below where it is shown in your results.
Your confidence interval will be higher or lower than your specified value as it is based on your actual sample proportion, rather than your estimated proportion. It also depends on how accurate the results you are seeking are (determined by your confidence level). A higher confidence level results in a wider confidence interval.
Check out the margin of error for different survey sample sizes under the standard 90% level of confidence.
4. Sample proportion
Your sample proportion (expressed as a percentage) indicates your estimated results and is calculated using a Quick Feedback study or previous survey results. Otherwise, 50% is a safe sample proportion to use without hindering the accuracy of your calculated sample size.
What is the formula for determining sample size?
The formula for calculating sample size is:
- n is the sample size,
- N is the population size,
- z is the confidence level (in percent, such as 90% = 0.9 ),
- p is the sample proportion (in percent, such as 50% = 0.5 ),
- e is the margin of error (in percent, such as 5% = 0.05 ).
What is a good sample size for a market research survey?
The ideal sample size for your study will depend on your population size, confidence level, and confidence interval. The survey design and methodology you use may also require you to adjust your sample size.
A good sample size will satisfy your criteria for accuracy in quantitative research results. It is usually determined by a combination of expected confidence, budget and resource availability for analysis.
Generally, the bigger the sample size, the more accurate your results will be. However, you should consider that large sample sizes are costlier and can complicate your study. You can use our sample size calculator to determine the minimum sample size for your project to ensure your survey is accurate and cost-effective.
What sample size do I need for 95 confidence?
Once you have selected your confidence level as 95%, you will need to determine your confidence interval and population size to calculate the sample size required for your study.
The sample size will be larger for 95% confidence than 90%, if all other factors remain the same.
Even though we recommend using 90% confidence level to achieve the right balance between cost and precision, you can increase it up to 99 percent. However, 99% confidence more than doubles the size of the required sample, compared to 90% confidence. This might produce unnecessary bloat of data for most quantitative research projects .
How do you find the sample size when given the margin of error?
To calculate sample size using your margin of error (confidence interval), you must also know your confidence level and population size.
The margin of error is usually expressed as ± value. This means your survey results can represent a range of values plus or minus the value of the margin of error.
Consider a survey that indicates that 40% of car owners in the USA would not consider the colour red for their next car. With a 5% margin of error, you should express your findings as 35-45% of car owners in the USA would not consider a red car. To gain more accurate insights , you could lower your margin of error to 2%, for example, and expect your findings to lie within a smaller confidence interval of 38-42%.
Why does the margin of error decrease as the sample size increases?
You will see in our sample size calculator, reducing your margin of error results in a large increase in recommended sample size.
It should be noted that this is not a linear relationship, increasing sample size will result in diminishing returns in the margin of error reduction. For example, the following chart illustrates the relationship between the margin of error and sample size, for a population of 1 million, seeking a 90% confidence interval, with a 0.5 sample proportion.
As shown above, moving from a 5% margin of error to a 1% margin of error would require a sample size over 20 times as large.
Why is a small sample size bad? Why is a larger sample size better? Why must sample size be greater than 30?
How do you justify a small sample size in quantitative research.
A small sample size can be justified when:
- The whole population is small. For example, in B2B research, when there are only 100 customers, then it is OK to sample ~30 to get a view of the opinions of the whole customer base.
- The cost of sampling is prohibitive.
Please note, it is not justifiable for most consumer surveys as they require a sample of hundreds of consumers from your product category, including current users and potential buyers. Conjointly provides numerous options and delivers quality respondents straight into your survey, starting at only $0.90 per response.
How does sample size affect validity of a study?
If sample size is not large enough for your study, the internal and external validity will be compromised and it can also result in cases of bias. A higher sample size results in more accurate results. Sample size is only one of many factors that affect the validity of your study.
You should also consider that data can still be useful in some instances even if you do not meet the required sample size for your study. For example, a customer satisfaction survey with open-ended questions can still provide meaningful insights as detailed consumer feedback is indispensable to market research.
Read these articles next:
How to test your figma designs with consumers.
Looking for a straightforward approach to validate your Figma designs with real consumers? Market Test allows you to gather quick human feedback directly on your Figma designs in under two hours — no tester recruitment or subscription needed.
Writing a Market Research Report: 5 Top Tips
Writing a market research report is a tough skill to master. Read our 5 top tips to get you started for writing a successful market research report.
Kano Model or MaxDiff Analysis?
Should you use Kano or MaxDiff for feature selection? We compare the two and draw practical recommendations.
Which one are you?
I am new to conjointly, i am already using conjointly, cookie consent.
Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.
For more information on Conjointly's use of cookies, please read our Cookie Policy .
Do you want to be updated on new features from Conjointly?
We send occasional emails to keep our users informed about new developments on Conjointly , such as new types of analysis and features.
Subscribe to updates from Conjointly
You can always unsubscribe later. Your email will not be shared with other companies.
Calculate your ideal sample size
Last updated
11 May 2023
Reviewed by
Miroslav Damyanov
Whether you're conducting market research , medical trials, or social science studies, understanding how to calculate your ideal sample size is essential for a successful research project .
Make research less tedious
Dovetail streamlines research to help you uncover and share actionable insights
- What is a sample size?
The sample size is the number of participants or data points a researcher needs to collect to make inferences about a larger population. Researchers use sample size to conclude a population.
For example, if a researcher wants to know the average height of adult males in the United States, the population would be all adult males in the US. The researcher would collect a sample of adult males, measure their height, and use this information to estimate the average size of all adult males in the US.
- Understanding sample size
Comprehending sample size is vital for conducting meaningful research that provides reliable and accurate results. Here are some key concepts that can help you better understand this critical aspect of research:
Representativeness
A sample is considered emblematic if it accurately reflects the population characteristics from which it’s drawn. To ensure representativeness, researchers should use appropriate sampling methods , such as random or stratified sampling .
Confidence level
This is the degree of certainty the results obtained from a sample accurately represent the population. A confidence level of 95% means there is a 95% chance the population parameter falls within the confidence interval .
The margin of error
The margin of error is the sampling error expected in the results due to using a cross-section instead of the entire population.
This refers to the ability of a study to detect an actual effect—if it exists. A study with high power has a greater chance of detecting a significant impact, while a study with low power may fail to see the effect, even if it exists.
Effect size
This is the magnitude of the difference between groups or the strength of the relationship between variables. The larger the effect size, the stronger the relationship.
By selecting an appropriate sample size, researchers can ensure their findings represent the population being studied and have the necessary level of precision and confidence.
Does having a statistically significant sample size matter?
A statistically significant sample size is the minimum number of participants required to detect a meaningful difference in the studied population. Statistical significance doesn't guarantee the validity or importance of the study results.
However, it provides evidence that the observed differences in the sample are unlikely coincidental. Therefore, a statistically significant sample size is vital in drawing valid conclusions and making informed decisions based on the study results.
- How to calculate sample size
Quantifying the ideal sample size requires careful consideration of several factors, including the research question , the desired accuracy, and the confidence level. Here's a general overview of how to calculate sample size:
Power analysis is a statistical method used to determine the ideal sample size based on the effect size, the significance level, and the study's desired power.
Confidence intervals are an analytical method used to estimate the range of values probable to contain the actual population variable with a certain confidence level.
The margin of error is a demographic method used to gauge the scope of values likely to have the true population parameter with a certain precision level.
The sample size calculation may differ depending on the statistical method and study design.
Sample size calculator .css-5oqtrw{background:transparent;border:0;color:#0C0020;cursor:pointer;display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;font-size:18px;font-weight:600;line-height:40px;outline:0;padding:0;} .css-17ofuq7{-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;background:transparent;border:0;color:inherit;cursor:pointer;-webkit-flex-shrink:0;-ms-flex-negative:0;flex-shrink:0;background:transparent;border:0;color:#0C0020;cursor:pointer;display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;font-size:18px;font-weight:600;line-height:40px;outline:0;padding:0;}.css-17ofuq7:disabled{opacity:0.6;pointer-events:none;} .css-7jswzl{-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;display:inline-block;height:28px;-webkit-box-pack:center;-ms-flex-pack:center;-webkit-justify-content:center;justify-content:center;width:28px;-webkit-text-decoration:none;text-decoration:none;}.css-7jswzl svg{height:100%;width:100%;margin-bottom:-4px;}
Maximize your research’s impact with the right sample size and get an accurate representation of your target audience.
Sample size
The total number of people whose opinion or behavior your sample will represent.
The probability that your sample accurately reflects the attitudes of your population. The industry standard is 95%.
The range (measured as a percentage) that your population’s responses may deviate from your sample’s.
Sample size formula
The formulas for calculating sample size depend on the statistical method used. Here are the commonly used formulas:
Power analysis : N = [(Zα/2 + Zβ) / ES] ^ 2
N = sample size
Zα/2 = the critical value of the standard normal distribution for a specified level of significance
Zβ = the critical value of the standard normal distribution for a particular power of the study
ES = the effect size, representing the magnitude of the difference or effect the study tries to detect
Confidence intervals : n = [(z * σ) / E] ^ 2
z = the critical value of the standard normal distribution for a specified level of confidence
σ = the standard deviation of the population
E = the desired margin of error
The margin of error : MOE = Z * (σ / √n)
Z = the z-score associated with the desired level of confidence (e.g., for 95% confidence, Z = 1.96)
n = the sample size
Margin of error calculator
Optimize your research’s impact when you improve the margin of error.
Margin of error
The number of people who took your survey.
These formulas are general guidelines, and researchers should consult with a statistician or use statistical software to ensure the sample size calculation is appropriate for their particular research question and study design.
Is a larger sample size better?
Yes, a larger sample size is better. A larger sample size increases the statistical power of a study, meaning it's more likely to detect actual effects or differences between groups.
Why use a sample size calculator?
A sample size calculator is used to determine the optimal sample size needed to obtain reliable and valid results in a study. It considers several factors, including the desired level of statistical power, the expected effect size, and the significance level.
Should you be using a customer insights hub?
Do you want to discover previous research faster?
Do you share your research findings with others?
Do you analyze research data?
Start for free today, add your research, and get to key insights faster
Editor’s picks
Last updated: 18 April 2023
Last updated: 27 February 2023
Last updated: 6 February 2023
Last updated: 15 January 2024
Last updated: 6 October 2023
Last updated: 5 February 2023
Last updated: 16 April 2023
Last updated: 7 March 2023
Last updated: 9 March 2023
Last updated: 12 December 2023
Last updated: 11 March 2024
Last updated: 13 May 2024
Latest articles
Related topics, .css-je19u9{-webkit-align-items:flex-end;-webkit-box-align:flex-end;-ms-flex-align:flex-end;align-items:flex-end;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;-webkit-box-flex-wrap:wrap;-webkit-flex-wrap:wrap;-ms-flex-wrap:wrap;flex-wrap:wrap;-webkit-box-pack:center;-ms-flex-pack:center;-webkit-justify-content:center;justify-content:center;row-gap:0;text-align:center;max-width:671px;}@media (max-width: 1079px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}}@media (max-width: 799px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}} decide what to .css-1kiodld{max-height:56px;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;}@media (max-width: 1079px){.css-1kiodld{display:none;}} build next, decide what to build next.

Users report unexpectedly high data usage, especially during streaming sessions.

Users find it hard to navigate from the home page to relevant playlists in the app.

It would be great to have a sleep timer feature, especially for bedtime listening.

I need better filters to find the songs or artists I’m looking for.
Log in or sign up
Get started for free
.webp)
Research 101
How to Calculate Your Sample Size Using a Sample Size Formula

Patrick Hyland
November 25, 2021
Advanced Research
Maria Noesi
How To Calculate Your Sample Size Using a Sample Size Formula
Calculate sample size with a margin of error using these simple sample size formulas for your market research.

Anika Nishat
March 22, 2024
Calculating your sample size
During the course of your market research , you may be unable to reach the entire population you want to gather data about. While larger sample sizes bring you closer to a 1:1 representation of your target population, working with them can be time-consuming, expensive, and inconvenient. However, small samples risk yielding results that aren’t representative of the target population.
Luckily, you can easily identify an ideal subset that represents the population and produces strong, statistically significant results that don’t gobble up all of your resources. In this article, we'll teach how to calculate sample size with a margin of error to identify that subset.
Five steps to finding your sample size
- Define population size or number of people
Designate your margin of error
- Determine your confidence level
- Predict expected variance
- Finalize your sample size
Follow these five steps to ensure you get the right selection size for your research needs.
Download: The State of AI in Market Research

Define the size of your population
Your sample size needs will differ depending on the true population size or the total number of people you’re looking to conclude on. That’s why determining the minimum number of individuals required to represent your selection is an important first step.
Defining the size of your population can be easier said than done. While there is a lot of population data available, you may be targeting a complex population or for which no reliable data currently exists.
Knowing the size of your population is more important when dealing with relatively small, easy-to-measure groups of people. If you’re dealing with a larger population, take your best estimate, and roll with it.
This is the first step in a sample size formula, yielding more accurate results than a simple estimate – and accurately reflecting the population.

Random sample errors are inevitable whenever you’re using a subset of your total population. Be confident that your results are accurate by designating how much error you intend to permit: that’s your margin of error.
Sometimes called a "confidence interval," a margin of error indicates how much you’re willing for your sample mean to differ from your population mean . It’s often expressed alongside statistics as a plus-minus (±) figure, indicating a range which you can be relatively certain about.
For example, say you take a sample proportion of your colleagues with a designated 3% margin of error and find that 65% of your office uses some form of voice recognition technology at home. If you were to ask your entire office, you could be sure that in reality, as low as 62% and as high as 68% might use some form of voice recognition technology at home.

Determine how confident you can be
Your confidence level reveals how certain you can be that the true proportion of the total population would pick an answer within a particular range. The most common confidence levels are 90%, 95%, and 99%. Researchers most often employ a 95% confidence level.
Don’t confuse confidence levels for confidence intervals (i.e., mean of error). Remember the distinction by thinking about how the concepts relate to each other to sample more confidently.
In our example from the previous step, when you put confidence levels and intervals together, you can say you’re 95% certain that the true percentage of your colleagues who use voice recognition technology at home is within ± three percentage points from the sample mean of 65%, or between 62% and 68%.
Your confidence level corresponds to something called a "z-score." A z-score is a value that indicates the placement of your raw score (meaning the percent of your confidence level) in any number of standard deviations below or above the population mean.
Z-scores for the most common confidence intervals are:
- 90% = 2.576
- 99% = 2.576
If you’re using a different confidence interval, use this z-score table to find the correct value for your calculation.

Decide the variance you expect
The last thing you’ll want to consider when calculating your sample size is the amount of variance you expect to see among participant responses.
Standard deviation measures how much individual sample data points deviate from the average population.
Don’t know how much variance to expect? Use the standard deviation of 0.5 to make sure your group is large enough.
Read: Best Practices for Writing Discussion Guides (eBook)

Finding your ideal sample size
Now that you know what goes into determining sample size, you can calculate sample size online. Or, calculate it the old-fashioned way: by hand.
Below, find two sample size calculations - one for the known population proportion and one for the unknown population.
Sample size for known population

Sample size for unknown population

Here’s how the calculations work out for our voice recognition technology example in an office of 500 people, with a 95% confidence level and 5% margin of error:

There you have it! 197 respondents are needed.
You can tweak some things if that number is too big to swallow.
Try increasing your margin of error or decreasing your confidence level which will reduce the number of respondents necessary but increase chances for errors.
Summing Up Sample Size
Calculating sample size sounds complicated - but, utilizing an easy sample size formula and even calculators are now available to make this tedious part of research faster!
Now, it's time to recruit your sample and run a focus group or even a customer satisfaction survey . Whatever you decide, you now have the information needed to make decisions with confidence.
Want to whip your research skills into shape? Check out our go-to eBook on writing discussion guides !

Want to Prevent Culture Drift? Take a Temporal Perspective

Multi-Language Conversations: Unlocking Global Research for All

Rethinking insights: The rise of conversational research
Stay up-to date..
Stay ahead of the curve. Get it all. Or get what suits you. Our 101 material is great if you’re used to working with an agency. Are you a seasoned pro? Sign up to receive just our advanced materials.

Get insights in your inbox . Sign up to stay up to date on the latest research tactics and breakthroughs.

©All Rights Reserved 2024. Read our Privacy policy
No data capture tricks. No bull SEO content for ranking. Just good, solid, honest, research ed.
By entering your email address, you agree to receive marketing communications in accordance with our privacy policy.

Request a demo
Dive Deeper
Sample Size Calculator
What is sample size, sample size formula.
| Desired Confidence Level | Z-Score |
|---|---|
| 70% | 1.04 |
| 75% | 1.15 |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.645 |
| 91% | 1.70 |
| 92% | 1.75 |
| 93% | 1.81 |
| 94% | 1.88 |
| 95% | 1.96 |
| 96% | 2.05 |
| 97% | 2.17 |
| 98% | 2.33 |
| 99% | 2.576 |
| 99.5% | 2.807 |
| 99.9% | 3.29 |
| 99.99% | 3.89 |
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian J Psychol Med
- v.42(1); Jan-Feb 2020
Sample Size and its Importance in Research
Chittaranjan andrade.
Clinical Psychopharmacology Unit, Department of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bengaluru, Karnataka, India
The sample size for a study needs to be estimated at the time the study is proposed; too large a sample is unnecessary and unethical, and too small a sample is unscientific and also unethical. The necessary sample size can be calculated, using statistical software, based on certain assumptions. If no assumptions can be made, then an arbitrary sample size is set for a pilot study. This article discusses sample size and how it relates to matters such as ethics, statistical power, the primary and secondary hypotheses in a study, and findings from larger vs. smaller samples.
Studies are conducted on samples because it is usually impossible to study the entire population. Conclusions drawn from samples are intended to be generalized to the population, and sometimes to the future as well. The sample must therefore be representative of the population. This is best ensured by the use of proper methods of sampling. The sample must also be adequate in size – in fact, no more and no less.
SAMPLE SIZE AND ETHICS
A sample that is larger than necessary will be better representative of the population and will hence provide more accurate results. However, beyond a certain point, the increase in accuracy will be small and hence not worth the effort and expense involved in recruiting the extra patients. Furthermore, an overly large sample would inconvenience more patients than might be necessary for the study objectives; this is unethical. In contrast, a sample that is smaller than necessary would have insufficient statistical power to answer the primary research question, and a statistically nonsignificant result could merely be because of inadequate sample size (Type 2 or false negative error). Thus, a small sample could result in the patients in the study being inconvenienced with no benefit to future patients or to science. This is also unethical.
In this regard, inconvenience to patients refers to the time that they spend in clinical assessments and to the psychological and physical discomfort that they experience in assessments such as interviews, blood sampling, and other procedures.
ESTIMATING SAMPLE SIZE
So how large should a sample be? In hypothesis testing studies, this is mathematically calculated, conventionally, as the sample size necessary to be 80% certain of identifying a statistically significant outcome should the hypothesis be true for the population, with P for statistical significance set at 0.05. Some investigators power their studies for 90% instead of 80%, and some set the threshold for significance at 0.01 rather than 0.05. Both choices are uncommon because the necessary sample size becomes large, and the study becomes more expensive and more difficult to conduct. Many investigators increase the sample size by 10%, or by whatever proportion they can justify, to compensate for expected dropout, incomplete records, biological specimens that do not meet laboratory requirements for testing, and other study-related problems.
Sample size calculations require assumptions about expected means and standard deviations, or event risks, in different groups; or, upon expected effect sizes. For example, a study may be powered to detect an effect size of 0.5; or a response rate of 60% with drug vs. 40% with placebo.[ 1 ] When no guesstimates or expectations are possible, pilot studies are conducted on a sample that is arbitrary in size but what might be considered reasonable for the field.
The sample size may need to be larger in multicenter studies because of statistical noise (due to variations in patient characteristics, nonspecific treatment characteristics, rating practices, environments, etc. between study centers).[ 2 ] Sample size calculations can be performed manually or using statistical software; online calculators that provide free service can easily be identified by search engines. G*Power is an example of a free, downloadable program for sample size estimation. The manual and tutorial for G*Power can also be downloaded.
PRIMARY AND SECONDARY ANALYSES
The sample size is calculated for the primary hypothesis of the study. What is the difference between the primary hypothesis, primary outcome and primary outcome measure? As an example, the primary outcome may be a reduction in the severity of depression, the primary outcome measure may be the Montgomery-Asberg Depression Rating Scale (MADRS) and the primary hypothesis may be that reduction in MADRS scores is greater with the drug than with placebo. The primary hypothesis is tested in the primary analysis.
Studies almost always have many hypotheses; for example, that the study drug will outperform placebo on measures of depression, suicidality, anxiety, disability and quality of life. The sample size necessary for adequate statistical power to test each of these hypotheses will be different. Because a study can have only one sample size, it can be powered for only one outcome, the primary outcome. Therefore, the study would be either overpowered or underpowered for the other outcomes. These outcomes are therefore called secondary outcomes, and are associated with secondary hypotheses, and are tested in secondary analyses. Secondary analyses are generally considered exploratory because when many hypotheses in a study are each tested at a P < 0.05 level for significance, some may emerge statistically significant by chance (Type 1 or false positive errors).[ 3 ]
INTERPRETING RESULTS
Here is an interesting question. A test of the primary hypothesis yielded a P value of 0.07. Might we conclude that our sample was underpowered for the study and that, had our sample been larger, we would have identified a significant result? No! The reason is that larger samples will more accurately represent the population value, whereas smaller samples could be off the mark in either direction – towards or away from the population value. In this context, readers should also note that no matter how small the P value for an estimate is, the population value of that estimate remains the same.[ 4 ]
On a parting note, it is unlikely that population values will be null. That is, for example, that the response rate to the drug will be exactly the same as that to placebo, or that the correlation between height and age at onset of schizophrenia will be zero. If the sample size is large enough, even such small differences between groups, or trivial correlations, would be detected as being statistically significant. This does not mean that the findings are clinically significant.
Financial support and sponsorship
Conflicts of interest.
There are no conflicts of interest.
- Sign Up Now
- -- Navigate To -- CR Dashboard Connect for Researchers Connect for Participants
- Log In Log Out Log In
- Recent Press
- Papers Citing Connect
- Connect for Participants
- Connect for Researchers
- Connect AI Training
- Managed Research
- Prime Panels
- MTurk Toolkit
- Health & Medicine
- Conferences
- Knowledge Base
- A Researcher’s Guide To Statistical Significance And Sample Size Calculations
Determining Sample Size: How Many Survey Participants Do You Need?

Quick Navigation:
How to calculate a statistically significant sample size in research, determining sample size for probability-based surveys and polling studies, determining sample size for controlled surveys, determining sample size for experiments, how to calculate sample size for simple experiments, an example sample size calculation for an a/b test, what if i don’t know what size difference to expect, part iii: sample size: how many participants do i need for a survey to be valid.
In the U.S., there is a Presidential election every four years. In election years, there is a steady stream of polls in the months leading up to the election announcing which candidates are up and which are down in the horse race of popular opinion.
If you have ever wondered what makes these polls accurate and how each poll decides how many voters to talk to, then you have thought like a researcher who seeks to know how many participants they need in order to obtain statistically significant survey results.
Statistically significant results are those in which the researchers have confidence their findings are not due to chance . Obtaining statistically significant results depends on the researchers’ sample size (how many people they gather data from) and the overall size of the population they wish to understand (voters in the U.S., for example).
Calculating sample sizes can be difficult even for expert researchers. Here, we show you how to calculate sample size for a variety of different research designs.
Before jumping into the details, it is worth noting that formal sample size calculations are often based on the premise that researchers are conducting a representative survey with probability-based sampling techniques. Probability-based sampling ensures that every member of the population being studied has an equal chance of participating in the study and respondents are selected at random.
For a variety of reasons, probability sampling is not feasible for most behavioral studies conducted in industry and academia . As a result, we outline the steps required to calculate sample sizes for probability-based surveys and then extend our discussion to calculating sample sizes for non-probability surveys (i.e., controlled samples) and experiments.
Determining how many people you need to sample in a survey study can be difficult. How difficult? Look at this formula for sample size.
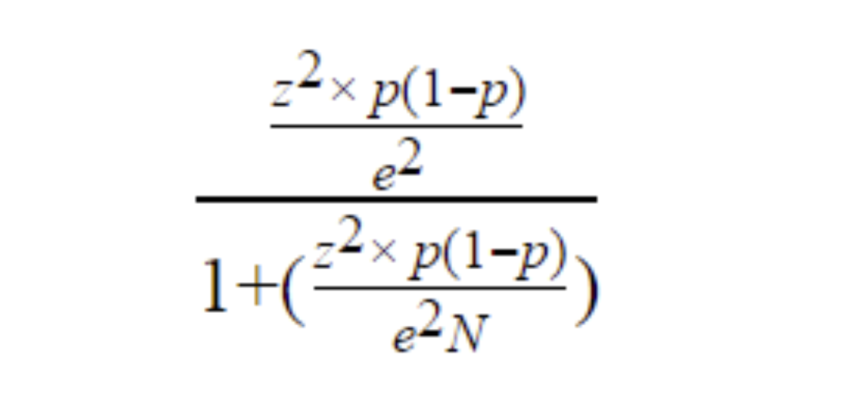
No one wants to work through something like that just to know how many people they should sample. Fortunately, there are several sample size calculators online that simplify knowing how many people to collect data from.
Even if you use a sample size calculator, however, you still need to know some important details about your study. Specifically, you need to know:
- What is the population size in my research?
Population size is the total number of people in the group you are trying to study. If, for example, you were conducting a poll asking U.S. voters about Presidential candidates, then your population of interest would be everyone living in the U.S.—about 330 million people.
Determining the size of the population you’re interested in will often require some background research. For instance, if your company sells digital marketing services and you’re interested in surveying potential customers, it isn’t easy to determine the size of your population. Everyone who is currently engaged in digital marketing may be a potential customer. In situations like these, you can often use industry data or other information to arrive at a reasonable estimate for your population size.
- What margin of error should you use?
Margin of error is a percentage that tells you how much the results from your sample may deviate from the views of the overall population. The smaller your margin of error, the closer your data reflect the opinion of the population at a given confidence level.
Generally speaking, the more people you gather data from the smaller your margin of error. However, because it is almost never feasible to collect data from everyone in the population, some margin of error is necessary in most studies.
- What is your survey’s significance level?
The significance level is a percentage that tells you how confident you can be that the true population value lies within your margin of error. So, for example, if you are asking people whether they support a candidate for President, the significance level tells you how likely it is that the level of support for the candidate in the population (i.e., people not in your sample) falls within the margin of error found in your sample.
Common significance levels in survey research are 90%, 95%, and 99%.
Once you know the values above, you can plug them into a sample size formula or more conveniently an online calculator to determine your sample size.
The table below displays the necessary sample size for different sized populations and margin of errors. As you can see, even when a population is large, researchers can often understand the entire group with about 1,000 respondents.



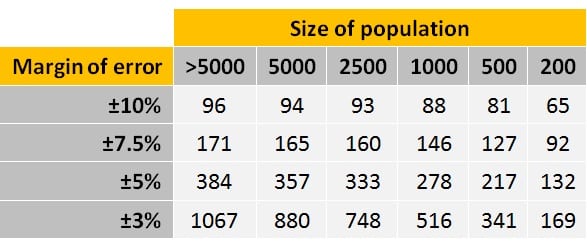



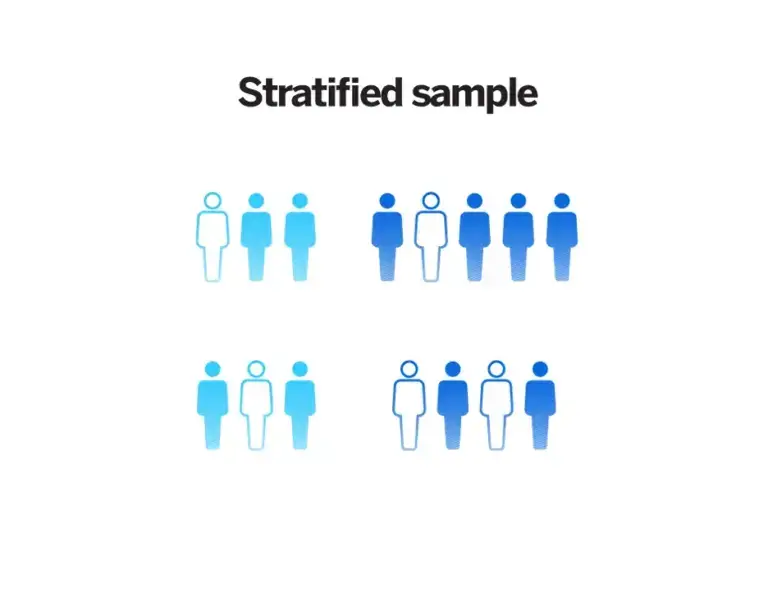
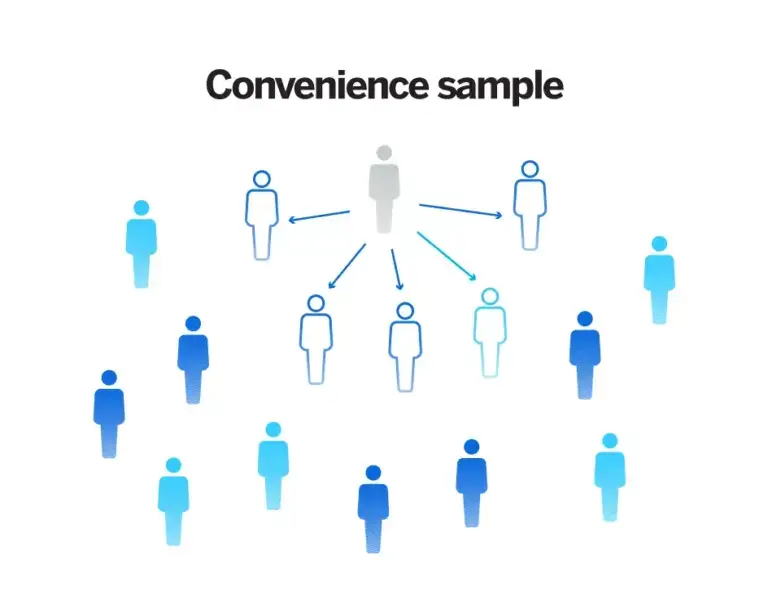
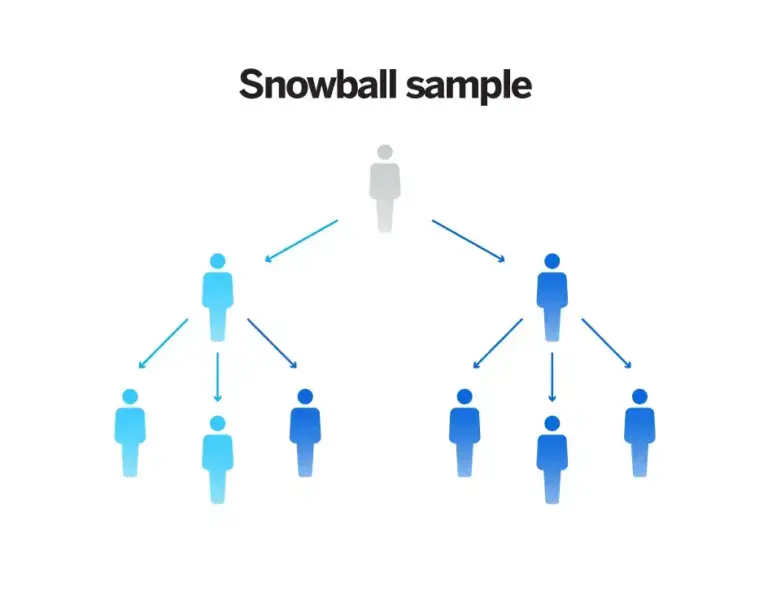
IMAGES
VIDEO
COMMENTS
Find your Z-score. The Z-score is a constant value automatically set based on your confidence level. It indicates the "standard normal score," or the number of standard deviations between any selected value and the average/mean of the population.
3) Plan for a sample that meets your needs and considers your real-life constraints. Every research project operates within certain boundaries - commonly budget, timeline and the nature of the sample itself. When deciding on your sample size, these factors need to be taken into consideration.
Stage 2: Calculate sample size. Now that you've got answers for steps 1 - 4, you're ready to calculate the sample size you need. This can be done using an online sample size calculator or with paper and pencil. 1. Find your Z-score. Next, you need to turn your confidence level into a Z-score.
Some factors that affect the width of a confidence interval include: size of the sample, confidence level, and variability within the sample. There are different equations that can be used to calculate confidence intervals depending on factors such as whether the standard deviation is known or smaller samples (n 30) are involved, among others.
2.58. Put these figures into the sample size formula to get your sample size. Here is an example calculation: Say you choose to work with a 95% confidence level, a standard deviation of 0.5, and a confidence interval (margin of error) of ± 5%, you just need to substitute the values in the formula: ( (1.96)2 x .5 (.5)) / (.05)2.
In the existing research literatures, the sample size statement is written in various styles. This paper recommends for the sample size statement to start by reminding the readers or reviewers about the main objective of study. Hence, this paper recommends all the elements from Step 1 until Step 4 (study objective, appropriate statistical ...
Sample size is the number of observations or data points collected in a study. It is a crucial element in any statistical analysis because it is the foundation for drawing inferences and conclusions about a larger population. When delving into the world of statistics, the phrase "sample size" often pops up, carrying with it the weight of ...
For education surveys, we recommend getting a statistically significant sample size that represents the population.If you're planning on making changes in your school based on feedback from students about the institution, instructors, teachers, etc., a statistically significant sample size will help you get results to lead your school to success.
There are many "human" factors that go into selecting a sample size including budget, prior research (you can use a sample size from previous research) and tables constructed from previous research. How to use Excel Sampling to find a Sample: Steps. Step 1: Enter your data items into Excel. You can enter your data into rows or columns.
Sample size calculation formula. The equation that our sample size calculator uses is: n_1 = Z^2\cdot p \cdot \frac {1-p} {\mathrm {ME}^2} n1 = Z 2 ⋅ p ⋅ ME21 − p. where: Z Z — The z-score associated with the confidence level you chose. Our statistical significance calculator calculates this value automatically, but if you want to learn ...
Determining the right sample size for your survey is one of the most common questions researchers ask when they begin a market research study. Luckily, sample size determination isn't as hard to calculate as you might remember from an old high school statistics class. Before calculating your sample size, ensure you have these things in place:
An appropriate sample size is crucial for achieving statistically significant and reliable research results, balancing accuracy and practicality. Key factors influencing sample size calculation include population size, margin of error, and confidence level, which combine to determine the necessary sample size for robust data representation.
The ideal sample size for your study will depend on your population size, confidence level, and confidence interval. The survey design and methodology you use may also require you to adjust your sample size.. A good sample size will satisfy your criteria for accuracy in quantitative research results.
A small sample size can result in unreliable results, while a large sample size can waste resources and time. Therefore, calculating your ideal sample size is crucial to ensure your study provides reliable and valid results. Whether you're conducting market research, medical trials, or social science studies, understanding how to calculate your ...
A z-score is a value that indicates the placement of your raw score (meaning the percent of your confidence level) in any number of standard deviations below or above the population mean. Z-scores for the most common confidence intervals are: 90% = 2.576. 95% = 1.96. 99% = 2.576. If you're using a different confidence interval, use this z ...
Stage 2: Calculate sample size. Now that you've got answers for steps 1 - 4, you're ready to calculate the sample size you need. This can be done using the online sample size calculator above or with paper and pencil. 5. Find your Z-score. Next, you need to turn your confidence level into a Z-score.
It is the ability of the test to detect a difference in the sample, when it exists in the target population. Calculated as 1-Beta. The greater the power, the larger the required sample size will be. A value between 80%-90% is usually used. Relationship between non-exposed/exposed groups in the sample.
Sample size is a term used in market research to define the number of subjects included in a survey, study, or experiment. In surveys with large populations, sample size is incredibly important. The reason for this is because it's unrealistic to get answers or results from everyone - instead, you can take a random sample of individuals that ...
You can use this free sample size calculator to determine the sample size of a given survey per the sample proportion, margin of error, and required confidence level. ... The accuracy of the research outputs also varies according to the percentage of the sample that chooses a given response. If 98% of the population select "Yes" and 2% select ...
The sample size for a study needs to be estimated at the time the study is proposed; too large a sample is unnecessary and unethical, and too small a sample is unscientific and also unethical. The necessary sample size can be calculated, using statistical software, based on certain assumptions. If no assumptions can be made, then an arbitrary ...
The reason why sample size calculators for experiments are hard to find is simple: experiments are complex and sample size calculations depend on several factors. The guidance we offer here is to help researchers calculate sample size for some of the simplest and most common experimental designs: t-tests, A/B tests, and chi square tests.
A good maximum sample size is usually around 10% of the population, as long as this does not exceed 1000. For example, in a population of 5000, 10% would be 500. In a population of 200,000, 10% would be 20,000. This exceeds 1000, so in this case the maximum would be 1000. Even in a population of 200,000, sampling 1000 people will normally give ...
Our sample size calculator will work out the answer based on your project's scope, participant characteristics, researcher expertise, and methodology. Just answer 4 quick questions to get a super actionable, data-backed recommendation for your next study. Do the math How it works.
By accurately estimating the effective sample size, researchers can enhance the efficiency and validity of Bayesian analyses in the context of historical data borrowing. Keywords: Power prior method; Information borrowing ... Register to receive personalised research and resources by email. Sign me up. Taylor and Francis Group Facebook page ...
Sampling: The process and method of selecting your sample; Free eBook: 2024 Market Research Trends. Why is sampling important? Although the idea of sampling is easiest to understand when you think about a very large population, it makes sense to use sampling methods in research studies of all types and sizes.