1.1 explain the use of different problem solving techniques

We write, we don’t plagiarise! Every answer is different no matter how many orders we get for the same assignment. Your answer will be 100% plagiarism-free, custom written, unique and different from every other student.

I agree to receive phone calls from you at night in case of emergency

Please share your assignment brief and supporting material (if any) via email here at: [email protected] after completing this order process.

Important Note: Your order at Assignment Experts is protected by Consumer Law UK; also, we use 3rd party merchant support “PayPal” for all online transactions to provide you with the most protected online buying experience.

Custom-Written, AI & Plagiarism-Free with Passing "Guaranteed"

1.1 Explain the use of different problem-solving techniques

Unit 34: contribute to the improvement of business performance, unit reference number: d/506/1911 qcf level: 3, credit value: 6, guided learning hours: 33, unit type: competence.

Unit summary

Problem solving and decision-making are important skills for business and life. Problems that arise in any aspect of a business could lead to disagreements, work errors, poor quality and loss of profits. There are processes and techniques to improve decision-making, the quality of potential solutions and decisions that deliver tangible benefits and an overall improvement in the efficiency and effectiveness of the business.

This unit covers the knowledge and skills required to solve problems in any context and contribute to the achievement of process and quality improvements. You will consider the types of problems that can arise at work and ways that these can be resolved using a decision-making approach. You will be required to contribute to the identification of the root cause of problems, examine the key stages in the decision- making process and determine the corrective actions that need to be implemented to meet organisation, legal or regulatory requirements.

You will use a variety of business improvement models, such as Kaizen and Six Sigma, and a range of techniques including 5 Whys, Boston Matrix, Ishakawa (Fishbone) Diagram to solve problems and develop a resource plan (master schedule) that will establish quantifiable objectives and targets for the improvement activity. You will contribute to the development of standard operating procedures (SOPs) that could relate to the maintenance of equipment, health and safety practices and procedures, process procedures or quality improvements

Learning outcomes and assessment criteria

To pass this unit, the learner needs to demonstrate that they can meet all the learning outcomes for the unit. The assessment criteria outline the requirements the learner is expected to meet to achieve the unit.

Unit amplification: Unit 34: Contribute to the Improvement of Business Performance

Ac1.1: explain the use of different problem-solving techniques.

• Problem-solving techniques: brainstorming, workshops; SWOT analysis (strengths, weaknesses, opportunities, threats); PESTLE analysis (political, economic, social, technological, legal, environmental); risk analysis, RCA (root cause analysis); Pareto Principle; PDCA (plan, do, check, act); 5-why analysis
• Use: e.g. to create new ideas, to improve decision-making, to improve quality of decisions
• Organisational and legal constraints: contracts and agreements; employee relations; skills and experience of staff; existing policies and procedures; budget; technology; values and ethics; legal or regulatory barriers, e.g. health and safety, equality, data protection
• Internal: team leader, oversees and takes responsibility for problem solving; team members, affected by the problem, provide feedback, options, solutions; senior managers, agree solutions and finance
• External: potential users/customers ,feedback; suppliers, feedback; competitors, sales; regulatory bodies, compliance checking

AC1.2: Explain the organisational and legal constraints relating to problem-solving

Ac1.3: describe the role of stakeholders in problem-solving, ac1.4: describe the steps in the business decision-making process.

• Identify the problem: recognising the problem, symptoms, recognising waste
• Gather data and information: fact finding, use of management reports and performance indicators
• Consider options and solutions: advantages and disadvantages of each option; potential problems and risks; analysis, 5 Whys, cause and effect
• Adopt the recommendation: make the decision, responsibility for decision
• Implications: how the solution will be implemented; responsibility for implementation; risks of implementing the solution; avoiding recurrence of problem(s); developing monitoring system; communication (internal, external)
• Continuous improvement: definition
• Purpose: e.g. improve standards, improve quality, improve productivity, reduce waste
• Benefits: business efficiency, effective team working, motivated employees, effective resource management, customer satisfaction

AC1.5: Analyse the implications of adopting recommendations and implementing decisions to solve business problems

Ac2.1: describe the purpose and benefits of continuous improvement, ac2.2: analyse the features, use and constraints of different continuous improvement techniques and models.

Continuous improvement models: Kaizen, PDCA, Six Sigma, DMAIC

• Features: structured approach to problem solving, improvements based on smaller changes, ideas generated from within the organisation
• Uses: continuous improvement, innovation, develop a design, reduce waste, improvement in productivity and efficiency
• Constraints: commitment over time, change in mind-set, resistance to change

Continuous improvement techniques

• Features: master schedule, SIPOC, problem and goal statements, time bound visual plans, commercial and bespoke software task management systems, responsibility and accountability
• Use: to determine the ‘what, why, how and when’, to provide structure
• Constraints: limits of stakeholder engagement, timescales
• Features: key stakeholder involvement, RACI Matrix, Boston Matrix
• Use: to capture ideas, to remove barriers, to ensure individual buy- in and engagement throughout the process, to prioritise areas to be addressed and timescales required, to identify the significance/extent of a problem
• Constraints: networking skills, communication skills, lack of ownership or accountability, lack of hard data/evidence, differing attitudes and objectives
• Features: effective communication processes, visual aids, e.g. signs, charts, display or performance boards, company handbooks, key performance indicators, standard operating procedures, voice of the customer
• Use: to provide current status at a glance, standardisation of approach, identification of non-standard approaches, to increase employee involvement and motivation, to raise productivity and quality, to facilitate faster decision-making
• Constraints: currency and value if not maintained, timely dissemination of information to participants
• Features: brainstorming, affinity diagram, Ishakawa Fishbone diagram, 5 Whys, RCA, data gathering
• Use: to eliminate problems, to treat the cause not the symptoms, to add value by improving business processes, e.g. efficiency, service, health and safety
• Constraints: timescales, knowledge of the problem, desire to jump to the solution
• Brainstorm costs and benefits: costs, actual costs, unexpected costs; benefits, staff, stakeholders, environment, business efficiency, service
• Assign monetary value to benefits: minimising future loss, return on investment, profit
• Importance of feedback: gathers different viewpoints, enables reflection, resolves further problems, confirms solution is fit-for- purpose, celebrates success, motivational, maintains continuous improvement cycle

AC2.3: Explain how to carry out a cost-benefit analysis

Ac2.4: explain the importance of feedback from customers and other stakeholders in continuous improvement, information for tutors: unit 34: contribute to the improvement of business performance, suggested resources.

Evans V – Key Strategy Tools: The 80+ Tools for Every Manager to Build a Winning Strategy , 1st Edition (FT Publishing International, 2013)

ISBN 9780273778868

Liker J – The Toyota Way: Fourteen Management Principles from the World’s Greatest Manufacturer , Reissue Edition (McGraw-Hill Education, 2004)

ISBN 9780071392310

Weiss AE – Key Business Solutions : Essential Problem-Solving Tools and Techniques That Every Manager Needs to Know, 1st Edition (FT Prentice Hall, 2011) ISBN 9780273750291

www.bbc.co.uk/news/business – BBC website: business news section www.bized.co.uk – a business education resource site

www.business.com – business skills for personal and professional development

www.businesscasestudies.co.uk – business studies learning resources including the ‘Times 100’ business case studies

www.thecqi.org – quality management approach based on planning, measurement and improvement

www.efqm.org – European Foundation for Quality Management: helping European organisations learn from each other and improve performance

www.managers.org.uk – professional body promoting management and leadership excellence

www.mindtools.com – business skills that help you excel at work

This unit is internally assessed. To pass this unit the evidence that the learner presents for assessment must demonstrate that they have met the required standard specified in the learning outcomes and assessment criteria and the requirements of the Assessment Strategy.

To ensure that the assessment tasks and activities enable learners to produce valid, sufficient, authentic and appropriate evidence that meets the assessment criteria, centres should apply the Unit Assessment guidance and the requirements of the Assessment Strategy below.

Wherever possible, centres should adopt a holistic approach to assessing the units in the qualification. This gives the assessment process greater rigour and minimises repetition, time and the burden of assessment on all parties involved in the process.

Unit assessment requirements

This unit must be assessed in the workplace in accordance with the Skills CFA Assessment Strategy for Business Administration, Customer Service and Management and Leadership, in Annexe A . Simulation is not allowed for this unit.

All evidence of occupational competence should be generated through performance under workplace conditions; this includes evidence of achievement for knowledge- based learning outcomes and associated assessment criteria.

Unit assessment guidance

This guidance supports assessors in making decisions about how best to assess each unit and the evidence needed to meet the requirements. Centres can adapt the guidance as appropriate for learners and the particular assessment context.

Possible sources of evidence for demonstrating achievement of this unit could be through direct observation, professional discussion or review of work products relating to the improvement of business performance. A holistic approach to assessment is recommended.

For AC1.1; AC1.2; AC1.3; AC1.4 and AC2.2, learners could provide examples of the types of problems that exist in their workplace with an explanation of the techniques used to determine the cause. Learners could provide a description of the stakeholders involved in this process and their roles. Learners could explain the limitations of problem-solving from an organisation and legal point of view.

Professional discussion or reflective accounts could be used demonstrate the learners’ achievement of the knowledge-based criteria that could also link to AC2.1; AC2.3 and AC2.4. Learners could describe the purpose and benefits of continuous improvements in their work environment and provide an analysis of the features, use and limitations of a range of business improvement techniques and models and justify the preferred solution. This could also be linked to the competence-based criteria. Learners could provide a cost-benefit analysis and provide an explanation of how this was carried out. Work products could include evidence of minutes of meetings, process maps and diagrams, master schedules, feedback from stakeholders, presentation notes, reports to management/sponsors, resource plans and performance measures relating to cost, quality, delivery and responsibilities, analysis and evaluation, standard operating procedures showing agreed changes.

Evidence could also include photographic evidence of Kaizen events and information centres. This assessment method could be used for all competence-based assessment criteria in learning outcomes 3 and 4 to demonstrate the learner’s use of a range of business improvement techniques and models when solving business problems and contributing to improvement activities.

For AC1.5 and AC2.3 learners could analyse the various business improvement models available in their work environment. Learners could review product evidence of the possible solutions to problems, such as minutes of meetings, diagrams and process maps and workshop recommendations to provide an analysis of the implications involved in adopting recommendations and decisions

To provide corroborating evidence for the assessment criteria in learning outcome 3 and 4 a reflective account could be used to document the learner’s own role, responsibilities and skills. For example the learner could reflect on the criteria or standards they used to evaluate the scope of a particular problem, discuss the advantages and disadvantages of the different courses of action to solve the problem and explain the rationale for action chosen to solve the problem.

Witness testimony could be used to support the evidence from direct observation or work products.

Evidence of Recognition of Prior Learning (RPL) can be used in the unit to confirm competence. Wherever possible, the learning outcomes in this unit should be assessed holistically across the qualification.

The services provided by Assignment Experts UK are 100% original and custom written. We never use any paraphrasing tool, any software to generate content for e.g. Chat GPT and all other content writing tools. We ensure that the work produced by our writers is self-written and 100% plagiarism-free.

International House, 12 Constance Street, London, United Kingdom, E16 2DQ

UK Registered Company # 11483120

100% Pass Guarantee

Still not convinced.

We've produced some samples of what you can expect from our Academic Writing Service - these are created by our writers to show you the kind of high-quality work you'll receive. Take a look for yourself!

View Our Samples

Recent Uploads

1.1 explain the types of information to be managed by a system | ..., 1.1 assess the suitability of a range of techniques for monitorin ..., 1.1 assess the suitability of a range of monitoring techniques fo ..., 1.1 describe methods of collecting data for customer research | u ....

Login and registration

• Forgot Username?
• Forgot Password?

Comparison of problem-solving methods and techniques

Problem-solving is an essential skill in everyday life, in the professional world, and even in scientific research. However, with the multitude of approaches, methods, and techniques available, it can be challenging to navigate. Each problem is unique and may require a different approach. We will attempt to clarify the landscape of these approaches and methods by explaining their primary differences and when to use them, all summarized in the image above.

1 Comprehensive Problem-Solving approaches

This category encompasses complete and structured methods for tackling problem-solving in a systematic way. These approaches are designed to guide individuals or teams throughout the problem-solving process, providing clear and ordered steps to follow.

The DMAIC approach is a structured problem-solving method, divided into five main steps:

• Define : Identify the problem, set objectives, and define the scope of analysis.
• Measure : Gather data to assess the current performance of the process and measure variability.
• Analyze : Dive deep into the data to identify the root causes of the problem.
• Improve : Develop and implement solutions to eliminate the identified problem causes.
• Control : Establish control mechanisms to monitor results and maintain long-term improvements.

Distinctiveness from other comprehensive problem-solving approaches:

The DMAIC approach stems from the Six-Sigma philosophy and places a greater emphasis than other global methods on quantified data, through measurement, and quantitative statistical analyses.

Preferred application

DMAIC is suitable for any type of recurring problem-solving, from medium to high complexity, occurring in an organization's processes or operations. Especially for problems that require quantitative data analyses.

1.2 8D Method

The 8D method is a structured problem-solving approach which stands for "eight disciplines" summarized as follows:

• Form a multidisciplinary team : Create a problem-solving team composed of people with diverse skills.
• Define the problem : Clearly identify the problem, its scope, and the resolution objectives.
• Implement immediate measures : If necessary, take emergency actions to contain the problem.
• Identify causes : Pinpoint the root causes of the problem.
• Develop corrective actions : Design corrective actions to eliminate the immediate causes.
• Implement corrective actions : Execute the corrective actions and monitor their effectiveness.
• Prevent recurrence : Validate that corrective actions are effective and prevent the problem's recurrence.
• Acknowledge the involved individuals : Document the resolution process and recognize the team's contributions.

It explicitly introduces a step to implement immediate actions before identifying the root causes.

Even though the method applies to recurring problem-solving, from medium to high complexity, it tends to be mainly used for medium complexity problems that require urgent actions.

1.3 The A3 method

The A3 method originates from the Toyota Production System (TPS). At Toyota, the A3 paper format was adopted to document, visualize, and share problems, analyses, and solutions concisely. This format has become a principle for reporting, and particularly applied in problem solving. It is more a principle than a method. The steps in the A3 method are not specified, but often follow the example below:

• Describe the current situation
• Define the objective
• Identify the root causes
• Define the corrective actions
• Define the implementation plan
• Track the results
• Learn from the experience

It emphasizes clarity of communication through a simple, visual document containing concise information.

Although the method applies to recurring problem-solving, from medium to high complexity, it tends to be primarily used for medium complexity problems.

1.4 The Change or Transformation project

The Transformation, or Change approach, is a comprehensive method for solving complex problems related to an organization and its operational methods (organization, governance, management methods, processes, staff skills, and motivations...). It involves conducting an in-depth diagnostic of the organization to identify its strengths, weaknesses, opportunities, and threats, then using this information to draft a transformation or improvement plan which will involve a significant part of change management. This approach relies on a holistic analysis of the current company situation, followed by designing and implementing a project aiming to achieve specific change or improvement goals. 

There isn't truly a Change/Transformation approach that has established its "brand", acronyms, and standard structure like DMAIC, 8D, etc. However, all Transformation projects apply similar approaches, and they are frequent enough that this approach deserves to be on our list. It places a more particular emphasis on organizational, managerial, and human aspects, even though process improvement is also part of its scope.

This method mainly applies to solving recurring problems of high complexity of organizational and human nature (organization, governance, management, skills, and motivation...) especially across multiple departments or services of the organization.

1.5 The PDCA method

The PDCA (Plan, Do, Check, Act) is a continuous improvement cycle used to solve problems, enhance processes, and achieve goals. Here's a brief description of each step:

• Plan: Identify the problem or the objective, set goals, design an action plan, and choose methods to achieve them.
• Do: Implement the action plan by executing the planned activities.
• Check: Evaluate the results obtained against the set objectives, by collecting data and checking performance.
• Act: Take measures to adjust, correct, and improve the plan based on the results of the evaluation. Repeat the cycle to continue improvement.

Distinguishing feature compared to other global problem-solving approaches:

PDCA is more of a continuous improvement principle based on a cycle that continually repeats to solve problems, enhance processes, or achieve objectives. It is more generic and can be applied to various situations.

PDCA is often used for incremental improvements and regular adjustments in a process or activity. It is less used to solve complex, identified, or chronic problems and to bring about significant improvements.

The Kaizen event, often referred to as "Kaizen Blitz" or simply "Kaizen," stemming from Toyota's production philosophy, is a targeted and intensive approach aimed at rapidly improving a process, product, or service within an organization.

It typically lasts from a few days to a week, brings together a multidisciplinary team, and follows a procedure of analysis, ideation, rapid implementation, and review.

Although Kaizen covers the entire problem-solving process, it is more focused, both in terms of duration (a few days) and scope compared to broader approaches.

It is particularly suitable for low or medium complexity problems, aiming to achieve immediate and visible improvements, often focused on process efficiency and waste reduction, within a continuous improvement context.

1.7 Conclusion on global problem-solving approaches

Except for Kaizen, which is more targeted than the others, the differences lie mainly in certain aspects more or less highlighted by one method or another.

The effectiveness of the method used will probably depend more on the way (rigor, demand, flexibility, commitment of individuals, etc.) it is implemented than the method itself.

2 Specific methods used within the problem-solving process

2.1 5w2h method.

The method is a management and organization tool used to ask essential questions in order to gather specific and relevant information on a given subject. The letters 5W2H represent the initials of each question  as follows:

• What? : This question aims to clearly define the object or subject under examination. It's the first step to ensure everyone understands what's being discussed.
• Who? : This pertains to determining who is involved or affected by the subject. This could include individuals, teams, departments, or other stakeholders.
• Where? : This question seeks to identify places or locations related to the subject. This could mean physical locations, specific departments in an organization, or even geographical areas.
• When? : It's essential to determine the timeline or time frame associated with the subject. This can include deadlines, due dates, specific moments, and so on.
• Why? : The "Why?" question seeks to comprehend the motivations, reasons, or objectives behind the subject. It helps explore the reasons leading to a particular situation or decision.
• How? : This question delves into the methods, processes, or means used concerning the subject. It aids in understanding the steps or actions required to achieve a goal.
• How much? : This involves quantifying elements related to the subject. This can comprise figures, measurements, financial resources, quantities, and more.

The most appropriate use of the 5W2H method is typically in the Problem Definition phase for the following reasons:

• Clarifying the subject: The "What?" question helps to precisely define what the project is about, avoiding ambiguity.
• Identifying stakeholders: By answering the "Who?" question, the team can determine who's involved in the process or problem to be solved, which is vital for stakeholder management.
• Location: The "Where?" question helps identify the physical places or areas of the organization affected by the project.
• Scheduling: By answering the "When?" question, timelines and deadlines for the project can be set.
• Understanding methods and resources: The "How?" and "How much?" questions help understand existing processes, available resources, and measurements related to the problem.
• Understanding motivations: Finally, the "Why?" question can assist in grasping why the problem is crucial to solve.

2.2 Ishikawa method for identifying root causes

The Ishikawa diagram , also known as the fishbone diagram, is a problem-solving technique used to identify and analyze the root causes of a specific issue. It was developed by Japanese statistician Kaoru Ishikawa. Here's how it works:

• Problem identification: The team clearly identifies the problem or adverse effect that needs resolving. This issue is typically written at the far right of a fish-shaped diagram.
• Diagram creation: A fish-shaped diagram is drawn with a horizontal line representing the problem to solve. This line resembles a fish's spine.
• Cause categories: On the diagram, "spines" are drawn perpendicular to the central spine of the fish. These represent different cause categories that might contribute to the problem. Common categories include the "5 M's" (Material, Manpower, Methods, Environment, Machines) or the "4 P's" (Product, Processes, People, Partners).
• Identifying potential causes: The team then contemplates potential causes for each category and notes them along the corresponding spines. These causes are often identified through brainstorming sessions.
• Analyze and identify root causes: Once all potential causes are recognized, the team analyzes each to determine if it's genuinely linked to the problem and if there are deeper underlying reasons, in order to pinpoint the root causes. Techniques like Pareto charts, data analysis, or the "5 whys" can be employed to identify and prioritize causes based on their significance.

One can argue that the essence of the Ishikawa method lies mainly within stages 1 to 4, up to the identification of potential causes.

Step 5 is more an extension of the Ishikawa method involving the use of other data analysis methods, such as Pareto charts, statistical analyses, or other in-depth investigative techniques.

The Ishikawa method is suitable for two phases of the problem-solving process:

• Problem Definition: The "core" of the Ishikawa method is apt as it allows for the identification of potential causes to clarify the problem's scope and the extent of subsequent analyses. Indeed, the analysis and identification of root causes stage is lengthier and more resource-intensive and will thus be more suitable for the next phase.
• Identifying causes: Both the core of the method and its extension to other methods are used here. The strength of the Ishikawa method is its ability to identify and structure analysis axes using complementary approaches. It's also common to undertake the "core" of the method in the problem definition phase and continue it in this stage (after validating the continuation of the problem-solving process).

2.3 Process mapping and critique

If problem solving is oriented towards improving a process, then the method of process mapping is suitable. This method aims to understand, analyze, and improve a process by visualizing it in detail and identifying optimization opportunities. Within this framework, this method can be applied at two stages of the problem-solving process:

• Problem definition: At this stage, a high-level map will be preferred, for example, a simplified flow diagram, such as a SIPOC . This is generally sufficient to identify the main opportunities to explore later and to clarify the problem definition.
• Cause identification: In this case, and especially for complex problems or significant processes, a detailed mapping that includes all steps, subprocesses, tasks, and interactions will be favored. This can be complemented by a SIPOC map if major issues are identified concerning the documents used (inputs, outputs) and the providers or customers of these documents.

2.4 Structured questionnaires

Questionnaires are generally categorized under general techniques of the following chapter. However, since we are referring here to two very specific types of questionnaires designed for problem-solving, we place them in this category.

• Scoping - Survey: A structured but simple questionnaire (some open questions and performance perception scores) is answered by a selection of organization leaders (scoping) or by a large number of employees (survey).
• Assessment against a benchmark: A very precise questionnaire answered by a selection of leaders or experts to assess how certain practices are conducted and if they match the state of the art (the benchmark).

These two types of questionnaires are used in two different phases:

• Scoping - survey is appropriate in the problem definition phase
• Assessment against a benchmark is used in the root cause identification phase

2.5 Benefit/Ease Matrix

The Benefit/Ease matrix is a tool that allows for the evaluation and ranking of potential actions based on two key criteria:

• Benefit: Benefits, whether qualitative or quantitative, expected from the implementation of each action.
• Ease: This represents the ease with which the proposed actions can be implemented or carried out. Ease depends on various factors such as available resources, required skills, legal constraints, or local conditions.

3 General techniques used in problem-solving

This category includes methods that are not specifically designed for use in problem-solving, but can be. They can also be more of techniques or principles rather than actual methods. Therefore, they can be integrated or used with more specific methods. For example, the "5 whys" can be used in the Ishikawa method to delve deeper into the causes indicated on each fishbone.

3.1 Brainstorming

Brainstorming is a technique for generating ideas creatively and collaboratively. It aims to gather a group of people to explore ideas, solutions, or concepts by encouraging free thought, creativity, and diversity of perspectives.

It is mainly used in the phases of:

• Problem definition: Brainstorming can be used to gather initial ideas about areas that deserve particular attention, identify problems or opportunities requiring improvement.
• Action definition: Brainstorming is particularly useful in this phase as it promotes the generation of a wide range of potential solutions to identified problems. It allows the team to think creatively about process changes, improvements, and innovations that could effectively solve the problems.

3.2 The 5 whys

The "5 Whys" is more of a technique than a method. It involves repeatedly asking the question "Why?" typically until the root cause of a problem is reached. The goal is to move beyond the obvious symptoms of a problem to identify underlying factors contributing to its occurrence.

3.3 Affinity diagram

The affinity diagram method, also known as the KJ method, is a group management technique used to organize and group ideas, information, or problems into logical categories. It consists of collecting items related to a subject, displaying them randomly, and then grouping them based on similarities or relations.

3.4 Quantitative data analysis

Data analysis is an essential element of problem-solving. However, the level of analysis, especially when it comes to quantitative analysis, varies greatly. Thus, we propose a categorization of analysis methods by complexity level to better indicate which analyses to use and when.

3.4.1 Categorization of analyses

Here is a categorization from the simplest to the most complex, with illustrations for each type, for quantitative analyses:

• Basic statistics (mean, median, mode, variance, standard deviation)
• Graphs (bar charts, histograms, pie charts)
• Pareto charts
• Scatter plots
• Correlation analyses
• Hypothesis tests (t-test, ANOVA)
• Confidence intervals
• Linear and logistic regression
• Decision trees and random forests
• Simple simulation
• Optimization (linear programming, network optimization)
• Neural networks
• Clustering (like K-means)
• Deep learning techniques

3.4.2 When to use them during problem-solving?

It depends both on the stage and on the complexity of identifying the real root causes, especially through a quantitative analysis.

• Problem definition phase: Generally, descriptive analyses are sufficient at this stage.
• Cause identification phase: Descriptive analyses are naturally used. Exploratory analyses, and even inferential/predictive analyses, are often used for specific causes. For instance, when calculating the capability of a process and verifying that it meets requirements (such as the defect rate, non-quality rate, etc.). This is even the basis of the approach and the term "six sigma", which requires less than 3.4 defects per million. For very specific and complex problems, advanced methods (simulations, AI) may be used.
• Action definition phase: The main data analysis performed here is estimating the impacts of the actions, which is usually a descriptive analysis. However, it may happen that you simulate and compare several scenarios by performing sensitivity analyses, exploratory, or even predictive types. It is also likely that with the maturation of AI-based techniques, these tools will be used more and more to make action recommendations.

3.5 The Business Case

In the context of problem-solving, the "Business Case" identifies the gains, costs, investments, and financial risks associated with solving the problem. It supports several actions, such as deciding to continue the problem-solving process, prioritizing causes and actions, or tracking results:

• Problem definition: At this stage, the Business Case is used to decide whether to proceed with the analysis and action definition phases. The Business Case is generally vague at this stage due to a lack of many data.
• Cause identification: An estimated quantitative impact of the different causes can help focus on the causes generating the greatest financial losses.
• Action definition: The Business Case is established at the end of the phase to decide whether or not to implement the actions. This time it is more precise because all the necessary data could be collected in the previous phases.
• Measuring results: The Business Case is then used to verify that the impact of the solutions not only brings operational benefits but also translates into the organization's accounts.

The Business Case is used more the more complex the problem is, and therefore costly to solve. It will then be necessary to justify the investment in human and financial resources to solve the problem. It will be used less for simple problems, or in a very simplified way, for example, when the "Kaizen" method is used.

You may also access our unique directory of management best practices by function and industry

When you subscribe to the blog, we will send you an e-mail when there are new updates on the site so you wouldn't miss them.

Related Posts

A3 is a principle, not a problem-solving method !!

The pdca cycle or deming wheel: how and why to use it, the 5 whys method: how and when to use it, 5w2h or 5w1h methods: how and when to use them, 8d method (8 disciplines), ishikawa diagram and root cause analysis, continuous improvement process : a challenge for significant benefits, dmaic process: a methodology to implement six sigma, what is an operational audit of the organisation, improvement and innovation excellence.

• Professional Services
• Creative & Design
• See all teams
• Project Management
• Workflow Management
• Task Management
• Resource Management
• See all use cases

Apps & Integrations

• Microsoft Teams
• See all integrations

Explore Wrike

• Book a Demo
• Take a Product Tour
• Start With Templates
• Customer Stories
• ROI Calculator
• Find a Reseller
• Mobile & Desktop Apps
• Cross-Tagging
• Kanban Boards
• Project Resource Planning
• Gantt Charts
• Custom Item Types
• Dynamic Request Forms
• Integrations
• See all features

Learn and connect

• Resource Hub
• Educational Guides

Become Wrike Pro

• Submit A Ticket
• Help Center
• Premium Support
• Community Topics
• Training Courses
• Facilitated Services
• Productivity

Problem-Solving Techniques and Tips (That Actually Work)

June 14, 2022 - 10 min read

Solving complex problems may be difficult but it doesn't have to be excruciating. You just need the right frame of mind and a process for untangling the problem at hand.

Luckily for you, there are plenty of techniques available to solve whatever problems come at you in the workplace.

When faced with a doozy of a problem, where do you start? And what problem-solving techniques can you use right now that can help you make good decisions?

Today's post will give you tips and techniques for solving complex problems so you can untangle any complication like an expert.

How many steps are there in problem-solving?

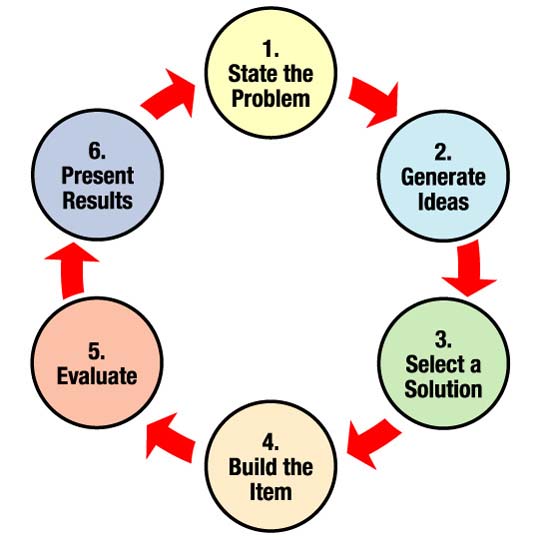
At its core, problem-solving is a methodical four-step process. You may even recall these steps from when you were first introduced to the Scientific Method.

• First, you must define the problem . What is its cause? What are the signs there's a problem at all?
• Next, you identify various options for solutions. What are some good ideas to solve this?
• Then, evaluate your options and choose from among them. What is the best option to solve the problem? What's the easiest option? How should you prioritize?
• Finally, implement the chosen solution . Does it solve the problem? Is there another option you need to try?

When applying problem-solving techniques, you will be using a variation of these steps as your foundation.

Takeaway: Before you can solve a problem, seek to understand it fully.

Creative problem-solving techniques

Time to get creative! You might think this will just be a list of out-of-the-box ways to brainstorm ideas. Not exactly.

Creative problem solving (CPS) is actually a formal process formulated by Sidney Parnes and Alex Faickney Osborn , who is thought of as the father of traditional brainstorming (and the "O" in famous advertising agency BBDO).

Their creative problem solving process emphasizes several things, namely:

• Separate ideation from evaluation . When you brainstorm creative ideas, have a separate time for writing it all down. Focus on generating lots of ideas. Don't prioritize or evaluate them until everything is captured.
• Judging will shut it down . Nothing stops the flow of creative ideas faster than judging them on the spot. Wait until the brainstorming is over before you evaluate.
• Restate problems as questions . It's easier to entice a group into thinking of creative ideas when challenges are stated as open-ended questions.
• Use "Yes and" to expand ideas . Here's one of the basic tenets of improv comedy. It's way too easy to shut down and negate ideas by using the word "but" (i.e. "But I think this is better..."). Avoid this at all costs. Instead, expand on what was previously introduced by saying "Yes, and..." to keep ideas flowing and evolving.

Takeaway: When brainstorming solutions, generate ideas first by using questions and building off of existing ideas. Do all evaluating and judging later.

Problem-solving tips from psychology

If you take a look at the history of problem-solving techniques in psychology, you'll come across a wide spectrum of interesting ideas that could be helpful.

Take it from experience

In 1911, the American psychologist Edward Thorndike observed cats figuring out how to escape from the cage he placed them in. From this, Thorndike developed his law of effect , which states: If you succeed via trial-and-error, you're more likely to use those same actions and ideas that led to your previous success when you face the problem again.

Takeaway: Your past experience can inform and shed light on the problem you face now. Recall. Explore.

Barriers to reproductive thinking

The Gestalt psychologists  built on Thorndike's ideas when they proposed that problem-solving can happen via reproductive thinking — which is not about sex, but rather solving a problem by using past experience and reproducing that experience to solve the current problem.

What's interesting about Gestalt psychology is how they view barriers to problem-solving. Here are two such barriers:

• Are you entrenched? Look up mental set or entrenchment . This is when you're fixated on a solution that used to work well in the past but has no bearing to your current problem. Are you so entrenched with a method or idea that you use it even when it doesn't work? As Queen Elsa sang, "Let it go!" 
• Are you thinking of alternative uses? There is a cognitive bias called functional fixedness which could thwart any of your critical thinking techniques by having you only see an object's conventional function. For example, say you need to cut a piece of paper in half but only have a ruler. Functional fixedness would lead you to think the ruler is only good for measuring things. (You could also use the ruler to crease the paper, making it easier to tear it in half.)

Takeaway: Think outside of the box! And by box, we mean outside of the past experience you're holding on to, or outside any preconceived ideas on how a tool is conventionally used.

More problem-solving tools

Hurson's productive thinking model.

In his book "Think Better," author and creativity guru Tim Hurson proposed a six-step model for solving problems creatively. The steps in his Productive Thinking Model are:

• Ask, "What is going on?" Define the problem and its impact on your company, then clarify your vision for the future.
• Ask, "What is success?" Define what the solution must do, what resources it needs, its scope, and the values it must uphold.
• Ask, "What is the question?" Generate a long list of questions that, when answered, will solve the problem.
• Generate answers . Answer the questions from step three.
• Forge the solution . Evaluate the ideas with potential based on the criteria from step two. Pick a solution.
• Align resources . Identify people and resources to execute the solution.

Use a fishbone diagram to see cause and effect

The most important part of defining the problem is looking at the possible root cause. You'll need to ask yourself questions like: Where and when is it happening? How is it occurring? With whom is it happening? Why is it happening?

You can get to the root cause with a fishbone diagram (also known as an Ishikawa diagram or a cause and effect diagram).

Basically, you put the effect on the right side as the problem statement. Then you list all possible causes on the left, grouped into larger cause categories. The resulting shape resembles a fish skeleton. Which is a perfect way to say, "This problem smells fishy."

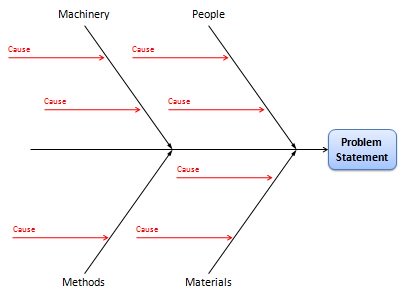
Use analogies to get to a solution

Analogical thinking uses information from one area to help with a problem in a different area. In short, solving a different problem can lead you to find a solution to the actual problem. Watch out though! Analogies are difficult for beginners and take some getting used to.

An example: In the "radiation problem," a doctor has a patient with a tumor that cannot be operated on. The doctor can use rays to destroy the tumor but it also destroys healthy tissue.

Two researchers, Gick and Holyoak , noted that people solved the radiation problem much more easily after being asked to read a story about an invading general who must capture the fortress of a king but be careful to avoid landmines that will detonate if large forces traverse the streets. The general then sends small forces of men down different streets so the army can converge at the fortress at the same time and can capture it at full force.

Ask "12 what elses"

In her book " The Architecture of All Abundance ," author Lenedra J. Carroll (aka the mother of pop star Jewel) talks about a question-and-answer technique for getting out of a problem.

When faced with a problem, ask yourself a question about it and brainstorm 12 answers ("12 what elses") to that problem. Then you can go further by taking one answer, turning it into a question and generating 12 more "what elses." Repeat until the solution is golden brown, fully baked, and ready to take out of the oven.

Start using these techniques today

Hopefully you find these different techniques useful and they get your imagination rolling with ideas on how to solve different problems.

And if that's the case, then you have four different takeaways to use the next time a problem gets you tangled up:

• Don't start by trying to solve the problem. First, aim to understand the root of the problem.
• Use questions to generate ideas for solving the problem.
• Look to previous problems to find the answers to new ones.
• Clear your preconceived ideas and past experiences before attempting to tackle the problem.

How to solve problems with Wrike

Empower your team to be even more productive with Wrike's project management and collaboration tools. With documents, revisions, and project -related communication all in one place, employees can use Wrike as a single source of truth for all project information.

Get 360-degree visibility of all your work and identify problems before they occur — see schedule or resource conflicts on Gantt charts, easily view progress with custom statuses, and move work along with automated approvals.

Want to streamline your processes and ease future problem-solving? Get started with a free two-week trial of Wrike today.

What are your favorite problem-solving techniques?

Do you have a problem-solving technique that has worked wonders for your organization? Hit the comments below and share your wisdom!

Lionel Valdellon

Lionel is a former Content Marketing Manager of Wrike. He is also a blogger since 1997, a productivity enthusiast, a project management newbie, a musician and producer of electronic downtempo music, a father of three, and a husband of one.

Sorry, this content is unavailable due to your privacy settings. To view this content, click the “Cookie Preferences” button and accept Advertising Cookies there.

• Soft skills
• What is a credential?
• Why do a credential?
• How do credentials work?
• Selecting your level
• How will I be assessed?
• Benefits for professionals
• Benefits for organisations
• Benefits for postgraduates

Problem solving techniques: Steps and methods

Posted on May 29, 2019

Constant disruption has become a hallmark of the modern workforce and organisations want problem solving skills to combat this. Employers need people who can respond to change – be that evolving technology, new competitors, different models for doing business, or any of the other transformations that have taken place in recent years.

In addition, problem solving techniques encompass many of the other top skills employers seek . For example, LinkedIn’s list of the most in-demand soft skills of 2019 includes creativity, collaboration and adaptability, all of which fall under the problem-solving umbrella.

Despite its importance, many employees misunderstand what the problem solving method really involves.

What constitutes effective problem solving?

Effective problem solving doesn’t mean going away and coming up with an answer immediately. In fact, this isn’t good problem solving at all, because you’ll be running with the first solution that comes into your mind, which often isn’t the best.

Instead, you should look at problem solving more as a process with several steps involved that will help you reach the best outcome. Those steps are:

• Define the problem
• List all the possible solutions
• Evaluate the options
• Select the best solution
• Create an implementation plan
• Communicate your solution

Let’s look at each step in a little more detail.

1. Define the problem

The first step to solving a problem is defining what the problem actually is – sounds simple, right? Well no. An effective problem solver will take the thoughts of everyone involved into account, but different people might have different ideas on what the root cause of the issue really is. It’s up to you to actively listen to everyone without bringing any of your own preconceived notions to the conversation. Learning to differentiate facts from opinion is an essential part of this process.

An effective problem solver will take the opinions of everyone involved into account

The same can be said of data. Depending on what the problem is, there will be varying amounts of information available that will help you work out what’s gone wrong. There should be at least some data involved in any problem, and it’s up to you to gather as much as possible and analyse it objectively.

2. List all the possible solutions

Once you’ve identified what the real issue is, it’s time to think of solutions. Brainstorming as many solutions as possible will help you arrive at the best answer because you’ll be considering all potential options and scenarios. You should take everyone’s thoughts into account when you’re brainstorming these ideas, as well as all the insights you’ve gleaned from your data analysis. It also helps to seek input from others at this stage, as they may come up with solutions you haven’t thought of.

Depending on the type of problem, it can be useful to think of both short-term and long-term solutions, as some of your options may take a while to implement.

3. Evaluate the options

Each option will have pros and cons, and it’s important you list all of these, as well as how each solution could impact key stakeholders. Once you’ve narrowed down your options to three or four, it’s often a good idea to go to other employees for feedback just in case you’ve missed something. You should also work out how each option ties in with the broader goals of the business.

There may be a way to merge two options together in order to satisfy more people.

4. Select an option

Only now should you choose which solution you’re going to go with. What you decide should be whatever solves the problem most effectively while also taking the interests of everyone involved into account. There may be a way to merge two options together in order to satisfy more people.

5. Create an implementation plan

At this point you might be thinking it’s time to sit back and relax – problem solved, right? There are actually two more steps involved if you want your problem solving method to be truly effective. The first is to create an implementation plan. After all, if you don’t carry out your solution effectively, you’re not really solving the problem at all. 

Create an implementation plan on how you will put your solution into practice. One problem solving technique that many use here is to introduce a testing and feedback phase just to make sure the option you’ve selected really is the most viable. You’ll also want to include any changes to your solution that may occur in your implementation plan, as well as how you’ll monitor compliance and success.

6. Communicate your solution

There’s one last step to consider as part of the problem solving methodology, and that’s communicating your solution . Without this crucial part of the process, how is anyone going to know what you’ve decided? Make sure you communicate your decision to all the people who might be impacted by it. Not everyone is going to be 100 per cent happy with it, so when you communicate you must give them context. Explain exactly why you’ve made that decision and how the pros mean it’s better than any of the other options you came up with.

Prove your problem solving skills with Deakin

Employers are increasingly seeking soft skills, but unfortunately, while you can show that you’ve got a degree in a subject, it’s much harder to prove you’ve got proficiency in things like problem solving skills. But this is changing thanks to Deakin’s micro-credentials. These are university-level micro-credentials that provide an authoritative and third-party assessment of your capabilities in a range of areas, including problem solving. Reach out today for more information .

.css-s5s6ko{margin-right:42px;color:#F5F4F3;}@media (max-width: 1120px){.css-s5s6ko{margin-right:12px;}} Join us: Learn how to build a trusted AI strategy to support your company's intelligent transformation, featuring Forrester .css-1ixh9fn{display:inline-block;}@media (max-width: 480px){.css-1ixh9fn{display:block;margin-top:12px;}} .css-1uaoevr-heading-6{font-size:14px;line-height:24px;font-weight:500;-webkit-text-decoration:underline;text-decoration:underline;color:#F5F4F3;}.css-1uaoevr-heading-6:hover{color:#F5F4F3;} .css-ora5nu-heading-6{display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;-webkit-box-pack:start;-ms-flex-pack:start;-webkit-justify-content:flex-start;justify-content:flex-start;color:#0D0E10;-webkit-transition:all 0.3s;transition:all 0.3s;position:relative;font-size:16px;line-height:28px;padding:0;font-size:14px;line-height:24px;font-weight:500;-webkit-text-decoration:underline;text-decoration:underline;color:#F5F4F3;}.css-ora5nu-heading-6:hover{border-bottom:0;color:#CD4848;}.css-ora5nu-heading-6:hover path{fill:#CD4848;}.css-ora5nu-heading-6:hover div{border-color:#CD4848;}.css-ora5nu-heading-6:hover div:before{border-left-color:#CD4848;}.css-ora5nu-heading-6:active{border-bottom:0;background-color:#EBE8E8;color:#0D0E10;}.css-ora5nu-heading-6:active path{fill:#0D0E10;}.css-ora5nu-heading-6:active div{border-color:#0D0E10;}.css-ora5nu-heading-6:active div:before{border-left-color:#0D0E10;}.css-ora5nu-heading-6:hover{color:#F5F4F3;} Register now .css-1k6cidy{width:11px;height:11px;margin-left:8px;}.css-1k6cidy path{fill:currentColor;}

• Collaboration |
• Turn your team into skilled problem sol ...

Turn your team into skilled problem solvers with these problem-solving strategies

Picture this, you're handling your daily tasks at work and your boss calls you in and says, "We have a problem." 

Unfortunately, we don't live in a world in which problems are instantly resolved with the snap of our fingers. Knowing how to effectively solve problems is an important professional skill to hone. If you have a problem that needs to be solved, what is the right process to use to ensure you get the most effective solution?

In this article we'll break down the problem-solving process and how you can find the most effective solutions for complex problems.

What is problem solving? 

Problem solving is the process of finding a resolution for a specific issue or conflict. There are many possible solutions for solving a problem, which is why it's important to go through a problem-solving process to find the best solution. You could use a flathead screwdriver to unscrew a Phillips head screw, but there is a better tool for the situation. Utilizing common problem-solving techniques helps you find the best solution to fit the needs of the specific situation, much like using the right tools.

Decision-making tools for agile businesses

In this ebook, learn how to equip employees to make better decisions—so your business can pivot, adapt, and tackle challenges more effectively than your competition.

4 steps to better problem solving

While it might be tempting to dive into a problem head first, take the time to move step by step. Here’s how you can effectively break down the problem-solving process with your team:

1. Identify the problem that needs to be solved

One of the easiest ways to identify a problem is to ask questions. A good place to start is to ask journalistic questions, like:

Who : Who is involved with this problem? Who caused the problem? Who is most affected by this issue?

What: What is happening? What is the extent of the issue? What does this problem prevent from moving forward?

Where: Where did this problem take place? Does this problem affect anything else in the immediate area? 

When: When did this problem happen? When does this problem take effect? Is this an urgent issue that needs to be solved within a certain timeframe?

Why: Why is it happening? Why does it impact workflows?

How: How did this problem occur? How is it affecting workflows and team members from being productive?

Asking journalistic questions can help you define a strong problem statement so you can highlight the current situation objectively, and create a plan around that situation.

Here’s an example of how a design team uses journalistic questions to identify their problem:

Overarching problem: Design requests are being missed

Who: Design team, digital marketing team, web development team

What: Design requests are forgotten, lost, or being created ad hoc.

Where: Email requests, design request spreadsheet

When: Missed requests on January 20th, January 31st, February 4th, February 6th

How : Email request was lost in inbox and the intake spreadsheet was not updated correctly. The digital marketing team had to delay launching ads for a few days while design requests were bottlenecked. Designers had to work extra hours to ensure all requests were completed.

In this example, there are many different aspects of this problem that can be solved. Using journalistic questions can help you identify different issues and who you should involve in the process.

2. Brainstorm multiple solutions

If at all possible, bring in a facilitator who doesn't have a major stake in the solution. Bringing an individual who has little-to-no stake in the matter can help keep your team on track and encourage good problem-solving skills.

Here are a few brainstorming techniques to encourage creative thinking:

Brainstorm alone before hand: Before you come together as a group, provide some context to your team on what exactly the issue is that you're brainstorming. This will give time for you and your teammates to have some ideas ready by the time you meet.

Say yes to everything (at first): When you first start brainstorming, don't say no to any ideas just yet—try to get as many ideas down as possible. Having as many ideas as possible ensures that you’ll get a variety of solutions. Save the trimming for the next step of the strategy. 

Talk to team members one-on-one: Some people may be less comfortable sharing their ideas in a group setting. Discuss the issue with team members individually and encourage them to share their opinions without restrictions—you might find some more detailed insights than originally anticipated.

Break out of your routine: If you're used to brainstorming in a conference room or over Zoom calls, do something a little different! Take your brainstorming meeting to a coffee shop or have your Zoom call while you're taking a walk. Getting out of your routine can force your brain out of its usual rut and increase critical thinking.

3. Define the solution

After you brainstorm with team members to get their unique perspectives on a scenario, it's time to look at the different strategies and decide which option is the best solution for the problem at hand. When defining the solution, consider these main two questions: What is the desired outcome of this solution and who stands to benefit from this solution? 

Set a deadline for when this decision needs to be made and update stakeholders accordingly. Sometimes there's too many people who need to make a decision. Use your best judgement based on the limitations provided to do great things fast.

4. Implement the solution

To implement your solution, start by working with the individuals who are as closest to the problem. This can help those most affected by the problem get unblocked. Then move farther out to those who are less affected, and so on and so forth. Some solutions are simple enough that you don’t need to work through multiple teams.

After you prioritize implementation with the right teams, assign out the ongoing work that needs to be completed by the rest of the team. This can prevent people from becoming overburdened during the implementation plan . Once your solution is in place, schedule check-ins to see how the solution is working and course-correct if necessary.

Implement common problem-solving strategies

There are a few ways to go about identifying problems (and solutions). Here are some strategies you can try, as well as common ways to apply them:

Trial and error

Trial and error problem solving doesn't usually require a whole team of people to solve. To use trial and error problem solving, identify the cause of the problem, and then rapidly test possible solutions to see if anything changes. 

This problem-solving method is often used in tech support teams through troubleshooting.

The 5 whys problem-solving method helps get to the root cause of an issue. You start by asking once, “Why did this issue happen?” After answering the first why, ask again, “Why did that happen?” You'll do this five times until you can attribute the problem to a root cause. 

This technique can help you dig in and find the human error that caused something to go wrong. More importantly, it also helps you and your team develop an actionable plan so that you can prevent the issue from happening again.

Here’s an example:

Problem: The email marketing campaign was accidentally sent to the wrong audience.

“Why did this happen?” Because the audience name was not updated in our email platform.

“Why were the audience names not changed?” Because the audience segment was not renamed after editing. 

“Why was the audience segment not renamed?” Because everybody has an individual way of creating an audience segment.

“Why does everybody have an individual way of creating an audience segment?” Because there is no standardized process for creating audience segments. 

“Why is there no standardized process for creating audience segments?” Because the team hasn't decided on a way to standardize the process as the team introduced new members. 

In this example, we can see a few areas that could be optimized to prevent this mistake from happening again. When working through these questions, make sure that everyone who was involved in the situation is present so that you can co-create next steps to avoid the same problem. 

A SWOT analysis

A SWOT analysis can help you highlight the strengths and weaknesses of a specific solution. SWOT stands for:

Strength: Why is this specific solution a good fit for this problem? 

Weaknesses: What are the weak points of this solution? Is there anything that you can do to strengthen those weaknesses?

Opportunities: What other benefits could arise from implementing this solution?

Threats: Is there anything about this decision that can detrimentally impact your team?

As you identify specific solutions, you can highlight the different strengths, weaknesses, opportunities, and threats of each solution. 

This particular problem-solving strategy is good to use when you're narrowing down the answers and need to compare and contrast the differences between different solutions. 

Even more successful problem solving

After you’ve worked through a tough problem, don't forget to celebrate how far you've come. Not only is this important for your team of problem solvers to see their work in action, but this can also help you become a more efficient, effective , and flexible team. The more problems you tackle together, the more you’ll achieve. 

Looking for a tool to help solve problems on your team? Track project implementation with a work management tool like Asana .

Related resources

Don’t let your digital tools sabotage the employee experience

12 tips for effective communication in the workplace

Unmanaged business goals don’t work. Here’s what does.

How Asana uses work management to drive product development

Chapter 1: General Problem Solving

1.1 why it matters: general problem solving, why understand the basics of problem solving, critical thinking.

Thinking comes naturally. You don’t have to make it happen—it just does. But you can make it happen in different ways. For example, you can think positively or negatively. You can think with “heart” and you can think with rational judgment. You can also think strategically and analytically, and mathematically and scientifically. These are a few of the ways in which the mind can process thought.

What are some forms of thinking you use? When do you use them, and why?

As a college student, you are tasked with engaging and expanding your thinking skills. One of the most important of these skills is critical thinking. Critical thinking is important because it relates to nearly all tasks, situations, topics, careers, environments, challenges, and opportunities. It’s a “domain-general” thinking skill—not a thinking skill that’s reserved for one subject alone or restricted to a particular subject area.

Great leaders have highly attuned critical thinking skills, and you can too. In fact, you probably have a lot of these skills already. Of all your thinking skills, critical thinking may have the greatest value.

What Is Critical Thinking?

Critical thinking is clear, reasonable, reflective thinking focused on deciding what to believe or do. It means asking probing questions like, “How do we know?” or “Is this true in every case or just in this instance?” It involves being skeptical and challenging assumptions, rather than simply memorizing facts or blindly accepting what you hear or read.

Who are critical thinkers, and what characteristics do they have in common? Critical thinkers are usually curious and reflective people. They like to explore and probe new areas and seek knowledge, clarification, and new solutions. They ask pertinent questions, evaluate statements and arguments, and they distinguish between facts and opinion. They are also willing to examine their own beliefs, possessing a manner of humility that allows them to admit lack of knowledge or understanding when needed. They are open to changing their mind. Perhaps most of all, they actively enjoy learning, and seeking new knowledge is a lifelong pursuit.

This may well be you!

The following video, from Lawrence Bland, presents the major concepts and benefits of critical thinking.

Critical Thinking and Logic

Critical thinking is fundamentally a process of questioning information and data. You may question the information you read in a textbook, or you may question what a politician or a professor or a classmate says. You can also question a commonly-held belief or a new idea. With critical thinking, anything and everything is subject to question and examination for the purpose of logically constructing reasoned perspectives.

Questions of Logic in Critical Thinking

Let’s use a simple example of applying logic to a critical-thinking situation. In this hypothetical scenario, a man has a PhD in political science, and he works as a professor at a local college. His wife works at the college, too. They have three young children in the local school system, and their family is well known in the community. The man is now running for political office. Are his credentials and experience sufficient for entering public office? Will he be effective in the political office? Some voters might believe that his personal life and current job, on the surface, suggest he will do well in the position, and they will vote for him. In truth, the characteristics described don’t guarantee that the man will do a good job. The information is somewhat irrelevant. What else might you want to know? How about whether the man had already held a political office and done a good job? In this case, we want to ask, How much information is adequate in order to make a decision based on logic instead of assumptions?

The following questions are ones you may apply to formulating a logical, reasoned perspective in the above scenario or any other situation:

• What’s happening? Gather the basic information and begin to think of questions.
• Why is it important? Ask yourself why it’s significant and whether or not you agree.
• What don’t I see? Is there anything important missing?
• How do I know? Ask yourself where the information came from and how it was constructed.
• Who is saying it? What’s the position of the speaker and what is influencing them?
• What else? What if? What other ideas exist and are there other possibilities?

Problem-Solving with Critical Thinking

For most people, a typical day is filled with critical thinking and problem-solving challenges. In fact, critical thinking and problem-solving go hand-in-hand. They both refer to using knowledge, facts, and data to solve problems effectively. But with problem-solving, you are specifically identifying, selecting, and defending your solution.

Problem-Solving Action Checklist

Problem-solving can be an efficient and rewarding process, especially if you are organized and mindful of critical steps and strategies. Remember, too, to assume the attributes of a good critical thinker. If you are curious, reflective, knowledge-seeking, open to change, probing, organized, and ethical, your challenge or problem will be less of a hurdle, and you’ll be in a good position to find intelligent solutions.

Critical Thinking, Problem Solving, and Math

In previous math courses, you’ve no doubt run into the infamous “word problems.” Unfortunately, these problems rarely resemble the type of problems we actually encounter in everyday life. In math books, you usually are told exactly which formula or procedure to use, and are given exactly the information you need to answer the question. In real life, problem solving requires identifying an appropriate formula or procedure, and determining what information you will need (and won’t need) to answer the question.

In this section, we will review several basic but powerful algebraic ideas: percents , rates , and proportions . We will then focus on the problem solving process, and explore how to use these ideas to solve problems where we don’t have perfect information.

• "Student Success-Thinking Critically In Class and Online."  Critical Thinking Gateway . St Petersburg College, n.d. Web. 16 Feb 2016. ↵
• Critical Thinking Skills. Authored by : Linda Bruce. Provided by : Lumen Learning. Located at : https://courses.lumenlearning.com/collegesuccess-lumen/chapter/critical-thinking-skills/ . Project : College Success. License : CC BY: Attribution
• Critical Thinking. Authored by : Critical and Creative Thinking Program. Located at : http://cct.wikispaces.umb.edu/Critical+Thinking . License : CC BY: Attribution
• Thinking Critically. Authored by : UBC Learning Commons. Provided by : The University of British Columbia, Vancouver Campus. Located at : http://www.oercommons.org/courses/learning-toolkit-critical-thinking/view . License : CC BY: Attribution
• Problem Solving. Authored by : David Lippman. Located at : http://www.opentextbookstore.com/mathinsociety/ . Project : Math in Society. License : CC BY-SA: Attribution-ShareAlike
• Critical Thinking.wmv. . Authored by : Lawrence Bland. Located at : https://youtu.be/WiSklIGUblo . License : All Rights Reserved . License Terms : Standard YouTube License

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

How to Solve Problems

• Laura Amico

To bring the best ideas forward, teams must build psychological safety.

Teams today aren’t just asked to execute tasks: They’re called upon to solve problems. You’d think that many brains working together would mean better solutions, but the reality is that too often problem-solving teams fall victim to inefficiency, conflict, and cautious conclusions. The two charts below will help your team think about how to collaborate better and come up with the best solutions for the thorniest challenges.

• Laura Amico is a former senior editor at Harvard Business Review.

Partner Center

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

1.1 KEY CONCEPT: Problem-Solving Approach to Communications Tasks

In the workplace, many of the communication tasks you perform are designed to solve a problem or improve a situation. Whether you are doing work for a client, for your employer, with your team, or for someone else, you will typically use some sort of design process to tackle and solve the problem. A clearly articulated design process provides you with a clear, step-by-step plan for finding the best solution for your situation.

Take a moment to search the Internet for the term “design process” and look at “images.” You will find many variations. Have a look at several of them and see if you can find a common pattern.

One commonality you will likely find in examining other people’s design process diagrams is this: the first step in designing any solution is to clearly define the problem . Figure 1.1.1 shows NASA’s basic design process. Think about the kind of communication that each step of this process might entail.

You cannot begin to work on solutions until you have a clear definition of the problem and the goals you want to achieve. This critical first stage of the design process requires that you effectively communicate with the “client” or whoever has the “problem” that needs solving. Poor communication at this stage can derail a project from the start.

Before we examine the step-by-step process to developing a business/research problem, the video below will review the importance of clearly defining a business/research problem.

• Need Statement: recognizes and describes the need for a solution or improvement to an “unsatisfactory situation.”  It answers the questions, “what is wrong with the way things are currently? What is unsatisfactory about the situation? What negative effects does it cause?” You may need to do research and supply data to quantify the negative effects.
• Goal Statement: describes what the improved situation would look like once a solution has been implemented. The goal statement defines the scope of your search for a solution. At this point, do not describe your solution, only the goal that any proposed solution should achieve. The broader you make your goal, the more numerous and varied the solution can be; a narrowly focused goal limits the number and variety of possible solutions.
• Objectives : define measurable, specific outcomes that any feasible solution should optimize (aspects you can use to “grade” the effectiveness of the solution). Objectives provide you with ways to quantifiably measure how well any solution will solve the problem; ideally, they will allow you to compare multiple solutions and figure out which one is most effective (which one gets the highest score on meeting the objectives?).
• Constraints :  define the limits that any feasible solution must adhere to in order to be acceptable (pass/fail conditions, range limits, etc .). The keyword here is must — constraints are the “go/no go” conditions that determine whether a solution is acceptable or not.  These often include budget and time limits, as well as legal, safety and other regulatory requirements.

Knowledge Check

Communication as Solution

This model can apply to a communications task as well as more physical design tasks. Imagine your communications task as something that will solve a problem or improve a situation. Before you begin drafting this document or presentation, define the problem you want to solve with this document:

• A potential client lacks sufficient information on whether the solution I have proposed to solve the client’s problem will be feasible, affordable, and effective.
• My instructor lacks sufficient examples of my written work to assign a grade for how well I met the course learning objectives. 
• Provide the client with enough information, in an effective and readable format, to make a decision (ideally, to hire you to build the solution for the problem).
• Provide my instructor with samples of my writing that demonstrate my achievement of the course learning objectives (provide relevant and complete  information in a professionally appropriate forma t, using evidence-based argument; earn an A+ grade on the assignment. )
• Review the client’s RFP to see what specific objectives it lists and how your proposal will be assessed.
• Review the Assignment Description and G rading Rubric for your assignment to determin e specific requirements and objectives that your instructor will use to evaluate your work.
• How much time is your audience willing to spend on this? How long can you make your document or presentation? (word length/time limit)
• What format and style do they require? Is there a Style Guide you must follow? A template you can use?
• How much time do you have to create it?  Do you have a deadline? (due date)
• Are there requirements for using sources? (academic integrity rules)

In addition to the process above, the following video provides a slightly different problem solving process; however, it incorporates many of the same principles described above.

( How to Solve a Problem in Four Steps , 2015)

Keep in mind that the document you produce is evaluated in terms of how well it responds to the “problem” — that is, how well it meets the overall goal and demonstrates achievement of specific objectives while abiding by constraints.

EXERCISE 1.2 Define a problem

Think of a problem or an “unsatisfactory situation” that you have recently experienced.  It could be as simple as It’s 8 p.m., I haven’t had dinner yet, and I’m hungry . Use Hymen’s Problem Formulation schema to formally define the problem — without proposing any particular solutions. Your problem definition should ideally allow a multitude of possible solutions that adhere to the following:

• Need/Unsatisfactory situation?
• What is your goal?
• What are some measurable objectives you want to achieve?
• What are your constraints?

Map out your analysis to find the most logical next steps.

100% Effective. (2015). What is a Problem Statement? [Video]. Youtube. https://www.youtube.com/watch?v=vjCCC2kFJcQ&t=43s

DecisionSkills. (2015). How to solve a problem in four steps [Video]. Youtube. https://www.youtube.com/watch?v=QOjTJAFyNrU

Hyman, B. (2002). Ch. 2: Problem formulation. In Fundamentals of engineering design. Upper Saddle River, NJ: Prentice Hall, pp. 40-54.

NASA. (2018, January 30 updated). NASA design process . NASA STEM Engagement.  https://www.nasa.gov/audience/foreducators/best/index.html Used for educational and noncommercial purposes.

Technical Writing Essentials Copyright © 2019 by Suzan Last is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

The general systems approach to problem-solving

Cite this chapter.

149 Accesses

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Further reading

Blanchard, B.S. and Fabrychy, W.J. (1981), Systems Engineering and Analysis , Prentice-Hall.

Google Scholar  

Cleland, D.I. and William, R.K. (1983), Systems Analysis and Project Management , McGraw-Hill.

Wilson, B. (1984), Systems: Concepts, Methodologies, and Applications , John Wiley.

Blanchard, B.S. and Fabrychy, W.J. (1981) Systems Engineering and Analysis Prentice-Hall.

Box, G.E.P. and Draper, N.R. (1969) Evolutionary Operation Wiley.

Checkland, P. (1981) Systems Thinking, Systems Practice John Wiley.

Cleland, D.I. and King, W.R. (1983) Systems Analysis and Project Management McGraw-Hill.

Dandy, G.C. and Warner, R.F. (1989) Planning and Design of Engineering Systems Unwin Hyman.

Pidd, M. (1984) Computer Simulation in Management Science John Wiley.

Sandquist, G.M. (1985) Introduction to System Science Prentice-Hall.

Wilson, B. (1984) Systems: Concepts, Methodologies, and Applications John Wiley.

Wu, B. (1990) WIP cost-related effectiveness measure for the application of an IBE to simulation analysis, Computer-Integrated Manufacturing Systems , 3 (3).

Download references

Author information

Authors and affiliations.

Department of Manufacturing and Engineering Systems, Brunel University, Middlesex, UK

You can also search for this author in PubMed   Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 1992 B. Wu

About this chapter

Wu, B. (1992). The general systems approach to problem-solving. In: Manufacturing Systems Design and Analysis. Springer, Dordrecht. https://doi.org/10.1007/978-94-011-3128-5_4

Download citation

DOI : https://doi.org/10.1007/978-94-011-3128-5_4

Publisher Name : Springer, Dordrecht

Print ISBN : 978-0-412-40840-3

Online ISBN : 978-94-011-3128-5

eBook Packages : Springer Book Archive

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• v.9(5); 2023 May
• PMC10208825

Development and differences in mathematical problem-solving skills: A cross-sectional study of differences in demographic backgrounds

Ijtihadi kamilia amalina.

a Doctoral School of Education, University of Szeged, Hungary

Tibor Vidákovich

b Institute of Education, University of Szeged, Hungary

Associated Data

Data will be made available on request.

Problem-solving skills are the most applicable cognitive tool in mathematics, and improving the problem-solving skills of students is a primary aim of education. However, teachers need to know the best period of development and the differences among students to determine the best teaching and learning methods. This study aims to investigate the development and differences in mathematical problem-solving skills of students based on their grades, gender, and school locations. A scenario-based mathematical essay test was administered to 1067 students in grades 7–9 from schools in east Java, Indonesia, and their scores were converted into a logit scale for statistical analysis. The results of a one-way analysis of variance and an independent sample t -test showed that the students had an average level of mathematical problem-solving skills. The number of students who failed increased with the problem-solving phase. The students showed development of problem-solving skills from grade 7 to grade 8 but not in grade 9. A similar pattern of development was observed in the subsample of urban students, both male and female. The demographic background had a significant effect, as students from urban schools outperformed students from rural schools, and female students outperformed male students. The development of problem-solving skills in each phase as well as the effects of the demographic background of the participants were thoroughly examined. Further studies are needed with participants of more varied backgrounds.

1. Introduction

Problem-solving skills are a complex set of cognitive, behavioral, and attitudinal components that are situational and dependent on thorough knowledge and experience [ 1 , 2 ]. Problem-solving skills are acquired over time and are the most widely applicable cognitive tool [ 3 ]. Problem-solving skills are particularly important in mathematics education [ 3 , 4 ]. The development of mathematical problem-solving skills can differ based on age, gender stereotypes, and school locations [ [5] , [6] , [7] , [8] , [9] , [10] ]. Fostering the development of mathematical problem-solving skills is a major goal of educational systems because they provide a tool for success [ 3 , 11 ]. Mathematical problem-solving skills are developed through explicit training and enriching materials [ 12 ]. Teachers must understand how student profiles influence the development of mathematical problem-solving skills to optimize their teaching methods.

Various studies on the development of mathematical problem-solving skills have yielded mixed results. Grissom [ 13 ] concluded that problem-solving skills were fixed and immutable. Meanwhile, other researchers argued that problem-solving skills developed over time and were modifiable, providing an opportunity for their enhancement through targeted educational intervention when problem-solving skills developed quickly [ 3 , 4 , 12 ]. Tracing the development of mathematical problem-solving skills is crucial. Further, the results of previous studies are debatable, necessitating a comprehensive study in the development of students’ mathematical problem-solving skills.

Differences in mathematical problem-solving skills have been identified based on gender and school location [ [6] , [7] , [8] , [9] , [10] ]. School location affects school segregation and school quality [ 9 , 14 ]. The socioeconomic and sociocultural characteristics of a residential area where a school is located are the factors affecting academic achievement [ 14 ]. Studies in several countries have shown that students in urban schools demonstrated better performance and problem-solving skills in mathematics [ 9 , 10 , 15 ]. However, contradictory results have been obtained for other countries [ 6 , 10 ].

Studies on gender differences have shown that male students outperform female students in mathematics, which has piqued the interest of psychologists, sociologists, and educators [ 7 , 16 , 17 ]. The differences appear to be because of brain structure; however, sociologists argue that gender equality can be achieved by providing equal educational opportunities [ 8 , 16 , 18 , 19 ]. Because the results are debatable and no studies on gender differences across grades in schools have been conducted, it would be interesting to investigate gender differences in mathematical problem-solving skills.

Based on the previous explanations, teachers need to understand the best time for students to develop mathematical problem-solving skills because problem-solving is an obligatory mathematics skill to be mastered. However, no relevant studies focused on Indonesia have been conducted regarding the mathematical problem-solving skill development of students in middle school that can provide the necessary information for teachers. Further, middle school is the important first phase of developing critical thinking skills; thus relevant studies are required in this case [ 3 , 4 ]. In addition, a municipal policy-making system can raise differences in problem-solving skills based on different demographic backgrounds [ 10 ]. Moreover, the results of previous studies regarding the development and differences in mathematical problem-solving skills are debatable. Thus, the present study has been conducted to meet these gaps. This study investigated the development of mathematical problem-solving skills in students and the differences owing demographic backgrounds. Three aspects were considered: (1) student profiles of mathematical problem-solving skills, (2) development of their mathematical problem-solving skills across grades, and (3) significant differences in mathematical problem-solving skills based on gender and school location. The results of the present study will provide detailed information regarding the subsample that contributes to the development of mathematical problem-solving skills in students based on their demographic backgrounds. In addition, the description of the score is in the form of a logit scale from large-scale data providing consistent meaning and confident generalization. This study can be used to determine appropriate teaching and learning in the best period of students’ development in mathematical problem-solving skills as well as policies to achieve educational equality.

2. Theoretical background

2.1. mathematical problem-solving skills and their development.

Solving mathematical problems is a complex cognitive ability that requires students to understand the problem as well as apply mathematical concepts to them [ 20 ]. Researchers have described the phases of solving a mathematical problem as understanding the problem, devising a plan, conducting out the plan, and looking back [ [20] , [24] , [21] , [22] , [23] ]. Because mathematical problems are complex, students may struggle with several phases, including applying mathematical knowledge, determining the concepts to use, and stating mathematical sentences (e.g., arithmetic) [ 20 ]. Studies have concluded that more students fail at later stages of the solution process [ 25 , 26 ]. In other words, fewer students fail in the phase of understanding a problem than during the plan implementation phase. Different studies have stated that students face difficulties in understanding the problem, determining what to assume, and investigating relevant information [ 27 ]. This makes them unable to translate the problem into a mathematical form.

Age or grade is viewed as one factor that influences mathematical problem-solving skills because the skills of the students improve over time as a result of the teaching and learning processes [ 28 ]. Neuroscience research has shown that older students have fewer problems with arithmetic than younger students; however, the hemispheric asymmetry is reduced [ 29 ]. In other words, older students are more proficient, but their flexibility to switch among different strategies is less. Ameer & Sigh [ 28 ] obtained similar results and found a considerable difference in mathematical achievement; specifically, older students performed better than younger students in number sense and computation using one-way analysis of variance (ANOVA) ( F ) of F (2,411) = 4.82, p  < 0.01. Molnár et al. [ 3 ] found that the student grade affects domain-specific and complex problem-solving skills. They observed that the development of problem-solving skills was noticeable across grades in elementary school but stopped in secondary school. The fastest development of domain-specific problem-solving occurred in grades 7 and 8 [ 3 ], but the fastest development of complex problem-solving occurred in grades 5–7 [ 3 ]. No development was detected between grades 4 and 5 as well as grades 6 and 7 for domain-specific and complex problem-solving skills, respectively. Similarly, Greiff et al. [ 4 ] concluded that students developed problem-solving skills across grades 5–11 with older students being more skilled. However, the grade 9 students deviated from the development pattern, and their problem-solving skills dropped. The theories from Molnár et al. [ 3 ] and Greiff et al. [ 4 ] are the benchmark cases herein.

The above studies showed that problem-solving skills mostly developed during compulsory schooling and developed most quickly in specific grades. This indicates that specific development times can be targeted to enhance the problem-solving skills [ 3 ]. However, Jabor et al. [ 30 ] observed contradictory results showing statistically significant differences with small effects in mathematical performance between age groups: those under the age of 19 outperformed those over the age of 19 years old. Grissom [ 13 ] observed a negative correlation between age and school achievement that remained constant over time.

2.2. Effects of school location and gender on mathematical problem-solving skills

School location has been shown to affect mathematical achievement [ 9 , 14 ]. In 15 countries, students in rural schools performed considerably worse than students in urban schools in mathematics [ 9 , 10 ], science and reading [ 9 ]. In addition, Nepal [ 15 ] discovered that urban students significantly outperformed rural students in mathematical problem-solving skills ( t  = −5.11, p  < 0.001) and achievement ( t  = −4.45, p  < 0.001) using the results of an independent sample t -test (t). However, other countries have found that rural students outperformed urban students in mathematics [ 6 , 10 ]. These variations may be attributed to a lack of instructional resources (e.g., facilities, materials, and programs), professional training (e.g., poorly trained teachers), and progressive instruction [ 6 ]. The results of Williams's study [ 10 ] serve as the basis for the current study.

Gender differences in mathematics have received attention because studies show that male students outperform female students on higher-level cognitive tasks [ 31 ]. This is a shift from a meta-analysis study that found gender differences in mathematics to be insignificant and favored female students [ 32 ]. At the college level, female students slightly outperform male students in computation while male students outperform female students in problem solving. However, no gender differences have been observed among elementary and middle school students. This result was strengthened by other meta-analysis studies [ 7 , 8 ], which concluded that there was no gender difference in mathematical performance and problem-solving skills [ 15 , [33] , [35] , [34] ]. Gender similarity in mathematics is achieved when equal learning opportunities and educational choices are provided and the curriculum is expanded to include the needs and interests of the students [ 16 , 18 , 31 ].

From a sociological perspective, gender similarity in mathematics makes sense. If there is a gender difference in mathematics, this has been attributed to science, technology, engineering, and mathematics (STEM) being stereotyped as a male domain [ 8 ]. Stereotypes influence beliefs and self-efficacy of students and perceptions of their own abilities [ 8 , 19 ]. This is the reason for the low interest of female students in advanced mathematics courses [ 18 , 19 ]. However, Halpern et al. [ 16 ] found that more female students are entering many occupations that require a high level of mathematical knowledge. Moreover, Anjum [ 36 ] found that female students outperformed male students in mathematics. This may be because female students prepared better than the male students before the test and were more thorough [ 36 , 37 ]. The study of Anjum [ 36 ] is one of the basis cases of the current study.

Differences in brain structure support the argument that there are gender differences in mathematical performance [ 16 , 17 ]. Females have less brain lateralization (i.e., symmetric left and right hemispheres), which helps them perform better verbally. Meanwhile, males have more brain lateralization, which is important for spatial tasks [ 17 ]. In addition, the male hormone testosterone slows the development of the left hemisphere [ 16 ], which improves the performance of right brain-dominant mathematical reasoning and spatial tasks.

3.1. Instrumentation

In this study, a science-related mathematical problem-solving test was used. This is a mathematics essay test where the problems are in the form of scenarios related to environmental management. Problems are solved by using technology as a tool (e.g., calculator, grid paper). The test was developed in an interdisciplinary STEM framework, and it is targeted toward grades 7–9. There were six scenarios in total: some were given to multiple grades, and others were specific to a grade. They included ecofriendly packaging (grade 7), school park (grade 7), calorie vs. greenhouse gas emissions (grades 7–9), floodwater reservoir (grade 8), city park (grades 8–9), and infiltration well (grade 9). These scenarios cover topics such as number and measurement, ratio and proportion, geometry, and statistics. Every scenario had a challenge, and students were provided with eight metacognitive prompt items to help them explore their problem-solving skills.

The test was administered by using paper and pencils for a 3-h period with a break every hour. At the end of the test, students were asked to fill in their demographic information. Each prompt item had a maximum score of 5 points: a complete and correct answer (5 points), a complete answer with a minor error (4 points), an incomplete answer with a minor error (3 points), an incomplete answer with a major error (2 points), and a completely wrong and irrelevant answer (1 point). Each scenario had a maximum total score of 40 points.

The test was validated to determine whether it contained good and acceptable psychometric evidence. It had an acceptable content validity index (CVI >0.67), moderate intraclass correlation coefficient (ICC) (rxx = 0.63), and acceptable Cronbach's alpha (α = 0.84). The construct validity indicated all scenarios and prompt items were fit (0.77 ≤ weighted mean square ≤1.59) with an acceptable discrimination value (0.48 ≤ discrimination value ≤ 0.93), acceptable behavior of the rating score, and good reliability (scenario reliability = 0.86; prompt item reliability = 0.94).

3.2. Participants

The test was administered to grades 7–9 students in east Java, Indonesia (n = 1067). The students were selected from A-accreditation schools in urban and rural areas; random classes were selected for each grade. The majority of the students were Javanese (95.01%), with the remainder being Madurese (3.3%) and other ethnicities. Table 1 describes the demographics of the participants.

Demographic characteristics of participants.

3.3. Data analysis

Data were collected between July and September 2022. Prior to data collection, ethical approval was sought from the institutional review board (IRB) of the Doctoral School of Education, University of Szeged and was granted with the ethical approval number of 7/2022. In addition, permission letters were sent to several schools to request permission and confirm their participation. The test answers of the students were scored by two raters – the first author of this study and a rater with master's degree in mathematics education – to ensure that the rating scale was consistently implemented. The results showed good consistency with an ICC of 0.992 and Cronbach's alpha of 0.996.

The scores from one of the raters were converted to a logit scale by weighted likelihood estimation (WLE) using the ConQuest software. A logit scale provides a consistent value or meaning in the form of intervals. The logit scale represents the unit interval between locations on the person–item map. WLE was chosen rather than maximum likelihood estimation (MLE) because WLE is more central than MLE, which helps to correct for bias [ 38 ]. The WLE scale was represented by using descriptive statistics to profile the students' mathematical problem-solving skills in terms of the percentage, mean score ( M ) and standard deviation ( SD ) for each phase. The WLE scale was also used to describe common difficulties for each phase. The development of students’ mathematical problem-solving skills across grades was presented by a pirate plot, which is used in R to visualize the relationship between 1 and 3 categorical independent variables and 1 continuous dependent variable. It was chosen because it displays raw data, descriptive statistics, and inferential statistics at the same time. The data analysis was performed using R studio version 4.1.3 software with the YaRrr package. A one-way ANOVA was performed to find significant differences across grades. An independent sample t -test was used to analyze significant differences based on gender and school location. The descriptive statistics, one-way ANOVA test, and independent sample t -test were performed using the IBM SPSS Statistics 25 software.

4.1. Student profiles

The scores of students were converted to the WLE scale, where a score of zero represented a student with average ability, a positive score indicated above-average ability, and a negative score indicated below-average ability. A higher score indicated higher ability. The mean score represented a student with average mathematical problem-solving skills ( M  = 0.001, SD  = 0.39). Overall, 52.1% of students had a score below zero. The distribution of scores among students was predominantly in the interval between −1 and 0. When the problem-solving process was analyzed by phase, the results showed that exploring and understanding were the most mastered problem-solving skills ( M  = 0.24, SD  = 0.51). Only 27.9% of students had below-average scores for the exploring and understanding phases, which indicates that they mostly understood the given problem and recognized the important information. However, the problem-solving skills decreased with higher phases. The students had below-average abilities in the phases of representing and formulating ( M  = −0.01, SD  = 0.36), planning and executing ( M  = −0.15, SD  = 0.41), and monitoring and reflecting ( M  = −0.16, SD  = 0.36). About 57.9% of the students had below-average scores for the representing and formulating phase, which indicates that they had problems making hypotheses regarding science phenomena, representing problems in mathematical form, and designing a prototype. The obvious reason for their difficulty with making hypotheses was that they did not understand simple concepts of science (e.g., CO 2 vs. O 2 ). In the planning and executing phase, 66.8% of the students failed to achieve a score greater than zero. This happened because they failed to apply mathematical concepts and procedures. Because they were unable to plan and execute a strategy, this affected the next phase of the problem-solving process. In the monitoring and reflecting phase, 68.0% of the students had a below-average score.

4.2. Development of mathematical problem-solving skills across grades

The development of the mathematical problem-solving skills of the students across grades was observed based on the increase in the mean score. The problem-solving skills developed from grade 7 to grade 8. The students of grade 7 had a mean score of −0.04 while grade 8 students had the highest mean score of 0.03. The students in grades 7 and 8 also showed more varied problem-solving skills than the grade 9 students did. In contrast, the grade 9 students showed a different pattern of development, and their mean score dropped to 0.01. Although the difference was not large, further analysis was needed to determine its significance.

Fig. 1 displays the development of the mathematical problem-solving skills of the students. The dots represent raw data or WLE scores. The middle line shows the mean score. The beans represent a smoothed density curve showing the full data distribution. The scores of the students in grades 7 and 9 were concentrated in the interval between −0.5 and 0. However, the scores of the grade 8 students were concentrated in the interval between 0 and 0.5. The scores of the students in grades 7 and 8 showed a wider distribution than those of the grade 9 students. The bands which overlap with the line representing the mean score, define the inference around the mean (i.e., 95% of the data are in this interval). The inference of the WLE score was close to the mean.

Differences in students' mathematical problem-solving skills across grades.

Note : PS: Problem-Solving Skills of Students.

The one-way ANOVA results indicated a significant difference among the problem-solving skills of the students of grades 7–9 ( F (1,066) = 3.01, p  = 0.046). The students of grade 8 showed a significant difference in problem-solving skills and outperformed the other students. The students of grades 7 and 9 showed no significant difference in their mathematical problem-solving skills. Table 2 presents the one-way ANOVA results of the mathematical problem-solving skills across grades.

One-way ANOVA results of the mathematical problem-solving across grades.

Note. Post hoc test: Dunnett's T3. 7, 8, and 9: subsample grade. <: direction of significant difference ( p  < 0.05).

Fig. 2 shows the development of the mathematical problem-solving skills of the students across grades based on school location and gender. The problem-solving skills of the urban students increased from a mean score of 0.07 in grade 7 to 0.14 in grade 8. However, the mean score of urban students in grade 9 dropped. In contrast, the mean scores of the rural students increased continuously with grade. The improvements were significant for both the rural ( F (426) = 10.10, p  < 0.001) and urban ( F (639) = 6.10, p  < 0.01) students. For the rural students, grade 9 students showed a significant difference in problem-solving skills. In contrast, urban students in grades 8 and 9 showed significant differences in problem-solving skills but not in grade 7.

Differences in students' mathematical problem-solving skills across grades and different demographic backgrounds.

(a) Differences in students grade 7 of mathematical problem-solving skills across grades and different demographic backgrounds

(b) Differences in students grade 8 of mathematical problem-solving skills across grades and different demographic backgrounds

(c) Differences in students grade 9 of mathematical problem-solving skills across grades and different demographic backgrounds

Note: WLE_PS: The students' problem-solving skills in WLE scale; F: Female; M: Male; ScLoc: School location; R: Rural; U: Urban.

When divided by gender, both female and male students showed improvements in their problem-solving skills from grades 7 and 8. However, female students in grade 9 showed a stable score while the scores of male students in grade 9 declined. Only male students in grade 7 showed a significant difference in the mean score. In urban schools, the scores of male and female students increased and decreased, respectively, from grade 7 to grade 8. Male students in rural schools showed an increase in score from grade 7 to grade 9. However, the scores of female students in rural schools decreased from grade 7 to grade 8. Table 3 presents the one-way ANOVA results for the mathematical problem-solving skills of the students considering gender and school location.

One-way ANOVA results for mathematical problem-solving skills across grades and different demographic backgrounds.

Fig. 2 shows that the distributions of the male and female scores of students were similar for every grade except rural grade 9 students. The scores of the rural female students were concentrated in the interval between 0 and 0.5 while the scores of the rural male students were mostly below 0. The scores of rural students in grade 7 and urban students in grade 9 (both male and female) were concentrated in the interval between −0.5 and 0. The scores of urban students in grades 7 and 8 were concentrated in the interval between −0.5 and 0.5.

Fig. 3 shows a detailed analysis of the development of mathematical problem-solving skills across grades for each phase of the problem-solving process. Similar patterns were observed in the exploring and understanding and the representing and formulating phases: the mean score increased from grade 7 to grade 8 but decreased from grade 8 to grade 9. Grade 8 students had the highest mean score and differed significantly from the scores of students in other grades.

Differences in students' mathematical problem-solving skills in every phase across grades: (1) Exploring & understanding, (2) Representing & formulating, (3) Planning & executing, (4) Monitoring & reflecting.

(a) Differences in students' mathematical problem-solving skills in exploring and understanding phase

(b) Differences in students' mathematical problem-solving skills in representing and formulating phase

(c) Differences in students' mathematical problem-solving skills in planning and executing phase

(d) Differences in students' mathematical problem-solving skills in monitoring and reflecting phase

Note: WLE_Exp_Un: The WLE score in exploring and understanding; WLE_Rep_For: The WLE score in representing and formulating; WLE_Plan_Ex: The WLE score in planning and executing; WLE_Mon_Ref: The WLE score in monitoring and reflecting.

The scores of the students for the planning and executing phase increased with grade. However, the difference was only significant at grade 9. Grades 7 and 8 students showed an increase in score, but the improvement was not significant. There was no pattern detected in the monitoring and reflecting phase. The score was stable for grades 7 and 8 students but improved for grade 9 students. The mean score for each phase and the one-way ANOVA results are presented in Table 4 .

One-way ANOVA results for every phase of problem-solving across grades.

Fig. 3 shows that the distributions of the problem-solving skills of the students were similar across grades and phases. However, the distributions were different for grade 9 students in the representing and formulating, planning and executing, and monitoring and reflecting phases, where 95% of the data were in the interval between −0.5 and 0.5.

4.3. Effects of demographic background

4.3.1. school location.

The mathematical problem-solving skills of the students differed significantly based on school location. Urban students scored higher than rural students. The results of the t -test for mathematical problem-solving skills based on school location are presented in Table 5 .

T-test results for mathematical problem-solving skills based on school location.

The effects of the school's location on the performances of male and female students were analyzed. The results showed that the scores of the female students differed significantly based on school location ( t (613) = −6.09, p  < 0.001). Female students in urban schools ( M  = 0.18, SD  = 0.39) outperformed female students in rural schools ( M  = −0.08, SD  = 0.37). Similar results were observed for male students with urban students ( M  = −0.01, SD  = 0.35) outperforming rural students ( M  = −0.12, SD  = 0.39) by a significant margin ( t (382.764) = −3.25, p  < 0.01).

When analyzed by grade, grades 7 and 8 students contributed to the difference based on school location with t (377.952) = −6.34, p  < 0.001 and t (300.070) = −5.04, p  < 0.001, respectively. Urban students in grades 7 and 8 performed significantly better than their rural counterparts did. However, there was no significant difference between rural and urban students in grade 9 ( t (354) = 0.71, p  = 0.447).

4.3.2. Gender

Male and female students showed a significant difference in their mathematical problem-solving skills. Overall, female students outperformed male students. The detailed results of the independent sample t -test for mathematical problem-solving skills based on gender are presented in Table 6 .

T-test results for mathematical problem-solving skills based on gender.

The results were analyzed to determine whether the school location contributed to the gender difference. The gender difference was most significant among urban students ( t (596.796) = −4.36, p  < 0.001). Female students from urban schools ( M  = 0.12, SD  = 0.39) outperformed male students from urban schools ( M  = −0.01, SD  = 0.35). There was no significant difference between female and male students from rural schools ( t (425) = −1.31, p  = 0.191).

Grades 7 and 9 students contributed to the gender difference with t (372.996) = −3.90, p  < 0.001 and t (354) = −2.73, p  < 0.01, respectively. Female students in grades 7 and 9 outperformed their male counterparts. However, there was no significant gender difference among grade 8 students ( t (329) = −0.10, p  = 0.323).

5. Discussion

The mathematical problem-solving skills of the students were categorized as average. In addition, the difficulties of students increased in line with the problem-solving phase. Fewer students failed the exploring and understanding phase than the subsequent phases. This confirms the results of previous studies indicating that more students failed further along the problem-solving process [ 25 , 26 ]. Because the problem-solving process is sequential, students who have difficulty understanding a problem will fail the subsequent phases [ 27 ].

The development of mathematical problem-solving skills was evaluated according to the mean WLE score. The mathematical problem-solving skills of the students developed from grade 7 to grade 8 based on the increase in their mean scores. However, the development dropped in grade 9. This agrees with previous results that concluded that higher grades had the highest problem-solving skills, but the fastest skill development took place in grades 7–8 after which it dropped [ 3 , 4 ]. These results indicate that the mathematical problem-solving skills of the students should improve and be strengthened in grades 7–8, which will help them perform better in grade 9.

In this study, the effects of the demographic background of the students were analyzed in detail, which is an aspect missing from previous studies. The results showed that the mathematical problem-solving skills of urban students increased from grade 7 to grade 8 but decreased in grade 9. The same pattern was found among male and female students. However, a different pattern was observed for rural students, where the skills of grade 9 students continued to increase. The different patterns may be attributed to a structural reorganization of cognitive processes at a particular age [ 3 ]. However, more research is needed on the effects of the demographic backgrounds of students on mathematical problem-solving skills. These results were different from previous results because the previous studies only analyzed the development in general, without focusing on their demographic background. Hence, different patterns of development were observed when it was thoroughly examined.

Because solving problems is a cognitive process, the development of problem-solving skills for particular phases and processes needed to be analyzed. The students showed the same pattern for knowledge acquisition (i.e., exploring and understanding, and representing and formulating phases), with an increase in skill from grade 7 to grade 8 but a decrease in grade 9. However, the students showed increasing skill in knowledge application (i.e., planning and executing, as well as monitoring and reflecting phases) across grades. This means that the difference between the mean scores in grade 9 was not significant across phases. Grade 9 students had lower scores than grade 8 students for the knowledge acquisition phase but higher scores for the knowledge application phase. In contrast, the gap between the mean scores of grades 7 and 8 was large across phases.

These results proved that there is a significant difference in the mathematical problem-solving skills of students based on their demographic backgrounds. The urban students outperformed rural students, which confirms the results of previous studies [ 9 , 10 , 15 ]. The difference can be attributed to the availability of facilities, teacher quality, and interactive teaching and learning instruction [ 6 ]. In Indonesia, the policies for the public educational system for middle schools are set at the municipal level. This means that each city has its own policies for teacher training, teacher recruitment, teaching and learning processes, facilities, etc. Urban schools mostly have stricter policies as well as various programs to help students improve their knowledge and skills. In addition, they have supportive facilities for teaching and learning. This unequal environment is the strongest reason for the difference in mathematical problem-solving skills.

The results were analyzed in detail to observe which groups in the rural and urban schools contributed to the difference. Both male and female students in urban schools performed better than their counterparts in rural schools did. In addition, urban students in grades 7 and 8 outperformed their rural counterparts. There was no significant difference between urban and rural students in grade 9. This may be because grade 9 is the last grade in middle school, so students have to prepare for high school entrance requirements, including exam and/or grade point average scores. Hence, both rural and urban schools focus much effort on the teaching and learning process in this grade.

In this study, the female students surprisingly had better mathematical problem-solving skills than the male students did. This confirmed the results of the meta-analysis by Hyde et al. [ 32 ] and study by Anjum [ 36 ], which found that female students slightly outperformed male students in mathematics. This difference may be because of motivation and attitude [ 39 , 40 ]. Female Indonesian students are typically more diligent, thorough, responsible, persistent, and serious with their tasks.

A detailed analysis was performed to evaluate which group of students contributed to the gender differences. The results showed that female students outperformed male students in urban schools. This may be because male students at urban schools typically display an unserious attitude toward low-stake tests. In addition, female students outperformed their male counterparts in grades 7 and 9. The reason for this difference requires further analysis.

6. Conclusion

Studying the problem-solving skills of students is crucial to facilitating their development. In this study, the conclusions are presented as follows:

• • The mathematical problem-solving skills of the students were categorized as average. More students failed at higher phases of the problem-solving process.
• • Students showed development of their mathematical problem-solving skills from grade 7 to grade 8 but a decline in grade 9. The same pattern was detected across grades for urban students, both female and male. However, the problem-solving skills of rural students increased with the grade.
• • A similar development was observed for the individual problem-solving phases. In the knowledge acquisition phase, the problem-solving skills of the students developed from grade 7 to grade 8 but decreased in grade 9. However, problem-solving skills increased across grades in the knowledge application phase.
• • The school location was shown to have a significant effect on the mathematical problem-solving skills of the students. Urban students generally outperform students in rural schools. However, gender and grade contributed to differences in mathematical problem-solving skills based on school location. Female and male urban students in grades 7 and 8 outperformed their rural counterparts.
• • In general, female students outperformed male students in mathematical problem-solving skills, particularly those from urban schools and in grades 7 and 9.

The sampling method and the number of demographic backgrounds limited the scope of this study. Only students from A-accreditation schools were selected because higher-order problem-solving skills were considered assets. Moreover, the study only included three demographic factors: grade, gender, and school location. More demographic information, such as school type, can be added (public or private schools). Hence, future studies will need to broaden the sample size and consider more demographic factors. Despite these limitations, this study can help teachers determine the best period for enhancing the development of mathematical problem-solving skills. Moreover, the differences in mathematical problem-solving skills due to demographic background can be used as a basis for educational policymakers and teachers to provide equal opportunity and equitable education to students.

Author contribution statement

Ijtihadi Kamilia Amalina: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Tibor Vidákovich: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.

Funding statement

This work was supported by University of Szeged Open Access Fund with the grant number of 6020.

Data availability statement

Additional information.

No additional information is available for this paper.

Declaration of competing interest

No potential conflict of interest was reported by the authors.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Use a Problem Solving Strategy

• Last updated
• Save as PDF
• Page ID 29036

Learning Objectives

By the end of this section, you will be able to:

• Use a problem solving strategy for word problems
• Solve number word problems
• Solve percent applications
• Solve simple interest applications

Before you get started, take this readiness quiz.

• Translate “six less than twice \(x\)” into an algebraic expression. If you missed this problem, review [link] .
• Convert 4.5% to a decimal. If you missed this problem, review [link] .
• Convert 0.6 to a percent. If you missed this problem, review [link] .

Have you ever had any negative experiences in the past with word problems? When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. Realize that your negative experiences with word problems are in your past. To move forward you need to calm your fears and change your negative feelings.

Start with a fresh slate and begin to think positive thoughts. Repeating some of the following statements may be helpful to turn your thoughts positive. Thinking positive thoughts is a first step towards success.

• I think I can! I think I can!
• While word problems were hard in the past, I think I can try them now.
• I am better prepared now—I think I will begin to understand word problems.
• I am able to solve equations because I practiced many problems and I got help when I needed it—I can try that with word problems.
• It may take time, but I can begin to solve word problems.
• You are now well prepared and you are ready to succeed. If you take control and believe you can be successful, you will be able to master word problems.

Use a Problem Solving Strategy for Word Problems

Now that we can solve equations, we are ready to apply our new skills to word problems. We will develop a strategy we can use to solve any word problem successfully.

EXAMPLE \(\PageIndex{1}\)

Normal yearly snowfall at the local ski resort is 12 inches more than twice the amount it received last season. The normal yearly snowfall is 62 inches. What was the snowfall last season at the ski resort?

Try It! \(\PageIndex{1}\)

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was three more than twice the number of notebooks. He bought seven textbooks. How many notebooks did he buy?

He bought two notebooks

Try It! \(\PageIndex{2}\)

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?

He did seven crossword puzzles

We summarize an effective strategy for problem solving.

PROBLEM SOLVING STRATEGY FOR WORD PROBLEMS

• Read the problem. Make sure all the words and ideas are understood.
• Identify what you are looking for.
• Name what you are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
• Solve the equation using proper algebra techniques.
• Check the answer in the problem to make sure it makes sense.
• Answer the question with a complete sentence.

Solve Number Word Problems

We will now apply the problem solving strategy to “number word problems.” Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.

EXAMPLE \(\PageIndex{2}\)

The sum of seven times a number and eight is thirty-six. Find the number.

Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.

Try It! \(\PageIndex{3}\)

The sum of four times a number and two is fourteen. Find the number.

Try It!  \(\PageIndex{4}\)

The sum of three times a number and seven is twenty-five. Find the number.

Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far, we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

EXAMPLE \(\PageIndex{3}\)

The sum of two numbers is negative fifteen. One number is nine less than the other. Find the numbers.

Try It!  \(\PageIndex{5}\)

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

\(−15,−8\)

Try It!  \(\PageIndex{6}\)

The sum of two numbers is negative eighteen. One number is forty more than the other. Find the numbers.

\(−29,11\)

Some number problems involve consecutive integers . Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:

\[\begin{array}{rrrr} 1, & 2, & 3, & 4 \\ −10, & −9, & −8, & −7\\ 150, & 151, & 152, & 153 \end{array}\nonumber\]

Notice that each number is one more than the number preceding it. Therefore, if we define the first integer as \(n,\) the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\).

\[\begin{array}{ll} n & 1^{\text{st}} \text{integer} \\ n+1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; & 2^{\text{nd}}\text{consecutive integer} \\ n+2 & 3^{\text{rd}}\text{consecutive integer} \;\;\;\;\;\;\;\; \text{etc.} \end{array}\nonumber\]

We will use this notation to represent consecutive integers in the next example.

EXAMPLE \(\PageIndex{4}\)

Find three consecutive integers whose sum is \(−54\).

Try It!  \(\PageIndex{7}\)

Find three consecutive integers whose sum is \(−96\).

\(−33,−32,−31\)

Try It!  \(\PageIndex{8}\)

Find three consecutive integers whose sum is \(−36\).

\(−13,−12,−11\)

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers . Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

\[24, 26, 28\nonumber\]

\[−12,−10,−8\nonumber\]

Notice each integer is two more than the number preceding it. If we call the first one \(n,\) then the next one is \(n+2\). The one after that would be \(n+2+2\) or \(n+4\).

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 63, 65, and 67.

\[63, 65, 67\nonumber\]

\[n,n+2,n+4\nonumber\]

Does it seem strange to have to add two (an even number) to get the next odd number? Do we get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you do not have to do anything different. The pattern is still the same—to get to the next odd or the next even integer, add two.

EXAMPLE \(\PageIndex{5}\)

Find three consecutive even integers whose sum is \(120\).

Try It!  \(\PageIndex{9}\)

Find three consecutive even integers whose sum is 102.

\(32, 34, 36\)

Try It!  \(\PageIndex{10}\)

Find three consecutive even integers whose sum is \(−24\).

\(−10,−8,−6\)

When a number problem is in a real life context, we still use the same strategies that we used for the previous examples.

EXAMPLE \(\PageIndex{6}\)

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,400. This was $1,600 less than six times the cost in 1975. What was the average cost of a car in 1975?

The average cost was $5,000.

Try It!  \(\PageIndex{11}\)

US Census data shows that the median price of new home in the U.S. in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?

The median price was $19,300.

Solve Percent Applications

There are several methods to solve percent equations. In algebra, it is easiest if we just translate English sentences into algebraic equations and then solve the equations. Be sure to change the given percent to a decimal before you use it in the equation.

EXAMPLE \(\PageIndex{7}\)

Translate and solve:

• What number is 45% of 84?
• 8.5% of what amount is $4.76?
• 168 is what percent of 112?

Try It!  \(\PageIndex{12}\)

• What number is 45% of 80?
• 7.5% of what amount is $1.95?
• 110 is what percent of 88?

a. 36   b. $26   c. \(125 \% \)

Try It!  \(\PageIndex{13}\)

• What number is 55% of 60?
• 8.5% of what amount is $3.06?
• 126 is what percent of 72?

a. 33   b. $36   c. \(175 \% \)

Now that we have a problem solving strategy to refer to, and have practiced solving basic percent equations, we are ready to solve percent applications. Be sure to ask yourself if your final answer makes sense—since many of the applications we will solve involve everyday situations, you can rely on your own experience.

EXAMPLE \(\PageIndex{8}\)

The label on Audrey’s yogurt said that one serving provided 12 grams of protein, which is 24% of the recommended daily amount. What is the total recommended daily amount of protein?

Try It!  \(\PageIndex{14}\)

One serving of wheat square cereal has 7 grams of fiber, which is 28% of the recommended daily amount. What is the total recommended daily amount of fiber?

Try It!  \(\PageIndex{15}\)

One serving of rice cereal has 190 mg of sodium, which is 8% of the recommended daily amount. What is the total recommended daily amount of sodium?

Remember to put the answer in the form requested. In the next example we are looking for the percent.

EXAMPLE \(\PageIndex{9}\)

Veronica is planning to make muffins from a mix. The package says each muffin will be 240 calories and 60 calories will be from fat. What percent of the total calories is from fat?

Try It!  \(\PageIndex{16}\)

Mitzi received some gourmet brownies as a gift. The wrapper said each 28% brownie was 480 calories, and had 240 calories of fat. What percent of the total calories in each brownie comes from fat? Round the answer to the nearest whole percent.

Try It!  \(\PageIndex{17}\)

The mix Ricardo plans to use to make brownies says that each brownie will be 190 calories, and 76 calories are from fat. What percent of the total calories are from fat? Round the answer to the nearest whole percent.

It is often important in many fields—business, sciences, pop culture—to talk about how much an amount has increased or decreased over a certain period of time. This increase or decrease is generally expressed as a percent and called the percent change .

To find the percent change, first we find the amount of change, by finding the difference of the new amount and the original amount. Then we find what percent the amount of change is of the original amount.

FIND PERCENT CHANGE

\[\text{change}= \text{new amount}−\text{original amount}\]

change is what percent of the original amount?

EXAMPLE \(\PageIndex{10}\)

Recently, the California governor proposed raising community college fees from $36 a unit to $46 a unit. Find the percent change. (Round to the nearest tenth of a percent.)

Try It!  \(\PageIndex{18}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 2011, the IRS increased the deductible mileage cost to 55.5 cents from 51 cents.

\(8.8 \% \)

Try It!  \(\PageIndex{19}\)

Find the percent change. (Round to the nearest tenth of a percent.) In 1995, the standard bus fare in Chicago was $1.50. In 2008, the standard bus fare was 2.25.

Applications of discount and mark-up are very common in retail settings.

When you buy an item on sale, the original price has been discounted by some dollar amount. The discount rate , usually given as a percent, is used to determine the amount of the discount . To determine the amount of discount, we multiply the discount rate by the original price.

The price a retailer pays for an item is called the original cost . The retailer then adds a mark-up to the original cost to get the list price , the price he sells the item for. The mark-up is usually calculated as a percent of the original cost. To determine the amount of mark-up, multiply the mark-up rate by the original cost.

\[ \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\]

The sale price should always be less than the original price.

\[\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\]

The list price should always be more than the original cost.

EXAMPLE \(\PageIndex{11}\)

Liam’s art gallery bought a painting at an original cost of $750. Liam marked the price up 40%. Find

• the amount of mark-up and
• the list price of the painting.

Try It!  \(\PageIndex{20}\)

Find a. the amount of mark-up and b. the list price: Jim’s music store bought a guitar at original cost $1,200. Jim marked the price up 50%.

a. $600 b. $1,800

Try It!  \(\PageIndex{21}\)

Find a. the amount of mark-up and b. the list price: The Auto Resale Store bought Pablo’s Toyota for $8,500. They marked the price up 35%.

a. $2,975 b. $11,475

Solve Simple Interest Applications

Interest is a part of our daily lives. From the interest earned on our savings to the interest we pay on a car loan or credit card debt, we all have some experience with interest in our lives.

The amount of money you initially deposit into a bank is called the principal , \(P,\) and the bank pays you interest, \(I.\) When you take out a loan, you pay interest on the amount you borrow, also called the principal.

In either case, the interest is computed as a certain percent of the principal, called the rate of interest , \(r.\) The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable \(t,\) (for time) represents the number of years the money is saved or borrowed.

Interest is calculated as simple interest or compound interest. Here we will use simple interest.

SIMPLE INTEREST

If an amount of money, \(P,\) called the principal, is invested or borrowed for a period of \(t\) years at an annual interest rate \(r,\) the amount of interest, \(I,\) earned or paid is

\[ \begin{array}{ll} I=Prt \; \; \; \; \; \; \; \; \; \; \; \; \text{where} & { \begin{align*} I &= \text{interest} \\ P &= \text{principal} \\ r &= \text{rate} \\ t &= \text{time} \end{align*}} \end{array}\]

Interest earned or paid according to this formula is called simple interest .

The formula we use to calculate interest is \(I=Prt\). To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.

EXAMPLE \(\PageIndex{12}\)

Areli invested a principal of $950 in her bank account that earned simple interest at an interest rate of 3%. How much interest did she earn in five years?

\( \begin{aligned} I & = \; ? \\ P & = \; \$ 950 \\ r & = \; 3 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\begin{array}{ll} \text{Identify what you are asked to find, and choose a} & \text{What is the simple interest?} \\ \text{variable to represent it.} & \text{Let } I= \text{interest.} \\ \text{Write the formula.} & I=Prt \\ \text{Substitute in the given information.} & I=(950)(0.03)(5) \\ \text{Simplify.} & I=142.5 \\ \text{Check.} \\ \text{Is } \$142.50 \text{ a reasonable amount of interest on } \$ \text{ 950?} \; \;\;\;\;\; \;\;\;\;\;\; \\ \text{Yes.} \\ \text{Write a complete sentence.} & \text{The interest is } \$ \text{142.50.} \end{array}\)

Try It!  \(\PageIndex{22}\)

Nathaly deposited $12,500 in her bank account where it will earn 4% simple interest. How much interest will Nathaly earn in five years?

He will earn $2,500.

Try It!  \(\PageIndex{23}\)

Susana invested a principal of $36,000 in her bank account that earned simple interest at an interest rate of 6.5%. How much interest did she earn in three years?

She earned $7,020.

There may be times when we know the amount of interest earned on a given principal over a certain length of time, but we do not know the rate.

EXAMPLE \(\PageIndex{13}\)

Hang borrowed $7,500 from her parents to pay her tuition. In five years, she paid them $1,500 interest in addition to the $7,500 she borrowed. What was the rate of simple interest?

\( \begin{aligned} I & = \; \$ 1500 \\ P & = \; \$ 7500 \\ r & = \; ? \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\text{Identify what you are asked to find,} \qquad \quad \text{What is rate of simple interest?} \\ \begin{align*} &\text{and choose a variable to represent it.} &  \text{Let }r \;&= \;\text{ rate of interest} \\ &\text{Write the formula.} & I \;&= \;Prt \\ &\text{Substitute in the given information.} & 1,500\; &= \;(7,500)r(5) \\ &\text{Multiply.} & 1,500 \; &= \; 37,500r \\ &\text{Divide.} & 0.04 \; &=\; r \\ &\text{Change to percent form} &  r\; &= \; 4\% \end{align*}\)

\(\begin{align*} I \; &= \; Prt \\ 1,500 \; &\stackrel{?}{=}\; (7,500)(0.04)(5)\\ 1,500 \; &= \;1,500✓ \end{align*}\)

Write a complete sentence.                    The rate of interest was \(4\%.\)

Try It!  \(\PageIndex{24}\)

Jim lent his sister $5,000 to help her buy a house. In three years, she paid him the $5,000, plus $900 interest. What was the rate of simple interest?

The rate of simple interest was 6%.

Try It!  \(\PageIndex{25}\)

Loren lent his brother $3,000 to help him buy a car. In four years, his brother paid him back the $3,000 plus $660 in interest. What was the rate of simple interest?

The rate of simple interest was 5.5%.

In the next example, we are asked to find the principal—the amount borrowed.

EXAMPLE \(\PageIndex{14}\)

Sean’s new car loan statement said he would pay $4,866,25 in interest from a simple interest rate of 8.5% over five years. How much did he borrow to buy his new car?

\( \begin{aligned} I & = \; 4,866.25 \\ P & = \; ? \\ r & = \; 8.5 \% \\ t & = \; 5 \text{ years} \end{aligned}\)

\(\text{Identify what you are asked to find,} \qquad \quad \text{What is the amount borrowed (the principal)?} \\ \begin{align*} &\text{and choose a variable to represent it.} &  \text{Let }P \;&= \;\text{ principal borrowed} \\ &\text{Write the formula.} & I \;&= \;Prt \\ &\text{Substitute in the given information.} & 4,866.25\; &= \;P(0.085)(5) \\ &\text{Multiply.} & 4,866.25 \; &= \; 0.425P \\ &\text{Divide.} & 11,450 \; &=\; P \end{align*}\)

\(\begin{align*} I \; &= \; Prt \\ 4,866.25 \; &\stackrel{?}{=}\; (11,450)(0.085)(5)\\ 4,866.25 \; &= \;4,866.25✓ \end{align*}\)

Write a complete sentence.                    The principal was \($11,450.\)

Try It!  \(\PageIndex{26}\)

Eduardo noticed that his new car loan papers stated that with a 7.5% simple interest rate, he would pay $6,596.25 in interest over five years. How much did he borrow to pay for his car?

He paid $17,590.

Try It!  \(\PageIndex{27}\)

In five years, Gloria’s bank account earned $2,400 interest at 5% simple interest. How much had she deposited in the account?

She deposited $9,600.

Access this online resource for additional instruction and practice with using a problem solving strategy.

• Begining Arithmetic Problems

Key Concepts

\(\text{change}=\text{new amount}−\text{original amount}\)

\(\text{change is what percent of the original amount?}\)

• \( \begin{align*} \text{amount of discount} &= \text{discount rate}· \text{original price} \\ \text{sale price} &= \text{original amount}– \text{discount price} \end{align*}\)
• \(\begin{align*} \text{amount of mark-up} &= \text{mark-up rate}·\text{original price} \\ \text{list price} &= \text{original cost}–\text{mark-up} \end{align*}\)
• If an amount of money, \(P,\) called the principal, is invested or borrowed for a period of t years at an annual interest rate \(r,\) the amount of interest, \(I,\) earned or paid is: \[\begin{aligned} &{} &{} &{I=interest} \nonumber\\ &{I=Prt} &{\text{where} \space} &{P=principal} \nonumber\\ &{} &{\space} &{r=rate} \nonumber\\ &{} &{\space} &{t=time} \nonumber \end{aligned}\]

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 1.7: Use a Problem-Solving Strategy

Learning Objectives

By the end of this section, you will be able to:

• Approach word problems with a positive attitude
• Use a problem-solving strategy for word problems
• Solve number problems

Approach Word Problems with a Positive Attitude

“If you think you can… or think you can’t… you’re right.”—Henry Ford

The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?

How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?

Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.

Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!

Use a Problem-Solving Strategy for Word Problems

We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.

Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.

Use a Problem-Solving Strategy to Solve Word Problems.

• Read the problem. Make sure all the words and ideas are understood.
• Identify what we are looking for.
• Name what we are looking for. Choose a variable to represent that quantity.
• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?

Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.

• In this problem, is it clear what is being discussed? Is every word familiar?

Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!

• In this problem, the words “what was the original price of the purse” tell us what we need to find.

Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.

Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.

Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.

Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.

• Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.

Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”

• The answer to the question is: “The original price of the purse was $36.”

If this were a homework exercise, our work might look like this:

Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?

Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?

Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?

Let’s try this approach with another example.

Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?

Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?

Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?

Solve Number Problems

Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.

The difference of a number and six is 13. Find the number.

The difference of a number and eight is 17. Find the number.

The sum of twice a number and seven is 15. Find the number.

Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.

The sum of four times a number and two is 14. Find the number.

The sum of three times a number and seven is 25. Find the number.

Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.

One number is five more than another. The sum of the numbers is 21. Find the numbers.

One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.

The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.

The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.

The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.

One number is ten more than twice another. Their sum is one. Find the numbers.

One number is eight more than twice another. Their sum is negative four. Find the numbers.

Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.

 Examples of consecutive integers are:

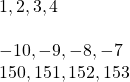
The sum of two consecutive integers is 47. Find the numbers.

Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81

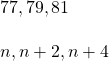
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?

Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2

Find three consecutive even integers whose sum is 84

TRY IT 10.1

Find three consecutive even integers whose sum is 102

TRY IT 10.2

A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?

TRY IT 11.1

According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?

TRY IT 11.2

The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?

$24,000

Key Concepts

• Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.

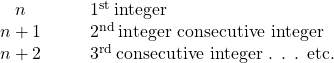
Consecutive even integers are even integers that immediately follow one another.

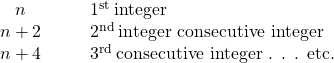
Consecutive odd integers are odd integers that immediately follow one another.

Practice Makes Perfect

Use the approach word problems with a positive attitude.

In the following exercises, prepare the lists described.

In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.

In the following exercises, solve each number word problem.

Everyday Math

Writing exercises, attributions.

This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.

Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book