

Alta Sierra Intermediate
- Math 8 Unit 1
Math 8 Unit 1 - Illustrative Mathematics Online Resources
|
| |||||
|
| |||||
|
| |||||
|
|
|
|
|
|
|
| 1 – Moving in the Plane |
|
| |||
| 2 – Naming the Moves |
|
| |||
| 3 – Grid Moves |
|
|
| ||
| 4 – Making the Moves |
|
| |||
| 5 – Coordinate Moves |
|
|
|
| |
| 6 – Describing Transformations |
|
|
|
| |
| 7 – No Bending or Stretching |
|
|
|
| |
| 8 – Rotation Patterns |
|
| |||
| 9 – Moves in Parallel |
|
| |||
| 10 – Composing Figures |
|
| |||
| 11 – What is the Same? |
|
| |||
| 12 – Congruent Polygons |
|
|
|
| |
| 13 – Congruence |
|
| |||
| 14 – Alternate Interior Angles |
|
|
|
| |
| 15 – Adding the Angles in a Triangle |
|
|
|
| |
| 16 – Parallel Lines and the Angles in a Triangle |
|
|
|
| |
| 17 – Rotate and Tessellate |
| ||||
| Unit 1 Review |
| ||||
- Math 8 Unit 2
- Math 8 Unit 3
- Math 8 Unit 4
- Math 8 Unit 5
- Math 8 Unit 6
- Math 8 Unit 7
- Math 8 Unit 8

Experience Teachmint X - AI driven Interactive Flat Panels and Smart Boards
More from Feroza Aziz Shaikh
Recommended content, learn from anywhere on any device.
Top Leader by G2
Top Performer by SourceForge
Top Leader by SoftwareSuggest
Ranked Amongst Top 25 Companies by LinkedIn
ISO27001 Certified
Most Preferred Workplace
We use cookies to enhance site navigation and analyse usage, read our Privacy Policy for more.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 1: Algebra foundations
Unit 2: solving equations & inequalities, unit 3: working with units, unit 4: linear equations & graphs, unit 5: forms of linear equations, unit 6: systems of equations, unit 7: inequalities (systems & graphs), unit 8: functions, unit 9: sequences, unit 10: absolute value & piecewise functions, unit 11: exponents & radicals, unit 12: exponential growth & decay, unit 13: quadratics: multiplying & factoring, unit 14: quadratic functions & equations, unit 15: irrational numbers, unit 16: creativity in algebra.
Talk to our experts
1800-120-456-456
CBSE Maths Chapter 1 Rational Numbers Class 8 Extra Questions
- Class 8 Important Question
- Chapter 1: Rational Numbers

Boost Your Performance in CBSE Mathematics Exam Chapter 1 with Class 8 Rational Numbers Important Questions PDF
Class 8 lays down the foundational concepts for mathematics. These concepts are important as many other concepts you will learn in higher classes are based upon these. Obtaining an in-depth understanding of these concepts then becomes fairly important. To help students in this, Rational Numbers Class 8 Extra Questions pdf is prepared by our subject experts at Vedantu. Vedantu is a platform that provides free NCERT Solution and other study materials for students.
These are prepared to keep in mind the examination pattern to help students in scoring well. Also, it provides accurate and reliable study material free of cost to all the students. The list of Class 8 Rational Numbers Important Questions is prepared carefully studying the previous year question paper and examination pattern. You can also download NCERT Maths Class 8 to help you to revise complete syllabus and score more marks in your examinations. Science students who are looking for NCERT Solutions for Class 8 Science will also find the solutions curated by our Master Teachers really helpful. Download important questions for class 8 Maths chapter 1 pdf here.

Chapter 1 Class 8 Rational Numbers Important Questions (Short and Long Answer Questions)
Very Short Answer Questions 1 Marks
1. The additive inverse of $\dfrac{3}{4}$ is ____
Ans: Additive inverse of any number is a number that can be added to a number to get $0$.
Hence, the additive inverse of $\dfrac{\text{3}}{\text{4}}$ is $\text{-}\dfrac{\text{3}}{\text{4}}$ .
2. Multiplicative inverse of is $\dfrac{1}{8}$
Ans: Multiplicative inverse of any number is a number that can be multiplied to a number to get $1$.
The multiplicative inverse of $\dfrac{\text{p}}{\text{q}}$ is $\dfrac{\text{q}}{\text{p}}$ .
Hence, the multiplicative inverse of $\dfrac{1}{8}$ is $8$.
3. A Rational number between $3$ and $4$ is ____
Ans: The rational number of any number can be calculated as;
$\dfrac{\left( \text{p+q} \right)}{\text{2}}$
Hence, the required rational number is;
$\dfrac{\left( 3+4 \right)}{2}=\dfrac{7}{2}$
Hence, $\dfrac{7}{2}$ is a rational number between $3$ and $4$.
4. Reciprocal of $-2$ is ___
Ans: Reciprocal of any number will be the inverse of that number.
That is, the reciprocal of $a$ is $\dfrac{1}{a}$ .
Hence, the reciprocal of $-2$ is $-\dfrac{1}{2}$ .
5. Zero has ____ reciprocal
Ans: The product of any number with $0$ will be $0$ and hence, zero has no reciprocal.
6. Reciprocal of a negative number is _______
Ans: The product of any negative number with any number will be negative and hence, the reciprocal of a negative number will be negative .
7. Whole numbers start from______
Ans: The numbers that start from $0$, are called whole numbers.
8. There are _____ rational numbers between $3$ and $4$.
Ans: Infinite rational numbers are between $3$ and $4$.
9. What are the multiplicative and additive identities of rational numbers?
Ans: 0 and 1 are the additive and multiplicative identity of rational numbers respectively.
10. Write the additive inverse of $\dfrac{19}{-6}$ and $-\dfrac{2}{3}$
Ans: $\dfrac{19}{-6}$ and $-\dfrac{2}{3}$ = $\dfrac{2}{3}$
11. Write the multiplicative inverse of $-\dfrac{13}{19}$ and $-7$
Ans: $-\dfrac{13}{19} = -\dfrac{19}{13}$ and $-7 = -\dfrac{1}{7}$
12. Mention a rational number which has no reciprocal.
Ans: A rational number “0” has no reciprocal or multiplicative inverse.
13. Mention any 4 rational numbers which are less than 5.
Ans: -1, 1, 2, and 3.
Short Answer Questions 2 Marks
14. Sum of two numbers is $\dfrac{3}{4}$, one of the number is $\dfrac{1}{8}$ .Find the other one.
Ans: Let the other number be $\text{x}$.
The sum of $\text{x}$ and $\dfrac{1}{8}$ is $\dfrac{3}{4}$ . Therefore, we have
\[\begin{align} & \Rightarrow \text{x}+\dfrac{1}{8}=\dfrac{3}{4} \\ & \Rightarrow \text{x}=\dfrac{3}{4}-\dfrac{1}{8} \\ & \Rightarrow \text{x}=\dfrac{\left( 3\times 2 \right)-1}{8} \\ \end{align}\] Since, $[\text{LCM}=8]$ Therefore, $\begin{align} & \Rightarrow \text{x}=\dfrac{6-1}{8} \\ & \Rightarrow \text{x}=\dfrac{5}{8} \\ \end{align}$
Therefore, the sum of $\dfrac{5}{8}$ and $\dfrac{1}{8}$ is $\dfrac{3}{4}$.
15. Simplify $\left( \dfrac{-8}{13} \right)+\left( \dfrac{-3}{26} \right)$
Ans: The given dfraction is;
$\dfrac{-8}{13}-\dfrac{3}{26}$
By simplifying above dfraction, we get
$\Rightarrow \dfrac{\left( -8\times 2 \right)-3}{26}$
Since, $[\text{LCM}=26]$
$\begin{align} & \Rightarrow \dfrac{-16-3}{26} \\ & \Rightarrow -\dfrac{19}{26} \\ \end{align}$
Therefore, $\left( \dfrac{-8}{13} \right)+\left( \dfrac{-3}{26} \right)=-\dfrac{19}{26}$ .
16. What number to be multiplied with $\dfrac{1}{4}$ so as to get the product as $-\dfrac{5}{16}$
Ans: Let the number be $\text{x}$ .
The product can be written as;
$\Rightarrow \dfrac{1}{4}\times \text{x}$ and,
Product of $\text{x}$ and $\dfrac{1}{4}$ is $-\dfrac{5}{16}$ .
Therefore, we have
\[\begin{align} & \Rightarrow -\dfrac{5}{16}=\dfrac{1}{4}\times \text{x} \\ & \Rightarrow \text{x}=4\times \left( -\dfrac{5}{16} \right) \\ \end{align}\]
Therefore, we get
$\Rightarrow \text{x}=-\dfrac{5}{4}$
Hence, $-\dfrac{5}{4}$ is the number to be multiplied with $\dfrac{1}{4}$ so as to get the product as $-\dfrac{5}{16}$.
17. Represent $-\dfrac{2}{7}$ on the number line.
Ans: $-\dfrac{2}{7}$ is a rational number.
$-\dfrac{2}{7}$ on a Number Line, can be represented as follows;
18. Divide $\dfrac{1}{2}$by $\left[ \dfrac{-1}{3}+\dfrac{2}{5} \right]$
Ans: The given fraction is;
$\left[ \dfrac{-1}{3}+\dfrac{2}{5} \right]$
By simplifying above fraction, we get
\[\begin{align} & \Rightarrow -\dfrac{1}{3}+\dfrac{2}{5} \\ & \Rightarrow \dfrac{\left( -1.5 \right)+\left( 2.3 \right)}{15} \\ \end{align}\]
Since, $[\text{LCM}=15]$ , therefore
\[\begin{align} & \Rightarrow \dfrac{-5+6}{15} \\ & \Rightarrow \dfrac{1}{15} \\ \end{align}\]
On dividing $\dfrac{1}{2}$ by $\dfrac{1}{15}$ , we get
\[\begin{align} & \Rightarrow \dfrac{1}{2}\div \dfrac{1}{15} \\ & \Rightarrow \dfrac{1}{2}\times \dfrac{15}{1} \\ & \Rightarrow \dfrac{15}{2} \\ \end{align}\]
19. Find three rational number between $-4$and $4$ Represent them on line.
Ans: The three rational numbers between $-4$ and $4$ are $-2,-1,1$ .
On a number line, the mentioned rational numbers are represented as follows:
20. Define by example of addition
(a) Associative Property
Ans: Associative Property can be stated as while addition or multiplication of any two grouped numbers, the interchange of those numbers won’t get affected on resultant addition or multiplication.
$\Rightarrow \text{a+b = b+a}$
The following example shows how the associative property gets used to solve it;
We can solve $9+7$ by using Associative Property; we get
$\begin{align} & \Rightarrow \left( 7+9 \right)=\left( 9+7 \right) \\ & \Rightarrow 7+9=16 \\ \end{align}$ and
$\Rightarrow 9+7=16$
Therefore, according to the property, we can add or multiply regardless of how the numbers are grouped.
Short Answer Questions 3 Marks
21. Simplify $\left[ \dfrac{6}{7}+\dfrac{3}{8}-\dfrac{1}{2} \right]\dfrac{4}{3}$ and find its reciprocal.
Hence, by solving above dfraction, we get
$\Rightarrow \left[ \dfrac{6\times 8+3\times 7-1\times 28}{56} \right]\dfrac{4}{3}$
(Since the LCM of $7,8$ and $2$ is $56$ )
\[\begin{align} & \Rightarrow \left[ \dfrac{48+21-28}{56} \right]\times \dfrac{4}{3} \\ & \Rightarrow \dfrac{41}{56}\times \dfrac{4}{3} \\ & \Rightarrow \dfrac{41}{42} \\ \end{align}\]
Reciprocal of $\dfrac{41}{42}$ is
$\Rightarrow \dfrac{1}{\dfrac{41}{42}}=1\times \dfrac{42}{41}$
\[\Rightarrow \dfrac{42}{41}\]
Hence, reciprocal of $\left[ \dfrac{6}{7}+\dfrac{3}{8}-\dfrac{1}{2} \right]\dfrac{4}{3}$ is \[\dfrac{42}{41}\] .
22. Find three Rational Number between $3$ and $4$. Represent them on the Number line.
Ans: $3$ can be written as
\[\begin{align} & \Rightarrow 3\times \dfrac{10}{10} \\ & \Rightarrow \dfrac{30}{10} \\ \end{align}\] $4$ can be written as \[\begin{align} & \Rightarrow 4\times \dfrac{10}{10} \\ & \Rightarrow \dfrac{40}{10} \\ \end{align}\]
Hence, the three Rational Numbers are $\dfrac{31}{10},\dfrac{32}{10},\dfrac{33}{10}$ .
$\dfrac{31}{10},\dfrac{32}{10},\dfrac{33}{10}$ these numbers can be represented on a Number line, are as follows;
23. Use appropriate property and find $-\dfrac{1}{6}\times \dfrac{4}{7}+\dfrac{1}{2}-\dfrac{3}{7}\times \dfrac{1}{6}$
Ans: The given dfraction is;
$-\dfrac{1}{6}\times \dfrac{4}{7}+\dfrac{1}{2}-\dfrac{3}{7}\times \dfrac{1}{6}$
By using associative property $\left( \text{a+b = b+a} \right)$ , we can be simplifying the above dfraction as follows;
\[\begin{align} & \Rightarrow -\dfrac{1}{6}\times \dfrac{4}{7}-\dfrac{3}{7}\times \dfrac{1}{6}+\dfrac{1}{2} \\ & \Rightarrow -\dfrac{1}{6}\times \dfrac{4}{7}-\dfrac{1}{6}\times \dfrac{3}{7}+\dfrac{1}{2} \\ & \Rightarrow -\dfrac{1}{6}\left[ \dfrac{4}{7}+\dfrac{3}{7} \right]+\dfrac{1}{2} \\ & \Rightarrow -\dfrac{1}{6}\times \dfrac{7}{7}+\dfrac{1}{2} \\ \end{align}\]
\[\begin{align} & \Rightarrow \dfrac{-1+3}{6} \\ & \Rightarrow \dfrac{2}{6} \\ & \Rightarrow \dfrac{1}{3} \\ \end{align}\]
Hence, $-\dfrac{1}{6}\times \dfrac{4}{7}+\dfrac{1}{2}-\dfrac{3}{7}\times \dfrac{1}{6}=\dfrac{1}{3}$ .
24. Find the multiplicative inverse of following
\[\dfrac{1}{6}\]
Ans: Multiplicative inverse of any number is a number which can be multiplied to a number to get $1$ .
Hence, the multiplicative inverse of $\dfrac{1}{6}$ is
\[\begin{align} & \Rightarrow \dfrac{1}{6}\times \text{x}=1 \\ & \Rightarrow \text{x}=6 \\ \end{align}\]
Therefore, the multiplicative inverse of $\dfrac{1}{6}$ is $6$ .
$-\dfrac{3}{8}$
Hence, the multiplicative inverse of $\dfrac{-3}{8}$ is
$\begin{align} & \Rightarrow -\dfrac{3}{8}\times \text{x}=1 \\ & \Rightarrow \text{x}=-\dfrac{8}{3} \\ \end{align}$
Therefore, the multiplicative inverse of $-\dfrac{3}{8}$ is $-\dfrac{8}{3}$.
$\dfrac{4}{19}$
Hence, the multiplicative inverse of $\dfrac{4}{19}$ is
\[\begin{align} & \Rightarrow \dfrac{4}{19}\times \text{x}=1 \\ & \Rightarrow \text{x}=\dfrac{19}{4} \\ \end{align}\]
Therefore, the multiplicative inverse of $\dfrac{4}{19}$ is $\dfrac{19}{4}$ .
Long Answer Questions 4 or 5 Marks
25. Find three Rational number between $\dfrac{3}{6}$ and $\dfrac{3}{4}$
Hence, the mean of two Rational numbers is a Rational number.
For given numbers;
$\dfrac{3}{6}=\dfrac{1}{2}$ and $\dfrac{3}{4}$
Mean can be calculated as;
\[\begin{align} & \Rightarrow \dfrac{\dfrac{1}{2}+\dfrac{3}{4}}{2} \\ & \Rightarrow \dfrac{\dfrac{5}{4}}{2} \\ & \Rightarrow \dfrac{5}{8} \\ \end{align}\]
Since, $\dfrac{1}{2}<\dfrac{5}{8}<\dfrac{3}{4}$ ;
Now Mean of $\dfrac{1}{2}$ and $\dfrac{5}{8}$
\[\begin{align} & \Rightarrow \dfrac{\dfrac{1}{2}+\dfrac{5}{8}}{2} \\ & \Rightarrow \dfrac{\dfrac{9}{8}}{2} \\ & \Rightarrow \dfrac{9}{16} \\ \end{align}\]
Since, \[\dfrac{1}{2}<\dfrac{9}{16}<\dfrac{5}{8}\]
Mean of $\dfrac{5}{8}$ and $\dfrac{3}{4}$
\[\begin{align} & \Rightarrow \dfrac{\dfrac{5}{8}+\dfrac{3}{4}}{2} \\ & \Rightarrow \dfrac{5+6}{8\times 2} \\ & \Rightarrow \dfrac{11}{16} \\ \end{align}\]
$\therefore \dfrac{5}{8}<\dfrac{11}{16}<\dfrac{3}{4}$
Hence, $\dfrac{9}{16},\dfrac{5}{8},\dfrac{11}{16}$ are the three rational numbers are between $\dfrac{3}{6}$ and $\dfrac{3}{4}$ .
26.
Reciprocal of $-\dfrac{1}{2}$
Ans: Reciprocals of any number are going to be the inverse of that number.
Hence, the reciprocal of $-\dfrac{1}{2}$ is;
$\dfrac{1}{-\dfrac{1}{2}}=-2$
Therefore, Reciprocal of $-\dfrac{1}{2}$ is $-2$ .
Additive inverse of $\dfrac{4}{9}$
Ans: Additive inverse of any number is a number which can be added to a number to get $0$ .
For the given number, we get
$\Rightarrow \dfrac{4}{9}+x=0$
$\Rightarrow $ $x=-\dfrac{4}{9}$
Therefore, an additive inverse of $\dfrac{4}{9}$ is $-\dfrac{4}{9}$ .
Multiplicative inverse of $\left[ \dfrac{1}{6}+\dfrac{4}{9} \right]\times \dfrac{4}{3}$
Ans: Multiplicative inverse of any number is a number which can be multiplied to a number to get $1$ .
For given number, we get
$\begin{align} & \Rightarrow \left[ \dfrac{1}{6}+\dfrac{4}{9} \right]\times \dfrac{4}{3} \\ & \Rightarrow \dfrac{(1\times 3+2\times 4)}{18}\times \dfrac{4}{3} \\ & \Rightarrow \dfrac{(3+8)}{18}\times \dfrac{4}{3} \\ \end{align}$ Therefore, $\begin{align} & \Rightarrow \dfrac{11}{18}\times \dfrac{4}{3} \\ & \Rightarrow \dfrac{22}{27} \\ \end{align}$
Hence, multiplicative inverse of $\left[ \dfrac{1}{6}+\dfrac{4}{9} \right]\times \dfrac{4}{3}$ is $\dfrac{27}{22}$ .
27. Match the correct
(a) Whole number
(b) Natural number
(c) Integer
(d) Rational Number
Ans: The correct pairs are as follows;
(a) (ii)
(b) (iii)
(c) (i)
(d) (iv)
Whole numbers starts from $0$ .
Natural numbers are positive numbers and starts from $1$.
Integers will be positive, negative or $0$ numbers.
Rational numbers are the dfractional numbers.
Important Questions for Class 8 Rational Numbers Free PDF Download
The pdf contains the list of important questions for class 8 rational numbers. These questions are handpicked by our subject experts as these questions have the highest probability of coming in the examinations. Also, these questions are a great revision tool students can use. Solving these questions will help students in obtaining a better understanding of the type of questions asked in the examinations and how to format their answers correctly.
The chapter Rational Numbers is part of the syllabus for SA-I examinations which is for a total of 40 marks. The weightage of this chapter in the examination is 6 marks and a total of three questions are asked from this chapter- one very short answer type question, one short answer type question and one long answer type question.
Subtopics Covered in Detail in Chapter 1 - Rational Numbers
The subtopics that are covered in the detail in the chapter are:
Properties of Rational Numbers.
Closure property
Commutative property
Associativity property
The role of 0
- The role of 1
- Negative of a number
Distributivity of multiplication over addition for rational numbers
Representation of rational numbers on the Number Line.
Rational numbers between two rational numbers.
Rational numbers are of the type p/q where p and q are integers and q ≠ 0. Simply rational numbers can be defined as fractions that can be represented on the number line. Let us look at the concepts that govern rational numbers.
- Properties of Rational Numbers
The properties we are going to discuss are basic mathematical properties that are applicable on integers as well. Let us discuss the properties one by one:
Closure Property
The result of addition, multiplication and subtraction between any two rational numbers is also a rational number. This property is true for all mathematical properties except division because division by 0 is not defined. So divisions other than 0 are included in the closure property.
Commutative Property
The commutative property is true only for addition and multiplication of rational numbers. For any two rational numbers: Commutative property of addition: $a + b = b + a$ $\dfrac{2}{5} + \dfrac{3}{5} = \dfrac{3}{5} + \dfrac{2}{5}$ Commutative property of multiplication: $a \times b = b \times a$ $\dfrac{3}{7} \times \dfrac{2}{7} = \dfrac{2}{7} \times \dfrac{3}{7}$
Associative Property
Rational numbers follow the property of association only for addition and multiplication. Let a, b and c be three rational numbers: Associative property for addition: $a + (b + c) = (a + b) + c$ Associative property for multiplication: $a \times (b \times c) = (a \times b) \times c$
Distributive Property
Rational numbers follow distributive property for addition and multiplication only. For any three rational numbers p,q and r. $p \times (q + r) = (p \times q) + (p \times r)$
Identity Property
The additive identity for any rational number is 0 and the multiplicative identity is 1.
Inverse Property
For a given rational number $\dfrac{x}{y}$, Additive inverse: $-\dfrac{x}{y}$ Multiplicative inverse: $\dfrac{y}{x}$
Representation of Rational Numbers on the Number Line
Rational numbers can also be represented on the number line just like other whole numbers or integers. 0 represents the origin. Negative rational numbers are present to the left and the positive rational numbers are located on the right side of the number line.
Representation of a rational number can be categorised into:
Proper Fraction: When the value of the numerator is less than the value of denominator, the fraction is called proper fraction and the value is less than one.
Improper Fraction: In case of the improper fraction, the value of the numerator is greater than the value of the denominator. First, we convert the given fraction into a mixed fraction to get a better picture of where the number exists on the number line.
To represent the rational number we divide the distance between the two whole numbers into the number of subunits denoted by the denominator.
The number can also be represented using the process of successive magnification where we convert the rational number into decimal expansion and represent the decimal places successively.
Rational Number Between Two Rational Numbers
The different methods using which rational numbers between two rational numbers can be found are:
The basic method that is used to find the number between two rational numbers is dividing their sum by 2.
A rational number between 5 and 6 can be calculated by $\dfrac{5 + 6}{2} = \dfrac{11}{2}$ $\dfrac{11}{2}$ is a rational number between 5 and 6.
For numbers with a common denominator, rational numbers between them can be easily found.
Rational numbers between $\dfrac{4}{9}$ and $\dfrac{8}{9} are $\dfrac{5}{9}$, $\dfrac{6}{9}$, $\dfrac{7}{9}$. Rational numbers between $-\dfrac{2}{3}$ and $\dfrac{2}{3}$ are: $-\dfrac{1}{3}, 0, \dfrac{1}{3}$
In the case of different denominators, the first step is to make the denominators of the fraction similar before finding the rational numbers between them.
To find the rational number between $\dfrac{1}{5}$ and $\dfrac{14}{15}$, make the denominators of both the rational numbers equal. So, $\dfrac{1 \times 3}{5 \times 3} = \dfrac{3}{15}$ The rational numbers between them are $\dfrac{4}{15}, \dfrac{5}{15}, \dfrac{6}{15}, \dfrac{7}{15} …. \dfrac{12}{15}, \dfrac{13}{15}$ etc.
List of Important Class 8 Maths Rational Numbers Important Questions
The pdf class 8 maths chapter 1 important questions contains different types of questions that cover all the sub-topics of the entire chapter. Important questions from each topic are included in the pdf to give the students a clear and logical understanding of the chapter. Some of the important questions that are commonly asked in the examination from this chapter are:
- Find the rational number between $\dfrac{2}{3}$ and $\dfrac{4}{5}$.
Determine the rational numbers lying between $-\dfrac{1}{2}$ and $\dfrac{1}{2}$.
Simplify: $\dfrac{3}{4} + \dfrac{(-5)}{8}$.
Simplify: $-\dfrac{2}{3} - \dfrac{4}{5}$.
Solve: $\dfrac{3}{7} \times \dfrac{5}{6}$.
Solve: $-\dfrac{2}{5} \div \dfrac{3}{4}$.
Determine whether the following numbers are rational or irrational: $\sqrt{16}, \sqrt{5}, -3.25, 0.8888 …$
Find the rational number between 1.5 and 1.6.
Simplify: $-\dfrac{7}{9} + \dfrac{(-4)}{9} - \dfrac{1}{3}$.
Find the value of 'x' if $\dfrac{2}{3} \div x = \dfrac{4}{5}$.
Benefits of Class 8 Maths Rational Numbers Important Questions PDF
Rational numbers are a scoring chapter for students. If students prepare the questions from the pdf, they will be able to answer all the questions that are asked from the chapter. Students can be asked short answer type questions from the properties of rational numbers and long answer type questions from the representation of rational numbers on a number line or a rational number between rational numbers.
The benefits of the pdf containing important questions for class 8 maths chapter 1 are given below:
The pdf is prepared in accordance with the examination guidelines to help students to score well in the examinations.
The list of important questions is prepared by the subject experts who have years of experience in teaching.
The list is prepared after thorough research of previous year question papers and incorporating the revisions in the syllabus.
The pdf also contains solutions students can refer to in case of any doubts.
Practising questions from the pdf will improve the student’s understanding of the concepts and the examination pattern.

Chapterwise Important Questions for Class 8 Maths
Planning your schedule is extremely important if you want to score good marks in the upcoming examinations. To help you in this, the Class 8 Chapterwise Important Questions is given below.
Chapter 2 - Linear Equations in One Variable
Chapter 3 - Understanding Quadrilaterals
Chapter 4 - Practical Geometry
Chapter 5 - Data Handling
Chapter 6 - Squares and Square Roots
Chapter 7 - Cubes and Cube Roots
Chapter 8 - Comparing Quantities
Chapter 9 - Algebraic Expressions and Identities
Chapter 10 - Visualising Solid Shapes
Chapter 11 - Mensuration
Chapter 12 - Exponents and Powers
Chapter 13 - Direct and Inverse Proportions
Chapter 14 - Factorisation
Chapter 15 - Introduction to Graphs
Chapter 16 - Playing with Numbers
Mastering the concepts of rational numbers in CBSE Class 8 Maths is crucial for building a strong foundation in Mathematics. By practicing these important questions, you will gain confidence in solving problems related to rational numbers and improve your overall understanding of the chapter. It will also test your level of understanding of the chapter and highlight your weaker sections. Make sure to revise the concepts and formulas related to rational numbers and attempt additional practice questions to enhance your problem-solving skills further. Download the Class 8 Maths Rational Numbers Important Questions pdf and kickstart your preparations for the examination. Best of luck with your studies!

FAQs on CBSE Maths Chapter 1 Rational Numbers Class 8 Extra Questions
1. How are Important Questions for CBSE Class 8 Maths Chapter 1 Rational Numbers useful for students?
Ans: Vedantu’s curated list of important questions for Class 8 Maths Chapter 1 Rational Numbers are extremely useful for students. The study materials provided for free by e-learning platforms like Vedantu provide extra questions for practice and help in scoring well in the subject. At Vedantu, these questions are solved by expert teachers. By referring to the important questions PDF for Class 8 Maths Chapter 1 Rational Numbers, students will be able to practice the chapter effectively. These questions also help in revision during exam time. In case students are not able to solve any of the questions of the chapter, they can refer to the solutions provided by Vedantu.
2. Where can I find Important Questions for Class 8 Maths Chapter 1 Rational Numbers?
Ans: Vedantu, a premier online learning platform, provides a well-prepared set of Important Questions for Class 8 Maths Chapter 1 as well as other chapters. Students can trust Vedantu for such a resource as it offers relevant questions that can be asked in the exams. Vedantu provides a free PDF of Important Questions for Class 8 Maths Chapter 1 Rational Numbers along with answers. These solutions are prepared by subject matter experts. These are extremely helpful in exam preparation and provide effective revision during exams.
3. Why must students solve important questions for Class 8 Maths Chapter 1 Rational Numbers during exam preparation?
Ans: Solving extra questions for Class 8 Maths CBSE chapters is really helpful during exams. The list of important questions for Class 8 Maths Chapter 1 Rational Numbers allows students to have a thorough practice. Students will also get familiar with all types of questions that can be asked in the exam. The important questions are picked by a panel of experts to cover all the important topics of the chapters. The questions are selected after referring to the exam pattern and observing the previous year question papers. Vedantu provides important questions free PDF for CBSE Maths examination of Class 8 Chapter 1 that can be utilized at the time of revision. These are really helpful in scoring well in the paper as it will boost students’ confidence while appearing for the board exam.
4. What are the contents of the Class 8 Maths Chapter 1 Rational Numbers NCERT textbook?
Following are the subtopics of Class 8 Maths Chapter 1 Rational Numbers:
- Introduction
- Commutativity
- Associativity
- The role of zero
- Representation of Rational Numbers on the Number Line.
- Rational Numbers between Two Rational Numbers.
5. Why are NCERT Solutions of Chapter 1 of Class 8 Maths Important?
Ans: NCERT Solutions for Chapter 1 of Class 8 Maths Chapter 1 is important because students can understand the concepts easily by solving the NCERT questions. NCERT questions are also important for their exams. Students will get questions based on a similar pattern in their final exams. NCERT Solutions given on Vedantu can help students to score good marks in maths. They can practice all NCERT questions for Chapter1 to score good marks in the math exam.
6. What are the Important Topics Covered in NCERT Solutions of Chapter 1 of Class 8 Maths?
Ans: Chapter 1 of Class 8 Maths is based on rational numbers. The chapter covers the different topics related to rational numbers such as properties of rational numbers, representing rational numbers on a number line, and how to find a rational number between two rational numbers. Students should practice all questions related to the NCERT Solutions for Chapter 1 of Class 8 Maths to understand all topics.
7. What are the properties of rational numbers?
Properties of rational numbers includes commutative, associative, additive, and closure properties. Students must understand the different properties of rational numbers to get high marks in Class 8 Maths.
8. What do you mean by associative property of rational numbers according to Chapter 1 of Class 8 Maths?
Ans: The associative property of rational numbers means that if you add three or more rational numbers in any sequence the result will be the same. Rational numbers follow the associative property of addition and multiplication. According to the associative property of multiplication, if you multiply two or more rational numbers in any sequence the result will be the same. Thus, according to this property, students can add or multiply two or more rational numbers in any order to get the right result.
9. What is the closure property of rational numbers according to Chapter 1 of Class 8 Maths?
Ans: The closure property of rational numbers states that if you add, subtract, or multiply two rational numbers you will get a rational number. Rational numbers are not closed for division because if you divide a rational number by zero, you will not get a rational number. Thus, the closure property of rational numbers does not fit for division.
10. What are terminating and non-terminating decimals in rational numbers?
Terminating decimals are rational numbers with decimal representations that end, such as 0.25 or 0.5. Non-terminating decimals are rational numbers with decimal representations that continue indefinitely, either repeating or not repeating in a pattern.
11. Are there any specific techniques for solving problems involving rational numbers?
One useful technique is to convert mixed numbers to improper fractions before performing operations. Additionally, when adding or subtracting fractions, it's helpful to find a common denominator to make calculations easier.
12. What are some real-life examples of rational numbers?
Examples of rational numbers in real life include measurements such as distances, weights, and temperatures, as well as fractions representing parts of a whole, such as $\dfrac{3}{4}$ of a pizza or $\dfrac{2}{5}$ of a liter.
13. How can I practice Class 8 Maths Rational Numbers Important Questions?
You can practice extra questions on rational numbers by downloading additional worksheets or PDFs available online or using textbooks with supplementary exercises. These resources typically provide a variety of problems to reinforce your understanding of the topic.
14. What is the difference between rational and irrational numbers?
Rational numbers can be expressed as fractions, while irrational numbers cannot be expressed as fractions and have non-terminating and non-repeating decimal expansions. For example, $\sqrt{2}$ and $\pi$ are irrational numbers.
15. How can we perform operations on rational numbers?
Operations such as addition, subtraction, multiplication, and division can be performed on rational numbers using rules similar to those for integers. For division, we need to ensure that the divisor is not zero.
Chapterwise Important Questions for CBSE Class 8 Maths
Cbse study materials.
Math Assignment Unit 3
- Mathematics
Make Math and English fun for kids
With Prodigy, kids practice standards-aligned skills in Math and English as they play our fun, adaptive learning games. All with teacher and parent tools to support their learning in class and at home.
Master Math Grades 1-8 & English Grades 1-6
91% of parents said their children enjoy using Prodigy Math*
" Prodigy is a great way to get kids who don't like math into math. "
Caralena Luthi

" In less than 12 months... I’ve got kids that have elevated two to three grade levels. That’s huge when you look at those kids who’ve grown three grade levels with everything that’s going on. "
5th Grade Teacher

" Having access to Prodigy really helps supplement our math learning and tells me what areas of the curriculum I need to add more focus on. I think all teachers should use Prodigy if possible because it is an amazing learning tool. "
6th Grade Teacher

*In one survey of parents commissioned by Prodigy Education.
Our mission is to help every student in the world love learning!
That’s why all of our standards-aligned educational content is free and students can play prodigy at school or at home..
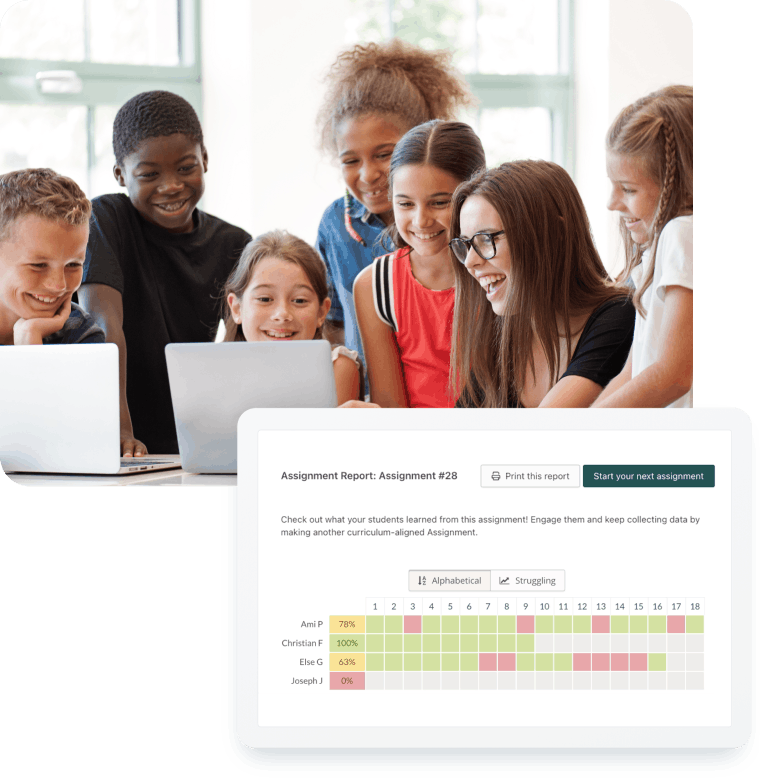
Here's how nearly one million teachers use Prodigy in the classroom at no cost!
Help students master math standards with a fun and engaging gameplay experience
Adjust and align Prodigy's in-game math content with your lesson plans
Track student development to decide where to best spend your time
No trial period, no hidden costs for educators. Our optional parent memberships ensure Prodigy stays free for all teachers.
Students reported an average of twice the level of math enjoyment in just a few months.
In one school district, students mastered an average of 68% more math skills per month .
96%** of parents and teachers were satisfied with the educational impact of Prodigy Math.
**Based on a survey of parents and a survey of teachers commissioned by Prodigy Education.
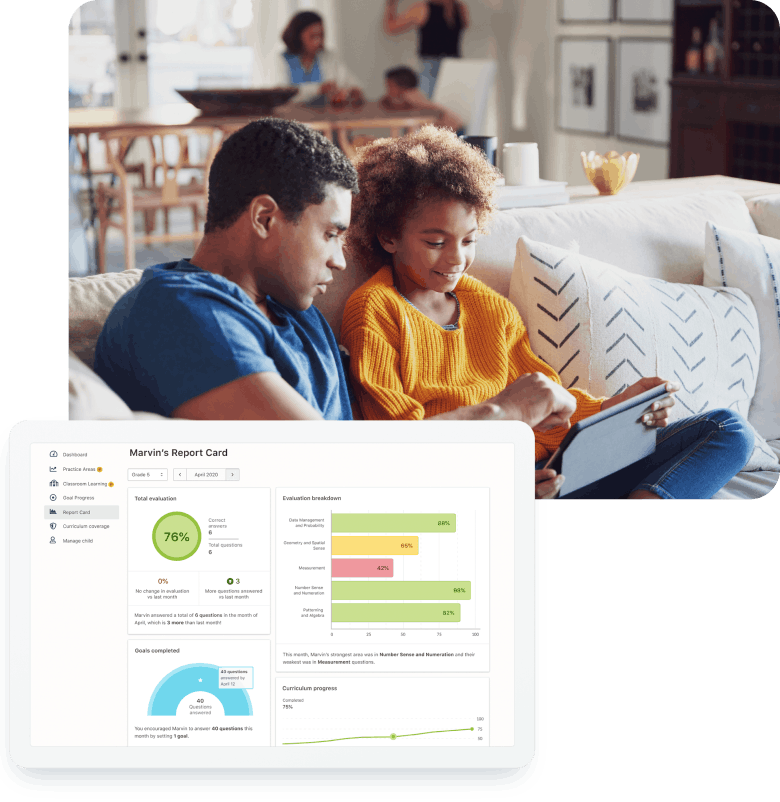
Invest in your child's learning journey with engaging games that make learning fun!
Help your child improve their math skills and confidence in a fun, safe and secure environment
Motivate learning, track their progress and inspire them to practice new skills
Get insights into their classroom progress with a Prodigy parent account
Optional Prodigy memberships provide additional features that are engaging and promote more math practice - and they also help us keep Prodigy free for all teachers!
Learning made fun, in more ways than one
Our safe, curriculum-aligned games make online learning an adventure!
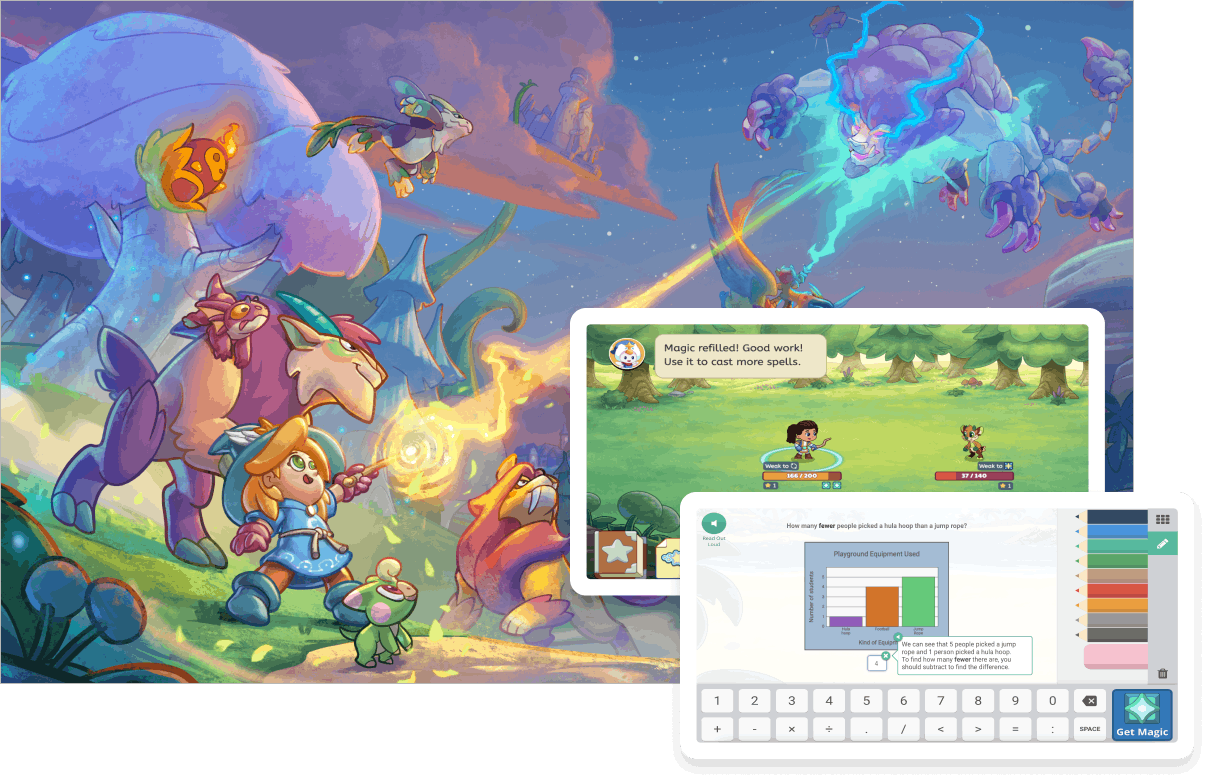
Prodigy Math
Discover the magic of math! Players embark on a journey filled with quests, battles, spells and rewards. Every battle brings more skill-building math questions for students to solve.
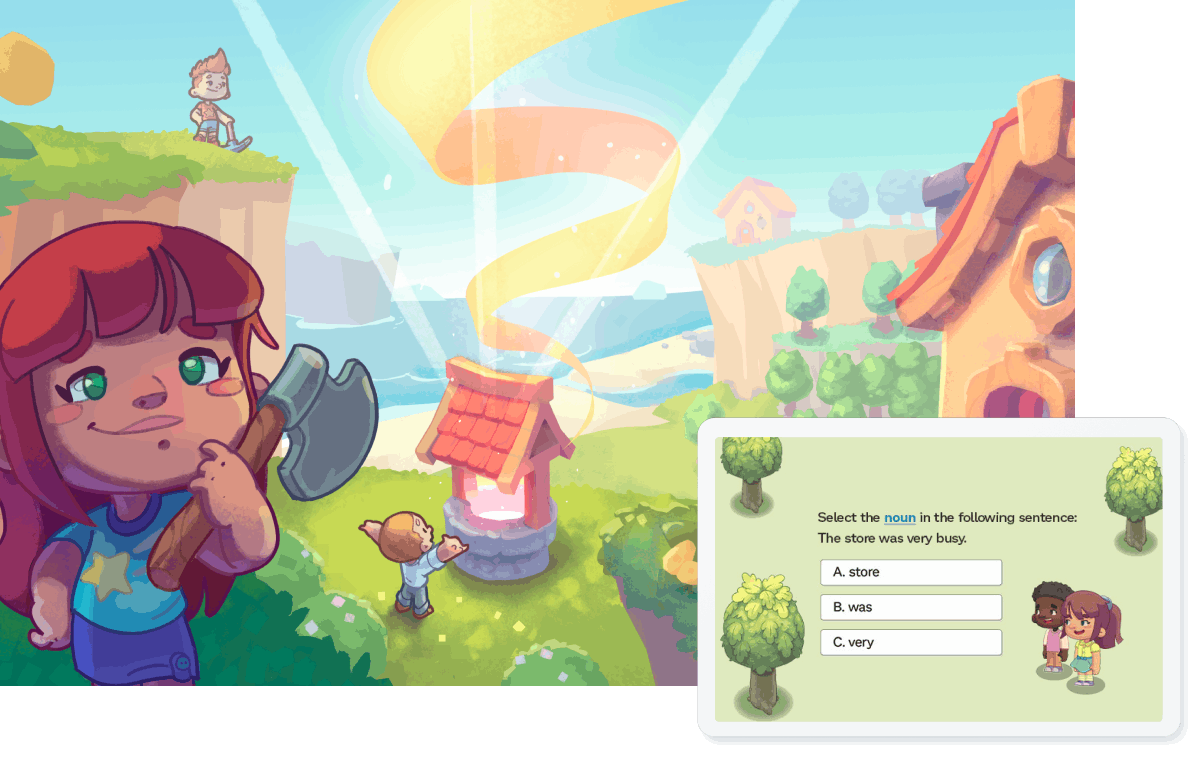
Prodigy English
Power your imagination! Create a custom-built world through reading and language practice. Every correct answer gives students more energy to gather supplies and build up your village.

Aligned to your curriculum
Prodigy Math provides comprehensive math curriculum coverage, including Common Core, TEKS and many more state-specific standards. Prodigy English also aligns with Common Core, with more skills and coverage on the way!
Ready to kickstart a learning adventure?


IMAGES
VIDEO
COMMENTS
Up next for you: Course challenge Test your knowledge of the skills in this course. Start Course challenge. Square roots review. Community questions. Learn eighth grade math—functions, linear equations, geometric transformations, and more. (aligned with Common Core standards)
The ultimate collection of free 8th grade math worksheets. All of our 8th grade math worksheets are topic-specific, printable (they are available as pdf files), and include a complete answer key. This is the only 8th grade math worksheets library you will ever need--simply pick your topic, select a worksheet, click and download.
All the numbers in the number system are classified into different sets and those are called sets of numbers. Examples of sets: Real Numbers, Rational numbers, INtegers, Whole numbers, Natural numbers
Unit 1. 8.1 Rigid Transformations and Congruence. Rigid Transformations. Lesson 1 Moving in the Plane; Lesson 2 Naming the Moves; Lesson 3 Grid Moves ; Lesson 4 Making the Moves; Lesson 5 Coordinate Moves; Lesson 6 ... Open Up Resources 6-8 Math is published as an Open Educational Resource.
Grade 8 Math. Units. Unit. 1. Lesson 1 Moving in the Plane. Lesson 2 Naming the Moves. Lesson 3 Grid Moves . Lesson 4 Making the Moves. Lesson 5 Coordinate Moves. Lesson 6 Describing Transformations. Lesson 7 No Bending or Stretching. Lesson 8 Rotation Patterns.
denoted by a number or variable in the superscript place of the base, which designates how many times the base will be multiplied by itself if it is positive or by its inverse if it is negative. If the power is 1, the base will be multiplied by 1 and will not change. If the power is 0, the simplified form will equal 1.
Solution. To get from Position 1 to Position 2, the shape moves up. To get from Position 2 to Position 3, the shape rotates 90 degrees counterclockwise. To get from Position 3 to Position 4, the shape moves down and to the right. To get from Position 4 to Position 5 the shape rotates 90 degrees clockwise. To get from Position 5 to Position 6 ...
Unit 1: Get ready for numbers and operations. 0/1100 Mastery points. Converting fractions to decimals Exponents Evaluating exponent expressions. Order of operations Powers of ten Multiplying and dividing with powers of ten Estimating with multiplying and dividing decimals.
Learn eighth grade math aligned to the Eureka Math/EngageNY curriculum —functions, linear equations, geometric transformations, and more. If you're seeing this message, it means we're having trouble loading external resources on our website. ... Unit 1 Unit 1: Module 1: Integer exponents and scientific notation. Multiply powers; Powers of ...
1.2 Triangle Square Dance. Your teacher will give you three pictures. Each shows a different set of dance moves. Arrange the three pictures so one of you can see them right way up. Choose who will start the game. The starting player chooses one of the three applets below and describes the dance to the other player. After one round, trade roles.
Plane and Solid Figures Student Resources MathLinks: Grade 8 (2nd ed.) ©CMAT Unit 1: Student Packet 29 Transversals and Parallel Lines In this figure, line k is a transversal. Lines m and n are NOT parallel. When two lines in a plane are cut (crossed) at two points by a transversal, eight
The number can now be written as 3.829 x 103. You can check the number by multiplying 3.829 x (10 x 10 x 10) = 3.829 x 1,000 = 3,829. If you have a number like 700, you can drop the zeros when writing scientific notation. 700 = 7 x 102. Unit 1: Number and Operations: Practice Activity 4.
8th Grade, Unit 1, Open Up Resources - Illustrative Mathematics Tutorials Playlist. Search #811math #812math #813math to find individual tutorials fast!
a single numeral; the number 359 has 3 digits: 3,5,9. following each other (4,5,6) answer when you add. answer when you subtract. answer when you multiply. answer when you divide. Study with Quizlet and memorize flashcards containing terms like variable, like terms, coefficient and more.
Math 8 Unit 1 - Illustrative Mathematics Online Resources. Grade 8 Illustrative Mathematics - Unit 1: Rigid Transformations and Congruence. Download PDF of Student Edition. Download PDF of Student Practice Work (Homework) Unit Summary for Parents - PDF File. Lesson Topic.
Lesson 16 Parallel Lines and the Angles in a Triangle. Let's see why the angles in a triangle add to 180 degrees. Lesson Activities. Practice Problems.
Grade 8 Math In-Class Assignment Unit 1. Squares and Square Roots. Sections 1.1 - 1. 4. Name: _____ Selected Response. Place the letter of the best response in the blank to the left.
Assignment of Grade 8, Maths & Maths UNIT 1 Ex 1.1 - Study Material. Page 4 : he a. and, , AO EE OSM Oe , , , in this exercise you have;, , » used factor trees to write an integer as a product of prime tactors, , » found the HCF of two integers by first writing each one, as a product of prime numbers, , found the LCM of two integers by first writing each one, , as a product of prime numbers ...
View grade_8_math_-_unit_1_assignment_1_2015.docx from MATH 8 at Cando Community School. Grade 8 Math In-Class Assignment Unit 1 Squares and Square Roots Sections 1.1 - 1.4 Name: _ Selected Response.
The Algebra 1 course, often taught in the 9th grade, covers Linear equations, inequalities, functions, and graphs; Systems of equations and inequalities; Extension of the concept of a function; Exponential models; and Quadratic equations, functions, and graphs. Khan Academy's Algebra 1 course is built to deliver a comprehensive, illuminating, engaging, and Common Core aligned experience!
View grade_8_math_-_unit_1_assignment_1_2015_workings.pdf from MATH 8 at Cando Community School. Grade 8 Math In-Class Assignment Unit 1 Squares and Square Roots Sections 1.1 - 1.4 Name: _ Selected AI Homework Help
Operations such as addition, subtraction, multiplication, and division can be performed on rational numbers using rules similar to those for integers. For division, we need to ensure that the divisor is not zero. Download CBSE Maths Chapter 1 Rational Numbers Class 8 Extra Questions PDF for free to Secure good marks.
Unit 1: Downloads. Unit Downloads are offered as additional resources to support teachers in making instructional decisions that allow them to better meet the needs of their students. Each resource is tied directly to the curriculum and is intended to be used with the lessons within each unit. ... OUR 6-8 Math is published as an Open ...
Math Assignment Unit 3. Task 1. Imagine a scenario involving a bungee jumper leaping from a bridge, with the jumper's height above the river surface modeled by the equation h (t) = -0.5 + v0t + h0 , where h is 𝑡 2 measured in meters, t is in seconds, v0 represents the jumper's initial velocity in meters per second, and h0 is the initial ...
Master Math Grades 1-8 & English Grades 1-6. 91% of parents said their children enjoy using Prodigy Math* "Prodigy is a great way to get kids who don't like math into math." Caralena Luthi. ... Optional Prodigy memberships provide additional features that are engaging and promote more math practice - and they also help us keep Prodigy free for ...
Sign in to access your AP or Pre-AP resources and tools including AP Classroom.