how to draw null hypothesis distribution

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• College University and Postgraduate
• Academic Writing

Writing Null Hypotheses in Research and Statistics

Last Updated: January 17, 2024 Fact Checked

This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a High School Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 24,695 times.

Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Start by recognizing that the basic definition of "null" is "none" or "zero"—that's your biggest clue as to what a null hypothesis should say. Keep reading to learn everything you need to know about the null hypothesis, including how it relates to your research question and your alternative hypothesis as well as how to use it in different types of studies.

Things You Should Know

• Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

• Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.

What is a null hypothesis?

• Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
• Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.

Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

• For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

• You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
• In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.

How do I test a null hypothesis?

• Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
• Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
• Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
• Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source

Templates for Null Hypotheses

• Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

• Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

• Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

• Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .

• ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
• ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
• ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
• ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
• ↑ https://online.stat.psu.edu/statprogram/reviews/statistical-concepts/hypothesis-testing
• ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
• ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html

About This Article

• Send fan mail to authors

Reader Success Stories

Dec 3, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

Get all the best how-tos!

Sign up for wikiHow's weekly email newsletter

Null Hypothesis – Simple Introduction

A null hypothesis is a precise statement about a population that we try to reject with sample data. We don't usually believe our null hypothesis (or H 0 ) to be true. However, we need some exact statement as a starting point for statistical significance testing.

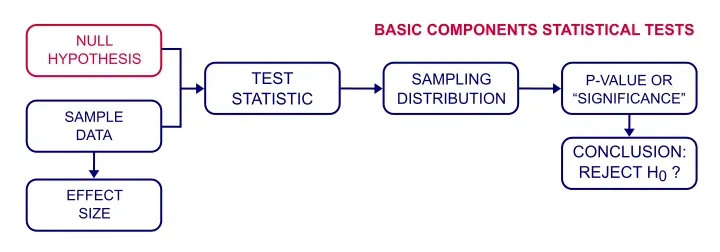
Null Hypothesis Examples

Often -but not always- the null hypothesis states there is no association or difference between variables or subpopulations. Like so, some typical null hypotheses are:

• the correlation between frustration and aggression is zero ( correlation analysis );
• the average income for men is similar to that for women ( independent samples t-test );
• Nationality is (perfectly) unrelated to music preference ( chi-square independence test );
• the average population income was equal over 2012 through 2016 ( repeated measures ANOVA ).
• Dutch, German, French and British people have identical average body weigths .the average body weight is equal for D

“Null” Does Not Mean “Zero”

A common misunderstanding is that “null” implies “zero”. This is often but not always the case. For example, a null hypothesis may also state that the correlation between frustration and aggression is 0.5. No zero involved here and -although somewhat unusual- perfectly valid. The “null” in “null hypothesis” derives from “nullify” 5 : the null hypothesis is the statement that we're trying to refute, regardless whether it does (not) specify a zero effect.

Null Hypothesis Testing -How Does It Work?

I want to know if happiness is related to wealth among Dutch people. One approach to find this out is to formulate a null hypothesis. Since “related to” is not precise, we choose the opposite statement as our null hypothesis: the correlation between wealth and happiness is zero among all Dutch people. We'll now try to refute this hypothesis in order to demonstrate that happiness and wealth are related all right. Now, we can't reasonably ask all 17,142,066 Dutch people how happy they generally feel.

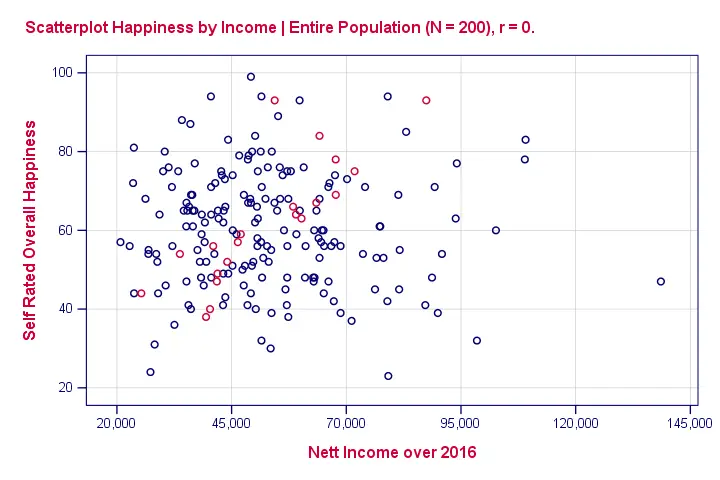
So we'll ask a sample (say, 100 people) about their wealth and their happiness. The correlation between happiness and wealth turns out to be 0.25 in our sample. Now we've one problem: sample outcomes tend to differ somewhat from population outcomes. So if the correlation really is zero in our population, we may find a non zero correlation in our sample. To illustrate this important point, take a look at the scatterplot below. It visualizes a zero correlation between happiness and wealth for an entire population of N = 200.

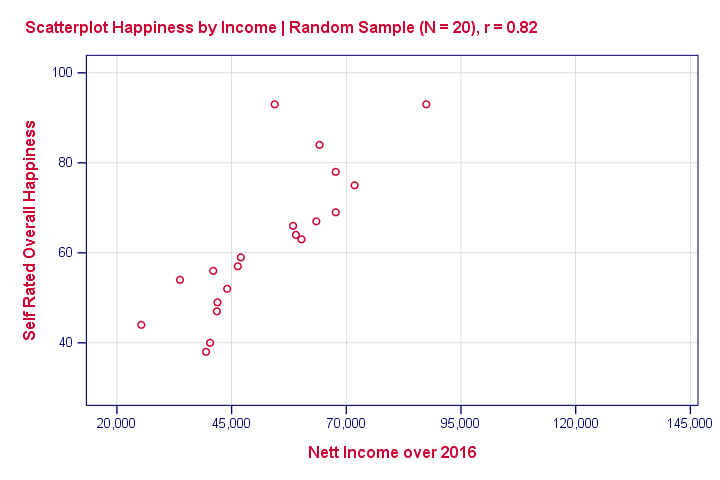
Now we draw a random sample of N = 20 from this population (the red dots in our previous scatterplot). Even though our population correlation is zero, we found a staggering 0.82 correlation in our sample . The figure below illustrates this by omitting all non sampled units from our previous scatterplot.

This raises the question how we can ever say anything about our population if we only have a tiny sample from it. The basic answer: we can rarely say anything with 100% certainty. However, we can say a lot with 99%, 95% or 90% certainty.

Probability

So how does that work? Well, basically, some sample outcomes are highly unlikely given our null hypothesis . Like so, the figure below shows the probabilities for different sample correlations (N = 100) if the population correlation really is zero.

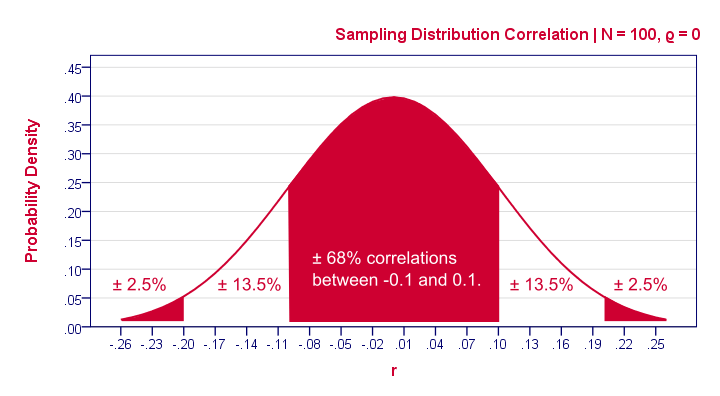
A computer will readily compute these probabilities. However, doing so requires a sample size (100 in our case) and a presumed population correlation ρ (0 in our case). So that's why we need a null hypothesis . If we look at this sampling distribution carefully, we see that sample correlations around 0 are most likely: there's a 0.68 probability of finding a correlation between -0.1 and 0.1. What does that mean? Well, remember that probabilities can be seen as relative frequencies. So imagine we'd draw 1,000 samples instead of the one we have. This would result in 1,000 correlation coefficients and some 680 of those -a relative frequency of 0.68- would be in the range -0.1 to 0.1. Likewise, there's a 0.95 (or 95%) probability of finding a sample correlation between -0.2 and 0.2.

We found a sample correlation of 0.25. How likely is that if the population correlation is zero? The answer is known as the p-value (short for probability value): A p-value is the probability of finding some sample outcome or a more extreme one if the null hypothesis is true. Given our 0.25 correlation, “more extreme” usually means larger than 0.25 or smaller than -0.25. We can't tell from our graph but the underlying table tells us that p ≈ 0.012 . If the null hypothesis is true, there's a 1.2% probability of finding our sample correlation.

Conclusion?

If our population correlation really is zero, then we can find a sample correlation of 0.25 in a sample of N = 100. The probability of this happening is only 0.012 so it's very unlikely . A reasonable conclusion is that our population correlation wasn't zero after all. Conclusion: we reject the null hypothesis . Given our sample outcome, we no longer believe that happiness and wealth are unrelated. However, we still can't state this with certainty.

Null Hypothesis - Limitations

Thus far, we only concluded that the population correlation is probably not zero . That's the only conclusion from our null hypothesis approach and it's not really that interesting. What we really want to know is the population correlation. Our sample correlation of 0.25 seems a reasonable estimate. We call such a single number a point estimate . Now, a new sample may come up with a different correlation. An interesting question is how much our sample correlations would fluctuate over samples if we'd draw many of them. The figure below shows precisely that, assuming our sample size of N = 100 and our (point) estimate of 0.25 for the population correlation.

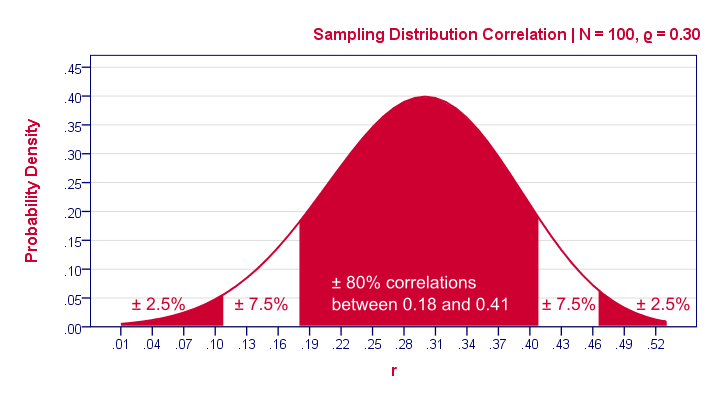
Confidence Intervals

Our sample outcome suggests that some 95% of many samples should come up with a correlation between 0.06 and 0.43. This range is known as a confidence interval . Although not precisely correct, it's most easily thought of as the bandwidth that's likely to enclose the population correlation . One thing to note is that the confidence interval is quite wide. It almost contains a zero correlation, exactly the null hypothesis we rejected earlier. Another thing to note is that our sampling distribution and confidence interval are slightly asymmetrical. They are symmetrical for most other statistics (such as means or beta coefficients ) but not correlations.

• Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
• Cohen, J (1988). Statistical Power Analysis for the Social Sciences (2nd. Edition) . Hillsdale, New Jersey, Lawrence Erlbaum Associates.
• Field, A. (2013). Discovering Statistics with IBM SPSS Newbury Park, CA: Sage.
• Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
• Van den Brink, W.P. & Koele, P. (2002). Statistiek, deel 3 [Statistics, part 3]. Amsterdam: Boom.

Tell us what you think!

This tutorial has 17 comments:.

By John Xie on February 28th, 2023

“stop using the term ‘statistically significant’ entirely and moving to a world beyond ‘p < 0.05’”

“…, no p-value can reveal the plausibility, presence, truth, or importance of an association or effect.

Therefore, a label of statistical significance does not mean or imply that an association or effect is highly probable, real, true, or important. Nor does a label of statistical nonsignificance lead to the association or effect being improbable, absent, false, or unimportant.

Yet the dichotomization into ‘significant’ and ‘not significant’ is taken as an imprimatur of authority on these characteristics.” “To be clear, the problem is not that of having only two labels. Results should not be trichotomized, or indeed categorized into any number of groups, based on arbitrary p-value thresholds.

Similarly, we need to stop using confidence intervals as another means of dichotomizing (based, on whether a null value falls within the interval). And, to preclude a reappearance of this problem elsewhere, we must not begin arbitrarily categorizing other statistical measures (such as Bayes factors).”

Quotation from: Ronald L. Wasserstein, Allen L. Schirm & Nicole A. Lazar, Moving to a World Beyond “p<0.05”, The American Statistician(2019), Vol. 73, No. S1, 1-19: Editorial.

By Ruben Geert van den Berg on February 28th, 2023

Yes, partly agreed.

However, most students are still forced to apply null hypothesis testing so why not try to explain to them how it works?

An associated problem is that "significant" has a normal language meaning. Most people seem to confuse "statistically significant" with "real-world significant", which is unfortunate.

By the way, this same point applies to other terms such as "normally distributed". A normal distribution for dice rolls is not a normal but a uniform distribution ;-)

Keep up the good work!

SPSS tutorials

Privacy Overview

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 29 April 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.3: Test Statistics and Sampling Distributions

• Last updated
• Save as PDF
• Page ID 4009

• Danielle Navarro
• University of New South Wales

At this point we need to start talking specifics about how a hypothesis test is constructed. To that end, let’s return to the ESP example. Let’s ignore the actual data that we obtained, for the moment, and think about the structure of the experiment. Regardless of what the actual numbers are, the form of the data is that X out of N people correctly identified the colour of the hidden card. Moreover, let’s suppose for the moment that the null hypothesis really is true: ESP doesn’t exist, and the true probability that anyone picks the correct colour is exactly θ=0.5. What would we expect the data to look like? Well, obviously, we’d expect the proportion of people who make the correct response to be pretty close to 50%. Or, to phrase this in more mathematical terms, we’d say that X/N is approximately 0.5. Of course, we wouldn’t expect this fraction to be exactly 0.5: if, for example we tested N=100 people, and X=53 of them got the question right, we’d probably be forced to concede that the data are quite consistent with the null hypothesis. On the other hand, if X=99 of our participants got the question right, then we’d feel pretty confident that the null hypothesis is wrong. Similarly, if only X=3 people got the answer right, we’d be similarly confident that the null was wrong. Let’s be a little more technical about this: we have a quantity X that we can calculate by looking at our data; after looking at the value of X, we make a decision about whether to believe that the null hypothesis is correct, or to reject the null hypothesis in favour of the alternative. The name for this thing that we calculate to guide our choices is a test statistic .

Having chosen a test statistic, the next step is to state precisely which values of the test statistic would cause is to reject the null hypothesis, and which values would cause us to keep it. In order to do so, we need to determine what the sampling distribution of the test statistic would be if the null hypothesis were actually true (we talked about sampling distributions earlier in Section 10.3.1). Why do we need this? Because this distribution tells us exactly what values of X our null hypothesis would lead us to expect. And therefore, we can use this distribution as a tool for assessing how closely the null hypothesis agrees with our data.

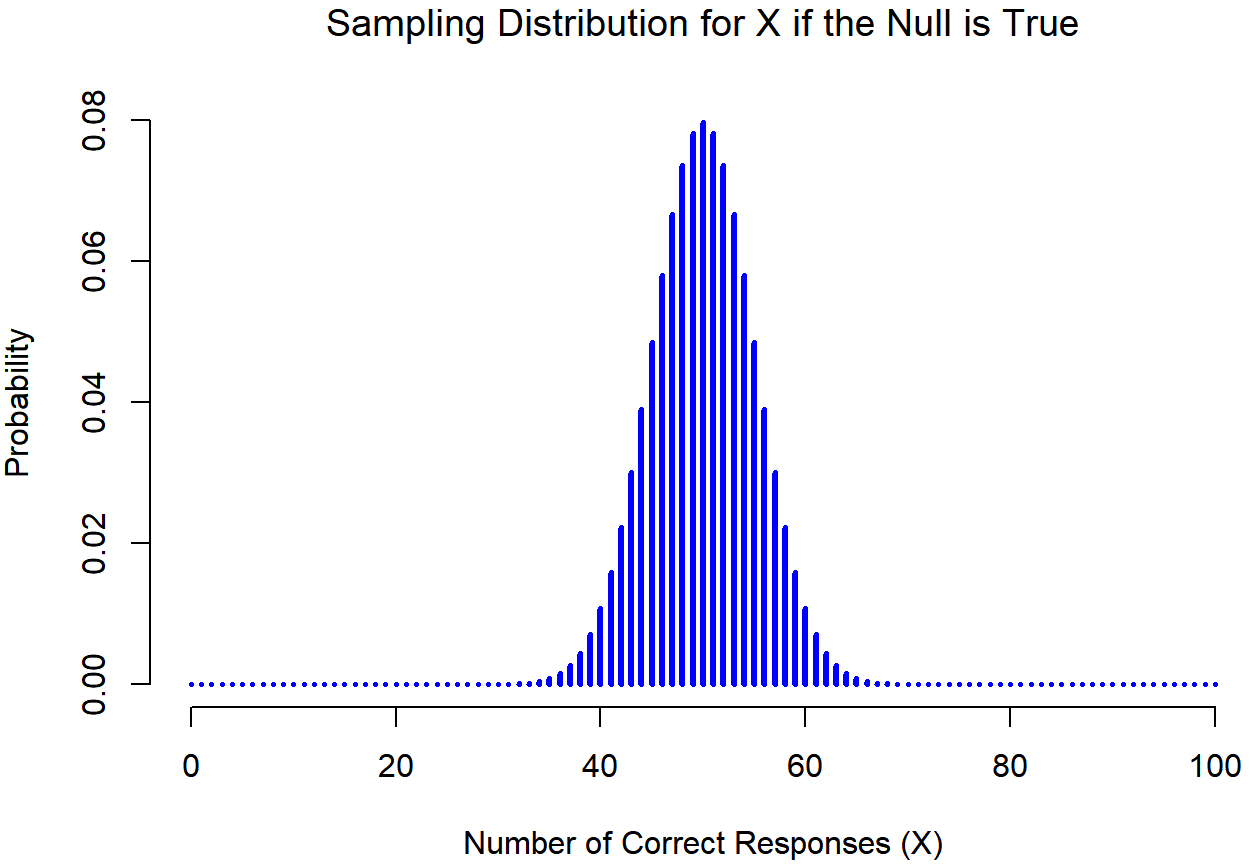
How do we actually determine the sampling distribution of the test statistic? For a lot of hypothesis tests this step is actually quite complicated, and later on in the book you’ll see me being slightly evasive about it for some of the tests (some of them I don’t even understand myself). However, sometimes it’s very easy. And, fortunately for us, our ESP example provides us with one of the easiest cases. Our population parameter θ is just the overall probability that people respond correctly when asked the question, and our test statistic X is the count of the number of people who did so, out of a sample size of N. We’ve seen a distribution like this before, in Section 9.4: that’s exactly what the binomial distribution describes! So, to use the notation and terminology that I introduced in that section, we would say that the null hypothesis predicts that X is binomially distributed, which is written

X∼Binomial(θ,N)

Since the null hypothesis states that θ=0.5 and our experiment has N=100 people, we have the sampling distribution we need. This sampling distribution is plotted in Figure 11.1. No surprises really: the null hypothesis says that X=50 is the most likely outcome, and it says that we’re almost certain to see somewhere between 40 and 60 correct responses.

Statistics Made Easy

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3  = … = μ k  (all of the group means are equal)
• H A : At least one group mean is different   from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).

A two-way ANOVA tests three null hypotheses at the same time:

• All group means are equal at each level of the first variable
• All group means are equal at each level of the second variable
• There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.

The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam. 

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

• The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
• The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
• The p-value for the interaction between watering  frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Something Out of Nothing? The Influence of Double-Zero Studies in Meta-analysis of Adverse Events in Clinical Trials

• Original Paper
• Open access
• Published: 01 May 2024

Cite this article

You have full access to this open access article

• Zhaohu Fan 1 ,
• Dungang Liu   ORCID: orcid.org/0000-0001-5340-9465 4 ,
• Yuejie Chen 2 &
• Nanhua Zhang 3  

In addition to clinical efficacy, safety is another important outcome to assess in randomized controlled trials. It focuses on the occurrence of adverse events, such as stroke, deaths, and other rare events. Because of the low or very low rates of observing adverse events, meta-analysis is often used to pooled together evidence from dozens or even hundreds of similar clinical trials to strengthen inference. A well-known issue in rare-event meta-analysis is that some or even majority of the available studies may observe zero events in both the treatment and control groups. The influence of these so-called double-zero studies has been researched in the literature, which nevertheless focuses on reaching a dichotomous conclusion—whether or not double-zero studies should be included in the analysis. It has not been addressed when and how they contribute to inference, especially for the odds ratio. This paper fills this gap using comparative analysis of real and simulated data sets. We find that a double-zero study contributes to the odds ratio inference through its sample sizes in the two arms. When a double-zero study has an unequal allocation of patients in its two arms, it may contain non-ignorable information. Exclusion of these studies, if taking a significant proportion of the study cohort, may result in inflated type I error, deteriorated testing power, and increased estimation bias.

Avoid common mistakes on your manuscript.

1 Introduction

Efficacy and safety are pivotal issues in clinical treatments and procedures. Clear and sufficient evidence, demonstrating a new treatment or procedure is effective and safe, is required before its approval by the Food and Drug Administration [ 18 ]. Different from efficacy assessment aiming to prove effectiveness, a safety study seeks to identify adverse effects potentially associated with the new treatment [ 18 ]. The adverse effects are detected by capturing certain adverse events, which are those events with dangerous and unwanted tendencies, such as death, stock, and heart failure. Oftentimes, the adverse events of interest are rarely observed, as their occurrence rate could be extremely low. As a result, a single clinical trial, even with hundreds of patients enrolled, may be powerless to detect safety issues, if there is any. In this so-called rare-event situation, synthesis of the evidence from dozens or even hundreds of clinical trials may be the only way to make a reliable and meaningful conclusion [ 8 ]. This evidence synthesis process is often termed as meta-analysis in statistical and clinical literature. In the past decade, meta-analysis has been recognized and demonstrated as an effective tool in the discovery of safety issues. For example, in a high-profile meta-analysis of 48 clinical trials, Nissen and Wolski [ 12 ] concluded that the diabetic drug Rosiglitazone had a significant association with myocardial infarction. Such a discovery would not be possible if the 48 trials were not pooled together, as an analysis of any single-trial data did not yield statistical significance.

A common issue in meta-analysis of adverse events is the existence of the so-called double-zero studies. A double-zero study is a situation in which no adverse events occur in either the control or treatment arm of a study. Such studies may take a great proportion in the study cohort when the event rates are very low. There are extensive discussions on how to deal with double-zero studies in the literature (see, e.g., [ 2 , 6 , 8 , 9 , 19 , 26 ]). A consensus so far is that the common continuity correction (i.e., adding 0.5 to zeros) may result in severe bias [ 8 , 9 , 14 , 19 ]. However, there is still an unsettling question—when and how double-zero studies contribute to inference?

The impact of double-zero studies on statistical inference for the odds ratio (or relative risk) has been researched in the literature. Note that the odds ratio and relative risk have similar values when event rates are low. Some argue that in theory such studies provide information for inference. For example, Xie et al. [ 23 ] showed that double-zero studies can contribute to the full likelihood of the common odds ratio and therefore they contain information for meta-analysis inference. Nevertheless, others have reported numerical results that are not consistent or even contradictory to each other. For example, in the analysis of 60 clinical trials on the coronary artery bypass grafting, Kuss [ 7 ] observed the relative risk changed little with the 35 double-zero studies either included or excluded. In their development of an exact meta-analysis approach, Liu et al. [ 9 ] and Yang et al. [ 26 ] observed that the inclusion of double-zero studies always results in wider confidence intervals for the odds ratio and relative risk, which implies that the influence of double-zero studies may make inference conservative and potentially less efficient. Ren et al. [ 14 ] showed odds ratio disagreement between inclusion and exclusion of double-zero studies (c.f. Tables 3-4 therein) in 386 real data meta-analyses. But their comparison in this regard was limited to the inverse-variance method and Mantel-Haenszel method which required continuity corrections to incorporate double-zero studies. Xu et al. [ 25 ] used the generalized linear mixed model and performed a similar comparison in 442 meta-analyses. They reported noticeable numerical changes (e.g., odds ratio direction or statistical significance) when double-zero studies were excluded from meta-analysis. Xu et al. [ 24 ] used Doi’s inverse variance heterogeneity (IVhet) model with continuity corrections (of 0.5) to include double-zero studies, which led to improved performance. However, they noted that this may be due to the addition of 0.5 to zero cells. So far, the focus of the existing literature is on reaching a dichotomous conclusion—whether or not double-zero studies should be included in the analysis. There is still a lack of clear understanding of when and how double-zero studies contribute to the odds ratio inference.

The goal of this paper is to use real and simulated data analyses to explain when and how double-zero studies contribute to the odds ratio inference. We use as a prototype of the cohort of Kuss [ 7 ]’s 60 clinical trials on the coronary artery bypass grafting (CABG) to generate new data for our numerical investigation. We use a classical binomial-normal hierarchical model [ 4 , 16 ] and conduct fixed- and random-effects analysis. Our finding is that a double-zero study contribute to the odds ratio inference through its sample sizes in the two arms. Roughly speaking, a double-zero study with an unequal allocation in the two arms (e.g., \(n_c > n_t\) ) contains non-ignorable information for inference. Exclusion of these studies will lead to inflated type I error, deteriorated testing power, and increased estimation bias.

The rest of the article is organized as follows. In Sect.  2 , we review the binomial-normal hierarchical model and a fully Bayesian inference for the odds ratio. In Sect.  3 , we conduct a case study of Kuss [ 7 ]’s CABG data, through which we explain heuristically and numerically how the arm sizes of a double-zero study contribute to inference. The insights are used to guide the design of simulation studies in Sect.  4 , where the impact of double-zero studies is demonstrated. In Sect.  5 , we repeat the same investigation but in a random-effects model setting. The paper is concluded with a discussion in Sect.  6 .

2 A Classical Meta-analysis Model for Odds Ratios

Given K independent clinical trials, we use the classical binomial-normal hierarchical model to make inference [ 4 , 16 , 17 ]. We assume that in the i th study, the numbers of (adverse) events \(Y_{ci}\) and \(Y_{ti}\) , in the control and treatment arms, respectively, follow binomial distributions

where \(n_{ci}\) and \(n_{ti}\) are the numbers of participants. The goal is to compare the probability \(p_{ci}\) of the control arm with the probability \(p_{ti}\) of the treatment arm. To gauge the difference between \(p_{ci}\) and \(p_{ti}\) , we consider the odds ratios \(\theta _{i}=\frac{p_{ti}}{1-p_{ti}}/\frac{p_{ci}}{1-p_{ci}}\) . The odds ratio is a risk measure commonly used in clinical trials, and it is studied in [ 9 , 14 , 23 ] in meta-analysis of rare events.

The logarithm of the odds ratios is \(\delta _i=\log (\theta _{i})= \log (\frac{p_{ti}}{1-p_{ti}})-\log (\frac{p_{ci}}{1-p_{ci}})=logit(p_{ti})-logit(p_{ci})\) . Using the log odds ratios \(\delta _{i}\) , the model can be reparameterized as

where \(\mu _{ci}\) is the baseline probability in the control arm of the i th study. In the classical fixed-effects model, the treatment effects \(\delta _{i}\) are fixed and identical across all the studies, i.e., \(\delta _{i}=\delta\) . The fixed-effects assumption can be relaxed to allow \(\delta _i\) to vary across studies. This so-called random-effects model will be examined later in this paper. In both fixed- and random-effects models, the baseline effects \(\mu _{ci}\) are allowed to vary between studies. Oftentimes, they are assumed to follow a normal distribution

where a and b are nuisance parameters.

In this paper, we use a fully Bayesian method to make inference about \(\delta\) . We follow the convention to specify its non-informative prior as \(\delta \sim {\mathcal {N}}(0, 10^4)\) . The non-informative priors for the two nuisance parameters a and b in Eq. ( 2 ) can be specified as \(a\sim {\mathcal {N}}(0,10^{4})\) and \(b^2\sim {{\mathcal {I}}}{{\mathcal {G}}}(10^{-3}, 10^{-3})\) (see, e.g., [ 16 , 17 , 21 ]). We draw posterior samples using Markov Chain Monte Carlo via Gibbs sampling. Our implementation of Gibbs sampling uses the R package Rjags which calls the computing programs in JAGS [ 13 ]. Specifically, we run three Markov chains with distinct starting values to ensure that they converge to the same distribution. In each Markov chain, we use 10,000 burn-in iterations followed by 50,000 iterations to collect posterior samples. To reduce autocorrelation within the samples, we implement a thinning process, selecting every fourth value from the posterior samples of each chain.

3 A Case Study of Coronary Artery Bypass Grafting

Ischaemic heart disease refers to a condition of insufficient blood supply to the myocardium. A medical therapy for this condition is coronary artery bypass grafting (CABG) surgery (see, e.g., [ 1 , 10 , 27 ]). Traditionally, a CABG surgery is performed with cardiopulmonary bypass to provide artificial circulation, and the coronary artery bypass can be performed with the heart stopped. This procedure is called “on-pump” CABG. The on-pump CABG operation, however, may result in adverse events, such as myocardial, pulmonary, renal, coagulation, and cerebral complications (see, e.g., [ 11 , 20 ]). In an effort to reduce the occurrence of adverse events, “off-pump” CABG, a relatively new procedure that does not require cardiopulmonary bypass, has been developed and used in recent years (see, e.g., [ 5 , 11 , 15 ]).

To compare the off-pump and on-pump methods, [ 11 ] collected 60 studies to examine the occurrence of postoperative strokes. Out of the 60 studies, 35 studies did not observe any postoperative strokes in either arm. The full data set is displayed in Table 1 . In their analysis, [ 11 ] calculated the relative risk using the standard inverse-variance method. The relative risk was 0.73 with a \(95\%\) confidence interval of [0.53, 0.99] with the p value being 0.04. Therefore, they concluded that the off-pump method results in lower chance of postoperative strokes. Yet, their analysis ignored all of the 35 double-zero studies, which accounted for 58.3 \(\%\) of the available studies.

To investigate the impact of the 35 double-zero studies, [ 7 ] compared the results by excluding and including them in the beta-binomial model (which is different from the model used in [ 11 ]). When the double-zero studies were excluded, the relative risk was 0.53 with a \(95\%\) confidence interval of [0.31,0.91]. When the double-zero studies were included, the relative risk was 0.51 with a \(95\%\) confidence interval of [0.28, 0.92]. The results in the two scenarios are similar to each other, which suggests that information in the double-zero studies may be negligible for inference. However, this conclusion contradicts arguments made in other existing publications [ 9 , 19 , 22 , 24 , 25 , 26 ].

Our intuition is that a double-zero study may contain useful information in the sample size of each of its arm. To illustrate this, we start with a toy example and then use the proof-by-contradiction method to re-analyze the CABG data set. Suppose the number of adverse events follows a binomial distribution \(Y\sim \text {Binomial} (n,p)\) , and we observe no event, i.e., \(y=0\) . If the sample size \(n=10\) , the Bayesian method with a non-informative prior \(\text {Beta} (1,1)\) on p yields a mean estimate \({\hat{p}}=0.083\) with a \(95\%\) credible interval (0.002, 0.285). However, if \(n=1000\) , the same inference procedure yields a mean estimate \({\hat{p}}=0.001\) with a \(95\%\) credible interval (0.000, 0.004). The upper end 0.004 is much smaller than 0.285, and it is closer to 0. This implies that observing a zero event out of a larger sample size gives more confidence that the underlying probability is closer to zero. In other words, the same observation \(y=0\) but with different sample sizes ( \(n=10\) or \(n=1000\) ) may yield very different results.

To further manifest how the sample sizes of the two arms of a double-zero study may contribute to meta-analytical inference, we use the proof-by-contradiction method. We begin with an assumption that a double-zero study does not contribute any information to statistical inference, even through the sample sizes of its two arms. If this assumption is true, we can arbitrarily change its \(n_{ci}\) or \(n_{ti}\) and expect no or minimal numerical change in analysis result. For the CABG data set, we increase \(n_{ci}\) of the control arms in the 35 double-zero studies (only) and monitor the change in numerical results. Specifically, we multiply \(n_{ci}\) in the double-zero studies by the factors 2, 3, 4, and 5. Note that we do not alter the sample sizes in non-double-zero studies. We only alter the control-arm size \(n_{ci}\) in the 35 double-zero studies, which means any numerical change observed in subsequent analysis is due to the alteration of \(n_{ci}\) in the context of observing 0 event out of \(n_{ci}\) patients in the control arm.

Table 2 shows the odds ratio estimates and credible intervals obtained using the method presented in Sect. 2 . When the scale factor is 1, results are shown for the analysis of the original CABG data set (the first row of Table 2 ). When the scale factor is larger than 1, the sample size \(n_{ci}\) of the control arm of the 35 double-zero studies has been increased. Table 2 shows that when all the 35 double-zero studies are excluded from the analysis, the odds ratio estimates and credible intervals change little, regardless of the scale factors. This is in line with our expectation as we have only altered \(n_{ci}\) in the double-zero studies and the data in those non-double-zero studies remain the same. On the other hand, when the 35 double-zero studies are included in the analysis, scaling up \(n_{ci}\) clearly moves the odds ratio estimate toward 1 (i.e., from 0.705 to 0.787). In particular, when the scaling factor is 2 (e.g., \(n_{ci}\) is doubled), the upper end of the credible interval becomes \(1.006 > 1\) , which indicates a non-significant difference between the off-pump and on-pump methods. This is in contrast with the analysis of the original data set (scale factor = 1) where the upper limit of the credible interval is \(0.942 < 1\) , which indicates a significant difference between the two surgical methods. To summarize, the numerical changes seen after \(n_{ci}\) of the double-zero studies scaled up contradicts the assumption that a double-zero study does not contribute any information to inference. In fact, our experiment here (by altering \(n_{ci}\) in double-zero studies only) has provided numerical evidence that \(n_{ci}\) (or \(n_{ti}\) ) can contribute to meta-analysis nonignorable information that may change the significance conclusion.

The numerical evidence in this section has provides critical insights into when and how a double-zero study may contribute to the inference. Roughly put, if a double-zero study contributes to the overall inference, it is through the sample sizes \(n_{ci}\) and \(n_{ti}\) of its two arms, and this contribution is more manifest when its two arms have unequal allocations (e.g., \(n_{ci}>> n_{ti}\) ). The simulation studies in the following section will further demonstrate this heuristic statement by considering different allocations in the two arms in trial designs.

4 Simulation studies

The goal of our simulation studies is to compare the “full analysis” that includes all available data with “partial analysis” that excludes double-zero studies. We assess their performance with respect to the type I error, testing power, and estimation bias. We consider a variety of settings by varying (1) the odds ratio, (2) the number of subjects in each clinical study, and (3) the total number of clinical studies. Our results are based on 1000 simulation repetitions.

We simulate \(Y_{ci}\) and \(Y_{ti}\) for K independent studies from Model ( 1 ). To ensure low or very low baseline event rates, we set the parameters Eq. ( 2 ) as \(a=\textrm{logit}(p_{\max }/2)\) and \(b=\big (\textrm{logit}(p_{\max })-a\big )/3\) . The value of \(p_{\max }\) controls the upper bound of the baseline probabilities \(p_{ci}\) . When \(p_{\max }=1\%\) or \(0.5\%\) , we summarize the distribution of \(p_{ci}\) ’s in Table 3 . For example, when \(p_{\max }=1\%\) , the \(99\%\) quantile of the the baseline probabilities is \(0.86\%\) .

4.1 Equal allocation

We begin with an equal allocation setting where the sample sizes of the treatment and control groups are the same for each clinical study (e.g., \(n_{ci}=n_{ti}=200\) ). We set (i) the total number of clinical studies \(K=60\) or 180, (ii) \(p_{{\max }}=0.5\%\) , and (iii) the odds ratio \(\theta =1, 1.2, 1.4, 1.6, 1.8\ \text {and}\ 2\) . Table 4 shows that the varying odds ratios result in different percentages of the double-zero studies ranging between \(23\%\) and \(37\%\) . Our goal is to test testing power when the null hypothesis is \(H_0\) : the odds ratio \(\theta =1\) .

We compare the full and partial analyses in terms of the type I error and testing power. When \(K=60\) , the top panel of Table 4 shows that these two types of analyses produce similar type I error rates, both of which are close to the \(5\%\) nominal level. The partial analysis also yields similar testing power to that of the full analysis across all the odds ratios greater than 1. This observation implies that in this equal allocation setting, the partial analysis may perform as well as the full analysis. In other words, the inclusion/exclusion of double-zero studies has little influence on the inference even when double-zero studies take a significant proportion (23–37%) of the available studies. This conclusion holds when the number of studies increases to \(K=180\) as seen in the bottom panel of Table 4 .

In Table 5 , we examine the bias in odds ratio estimates produced by the partial and full analyses. The results show that both partial and full analyses yield small biases, which are comparable to each other. This observation suggests that in this equal allocation setting, the inclusion/exclusion of double-zero studies has negligible influence on the estimation bias. This conclusion holds for both \(K=60\) and \(K=180\) .

We use Gelman–Rubin diagnostic test to assess convergence of Markov chains [ 3 ]. For example, Table 6 presents a summary of the Gelman–Rubin diagnostic test statistics for the equal allocation setting where \(K= 60\) . The mean and maximum statistics show that Gelman–Rubin diagnostic test statistics in all 1000 simuation replications are close to 1, indicating satisfactory convergence of Markov Chains.

4.2 Unequal allocation

Unequal allocation ( \(n_{ci}>n_{ti}\) ). We continue to carry out our comparative analyses but using an unequal allocation setting, where the sample sizes of the treatment and control groups could be very different. The simulation setting is similar to the previous one except that 120 out of 180 clinical studies are unequally allocated. Specifically, we set \(n_{ci}=100\) in the control arm and \(n_{ti}=50\) in the treatment arm. For the remaining 60 studies, the treatment and control groups have equal sample sizes (e.g., \(n_{ci}=n_{ti}=200\) ). The total sample size ( \(n_{ci}+n_{ti}\) ) is not comparable across all the studies, which is intentional as it is not uncommon (see the meta-data in [ 12 ]).

In this setting that contains unequal-allocation studies, we continue to compare the full and partial analyses in terms of the type I error and testing power. When \(p_{\max }=0.5\%\) , the number of double-zero studies in each meta-analysis ranges from 86 to 104 (the proportion ranging from 48 to \(58\%\) ). The top panel of Table 7 shows that the type I error produced by the partial analysis is \(10.10\%\) , which is twice as large as the 5 \(\%\) nominal level. In contrast, the full analysis yields a type I error of \(4.80\%\) , which is close to the 5 \(\%\) nominal level. Furthermore, the partial analysis has much lower testing power across all the odds ratios greater than 1, when compared to that of the full analysis. For example, if we examine the odds ratio = 1.4 in the third column of Table 7 , the testing power of the partial analysis is 15.20 \(\%\) , which is less than a half of that of the full analysis (33.50 \(\%\) ). These observations demonstrate that in this unequal allocation setting, the full analysis outperforms the partial analysis. The exclusion of double-zero studies from the analysis can result in substantially inflated type I error and substantially undermined testing power. When \(p_{\max }\) increases to 1 \(\%\) , the bottom panel of Table 7 shows that the exclusion of double-zero studies severely inflates the type I error (e.g., 11.30 \(\%\) ) and adversely undermines its power as well (e.g., 10.30 \(\%\) as compared to 21.90 \(\%\) from the full analysis when the odds ratio is 1.2).

In Table 8 , we examine the bias in odds ratio estimates produced by the partial and full analyses. When \(p_{\max }\) = \(0.5\%\) , the top panel shows that the estimation bias in the partial analysis is double or even triple of those produced in the full analysis across all the odds ratios considered. For example, when the odds ratio is 1.2, the bias produced from the partial analysis is \(-\) 0.09. which is three times as large as bias (0.03) produced by the partial analysis. When \(p_{\max }=1\%\) , our observation in the bottom panel of Table 8 is similar. The full analysis shows much smaller bias. These observations again confirms double-zero studies can contain useful information for inference in the unequal-allocation setting, and including them in the analysis can decrease the estimation bias.

We carry out additional simulations when the total number of studies K is much smaller \((e.g., K=60)\) , and the total sample size \((n_{ci}+n_{ti})\) is comparable across all the clinical studies \((e.g.,(n_{\text {ci}} = 300, n_{\text {ti}} = 100)\) and \(({n_{\text {ci}}} = 200, {n_{\text {ti}}} = 200))\) . The results are similar and can be found in Supplementary Materials A.

Unequal allocation ( \(n_{ci}<n_{ti}\) ). We consider another unequal-allocation setting but set \(n_{ci}=200 < n_{ti}=400\) in 120 studies, out of the 180 simulated studies. Treatment and control arms have equal sample sizes in the remaining 60 studies (i.e., \(n_{ci}=n_{ti}=200\) ).

Table 9 shows that the type I error produced by the partial analysis is slightly inflated (7.00 \(\%\) ), whereas the type I error (6.20 \(\%\) ) yielded by the full analysis is closer to the 5 \(\%\) nominal level. On the other hand, the full analysis yields higher testing power than that of the partial analysis across all the odds ratios greater than 1 (e.g., 49.60 \(\%\) versus 41.10 \(\%\) when the odds ratio = 1.3). For example, the full analysis has an increase of 2.0–8.5 \(\%\) in testing power across odds ratios, when compared to that of partial analysis. These observations indicate that the full analysis outperforms the partial analysis. Meta-analyses with double-zero studies can have greater testing power in an unequal-allocation setting.

In Supplementary Materials B, we compare bias in odds ratio estimates between partial and full analyses. The full analysis shows much smaller bias (see Table S3 for details).

5 Results in a Random-Effects Model Setting

In this section, we examine the difference between the partial and full analyses in a random-effects model setting. In the random-effects model, the treatment effects \(\delta _{i}\) ’s are assumed to be drawn from a normal distribution \(\delta _{i}\sim N(\delta ,\sigma ^2)\) . More specifically,

In the random-effects model, the parameter of interest is the mean parameter \(\delta\) of the distribution of \(\delta _i\) in Model ( 3 ). The non-informative priors for \(\delta\) and \(\sigma ^2\) can be specified as \({\mathcal {N}}(0,10^{4})\) and \({{\mathcal {I}}}{{\mathcal {G}}}(10^{-3},10^{-3})\) , respectively (see, e.g., [ 16 , 21 ]). The priors for both a and b can be specified in the same way as in the fixed-effects model.

We simulate data from Model ( 3 ) to compare the full and partial analyses. We set the parameter \(\sigma\) =0.1 to mimic the heterogeneity in the last column of Table 11 . The rest of simulation settings is similar to that of the fixed-effects model in Sect.  4.2 , unequal allocation ( \(n_{ci}>n_{ti}\) ). Table 10 shows that the type I error produced by the partial analysis is severely inflated (11.30 \(\%\) ), whereas the type I error (6.90 \(\%\) ) yielded by the full analysis is close to the 5 \(\%\) nominal level. On the other hand, when the odds ratios are greater than 1, the full analysis yields higher testing power than the partial analysis (e.g., 60.20 \(\%\) versus 48.80 \(\%\) when the odds ratio=1.6). These observations indicate the inclusion of double-zero studies increases testing power while reducing the type I error.

Similar to the real data analysis conducted in Sect.  3 , we assume that a double-zero study does not contribute to statistical inference, even when taking into consideration the sample sizes of both arms. If this premise is true, we can alter the sample size \(n_{ci}\) or \(n_{ti}\) and expect little or no numerical change in the analysis results. Specifically, we increase the sample size of the control arm by multiplying it by the factors of 2, 3, 4, and 5.

Table 11 shows odds ratio estimates, credible intervals and estimates of the heterogeneity parameter \(\sigma\) obtained using the method presented in Sect.  5 . When the scale factor is set to 1, analysis results are shown for the original CABG data set (the first row of Table 11 ). When the scale factor exceeds 1, the sample size \(n_{ci}\) of the control arm in the 35 double-zero studies has been increased. Table 11 shows when all of the 35 double-zero studies are removed from the analysis, the odds ratio estimates, credible intervals, and heterogeneity estimates remain almost unchanged, regardless of the scale factors. This is consistent with our expectations, as we have only modified \(n_{ci}\) in the double-zero studies, while the data in the non-double-zero studies remains unchanged (from the second to the fourth columns of Table 11 ). Conversely, when the 35 double-zero studies are incorporated into the analysis, increasing \(n_{ci}\) leads to a noticeable shift of the odds ratio estimate towards 1 (from 0.555 to 0.706). Furthermore, if the scaling factor is set to 3 (i.e., \(n_{ci}\) is tripled), the upper end of the credible interval becomes \(1.028 > 1\) . This suggests that there is no significant difference between the off-pump and on-pump methods. This stands in contrast to the analysis of the original dataset (scale factor = 1), in which the upper bound of the credible interval is \(0.866 < 1\) , indicating a significant difference between the two surgical methods. In summary, the numerical alterations observed after scaling up \(n_{ci}\) in the double-zero studies contradict the assumption that a double-zero study does not provide any information for inference. In fact, our experiment here (by modifying \(n_{ci}\) solely in the double-zero studies) has provided numerical proof that \(n_{ci}\) (or \(n_{ti}\) ) can supply non-ignorable information to meta-analysis that may alter the conclusion of significance.

In Supplementary Materials B, we examine bias in odds ratio estimates produced by the partial and full analyses. The full analysis shows much smaller bias (see Table S4 for details).

6 Discussion

Rare adverse events, such as strokes and deaths, are of crucial concerns in safety studies of clinical treatments and procedures. However, their low occurrence rates pose challenges and questions for statistical inference. Many of them are surrounding double-zero studies. The debate concerning the inclusion and exclusion of double-zero studies was prominently sparked by the high-profile study by [ 12 ]. To examine the safety of the diabetic drug Rosiglitazone, they used Peto’s method through which double-zero studies did not contribute anything to the inference. This practice has been questioned by many statisticians, leading to two lines of research. One line has focused on the development of new methods that can incorporate double-zero studies without using 0.5 corrections (see the review article by [ 8 ]). The other line has attempted to reach a inclusion/exclusion conclusion, which is nevertheless dichotomous (see the references cited in the introduction). Before recommending an action (inclusion/exclusion), one question needs to be answered; that is, when and how double-zero studies contribute to the odds ratio inference. This is the main purpose of our investigation, and we intentionally avoid advocating a specific inclusion/exclusion action. As shown in our paper, double-zero studies may contribute significantly in some scenarios while in other scenarios they contribute little.

Through numerical studies, we have empirically found that when the following two conditions are met, double-zero studies may likely contribute to the odds ratio inference to a notable extent.

The group of non-double-zero studies itself contains adequate information for double-zero studies to borrow.

There is a substantial number of double-zero studies with unequal allocation in the two arms.

Basically, to see notable impact of double-zero studies, Condition (i) says that the number of non-double-zero studies \(K_\mathrm{non-DZ}\) can not be small. Otherwise, there is not adequate information to borrow from. Condition (ii) says that the number of double-zero studies with unequal allocations \(K_\mathrm{DZ-uneqaul}\) should be (moderately) large. Otherwise, the impact of double-zero studies may not accumulate sufficiently to make a practical difference. These two conditions can be explained more intuitively in a non-meta-analysis setting where all the K studies have the same baseline probability and odds ratio. In this setting, we can stack the data throughout the K studies and form a single 2 by 2 contingency table to draw an inference. If Condition (i) is not met and \(K_\mathrm{non-DZ}\) is too small, the odds ratio inference may be too unreliable as the numerators of the control and treatment arms may be small. If Condition (ii) is not met and \(K_\mathrm{DZ-uneqaul}\) is not large, we may not see disproportionate increases in the denominators of the control and treatment arms and thus a difference in the odds ratio inference. An implication is that if the total number of studies K is small, at least one of the two conditions cannot be met, and therefore, the impact of double-zero studies may not be significant enough to make a clinical difference.

When the impact of double-zero studies is non-ignorable, our finding is that they contribute to odds ratio inference through the sample sizes in their two arms. When a double-zero study has unequal allocation in its two arms, it may contain non-ignorable information. If double-zero studies as such make up a large proportion of the study cohort, they should not be excluded from analysis. If excluded, the inference may not be valid or efficient as we have seen severely inflated type I error, deteriorated testing power, and increased estimation bias in our numerical study.

In practice, study level characteristics may explain the variation in the prevalences of adverse event outcomes as well as the differences between active treatment and control. These factors may be accounted for in meta-analyses through meta-regression. It is interesting to examine how double-zero studies may impact inference especially when the site-level characteristics may be related to the occurrence of double-zero studies.

Alexander JH, Smith PK (2016) Coronary-artery bypass grafting. N Engl J Med 374:1954–1964

Article   Google Scholar  

Bradburn MJ, Deeks JJ, Berlin JA, Russell Localio A (2007) Much ado about nothing: a comparison of the performance of meta-analytical methods with rare events. Stat Med 26:53–77

Article   MathSciNet   Google Scholar  

Brooks SP, Gelman A (1998) General methods for monitoring convergence of iterative simulations. J Comput Graph Stat 7:434–455

Günhan BK, Röver C, Friede T (2020) Random-effects meta-analysis of few studies involving rare events. Res Synth Methods 11:74–90

Hannan EL, Wu C, Smith CR, Higgins RS, Carlson RE, Culliford AT, Gold JP, Jones RH (2007) Off-pump versus on-pump coronary artery bypass graft surgery: differences in short-term outcomes and in long-term mortality and need for subsequent revascularization. Circulation 116:1145–1152

Sweeting JM, Sutton JA, Lambert PC (2004) What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Stat Med 23:1351–1375

Kuss O (2015) Statistical methods for meta-analyses including information from studies without any events-add nothing to nothing and succeed nevertheless. Stat Med 34:1097–1116

Liu D (2019) Meta-analysis of rare events. In: Wiley StatsRef: statistics reference. Online 1–7. https://doi.org/10.1002/9781118445112.stat08167

Liu D, Liu RY, Xie M-G (2014) Exact meta-analysis approach for discrete data and its application to 2 \(\times\) 2 tables with rare events. J Am Stat Assoc 109:1450–1465

Lorenzen US, Buggeskov KB, Nielsen EE, Sethi NJ, Carranza CL, Gluud C, Jakobsen JC (2019) Coronary artery bypass surgery plus medical therapy versus medical therapy alone for ischaemic heart disease: a protocol for a systematic review with meta-analysis and trial sequential analysis. Syst Rev 8:1–14

Møller CH, Penninga L, Wetterslev J, Steinbrüchel DA, Gluud C (2012) Off-pump versus on-pump coronary artery bypass grafting for ischaemic heart disease. Cochrane Database Syst Rev 3:CD007224

Nissen SE, Wolski K (2007) Effect of rosiglitazone on the risk of myocardial infarction and death from cardiovascular causes. N Engl J Med 356:2457–2471

Plummer M, Stukalov A, Denwood M (2022) rjags: Bayesian graphical models using MCMC. R package version 4.13

Ren Y, Lin L, Lian Q, Zou H, Chu H (2019) Real-world performance of meta-analysis methods for double-zero-event studies with dichotomous outcomes using the Cochrane Database of Systematic Reviews. J Gen Intern Med 34:960–968

Shroyer AL, Grover FL, Hattler B, Collins JF, McDonald GO, Kozora E, Lucke JC, Baltz JH, Novitzky D (2009) On-pump versus off-pump coronary-artery bypass surgery. N Engl J Med 361:1827–1837

Smith TC, Spiegelhalter DJ, Thomas A (1995) Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med 14:2685–2699

Sutton AJ, Abrams KR (2001) Bayesian methods in meta-analysis and evidence synthesis. Stat Methods Med Res 10:277–303

Thaul S (2012) How FDA approves drugs and regulates their safety and effectiveness. Congressional Research Service

Tian L, Cai T, Pfeffer MA, Piankov N, Cremieux P-Y, Wei L (2009) Exact and efficient inference procedure for meta-analysis and its application to the analysis of independent 2 \(\times\) 2 tables with all available data but without artificial continuity correction. Biostatistics 10:275–281

Van Dijk D, Jansen EW, Hijman R, Nierich AP, Diephuis JC, Moons KG, Lahpor JR, Borst C, Keizer AM, Nathoe HM et al (2002) Cognitive outcome after off-pump and on-pump coronary artery bypass graft surgery: a randomized trial. J Am Med Assoc 287:1405–1412

Warn DE, Thompson S, Spiegelhalter DJ (2002) Bayesian random effects meta-analysis of trials with binary outcomes: methods for the absolute risk difference and relative risk scales. Stat Med 21:1601–1623

Xiao M, Lin L, Hodges JS, Xu C, Chu H (2021) Double-zero-event studies matter: a re-evaluation of physical distancing, face masks, and eye protection for preventing person-to-person transmission of COVID-19 and its policy impact. J Clin Epidemiol 133:158–160

Xie M-G, Kolassa J, Liu D, Liu R, Liu S (2018) Does an observed zero-total-event study contain information for inference of odds ratio in meta-analysis? Stat Interface 11:327–337

Xu C, Furuya-Kanamori L, Islam N, Doi SA (2022) Should studies with no events in both arms be excluded in evidence synthesis? Contemp Clin Trials 122:e106962

Xu C, Li L, Lin L, Chu H, Thabane L, Zou K, Sun X (2020) Exclusion of studies with no events in both arms in meta-analysis impacted the conclusions. J Clin Epidemiol 123:91–99

Yang G, Liu D, Wang J, Xie M-G (2016) Meta-analysis framework for exact inferences with application to the analysis of rare events. Biometrics 72:1378–1386

Yusuf S, Zucker D, Passamani E, Peduzzi P, Takaro T, Fisher L, Kennedy J, Davis K, Killip T, Norris R et al (1994) Effect of coronary artery bypass graft surgery on survival: overview of 10-year results from randomised trials by the Coronary Artery Bypass Graft Surgery Trialists Collaboration. Lancet 344:563–570

Download references

Author information

Authors and affiliations.

Information Technology Management, Scheller College of Business, Georgia Institute of Technology, Atlanta, GA, USA

LexisNexis, Raleigh, NC, USA

Yuejie Chen

Division of Biostatistics and Epidemiology, Cincinnati Children’s Hospital Medical Center and College of Medicine, University of Cincinnati, Cincinnati, OH, USA

Nanhua Zhang

Department of Operations, Business Analytics and Information Systems, Carl H. Lindner College of Business, University of Cincinnati, Cincinnati, OH, USA

Dungang Liu

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Dungang Liu .

Ethics declarations

Ethical standards.

No external funding or grants were received to support this work. Yuejie Chen was an undergraduate student at the University of Cincinnati and graduate student at North Carolina State University, and she is currently Data Analyst at LexisNexis, Raleigh, North Carolina. The real data presented in Table 1 were originally published in [ 11 ].

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file 1 (pdf 45 KB)

Rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Fan, Z., Liu, D., Chen, Y. et al. Something Out of Nothing? The Influence of Double-Zero Studies in Meta-analysis of Adverse Events in Clinical Trials. Stat Biosci (2024). https://doi.org/10.1007/s12561-024-09431-y

Download citation

Received : 24 March 2023

Revised : 24 November 2023

Accepted : 28 January 2024

Published : 01 May 2024

DOI : https://doi.org/10.1007/s12561-024-09431-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Adverse event
• Clinical trial
• Unequal allocation
• Find a journal
• Publish with us
• Track your research