8.1 finding the average value of a function homework answers

Find what you need to study

8.1 Finding the Average Value of a Function on an Interval

2 min read • february 15, 2024

Anusha Tekumulla

Attend a live cram event

Review all units live with expert teachers & students

Welcome back to AP Calculus with Fiveable! This topic focuses on finding the average value of a continuous function using definite integrals.

🔢 Average Value of a Function

The average value of a function will allow us to solve problems that involve the accumulation of change over an interval, which will later be used to understand more difficult topics of integration.

For questions that require the average value of a function, we are never given a finite number of data points. Therefore, we must use integration to determine what the average value is.

This idea is fairly simple once you memorize a key piece of information: if f is continuous on [ a , b ] , [a,b], [ a , b ] , then the average value of f on [ a , b [a,b [ a , b ] is the following.

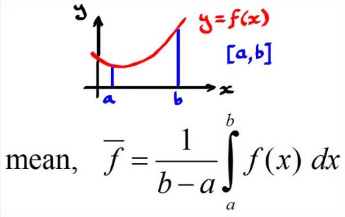
Image Courtesy of ExamSolutions

🔍Average Value of a Function Steps

Here are some steps to help break down the formula!

Set up the integral so that you integrate f(x) from a to b with respect to x, which will calculate the area under the curve between these two limits.
Then place the fraction in front of the integral, which is simply the reciprocal of the difference between a and b.
Evaluating this expression allows you to get the average y-value of this function between [ a , b ] [a,b] [ a , b ]

✏️ Average Value of a Function Walkthrough

If the formula still seems a little difficult to understand due to its notation, practice questions are the best way to better understand its use!

Consider the function f ( x ) = 2 x 2 − 3 x + 5 f(x) = 2x^2-3x+5 f ( x ) = 2 x 2 − 3 x + 5 on the interval [1,4]. Find the average value of this function on the interval.

In this case, a = 1 and b = 4. So we begin by subbing the 1 and 4 into both the denominator of the fraction in front of the integral and the limits of the integral.

Next, take the integral of f(x).

Finally, we can sub in the limits and evaluate.

Time for you to practice some questions yourself! ⬇️

📝 Average Value of a Function Practice Problems

Give each of these problems a try before you move onto the solutions!

What is the average value of 5 x 2 + 4 5x^2+4 5 x 2 + 4 on the interval 0 ≤ x ≤ 6 0\le x\le 6 0 ≤ x ≤ 6 ?
What is the average value of x 3 − x 2 x^3-x^2 x 3 − x 2 on the interval 2 ≤ x ≤ 5 2\le x\le 5 2 ≤ x ≤ 5 ?
What is the average value of s i n ( x ) + c o s ( x ) sin(x)+cos(x) s in ( x ) + cos ( x ) on the interval 0 ≤ x ≤ π 0\le x\le \pi 0 ≤ x ≤ π ?

Average Value of a Function Question Solutions

Question 1 solution, question 2 solution, question 3 solution.

Great job! This topic often shows up as part (a) of FRQs, so keep this in mind for the AP.

Stay Connected

AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.

AP Calculus AB : 8.1 Finding the Average Value of a Function on an Interval- Exam Style questions with Answer- MCQ

AP Physics AP Calculus AP Chemistry AP Biology

What is the average (mean) value of $3t^{3}-t^{2} $over the interval$ -1\leq t\leq 2 $?

(A)$\frac{11}{4} $ (B)$\frac{7}{2} $ (C)8 (D)$\frac{33}{4}$ (E) 16

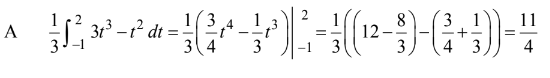
8.1 finding the average value of a function homework answers

The average value of $\sqrt{x}$ over the interval 0 ≤ 2 ≤ x is

(A)$\frac{1}{3}\sqrt{2}$ (B)$\frac{1}{2}\sqrt{2}$ (C)$\frac{2}{3}\sqrt{2} $ (D) 1 (E)$\frac{4}{3}\sqrt{2}$

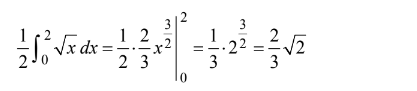
If the position of a particle on the x-axis at time t is $−5t^{2}$ , then the average velocity of the particle for 0 ≤ t ≤ 3 is (A) −45 (B) −30 (C) −15 (D) −10 (E) −5

Let $x(t)=5t^2$ be the position at time t. Average velocity\frac{x(3)-x(0)}{3-0}=\frac{-45-0}{3}=-15\)

What is the average value of $y=x^2\sqrt{x^3+1}$ on the interval [0, 2] ?

(A) $\frac{26}{9}$ (B)$\frac{52}{9}$ (C) $\frac{26}{3}$ (D) $\frac{52}{3}$ (E) 24

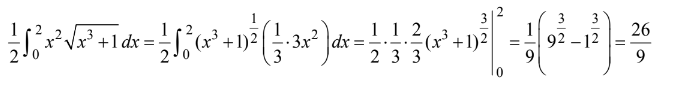
What is the average value of y for the part of the curve$ y= 3x-x^{2}$ which is in the first quadrant ?

(A) –6 (B) –2 (C) $\frac{3}{2}$ (D) $\frac{9}{4}$ (E)$\frac{9}{2}$

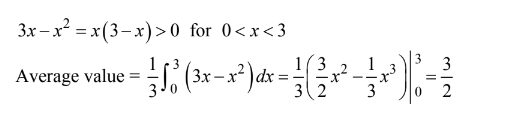
Find what you need to study

8.1 Finding the Average Value of a Function on an Interval

2 min read • february 15, 2024

Anusha Tekumulla

Attend a live cram event

Review all units live with expert teachers & students

Welcome back to AP Calculus with Fiveable! This topic focuses on finding the average value of a continuous function using definite integrals.

🔢 Average Value of a Function

The average value of a function will allow us to solve problems that involve the accumulation of change over an interval, which will later be used to understand more difficult topics of integration.

For questions that require the average value of a function, we are never given a finite number of data points. Therefore, we must use integration to determine what the average value is.

This idea is fairly simple once you memorize a key piece of information: if f is continuous on [ a , b ] , [a,b], [ a , b ] , then the average value of f on [ a , b [a,b [ a , b ] is the following.

Image Courtesy of ExamSolutions

🔍Average Value of a Function Steps

Here are some steps to help break down the formula!

Set up the integral so that you integrate f(x) from a to b with respect to x, which will calculate the area under the curve between these two limits.
Then place the fraction in front of the integral, which is simply the reciprocal of the difference between a and b.
Evaluating this expression allows you to get the average y-value of this function between [ a , b ] [a,b] [ a , b ]

✏️ Average Value of a Function Walkthrough

If the formula still seems a little difficult to understand due to its notation, practice questions are the best way to better understand its use!

Consider the function f ( x ) = 2 x 2 − 3 x + 5 f(x) = 2x^2-3x+5 f ( x ) = 2 x 2 − 3 x + 5 on the interval [1,4]. Find the average value of this function on the interval.

In this case, a = 1 and b = 4. So we begin by subbing the 1 and 4 into both the denominator of the fraction in front of the integral and the limits of the integral.

Next, take the integral of f(x).

Finally, we can sub in the limits and evaluate.

Time for you to practice some questions yourself! ⬇️

📝 Average Value of a Function Practice Problems

Give each of these problems a try before you move onto the solutions!

What is the average value of 5 x 2 + 4 5x^2+4 5 x 2 + 4 on the interval 0 ≤ x ≤ 6 0\le x\le 6 0 ≤ x ≤ 6 ?
What is the average value of x 3 − x 2 x^3-x^2 x 3 − x 2 on the interval 2 ≤ x ≤ 5 2\le x\le 5 2 ≤ x ≤ 5 ?
What is the average value of s i n ( x ) + c o s ( x ) sin(x)+cos(x) s in ( x ) + cos ( x ) on the interval 0 ≤ x ≤ π 0\le x\le \pi 0 ≤ x ≤ π ?

Average Value of a Function Question Solutions

Question 1 solution, question 2 solution, question 3 solution.

Great job! This topic often shows up as part (a) of FRQs, so keep this in mind for the AP.

Stay Connected

AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.

Snapsolve any problem by taking a picture. Try it in the Numerade app?

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.8: Average Value of a Function

Last updated
Save as PDF
Page ID 32819

5.4 Average Value of a Function

We often need to find the average of a set of numbers, such as an average test grade. Suppose you received the following test scores in your algebra class: 89, 90, 56, 78, 100, and 69. Your semester grade is your average of test scores and you want to know what grade to expect. We can find the average by adding all the scores and dividing by the number of scores. In this case, there are six test scores. Thus,

\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33.\]

Therefore, your average test grade is approximately 80.33, which translates to a B− at most schools.

Suppose, however, that we have a function $v(t)$ that gives us the speed of an object at any time t, and we want to find the object’s average speed. The function $v(t)$ takes on an infinite number of values, so we can’t use the process just described. Fortunately, we can use a definite integral to find the average value of a function such as this.

Let $f(x)$ be continuous over the interval $[a,b]$ and let $[a,b]$ be divided into n subintervals of width $Δx=(b−a)/n$. Choose a representative $x^∗_i$ in each subinterval and calculate $f(x^∗_i)$ for $i=1,2,…,n.$ In other words, consider each $f(x^∗_i)$ as a sampling of the function over each subinterval. The average value of the function may then be approximated as

\[\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n},\]

which is basically the same expression used to calculate the average of discrete values.

But we know $Δx=\dfrac{b−a}{n},$ so $n=\dfrac{b−a}{Δx}$, and we get

\[\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\dfrac{(b−a)}{Δx}}.\]

Following through with the algebra, the numerator is a sum that is represented as $\sum_{i=1}^nf(x∗i),$ and we are dividing by a fraction. To divide by a fraction, invert the denominator and multiply. Thus, an approximate value for the average value of the function is given by

$\dfrac{\sum_{i=1}^nf(x^∗_i)}{\dfrac{(b−a)}{Δx}}=(\dfrac{Δx}{b−a})\sum_{i=1}^nf(x^∗_i)=(\dfrac{1}{b−a})\sum_{i=1}^nf(x^∗_i)Δx.$

This is a Riemann sum. Then, to get the exact average value, take the limit as n goes to infinity. Thus, the average value of a function is given by

$\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx.$

Definition: average value of the function

Let $f(x)$ be continuous over the interval $[a,b]$. Then, the average value of the function $f(x)$ (or $f_{ave}$) on $[a,b]$ is given by

\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)dx.\]

Example $\PageIndex{8}$: Finding the Average Value of a Linear Function

Find the average value of $f(x)=x+1$ over the interval $[0,5].$

First, graph the function on the stated interval, as shown in Figure.

$CNX_Calc_Figure_05_02_017.jpeg$

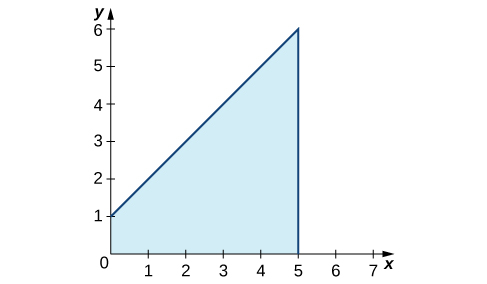
Figure $\PageIndex{10}$: The graph shows the area under the function $(x)=x+1$ over $[0,5].$

The region is a trapezoid lying on its side, so we can use the area formula for a trapezoid $A=\dfrac{1}{2}h(a+b),$ where h represents height, and a and b represent the two parallel sides. Then,

$∫^5_0x+1dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}$.

Thus the average value of the function is

$\dfrac{1}{5−0}∫^5_0x+1dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}$.

Exercise $\PageIndex{7}$

Find the average value of $f(x)=6−2x$ over the interval $[0,3].$

Use the average value formula, and use geometry to evaluate the integral.

Key Concepts

The definite integral can be used to calculate net signed area, which is the area above the x-axis less the area below the x-axis. Net signed area can be positive, negative, or zero.
The average value of a function can be calculated using definite integrals.

Key Equations

Definite Integral

$\displaystyle∫^b_af(x)dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org .

HIGH SCHOOL

ACT Tutoring
SAT Tutoring
PSAT Tutoring
ASPIRE Tutoring
SHSAT Tutoring
STAAR Tutoring

GRADUATE SCHOOL

MCAT Tutoring
GRE Tutoring
LSAT Tutoring
GMAT Tutoring
AIMS Tutoring
HSPT Tutoring
ISAT Tutoring
SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

Elementary Math
Pre-Calculus
Trigonometry

science tutoring

Foreign languages.

Mandarin Chinese

elementary tutoring

Computer Science

Search 350+ Subjects

Video Overview
Tutor Selection Process
Online Tutoring
Mobile Tutoring
Instant Tutoring
How We Operate
Our Guarantee
Impact of Tutoring
Reviews & Testimonials
Media Coverage
About Varsity Tutors

Calculus AB : Find Average Value

Study concepts, example questions & explanations for calculus ab, all calculus ab resources, example questions, example question #1 : find average value.

Which of the following theorems is related to finding the Average Value of a Function?

Mean Value Theorem for Integrals

Extreme Value Theorem

Fundamental Theorem of Calculus

Intermediate Value Theorem