the unit circle algebra 2 with trigonometry homework answers

A free service from Mattecentrum

Circular functions

• Circular relations I
• Circular relations II
• Circular relations III
• Circular relations IV
• Circular relations V

The circle below is drawn in a coordinate system where the circle's center is at the origin and has a radius of 1. This circle is known as a unit circle.

The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. If you picture a right triangle with one side along the x -axis:

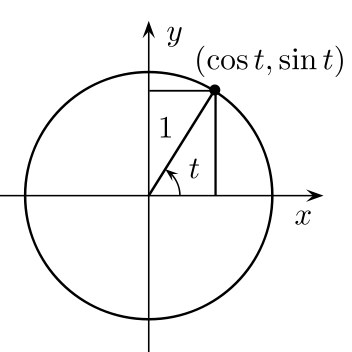
then the cosine of the angle would be the x -coordinate and the sine of the angle would be the y -coordinate. Since both the coordinates are defined by using a unit circle, they are often called circular functions.

Solve the equation sin v = 0.5 with the unit circle.

If we examine the figure below, it is evident that there are two solutions to the problem:

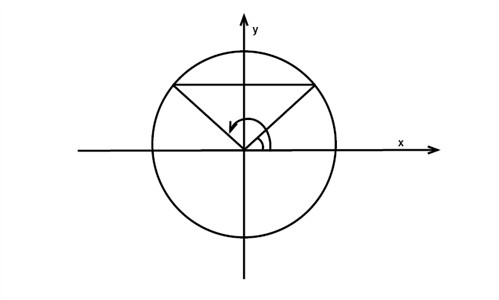
We arrive at the first solution by using a pocket calculator and keying:

$$v=\sin^{-1}0.5=30^{\circ}$$

Since half a revolution is 180 degrees, we ascertain the other angle by:

$$180-v=180-30=150^{\circ}$$

Video lesson

Solve the given equation using the unit circle Sin Ѳ = -1

• Geometry Overview
• SAT Overview
• ACT Overview

Lesson The Amazing Unit Circle: Trigonometric Identities

Trigonometry

Do you like studying angles and triangles? Then you’ll love learning trigonometry! Trigonometry is a branch of math that looks at the relationships between side lengths of triangles and their corresponding angles. You’ll be able to use your knowledge of geometry and algebra to derive and employ the trigonometric identities. Trigonometry is essential to the understanding of precalculus .

Still need help after using our trigonometry resources? Use our service to find a trigonometry tutor .

This lesson reviews the specific types of triangles as well as fundamental trigonometric identities like sine, cosine and tangent. The ratios of those identities help solve for missing side lengths of triangles and the Pythagorean theorem cannot be used.

Complex numbers are written in the form x+yi, where the y-axis represents the imaginary axis. In polar coordinate form, “x+yi” is written as r(cosθ + i sinθ) where r is the distance from the origin.

This lesson investigates how different trigonometric identities are derived. Read on to learn how to use Euler’s Formula is used to find some important trigonometric identities!

This lesson is all about the special relationship between trigonometric functions (like sin, cos, and tan) and their doubles or halves. These formulas are important to know, because they can simplify a much harder equation.

An inverse trig function allows you to input a number and get an angle measure as an output. Typically, you’ll be working in radians when you use inverse trig functions. These functions are read as “arc” + “name of function;” for example, “the arcsine of x,” or sin -1 (x).

The Law of Sines describes a proportion that can be used to solve for unknown sides and angles in a triangle. Basically, the proportion states that a side length of a triangle, a, directly corresponds to the sine of its opposite angle, A.

This lesson breaks down tricky logarithmic functions into their basic components: the base (b), the fixed input value (y), and the output of the function, x.The logarithm is therefore written as b x = y. This lesson also goes over Product Identity, Quotient Identity, Power Identity, and changing bases.

Both polar and rectangular coordinates refer to a point on a chart or graph. Often times, the Pythagorean theorem is used to find the corresponding coordinates. Read this lesson for quick conversion tips!

Did you know the Pythagorean theorem, a 2 + b 2 = c 2 , is closely related to the trigonometric identity sin(θ) 2 + cos(θ) 2 = 1? Read this lesson to learn how to apply the Pythagorean Identity.

Converting radians to degrees (and vice versa!) is simply another method of unit conversion. To convert, one must understand the relationship between radians and degrees, which is basically π = 180°. Read the entire lesson to discover how to perform this conversion flawlessly!

This lesson describes what to do when you see the reciprocal of a function – for example, how do you evaluate 1 / cos(x) ? Read this lesson to find out!

An exponential function looks like this: f(x) = ab x . This lesson goes over the difference between exponential growth and exponential decay, as well as other ways to look at exponential functions.

The unit circle is one of the most fundamental concepts in math. Here, you’ll be able to revisit the four quadrants as well as static angle measurements (both in radiants and degrees) that are found in each of the quadrants.

Subpages include:

Cartesian Circle

Cartesian versus Polar Coordinates

How to Memorize the Unit Circle

• The members of the city cultural center have decided to put on a play once a night for a week. Their auditorium holds
• Nine subtracted from w is greater than or equal to -22
• In a game, you have a 1/22 probability of winning $135 and a 21/22 probability of losing $10. What is your expected winning?
• Help me answer this

Alg2.6 Trigonometric Functions

In this unit, students are introduced to trigonometric functions. While they have studied a variety of function types with different key features previously, this is the first time students are asked to consider periodic functions, that is, functions whose output values repeat at regular intervals. Students first consider circular motion and learn to use right triangle trigonometry to identify the coordinates of a point on a circle. The unit circle is introduced, and students study the symmetry of its coordinates and reason about radian angles knowing a full circle has an angle of \(2\pi\) . From the unit circle, the domain of cosine, sine, and tangent are expanded and students begin to think about them as functions. Students graph these functions using their knowledge of the unit circle and expand the domain of the functions a second time to angles beyond \(2\pi\) and less than 0. The second half of this unit builds directly on the work of the previous unit by having students apply their knowledge of transformations to trigonometric functions and use these functions to model periodic situations.

The Unit Circle

• 1 Moving in Circles
• 2 Revisiting Right Triangles
• 3 The Unit Circle (Part 1)
• 4 The Unit Circle (Part 2)
• 5 The Pythagorean Identity (Part 1)
• 6 The Pythagorean Identity (Part 2)
• 7 Finding Unknown Coordinates on a Circle

Periodic Functions

• 8 Rising and Falling
• 9 Introduction to Trigonometric Functions
• 10 Beyond $2\pi$
• 11 Extending the Domain of Trigonometric Functions

Trigonometry Transformations

• 13 Amplitude and Midline
• 14 Transforming Trigonometric Functions
• 15 Features of Trigonometric Graphs (Part 1)
• 16 Features of Trigonometric Graphs (Part 2)
• 17 Comparing Transformations
• 18 Modeling Circular Motion

Putting It All Together

• 19 Beyond Circles

• Algebra 2 Course - Unit 19The Unit C . . .

Algebra 2 Course - Unit 19 The Unit Circle, Degrees and Radians, Inverse Trig Functions, Trig Equations

Covers the unit circle in degrees and radians, converting between degrees and radians, inverse trig functions (ArcSin, ArcCos, etc), solving trigonometric equations, and more.

Lesson 1: The Unit Circle in Degrees - Part 1

In this lesson, you will learn how to use the unit circle in degrees.... View the lesson

In this lesson, you will learn how to use the unit circle in degrees to find the sin, cos, and tangent of an angle.... View the lesson

In this lesson, you will learn what radian angle measure is and why we use radians in trigonometry and precalculus.... View the lesson

In this lesson, you will learn how to use the unit circle in radians.... View the lesson

In this lesson, you will learn how to use the unit circle to find the sin, cos, and tangent of an angle in radians.... View the lesson

In this lesson, you will learn about the inverse trig functions ArcSin, ArcCos, and ArcTan.... View the lesson

In this lesson, you will learn how to solve equations that involve trigonometric functions.... View the lesson

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Trigonometry

Unit 1: right triangles & trigonometry, unit 2: trigonometric functions, unit 3: non-right triangles & trigonometry, unit 4: trigonometric equations and identities, review articles.

Math  /  11th Grade  /  Unit 6: Unit Circle and Trigonometric Functions

Unit Circle and Trigonometric Functions

Students discover trigonometry, which allows them to synthesize knowledge of transformations and properties of other functions while offering a new perspective on functions through periodicity.

Unit Summary

High school math sequences typically include trigonometric functions as the final example of functions in the curriculum. Trigonometry offers an opportunity to synthesize knowledge of transformations and properties of other functions while offering a new perspective on functions through periodicity. 

Trigonometry supports calculus, as the trigonometric functions have fascinating relationships through differentiation and integration and offer a great opportunity to practice calculus skills involving rate of change and accumulation.

While trigonometry is necessary for calculus, it also offers avenues to explore for their own sake. Students must connect geometric interpretations of sine and cosine, the unit circle, and the sine and cosine function and look at these three different mathematical structures as examples of the same underlying idea. Trigonometry also offers an opportunity to model periodic contexts in the world and to better understand phenomena around us.

Pacing: 16 instructional days (14 lessons, 1 flex day, 1 assessment day)

The following assessments accompany Unit 6.

Use the resources below to assess student understanding of the unit content and action plan for future units.

Post-Unit Assessment

Intellectual Prep

Suggestions for how to prepare to teach this unit

Internalization of Standards via the Unit Assessment

• Standards that each question aligns to
• Purpose of each question: spiral, foundational, mastery, developing
• Strategies and representations used in daily lessons
• Relationship to Essential Questions of unit 
• Lesson(s) that assessment points to

Internalization of Trajectory of Unit

• Read and annotate “Why This Unit.”
• Notice the progression of concepts through the unit using the “Unit at a Glance.”
• Essential questions
• Connection to assessment questions 
• Answer the essential questions.

Unit-Specific Intellectual Prep

• Read " Intuitive Understanding of Sine Waves " on BetterExplained. It explains sine and cosine very well.

Essential Understandings

The central mathematical concepts that students will come to understand in this unit

• Periodic phenomena are modeled by the trigonometric functions of  $${f(x)=\mathrm{sin}(x)}$$ , $${f(x)=\mathrm{cos(x)}}$$ , and $${f(x)=\mathrm{tan(x)}}$$ . These functions are characterized by their period, amplitude, midline, and phase shift and can be expressed algebraically in multiple ways.
• Trigonometric functions represent values on the unit circle, and trigonometric functions and the Pythagorean theorem connect geometric and functional representations of trigonometry.
• Trigonometric functions are useful in modeling periodic phenomena in the world, and the features of trigonometric functions correspond to useful features of real-world situations.

Terms and notation that students learn or use in the unit

The materials, representations, and tools teachers and students will need for this unit

• Unit circle
• Interactive graphing software
• Trigonometry-specific graphing paper is very helpful for this unit

Topic A: Trigonometric Ratios in Application and on the Unit Circle

Sketch sine graphs to model contextual situations and identify features of sine graphs.

F.IF.B.4 F.IF.C.7.E F.TF.A.4 F.TF.B.5

Sketch cosine graphs to model contextual situations and identify features of cosine graphs.

F.IF.B.4 F.IF.C.7.E F.TF.B.5

Find values of specific points on the unit circle using geometry.

F.TF.A.2 F.TF.A.4

Evaluate sines and cosines of points at reference angles on the unit circle.

Describe the relationship between the unit circle and tangent.

F.TF.A.2 F.TF.A.3

Define and evaluate the trigonometric functions of tangent, cosecant, secant, and cotangent.

Convert between degrees and radians and evaluate trigonometric functions written in radians.

F.TF.A.1 F.TF.A.3

Evaluate transformations of sine, cosine, and tangent such as  $${2{\pi-x}}$$ ,  $${\pi-x}$$ , and  $${\pi+x}$$ .

Create a free account to access thousands of lesson plans.

Already have an account? Sign In

Topic B: Graphing Sine, Cosine, and Target

Graph transformations of sine and cosine functions (Part I).

F.IF.C.7.E F.TF.A.1 F.TF.A.3 F.TF.A.4

Graph transformations of sine and cosine functions (Part II).

F.BF.B.3 F.IF.C.7.E

Graph transformations of tangent functions.

Identify equations and graphs of all six trigonometric functions.

F.BF.B.3 F.TF.A.3 F.TF.B.5

Model contextual situations using trigonometric functions (Part I).

F.TF.A.3 F.TF.B.5

Model contextual situations using trigonometric functions (Part II).

Common Core Standards

Major Cluster

Supporting Cluster

Additional Cluster

Core Standards

The content standards covered in this unit

Building Functions

F.BF.B.3 — Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology. Include recognizing even and odd functions from their graphs and algebraic expressions for them.

Interpreting Functions

F.IF.B.4 — For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.

F.IF.C.7 — Graph functions expressed symbolically and show key features of the graph, by hand in simple cases and using technology for more complicated cases. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.

F.IF.C.7.E — Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.

Trigonometric Functions

F.TF.A.1 — Understand radian measure of an angle as the length of the arc on the unit circle subtended by the angle.

F.TF.A.2 — Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle.

F.TF.A.3 — Use special triangles to determine geometrically the values of sine, cosine, tangent for π/3, π/4 and π/6, and use the unit circle to express the values of sine, cosine, and tangent for π-x, π+x, and 2π-x in terms of their values for x, where x is any real number.

F.TF.A.4 — Use the unit circle to explain symmetry (odd and even) and periodicity of trigonometric functions.

F.TF.B.5 — Choose trigonometric functions to model periodic phenomena with specified amplitude, frequency, and midline. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.

Foundational Standards

Standards covered in previous units or grades that are important background for the current unit

G.C.A.2 — Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.

G.C.B.5 — Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

Expressing Geometric Properties with Equations

G.GPE.B.5 — Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point).

G.GPE.B.7 — Use coordinates to compute perimeters of polygons and areas of triangles and rectangles, e.g., using the distance formula. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.

7.G.B.4 — Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.

8.G.B.6 — Explain a proof of the Pythagorean Theorem and its converse.

8.G.B.7 — Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.

8.G.B.8 — Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

Similarity, Right Triangles, and Trigonometry

G.SRT.C.6 — Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.

G.SRT.C.7 — Explain and use the relationship between the sine and cosine of complementary angles.

G.SRT.C.8 — Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. Modeling is best interpreted not as a collection of isolated topics but in relation to other standards. Making mathematical models is a Standard for Mathematical Practice, and specific modeling standards appear throughout the high school standards indicated by a star symbol (★). The star symbol sometimes appears on the heading for a group of standards; in that case, it should be understood to apply to all standards in that group.

G.SRT.D.10 — Prove the Laws of Sines and Cosines and use them to solve problems.

G.SRT.D.11 — Understand and apply the Law of Sines and the Law of Cosines to find unknown measurements in right and non-right triangles (e.g., surveying problems, resultant forces).

G.SRT.D.9 — Derive the formula A = 1/2 ab sin(C) for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side.

Standards for Mathematical Practice

CCSS.MATH.PRACTICE.MP1 — Make sense of problems and persevere in solving them.

CCSS.MATH.PRACTICE.MP2 — Reason abstractly and quantitatively.

CCSS.MATH.PRACTICE.MP3 — Construct viable arguments and critique the reasoning of others.

CCSS.MATH.PRACTICE.MP4 — Model with mathematics.

CCSS.MATH.PRACTICE.MP5 — Use appropriate tools strategically.

CCSS.MATH.PRACTICE.MP6 — Attend to precision.

CCSS.MATH.PRACTICE.MP7 — Look for and make use of structure.

CCSS.MATH.PRACTICE.MP8 — Look for and express regularity in repeated reasoning.

Exponential Modeling and Logarithms

Trigonometric Identities and Equations

Request a Demo

See all of the features of Fishtank in action and begin the conversation about adoption.

Learn more about Fishtank Learning School Adoption.

Contact Information

School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.

Effective Instruction Made Easy

Access rigorous, relevant, and adaptable math lesson plans for free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.2: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 1515

Learning Objectives

• Use right triangles to evaluate trigonometric functions.
• Find function values for 30°(\(\dfrac{\pi}{6}\)),45°(\(\dfrac{\pi}{4}\)),and 60°(\(\dfrac{\pi}{3}\)).
• Use equal cofunctions of complementary angles.
• Use the definitions of trigonometric functions of any angle.
• Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x -axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

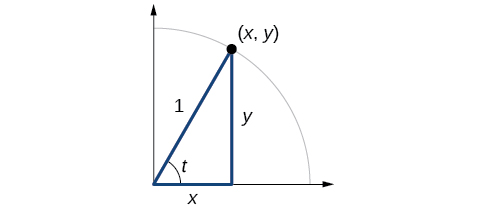
\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in Figure \(\PageIndex{2}\).

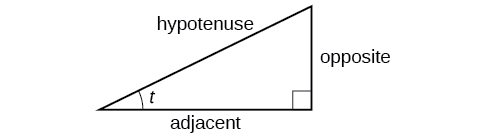
Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

• Find the sine as the ratio of the opposite side to the hypotenuse.
• Find the cosine as the ratio of the adjacent side to the hypotenuse.
• Find the tangent is the ratio of the opposite side to the adjacent side.

Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

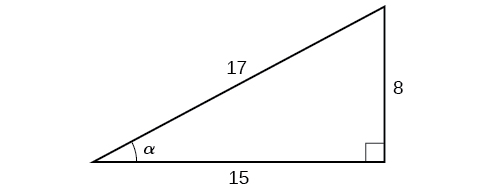
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Exercise \(\PageIndex{1}\)

Given the triangle shown in Figure \(\PageIndex{4}\), find the value of \(\sin t\).

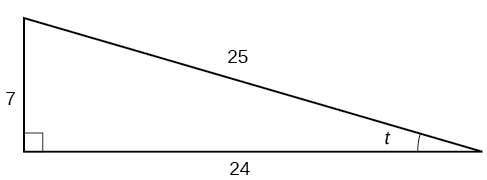
\(\frac{7}{25}\)

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

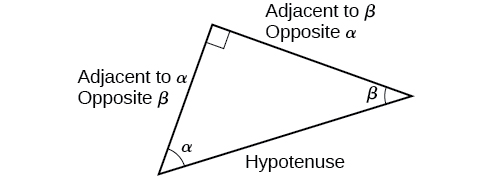
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles

• If needed, draw the right triangle and label the angle provided.
• Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
• sine as the ratio of the opposite side to the hypotenuse
• cosine as the ratio of the adjacent side to the hypotenuse
• tangent as the ratio of the opposite side to the adjacent side
• secant as the ratio of the hypotenuse to the adjacent side
• cosecant as the ratio of the hypotenuse to the opposite side
• cotangent as the ratio of the adjacent side to the opposite side

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure \(\PageIndex{6}\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).

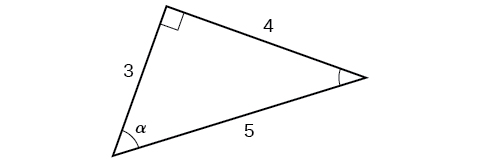
\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Exercise \(\PageIndex{2}\)

Using the triangle shown in Figure \(\PageIndex{7}\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).

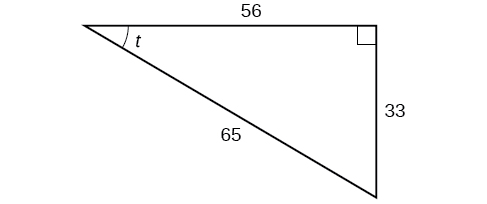
\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

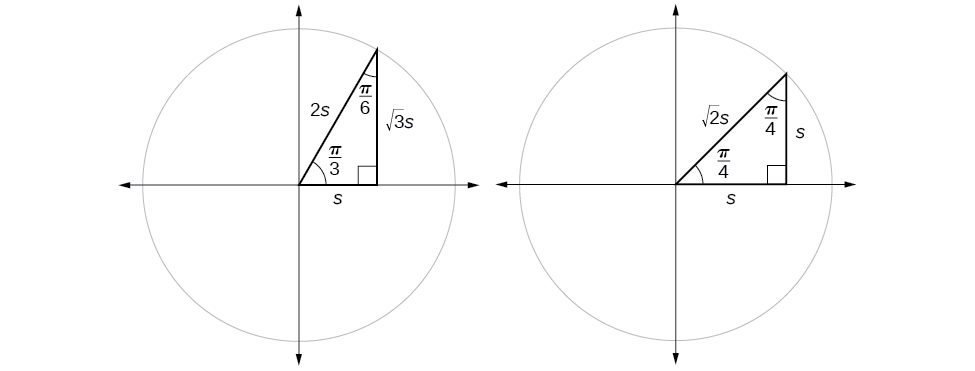
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

• Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
• Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercise \(\PageIndex{3}\)

Find the exact value of the trigonometric functions of \(\frac{π}{4}\) using side lengths.

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

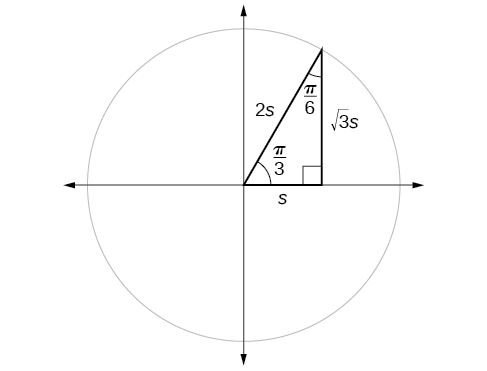
This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

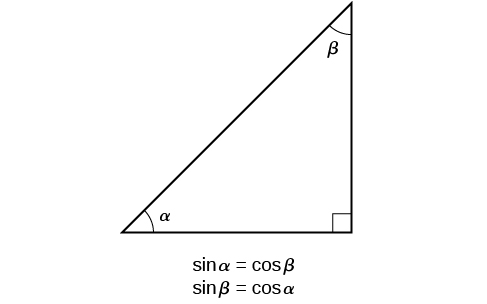
Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Exercise \(\PageIndex{4}\)

If \(\csc (\frac{π}{6})=2,\) find \( \sec (\frac{π}{3}).\)

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

how to: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure \(\PageIndex{11}\).

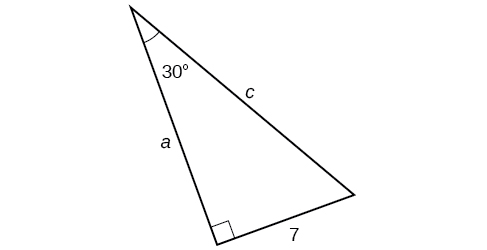
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

We rearrange to solve for \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

We can use the sine to find the hypotenuse.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Again, we rearrange to solve for \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Exercise \(\PageIndex{5}\):

A right triangle has one angle of \(\frac{π}{3}\) and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\) missing angle is \(\frac{π}{6}\)

Using Right Triangle Trigonometry to Solve Applied Problems

Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

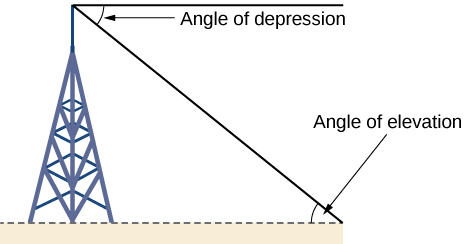
how to: Given a tall object, measure its height indirectly

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

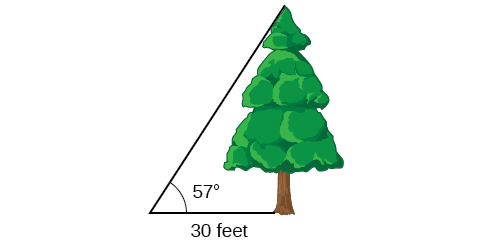
We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.

Exercise \(\PageIndex{6}\):

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of \(\frac{5π}{12}\) with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

• Finding Trig Functions on Calculator
• Finding Trig Functions Using a Right Triangle
• Relate Trig Functions to Sides of a Right Triangle
• Determine Six Trig Functions from a Triangle
• Determine Length of Right Triangle Side

Visit this website for additional practice questions from Learningpod.

Key Equations

Cofunction Identities

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example .
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See Example .
• We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See Example .
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See Example .
• We can use trigonometric functions of an angle to find unknown side lengths.
• Select the trigonometric function representing the ratio of the unknown side to the known side. See Example .
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
• The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example .