quadratic assignment problem formulation

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

• 1 Introduction
• 2.1 Koopmans-Beckman Mathematical Formulation
• 2.2.1 Parameters
• 2.3.1 Optimization Problem
• 2.4 Computational Complexity
• 2.5 Algorithmic Discussions
• 2.6 Branch and Bound Procedures
• 2.7 Linearizations
• 3.1 QAP with 3 Facilities
• 4.1 Inter-plant Transportation Problem
• 4.2 The Backboard Wiring Problem
• 4.3 Hospital Layout
• 4.4 Exam Scheduling System
• 5 Conclusion
• 6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

• Dynamic Program
• Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

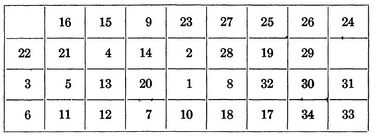
In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

• ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
• ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
• ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
• ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
• ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
• ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

Navigation menu

• Analysis of Algorithms
• Backtracking
• Dynamic Programming
• Divide and Conquer
• Geometric Algorithms
• Mathematical Algorithms
• Pattern Searching
• Bitwise Algorithms
• Branch & Bound
• Randomized Algorithms
• Art Gallery Problem
• Transform and Conquer Technique
• Implementation of Exact Cover Problem and Algorithm X using DLX
• Preemptive Priority CPU Scheduling Algorithm
• Introduction to Exact Cover Problem and Algorithm X
• Introduction to Grover's Algorithm
• Approximation Algorithms
• What Does Big O(N^2) Complexity Mean?
• How to develop an Algorithm from Scratch | Develop Algorithmic Thinking
• Algorithm definition and meaning
• Representation Change in Transform and Conquer Technique
• How to write a Pseudo Code?
• Print numbers 1 to N using Indirect recursion
• Genetic Algorithms
• The Role of Algorithms in Computing
• Trial division Algorithm for Prime Factorization
• Mo's Algo with update and without update
• Instance Simplification Method in Transform and Conquer Technique
• Make n using 1s and 2s with minimum number of terms multiple of k

Quadratic Assignment Problem (QAP)

The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.

The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.

The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.

The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.

There are various types of algorithms for different problem structures, such as:

• Precise algorithms
• Approximation algorithms
• Metaheuristics like genetic algorithms and simulated annealing
• Specialized algorithms

Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.

Facilities cost matrix:

Flow matrix:

To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.

The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.

The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.

To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.

Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.

Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.

Please Login to comment...

Similar reads.

Improve your Coding Skills with Practice

Quadratic Assignment Problem

The objective of the Quadratic Assignment Problem (QAP) is to assign \(n\) facilities to \(n\) locations in such a way as to minimize the assignment cost. The assignment cost is the sum, over all pairs, of the flow between a pair of facilities multiplied by the distance between their assigned locations.

Problem Statement

The quadratic assignment problem (QAP) was introduced by Koopmans and Beckman in 1957 in the context of locating “indivisible economic activities”. The objective of the problem is to assign a set of facilities to a set of locations in such a way as to minimize the total assignment cost. The assignment cost for a pair of facilities is a function of the flow between the facilities and the distance between the locations of the facilities.

Consider a facility location problem with four facilities (and four locations). One possible assignment is shown in the figure below: facility 2 is assigned to location 1, facility 1 is assigned to location 2, facility 4 is assigned to location 3, and facility 4 is assigned to location 3. This assignment can be written as the permutation \(p = \{2, 1, 4, 3\}\), which means that facility 2 is assigned to location 1, facility 1 is assigned to location 2, facility 4 is assigned to location 3, and facility 4 is assigned to location 3. In the figure, the line between a pair of facilities indicates that there is required flow between the facilities, and the thickness of the line increases with the value of the flow.

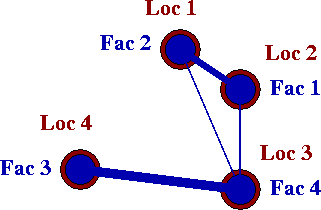
To calculate the assignment cost of the permutation, the required flows between facilities and the distances between locations are needed.

Then, the assignment cost of the permutation can be computed as \(f(1,2) \cdot d(2,1) + f(1,4) \cdot d(2,3) + f(2,4) \cdot d(1,3) + f(3,4) \cdot d(3,4)\) = \(3 \cdot 22 + 2 \cdot 40 + 1 \cdot 53 + 4 \cdot 55\) = 419. Note that this permutation is not the optimal solution.

Mathematical Formulation

Here we present the Koopmans-Beckmann formulation of the QAP. Given a set of facilities and locations along with the flows between facilities and the distances between locations, the objective of the Quadratic Assignment Problem is to assign each facility to a location in such a way as to minimize the total cost.

Sets \(N = \{1, 2, \cdots, n\}\) \(S_n = \phi: N \rightarrow N\) is the set of all permutations

Parameters \(F = (f_{ij})\) is an \(n \times n\) matrix where \(f_{ij}\) is the required flow between facilities \(i\) and \(j\) \(D = (d_{ij})\) is an \(n \times n\) matrix where \(d_{ij}\) is the distance between locations \(i\) and \(j\)

Optimization Problem \(\text{min}_{\phi \in S_n} \sum_{i=1}^n \sum_{j=1}^n f_{ij} \cdot d_{\phi(i) \phi(j)}\)

The assignment of facilities to locations is represented by a permutation \(\phi\), where \(\phi(i)\) is the location to which facility \(i\) is assigned. Each individual product \(f_{ij} \cdot d_{\phi(i) \phi(j)}\) is the cost of assigning facility \(i\) to location \(\phi(i)\) and facility \(j\) to location \(\phi(j)\).

Solve some QAPs!

Follow the links below to test your skill at finding good solutions to QAPs of various sizes. Notice that as the problem size increases, it becomes much more difficult to find an optimal solution. As \(n\) increases beyond a small number, it becomes impossible to enumerate and evaluate all possible assignment vectors. Instead, advanced solution algorithms are required to solve larger instances.

QAP of size 4

Qap of size 5, qap of size 6, qap of size 7, qap of size 8, qap of size 9.

• Anstreicher, K.M. 2003. Recent advances in the solution of quadratic assignment problems. Mathematical Programming Series B 97 , 27 - 42.
• Çela, E. 1998. The Quadratic Assignment Problem: Theory and Algorithms . Kluwer Academic Publishers, Dordrecht.
• Koopmans, T. C. and M. J. Beckmann. 1957. Assignment problems and the location of economic activities. Econometrica 25 , 53 - 76.
• QAPLIB Home Page

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

The Quadratic Assignment Problem

Related Papers

Encyclopedia of Optimization

Panos Pardalos

Panos M Pardalos

Abstract This paper aims at describing the state of the art on quadratic assignment problems (QAPs). It discusses the most important developments in all aspects of the QAP such as linearizations, QAP polyhedra, algorithms to solve the problem to optimality, heuristics, polynomially solvable special cases, and asymptotic behavior.

Güneş Erdoğan

The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we analyze the binary structure of the QAP and present new IP formulations. We focus on “flow-based” formulations, strengthen the formulations with valid inequalities, and report computational experience with a branch-and-cut algorithm. Next, we present new classes of instances of the QAP that can be completely or partially reduced to the Linear Assignment Problem and give procedures to check whether or not an instance is an element of one of these classes. We also identify classes of instances of the Koopmans-Beckmann form of the QAP that are solvable in polynomial time. Lastly, we present a strong lower bound based on Bender’s decomposition.

Cesar Beltran-Royo

Pesquisa Operacional

Paulo Boaventura Netto

We investigate the classical Gilmore-Lawler lower bound for the quadratic assignment problem. We provide evidence of the difficulty of improving the Gilmore-Lawler bound and develop new bounds by means of optimal reduction schemes. Computational results are reported indicating that the new lower bounds have advantages over previous bounds and can be used in a branch-and-bound type algorithm for the quadratic assignment problem.

Computers & Operations Research

Ricardo P M Ferreira

Ilyes Beltaef

RELATED PAPERS

Paulo Gonçalves

Dennis Heffley

Franz Rendl

Vittorio Maniezzo

New ideas in optimization

Marco Dorigo

Álvaro M. Valdebenito B.

Journal of Combinatorial Optimization

Madalina Drugan

Ali Safari Mamaghani

Informs Journal on Computing

Dushyant Sharma

Mathematics of Operations Research

Discrete Applied Mathematics

catherine roucairol

IEEE Transactions on Knowledge and Data Engineering

Cut Latifah

European Journal of Operational Research

Bernard Mans

Teodor Crainic

Applied Mathematical Sciences

Hassan Mishmast Nehi

Panos M Pardalos , John Mitchell

Paulo Boaventura-Netto

Ajay Bidyarthy

Yugoslav Journal of …

Journal of Industrial Engineering International

Hossein Karimi

NURDIYANA JAMIL

Ajith Abraham

IEEE Transactions on Information Theory

David Malah

Tansel Dökeroğlu

Matteo Fischetti

Sunderesh Heragu

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

(Stanford users can avoid this Captcha by logging in.)

• Send to text email RefWorks EndNote printer

The Quadratic Assignment Problem : Theory and Algorithms

Available online.

• SpringerLink

More options

• Find it at other libraries via WorldCat
• Contributors

Description

Creators/contributors, contents/summary.

• Preface. List of Figures. List of Tables.
• 1. Problem Statement and Complexity Aspects.
• 2. Exact Algorithms and Lower Bounds.
• 3. Heuristics and Asymptotic Behavior.
• 4. QAPs on Specially Structured Matrices.
• 5. Two More Restricted Versions of the QAP.
• 6. QAPs Arising as Optimization Problems in Graphs.
• 7. On the Biquadratic Assignment Problem (BIQAP). References. Notation Index. Subject Index.
• (source: Nielsen Book Data)

Bibliographic information

• Stanford Home
• Maps & Directions
• Search Stanford
• Emergency Info
• Terms of Use
• Non-Discrimination
• Accessibility

© Stanford University , Stanford , California 94305 .

Operations Research - Definition and formulation of Assignment Problem | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research, definition and formulation of assignment problem.

Definition and formulation

Consider the problem of assigning n jobs to n machines (one job to one machine). Let C ij be the cost of assigning i th job to the j th machine and x ij represents the assignment of i th job to the j th machine.

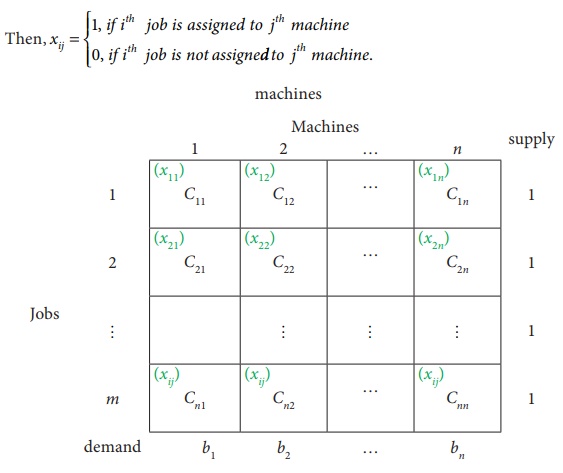
 x ij is missing in any cell means that no assignment is made between the pair of job and machine.( i.e ) x ij = 0.

x ij presents in any cell means that an assignment is made their.In such cases x ij = 1

The assignment model can be written in LPP as follows

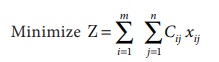
Subject to the constrains

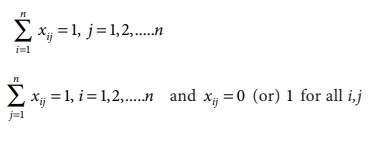
The optimum assignment schedule remains unaltered if we add or subtract a constant from all the elements of the row or column of the assignment cost matrix.

If for an assignment problem all C ij > 0 then an assignment schedule (x ij ) which satisfies ∑ C ij x ij   = 0 must be optimal.

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Semidefinite Programming Approaches to the Quadratic Assignment Problem

Cite this chapter.

• Henry Wolkowicz 5  

Part of the book series: Combinatorial Optimization ((COOP,volume 7))

565 Accesses

5 Citations

The Quadratic Assignment Problem, QAP, is arguably the hardest of the NP-hard problems. One of the main reasons is that it is very difficult to get good quality bounds for branch and bound algorithms. We show that many of the bounds that have appeared in the literature can be ranked and put into a unified Semidefinite Programming, SDP, framework. This is done using redundant quadratic constraints and Lagrangian relaxation. Thus, the final SDP relaxation ends up being the strongest.

Research partially supported by The Natural Sciences Engineering Research Council Canada.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Adams, W. and Johnson, T. (1994). Improved linear programming-based lower bounds for the quadratic assignment problem. In Proceedings of the DIMACS Workshop on Quadratic Assignment Problems , volume 16 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science , pages 43–75. American Mathematical Society.

Google Scholar  

Anjos, M. and Wolkowicz, H. (1999). A strengthened SDP relaxation via a second lifting for the Max-Cut problem. Technical Report Research Report, CORR 99–55, University of Waterloo, Waterloo, Ontario. 28 pages.

Anstreicher, K. (1999). Eigenvalue bounds versus semidefinite relaxations for the quadratic assignment problem. Technical report, University of Iowa, Iowa City, IA.

Anstreicher, K. and Brixius, N. (1999). A new bound for the quadratic assignment problem based on convex quadratic programming. Technical report, University of Iowa, Iowa City, IA.

Anstreicher, K., Chen, X., Wolkowicz, H., and Yuan, Y. (1999). Strong duality for a trust-region type relaxation of QAP. Linear Algebra Appl ., To appear.

Anstreicher, K. and Wolkowicz, H. (1999). On Lagrangian relaxation of quadratic matrix constraints. SIAM J. Matrix Anal. Appl ., To appear.

Assad, A. and Xu, W. (1985). On lower bounds for a class of quadratic {0, 1} programs. Operations Research Letters , 4:175–180.

Article   MathSciNet   MATH   Google Scholar  

Barker, G. and Carlson, D. (1975). Cones of diagonally dominant matrices. Pacific J. of Math ., 57:15–32.

Bhatia, R. (1987). Perturbation Bounds for Matrix Eigenvalues : Pitman Research Notes in Mathematics Series 162 . Longman, New York.

MATH   Google Scholar  

Borwein, J. and Wolkowicz, H. (1981). Regularizing the abstract convex program. J. Math. Anal. Appl ., 83(2):495–530.

Carraresi, P. and Malucelli, F. (1992). A new lower bound for the quadratic assignment problem. Oper.. Res ., 40(suppl. 1):S22–S27.

Article   MathSciNet   Google Scholar  

Carraresi, P. and Malucelli, F. (1994). A reformulation scheme and new lower bounds for the QAP. In Pardalos, P. and Wolkowicz, H., editors, Quadratic assignment and related problems (New Brunswick, NJ, 1993) , pages 147–160. Amer. Math. Soc., Providence, RI.

Celis, M., Dennis Jr., J., and Tapia, R. (1984). A trust region strategy for nonlinear equality constrained optimization. In Proceedings of the SIAM Conference on Numerical Optimization, Boulder, CO . Also available as Technical Report TR84–1, Department of Mathematical Sciences, Rice University, Houston, TX.

Edelman, A., Arias, T., and Smith, S. (1999). The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl ., 20(2):303–353 (electronic).

Finke, G., Burkard, R., and Rendl, F. (1987). Quadratic assignment problems. Ann. Discrete Math ., 31:61–82.

MathSciNet   Google Scholar  

Frieze, A. M. and Yadegar, J. (1983). On the quadratic assignment problem. Discrete Applied Mathematics , 5:89–98.

Fujie, T. and Kojima, M. (1997). Semidefinite programming relaxation for nonconvex quadratic programs. J. Global Optim ., 10(4) : 367–380.

Gilmore, P. (1962). Optimal and suboptimal algorithms for the quadratic assignment problem. SIAM Journal on Applied Mathematics , 10:305–313.

Grötschel, M., Lovász, L., and Schrijver, A. (1988). Geometric Algorithms and Combinatorial Optimization . Springer Verlag, Berlin-Heidelberg.

Book   MATH   Google Scholar  

Hadley, S., Rendl, F., and Wolkowicz, H. (1990). Bounds for the quadratic assignment problems using continuous optimization. In Integer Programming and Combinatorial Optimization . University of Waterloo Press.

Hadley, S., Rendl, F., and Wolkowicz, H. (1992). A new lower bound via projection for the quadratic assignment problem. Math. Oper. Res ., 17(3):727–739.

Helmberg, C., Poljak, S., Rendl, F., and Wolkowicz, H. (1995). Combining semidefinite and polyhedral relaxations for integer programs. In Integer Programming and Combinatorial Optimization (Copenhagen, 1995) , pages 124–134. Springer, Berlin.

Chapter   Google Scholar  

Jünger, M. and Kaibel, V. (1995). A basic study of the qap-polytope. Technical Report Technical Report No. 96.215, Institut für Informatik, Universität zu Köln, Germany.

Karisch, S., Rendl, F., and Wolkowicz, H. (1994). Trust regions and relaxations for the quadratic assignment problem. In Quadratic assignment and related problems (New Brunswick, NJ, 1993) , pages 199–219. Amer. Math. Soc., Providence, RI.

Koopmans, T. C. and Beckmann, M. J. (1957). Assignment problems and the location of economic activities. Econometrica , 25:53–76.

Kruk, S. and Wolkowicz, H. (1998). SQ 2 P, sequential quadratic constrained quadratic programming. In xiang Yuan, Y., editor, Advances in Nonlinear Programming , volume 14 of Applied Optimization , pages 177–204. Kluwer, Dordrecht. Proceedings of Nonlinear Programming Conference in Beijing in honour of Professor M.J.D. Powell.

Lawler, E. (1963). The quadratic assignment problem. Management Sci ., 9:586–599.

Li, Y., Pardalos, P., Ramakrishnan, K., and Resende, M. (1994). Lower bounds for the quadratic assignment problem. Ann. Oper Res ., 50: 387–410. Applications of combinatorial optimization.

Lovász, L. and Schrijver, A. (1991). Cones of matrices and set-functions and 0–1 optimization. SIAM J. Optim ., 1(2):166–190.

Pardalos, P., Rendl, F., and Wolkowicz, H. (1994). The quadratic assignment problem: a survey and recent developments. In Pardalos, P. and Wolkowicz, H., editors, Quadratic assignment and related problems (New Brunswick, NJ, 1993) , pages 1–42. Amer. Math. Soc., Providence, RI.

Pardalos, P. and Wolkowicz, H., editors (1994). Quadratic Assignment and Related Problems . American Mathematical Society, Providence, RI. Papers from the workshop held at Rutgers University, New Brunswick, New Jersey, May 20–21, 1993.

Pataki, G. (2000). Geometry of Semidefinite Programming. In Wolkowicz, H., Saigal, R., and Vandenberghe, L., editors, HANDBOOK OF SEMIDEFINITE PROGRAMMING: Theory, Algorithms, and Applications . Kluwer Academic Publishers, Boston, MA. To appear.

Poljak, S., Rendl, F., and Wolkowicz, H. (1995). A recipe for semidefinite relaxation for (0, 1) -quadratic programming. J. Global Optim ., 7(1):51–73.

Ramana, M., Tuncel, L., and Wolkowicz, H. (1997). Strong duality for semidefinite programming. SIAM J. Optim ., 7(3):641–662.

Rendl, F. and Wolkowicz, H. (1992). Applications of parametric programming and eigenvalue maximization to the quadratic assignment problem. Math. Programming , 53(1, Ser. A):63–78.

Rendl, R. and Wolkowicz, H. (1999). Testing bounds for the quadratic assignment problem. Technical Report in progress, University of Waterloo, Waterloo, Canada.

Resende, M., Ramakrishnan, K., and Drezner, Z. (1995). Computing lower bounds for the quadratic assignment problem with an interior point algorithm for linear programming. Oper. Res ., 43(5):781–791.

Rijal, M. (1995). Scheduling, design and assignment problems with quadratic costs. PhD thesis, New York University, New York, USA.

Shor, N. (1987). Quadratic optimization problems. Izv.. Akad. Nauk SSSR Tekhn. Kibernet ., 222(1):128–139, 222.

Stern, R. and Wolkowicz, H. (1995). Indefinite trust region subproblems and nonsymmetric eigenvalue perturbations. SIAM J. Optim ., 5(2):286–313.

Stiefel, E. (1935–36). Richtungsfelder und fernparallelismus in n-dimensionalem mannig faltigkeiten. Commentarii Math. Helvetici , 8:305–353.

Wolkowicz, H. (2000a). A note on lack of strong duality for quadratic problems with orthogonal constraints. Technical report, University of Waterloo.

Wolkowicz, H. (2000b). Semidefinite and Lagrangian relaxations for hard combinatorial problems. In Powell, M., editor, Proceedings of 19th IFIP TC7 CONFERENCE ON System Modeling and Optimization, July, 1999, Cambridge , page 35. Kluwer Academic Publishers, Boston, MA. To appear.

Zhao, Q., Karisch, S., Rendl, F., and Wolkowicz, H. (1998). Semidefinite programming relaxations for the quadratic assignment problem. J. Comb. Optim ., 2(1):71–109.

Download references

Author information

Authors and affiliations.

Department of Combinatorics and Optimization , Waterloo, Ontario, N2L 3G1, Canada

Henry Wolkowicz

You can also search for this author in PubMed   Google Scholar

Editor information

Editors and affiliations.

University of Florida, USA

Panos M. Pardalos

Princeton University, USA

Leonidas S. Pitsoulis

Rights and permissions

Reprints and permissions

Copyright information

© 2000 Springer Science+Business Media Dordrecht

About this chapter

Wolkowicz, H. (2000). Semidefinite Programming Approaches to the Quadratic Assignment Problem. In: Pardalos, P.M., Pitsoulis, L.S. (eds) Nonlinear Assignment Problems. Combinatorial Optimization, vol 7. Springer, Boston, MA. https://doi.org/10.1007/978-1-4757-3155-2_7

Download citation

DOI : https://doi.org/10.1007/978-1-4757-3155-2_7

Publisher Name : Springer, Boston, MA

Print ISBN : 978-1-4419-4841-0

Online ISBN : 978-1-4757-3155-2

eBook Packages : Springer Book Archive

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research